算法分析作业
[学习]算法设计与分析作业第56章v
![[学习]算法设计与分析作业第56章v](https://img.taocdn.com/s3/m/8d094c915901020206409c78.png)
(单位:s)
22个基站
42个基站
旅行商问题
针对昆明LTE网络,选取部分基站,计算基站间的 距离,在部分基站间引入边,得到
1)图1. n=15个基站顶点组成的图,以图中基站顶点 作为城市
——从n=22的基站图中,去除2组、7个位置相邻的 基站:2, 12, 15; 4, 6, 8,18
——对应地,从22个基站顶点的邻接矩阵(.xls)中, 去除这7个基站对应的行、列, 得到15个基站顶点的邻接矩阵
分析结果
1. 算法运行数据,记录在(前一张)表格中 2. <lgn, lgt(n)>散点图 3. 线性回归表达式lgt(n) = k* lgn + b
不许抄袭!
不同台式机、笔记本电脑的硬件配置不同 ,在2台不同机器上程序运行时间t(n)不可 能完全相同!!!
图的m着色问题
从昆明LTE网络中,选取部分基站,计算基站间的 距离,在部分基站间引入边,得到
方法 根据资料/讲义,算法在一个随机解上的最坏复杂度为O(n3) 假设: t(n)=O(nk),则 lgt(n) ~klgn,
通过对数据<n, lgn, lgt(n)>的线性回归分析,以lgn为自变量x ,以lgt(n)为因变量y,得到回归表达式 y = k*x +b,判断: 1)阶次k的范围( ? ≤ k ≤ ?), 2)t(n) ~ C nk
模,但需要保持10组数据。
例如,如果问题规模n=500,000时,算法运行时间 已经达到4小时左右,可以在5,000至500,000间取 10个不同的n值。考察这10个问题规模n下的算法 运行时间
此时,n可以取值:
5,000
10,000
50,000
东师21秋学期《算法分析与设计》在线作业1(答案)

东师21秋学期《算法分析与设计》在线作业1(答案)一、单选题1. 字符串”China Beijing”的长度是()A.12B. 13C. 14D. 15正确答案. B2. 一棵二叉树中共有70个叶子结点与80个度为1的结点,则该二叉树的总结点数为()。
A.219B. 221C. 229D. 231正确答案. A3. 栈和队列的共同点是()A.都是先进先出B. 都是先进后出C. 只允许在端点处插入和删除元素D. 没有共同点正确答案. C4. 使用简单选择排序法对n个数进行排序要进行()趟比较。
A. NB. n-1C. n+1D. 不一定正确答案. B5. 下面给出的四种排序方法中,排序过程中的比较次数与排序方法无关的是()。
A. 选择排序法B. 插入排序法C. 快速排序法D. 堆积排序法正确答案. A6. 图中有关路径的定义是()。
A. 由顶点和相邻顶点序偶构成的边所形成的序列B. 由不同顶点所形成的序列C. 由不同边所形成的序列D. 上述定义都不是正确答案. A7. 执行memset(s,'a',4)后,s的值为()。
A. "aaaa"B. "a4"C. "4a"D. "eeee"正确答案. A8. 一个算法的评价主要从空间复杂度和()来考虑。
A. 时间复杂度B. 算法有效性C. 算法有穷性D. 算法可读性正确答案. A9. 下面的时间复杂度按数量级递增的顺序排列,正确的是注释从功能上可以分为()。
A. 平方阶O(n2),对数阶O(log2n),指数阶O(2n)B. 线性对数阶O(nlog2n),指数阶O(2n),立方阶O(n3)C. 常数阶O(1),线性阶O(n),指数阶O(2n)D. k次方阶O(nk),指数阶O(2n),对数阶O(log2n)正确答案. C10. ()嵌在源程序体中,用于描述其后的语句或程序段做什么工作,也就是解释下面要做什么,或是执行了下面的语句会怎么样。
算法分析与设计作业及参考答案样本

《算法分析与设计》作业( 一)本课程作业由两部分组成。
第一部分为”客观题部分”, 由15个选择题组成, 每题1分, 共15分。
第二部分为”主观题部分”,由简答题和论述题组成, 共15分。
作业总分30分, 将作为平时成绩记入课程总成绩。
客观题部分:一、选择题( 每题1分, 共15题)1、递归算法: ( C )A、直接调用自身B、间接调用自身C、直接或间接调用自身 D、不调用自身2、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的字问题, 这些子问题: ( D )A、相互独立B、与原问题相同C、相互依赖D、相互独立且与原问题相同3、备忘录方法的递归方式是:( C )A、自顶向下B、自底向上C、和动态规划算法相同D、非递归的4、回溯法的求解目标是找出解空间中满足约束条件的:( A )A、所有解B、一些解C、极大解D、极小解5、贪心算法和动态规划算法共有特点是: ( A )A、最优子结构B、重叠子问题C、贪心选择D、形函数6、哈夫曼编码是: ( B)A、定长编码B、变长编码C、随机编码D、定长或变长编码7、多机调度的贪心策略是: ( A)A、最长处理时间作业优先B、最短处理时间作业优先C、随机调度D、最优调度8、程序能够不满足如下性质: ( D )A、零个或多个外部输入B、至少一个输出C、指令的确定性D、指令的有限性9、用分治法设计出的程序一般是: ( A )A、递归算法B、动态规划算法C、贪心算法D、回溯法10、采用动态规划算法分解得到的子问题:( C )A、相互独立B、与原问题相同C、相互依赖D、相互独立且与原问题相同11、回溯法搜索解空间的方法是: ( A )A、深度优先B、广度优先C、最小耗费优先D、随机搜索12、拉斯维加斯算法的一个显著特征是它所做的随机选性决策有可能导致算法: ( C )A、所需时间变化B、一定找到解C、找不到所需的解D、性能变差13、贪心算法能得到: ( C )A、全局最优解B、 0-1背包问题的解C、背包问题的解 D、无解14、能求解单源最短路径问题的算法是: ( A )A、分支限界法B、动态规划C、线形规划D、蒙特卡罗算法15、快速排序算法和线性时间选择算法的随机化版本是:( A )A、舍伍德算法B、蒙特卡罗算法C、拉斯维加斯算法D、数值随机化算法主观题部分:二、写出下列程序的答案( 每题2.5分, 共2题)1、请写出批处理作业调度的回溯算法。
作业调度之最短作业优先算法5例题解析

作业调度之最短作业优先算法5例题解析例题一、某系统采用不能移动已在主存储器中作业的可变分区方式管理主存储器,现有供用户使用的主存空间100K,系统配有4台磁带机,有一批作业见下表:作业序号进输入井时间要求计算时间需要主存容量申请磁带机数110:0025分钟15K2台210:2030分钟60K1台310:3010分钟50K3台410:3520分钟10K2台510:4015分钟30K2台按计算时间最短者优先算法如下表:我的解释:系统首先装入1、2、4,但1结束时4沿未到达,因此先执行2;2执行完毕后,资源可以分配给3或5,考虑5的时间短优先分配5并执行,执行完5后,主存中只有4已就绪并等待执行,因此开始执行4,执行4的同时系统会将作业3装入主存,最后自然执行作业3;因此最后的顺序是:1\2\5\4\3作业序号进输入井时间进入主存时间开始计算时间结束计算时间周转时间解释110:0010:1010:00102525此时输入井中只有一个作业且满足资源要求,因此被选中运行。
2102010:2010:2510:5535作业2到达输入井,满足资源要求,装入主存,等到作业1运行完毕进入运行。
510:4010:5510:5511:1030由于作业3要求主存空间无法满足,因此作业4先行一步装入主存,当作业2让出处理器的同时,作业5满足资源要求进入主存就绪。
根据算法作业5先进入处理器运行最后作业3装入主存并运行平均周转时间:(25+35+30+55+70/5=43分钟 [分析]解答本题时应注意如下几个问题:第一,系统采用的是多道程序设计技术,但没有限定并行工作的道数,因此, 只要当前尚未分配的资源可以满足在输入井中等待的某些作业的要求时,作业 调度可以按照给定的算法从中选择一个或多个作业装人主存储器;第二,采用可变分区方式管理主存储器,但没给出主存空间的分配算法,因而,只要有合适的空间就可分配,题中还规定可用移动技术来合并分散的空闲区; 第三,对磁带机采用静态分配;第四,进程调度采用可抢占的最高优先级调度算法,即对已被装人主存储器的作业而言优先级高的作业可抢占处理器执行;第五,虽然作业需要使用磁带机,但题意中已提示忽略磁带机和调度所花的时问,所以,解题时不必考虑外围设备的启动二八D 中断等复杂情况,只需把它们当作纯计算型的作业; 第六,由于没有规定什么时候开始进行作业调度,故在一般情况下只要输入井中有等待处理的作业就可按选定的算法去选择满足必要条件的作业。
《算法分析与设计》课后作业

《算法分析与设计》各章课后作业第一章 课后作业1. 设某算法在输入规模为n 时的计算时间为T(n)=10*2n。
若在甲台计算机上实现并完成该算法的时间为t 秒,现有一台运行速度是甲的64倍的另一台计算机乙,问在乙计算机上用同一算法在t 秒内能解决的问题的规模是多大?2.按照渐近阶从低到高的顺序排列以下表达式:4n 2,logn ,3n,20n ,2,n 2/3。
又n!应该排在哪一位?第二章 课后作业1. 用展开法求解下列递推关系:T(n)=⎩⎨⎧>+=1n )()2/(20n )1(n O n T O,写出T(n)的大O 记号表示。
2. 下面是实现在a[0]<=a[1]<=…<=a[n-1]中搜索x 的二分搜索算法,请根据二分 搜索技术在下划线处填充语句。
算法描述如下: template<class Type>public static int BinarySearch(int []a, int x, int n) { //在a[0]<=a[1]<=…<=a[n-1]中搜索 x // 找到x 时返回其在数组中的位置,否则返回-1 int left = 0; int right = n - 1; while ( ) {int middle = ;if(x == a[middle]) return ; if(x > a[middle]) left = middle + 1; else right= ; }return -1; // 未找到x}第三章课后作业1、选择题。
(1)下列算法中通常以自底向上的方式求解最优解的是()。
A、备忘录法B、动态规划法C、贪心法D、回溯法(2)备忘录方法是那种算法的变形。
()A、分治法B、动态规划法C、贪心法D、回溯法(3)矩阵连乘问题的算法可由()设计实现。
A、分支界限算法B、动态规划算法C、贪心算法D、回溯算法2.计算题。
算法分析作业

算法分析作业 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】算法分析练习题(一)一、选择题1、二分搜索算法是利用(A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法2、下列不是动态规划算法基本步骤的是(A )。
A、找出最优解的性质B、构造最优解C、算出最优解D、定义最优解3.下列算法中通常以自底向上的方式求解最优解的是(B )。
A、备忘录法B、动态规划法C、贪心法D、回溯法4、衡量一个算法好坏的标准是(C )。
A 运行速度快B 占用空间少C 时间复杂度低D 代码短5、以下不可以使用分治法求解的是(D )。
A 棋盘覆盖问题B 选择问题C 归并排序D 0/1背包问题6. 实现循环赛日程表利用的算法是(A )。
A、分治策略B、动态规划法C、贪心法D、回溯法7.备忘录方法是那种算法的变形。
( B )A、分治法B、动态规划法C、贪心法D、回溯法8.最长公共子序列算法利用的算法是(B )。
A、分支界限法B、动态规划法C、贪心法D、回溯法9.实现棋盘覆盖算法利用的算法是(A )。
A、分治法B、动态规划法C、贪心法D、回溯法10. 矩阵连乘问题的算法可由(B)设计实现。
A、分支界限算法B、动态规划算法C、贪心算法D、回溯算法11、Strassen矩阵乘法是利用(A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法12、使用分治法求解不需要满足的条件是(A )。
A 子问题必须是一样的B 子问题不能够重复C 子问题的解可以合并D 原问题和子问题使用相同的方法解13、下列算法中不能解决0/1背包问题的是(A )A 贪心法B 动态规划C 回溯法D 分支限界法14.实现合并排序利用的算法是(A )。
A、分治策略B、动态规划法C、贪心法D、回溯法15.下列是动态规划算法基本要素的是(D )。
A、定义最优解B、构造最优解C、算出最优解D、子问题重叠性质16.下列算法中通常以自底向下的方式求解最优解的是(B )。
【图文】算法分析与设计大作业

算法理论、教改类题目学习大量相关算法(程序),总结出对应方法的一些特点,将其写成论文形式,并以足够的例子作为佐证。
24.论分治法、动态规划、贪心法的区别 25.论递归程序向非递归程序的转换 26.论应用型本科院校算法课程的教学目标和教学方法 27.论二叉树在计算机科学与技术中的应用 28.数据库索引的算法解释 29.论贪心法的适用范围 30.解空间搜索方法的选择依据 31.分治法算法分析综述
算法应用、算法研究类题目查阅大量相关资料,对相关内容给出初步的结果。
31.基于UCCI的中国象棋对弈引擎开发技术研究 32.五子棋对弈关键技术研究33.黑白棋对弈关键技术研究 34.数独初始局面生成算法研究 35.支持按文件名搜索的索引构造技术研究 36.通用回溯算法演示系统设计 37.通用分支限界算法演示系统设计 38.通用排序算法演示系统设计 39.通用动态规划算法演示系统设计
40.论文阅读和翻译类题目• 给出一个英文文献,用准确的语言将其翻译为中文,不需要逐字逐句翻译,但主要观点、算法思想和算法过程表述清楚、准确、充分。
格式要求• 论文正文中不得出现大段代码(超过10行)• 标题样式需规范• 参考文献不低于10篇,参考文献格式和标注位置须规范。
中科院计算机算法设计与分析各章作业+历年习题

5.下面那些规则是正确的?为什么? 1). f (n) O( F (n)), g (n) O(G(n)) f (n) / g (n) O( F (n) / G(n)) ;错 2). f (n) O( F (n)), g (n) O(G(n)) f (n) / g (n) ( F (n) / G(n)) ;错 3). f (n) O( F (n)), g (n) O(G(n)) f (n) / g (n) ( F (n) / G(n)) ;错 4). f (n) ( F (n)), g (n) (G(n)) f (n) / g (n) ( F (n) / G(n)) ;错 5). f (n) ( F (n)), g (n) (G(n)) f (n) / g (n) ( F (n) / G(n)) 。错 6).
7
对顶点个数进行归纳。 当顶点数|v(D)|=2 时,因为每个点的入度和出度相等,易得构成有向 Euler 环游。 假设顶点数|v(D)|=k 时结论成立,则 当顶点数|v(D)|=k + 1 时,任取 v∈v(D).设 S={以 v 为终点的边},K={以 v 为始点的边},因为 v 的入度和出度相等,故 S 和 K 中边数相等。记 G=D-v.对 G 做如下操作: 任取 S 和 K 中各一条边 e1、e2 ,设在 D 中 e1 v1v , e2 vv2 ,则对 G 和 S 做如下操作 G G v1v2 , S S {e2} ,重复此步骤直到 S 为空。这个过程最终 得到的 G 有 k 个顶点,且每个顶点的度与在 G 中完全一样。由归纳假设,G 中 存在有向 Euler 环游,设为 C。在 G 中从任一点出发沿 C 的对应边前行,每当遇 到上述添加边 v1v2 时, 都用对应的两条边 e1, e2 代替, 这样可以获得有向 Euler 环游。 3)G 是至少有三个顶点的无向图,则 G 包含 Euler 环游等价于 G 中无奇度顶 点。 (即任意顶点的度为偶数) 。 3. 设 G 是具有 n 个顶点和 m 条边的无向图, 如果 G 是连通的, 而且满足 m = n-1, 证明 G 是树。
算法分析与设计作业及参考答案

算法分析与设计作业及参考答案作业题目1、请分析冒泡排序算法的时间复杂度和空间复杂度,并举例说明其在实际中的应用场景。
2、设计一个算法,用于在一个未排序的整数数组中找到第二大的元素,并分析其时间复杂度。
3、比较贪心算法和动态规划算法的异同,并分别举例说明它们在解决问题中的应用。
参考答案1、冒泡排序算法时间复杂度:冒泡排序的基本思想是通过相邻元素的比较和交换,将最大的元素逐步“浮”到数组的末尾。
在最坏情况下,数组完全逆序,需要进行 n 1 轮比较和交换,每一轮比较 n i 次(i 表示当前轮数),所以总的比较次数为 n(n 1) / 2,时间复杂度为 O(n^2)。
在最好情况下,数组已经有序,只需要进行一轮比较,时间复杂度为 O(n)。
平均情况下,时间复杂度也为 O(n^2)。
空间复杂度:冒泡排序只在原数组上进行操作,不需要额外的存储空间,空间复杂度为 O(1)。
应用场景:冒泡排序算法简单易懂,对于规模较小的数组,或者对算法的简单性要求较高而对性能要求不是特别苛刻的场景,如对少量数据进行简单排序时,可以使用冒泡排序。
例如,在一个小型的学生成绩管理系统中,需要对一个班级的少量学生成绩进行排序展示,冒泡排序就可以满足需求。
2、找到第二大元素的算法以下是一种使用遍历的方法来找到未排序整数数组中第二大元素的算法:```pythondef find_second_largest(arr):largest = arr0second_largest = float('inf')for num in arr:if num > largest:second_largest = largestlargest = numelif num > second_largest and num!= largest:second_largest = numreturn second_largest```时间复杂度分析:这个算法需要遍历数组一次,所以时间复杂度为O(n)。
算法设计与分析作业答案

CS330:Introduction To Algorithm Spring2014Lecture2:Asymptotic AnalysisTF:Xianrui Meng Scribes:Raman Bahdanouski,Ellie VialExercise1Suppose you have algorithms with thefive running times listed below.How much slower do each of these algorithms get when you(a)double the input size,or(b)increase the input size by one?1.n2;2.n3;3.100n2;4.nlog(n);5.2n;SolutionFor doubling the input:1.f(n)=n2;f (2n)=4n2.;So the running time of the algorithm gets4times slower.2.f(n)=n3;f (2n)=8n3.;So the running time of the algorithm gets8times slower.3.f(n)=100n2;f (2n)=400n2.;So the running time of the algorithm gets4times slower.4.f(n)=nlog(n);f (2n)=2n∗log(2n)=2n∗(log(n)+log(2))=2n∗log(n)+2n∗log(2).;So the runningtime of the algorithm increases by2n∗log(n)+2n∗log(2).5.f(n)=2n;f (2n)=22n;f(2n)−f(n)=22n−2n=(2n)∗(2n−1);So the running time of the algorithmgets slower by the factor of(2n−1).For increasing the input by one:1.f(n)=n2;f (n+1)=n2+2n+1.;So the running time of the algorithm increases by2n+1.2.f(n)=n3;f (n+1)=n3+3n2+3n+1.;So the running time of the algorithm increases by3n2+3n+1.3.f(n)=100n2;f (n+1)=100(n2+2n+1).;So the running time of the algorithm increases by100(2n+1).4.f(n)=nlog(n);f(n+1)=(n+1)∗log(n+1);f(n+1)−f(n)=(n+1)∗log(n+1)−nlog(n)=n∗log(n+1)+log(n+1)−nlog(n)=log(n+1)+n∗(log(n+1)−log(n));So the running time increases by log(n+1)+n∗(log(n+1)−log(n)).5.f(n)=2n;f (n+1)=2n+1=2∗2n;So the running time of the algorithm doubles.2-12-2Lecture 2:Asymptotic Analysis Exercise 3Take the following list of functions and arrange them in ascending order of growth rate.That is,if function g(n)immediately follows function f(n)in your list,it should be the case that f(n)is O(g(n)).•f 1(n )=n 2.5•f 2(n )=√2n•f 3(n )=n +10•f 4(n )=10n•f 5(n )=100n•f 6(n )=n 2log (n )SolutionWe can start approaching this problem by putting f 4and f 5at end of the list,because these functions are exponential and will grow the fastest.f 4<f 5because 10<100.Other four functions are polynomial and will grower slower then exponential.We can represent f 1and f 2as:n 2.5=n 2∗√2n ;and √2n =2n 0.5.Now,we can say that out of all polynomial functions f 2will be the slowest because it has the smallest degree.Morover,and will be bounded by f 3because it has a higher degree of 1.Furthermore,f 1and f 6will be beween exponential f 4and f 5and polynomial f 2and f 3,because polynomial functions grow slower and both f 4and f 5and have the highest degree of 2out of all other polynomial functions.And f 6will be bounded by f 1because f 6=n 2log (n )and f 1=n 2√2n and log (n )=O (√2n ).Therefore the final order will be:f 2(n )<f 3(n )<f 6(n )<f 1(n )<f 4(n )<f 5(n )Lecture2:Asymptotic Analysis2-3Exercise5Assume you have functions f and g such that f(n)is O(g(n)).For each of the following statemenets,decided whether you think it is true or false and give a proof or counterexample.1.log f(n)is O(log g(n)).2.2f(n)is O(2g(n)).3.f(n)2is O(g(n)2).Solution1.False.Disprove by counterexample.Suppose f(n)=2and g(n)=1.This holds under the assumtion stated that f(n)is O(g(n))for all n, then2<C1for any constant C>2.However,log f(n)is not in O(log g(n))in the case that f(n)=2 and g(n)=1since log2>C∗log(1)=1>C∗0for any n and any constant C.To make the statement hold,assume there exists n1such that g(n)>2for all n>n1.By this assumption,there exists some n0for all n1>n0,such that f(n)<C∗g(n)for some constant C.Thus,when n>max(n0,n1),then log f(n)<log C+log g(n)<log C∗log O(g(n)),which means that log f(n))=O(log g(n)).2.False.Disprove by counterexample.Suppose f(n)=2n and g(n)=n.This holds under the assumtion that f(n)is O(g(n))for all n, 2n<Cn for any constant C>3.However,22n is not in O(2n)in the case if f(n)=2n and g(n)=n because22n>>C∗2n⇒1>C∗0for any n>0and any constant C.Thus2f(n)>O(2g(n))3.True.∃some n0∀n>n0,s.t.f(n)<C∗g(n)for some constant C,Therefore,for any positive n,f(n)2<(C∗g(n))2because f(n)2<C2∗g(n)2for all C>0.。
《算法分析与设计》作业答案

《算法分析与设计》作业1、考虑,10≤≤i x 而不是x i ∈{0,1}的连续背包问题。
一种可行的贪婪策略是:按价值密度非递减的顺序检查物品,若剩余容量能容下正在考察的物品,将其装入;否则,往背包内装如此物品的一部分。
(a) 对于n=3,w=[100,10,10],p=[20,15,15],以及c=105,上述装入法获得结果是什么?(b)证明这种贪婪算法总能获得最优解。
(c) 用伪代码描述此算法。
答:(a )利用贪婪算法,按价值密度考察的背包为w2,w3,w1;背包w2和w3重20,还可以容纳85,由于10≤≤i x ,背包w1还可以装入x1=0.85,则背包内物品总价值为15+15+20*0.85=47.(b )假设已按价值密度排好序,考察w1,w2,……,wi ,……,对应的价值为p1,p2,……,pi,……如果装到pi-1再装pi 时,恰好要取xi 个wi 。
(,10≤≤i x ) 因为比它价值密度大的都已装载完,所以此时获得的为最优解。
(c )算法描述如下: template <class T>int ContainerLoading( int x[], T w[], T c, int n ) {int *t = new int[n+1]; IndirectSort(w, t, n); for( int i=1; i<=n; i++) x[i] = 0;for(i=1; i<=n && w[t[i]]<=c; i++){ x[t[i]] = 1; c += w[t[i]]; } delete []t; }2、证明当且仅当二分图没有覆盖时,下述算法找不到覆盖。
m=0; //当前覆盖的大小对于A中的所有i,New[i]=Degree[i]对于B中的所有i,Cov[i]=falsewhile(对于A中的某些i,New[i]>0) {设v是具有最大的New[i]的顶点;C[m++]=v;for(所有邻接于v的顶点j) {If(!Cov[j]) {Cov[j] = true;对于所有邻接于j的顶点,使其New[k]减1}}}if (有些顶点未被覆盖) 失败else 找到一个覆盖2)给出一个具有覆盖的二分图,使得上述算法找不到最小覆盖。
算法分析作业--第5章

按l1≥ l2 ≥ l3 ≥ l4 ≥ l5次序得到 A={10,6,5},B={9,8},最大值是21.
若令A={10,9},B={8,6,5},最大值是19. 这种方式更优。
故命题得证。
① 当n=7,(p1 ,…, p7)=(3,5,20,18,1,6,30) 和(d1,…,d7)=(1,3,4,3,2,1,2)时,算法5.4所生 成的解是什么?
将以上数据情况的背包问题记为I。设FG(I)是 物品按pi的非增次序输入时由GREEDYKNAPSACK所生成的解,FO(I)是一个最优解。 问FO(I)/ FG(I)是多少?
当物品按wi的非降次序输入时,重复②的讨 论。
i 1234 5
p 10 5 15 7 6
w2 3 5 7 1
p/w 5 5/3 3 1 6
③ 证明按fi/li的非增次序来存放程序时ERT取最 小值。
I:
(l1,l2)=(10,12) (f1,f2)=(0.4,0.6)
ERT(I)=10*0.4+(10+12)*0.6=17.2 ERT(I’)=12*0.6+(10+12)*0.4=16
I:
(l1,l2)=(2,1) (f1,f2)=(0.6,0.4)
x 1 2/3 1
1
n=7,m=15
根据贪心(x5,x1,x6,x3,x7,x2,x4)= (1,1,1,1,1,2/3,0)即
(x1,x2,x3,x4,x5,x6,x7)=(1,2/3,1,0,1,1,1 ) FO(I)=166/3。
67 18 3 41 9/2 3 11
i 1234 5
算法分析与设计作业参考答案

《算法分析与设计》作业参考答案作业一一、名词解释:1.递归算法:直接或间接地调用自身的算法称为递归算法。
2.程序:程序是算法用某种程序设计语言的具体实现。
二、简答题:1.算法需要满足哪些性质?简述之。
答:算法是若干指令的有穷序列,满足性质:(1)输入:有零个或多个外部量作为算法的输入。
(2)输出:算法产生至少一个量作为输出。
(3)确定性:组成算法的每条指令清晰、无歧义。
(4)有限性:算法中每条指令的执行次数有限,执行每条指令的时间也有限。
2.简要分析分治法能解决的问题具有的特征。
答:分析分治法能解决的问题主要具有如下特征:(1)该问题的规模缩小到一定的程度就可以容易地解决;(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质; (3)利用该问题分解出的子问题的解可以合并为该问题的解;(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
3.简要分析在递归算法中消除递归调用,将递归算法转化为非递归算法的方法。
答:将递归算法转化为非递归算法的方法主要有:(1)采用一个用户定义的栈来模拟系统的递归调用工作栈。
该方法通用性强,但本质上还是递归,只不过人工做了本来由编译器做的事情,优化效果不明显。
(2)用递推来实现递归函数。
(3)通过Cooper 变换、反演变换能将一些递归转化为尾递归,从而迭代求出结果。
后两种方法在时空复杂度上均有较大改善,但其适用范围有限。
三、算法编写及算法应用分析题: 1.冒泡排序算法的基本运算如下: for i ←1 to n-1 dofor j ←1 to n-i do if a[j]<a[j+1] then交换a[j]、a[j+1];分析该算法的时间复杂性。
答:排序算法的基本运算步为元素比较,冒泡排序算法的时间复杂性就是求比较次数与n 的关系。
(1)设比较一次花时间1;(2)内循环次数为:n-i 次,(i=1,…n ),花时间为:∑-=-=in j i n 1)(1(3)外循环次数为:n-1,花时间为:2.设计一个分治算法计算一棵二叉树的高度。
十六皇后-《算法分析与设计》作业报告

十六皇后问题【问题描述】八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。
该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
高斯认为有76种方案。
1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。
计算机发明后,有多种计算机语言可以解决此问题。
十六皇后是对八皇后的一个延伸,只不过是皇后的数目增多。
【基本要求】设计16皇后的程序,要求如下:⏹输出其中的一个解⏹输出其总共有多少个解⏹要有计时器,计算并显示运行时间。
【问题求解】1 需求规格说明要求根据已学的回溯算法,在原有8皇后的回溯算法基础上加以改进,从而提高效率,降低时间复杂度或是空间复杂度。
2 总体分析与设计2.1 设计思想:皇后问题是回溯算法的典型应用,我们试探性的在每一行放置一个皇后,皇后位置要求与其他皇后在不同一列和正负45°对角线上,如果某一行没有合适的位置,那么需要回溯到上一行,上一行重新选择一个合法的位置,当所有的行都正确放置了皇后,那么这便是一个合法解。
算法1:利用一个二维数组保存整个棋盘,元素可以放置皇后置为1,不能放置皇后置为0。
判断某一位置能否放置皇后需要进行如下判断(1)一列上只能有一个皇后;(2)135°斜对角线上只能有一个皇后;(3)45°对角线上只能有一个皇后。
算法2:算法1可以找到正确解,但是发现大可不必利用二维数组保存皇后位置,可以改进为用一维数组来存储结果,数组下标代表行,数组中值代表当前行的皇后位置,便可节省大量空间。
判断某一位置能否放置皇后只需要一遍循环。
改进算法:当计算出一个解之后,便可根据矩阵列对称性找到另一个解,那么时间和空间会节省一半。
2.2 算法流程:图 1. 算法流程3 算法实现3.1 类图设计:图 2. 类图⏹NQueenTestMain:测试类,控制台界面,提供用户选择算法,输入皇后数目,是否打印结果,以及运行时间显示。
算法分析期末试题集答案

算法分析期末试题集答案1.应⽤Johnson法则的流⽔作业调度采⽤的算法是(D)A. 贪⼼算法B. 分⽀限界法C.分治法D. 动态规划算法2.Hanoi塔问题如下图所⽰。
现要求将塔座A上的的所有圆盘移到塔座B上,并仍按同样顺序叠置。
移动圆盘时遵守Hanoi塔问题的移动规则。
由此设计出解Hanoi塔问题的递归算法正确的为:(B)Hanoi塔3. 动态规划算法的基本要素为(C)A. 最优⼦结构性质与贪⼼选择性质B.重叠⼦问题性质与贪⼼选择性质C.最优⼦结构性质与重叠⼦问题性质D. 预排序与递归调⽤4. 算法分析中,记号O表⽰(B),记号Ω表⽰(A),记号Θ表⽰(D)。
A.渐进下界B.渐进上界C.⾮紧上界D.紧渐进界E.⾮紧下界5. 以下关于渐进记号的性质是正确的有:(A)A.f(n)(g(n)),g(n)(h(n))f(n)(h(n))=Θ=Θ?=ΘB. f(n)O(g(n)),g(n)O(h(n))h(n)O(f(n))==?=C. O(f(n))+O(g(n)) = O(min{f(n),g(n)})D. f(n)O(g(n))g(n)O(f(n))=?=6.能采⽤贪⼼算法求最优解的问题,⼀般具有的重要性质为:(A)A. 最优⼦结构性质与贪⼼选择性质B.重叠⼦问题性质与贪⼼选择性质C.最优⼦结构性质与重叠⼦问题性质D. 预排序与递归调⽤7. 回溯法在问题的解空间树中,按(D)策略,从根结点出发搜索解空间树。
A.⼴度优先B. 活结点优先 C.扩展结点优先 D. 深度优先8. 分⽀限界法在问题的解空间树中,按(A)策略,从根结点出发搜索解空间树。
A.⼴度优先B. 活结点优先 C.扩展结点优先 D. 深度优先9. 程序块(A)是回溯法中遍历排列树的算法框架程序。
A.10. 回溯法的效率不依赖于以下哪⼀个因素?(C )A.产⽣x[k]的时间;B.满⾜显约束的x[k]值的个数;C.问题的解空间的形式;D.计算上界函数bound的时间;E.满⾜约束函数和上界函数约束的所有x[k]的个数。
北航研究生 算法设计与分析大作业一
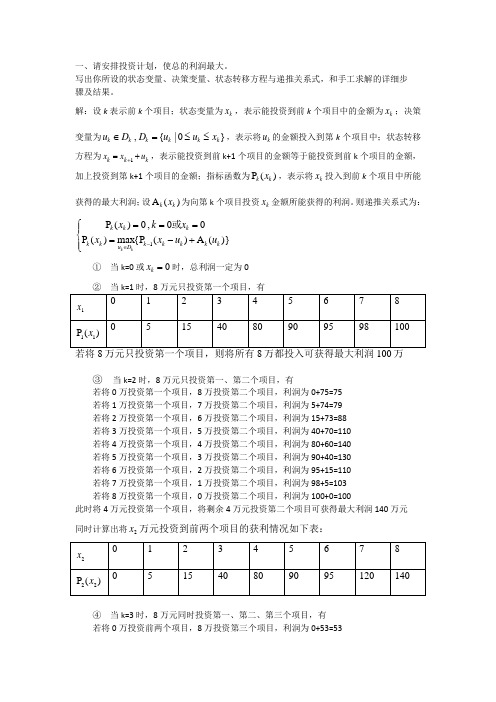
一、请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步 骤及结果。
解:设k 表示前k 个项目;状态变量为k x ,表示能投资到前k 个项目中的金额为k x ;决策变量为}0|{ , k k k k k k x u u D D u ≤≤=∈,表示将k u 的金额投入到第k 个项目中;状态转移方程为k k k u x x +=+1,表示能投资到前k+1个项目的金额等于能投资到前k 个项目的金额,加上投资到第k+1个项目的金额;指标函数为)(P k k x ,表示将k x 投入到前k 个项目中所能获得的最大利润;设)(A k k x 为向第k 个项目投资k x 金额所能获得的利润。
则递推关系式为:⎪⎩⎪⎨⎧+-====-∈)}(A )({P max )(P 00 , 0)(P 1k k k k k D u kk k k k u u x x x k x k k 或① 当k=0或0=k x 时,总利润一定为0③ 当k=2时,8万元只投资第一、第二个项目,有若将0万投资第一个项目,8万投资第二个项目,利润为0+75=75若将1万投资第一个项目,7万投资第二个项目,利润为5+74=79 若将2万投资第一个项目,6万投资第二个项目,利润为15+73=88 若将3万投资第一个项目,5万投资第二个项目,利润为40+70=110 若将4万投资第一个项目,4万投资第二个项目,利润为80+60=140 若将5万投资第一个项目,3万投资第二个项目,利润为90+40=130 若将6万投资第一个项目,2万投资第二个项目,利润为95+15=110 若将7万投资第一个项目,1万投资第二个项目,利润为98+5=103 若将8万投资第一个项目,0万投资第二个项目,利润为100+0=100此时将4万元投资第一个项目,将剩余4万元投资第二个项目可获得最大利润140万元 同时计算出将2x 万元投资到前两个项目的获利情况如下表:④ 当k=3时,8万元同时投资第一、第二、第三个项目,有 若将0万投资前两个项目,8万投资第三个项目,利润为0+53=53若将1万投资前两个项目,7万投资第三个项目,利润为5+52=57若将2万投资前两个项目,6万投资第三个项目,利润为15+51=66若将3万投资前两个项目,5万投资第三个项目,利润为40+50=90若将4万投资前两个项目,4万投资第三个项目,利润为80+45=125若将5万投资前两个项目,3万投资第三个项目,利润为90+40=130若将6万投资前两个项目,2万投资第三个项目,利润为95+26=121若将7万投资前两个项目,1万投资第三个项目,利润为120+4=124若将8万投资前两个项目,0万投资第三个项目,利润为140+0=140此时将4万元投资第一个项目,将剩余4万元投资第二个项目,第三个项目投资0元,可获得最大利润140万元。
算法分析期末考试集答案(套)

算法分析期末考试集答案(套)《算法分析与设计》⼀、解答题 1. 机器调度问题。
问题描述:现在有n 件任务和⽆限多台的机器,任务可以在机器上得到处理。
每件任务的开始时间为s i ,完成时间为f i ,s i问题实例:若任务占⽤的时间范围是{[1,4],[2,5],[4,5],[2,6],[4,7]},则按时完成所有任务最少需要⼏台机器?(提⽰:使⽤贪⼼算法)画出⼯作在对应的机器上的分配情况。
2. 已知⾮齐次递归⽅程:f (n)bf (n 1)g(n)f (0)c =-+??=? ,其中,b 、c 是常数,g(n)是n 的某⼀个函数。
则f(n)的⾮递归表达式为:nnn i i 1f (n)cb b g(i)-==+∑。
现有Hanoi 塔问题的递归⽅程为:h(n)2h(n 1)1h(1)1=-+??=? ,求h(n)的⾮递归表达式。
解:利⽤给出的关系式,此时有:b=2, c=1, g(n)=1, 从n 递推到1,有:n 1n 1n 1i i 1n 1n 22n h(n)cbb g(i)22 (22121)----=--=+=+++++=-∑3. 单源最短路径的求解。
问题的描述:给定带权有向图(如下图所⽰)G =(V,E),其中每条边的权是⾮负实数。
另外,还给定V 中的⼀个顶点,称为源。
现在要计算从源到所有其它各顶点的最短路长度。
这⾥路的长度是指路上各边权之和。
这个问题通常称为单源最短路径问题。
解法:现采⽤Dijkstra 算法计算从源顶点1到其它顶点间最短路径。
请将此过程填⼊下表中。
4. 请写出⽤回溯法解装载问题的函数。
装载问题:有⼀批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i 的重量为wi ,且121nii w c c=≤+∑。
装载问题要求确定是否有⼀个合理的装载⽅案可将这n 个集装箱装上这2艘轮船。
如果有,找出⼀种装载⽅案。
解:void backtrack (int i){// 搜索第i 层结点if (i > n) // 到达叶结点更新最优解bestx,bestw;return; r -= w[i];if (cw + w[i] <= c) {// 搜索左⼦树43 2 1 100 30 maxint10 - {1} 初始 dist[5] dist[4] dist[3] dist[2] u S 迭代x[i] = 1;cw += w[i];backtrack(i + 1);cw -= w[i]; }if (cw + r > bestw) {x[i] = 0; // 搜索右⼦树backtrack(i + 1); }r += w[i];}5. ⽤分⽀限界法解装载问题时,对算法进⾏了⼀些改进,下⾯的程序段给出了改进部分;试说明斜线部分完成什么功能,以及这样做的原因,即采⽤这样的⽅式,算法在执⾏上有什么不同。
算法作业讲解

Sch1-1:设n个不同的整数排好序后存于T[1..n]中,若 存在一个下标i(1≤ i ≤ n),使得T[i]=i。试设计一个 有效算法找到这个下标,要求算法在最坏情形下的 计算时间为O(log n)。
解答要点:采用二分查找,当T[mid]>mid时, 在前半部分寻找,当T[mid]<mid时,在后半部 分需找,相等时即找到。ຫໍສະໝຸດ c[i][j]
min
x[i] y[ j 1] and x[i1] y[j]
c[i 1][ j] cost(delete) c[i][ j 1] cost(insert)
always always
(b):
(1)如果x[j]==y[j],1分;对应的是copy操作; (2)如果x[i]!=y[j]并且两者都不是空格,-1分;对应的是 replace操作; (3)如果x[j]或者y[j]是空格,-2分,对应的是insert和delete 操作。
解答要点:设法将ac、bd、ad和bc四次乘法 变为只用3次乘法。保留ac、bd,于是
(ad+bc)= (a+b)(c+d)-ac-bd 只需计算ac、bd和(a+b)(c+d)三次乘法即可。
15.2-1:对矩阵规模序列<5,10,3,12,5,50,6>,求矩阵 链最优括号化方案。
解答要点:递归求解公式为:
16.2-5:设计一个高效算法,对实数线上给定的一个 点集{x1,x2 … xn},求一个单位长度闭区间集合,包含 所有给定的点,并要求此集合最小。证明你的算法 是正确的。
解答要点:对点集进行排序得到{y1,y2, … yn},贪心 的从左到右进行选择,比如选择[ y1,y1 +1]区间,则 属于此区间内的点均可消去。
中科大算法设计与分析分布式算法部分作业部分答案

1. 分析在同步和异步模型下汇集算法的复杂性。 分析在同步和异步模型下பைடு நூலகம்集算法的复杂性。
解:与广播算法分析时间复杂性的步骤一致,一两句的说明 与广播算法分析时间复杂性的步骤一致, 不是分析。 不是分析。 <1> 同步模型 引理:在汇集算法的每个容许执行里, 引理:在汇集算法的每个容许执行里,树中每个高为 t 轮里收到所有孩子的msg。 子树根结点在第 t 轮里收到所有孩子的msg。 归纳证明。。。 归纳证明。。。 定理:当生成树高为 d 时,存在一个时间复杂度为O(d)的 定理: 存在一个时间复杂度为O(d)的 同步汇集算法。 同步汇集算法。 <2> 异步模型 引理:在汇集算法的每个容许的执行里, 引理:在汇集算法的每个容许的执行里,树中每个高为 t 收到所有孩子的msg。 的子树根结点在时刻 t 收到所有孩子的msg。 归纳证明。。。 归纳证明。。。 定理: 存在一个时间复杂度为O(d)的 定理:当生成树高为 d 时,存在一个时间复杂度为O(d)的 异步汇集算法。 异步汇集算法。
6.
证明同步环上不存在匿名的、 证明同步环上不存在匿名的、一致性的 Leader选举算法 Leader选举算法。 选举算法。
解:由Lemma3.1可得。 解:由Lemma3.1可得。 假设R是大小为n>1的环(非均匀),A 假设R是大小为n>1的环(非均匀),A是其上的一 个匿名算法,它选中某处理器为leader。因为环是 个匿名算法,它选中某处理器为leader。因为环是 同步的且只有一种初始配置,故在R 同步的且只有一种初始配置,故在R上A只有唯一的 合法执行。 Lemma3.1: 在环R上算法A Lemma3.1: 在环R上算法A的容许执行里,对于每 轮k,所有处理器的状态在第k轮结束时是相同的。 ,所有处理器的状态在第k Note:每个处理器同时宣布自己是Leader! Note:每个处理器同时宣布自己是Leader!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法分析练习题(一)一、选择题1、二分搜索算法是利用( A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法2、下列不是动态规划算法基本步骤的是( A )。
A、找出最优解的性质B、构造最优解C、算出最优解D、定义最优解3.下列算法中通常以自底向上的方式求解最优解的是( B )。
A、备忘录法B、动态规划法C、贪心法D、回溯法4、衡量一个算法好坏的标准是( C )。
A 运行速度快B 占用空间少C 时间复杂度低D 代码短5、以下不可以使用分治法求解的是( D )。
A 棋盘覆盖问题B 选择问题C 归并排序D 0/1 背包问题6. 实现循环赛日程表利用的算法是( A )。
A、分治策略B、动态规划法C、贪心法D、回溯法7. 备忘录方法是那种算法的变形。
( B )A、分治法B、动态规划法C、贪心法D、回溯法8.最长公共子序列算法利用的算法是( B )。
A、分支界限法B、动态规划法C、贪心法D、回溯法9.实现棋盘覆盖算法利用的算法是( A )。
A、分治法B、动态规划法C、贪心法D、回溯法10. 矩阵连乘问题的算法可由(B)设计实现。
A、分支界限算法B、动态规划算法C、贪心算法D、回溯算法11、Strassen 矩阵乘法是利用( A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法12、使用分治法求解不需要满足的条件是( A )。
A 子问题必须是一样的B 子问题不能够重复C 子问题的解可以合并D 原问题和子问题使用相同的方法解13、下列算法中不能解决0/1 背包问题的是(A )A 贪心法B 动态规划C 回溯法D 分支限界法14.实现合并排序利用的算法是( A )。
A、分治策略B、动态规划法C、贪心法D、回溯法15.下列是动态规划算法基本要素的是( D )。
A、定义最优解B、构造最优解C、算出最优解D、子问题重叠性质16.下列算法中通常以自底向下的方式求解最优解的是( B )。
A、分治法B、动态规划法C、贪心法D、回溯法17、合并排序算法是利用( A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法18.实现大整数的乘法是利用的算法( C )。
A、贪心法B、动态规划法C、分治策略D、回溯法19. 实现最大子段和利用的算法是( B )。
A、分治策略B、动态规划法C、贪心法D、回溯法20. 一个问题可用动态规划算法或贪心算法求解的关键特征是问题的( B )。
A、重叠子问题B、最优子结构性质C、贪心选择性质D、定义最优解21. 实现最长公共子序列利用的算法是( B )。
A、分治策略B、动态规划法C、贪心法D、回溯法二、填空题1. 算法的复杂性有时间复杂性和空间复杂性之分。
2、程序是算法用某种程序设计语言的具体实现。
3、算法的“确定性”指的是组成算法的每条指令是清晰的,无歧义的。
4. 矩阵连乘问题的算法可由动态规划设计实现。
5、算法是指解决问题的一种方法或一个过程。
6、从分治法的一般设计模式可以看出,用它设计出的程序一般是递归算法。
7、矩阵连乘问题的算法可由动态规划设计实现。
8. 动态规划算法的基本思想是将待求解问题分解成若干子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
9. 算法是由若干条指令组成的有穷序列,且要满足输入、输出、确定性和有限性四条性质。
10、大整数乘积算法是用分治法来设计的。
11. 快速排序算法是基于分治策略的一种排序算法。
12. 动态规划算法的两个基本要素是. 性质和性质。
13. 任何可用计算机求解的问题所需的时间都与其规模有关。
14. 快速排序算法的性能取决于划分的对称性。
15、出自于“平衡子问题”的思想,通常分治法在分割原问题,形成若干子问题时,这些子问题的规模都大致相同。
16、使用二分搜索算法在n 个有序元素表中搜索一个特定元素,在最佳情况下,搜索的时间复杂性为O(),在最坏情况下,搜索的时间复杂性为O(logn )。
17、已知一个分治算法耗费的计算时间T(n) ,T(n) 满足如下递归方程:T ( n) O2T(1)(n / 2) O(n )nn22解得此递归方可得T(n)= O (nlogn )。
18、动态规划算法有一个变形方法备忘录方法。
这种方法不同于动态规划算法“自底向上”的填充方向,而是“自顶向下”的递归方向,为每个解过的子问题建立了备忘录以备需要时查看,同样也可避免相同子问题的重复求解。
19、递归的二分查找算法在divide 阶段所花的时间是O(1) ,conquer阶段所花的时间是T(n/2) ,算法的时间复杂度是O( log n) 。
20、用动态规划算法计算矩阵连乘问题的最优值所花的时间是O(n3) ,子问题空间大小是O(n2) 。
21、一个算法的优劣可以用(时间复杂度)与(空间复杂度)与来衡量。
22、直接或间接地调用自身的算法称为(递归算法)。
23、记号在算法复杂性的表示法中表示(渐进确界或紧致界)。
24、在分治法中,使子问题规模大致相等的做法是出自一种(平衡子问题)的思想。
25、动态规划算法适用于解(具有某种最优性质)问题。
26、最优子结构性质的含义是(问题的最优解包含其子问题的最优解)。
27、按照符号O的定义O(f)+O(g) 等于O(max{f(n),g(n)}) 。
28、二分搜索技术是运用(分治)策略的典型例子。
29、动态规划算法中,通常不同子问题的个数随问题规模呈(多项式)级增长。
30、(最优子结构性质)和(子问题重叠性质)是采用动态规划算法的两个基本要素。
三、算法填空1. 最大子段和: 动态规划算法int MaxSum(int n, int a[]){int sum=0, b=0 ;//sum 存储当前最大的b[j], b 存储b[j]for(int j=1 ;j<=n ;j++) {if(b>0)b+=a[j] ;else b=a[i] ;//一旦某个区段和为负,则从下一个位置累和if (b>sum) sum=b ;}return sum ;}2. 快速排序template<class Type>void QuickSort (Type a[], int p, int r){if (p<r) {int q=Partition(a,p,r);QuickSort (a,p,q-1); //对左半段排序QuickSort(a,q+1,r) ; //对右半段排序}}四、简答题1、写出下列复杂性函数的偏序关系(即按照渐进阶从低到高排序):n n n n n n n2 n n 3 23 log ! log 102、将所给定序列a[1:n] 分为长度相等的两段a[1:n/2] 和a[n/2+1:n] ,分别求出这两段的最大子段和,则a[1:n] 的最大子段和有哪三种情形?3、请说明动态规划方法为什么需要最优子结构性质。
最优子结构性质是指大问题的最优解包含子问题的最优解。
动态规划方法是自底向上计算各个子问题的最优解,即先计算子问题的最优解,然后再利用子问题的最优解构造大问题的最优解,因此需要最优子结构4、设计动态规划算法的主要步骤是怎么的?请简述。
参考解答:(1 )找出最优解的性质,并刻划其结构特征。
(6 分) (2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息,构造最优解。
5、分治法所能解决的问题一般具有哪几个特征?请简述。
参考解答:(1)该问题的规模缩小到一定的程度就可以容易地解决;(6 分) (2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;(3)利用该问题分解出的子问题的解可以合并为该问题的解;(4)原问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
6、算法的要特性是什么?参考解答:确定性、可实现性、输入、输出、有穷性7、算法分析的目的是什么?参考解答:分析算法占用计算机资源的情况,对算法做出比较和评价,设计出额更好的算法。
8、算法的时间复杂性与问题的什么因素相关?参考解答:算法的时间复杂性与问题的规模相关,是问题大小n 的函数。
9、算法的渐进时间复杂性的含义?参考解答:当问题的规模n 趋向无穷大时,影响算法效率的重要因素是T(n) 的数量级,而其他因素仅是使时间复杂度相差常数倍,因此可以用T(n) 的数量级( 阶) 评价算法。
时间复杂度T(n) 的数量级( 阶) 称为渐进时间复杂性。
10 简述渐进时间复杂性上界的定义。
参考解答:T(n) 是某算法的时间复杂性函数,f(n) 是一简单函数,存在正整数No和C,n〉No,有T(n)<f(n) ,这种关系记作T(n)=O(f(n)) 。
11 快速排序算法最坏情况下需要多少次比较运算?参考解答:最坏情况下快速排序退化成冒泡排序,需要比较n2 次。
12 阐述归并排序的分治思路。
参考解答:讲数组一分为二,分别对每个集合单独排序,然后将已排序的两个序列归并成一个含n 个元素的分好类的序列。
如果分割后子问题还很大,则继续分治,直到一个元素。
13 快速排序的基本思想是什么。
参考解答:快速排序的基本思想是在待排序的N个记录中任意取一个记录,把该记录放在最终位置后,数据序列被此记录分成两部分。
所有关键字比该记录关键字小的放在前一部分,所有比它大的放置在后一部分,并把该记录排在这两部分的中间,这个过程称作一次快速排序。
之后重复上述过程,直到每一部分内只有一个记录为止。
14 分治法的基本思想是什么?将一个规模为N 的问题分解为K 个规模较小的子问题,这些子问题相互独立且与原问题性质相同。
求出子问题的解,就可得到原问题的解。
即一种分目标完成程序算法,简单问题可用二分法完成。
15 设计动态规划算法的主要步骤?参考解答:(1 )找出最优解的性质,并刻划其结构特征。
(6 分) (2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息,构造最优解。
16 分治法与动态规划法的异同共同点:将待求解的问题分解成若干子问题,先求解子问题,然后再从这些子问题的解得到原问题的解。
不同点:1、适合于用动态规划法求解的问题,分解得到的各子问题往往不是相互独立的;而分治法中子问题相互独立。
2、动态规划法用表保存已求解过的子问题的解,再次碰到同样的子问题时不必重新求解,而只需查询答案,故可获得多项式级时间复杂度,效率较高;而分治法中对于每次出现的子问题均求解,导致同样的子问题被反复求解,故产生指数增长的时间复杂度,效率较低。
17 分治法所能解决的问题一般具有的几个特征?参考解答:(1)该问题的规模缩小到一定的程度就可以容易地解决;(6 分) (2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;(3)利用该问题分解出的子问题的解可以合并为该问题的解;(4)原问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
