离散相似法仿真
离散相似法

3.1时域离散相似法的基本原理
仿真计算过程:
原连续系统 离散后系统
输入信号 u(t) uh(kT)
2012-12-17
3-0 离散控制系统基本原理
3-0 离散控制系统基本原理
4 离散控制系统:
5 x(t) 和 x(kT) 的数学描述
系统中既含有连续信号[x(t), e(t), u(t)],又含有采样 信号[x*(t)]或者数字信号[x(kT), u(kT)]的系统。 离散控制系统是由连续的控制对象、离散的控制器、 采样器和保持器等几个环节所组成。
控制系统建模与仿真 rjliu@ 19
1.连续系统的离散化:微分方程-》差分方程
Ax Bu, x y Cx Du x (0) x0 , t 0
2012-12-17
2012-12-17
控制系统建模与仿真 rjliu@
20
对系统进行离散化:(T为采样周期)
控制系统建模与仿真 rjliu@ 5 2012-12-17 控制系统建模与仿真 rjliu@ 6
2 采样信号 x*(t)
3 数字信号 x(kT)
2012-12-17
北京交通大学
1
控制系统建模与仿真 rjliu@
3-0 离散控制系统基本原理
数值积分的计算,是根据计算步长h,一步一步的逐步计 算,得到t1,t2, …,tk (采样点)的数值x1, x2,…, xk 。 对原连续的系统进行了离散化处理。求解时,用一个等价 离散模型,代替原连续系统。 在自动控制领域,随着计算机的引入和广泛应用,形成了 一套系统的理论——计算机控制(离散控制,数字控制)。 我们可以从连续系统离散化的角度出发,用控制理论中采 样和信号重构的理论,建立离散模型,并用计算机控制的 理论分析计算。 离散后的系统和原来的连续系统是相似的(输入输出信号 在采样点上是近似相等的),所以叫做离散相似法。
自动控制系统仿真离散相似法算法的改进

自动控制系统仿真离散相似法算法的改进随着现代控制理论的不断发展和应用,控制系统仿真已经成为了控制工程中不可或缺的一部分。
在控制系统的设计和调试过程中,仿真技术可以有效地减少成本和时间,提高系统的可靠性和性能。
而自动控制系统仿真离散相似法算法的改进则是控制系统仿真技术发展的重要方向之一。
本文将介绍自动控制系统仿真离散相似法算法的基本原理和常见问题,并提出一种改进算法,旨在提高仿真精度和效率。
一、自动控制系统仿真离散相似法算法的基本原理自动控制系统仿真离散相似法算法,又称为模型缩放法,是一种将实际系统模型缩放到仿真系统模型的方法。
该方法的基本原理是利用相似性原理,通过对实际系统和仿真系统的物理量进行比较,确定缩放比例,将实际系统的模型缩放到仿真系统的模型上,从而实现实际系统的仿真。
具体来说,自动控制系统仿真离散相似法算法主要包括以下步骤:1. 确定实际系统和仿真系统的相似性参数,包括物理量、时间常数、频率响应等。
2. 根据相似性参数,计算缩放比例并将实际系统模型缩放到仿真系统模型上。
3. 将仿真系统模型输入仿真软件进行仿真,得到仿真结果。
4. 将仿真结果与实际系统的实测数据进行比较,调整仿真模型参数,提高仿真精度。
二、自动控制系统仿真离散相似法算法的常见问题虽然自动控制系统仿真离散相似法算法具有很多优点,例如可以减少实验成本和时间、提高仿真精度和效率等,但在实际应用中也存在一些问题和挑战。
1. 相似性参数的确定问题相似性参数的确定是自动控制系统仿真离散相似法算法的关键步骤,但也是比较困难的。
一方面,实际系统和仿真系统的物理量和特性可能存在差异,需要考虑到各种因素的影响;另一方面,相似性参数的确定需要大量的实验数据和理论分析,耗时耗力。
2. 缩放比例的确定问题缩放比例的确定是自动控制系统仿真离散相似法算法的另一个关键步骤,但也存在一定的难度。
缩放比例的确定需要考虑到实际系统和仿真系统的物理量和特性之间的差异,同时还需要考虑到仿真系统的精度和效率等因素,因此需要进行一定的试验和分析。
自动控制系统仿真实验三离散相似法数字仿真

实验三 离散相似法数字仿真一、实验目的1、掌握离散相似法仿真方法二、实验内容用离散相似法仿真程序(参考课本sp4-4m )重现实验三输出Y1的数据和曲线,并与四阶龙格一库塔法比较精度。
在下图中,若各环节传递函数已知为;01s .010044.0)s (G9 ;01s .011.0)s (G8 ;s 130)s (G7;15s .0121.0)s (G6 ;0067s .0170)s (G5 ;051s .015s .01G4(s);01s .011G3(s) ;085s .017s .01)s (2G ;s 01.011)s (1G +=+==+=+=+=+=+=+=但G10(s)=0.212;重新列写联接矩阵W,W0和非零元素阵Wij ,编写程序,求出y7响应曲线。
三、实验步骤1、整理状态空间矩阵:1098765432110987654321*0000000001*000100000000010000000000100000000010000010000100000000001000001000010000000000100100000001000000000y y y y y y y y y y y u u u u u u u u u u ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡2、重新列写联接矩阵W,W0和非零元素阵Wij1y 2y 3y 4y 5y 6y 8y 9y 10y⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=0001000000000100000000001000000000100000100001000000000010000010000100000000001001000000010000000000W ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=00000000010W 10121129132143148154165161017618619711071IJ W ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 3、实验仿真程序(1)离散相似法仿真 P=[1 0.01 1 0; 0 0.085 1 0.17; 1 0.01 1 0;0 0.051 1 0.15; 1 0.0067 70 0; 1 0.15 0.21 0; 0 1 130 0;1 0.01 0.1 0;1 0.01 0.0044 0]; WIJ=[1 0 1;2 1 1;2 9 -1;3 2 1;4 3 1; 4 8 -1;5 4 1;6 5 1;6 7 -0.212; 7 6 1; 8 6 1; 9 7 1]; n=9; Y0=1;Yt0=[0 0 0 0 0 0 0 0 0]; h=0.001; T=0; T0=0; Tf=5;Nout=7; A=P(:,1); B=P(:,2);C=P(:,3); D=P(:,4);m=length(WIJ(:,1)); W0=zeros(n,1); W=zeros(n,n); for k=1:mif(WIJ(k,2)==0);W0(WIJ(k,1))=WIJ(k,3); else W(WIJ(k,1),WIJ(k,2))=WIJ(k,3); end; end;for i=1:nif(A(i)==0); FI(i)=1;FIM(i)=h*C(i)/B(i); FIJ(i)=h*h*C(i)/B(i)/2; FIC(i)=1;FID(i)=0; if(D(i)~=0); FID(i)=D(i)/B(i); elseend;elseFI(i)=exp(-h*A(i)/B(i));FIM(i)=(1-FI(i))*C(i)/A(i); FIJ(i)=h*C(i)/A(i)-FIM(i)*B(i)/A(i); FIC(i)=1;FID(i)=0; if(D(i)~=0); FIM(i)=(1-FI(i))*D(i)/A(i); FIJ(i)=h*D(i)/A(i)-FIM(i)*B(i)/A(i); FIC(i)=C(i)/D(i)-A(i)/B(i); FID(i)=D(i)/B(i); else end; end; end; Y=zeros(n,1); X=Y;y=0;Uk=zeros(n,1);Ub=Uk; t=T0:h:Tf; N=length(t); for k=1:N-1 Ub=Uk;Uk=W*Y+W0*Y0; Udot=(Uk-Ub)/h; Uf=2*Uk-Ub;X=FI'.*X+FIM'.*Uk+FIJ'.*Udot; Y=FIC'.*X+FID'.*Uf; y=[y,Y(Nout)]; end;plot(t,y)(2)四阶龙格一库塔法: p=[1 0.01 1 0;0 0.085 1 0.17; 1 0.01 1 0; 0 0.051 1 0.15; 1 0.0067 70 0; 1 0.15 0.21 0; 0 1 130 0; 1 0.01 0.1 0;1 0.01 0.0044 0]; WIJ=[1 0 1;2 1 1; 2 9 -1;3 2 1;4 3 1; 4 8 -1;5 4 1;6 5 1;6 7 -0.212; 7 6 1; 8 6 1; 9 7 1]; n=9; y0=1;yt0=[0 0 0 0 0 0 0 0 0]; h=0.01; T=0; T0=0; Tf=10;nout=7;A=diag(p(:,1)); B=diag(p(:,2)); C=diag(p(:,3)); D=diag(p(:,4)); m=length(WIJ(:,1)); w0=zeros(n,1); w=zeros(n,n); for k=1:mif (WIJ(k,2))==0;w0(WIJ(k,1))=WIJ(k,3); elsew(WIJ(k,1),WIJ(k,2))=WIJ(k,3); end; end;Q=B-D*w; Qn=inv(Q); R=C*w-A; V1=C*w0; Ab=Qn*R; b1=Qn*V1; Y=yt0'; y=Y(nout);t=T0;N=round((Tf-T0)/h);for i=1:Nk1=Ab*Y+b1*y0;k2=Ab*(Y+h*k1/2)+b1*y0;k3=Ab*(Y+h*k2/2)+b1*y0; k4=Ab*(Y+h*k3)+b1*y0;Y=Y+h*(k1+2*k2+2*k3+k4)/6; y=[y,Y(nout)]; T=[T,t+h]; t=t+h; end;[T',y']; plot(T,y)4、仿真结果 (1)离散相似法:(2)四阶龙格一库塔法:。
第4-1章 时域离散相似法Matlab编程

当T=0.1时,计算结果与c2d函数得 到的结果一致。
3
4.2 针对离散状态空间模型的仿真程序
离散状态空间 模型为
x[( k 1)T ] Gx (k T) Hu (k T) y (k T) Cx(k T) Du (k T)
对此模型编写仿真程序,只需要按模型方程迭代即可。 function [t,y]=w_DiscreteSimu(tstart,tstop,h,x0,u0,G,H,C,D) % 函数功能:对线性离散系统x(k+1)=G*X(k)+H*u(k), y(k)=C*x(k)+D*u(k)进行仿真 % 输入参数:tstart, tstop,h 分别是起始时间、结束时间和仿真步 % 长,是标量 % x0,u0是状态、输入的初值,都是列向量 % G,H,C,D是线性离散状态空间模型的系数矩阵 % 输出参数:t是仿真结果的时间序列 % y是仿真结果系统的输出序列
5
【例4.2.1】对下面的连续系统,采用数值积分法和离散相似法仿真。
2 G( s) 2 s 3s 2
解:该系统连续状态空间模型矩阵为
1 0 0 A 2 3 , B 1 , C 2 0
其离散状态空间模型矩阵为
2e T e 2T G (T ) 2T T 2e 2e
12
function [t,p]=w_DisNodesSimu2(tstart,tstop,h,x0,y0,r0,W,W0,G,H,C,D,Q)
t=[tstart:h:tstop];%t数一个行序列 cntt=size(t,2);%返回列数 cnty=size(Q,1);%返回y的维数 p=zeros(cnty,cntt);%构造一个空矩阵,用来存储结果 p(:,1)=Q*y0; % for i=1:1:cntt-1 u=W*y0+W0*r0; x0=G*x0+H*u; y0=C*x0+D*u; p(:,i+1)=Q*y0 ;%将y0作为输出的第1列 end
面向结构图的离散相似法仿真
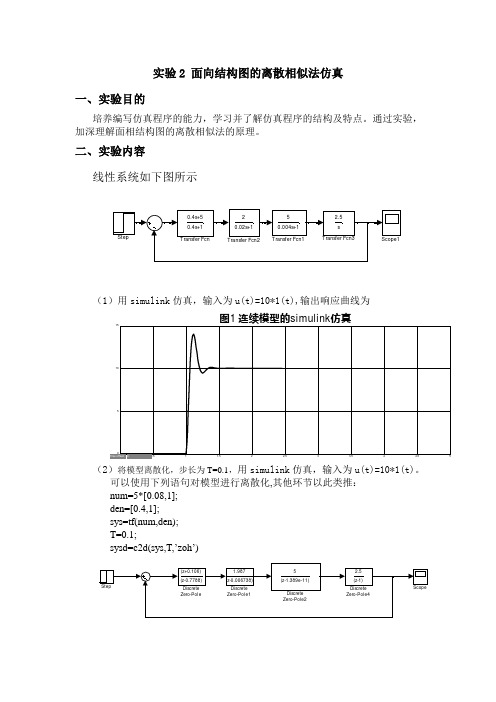
实验2 面向结构图的离散相似法仿真一、实验目的培养编写仿真程序的能力,学习并了解仿真程序的结构及特点。
通过实验,加深理解面相结构图的离散相似法的原理。
二、实验内容线性系统如下图所示2.5s Transfer Fcn320.02s+1Transfer Fcn250.004s+1Transfer Fcn10.4s+50.4s+1Transfer FcnStepScope1(1)用simulink 仿真,输入为u(t)=10*1(t),输出响应曲线为00.51 1.52 2.53 3.54 4.5551015图1 连续模型的simulink 仿真(2)将模型离散化,步长为T=0.1,用simulink 仿真,输入为u(t)=10*1(t)。
可以使用下列语句对模型进行离散化,其他环节以此类推: num=5*[0.08,1]; den=[0.4,1]; sys=tf(num,den); T=0.1;sysd=c2d(sys,T,’zoh ’)StepScope2.5(z-1)Discrete Zero-Pole45(z-1.389e-11)Discrete Zero-Pole21.987(z-0.006738)Discrete Zero-Pole1(z+0.106)(z-0.7788)Discrete Zero-Pole02468101214161820-0.50.511.522.533.5x 1010图2 离散模型的simulink仿真(T=0.1)由图2可知,当离散步长T=0.1时,系统是发散的,不稳定。
(3)采用离散化步长T=0.1,写出系统完整的按环节离 散化模型。
环节分为数4个环节,按从左至右依次编号为①②③④I 环节之间的连接方程II 环节内部离散模型①超前滞后环节②惯性环节)()(10)()()1(4.0)()1(11115.215.21k u k x k y k u e k x e k x T T +=-+=+--)()()()1(2)()1(222502502k x k y k u e k x e k x T T =-+=+--③惯性环节④积分环节)()()()1(5)()1(33325032503k x k y k u e k x e k x T T =-+=+--)()()(T 5.2)()1(44444k x k y k u k x k x =+=+)()()()()()()()()(34231241k y k u k y k u k y k u k y k r k u ===-=)(0001)(010*******011-000)()()(0k r k y k r W k y W k u ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=⋅+⋅=得到环节内部动态方程环节输出方程系统输出方程(4)仿真程序为分别采用步长T=0.001,0.01,0.1,0.5,进行仿真,得出下列图形)(0001)(11110)()()(k u k x k u D k x C k y ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⋅+⋅=())(1000)()(k y k y Q k p =⋅=)(T 5.2)1(5)1(2)1(4.0)(1)()()1(250505.2250505.2k u e e e k x e e e k Hu k Gx k x T TT T T T ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+=+------function[t,p]=w_DisNodesSimu(tstart,tstop,h,x0,y0,r0,W,W0,G,H,C,D,Q)t=[tstart:h:tstop];%t 数一个行序列 cntnodes=size(W,1);%得到环节的个数 cntt=size(t,2);%返回列数cnty=size(Q,1);%返回y 的维数 p=zeros(cnty,cntt);%构造一个空矩阵,用来存储结果 p(:,1)=Q*y0; % for i=1:1:cntt-1for j=1:1:cntnodes u(j)=W(j,:)*y0+W0(j,:)*r0; x0(j)=G(j,j)*x0(j)+H(j,j)*u(j); y0(j)=C(j,j)*x0(j)+D(j,j)*u(j); end ; p(:,i+1)=Q*y0 ;%将y0作为输出的第1列endfunction simutstart=0;tstop=20;x0=[0;0;0;0];u0=[10];h =0.1;%面向环节离散化仿真W=[0,0,0,-1;1,0,0,0;0,1,0,0;0,0,1,0]; W0=[1,0,0,0]';C=diag([10,1,1,1]); D=[1,0,0,0;0,0,0,0;0,0,0,0;0,0,0,0]; Q=[0,0,0,1];G=diag([exp(-2.5*h),exp(-50*h),exp(-250*h),1]);H=diag([(1-exp(-2.5*h))/2.5,2*(1-exp(-50*h)),5*(1-exp(-250*h)),2.5*h]); y0=x0;[t,y1]=w_DisNodesSimu(tstart,tstop,h,x0,y0,u0,W,W0,G,H,C,D,Q);stairs(t,y1,'-b*');xlabel('x');ylabel('y');title('图3 逐个环节刷新(T=0.1)');2468101214161820-2.5-2-1.5-1-0.50.51x 10103xy图3 逐个环节刷新(T=0.1)246810121416182002468101214xy图4 逐个环节刷新(h=0.01)246810121416182002468101214xy图5 逐个环节刷新(T=0.001)02468101214161820-8-7-6-5-4-3-2-11x 1067xy图6 逐个环节刷新(T=0.5)分析上面的曲线可知,当逐个环节刷新,离散步长为T=0.1时,与simulink仿真的结果一致,系统均不稳定;当离散步长为T=0.01,0.001时,曲线表现为收敛,及系统稳定;当离散步长为T=0.5时,曲线发散,系统不稳定。
ch2.3 连续系统仿真的离散相似法

12
5. Ga的迭代计算
Ga
T
At t G e Bdt a 0 T T
0
2` 3 3` 4 1 A t A t 2 Bdt It At T 2! 3!
1 T 2 AT 3 A2`T 4 A3`T 5 I B T 2 3 4 2! 5 3! T AT A T A T I 2 3 1! 4 2! 5 3! B
kAT G ( k 1 ) a ( k 1 )( k 1 )
13
6. 折半-加倍措施
T T T F ( ), G ( ), G () F ( T ), G ( T ), G ( T ) a a 2 2 2
T T F e e e F () F () 2 2
k
k
A Tk k !
k
矩阵R的范数
N 1 2 2 3 3 A TN1 A T A T A T 1 (N1 )! N 2 ( N 3 )( N 2 ) ( N 4 )( N 3 )( N 2 ) N 1 2 2 3 3 A TN1 A T A T A T 1 2 3 (N1 )! N 2 ( N 2 ) ( N 2 )
1
本章从连续系统离散化的角度出发,建立连续系 统模型的等价离散化模型,并用采样系统的理论和方
法介绍另一种常用的仿真算法—离散相似算法。
建立离散化模型采用的是: 1. 采样(sampling) 2. 信号重构(signal reconstruction)技术
22
ห้องสมุดไป่ตู้
离散相似算法的特点:
计算机与CAD仿真第4章连续系统按环节离散化的数字仿真

xk 1 Gxk Hu k uk yk 1 c x d uk 1
a T b Ge T a a (T ) c T c d (1 e b ) H e b b a 0 T a a (T ) c T c d 2 (aT b be b ) e b b a 0 ad c 1 cb d d b
表4-2 非线性环节标志
标 志 FZ=0
FZ=1 FZ=2
说 明 典型环节前后均无非线性环节
典型环节前有饱和非线性环节,应修正其输入u 典型环节前有死区非线性环节,应修正其输入u
FZ=3
FZ=4 FZ=5
典型环节前有滞环非线性环节,应修正其输入u 典型环节前有继电器非线性环节,应修正其输 入u 典型环节后有饱和非线性环节,应修正其输出x 典型环节后有死区非线性环节,应修正其输出x
sX(s) X(0) AX(s) BU(s)
或者:
( sI A) X( s) X(0) BU( s)
sI A1
1
上式两边左乘
,可得
1
X(s) (sI A) X(0) (sI A) BU(s)
令: L1[(sI A) 1 ] Φ(t ) ,称为系统状态转移矩阵。
x[(k 1)T ] Gx(kT ) Hu (kT ) u(kT )
G e AT
T
式中:
H
e A(T t ) Bdt
0
T
te A(T t ) Bdt
0
2. 关于离散相似法的几点说明及结论
1. 它是一个递推算法(但不是数值积分法)。
2.G, H ,
7.离散相似法仿真

7.2
典型环节的离散模型
按照前面的讨论,我们将常见的典型环节由传递函数表 达式推导出其离散系数及离散状态方程。
7.2.1 典型线性动态环节 ˆ (T ) Φ Φ m (T ) , Φ(T ) , m 的计算
• 典型线性动态环节有:积分、比例积分、惯性、超前-滞 后、比例五种。均以(Ci+Dis)/(Ai+Bis)形式描述。根据每种 情况的Ai,Bi,Ci,Di取值,确定分别所对应的线性环节 类型,进而计算出该环节的状态转移矩阵的值,包括下面 几个。
离散相似法仿真
本章主要教学内容
离散相似法原理 典型环节的离散模型 线性系统离散相似法仿真 非线性系统离散相似法仿真 采样系统仿真分析
7.1
7.1.1 仿真算法描述
离散相似法原理
所谓离散相似法,就是将一个连续系统进行离散化处理, 从而得到等价的系统离散模型,此种方法按系统的动态结 构图建立仿真模型。 在计算过程中,按各典型环节离散相似模型,根据环节 的输入来计算环节的输出。 1. 环节的离散化模型 将连续系统按图7-1所示对其进行离散化处理,在系统的 输入、输出端加上虚拟采样开关,T为采样周期。为保证输 入信号复现原信号,在输入端加上一个保持器。
Ts = 10 T
如果给定系统开环截止频率时,系统的采样周期也可 以按下式进行选择:
1 Ts = (30 ~ 50)ω c
2.
保持器特性对仿真精度的影响
为使经采样后的信号无失真地复现,要在系统中加入保持器。虽然零
阶保持器比较容易实现,但其精度较低。为了提高控制精度,可以采用 三角保持器,它复现信号的高频部分失真较小,并且无相位滞后,可以 得到比较满意的结果。 此外,为了提高精度还可以采用校正补偿措施,在离散模型中加入 一个确定的校正环节,适当调整参数,可使离散模型尽可能地接近原型。
系统仿真技术_Chapter 3 时域离散相似法(1)

等效转移法(续)
得到新的状态方程:
X * A* X * B *u * * Y C * X *
A*、B*阵的各元素ai*、bi*与原来的ai、bi 相比较,分别乘以Ti+1、T i,时间常数加大, 状态矩阵计算的收敛性则大大加快。需要 注意的是,仿真结果的时间比例尺也放大 了1/T倍。
离散相似化
连续时间模型
离散时间模型
时域离散相似化
离 散 相 似 化
连续时间响应
离散时间响应
频域离散相似化
传递函数
脉冲传递函数
“离散相似法”
――对状态方程离散化得时域离散相似模 型――时域离散相似法 ――对传递函数作离散化处理得离散传递 函数,称为频域离散相似模型――频域离 散相似法
3.1 时域离散相似法基本原理
e
AT AiT i AiT i M R i! i 0 i L 1 i! L
AT
AiT i , i! i 0
A0 I
(12)
(13)
要求: rij E mij E 10 d , d为正整数 rmax E mmin 或 (14) 其中ri j和mi j对应为R与M的元素,rmax为ri j中最 大元素。
0
0
x(kT) e
AkT
~ x(0) e A( kT ) Bu ( )d
kT
基本方法 (续)
将(4)式-(3)式乘以eAT,可得:
x[(k 1)T ] e x(kT)
AT ( k 1)T kT
~ e A[(k 1)T ] Bu ( )d
(5)
(5)式右端的积分与k无关,故可令k=0。 若信号重构器使kT与(k+1)T之间的 u (t ) 不变, ~ ~ 积分式中的 u ( )保持常数 u () u( kT ) ,那么,(5) 式可改写为:
离散相似法仿真

实验名称:将传递函数为s s 2612 的环节与单位反馈组成系统,将其离散化1.实验原理1 )离散相似法 所谓离散相似法,就是将一个连续系统进行离散化处理,从而得到等价的系统离散模型,此种方法按系统的动态结构图建立仿真模型。
在计算过程中,按各典型环节离散相似模型,根据环节的输入来计算环节的输出。
2) 环节的离散化模型将连续系统按下图所示对其进行离散化处理,在系统的输入、输出端加上虚拟采样开关,T 为采样周期。
为保证输入信号复现原信号,在输入端加上一个保持器。
使用零阶保持器,可得到离散化状态方程的解:3) 仿真算法实现过程当给定连续系统的动态结构图后,将其等效为各典型环节的组合,按前面讨论的典型环节离散系数 表达式,经程序处理,事先将各环节的类型、参数、初始条件、各环节连接关系矩阵、输入输出连接矩阵等参量送入程序中,既可通过离散相似的模型求出在特定信号作用下,系统中各环节输出变量的变化情况,从而得到系统的仿真结果。
3.实验方案1)连续系统的结构图这是一个单位反馈的二阶系统。
2)引入采样开关将其离散Zero-Order (零阶保持器)及采样开关对系统进行离散化,采用状态转移法进行离散化3)将传递函数转化成状态方程并对其进行离散化传递函数 1261)()()(2++==s s s U s Y s G 变形得)()()(2)(62s U s Y s sY s Y s =++假设其为零状态响应取Laplace 反变换得u y y y =+''+''26将其转变成状态方程有u x x ⎥⎦⎤⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡--=10016131x y ]01[=通过求矩阵指数及相关变化将状态方程离散化得)(]01[)()()()1(k u k y k Bu k x A k x =+=+由于矩阵A ,B 过于复杂,这里简写,详细表达式见后面程序4.实验程序1)由传递函数求状态方程建立传递函数并转化为状态方程clearclcA = tf2ss([1],[6 2 1]) %建立传递函数模型%并转化为状态方程运行结果:2)将状态方程离散化对应脚本程序:A =[-1/3 -1/6;1 0] %syms s tB= [s 0;0 s] % SID = inv(B-A) %求逆矩阵AI = ilaplace(D,s,t)%laplace 变换 求A 阵BI = AI*[0 ;1]BI =int(BI,'0','t') %积分求B 阵pretty(AI) %A 转化陈易读形式。
自动控制系统仿真离散相似法算法的改进

自动控制系统仿真离散相似法算法的改进自动控制的发展已经成为现代工程工作的一个必要部分,系统仿真也成为了许多项目的重要环节。
然而,仿真的准确性和效率却成为了人们关注和追求的目标。
离散相似法是目前仿真中常用的一种方法,而其算法的改进也一直是研究的焦点。
本文介绍离散相似法算法改进的相关信息,包括原理、目的、方法和效果等方面。
1. 原理离散相似法是一种将实际工程中的连续系统仿真成离散系统的一种方法,是工程仿真中最常用的方法之一。
离散相似法的基本原理是利用与实际系统的定义特性相同的代理模型以及在系统状态变化点上的数据来重构系统。
其原理如下:(1) 基于实际系统定义特性的代理模型代理模型是实际系统的模拟模型,在仿真中被用来模拟实际系统的动态行为。
它的定义特性应与实际系统的定义特性相同,且其输入输出特性应能仿真实际系统的输入输出行为。
通常,这种输入输出特性可能包括时间延迟、频率响应、非线性特性以及各种噪声特性等内容。
(2)基于系统状态变化点上的数据的重构操作系统状态变化点是指仿真过程中离散系统状态向连续系统状态的转化点。
在这些状态变化点处,数据被采样并分析,被用来确定仿真过程中的离散系统参数,包括时延、频率响应等内容。
这些参数被用来重构仿真过程中的连续系统,并最终用于评价仿真结果。
这种操作可以保证仿真结果与实际系统间的相似性并提高仿真的准确度和效率。
2. 目的离散相似法算法的改进,主要是为了提高其仿真效率和准确性,是一个基于最优控制方法的研究方向。
主要目的包括:(1) 改进仿真精度离散相似法算法需要保证仿真精度,在模型参数的测定以及模型拟合方面采用多种优化控制方法,从而实现最优参数测定和最优模型拟合,减少误差的产生,达到最佳仿真效果。
(2) 优化计算过程随着计算技术的发展,优化计算过程成为了提高仿真速度的重要手段。
离散相似法算法的改进直接关系到仿真计算的速度和效率。
因此,在研究离散相似法的改进时,优化计算过程也成为了关注的焦点。
实验3-连续系统离散相似法数字仿真实验

实验3 连续系统离散相似法的数字仿真实验(1) 掌握以系统结构图形式描述的连续系时域离散相似法的数字仿真方法和步骤。
(2) 学会利用时域离散相似法分析线性和非线性控制系统的动态性能以及典型非线性环节对控制系统动态性能的影响。
【实验内容】含死区环节的非线性控制系统的结构图如图A.2所示(1)按实验目的、要求和已知条件,建立系统的Simulink模型,并且用RK4法,求出c=0,0.1,0.5,1.0情况下(c=0相当于IV环节为1,即没有加入死去环节)系统的单位阶跃响应作为标准解。
(2)求出图A.2中传递函数对应的状态空间模型,并在该模型前加入虚拟的采样开关和零阶保持器,得到离散化状态空间模型。
(3)在c=0,0.1,0.5,1.0情况下,利用时域离散相似法编程完成对该系统的仿真研究。
(1)搭建simulink模型编写脚本文件:c=0;h1=plot(tout,y,'k'); set(h1,'LineWidth',1) hold on ;sim('lab3');c=0.1;h2=plot(tout,y,'r'); set(h2,'LineWidth',1) hold on ;sim('lab3');c=0.5;h3=plot(tout,y,'b'); set(h3,'LineWidth',1) hold on ;sim('lab3')c=1;h4=plot(tout,y,'m'); set(h4,'LineWidth',1) hold on;sim('lab3');grid绘制出单位阶跃相应图像:(2)输入程序求出状态空间模型(3)编程实现离散相似算法clc;clear;G=tf([8 10],[0.1 1 0 0]);G1=ss(G);T=0.01;sysd=c2d(G1,T);Ad=sysd.a;Bd=sysd.b;Cd=sysd.c;Dd=sysd.d;X=[0;0;0];yt=0;tt=0;R=1;c=0;M=10/T;for k=1:ME=R-yt(end);X=Ad*X+Bd*E;Y=Cd*X+Dd*E; if Y<=cY=Y+c;elseif Y>=cY=Y-c;elseY=0;endyt=[yt,Y];tt=[tt,k*T]; endplot(tt,yt,'k')1.c=02.C=0.13.C=0.54.C=1。
计算机仿真教案04-2-第四章 离散相似法的连续系统仿真

经整理后,得:(sI-A)X(s)=X(0)+BU(s)
X(s)=(sI-A)-1X(0)+(sI-A)-1BU(s)
(3-2-2)
L1[ 1 ]eat 因为, sa
标量,拉氏反变换
L1[s(IA )1]eAt 令F(t)=eAt,称F(t)为系统的状态转移同矩理阵
拉氏卷积定理:若£[f1(t)]=F1(s), £[f2(t)]=F2(s) 则有,
在零初始条件下,线性定常采样系统的输出采 样信号的Z变换与输入采样信号的Z变换之比称 为采样系统的脉冲传递函数。
脉冲传递函数又可表示为: G(Z)=Z[Gh(s)Ga(s)]
保持器传递函数
系统传递函数
(3-2-10)
选择不同的保持器,将得不同的G(Z),例 如选零阶保持器,则由(3-2-10)得,
式(3-2-5)-eAT×式(3-2-4),得
x [k (1 ) T ] e A x ( T k) T e A ( k 1 ) T( k 1 ) T e A B () d u kT
现作变量置换,τ=kT+t, dτ=dt 所以,(3-2-6)变成
(3-2-6)
x [k ( 1 ) T ] e A x T ( k)T T e A ( T t)B ( k u T t) dt 0 (3-2-7) 离散状态方程
2 4 12 2 4 12
利用矩阵指数函数的计算,可方便计算出其余的两 个系数,例如:
对于
m (T )
T e A ( T t ) Bdt
0
令 =T-t,则有, m ( T )
T e A ( T t ) Bdt
0
eAT (AT)i /i! i0
仿真技术实验程序及思考题解答(仅供参考)

实验一 连续系统的数字仿真一、实验目的1. 熟悉Matlab 中m 文件的编写;2. 掌握龙格-库塔法的基本原理。
二、实验设备计算机、MATLAB 软件三、实验内容假设单变量系统如图所示。
试根据四阶龙格-库塔法,求系统输出y 的动态响应。
1.首先把原系统转化为状态空间表达式:⎪⎩⎪⎨⎧=+=•CXy bu AX X ,根据四阶龙格-库塔公式,可得到: ⎪⎩⎪⎨⎧=++++=+++1143211)22(6k k k k CX y K K K K h X X (1) 其中: ⎪⎪⎪⎩⎪⎪⎪⎨⎧+++=+++=+++=+=)()()2()2()2()2()(3423121h t bu hK X A K h t bu K h X A K h t bu K h X A K t bu AX K k k k k k k k k (2) 根据(1)、(2)式编写仿真程序。
2.在Simulink 环境下重新对上述系统进行仿真,并和1中结果进行比较。
四、实验结果及分析要求给出系统输出响应曲线,并分析计算步长对龙格-库塔法的影响。
计算步长对龙格-库塔法的影响:单从每一步看,步长越小,截断误差就越小,但随着步长的缩小,在一定求解范围内所要完成的步数就增加,不但引起计算量的增大,而且可能导致舍入误差严重积累,因此同积分的数值计算一样,微分方程的解法也有选择步长的问题。
源程序:r=5;numo=[1];deno=[1 4 8 5];numh=1;denh=1;[num,den]=feedback(numo,deno,numh,denh);[A,b,C,d]=tf2ss(num,den);Tf=input('仿真时间 Tf= ');h=input('计算步长 h=');x=[zeros(length(A),1)];y=0;t=0;for i=1:Tf/h;K2=A*(x+h*K1/2)+b*r;K3=A*(x+h*K2/2)+b*r;K4=A*(x+h*K3)+b*r;x=x+h*(K1+2*K2+2*K3+K4)/6;y=[y;C*x];t=[t;t(i)+h];endplot(t,y)Tf=5 h=0.02五、思考题1.试说明四阶龙格-库塔法与计算步长关系,它与欧拉法有何区别。
钱雪军-第4章 连续系统仿真——离散相似法2

4.2.2 保持器
系统辨识与仿真
通过保持器对采样后输入信号的重构,通常可采用三种类型的保持器。
◨ 零阶保持器
◨ 一阶保持器
◨ 三角保持器
▶三种保持器比较:零阶保持器最简单,但重构信号的误差较大; 三角保持器最复杂,恢复信号的失真最小。
▶常用的还是零阶或一阶保持器,特别是零阶。
零阶保持器
u(t)
t0
u(t)
u*(t)
保持器
T
uk(t) x(t) = Ax(t) + Bu(t) x(t)
x*(t)
T
图4.2 状态空间模型离散化原理结构图
4.2.1 采样定理
系统辨识与仿真
采样频率ωs大于或等于两倍的采样器输入连续信号e(t)频谱 中的最高频率ωmax。即ωs>=2ωmax,这就是香农采样定理。
抽样频率小于模拟信号最好频率的2倍会造成频谱混叠 。
比较G(z)与G(s),可以得到置换关系 s ≈ 2 ( z −1) T (z +1)
映射关系
系统辨识与仿真
1+ Ts
考虑到
z
≈
1
−
2 Ts
将 s = σ + jω 代入上式,可得
2
1+ Ts 1+ T (σ + jω) 1+ T σ + j T ω
(1+ T σ )2 + (T ω)2
z
≈
2 1− Ts
◆为了使输入信号u(t)离散化后仍能保持原来的变化规律, 在输入采样开关后设置信号保持器(亦称为信号重构器), 复现原输入信号u(t),其结构如图4.1。
u(t)
u*(t) 保持器
第5-1章 频域离散相似法仿真Matlab编程

arru(m+1)
u(k-1)
…..
u(k-m+1)
u(k-m)
2
函数原型定义
function [t,y]=GZSimu(tstart,tstop,h,num,den,iniu,iniy,u) % 函数功能:对Z传递函数进行仿真 % 输入参数:tstart, tstop,h 分别是起始时间、结束时间和仿真步长,是 标量 % num,den是Z传递函数的分子分母多项式系数 % iniu,iniy是u,y的初始值,维数与num,den一致,第1个元素存最新 的 % u是系统输入 % 输出参数:t是仿真结果的时间序列 % y是仿1 G ( s) sK
采用单零点补偿
e
Ts
(1 Ts)
经计算得到系统的补偿离散模型为
X ( z ) z (1 e KT ) U ( z ) K ( z e KT )
取K=2,步长0.5时,
X ( z) 0.3161 z U ( z ) z 0.3679
an y(k ) an1 y(k 1) a0 y(k n) bmu(k ) b0u(k m)
将y(k)的系数归一化
an y (k ) a1n an 1 y (k 1) a0 y (k n)
1 an
bmu (k ) b0u (k m)
XX=ones(n,n);baseitem=[1]; for i=1:1:n-1 %计算(z+1)^n的系数 baseitem=conv(baseitem,[1,1]);end; XX(1,:)=baseitem; for i=2:n for j=2:n XX(i,j)=XX(i-1,j)-XX(i,j-1)-XX(i-1,j-1);
时域离散相似法

第三章 时域离散相似法用数字计算机对一个连续系统进行仿真时,必须将这个系统看作一个时间离散系统。
也就是说,我们只能计算到各状态量在各计算步距点上的数值,它们是一些时间离散点的数值。
在第二章中主要是从数值积分法的角度来讨论数字仿真问题,没有显式地涉及到“离散”这个概念。
史密斯从控制和工程的概念出发提出离散相似问题[1],并导出离散相似法。
所谓“离散相似法”就是将一个连续系统进行离散化处理,然后求得与它等价的离散模型。
由于连续系统的模型可以用传递函数来表示,也可以用状态空间模型来表示,因此,与连续系统等价的离散模型可以通过两个途径获得,其一是对传递函数作离散化处理得离散传递函数(或脉冲传递函数),称为频域离散相似模型。
其二是基于状态方程离散化,得到时域离散相似模型。
本章介绍时域离散相似法,第四章介绍频域离散相似法。
3.1 时域离散相似法基本原理3.1.1基本方法假设有一个连续系统,它由以下状态方程描述:xAx B =+u (3.1) 对于(3.1)式描述的连续系统进行离散化处理,如图3.1所示。
在系统的输入端加上虚拟采样开关和虚拟信号重构器,输出端加一个虚拟采样开关。
虚拟采样周期为T 且同步。
其中,u (t )是系统输入;u (k )是加虚拟采样开关后,在kT 时刻系统输入;x (k )是加虚拟采样开关后在kT 时刻系统输出;~()ut 、~()x t 是等价的连续信号。
只要~()ut 能足够精确地表示u (t ),那么~()x t 也就能足够精确地表示x t (),这样,就能获得与连续系统等价的时域离散相似模型。
对该连续系统进行离散化处理后可以得到系统离散相似模型如式3.2所示:x [(k +1)T )]=)(T Φ x (kT )+)(T m Φ u (kT )+ Φm (T) ()u kT (3.2) 其中:T 是采样时间间隔(或称采样周期);u (k )、x (k )为系统kT 时刻的输入及状态量;)(ˆ)()(T T T mm ΦΦΦ、、为离散化后与系统模型有关的系数。
线性定常系统离散相似法仿真的快速算法

线性定常系统离散相似法仿真的快速算法
金炜东
【期刊名称】《控制理论与应用》
【年(卷),期】1993(010)005
【摘要】考虑线性定常系统的数字仿真,状态变量的计算步长为T,而系统输出的计算间隔常常为NT。
本文通过以多项式插值函数逼近系统输入,利用增广矩阵法的结果,给出了基于离散相似法的一类仿真算法。
当N较大时,与一般同类算法相比,本文算法使计算量显著减小。
【总页数】6页(P599-604)
【作者】金炜东
【作者单位】无
【正文语种】中文
【中图分类】TP271
【相关文献】
1.边续线性定常系统的高精度,高数值稳定性,快速仿真算法 [J], 任兴权;薛定宇
2.连续系统离散相似法仿真的排序算法 [J], 李胜勇;常谦
3.自动控制系统仿真离散相似法算法的改进 [J], 常谦;王兆安
4.自动控制系统仿真离散相似法算法的改进 [J], 常谦;王兆安
5.不同决策输入下系统的通用离散相似仿真算法 [J], 王侃
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称:将传递函数为
s s 2612 的环节与单位反馈组成系统,将其离散化
1.实验原理
1 )离散相似法 所谓离散相似法,就是将一个连续系统进行离散化处理,从而得到等价的系统离散模型,此种方法按系统的动态结构图建立仿真模型。
在计算过程中,按各典型环节离散相似模型,根据环节的输入来计算环节的输出。
2) 环节的离散化模型
将连续系统按下图所示对其进行离散化处理,在系统的输入、输出端加上虚拟采样开关,T 为采样周期。
为保证输入信号复现原信号,在输入端加上一个保持器。
使用零阶保持器,可得到离散化状态方程的解:
3) 仿真算法实现过程
当给定连续系统的动态结构图后,将其等效为各典型环节的组合,按前面讨论的典型环节离散系数 表达式,经程序处理,事先将各环节的类型、参数、初始条件、各环节连接关系矩阵、输入输出连接矩阵等参量送入程序中,既可通过离散相似的模型求出在特定信号作用下,系统中各环节输出变量的变化情况,从而得到系统的仿真结果。
3.实验方案
1)连续系统的结构图
这是一个单位反馈的二阶系统。
2)引入采样开关将其离散
Zero-Order (零阶保持器)及采样开关对系统进行离散化,采用状态转移法进行离散化
3)将传递函数转化成状态方程并对其进行离散化
传递函数 1261)()()(2++==
s s s U s Y s G 变形得)()()(2)(62s U s Y s sY s Y s =++
假设其为零状态响应取Laplace 反变换得
u y y y =+''+''26
将其转变成状态方程有
u x x ⎥⎦⎤⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡--=10016131
x y ]01[=
通过求矩阵指数及相关变化将状态方程离散化得
)(]01[)()
()()1(k u k y k Bu k x A k x =+=+
由于矩阵A ,B 过于复杂,这里简写,详细表达式见后面程序
4.实验程序
1)由传递函数求状态方程
建立传递函数并转化为状态方程
clear
clc
A = tf2ss([1],[6 2 1]) %建立传递函数模型
%并转化为状态方程
运行结果:
2)将状态方程离散化
对应脚本程序:
A =[-1/3 -1/6;1 0] %
syms s t
B= [s 0;0 s] % SI
D = inv(B-A) %求逆矩阵
AI = ilaplace(D,s,t)%laplace 变换 求A 阵
BI = AI*[0 ;1]
BI =int(BI,'0','t') %积分求B 阵
pretty(AI) %A 转化陈易读形式。
pretty(BI) %B
运行结果:(这里是离散后的A ,B 阵)
AI =
[ (cos((5^(1/2)*t)/6) - (5^(1/2)*sin((5^(1/2)*t)/6))/5)/exp(t/6)
-(5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6));
(6*5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6))
(cos((5^(1/2)*t)/6) + (5^(1/2)*sin((5^(1/2)*t)/6))/5)/exp(t/6)]
BI=
[(6*5^(1/2)*(sin((5^(1/2)*t)/6)/6 + (5^(1/2)*cos((5^(1/2)*t)/6))/6))/(5*exp(t/6)) - 1;
(4*5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6)) - (2*cos((5^(1/2)*t)/6))/exp(t/6) + 2] 3)由离散后的状态仿真求响应,这里以阶跃相应为例(u = 10)
对应脚本程序:
clear %假设为零状态响应
clc
close
t = 0.1 %采样周期0.1s
A =[(cos((5^(1/2)*t)/6) - (5^(1/2)*sin((5^(1/2)*t)/6))/5)/exp(t/6) -(5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6));
(6*5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6)) (cos((5^(1/2)*t)/6) + (5^(1/2)*sin((5^(1/2)*t)/6))/5)/exp(t/6)]
B = [1 - (6*5^(1/2)*(sin((5^(1/2)*t)/6)/6 + (5^(1/2)*cos((5^(1/2)*t)/6))/6))/(5*exp(t/6));
(2*cos((5^(1/2)*t)/6))/exp(t/6) - (4*5^(1/2)*sin((5^(1/2)*t)/6))/(5*exp(t/6)) - 2]
y0 = 0 %初值
uN = 50
t = 0.1; %步长0.1
u =0:t:uN;
N = length(u);
x0 = [0;0] %零初始状态
dy = 0
uc = 10; %阶跃输入u = 10
j = 1
yk = 0;
for j = 1:N
% xk = diffsubf(x0,1,t,A,B)
yk = [1 0]*x0;
xk =A*x0 +B*uc;
x0 = xk;
data(j) = yk(1);
end
for j = 1:N %与真实值比较
comparedata(j) =10 - (10*(cos((5^(1/2)*u(j))/6) + (5^(1/2)*sin((5^(1/2)*u(j))/6))/5))/exp(u(j)/6);
end
plot(u,data,'r-',u,comparedata,'bO')
legend('相似法','解析法',4)
grid on
4)运行结果:
4.实验结果分析
在最终图像中,相似法与解析法所得结果完全重合,说明此次使用的相似离散法有很高的精度。
从响应曲线可以看出该系统在阶跃输入下超调量约为23%,调节时间约为25s。
稳态精度较高。
具有较好的稳定性。
