代密码学第十一讲：基于身份的密码体制
现代密码学课后题答案
《现代密码学习题》答案第一章判断题×√√√√×√√选择题1、1949年，（ A ）发表题为《保密系统的通信理论》的文章，为密码系统建立了理论基础，从此密码学成了一门科学。
A、ShannonB、DiffieC、HellmanD、Shamir2、一个密码系统至少由明文、密文、加密算法、解密算法和密钥5部分组成，而其安全性是由（ D）决定的。
A、加密算法B、解密算法C、加解密算法D、密钥3、计算和估计出破译密码系统的计算量下限，利用已有的最好方法破译它的所需要的代价超出了破译者的破译能力（如时间、空间、资金等资源），那么该密码系统的安全性是（ B ）。
A无条件安全B计算安全C可证明安全D实际安全4、根据密码分析者所掌握的分析资料的不通，密码分析一般可分为4类：唯密文攻击、已知明文攻击、选择明文攻击、选择密文攻击，其中破译难度最大的是（ D ）。
A、唯密文攻击B、已知明文攻击C、选择明文攻击D、选择密文攻击填空题：5、1976年，和在密码学的新方向一文中提出了公开密钥密码的思想，从而开创了现代密码学的新领域。
6、密码学的发展过程中，两个质的飞跃分别指 1949年香农发表的保密系统的通信理论和公钥密码思想。
7、密码学是研究信息寄信息系统安全的科学，密码学又分为密码编码学和密码分析学。
8、一个保密系统一般是明文、密文、密钥、加密算法、解密算法 5部分组成的。
9、密码体制是指实现加密和解密功能的密码方案，从使用密钥策略上，可分为对称和非对称。
10、对称密码体制又称为秘密密钥密码体制，它包括分组密码和序列密码。
第二章判断题：×√√√选择题：1、字母频率分析法对（B ）算法最有效。
A、置换密码B、单表代换密码C、多表代换密码D、序列密码2、（D）算法抵抗频率分析攻击能力最强，而对已知明文攻击最弱。
A仿射密码B维吉利亚密码C轮转密码D希尔密码3、重合指数法对（C）算法的破解最有效。
A置换密码B单表代换密码C多表代换密码D序列密码4、维吉利亚密码是古典密码体制比较有代表性的一种密码，其密码体制采用的是（C ）。
现代密码学课后题答案
《现代密码学习题》答案第一章判断题×√√√√×√√选择题1、1949年，（ A ）发表题为《保密系统的通信理论》的文章，为密码系统建立了理论基础，从此密码学成了一门科学。
A、ShannonB、DiffieC、HellmanD、Shamir2、一个密码系统至少由明文、密文、加密算法、解密算法和密钥5部分组成，而其安全性是由（ D）决定的。
A、加密算法B、解密算法C、加解密算法D、密钥3、计算和估计出破译密码系统的计算量下限，利用已有的最好方法破译它的所需要的代价超出了破译者的破译能力（如时间、空间、资金等资源），那么该密码系统的安全性是（ B ）。
A无条件安全B计算安全C可证明安全D实际安全4、根据密码分析者所掌握的分析资料的不通，密码分析一般可分为4类：唯密文攻击、已知明文攻击、选择明文攻击、选择密文攻击，其中破译难度最大的是（ D ）。
A、唯密文攻击B、已知明文攻击C、选择明文攻击D、选择密文攻击填空题：5、1976年，和在密码学的新方向一文中提出了公开密钥密码的思想，从而开创了现代密码学的新领域。
6、密码学的发展过程中，两个质的飞跃分别指 1949年香农发表的保密系统的通信理论和公钥密码思想。
7、密码学是研究信息寄信息系统安全的科学，密码学又分为密码编码学和密码分析学。
8、一个保密系统一般是明文、密文、密钥、加密算法、解密算法 5部分组成的。
9、密码体制是指实现加密和解密功能的密码方案，从使用密钥策略上，可分为对称和非对称。
10、对称密码体制又称为秘密密钥密码体制，它包括分组密码和序列密码。
第二章判断题：×√√√选择题：1、字母频率分析法对（B ）算法最有效。
A、置换密码B、单表代换密码C、多表代换密码D、序列密码2、（D）算法抵抗频率分析攻击能力最强，而对已知明文攻击最弱。
A仿射密码B维吉利亚密码C轮转密码D希尔密码3、重合指数法对（C）算法的破解最有效。
A置换密码B单表代换密码C多表代换密码D序列密码4、维吉利亚密码是古典密码体制比较有代表性的一种密码，其密码体制采用的是（C ）。
基于身份的加密IBE研究与启示 PPT
CPK产品
• 组合公钥加密IC卡, 北京密海信息技术有限公司, can not get extra information. • CPK认证系统,北京密海信息技术有ion Architecture
KMC
负责初始化系统的公/私 钥因子矩阵，发布公钥 因子矩阵，接受名字管 理中心的申请，产生指 定终端实体的私钥并将 其返回给名字管理中心 制定整个系统的 安全实施策略并 负责管理密钥管 理中心的实体
Directory Server
IBE历史
• 1984年Adi Shamir首次正式提出IBE的概念; • 1999年南相浩教授提出CPK (Combined Public Key),2005年公布 • 2001年Cocks在密码学与编码IMA国际会议上提出了一种 可以应用的IBE方案,但效率非常低; • 2001年Dan Boneh和Franklin Matt提出了DB/FM方案;
Combined Public Key
• 无须在线认证数据库系统的支持，颁发的是ID证书。 • 采用了种子矩阵算法，只需要保留很少的公钥参数，甚 至可以在手机等小终端上得到普遍的使用，其认证规模 极大。 • 适合网络世界中代理、进程、主体的身份认证。 • CPK认证体系要远远优于PKI和IBE体系。
Identity based Encryption
(DB/FM)
• 其特点是取消了第三方认证的CA机构，颁发的是ID证书。 • 依然保留了在线认证服务，需要保留大量的用户证书， 仍然需要建立在线的证书数据库系统。 • 认证管理能力低，管理成本比PKI大大减少。 • 该方法仍然不适合网络世界中代理、进程、主体的身份 认证。
QNS是中国信息产业商会的咨询结构,其认为:从理论上讲，规模化的信任系统只 能“由上而下”地构筑，因此，政府的主导作用和顶层的理念和整体设计是至 关重要的。 • 由QNS工作室提出“国家组合公钥(CPK)基础设施”NCI(National CPK Infrastructure)的设想。NCI理念，同美国的《紧急报告》不谋而合，但是美 国只提出了问题，还没有找到解决方案。 • 在《银行行为监管》、《银行行为控制》两本书中已给出了全面而可行的解决 方案。 • NCI理念包括CPK-inside的芯片，NCI企业联盟，NCI论坛等；以《软件行为学》 和《CPK认证算法》作为主要理论和技术支撑，逐步开展八个方面的可信平台 建设。 • NCI理念的形成和兴起，将标志着我国自主开发可信网络世界安全的新时代的 到来，宣告跟随外国技术的狭义信息安全时代和PKI时代的结束。
基于身份的密码体制在空管信息安全中的应用
基于身份的密码体制在空管信息安全中的应用随着信息化技术的不断发展，航空交通的管理和控制越来越离不开计算机和网络技术的支持。
然而，随着计算机和网络系统的广泛应用，信息安全问题也愈加突出，特别是对于航空交通管理这样的关系到民众安全的行业，信息安全问题更是不容小觑。
为了确保空管信息系统的安全性和可信性，身份的密码体制应用于空管信息安全已成为一个非常现实和必要的选择。
身份的密码体制是一种在消息传输中保证通信安全的常用方法，其中，身份认证、密钥交换和消息加密是基本环节。
身份认证的目的是确认通信双方的身份信息，在通信之前要求通信双方进行身份认证，能够大大降低信息泄露的风险。
密钥交换是为了建立对称加密算法的密钥，保证信息传输的机密性。
消息加密是在通信传输过程中，利用密钥对明文消息进行加密，保证传输中消息的完整性和保密性。
这三个环节共同构成了身份的密码体制。
身份的密码体制可应用于航空交通管理的多个领域，如空管数据通信、雷达通信、导航通信、电子地图、航班管理和恶意攻击检测等方面，以保障空管系统的安全和可靠运行。
以下是航空交通管理中身份的密码体制应用的几个方面：1. 空管数据通信：空管数据通信是空管系统内部数据流转的重要组成部分，包括航路信息、飞行计划、雷达跟踪数据等。
对这些数据的泄露可能导致恶意攻击者得到真实的飞行情况，造成重大后果。
利用身份的密码体制建立安全通信链路，实现身份认证、密钥交换和数据加密，可以保证通信数据的机密性和完整性，并有效防止数据泄露。
2. 雷达通信：雷达通信是空管系统中的核心组成部分，是实现飞机跟踪和航班管理的不可或缺的手段。
然而，雷达通信也面临着恶意攻击者窃取信息和干扰雷达系统正常运行的风险。
在这方面，身份的密码体制可以通过身份认证和消息加密确保雷达通信的安全性，使得攻击者无法获取雷达数据或干扰雷达系统正常工作。
3. 导航通信：导航通信是航班导航的基础，能够提供飞机导航信息的接入服务、高精度的导航数据和预警信息的提供、以及飞机与地面通信的互联互通等功能。
基于身份的公钥密码学
在通常意义下的公钥密码学中，公钥 (public-key) 是借助某个有效单向函数作用 ek ek d 于私钥(private-key)而产生的。也就是说， d 对事先选定好的一个有效单向函数，有 public-key ＝ F (private-key). （7.1） 这种公钥看起来有一定的随机性。即从公 钥本身，看不出该公钥与公钥所有者之间 有任何的联系。当有一条机密信息要用某 一公钥加密后发送给指定的接受者时，发 送者必须确定这个看起来有点随机性的公
19:37 8
Shamir提出的基于身份（ID）的数字签名 体制由下列四个步骤组成：
参数建立(Setup):
TA完成：产生整个系统 的参数及主密钥(master-key)。 用户私钥生成(User-key-generation): TA 完成：利用master-key及用户传输的任意比 特串id，产生相对于id的用户的私(privatekey)。 签名(Sign): 签名者完成： 对输入的信息m， 用签名者的私钥对信息m进行签名sig。 验证(Verify): 用户完成： 对输入的信息m 及相应的签名sig，利用id验证签名的 真 伪性。
19:37 7
由于用户的私钥由TA生成，所以用户必须 绝对无条件地信任TA，也就是说，用户不 用担心TA读取了用户之间所有的秘密通 信，或伪造他们的签名。因此，基于身份 的密码系统只适用在用户接受对TA无条 件信任的环境。比如在雇主可完全知道他 的所有雇员的来往信息的环境中，雇主就 可担当TA的角色。 7. 1. 1 Shamir的基于身份的数字签名体，公钥是经由私钥来生成的，私钥是 事先精心挑选好的。 在Shamir的基于身份的公钥密码系统. TA由(7. 2)生成用户私钥的计算一般不公开。 在TA为用户生成私钥前，TA需要彻底检验 用户的身份信息，用户提供的身份信息必须 能使TA确信它能唯一准确地识别出用户。 这类似于在一般公钥密码系统中，CA在签 发公钥证书给用户之前需要对用户作身份检 验。
基于身份的加密体制
基于⾝份的加密体制动机基于⾝份加密技术是为了解决公钥加密算法中数字证书管理的困难性⽽提出的，基于⾝份加密技术使⽤⽤户的⾝份 ( 如 ID 和邮箱等 ) 作为公钥，由可信的第三⽅（PKG）产⽣⽤户的私钥。
基于⾝份加密技术是⼀种公钥加密技术，可实现⾝份鉴别、消息加密、数字签名和协商会话密钥。
算法a)系统初始化算法setup。
该算法的输⼊是安全参数k，输出是系统参数params和主密钥msk。
该算法由PKG执⾏。
b)私钥⽣成算法keyGen。
该算法的输⼊是params、主密钥msk和⾝份ID，输出是ID对应的私钥d。
该算法由PKG执⾏。
c)加密算法encrypt。
该算法的输⼊是params、⾝份ID和消息M，输出是密⽂C。
该算法由加密者执⾏。
d)解密算法decrypt。
该算法的输⼊是params、密⽂C和私钥d，输出是消息M。
该算法由解密者执⾏。
安全模型1)系统参数⽣成挑战者选择安全参数k，并运⾏setup 算法⽣成系统参数params和主密钥msk；挑战者将params发送给敌⼿，并保存msk。
阶段1敌⼿提出⼀系列询问，询问是a)私钥询问<IDi.>或者b)解密询问<IDi，Ci>2)挑战敌⼿结束阶段1的询问，输出长度相等的明⽂M0,M1和⾝份ID*。
要求在阶段1中敌⼿没有询问过ID*。
的私钥。
挑战者随机选择b∈{0，1}，计算C*=encrypt (params，ID*，Mb)，并把C*作为挑战发送给敌⼿。
阶段2敌⼿提出⼀系列询问，询问是a)私钥询问<IDi.>或者b)解密询问<IDi，Ci>，其中IDi≠ID*，<IDi,Ci>≠<ID*，C*>询问都是适应性的，也就是说当前询问依赖于以前询问的结果。
3)猜测敌⼿输出b'∈{0，1}。
如果b'=b,则敌⼿赢得游戏。
把上⾯的敌⼿A称为IND-ID-CCA2敌⼿，定义优势如果优势可以忽略，则IBE⽅案是不可区分适应性选择密⽂攻击(IND-ID-CCA2)安全的。
基于身份的密码体制研究及其在移动支付业务中的应用
二、问题陈述
五、结论与展望
五、结论与展望
本次演示通过对身份密码体制的安全问题进行研究，提出了一系列有效的解 决方案和优化方案，为提高身份密码体制的安全性和可靠性提供了重要参考。然 而，随着网络攻击手段的不断升级和变化，身份密码体制的研究仍需以下问题和 挑战：
五、结论与展望
1、密码算法的复杂性和强度：随着计算能力的提高，密码算法需要更高的复 杂度和强度来确保安全性。因此，研究更加复杂和强大的密码算法是未来身份密 码体制研究的重要方向。
相关技术综述
相关技术综述
传统密码学主要分为对称密码学和非对称密码学。对称密码学中加密和解密 使用相同的密钥，而非对称密码学则使用公钥和私钥。基于身份的密码体制是一 种新型的密码学技术，其主要特点是将用户的身份信息作为密码学的关键元素， 而不是传统的密钥。
相关技术综述
在基于身份的密码体制中，用户的身份信息经过一定的算法处理后生成一个 公钥和一个私钥。公钥用于加密和身份认证，私钥用于解密和签名。由于用户的 身份信息是可信任的，因此可以避免传统密码学中密钥管理的难题。
基于身份的密码体制研究及 其在移动支付业务中的应用
目录
01 相关技术综述
03 参考内容
02
基于身份的密码体制 设计
内容摘要
随着移动支付业务的快速发展，保障支付安全变得越来越重要。基于身份的 密码体制作为一种新型的密码学技术，在移动支付业务中发挥重要作用。本次演 示将对基于身份的密码体制进行详细介绍，并分析其在移动支付业务中的应用及 安全性。
【国家自然科学基金】_基于身份的密码体制_基金支持热词逐年推荐_【万方软件创新助手】_20140731
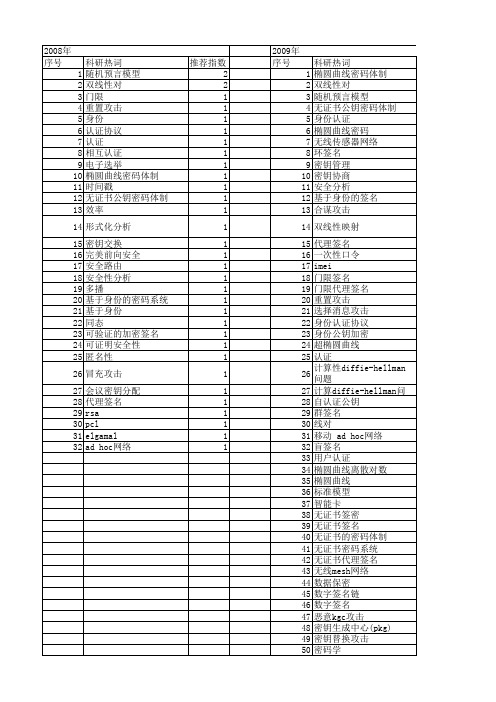
安全椭圆曲线 1 安全中介 1 安全 1 存储 1 多重数字签名 1 多签密 1 基于身份的密码系统 1 基于身份的加密 1 基于身份的公钥系统 1 基于身份的公钥密码系统 1 基于身份的公钥密码体制 1 基于身份加密 1 基于虹膜信息的签名方案 1 基于id身份认证 1 在线/离线签密 1 团队 1 合谋攻击 1 可验证秘密共享 1 可认证的密钥协商 1 可撤销匿名性 1 半可信第三方 1 匿名路由协议 1 公钥加密 1 信任评估 1 伪造攻击 1 不可追踪性 1 不可伪造性 1 一次性口令 1 weil/tate对 1 tinyos 1 shamir门限方案 1 rsa密码体制 1 rabin-pss-mr体制 1 miller算法 1 imei 1 elgamal体制 1 diffie-hellman密钥协商 1 decisionalbilineardiffie-hellman假设 1 bdh问题 1 ad hoc 1
推荐指数 6 6 4 4 3 3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 椭圆曲线密码体制 双线性对 随机预言模型 无证书公钥密码体制 身份认证 椭圆曲线密码 无线传感器网络 环签名 密钥管理 密钥协商 安全分析 基于身份的签名 合谋攻击 双线性映射 代理签名 一次性口令 imei 门限签名 门限代理签名 重置攻击 选择消息攻击 身份认证协议 身份公钥加密 超椭圆曲线 认证 计算性diffie-hellman问题 计算diffie-hellman问题 自认证公钥 群签名 线对 移动 ad hoc网络 盲签名 用户认证 椭圆曲线离散对数 椭圆曲线 标准模型 智能卡 无证书签密 无证书签名 无证书的密码体制 无证书密码系统 无证书代理签名 无线mesh网络 数据保密 数字签名链 数字签名 恶意kgc攻击 密钥生成中心(pkg) 密钥替换攻击 密码学 安全组播 安全
基于身份的密码体制在空管信息安全中的应用
基于身份的密码体制在空管信息安全中的应用1. 引言1.1 研究背景随着空中交通的快速发展和信息化程度的提升，空管系统的安全性问题日益受到重视。
传统的密码体制在保障信息安全方面存在一定的局限性，例如易受到密码破解攻击，无法有效应对身份伪装等问题。
为了提升空管系统的信息安全性，基于身份的密码体制成为了当前研究的热点之一。
基于身份的密码体制是一种新型的密码技术，它不再依赖传统的密码方式来验证用户的身份，而是基于用户的身份信息进行加密和解密操作。
通过使用信任中心来分配身份标识，可以有效防止身份伪装和信息泄露等安全威胁。
在空管系统中应用基于身份的密码体制，可以提高用户身份验证的准确性和安全性，防止非法入侵和数据篡改等危险行为。
基于身份的密码体制还能够简化密钥管理过程，降低系统维护的成本，提高整个系统的可靠性和稳定性。
基于身份的密码体制在空管信息安全中具有重要的应用价值，是当前空管系统安全性提升的必然选择。
通过深入研究该技术在空管领域的应用，可以进一步加强空管系统的信息安全防护能力，确保航空安全和信息安全得到有效的保障。
1.2 研究目的研究目的是为了探讨基于身份的密码体制在空管信息安全中的应用，深入了解其原理和特点，分析其在空管系统中的具体实施方式和效果。
通过研究，可以为空中交通管制系统提供更加安全可靠的信息保护措施，防范可能存在的安全漏洞和威胁。
研究目的也在于评估基于身份的密码体制在空管领域中的实际应用价值，探讨其优势和不足之处，为未来的相关研究和技术开发提供参考和指导。
通过深入研究基于身份的密码体制在空管信息安全中的应用，旨在提高空中交通管制系统的整体安全性和数据保护能力，为航空运输业的安全和发展作出贡献。
1.3 研究意义研究基于身份的密码体制在空管信息安全中的应用，不仅可以提升空管系统的安全性和可靠性，还可以有效减少安全漏洞的发生，保护重要数据和通信的隐私性。
基于身份的密码体制还可以简化身份验证流程，提高系统的用户友好性和操作便捷性，为空管系统的运行和管理提供更加便利的手段。
(最新整理)5G时代信息通信网络安全与技术发展(2019全3套题)
5G时代信息通信网络安全与技术发展(2019全3套题)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（5G时代信息通信网络安全与技术发展(2019全3套题)）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为5G时代信息通信网络安全与技术发展(2019全3套题)的全部内容。
5G时代信息通信网络安全与技术发展（继续教育考试第一套题）一、单选题（共30题，每题2分）1 ．（)标签工作频率是3-30MHZ.A．低频电子标签B．高频电子标签C．特高频电子标签D．微波标签参考答案：B2 ．以下关于企事业单位人员的管理说法不对的是（）。
A．应该在新员工聘用阶段就提出安全责任问题B．应该开展对用户的安全管理规程和正确使用信息处理设备的培训C．只有组织中的信息安全部门人员，应该接收适当的信息安全教育和培训D．应该使所有雇员和签约人员知道可能影响组织资产安全的不同种类事件的各种报告程序参考答案：C3 ．下面系统不属于第三代移动通信系统。
（ )A．GSMB．CDMA2000C．WCDMAD．TD—SCDMA参考答案：A4 ．按照密码系统对明文的处理方法，密码系统可以分为（）A．置换密码系统和移位密码系统B．密码学系统和密码分析学系统C．对称密码系统和非对称密码系统D．分组密码系统和序列密码系统参考答案:C5 ．软切换是指_______。
A．不同基站NodeB间切换B．同基站不同扇区间切换C．不同RNC间切换D．异频切换参考答案:A6 ．机器人中的皮肤采用的是（）A．气体传感器B．味觉传感器C．光电传感器D．温度传感器参考答案:D7 ．以下哪个设备属于智慧农业的(）A．遥控精灵B．智能窗帘C．土壤水分温度传感器D．人体红外线传感器参考答案:C8 ． AES的最小分组长度为（）A．128B．64C．56D．256参考答案:A9 ．基于身份的密码体制中，以下哪一个不能作为用户公钥（ )A．用户名字B．用户邮箱C．用户住址D．用户私钥参考答案：D10 ． 8位二进制表示的图像如果进行位面分解,最高位的1代表的灰度是（）A．128B．64C．16D．8参考答案：A11 ．一般来说，以下加密算法中加密速度最快的是( ）A．RSAB．DESC．AESD．序列密码参考答案：D12 ．利用公开密钥算法进行数据加密时，采用的方式是（ ) A．发送方用公开密钥加密，接收方用公开密钥解密。
基于身份的加密体制研究综述
第一个真正 实用 的 ＩＥ方 案 直到 ２０ Ｂ ０ １年才 由 Ｂ ｎｈ等 ｏｅ 人 提出。该加密方 案使 用 双线性 对 进行 构造 ， 于双 线性 基
第２ ７卷 第 １期 ２１ ０ ０年 １月
计 算 机 应 用 研 究
Ａｐ ｌ ａ ｉｎ Ｒｅ ｅ ｒ ｈ ｏ ｍｐ ｔｒ ｐ ｉ ｔｏ ｓ ａ ｃ ｆＣｏ ｕ ｅ ｓ ｃ
Ｖ０ ． ７ Ｎｏ １ １２ ．
Ｊｎ ２ １ ａ． ００
基 于 身份 的加 密 体 制研 究综 述 水
曾梦岐 ， 卿
摘
昱， 谭平璋 ， 杨
宇， 周楝淞
（ 中国电子科 技 集 团公 司 第三十研 究 所 ，成都 ６ ０ ４ ） １０ １
要 ：着 重对基 于身份 的加 密 （Ｂ 体 制进 行综 述性 的研 究 ： Ｉ Ｅ） 通过 与传 统的 Ｐ Ｉ Ｋ 进行 比较 引 出 Ｉ Ｅ加 密体制 ， Ｂ
提 出有 价值 的 问题供 进 一步研 究 。 关 键词 ：基 于身份 的加 密 ； Ｋ ； 圆曲线 ； 线性 映射 ＰＩ 椭 双
中图分 类号 ：Ｔ ３ ９ ２ Ｐ ０ ． 文献 标 志码 ：Ａ 文章编 号 ：１０ —６ ５ ２ １ ） １０ ２ — ５ ０ １ ３ ９ （ ０ ０ ０ —０ ７ ０
０ 引言
ＩＥ也 即基 于 标 志 的加 密 ， 一 种 公 钥 密 码 体 制 ， 直 接 Ｂ 是 它
到用 户手 中。１８ ９ ７年 Ｔ ｎｋ 基于离散对 数问题和大 整数的 ａａａ
分 解 问 题 提 出一 个 修 改 的 ＩＥ实 现 方 案 ， 引入 了 门 限 的概 念 Ｂ 并
利用用户 的惟一身 份标 志作为公 钥 ， 不采用 数字证 书 的概念 ， 用户使用 和后 台管 理都很 简单 ， 有广泛 的应用前景 。而在传统 的 ＰＩ Ｋ 技术 中 ， 由于每个用户需要 事先 申请 数字证 书 ， 用户使 用复杂 ， 台管理也异常繁琐 。为 了让读者对 ＩＥ有个对 比性 后 Ｂ 的认 识 ， １给 出了传统 的 Ｐ Ｉ Ｉ Ｅ的 比较 。在 Ｐ Ｉ Ｃ 表 Ｋ与 Ｂ Ｋ 中 Ａ （ ｅ ｉｃｔ ａ ｔｏ ｔ） 应 ＩＥ中的 Ｔ ｔ ｓ ｄａ ｔ ｒｙ ， 中 ｃｒｆ ａｅ ｕｈｒｙ 对 ｔ ｉ ｉ Ｂ Ａ（ｒ ｔ ｕｈ ｉ ） 其 ｕｅ ｏｔ
基于身份密码体制及其应用的研究
2、电子政务：电子政务系统中使用身份密码体制可以对用户进行身份认证和 访问控制，确保只有合法用户可以访问敏感信息和办理业务。
3、社交网络：社交网络平台也采用身份密码体制进行用户身份验证，从而保 护用户的个人隐私和信息安全。
尽管身份密码体制在上述应用场景中发挥了重要作用，但也存在一些不足之处， 如密码泄露、重复使用等问题。因此，在应用身份密码体制时需要注意以下几 点：
身份密码体制的优势在于，它可以根据用户的不同身份信息设定不同的访问权 限，从而实现细粒度的访问控制。同时，身份密码体制还可以防止非法用户获 取敏感信息，保护用户的隐私和安全。然而，身份密码体制也存在一些争议焦 点，如密码泄露、重复使用等安全问题。
三、身份密码体制的组成
身份密码体制主要由密码算法和密钥管理组成。密码算法是身份密码体制的核 心，用于将原始数据进行加密和解密。常见的密码算法包括对称加密算法和非 对称加密算法。对称加密算法使用相同的密钥进行加密和解密，而非对称加密 算法使用公钥和私钥进行加密和解密。
基于身份密码体制及其应用的研究
01 一、引言
目录
02 二、概述
03
三、身份密码体制的 组成
04
四、身份密码体制的 应用
05 五、未来发展方向
随着信息技术的快速发展和网络应用的普及，网络安全问题越来越受到人们的。 身份密码体制是解决网络安全问题的一个重要手段。本次演示将对身份密码体 制及其应用进行深入研究，介绍其基本概念、组成、应用及未来发展方向。
一、引言
身份密码体制是一种基于用户身份信息的密码系统，广泛应用于各类网络应用 中。身份密码体制通过验证用户的身份信息，确保只有合法用户能够访问相应 的资源。随着网络攻击的不断增加，身份密码体制在保护用户隐私和网络信息 安全方面发挥着越来越重要的作用。
基于身份的密码学及其在认证与授权中的应用
基于身份的密码学及其在认证与授权中的应用密码学是一门研究如何保障信息安全的学科，而基于身份的密码学则是在密码学的基础上，通过对身份的验证和认证，进一步提升信息的安全性。
本文将介绍基于身份的密码学的概念、原理，并探讨其在认证与授权中的应用。
一、基于身份的密码学概述基于身份的密码学（Identity-based cryptography）是指使用主体的身份作为公钥的密码学体系。
传统的公钥密码学中，需要使用者拥有自己的公私钥对，且公钥需要发布到认证机构或者密钥分发中心进行认证，而基于身份的密码学通过绑定主体的身份信息，克服了传统公钥密码学中的公钥分发问题。
二、基于身份的密码学的原理基于身份的密码学的核心原理是将主体的身份信息作为公钥生成算法的输入，通过某种特定的数学运算，从主体的身份信息中生成对应的私钥。
当主体需要进行加密或解密操作时，只需使用生成的私钥即可，无需像传统公钥密码学那样需要进行公私钥的配对。
三、基于身份的密码学在认证中的应用1. 身份认证基于身份的密码学可以应用于身份认证领域，代替传统的用户名密码登录方式。
用户只需提供自己的身份信息，系统即可生成对应的私钥进行身份验证，免去了用户记忆复杂密码的烦恼，同时提升了身份认证的安全性。
2. 数字签名基于身份的密码学可以用于生成数字签名，确保数据的完整性和不可篡改性。
发送方使用自己的私钥对数据进行签名，接收方使用发送方的公钥进行验证，从而确保数据未被篡改过。
四、基于身份的密码学在授权中的应用1. 权限控制基于身份的密码学可以用于实现精细化的权限控制。
系统可以根据用户的身份信息，生成对应的私钥，通过私钥的控制来实现对资源的访问控制，确保只有经过授权的用户才能访问特定的资源。
2. 数字版权保护基于身份的密码学可以应用于数字版权保护领域，通过对每一个数字内容进行身份识别，确保只有合法拥有者才能对数字内容进行访问和复制，有效保护了数字版权的权益。
五、结论基于身份的密码学通过利用主体的身份信息作为公钥生成的基础，提供了一种新的安全通信方式。
基于身份的公钥密码体制
A B pub A B B A pub B A
9.5基于身份的签密体制
2003年，Libert和Quisquater提出了一个基 于身份的签密方案，由四个算法组成：系 统建立、密钥提取、签密和解签密。
1．系统建立 设G1为由P生成的循环加法群，阶为q，G2为具有相同阶q的循环乘法群，：为一个双线性映射。 明文空间为{0,1}n，E和D分别表示一个对称密码体制（如AES）的加密和解密算法。定义三个安全 的哈希函数：、：和：。PKG随机选择一个主密钥，计算Ppub=sP。PKG公开系统参数{G1, G2, q, n, ê, P, Ppub, H1, H2, H3, E, D}，保密主密钥s。 2．密钥提取 给定一个用户的身份ID，PKG计算该用户的私钥SID=sQID并把此值安全地发送给该用户，其中 QID=H1（ID）为该用户的公钥。在这里我们设发送者的身份为IDA，公钥为QA，私钥为SA，接收 者的身份为IDB，公钥为QB，私钥为SB。 3．签密 对于消息m，发送者执行以下步骤： ① 随机选择。 ② 计算和。 ③ 计算和。 对消息m的签密密文为（c, r, S）。 4．解签密 当收到签密密文（c, r, S）时，接收者执行以下步骤： ① 计算。 ② 计算。 ③ 计算。 ④ 当且仅当r=H3（c, k1）成立时接受该密文。
相关难问题
（1）计算性Diffie-Hellman问题（Computational Diffie-Hellman Problem, CDHP）给定（P, aP, bP），计算abP∈G1，这里是未知 的整数。 （2）判定性Diffie-Hellman问题（Decisional Diffie-Hellman Problem, DDHP）给定（P, aP, bP, cP），判断c = ab mod q是否成立，这里 是未知的整数。如果（P, aP, bP, cP）满足这个条件，我们称它为一 个“Diffie-Hellman元组”。 （3）双线性Diffie-Hellman问题（Bilinear Diffie-Hellman Problem, BDHP）给定（P, aP, bP, cP），计算，这里是未知的整数。 （4）判定性双线性Diffie-Hellman问题（Decisional Bilinear DiffieHellman Problem, DBDHP）给定（P, aP, bP, cP）和h∈G2，判断 是否成立，这里是未知的整数。 容易看出，在G1中的DDHP是容易的。已知（P, aP, bP, cP），判断 c = ab mod q是否成立等价与判断下式是否成立：
基于身份的密码体制研究及保密系统实现
桂林电子科技大学
及保密系统实现
（英文） Research on Identity-based Cryptography and Implementation
of Secure Communication System
研 究 生 研 究 生
学 姓
I
万方数据
Abstract
Abstract
Identity-based cryptography is an emerging and developing public key cryptosystem. Compared with the traditional public key cryptosystem based on digital certificate, identity-based cryptography can ensure the security of information exchange without the two sides’ key- exchange and third party’s prov iding certifica tion services. What’s more, identity-based cryptography mainly based on the elliptic curve theory and bilinear pairing theory. In this paper, identity-based cryptography application as the research content, with security, fast, efficient, and low communication bandwidth requirement network secure communication systems as the design goal, studying selection of elliptic curve and bilinear pairing, studying construction and implementation of Encryption algorithm and signature algorithm, studying design and Analysis of mutual authenticated protocol. Related research has a certain reference value to speed up the application process of the system based on identity based cryptography. The main work and research results are summarized as follows: 1. We studied how to ensure parameters of elliptic curve according to the specific performance requirements. With fast and security performance requirements, we ensure parameters of elliptic curve, order of the group and selection of bilinear pairing, and reaching a set of elliptic curve parameters which are suitable for the performance of the system. 2. Taking this paper’s parameters of elliptic curve as input, we completed the construction and implementation of Encryption algorithm and signature algorithm, then an analytic comparison is made between two kinds of encryption algorithm and signature algorithm in both their security, cost and communication bandwidth, and selected the appropriate algorithm for the performance of the system. 3. A challenge-response mutual authenticated protocol based on IBC is proposed. We implemented our protocol with this paper’s encryption algorithm and signature algorithm, and particularly discussed the security of our protocol. Then an analytic comparison is made between our protocol and traditional challenge-response mutual authenticated protocol based on digital certificate in communication bandwidth cost, calculating cost and System complexity. 4. With design and development of an enterprise network secure communication systems, we implemented the communication systems based on IBC with our theory,
基于身份的密码体制在空管信息安全中的应用
基于身份的密码体制在空管信息安全中的应用随着科技的飞速发展，航空管制系统在保障飞行安全和提高空中交通效率方面发挥着越来越重要的作用。
空管信息系统的安全性问题也成为了正在面临的挑战。
在这样的情况下，如何保障空管系统的信息安全就显得非常关键。
而基于身份的密码体制正是一种能够有效提升空管信息安全的技术手段。
一、基于身份的密码体制简介基于身份的密码体制（Identity-based cryptography）是一种基于用户身份信息生成密钥对的密码体制。
通常而言，传统的公钥密码学需要使用证书颁发机构（CA）来进行身份验证，而基于身份的密码体制则使用了用户的身份信息作为公钥的一部分，从而避免了依赖CA的问题。
这种密码体制的独特性使得其在信息安全领域有着广泛的应用前景。
1. 加强身份验证空管系统中涉及数量庞大的用户和设备，如飞行员、地面人员、航空公司等，在信息交流和数据传输中，确保每一个用户的身份都是合法的是至关重要的。
传统的身份验证方法可能存在着漏洞，例如密码被盗用、证书伪造等问题。
而基于身份的密码体制通过使用用户的身份信息直接生成公钥，能够有效加强对用户身份的验证，提升系统的安全性。
2. 保障通信安全在空管系统中，通信的安全性直接关系到航空安全和信息泄露问题。
基于身份的密码体制可以用于数据的加密和解密，保障通信内容的机密性，防止数据被黑客攻击和窃取。
而传统的加密方法可能会面临证书失效、私钥泄露等问题，基于身份的密码体制能够有效解决这些问题，提升通信安全性。
3. 管理密钥密钥管理是保障信息安全的重要环节，而基于身份的密码体制的密钥管理相对来说更加简单和高效。
由于基于身份的密码体制使用了用户的身份信息来生成密钥对，因此不再需要传统的公钥证书颁发机构来进行密钥管理，这样能够减少了密钥管理的复杂性和成本。
4. 防范身份盗用虽然基于身份的密码体制在空管信息安全中有着广泛的应用前景，但也面临着一些挑战。
1. 系统性能问题基于身份的密码体制在加密和解密过程中会涉及到对用户身份信息的计算和处理，而这些运算可能会对系统的性能产生一定的影响。
代密码学第十一讲：基于身份的密码体制
IBC是一种非对称密码体系，与以往公钥密 码系统的不同在于任意的字符串可以作为用 户的公钥，例如每个人的身份标识，email 地址，电话号码等。 不需要CA系统将用户的身份和用户的公钥 绑定。
5
基于身份的密码体制
使用公钥加密邮件 “alice@”
是否可以像PKI系统， 由用户自己生成私钥？ 基于IBC的安全电子邮件系统
安全anklin IBE Scheme
初始化 (t)
用 t 生成一个素数 q 生成阶为q的循环群 G1, G2, 及一个双线性映射e: G1×G1 → G2 任意选取一个生成元 g∈G1 选取一个随机数 s∈Zq* 令 P= sg 选取两个密码学hash函数: H1:{0,1}* →G1* 和 H2:G2 → {0,1}n
3
本讲主要内容
基于身份的密码系统（IBC）的提出 基于身份的加密体制（IBE）的定义
Boneh-Franklin IBE方案 Shamir IBS方案
基于身份的签名体制（IBS）的定义
基于身份的密钥协商（IBKA）的定义
Scott IBS方案
IBC的应用 公开问题
4
基于身份的密码体制
CA/PKG
master-key
6
基于身份的密码体制
私钥生成（PKG） 系统的PKG中心拥有一对主密钥（master key），它公布主密钥中的公钥，自己保存 私钥； PKG中心输入自己的私钥和用户的公钥，得到 用户的公钥，并安全传回给用户； 用户输入这个私钥和PKG中心的公钥，检查收 到的私钥是否正确。
加密 (M)
基于身份的密码体制在空管信息安全中的应用
基于身份的密码体制在空管信息安全中的应用随着信息技术的发展，空中交通管制系统的安全问题日益引人注目。
为了保障空管系统的安全，采用了多种安全技术，其中基于身份的密码体制是一种重要的安全技术，能够有效防止未经授权的用户访问系统资源，保护数据的机密性和完整性。
本文将探讨基于身份的密码体制在空管信息安全中的应用。
1. 基于身份的密码体制的概念身份是指用户的个人信息，如用户名、密码、指纹、证书等。
基于身份的密码体制是一种基于用户身份进行认证授权的密码体制。
它通过验证用户身份的合法性来决定用户是否有权访问系统中的资源或服务，从而控制用户的访问权限。
在空管系统中，应用基于身份的密码体制能够有效地保护系统安全，提高系统可靠性和稳定性。
（1）用户身份认证空管系统包含众多用户，如空管人员、航空公司工作人员、机场管理人员等。
为了保障系统安全，必须对用户身份进行认证授权。
基于身份的密码体制通过密码认证、公钥认证、指纹认证等方式对用户身份进行验证，确保用户的合法性。
只有通过身份认证的用户才能访问系统资源或服务，从而避免未经授权的用户对系统资源的访问。
（2）授权管理基于身份的密码体制能够实现对用户的权限控制。
管理员可以根据用户的身份确定用户的权限范围，从而控制用户对系统资源的访问权限。
多级授权模式可以实现精细化的控制，只有经过合法授权的用户才能访问敏感数据和系统资源，有效提高了系统的安全性。
（3）追踪管理基于身份的密码体制可实现对用户操作的追踪管理，能够记录用户的操作行为，及时发现异常情况。
例如，当某一用户进行了异常操作时，管理员可以通过追踪管理及时发现并进行应对，从而有效提高了系统的安全性和稳定性。
（4）安全审计基于身份的密码体制可实现安全审计，对系统进行全面的安全控制和监督。
安全审计是指对系统操作进行记录、分析和审查，发现系统安全漏洞并提供完善的安全防护措施。
安全审计是一种综合性的安全管理手段，可以对系统的安全性进行定量评估，为系统的进一步优化提供数据支持。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
基于身份的加密体制
1984年以色列科学家Shamir提出了基于身份的密 码系统的概念（IBC）。 2001年，D. Boneh和M. Franklin , R. Sakai, K. Ohgishi 和 M. Kasahara利用椭圆曲线上的双线性 对设计了基于身份的加密算法。 2001年C. Cocks利用平方剩余难题设计了基于身 份的加密算法。 D. Boneh和M. Franklin提出的IBC (BF-IBC)的安全 性可以证明并且有较好的效率，所以引起了极大 的反响。
21
Shamir IBS Scheme
效率 签名和验证分别需要 2 integer exponentiations, 1 integer multiplication and 1 hash operation. 安全性：分解因子问题困难Integer Factorization Problem (IFP).
Boneh和Franklin的团队的努力, IBE 被应用 于 Debian GNU/Linux.
source code is available at http : ///ibe/download.html
Shamus Software 也开发了包含 BF-IBE 的 密码，称为 “MIRACL”24
Scott IB Key Agreement
密钥协商: 1. A 选取一个随机数 a < r, 计算 TA = e(sA,QB)^a; 把 TA发送给 B. 2. B选取一个随机数 b < r,计算 TB = e(sB,QA)^b; 把 TB发送给 A. 3. A 计算 KAB = TB^a，同样地，B计算KBA = TA^b 如果A和B正确执行协议，他们将计算出共享的密钥： KAB = KBA = e(QA,QB)^{sab}
19
验证（ Verify ）
Shamir IBS Scheme
Shamir提出了一个采用RSA算法的IBS算法。 初始化: 1. 选取两个大素数p，q，计算它们的乘积n；选 取与Φ(n)互素的整数 e ; 选取一个单向函数h. 参数: n, e, h； 主密钥: n 的因子. 提取私钥: 给定用户的 ID, PKG计算用户的私钥 g ，满足 g^e =ID mod n.
M
27
Scott IB Key Agreement
A e(g,QB)sma e(sA,QB)a B
e(sB,QA)b
e(P,QB)m
M发送其它值 是否可行？
e(QA,QB)asm
M
28
Scott IB Key Agreement
A QA,P sA 求e(sA,QB) QA,QB,P B QB,P sB 求e(sB,QA) 求e(QA,QB)s
14
Boneh-Franklin IBE Scheme
初始化(t)
M = {0,1}n C = G1* × {0,1}n
params = q, G1, G2, e, n, g, P, H1, H2 master-key = s
私钥生成(ID)
dID=s H1(ID)
15
Boneh-Franklin IBE Scheme
30
一轮通信的3方密钥协商协议
多方密钥协商 1轮3方密钥协商: A: 发送 aQ，计算e(bQ,cQ)^a； B: 发送 bQ，计算e(aQ,cQ)^b； C: 发送 cQ，计算e(aQ,bQ)^c； 共享密钥：e(Q,Q)^{abc}
猜想：若存在n次线性对，则存在1轮n方密钥协商
31
IBC的应用
身份鉴别的定义 口令认证协议 挑战应答协议 对身份识别协议的攻击和对策
4
本讲主要内容
基于身份的密码系统（IBC）的提出 基于身份的加密体制（IBE）的定义
Boneh-Franklin IBE方案 Shamir IBS方案
基于身份的签名体制（IBS）的定义
基于身份的密钥协商（IBKA）的定义
9
基于身份的加密体制
初始化
输入: 安全参数 t 输出: 系统参数params和主密钥master-key
提取私钥
输入: 系统参数params和主密钥master-key 用户身份 ID∈{0,1}* 输出: 用户私钥dID
10
基于身份的加密体制
加密
输入: 系统参数params,明文M∈M， 明文接收者公钥（身份）ID∈{0,1}*, 输出: 密文C 输入: 系统参数params,密文C ∈C ，接收者私 钥dID, 输出: 明文M
11
解密
双线性映射
e : G1× G1 → G2
G1 和 G2 是阶为p的循环群
任给 x, y ∈ G1 和任意整数 a, b ∈ Zp e(ax,by) = e(x,y)ab
双线性映射
非退化性（Non-Degenerate）
存在 x,y ∈ G1 使得 e(x,y) ≠ 1G2
33
IBC的应用
IEEE P1363.3的基于标识的密码技术工作组正在 进行相关算法的标准化工作 。 ISO/IEC已经标准化了两个基于身份的签名算法。 2007年，国家密码局组织了国家标识密码体系IBC 标准规范( Identity-Based Cryptograph)的编写和 评审工作。由五位院士和来自党政军、科研院所 的密码专家组成了评审组，对该标准规范在安全 性、可靠性、实用性和创新性等方面进行了多次 严格审查, 2007年12月16日国家IBC标准正式通过 了评审。
Stanford 和Shamus图书馆开发使用 C/C++. 似乎还没有Java implementation of IBE
32
IBC的应用
现实应用中，Voltage Security 开发了包含 IBE的 email 系统，它为Outlook, pine, hotmail, and Yahoo提供插件. Hewlett Packard Lab (布里斯托尔Bristol,UK) 的研究员开发健康保健信息系统使用了IBE 系统.
23
密钥协商（ Key Agreement ）
Scott IB Key Agreement
（基于Weil对 和Tate 对） 初始化: PKG 选取一个满足 p = 3 mod 4且 p + 1=c*r， 其中c, r亦为素数；选取一个将0-1数据映射到椭 圆曲线上点的hash函数H : {0, 1}∗ → G1.；选取 一个随机数 s ∈ Fq 作为主密钥. params: <G1,G2, e, P, q,H>； master-key: s 提取私钥: 设用户 A 的身份是 IDA, PKG 计算他的私钥 QA = H(IDA).；SA = sQA.
是否可以像PKI系统， 由用户自己生成私钥？ 基于IBC的安全电子邮件系统
CA/PKG
master-key
7
基于身份的密码体制
私钥生成（PKG） 系统的PKG中心拥有一对主密钥（master key），它公布主密钥中的公钥，自己保存 私钥； PKG中心输入自己的私钥和用户的公钥，得到 用户的公钥，并安全传回给用户； 用户输入这个私钥和PKG中心的公钥，检查收 到的私钥是否正确。
22
基于身份的密钥协商体制
初始化（Setup）
输入: 安全参数 t 输出: 系统参数params和主密钥master-key
提取私钥（ Extract ）
输入: 系统参数params和主密钥master-key 用户身份 ID∈{0,1}* 输出: 用户私钥dID 输入: 系统参数params和用户私钥dID 输出：会话密钥K
《现代密码学》第十一章
基于身份的密码体制
1
精品课程网站测试
用户名：student1,…,student9 密码111111
2
作业
5月31日之前，作业提交 作业提交名单查询 6月10日之前，作业补交，之后提交作业不 再记录
3
上节主要内容
20
Shamir IBS Scheme
签名: A 用私钥 g 签署消息 m: 1. 选取随机整数 r，计算t = r^e mod n 2. 计算s = g*r^h(t,m) mod n Signature: σ = <s, t>∈ Zn × Zn. 验证: 验证者收到签名 σ = <s’, t’> ，消息m’和签名者 的公钥(身份ID),验证下式是否成立 s’^e= ID*t’ ^h(t’,m’) mod n.
是否存在 中间人攻击
25
Scott IB Key Agreement
A e(sA,QB)a B e(sB,QA)b
e(QA,QB)abs
e(QA,QB)abs
26
Scott IB Key Agreement
A e(QA,QB)ma e(sA,QB)a B
e(sB,QA)b
e(QA,QB)m
e(QA,QB)asm
加密 (M)
选取随机数 r∈Zq* R=rg, M⊕H2(e(H1(ID),P)r)
解密(C=(U, V))
V ⊕ H2(e(dID,U))
正确性证明 H2(e(dID,U)) =H2(e(sH1(ID), rg) )= H2(e(H1(ID), g)sr =H2(e(H1(ID), sg)r )= H2(e(H1(ID),P)r)