二进制乘法器的VHDL设计
VHDL的乘法器设计——数字电路课程设计

cout=>c4,s=>s4(1));
------------------------------last u12:full_adder port map (a=>d4(1),b=>d4(2),cin=>d4(3),
【第二章】:设计思路及方案 算法结构(无符号)
由上图可见,乘法的运算最终是加法的运算,两个 4BIT 输入,输出为 7BIT。 模块一、半加器:单比特输入相加,
模块二、全加器:由两个半加器组成,有一个进位输入,
模块三、进位保留加法器:
3
最终程序结构图
流水设计的原理:在前向割集上加入四级流水
图一 图二
elsif clk'event and clk='1' then
--------------------------------------first d1(1)<= x(1); d1(2)<= x(2); d1(3)<= x(3);
7
d1(4)<= x(4); d1(5)<= x(5); d1(6)<= x(6); d1(7)<=c1(1) ; d1(8)<=s1(1); d1(9)<= x(9); d1(10)<=x(10); d1(11)<=c1(2); d1(12)<=s1(2); d1(13)<=x(13); d1(14)<=c1(3) ; d1(15)<=s1(3) ; d1(16)<=x(16);
EDA实验--8位二进制乘法电路

EDA数字系统设计实验——8位二进制乘法电路学院:电子工程学院学号:0210****姓名:***8位二进制乘法电路1.选题目的:通过八位二进制乘法器设计实验,进一步熟悉VHDL语言的电路设计,及数字电路的基本知识,为以后进一步在数字电路学习上奠定基础。
2.设计要求8位二进制乘法采用移位相加的方法。
即用乘数的各位数码,从低位开始依次与被乘数相乘,每相乘一次得到的积称为部分积,将第一次(由乘数最低位与被乘数相乘)得到的部分积右移一位并与第二次得到的部分积相加,将加得的和右移一位再与第三次得到的部分积相加,再将相加的结果右移一位与第四次得到的部分积相加。
直到所有的部分积都被加过一次。
例如:被乘数(M7M6M5M4M3M2M1M0)和乘数(N7N6N5N4N3N2N1N0)分别为11010101和10010011,其计算过程如下:1 1 0 1 0 1 0 1× 1 0 0 1 0 0 1 11 1 0 1 0 1 0 1 N0与被乘数相乘的部分积,部分积右移一位1 1 0 1 0 1 0 1 N1与被乘数相乘的部分积+ 1 1 0 1 0 1 0 11 0 0 1 1 1 1 1 1 11 0 0 1 1 1 1 1 1 1 两个部分积之和,部分积之和右移一位+ 0 0 0 0 0 0 0 0 N2与被乘数相乘的部分积0 1 0 0 1 1 1 1 1 1 10 1 0 0 1 1 1 1 1 1 1 与前面部分积之和相加,部分积之和右移一+ 0 0 0 0 0 0 0 0 N4与被乘数相乘的部分积· · ·· · · N7与被乘数相乘的部分积+ 1 1 0 1 0 1 0 11 1 1 1 0 1 0 0 1 0 0 1 1 1 1 与前面部分积之和相加0 1 1 1 1 0 1 0 0 1 0 0 1 1 1 右移一位得到最后的积为了实现硬件乘法器,根据上面的乘法的计算过程可以得出3点:一是只对两个二进制数进行相加操作,并用寄存器不断累加部分积;而是将累加的部分积左移(复制的被乘数不移动);三是乘数的对应位若为0时,对累加的部分积不产生影响(不操作)。
vhdl 四输入表决器 二位二进制乘法器 一位二进制全减器等源代码及仿真波形

将8421BCD转换为余3码源代码:Library ieee;Use ieee.std_logic_1164.all;Entity bcd isPort(a:in std_logic_vector(3 downto 0);y:out std_logic_vector(3 downto 0));End;Architecture rtl of bcd isBeginProcess(a)BeginCase a isWhen"0000"=>y<="0011";When"0001"=>y<="0100";When"0010"=>y<="0101";When"0011"=>y<="0110";When"0100"=>y<="0111";When"0101"=>y<="1000";When"0110"=>y<="1001";When"0111"=>y<="1010";When"1000"=>y<="1011";When"1001"=>y<="1100";When others=>y<="ZZZZ";End case;End process;End;仿真图形:(仿真结果均有延时,大约20ns)四输入表决器源代码:Library ieee;Use ieee.std_logic_1164.all;Entity bjq isPort(i:in std_logic_vector(3 downto 0);f:out std_logic);End;Architecture nm2 of bjq isBeginProcess(i)Begincase i isWhen"0000"=>f<='0';When"0001"=>f<='0';When"0010"=>f<='0';When"0011"=>f<='0';When"0100"=>f<='0';When"0101"=>f<='0';When"0110"=>f<='0';When"0111"=>f<='1';When"1000"=>f<='0';When"1001"=>f<='0';When"1010"=>f<='0';When"1011"=>f<='1';When"1100"=>f<='0';When"1101"=>f<='1';When"1110"=>f<='1';When"1111"=>f<='1';When others=>f<='Z';End case;End process;End;仿真图形:2位二进制相乘电路源代码:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity multi isport(A,B:in std_logic_vector(1 downto 0);F:out std_logic_vector(3 downto 0));end;architecture bhv of multi isbeginprocess(A,B)beginif(A="01" and B="01" )thenF<="0001";elsif(A="01" and B="10")thenF<="0010";elsif(A="01" and B="11")thenF<="0011";elsif(A="10" and B="01")thenF<="0010";elsif(A="10" and B="10")thenF<="0100";elsif(A="10" and B="11")thenF<="0110";elsif(A="11" and B="01")thenF<="0011";elsif(A="11" and B="10")thenF<="0110";elsif(A="11" and B="11")thenF<="1001";elseF<="0000";end if;end process;end;仿真图形:一位二进制全减器源代码:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity subtracter isport(A,B,Ci:in std_logic;F,Co:out std_logic);end;architecture bhv of subtracter isbeginprocess(A,B,Ci)beginif(A='0' and B='0' and Ci='0')thenF<='0';Co<='0';elsif(A='0' and B='0' and Ci='1')thenF<='1';Co<='1';elsif(A='0' and B='1' and Ci='0')thenF<='1';Co<='1';elsif(A='0' and B='1' and Ci='1')thenF<='0';Co<='1';elsif(A='1' and B='0' and Ci='0')thenF<='1';Co<='0';elsif(A='1' and B='0' and Ci='1')thenF<='0';Co<='0';elsif(A='1' and B='1' and Ci='0')thenF<='0';Co<='0';elseF<='1';Co<='1';end if;end process;end;仿真图形:开关控制电路源代码:Library ieee;Use ieee.std_logic_1164.all;Entity switch_control isPort(a,b,c:in std_logic;y:out std_logic);End;Architecture nm5 of switch_control isBeginProcess(a,b,c);V ariable comb:std_logic_vector(2 downto 0);BeginComb:=a&b&c;Case comb isWhen"000"=>y<='0';When"001"=>y<='1';When"011"=>y<='0';When"010"=>y<='1';When"110"=>y<='0';When"111"=>y<='1';When"101"=>y<='0';When"100"=>y<='1';When others=>y<='X';End case;End process;End;仿真图形:。
基于VHDL的乘法器的设计与对比

基于VHDL的乘法器的设计与对比赵杰【摘要】Multiplier is the core of digital signal calculation. It is also the key component of data processing and microprocessor. 8-bits multiplier is taken as the example. The simple parallel multiplier, the shift summation multiplier and the addition tree multiplier were introduced. They were described using VHDL. The three kinds of multipliers are simulated respectively through the Quartus II platform. Their simulation results were given. At the end of paper, the three multipliers were compared and discussed in the resource occupancy and operation speed.%在数字系统中,乘法器是进行数字信号运算的核心运算单元,同时也是微处理器中进行数据处理的关键部分。
以8位乘法器为例,根据简单并行乘法器、加法器树乘法器和移位相加乘法器的基本原理,利用VHDL分别进行描述和实现。
对三种乘法器分别通过QuartusⅡ软件平台进行仿真,再做进一步比较和讨论。
结果表明,三种乘法器在运行速度和资源占用上各有利弊,实践中可根据设计要求和硬件条件选择使用。
【期刊名称】《商洛学院学报》【年(卷),期】2015(000)006【总页数】4页(P3-6)【关键词】乘法器;移位相加;加法器树;仿真【作者】赵杰【作者单位】商洛学院电子信息与电气工程学院,陕西商洛 726000【正文语种】中文【中图分类】TP332.22乘法器在数字信号处理过程中发挥着重要的作用,在语音、图像处理、通信等领域中扮演着举足轻重的角色,它的运算速度与信号处理和整体效率的性能直接相关,并且在很大程度上左右着系统功能[1-3]。
基于VHDL语言的乘法器的设计

利用VHDL設計乘法器Implement of Multiplier by Using VHDL許地申Dih-Shen Hsu中華技術學院電機系副教授Associate ProfessorDepartment of Electrical EngineeringChina Institute of Technology摘 要在計算機結構裡加,減,乘,除是常被用到的運算,本文提出以非常高速積體電路硬體描述語言(VHDL)來描述硬體,說明如何將兩個運算元作相乘的運算。
我們首先以無號數整數做乘法運算來說明其原理,設計其電路結構。
其實在VHDL 程式中,我們更可以載入STD_LOGIC_ARITH與STD_LOGIC_UNSIGNED元件盒之後,直接進行乘法運算,既簡單又容易擴充。
最後,我們將以4-bit X 4-bit 的例子來做電路描述、電路合成、電路模擬並以七段顯示器將其結果顯示出來。
關鍵字:非常高速積體電路硬體描述語言、電路描述、電路合成、電路模擬AbstractWe have known operation that perform addition, subtraction, multiplication, and division. In this paper we are presented primarily to describe hardware using by VHDL. We can explain how multiplication may be performed for two operand. Multiplication of unsigned numbers illustrates the main issues involved in the design of multiplier circuit. In fact, after the STD_LOGIC_ARITH and STD_LOGIC_UNSIGNED packages were added to the VHDL program, it became not only simple but also easy to extended. Next, consider a 4 x 4 example to circuit description, circuit synthesis, and circuit simulation by using VHDL. Finally, this approach can also be displayed by 7-segment.Keyword : VHDL , circuit description , circuit synthesis, circuit simulation壹.簡介VHDL是Very High Speed Integrated Circuit Hardware Description Language 的英文縮寫。
两位乘法 verilog hdl

一、介绍Verilog HDL(硬件描述语言)是一种用于建模电子系统的硬件描述语言,常用于数字电路设计和验证。
在Verilog HDL中,实现两位乘法器是一个常见的需求,本文将介绍如何使用Verilog HDL设计和实现一个两位乘法器。
二、两位乘法器的原理两位乘法器是用于计算两个二进制数的乘积的电路。
对于两个n位的二进制数A和B,它们的乘积可以使用shift-and-add算法来计算。
具体来说,可以将A拆分为A[0]和A[1],B拆分为B[0]和B[1],然后计算A[0]*B[0]、A[0]*B[1]、A[1]*B[0]和A[1]*B[1],最后将它们的和相加即可得到A*B的结果。
三、Verilog HDL的实现使用Verilog HDL可以轻松地实现两位乘法器。
以下是一个简单的Verilog HDL代码实现:```verilogmodule two_bit_multiplier(input [1:0] A, // 两位输入input [1:0] B,output [3:0] result // 四位输出);reg [3:0] temp; // 临时变量用于保存计算的结果always (A or B) begintemp[0] = A[0] B[0]; // 计算A[0]*B[0]temp[1] = A[0] B[1]; // 计算A[0]*B[1]temp[2] = A[1] B[0]; // 计算A[1]*B[0]temp[3] = A[1] B[1]; // 计算A[1]*B[1]result = {temp[3],temp[2]+temp[1],temp[0]}; // 将计算结果相加并输出endendmodule```上述Verilog HDL代码描述了一个两位乘法器模块。
模块有两个2位输入A和B,以及一个4位输出result。
通过使用always块来计算A 和B的乘积,并将结果存储在temp变量中;将temp中的值相加并输出到result中。
第3章二进制乘法器的VHDL设计
0 00 0 0 00 0
1011
0 01 0 1 10 0
+
1011
0 10 1 1 00 0
r 1 0 0 0 1 11 1 r 1 0 0 0 1 1 1 1
★二进制数相乘可以用移位相加计算
3.5 乘法器及其VHDL表述
3.5.3 移位相加型乘法器的VHDL表述方法--(11)例3-13
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; use ieee.std_logic_arith.all; entity mult4b is
3.5 乘法器及其VHDL表述
3.5.1 统计位矢中含‘1’个数的电路模块设计⑩【例3-12】
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
entity cntc is
port(din :in std_logic_vector(7 downto 0);
❖左移,SRA算术右移,ROL逻辑循环左移 ,ROR逻辑循环右移
3.5 乘法器及其VHDL表述
例3-13仿真结果
UNSIGNED
由INTEGER, UNSDGNED,
SIGNED 转换为
STD_LOGIC_VECTOR
❖2、generic参数定义语句
类属GENERIC常用来定义实体端口大小,数据宽度, 元件例化数目等。一般在简单的设计中不常用。
3.5 乘法器及其VHDL表述
❖3、整数数据类型integer
s:integer :=4; SIGNAL C :INTEGER RANGE 1 TO 7; 实际上一个整数是由32位二进制码表示的带符 号数的范围。
9X9乘法表VHDL

9*9乘法器的VHDL的设计1 设计任务制作一个9*9乘法器2 设计说明输入两个四位二进制信号a,b分别作为被乘数和乘数,以8421bcd码编号,输入一个一位信号oc作为控制信号;输出两个四位二进制信号c,d分别作为结果的十位和个位,以8421bcd码编号。
3 设计结果3.1 原理图图1 原理图3.2 信号表a:被乘数,用4位二进制8421bcd码表示;b:乘数,用4位二进制8421bcd码表示;oc:控制信号;c:结果的十位,用4位二进制8421bcd码表示;d:结果的个位,用4位二进制8421bcd码表示;图2 信号表3.3仿真结果图3 oc、a、b分别为0、2、8和0、4、3时结果图4 oc、a、b分别为1、2、8和1、4、3时结果图5 oc、a、b分别为0、10、8和0、4、11时结果3.4 电路图图6 原理图3.5 程序清单LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY mul9 ISPORT (oc: IN std_logic;a,b: IN std_logic_vector (3 downto 0);c,d: OUT std_logic_vector(3 downto 0));END;ARCHITECTURE one OF mul9 ISBEGINPROCESS(a,b)BEGINIF(oc = '1') THENIF(a = "0001") THENCASE b ISWHEN "0001" =>c <= "0000"; d <= "0001"; WHEN "0010" =>c <= "0000"; d <= "0010";WHEN "0011" =>c <= "0000"; d <= "0011"; WHEN "0100" =>c <= "0000"; d <= "0100";WHEN "0101" =>c <= "0000"; d <= "0101"; WHEN "0110" =>c <= "0000"; d <= "0110";WHEN "0111" =>c <= "0000"; d <= "0111"; WHEN "1000" =>c <= "0000"; d <= "1000";WHEN "1001" =>c <= "0000"; d <= "1001"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;CASE b ISWHEN "0001" =>c <= "0000"; d <= "0010"; WHEN "0010" =>c <= "0000"; d <= "0100";WHEN "0011" =>c <= "0000"; d <= "0101"; WHEN "0100" =>c <= "0000"; d <= "1000";WHEN "0101" =>c <= "0001"; d <= "0000"; WHEN "0110" =>c <= "0001"; d <= "0010";WHEN "0111" =>c <= "0001"; d <= "0100"; WHEN "1000" =>c <= "0001"; d <= "0110";WHEN "1001" =>c <= "0001"; d <= "1000"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;ELSIF(a = "0011") THENCASE b ISWHEN "0001" =>c <= "0000"; d <= "0101"; WHEN "0010" =>c <= "0000"; d <= "0110";WHEN "0011" =>c <= "0000"; d <= "1001"; WHEN "0100" =>c <= "0001"; d <= "0010";WHEN "0101" =>c <= "0001"; d <= "0101"; WHEN "0110" =>c <= "0001"; d <= "1000";WHEN "0111" =>c <= "0010"; d <= "0001"; WHEN "1000" =>c <= "0010"; d <= "0100";WHEN "1001" =>c <= "0010"; d <= "0111"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;CASE b ISWHEN "0001" =>c <= "0000"; d <= "0100"; WHEN "0010" =>c <= "0000"; d <= "1000";WHEN "0011" =>c <= "0001"; d <= "0010"; WHEN "0100" =>c <= "0001"; d <= "0110";WHEN "0101" =>c <= "0010"; d <= "0000"; WHEN "0110" =>c <= "0010"; d <= "0100";WHEN "0111" =>c <= "0010"; d <= "1000"; WHEN "1000" =>c <= "0011"; d <= "0010";WHEN "1001" =>c <= "0011"; d <= "0101"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;ELSIF(a = "0101") THENCASE b ISWHEN "0001" =>c <= "0000"; d <= "0101"; WHEN "0010" =>c <= "0001"; d <= "0000";WHEN "0011" =>c <= "0001"; d <= "0101"; WHEN "0100" =>c <= "0010"; d <= "0000";WHEN "0101" =>c <= "0010"; d <= "0101"; WHEN "0110" =>c <= "0011"; d <= "0000";WHEN "0111" =>c <= "0011"; d <= "0101"; WHEN "1000" =>c <= "0100"; d <= "0000";WHEN "1001" =>c <= "0100"; d <= "0101"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;CASE b ISWHEN "0001" =>c <= "0000"; d <= "0110"; WHEN "0010" =>c <= "0001"; d <= "0010";WHEN "0011" =>c <= "0001"; d <= "1000"; WHEN "0100" =>c <= "0010"; d <= "0100";WHEN "0101" =>c <= "0011"; d <= "0000"; WHEN "0110" =>c <= "0011"; d <= "0110";WHEN "0111" =>c <= "0100"; d <= "0010"; WHEN "1000" =>c <= "0100"; d <= "1000";WHEN "1001" =>c <= "0101"; d <= "0100"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;ELSIF(a = "0111") THENCASE b ISWHEN "0001" =>c <= "0000"; d <= "0111"; WHEN "0010" =>c <= "0001"; d <= "0100";WHEN "0011" =>c <= "0010"; d <= "0001"; WHEN "0100" =>c <= "0010"; d <= "1000";WHEN "0101" =>c <= "0011"; d <= "0101"; WHEN "0110" =>c <= "0100"; d <= "0010";WHEN "0111" =>c <= "0100"; d <= "1001"; WHEN "1000" =>c <= "0101"; d <= "0110";WHEN "1001" =>c <= "0110"; d <= "0011"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;CASE b ISWHEN "0001" =>c <= "0000"; d <= "1000"; WHEN "0010" =>c <= "0001"; d <= "0110";WHEN "0011" =>c <= "0010"; d <= "0110"; WHEN "0100" =>c <= "0011"; d <= "0010";WHEN "0101" =>c <= "0100"; d <= "0000"; WHEN "0110" =>c <= "0100"; d <= "1000";WHEN "0111" =>c <= "0101"; d <= "0110"; WHEN "1000" =>c <= "0110"; d <= "0100";WHEN "1001" =>c <= "0111"; d <= "0010"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;ELSIF(a = "1001") THENCASE b ISWHEN "0001" =>c <= "0000"; d <= "1001"; WHEN "0010" =>c <= "0001"; d <= "1000";WHEN "0011" =>c <= "0010"; d <= "0111"; WHEN "0100" =>c <= "0010"; d <= "0110";WHEN "0101" =>c <= "0100"; d <= "0101"; WHEN "0110" =>c <= "0101"; d <= "0100";WHEN "0111" =>c <= "0101"; d <= "0110"; WHEN "1000" =>c <= "0111"; d <= "0010";WHEN "1001" =>c <= "1000"; d <= "0001"; WHEN OTHERS =>c <= "0000"; d <= "0000";END CASE;ELSEc <= "0000";d <= "0000";END IF;ELSE c <= "0000"; d <= "0000";END IF;END PROCESS;END one;4 实验总结通过这次课程设计,我进一步加深了对电子设计自动化的了解。
基于VHDL语言的组合乘法器设计与仿真

i ii 《现代电子技术》20 05 年第 18 期总第 20 9 期þ 集 成 电 路 ü基于 VH DL 语言的组合乘法器设计与仿真刘姝延1 , 吴 志2 , 丁 红1 , 马秋明1( 1. 烟台师范学院 物理与电子工程学 院 山东 烟台 26 40 25; 2 . 烟台师范学院 基建处 山东 烟台 26 40 25 )摘 要: 基于 V H DL 的数字系统设计具有设计技术 齐全、方法灵活、支持广泛等优点, 同时也是 E DA 技术的重要 组成 部分。
文章用 V H DL 语言设计了左移法和进位节省法实现的两种组 合乘法器, 通过功能仿真 , 对两种乘法器的性能进 行了 比较, 从而得知后者的传输延迟时间小, 即速度较快 。
通过设 计实例, 介绍了利用 VH D L 语言进行数字系统设计的方法。
关键词: V H D L ; 组合乘法器; 左移法; 进位节省法中图分类号: T N 7 9 文 献标识码: B 文章编号: 1 00 4 37 3X ( 2 00 5) 18 0 77 0 2Design an d Simulation of Combin a tion a l Mu l t ip l ier Based on VH DL LanguageL I U Sh u y a n 1 , WU Zh i 2 , D I N G H o n g 1 , MA Q i u m i n g 1( 1 . Scho o l o f P hy s i cs a nd Elect ro nic E ng ineer ing , Ya nt ai Nor m a l Un iver si t y, Yant ai, 2 64 02 5, Ch ina;2 . Dep ar tmen t of Basic Bu ilding , Ya nt ai Nor m a l Un iver si t y, Yan t ai, 2 64 02 5, Ch ina)Abs t r a ct : Dig i t a l s y s t e ms u s i n g V H D L h a s t h e adv a n t a ges of comp r eh e n s i v e d e s i gn t e ch n o l o g i e s , fl e xi b l e des i g n met ho d s an d w i dera ng e s u p p o r t , it ′s al s o an i m po r t ant comp o n e n t o f E D A . T he co m b i n a t i o n a l mul t i p l i er s t o us e t w o met h o d s of left sh i f t s an d car rys a ve ar e des i g n e d i n V H D L la ng u a ge , by fun c t i o n a l s i mu l a t i o n , comp a r in g t h e pecu l i a ri t y o f t wo m ul t i p i er s , fi n d t h e car ry s a ve mu l t i - pl i er ′s del a y s h o r t e r , s p e ed fa st er. T h r o u g h d e si g n ex a mp l es , t h i s p a per in t r od u c es t h e met h o d of di g it al s y s t e ms des i g n based o nV H D L .Ke yw o rd s : VH D L ; comb i n a t i o n a l m ul t i p l i er ; met h o d o f left sh i ft ; met h o d o f carr y s a ve1 引 言随着计算机技术和大规模集成电路技术的发展, 传统 的通过 逻辑图 和布尔方 程设计 硬件电路 的方法 已大大落 后于当今 技术的发展, 取而代之 的是硬件描 述语言 H D L 使 用通用逻辑元、器件的限制, 电路尺寸大为缩小, 保密 程度大为提高。
eda乘法器设计

实验四乘法器设计一、实验目的1、掌握利用移位相加方法实现乘法运算的基本原理;2、通过一个4×4的二进制乘法器的设计,学习利用VHDL语言来描述简单的算法,3、熟悉VHDL语言的变量数据对象在描述算法中的作用;二、实验原理实现乘法运算的算法很多,比较常见的有以下几种方法:移位相加、查询表、逻辑树等。
这里主要介绍移位相加的方法。
这种方法实现起来相对简单,目前大多数的单片机和微处理器都采用这种方法。
但是这种方法的最大缺点是速度慢,8位乘法需要8个时钟周期才能得到结果。
根据运算过程中左移或者右移对象的不同,采用移位相加实现乘法运算又有两种算法:(1)部分和固定、部分积左移法(算法1)(2)部分和右移、部分积固定法(算法2)无论是从用时方面还是占用硬件资源方面看,算法2都要优于算法1。
在算法2中,部分积各位是固定的,部分和逐步右移。
下面以4位乘法运算为例,说明其工作原理。
假设4位被乘数X为X3X2X1X0, 乘数Y为Y3Y2Y1Y0, 4×4位结果得到8位的乘积S,将它存放在一个9位累加寄存器中。
累加器初始值为全零,即“000000000”。
算法2的运算过程如下:(1)移出乘数的最低位Y0乘以被乘数X得到第1个部分积S0;(2)第1个部分积S0与累加器S中高4位相加,结果仍然存放在累加器中,即S<=S+S0; (3)将累加器中内容向右移1位,结果仍然存放在累加器中;(4)移出乘数的次低位Y1, 乘以被乘数X得到第2个部分积S0;(5)第2个部分积S0 再与累加器S中高4位相加,结果仍然存放在累加器中,即S<=S+S0;……如此反复直到乘数中所有的位都被移出,第4个部分和与累加器中的值相加后右移,得到的和就是乘积。
算法2的流程图如下图4.1所示:在本实验中将设计一个如下图4.2所示的4位乘法器,输入信号X和Y分别是4位乘数和被乘数Y,CLK为输入时钟信号,START 是乘法启动信号。
(VHDL)8位二进制乘法器电路程序

8位二进制乘法电路该乘法器是有由8位加法器构成的以时序方式设计的8位乘法器,采用逐项移位相加的方法来实现相乘。
用乘数的各位数码,从低位开始依次与被乘数相乘,每相乘一次得到的积称为部分积,将第一次(由乘数最低位与被乘数相乘)得到的部分积右移一位并与第二次得到的部分积相加,将加得的和右移一位再与第三次得到的部分积相加,再将相加的结果右移一位与第四次得到的部分积相加。
直到所有的部分积都被加过一次。
例如:被乘数(M7M6M5M4M3M2M1M0)和乘数(N7N6N5N4N3N2N1N0)分别为11010101和10010011,其计算过程如下:下面分解8位乘法器的层次结构,分为以下4个模块:①右移寄存器模块:这是一个8位右移寄存器,可将乘法运算中的被乘数加载于其中,同时进行乘法运算的移位操作。
②加法器模块:这是一个8位加法器,进行操作数的加法运算。
③1位乘法器模块:完成8位与1位的乘法运算。
④锁存器模块:这是一个16位锁存器,同时也是一个右移寄存器,在时钟信号的控制下完成输入数值的锁存与移位。
按照上述算法,可以得到下图所示之框图和简单流程图。
图中8位移位寄存器reg_8存放乘数a,从a的最低位开始,每次从reg_8中移出一位,送至1×8位乘法器multi_1中,同时将被乘数加至multi_1中,进行乘法运算,运算的结果再送至8位加法器adder_8中,同时取出16位移位寄存器reg_16的高8位与之进行相加,相加后结果即部分积存入reg_16中,进行移位后并保存。
这样经过8次对乘数a的移位操作,所以的部分积已全加至reg_16中,此时锁存器reg_16存放的值即所要求的积。
(1)8位移位寄存器reg_8的设计(A )电路框图(B8位移位寄存器是在时钟(r8_clk'event and r8_clk='1')信号作用下,当r8_load='1'时,将8位乘数加载进入;而当r8_load='0'时,对数据进行移位操作,同时定义一个信号reg8用来装载新数据及移位后的操作数,完成这些操作后,寄存器的最低位reg8(0)传送给r8_out 输出。
乘法器vhdl课程设计

乘法器vhdl课程设计一、课程目标知识目标:1. 理解乘法器的原理及其在数字信号处理中的应用。
2. 掌握VHDL语言的基本语法和结构,能够使用VHDL进行简单的程序编写。
3. 学习并掌握利用VHDL设计乘法器的方法,理解其位运算和结构设计。
技能目标:1. 能够运用所学知识,独立设计并实现一个简单的乘法器VHDL程序。
2. 培养学生利用电子设计自动化(EDA)工具进行代码编写、仿真和测试的能力。
3. 提高学生的问题分析能力,学会使用VHDL解决实际的数字电路设计问题。
情感态度价值观目标:1. 培养学生对于电子信息和数字电路设计的兴趣,激发学生创新精神和探索欲望。
2. 增强团队合作意识,通过小组讨论和协作,提高学生之间的沟通能力和协作解决问题的能力。
3. 强化学生的工程伦理观念,了解所学技术在国家经济发展和国防建设中的重要性,树立正确的价值观。
本课程针对高年级电子信息工程及相关专业学生设计,结合学生已具备的基础知识和课程性质,以实践性和应用性为导向,旨在通过具体的乘法器VHDL课程设计,将理论知识与实践技能相结合,提升学生解决实际工程问题的能力。
通过本课程的学习,学生应能够展示出上述具体的学习成果。
二、教学内容1. 乘法器原理回顾:包括乘法器的基本工作原理,不同类型的乘法器结构对比,以及乘法器在数字信号处理中的应用。
- 相关教材章节:第三章“数字电路基础”,第5节“算术逻辑单元”。
2. VHDL语言基础:VHDL的基本语法,数据类型,信号与变量,运算符,顺序与并行语句,进程,实体和架构等。
- 相关教材章节:第五章“硬件描述语言VHDL”,第1-3节。
3. 乘法器的VHDL设计方法:- 位运算乘法器设计原理与实现。
- 流水线乘法器设计原理与实现。
- 相关教材章节:第五章“硬件描述语言VHDL”,第4节“VHDL设计实例”;第六章“数字信号处理器的硬件实现”,第2节“乘法器的硬件实现”。
4. EDA工具的应用:利用EDA工具进行VHDL代码的编写、编译、仿真和测试。
EDA--八位二进制乘法器

EDA课设:选题名称:八位二进制乘法电路(一)设计要求:分拍输入两个八位二进制数字,并四个数码管显示当前输入数字的十进制形式,通过使能端的控制,分拍输出这两位二进制数字的乘积并通过四个数码管显示成十进制。
(二)基本算法:8位二进制乘法采用移位相加的方法。
即用乘数的各位数码,从低位开始依次与被乘数相乘,每相乘一次得到的积称为部分积,将第一次(由乘数最低位与被乘数相乘)得到的部分积右移一位并与第二次得到的部分积相加,将加得的和右移一位再与第三次得到的部分积相加,再将相加的结果右移一位与第四次得到的部分积相加。
直到所有的部分积都被加过一次。
按照这种算法,可以得到下图所示之框图和简单流程图。
图中Y寄存器存放被乘数M,B寄存器存放乘数N,A累加器存放部分积。
A和Y中的数据在加法器中相加后送入A中,而A和B相级联又构成了一个16bit的移位寄存器,当它工作于移位模式时,可以实现数据的右移。
由于乘数的每一位不是0就是1 ,对应的部分积不是0就是被乘数本身,所以实际作部分积相加这一步时,只要根据乘数的对应位判断:如该位为 1 ,则将累加器中的数据加上被乘数再移位;如该位为0时,就不加被乘数而直接移位。
运算时首先将累加器A 清零,并将被乘数M和乘数N分别存入寄存器Y和B,然后依据寄存器B中最右一位B0(数据N0)确定第一个部分积。
将此部分积送入A累加器以后,将A连同寄存器B右移一位,部分积的最低位被移进寄存器B的最左位,乘数的最低位N0被移出寄存器B,而乘数的次低位N1被移至寄存器B的B0位。
第二次仍然依据B0位的数据(N1)来确定第二个部分积,将部分积与累加器中的数据相加后右移一位,N1又被移出寄存器,数据N2被移到B0位置……这样,经过8次部分积相加位的操作,完成1次乘法运算,乘数N恰好被移出寄存器B,寄存器B中保存的就是运算积的低8位数据。
移位相加的次数应用一个计数器来控制,每移位一次,计数器计一个数。
当计数器计得8个数时,发出一个信号,使电路停止操作,并输出运算结果(流程图是按减法计数器设计的,也可使用加法计数器)。
利用VHDL设计乘法器

在计算机结构里加,减,乘,除是常被用到的运算,本文提出以非常高速积体电路硬体描述语言(VHDL)来描述硬体,说明如何将两个运算元作相乘的运算。
我们首先以无号数整数做乘法运算来说明其原理,设计其电路结构。
其实在VHDL 程式中,我们更可以载入STD_LOGIC_ARITH与STD_LOGIC_UNSIGNED元件盒之后,直接进行乘法运算,既简单又容易扩充。
最后,我们将以4-bit X 4-bit的例子来做电路描述、电路合成、电路模拟并以七段显示器将其结果显示出来。
关键字:非常高速积体电路硬体描述语言、电路描述、电路合成、电路模拟Abstract We have known operation that perform addition, subtraction, multiplication, and division. In this paper we are presented primarily to describe hardware using by VHDL. We can explain how multiplication may be performed for two operand. Multiplication of unsigned numbers illustrates the main issues involved in the design of multiplier circuit. In fact, after the STD_LOGIC_ARITH and STD_LOGIC_UNSIGNED packages were added to the VHDL program, it became not only simple but also easy to extended. Next, consider a 4 x 4 example to circuit description, circuit synthesis, and circuit simulation by using VHDL. Finally, this approach can also be displayed by 7-segment.Keyword : VHDL , circuit description , circuit synthesis, circuit simulation利用VHDL 设计乘法器一.简介VHDL是V ery High Speed Integrated Circuit Hardware Description Language 的英文缩写。
quartusII软件做4的位乘法器设计(vhdl语言)

quartusII软件做4的位乘法器设计(vhdl语⾔)⽤quartus II 软件设计4位乘法器1. 并⾏乘法的算法:下⾯根据乘法例题来分析这种算法,题中M4,M3,M2,M1是被乘数,⽤M表⽰。
N4,N3,N2,N1是乘数,⽤N表⽰2.乘法模块Library ieee;Use ieee.std_logic_1164.all;Use ieee.std_logic_unsigned.all;Entity and4a isPort(a:in std_logic_vector(3 downto 0);en:in std_logic;r:out std_logic_vector(3 downto 0));End and4a;Architecture behave of and4a isBeginProcess(en,a(3 downto 0))Beginr<=a;Elser<="0000";End if;End process;End behave;3.加法模块Library ieee;Use ieee.std_logic_1164.all;Entity ls283 isPort (o1,o2:in std_logic_vector(3 downto 0); res:out std_logic_vector(4 downto 0));Architecture behave of ls283 isBeginProcess(o1,o2)Beginres<=('0'&o1)+('0'&o2);End process;End behave;4.主程序Library ieee;Use ieee.std_logic_1164.all;Use ieee.std_logic_unsigned.all;Entity mul4p isPort (op1,op2:in std_logic_vector(3 downto 0);result:out std_logic_vector(7 downto 0));End mul4p;Architecture count of mul4p iscomponent and4a port (a:in std_logic_vector(3 downto 0); en:in std_logic;r:out std_logic_vector(3 downto 0)); End component; Component ls283 port (o1,o2:in std_logic_vector(3 downto 0); res:out std_logic_vector(4 downto 0)); End component; Signal sa:std_logic_vector(3 downto 0);Signal sb:std_logic_vector(4 downto 0);Signal sc:std_logic_vector(3 downto 0);Signal sd:std_logic_vector(4 downto 0);Signal se:std_logic_vector(3 downto 0);Signal sf:std_logic_vector(3 downto 0);Signal sg:std_logic_vector(3 downto 0);--signal tmp1:std_logic;Beginsg<=('0'&sf (3 downto 1));--tmp1<=op1(1);u0:and4a port map(a=>op2,en=>op1(1),r=>se);U1:and4a port map(a=>op2,en=>op1(3),r=>sa);U2:ls283 port map(o1=>sb(4 downto 1),o2=>sa,res=>result(7 downto 3)); U3:and4a port map(a=>op2,en=>op1(2),r=>sc);U4:ls283 port map(o1=>sc,o2=>sd(4 downto 1),res=>sb);u5:ls283 port map(o1=>sg,o2=>se,res=>sd);u6:and4a port map(a=>op2,en=>op1(0),r=>sf);result(0)<=sf(0);result(1)<=sd(0);result(2)<=sb(0);--result(7 downto 0)<="00000000";End count;5.仿真波形图6.引脚分配图7.硬件下载编程与硬件实现在实现硬件测试时,选择8个按键作为4个数据的输⼊信号,⽤8个LED灯作为运算结果数据输出指⽰,每4个数作为⼀个⼆进制数值,通过LED灯的亮灭来显⽰乘法的运算结果。
用VHDL语言描述和实现乘法累加器设计

设计应完成的功能要求:(1)乘法累加器的结构如下图所示,5位的被乘数X和5位的乘数Y输入后,暂存在寄存器5位的寄存器A和B中,寄存器A和B的输出首先相乘,得到10位乘积,该乘积通过选择信号sel的控制,可以和10位寄存器C的输出相加,相加结果保存在寄存器C中,实现乘法累加功能;也可以通过sel选择全零和乘积相加,实现乘法功能。
寄存器C的输出也是系统输出Z。
:用VHDL语言描述和实现乘法累加器设计(2)要求乘法器和加法器都采用电路描述,不采用算法描述。
(3)要求寄存器A,B,C具有异步清零功能,全部寄存器采用相同的时钟和清零信号。
(4)设计的最终输出是设计报告。
设计报告的内容要求:(1)设计报告的格式采用标准的深圳大学设计报告格式(2)设计报告应包括该电路的总体结构图和主要功能模块组成图;(3)设计报告应根据总体结构图,说明VHDL代码编写的设计思路和基本原理;(4)设计报告应完成该电路的VHDL代码设计;(5)设计报告应完成该电路的VHDL仿真分析。
一、实验目的用VHDL语言描述和实现乘法累加器设计二、实验内容和步骤一.总体结构图设计思路和原理:首先,寄存器A、B、C具有异步清零功能,rest在clk之前调用,当复位信号rest 为1时,寄存器A、B、C复位,当rest为0时,并且在它们同一时钟clk的上升沿到来时,输出将等于输入,起到了数据锁存功能。
同时,寄存器的输出Z既是整个结果的输出,也可以被内部引用,因此在定义Z的端口时,把端口类型定义为buffer。
5位的被乘数X和5位的乘数Y输入后,暂存在寄存器5位的寄存器A和B中,通过寄存器A、B的寄存,能够让不同时到达的数据X和Y能够在同一时钟的控制下同时参与运算,寄存器A和B的输出分别为x_temp和y_temp,他们首先相乘,得到10位乘积mul,该乘积通过选择信号sel的控制,当sel为1时,acc=z,即乘积mul可以和10位寄存器C的输出相加,相加结果保存在寄存器C中,实现乘法累加功能;当sel为0时,acc为全零,即选择全零和乘积相加,实现乘法功能。
VHDL加法器与乘法器
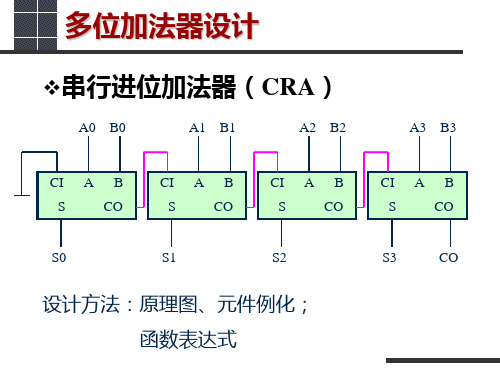
串行进位加法器( 串行进位加法器(CRA) )
A0 B0 A1 B1 A2 B2 A3 B3
CI S
A
B CO
CI S
A
B CO
CI S
A
B CO
CI S
A
B CO
S0
S1
S2
S3
CO
设计方法:原理图、元件例化; 函数表达式
多位加法器设计
选择进位加法器( 选择进位加法器(CSLA) )
移位相加乘法器
BEGIN IF ST = '1' THEN -REGA := "00000000" & A; REGB := B; RESULT <= (OTHERS => '0'); SOUT <= '0'; REGRES := (OTHERS => '0'); CNT := (OTHERS => '0'); ELSIF CLK'EVENT AND CLK='1' THEN -IF REGB(0)='1' THEN -REGRES := REGRES + REGA; END IF; REGA(15 DOWNTO 1) := REGA(14 DOWNTO 0); -REGA(0):= '0'; -REGB(6 DOWNTO 0) := REGB(7 DOWNTO 1); -CNT := CNT + 1; -IF CNT="000" THEN -RESULT <= REGRES; -SOUT <= '1'; REGA := "00000000" & A; REGB := B;-REGRES := (OTHERS => '0'); -END IF; END IF; END PROCESS; END ARCHITECTURE; 初始化, 初始化,置位
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
11 0 1
a0 0 0 0 0 1 0 1 1
r1 0 0 0 0 0 0 0 0
i=0 r1 0 0 0 0 1 0 1 1
i=1 r1 0 0 0 0 1 0 1 1
i=2 a0 0 0 1 0 1 1 0 0
r1 0 0 1 1 0 1 1 1
i=3 a0 0 1 0 1 1 0 0 0
r1 1 0 0 0 1 1 1 1
3.5 乘法器及其VHDL表述
3.5.1 统计位矢中含‘1’个数的电路模块设计⑩【例3-12】
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
entity cntc is
port(din :in std_logic_vector(7 downto 0);
UNSIGNED
由INTEGER, UNSDGNED,
SIGNED 转换为
STD_LOGIC_VECTOR
❖2、generic参数定义语句
类属GENERIC常用来定义实体端口大小,数据宽度, 元件例化数目等。一般在简单的设计中不常用。
3.5 乘法器及其VHDL表述
❖3、整数数据类型integer
s:integer :=4; SIGNAL C :INTEGER RANGE 1 TO 7; 实际上一个整数是由32位二进制码表示的带符 号数的范围。
量在赋值前必须通过定义,可以在变量定义语句中赋初值
,但对变量赋初值是没有实际意义的。
❖ 变量的赋值符号是“ :=”。
❖ 小提示: 变量与信号赋初值语句仅可用于仿真,在综合 时被忽略,不起作用。
3.5 乘法器及其VHDL表述
❖相关语法 ❖2、for loop循环语句
for loop循环语句是典型的顺序语句,分为递减方式和递增 方式,格式分别为: (1) 递减方式 FOR I IN 起始值 DOWNTO 结束值 LOOP 顺序语句 END LOOP; (2) 递增方式 FOR I IN 起始值 TO 结束值 LOOP 顺序语句 END LOOP;
3.4.3 8位加法器设计
思考:什么时候用到unsigned或signed程序包呢?
3.4.3 8位加法器设计
语法说明 1、std_logic_unsigned程序包
STD_LOGIC_SIGNED STD_LOGIC_UNSIGNED
定义基于STD_LOGIC与 STD_LOGIC_VECTOR数据类型上的有符号 的算术运算 定义基于STD_LOGIC与 STD_LOGIC_VECTOR类型上的无符号的算 术运算
if (b(i)='1') then r1:=r1+to_stdlogicvector(to_bitvector(a0)sll(i)); end if; end loop; r<=r1; end process; end architecture one;
3.5 乘法器及其VHDL表述
a
10 1 1
3.4.3 8位加法器设计
⑨【例3-11】 library ieee;
use ie思ee.s考td_:logic由_11一64.a位ll; 二进制半加器、全加器
use ieee.std_logic_unsigned.all; --此程序包中包含算术操作符的重载函数
entity的add实er8b现is ,如何实现多位二进制加法器? port(a,b :in std_logic_vector(7 downto 0); cin:in std_logic; cout:out std_logic; dout:out std_logic_vector(7 downto 0)); end entity adder8b; architecture bhv of adder8b is signal data:std_logic_vector(8 downto 0); begin data<=('0'&a)+('0'&b)+("00000000"&cin); cout<=data(8); dout<=data(7 downto 0); end architecture bhv;
0 00 0 0 00 0
1011
0 01 0 1 10 0
+
1011
0 10 1 1 00 0
r 1 0 0 0 1 11 1 r 1 0 0 0 1 1 1 1
★二进制数相乘可以用移位相加计算
3.5 乘法器及其VHDL表述
3.5.3 移位相加型乘法器的VHDL表述方法--(11)例3-13
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; use ieee.std_logic_arith.all; entity mult4b is
cnth:out std_logic_vector(3 downto 0));
end cntc;
architecture bhv of cntc is
begin
process(din)
variable q:std_logic_vector(3 downto 0);
begin
q:="0000";
for n in 0 to 7 loop
VARABLE 变量名称:数据类型 := 初值;
❖1、变量variable
❖
在VHDL程序中,常用的数据对象分为三种类型,
即常数(CONSTANT)、变量(VARIABLE)和信号(
SIGNAL)。
❖ 变量只能在进程和子程序中定义和使用,不能在进程
外部定义使用,变量属于局部量,在进程内部主要用来暂
存数据。对变量操作有变量定义语句和变量赋值语句,变
r 1 00 0 11 1 1
3.5 乘法器及其VHDL表述
❖相关语法 ❖1、std_logic_arith程序包
STD_LOGIC_ARITH CONV_INTEGER
由UNSIGNED, SIGNED 转换
CONV_UNSIGNED
为INTEGER
CONV_STD_LOGIC_VECTOR 由SIGNED, INTEGER转换为
3.5 乘法器及其VHDL表述
例3-12 仿真结果
3.5 乘法器及其VHDL表述
a=1011,b=1101,r=a*b
思考二进制乘法的规律
a
1 01 1 a 0 0 0 0 1 0 1 1
b
1 10 1 b 0 0 0 0 1 1 0 1
*
1 01 1 * 0 0 0 0 1 0 1 1
0 0 00
Review
component 元件名 is port (端口名表) ;
end component 文件名 ;
port map
元件例化语句: 元件声明语句或定义语句; 元件连接语句
u1 : h_adder PORT MAP(a=>ain,b=>bin,co=>net2,so=>net1);
元件例化语句用在哪里呢? 什么时候需要用到元件例化语句呢?
generic(s:integer :=4); port(a,b :in std_logic_vector((s-1) downto 0);
r:out std_logic_vector((2*s-1) downto 0)); end entity mult4b; architecture one of mult4b is signal a0:std_logic_vector((2*s-1) downto 0); begin a0<=conv_std_logic_vector(0,s)&a; process(a,b) variable r1:std_logic_vector((2*s-1) downto 0); begin r1:=(others=>'0'); for i in 0 to (s-1) loop
--n是loop的循环变量
if (din(n)='1') then q:=q+1;
end if;
end loop;
cnth<=q;
end process;
end bhv;
3.5 乘法器及其VHDL表述
作业2:设计一个统 计32位矢量型数据 中1的个数的程序
3.5 乘法器及其VHDL表述
❖相关语法
LIBRARY IEEE; USE IEEE.STD_LOGIC_1164.ALL; USE IEEE.STD_LOGIC_UNSIGNED.ALL;
3.4.3 8位加法器设计
例3-11 仿真结果
思考 ❖如何实现n位的二进制加法器? ❖作业1:编写一个16位的二进制加法器。 ❖如何用VHDL实现二进制乘法器? ❖二进制乘法和加法有什么关系呢?
❖左移,SRA算DL表述
例3-13仿真结果
由STD_LOGIC转换为BIT 由
TO_BITVECTOR
STD_LOGIC_VECTOR转换
为 BIT_VECTOR
TO_STDULOGIC
由BIT转换为STD_LOGIC
TO_STDULOGICVECTER 由BIT_VECTOR转换为
STD_LOGIC_VECTOR
❖7、移位操作符
❖SLL逻辑左移,SRL逻辑右移,SLA算术
❖4、conv_std_logic_vector ❖a0<=conv_std_logic_vector(0,s)&a ❖5、省略赋值操作符 ❖r1:=(others=>'0')
