邯郸市一中理科实验班真题8
邯郸市一中理科实验班真题7

邯郸市一中理科实验班试卷7一、选择题(本大题共10小题,每小题4分,共40分)将正确答案填在答题纸内的方格内1、化简2)14.3-π(的结果是()A 、0B 、14.3-πC 、π-14.3D 、π2、已知4468.01996.0=,413.1996.1=,则下列结论正确的是()A 、4468.001996.0=B 、01413.00001996.0=C 、3.1416.199=D 、13.1496.19=3、如果多项式200842222++++=b a b a P ,则P 的最小值是()A 、2005B 、2006C 、2007D 、20084、若一个三角形两边的中垂线的交点在第三边上,则这个三角形是()A 、锐角三角形B 、钝角三角形C 、直角三角形D 、不能确定5、若不等式{223+-x >>a x <(x 为未知数)无解,则函数41)3(2---=x x a y 的图象与x 轴()A 、相交于一点B 、没有交点C 、相交于一点或两点D 、相交于一点或无交点6、已知反比例函数xy 1-=的图象关于一次函数)0(a <b ax y +=的图象对称,则使反比例函数的值小于一次函数值x 的取值范围是()A 、a a b b <x <a a b b 242422-+----B 、1-x <或01<x <C 、1-≤x 或10≤≤x D 、11<x <-7、如图矩形ABCD 中,AB =1,BC =2,以B 为圆心,BC 为半径画弧交AD 于F ,交BA 的延长线于E ,则阴影部分面积为()A 、334-πB 、2334-πC 、2332-πD 、332-π8、已知矩形ABCD ,E 是AB 上的一点,CE ⊥EF ,EF 交AD于点F ,若BE =2,矩形周长为16,CE =EF ,则CB 的长为()A 、3B 、4C 、5D 、69、若等腰三角形一腰上的高与另一腰的夹角为45°,则这个等腰三角形的底角为()A 、67°50°B 、22.5°C 、22.5°或67.5°D 、67.5°10、有一个盛水的容器,由悬在它上空的一条水管均匀地注水,最后把容器注满。
邯郸一中直升班物理招考样题
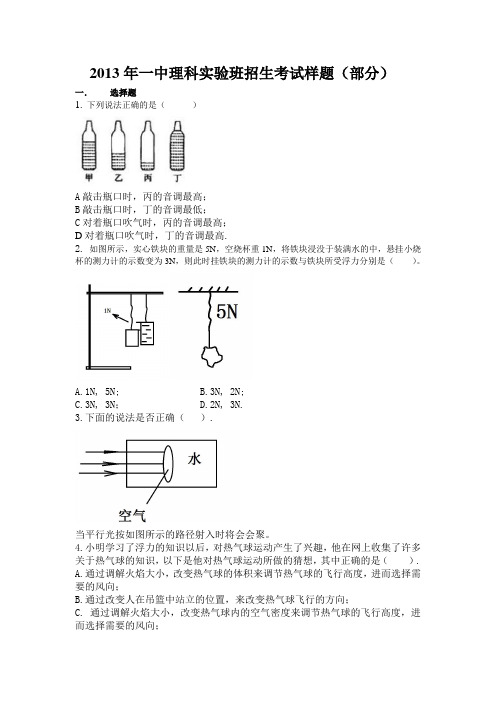
2013年一中理科实验班招生考试样题(部分)一.选择题1.下列说法正确的是()A敲击瓶口时,丙的音调最高;B敲击瓶口时,丁的音调最低;C对着瓶口吹气时,丙的音调最高;D对着瓶口吹气时,丁的音调最高.2.如图所示,实心铁块的重量是5N,空烧杯重1N,将铁块浸没于装满水的中,悬挂小烧杯的测力计的示数变为3N,则此时挂铁块的测力计的示数与铁块所受浮力分别是()。
A.1N, 5N;B.3N, 2N;C.3N, 3N;D.2N, 3N.3.下面的说法是否正确().当平行光按如图所示的路径射入时将会会聚。
4.小明学习了浮力的知识以后,对热气球运动产生了兴趣,他在网上收集了许多关于热气球的知识,以下是他对热气球运动所做的猜想,其中正确的是().A.通过调解火焰大小,改变热气球的体积来调节热气球的飞行高度,进而选择需要的风向;B.通过改变人在吊篮中站立的位置,来改变热气球飞行的方向;C. 通过调解火焰大小,改变热气球内的空气密度来调节热气球的飞行高度,进而选择需要的风向;D.通过调解火焰喷射的方向,来改变热气球飞行的方向.5.如图所示,有两个高度相同的柱体,对水平地面的压强相等,如从顶部割去相同的高度,则剩余的部分对水平地面的压强().A. A大B.B大C.一样大D.无法确定二.填空题1.当潜水艇下潜的时候(从未露出水面时开始),受到的压强,受到的浮力。
(选填“变大”、“变小”或“不变”)。
当潜水艇执行任务从长江潜行到东海时,受到的浮力(选填“变大”、“变小”或“不变”)。
一艘轮船从长江驶入东海,船身将会(选填“上浮一些”、“下沉一些”或“不变”)(其他的实在想不起来了)三.作图题1.如图所示,想将水平面上的长方体木块用最小的力从左搬动,画出力的示意图(保留作图痕迹);2.画出对应的光学元件。
四.实验探究题1.如图所示是探究“平面镜成像的特点”的情景:(1)为了便于观察,该实验最好在 环境中进行(填“较明亮”或“较黑暗”)采用透明玻璃板替代平面镜的作用是 。
邯郸市一中理科实验班提前招生 化学试卷

邯郸市一中理科实验班提前招生化学试卷可能用到的相对原子质量:H—1 S—32 Cl—35.5 K—39 Ca—40 C—12 N—14 O—16 Na—23 I---127 Mg—24 Fe—56 Cu—64 Ba—137第Ⅰ卷Ⅰ一、选择题(共20 分)1、法国科学家拉瓦锡研究空气的组成时给固体氧化汞加强热,氧化汞受热时的变化可用下图表示(图中表示汞原子,表示氧原子),下列说法错误的是( )A.氧化汞受热时能分解成汞和氧气B.原子在化学变化中不能再分C.氧化汞分子是由氧原子和汞原子构成的D.所有物质都是由分子构成的2、正确的化学实验操作对实验结果、人身安全非常重要。
下图中的实验操作正确的是()3、铁酸钠是水处理过程中使用的一种新型净水剂。
铁酸钠之所以能净水,是因为该物质既能消毒杀菌、其反应后的产物又能吸附杂质。
制取铁酸钠(M)的化学方程式为2Fe NO3)+16NaOH+3CI2===2M+6Na NO3+6NaCI+8H2O 则M 的化学式是()A.NaFeO4B.Na2FeO4C.NaFe2O4D.Na2Fe3O84、查阅相关文章知道,用于测定磷含量的试剂是铝酸铵,化学式为(NH4)2MoO4,请问铝酸铵中铝(Mo)元素化合价为()A 、+6B 、+5 C、+4 D、+35、木炭氧化铜和铁粉都是黑色粉末,用化学方法鉴别它们最理想的试剂是下列物质中的()A、稀硫酸B、硫酸铜溶液C、氢氧化钠溶液D、水溶解度/g A6、右图是A、B 两固体物质的溶解度曲线,在t1℃时,将25gA和25gB 分别加到各有50g水中的甲、乙烧杯中,充分溶解,下列说法错误的是()A、t1℃时,A、B 两物质饱和溶液中溶质的质量分数相同B、若A物质中混有少量B物质,可用降温结晶方法提纯AC、由t1℃升温至t2℃,甲烧杯里A 物质溶液中溶质的质量分数不变D、由t1℃升温至t2℃,乙烧杯中B物质溶液的质量不变7、铜和铝是日常生活和生产中重要金属,钛(Ti)有许多的神奇功能,越来越引起人们的关注,依据三种金属的性质和用途,判断下列说法错误的是:()A 钛和钛合金放在海水中数年,取出后仍光亮如初,这说明金属钛具有很强的抗腐蚀性。
2024学年邯郸市第一中学高三第一次联考(4月)物理试题试卷

2024学年邯郸市第一中学高三第一次联考(4月)物理试题试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图所示,一定质量的理想气体从状态A 变化到状态B ,再到状态C ,最后变化到状态A ,完成循环。
下列说法正确的是( )A .状态A 到状态B 是等温变化B .状态A 时所有分子的速率都比状态C 时的小 C .状态A 到状态B ,气体对外界做功为0012p VD .整个循环过程,气体从外界吸收的热量是0012p V 2、如图所示,相距为L 的两条足够长的光滑平行不计电阻的金属导轨与水平面夹角为θ,处于方向垂直导轨平面向下且磁感应强度为B 的匀强磁场中。
将金属杆ab 垂直放在导轨上,杆ab 由静止释放下滑距离x 时速度为v 。
已知金属杆质量为m ,定值电阻以及金属杆的电阻均为R ,重力加速度为g ,导轨杆与导轨接触良好。
则下列说法正确的是( )A .此过程中流过导体棒的电荷量q 等于2BLx RB .金属杆ab 下滑x 时加速度大小为g sinθ-22B L x mRC .金属杆ab 下滑的最大速度大小为22sin mgR B Lθ D .金属杆从开始运动到速度最大时, 杆产生的焦耳热为12mgx sin θ-322244sin m g R B Lθ 3、米歇尔•麦耶和迪迪埃•奎洛兹因为发现了第一颗太阳系外行星﹣飞马座51b 而获得2019年诺贝尔物理学奖。
飞马座51b 与恒星相距为L ,构成双星系统(如图所示),它们绕共同的圆心O 做匀速圆周运动。
设它们的质量分别为m 1、m2且(m1<m2),已知万有引力常量为G.则下列说法正确的是()A.飞马座51b与恒星运动具有相同的线速度B.飞马座51b与恒星运动所受到的向心力之比为m1:m2C.飞马座51b与恒星运动轨道的半径之比为m2:m1D.飞马座51b与恒星运动周期之比为m1:m24、如图所示,正六边形的物体上受四个共点力的作用下保持平衡。
2003年邯郸市一中理科实验班选拔数学试题

2003年邯郸市一中理科实验班选拔试卷一、填空题(每小题3分,共24分)1、 某种半导体收音机,原来每台售价96元,由于两次降价,现在每台售价54元,平均每次降价的百分数 .2、 等腰三角形、等边三角形、等腰梯形、平行四边形、矩形、菱形、正方形、弓形、扇形、圆,这些图形中是中心对称图形而不是轴对称图形的是 . 3、 已知点()1,P a 在反比例函数()0ky k x=≠的图象上,其中223(a m m m =++为实数),则这个函数的图象在第 象限,在每个象限内,y 随x 的增大而 .4、 抛物线2y x bx c =-++= .5、 若不等式组2123x a x b -<⎧⎨->⎩的解集为11x -<<,那么(1)(1)a b +-= .6、 在实数范围内分解因式,2481x x +-= .7、 若扇形的圆心角为150°,弧长为20πcm ,则扇形的面积为 .8、 如图:AB 为半圆的直径,点C 、D 是半圆周的三等分点,若AB =2,则ACD S ∆= .二、选择题(每小题3分,共24分)9、若2222122a b a b ab ab +++-=,则a b +的值为( )A 、2或2-B 、2或2-或0C 、2D 、2- 10、下列结论正确的是( )A 、正三角形是中心对称图形B 、若 225x ab +-与13y ab 是同类项,则2x y ∙=-C 、0.01988-用科学计数法表示为21.98810-⨯D 、在221,,0.53a bxy y x -+这三个代数式中,只有20.5xy y -+是整式 11、如图:三条公路两两相交,交点分别是A 、B 、C ,现计划修一油库,要求油库到三条公路的距离相等,则可供选择的油库地址有( )A 、1处B 、2处C 、3处D 、4处12、若三角形面积为215cm ,它的底边acm 是这个底边上的高的函数,则这个函数图象大致是( )13、以下四点中,有三点在同一条直线上,另外一点与它们不在一条直线上,该点为( ) A 、()1,1 B 、()2,1- C 、()1,5- D 、()3,014、股市交易中每买、卖一次需交千分之七点五的各种费用,某投资者以每股10元的价格买入上海某股票1000股,当股票涨到12元时全部卖出,该投资者实际盈利为( )A 、2000元B 、1985元C 、1835元D 、1910元 15、若方程2220x kx x k +-+=有两个正的实数根,则k 为( )A 、 104k k ≤≠且 B 、14k < C 、 102k k <≠且 D 、12k ≤16、两条宽都为1的纸条,交叉重叠放在一起,且它们的交角为30︒,则它们重叠部分的面积为( )A 、2BC 、12D 、4三、解答题17、(本题4分)计算:222a b ab a b b a a b-++--,其中1,1a b =.18、(本题6分)平行四边形ABCD 周长为110cm ,面积为6002cm ,AB :BC =6:5,DE AB E ⊥于,D F B CF ⊥于,求:cos EDF ∠.19、(本题9分)如图:已知两圆内切与P ,大圆的弦AB 切小圆于C . (1)求证:APC BPC ∠=∠;(2)若两圆继续运动,当两圆相交时,如图,此时的1APC ∠与2BP C ∠是否存在等量关系?若有请给予证明,若没有请说明理由.20、(本题9分)将一张正方形纸剪成四个大小一样的小正方形,然后将其中的一片小正方形又剪成四个小正方形,如此循环下去. (1(2)如果剪n 次共有n S 个正方形,请用含n 的代数式表示n S(3)按上面的方法能否将一个足够大的正方形剪成2002个完整的正方形?为什么?(4)若原正方形的边长为1单位长度,第n 次所剪的正方形的边长为n a ,请用含n 的代数式表示n a1a = 2a = 3a = 4a =(5)比较大小123.........n a a a a ++++ 1 ,,>=<(用填空).21、(本题12分)如图,守门员在O 处开出一高球,此时球从离地面1米A 处飞出(A 在y 轴上),运动员乙在距O 点6米处发现球在自己头正上方达到最高点,距地面4米,据实验:足球在草坪上弹起后的抛物线与原来的形状相同,且高度减少到原来的一半. (1)求足球开始飞出的抛物线解析式; (2)求球第一次落地点距守门员有多少米?(3)运动员乙要抢到第二个落点,他应再向前跑多少米?22、(本题12分)ABC ∆是等边三角形,AB =8cm ,一动点P 从C 开始沿CA 边向A 点以1cm /s 的速度移动,同时另一动点D 从点B 开始沿AB 的延长线以2cm /s 的速度移动,PD 与BC 交于O . (1)点D 移动到什么位置时,30PDB ∠=︒;(2)若OBD ∆面积用y 表示,写出y 关于时间t 的关系式,并注明自变量取值范围; (3)OBD ∆面积存在最大值吗?若存在,求出最大值;若不存在,请说明理由.。
邯郸市一中理科实验班真题6

28、已知抛物线 y ax2 bx 1经过点 A(1,0)、B(-m,0),其中 m >0,且与 y 轴交于点 C, (1)求 a、b 的值(用含 m 的式子表示);(2)⊙ m 过 A、B、C 三点,求∠BMC 的度数; (3)在 x 轴上方,若抛物线上存在点 P,使得以 A、B、P 为顶点的三角形与△ABC 相似,求 m 的值。((1)4 分,(2)4 分,(3)5 分,本题共 13 分)
C、 a a3 a4
D、 a2 a5 a10
2、下列命题正确的是(
)
A、对角线相等的四边形是矩形
B、对角线互相平分的四边形是平行四边形
B、对角线互相垂直的四边形是菱形
D、对角线互相垂直且相等的四边形是正方形
3、地球绕太阳每小时转动通过的路程是 110000 千米,用科学记数法表示为( )
26、如图,PA 是⊙0 的切线,切点为 A,割线 PCB 交⊙0 交于 C、B 两点,半径 OD⊥BC,垂足为 E,AD 交 PB 于点 F,(1)求证:PA=PF; (2)若 F 是 PB 的中点,CF=1.5,求切线 PA 的长。((1)5 分,(2) 6 分)
27、已知⊙0 的弦 AB=10,P 是弦 AB 所对优弧上的一个点, tan APB 2 ,若△APB 是等腰 三角形,求△APB 的面积。(11 分)
A、11104 千米
B、1.1105 千米
C、 0.11106 千米
D、115 千米
4、函数Hale Waihona Puke y x 3 的自变量的取值范围是(
)
x2
A、 x 2
B、 x2
C、 x 2
D、 x2 且 x 3
5、方程 x2 6x 0 的根是(
邯郸一中2015-2016学年高一下学期期中物理试题及答案(实验班)

2015-2016学年河北省邯郸一中高一(下)期中物理试卷(实验班)一、选择题(1-9题是单选题,10-14是多选题.每小题4分,共56分,少选得2分,错选不得分.)1.在力学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法中不正确的是()A.伽利略首先将实验事实和逻辑推理(包括数学推演)和谐地结合起来B.牛顿总结出了万有引力定律并用实验测出了引力常量C.笛卡尔对牛顿第一定律的建立做出了贡献D.开普勒通过研究行星观测记录,发现了行星运动三大定律2.地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,要使赤道上的物体“飘”起来,则地球的转速应为原来的()A.倍B.倍C.倍 D.倍3.有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则()A.a的向心加速度等于重力加速度gB.在相同时间内b转过的弧长最长C.c在4小时内转过的圆心角是D.d的运动周期有可能是20小时4.火星和地球绕太阳运行的轨道可近似视为圆形,若已知火星和地球绕太阳运行的周期之比,则由此可求得()A.火星和地球受到太阳的万有引力之比B.火星和地球绕太阳运行速度大小之比C.火星和地球表面的重力加速度之比D.火星和地球的第一宇宙速度之比5.用一根细线一端系一小球(可视为质点),另一端固定在一光滑锥顶上,如图所示,设小球在水平面内做匀速圆周运动的角速度为ω,细线的张力为F T,则F T随ω2变化的图象是下图中的()A.B.C.D.6.一滑块在水平地面上沿直线滑行,t=0时其速度为1m/s.从此刻开始滑块运动方向上再施加一水平面作用F,力F和滑块的速度v随时间的变化规律分别如图a和图b所示.设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是()A.W1=W2=W3B.W1<W2<W3C.W1<W3<W2D.W1=W2<W37.光滑水平面上静置一质量为M的木块,一颗质量为m的子弹以水平速度v1射入木块,以v2速度穿出,对这个过程,下列说法正确的是()A.子弹对木块做的功等于B.子弹对木块做的功等于子弹克服阻力做的功C.子弹对木块做的功等于木块获得的动能与子弹跟木块摩擦生热的内能之和D.子弹损失的动能等于木块获得的动能跟子弹与木块摩擦转化的内能和8.有一个固定的光滑直杆与水平面的夹角为53°,杆上套着一个质量为m=2kg 的滑块(可视为质点).用不可伸长的细绳将滑块m与另一个质量为M=2.7kg 的物块通过光滑的定滑轮相连接,细绳因悬挂M而绷紧,此时滑轮左侧细绳恰好水平,其长度L=,p点与滑轮的连线与直杆垂直(如图所示).现将滑块m从图中O点由静止释放,(整个运动过程中M不会触地,g=10m/s2).则滑块m滑至P点时的速度大小为()A.5m/s B.5m/s C.m/s D.2m/s9.物体在万有引力场中具有的势能叫做引力势能.取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距离质量为M0的引力源中心为r0时.其引力势能E P=﹣(式中G为引力常数),一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行,已知地球的质量为M,由于受高空稀薄空气的阻力作用.卫星的圆轨道半径从r1逐渐减小到r2.若在这个过程中空气阻力做功为W f,则在下面给出的W f的四个表达式中正确的是()A.W f=﹣GMm(﹣)B.W f=﹣(﹣)C.W f=﹣(﹣) D.W f=﹣(﹣)10.一颗在地球赤道上空绕地球运转的同步卫星,距地面高度为h,已知地球半径为R,自转周期为T,地面重力加速度为g,则这颗卫星运转的速度大小是()A.(R+h)B.RC.D.11.在圆轨道运动的质量为m的人造地球卫星,它到地面的距离等于地球半径R,已知地面上的重力加速度为g,则()A.卫星运动的速度为B.卫星运动的周期为。
2004年邯郸市一中理科实验班选拔数学试题

2004年邯郸市一中理科实验班选拔数学试题一、填空题(本大题共12小题,每小题3分,共36分)1、一件原价80元的衣服,现降价25%出售,如果再征收10%的税,则衣服售价应为 元.2、如图,AB 是O 的直径,DE 切O 与C ,欲使AE ⊥DE ,须添加的一个条件是 (不另外添加线和点).3、在边长为6的正三角形上截去三个三角形,得到一个正六边形,它的面积是 .4、已知反比例函数ky x=经过(4,2)P -,则直线y kx k =-不经过第 象限. 5、已知AB 、CD 为O 的两条直径,弦CE//AB ,EC 度数为40︒,则BOC ∠= . 6、函数2356x y x x +=-+中自变量的取值范围是 . 7、已知点(3,0)A 、(1,0)B -两点,分别以A 、B 为圆心的两圆相交于M (1,2)a --和(1,22)N b a -,则a b = .8、因式分解:222x xy y x y ----= .9、某种活期储蓄的月利率为0.16%,存在10000元本金,按国家规定,取款时应缴纳利息部分20%的利息税,则这种活期储蓄扣除利息税后实得本息和(y 元)与所存月x 之间的函数关系是 .10、股市交易中每买卖一次需交千分之六的费用,某投资者以每股10元的价格买入某种股票1000股,当股票涨到12元时全部卖出,该投资者实际赢利为 . 11、已知一组数据12,,......n a a a 方差是2,那么数据132,a + 232a +,……32n a +方差是 .12、在函数21a y x+=(a 为常数)图象上有三点11(1,)A y -、22(2,)A y 、33(3,)A y ,则1y 、2y 、3y 由小到大排列的顺序为 . 二、选择题(本大题共12小题,每小题3分,共36分)13、若1x m =-、21y m =+则y x 与之间的关系为( )A 、2y x =+B 、21y x =-C 、32y x =-D 、23y x =+ 14、二次函数2y x mx n =++,若21,m n +=则它的图象必经过的点是( ) A 、(2,-5) B 、(5,-2) C 、(-2,-5) D 、(2,5) 15、化简:31x x x---=( ) A 、(1)x x -- B 、(1)x x -- C 、(1)x x -+ D 、(1)x x -16、若1x 、2x 是两个不等的实数,且满足21121x x -=,22221x x -=,那么12x x ⋅=( ) A 、2 B 、2- C 、1 D 、1- 17、如果圆锥的侧面展开图是半圆,那么这个圆锥的顶角是( )度. A 、30° B 、45° C 、60° D 、90°18、等腰梯形各边都与O 相切,若O 的半径为3cm ,梯形腰长为8cm ,则梯形面积为( )A 、242cm B 、362cm C 、482cm D 、602cm 19、已知a 、b 、c 是ABC △的三边长,则方程2()04ccx a b x +++=的根满足( ) A 、无实数根 B 、有两个不等的正实数根 C 、有两个不等的负实数根 D 、有两个异号的实数根20、有一块直角三角形纸片,两直角边AC =6cm ,BC =8cm .现将直角边AC 沿直线AD 折叠,使它落在AB 上,且与AE 重合,则CD =( ) A 、2cm B 、3cm C 、4cm D 、5cm21、由于被墨水污染,一道数学题仅能见如下文字:已知:二次函数2y x bx c =++的图象过点(1,0).求证:这个二次函数的图象关于直线2x =对称.据现有信息,题中的二次函数图象不具有的性质是( )A 、过点(3,0)B 、顶点是(-2,-2)C 、在x 轴上截取线段长2D 、与y 轴交点为(0,3) 22、若不等式组2x x a>⎧⎨≤⎩有解,则a 的取值范围是( )A 、2a ≥B 、2a ≤C 、2a >D 、2a <23、四边形的两条对角线相等且互相垂直,那么这个四边形一定是( ) A 、菱形 B 、矩形 C 、正方形 D 、以上都不对24、已知BE 、CF 是ABC △的两条高,ABC △的面积为642cm ,AEF △面积为362cm ,则cos A 的值为( )A 、14 B 、916 C 、34 D 、1344或 三、解答题25、(本题满分7分)如图,O 的直径AB 和弦CD 相交与点E ,已知AE =6cm ,EB =2cm ,30CEA ∠=︒,求CD 的长.26、(本题满分7分)化简:a ab ab b ab ab b a b ⎡⎤+-+⎢⎥+-⎣⎦其中23a =+,23b =-.27、(本题满分7分)是否存在这样的非负整数m ,使关于x 的一元二次方程22(21)10m x m x --+=有两个实数根,若存在,请求出m 的值,若不存在,请说明理由.28、(本题满分7分)在直角三角形ABC 中,90C ∠=︒,45BDC ∠=︒,A 在CD 延长线上,且AD =DB ,求tan BAC ∠.29、(本题满分7分)如图1,图形ABCD 是由铁栏杆围成的菱形花坛(4590α︒≤≤︒),由于修路的需要把铁栏杆DC 、BC 变成以AD 、AB 为半径的弧(如图2),那么扇形ABCD 的面积与菱形ABCD 的面积相比是否发生变化?若变化说明增加(或减少)了多少?若不变,请说明理由.30、(本题满分7分)《代数》第二册104页例2,解方程11322x x x -=---.解:方程两边同乘以(2)x -约去分母,得113(2)x x =---解这个整式方程得2x =,检验:当2x =时,20x -=,所以2x =是增根,原方程无解.请你根据这个方程的特点,用另一种方法解这个方程.31、(本题满分7分)AB 是O 的直径,AE 平分BAF ∠,交O 于点E ,过E 作直线与AF 垂直,交AF 延长线于D 点,且交AB 延长线于C 点. (1)求证:CD 与O 相切于E 点; (2)若CE ⋅DE =154,AD =3,求O 的直径以及AED ∠的正切值.32、(本题满分9分)某单位用车,出于经济效益原因不计划买车,他们打算与一个体车主或与一出租车公司的一家签订用车合同,若汽车每月行驶x 千米,应付个体车主月租费1y 元,付给出租车公司月租费2y 元,1y 、2y 与x 的函数关系如图所示,看图后回答: (1)付给出租车公司月租费2y (元)与每月行驶路程x (千米)函数关系: ①当0400x ≤≤时,2y = ; ②当400x >时,2y = ; (2)写出1y 与x 之间函数关系,并指出x 的取值范围;(3)写出每月行驶的路程x (千米)在何范围内时,租用出租车公司的车较便宜? (4)若此单位估计每月行使1500千米,用哪家的车费用便宜?33、(本题满分9分)已知矩形ABCD (字母顺序为逆时针方向),边AB =3,对角线BD =13,将此矩形置于直角坐标系xOy 中,使边AB 在x 轴上,直线2y x =-与x 轴、y 轴分别交于F 、E 两点,且经过矩形顶点C . (1)求矩形顶点A 、B 、C 、D 的坐标;(2)若抛物线2y ax bx c =++经过E 、A 、B 三点,求该抛物线的解析式; (3)判断上述抛物线顶点是否会落在矩形ABCD 内,并说明理由.34、(本题满分11分)如图,一位同学在距篮筐水平距离4米处跳起投篮,篮球运行的路线是抛物线,篮球运行的水平距离为2.5米时达到最大高度3.5米,然后准确地落入篮筐,已知篮筐到地面的距离为3.05米.(1)建立如图所示的坐标系,求抛物线的解析式;(2)该运动员身高1.6米,在此次跳投中,球在头顶上方0.35米处出手,问球出手时他跳离地面的高度是多少?。
河北省邯郸市第一实验中学2021年高一数学理测试题含解析

河北省邯郸市第一实验中学2021年高一数学理测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知集合A={x|﹣1<x<3},B={x|﹣2<x<1,x∈z},则A∩B=()A.{0} B.[﹣1,1] C.{﹣1,0,1,2} D.D=[﹣2,3]参考答案:A【考点】交集及其运算.【分析】列举出B中的元素确定出B,找出A与B的交集即可.【解答】解:∵A={x|﹣1<x<3},B={x|﹣2<x<1,x∈Z}={﹣1,0},∴A∩B={0},故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2. 如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=,且点E到平面ABCD的距离为2,则该多面体的体积为()A.B.5 C.6 D.参考答案:D【考点】棱柱、棱锥、棱台的体积.【分析】法一:取AB中点G,CD中点H,连结GE、GH、EH,该多面体的体积V ABCDEF=V BCF﹣GHE+V E﹣AGHD,由此能求出结果.法二:连接BE、CE,求出四棱锥E﹣ABCD的体积V E﹣ABCD=6,由整个几何体大于四棱锥E﹣ABCD的体积,能求出结果.【解答】解法一:取AB中点G,CD中点H,连结GE、GH、EH,∵在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=,且点E到平面ABCD的距离为2,∴该多面体的体积:V ABCDEF=V BCF﹣GHE+V E﹣AGHD=S△BCF×EF+=+=.故选:D.解法二:如下图所示,连接BE、CE则四棱锥E﹣ABCD的体积V E﹣ABCD=×3×3×2=6,又∵整个几何体大于四棱锥E﹣ABCD的体积,∴所求几何体的体积V ABCDEF>V E﹣ABCD,故选:D.3. 函数y=a x﹣2(a>0,a≠1)的图象必经过点()A.(0,1)B.(1,1)C.(2,0)D.(2,1)参考答案:D【考点】指数函数的单调性与特殊点.【分析】根据指数函数y=a x过定点(0,1)的性质,即可推导函数y=a x﹣2(0<a≠1)的图象过定点(2,1).【解答】解:∵指数函数y=a x过定点(0,1),∴将y=a x向右平移2个单位,得到y=a x﹣2,则函数y=a x﹣2(0<a≠1)的图象过定点(2,1).故选:D4. 已知数列{a n}为等比数列,且,则()A. B. C. D.参考答案:A【分析】根据等比数列性质知:,得到答案.【详解】已知数列为等比数列故答案选A【点睛】本题考查了等比数列的性质,属于简单题.5. 已知a=,b=,c=,则a、b、c的大小关系是()A.c<a<b B.a<b<c C.b<a<c D.c<b<a参考答案:D∵,可得是单调减函数,∵,∴,∵,可得为减函数,∵,∴,综上可得,故选D. 6. 已知实数满足若目标函数的最小值为,则实数等于() A.3 B.4 C.5 D.7参考答案:C7. 已知函数的一条对称轴为直线,一个对称中心为点,则有()A. 最小值2B. 最大值2C. 最小值1D. 最大值1参考答案:A【分析】将代入余弦函数对称轴方程,可以算出关于的一个方程,再将代入余弦函数的对称中心方程,可求出另一个关于的一个方程,综合两个等式可以选出最终答案.【详解】由满足余弦函数对称轴方程可知,再由满足对称中心方程可知,综合可知的最小值为2,故选A.【点睛】正弦函数的对称轴方程满足,对称中心满足;余弦函数的对称轴方程满足,对称中心满足;解题时一定要注意这个条件,缩小范围.8. 已知偶函数与奇函数的定义域都是,它们在上的图象如图所示,则使关于的不等式成立的的取值范围为 ( )A、 B、C、 D、参考答案:D9. 过点(3,1)作圆的两条切线,切点分别为A,B,则直线AB的方程为A. 2x+y-3=0B. 2x-y-3=0C. 4x-y-3=0D. 4x+y-3=0参考答案:A略10. 同时掷2枚硬币,那么互为对立事件的是()A.恰好有1枚正面和恰有2枚正面B.至少有1每正面和恰好有1枚正面C.至少有2枚正面和恰有1枚正面D.最多有1枚正面和恰有2枚正面参考答案:C【考点】互斥事件与对立事件.【专题】计算题;规律型;概率与统计.【分析】利用对立事件的概念求解.【解答】解:恰好有1枚正面和恰好有2枚正面有可能同时不发生,不互为对立事件,故A错误;至少有1枚正面和恰好有1枚正面有可能同时发生,不互为对立事件,故B错误;至少有2枚正面和恰好有1枚正面有可能同时不发生,不互为对立事件,故C错误.最多有1枚正面和至少有2枚正面不可能同时发生,也不可能同时不发生,互为对立事件,故D正确;故选:C.【点评】本题考查对立事件的判断,是基础题,解题时要注意对立事件的性质的合理运用.二、填空题:本大题共7小题,每小题4分,共28分11. 设集合A={1,2,3},B={2,4,5},则A∩B=___________.参考答案:{2}。
河北省邯郸市第一中学2017-2018学年高一上学期入学考试理科综合试题 Word版含答案

邯郸一中2017-2018学年第一学期入学试卷科目理综年级高一(直升实验班)相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 Si-28 S-32 Cl-35.5 K-39 Ca-40 Fe-56 Cu-64 Zn-65 Mn-55 Ba-137第I卷(共80分)一、化学选择题(每道题只有一个选项是正确的,每题2分,共16题,共32分)1、下列有关电解质及氧化还原反应的叙述,正确的是()A.某化合物溶于水导电,则该化合物为电解质B.NaCl溶液在电流作用下电离成Na+ 和Cl-C.在氧化还原反应中,非金属单质一定是氧化剂D.元素由化合态变成游离态时,它可能被氧化,也可能被还原2、在两个密闭容器中,分别充有质量相同的甲、乙两种气体,若两容器的温度和压强均相同,且甲的密度大于乙的密度,则下列说法正确的是()A.甲的分子数比乙的分子数多B.甲的摩尔体积比乙的摩尔体积小C.甲的物质的量比乙的物质的量少D.甲的相对分子质量比乙的相对分子质量小3、分类是学习和研究化学的一种常用的科学方法。
下列分类合理的是()①根据酸分子中含有H原子个数将酸分为一元酸、二元酸等;②碱性氧化物一定是金属氧化物;③根据丁达尔现象可将分散系分为胶体、溶液和浊液;④SiO2是酸性氧化物,能与NaOH溶液反应;⑤根据反应的热效应将化学反应分为放热反应和吸热反应.A.②③ B.②④⑤ C.①②④ D.②③④⑤4、在NaCl和NaBr的混合溶液中,Na+、Br—、Cl—的物质的量浓度之比不可能出现的是()A.5:3:2 B.3:2:2 C.5:4:1 D.3:2:15、标准状况下VL氨气溶解在1L水中(水的密度近似为1g/mL),所得溶液的密度为ρg/mL,质量分数为W,物质的量浓度为c mol/L,则下列选项不正确的是()A.ρ=(17V+22400 )/ (22.4+22.4V) B.W=17c/(1000ρ)C.W=17V/(17V+22400) D.c=1000Vρ/(17V+22400)6、只给出下列甲中和乙中对应的量,不能组成一个求物质的量的公式的是( )A.②③④ B .③④⑤ C .③④ D .③7、下列关于同温同压下的两种气体12C 18O 和14N 2的判断正确的是( )A .体积相等时密度相等B .原子数相等时具有的中子数相等C .体积相等时具有的电子数相等D .质量相等时具有的质子数相等8、我国科学家通过测量SiO 2中26Al 和10Be 两种元素的比例来确定“北京人”年龄,这种测量方法叫铝铍测年法.关于26Al 和10Be 的说法不正确的是( )A .10Be 和9Be 是中子数不同质子数相同的不同原子B .10Be 的原子核内中子数比质子数多C .2.6g 26Al 3+中所含的电子数约为6.02×1023D .26Al 3+和26Mg 2+的质子数、中子数和电子数均不相同9、质子数和中子数之和为A ,核内中子数为N 的R 2+离子与16O 所形成的Wg 氧化物中所含质子的物质的量为 ( )A .()816+-+N A A W mol B .()1016+-+N A A W mol C .(A-N+8)mol D .()6+-N A A W mol 10、实验室有下列试剂,其中必须用带橡胶塞的试剂瓶保存的是( )①NaOH 溶液 ②水玻璃 ③Na 2S 溶液 ④Na 2CO 3溶液 ⑤NH 4Cl 溶液 ⑥澄清石灰水⑦浓HNO 3⑧浓H 2SO 4A .①⑥B .①②③④⑥C .①②③⑥⑦⑧D .⑤⑦⑧11、下列关于某些离子的检验及结论,一定正确的是( )A .加入稀盐酸产生无色气体,将该气体通入澄清石灰水中变浑浊,则一定有CO 32﹣B .加入氯化钡溶液有白色沉淀产生,再加盐酸,沉淀不消失,则一定有SO 42﹣C .加入稀硝酸无明显现象,再加入硝酸银有白色沉淀产生,则一定有Cl ﹣D .加入Na 2CO 3 溶液产生白色沉淀,再加盐酸,白色沉淀消失,则一定有Ba 2+12、设N A 为阿伏加德罗常数的值,下列说法正确的是( )A .14 g 乙烯和丙烯的混合物中总原子数为2N A 个B.在1mol的CH5+中所含的电子数为10N AC.16g CH4与18 g NH4+所含质子数相等D.11.2 L的甲烷气体含有甲烷分子数一定为0.5N A个13、下列电离..方程式正确的是()S 2H+ + S2-B.NaHSO4Na + + HSO4-A.HNa+ + H++CO32-D.HCO3-CO32-+ H+C.NaHCO14、下列离子方程式书写正确的是()A.氯气溶于水:H2O+Cl2═2H++ClOˉ+ClˉB.锌片插入稀H2SO4溶液中:Zn+2H+=Zn2++H2↑C.氢氧化钡溶液与稀硫酸反应:H++SO42-+OH-+Ba2+═H2O+BaSO4↓D.碳酸钙溶于稀盐酸:CO32-+2H+=H2O+CO2↑15、下列反应不属于...氧化还原反应的是()A.2F2+2H2O=4HF+O2B.Cl2+H2O=HCl+HClOC.BrCl+H2O=HCl+HBrO D.2Cl2+2Ca(OH)2=CaCl2+Ca(ClO)2+2H2O16、根据反应2KClO3+I2=2KIO3+Cl2↑判断,下列结论不正确的是()A.I2具有还原性B.该反应属于置换反应C.氧化剂是KClO3D.当生成1mol Cl2时,转移2mol电子二、化学选择题(每题有1-2个答案是正确的,每题4分,共12题,共48分,漏选给2分,多选错选不给分)17、下列物质的水溶液能导电,但该物质属于非电解质的是()A.Cu B.CO2C.NH3D.CH3CH2OH(乙醇)18、在强酸性或强碱性溶液中都不能大量共存的一组离子是()A.Ba2+、Fe2+、Br一、NO3—B.Na+、Ca2+、HCO3—、NO3—C.A13+、NH4+、SO42—、Na+D.Na+、K+、NO3—、SO42—19、下列说法正确的是()A.将25gKCl溶液蒸干得到5gKCl固体,则原溶液中溶质的质量分数为20%B.某物质中只含有一种元素,则该物质一定是纯净物C.只有一种元素的阳离子和一种元素的阴离子构成的物质一定是纯净物D.盐形成的溶液中,既不能电离出H+,也不能电离出OH-20、有以下四种物质:①标况下11.2LCO2②1gH2③1.204×1024个N2④4℃时18mLH2O,下列说法不正确的是()A.分子个数:③>④>①=② B.原子个数:③>④>①>②C.体积:③>④>①=② D.质量:③>①>④>②21、实验室里需要480 mL 0.1 mol/L的硫酸铜溶液,以下操作正确的是()A.称取7.68 g硫酸铜,加入500 mL水B.称取12.0 g胆矾配成500 mL溶液C.称取8.0 g硫酸铜,加入500 mL水D.称取12.5 g胆矾配成500 mL溶液22、设N A为阿伏加罗常数的值,下列叙述正确的是()A.在标况下,11.2 L NO与11.2 L O2混合后所含分子数为0.75N AB.常温常压下,16gO3所含的电子数为8N AC.5NH4NO3△2HNO3+4N2↑+9H2O反应中,生成28gN2时,转移的电子数目为3.75N AD.铝跟氢氧化钠溶液反应生成1mol氢气时,转移的电子数为N A23、粗盐中含有不溶性泥沙,可溶性的CaCl2、MgCl2以及一些硫酸盐等。
河北省邯郸市第一中学2018学年高一理科实验班上学期入学考试理综生物试题 含解析

生物选择题(每题2分,共52分)44.细胞学说的建立过程,是科学家探究、开拓、继承、修正和发展的过程,充满了耐人寻味的曲折,下列说法正确的是()A.英国科学家虎克最终建立了细胞学说B.德国科学家施莱登和施旺是细胞的发现者和命名者C.德国科学家魏尔肖的名言是“所有的细胞都来源于先前存在的细胞”D.细胞学说揭示了生物界的统一性和多样性【答案】C【解析】德国科学家施莱登和施旺最终建立了细胞学说,A错误;英国科学家虎克是细胞的发现者和命名者,B错误;德国科学家魏尔肖的名言是“所有的细胞都来源于先前存在的细胞”,C正确;细胞学说揭示了生物界的统一性,D错误。
【考点定位】细胞学说【名师点睛】1.英国科学家虎克利用自制的显微镜观察植物的木栓组织,是细胞的发现者和命名者。
2.德国科学家魏尔肖总结出“细胞通过分裂产生新细胞”,他的名言是“所有的细胞都来源于先前存在的细胞”。
3.细胞学说没有揭示生物界的多样性,只揭示了生物界的统一性,即一切动植物都是由细胞发育而来,并且由细胞核细胞产物所构成。
45.下列各组合中,能体现生命系统的层次由简单到复杂的正确顺序是()①一个大西瓜②血液③白细胞④蝗虫⑤血红蛋白⑥SARS病毒⑦同一片草原上的所有绵羊⑧森林中的所有鸟⑨一片桃园⑩池塘中所有生物A.⑤⑥③②①④⑦⑩⑨ B.③②①④⑦⑩⑨ C.③②①④⑦⑧⑩⑨ D.⑤②①④⑦⑩⑨【答案】B【解析】生命系统的层次由简单到复杂的正确顺序是:细胞→组织→器官→系统→个体→种群→群落→生态系统→生物圈;①一个大西瓜属于果实器官,②血液属于结缔组织,③白细胞是一种血细胞,④蝗虫属于个体;⑤血红蛋白是细胞产物,不属于生命系统结构层次;⑥SARS病毒没有细胞结构,不属于生命系统结构层次;⑦同一片草原上的所有绵羊构成一个种群,⑧森林中的所有鸟构成多个种群,⑨一片桃园属于生态系统,⑩池塘中所有生物构成群落,所以B正确,ACD错误。
【考点定位】生命系统的结构层次【名师点睛】1.生命系统的层次由简单到复杂的顺序是:细胞→组织→器官→系统→个体→种群→群落→生态系统→生物圈,其中细胞是最基本的结构层次,生物圈是最大的结构层次。
2024年河北省邯郸市第一中学高三物理第一学期期末联考模拟试题含解析

2024年河北省邯郸市第一中学高三物理第一学期期末联考模拟试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图,两个小球分别被两根长度不同的细绳悬于等高的悬点,现将细绳拉至水平后由静止释放小球,当两小球通过最低点时,两球一定有相同的( )A.速度B.角速度C.加速度D.机械能2、如图所示,图甲是旋转磁极式交流发电机简化图,其矩形线圈在匀强磁场中不动,线圈匝数为10匝,内阻不可忽略。
产生匀强磁场的磁极绕垂直于磁场方向的固定轴OO′(O′O沿水平方向)匀速转动,线圈中的磁通量随时间按如图乙所示正弦规律变化。
线圈的两端连接理想变压器,理想变压器原、副线圈的匝数比n1∶n2=2∶1,电阻R1=R2=8Ω。
电流表示数为1A。
则下列说法不正确的是()A.abcd线圈在图甲所在的面为非中性面B.发电机产生的电动势的最大值为2VC.电压表的示数为10VD.发电机线圈的电阻为4Ω3、一滴水的质量为0.05g,水滴间隔相等的时间从距石头上方5m处由静止下落,水滴和石头的撞击时间为0.01s,重力加速度g取10m/s2,不计空气阻力。
若在一滴水撞击石头的同时下一滴水开始落下,则一天时间内水滴对石头作用力的总冲量大小约为()A.1N▪s B.10N▪s C.20N▪s D.40N▪s4、如图所示,实线为两个点电荷Q1、Q2产生的电场的电场线,虚线为正电荷从A点运动到B点的运动轨迹,则下列判断正确的是()A.A点的场强小于B点的场强B.Q1的电荷量大于Q2的电荷量C.正电荷在A点的电势能小于在B点的电势能D.正电荷在A点的速度小于在B点的速度5、如图所示,两条光滑金属导轨平行固定在斜面上,导轨所在区域存在垂直于斜面向上的匀强磁场,导轨上端连接一t 时,一导体棒由静止开始沿导轨下滑,下滑过程中导体棒与导轨接触良好,且方向始终与斜面底边平行。
河北省邯郸市第一中学2014-2015学年高二上学期(实验班)限时练习数学试题(2014-11-23)Word版含答案

邯郸市第一中学高二实验班数学限时练1.若函数1)(23+-=ax x x f 在)2,0(上单调递减,则实数a 的取值范围为( )A .3≥aB .3=aC .3≤aD .30<a< 2.函数x x x f +=1cos )(在)1,0(处的切线方程是( ) A .01=-+y x B .012=-+y xC .012=+-y xD .01=+-y x3.函数xx x f 1ln )(-=的单调增区间是( ) A .),1(+∞- B .),0(+∞ C .),1(+∞ D .)1,(--∞4.若函数1ln 21)(2+-=x x x f 在其定义域内的一个子区间)1,1(+-k k 内不是单调函数,则实数k 的取值范围( )A .1+∞[,)B . 312[,) C . 12[,) D . 322[,) 5.函数()331f x x x =--,若对于区间[-3,2]上的任意x 1,x 2,都有|f(x 1)-f(x 2)|≤t ,则实数t 的最小值是( )A .20B .18C .3D .06.已知在R 上可导的函数()f x 的图象如图所示,则不等式()()0f x f x ⋅'<的解集为( )A .(2,0)-B .(,2)(1,0)-∞-⋃-C .(,2)(0,)-∞-⋃+∞D .(2,1)(0,)--⋃+∞7.设,若,则,,的大小关系为( )A .B .C .D .8.已知函数32()f x x bx cx =++的图象如图所示,则2221x x+等于( )A .32B .34C .38D .316 9.已知函数在区间(0,1)内任取两个实数p,q ,且p≠q ,不等式恒成立,则实数的取值范围为( )A .B .C .D .10.函数)(x f 的导函数为)(x f ',对x ∀∈R ,都有2()()f x f x '>成立,若2)4ln (=f ,则不等式2()x f x e >的解是( )A .ln 4x >B .0ln 4x <<C .1x >D .01x <<11.若函数()f x 在R 上可导,且满足()()0f x xf x '->,则( )A .()()313f f <B .()()313f f >C .()()313f f =D .()()13f f =12.定义在(0,)+∞上的单调递减函数()f x ,若()f x 的导函数存在且满足'()()f x x f x >,则下列不等式成立的是( )A .3(2)2(3)f f <B .3(4)4(3)f f <C .2(3)3(4)f f <D .(2)2(1)f f <13.定义在R 上的函数()f x 满足:104'+>=()(),(),f x f x f 则不等式3>+()x x e f x e (其中e 为自然对数的底数)的解集为( )A .(0,)+∞B .(,0)(3,)-∞+∞ C .(,0)(0,)-∞+∞ D .(3,)+∞14.定义在R 上的函数满足,且对任意都有,则不等式的解集为( )A .(1,2)B .(0,1)C .D .(-1,1)15.函数)(x f 是R 上的可导函数,0x ≠时, ()()0f x f x x'+>,则函数1()()g x f x x =+的零点个数为( )A .3B .2C .1D .016.若定义在R 上的函数f(x)的导函数为,且满足,则与的大小关系为( )A . <B . =C . >D .不能确定17.定义在R 上的函数f(x)的导函数为f′(x),已知f(x +1)是偶函数,(x -1)f′(x)<0.若x 1<x 2,且x 1+x 2>2,则f(x 1)与f(x 2)的大小关系是( )A .f(x 1)<f(x 2)B .f(x 1)=f(x 2)C .f(x 1)>f(x 2)D .不确定18.设函数3()f x x x =+,x R ∈.若当02πθ<<时,不等式0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是( )A .(,1]-∞B .[1,)+∞C .1(,1)2D .1(,1]219.设函数在上的导函数为,在上的导函数为,若在上,恒成立,则称函数在上为“凸函数”.已知当时,在上是“凸函数”.则在上( )A .既有极大值,也有极小值B .既有极大值,也有最小值C .有极大值,没有极小值D .没有极大值,也没有极小值20.设函数()f x 在R 上存在导数'()f x ,对任意的x ∈R ,有2()()f x f x x -+=,且x ∈(0,+∞)时,'()f x x >.若(2)()22f a f a a --≥-,则实数a 的取值范围为( )A .[1,+∞)B .(-∞,1]C .(-∞,2]D .[2,+∞)AABBA BBCAA BAADD CCACB。
河北省邯郸市第一中学2016-2017学年高二(实验、平行班)上学期开学考试物理试题 解析版 Word版含解析

河北省邯郸市第一中学2016-2017学年高二上学期开学考试 物理试题年级 高二 科目 物理 命题人 审核人一.不定项选择题(每题4分,共计60分,多选、不选或错选均不得分,漏选得2分) 1.重粒子肿瘤治疗装置中的回旋加速器可发射+5价重离子束,其电流强度为1.2×10-5A ,则在1s 内发射的重离子个数为(e=1.6×10-19C )A .3.0×1012B .1.5×1013C .7.5×1013D .3.75×1014 【答案】B考点:电流强度的定义式。
【名师点睛】根据电流的定义式,求出每秒发射的电荷量,结合每个重离子所带电荷数,即可计算出每秒发射的重离子个数。
2.如图所示,斜面体P 放在水平面上,物体Q 放在斜面上。
Q 受一水平作用力F ,Q 和P 都静止。
这时P 对Q 的静摩擦力和水平面对P 的静摩擦力分别为1f F 、2f F 。
现使力F 变大,系统仍静止,则A .1f F 、2f F 都变大B .1f F 变大,2f F 不一定变大C .2f F 变大,1f F 不一定变大D .1f F 、2f F 都不一定变大 【答案】C试题分析:对物体Q 受力分析,受推力、重力、支持力,可能有摩擦力,如图1;对P 、Q 整体分析如图2①当θθcos sin F mg >时,摩擦力沿着斜面向上,大小为θθcos sin 1F mg F f -=,当F 增大时,1f F 变小;②当θθcos sin F mg =时,摩擦力为零,F 增大时,1f F 变大;③当θθcos sin F mg <时,摩擦力沿着斜面向下,大小为θθsin cos 1mg F F f -=,F 增大时,1f F 变大;对整体受力分析,则有:F F f =2,F 变大则2f F 一定变大;故C 正确,ABD 错误;故选C 。
考点:共点力平衡的条件及其应用。
2008年邯郸市一中理科实验班选拔数学试题

2008年邯郸市一中冬令营活动数学试卷一、选择题:(本大题10小题,每题4分,共40分)1、已知1>a ,下列式子中正确的是( ) A 、a a >1B 、a a >C 、aa 11< D 、()a a -=-1122、若,0132=+-m m 则=+221m m ( ) A 、5 B 、6 C 、7 D 、93、如图,在梯形ABCD 中,BC AD //,对角线交于点P ,若4=∆APD S ,8=∆PCD S ,则 =A B C D S 梯形( )A 、36B 、24C 、30D 、324、若a 、b 、c 为三角形三边,且满足0222=---++ac bc ab c b a ,则三角形为( ) A 、等腰直角三角形 B 、等边三角形 C 、斜三角形 D 、直角三角形 5、若等腰三角形腰上的高是腰长的一半,则顶角的度数为( ) A 、︒30 B 、︒150 C 、︒45 D 、︒30或︒1506、已知函数)21(1222≤≤---=x ax x y 的最大值是4,若2>a ,则a = ( ) A 、2 B 、4 C 、7.5 D 、87、若k bca a cbc b a =+=+=+且0≠++c b a ,则直线k kx y +=的图象过第( )象限. A 、一、二、三 B 、二、三 C 、二、三、四 D 、一、四8、如图,圆心为O 直径为MN 的半圆上有不同的两点A 、B ,在ON 上有一点P ,︒=∠=∠10OBP OAP ,若弧MA 的度数是︒40,则弧BN 的度数是( ) A 、︒10 B 、︒15 C 、︒20 D 、︒259、如图,在四边形ABCD 中,2==BC AB ,且︒=∠=∠90C B ,E 为BC 上一动点,当︒=∠45DAE 时,则DE 边上的高AF =( )A 、2B 、3C 、4D 、510、如图五边形ABCDE 中,,6,5,4,8====EA DE BC AB 且︒=∠=∠=∠90E B A ,N 为CD 上一动点,作AE NM AB NL ⊥⊥,,垂足分别为L 和M ,则矩形MALN 的最大面积为( ) A 、364 B 、386 C 、398 D 、34二、填空题:(每题4分,共40分)11、分解因式:=+---142222ab b a b a .12、已知直线1423-=-a y x 与直线a y x =+交点在第一象限,则a 的取值范围是 . 13、若y x a -=-62,其中a y x ,,为正整数,则=-+a y x .14、设b a ≠为两个实数,满足23,2322=-+=b b a a ,则=+abb a . 15、已知抛物线在x 轴上截得的线段长为4,且当3=x 时有最大函数值10,则此函数解析式是 .16、在平面直角坐标系中有())1,5(4,1-B A 和两点,P 为x 轴上一点,当P A 与PB 的差最大时P 点坐标是 ,此时最大值是 . 17、解方程组⎪⎩⎪⎨⎧=++=+++2312y xy x y x y x 的解为 .18、如图,已知在梯形ABCD 中,AB //DC ,中位线EF =7cm ,对角线BD AC ⊥,︒=∠30BDC ,求梯形的高AH = .19、如图,在ABC Rt ∆中,︒=∠90C ,点O 为斜边AB 上一点,以O 为圆心,OA 为半径的圆恰好切BC 于点D ,交AC 于E 点,若︒=∠40B ,则=∠EDC .20、若不等式组⎩⎨⎧>-+>-0504a x x a 无解,则a 的取值范围是 .三、解答题:21、(6分)计算:()102332.02160sin 225-⎪⎪⎭⎫ ⎝⎛-+--+︒+-.22、(8分)解方程:98876554-----=-----x x x x x x x x .23、(10分)已知关于1x 、2x 是方程:02-2=+a x x 的两个实数根,且23221-=+x x . (1)求1x 、2x 及a 的值; (2)求21213123x x x x ++-的值.24、(10分)如图,过正方形ABCD 的顶点C ,作对角线BD 的平行线CP ,在CP 上有一点E ,使BE =BD ,求CBE ∠的度数.25、(10分)如图,在平面直角坐标系中,ABC ∆为直角三角形,︒=∠90ACB ,点B ,C 的坐标分别为(-5,0)、(-1,0).现有半径为1.5,圆心在x 轴上沿x 轴向左运动的动圆,当圆心运动到点1O 的位置时,1O 与x 轴相交于E 点,与AC 相切于C 点,与AB 有公共点D ,且BD =2.(1)1O 是否与AB 相切,为什么?(2)已知抛物线c bx ax y ++=2的对称轴垂直于x 轴,其顶点在线段AB 上运动,是否存在同时经过C ,E 两点的抛物线?若存在,请求出抛物线的解析式,若不存在,请说明理由.26、(12分)做小家电生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能出售A 、B 两种商品合计30件,并且每售出一件A 商品,甲店能获利30元,乙店能获利27元;每售出一件B 商品,甲店能获利40元,乙店能获利36元.某日,王老板进A 商品35件,B 商品25件,怎样平均分给每个店铺各30件,使得在保证乙店获利不少于950元的前提下,王老板获利最大,最大的总利润是多少?27、(14分)已知0<a ,0≤b ,0>c ,且ac b ac b 242-=-,求ac b 42-的最小值.。
2009年邯郸市一中理科实验班选拔数学试题

2009九年级数学调研试卷(邯郸一中)一、选择题(每小题5分,共35分)1、下面形状的四张纸板,按图中线经过折叠可以围成一个直三棱柱的是( )2、命题:①三点确定一个圆;②平分弦的直径垂直于弦,并且平分弦所对的两条弧;③对角线相等的四边形是矩形;④如果顺次连接梯形四条边中点所得的图形是菱形,那么这个梯形是等腰梯形.其中真命题的个数是( )A 、0个B 、1个C 、2个D 、3个 3、函数()31y x x x =-+中,自变量x 的取值范围是( )A 、0x ≥B 、1x ≥C 、1x ≥或0x =D 、01x ≤≤4、如图,60ACB ∠=︒,半径为4的O 切BC 于点C ,若将O 在CB 上向右滚动,则当滚动到O 与CA 也相切时,圆心O 移动的水平距离为( ) A 、4π B 、8π C 、43 D 、85、如图,在直角梯形ABCD 中,AD //BC ,点E 是边CD 的中点,若AB =AD +BC ,52BE =,则梯形ABCD 的面积为( ) A 、254 B 、252 C 、258D 、256、如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是( ) A 、1925 B 、1025 C 、625 D 、5257、设a 、b 、c 分别是△ABC 的三条边的长,且a a bb a b c+=++,则它的内角A ∠、B ∠的关系是( )A 、2B A ∠>∠ B 、2B A ∠=∠C 、2B A ∠<∠D 、不确定二、填空题(每小题5分,共35分)8、关于x 的一元二次方程()22110a x x a -++-=一根为0,则a = .9、若关于x 的分式方程3177ax x -=++在实数范围内无解,则实数a = . 10、如图,△ABC 中,AB =AC =8,D 、E 、F 为BC 、AB 、AC 上的点,DE =DB ,DF =DC ,BE +CF =6,则BC = .11、实数a 、b 、c 满足2823a c +=-,2617b a +=-,2214c b +=,则a b c ++= . 12、如图,O 的圆心在梯形ABCD 的底边AB 上,并与其它三边均相切,若AB =10,AD =6,则BC 的长为 .13、已知方程()2330x a x +-+=在实数范围内恒有解,并且恰有一个解大于1小于2,则a 的取值范围是 .14、已知m 、n 是实数,且223m mn n ++=,设22t m mn n =-+,则t 的取值范围为 .三、解答题(共8题,共80分)15、(6分)正数x 、y ,若()()()()222222315x y y x y x x y xy --+-=+-. 求3x y x y-+的值.16、(6分)若干个1与2排成一行:1,2,1,2,2,1,2,2,2,1,2,….规则是:第1个数是1,第2个数是2,第3个数是1.一般地,先写一行1,再在第k 个1与第k +1个1之间插入k 个2(k =1,2,3,…). 试问:(1)第2009个数是1还是2? (2)前2009个数的和是多少?(3)前2009个数两两乘积的和是多少?17、(8分)解方程116x x x +-++=.18、(10分)若m 是不小于1-的实数,关于x 的方程()2222330x m x m m +-+-+=有两个不相等的实数根1x 、2x . (1)若22126x x +=,求m 的值;(2)求22121211mx mx x x +--的最大值.19、(10分)已知如图,矩形OABC 的长3OA =,宽1OC =,将△AOC 沿AC 翻折得△APC .(1)填空:PCB ∠= ,P 点坐标为 ; (2)若P 、A 两点在抛物线243y x bx c =-++上,求b 、c 的值,并说明点C 在此抛物线上;(3)在(2)中的抛物线CP 段(不包括C 、P 点)上,是否存在一点M ,使得四边形MCAP 的面积最大?若存在,求出这个最大值及此时M 点的坐标;若不存在,请说明理由.20、(10分)若三个完全平方数之和能被9整除,那么试证明可以从这三个数中选出两个来,使得这两个完全平方数之差也能被9整除. 21、(14分)(1999年福州中考)如图,已知O 和'O 相交于A 、B 两点,过点A 作'O 的切线交O 于点C ,过点B 作两圆的割线分别交O 、'O 于E 、F ,EF 与AC 相交于点P .(1)求证:PA PE PC PF ⋅=⋅;(2)求证:22PE PFPC PB=; (3)当O 与'O 为等圆时,且::3:4:5PC CE EP =时,求△PEC 与△F AP 的面积的比值.22、(16分)整数0a 、1a 、2a 、3a 、…、2008a 、2009a 满足条件:00a =,101a a =+,211a a =+,321a a =+,…,200920081a a =+.求:012320082009...a a a a a a ++++++的最小值.。
2010邯郸市一中实验班提前招生数学试卷

2010九年级数学调研试卷(邯郸一中)一、选择题(本大题共6题,每题4分,共24分)1、下列计算正确的是( ) A 、326a a a ⋅= B 、()326aa = C 、23235a a a += D 、333322a a a ÷=2、不等式组21318x x -≥-⎧⎨->⎩的解集在数轴上可表示为( )3、用换元法解分式方程13101x x x x --+=-时,如果设1x y x -=,将原方程化为关于y 的整式方程,那么这个整式方程是( )A 、2310y y -+= B 、230y y +-= C 、2310y y -+= D 、2310y y --= 4、下列图象中,以方程220y x --=的解为坐标的点组成的图象是( )5、如图,E 、F 、G 、H 分别为正方形ABCD 的边AB 、BC 、CD 、DA 上的点,且AE =BF =CG =DH =13AB .则图中阴影部分的面积与正方形ABCD 的面积之比为( ) A 、25 B 、49 C 、12 D 、356、已知点A 的坐标为(a ,b ),O 为坐标原点,连接OA ,将线段OA 绕点O 按逆时针方向旋转90°得1OA ,则点1A 的坐标为( )A 、(-a ,b )B 、(a ,-b )C 、(-b ,a )D 、(b ,-a )二、填空题(本大题共12题,每题4分,共48分)7、甲、乙两同学近期4次数学单元测试成绩的平均分相同,甲同学成绩的方差2=3.2S 甲,乙同学成绩的方差2=4.1S 乙,则他们的数学测试成绩谁较稳定 (填甲或乙). 8、已知关于x 的方程260x kx --=的一个根为3x =,则实数k 的值为 . 9、若1x 、2x 是一元二次方程210x x --=的两个实数根,则1211x x += . 10、王鹏同学在练习“描点法”画二次函数()20y ax bx c a =++≠的图象时,列了如下表格:x ... ﹣2 ﹣1 0 1 2 ... y...﹣6.5﹣4﹣2.5﹣2﹣2.5...根据表格上的信息可以知道该二次函数()20y ax bx c a =++≠在3x =时,y = .11、如图,点A (m ,m +1)、B (m +3,m -1)都在反比例函数ky x=的图象上,则m 、k 的值分别是 .12、如图,AOB ∠是放置在正方形网格中的一个角,则cos AOB ∠的值是 .13、如图,在两个同心圆中,三条直径把大圆分成六等份,若在这个圆面上均匀地撒一把豆子,则豆子落在阴影部分的概率是 .14、如图,一块砖的外侧面积为x ,那么图中残留部分墙面的面积为 .15、如图,在12×6的网格图中(每个小正方形的边长均为1个单位长),⊙A 的半径为1,⊙B 的半径为2,要使⊙A 与静止的⊙B 相切,那么⊙A 由图示位置需向右平移 个单位长.16、如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接BC ,若34A ∠=︒,则C ∠= .17、对于每个非零自然数n ,抛物线()2211(1)1n y x x n n n n +=-+++与x 轴交于n A 、n B 两点,以n n A B 表示这两点间的距离,则11223320092009A B A B A B A B +++⋅⋅⋅+的值是 .18、在Rt ABC △中,90BAC ∠=︒,3AB =,M 为边BC 上的点,连接AM (如图所示).如果将△ABM 沿直线AM 翻折后,点B 恰好落在边AC 的中点处,那么点M 到AC 的距离是 .三、解答题(本大题共7题,合计78分)19、(10分)给定下面一列分式:3x y ,52x y -,73x y ,94x y-,…,(其中0x ≠).(1)把任意一个分式除以前面一个分式,你发现了什么规律?(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.20、(10分)已知关于x 的方程221=0x kx -+的一个解与方程2141x x+=-的解相同. (1)求k 的值;(2)求方程221=0x kx -+的另一个解.21、(10分)如图,在平面直角坐标系中,四边形OABC 的等腰梯形,BC //OA ,OA =7,AB =8,60COA ∠=︒,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合.连接CP ,过点P 作PD 交AB 于点D . (1)求点B 的坐标;(2)当点P 运动什么位置时,使得CPD OAB ∠=∠,且58BD AB =,求这时点P 的坐标.22、(10分)“农民也可以报销医疗费了!”这是某市推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图. 根据以上信息,解答以下问题:(1)本次调查了多少村民,被调查的村民中,有多少人参加合作医疗得到了返回款; (2)该乡若有10 000村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9 680人,假设这两年的年增长率相同,求这个年增长率.23、(12分)已知一次函数与反比例函数的图象交于点P(-3,m)、Q(2,-3).(1)求这两个函数的函数关系式;(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;(3)当x取何值时,一次函数的值大于反比例函数的值?当x为何值时,一次函数的值小于反比例函数的值?24、(12分)东方商厦专销某品牌的计算器,已知每只计算器的进价是12元,售价是20元.为了促销,商厦决定:凡是一次性购买10只以上(不含10只)的顾客,每多买1只计算器,其购买的每只计算器的售价就降低0.10元(假设顾客购买了18只计算器,则每只计算器售价为:20﹣0.10×(18﹣10)=19.20元,顾客应付的购货款为:18×19.20=345.60元),但最低售价为16元/只.(1)求顾客至少一次性购买多少只计算器,才能以最低价购买?(2)设顾客一次性购买x(10<x≤50)只计算器时,东方商厦可获利润y(元),试求y与x之间的函数关系式及商厦的最大利润;(3)有一天,一位顾客一次性购买了46只计算器,另一位顾客一次性购买了50只计算器,结果商厦发现卖50只反而比卖46只赚的钱少.为了使每次获利随着销量的增大而增大,在其他促销条件不变的情况下,商厦应将最低价16元/只至少提高到多少?为什么?25、(14分)如图,已知AB是O的直径,AC是O的弦,点D是ABC的中点,弦DE ⊥AB,垂足为F,DE交AC于点G.(1)图中有哪些相等的线段?(要求:不再标注其它字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程)(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG 是否成立?若成立,请证明;若不成立,请说明理由;(3)在满足第(2)问的条件下,已知AF=3,43FB ,求AG与GM的比.(第(1)的结论可直接利用)。
2021—2021学年度河北省邯郸一中第一学期高三8月考试(实验班)高中化学

2021—2021学年度河北省邯郸一中第一学期高三8月考试〔实验班〕高中化学化学试卷第I卷〔60分〕一、选择题:〔此题包括12小题,每题2分,共24分。
每题只有一个选项符合题意〕1 •化学与生活、社会紧密相关。
以下讲法不正确的选项是〔〕A •利用太阳能等清洁能源代替化石燃料,有利于节约资源、保护环境B. 凡含有食品添加剂的食物对人体健康均有害,不可食用C. 为防止电池中的重金属等污染土壤和水体,应积极开发废电池的综合利用技术D. 提倡人们购物时不用塑料袋,是为了防止白色污染2 •以下文字表述与反响方程式对应且正确的选项是〔〕A .溴乙烷中滴入AgNO 3溶液检验其中的溴元素:Br-+Ag+==AgBr JB. 用醋酸除去水垢:CaCO3 + 2H+==Ca2+ + H2O + CO2 T+电解C. 用惰性电极电解饱和氯化钠溶液:2C「+ 2HH2 f + QfD. 实验室用液溴和苯在催化剂作用下制溴苯:0 + Br2 Fe B3・+ HBr3 .用N A表示阿伏加德罗常数的值。
以下表达错误的选项是〔〕A. 在H2O2+ Cl2= 2HC1 + 02反响中,每生成32g氧气,那么转移2N A个电子B. 标准状况下,22.4L己烷中共价键数目为19N AC. 由CO2和O2组成的混合物中共有N A个分子,其中的氧原子数为2N AD. 一定温度下,1L0.5mol L-1NH4Cl溶液与2L0.25mol L・-1NH4CI溶液含NH4+物质的量不同4. 以下现象或事实可用同一原明白得释的是〔〕A .浓硫酸和浓盐酸长期暴露在空气中浓度降低B. 氯水和二氧化硫均可使品红试液褪色C. 漂白粉和水玻璃长期暴露在空气中变质D. 乙炔和乙烯使溴的四氯化碳溶液褪色5. 只靠一组镍氢电池驱动,一台试运行的混合动力公交车两年内跑了10万公里。
大功率镍氢动力电池及其治理模块,是国家〞十五〃863打算电动汽车重大专项中一项重要课题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
邯郸一中立刻实验班真题8
一、选择题(每小题4分,共48分)
1、在6张完全相同的卡片上分别画上线段、等边三角形、平形四边形、直角梯形、正方形和圆。
在看不见图形的情况下随机摸出1张,这张卡片上的图形是中心对称图形的概率是()
A、61
B、31
C、21
D、
322、关于x 的方程:014)5(2=---x x a 有实数根,则a 满足()A、1
≥a B、a>1且a≠5
C、a≥1且a≠5
D、a≠5
3、若a <1,化简=--1)1(2a ()A、a-2
B、2-a
C、a
D、-a
4、有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离相等;④半径相等的两个半圆是等弧。
其中正确的的有()
A、4个
B、3个
C、2个
D、1个
5、要使1
21
3-+-x x 有意义,则x 应满足()
A、
3
21≤≤x B、3≤x 且21≠x C、21<x <3D、2
1
<x ≤36、如图,两圆相交于A、B 两点,小圆经过大圆的圆心O,点C、D 分别在两圆上,若∠100°,
则∠ACB 的度数为()
A、35°
B、40°
C、50°
D、80°
7、抛物线:c bx x y ++=2图象向右平移2个单位再向下平移3个单位,所得图象的解析式为322--=x x y ,则b 、c 的值为()A、b=2,c-2
B、b=2,c=0
C、b=-2,c=-1
D、b=-3,c=2
8、已知两圆的半径R、r 分别为方程062=+-x x 的两根,两圆的圆心距为1,两圆的位置关系是()A、外离
B、内切
C、相交
D、外切
9、如图,如果从半径为9cm 的圆形纸片上剪去3
1
扇形,
将剩下部分折成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A、6cm
B、cm
53
C、8
cm D、cm
3510、正方形ABCD 在坐标系中的位置如图所示,将正方形ABCD 绕D 点顺时针方向旋转90度后,B 点的坐标为()
A、(-2,2)
B、(4,1)
C、(3,1)
D、(4,0)
11、如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN=30°
B 为AN 弧的中点,P 是直径MN 上一动,则PA+PB 的最小值为()
A、2
2B、2
C、1
D、2
12、已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表,则下列判断中正确的是(
)x …-1013…y
…
-3
1
3
1
…
A、抛物线开口向上
B、抛物线与y 轴交于负半轴
C、当x=4时,y>0
D、方程02=++c bx ax 的正根在3与4之间
二、空题(每题4分,共24分)
13、如图,△ABC,点D 在边AB 上,满足:∠ACD=∠ABC,若AC=2,AD=1,则DB=
14、设a、b 是一元二次方程0200932=-+x 的两个实数根,则022=++b a a
的值为。
15、如科,是一张宽m 的矩形台球桌ABCD,一球从点M(点M 在长边CD 上)出发沿虚线MN
射向边BC,然后反弹到边AB 上的P 点。
如果MC=n,∠CMN=a,那么P 点与B 点的距离为。
16、如图,是二次函数c bx ax y ++=2图象的一部分,其对称轴为直线1=x ,若其与x 轴一
交点A(3,0),则由图象可知,不等式c bx ax ++2<0的解集是。
17、如图,等边三菜形ABC 中,D、E 分别为AB、BC 边上的点,AD=BE,AE 与CD 交于点F,
AG⊥CD 于点G,则AF
AG
的值为。
18、如图,已知A、B 两点的坐标分别为)(0,32、(0,2)、
P 是△AOB 的外接圆上的一点,且∠AOP=45°,则点P 的坐标为。
三、解答题:
19、(本题满分8分)如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有
数字1、3、6,指日针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘)。
(1)请用树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果。
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率。
20、(本题满分12分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210元。
如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元)。
设每件商品的售价上涨x 元(x 为正整数),每个月的销售利润为y 元。
(1)求y 与x 的函数关系式并直接写出自变量x 的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润恰为
2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
21、(本题满分10分)在东西方向的海岸线ι上有一长为1km 的码头MN(如图),在码头西端M 的正西19.5km 处有一观察站A。
某时刻测得一艘匀速直线航行的轮船位于A 的北偏西30°,且与A 相距40km 的B 处。
经过1小时20分钟,又测得该轮船位于A 的北偏东60°,且与A 相距km 38的C 处。
(1)求该轮船航行的速度(保留精确结果)。
(2)如果该轮船不改变航向继续航行,那么轮船能否正好至码头MN 靠岸?请说明理由。
22、(本题满分12分)如图,Rt△ABC 中,∠C=90°,AB=5
5
sin 52=
B ,,点P 为边B
C 上一动点,PD∥AB,P
D 交AC 于点D,连接AP。
(1)求AC、BC 的长:
(2)设PC 的长为x,△ADP 的面积为y。
当x 为何值时,
y 最大,并求出最大值。
23、(本题满分12分),在日常生活中,我们经常有目的地收集数据,分析数据,作出预测。
(1)下图是小芳家2009年全年月用电量的条形统计图。
根据图中提供的信息,回答下列问题:
①2009年小芳家月用电量最小的是月,四个季度中用电量最大的是第季度;
②求2009年5月至6月用电量的月增长率;
(2)今年小芳家添置了新电器。
已知今年5月份的用电量是120千瓦时,根据2009年5月至7月用电量的增长趋势,预计今年7月份的用电量将达到240千瓦时。
假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,预计小芳家今年6月份的用电量是多少千瓦时?
24、(本题满分12分)如图,⊙O是△ABC的外接圆,FH⊙O的切线,切点为F,FH/BC,连
接AF交BF于E,∠ABC的平分线BD交AF于D,连接BF。
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,BD=3,求AD的长。
25、(本题满分12分)在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、B(3,
33
2
)
三点
(1)求此抛物线的解析式;
(2)以OA的中点M为圆心,OM长为半径作⊙M,在91)中的抛物线上是否存在这样的点P,过点P作⊙M的切线m,且m与x轴的夹角为30°,若存在,请求出此时点P的坐标,若不存在,请说明理由。
(注意:本题中的结果可保留根号)。
