2013年中考数学专题复习 圆与圆的位置关系(含答案)
圆与圆的位置关系(含答案)

圆与圆的位置关系一、选择题1.若两圆相切,圆心距是7,其中一圆的半径为10,则另一个圆的半径为__________. 【答案】3或172.已知两圆的半径R 、r 分别为方程0652=+-x x 的两根,两圆的圆心距为1,两圆的位置关系是A .外离B .内切C .相交D .外切 【答案】B3.已知⊙O 1与⊙O 2相切,⊙O 1的半径为3 cm ,⊙O 2的半径为2 cm ,则O 1O 2的长是 A .1 cm B .5 cmC .1 cm 或5 cmD .0.5cm 或2.5cm【答案】C4.已知两圆的半径分别为3cm ,5 cm ,且其圆心距为7cm ,则这两圆的位置关系是(A )外切 (B )内切 (C )相交 (D )相离 【答案】C5.⊙O 1的半径为3cm ,⊙O 2的半径为5cm ,圆心距O 1O 2=2cm ,这两圆的位置关系是A .外切B .相交C .内切D .内含 【答案】C6.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是(A)内切 (B)相交 (C)外切 (D)外离 【答案】B7.如图为某机械装置的截面图,相切的两圆⊙O 1,⊙O 2均与⊙O 的弧AB 相切,且O 1O 2∥l 1( l 1为水 平线),⊙O 1,⊙O 2的半径均为30 mm,弧AB 的最低点到l 1的距离为30 mm,公切线l 2与l 1间的 距离为100 mm.则⊙O 的半径为( )A.70 mmB.80 mmC.85 mmD.100 mm 【答案】B8.已知⊙O 1、⊙O 2的半径分别是12r =、24r =,若两圆相交,则圆心距O 1O 2可能取的值是( ). A 、2 B 、4 C 、6 D 、8 【答案】B .9.外切两圆的半径分别为2 cm 和3cm ,则两圆的圆心距是A .1cmB .2cmC .3cmD .5cm【答案】D第10题图AB单位:mml 1l 210.已知两圆的半径分别是3和2,圆心的坐标分别是(0,2)和(0,-4),那么两圆的位置关系是( )A.内含B.相交C.相切D.外离 【答案】D11.已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d 的取值满足 ()A .9d >B . 9d =C . 39d <<D .3d = 【答案】D12.如图(四)在边长为1的小正方形组成的网格中,半径为2的1O 的圆心1O 在格点上,将一个与1O 重合的等圆向右平移2个单位,再向上平移2个单位得到2O ,则2O 与1O 的位置关系是( )A .内切B .外切C .相交D .外离图(四) 【答案】C13.已知圆O 1、圆O 2的半径不相等,圆O 1的半径长为3,若圆O 2上的点A 满足AO 1 = 3,则圆O 1与圆O 2的位置关系是( )A.相交或相切B.相切或相离C.相交或内含D.相切或内含 【答案】A14.两圆的圆心距为7cm ,半径分别为5cm 和2cm ,则两圆的位置关系是( )A .内切B .外切C .外离D .内含 【答案】B15.已知两圆的半径分别是2㎝和4㎝,圆心距是6㎝,那么这两圆的位置关系是 (A )外离 (B )外切 (C )相交 (D )内切 【答案】B16.如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A 的半径为1,⊙B 的半径为2,将⊙A 由图示位置向右平移1个单位长后,⊙A 与静止的⊙B 的位置关系是( ).A.内含B.内切C.相交D.外切【答案】D17. 若两圆的半径分别为2和3,圆心距为5,则两圆的位置关系为A.外离B.外切C.相交D.内切 【答案】B18. 已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( ) (A )相交 (B )外切 (C )外离 (D )内含 【答案】A 19. 已知⊙O 1的半径为5㎝, ⊙O 2的半径为6㎝,两圆的圆心距O 1 O 2=11㎝,则两圆的位置关系为( )A .内切B . 外切C .相交D .外离 【答案】B20.如图,两圆相交于A ,B 两点,小圆经过大圆的圆心O ,点C ,D 分别在两圆上,若100ADB ∠=︒,则ACB ∠的度数为 A .35︒B .40︒C .50︒D .80︒【答案】B21.已经⊙O 1、⊙O 2的半径分别为5cm,、8cm ,且他们的圆心距为8cm ,则⊙O 1与⊙O 2的位置关系为( )A .外离B .相交C .相切D .内含 【答案】B22.已知⊙1O 和⊙2O 的半径分别为2cm 和3cm ,两圆的圆心距为5cm ,则两圆的位置关系是( ) A .外切 B .外离 C .相交 D .内切 【答案】A23.有四个命题:①两条直线被第三条直线所截,同旁内角互补;②有两边和其中一边的对角对应相等的两个三角形全等;③菱形既是轴对称图形又是中心对称图形;④两圆的半径分别是3和4,圆心距为d ,若两圆有公共点,则.71<<d 其中正确的命题有( ) A .1个 B .2个 C .3个 D .4个 【答案】A24.已知方程0452=+-x x 的两根分别为⊙1与⊙2的半径,且O 1O 2=3,那么两圆的位置关系是( ) A .相交 B .外切 C .内切 D .相离 【答案】C25.已知⊙O 1与⊙O 2的半径分别为2和3,两圆相交,则两圆的圆心距m 满足( )A .m =5B .m =1C .m >5D .1<m <5 【答案】D26.已知两圆的半径分别为R 和r (R >r ),圆心距为d .如图,若数轴上的点A 表示R -r ,点B 表示R +r ,当两圆外离时,表示圆心距d 的点D 所在的位置是(A )在点B 右侧 (B )与点B 重合(C )在点A 和点B 之间 (D )在点A 左侧 【答案】A27.已知大圆的半径为5,小圆的半径为3,两圆圆心距为7,则这两圆的位置关系为( ) A .外离 B .外切 C.相交 D .内含 【答案】C28.在数轴上,点A 所表示的实数是-2,⊙A 的半径为2,⊙B 的半径为1,若⊙B 与⊙A 外切,则在数轴上点B 所表示的实数是: ( )A .1B .-5C .1或 -5D .―1或―3 【答案】C29.如图,两圆相交于A ,B 两点,小圆经过大圆的圆心O ,点C ,D 分别在两圆上,若100ADB ∠=︒,则ACB ∠的度数为A .35︒B .40︒C .50︒D .80︒【答案】B30.)已知两圆半径分别为4和7,圆心距为3,那么这两个圆的位置关系是() A.内含 B.内切 C.相交 D.外切【答案】B31.两圆的半径分别为2和1,圆心距为3,则反映这两圆位置关系的为图( )。
薛城四中褚召祥圆和圆的位置关系复习

教学过程一、明确考试要求师:同学们,圆和圆的位置关系是初中数学的重要内容,在中考中经常和平行四边形、三角形、函数等内容相联系,今天这节课我们就来复习考点三:圆和圆的位置关系(板书课题).首先请同学们了解一下中考对这部分内容的要求:(可以让学生齐读一下此部分的中考要求)1. 探索并了解圆和圆的位置关系.2. 探索并掌握两圆的圆心距d与两圆的半径R,r之间的关系.设计意图:让学生明白圆和圆的位置关系的重要性,以及中考对这一部分的要求,使学生做到心中有数,有的放矢,在这里起到一个总领作用.二、回顾基础知识师:下面请同学们用五分钟的时间完成以下问题.(注:教案中出现的知识点及后面题组中的题目都以答题纸的形式出现)1.请说出圆与圆的五种位置关系:2.圆与圆的位置关系的性质和判定:设两个圆的半径为R和r(R>r),圆心距为d,则:1、两圆内切.两圆相切 2、两圆外切.3、两圆相交.4、两圆外离两圆相离 .5、两圆内含.3.如果两圆相切,连心线;如果两圆相交,连心线 .设计意图:第1个题目考查圆和圆的五种位置关系,第2个题目考查的是两圆的圆心距d与两圆的半径R,r之间的关系,第3小题是让学生掌握两圆相切相交时连心线的重要性质,让学生在解决这些问题的过程中,回顾本考点的基础知识.通过小组合作及时纠错、讲解、补充,让学生加深对本考点知识的理解,体会小组合作的必要性.在学生充分思考、交流及查找相应课本的基础上,让学生在课前梳理本章的知识框架,为后面的题组训练打好基础,以帮助学生更好的掌握本部分知识.三、组织题组训练考点一.圆与圆的位置关系1.如图,是北京奥运会自行车比赛项目标志,则图中两轮所在圆的位置关系是()A.内含 B.相交 C.相切 D.外离分析:从图形可以看出,图中两轮所在圆的位置关系是外离,故,选择D.点评:以北京奥运会自行车比赛项目标志为载体,设计题目,内容新颖,寓教于乐,能够使同学们在玩中学,学中玩,从而增长知识,2.右图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是( )A .外离B .相交C .外切D .内切分析:由图可以发现,图标中两圆的位置关系是外切,故选择C. 点评:以社会热点问题为载体,考查了同学们关注社会,关注生活的能力。
(全国100套)2013年中考数学试卷分类汇编 圆与圆的位置关系

圆与圆的位置关系1、(2013年某某)如图,圆O 1、圆O 2的圆心O 1、O 2在直线l 上,圆O 1的半径为2 cm ,圆O 2的半径为3 cm ,O 1O 2=8 cm 。
圆O 1以1 cm/s 的速度沿直线l 向右运动,7s 后停止运动,在此过程中,圆O 1与圆O 2没有出现的位置关系是(A) 外切 (B) 相交 (C) 内切 (D) 内含答案:D解析:7s 后两圆刚好内切,所以,外切、相交、内切都有,没有内含,选D 。
(2013凉山州)已知⊙O 1和⊙O 2的半径分别为2cm 和3cm ,圆心距O 1O 2为5cm ,则⊙O 1和⊙O 2的位置关系是( )A .外离B .外切C .相交D .内切考点:圆与圆的位置关系.分析:由⊙O 1与⊙O 2的半径分别为2cm 和3cm ,且圆心距O 1O 2为5cm ,根据两圆位置关系与圆心距d ,两圆半径R ,r 的数量关系间的联系即可得出两圆位置关系.解答:解:∵⊙与⊙O 2的半径分别为2cm 和3cm ,且圆心距O 1O 2为5cm ,又∵2+3=5,∴两圆的位置关系是外切.故选B .点评:此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d ,两圆半径R ,r 的数量关系间的联系.2、(2013•某某)两个圆的半径分别为2和3,当圆心距d=5时,这两个圆的位置关系是( )A . 内含B . 内切C . 相交D . 外切考点:圆与圆的位置关系. 分由两个圆的半径分别为2和3,圆心之间的距离是d=5,根据两圆位置关系与圆心距析:d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵两个圆的半径分别为2和3,圆心之间的距离是d=5,又∵2+3=5,∴这两个圆的位置关系是外切.故选D.点评:此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.3、(2013•某某)已知⊙O1和⊙O2的半径分别是方程x2﹣4x+3=0的两根,且两圆的圆心距等于4,则⊙O1与⊙O2的位置关系是()A.外离B.外切C.相交D.内切考点:圆与圆的位置关系;解一元二次方程-因式分解法分析:由⊙O1与⊙O2的半径r1、r2分别是方程x2﹣4x+3=0的两实根,解方程即可求得⊙O1与⊙O2的半径r1、r2的值,又由⊙O1与⊙O2的圆心距等于4,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵x2﹣4x+3=0,∴(x﹣3)(x﹣1)=0,解得:x=3或x=1,∵⊙O1与⊙O2的半径r1、r2分别是方程x2﹣6x+8=0的两实根,∴r1+r2=3+1=4,∵⊙O1与⊙O2的圆心距d=4,∴⊙O1与⊙O2的位置关系是外切.故选B.点评:此题考查了圆与圆的位置关系与一元二次方程的解法.注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.4、(12-3圆与圆的位置关系·2013东营中考)已知1O ⊙的半径1r =2,2O ⊙的半径2r 是方程321x x =-的根,1O ⊙与2O ⊙的圆心距为1,那么两圆的位置关系为( ) A .内含B .内切C .相交D .外切7.D.解析:解方程321x x =-得,x=3,经检验x=3是原方程的根,所以23r =,因为211r r -=,所以两圆外切.5、(2013•某某)如图,已知⊙O 1的半径为1cm ,⊙O 2的半径为2cm ,将⊙O 1,⊙O 2放置在直线l 上,如果⊙O 1在直线l 上任意滚动,那么圆心距O 1O 2的长不可能是( )A . 6cmB . 3cmC . 2cmD .考点:圆与圆的位置关系. 分析:根据在滚动的过程中两圆的位置关系可以确定圆心距的关系. 解答: 解:∵⊙O 1的半径为1cm ,⊙O 2的半径为2cm , ∴当两圆内切时,圆心距为1,∵⊙O 1在直线l 上任意滚动,∴两圆不可能内含,∴圆心距不能小于1,故选D .点评:本题考查了两圆的位置关系,本题中两圆不可能内含.6、(2013某某)如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为()A.8 B.4 C.4π+4D.4π﹣4考点:扇形面积的计算;圆与圆的位置关系.分析:首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.解答:解:如图所示:可得正方形EFMN,边长为2,正方形中两部分阴影面积为:4﹣π,∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,∵⊙O的半径为2,∴O1,O2,O3,O4的半径为1,∴小圆的面积为:π×12=π,扇形COB的面积为:=π,∴扇形COB中两空白面积相等,∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.故选:A.点评:此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.7、(2013•某某)如图,以等腰直角△ABC两锐角顶点A 、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为()A.B.C.D.考点:扇形面积的计算;相切两圆的性质.3718684分析:根据题意可判断⊙A 与⊙B 是等圆,再由直角三角形的两锐角互余,即可得到∠A+∠B=90°,根据扇形的面积公式即可求解.解答:解:∵⊙A与⊙B恰好外切,∴⊙A与⊙B是等圆,∵AC=2,△ABC是等腰直角三角形,∴AB=2,∴两个扇形(即阴影部分)的面积之和=+==πR2=.故选B.点评:本题考查了扇形的面积计算及相切两圆的性质,解答本题的关键是得出两扇形面积之和的表达式,难度一般.8、(2013•某某)如图,⊙O1,⊙O2、相交于A、B两点,两圆半径分别为6cm和8cm,两圆的连心线O1O2的长为10cm,则弦AB的长为()A.B.C.D.考点:相交两圆的性质.分析:根据相交两圆的性质得出AC=AB,进而利用勾股定理得出AC的长.解答:解:连接AO1,AO2,∵⊙O1,⊙O2相交于A、B两点,两圆半径分别为6cm和8cm,两圆的连心线O1O2的长为10cm,∴O1O2⊥AB,∴AC=AB,设O1C=x,则O2C=10﹣x,∴62﹣x2=82﹣(10﹣x)2,解得:x=3.6,∴AC2=62﹣x22=23.04,∴AC=,∴弦AB的长为:.故选:B.点评:此题考查了相交圆的性质与勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.9、(2013•湘西州)已知⊙O1与⊙O2的半径分别为3cm和5cm,若圆心距O1O2=8cm,则⊙O1与⊙O2的位置关系是()A.相交B.相离C.内切D.外切考点:圆与圆的位置关系.3718684分析:由两圆的半径分别为3cm和5cm,圆心距为8cm,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵两圆的半径分别为3cm和5cm,圆心距为8cm,又∵5+3=8,∴两圆的位置关系是:外切.故选D.点评:此题考查了圆与圆的位置关系.注意掌握两圆位置关系与圆心距d,两圆半径R,r 的数量关系间的联系是解此题的关键.10、(2013•某某)已知⊙O1与⊙O2的半径分别为2cm和3cm,若O1O2=5cm.则⊙O1与⊙O2的位置关系是()A.外离B.相交C.内切D.外切考点:圆与圆的位置关系.分析:由⊙O1、⊙O2的半径分别是2cm和3cm,若O1O2=5cm,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出⊙O1和⊙O2的位置关系.解答:解:∵⊙O1、⊙O2的半径分别是2cm和3cm,若O1O2=5cm,又∵2+3=5,∴⊙O1和⊙O2的位置关系是外切.故选D.点评:此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R﹣r<d<R+r(R≥r);④两圆内切⇔d=R﹣r(R>r);⑤两圆内含⇔d<R﹣r(R>r).11、(2013某某某某4分、4)⊙O1的半径为1cm,⊙O2的半径为4cm,圆心距O1O2=3cm,这两圆的位置关系是()A.相交 B.内切 C.外切 D.内含考点:圆与圆的位置关系.分析:两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r,则两圆相离;若d=R+r,则两圆外切;若d=R﹣r,则两圆内切;若R﹣r<d<R+r,则两圆相交.本题可把半径的值代入,看符合哪一种情况.解答:解:∵R﹣r=4﹣1=3,O1O2=3cm.∴两圆内切.故选B.点评:本题主要考查两圆的位置关系与数量之间的联系.12、(2013凉山州)如图,Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为.考点:扇形面积的计算;勾股定理;相切两圆的性质.专题:计算题.分析:根据题意,可得阴影部分的面积等于圆心角为90°的扇形的面积.解答:解:∵∠C=90°,AC=8,BC=6,∴AB=10,∴扇形的半径为5,∴阴影部分的面积==π.点评:解决本题的关键是把两个阴影部分的面积整理为一个规则扇形的面积.13、(2013•某某)在同一平面内,已知线段AO=2,⊙A的半径为1,将⊙A绕点O按逆时针方向旋转60°得到的像为⊙B,则⊙A与⊙B的位置关系为外切.考点:圆与圆的位置关系;旋转的性质.专题:计算题.分析:根据旋转的性质得到△OAB为等边三角形,则AB=OA=2,而⊙A、⊙B的半径都为1,根据圆与圆的位置关系即可判断两圆的位置关系.解答:解:∵⊙A绕点O按逆时针方向旋转60°得到的⊙B,∴△OAB为等边三角形,∴AB=OA=2,∵⊙A、⊙B的半径都为1,∴AB等于两圆半径之和,∴⊙A与⊙B外切.故答案为外切.点评:本题考查了圆与圆的位置关系:两圆的半径分别为R、r,两圆的圆心距为d,若d=R+r,则两圆外切.也考查了旋转的性质.14、(2013•某某)若两圆的半径分别是2和3,圆心距是5,则这两圆的位置关系是外切.考点:圆与圆的位置关系.分析:两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d<R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.解答:解:∵两圆半径分别为2和3,圆心距为5,则2+3=5,∴两圆外切.故答案为:外切.点评:本题主要考查了两圆的位置关系.两圆的位置关系有:外离(d>R+r)、内含(d<R ﹣r)、相切(外切:d=R+r或内切:d=R﹣r)、相交(R﹣r<d<R+r ).15、(2013•某某)如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=4cm,P 为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的X围是d >5cm或2cm≤d<3cm.考点:圆与圆的位置关系.分析:根据两圆内切和外切时,求出两圆圆心距,进而得出d的取值X围.解答:解:连接OP,∵⊙O的半径为4cm,1cm为半径的⊙P,⊙P与⊙O没有公共点,∴d>5cm时,两圆外离,当两圆内切时,过点O作OD⊥AB于点D,O′P=4﹣1=3cm,OD==2(cm),∴以1cm为半径的⊙P与⊙O没有公共点时,2cm≤d<3cm,故答案为:d>5cm或2cm≤d<3cm.点评: 此题主要考查了圆与圆的位置关系,根据图形进行分类讨论得出是解题关键.16、(2013年某某)如右图,在边长为3的正方形ABCD 中,圆1O 与圆2O 外切,且圆1O 分别与DA 、DC 边相切,圆2O 分别与BA 、BC 边相切,则圆心距12O O 为. 答案:632解析:过O 1,O 2分别作O 1M ⊥CD, O 2N ⊥BC ,垂足为M,N设圆O 1半径为R,圆O 2半径为r, 则DO 1=2R ,BO 2=2r,又BD=32,所以2R +2r+r+R=32 解得R +r=6-32,即12O O =6-3217、(2013•某某州)如图所示,一半径为1的圆内切于一个圆心角为60°的扇形,则扇形的周长为 6+π .考相切两圆的性质;含30度角的直角三角形;切线的性质;弧长的计算.CDO 2O 1B分析:首先求出扇形半径,进而利用扇形弧长公式求出扇形弧长,进而得出扇形周长.解答:解:如图所示:设⊙O与扇形相切于点A,B,则∠CAO=90°,∠AOB=30°,∵一半径为1的圆内切于一个圆心角为60°的扇形,∴AO=1,∴CO=2AO=2,∴BC=2=1=3,∴扇形的弧长为:=π,∴则扇形的周长为:3+3+π=6+π.故答案为:6+π.点评:此题主要考查了相切两圆的性质以及扇形弧长公式等知识,根据已知得出扇形半径是解题关键.18、(2013•六盘水)若⊙A和⊙B相切,它们的半径分别为8cm和2cm,则圆心距AB为10或6 cm.考点:圆与圆的位置关系.专题:分类讨论.分本题应分内切和外切两种情况讨论.解答:解:∵⊙A和⊙B相切,∴①当外切时圆心距AB=8+2=10cm,②当内切时圆心距AB=8﹣2=6cm.故答案为:10或6.点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.外切时P=R+r;内切时P=R﹣r;注意分情况讨论.19、(2013•某某)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且O1O2=t+2,若这两个圆相切,则t= 2或0 .考点:圆与圆的位置关系;解一元二次方程-因式分解法.分析:先解方程求出⊙O1、⊙O2的半径,再分两圆外切和两圆内切两种情况列出关于t的方程讨论求解.解答:解:∵⊙O1、⊙O2的半径分别是方程x2﹣4x+3=0的两根,解得⊙O1、⊙O2的半径分别是1和3.①当两圆外切时,圆心距O1O2=t+2=1+3=4,解得t=2;②当两圆内切时,圆心距O1O2=t+2=3﹣1=2,解得t=0.∴t为2或0.故答案为:2或0.点评:考查解一元二次方程﹣因式分解法和圆与圆的位置关系,同时考查综合应用能力及推理能力.注意:两圆相切,应考虑内切或外切两种情况是解本题的难点.20、(2013•某某地区)已知⊙O1与⊙O2的半径分别是a,b,且a、b满足,圆心距O1O2=5,则两圆的位置关系是外切.考点:圆与圆的位置关系;非负数的性质:绝对值;非负数的性质:算术平方根.分析:首先根据求得a、b的值,然后根据半径与圆心距的关系求解即可.解答:解:∵,∴a﹣2=0,3﹣b=0解得:a=2,b=3∵圆心距O1O2=5,∴2+3=5∴两圆外切,故答案为:外切.点评:此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.21、(2013•某某)如图,⊙A、⊙B、⊙C两两外切,它们的半径都是a,顺次连接三个圆心,则图中阴影部分的面积是.考相切两圆的性质;扇形面积的计算.3718684点:根据三角形内角和定理以及扇形面积公式直接求出即可.分析:解解:∵⊙A、⊙B、⊙C两两外切,它们的半径都是a,答:∴阴影部分的面积是:=.故答案为:.点此题主要考查了扇形面积求法,根据已知得出扇形圆心角的和是解题关键.评:22、(2013•某某)如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为﹣π.考点:三角形的内切圆与内心.3718684分析:连接OB,以及⊙O与BC的切点,在构造的直角三角形中,通过解直角三角形易求得⊙O的半径,然后作⊙O与小圆的公切线EF,易知△BEF也是等边三角形,那么小圆的圆心也是等边△BEF的重心;由此可求得小圆的半径,即可得到四个圆的面积,从而由等边三角形的面积减去四个圆的面积和所得的差即为阴影部分的面积.解答:解:如图,连接OB、OD;设小圆的圆心为P,⊙P与⊙O的切点为G;过G作两圆的公切线EF,交AB于E,交BC于F,则∠BEF=∠BFE=90°﹣30°=60°,所以△BEF是等边三角形.在Rt△OBD中,∠OBD=30°,则OD=BD•tan30°=1×=,OB=2OD=,BG=OB﹣OG=;由于⊙P是等边△BEF的内切圆,所以点P是△BEF的内心,也是重心,故PG=BG=;∴S⊙O=π×()2=π,S⊙P=π×()2=π;∴S阴影=S△ABC﹣S⊙O﹣3S⊙P=﹣π﹣π=﹣π.故答案为﹣π.点评:此题主要考查了等边三角形的性质、相切两圆的性质以及图形面积的计算方法,难度适中.23、(2013•某某)若⊙O1和⊙O2的圆心距为4,两圆半径分别为r1、r2,且r 1、r2是方程组的解,求r1、r2的值,并判断两圆的位置关系.考点:圆与圆的位置关系;解二元一次方程组.分析:首先由r1、r2是方程组的解,解此方程组即可求得答案;又由⊙O1和⊙O2的圆心距为4,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系得出两圆位置关系.解答:解:∵,①×3﹣②得:11r2=11,解得:r2=1,吧r2=1代入①得:r 1=4;∴,∵⊙O1和⊙O2的圆心距为4,∴两圆的位置关系为相交.点评:此题考查了圆与圆的位置关系与方程组的解法.注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.24、(2013某某压轴题)在矩形ABCD 中,点P 是边AD 上的动点,联结BP ,线段BP 的垂直平分线交边BC 于点Q ,垂足为点M ,联结QP (如图10).已知13AD =,5AB =,设AP x BQ y ==,. (1)求y 关于x 的函数解析式,并写出x 的取值X 围;(2)当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时,求x 的值;(3)点E 在边CD 上,过点E 作直线QP 的垂线,垂足为F ,如果4EF EC ==,求x 的值.DC备用图QM DP图10。
鲁教版中考数学一轮复习 圆 专题2 与圆有关的位置关系(含答案)

第六单元圆专题2 与圆有关的位置关系考点1 点和圆、直线和圆的位置关系1.已知平面内有⊙O和点A,B,若⊙O半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⊙O的位置关系为( )A.相离B.相交C.相切D.相交或相切2.点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9 cm,则⊙O 的半径是___________.3.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点.若以1cm为半径的⊙O与直线a相切,则OP的长为___________.考点2 切线的性质与判定1.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则∠ACB的大小为( )A.35°B.45°C.55°D.65°2.如图,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线3.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )A.1B.2C.√2C.√34.如图,在▱ABCD中,AD=12,以AD为直径的⊙O与BC相切于点E,连接OC.若OC=AB,则▱ABCD 的周长为____________.5.如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC.当△OAC是直角三角形时,其斜边长为_____________.6.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=___________.7.如图,PA是以AC为直径的⊙O的切线,切点为A,过点A作AB⊥OP,交⊙O于点B. (1)求证:PB是⊙O的切线;,求PO的长.(2)若CC=6,cos∠CCC=358.如图,AB为⊙O的直径,四边形ABCD内接于⊙O,对角线AC,BD交于点E,⊙O的切线AF交BD的延长线于点F,切点为A,且∠CAD=∠ABD.(1)求证:AD=CD;(2)若AB=4,BF=5,求sin∠BDC的值.̂上一点,连接AE并延长至点C,使9.已知:如图,AB是⊙O的直径,E为⊙O上一点,D是AE∠CBE=∠BDE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:AD²=DF· DB.考点3 三角形的外接圆与内切圆1.如图,已知点O是△ABC的外心,∠A=40°,连接BO,CO,则∠BOC的度数是( )A.60°B.70°C.80°D.90°2.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD是⊙O的直径,若AD=3,则CC=( )C.2√3C.3√3 C.3D.43.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h,r,R,则下列结论不正确的是( )A.h=R+rB.R=2rC.C=√34C C.C=√33C4.如图,△ABC内接于⊙O,∠A=50°,点D是BC的中点,连接OD,OB,OC,则∠BOD=_______.5.如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为_____________.6.已知△ABC的三边a,b,c满足b+|c-3|+C2−8C=4√C−1−19,则△ABC的内切圆半径=____________.专题检测一、选择题(每小题4分,共40分)1.平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )A.点P在⊙O外B.点P在⊙O上C.点P在⊙O内D.无法判断2.已知⊙O的半径为5,点O到直线l的距离为3,则⊙O上到直线l的距离为2的点共有( )A.1个B.2个C.3个D.4个3.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )A.75°B.70°C.65°D.60°̂上一点,则∠EPF的4.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是DF度数是( )A.65°B.60°C.58°D.50°5.如图,PA,PB是⊙O的切线,A,B是切点,若∠P=70°,则∠ABO=( )A.30°B.35°C.45°D.55°6.如图,长方形ABCD中,AB=4,AD=3,圆B 半径为1,圆A与圆B内切,则点C、D与圆A的位置关系是( )A.点C在圆A外,点D在圆A内B.点C在圆A外,点D在圆A外C.点C在圆A上,点D在圆A内D.点C在圆A内,点D在圆A外7.如图,在等腰△ABC中, AB=AC=2√5,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分EF的长为半径作弧相交于点H,作射线AH;别以点E,F为圆心,大于12AB的长为半径作弧相交于点M,N,作直线②分别以点A,B为圆心,大于12MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为( )A.2√5B.10C.4D.58.如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,若OB=6 cm,OC=8cm,则BE+CG的长等于( )A.13 cmB.12 cmC.11 cmD. 10 cm9.如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD与⊙O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于( )A.35B.23C.34D.4510.如图,点A的坐标为(-3,2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A于点Q,在所有P点中,使得PQ长最小时,点P的坐标为( )A.( 0,2)B.( 0,3)C.( -2,0)D.( -3,0)二、填空题(每小题4分,共24分)11.点A(0,3),点B(4,0),则点O(0,0)在以AB为直径的圆 (填“内”“上”或“外”).12.如图,在△ABC中,D是边BC上的一点,以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为___________.13.点O是△ABC的外心,若∠BOC=110°,则∠BAC为 .14.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .15.如图,PA,PB是⊙O的切线,A,B是切点.若∠P=50°,则∠AOB= .16.如图,两个圆都是以点O为圆心,大圆的弦AB是小圆的切线,点P为切点,AB=10,则图中圆环的面积为 .三、解答题(共36分)17.(12分)阅读下列材料:平面上两点P₁(x₁,y₁),P₂(x₂,y₂)之间的距离表示为|P1P2|=√(x1−x2)2+(y1−y2)2,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为√(x−a)2+(y−b)2=r,变形可得 (x-a)²+(y-b)²=r², 我们称其为圆心为C(a,b),半径为r的圆的标准方程.例如:由圆的标准方程(x-1)²+(y-2)²=25 可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.(1)圆心为C(3,4),半径为2的圆的标准方程为 ;(2)若已知⊙O的标准方程为(x-2)²+y²=2²,圆心为C,请判断点A(3,-1)与⊙O的位置关系.18.(12分)已知△ABC内接于⊙O,AB=AC,∠BAC=42°,点D是⊙O上一点.(1)如图①,若BD为⊙O的直径,连接CD,求∠DBC和∠ACD的大小;(2)如图②,若CD∥BA,连接AD,过点D作⊙O的切线,与OC的延长线交于点E,求∠E的大小.19.(12分)如图,在△ABC中,∠ACB=90°,BO为△ABC的角平分线,以点O为圆心,OC为半径作⊙O与线段AC交于点D.(1)求证:AB为⊙O的切线;,AD=2,求BO的长.(2)若tanA=34参考答案考点1 点和圆、直线和圆的位置关系1.D ⊙O的半径为2 cm,线段OA=3cm,OB=2cm,即点A到圆心O的距离大于圆的半径,点B 到圆心O的距离等于圆的半径,∴点A在⊙O外,点B在⊙O上,∴直线AB 与⊙O的位置关系为相交或相切.2.6.5cm或2.5cm 分为两种情况:①当点在圆内时,如图1,∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,∴直径AB=4+9=13(cm),∴半径r=6.5 cm;②当点在圆外时,如图2,∵点到圆上的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=9-4=5(cm),∴半径r=2.5cm.3.3cm或5cm ∵直线a⊥b,O为直线b上一动点,∴⊙O与直线a相切时,切点为H,∴OH=1 cm. 当点O在点H的左侧,⊙O与直线a相切时,OP=PH-OH=4-1=3(cm);当点O在点H的右侧,⊙O与直线a相切时,OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm.考点2 切线的性质与判定1.C ∵BC是⊙O的切线,AB是⊙O的直径,∴AB⊥BC,∴∠ABC=90°,∴∠ACB=90°-∠BAC=90°-35°=55°.2.B 由切线长定理,得PA=PB,∴△BPA 是等腰三角形,故A正确;由圆的对称性可知AB⊥PD,但不一定平分,故B不一定正确;如图,连接OB,OA,由切线的性质,得∠OBP=∠OAP=90°,∴点A,B,P在以OP为直径的圆上,故C正确;∵△BPA是等腰三角形,PD⊥AB,∴PC为△BPA的边AB上的中线,故D正确.3.D 如图,连接OB.∵四边形OABC是菱形.∴OA=AB.∵OA=OB,∴OA=AB=OB,∴∠AOB=60°.∵BD是⊙O的切线,∴∠DBO=90°.∵OB=1,∴BD=√3OB=√3.4.24+6√5如图,连接OE,过点C作CF⊥AD交AD于点F,∵四边形ABCD为平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠EOD+∠OEC =180°,∵⊙O与BC相切于点E,∴OE⊥BC,∴∠OEC=90°,∴∠EOD=90°,∵CF⊥AD,∴∠CFO=90°,∴四边形OECF为矩形,∴FC=OE,OD=3,∵AD为直径,AD=12,∴FC=OE=OD= 12在Rt△OFC中,由勾股定理得OC²=OF²+FC²=3²+6²=45.∴AB=OC=3√5,∴平行四边形ABCD的周长为12+12+3√5+3√5=24+6√5.5.2√3或2√2连接OB,∵BC是⊙O的切线,∴∠OBC=90°.∵BC=OA,∴OB=BC=2,∴△OBC是等腰直角三角形,∴∠BCO=45°,∴∠ACO≤45°.当△OAC是直角三角形时,①若∠AOC=90°,∴OC=√2OB=2√2,∴AC=√OA2+OC2=√22+(2√2)2=2√3;②若∠OAC=90°,∵BC是⊙O的切线,∴∠CBO=∠OAC=90°.∵BC=OA=OB,∴△OBC是等腰直角三角形,∴OC= 2√2.6.27°∵ PA切⊙O于点A,∴∠OAP=90°.∵∠P=36°, ∴∠AOP=54°. ∴∠B=12∠AOP=27 ∘.7.(1)证明连接OB,如图,∵PA是以AC为直径的⊙O的切线,切点为A,∴∠PAO=90°, ∵OA=OB,AB⊥OP,∴∠POA=∠POB,在△PAO和△PBO中, {AO=BO,∠POA=∠POB,OP=OP,∴△PAO≌△PBO(SAS),∴∠PBO=∠PAO=90°,即OB⊥PB,又∵OB为⊙O的半径,∴PB是⊙O的切线;(2)解设OP与AB交于点D.∵AB⊥OP,AB=6,∴DA=DB=3,∠PDA =∠PDB=90°,∵cos∠PAB=35=DAPA=3PA,∴PA=5,∴PD=√PA2−AD2=√52−32=4,在Rt△APD和Rt△APO中,cos∠APD= PDPA ,cos∠APO=PAPO,8.(1)证明∵∠CAD=∠ABD,∠ABD=∠ACD,∴∠ACD=∠CAD,∴AD=CD;(2)解∵AF是⊙O的切线,∴∠FAB=90°.∵AB是⊙O的直径,∴∠ACB=∠ADB=∠ADF=90°,∴∠ABD+∠BAD=∠BAD+∠FAD=90°. ∴∠ABD=∠FAD.∵∠ABD=∠CAD,∠CAD=∠EAD,∴∠FAD=∠EAD.∵AD=AD,∴△ADF≌△ADE(ASA).∴AF=AE,DF=DE.∵AB=4,BF=5,∴AF =√BF 2−AB 2=3,∴AE=AF=3. ∵S △ABF =12AB ⋅AF =12BF ⋅AD, ∴AD =AB⋅AF BF=4×35=125,∴DE =√AE 2−AD 2=√32−(125)2=95, ∴BE =BF −2DE =75.∵∠AED=∠BEC,∠ADE=∠BCE=90°.∴△BEC ∽△AED. ∴BEAE =BCAD , ∴BC =BE⋅AD AE=2825, ∴sin ∠BAC =BC AB =725.∵∠BDC=∠BAC,∴sin ∠BDC =725.9.证明 (1)∵AB 是⊙O 的直径,∴∠AEB=90°,∴∠EAB+∠EBA=90°. ∵∠CBE=∠BDE,∠BDE=∠EAB,∴∠EAB=∠CBE,∴∠EBA+∠CBE=∠EBA+∠EAB=90°,即∠ABC=90°,∴CB ⊥AB. ∵AB 是⊙O 的直径,∴BC 是⊙O 的切线. (2)∵BD 平分∠ABE,∴∠ABD=∠DBE. ∵∠DAF=∠DBE,∴∠DAF=∠DBA.∵∠ADB=∠FDA,∴△ADF ∽△BDA, ∴ADBD =DFAD ,∴AD ²=DF ·DB. 考点3 三角形的外接圆与内切圆1.C ∵点O 为△ABC 的外心,∠A=40°, ∴∠A =12∠BOC,∴∠BOC =2∠A =80 ∘. 2.C 过点O 作OE ⊥BC 于点E,如图所示:∵∠BAC=120°,AB=AC,∴∠ABC=∠ACB=30°,又 ∵AB̂对应的圆周角为∠ACB 和∠ADB,∴∠ACB=∠ADB=30°, 而BD 为直径,∴∠BAD=90°,在Rt △BAD 中,∠ADB=30°,AD=3, ∴cos30 ∘=ADBD =3BD =√32,∴BD =2√3,∴OB =√3,又∵∠ABD=90°-∠ADB=90°-30°=60°,∠ABC=30°,∴∠OBE=30°. 又∵OE ⊥BC,∴△OBE 为直角三角形. ∴cos ∠OBE =cos30 ∘−BEOB =√3=√32, ∴BE =32.由垂径定理可得BC=2BE= 2×32=3.3.C 如图,∵△ABC是等边三角形.∴△ABC的内切圆和外接圆是同心圆,圆心为O. 设OE=r,AO=R,AD=h,∴h=R+r,故A正确;∵AD⊥BC,∴∠DAC=12∠BAC=12×60°=30°.在Rt△AOE中,∴R=2r,故B正确;∵OD=OE=r,AB=AC=BC=a,∴AE=12AC=12a,∴(12a)2+r2=(2r)2,(12a)2+(12R)2=R².∴r=√36a,R=√33a,故C错误,D正确.4.50°∵∠A=50° ,∴∠BOC=100°.∵OB=OC,∴△OBC为等腰三角形,又∵D为BC 中点,∴OD为BC上的中线,根据等腰三角形三线合一性质可得OD为∠BOC的平分线∴∠BOD=12∠BOC=50∘.5.(2,3) 根据A,B,C三点的坐标建立如图所示的坐标系.根据题意,得AB=√62+32=3√5,AC=√42+82=4√5,BC=√102+52=5√5.∵AB²+AC²=BC².∴∠BAC=90°.设BC的函数表达式为y=kx+b,代入B( -3,3),C(7,-2).得{3=−3k+b,−2=7k+b,解得{k=−12,b=32,∴BC的函数表达式为y=−12x+32.当y=0时,x=3,即G(3,0),∴点A与点G关于BD对称,射线BD是∠ABC的平分线.设点M为三角形的内心,内切圆的半径为r,在BD上找一点M,过点M作ME⊥AB,过点M作MF⊥AC,且ME=MF=r.∵∠BAC=90°,∴四边形MEAF为正方形, S ABC=12AB×AC=12AB×r+12AC×r+12BC×r,解得r=√5,即AE=EM=√5,∴BE=3√5−√5=2√5,∴BM=√BE2+EM2=5,∵B( -3,3),∴M(2,3).∴△ABC内心M的坐标为(2,3).6.1 ∵b+|c−3|+a2−8a=4√b−1−19,∴|c−3|+(a−4)2+(√b−1−2)2= 0,∴c=3,a=4,b=5.∵3²+4²=25=5²,∴c²+a²=b²,∴△ABC是直角三角形,∠ABC=90°.设内切圆的半径为r.根据题意,得S△ABC=12×3×4=12×3×r+12×4×r+12×r×5,∴r=1.(或者r=3+4−52=1)专题检测1.C2.C 如图,∵⊙O的半径为5,点O到直线l 的距离为3,∴CE=2,过点D作AB⊥ OC,垂足为D,交⊙O于A,B两点,且DE=2,∴⊙O上到直线l的距离为2的点为A,B,C,∴⊙O上到直线l的距离为2的点有3个.3.B4.B5.B 如图,连接OA.∵PA,PB是⊙O的切线,A,B是切点,∴∠PBO=∠PAO=90°,∵∠P=70°,∴∠BOA=360°—∠PBO—∠PAO-∠P=110°,∵OA=OB,∴∠ABO=∠BAO=12(180∘−∠BOA)=12(180 ∘−110 ∘)=35 ∘.6.C 两圆内切,圆心距等于半径之差的绝对值,设圆A的半径为R,则AB=R-1,∵AB =4,圆B半径为1,∴R=5,即圆A的半径等于5,∵AB=4,BC=AD=3,由勾股定理可知AC=5,∴AC=5=R,AD=3C在圆上,点D在圆内.7.D 如图,连接OC,设OA交BC于点T.∵AB=AC=2√5,AO平分∠BAC,∴AO⊥BC,BT=TC=4,∴AT=√AC2−CT2=√(2√5)2−42=2.在Rt△OCT中.有r²=(r-2)²+4²,解得r=5.8.D9.D 连接OC、OD、CD,CD交PA于点E,如图,∵PC,PD与⊙O相切,切点分别为C,D,∴OC⊥CP,PC=PD,OP平分∠CPD.∴OP⊥CD,∴CB̂=DB̂,∴∠COB=∠DOB,∵∠CAD=12∠COD,∴∠COB=∠CAD,在Rt△OCP中, OP=√OC2+PC2=√32+42=5,∴sin∠COP=PCOP =45,∴sin∠CAD=45.10.D 连接AQ、PA,如图,∵PQ切⊙A于点Q,∴AQ⊥PQ,∴∠AQP=90°,∴PQ=√AP2−AQ2=√AP2−1,当AP的长度最小时,PQ的长度最小,∵AP⊥x轴时,AP的长度最小,∴AP⊥x轴时,PQ的长度最小,∵A(-3,2),∴此时P点坐标为(-3,0).11.上 12.55°13.55°或125°分两种情况:(1)点A 与点O 在BC 边同侧时,如图1:∵∠BOC=110°,∴∠BAC =110 ∘×12=55 ∘. (2)点A 与点O 在BC 边两侧时,如图2:∵∠BOC=110°,即BĈ所对的圆心角为110°,∴BDC ̂所对的圆心角为:360°—110°=250°. ∴∠BAC =12×250 ∘=125 ∘. 14.4415.130° ∵PA,PB 是⊙O 的切线,A,B 是切点,∴OA ⊥PA,OB ⊥PB,∴∠OAP=∠OBP=90°,∵∠OAP+∠AOB+∠OBP +∠P=360°,∴∠AOB=360°—90°—90°-50°=130°. 16.25π 如图,连接OP 、OA,∵大圆的弦AB 是小圆的切线,∴OP ⊥AB, ∴AP=BP= 12AB =5, 由勾股定理得OA ²-OP ²=AP ²=25, ∴圆环的面积=π×OA ²-π×OP ²=π×(OA ²-OP ²)=25π.17.解 (1)圆心为C(3,4),半径为2的圆的标准方程为(x-3)²+( y-4)²=4.故答案为:(x-3)²+(y-4)²=4. (2)由题意得圆心为C(2.0),∵A (3,−1),∴AC =√(3−2)2+12= √2<2,∴点A 在⊙C 内部.18.解 (1)∵AB=AC,∴∠ABC=∠ACB= 12(180 ∘−∠BAC)=12×(180 ∘−42 ∘)=69 ∘,∵BD 为直径,∴∠BCD=90°,∵∠D=∠BAC=42°,∴∠DBC=90°-∠D=90°-42°=48°; ∴∠ACD=∠ABD=∠ABC-∠DBC=69°-48°=21°; (2)如图,连接OD,∵CD ∥AB,∴∠ACD=∠BAC=42°,∵四边形ABCD 为⊙O 的内接四边形,∴∠B+∠ADC=180°, ∴∠ADC=180°-∠B=180°-69°=111°,∴∠CAD=180°-∠ACD-∠ADC=180°-42°-111°=27°,∴∠COD=2∠CAD=54°, ∵DE 为切线,∴OD ⊥DE,∴∠ODE=90°,∴∠E=90°-∠DOE=90°-54°=36°. 19.(1)证明如图,过点O 作OH ⊥AB 于点H.∵∠ACB=90°,∴OC ⊥BC.∵BO 为△ABC 的角平分线,OH ⊥AB,∴OH=OC,即OH 为⊙O 的半径. ∵OH ⊥AB,∴AB 为⊙O 的切线.(2)解设⊙O 的半径为3x,则OH=OD=OC=3x.在Rt △AOH 中,∵tanA =34, ∴OHAH =34,∴3xAH =34,∴AH=4x, ∴AO =√OH 2+AH 2=√(3x )2+(4x )2=5x,∵AD=2,∴AO=OD+AD=3x+2,∴3x+2=5x,∴x=1,∴OA=3x+2=5,OH=OD=OC=3x=3 . ∴AC=OA+OC=5+3=8.在Rt △ABC 中, ∵tanA =BCAC ,∴BC =AC ⋅tanA =8×34=6, ∴OB =√OC 2+BC 2=√32+62=3√5.。
《圆与圆的位置关系》练习题(含答案)

10题B A O'O O 3O 218题O 1A 20题B A 19题16题P O 《圆与圆的位置关系》练习题1.⊙O 1与⊙O 2的半径分别为3cm 和8cm,①若两圆相切,则圆心距O 1O 2= ;②若O 1O 2=4㎝,则两圆 ;③若两圆相交,则圆心距O 1O 2的取值范围为 ;④若两圆有公共点,则圆心距O 1O 2的取值范围为 。
2.相切两圆的半径分别为8㎝和x ㎝,圆心距为10㎝,则x 的值为 。
3.⊙O 1与⊙O 2相切,⊙O 1的半径为6cm ,①若O 1O 2=4㎝,则⊙O 2的半径为 ;②若O 1O 2=8㎝,则⊙O 2的半径为 。
4.两圆半径之比为3︰5,若两圆相外切,且圆心距为8㎝,则两圆相内切时,圆心距为 .5.在平面直角坐标系中,A 、B 两点的坐标分别是(0,5)、(12,0),分别以A 、B 为圆心作⊙A 、⊙B ,①若两圆的半径分别是8、3,则两圆的位置关系为 ;②若两圆的半径分别是15、2,则两圆的位置关系为 ;③若两圆的半径分别是7、6,则两圆的位置关系为 ;④若⊙A 的半径为8㎝,则当⊙B 的半径为 时,两圆相切。
6.半径分别为2、4、6的三个圆两两外切,则以这三个圆的圆心为顶点的三角形的形状为 .7.△ABC 的三边分别为AB=5㎝、BC=6㎝、AC=7㎝,若分别以A 、B 、C 三点为圆心作⊙A 、⊙B 、⊙C ,它们两两外切,则⊙A 、⊙B 、⊙C 的半径分别为 。
8.若两圆半径分别为r 1、r 2,圆心距为d,关于x 的一元二次方程x 2-2r 1x+(r 2-d)2=0有两个相等的实数根,则这两圆的位置关系为 。
9. ⊙O 1与⊙O 2是等圆,且两圆交于A 、B 两点,⊙O 1经过⊙O 2的圆心O 2,连接O 1A 、O 1B 、O 2A 、O 2B ,则四边形O 1AO 2B 的形状为 。
10.如图所示,两个等圆⊙O 与⊙O ’相外切,则∠AOB 的度数为 。
圆与圆的位置关系(含答案)

圆与圆的位置关系班级:____________ 姓名:__________________一、选择题1.已知0<r<2+1,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是()A.外切B.相交C.外离D.内含2.若两圆x2+y2-2x+10y+1=0,x2+y2-2x+2y-m=0相交,则m的取值范围是() A.(-2,39) B.(0,81) C.(0,79) D.(-1,79)3.圆C1:x2+y2+4x-4y+7=0和圆C2:x2+y2-4x-10y+13=0的公切线有() A.2条B.3条C.4条D.0条4.已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是() A.(x-5)2+(y+7)2=25B.(x-5)2+(y+7)2=17或(x-5)2+(y+7)2=15C.(x-5)2+(y+7)2=9D.(x-5)2+(y+7)2=25或(x-5)2+(y+7)2=95.若圆(x-a)2+(y-b)2=b2+1始终平分圆(x+1)2+(y+1)2=4的周长,则a,b满足的关系式是() A.a2-2a-2b-3=0B.a2+2a+2b+5=0C.a2+2b2+2a+2b+1=0D.3a2+2b2+2a+2b+1=06.若集合A={(x,y)|x2+y2≤16},B={(x,y)|x2+(y-2)2≤a-1}且A∩B=B,则a的取值范围是() A.a≤1 B.a≥5 C.1≤a≤5 D.a≤57.两圆相交于A(1,3)和B(m,-1)两点,且两圆圆心都在直线x-y+c=0上,则m+c的值是() A.-1 B.2 C.3 D.08.若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称,且过点C(-a,a)的圆P与y轴相切,则圆心P的轨迹方程为()A.y2-2x+2y+8=0 B.y2+2x-2y+8=0C.y2+4x-4y+8=0 D.y2-4x+4y+8=0二、填空题9.若圆x2+y2=4与圆x2+y2-2ax+a2-1=0相内切,则a=________.10.集合A={(x,y)|x2+y2=4},B={(x,y)|(x-3)2+(y-4)2=r2},其中r>0 ,若A∩B中有且仅有一个元素,则r的值是__________.11.若⊙O:x2+y2=5与⊙O1:(x-m)2+y2=20(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是__________.12.已知点M在圆C1:(x+3)2+(y-1)2=4上,点N在圆C2:(x-1)2+(y+2)2=4上,则|MN|的最大值是__________.三、解答题13.a为何值时,两圆x2+y2-2ax+4y+a2-5=0和x2+y2+2x-2ay+a2-3=0.(1)外切;(2)内切.14.点M在圆心为C1的方程x2+y2+6x-2y+1=0上,点N在圆心为C2的方程x2+y2+2x+4y+1=0上,求|MN|的最大值.15.已知圆A:x2+y2+2x+2y-2=0,若圆B平分圆A的周长,且圆B的圆心在直线l:y=2x上,求满足上述条件的半径最小的圆B的方程.(选做题)16.如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得PM=2PN.试建立适当的坐标系,求动点P的轨迹方程.答案 1.B 2.D 3.B 4.D 5.B 6.D 7.C 8.C9.±110.3或711.412.913.解 将两圆方程写成标准方程,得(x -a )2+(y +2)2=9,(x +1)2+(y -a )2=4.设两圆的圆心距为d ,则d 2=(a +1)2+(-2-a )2=2a 2+6a +5.(1)当d =3+2=5,即2a 2+6a +5=25时,两圆外切,此时a =-5或2.(2)当d =3-2=1,即2a 2+6a +5=1时,两圆内切,此时a =-1或-2.14.解 把圆的方程都化成标准形式,得(x +3)2+(y -1)2=9,(x +1)2+(y +2)2=4.如图,C 1的坐标是(-3,1),半径长是3;C 2的坐标是(-1,-2),半径长是2.所以,|C 1C 2|=(-3+1)2+(1+2)2=13.因此,|MN |的最大值是13+5.15.解 设圆B 的半径为r ,因为圆B 的圆心在直线l :y =2x 上,所以圆B 的圆心可设为(t,2t ),则圆B 的方程是(x -t )2+(y -2t )2=r 2,即x 2+y 2-2tx -4ty +5t 2-r 2=0.①因为圆A 的方程为x 2+y 2+2x +2y -2=0,②所以②-①,得两圆的公共弦所在直线的方程为(2+2t )x +(2+4t )y -5t 2+r 2-2=0.③因为圆B 平分圆A 的周长,所以圆A 的圆心(-1,-1)必须在公共弦上,于是将x =-1,y =-1代入方程③并整理得r 2=5t 2+6t +6=5⎝⎛⎭⎫t +352+215≥215, 所以当t =-35时,r min =215. 此时,圆B 的方程是⎝⎛⎭⎫x +352+⎝⎛⎭⎫y +652=215. 16.以O 1O 2所在直线为x 轴,O 1O 2的垂直平分线为y 轴,建立平面直角坐标系,则O 1(-2,0),O 2(2,0).设动点P(x ,y).由题意得|PM|2=|O 1P|2-|O 1M|2=(x +2)2+y 2-1.同理,可得|PN|2=(x -2)2+y 2-1.∵|PM|=2|PN|,∴|PM|2=2|PN|2.∴(x +2)2+y 2-1=2[(x -2)2+y 2-1],即x 2+y 2-12x +3=0.∴动点P 的轨迹方程是x 2+y 2-12x +3=0.。
(完整版)初中中考复习之圆与圆的位置关系(精编含答案)

中考复习之圆与圆的位置关系一、选择题:1.如果两圆的半径长分别为 6 和2,圆心距为 3,那么这两个圆的位置关系是【】A.外离B.相切C.相交D.内含2.若两圆的半径分别为 2cm 和6cm,圆心距为 4cm,则这两圆的位置关系是【】A.内含 B.内切 C.外切 D.外离3.如图,用邻边分别为 a,b(a<b)的矩形硬纸板裁出以 a 为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则 a 与b 满足的关系式是【】A.b= a B.b= 5+1a2C.b=5a2D.b= 2a4.已知⊙O1与⊙O2外切,O1O2=8cm,⊙O1的半径为5cm,则⊙O2的半径是【】A.13cm.B. 8cmC. 6cmD. 3cm5.已知两圆半径分别为7,3,圆心距为4,则这两圆的位置关系为【】A.外离B.内切C.相交D.内含6.若⊙O1,⊙O2的半径是r1=2, r2=4,圆心距d=5,则这两个圆的位置关系是【】A.内切B.相交C.外切D.外离7.已知⊙O1、⊙O2的半径分别为3cm、5cm,且它们的圆心距为8cm,则⊙O1与⊙O2的位置关系是【】A.外切B.相交C.内切D.内含8.⊙O1和⊙O2的半径分别是3cm 和4cm,如果O1O2=7cm,则这两圆的位置关系是【】A.内含B.相交C.外切D.外离9.若两圆的半径分别为2 和4,且圆心距为7,则两圆的位置关系为【】A.外切B. 内切C. 外离D. 相交10.如图,平面直角坐标系中,⊙O半径长为 1.点⊙P(a,0),⊙P的半径长为 2,把⊙P向左平移,当⊙P与⊙O相切时,a 的值为【】(A)3 (B)1 (C)1,3 (D)±1,±311.已知两圆外切,圆心距为5cm,若其中一个圆的半径是3cm,则另一个圆的半径是【】A.8cm B.5cm C.3cm D.2cm12.⊙O1的半径为3 厘米,⊙O2的半径为2 厘米,圆心距O1O2=5 厘米,这两圆的位置关系是【】A.内含B.内切C.相交D.外切13.已知两圆的半径分别为1 和3,当这两圆内含时,圆心距d 的范围是【】A. 0<d<2B. 1<d<2C. 0<d<3D. 0≤d<214.圆心距为2 的两圆相切,其中一个圆的半径为1,则另一个圆的半径为【】(A)1 (B)3 (C)1 或2 (D)1 或315.第三十奥运会将于 2012 年7 月27 日在英国伦敦开幕,奥运会旗图案有五个圆环组成,下图也是一幅五环图案,在这个五个圆中,不存在的位置关系是【】 A 外离 B 内切 C 外切 D 相交16.已知两圆相外切,连心线长度是 10 厘米,其中一圆的半径为 6 厘米,则另一圆的半径是【】A.16 厘米B.10 厘米C.6 厘米D.4 厘米17.如果两圆的半径分别为4 和6,圆心距为10,那么这两圆的位置关系是【】A.内含B.外离C.相交D.外切18.已知⊙O1与⊙O2的半径分别为4 和6,O1O2=2,则⊙O1与⊙O2的位置关系是【】A.内切B.相交C.外切D.外离19.如图,⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm,⊙O与其他4个圆均相外切,图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,则四边形O1O4O2O3的面积为【】A.12cm2B.24cm2C.36cm2D.48cm220.已知两圆的半径分别是3 和4,圆心距的长为1,则两圆的位置关系为:【】A.外离B.相交C.内切D.外切21.已知两圆半径为5cm 和3cm,圆心距为3cm,则两圆的位置关系是【】A.相交B.内含C.内切D.外切22.定圆O 的半径是4cm,动圆P 的半径是2cm,动圆在直线l 上移动,当两圆相切时,OP 的值是【】A.2cm 或6cm B.2cm C.4cmD.6cm23.若两圆的半径是方程x2﹣5x+6=0 的两个根,且圆心距是5,则这两圆的位置关系是【】A.内切B.相交C.外切D.外离24.已知两圆的直径分别为2cm 和4cm,圆心距为3cm,则这两个圆的位置关系是【】A.相交B.外切C.外离D.内含25.已知两圆的半径分别为3cm、4cm,圆心距为8cm,则两圆的位置关系是【】A.外离B.相切C.相交D.内含二、填空题:1.半径分别为3cm 和4cm 的两圆内切,这两圆的圆心距为cm.2.如图,⊙M与⊙N外切,MN=10cm,若⊙M的半径为6cm,⊙N的半径为cm。
初中数学拔高九年级 专题23 圆与圆的位置关系(含答案)

专题23 圆与圆的位置关系【阅读与思考】两圆的半径与圆心距的大小量化确定圆与圆的外离、外切、相交、内切、内含五种位置关系.圆与圆相交、相切等关系是研究圆与圆位置关系的重点,解题中经常用到相关性质. 解圆与圆的位置关系问题,往往需要添加辅助线,常用的辅助线有: 1.相交两圆作公共弦或连心线;2.相切两圆作过切点的公切线或连心线;3.有关相切、相离两圆的公切线问题常设法构造相应的直角三角形. 熟悉以下基本图形和以上基本结论.【例题与求解】【例1】 如图,大圆⊙O 的直径a AB cm ,分别以OA ,OB 为直径作⊙O 1和⊙O 2,并在⊙O 与⊙O 1和⊙O 2的空隙间作两个等圆⊙O 3和⊙O 4,这些圆互相内切或外切,则四边形3241O O O O 的面积为________cm 2. (全国初中数学竞赛试题) 解题思路:易证四边形3241O O O O 为菱形,求其面积只需求出两条对角线的长.O O 2O 1O 3O 4BA【例2】 如图,圆心为A ,B ,C 的三个圆彼此相切,且均与直线l 相切.若⊙A ,⊙B ,⊙C 的半径分别为a ,b ,c (b a c <<<0),则a ,b ,c 一定满足的关系式为( ) A .c a b +=2 B .c a b +=2C .b ac 111+= D .ba c 111+= (天津市竞赛试题) 解题思路:从两圆相切位置关系入手,分别探讨两圆半径与分切线的关系,解题的关键是作圆的基本辅助线.lC A 1C 1B 1BA【例3】 如图,已知两圆内切于点P ,大圆的弦AB 切小圆于点C ,PC 的延长线交大圆于点D .求证: (1)∠APD =∠BPD ;(2)CB AC PC PB PA ∙+=∙2. (天津市中考试题)解题思路:对于(1),作出相应辅助线;对于(2),应化简待证式的右边,不妨从AC ·BC =PC ·CD 入手.PBCDA【例4】 如图⊙O 1和⊙O 2相交于点A 及B 处,⊙O 1的圆心落在⊙O 2的圆周上,⊙O 1的弦AC 与⊙O 2交于点D .求证:O 1D ⊥BC .(全俄中学生九年级竞赛试题)解题思路:连接AB ,O 1B ,O 1C ,显然△O 1BC 为等腰三角形,若证O 1D ⊥BC ,只需证明O 1D 平分∠B O 1C .充分运用与圆相关的角.O 1O 2D BCA【例5】 如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =1,AB =2,DC =22,点P 在边BC 上运动(与B ,C 不重合).设PC =x ,四边形ABPD 的面积为y . (1)求y 关于x 的函数关系式,并写出自变量x 的取值范围; (2)若以D 为圆心,21为半径作⊙D ,以P 为圆心,以PC 的长为半径作⊙P ,当x 为何值时,⊙D 与⊙P 相切?并求出这两圆相切时四边形ABPD 的面积. (河南省中考题) 解题思路:对于(2),⊙P 与⊙D 既可外切,也可能内切,故需分类讨论,解题的关键是由相切两圆的性质建立关于x 的方程.DCPBA【例6】 如图,ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ,延长AP 交BC 于点N ,求NCBN的值. (全国初中数学联赛试题) 解题思路:AB 为两圆的公切线,BC 为直径,怎样产生比例线段?丰富的知识,不同的视角激活想象,可生成解题策略与方法.N PB A CD【能力与训练】A 级1.如图,⊙A ,⊙B 的圆心A ,B 在直线l 上,两圆的半径都为1cm .开始时圆心距AB =4cm ,现⊙A ,⊙B 同时沿直线l 以每秒2cm 的速度相向移动,则当两圆相切时,⊙A 运动的时间为_______秒.(宁波市中考试题)2.如图,O 2是⊙O 1上任意一点,⊙O 1和⊙O 2相交于A ,B 两点,E 为优弧AB 上的一点,EO 2及延长线交⊙O 2于C ,D ,交AB 于F ,且CF =1,EC =2,那么⊙O 2的半径为_______.(四川省中考试题)(第1题图) (第2题图) (第3题图)3.如图,半圆O 的直径AB =4,与半圆O 内切的动圆O 1与AB 切于点M .设⊙O 1的半径为y ,AM 的长为x ,则y 与x 的函数关系是_________________.(要求写出自变量x 的取值范围)(昆明市中考试题)4.已知直径分别为151+和315-的两个圆,它们的圆心距为115-,这两圆的公切线的条数是__________.5.如图,⊙O 1和⊙O 2相交于点A ,B ,且⊙O 2的圆心O 2在圆⊙O 1的圆上,P 是⊙O 2上一点.已知∠A O 1B =60°,那么∠APB 的度数是( )A .60°B .65°C .70°D .75°(甘肃省中考试题) 6.如图,两圆相交于A 、B 两点,过点B 的直线与两圆分别交于C ,D 两点.若⊙O 1半径为5,⊙O 2的半径为2,则AC :AD 为( )A .52:3B .3:52C .1:52D .2:5(第5题图) (第6题图) (第7题图)7.如图,⊙O 1和⊙O 2外切于点T ,它们的半径之比为3:2,AB 是它们的外公切线,A ,B 是切点,AB =64,那么⊙O 1和⊙O 2的圆心距是( )A .65B .10C .610D .1339208.已知两圆的半径分别为R 和r (r R >),圆心距为d .若关于x 的方程0)(222=-+-d R rx x 有两相等的实数根,那么这两圆的位置关系是( )A .外切B .内切C .外离D .外切或内切lB A FC EB AD O 1O 2O 1B O M A O 1O 2PBAO 2DBCAO 1BATO 1O 2。
历年初三数学中考辅导之—圆和圆的位置关系及答案

中考数学辅导之—圆和圆的位置关系一、教材简析本单元主要研究圆和圆的位置关系,内容主要包括两个圆各种不同位置关系的概念;相交、相切两圆的性质以及两个圆的公切线。
其中两个圆不同位置关系的概念及相交、相切时的性质是本单元的重点。
同学们在学习过程中要注意与前面所学的圆的有关知识的联系。
当一条直线与两个圆相切时,这条直线就是这两个圆的公切线,而对于每一个圆来说,这条直线都是他们的切线。
因此,研究两圆的公切线问题,就是圆的切线的判定和性质在两个相关的圆中的应用。
由圆的轴对称性可以推出,任意两个圆组成的图形,一定是以连心线为轴的对称图形。
两圆相交、相切的性质,都是由这个对称性得到的。
所以在学习这一单元时,要随时复习巩固前面所学知识,并逐步学会运用这些知识来解决两圆位置关系中的新问题。
本单元学习过程中,涉及实际应用的问题较多,有计算题,也有作图题,要学会把实际问题抽象成数学问题,在关于两圆公切线长的计算中,要学会把它转化为解直角三角形的问题。
二、基本内容及应注意的问题1、圆和圆的位置关系的分类,既考虑了数(两圆公共点的个数),又考虑了形(两圆的相对位置),两圆的五种位置关系按公共点的个数(0,1,2)可分为三类:(1)没有公共点⇔相离外离内含(包括同心);(2)有1个公共点⇔相切外切内切;(3)有2个公共点⇔相交2、与点和圆、直线和圆的位置关系相类似,两圆的位置关系(形的关系)与两圆的半径、圆心距的大小(数量关系)有关。
(1)两圆外离⇔d>R+r(2)两圆外切⇔d=R+r(3)两圆相交⇔R-r<d<R+r(R≥r)(4)两圆内切⇔d=R-r(R>r)(5)两圆内含⇔d<R-r(R>r)这个结论是双向的,“⇒”是由两圆位置的关系,得到两圆半径与圆心距之间特定的数量关系,这是两圆位置关系的性质,利用这些性质可以把形的问题转化为数的问题来解决;“⇐”是根据两圆半径与圆心距之间的某种数量关系来判定两圆的位置关系,从而把判定形的问题,转向为数的问题来解决。
【复习专题】中考数学复习:点与圆的位置关系、直线与圆的位置关系及圆与圆的位置关系

点与圆的地点关系、直线与圆的地点关系及圆与圆的地点关系三只钟的故事一只小钟被主人放在了两只旧钟中间,两只旧钟滴答、滴答的走着。
一只旧钟对小钟说:“来吧,你也该工作了。
但是我有点担忧,你走完三千两百万次此后,唯恐会吃不用的。
”“天哪!三千两百万次。
”小钟惊讶不已,“要我做这么大的事?办不到,办不到!”另一支旧钟说:“别听他信口开河,不用惧怕,你只需每秒滴答摆一下就行了。
”“天下哪有这么简单的事情?”小钟将信将疑,“假如这样,我就试一试吧。
”小钟很轻松地每秒滴答摆一下,不知不觉中,一年过去了,它摆了三千两百万次。
成功就是这样,把简单的事做到极致,就能成功。
例 1.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于()A. 20 ° B. 25° C.40° D.50°例 2. 如图,△ABC的边AC与⊙O订交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为 B.已知∠A=30°,则∠ C的大小是()A. 30° B.45° C. 60° D. 40°例 3. 如图,在平面直角坐标系xOy中,半径为向平移,使⊙ P与 y 轴相切,则平移的距离为(2 的⊙P的圆心)P 的坐标为(﹣3, 0),将⊙P沿x轴正方(第 1 题图)A.1B.1或5C.3D.5例 4.如图,P为⊙O的直径BA延伸线上的一点,PC与⊙ O相切,切点为 C,点 D是⊙上一点,连结 P D.已知 PC=PD=B C.以下结论:(1)PD与⊙O相切;( 2)四边形PCBD是菱形;( 3)PO=AB;(4)∠PDB=120°.此中正确的个数为()A.4 个 B.3 个 C.2 个 D.1 个1.已知 Rt△ ABC,∠C=90°, 以 A 为圆心 ,AC 为半径作圆 , 则 B 在⊙ A;2.以 C为圆心 ,AB 的一半作圆 , 则 AB的中点⊙ C;3.认为 AB直径作圆 ,点 C在圆; ⊙C;4. 在中,以点C为圆心,以r=3为半径作圆,判断A、 B 两点和的地点关系 .5.在平面直角坐标系中,以点为圆心,为半径的圆与轴,与轴,点与的地点关系是6.已知正△ ABC,AO⊥BC,⊙ O切 AB 为 D,求证 : AC 为⊙ O切线 .7.已知点 A在⊙ E 上,BD 为直径 C 在 BD的延伸线上 ,AB=AC,∠ C=30° , 求证 AC为⊙ E 切线 .8.已知点 A 在⊙ E上, ∠D=∠ B =30° , 求证 AD为⊙ E 切线 .9.已知 AB=BC,AC交⊙ O与 D,AB 为直径 , DE ⊥ CB为在⊙ E 上 , 求证 DE为⊙ O切线 .10.已知 AB是⊙ O的直径 , BC 为⊙ O的切线 ,AC 交⊙ O于 D, E 是 BC的中点 , 求证 DE为⊙ O切线 .11.在△ ABC中,∠ C=90°, AD是∠ BAC的均分线, O是 AB上一点,以 OA为半径的⊙ O经过点 D.求证:BC 是⊙ O切线;12. 如图,、、都是的切线,,,则的度数为,周长为13.如图,,切于,两点,若,的半径为,则暗影部分的面积为14. 若⊙ C与 AB相切 ,AC=,CB=, 则⊙ C 的半径为 ;15.设⊙ P的半径为4cm,直线 m上一点 A到圆心的距离为4cm,则直线 m与⊙ P的地点关系是( )A.订交 B.相切 C.相离 D.相切或订交16. 如图 6,∠=900,O 为射线 BC上一点,以点O为圆心,为半径作圆。
中考总复习:圆的有关概念、性质与圆有关的位置关系--巩固练习(基础)

中考总复习:圆的有关概念、性质与圆有关的位置关系—巩固练习(基础)【巩固练习】一、选择题1. 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是( )A .相交B .相离C .内切D .外切2.如图,AB 是⊙O 的直径,点C 、D 在⊙O 上 ,∠BOD=110°,AC∥OD,则∠AOC 的度数 ( )A. 70°B. 60°C. 50°D. 40°3.如图所示,AB 是⊙O 的直径,CD 为弦,CD ⊥AB 于点E ,则下列结论中不成立的是( )A .∠COE =∠DOEB .CE =DEC .OE =BED .»»BDBC第2题 第3题 第5题 第6题4.(2015•黑龙江)如图,⊙O 的半径是2,AB 是⊙O 的弦,点P 是弦AB 上的动点,且1≤OP≤2,则弦AB 所对的圆周角的度数是( )A .60°B .120°C .60°或120°D .30°或150°5.如图所示,△ABC 内接于圆O ,∠A =50°;∠ABC =60°,BD 是圆O 的直径,BD 交AC 于点E ,连接DC ,则∠AEB 等于( )A .70°B .110°C .90°D .120°6.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配成与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )A .第①块B .第②块C .第③块D .第④块二、填空题7.(2015•雁江区模拟)如图,MN 是半径为2的⊙O 的直径,点A 在⊙O 上,∠AMN=30°,B 为弧AN 的中点,P 是直径MN 上一动点,则PA+PB 的最小值为 .8.如图所示,⊙O的直径AC=8 cm,C为⊙O上一点,∠BAC=30°,则BC=________cm.第8题第9题9.两圆有多种位置关系,图中(如图所示)不存在的位置关系是__________.10.如图所示,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C=______.11.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为 .第10题第11题第12题12.如图所示.B是线段AC上的一点,且AB:AC=2:5.分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为________.三、解答题13.已知AB与⊙O相切于点C,OA=OB.OA、OB与⊙O分别交于点D、E.(1) 如图①,若⊙O的直径为8,AB=10,求OA的长(结果保留根号);(2)如图②,连接CD、CE,若四边形ODCE为菱形.求ODOA的值.14. 如图所示,在Rt△ABC中,∠C=90°,O为直角边BC上一点,以O为圆心、OC为半径的圆恰好与斜边AB相切于点D,与BC交于另一点E.(1)求证:△AOC≌△AOD;(2)若BE=1,BD=3,求⊙O的半径及图中阴影部分的面积S.15.(2015•上城区二模)如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;(2)求证:CD⊥DF.l16. 如图,已知∠ABC=90°,AB=BC.直线与以BC为直径的圆O相切于点C.点F是圆O上异于B、Cl的动点,直线BF与相交于点E,过点F作AF的垂线交直线BC与点D.(1)如果BE=15,CE=9,求EF的长;(2)证明:①△CDF∽△BAF;②CD=CE;(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使CD,请说明你的理由.【答案与解析】一、选择题1.【答案】D;O O=7,根据圆与圆位置关系的判定可知两圆外切.【解析】两圆半径之和3+4=7,等于两圆圆心距122.【答案】D;【解析】由AB是⊙O的直径,点C、D在⊙O上,知OA=OC,根据等腰三角形等边对等角的性质和三角形内角和定理,得∠AOC=180°-2∠OAC.由AC∥OD,根据两直线平行,内错角相等的性质,得∠OAC=∠AOD.由AB是⊙O的直径,∠BOD=110°,根据平角的定义,得∠AOD=180°-∠BOD=70°.∴∠AOC=180°-2×70°=40°.故选D.3.【答案】C;【解析】由垂径定理知A、B、D都正确.4.【答案】C;【解析】作OD⊥AB,如图,∵点P是弦AB上的动点,且1≤OP≤2,∴OD=1,∴∠OAB=30°,∴∠AOB=120°,∴∠AEB=∠AOB=60°,∵∠E+∠F=180°,∴∠F=120°,即弦AB所对的圆周角的度数为60°或120°.故选C.5.【答案】B;【解析】∵∠A=50°,∴∠D=50°,又∵BD是直径,∴∠BCD=90°,∴∠DBC=90°-50°=40°,∠ABD=60°-40°=20°,∴∠BEC=50°+20°=70°,∴∠AEB=180°-70°=110°.6.【答案】B;【解析】因为第②块含有圆周的一部分,可以找到圆心,量出半径.其他块都不行.二、填空题7.【答案】2;【解析】如图,作点B关于MN的对称点B′,连接OA、OB′、AB′,由轴对称确定最短路线问题可知,AB′与M的交点即为所求的使PA+PB的值最小的点,∵∠AMN=30°,∴∠AON=2∠AMN=2×30°=60°,∵B为弧AN的中点,∴∠NOB′=×60°=30°,∴∠AOB′=90°,∴△AOB′是等腰直角三角形,∵⊙O的半径为2,∴AB′=2,即PA+PB的最小值为为2.8.【答案】4;【解析】因为AC为直径,根据直径所对的圆周角为直角,得∠ABC=90°,则BC=AC·sin∠BAC=4(am).9.【答案】相交;【解析】认真观察、判断可发现每两圆间不存在的位置关系是:相交.10.【答案】27°;【解析】如图,连结OB,由AB与⊙O相切于点B,得∠ABO=90°,因为∠A=36°,所以∠AOB=54°,所以∠C=27°.11.【答案】4;【解析】连接OC,则由直线PC是圆的切线,得OC⊥PC.设圆的半径为x,则在Rt△OPC中,PC=3,OC= x,OP=1+x,根据地勾股定理,得OP2=OC2+PC2,即(1+x)2= x2+32,解得x=4.即该半圆的半径为4.12.【答案】4:25;三、解答题13.【答案与解析】(1) 如图①,连接OC ,则OC=4.∵AB 与⊙O 相切于点C ,∴OC⊥AB. ∴在△OAB 中,由OA=OB ,AB=10得1AC AB 52==.∴ 在△RtOAB 中,OA ===.(2)如图②,连接OC ,则OC=OD.∵四边形ODCE 为菱形,∴OD=DC.∴△ODC 为等边三角形.∴∠AOC=60°.∴∠A=30°.∴1OC 1OD 1OC OA 2OA 2OA 2===,,即.14.【答案与解析】解:(1)∵ AB 切⊙O 于D ,∴OD ⊥AB .在Rt △AOC 和Rt △AOD 中,,.OC OD AO AO =⎧⎨=⎩ ∴Rt △AOC ≌Rt △AOD(HL).(2)设半径为r ,在Rt △ODB 中,,解得r =4.2223(1)r r +=+ 由(1)有AC =AD ,∴,2229(3)AC AC +=+ 解得AC =12,∴.22111112945482222S AC BC r πππ=-=⨯⨯-⨯=-g 15.【答案与解析】解:(1)∵∠ADB=∠ACB ,∠BAD=∠BFC ,∴∠ABD=∠FBC ,又∵AB=AD ,∴∠ABD=∠ADB ,∴∠CBF=∠BCF ,∵∠BFC=2∠DFC=80°,∴∠CBF==50°;(2)令∠CFD=α,则∠BAD=∠BFC=2α,∵四边形ABCD 是圆的内接四边形,∴∠BAD+∠BCD=180°,即∠BCD=180°﹣2α,又∵AB=AD ,∴∠ACD=∠ACB ,∴∠ACD=∠ACB=90°﹣α,∴∠CFD+∠FCD=α+(90°﹣α)=90°,∴∠CDF=90°,即CD ⊥DF .16.【答案与解析】解:(1)∵直线与以BC 为直径的圆O 相切于点C ,l ∴∠BCE=90°,又∵BC 为直径,∴∠BFC=∠CFE=90°.∴∠CFE=∠BCE.∵∠FEC=∠CEB,∴△CEF∽△BEC.∴CE EF BE EC =.∵BE=15,CE=9,即:9EF 159=,解得:EF=275.(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,∴∠ABF=∠FCD.同理:∠AFB=∠CFD.∴△CDF∽△BAF.②∵△CDF∽△BAF,∴CF CD BF BA =.又∵△CEF∽△BCF,∴CF CE BF BC =.∴CD CE BA BC=.又∵AB=BC,∴CE=CD.(3)当F 在⊙O 的下半圆上,且»»2BF BC 3=时,相应的点D 位于线段BC 的延长线上,且使CD.理由如下:CE.在Rt△BCE 中,tan∠CBE=CEBC =,∴∠CBE=30°,∴»CF所对圆心角为60°.∴F 在⊙O 的下半圆上,且»»2BF BC 3=.。
2013年浙教版九年级中考数学辅导(直线与圆、圆与圆的位置关系)
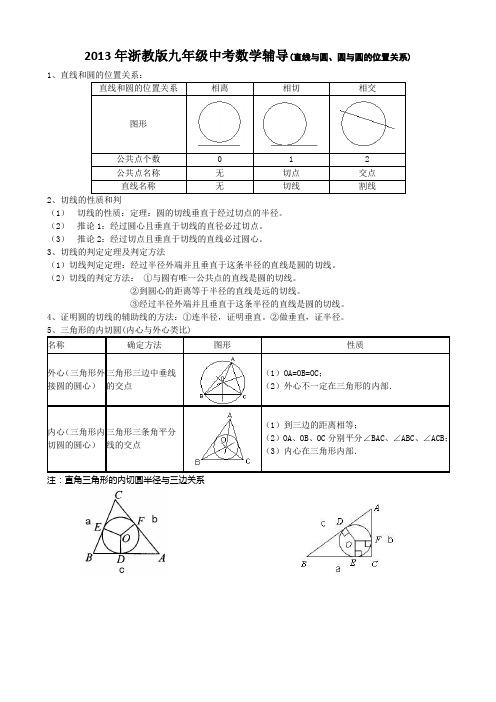
2013年浙教版九年级中考数学辅导(直线与圆、圆与圆的位置关系) 12、切线的性质和判(1)切线的性质:定理:圆的切线垂直于经过切点的半径。
(2)推论1:经过圆心且垂直于切线的直径必过切点。
(3)推论2:经过切点且垂直于切线的直线必过圆心。
3、切线的判定定理及判定方法(1)切线判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线。
(2)切线的判定方法:①与圆有唯一公共点的直线是圆的切线。
②到圆心的距离等于半径的直线是远的切线。
③经过半径外端并且垂直于这条半径的直线是圆的切线。
4、证明圆的切线的辅助线的方法:①连半径,证明垂直。
②做垂直,证半径。
5、三角形的内切圆(内心与外心类比)图1 图2 图3 6、切线长定理及切线长概念(1)切线长的概念:在经过员外一点的圆的切线上,这点和切点之间的线段的长,叫做这点倒圆的切线长。
(2) 切线长定理:从圆外一点可以引圆的两条切线,他们的切线长相等,这一点和圆心的连线评分两条切线的夹角。
7、与切线相交线有关的比例线段 (1)相交弦定理::如图1,弦AB 与CD 相交于点P ,则有:DP CP BP AP ∙=∙(2)切割线定理:如图2,切线PA 与割线PC 交于点P ,则有PC PB PA ∙=2(3)割线定理:如图3,割线PD 与PC 交于P ,则有PC PB PD PA ∙=∙(也叫切割线定理的推论)8、弦切角定理:弦切角:定点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
弦切角定理:弦切角等于它所夹的弧所对的圆周角。
9、圆与圆的位置关系一、选择题1、给出下列命题:①任意三角形一定有一个外接圆,并且只有一个外接圆; ②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形, 并且只有一个外切三角形,其中真命题共有( ) A.1个 B.2个 C.3个 D.4个2、一个点到圆的最小距离为4cm ,最大距离为9cm ,则该圆的半径是( ) A 、2.5 cm 或6.5 cm B 、2.5 cm C 、6.5 cm D 、5 cm 或13cm3、在平面直角坐标系中,以点(-1,2)为圆心,1为半径的圆必与( )4、两圆的半径分别为2和5,圆心距为7,则这两圆的位置关系为( ) A .外离 B .外切 C .相交 D .内切5、已知⊙O 1和⊙O 2的半径分别为1和5,圆心距为3,则两圆的位置关系是( )A.相交B.内含C.内切D.外切6、已知⊙O 1和⊙O 2的半径分别为3 cm 和4 cm ,圆心距O 1O 2=10 cm ,那么⊙O 1和⊙O 2的位置关系是( )A.内切B.相交C.外切D.外离 7、已知1O ⊙和2O ⊙相切,1O ⊙的直径为9cm ,2O ⊙的直径为4cm .则12O O 的长是( ) A .5cm 或13cmB .2.5cmC .6.5cmD .2.5cm 或6.5cm8、两圆的圆心坐标分别是(3,0)和(0,1),它们的半径分别是3和5,则这两个圆的位置关系是( ) A.相离 B.相交 C.外切 D.内切9、已知两圆相交,小圆半径为6,大圆半径为8,那么这两个圆的圆心距d 的取值范围是( )A.d>2B.d<14C.0<d<14D.2<d<14 10、如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( ) A .2 B .3 C . 3 D .2 3 11、△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )A .120°B .125°C .135°D .150° 12、同圆的内接正三角形与内接正方形的边长的比是( )A.26 B.43 C.36 D.3413、已知圆O 的半径为R ,AB 是圆O 的直径,D 是AB 延长线上一点,DC 是圆O 的切线,C 是切点,连结AC ,若∠CAB=30°,则BD 的长为( )A .2R BC .RD .2R 14、如图,AB 是⊙O 的直径,AD 是⊙O 的切线,点C 在⊙O 上,BC∥OD,AB =2,OD =3,则BC 的长为( )A .23B .32C D 15、如图PA 、PB 是⊙O 的切点,AC 是⊙O 的直径,∠P=40°,则∠BAC 得度数是 ( ) A.10° B.20° C.30° D.40°16、如图,直线AB 与⊙O 相切于点A ,⊙O 的半径为2,若∠OBA = 30°,则OB 的长为A .B .4C .D .2(第14题图) (第15题图) (第16题图)17、如图,AB 是⊙O 的直径,⊙O 交BC 的中点于D,DE⊥AC 于E,连接AD,则下列结论正确的个数是( ) ①AD⊥BC ②∠EDA=∠B ③OA=12AC ④DE 是⊙O 的切线18、如图,已知AB、AC分别为⊙O的直径和弦,D为BC⌒的中点,DE垂直于AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论一定错误的是()A、DE是⊙O的切线B、直径AB长为20cmC、弦AC长为16cmD、C为AD⌒的中点19、如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于()A、20°B、30°C、40°D、50°(第17题图)(第18题图)(第19题图)20、如图,O是正方形ABCD的对角线BD上一点,⊙O边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF对折,折痕EF与⊙O相切,此时点D恰好落在圆心O处.若DE=2,则正方形ABCD的边长是( ) A.3 B.4 C.2D.21、AD、AE和BC分别切⊙O于D、E、F,如果AD=20,则△ABC的周长为()A. 20B. 30C. 40D.213522、在⊙O中,直径AB、CD互相垂直,BE切⊙O于B,且BE=BC,CE交AB于F,交⊙O于M,连结MO并延长,交⊙O于N,则下列结论中,正确的是()A. CF=FMB. OF=FBC. BM⌒的度数是22.5° D. BC∥MN23、如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A = 100°,∠C = 30°,则∠DFE的度数是() A.55° B.60° C.65° D.70°(第20题图)(第21题图)(第22题图)(第23题图)24、如图所示,AB是⊙O的直径,弦AC、BD相交于E,则ABCD等于()A.AED∠tanB.AED∠cotC. AED∠sinD.AED∠cos25、如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是()A.2n R B.1()2n R C.11()2n R-D.1(2n R-26、已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为baab+的是(BDACEF(第24题图)(第25题图)27、如图,在Rt△ABC 中,∠ABC=90°,AB=8cm,BC =6cm ,分别以A,C 为圆心,以2AC的长为半径作圆,将Rt△ABC 截去两个扇形,则剩余(阴影)部分的面积为( )cm 2. A .2524π4-B .25π4C .524π4-D .2524π6-28、如图,△ABC 是直角边长为a 的等腰直角三角形,直角边AB 是半圆O 1的直径,半圆O 2过C 点且与半圆O 1相切,则图中阴影部分的面积是( ) A .2367a π- B .2365a π- C .2367a D .2365a 29、在Rt ABC ∆中,90A ∠=︒,点O 在BC 上,以O 为圆心的⊙O 分别与AB 、AC 相切于E 、F ,若A B a =, ACb =,则⊙O 的半径为( )AB 、a b ab +C 、ab a b +D 、2a b+30、正方形ABCD 中,AE 切以BC 为直径的半圆于E ,交CD 于F ,则:CF FD =( ) A 、1∶2 B 、1∶3 C 、1∶4 D 、2∶5CFBAFCBA(第27题图) (第28题图) (第29题图) (第30题图) 二、填空题31、如图,两个等圆⊙O 与⊙O ′外切,过点O 作⊙O ′的两条切线OA 、OB ,A 、B 是切点,则∠AOB = . 32、如图8,直线AB 与⊙O 相切于点B ,BC 是 ⊙O 的直径,AC 交⊙O 于点D ,连结BD ,则图 中直角三角形有 个.33、如图,DB 为半圆的直径,A 为BD 延长线上一点,AC 切半圆于点E ,BC ⊥AC 于点C ,交半圆于点F .已知BD =2,设AD =x ,CF =y ,则y 关于x 的函数解析式是 .34、如图,PA 、PB 分别与⊙O 相切于点A 、B ,⊙O 的切线EF 分别交PA 、PB 于点E 、F ,切点C 在 AB 上,若PA 长为2,则△PEF 的周长是_ _.35、如图,已知正方形纸片ABCD 的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA 恰好与⊙0相切于点A ′(△EFA ′与⊙0除切点外无重叠部分),延长FA ′交CD 边于点G ,则A ′G 的长是(第31题图) (第32题图)∙ABPCE F ∙O(第33题图) (第34题图)(第35题图)36、Rt △ABC 中,9068C AC BC ∠===°,,.则△ABC 的内切圆半径r =______.37、如图,施工工地的水平地面上,有三根外径都是1 m 的水泥管,两两相切地堆放在一起,其最高点到地面的距离是_________.38、如图,直径分别为CD 、CE 的两个半圆相切于点C ,大半圆M 的弦AB 与小半圆N 相切于点F ,且AB ∥CD ,AB=4,设 CD、 CE 的长分别为x 、y ,线段ED 的长为z ,则z (x+y )= .(第36题图) (第37题图) (第38题图)39、点A 、B 、C 、D 在同一圆上,AD 、BC 延长线相交于点Q ,AB 、DC 延长线相交于点P ,若∠A=50°,∠P =35°,则∠Q=________.40、已知三角形的内切圆半径为3cm ,三角形的周长为18cm ,则该三角形的面积为 . 41、如图,以O 为圆心的两个同心圆中,大圆的弦AB 与小圆相切于点C ,若大圆半径为10cm ,小圆半径为6cm ,则弦AB 的长为 cm .42、如图,已知AB 是⊙0的直径,BC 是和O 相切于点B 的切线,过⊙0上A 点的直线AD OC ∥,若2OA =且6AD OC +=,则CD = 。
【备战2013中考】2011和2012年各地中考数学试题分考点解析汇编圆与圆的位置关系

2011-2012全国各中考数学试题分考点解析汇编圆与圆的位置关系一、选择题1.(2011天津3分)已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是(A) 相交 (B) 相离 (C) 内切 (D) 外切【答案】D 。
【考点】圆与圆位置关系的判定。
【分析】两圆半径之和3+4=7,等于两圆圆心距12O O =7,根据圆与圆位置关系的判定可知两圆外切。
2.(2011重庆潼南4分)已知⊙O1与⊙O2外切,⊙O1的半径R=5cm ,⊙O2的半径r=1cm ,则⊙O1与⊙O2的圆心距是A 、1cmB 、4cmC 、5cmD 、6cm 【答案】D 。
【考点】圆与圆的位置关系。
【分析】根据两圆的位置关系的性质:相切(两圆圆心距离等于两圆半径之和或两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
由于两圆外切,故两圆圆心距离等于两圆半径之和;5cm +1cm =6cm 。
故选D 。
3.(2011浙江台州4分)如图是一个组合烟花的横截面,其中16个圆的半径相同,点A 、B 、C 、D 分别是四个角上的圆的圆心,且四边形ABCD 为正方形.若圆的半径为r ,组合烟花的高为h ,则组合烟花侧面包装纸的面积至少需要(接缝面积不计)A .rh π26B .rh rh π+24C .rh rh π212+D .rh rh π224+【答案】D 。
【考点】两圆相切的性质,扇形面积的计算。
【分析】由图形知,正方形ABCD 的边长为6r ,∴其周长为4×6r=24r ,∴截面的周长为:24r+2πr , ∴组合烟花的侧面包装纸的面积为:(24r+2πr )h=24rh+2πrh 。
故选D 。
4..(2011浙江温州4分)已知线段AB=7cm,现以点A为圆心,2cm为半径画⊙A;再以点B为圆心,3cm为半径画⊙B,则⊙A和⊙B的位置关系【来源:】A、内含B、相交C、外切D、外离【答案】D。
初升高衔接专题 圆和圆的位置关系(含答案)
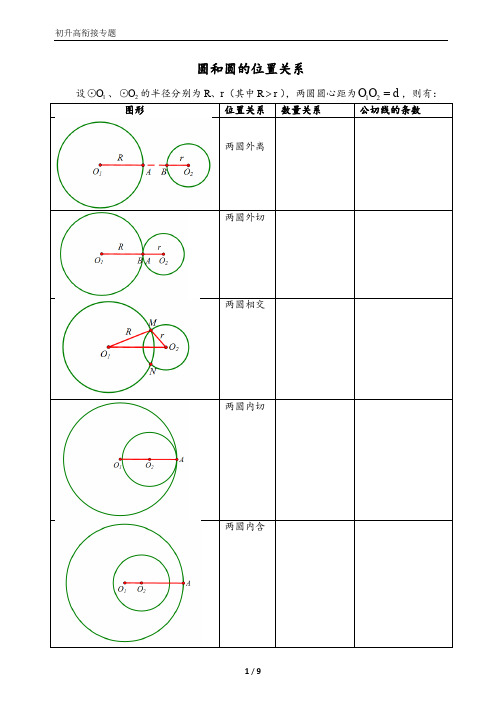
2.如图,⊙O1 与⊙O2 外离,AB,CD 是内公切线交于 P 点,O1O2 是圆心距,若 O1O2 10cm , 且⊙O1 的半径为 2cm,⊙O2 的半径为 3cm,求两条内公切线长及它们所夹锐角的度数.
D A
O1
P
C
O2 B
3.如图,矩形内放置 8 个半径为 1cm 的圆,其中相邻两个圆都相切,并且左上角和右下 角的两个圆和矩形的边相切,则该矩形的面积为__________.
∴ O1C2 O2C2 O1O22 ,即 (4 6)2 k2 (5k)2 ,解得 k 2 , ∴ O1O2 10 .
(2)18cm
9/9
A.外离
B.外切
C.相交
切
). D.内
(2)两圆的圆心距为 3,两圆的半径分别是方程 x2 4x 3 0 的两个根,则两圆的
位置关系是( ).
A.相交
B.外离
C.内含
D.外
切
(3)若两个圆相切于 A 点,它们的直径分别为 10cm、4cm,则这两个圆的圆心距为 __________.
(4)已知⊙O1 与⊙O2 两圆内含,O1O2 3 ,⊙O1 的半径为 5,那么⊙O2 的半径 r 的取值 范围是__________.
【提示】这道题主要考查多圆相切问题,连接圆心距.
【练出高分】
1(. 1)平面直角坐标系中,⊙O 的圆心在原点,半径为 3,⊙A 的圆心 A 的坐标为 ( 3, 1) ,
半径为 1,那么⊙O 与⊙A 的位置关系是____________. (2)已知两圆相切,两圆半径分别为 6cm 和 3cm,则圆心距为__________. 答:(1)内切;(2)9cm 或 3cm. 2.如图,⊙O1 与⊙O2 外离,AB,CD 是内公切线交于 P 点,O1O2 是圆心距,若 O1O2 10cm , 且⊙O1 的半径为 2cm,⊙O2 的半径为 3cm,求两条内公切线长及它们所夹锐角的度数.
中考数学专题复习(有答案)与圆有关的位置关系

第2节与圆有关的位置关系A组1.在平面直角坐标系中,以原点O为圆心,5为半径作圆,若点P的坐标为(4,3),则点P与⊙O的位置关系是(C)A.在⊙O外B.在⊙O内C.在⊙O上D.在⊙O内或在⊙O外2.平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为(C) A.0条B.1条C.2条D.无数条3.(2020天水)如图所示,P A,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=70°,则∠ACB的度数为(B)A.50°B.55°C.60°D.65°第3题图第4题图第5题图4.(2020上海改编)如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC于点D.若∠ABD=15°,则∠BAC=30°.5.(2020济宁)如图,在△ABC中,点D为△ABC的内心,∠A=60°,CD=2,BD=4.则△DBC的面积是(B)A.4 3 B.2 3C.2 D.46.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,以点O为圆心OC为半径作半圆.求证:AB为⊙O的切线.证明:作OM⊥AB于M.∵OA平分∠CAB,OC⊥AC,OM⊥AB,∴OC=OM.∵OC为半径,∴AB 是⊙O 的切线.B 组7.【新考法】如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m 和4m.按照输油中心O 到三条支路的距离相等来连接管道,则O 到三条支路的管道总长(计算时视管道为线,中心O 为点)是( B )A .2 mB .3 mC .4 mD .6 m8.(2020随州)如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作⊙O ,与BC 交于点M ,与AB 的另一个交点为E ,过M 作MN ⊥AB ,垂足为N .(1)求证:MN 是⊙O 的切线;(2)若⊙O 的直径为5,sin B =35,求ED 的长.(1)证明:如图,连接OM .∵OC =OM ,∴∠OCM =∠OMC .在Rt △ABC 中,CD 是斜边AB 上的中线,∴CD =12AB =BD . ∴∠DCB =∠DBC .∴∠OMC =∠DBC .∴OM ∥BD .∵MN ⊥BD ,∴OM ⊥MN .∵OM 过点O ,且OM =OC ,∴MN 是⊙O 的切线.(2)解:如图,连接DM ,CE .∵CD 是⊙O 的直径,∴∠CED =90°,∠DMC =90°.即DM ⊥BC ,CE ⊥AB ,由(1)知BD =CD =5,∴M 为BC 的中点.在Rt △BDM 中,sin B =DM BD =35,∴DM =3. ∴BM =BD 2-DM 2=4.∴BC =2BM =8.在Rt △CEB 中,sin B =CE BC =CE 8=35, ∴CE =245.∴在Rt △CDE 中,ED =CD 2-CE 2=75. C 组9.如图,AB 是⊙O 的直径,C 是⊙O 上一点,D 是AC ︵的中点,E 为OD 延长线上一点,且∠CAE =2∠C ,AC 与BD 交于点H ,与OE 交于点F .(1)求证:AE 是⊙O 的切线;(2)若DH =9,tan C =34,求直径AB 的长.(1)证明:∵D 是AC ︵的中点,∴OE ⊥AC .∴∠AFE =90°.∴∠E +∠EAF =90°.∵∠AOE =2∠C ,∠CAE =2∠C ,∴∠CAE =∠AOE .∴∠E +∠AOE =90°.∴∠EAO =90°.∴AE 是⊙O 的切线.(2)解:连接AD .在Rt △ADH 中,∵∠DAC =∠C ,∴tan ∠DAC =tan C =34. ∵DH =9,∴AD =12.在Rt △BDA 中,∵tan B =tan C =34, ∴sin B =35.∴AB =20.。
中考数学专题特训第二十四讲:与圆有关的位置关系(含详细参考答案)

中考数学专题复习第二十四讲与圆有关的位置关系【基础知识回顾】一、点与圆的位置关系:1、点与圆的位置关系有种,若圆的半径为r点P到圆心的距离为d则:点P在圆内<=> 点P在圆上<=>点P在圆外<=>2、过三点的圆:⑴过同一直线上三点作用,过三点,有且只有一个圆⑵三角形的外接圆:经过三角形各顶点的圆叫做三角形的外接圆的圆心叫做三角形的这个三角形叫做这个圆的⑶三角形外心的形成:三角形的交点,外心的性质:到相等【赵老师提醒:1、锐角三角形外心在三角形直角三角形的外心是锐角三角形的外心在三角形】一、直线与圆的位置关系:1、直线与圆的位置关系有种:当直线和圆有两个公共点时,叫做直线和圆直线叫圆的线,这的直线叫做圆的直线和圆没有公共点时,叫做直线和圆2、设Qo的半径为r,圆心o到直线l的距离为d,则:直线l与Qo相交<=>d r,直线l与Qo相切<=>d r直线l与Qo相离<=>d r3、切线的性质和判定:⑴性质定理:圆的切线垂直于经过切点的【赵老师提醒:根据这一定理,在圆中遇到切线时,常用连接圆心和切点,即可的垂直关系】⑵判定定理:经过半径的且这条半径的直线式圆的切线【赵老师提醒:在切线的判定中,当直线和圆的公共点标出时,用判定定理证明。
当公共点未标出时,一般可证圆心到直线的距离d=r来判定相切】4、切线长定理:⑴切线长定义:在经过圆外一点的圆的切线上,这点和切点之间的长叫做这点到圆的切线长。
⑵切线长定理:从圆外一点到圆的两条切线,它们的相等,并且圆心和这一点的连线平分的夹角5、三角形的内切圆:⑴与三角形各边都的圆,叫做三角形的内切圆,内切圆的圆心叫做三角形的⑵三角形内心的形成:是三角形的交点内心的性质:到三角形各的距离相等,内心与每一个顶点的连接线平分【赵老师提醒:三类三角形内心都在三角形若△ABC三边为a、b、c面积为s,内切圆半径为r,则s= ,若△ABC为直角三角形,则r= 】二、圆和圆的位置关系:圆和圆的位置关系有种,若Qo1半径为R,Qo2半径为r,圆心距外,则Qo1 与Qo2 外距<=> Qo1 与Qo2 外切<=>两圆相交<=> 两圆内切<=>两圆内含<=>【赵老师提醒:两圆相离无公共点包含和两种情况,两圆相切有唯一公共点包含和两种情况,注意题目中两种情况的考虑圆心同是两圆此时d= 】三、反证法:假设命题的结论,由此经过推理得出由矛盾判定所作的假设从而得到原命题成立,这种证明命题的方法叫反证法【赵老师提醒:反证法正题的关键是提出即假设所证结论的反面成立,择推理论证得出的矛盾可以与相矛盾,也可以与相矛盾,从而肯定原命题成立】【典型例题解析】考点一:切线的性质线,证明:AB=4PD.考点:切线的性质;等边三角形的判定与性质;含30度角的直角三角形;圆心角、弧、弦的关系;圆周角定理.专题:几何综合题.分析:(1)PO与BC的位置关系是平行;(2)(1)中的结论成立,理由为:由折叠可知三角形APO与三角形CPO全等,根据全等三角形的对应角相等可得出∠APO=∠CPO,再由OA=OP,利用等边对等角得到∠A=∠APO,等量代换可得出∠A=∠CPO,又根据同弧所对的圆周角相等得到∠A=∠PCB,再等量代换可得出∠COP=∠ACB,利用内错角相等两直线平行,可得出PO与BC平行;(3)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,再利用折叠的性质得到∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP 平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD,得证.解答:解:(1)PO与BC的位置关系是PO∥BC;(2)(1)中的结论PO∥BC成立,理由为:由折叠可知:△APO≌△CPO,∴∠APO=∠CPO,又∵OA=OP,∴∠A=∠APO,∴∠A=∠CPO,又∵∠A与∠PCB都为PB所对的圆周角,∴∠A=∠PCB,∴∠CPO=∠PCB,对应训练1.(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.(1)求证:AE平分∠CAB;(2)探求图中∠1与∠C的数量关系,并求当AE=EC时,tanC的值.考点:切线的性质;特殊角的三角函数值.专题:探究型.分析:(1)连接OE,则OE⊥BC,由于AB⊥BC,故可得出AB∥OE,进而可得出∠2=∠AEO,由于OA=OE,故∠1=∠AEO,进而可得出∠1=∠2;(2)由三角形外角的性质可知∠1+∠AEO=∠EOC,,因为∠1=∠AEO,∠OEC=90°,所以2∠1+∠C=90°;当AE=CE时,∠1=∠C,再根据2∠1+∠C=90°即可得出∠C的度数,由特殊角的三角函数值得出tanC即可.解答:(1)证明:连接OE,∵⊙O与BC相切于点E,∴OE⊥BC,∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,∵OP=OB,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠ACP=∠ABC,∴AB=AC;(2)延长AP交⊙O于D,连接BD,∵设圆半径为r,则OP=OB=r,PA=5-r,∴AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(25)2-(5-r)2,∴52-r2=(25)2-(5-r)2,解得:r=3,∴AB=AC=4,∵PD是直径,∴∠PBD=90°=∠PAC,∵∠DPB=∠CPA,∴△DPB∽△CPA,∴CP AP PD BP=,∴2553 33BP-=+,解得:PB=655.考点二:切线的判定(2)解:作BG⊥CD,垂足是G,在Rt△ABD中∵AB=10,sin∠DAB=35,又∵sin∠DAB=BD AB,∴BD=6∵C是弧AB的中点,∴∠ADC=∠CDB=45°,∴BG=DG=BDsin45°=6×22=32,∵∠DAB=∠DCB∴tan∠DCB=BGCG=34,∴CG=42,∴CD=CG+DG=42+32=72,∴S△CBD=12CD•BG=7232212⨯=.点评:本题考查的是切线的判定定理,涉及到圆周角定理、解直角三角形及三角形的面积公式,根据题意作出辅助线,构造出直角三角形是解答此题的关键.对应训练考点三:三角形的外接圆和内切圆例4 (2012•阜新)如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC能被半径至少为cm的圆形纸片所覆盖.考点:三角形的外接圆与外心;圆周角定理;锐角三角函数的定义.专题:计算题.分析:作圆O的直径CD,连接BD,根据圆周角定理求出∠D=60°,根据锐角三角函数的定义得出sin∠D= BCCD,代入求出CD即可.解答:解:作圆O的直径CD,连接BD,∵弧BC对的圆周角有∠A、∠D,∴∠D=∠A=60°,∵直径CD,A.r B.2r C.2r D.2r考点:三角形的内切圆与内心;矩形的判定;正方形的判定;切线长定理.专题:计算题.分析:连接OD、OE,求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=r,根据切线长定理得出MP=DM,NP=NE,代入MB+NB+MN得出BD+BE,求出即可.解答:解:连接OD、OE,∵⊙O是Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE是矩形,∵OD=OE,∴矩形ODBE是正方形,∴BD=BE=OD=OE=r,∵⊙O切AB于D,切BC于E,切MN于P,∴MP=DM,NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,故选C.点评:本题考查的知识点是矩形的判定、正方形的判定、三角形的内切圆和内心、切线长定理等,主要考查运用这些性质进行推理和计算的能力,题目比较好,难度也适中.对应训练4.(2012•台州)已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.(1)求证:△ABD≌△CBE;∴sin∠D=BCCD=45,∴CD=25 4,答:三角形ABC外接圆的直径是254.(2)解:连接IC、BI,且延长BI交AC于F,过I作IE⊥AB于E,∵AB=BC=5,I为△ABC内心,∴BF⊥AC,AF=CF,∵sin∠A=45=BFAB,∴BF=4,在Rt△ABF中,由勾股定理得:AF=CF=3,AC=2AF=6,∵I是△ABC内心,IE⊥AB,IF⊥AC,IG⊥BC,∴IE=IF=IG,设IE=IF=IG=R,∵△ABI、△ACI、△BCI的面积之和等于△ABC的面积,∴12AB×R+12BC×R+12AC×R=12AC×BF,即5×R+5×R+6×R=6×4,∴R=32,在△AIF中,AF=3,IF=32,由勾股定理得:AI=352.答:AI的长是352.点评:本题考查了三角形的面积公式,三角形的内切圆和内心,勾股定理,等腰三角形的性质,圆周角定理等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.考点三:圆与圆的位置关系例6(2012•毕节地区)第三十奥运会将于2012年7月27日在英国伦敦开幕,奥运会旗图案有五个圆环组成,如图也是一幅五环图案,在这个五个圆中,不存在的位置关系是()A.外离B.内切C.外切D.相交考点:圆与圆的位置关系.分析:根据两圆的位置关系易得到它们的位置关系有外切、外离、相交.解答:解:观察图形,五个等圆不可能内切,也不可能内含,并且有的两个圆只有一个公共点,即外切;有的两个圆没有公共点,即外离;有的两个圆有两个公共点,即相交.故选B.点评:本题考查了圆与圆的位置关系:若两圆的半径分别为R,r,圆心距为d,若d>R+r,两圆外离;若d=R+r,两圆外切;若R-r<d<R+r(R≥r),两圆相交;若d=R-r(R>r),两圆内切;若0≤d<R-r(R>r),两圆内含.对应训练6.(2012•德阳)在平面直角坐标系xOy中,已知点A(0,2),⊙A的半径是2,⊙P的半径是1,满足与⊙A及x轴都相切的⊙P有个.6.4考点:圆与圆的位置关系;坐标与图形性质;直线与圆的位置关系.分析:分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数.解答:解:如图,满足条件的⊙P有4个,故答案为4.点评:本题考查了圆与圆的位置关系、坐标与图形的性质及直线与圆的知识,能充分考虑到分内切和外切是解决本题的关键.【聚焦山东中考】1.(2012•济南)已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,若圆心距O1O2=5,则⊙O1和⊙O2的位置关系是()A.外离B.外切C.相交D.内切考点:圆与圆的位置关系.分析:先根据一元二次方程根与系数的关系,可知圆心距=两圆半径之和,再根据圆与圆的位置关系即可判断.解答:解:∵⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,∴两根之和=5=两圆半径之和,又∵圆心距O1O2=5,∴两圆外切.故选B.点评:此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断.圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R-r<d<R+r(R≥r);④两圆内切⇔d=R-r(R>r);⑤两圆内含⇔d<R-r(R>r).2.(2012•青岛)已知,⊙O1与⊙O2的半径分别是4和6,O1O2=2,则⊙O1与⊙O2的位置关系是()A.内切B.相交C.外切D.外离考点:圆与圆的位置关系.分析:由⊙O1与⊙O2的半径分别是4和6,O1O2=2,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵⊙O1与⊙O2的半径分别是4和6,O1O2=2,∴O1O2=6-4=2,∴⊙O1与⊙O2的位置关系是内切.故选A.点评:此题考查了圆与圆的位置关系.此题比较简单,注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.3.(2012•泰安)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为()A.π B.2πC.3π D.5π考点:切线的性质;弧长的计算.分析:连接OB,由于AB是切线,那么∠ABO=90°,而∠ABC=120°,易求∠OBC,而OB=OC,那么∠OBC=∠OCB,进而求出∠BOC的度数,在利用弧长公式即可求出BC的长.解答:解:连接OB,∵AB与⊙O相切于点B,∴∠ABO=90°,∵∠ABC=120°,∴∠OBC=30°,∵OB=OC,∴∠OCB=30°,∴∠BOC=120°,∴ BC 的长为nπr 180 =120×π×3 180 =2π,故选B.点评:本题考查了切线的性质、弧长公式,解题的关键是连接OB,构造直角三角形.4.(2012•潍坊)已知两圆半径r1、r2分别是方程x2-7x+10=0的两根,两圆的圆心距为7,则两圆的位置关系是()A.相交B.内切C.外切D.外离考点:圆与圆的位置关系;解一元二次方程-因式分解法.分析:首先解方程x2-7x+10=0,求得两圆半径r1、r2的值,又由两圆的圆心距为7,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵x2-7x+10=0,∴(x-2)(x-5)=0,∴x1=2,x2=5,即两圆半径r1、r2分别是2,5,∵2+5=7,两圆的圆心距为7,∴两圆的位置关系是外切.故选C.点评:此题考查了圆与圆的位置关系与一元二次方程的解法.此题比较简单,注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.5.(2012•济南)如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是.5.4848考点:切线的性质;勾股定理;矩形的性质.分析:首先取AC的中点O,过点O作MN∥EF,PQ∥EH,由题意可得PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,PL,KN,OM,OQ分别是各半圆的半径,OL,OK是△ABC的中位线,又由在Rt△ABC中,∠B=90°,AB=6,BC=8,即可求得个线段长,继而求得答案.解答:解:取AC的中点O,过点O作MN∥EF,PQ∥EH,∵四边形EFGH是矩形,∴EH∥PQ∥FG,EF∥MN∥GH,∠E=∠H=90°,∴PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,∵AB∥EF,BC∥FG,∴AB∥MN∥GH,BC∥PQ∥FG,∴AL=BL,BK=CK,∴OL=12BC=12×8=4,OK=12AB=12×6=3,∵矩形EFGH的各边分别与半圆相切,∴PL=12AB=12×6=3,KN=12BC=12×8=4,在Rt△ABC中,AC= ,∴OM=OQ=12AC=5,∴EH=FG=PQ=PL+OL+OQ=3+4+5=12,EF=GH=MN=OM+OK+NK=5+3+4=12,∴矩形EFGH的周长是:EF+FG+GH+EH=12+12+12+12=48.故答案为:48.点评:此题考查了切线的性质、矩形的性质,三角形中位线的性质以及勾股定理等知识.此题难度较大,解题的关键是掌握辅助线的作法,注意数形结合思想的应用.6.(2012•菏泽)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC= 度.6.23考点:切线的性质.专题:计算题.分析:由PA、PB是圆O的切线,根据切线长定理得到PA=PB,即三角形APB为等腰三角形,由顶角的度数,利用三角形的内角和定理求出底角的度数,再由AP为圆O的切线,得到OA与AP垂直,根据垂直的定义得到∠OAP为直角,再由∠OAP-∠PAB即可求出∠BAC 的度数.解答:解:∵PA,PB是⊙O是切线,∴PA=PB,又∠P=46°,∴∠PAB=∠PBA=180-462=67°,又PA是⊙O是切线,AO为半径,∴OA⊥AP,∴∠OAP=90°,∴∠BAC=∠OAP-∠PAB=90°-67°=23°.故答案为:23。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013中考数学专题复习圆与圆的位置关系
一、选择题
1. (2011浙江台州,8,4分)如图,图2 是一个组合烟花(图1)的横截面,其中16个圆
的半径相同,点O1、O2、O3、O4分布是四个角上的圆的圆心,且四边形O1O2O3O4正方形。
若圆的半径为r,组合烟花的高度为h,则组合烟花侧面包装纸的面积至少需要(解缝面积不计)()
A.26πrh
B. 24r h+πrh
C. 12r h-2πrh
D. 24r h+2πrh
【答案】D
2. (2011浙江温州,8,4分)已知线段AB=7cm.现以点A为圆心,2cm为半径画⊙A;
再以点B为圆心,3cm为半径画⊙B,则⊙A和⊙B的位置关系是()
A.内含B.相交C.外切D.外离
【答案】D
3. (2011台湾台北,25)如图(九),圆A、圆B的半径分别为4、2,且AB=12。
若作一
圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长?
A.3B.4 C.5 D .6
【答案】A
4. (2011台湾全区,25)若有两圆相交于两点,且圆心距离为13公分,则下列哪一选项
中的长度可能为此两圆的半径?
A.25公分、40公分B.20公分、30公分
C .1公分、10公分
D . 5公分、7公分 【答案】B
5. (2011台湾全区,32)图(十四)中,CA 、CD 分别切圆O 1于A 、D 两点,CB 、CE 分
别切圆O 2于B 、E 两点.若∠1=60∘,∠2=65∘,判断AB 、CD 、CE 的长度,下列关系何者正确?
A .A
B >CE >CD B .AB =CE >CD
C .AB >C
D >C
E D .AB =CD =CE 【答案】A
6. (2011浙江省舟山,5,3分)两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( ) (A )两个外离的圆 (B )两个外切的圆 (C )两个相交的圆
(D )两个内切的圆
【答案】D
7. (2011江苏扬州,4,3分)已知相交两圆的半径分别在4和7,则它们的圆心距可能是( ) A.2 B. 3 C. 6 D. 11 【答案】C
8. (2011山东济宁,5,3分)已知⊙O 1与⊙O 2相切,⊙O 1的半径为9 cm ,⊙O 2的半径为2 cm ,则O 1O 2的长是( ) A .1 cm B .5 cm C .1 cm 或5 cm D .0.5cm 或2.5cm
【答案】C
9. (2011福建泉州,5,3分)已知⊙O 1和⊙O 2的半径分别为2cm 和5cm ,两圆的圆心距
是3.5cm ,则两圆的位置关系是( ).
A .内含
B .外离
C .内切
D .相交
水平面
主视方向
(第5题)
【答案】D
10.(2011广东茂名,7,3分)如图,⊙1o 、⊙2o 相内切于点A ,其半径分别是8和4,将⊙2o 沿直线1
o 2o 平移至两圆相外切时,则点2o 移动的长度是
A .4
B .8
C .16
D .8 或16
【答案】D
11. (2011湖北襄阳,9,3分)在△ABC 中,∠C =90°,AC =3cm ,BC =4cm ,若⊙A ,⊙B 的半径分别为1cm ,4cm ,则⊙A ,⊙B 的位置关系是 A .外切
B .内切
C .相交
D .外离
【答案】A
12. (2011江苏盐城,5,3分)若⊙O 1、⊙O 2的半径分别为4和6,圆心距O 1O 2=8,则⊙O 1与⊙O 2的位置关系是
A .内切
B .相交
C .外切
D .外离 【答案】B
13. (2011重庆市潼南,7,4分) 已知⊙O 1与⊙O 2外切,⊙O 1的半径R=5cm, ⊙O 2的半径r =1cm ,则⊙O 1与⊙O 2的圆心距是 A .1cm B .4cm C .5cm D .6cm 【答案】D 二、填空题
1. (2011浙江省,16,3分)如图,图①中圆与正方形各边都相切,设这个圆的周长为C 1;
图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长为C 2;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长为C 3;……,依次规律,当正方形边长为2时,则C 1+ C 2+ C 3+…C 99+ C 100=
【答案】10100π
2. (2011浙江义乌,13,4分)已知⊙O 1与⊙O 2的半径分别为3和5,且⊙O 1与⊙O 2相切,则O 1O 2等于 ▲ . 【答案】2或8
3. (2011四川广安,14,3分)已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2
680x
x -+=
的两实根,若⊙O 1与⊙O 2的圆心距d =5.则⊙O 1与⊙O 2的位置关系是____ 【答案】相交
4. (2011江苏南通,18,3分)已知:如图,三个半圆以此相外切,它们的圆心都在x 轴的正半轴上并与直线y =
3
3
x 相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3,则当r 1=1时,r 3= ▲
【答案】9.
5. (2011广东肇庆,14,3分)已知两圆的半径分别为1和3,若两圆相切,则两圆的圆心距为 ▲ . 【答案】4或2
6. (2011山东枣庄,17,4分)如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a ,0),半径为5.如果两圆内含,那么a 的取值范围是________.
(a ,0) x y O · 3 5
【答案】-2<a <2 三、解答题
1. (2011江西,20,8分)有一种用来画圆的工具板(如图所示),工具板长21cm ,上面依次排列着大小不等的五个圆(孔),共中最大圆的直径为3cm ,其余圆的直径从左到右依次递减0.2cm .最大圆的左侧距工具板左侧边缘1.5cm ,最小圆的右侧距工具板右侧边缘1.5cm ,相邻两圆的间距d 均相等。
⑴直接写出其余四个圆的直径长; ⑵求相邻两圆的间距。
【答案】(1)其余四个圆的直径长分别为2.8cm ,2.6cm ,2.4cm ,2.2cm ; (2)因为工具板长21cm ,左、右侧边缘1.5cm ,
所以的五个圆(孔)及相邻两圆的间距之和为21-3=18(cm ).
d=[18-(3+2.8+2.6+2.4+2.2)]÷4=5
4
(cm ).
2. (2011江苏南京,26,8分)如图,在Rt △ABC 中,∠ACB=90°,AC=6㎝,BC=8㎝,P
为BC 的中点.动点Q 从点P 出发,沿射线PC 方向以2㎝/s 的速度运动,以P 为圆心,PQ 长为半径作圆.设点Q 运动的时间为t s .
⑴当t=1.2时,判断直线AB 与⊙P 的位置关系,并说明理由; ⑵已知⊙O 为△ABC 的外接圆,若⊙P 与⊙O 相切,求t 的值.
【答案】解:⑴直线AB 与⊙P 相切.
A
B C P Q O
(第26题)
如图,过点P 作PD ⊥AB, 垂足为D .
在Rt △ABC 中,∠ACB =90°,∵AC=6cm ,BC=8cm , ∴2210AB AC BC cm =
+=.∵P 为BC 的中点,∴PB=4cm .
∵∠PDB =∠ACB =90°,∠PBD =∠ABC .∴△PBD ∽△ABC . ∴
PD PB AC AB =,即4
610
PD =,∴PD =2.4(cm) . 当 1.2t =时,2 2.4PQ t ==(cm)
∴PD PQ =,即圆心P 到直线AB 的距离等于⊙P 的半径. ∴直线AB 与⊙P 相切.
⑵ ∠ACB =90°,∴AB 为△ABC 的外切圆的直径.∴1
52
OB AB cm ==. 连接OP .∵P 为BC 的中点,∴1
32
OP AC cm =
=. ∵点P 在⊙O 内部,∴⊙P 与⊙O 只能内切. ∴523t -=或253t -=,∴t =1或4. ∴⊙P 与⊙O 相切时,t 的值为1或4.
3. (2011湖北黄石,24,9分)已知⊙O 1与⊙O 2相交于A 、B 两点,点O 1在⊙O 2上,C
为O 2上一点(不与A ,B ,O 1重合),直线CB 与⊙O 1交于另一点D 。
(1)如图(8),若AC 是⊙O 2的直径,求证:AC =CD
(2)如图(9),若C 是⊙O 1外一点,求证:O 1C ⊥AD
(3)如图(10),若C 是⊙O 1内的一点,判断(2)中的结论是否成立。
【答案】(1)连接C O 1,AB ∵AC 是⊙O 2的直径
∴AB ⊥BD,AD ⊥C O 1 ∴AD 经过点O 1 ∵AO 1=DO 1 ∴AC =CD
(2)连接O 1 O 2,AO 1 ∵O 1 O 2⊥AB
∴∠AO 1O 2+∠AG O 1 ∵∠O 1AB =∠C 又∵∠D =
2
1
∠A O 1B =∠AO 1O 2 ∴∠C +∠D =900 ∴O 1C ⊥AD
(3)成立。
