数学实验答案-
数学实验练习二 参考答案

数学实验二实验内容:学习matlab的m文件编写和函数的编写,体会matlab编程特点,掌握matlab 的编程基本方法。
要求:一.学习ppt教案的例题代码,能正确的输入、运行代码;二.写出如下各段代码的作用,将以下各段循环执行的代码,改为不需要循环的矩阵和数组运行,并使用tic,toc测试不同代码的执行时间:%程序1,文件名:ex2_2_1.mticdx = pi/30;nx = 1 + 2*pi/dx;for i = 1:nxx(i) = (i-1)*dx;y(i) = sin(3*x(i));endtoc以上程序实现将[0,2*pi]间隔pi/30分成60等分,x和y分别为61个元素的数组,y为计算sin(3x)的值。
以上程序可以使用简单的matlab数组计算实现:x2=0:pi/30:2*pi;y2=sin(3*x2);大家可以比较一下,x1和x2完全相同,y和y2也完全相同。
%程序2,文件名:ex2_2_2.mticA=round(2+rand(50,60)*6); 生成一个在[2,8]上均匀分布的50*60随机数组[X,Y]=size(A); 求出其大小;X=50,Y=60minA=A(1,1); 设最小值为矩阵A的第1行1列的元素for i=1:Xfor j=1:Yif A(i,j)<minAminA=A(i,j);minX=i;minY=j;endendend 以上程序按行、列搜索矩阵A的最小值,若当前值A(I,j)小,则将最小值设为当前值;[minA ,minX,minY] 输出矩阵最小值minA及矩阵最小值所在的行minX、列minY。
toc上述程序可以使用find函数及min函数实现;此时只需: minA=min(A(:));[minX,minY]=find(A ’==minA,1);%注意此处需将矩阵A 转置,因为matlab 中是按列优先搜索的,而题目的程序是按行有限搜索。
数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年

数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年1.无向图中边的端点地位是平等的、边是无序点对。
而有向图中边的端点的地位不平等,边是有序点对,不可以交换。
参考答案:正确2.人口数量与下列因素都有关,人口基数、出生率、死亡率、年龄结构、性别比例、医疗水平、工农业生产水平、环境、生育政策等等。
参考答案:正确3.一元5次代数方程在复数范围内有多少个根?参考答案:54.任何贪心算法都能求出最优解。
参考答案:错误5.二维插值函数z=interp2(x0,y0,z0,x,y,’method’)中,method的缺省值是()参考答案:linear6.在当前文件夹和搜索路径中都有文件ex1.m,在命令行窗口输入ex1时,则执行的文件是当前文件夹中的ex1.m参考答案:正确7.下列关于Dijkstra算法的哪些说法正确参考答案:Dijkstra算法是求加权图G中从某固定起点到其余各点最短路径的有效算法;_Dijkstra算法的时间复杂度为O(n2),其中n为顶点数;_Dijkstra算法可用于求解无向图、有向图和混合图的最短路径问题;8.如果x=1: 2 : 10,则x(1)和x(5)分别是( )参考答案:1,99.人口是按指数规律无限增长的。
参考答案:错误10.在包汤圆问题的整个建模过程,包括了如下几个步骤(1)找出问题涉及的主要因素(变量),重新梳理问题使之更明确(2)作出简化、合理的假设(3)用数学的语言来描述问题(4)用几何的知识解决问题(5)模型应用参考答案:正确11.下面程序所解的微分方程组,对应的方程和初始条件为:(1)函数M文件weif.m:function xdot=weif(t, x)xdot=[3*x(1)+x(3);2*x(1)+6;-3*x(2)^2+2*x(3)];(2)脚本M文件main.m:x0=[1,2,3] ;[t,x]=ode23(‘weif’,[0,1],x0),plot(t,x’),figure(2),plot3(x( :,1),x( :,2),x( :,3)参考答案:___12.某公司投资2000万元建成一条生产线。
数学实验手册六年级下册答案

数学实验手册六年级下册答案1、下列说法有几种是正确的()(1)空间三点确定一个平面(2)一条直线和直线外一点确定一个平面(3)两条直线确定一个平面(4)两条平行直线确定一个平面[单选题] *A、1B、2(正确答案)C、3D、42、下列各对象可以组成集合的是()[单选题] *A、与1非常接近的全体实数B、与2非常接近的全体实数(正确答案)C、高一年级视力比较好的同学D、与无理数相差很小的全体实数3、已知10?=5,则100?的值为( ) [单选题] *A. 25(正确答案)B. 50C. 250D. 5004、22、在平面直角坐标系中,已知点P,在轴上有点Q,它到点P的距离等于3,那么点Q 的坐标是()[单选题] *(0,3)(0,5)(0,-1)(0,5)或(0,-1) (正确答案)5、28、若的三边之长都是整数,周长小于10,则这样的三角形共有()[单选题] *A. 6个,B. 7个,C. 8个,D. 9个(正确答案)6、1.在0,,3,2π,﹣23%,2021这六个数中,非正数有()个.[单选题] *A.2(正确答案)B.3C.4D.07、20.水文观测中,常遇到水位上升或下降的问题.我们规定:水位上升为正,水位下降为负;几天后为正,几天前为负.如果水位每天上升3cm,今天的水位为0cm,那么2天前的水位用算式表示正确的是()[单选题] *A.(+3)×(+2)B.(+3)×(﹣2)(正确答案)C.(﹣3)×(+2)D.(﹣3)×(﹣2)8、第三象限的角的集合可以表示为()[单选题] *A. {α|180°<α<270°}B. {α|180°+k·360°<α<270°+k·360°}(正确答案)C. {α|90°<α<180°}D. {α|90°+k·360°<α<180°+k·360°}9、一个直二面角内的一点到两个面的距离分别是3cm和4 cm ,求这个点到棱的距离为()[单选题] *A、25cmB、26cmC、5cm(正确答案)D、12cm10、由数字1、2、3、4、5可以组成多少个不允许有重复数字的三位数?()[单选题]*A、125B、126C、60(正确答案)D、12011、下列说法正确的是[单选题] *A.一个数前面加上“-”号,这个数就是负数B.零既不是正数也不是负数(正确答案)C.零既是正数也是负数D.若a是正数,则-a不一定是负数12、47.已知(x﹣2021)2+(x﹣2023)2=50,则(x﹣2022)2的值为()[单选题]* A.24(正确答案)B.23C.22D.无法确定13、300°是第()象限角?[单选题] *第一象限第二象限第三象限第四象限(正确答案)14、5. 下列对一元二次方程x2+x﹣3=0根的情况的判断,正确的是()[单选题] *A.有两个不相等实数根(正确答案)B.有且只有一个实数根C.有两个相等实数根D.没有实数根15、18.下列关系式正确的是(? ) [单选题] *A.-√3∈NB.-√3∈3C.-√3∈QD.-√3∈R(正确答案)16、30、等腰三角形ABC中,AB=2BC,且BC=12,则△ABC的周长为( ). [单选题]A. 48B. 60(正确答案)C. 48或60D. 3617、7人小组选出2名同学作正副组长,共有选法()种。
数学实验(南邮)答案2

第二次练习题1、 设⎪⎩⎪⎨⎧=+=+32/)7(11x x x x n n n ,数列}{n x 是否收敛?若收敛,其值为多少?精确到6位有效数字。
>> f=inline('(x+7/x)/2'); syms x; x0=3; for i=1:1:20 x0=f(x0);fprintf('%g,%g\n',i,x0); end 1,2.66667 2,2.64583 3,2.64575 4,2.64575 5,2.64575 6,2.64575 7,2.64575 8,2.64575 9,2.64575 10,2.64575 11,2.64575 12,2.64575 13,2.64575 14,2.64575 15,2.64575 16,2.64575 17,2.64575 18,2.64575 19,2.64575 20,2.64575本次计算运行到第三次结果稳定,可得: 数列}{n x 收敛,收敛到2.645752、 设 ,131211pp p n n x ++++= }{n x 是否收敛?若收敛,其值为多少?精确到17位有效数字。
学号为单号,取7=p >> s=0; for i=1:1:200 s=s+1/i^7;fprintf('%g,%20.17f\n',i,s); end1, 1.00000000000000000 2, 1.00781250000000000 3, 1.00826974737082750 4, 1.00833078252707750 5, 1.00834358252707750 6, 1.00834715477216210 7, 1.00834836903784100 8, 1.00834884587499920 9, 1.00834905495015730 10, 1.00834915495015730 …………………………… 181, 1.00834927738191870 182, 1.00834927738191890 183, 1.00834927738191920 184, 1.00834927738191940 185, 1.00834927738191960 186, 1.00834927738191980 187, 1.00834927738192000 188, 1.00834927738192030 189, 1.00834927738192050190, 1.00834927738192070 191, 1.00834927738192070 192, 1.00834927738192070 193, 1.00834927738192070 194, 1.00834927738192070 195, 1.00834927738192070 196, 1.00834927738192070 197, 1.00834927738192070 198, 1.00834927738192070 199, 1.00834927738192070 200, 1.00834927738192070运行至第190次后稳定,值为1.00834927738192070书上习题:(实验四) 1,2,4,7(1),8,12(改为:对例2,取 120,55,25,5.4=a 观察图形有什么变化.),13,14 。
数学实验1-3章习题答案
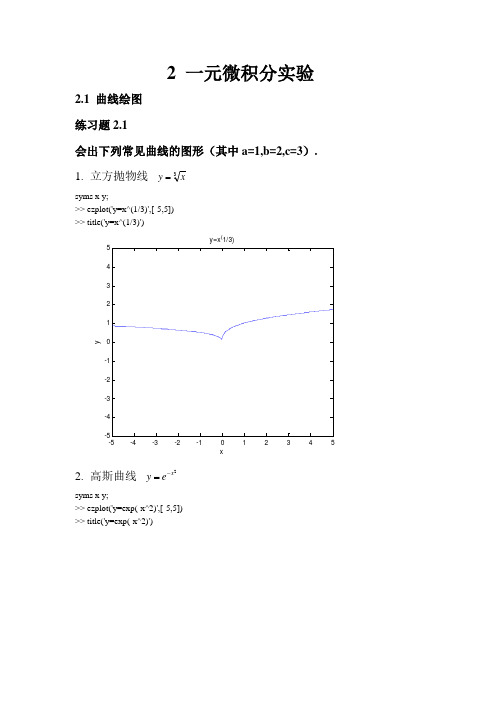
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
大学数学实验智慧树知到答案章节测试2023年黑龙江工程学院

绪论单元测试1.MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室)。
()A:错B:对答案:B2.MATLAB和、c语音并称为三大数学软件。
()A:对B:错答案:B3.MATLAB的基本数据单位是矩阵.( )A:对B:错答案:A4.matlab的优点有以下哪些?( )A:高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来;B:具有完备的图形处理功能,实现计算结果和编程的可视化;C:友好的用户界面及接近数学的自然化语言,使学者易于学习和掌握;D:功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
答案:ABCD5.MATLAB只能做高数、线代、概率的计算题,不能做其他的。
()A:对B:错答案:B6.matlab主要应用于以下哪些领域()A:工程计算、控制设计B:信号处理与通讯C:金融建模设计与分析等领域D:图像处理、信号检测答案:ABCD7.本课程仅仅学习了matlab的冰山一角。
()A:对B:错答案:A8.matlab也加入了对C,FORTRAN,C++,JAVA的支持。
()A:对B:错答案:A9.本课程只研究在matlab在高等数学、概率论、线性代数三大学科中的简单应用,姑且把matlab当做一个大型的计算器。
()A:对B:错答案:A10.“mathematica 可能是数学界最好的狙击枪,但MATLAB能给你一座军火库。
“这句话形容了矩阵运算、数据可视化、GUI(用户界面)设计、甚至是连接其他编程语言,MATLAB都能轻松实现。
()A:错B:对答案:B第一章测试1.定义变量的命令为syms ()A:错B:对答案:B2.正弦函数的函数命令为sinx ()A:错B:对答案:A3.余弦函数的函数命令为cos(x) ()A:对B:错答案:A4.matlab不区分输入法的半角和全角()A:对B:错答案:B5.matlab不区分函数命令的大小写()A:对B:错答案:B6.指数函数的函数命令为e^x ()A:对B:错答案:B7.floor(x)是指对x朝-∞方向取整()A:错B:对答案:B8.plot命令可以画离散数据的函数曲线图()A:错B:对答案:B9.ezplot命令可以画连续函数的曲线图()A:对B:错答案:A10.正切函数tanx 可以直接用plot命令画0到pi之间的图形()A:错B:对答案:A第二章测试1.计算极限:()A:-1/exp(1/3)B:1/exp(1/3)C:1D:0答案:B2.计算极限:()A:2B:-1C:1D:0答案:A3.计算极限:()A:INFB:-3/5C:0D:3/5答案:D4.计算极限:()A:-1/3B:0C:1/3D:1答案:C5.计算极限:()A:1B:0C:INFD:-1答案:B6.计算极限:()A:1B:0C:INFD:-1答案:D7.计算极限:()A:INFB:0C:1D:-1答案:B8.计算极限:()A:1/exp(1/3)B:-1/2C:0D:1/2答案:D9.计算极限:( )A:0B:2C:-1D:1答案:A10.计算极限:( )A:1B:-1C:0D:2答案:A第三章测试1.求由参数方程确定的函数的导数。
数学实验梁宝钰版课后答案

数学实验梁宝钰版课后答案1、11.11点40分,时钟的时针与分针的夹角为()[单选题] *A.140°B.130°C.120°D.110°(正确答案)2、已知10?=5,则100?的值为( ) [单选题] *A. 25(正确答案)B. 50C. 250D. 5003、1. 在实数0、-√3?、√2?、-2中,最小的是()[单选题] *A、-2(正确答案)B、-√3C、0D、√24、24.不等式x-3>5的解集为()[单选题] *A. x > 1B. x > 2(正确答案)C. x > 3D. x > 45、42.已知m、n均为正整数,且2m+3n=5,则4m?8n=()[单选题] * A.16B.25C.32(正确答案)D.646、已知直线l的方程为2x-y+7=0,()是直线l上的点[单选题] *A、(2,3)B、(2,4)(正确答案)C、(2,-3)D、(-2,-3)7、46.若a+b=7,ab=10,则a2+b2的值为()[单选题] *A.17B.29(正确答案)C.25D.498、8.数轴上一个数到原点距离是8,则这个数表示为多少()[单选题] *A.8或﹣8(正确答案)B.4或﹣4C.8D.﹣49、14.数﹣在数轴上的位置可以是()[单选题] *A.点A与点B之间(正确答案)B.点B与点O之间C.点O与点D之间D.点D与点E之间10、2.(2020·新高考Ⅱ,1,5分)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B=( ) [单选题] * A.{1,8}B.{2,5}C.{2,3,5}(正确答案)D.{1,2,3,5,7,8}11、7.如图,数轴上点M表示的数可能是()[单选题] *A.5B.﹣6C.﹣6(正确答案)D.612、以A(3,2),B(6,5),C(1,10)为顶点的三角形是()[单选题] *A、锐角三角形B、锐角三角形C、直角三角形(正确答案)D、无法判断13、点A的坐标为(3,4),点B的坐标为(5,8),则它们的中点坐标是(D)[单选题] *A、(3,4)B、(3,5)C、(8,12)D、(4,6)(正确答案)14、计算(-a)?·a的结果是( ) [单选题] *A. -a?B. a?(正确答案)C. -a?D. a?15、21.|x|>3表示的区间是()[单选题] *A.(-∞,3)B.(-3,3)C. [-3,3]D. (-∞,-3)∪(3,+ ∞)(正确答案)16、已知x-y=3,x2-y2=12,那么x+y的值是( ??) [单选题] *A. 3B. 4(正确答案)C. 6D. 1217、13.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是() [单选题] *A.(0,4)→(0,0)→(4,0)B.(0,4)→(4,4)→(4,0)C.(0,4)→(3,4)→(4,2)→(4,0)(正确答案)D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)18、260°是第()象限角?[单选题] *第一象限第二象限第三象限(正确答案)第四象限19、9.如图,下列说法正确的是()[单选题] *A.直线AB与直线BC是同一条直线(正确答案)B.线段AB与线段BA是不同的两条线段C.射线AB与射线AC是两条不同的射线D.射线BC与射线BA是同一条射线20、28、若的三边之长都是整数,周长小于10,则这样的三角形共有()[单选题] *A. 6个,B. 7个,C. 8个,D. 9个(正确答案)21、5.下列结论不正确的是[单选题] *A.若a > 0,b > 0,则a + b > 0B.若a < 0,b < 0,则a + b < 0C.若a > 0,b < 0,且|a| > |b|,则a + b > 0D.若a < 0,b > 0,且|a| > |b|,则a + b > 0(正确答案)22、11.小文买了一支温度计,回家后发现里面有一个小气泡(即不准确了),先拿它在冰箱里试一下,在标准温度是零下7℃时,显示为℃,在36℃的温水中,显示为32℃,那么用这个温度计量得的室外气温是23℃,则室外的实际气温应是()[单选题] *A.27℃(正确答案)B.19℃C.23℃D.不能确定23、北京、南京、上海三个民航站之间的直达航线,共有多少种不同的飞机票?()[单选题] *A、3B、4C、6(正确答案)D、1224、30.圆的方程+=4,则圆心到直线x-y-4=0的距离是()[单选题] *A.√2(正确答案)B.√2/2C.2√2D.225、下列计算正确是()[单选题] *A. 3x﹣2x=1B. 3x+2x=5x2C. 3x?2x=6xD. 3x﹣2x=x(正确答案)26、27.下列各函数中,奇函数的是()[单选题] *A. y=x^(-4)B. y=x^(-3)(正确答案)C .y=x^4D. y=x^(2/3)27、y=k/x(k是不为0的常数)是()。
高等数学实验教材答案

高等数学实验教材答案高等数学实验教材答案是学习高等数学实验课程的重要参考资料。
在这篇文章中,我将为大家提供一份高等数学实验教材的答案,以帮助学生更好地理解和掌握相关知识。
一、微分与导数1.1 定义与性质1.2 基本微分法则1.3 乘积法则、商法则与链式法则1.4 高阶导数与隐函数求导1.5 几何应用:切线与法线二、积分与不定积分2.1 定义与性质2.2 基本积分法则2.3 分部积分法2.4 有理函数的积分2.5 几何应用:定积分与曲线下面积三、微分方程3.1 一阶常微分方程3.2 高阶常微分方程3.3 可降阶的高阶常微分方程3.4 几何应用:曲线的凹凸性与拐点四、级数与幂级数4.1 数项级数与收敛性4.2 幂级数的收敛半径与收敛区间4.3 函数展开为幂级数4.4 幂级数展开与微分、积分的关系五、多元函数与偏导数5.1 多元函数的概念与性质5.2 偏导数及其计算5.3 隐函数与参数方程求导5.4 多元函数的极值与条件极值5.5 几何应用:方向导数与梯度六、重积分6.1 重积分的定义与性质6.2 二重积分的计算6.3 三重积分的计算6.4 极坐标、柱坐标与球坐标下的积分6.5 几何应用:质量、重心与转动惯量七、曲线积分与曲面积分7.1 第一类曲线积分7.2 第二类曲线积分7.3 常见曲线的参数方程与弧长7.4 曲面积分的概念与性质7.5 几何应用:质量、重心与转动惯量的曲面积分表示八、常微分方程与拉普拉斯变换8.1 齐次与非齐次线性常微分方程8.2 求解常系数齐次线性常微分方程8.3 非齐次线性常微分方程的常数变易法8.4 拉普拉斯变换的定义与性质8.5 拉普拉斯变换与求解微分方程以上是高等数学实验教材的答案大纲。
希望这份答案对广大学生们学习和理解高等数学实验课程有所帮助。
请将这份答案作为参考,并结合教材中的练习题进行实践,以巩固所学知识。
祝大家在高等数学实验课程中取得好成绩!。
数学实验期末试题及答案

数学实验期末试题及答案1. 选择题1) 请问下列哪个是无理数?A) 1.5B) √2C) 3/4D) 0.25答案: B) √22) 某公司某月原材料的消耗量为1000千克,该公司决定每个月的原材料消耗量要比上个月的消耗量减少20%。
请问第三个月的原材料消耗量是多少千克?A) 600B) 640C) 800D) 1000答案: C) 8003) 如果sinθ = 1/2,且θ位于第二象限,那么cosθ的值是?A) -1/2B) 1/2C) √3/2D) -√3/2答案: D) -√3/22. 填空题1) 若a = 3, b = -4,求 |ab| 的值。
答案: 122) 已知一组数据:3, 5, 7, 9, 11,求其中的众数。
答案: 无众数3) 若a + b = 8,a - b = 4,求a和b的值。
答案: a = 6, b = 23. 解答题1) 已知函数 f(x) = x^3 - 4x^2 + 3x + 2,求其在 x = 2 处的导数。
答案: f'(x) = 3x^2 - 8x + 3解释:根据函数求导法则,对于多项式函数,求导的结果是各项指数减1后的系数与原函数的积。
2) 某座山的高度为600米,山顶设有一个测量站A,山脚设有一个测量站B。
从A处以一定角度向上仰望山顶的角度为60°,从B处以一定角度向山顶仰望的角度为30°。
请问站A和站B之间的距离是多少?答案: 设山脚到山顶的距离为x,根据三角函数的定义可知:tan60° = 600 / xtan30° = 600 / (x + D)其中 D 为站A和站B之间的距离。
解方程组得:D = 300 / (√3 - 1) ≈ 254.5584. 应用题某饺子店每天销售不同种类的饺子,已知每天销售的饺子总数量为n,并且一包饺子里共有m个。
根据调查数据,销售饺子数量与价格之间存在以下函数关系:销售数量 = 100 - 2 * 价格若每天销售的饺子总数量为200,一包饺子有10个,请问该饺子店每个饺子的价格是多少?答案: 将已知数据带入函数关系得:200 = 100 - 2 * 价格即:2 * 价格 = 100解得:价格 = 50注意:以上为数学实验期末试题及答案的范例,实际试题及答案可能有所不同。
智慧树知到《数学实验》章节测试答案

智慧树知到《数学实验》章节测试答案绪论1、传统的数学实验包括测量手工操作制作模型实物或者教具演示等等。
A:对B:错答案: 对2、现代的数学实验以计算机软件应用为平台结合数学模型来模拟实验环境。
A:对B:错答案: 对第一章1、,则下列语句输出结果正确的是()A: >>A(2,1)↙ans=1B:>>B=A.A↙C:>>B=AA↙D:>>A(:,2)↙ans=(0,3)答案:>>B=A.*A↙2、要输入数组b=(3,4,5,6,7,8,9,10),下列语句不正确的是()B:b=3:1:10C: b=10:-1:3D: b=linspace(3,10,8)答案:b=10:-1:33、命令format rat, 0.5输出的结果是()A: ans=0.5000B: ans=+C: ans=0.50D:ans=1/2答案: ans=1/24、清除工作空间(workspace)的命令是().A: clcB: clearC: clfD: delete答案:clear5、如果x=1: 2 : 8,则x(1)和x(4)分别是()A: 1,8B: 1, 7C: 2, 8答案:1, 76、MATLAB表达式2*2^3^2的结果是( ) A:128B:4096C:262144D:256答案: 1287、sort([3,1,2,4])的运行结果是()A:4 3 2 1B:1 2 3 4C:1D:4答案: 1 2 3 48、image.pngA:feval(‘sin’,0.5pi)B:feval(sin(0.5pi)C:feval(sin, 0.5pi)D:feval(‘sin’, 0.5pi)答案: feval(‘sin’, 0.5pi)9、数组运算符与矩阵运算符是一样的。
A:对B:错答案: 错10、在输入矩阵时需要先定义矩阵的行数和列数。
A:对B:错答案: 错第二章1、在图形指定位置加标注的命令是()A: title(x,y,‘y=sin(x)’)B: xlabel(x,y,‘y=sin(x)’)C: text(x,y,‘y=sin(x)’)D:legend(x,y,‘y=sin(x)’)答案:text(x,y,‘y=sin(x)’)2、用来绘制二维条形统计图的命令是()A: barB: stairsC: fillD: full答案:bar3、绘制三维曲线下列语句组中有错误的语句是()A: >>t=0:pi/100:20piB: >>x=sin(t);y=cos(t)C: >>z=tsin(t)cos(t);D:>>plot3(x,y,z)答案:>>z=tsin(t)*cos(t);4、meshgrid函数的作用是()A: 绘制三维网格曲面B: 绘制三维实曲面C: 生成网格坐标矩阵D: 绘制带等高线的曲面答案:生成网格坐标矩阵5、为了使两个plot的图形在同一个坐标显示,可以使用()命令进行图形保持. A:hold onB:box onC:grid onD:subplot答案: hold on6、下列命令中中不是用来绘制曲面的是()A:meshB:surfC:sphereD:plot3答案: plot37、ezplot命令用来绘制隐函数的图形。
南邮数学实验答案

第一次练习题1、求032=-x e x 的所有根。
>>x=-5:0.01:5;y=exp(x)-3*x.^2;plot(x,y);grid on>> fsolve('exp(x)-3*x.^2',-1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =-0.4590>> fsolve('exp(x)-3*x.^2',1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =0.9100>> fsolve('exp(x)-3*x.^2',4)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =3.73312、求下列方程的根。
数学建模实验答案离散模型

实验09离散模型(2学时)(第8章离散模型)1. 层次分析模型(验证,编程)正互反阵最大特征根和特征向量的实用算法p263~264已知正互反阵注:[263]定理2 n阶正互反阵A的最大特征根≥n。
★(1) 用MATLAB函数求A的最大特征根和特征向量。
A为n×n正互反矩阵,算法步骤如下:a. 任取n 维非负归一化初始列向量(分量之和为1)(0)w ;b. 计算(1)(),0,1,2,k k wAw k +==%L ; c. (1)k w +%归一化,即令(1)(1)(1)1k k n k ii ww w+++==∑%%; d. 对于预先给定的精度ε,当(1)()||(1,2,,)k k i i w w i n ε+-<=L 时,(1)k w +即为所求的特征向量;否则返回到步骤b ;e. 计算最大特征根(1)()11k n i k i i w n w λ+==∑%。
注:☆(2) 用幂法函数求A 的最大特征根和特征向量。
A 为n×n 正互反矩阵,算法步骤如下:a. 将A 的每一列向量归一化得∑==n i ijij ij a a w 1~;b. 对ijw ~按行求和得∑==nj ij i w w 1~~; c. 将i w ~归一化T n n i i i i w w w w ww w ),,,(,~~211Λ==∑=即为近似特征向量;d. 计算∑==n i ii w Aw n 1)(1λ,作为最大特征根的近似值。
☆(3) 用和法函数求A 的最大特征根和特征向量。
根法(见[264])A 为n×n 正互反矩阵,算法步骤如下:a. 将A 的每一列向量归一化得∑==n i ijij ij a a w 1~; b. 对ijw ~按行求积并开n 次方得∏==n j nij i w w 11)~(~; c. 将i w ~归一化T n n i ii i w w w w w w w ),,,(,~~211Λ==∑=即为近似特征向量;d. 计算∑==n i ii w Aw n 1)(1λ,作为最大特征根的近似值。
高等数学(第三版)各章实验作业题答案

1. 作出函数[]53()3123,2,2f x x x x x =+-+∈-的图像.第1题图2. 求下列各极限.(1)1lim 1nn n →∞⎛⎫- ⎪⎝⎭; (2)sin lim x x x →∞;(3)0sin lim x x x →; (4)10lim x x e +→.解(1)11lim 1enn n →∞⎛⎫-= ⎪⎝⎭; (2)sin lim 0x x x →∞=;(3)0sin lim 1x xx →=; (4)12lim e x x e →3. 求方程20.2 1.70x x --=的近似解(精确到0.0001). 解 1 1.2077x ≈-,2 1.4077x ≈. 4. 探究高级计算器的其他功能.(略)1. 求函数3(21)y x x =-的导数; 操作:在命令窗口中输入:>> syms xy=x^3*(2*x -1); dy=diff(y) 按Enter 键,显示:dy = 3*x^2*(2*x -1)+2*x^3 继续输入:>> simplify(dy) % 将导数化简 按Enter 键,显示: ans =8*x^3-3*x^2即 3283y x x '=-. 2. 求函数()ln 1y x x =-+的二阶导数; 操作:在命令窗口中输入: >> syms xy=1-log(1+x); dy=diff(y,x,2) 按Enter 键,显示: dy = 1/(1+x)^2即 21(1)y x ''=+. 3.函数4322341y x x x x =-+-+在区间[-3,2]上的最小值. 操作:在命令窗口中输入:>>x=fminbnd('x^4-2*x^3+3*x^2-4*x+1',-3,2) y=x^4-2*x^3+3*x^2-4*x+1 按Enter 键,显示: x =1 y =-11.求下列不定积分(1)在命令窗口中输入: >> syms xint(x/(sqrt(x^2+1)),x)按键Enter 键,显示结果: ans = (x^2+1)^(1/2)即c +.(2)在命令窗口中输入: >> syms xint(x^3*cos(x))按键Enter 键,显示结果:ans =x^3*sin(x)+3*x^2*cos(x)-6*cos(x)-6*x*sin(x) 即332cos =sin 3cos 6cos 6sin x xdx x x x x x x x c +--+⎰. 2.求下列定积分(1)在命令窗口中输入: >> int((-3*x+2)^10,x,0,1) 点击Enter 键,显示结果: ans = 683/11 即1100683(-3+2)d =11x x ⎰. (2)在命令窗口中输入: >> int(x*sin(x),x,0,pi/2)点击Enter 键,显示结果: ans = 1 即 π20sin d =1x x x ⎰.3.求广义积分0e d x x x -∞⎰.操作:在命令窗口中输入: >>int(x*exp(x),x,-inf,0)按Enter 键,显示结果: ans =-1 即e d =1xx x -∞-⎰.1. 230y y y '''++=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y -4*Dy -5*y=0','x') 显示:y =C1*exp(5*x)+C2*exp(-x)即满足所给初始条件的特解为:512xx y c e c e -=-.2. 232sin xy y e x '''-=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y -3*Dy=2*exp(3*x)*sin(x)','x') 显示:y = -3/5*exp(3*x)*cos(x)-1/5*exp(3*x)*sin(x)+1/3*exp(x)^3*C1+C2即满足所给初始条件的特解为:33312311cos sin 553xxxy e x e x c e c =--++. 整理得:33213cos +sin 5xxy e x x ce c =-++()(令113c c =)3. +cos x y y y e x '''+=+,00x y ==,032x y ='=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y+Dy+y=exp(x)+cos(x)','y(0)=0', 'Dy(0)=3/2', 'x') 显示:y = -1/3*exp(-1/2*x)*cos(1/2*3^(1/2)*x)+1/3*exp(x)+sin(x)即满足所给初始条件的特解为:211cos()sin 323x xy e e x -=-++.1. 绘制平面曲线ln y x =. 操作:在命令窗口中输入: >> x=1:0.02: exp(2); y=log(x); plot(x,y);按Enter 键,显示下图:2. 绘制空间曲面2232z x y =-. 操作:在命令窗口输入 >>[x,y]=meshgrid(-4:0.5:4); z=-3*x.^2-2*y.^2; surf(x,y,z)按Enter 键,显示下图:3. 绘制空间曲线23,23.t t t x e y e z e ---⎧=⎪⎪=⎨⎪=⎪⎩操作:在命令窗口输入>>t=0:0.01:1;x=exp(-t);y=exp(-2*t)/4;z=3*exp(-3*t)/9;plot3(x,y,z)按Enter键,显示下图:实验6作业题1. 求函数cos z xy =的偏导数. 操作:在命令窗口中输入:>> dz_dx=diff('cos(x*y)', 'x ') 显示dz_dx = -sin(x*y)*y 继续输入:>> dz_dy=diff('cos(x*y)', 'y ') 显示:dz_dy =-sin(x*y)*x即sin zx xy x∂=-∂, sin z x xy y ∂=-∂2. 计算函数23y x y =-的极值.操作:在matlab 中依次选择“File\New\M -File ”,在弹出的M 文件编辑窗口中在命令窗口中输入:clear all;clc syms x y;z=x^3-6*x-y^3+3*y;dz_dx=diff(z,x); %计算z 对x 的偏导数 dz_dy=diff(z,y); %计算z 对y 的偏导数 [x0,y0]=solve(dz_dx,dz_dy); %求驻点x0,y0A_=diff(z,x,2); %计算z 对x 的二阶偏导数B_=diff(diff(z,x),y); %计算z 对x,y 的二阶混合偏导数 C_=diff(z,y,2); %计算z 对y 的二阶偏导数 x0=double(x0); %数据转换 y0=double(y0);n=length(x0); %计算x0中元素的个数 for i=1:nA_x=subs(A_, x,x0(i)); %把x=x0(i)(即x0的第i 个元素值)代入z 对x 的二阶偏导数A=subs(A_x, y,y0(i)); %继续把y=y0(i)(即y0的第i 个元素值)代入z 对x 的二阶偏导数,得到AB_x=subs(B_, x,x0(i)); %把x=x0(i)代入z 对x 、y 的二阶混合偏导数 B=subs(B_x, y,y0(i)); %继续把y=y0(i)代入二阶混合偏导数,得到B C_x=subs(C_, x,x0(i)); %把x=x0(i)代入z 对y 的二阶偏导数C=subs(C_x, y,y0(i)); %继续把y=y0(i)代入z 对y 的二阶偏导数,得到C D=A*C-B^2;text=['原函数在(',num2str(x0(i)), ', ',num2str(y0(i)), ')处' ]; if D>0fm=subs(x^3-6*x-y^3+3*y,{x,y},{x0(i),y0(i)}); %求函数值 if A>0disp([text, '有极小值',num2str(fm)]) %在命令窗口中输出 elsedisp([text, '有极大值',num2str(fm)])end end if D==0disp([text, '的极值情况还不确定,还需另作讨论' ]) end end保存后,选择M 文件编辑窗口中的“Debug\run ”,显示如下结果: 原函数在(1.4142,-1)处有极小值-7.6569 原函数在(-1.4142,1)处有极大值7.65693. 计算(2)d d Dx y x y -⎰⎰,D :顶点分别为(0,0),(1,1)和(0,1)的三角形闭区域;操作:在命令窗口中输入: >>syms x y;S=int(int(2*x-y,y,0,1-x),x,0,1) 显示: S=1/6即:二重积分1(2)d d =6Dx y x y -⎰⎰.实验7作业题1. 将函数xx f -=11)(展开为幂级数,写出展开至6次幂项. 操作:在命令窗口中输入: >> clear;clc syms x; f=1/(1-2*x); taylor(f,7,x) 显示:ans = 1+2*x+4*x^2+8*x^3+16*x^4+32*x^5+64*x^6即65432643216842111x x x x x x x ++++++=-. 2. 求函数2()tf t e =的拉氏变换.操作:在命令窗口中输入: >> clear;clc syms x;laplace(exp(2*t)) 显示: ans = 1/(s -2)即 21)(2-=s e L t. 3.求函数22()56s F s s s +=-+的拉氏逆变换.操作:在命令窗口中输入: >>syms silaplace((s+2)/(s^2-5*s+6)) 显示:ans =-4*exp(2*t)+5*exp(3*t)即 12256s L s s -+⎡⎤⎢⎥-+⎣⎦234e 5e t t =-+.。
数学实验第二次测验题及参考答案(09级)

数学实验第二次测验题及参考答案(09级)数学实验第二次测验题及参考答案一、写出下列MATLAB指令的运算结果.1. A=[1;2;3]; transpose(A)1 2 31 2 32. A=[1, 2, 3 ; 4, 5, 6 ]; B=A([1 2], [1,3]) , d=size(A)B =1 34 6d =2 33. a=1:3; b=linspace(1,3,3); x=sum(a.*b), y=cross(a, b)x = 14y = 0 0 04. A=[1,2, 3; 4,5,6; 7,8,9]; B=ones(3); C=A-BC =0 1 23 4 56 7 85. v=[1, 2, 3]; A=diag(v); E=eig(A), D=det(A)E=123D =66. x=[1,2,3,4,5]; [mean(x), median(x), range(x),sum(x), prod(x)]3 34 15 1207. x=[2,3,4]; a=cumsum(x) ,b=sort(x)a =2 5 9b =2 3 48.format rat; v=[1, 2, 3]; A=diag(v); inv(A)ans =1 0 00 1/2 00 0 1/39. [m,v]=normstat(1,4) % 求参数为1,4的正态分布的均值与方差m =1, v =16二、写出下列MATLAB指令的实验目的.1. dsolve('x*Dy+y-exp(-x)=0', 'y(1)=2*exp(1)', 'x')求微分方程0=-+'-x e y y x 在初始条件e y x 2|1==下的特解.2. u=[1,2,3],v=[0,3,2], w=[5, 2, 1]; dot(w, cross(u, v))计算向量u, v, w 的混合积.3. A=[1 2 3; 2 2 5; 3 5 1]; b=[1;2;3]; det(A); inv(A)*b利用逆矩阵解线性方程组=++=++=++3532522132321 321321x x x x x x x x x .4. A=[0 0 1; 0 1 1; 1 1 1; 1 0 0]; rref(A)求向量组)1,0,0(1=α,)1,1,0(2=α,)1,1,1(3=α,)0,0,1(4=α的秩.或对矩阵A 做行初等变换。
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a 与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6579 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3423 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2])(2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20);[theta,fai]=meshgrid(theta,fai); x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\ page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000 -1.00002.0000 1.0000 -0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b]) ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0 Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]'; >> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.0100 0.1200 0.0400 0.0900 >> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500 -0.0900 0.8000 -0.0100 -0.1200 -0.0400 0.9100 >> D=[17 17 17]';x=A\D x =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组3>> b=a([1 2 4],:)';c=a([3 5],:)'; >> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467%Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3))fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013%Exercise 1(1)roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi; x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小, x(2)最大。
数学实验答案

1.11 2 3 4;0 2 -1 1;1 -1 2 5;+1/2.*2 1 4 10;0 -1 2 0;0 2 3 -22.A=3 0 1;-1 2 1;3 4 2;B=1 0 2;-1 1 1;2 1 1 X=B+2*A/23.A=-4 -2 0 2 4;-3 -1 1 3 5absA>34.A=-2 3 2 4;1 -2 3 2;3 2 3 4;0 4 -2 5 detA;eigA;rankA;invA求计算机高手用matlab解决..>> A=-2;3;2;4;1;-2;3;2;3;2;3;4;0;4;-2;5求|A|>> absAans =2 3 2 41 2 3 23 2 3 40 4 2 5求rA>> rankAans =4求A-1>> A-1ans =-3 2 1 30 -3 2 12 1 2 3-1 3 -3 4求特征值、特征向量>> V;D=eigA %返回矩阵A的特征值矩阵D 与特征向量矩阵VV =0.7335 0.7335 -0.3804 - 0.0312i -0.3804 + 0.0312i-0.0024 + 0.5329i -0.0024 - 0.5329i -0.3907 - 0.0001i -0.3907 + 0.0001i-0.3166 - 0.0283i -0.3166 + 0.0283i -0.8280 -0.8280-0.0556 - 0.2718i -0.0556 + 0.2718i 0.0301 - 0.1235i 0.0301 + 0.1235iD =-3.1766 + 0.6201i 0 0 00 -3.1766 - 0.6201i 0 00 0 5.1766 + 0.7101i 00 0 0 5.1766 - 0.7101i将A的第2行与第3列联成一行赋给b>> b=A2;:;A:;3'b =1 -23 2 2 3 3 -21.a=roundunifrnd1;100i=7;while i>=0i=i-1;b=input'请输入一个介于0到100的数字: '; if b==adisp'You won';break;else if b>adisp'High';else if b<adisp'Low';endendendend结果a =82请输入一个介于0到100的数字: 50Low请输入一个介于0到100的数字: 75Low请输入一个介于0到100的数字: 85请输入一个介于0到100的数字: 82You won2.clear all;clc;n=input'请输入数字 n=';n1=floorn/100; %取出百位数字n1n2=modfloorn/10;10; %取出十位数字n2n3=modn;10 ; %取出个位数字n3if n1^3+n2^3+n3^3==nfprintf'%d是“水仙花数”'; n % 注意输出格式前须有%符号elsefprintf'%d不是“水仙花”'; n % 注意输出格式前须有%符号end结果请输入数字n=234234不是“水仙花数”>>3.price=input'请输入商品价格';switch fixprice/100case {0;1} %价格小于200rate=0;case {2;3;4} %价格大于等于200但小于500 rate=3/100;case num2cell5:9 %价格大于等于500但小于1000 rate=5/100;case num2cell10:24 %价格大于等于1000但小于2500 rate=8/100;case num2cell25:49 %价格大于等于2500但小于5000 rate=10/100;otherwise %价格大于等于5000rate=14/100;endprice=price*1-rate %输出商品实际销售价格结果请输入商品价格250price =242.5000Function f=myfunxx=input;s=pi*x*xl=pi*x^24、Function y=circlers=pi*x*xl=pi*x^24.syms rs=pi*r*rl=2*pi*r5. function fibonaccin;m f1=1;f2=1;for i=3:maxn;mfi=fi-1+fi-2;endfprintf'第%d项';mx=fmfprintf'前%d项';ns=f1:nCOMMAND WINDOW输入:fibonacci20;501.绘制])4,0[)(3sin(3π∈=x x e y x 的图像;要求用蓝色的星号画图;并且画出器官包络线3x e y ±=的图像;用红色的点划线画图..2.用fplot 和ezplot 命令绘出函数)21sin(32t ey t +=-在区间]10,0[上的图像.. 3.在同一图像窗口画三个子图要求使用指令gtext;axis;legend;title;xlabel;和ylabel : (3)]8,1[,sin 1∈=x x e y x1.x=0:pi/25:4*pi;y1=expx/3.*sin3*x;y2=expx/3;y3=-expx/3;plotx;y1;'b*';x;y2;'r-.';x;y3;'r-.'2.t=1:0.1:10y=exp-2*t/3.*sin1+2*t;plott;y;figurefplot 'exp-2*t/3.*sin1+2*t';1;10ezplot 'exp-2*t/3.*sin1+2*t';1;103.x=1:1/50:8;y=exp1./x.*sinx;subplot1;3;3;plotx;y;'b-';legend 'y=exp1/xsinx';grid on ;title 'y=exp1/xsinx';xlabel 'x 轴';ylabel 'y 轴'gtext '真棒';axisx1 x8 y1 y104.x=0:pi/50:2*pi;y1=sinx;y2=cosx;y3=sin2*x;plotx;y1;'k*--';x;y2;'rs-';x;y3;'bo--';grid ontitle '曲线y1=sinx;y2=cosx 与y3=sin2*x'xlabel 'x 轴';ylabel 'y 轴'gtext 'y1=sinx';gtext 'y2=cosx';gtext 'y3=sin2*x'legend 'y1=sinx';'y2=cosx';'y3=sin2*x'5.绘制圆锥螺线的图像并加各种标注;圆锥螺线的参数方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤≤==t z t t t t y t t t x 2)200(,6cos 6cos π 6.在同一图形窗口画半径为1的球面;柱面122=+y x 以及极坐标]2,0[,4sin 21πρ∈=t t7.用mesh 与surf 命令绘制三维曲面223y x z +=的图像;并使用不同的着色效果及光照效果.. 8.绘制由函数14169222=++z y x 形成的立体图;并通过改变观测点获得该图形在各个坐标平面上的投影..9.画三维曲面)2,2(522≤≤---=y x y x z 与平面3=z 的交线..5.t=1:pi/50:20*pi;x=t.*cospi/6.*t;y=t.*sinpi/6.*t;z=2*t;plot3x;y;z;grid on ;title '圆锥螺线'xlabel 'x 轴';ylabel 'y 轴';zlabel 'z 轴';axis square6. v=-2 2 -2 2 -2 2;subplot1;3;1;spheretitle'以半径为1的球面';xlabel'x 轴';ylabel'y 轴';zlabel'z 轴';axisvsubplot1;3;2;cylindertitle'柱面';xlabel'x 轴';ylabel'y 轴';zlabel'z 轴'subplot1;3;3;t=0:pi/100:2*pi;polart;1/2*sin4*ttitle'p=1/2*sin4t'7.X;Y=meshgrid-8:0.5:8;Z=X.^2+3*Y.^2;subplot1;2;1;meshX;Y;Z;shading interpsubplot1;2;2;surfX;Y;Z;shading flat8.xx;yy;zz=sphere40;x=xx*3;y=yy*4;z=zz*2;surfx;y;zaxis equal9.X;Y=meshgrid-2:0.1:2;Z1=5-X.^2+Y.^2;subplot1;3;1;meshX;Y;Z1;title'曲面';Z2=3*onessizeX;% 创建一个和y矩阵相同大小的纯1矩阵subplot1;3;2;meshX;Y;Z2;title'平面';r0=absZ1-Z2<=1;ZZ=r0.*Z2;YY=r0.*Y;XX=r0.*X;subplot1;3;3plot3XXr0~=0;YYr0~=0;ZZr0~=0;'*'title'交线'10.v=-22 -22 -22;x;y;z=sphere30;surf4*x;4*y;4*ztitle'半径为4的球面';axisv。
数学建模实验答案_微分方程模型

数学建模实验答案_微分⽅程模型实验07 微分⽅程模型(2学时)(第5章微分⽅程模型)1.(验证)传染病模型2(SI 模型)p136~138传染病模型2(SI 模型):0(1),(0)dik i i i i dt=-= 其中,i (t )是第t 天病⼈在总⼈数中所占的⽐例。
k 是每个病⼈每天有效接触的平均⼈数(⽇接触率)。
i 0是初始时刻(t =0)病⼈的⽐例。
1.1 画~dii dt曲线图p136~138取k =0.1,画出i dt di ~的曲线图,求i 为何值时dtdi达到最⼤值,并在曲线图上标注。
提⽰:fplot, fminbnd, plot, text, title, xlabel 1)画曲线图⽤fplot 函数,调⽤格式如下: fplot(fun,lims)fun 必须为⼀个M ⽂件的函数名或对变量x 的可执⾏字符串。
若lims取[xmin xmax],则x轴被限制在此区间上。
若lims取[xmin xmax ymin ymax],则y轴也被限制。
本题可⽤fplot('0.1*x*(1-x)',[0 1.1 0 0.03]);2)求最⼤值⽤求解边界约束条件下的⾮线性最⼩化函数fminbnd,调⽤格式如下:x=fminbnd('fun',x1,x2)fun必须为⼀个M⽂件的函数名或对变量x的可执⾏字符串。
返回⾃变量x在区间x1本题可⽤x=fminbnd('-0.1*x*(1-x)',0,1)y=0.1*x*(1-x)3)指⽰最⼤值坐标⽤线性绘图函数plot,调⽤格式如下:plot(x1,y1, '颜⾊线型数据点图标', x2,y2, '颜⾊线型数据点图标',…)本题可⽤hold on; %在上⾯的同⼀张图上画线(同坐标系)plot([0,x],[y,y],':',[x,x],[0,y],':');4)图形的标注使⽤⽂本标注函数text,调⽤格式如下:格式1text(x,y,⽂本标识内容, 'HorizontalAlignment', '字符串1')x,y给定标注⽂本在图中添加的位置。
数学实验(第二版)课后习题答案
贵州师范学院2012级数本一班李刚数学实验课后练习答案习题2.11. syms x y;>> x=-5:0.01:5;>> y=x.^1/2;>> plot(x,y)2. f plot('exp(-x.^2)',[-5,5])3. ezplot('x.^3+y.^3-3*x*y',[-5,5])4 . ezplot('y.^2-x.^3/(1-x)',[-5,5])5.t=0:0.1:2*pi;x=t-sin(t);y=2*(1-cos(t));plot(x,y)6. t=0:0.1:2*pi; x=cos(t).^3; >> y=sin(t).^3;>> plot(t,y)>>7: t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z)8: x =0:0.1:2*pi; r=x; polar(x,r)9: x =0:0.1:2*pi; r=exp(x); polar(x,r)10: x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)11: x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)12: x =0:0.1:2*pi; r=1+cos(x); polar(x,r)练习2.2 1:(1)(2):syms n; limit('sqrt(n+2)-2*(sqrt(n+1))+sqrt(n)',n,inf)Ans= 0 (3):: (4):(5):(6):2:3:fplot('x.^2*sin(x.^2-x-2)',[-2,2])练习2.3 1:(2):2:练习2.4 1:(1)(2):(3)(4):2:(1):syms x;int(x^(-x),x,0,1)ans =int(x^(-x),x = 0 .. 1)vpa(ans,10)ans =1.291285997(2):syms x;int(exp(2*x)*cos(x)^3,x,0,2*pi)ans =-22/65+22/65*exp(4*pi)(3):syms x; int(exp(x^2/2)/sqrt(2*pi),x,0,1)ans =-1125899906842624/5644425081792261*i*erf(1/2*i*2^(1/2))*pi^(1/2)*2^(1/2) >> vpa(ans,10)ans =.4767191345(4):syms x;int(x*log(x^4)*asin(1/x^2),x,1,3)ans =int(x*log(x^4)*asin(1/x^2),x = 1 .. 3)>> vpa(ans,10)ans =2.459772128(5):syms x ;int(exp(x^2/2)/sqrt(2*pi),x,-inf,inf)ans =Inf(6):syms x ;int(sin(x)/x,x,0,inf)ans =1/2*pi(7):syms x ;int(tan(x)/sqrt(x),x,0,1)Warning: Explicit integral could not be found. > In sym.int at 58ans =int(tan(x)/x^(1/2),x = 0 .. 1)>> vpa(ans,10)ans =.7968288892(8):syms x ;int(exp(-x^2/2)/(1+x^4),x,-inf,inf)ans =1/4*pi^(3/2)*2^(1/2)*(AngerJ(1/2,1/2)-2/pi^(1/2)*sin(1/2)+2/pi^(1/2)*cos(1/2)-WeberE(1/2,1/2 ))>> vpa(ans,10)ans =1.696392536(9):syms x ;int(sin(x)/sqrt(1-x^2),x,0,1)ans =1/2*pi*StruveH(0,1)>> vpa(ans,10)ans =.8932437410练习2.5(1):syms n;symsum(1/n^2^n,n,1,inf)ans =sum(1/((n^2)^n),n = 1 .. Inf)(2):s yms n ;symsum(sin(1/n),n,1,inf)ans =sum(sin(1/n),n = 1 .. Inf)(3):syms n ;symsum(log(n)/n^3,n,1,inf) ans =-zeta(1,3)(4):syms n ;symsum(1/(log(n))^n,n,3,inf) ans =sum(1/(log(n)^n),n = 3 .. Inf)(5):syms n;symsum(1/(n*log(n)),n,2,inf) ans =sum(1/n/log(n),n = 2 .. Inf)(6):yms n;symsum((-1)^n*n/(n^2+1),n,1,inf)ans =-1/4*Psi(1-1/2*i)+1/4*Psi(1/2-1/2*i)-1/4*Psi(1+1/2*i)+1/4*Psi(1/2+1/2*i)第三章练习3.11:(1):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=10*sin(sqrt(x.^2+y.^2))./(sqrt(1+x.^2+y.^2)); meshc(x,y,z)(2):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=4*x.^2/9+y.^2;meshc(x,y,z)(3):(4):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b); z=x.^2/3-y.^2/3; meshc(x,y,z)(5):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=x*y;>> meshc(x,y,z)(6):(7):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=sqrt(x.^2+y.^2); >> meshc(x,y,z)(8):(9):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b);>> z=atan(x./y);>> meshc(x,y,z)练习3.21;a=-1:0.1:1;>> b=0:0.1:2;>> [x,y]=meshgrid(a,b);>> z=x.*exp(-x.^2-y.^2);>> [px,py]=gradient(z,0.1,0.1);>> contour(a,b,z)>> hold on>> quiver(a,b,px,py)2:a=-2:0.1:1;>> b=-7:0.1:1;>> [x,y]=meshgrid(a,b);>> z=y.^3/9+3*x.^2.*y+9*x.^2+y.^2+x.*y+9; >> plot3(x,y,z)>> grid on3:[x,y]=meshgrid(-2*pi:0.2:2*pi); z=x.^2+2*y.^2;plot3(x,y,z)hold onezplot('x^2+y^2-1',[-2*pi,2*pi]) ; grid on4:t=0:0.03:2*pi;>> s=[0:0.03:2*pi]';>> x=(0*s+1)*cos(t);y=(0*s+1)*sin(t);z=s*(0*t+1); >> mesh(x,y,z)>> hold on>> [x,y]=meshgrid(-1:0.1:1);>> z=1-x+y;>> mesh(x,y,z)5:syms x y z dx dyz=75-x^2-y^2+x*y;zx=diff(z,x),zy=diff(z,y)zx =-2*x+yzy =-2*y+x练习3.31:ezplot('x^2+y^2-2*x',[-2,2]);>> grid onsyms x y ;s=int(int(x+y+1,y,-sqrt(1-(x-1)^2),sqrt(1-(x-1)^2)),x,0,2)s =2*pi2:syms r t ;>> s=int(int(sqrt(1+r^2*sin(t)),r,0,1),t,0,2*pi)s =int(1/2*((1+sin(t))^(1/2)*sin(t)^(1/2)+log(sin(t)^(1/2)+(1+sin(t))^(1/2)))/sin(t)^(1/2),t = 0 .. 2*pi) 3:syms x y z ;>> s=int(int(int(1/(1+x+y+z)^3,z,0,1-x-y),y,0,1-x),x,0,1)s =-5/16+1/2*log(2)4:s=vpa(int(int(x*exp(-x^2-y^2),y,0,2),x,-1,10))s =0.16224980455070416645061789474030练习3.41:(1):y=dsolve('Dy=x+y','y(0)=1','x')得:y =-1-x+2*exp(x)(2):y=dsolve('Dy=2*x+y^2','y(0)=0')y =tan(t*x^(1/2)*2^(1/2))*x^(1/2)*2^(1/2)练习4.11:(1):p=[5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -6 8 0 0 0 -5 0 0]; >> x=roots(p)x =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927(2): p=[8 36 54 23];x=roots(p)x =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.70632:p1=[1 0 -3 -2 -1];p2=[1 -2 5];[q2,r2]=deconv(p1,p2)q2 =1 2 -4r2 =0 0 0 -20 19 3:syms x;f=x^4+3*x^3-x^2-4*x-3;g=3*x^3+10*x^2+2*x-3;p1=factor(f),p2=factor(g)p1 =(x+3)*(x^3-x-1)p2 =(x+3)*(3*x^2+x-1)4:syms x ;f=x^12-1;p=factor(f)p =(-1+x)*(1+x^2+x)*(1+x)*(1-x+x^2)*(1+x^2)*(x^4-x^2+1)5: (1):p=[1 0 1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.0000 - 0.3536i-0.0000 + 0.3536i0.0000 - 0.3536i0.0000 + 0.3536ib =0.7071 + 0.7071i0.7071 - 0.7071i-0.7071 + 0.7071i-0.7071 - 0.7071ir =[](2):p=[1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.1768 - 0.1768i -0.1768 + 0.1768i0.1768 - 0.1768i0.1768 + 0.1768ib =0.7071 + 0.7071i0.7071 - 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071ir =[](3):p=[1 0 1];q=[1 1 -1 -1];[a,b,r]=residue(p,q)a =0.5000-1.00000.5000b =-1.0000-1.00001.0000r =[] (4): p=[1 1 0 0 0 -8];[a,b,r]=residue(p,q)a =-4-38b =-11r =1 1 1练习 4.21:(1):D=[2 1 3 1;3 -1 2 1;1 2 3 2;5 0 6 2];det(D)ans =6(2):syms a b c dD=[a 1 0 0 ;-1 b 1 0;0 -1 c 1;0 0 -1 d];det(D)ans =a*b*c*d+a*b+a*d+c*d+12:(1):D=[1 1 1 1; a b c d;a^2 b^2 c^2 d^2;a^3 b^3 c^3 d^3];det(D)ans =b*c^2*d^3-b*d^2*c^3-b^2*c*d^3+b^2*d*c^3+b^3*c*d^2-b^3*d*c^2-a*c^2*d^3+a*d^2*c^3+a *b^2*d^3-a*b^2*c^3-a*b^3*d^2+a*b^3*c^2+a^2*c*d^3-a^2*d*c^3-a^2*b*d^3+a^2*b*c^3+a^ 2*b^3*d-a^2*b^3*c-a^3*c*d^2+a^3*d*c^2+a^3*b*d^2-a^3*b*c^2-a^3*b^2*d+a^3*b^2*c(2): s yms a b x y zD=[a*x+b*y a*y+b*z a*z+b*x; a*y+b*z a*z+b*x a*x+b*y;a*z+b*x a*x+b*y a*y+b*z];det(D)ans =3*a^3*x*z*y+3*b^3*y*x*z-a^3*x^3-a^3*y^3-b^3*z^3-a^3*z^3-b^3*x^3-b^3*y^33: (1): D=[1 1 1 1;1 2 -1 4;2 -3 -1 -5;3 1 2 11];D1=[5 1 1 1;-2 2 -1 4;-2 -3 -1 -5;0 1 2 11];D2=[1 5 1 1;1 -2 -1 4;2 -2 -1 -5;3 0 2 11];D3=[1 1 5 1;1 2 -2 4;2 -3 -2 -5;3 1 0 11];D4=[1 1 1 5;1 2 -1 -2;2 -3 -1 -2;3 1 2 0];x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x1,x2,x3,x4x1 =1x2 =2x3 =3x4 =-1(2):D=[5 6 0 0 0;1 5 6 0 0;0 1 5 6 0;0 0 1 5 6;0 0 0 1 5]; D1=[1 6 0 0 0;0 5 6 0 0;0 1 5 6 0;0 0 1 5 6;1 0 0 1 5]; D2=[5 1 0 0 0;1 0 6 0 0;0 0 5 6 0;0 0 1 5 6;0 1 0 1 5]; D3=[5 6 1 0 0;1 5 0 0 0;0 1 0 6 0;0 0 0 5 6;0 0 1 1 5]; D4=[5 6 0 1 0;1 5 6 0 0;0 1 5 0 0;0 0 1 0 6;0 0 0 1 5]; D5=[5 6 0 0 1;1 5 6 0 0;0 1 5 6 0;0 0 1 5 0;0 0 0 1 1]; x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x5=det(D5)/det(D);x1,x2,x3,x4,x5x1 =2.2662x2 =-1.7218x3 =1.0571x4 =-0.5940x5 =0.3188练习 4.3 1:A=[1 2 0;3 4 -1; 1 1 -1];B=[1 2 3;-1 0 1;-2 4 -3];A',2+A,2*A-B,A*B,A^2,A^(-1)ans =1 3 12 4 10 -1 -1ans =3 4 25 6 13 3 1ans =1 2 -37 8 -34 -2 1ans =-1 2 51 2 162 -2 7ans =7 10 -214 21 -33 5 0ans =-3.0000 2.0000 -2.00002.0000 -1.0000 1.0000-1.0000 1.0000 -2.0000 2:(1):B=[2 4 3];B'ans =243(2):A=[1 2 3];B=[2 4 3];A.*B,B.*Aans =2 8 9ans =2 8 93:(1):A=[0 1 0;1 0 0;0 0 1];B=[1 0 0;0 0 1;0 1 0];C=[1 -4 3;2 0 -1;1 -2 0];A^(-1),B^(-1),X=A^(-1)*C*B^(-1) ans =0 1 01 0 00 0 1ans =1 0 00 0 10 1 0X =2 -1 01 3 -41 0 -2(2):>> A=[1 2 3;2 2 3;3 5 1];B=[1 0 0;2 0 0;3 0 0];A^(-1),x=A^(-1)*Bans =-1.0000 1.0000 0.00000.5385 -0.6154 0.23080.3077 0.0769 -0.1538x =1 0 00 0 00 0 0练习 4.41:(1):A=[4 2 -1;3 -1 2;11 3 0];b=[2;10;8];B=[A,b];rank(A),rank(B)ans =2ans =3(2):A=[2 1 -1 1;3 -2 1 -3;1 4 -3 5];b=[1;4;-2];B=[A,b];rank(A),rank(B)ans =2ans =2(3):A=[ 1 1 1 1; 1 2 -1 4;2 -3 -1 -5;3 1 2 11];b=[5;-2;-2;0];B=[A,b];rank(A),rank(B)ans =4ans =4(4):A=[ 1 1 2 -1; 2 1 1 -1;2 2 1 2];b=[0;0;0];B=[A,b];rank(A),rank(B)ans =3ans =32:syms a;A=[-2 1 1;1 -2 1;1 1 -2];b=[-2;a;a^2];B=[A,b];rank(A),rank(B)ans =2ans =3练习4.51:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 000 - 1.0000i(2):A=[0 0 1;0 1 0;1 0 0];[a,b]=eig(A)a =0.7071 0.7071 00 0 -1.0000-0.7071 0.7071 0b =-1 0 00 1 00 0 1(3):A=[4 1 -1;3 2 -6;1 -5 3];[a,b]=eig(A)a =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170b =-3.0527 0 00 3.6760 00 0 8.3766(4):A=[1 1 1 1;1 1 -1 -1;1 -1 1 -1;1 1 -1 1];[a,b]=eig(A)a =0.5615 0.3366 0.2673 -0.7683-0.5615 -0.3366 0.0000 -0.0000-0.5615 -0.3366 -0.5345 -0.6236-0.2326 0.8125 0.8018 -0.1447b =-1.4142 0 0 00 1.4142 0 00 0 2.0000 00 0 0 2.0000(5):A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10];[a,b]=eig(A)a =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209b =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887(6):A=[5 6 0 0 0;1 5 6 0 0 ;0 1 5 6 0 ;0 0 1 5 6; 0 0 0 1 5 ]; [a,b]=eig(A)a =0.7843 -0.7843 -0.9860 -0.9237 -0.92370.5546 0.5546 0.0000 0.3771 -0.37710.2614 -0.2614 0.1643 -0.0000 0.00000.0924 0.0924 0.0000 -0.0628 0.06280.0218 -0.0218 -0.0274 0.0257 0.02579.2426 0 0 0 00 0.7574 0 0 00 0 5.0000 0 00 0 0 2.5505 00 0 0 0 7.4495 2:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 00 0 - 1.0000i>> P=orth(a),B=P'*A*P,P*P'P =-0.7071 -0.70710 - 0.7071i 0 + 0.7071iB =0 + 1.0000i 0 - 0.0000i0 - 0.0000i 0 - 1.0000ians =1.0000 0 + 0.0000i0 - 0.0000i 1.0000>> inv(a)*A*a0 + 1.0000i 000 - 1.0000i3:(1):A=[2 0 0;0 3 2;0 2 3]; [a,b]=eig(A)a =0 1.0000 0-0.7071 0 0.70710.7071 0 0.7071b =1.0000 0 00 2.0000 00 0 5.0000>> P=orth(a),B=P'*A*P,P*P'P =-1.0000 0 -0.00000.0000 0.7071 0.7071-0.0000 -0.7071 0.7071B =2.0000 0.0000 0.00000.0000 1.0000 00.0000 0 5.0000ans =1.0000 -0.0000 0.0000-0.0000 1.0000 -0.00000.0000 -0.0000 1.0000(2):A=[1 1 0 -1;1 1 -1 0;0 -1 1 1;-1 0 1 1];[a,b]=eig(A)a =-0.5000 0.7071 0.0000 0.50000.5000 -0.0000 0.7071 0.50000.5000 0.7071 0.0000 -0.5000-0.5000 0 0.7071 -0.5000 b =-1.0000 0 0 00 1.0000 0 00 0 1.0000 00 0 0 3.0000 >> P=orth(a),B=P'*A*P,P*P'P =-0.5000 -0.4998 -0.4783 -0.52100.5000 -0.4822 0.5212 -0.49580.5000 0.4998 -0.4964 -0.5037-0.5000 0.5175 0.5031 -0.4786 B =-1.0000 0.0000 0.0000 0.00000.0000 2.9988 -0.0362 0.03440.0000 -0.0362 1.0007 -0.00060.0000 0.0344 -0.0006 1.0006 ans =1.0000 0.0000 0.0000 -0.00000.0000 1.0000 -0.0000 00.0000 -0.0000 1.0000 0.0000-0.0000 0 0.0000 1.0000练习5.3 1: [m,v]=unifstat(1,11)m =6v =8.33332:[m,v]=normstat(0,16)m =v =256>> s=sqrt(v)s =163:x=randn(200,6);s=std(x)s =0.9094 0.9757 0.9702 0.9393 0.9272 1.09824: x=normrnd(0,16,300,1);hist(x,10)练习 5.61:x=[352 373 411 441 462 490 529 577 641 692 743];y=[166 153 177 201 216 208 227 238 268 268 274];plot(x,y,'*')4:(1):x=[10 10 10 15 15 15 20 20 20 25 25 25 30 30 30];y=[25.2 27.3 28.7 29.8 31.1 27.8 31.2 32.6 29.7 31.7 30.1 32.3 29.4 30.8 32.8]; plot(x,y,'*')。
数学建模实验答案__数学规划模型二.

实验05 数学规划模型㈡(2学时)(第4章数学规划模型)1.(求解)汽车厂生产计划(LP,整数规划IP)p101~102(1) (LP)在模型窗口中输入以下线性规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3≥ 0并求解模型。
★(1) 给出输入模型和求解结果(见[101]):(2) (IP)在模型窗口中输入以下整数规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3均为非负整数并求解模型。
LINGO函数@gin见提示。
★(2) 给出输入模型和求解结果(见[102]模型、结果):2.(求解)原油采购与加工(非线性规划NLP ,LP 且IP )p104~107模型:已知 ⎪⎩⎪⎨⎧≤≤+≤≤+≤≤=)15001000(63000)1000500(81000)5000(10)(x x x x x xx c注:当500 ≤ x ≤ 1000时,c (x ) = 10 × 500 + 8( x – 500 ) = (10 – 8 ) × 500 + 8x112112221112212211112112122211122122max 4.8() 5.6()()500100015000.50.6,,,,0z x x x x c x x x x x x x x x x x x x x x x x x =+++-+≤++≤≤≥+≥+≥2.1解法1(NLP )p104~106将模型变换为以下的非线性规划模型:1121122212311122122111121121222123122312311122122max4.8()5.6()(1086)50010000.50.6(500)0(500)00,,500,,,,0z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++-+++≤++≤≥+≥+=++-=-=≤≤≥LINGO 软件设置:局部最优解,全局最优解,见提示。
数学实验(MATLAB版韩明版)2.1-2.4部分答案

数学实验(MATLAB版韩明版)2.1-2.4部分答案练习2.1画出下列常见曲线的图形(其中a=1,b=2,c=3)1.31xy =的图像:()55≤≤-x编程:>> x=-5:0.1:5; >> y=x.^(1/3); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y') >> legend('y=x.^(1/3)') >> title('y=x.^(1/3)') 图像:-5-4-3-2-101234500.20.40.60.811.21.41.61.8xyy=x.(1/3)y=x.(1/3)2.e x y -=2的图像:()55≤≤-x 编程:>> x=-5:0.1:5; >> y=exp(-x.^2); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y') >> legend('y=e^(-x^2)'); >> title('y=e^(-x^2)') 图像:-5-4-3-2-101234500.10.20.30.40.50.60.70.80.91xyy=e (-x 2)y=e (-x 2)=++=+=axy a y at x yx tt t313,1333222的图像:()55≤≤-x ,a=1编程:>> t=-5:0.1:5;>> x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> title('x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2)') >> legend('x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2)') 图像:-1.5-1-0.500.51 1.500.511.522.53xyx=3*t./(1+t.2);y=3*t.2./(1+t.2)4.?+=+=x a a y a x xyt tt t3223221,1的图像: ()55≤≤-t ,a=1 编程:>> t=-5:0.1:5;>> x=t.^2./(1+t.^2);y=t.^3./(1+t.^2); >> plot(x,y)>> xlabel('x');ylabel('y')>> title('x=t.^2./(1+t.^2);y=t.^3./(1+t.^2)') >> legend('x=t.^2./(1+t.^2);y=t.^3./(1+t.^2)') >> grid on 图像:0.10.20.30.40.50.60.70.80.91-5-4-3-2-1012345xyx=t.2./(1+t.2);y=t.3./(1+t.2)5.()()t b y t t a x cos 1,sin -=-=的图像:pi t pi *2*2≤≤-,a=1,b=2 编程:>> t=-2*pi:0.1:2*pi; >> x=t-sin(t);y=2*(1-cos(t)); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> legend('x=t-sin(t);y=2*(1-cos(t))') >> title('x=t-sin(t);y=2*(1-cos(t))') 图像:-8-6-4-20246800.511.522.533.54xyx=t-sin(t);y=2*(1-cos(t))x=t-sin(t);y=2*(1-cos(t))6.=+==ayx t a y t a x 32323233sincos ,的图像:pi t pi *2*2≤≤-,a=1 编程:>> t=-2*pi:0.1:2*pi; >> x=(cos(t)).^3;y=(sin(t)).^3; >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> title('x=(cos(t)).^3;y=(sin(t)).^3') 图像:-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81xyx=(cos(t)).3;y=(sin(t)).3x=(cos(t)).3;y=(sin(t)).37.ct z t b y t a x ===,sin ,cos 的图像:()pi t pi c b a *2*2,3,2,1≤≤-=== 编程:>> t=-2*pi:0.1:2*pi; >> x=cos(t);y=2*sin(t);z=3*t; >> plot3(x,y ,z)>> xlabel('x');ylabel('y');zlabel('z') >> grid on>> legend('x=cos(t);y=2*sin(t);z=3*t') >> title('x=cos(t);y=2*sin(t);z=3*t') 图像:-101-2-1012-20-101020xx=cos(t);y=2*sin(t);z=3*tyzx=cos(t);y=2*sin(t);z=3*t8.θa r =的图像:()pi a *20,1≤≤=θ编程:>> theta=0.0:0.1:2*pi; >> r=theta; >> polar(theta,r) >> grid on>> legend('r=theta') >> title('r=theta') 图像:24 68302106024090270120300150330180r=theta r=theta9.e a r θ=的图像:()pi a *20,1≤≤=θ编程:>> theta=-2*pi:0.1:2*pi; >> r=exp(theta); >> polar(theta,r) >> grid on >> title('r=exp(theta)') >> legend('r=exp(theta)') 图像:100200 300400 5003021060240902701203001503301800r=exp(theta)r=exp(theta)10.()?-==+yx ayxar 22222222,2cos θ的图像:1=a 编程:>> theta=0:0.1:2*pi;>> r=sqrt(abs(cos(2*theta))); >> polar(theta,r) >> grid on>> title('r=sqrt(abs(cos(2*theta)))'); >> legend('r=sqrt(abs(cos(2*theta)))') 图像:0.20.4 0.60.8 13021060240902701203001503301800r=sqrt(abs(cos(2*theta)))11.()==+xy a yxar 2222*222,2sin θ的图像:a=1编程:>> theta=0:0.1:2*pi;>> r=sqrt(abs(sin(2*theta))); >> polar(theta,r) >> grid on>> title('r=sqrt(abs(sin(2*theta)))') >> legend('r=sqrt(abs(sin(2*theta)))') 图像:0.4 0.60.8 13021060240902701203001503301800r=sqrt(abs(sin(2*theta)))12.)cos 1(θ+=a r 的图像:a=1 编程:>> theta=0:0.1:2*pi; >> r=1+cos(theta); >> polar(theta,r) >> grid on >> legend('r=1+cos(theta)') >> title('r=1+cos(theta)') 图像:0.51 1.52302106024090270120300150330180r=1+cos(theta)r=1+cos(theta)练习2.21.求出下列极限值. (1)nnn n33+∞→;(2)()n n n n ++-+∞→122lim;(3)x x x 2cot lim→;(4)??? ?→x m xx cos lim 0;(5)--→111lim1e xx x ;(6)??-+∞→x x xx 2lim .解:(1)编程:>> syms n >> limit((n^3+3^n)^(1/n),n,inf) ans = 3(2)编程:>> syms n>> limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf) ans =0(3)编程:>> syms x >> limit(x*cot(2*x),x,0) ans = 1/2(4)编程:>> syms x m >> limit((cos(m/x))^x,x,inf) ans =1(5)编程:>> syms x>> limit(1/x-1/(exp(x)-1),x,1) ans = (exp(1)-2)/(exp(1)-1) (6)编程:>> syms x >> limit(sqrt(x^2+x)-x,x,1) ans = 2^(1/2)-1 2.有个客户看中某套⾯积为180m 2,每平⽅⽶7500元的房⼦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(1)[1 2 3 4;0 2 -1 1;1 -1 2 5;]+(1/2).*([2 1 4 10;0 -1 2 0;0 2 3 -2])2.A=[3 0 1;-1 2 1;3 4 2],B=[1 0 2;-1 1 1;2 1 1]X=(B+2*A)/23.A=[-4 -2 0 2 4;-3 -1 1 3 5]abs(A)>34.A=[-2 3 2 4;1 -2 3 2;3 2 3 4;0 4 -2 5]det(A),eig(A),rank(A),inv(A)求计算机高手用matlab解决。
>> A=[-2,3,2,4;1,-2,3,2;3,2,3,4;0,4,-2,5]求|A|>> abs(A)ans =2 3 2 41 2 3 23 2 3 40 4 2 5求r(A)>> rank(A)ans =4求A-1>> A-1ans =-3 2 1 30 -3 2 12 1 2 3-1 3 -3 4求特征值、特征向量>> [V,D]=eig(A) %返回矩阵A的特征值矩阵D 与特征向量矩阵VV =0.7335 0.7335 -0.3804 - 0.0312i -0.3804 + 0.0312i -0.0024 + 0.5329i -0.0024 - 0.5329i -0.3907 - 0.0001i -0.3907 + 0.0001i-0.3166 - 0.0283i -0.3166 + 0.0283i -0.8280 -0.8280-0.0556 - 0.2718i -0.0556 + 0.2718i 0.0301 - 0.1235i 0.0301 + 0.1235iD =-3.1766 + 0.6201i 0 0 00 -3.1766 - 0.6201i 0 00 0 5.1766 + 0.7101i 00 0 0 5.1766 - 0.7101i将A的第2行与第3列联成一行赋给b>> b=[A(2,:),A(:,3)']b =1 -23 2 2 3 3 -21.a=round(unifrnd(1,100))i=7;while i>=0i=i-1;b=input('请输入一个介于0到100的数字:');if b==adisp('You won!');break;else if b>adisp('High');else if b<adisp('Low');endendendend结果a =82请输入一个介于0到100的数字:50Low请输入一个介于0到100的数字:75Low请输入一个介于0到100的数字:85请输入一个介于0到100的数字:82You won!2.clear all;clc;n=input('请输入数字n=');n1=floor(n/100); %取出百位数字n1n2=mod(floor(n/10),10); %取出十位数字n2n3=mod(n,10) ; %取出个位数字n3if n1^3+n2^3+n3^3==nfprintf('%d是“水仙花数”', n) % 注意输出格式前须有%符号elsefprintf('%d不是“水仙花”', n) % 注意输出格式前须有%符号end结果请输入数字n=234234不是“水仙花数”>>3.price=input('请输入商品价格');switch fix(price/100)case {0,1} %价格小于200rate=0;case {2,3,4} %价格大于等于200但小于500 rate=3/100;case num2cell(5:9) %价格大于等于500但小于1000 rate=5/100;case num2cell(10:24) %价格大于等于1000但小于2500 rate=8/100;case num2cell(25:49) %价格大于等于2500但小于5000 rate=10/100;otherwise %价格大于等于5000rate=14/100;endprice=price*(1-rate) %输出商品实际销售价格结果请输入商品价格250price =242.5000Function f=myfun(x)x=input;s=pi*x*xl=pi*x^24、Function y=circle(r)s=pi*x*xl=pi*x^24.syms rs=pi*r*rl=2*pi*r5. function fibonacci(n,m) f(1)=1;f(2)=1;for i=3:max(n,m)f(i)=f(i-1)+f(i-2);endfprintf('第%d项',m)x=f(m)fprintf('前%d项',n)s=f(1:n)COMMAND WINDOW输入:fibonacci(20,50)1.绘制])4,0[)(3sin(3π∈=x x e y x 的图像,要求用蓝色的星号画图;并且画出器官包络线3x e y ±=的图像,用红色的点划线画图。
2.用fplot 和ezplot 命令绘出函数)21sin(32t ey t +=-在区间]10,0[上的图像。
3.在同一图像窗口画三个子图要求使用指令gtext,axis,legend,title,xlabel,和ylabel : (3)]8,1[,sin 1∈=x x e y x1.x=0:pi/25:4*pi;y1=exp(x/3).*sin(3*x);y2=exp(x/3);y3=-exp(x/3);plot(x,y1,'b*',x,y2,'r-.',x,y3,'r-.')2.t=1:0.1:10y=exp(-2*t/3).*sin(1+2*t);plot(t,y);figurefplot('exp(-2*t/3).*sin(1+2*t)',[1,10])ezplot('exp(-2*t/3).*sin(1+2*t)',[1,10])3.x=1:1/50:8;y=exp(1./x).*sin(x);subplot(1,3,3),plot(x,y,'b-');legend('y=exp(1/x)sinx'),grid on ,title('y=exp(1/x)sinx'),xlabel('x 轴'),ylabel('y 轴')gtext('真棒'),axis([x1 x8 y1 y10])4.x=0:pi/50:2*pi;y1=sin(x);y2=cos(x);y3=sin(2*x);plot(x,y1,'k*--',x,y2,'rs-',x,y3,'bo--'),grid ontitle('曲线y1=sin(x),y2=cos(x)与y3=sin(2*x)')xlabel('x 轴'),ylabel('y 轴')gtext('y1=sin(x)'),gtext('y2=cos(x)'),gtext('y3=sin(2*x)')legend('y1=sin(x)','y2=cos(x)','y3=sin(2*x)')5.绘制圆锥螺线的图像并加各种标注,圆锥螺线的参数方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤≤==t z t t t t y t t t x 2)200(,6cos 6cos π 6.在同一图形窗口画半径为1的球面,柱面122=+y x 以及极坐标]2,0[,4sin 21πρ∈=t t7.用mesh 与surf 命令绘制三维曲面223y x z +=的图像,并使用不同的着色效果及光照效果。
8.绘制由函数14169222=++z y x 形成的立体图,并通过改变观测点获得该图形在各个坐标平面上的投影。
9.画三维曲面)2,2(522≤≤---=y x y x z 与平面3=z 的交线。
5.t=1:pi/50:20*pi;x=t.*cos(pi/6.*t);y=t.*sin(pi/6.*t);z=2*t;plot3(x,y,z);grid on ;title('圆锥螺线')xlabel('x 轴');ylabel('y 轴');zlabel('z 轴');axis square6. v=[-2 2 -2 2 -2 2];subplot(1,3,1),spheretitle('以半径为1的球面'),xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴'),axis(v) subplot(1,3,2),cylindertitle('柱面'),xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')subplot(1,3,3),t=0:pi/100:2*pi;polar(t,(1/2)*sin(4*t))title('p=(1/2)*sin(4t)')7.[X,Y]=meshgrid(-8:0.5:8);Z=X.^2+3*Y.^2;subplot(1,2,1);mesh(X,Y,Z);shading interpsubplot(1,2,2);surf(X,Y,Z);shading flat8.[xx,yy,zz]=sphere(40);x=xx*3;y=yy*4;z=zz*2;surf(x,y,z)axis equal9.[X,Y]=meshgrid(-2:0.1:2);-Z1=5-X.^2+Y.^2;subplot(1,3,1),mesh(X,Y,Z1),title('曲面');Z2=3*ones(size(X));% 创建一个和y矩阵相同大小的纯1矩阵subplot(1,3,2),mesh(X,Y,Z2),title('平面');r0=abs(Z1-Z2)<=1;ZZ=r0.*Z2;YY=r0.*Y;XX=r0.*X;subplot(1,3,3)plot3(XX(r0~=0),YY(r0~=0),ZZ(r0~=0),'*')title('交线')10.v=[-22 -22 -22];[x,y,z]=sphere(30);surf(4*x,4*y,4*z)title('半径为4的球面'),axis(v)- - -总结.。
