探索勾股定理3
探索勾股定理(公开课课件)

数学领域中的应用
三角函数
勾股定理与三角函数密切相关, 它可以用于求解三角函数的值, 以及推导三角函数的性质和公式。
解析几何
在解析几何中,勾股定理可以用于 求解直线、圆和曲线的方程,以及 解决几何问题。
数论
勾股定理在数论中也有应用,例如 在证明一些数学定理和猜想时,勾 股定理可以提供重要的思路和方法。
公式表示
勾股定理的公式可以表示为 a² + b² = c²,其中a和b是直角三角形的两条直角 边,c是斜边。
勾股定理的重要性
01
几何学基础
勾股定理是几何学中的一个基础定理,它为解决与直角三角形相关的问
题提供了重要的工具。
02 03
实际应用
勾股定理在现实生活中有着广泛的应用,例如建筑、航海、航空等领域。 通过应用勾股定理,我们可以解决与直角三角形相关的问题,从而更好 地理解和设计各种实际结构。
数学发展史
勾股定理在数学发展史上具有重要地位。它的证明和推广对于数学的发 展起到了重要的推动作用,也激发了人们对数学研究的兴趣和热情。
02 勾股定理的起源与历史
CHAPTER
毕达哥拉斯学派
毕达哥拉斯学派是古希腊时期的一个重要哲学和数学学派, 他们发现了音乐、政治、宇宙和数学之间的联系,并提出了 “万物皆数”的哲学思想。
CHAPTER
勾股定理的逆定理
勾股定理的逆定理
如果一个三角形的三边满足勾股定理 ,则这个三角形是直角三角形。
逆定理的证明
假设三角形ABC的三边满足勾股定理, 即$a^2 + b^2 = c^2$,根据余弦定 理,有$cos C = frac{a^2 + b^2 c^2}{2ab} = 0$,因此角C是直角。
《探索勾股定理》第三课时上课课件

B C
动手操作
五巧板的制作: 五巧板的制作:
I H D G
F E
练一练
1 、下列阴影部分是一个正方形,求此正方形的面积 下列阴影部分是一个正方形,
15厘米 厘米 17厘米 厘米
设正方形的边长为x厘米 解:设正方形的边长为 厘米 , 则 x2=172-152 x2=64 正方形的面积是64平方厘米 平方厘米。 答:正方形的面积是 平方厘米。
拓展练习 如图,受台风麦莎影响, 2、如图,受台风麦莎影响,一棵高 18m的大树断裂 的大树断裂, 18m的大树断裂,树的顶部落在离树根 折断后有多高 底部6米处,这棵树折断后有多高? 底部6米处,这棵树折断后有多高?
6米 米
补充练习: 补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东 、放学以后,小红和小颖从学校分手, 南方向和西南方向回家, 南方向和西南方向回家,若小红和小颖行走的速度都 分钟到家, 分钟到家, 是40米/分,小红用 分钟到家,小颖用 分钟到家, 米 分 小红用15分钟到家 小颖用20分钟到家 小红和小颖家的距离为 ( C ) A、600米; B、800米; C、1000米; D、不能确定 、 米 、 米 、 米 、 2、直角三角形两直角边分别为 厘米、12厘米,那么 、直角三角形两直角边分别为5厘米 厘米、 厘米 厘米, 斜边上的高是 ( D ) A、6厘米; 、 厘米 厘米; B、 8厘米; 厘米; 、 厘米 D、 60/13厘米; 厘米; 、 厘米 C、 80/13厘米; 、 厘米; 厘米
探索勾股定理(3)

课题:1.1探索勾股定理 (3)
教学目标:1、用拼图的方法验证勾股定理;
2、掌握勾股定理,并能运用它解决一些实际问题;
教学重点:掌握勾股定理,会运用它进行简单的计算及解决一些实际问题; 教学难点:用拼图的方法验证勾股定理;
导入方式:复习引入
一、课前练习:
1、 在Rt ΔABC 中,∠C=900,a=8,b=15,求c 。
2、 如图:Rt ΔABC 中,∠C=900,AC=10,BC=24,求AB 的长。
3、 完成书本P11知识技能#1。
二、知识点一:
1、课外阅读P12~13页, 从“朱青出入图”的拼图方法理解勾股定理的验证。
2、完成书本P26页#7题,动手验证勾股定理。
3、 试与同学交流一下你的体会。
4、 完成书本P14页议一议,
A C B
三、知识二:
1、完成书本P15随堂练习#1
2、求图中直角三角形的未知边长。
3、要修建一个育苗棚,棚高h =1.8 m,棚宽a =2.4 m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
5、 完成书本:P15页问题解决#1
4 3。
第3课时 探索勾股定理8月10号

第3课时 探索勾股定理(3)活动一:利用五巧板拼“朱青出入图”(1)取两幅五巧板,将其中的一幅拼成一个以C 为边长的正方形,将另外一幅五巧板拼成两个边长分别为a 、b 的正方形。
你能拼出“朱青出入图”来吗? (2)利用五巧板,你还能通过怎样的拼图验证勾股定理?与同伴交流。
活动二:观察下图,用数格子的方法判断图中三角形的三边长是否满足a 2+b 2=c 2。
四、师生互动:下面几个图是勾股定理的“无字证明”法,你能看懂吗?五、训练达标:1、一直角三角形的三边分别为2、3、x ,那么以x 为边长的正方形的面积 为2、等腰直角三角形三边的平方比为3、长方形的一条对角线的长为10cm ,一边长为6cm ,它的面积是4、一个直角三角形的三边为三个连续偶数,则它的三边长分别为5、Rt ∆ABC 中,︒=∠90C ,AB=2,则AB 2+BC 2+CA 2= .6、如图,学校有一块长方形花园,有极少数人为了避开拐角而走“捷径”,在花园内走出了一条“路”。
他们仅仅少走了_____步路(假设2步为1m )。
7、一个矩形的抽斗长为24cm ,宽为7cm,在里面放一根铁条,那么铁条最长可以是 . 8、等腰三角形的底边为10cm ,周长为36cm ,则它的面积是 cm 2.D'CBA9.直角三角形两直角边的比为3:4,面积是24,求这个三角形的周长.10.某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的卡车能否顺利通过该隧道?11.一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法。
如图,火柴盒的一个侧面ABCD 倒下到AB ’C ’D ’的位置,连接CC ’,设AB=a ,BC=b ,AC=c ,请利用四边形BCC ’D ’的面积证明勾股定理。
12. 如图,有一只小鸟在一棵高4m 的小树梢上捉虫子,它的伙伴在离该树12m ,高20m 的一棵大树的树梢上发出友好的叫声,它立刻以4m/s 的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?13、 如图,铁路上A 、B 两站(视为直线上两点)相距25村庄(视为两个点),DA ⊥AB 于A,CB ⊥AB 于B,已知DA=15CB=10㎞.现在要在铁路上建设一个土特产收购站E ,使得C D 两村到E 站的距离相等,则E 站应建在距A 站多少㎞处?14、在一棵树的10米高处有两只猴子,其中一只爬下树走向离树20米的池塘,而另一只猴子只爬到树顶后直扑池塘,如果两只猴子经过的路程相等,问这棵树有多高?15、以Rt △ABC 三边为直径作半圆,这三个半圆的面积S 1、S 2、S 3之间有什么关系?说明理由。
探索勾股定理3(1) - 副本
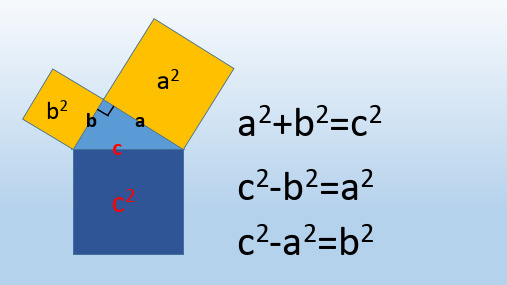
解:有勾股定理可求得:AB2=AC2+BC2 解AB=10cm,由题意可知AE=AC, DE=DC,∠ACD=∠AED=90° 所以BE=AB-AE=4cm
设DC=xcm,则BD=(8-x)cm 在Rt△BDE中,(8-x)2=x2+42 解得x=3,即CD的长为3cm
8
6
X
6 10
一架云梯AB长25m,如图斜靠在一面墙上梯子底端离墙7m (1) 这个梯子的顶端距离地面的高度AC是多少? (2) 如果梯子的顶端下滑了4m,那么梯子的底端在水平方向移 动的距离为 m 思考:梯子在下滑的过程中,什么量是不变的?
爬到点B处吃食,要爬行的最短路程 ( 取3)是
(B )
A.20cm B.10cm
C.14cm D.无法确定
2O
蛋糕 B
C
6
B
8
8
A
A
12
如图:一只蚂蚁从长为7cm、宽为5cm、高为9cm的长方形纸
箱的A点沿纸箱爬到B点,它所走的最短路线的长是 15 。
B
A
勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有
4.已知某个三角形的三边长分别为5,13,12,则此三角形的面积为( A )
A.30
B.60
C.78
D.不能确定
【解析】 ∵此三角形的三边长分别为5,13,12,而52+122=132,∴此三角
形为直角三角形,此三角形的面积为12×5×12=30.故选A.
• 5.三角形各边长度的平方比如下,其中不是直角三角形的是
解(2)∵a2=(m2-n2)2=m4-2m2n2+n4, b2=(m2+n2)2=m4+2m2n2+n4 c2=(2mn)2 =4m2n2
北师大版八年级数学上册《勾股定理3》课件

1
1
•1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” •2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 •3、反思自我时展示了勇气,自我反思是一切思想的源泉。 •4、好的教师是让学生发现真理,而不只是传授知识。 •5、数学教学要“淡化形式,注重实质.
6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/72021/11/72021/11/711/7/2021
▪ 1876年4月1日,伽菲尔德 在《新英格兰教育日志》 上发表了他对勾股定理的 这一证法。
▪ 1881年,伽菲尔德就任美 国第二十任总统。后来, 人们为了纪念他对勾股定 理直观、简捷、易懂、明 了的证明,就把这一证法 称为“总统”证法。
青九
刘
朱章 出算
徽
入术
图
无字证明
④
bc
⑤
③aຫໍສະໝຸດ ①②青无朱字出证入明图
▪ 赵爽:东汉末至三国时 代吴国人
▪ 为《周髀算经》作注, 并著有《勾股圆方图 说》。
▪ 赵爽的这个证明可谓别 具匠心,极富创新意识。 他用几何图形的截、割、 拼、补来证明代数式之 间的恒等关系。
毕达哥拉斯
在国外,相传勾股 定理是公元前500多年 时古希腊数学家毕达哥 拉斯首先发现的。因此 又称此定理为“毕达哥 拉斯定理”。法国和比 利时称它为“驴桥定 理”,埃及称它为“埃 及三角形”等。但他们 发现的时间都比我国要 迟得多。
青出
青方
青 出
青 入
朱
朱方 出
朱入 青入
青出
五巧板的制作 A
④
E
⑤
G
b
Hc
③
1.1探索勾股定理3

第一节探索勾股定理教学目标:1、 经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、 探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
重点难点:重点:了结勾股定理的由来,并能用它来解决一些简单的问题。
难点:勾股定理的发现 教学过程掌握勾股定理的内容,能利用勾股定理进行计算与证明。
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即:c 2=a 2+b 2(c 为斜边)。
它反映了直角三角形三边之间的数量关系,是解决直角三角形中计算问题以及解直角三角形的主要依据之一。
一、问题的提出:小明放学回家要经过一块长方形的麦地。
如图: 1、 小明本来应走大路从A 经B 到C 可是他却直接从A 到C ,为什么? 2、 为什么近、近多少? 3、用数学知识如何解答?二、量一量,算一算:1、直角三角形的两条直角边的长度分别为3㎝,4㎝和5㎝,12㎝请你量出斜边的长度。
2、进行有关的计算。
3、得出结论: 三、证明结论:利用拼合三角形的方法,如下:(1)b a a bca c cb a a a b a bc b c b b c aa b a b (1) (2)由(1)S ab c ab c 正=⨯+=+412222 A B C D由(2)S a b ab 正=++222 ∴+=++22222ab c a b ab ∴+=a b c 222(2)如图:S c S S S a b b a a b b a a b a b c a b 正正小正==+=⨯+-=++-=+∴=+222222222441222∆() 练习: 1、判断:(1)已知a 、b 、c 是三角形的三边,则∴+=a b c 222( ) (2)在直角三角形中两边的平方和等于第三边的平方。
( ) (3)在Rt ABC ∆90=∠B ∴+=a b c 222( ) 2、填空:在Rt ABC ∆中,∠=C 90(1)如果a=3,b=4,则c= (2)如果a=6,b=8,则c= (3)如果a=5,b=12,则c= (4) 如果a=15,b=20,则c=3、 解决新课开始提出的问题c ab ac b b c ba ac。
八年级数学上册《探索勾股定理》知识点北师大版

八年级数学上册《探索勾股定理》知识点
北师大版
八年级数学上册《探索勾股定理》知识点北师大版
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。
2.勾股定理逆定理:如果三角形三边长a,b,c满足
a2+b2=c2。
,那么这个三角形是直角三角形。
3.经过证明被确认正确的命题叫做定理。
我们把题设、结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的
逆命题。
(例:勾股定理与勾股定理逆定理)
4.直角三角形的性质
(1)、直角三角形的两个锐角互余。
可表示如下:
∠C=90° ∠A+∠B=90°
(2)、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°
可表示如下:BC= AB ∠C=90°
(3)、直角三角形斜边上的中线等于斜边的一半
∠ACB=90°
可表示为: CD= AB=BD=AD
D为AB的中点
5、摄影定理
在直角三角形中,斜边上的高线是两直角边在斜边
上的摄影的比例中项,每条直角边是它们在斜边上的摄
影和斜边的比例中项
∠ACB=90°
CD⊥AB
6、常用关系式
由三角形面积公式可得:AB CD=AC BC
7、直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理:如果三角形的三边长a,b,c有关系,那么这个三角形是直角三角形。
3.1 探索勾股定理(学生版) 2024-2025学年七年级数学上册同步课堂(鲁教版五四制)

3.1 探索勾股定理◆勾股定理的定义:直角三角形的两条直角边a 、b 的平方和等于斜边c 的平方,即:222a b c += .题型一 应用勾股定理求线段长1.(2024春•嘉祥县期中)如图,在ABC D 中,90C Ð=°,若1AC =,2AB =,则BC 的长是( )A .1BC.2D2.(2023秋•临淄区期末)如图,在Rt ABC D 中,90ACB Ð=°,3BC =,4AC =,CD AB ^于点D ,E是AB的中点,则DE的长为( )A.0.6B.0.7C.0.8D.0.9题型二应用勾股定理求面积1.(2024春•齐河县校级月考)如图,字母B所代表的正方形的面积是( )cmcm D.306 2cm B.15 2A.12 2cm C.144 22.(2022秋•郓城县期中)如图,在Rt ABCD中,90Ð=°,分别以各边为直径作半圆,图中阴影部分在C数学史上称为“希波克拉底月牙”,当4BC=时,则阴影部分的面积为( )AC=,2A.4B.4p C.8p D.83.(2024春•济南期末)已知,如图长方形ABCD中,3=,将此长方形折叠,使点BAD cmAB cm=,9D的面积为( )与点D重合,折痕为EF,则ABE6cm D.212cm3cm B.24cm C.2A.24.(2023秋•阳信县期末)如图,在Rt ABCAB=,则正方形ADEC和正方形BCFGÐ=°,若15D中,90C的面积和为( )A.225B.200C.150D.无法计算5.(2024春•沂水县校级月考)如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )A.50B.16C.25D.416.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )A.16B.25C.144D.169题型三勾股定理的证明1.(2024春•历下区期末)勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端,下面四幅图中不能证明勾股定理的是( )A.B.C.D.2.(2024春•梁山县校级月考)如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果直角三角形较长直角边的长为a,较短直角边的长为b,若7ab=,大正方形的面积为30,则小正方形的边长为( )A.16B.8C.4D.23.(2024春•阳谷县校级月考)如图是“赵爽弦图”,它是由4个全等的直角三角形拼成的图形,若大正方形的面积是29,小正方形的面积是9,设直角三角形较长直角边为b,较短直角边为a,则a b+的值是( )A .5B .6C .7D .84.(2024春•嘉祥县期中)如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a ,较短直角边为b ,则2()a b +的值是( )A .25B .17C .29D .225.(2023秋•邹平市期末)下面图形能够验证勾股定理的有( )A .0B .1C .2D .36.(2022春•兖州区期末)我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )A .B .C .D .7.(2024春•齐河县校级月考)如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,如果大正方形的面积为16,小正方形的面积为3,那么2()a b +的值为 .8.(2015秋•滕州市校级期末)如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两边长分别为3和5,则小正方形的面积为 .9.(2024春•河东区校级月考)阅读下列材料,并完成相应任务.教材第九章探索整式乘法法则时,我们用不同方法表示同一个图形的面积,直观地理解乘法法则.如图1,现有4张大小形状相同的直角三角形纸片,三边长分别是a 、b 、c ,将它们拼成如图2的大正方形.(1)观察:图2中,大正方形的面积可以用2()a b +表示,也可以用含a 、b 、c 的代数式表示为 ,那么可以得到等式: .整理后,得到a 、b 、c 之间的数量关系:222a b c +=,这就是著名的“勾股定理”,它反映了直角三角形的三边关系,即直角三角形的两直角边a 、b 与斜边c 所满足的关系式.(2)思考:爱动脑的小明通过图2得到启示,发现其它图形也能验证“勾股定理”,请你帮助小明画出该图形.(画出一种即可)(3)应用:如图3,在直角三角形ABC 中,90C Ð=°,3AC =,4BC =,那么AB = ,点D 为射线BC 上一点,将ACD D 沿AD 所在直线翻折,点C 的对应点为点1C ,如果点1C 在射线BA 上,那么CD = .(直接写出答案)10.(2024春•兰山区校级月考)如图①,直角三角形的两条直角边长分别是a ,()b a b <,斜边长为c .(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).①小正方形的边长为c ,大正方形的边长为 ;②由大正方形面积的不同表示方式可以得出等式 ,整理得 ,从而验证勾股定理;(2)应用:将两个这样的直角三角形按图③所示摆放,使BC 和CD 在一条直线上,连接AE .请你类比(1)中的方法用图③验证勾股定理.11.(2024春•昌乐县期中)公元3世纪,古人就通过拼图验证了勾股定理:在直角三角形中两直角边a 、b 与斜边c 满足关系式222a b c +=.还探索验证了勾股定理的逆定理:如果三角形三边满足222a b c +=,则这个三角形是直角三角形.(1)小明发现证明勾股定理的新方法:如图1,在正方形ACDE 边CD 上取点B ,连接AB ,得到Rt ACB D ,三边分别为a ,b ,c ,剪下ACB D 把它拼接到AEF D 的位置,如图2所示,请利用面积不变证明勾股定理.(2)一个零件的形状如图3,按规定这个零件中A Ð和C Ð都应是直角,小明测得这个零件各边尺寸(单位:)cm 如图③所示,这个零件符合要求吗?12.(2024春•长清区期中)(1)计算:(2)()a b a b ++= ;(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:图2: ;图3: ;(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:做4个全等的直角三角形,设它们的两条直角边分别为a ,b ,斜边为c ,再做1个长分别为c 的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:222a b c +=.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即222a b c +=.(4)如图5,在Rt ABC D 中,90ACB Ð=°,CD 是AB 边上高,4AC =,3BC =,求CD 的长度.。
北师大版数学八年级上册1《探索勾股定理》说课稿3

北师大版数学八年级上册1《探索勾股定理》说课稿3一. 教材分析《探索勾股定理》是北师大版数学八年级上册第一单元的一节重要内容。
本节课的主要目的是让学生通过探究、验证勾股定理,培养学生的动手操作能力、观察能力以及推理能力。
教材从学生的实际出发,设计了丰富的活动,让学生在活动中感受数学的美妙,体验到探究的乐趣。
二. 学情分析学生在学习本节课之前,已经掌握了实数、三角形等基本知识,具备了一定的观察、操作、推理能力。
但对于勾股定理的理解和应用,还需要通过本节课的学习来进一步深化。
同时,学生对于探究式学习方法还不太熟悉,需要在课堂上加以引导和培养。
三. 说教学目标1.知识与技能:学生能够理解勾股定理的含义,并会运用勾股定理解决一些实际问题。
2.过程与方法:学生通过自主探究、合作交流,培养观察、操作、推理能力。
3.情感态度与价值观:学生感受数学的美妙,体验探究的乐趣,培养对数学的兴趣。
四. 说教学重难点1.教学重点:学生能够理解并掌握勾股定理。
2.教学难点:学生能够运用勾股定理解决实际问题,并理解勾股定理的证明过程。
五. 说教学方法与手段1.教学方法:采用探究式学习方法,让学生在活动中自主发现、总结勾股定理。
2.教学手段:利用多媒体课件、实物模型等辅助教学,提高学生的学习兴趣和效果。
六. 说教学过程1.导入:通过一个有趣的数学故事,引导学生思考勾股定理的发现过程,激发学生的学习兴趣。
2.探究:让学生分组进行实践活动,利用提供的材料和工具,自主探究勾股定理。
3.交流:学生分组汇报探究过程和结果,其他同学进行评价、补充。
4.总结:教师引导学生总结勾股定理的证明过程,明确勾股定理的含义和应用。
5.练习:设计一些实际问题,让学生运用勾股定理进行解决,巩固所学知识。
七. 说板书设计板书设计要简洁明了,突出勾股定理的核心内容。
主要包括:勾股定理的定义、证明过程、应用示例等。
八. 说教学评价1.学生参与度:观察学生在课堂上的积极参与情况,是否能够主动思考、提出问题、与他人交流。
探索勾股定理ppt课件

边还是斜边或两种均有可能;
骤
(3)利用勾股定理进行计算
续表
1.1 探索勾股定理
返回目录
归纳总结
考
点
利用勾股定理解决实际问题的关键是利用数形结合思想
清
单 将实际问题转化成数学问题,建立直角三角形模型,再利用
解
读 勾股定理来解决.
1.1 探索勾股定理
返回目录
对点典例剖析
考
点
典例3 如图是一个长方形的大门,小强拿着一根竹竿要
方
法
)
技 100 和 36,则以 AD 为直径的半圆的面积是 (
巧
A. 4π
B. 8π
点
拨
C. 12π
D. 16π
1.1 探索勾股定理
返回目录
方
[解析] 因为在 Rt△ABD 中,∠ADB=90°,AB2=100,
法
技 BD2=36,所以 AD2=100-36=64,所以 AD=8,
巧
点
所以以 AD 为直径的半圆的面积是 π×( AD)2=8π.
行分类讨论.
1.1 探索勾股定理
返回目录
方 ■方法:利用勾股定理解决面积问题
法
如图,由直角三角形的三边向外作正方形、半圆或等边
技
巧 三角形,则有 S =S +S (S ,S ,S 分别代表三个图形的
1
2
3
1
2
3
点
拨 面积,其中 S1 代表以斜边为一边的图形的面积).
1.1 探索勾股定理
返回目录
例 如图,正方形 ABGF 和正方形 CDBE 的面积分别是
1.1 探索勾股定理
● 考点清单解读
北师大版八年级上册数学《探索勾股定理》勾股定理教学说课复习课件巩固

1.如图,一个长为2.5 m的梯子,一端放在离墙脚
1.5 m处,另一端靠墙,则梯子顶端距离墙脚( C )
A.0.2 m
B.0.4 m
C.2 m
D.4 m
课堂检测
基 础 巩 固 题
2.如图,在边长为1个单位长度的小正方形组成的网
格中,点A,B都是格点,则线段AB的长度为( A )
A.5
B.6
C.7
D.25
课堂检测
基 础 巩 固 题
3.如图,直线l上有三个正方形a,b,c,若a,c的
面积分别为3和4,则b的面积为( D )
A.16
B.12
C.9
D.7
课堂检测
基 础 巩 固 题
4.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,
一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至
部分称为“股”.
(在西方称为毕达
哥拉斯定理)
斜边称为 弦 .
弦
勾
股
勾2
+ 股2
= 弦2
a b c
2
2
2
四、探究活动
观察图片,分别求出正方形A,B,C的面
积。
能用直角三角
形的两直角边
的长a,b和斜
边长 c 来表示
图中正方形的
面积吗?
割补法
16
a
Sc c2
2
2
Sc a b
c
25
10
1
4km
所以BC2=9,所以BC=3,
因为20s=
h,
A
所以3÷ =540km.
答:飞机每小时飞行540km.
北师大版-数学-八年级上册-第一章第1节探索勾股定理(3) 作业

B北师大版八年级上第一章第1节探索勾股定理(3) 作业一、积累·整合1、如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的【 】.A.1倍B. 2倍C. 3倍D. 4倍2、 下列结论错误的是 【 】.A . 角度之比为1∶2∶3的三角形是直角三角形B .三个边长之比为3∶4∶5的三角形是直角三角形C .三个边长之比为8∶16∶17的三角形是直角三角形D .三个角度之比为1∶1∶2的三角形是直角三角形3、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程是 (π取3) 【 】. A. 20cm B. 10cm C. 14cm D. 无法确定4、一直角三角形的斜边长比一直角边长大2,另一直角边长为6,则斜边长为 【 】 A 4 B 8 C 10 D 125、在⊿ABC 中,若1,2,122+==-=n c n b n a ,则⊿ABC 是 【 】 A 锐角三角形 B 钝角三角形 C 等腰三角形 D 直角三角形6、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2.7、一部内部空间是长方体的电梯,长是3米,宽是2米,高是6米,这个电梯内能放入的最长的竹竿长度是 米。
二、拓展·应用8、如图,要从电线杆离地面8m 处向地面拉一条长10m 的电缆,求地面电缆固定点A 到电线杆底部B的距离.CA B9、如图,一根旗杆在离地面9 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆在折断之前有多高?9m12m10、某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。
今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答)三、探索·创新11、右图是历史上有名的“青朱出入图”,你能说明它的原理吗?12、如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理?第12题图简明答案1、B2、C3、B 解析:画出展开图,利用勾股定理求出斜边。
探索勾股定理ppt课件

欣赏下面一幅美丽的图案,仔细观察,你能发现这 幅图中的奥秘吗?带着疑问我们来一步认识
做一做 观察正方形瓷砖铺成的地面. (1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米;
AR P
CQ B
(3)正方形R的面积是 2 平方厘米.
左图 4
9
13
右图 16
9
25
分析表中数据,你发现了什么?
A的面积
左图
4
右图 16
B的面积 9 9
C的面积 13 25
结论 以直角三角形两直角边为边长的小 正方形的面积的和,等于以斜边为边长 的正方形的面积.
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的 平方.
几何语言 ∵在Rt△ABC中 ,∠C=90°, ∴.AC2+BC2=AB2 (勾股定理)
五、分层作业 课后思考
基础训练:1、小明的妈妈买了一部29in的电 视机。小明量了电视机的屏幕后,发现屏幕只 有58cm长和46cm宽,他觉得一定是销售员搞错 了。你同意他的想法吗?你能解释这是为什么 吗?
2、求下列图中未知数x,y的值
提高训练:1.今有池方一丈,葭生其中央,出水一 尺.引葭赴岸,适与岸齐.问水深、葭长各几何?译: 有一个一丈大小的池子,中央长有芦苇,高出水面 一尺长.把芦苇拽向岸边,刚好与到岸.请问水有多 深,芦苇有多高?
小男孩又问道:“如果两条直角边分别为5和7,那么这个直角 三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“ 那斜边的平方一定等于5的平方加上7的平方。”小男孩又说道 :“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无 法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回 家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演 算,终于弄清楚了其中的道理,并给出了简洁的证明方法。 1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了 他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十 任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、 明了的证明,就把这一证法称为“总统。”证法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:根据下列条件,分别判断以a、b、
c为边的三角形是不是直角三角形.
(1) a 7, b 3, c 2 2 2 (2) a , b 1, c 3 3
例2:已知ΔABC的三条边长分别为 a、b、c, 且
(
a m n b 2mn 2 2, , cm n m n, m , n 是正整数)。三角
义务教育课程标准实验教科书
《数学》八年级上册
勾股定理(3)
勾股定理:
直角三角形两直角边的平方和等角形是直 角三角形.
判定直角三角形的思路: 做一做:判定下列三角形是不是 直角三角形? 是否有两边的平方和等于第三
(1) a=7、b=25、c=24 边的平方。 (2)a=6、b=8、c=10 (3)a=5、b=12、c=13
2 2
形是直角三角形吗?请说明理由.
例3:如图,四边形ABCD中,AB=3,
BC=4,CD=12,AD=13,∠B=90°,
求四边形ABCD的面积。
D
A B C
说能出你这节课的收获和体验让大家 与你分享吗?
