2018 初三中考数学复习 平行线的证明 专题复习练习 含答案
中考数学专题复习全等三角形之辅助线做平行线

中考数学专题复习全等三角形(辅助线做平行线)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,△ABC是边长为4的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC至点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.1B.1.8C.2D.2.52.如图,⊥ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC到点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.0.5B.0.9C.1D.1.25评卷人得分二、填空题3.如图,四边形ABCD中,AC与BD相交于点O,且AC⊥BD,AC=BD=CD,点P 是⊥OCD角平分线的交点,点M是AB的中点,给出下列结论:⊥⊥CPD=135°;⊥BA=BP;⊥⊥P AC⊥⊥PDB;⊥S△ABP=S△DCP;⊥PM=12CD.其中正确的是___.(填序号)评卷人得分三、解答题4.如图,⊥ABC中,点D,E在边AB上,点F在边BC上,且AD=AC,EF=EC,⊥CEF=⊥A,连接DF.(1)在图1中找出与⊥ACE相等的角,并证明;(2)求证:⊥BDF=⊥EFC;(3)如图2,延长FD,CA交于点G,连接EG,若EG=AG,DE=kAE,求DG DF的值(用含k的代数式表示).5.如图所示:ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD CE=,连接DE交BC于点M.求让:MD ME=6.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.7.P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC 边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.8.如图,点P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE⊥AC于E,若BC=4,求DE的长.9.已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系.10.读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DB上,且⊥BAE=⊥CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明.图(1):延长DE到F使得EF=DE图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F图(3):过C点作CF⊥AB交DE的延长线于F.参考答案:1.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD⊥QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴△是等边三角形,AP PF∴=,⊥CQ=P A,⊥PF CQ=在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴⊥()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF∴=,=AE DC EF FD ED∴+=+,12DE AC∴=,4AC=,2DE∴=,故选:C.【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.2.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD≌QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴是等边三角形,AP PF∴=,在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴≌()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF ∴=,AE DC EF FD ∴+=+,12DE AC ∴=, 2AC =, 1DE ∴=,故选:C . 【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键. 3.⊥⊥⊥⊥ 【解析】 【分析】由角平分线的定义,可得⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,进而即可判断⊥;先证ACP DCP ≌,可得APD △是等腰直角三角形,进而得PAC PDB ≌,即可判断⊥;过点A 作AN ⊥BP 交PM 的延长线于点N ,可得AMN BMP ≌,再证明APN PDC ≌,从而得PM =12CD ,即可判断⊥;由ABP APM BMP APM AMN APN S S S S S S +=+==,即可判断⊥. 【详解】解:⊥AC ⊥BD ,点P 是⊥OCD 角平分线的交点,⊥⊥DOC =90°,⊥ODC +⊥OCD =90°,⊥CDP =12⊥CDO ,⊥DCP =12⊥DCO , ⊥⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,⊥⊥CPD =180°-(⊥CDP +⊥DCP )=135°,故⊥正确; ⊥CP ,DP 分别平分⊥DCO ,⊥CDO , ⊥⊥DCP =⊥ACP ,⊥CDP =⊥BDP , ⊥AC =CD ,PC =PC , ⊥ACP DCP ≌,⊥AP =DP ,⊥CAP =⊥CDP =⊥BDP ,⊥APC =⊥DPC =135°, ⊥⊥DP A =360°-135°-135°=90°,⊥APD △是等腰直角三角形, 又⊥AC =BD ,⊥CAP =⊥BDP,AP =DP , ⊥PAC PDB ≌,故⊥正确; ⊥⊥DPB =⊥APC=135°,PB =PC , ⊥⊥BPC =360°-135°-135°=90°,⊥BPC △是等腰直角三角形,找不到证明BA =BP 的条件,故⊥错误; 过点A 作AN ⊥BP 交PM 的延长线于点N ,⊥⊥N =⊥BPM ,⊥P AN +⊥APB =180°, ⊥点M 是AB 的中点,即AM =BM , 又⊥⊥AMN =⊥BMP , ⊥AMN BMP ≌,⊥MN =PM =12PN ,AN =PB =PC ,AMNBMPSS=,⊥⊥DP A =⊥BPC =90°, ⊥⊥APB +⊥DPC =180°, 又⊥⊥P AN +⊥APB =180°, ⊥⊥P AN =⊥DPC , 又⊥AP =DP ,AN =PC , ⊥APN PDC ≌,⊥CD =PN =2PM ,即:PM =12CD ,故⊥正确; ⊥APNPDCSS=,AMNBMPSS=,⊥ABPAPMBMPAPMAMNAPNS SSSSS+=+==,⊥ABPDCPSS=,故⊥正确.故正确的是⊥⊥⊥⊥. 【点睛】本题主要考查全等三角形的判定和性质,平行线的性质,等腰直角三角形的判定和性质,熟练掌握中线倍长模型和旋转全等模型,是解题的关键. 4.(1)⊥DEF =⊥ACE ,证明见解析;(2)见解析;(3)k 【解析】 【分析】(1)由三角形外角的性质可得出答案;(2)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥DEF ⊥⊥MEC (SAS ),由全等三角形的性质可得出⊥EDF =⊥EMC ,证出⊥EMD =⊥EFC ,则可得出结论;(3)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥EFG ⊥⊥ECD (ASA ),由全等三角形的性质可得出GF =DC ,证出GD =DM ,则根据平行线分线段成比例即可得出答案. 【详解】解:(1)⊥DEF =⊥ACE . 证明:⊥⊥DEC 是⊥ACE 的外角, ⊥⊥DEC =⊥A +⊥ACE , ⊥⊥DEC =⊥DEF +⊥CEF , ⊥⊥DEC +⊥CEF =⊥A +⊥ACE , ⊥⊥CEF =⊥A , ⊥⊥DEF =⊥ACE ;(2)证明:连接CD ,过点E作AC 的平行线与CD 交于点M ,⊥AD =AC ,⊥⊥ADC=⊥ACD,⊥EM⊥AC,⊥⊥EMD=⊥ACD,⊥CEM=⊥ACE,⊥⊥EDM=⊥EMD,⊥DEF=⊥CEM,⊥ED=EM,又⊥EF=EC,⊥⊥DEF⊥⊥MEC(SAS),⊥⊥EDF=⊥EMC,⊥⊥BDF+⊥EDF=⊥EMD+⊥EMC=180°,⊥⊥BDF=⊥EMC,⊥EM⊥AC,⊥⊥DEM=⊥A,⊥⊥A=⊥CEF,⊥⊥DEM=⊥CEF,⊥⊥DEM中,⊥EMD=1802DEM︒-∠,⊥FEC中,⊥EFC=1802CEF︒-∠,⊥⊥EMD=⊥EFC,⊥⊥BDF=⊥EFC;(3)连接CD,过点E作AC的平行线与CD交于点M,⊥EG=AG,⊥⊥GAE=⊥GEA,⊥⊥DAC+⊥GAE=⊥GEA+⊥GED=180°,⊥⊥DAC=⊥GED,⊥⊥CEF=⊥DAC,⊥⊥DEG=⊥CEF,⊥⊥DEG+⊥DEF=⊥CEF+⊥DEF,即⊥GEF=⊥DEC,⊥⊥DEF⊥⊥MEC,⊥⊥EFG=⊥ECD,DF=MC,又⊥EF=EC,⊥⊥EFG⊥⊥ECD(ASA),⊥GF=DC,⊥DC﹣MC=GF﹣DF,即GD=DM,⊥EM⊥AC,⊥DM DEk MC AE==,⊥GD DMk DF MC==.【点睛】本题考查了全等三角形的性质与判定,平行线分线段成比例,三角形的内角和定理,三角形的外角性质,添加辅助线证明三角形全等是解题的关键.5.见详解【解析】【分析】过点D作DE⊥AC,交BC于点E,根据等边三角形和平行线的性质得⊥MDE=⊥MEC,DE=CE,从而证明∆EMD≅∆CME,进而即可得到结论.【详解】过点D作DE⊥AC,交BC于点E,⊥ABC是等边三角形,⊥⊥B=⊥ACB=60°,⊥DE⊥AC,⊥⊥DEB=⊥ACB=60°,⊥MDE=⊥MEC,⊥BDE是等边三角形,⊥BD=DE,⊥DE=CE,又⊥⊥EMD=⊥CME,⊥∆EMD≅∆CME,⊥MDME =.【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理,添加辅助线,构造等边三角形和全等三角形,是解题的关键.6.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明△PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在△PDF和△QDC中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,△ABC是等边三角形,⊥⊥PFD=⊥QCD,△APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在△PFD和△QCD中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质,解题的关键是掌握等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质.7.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出⊥APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明⊥PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明⊥PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在⊥PDF和⊥QDC中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),⊥PD=DQ;(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,⊥ABC是等边三角形,⊥⊥PFD=⊥QCD,⊥APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在⊥PFD和⊥QCD中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.8.(1)详见解析(2)ED=2【解析】【分析】(1)过P作PF⊥BQ,可得△APF为等边三角形,所以AP=PF,再证△DCQ⊥⊥DFP,即可得PD=DQ;(2)根据等腰三角形三线合一的性质可得AE=EF,根据全等三角形对应边相等可得FD =CD,然后求出2DE=AC,代入数据进行计算即可得解.(1)证明:如图,过点P作PF⊥BC,则⊥DPF=⊥Q,⊥⊥ABC为等边三角形,⊥⊥APF是等边三角形,⊥AP=PF,又⊥AP=CQ,⊥PF=CQ,在△DPF和△DQC中,DPF QPDF QDC PF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DPF⊥⊥DQC(AAS),⊥DP=DQ;(2)⊥⊥P AF为等边三角形,PE⊥AC,可得AE=EF,由(1)知,⊥DPF⊥⊥DQC⊥FD=CD,⊥AC=AE+EF+FD+CD,⊥AC=2EF+2FD=2(EF+FD)=2ED,⊥AC=BC=4,⊥2ED=4,⊥ED=2.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线构造出等边三角形和全等三角形是解题的关键,也是本题的难点.9.(1)DM=EM.理由见详解;(2)成立,理由见详解;(3)MD=12ME.【解析】【分析】(1)DM=EM;过点E作EF//AB交BC于点F,然后利用平行线的性质和已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(2)成立;过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质与已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(3)MD=12ME.过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质和已知条件得到△DBM⊥⊥EFM,接着利用相似三角形的性质即可得到结论;(1)解:DM=EM;证明:过点E作EF//AB交BC于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDM FEMBMD FMEBD EF∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DBM⊥⊥EFM,⊥DM=EM.(2)解:成立;证明:过点E作EF//AB交CB的延长线于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDE FEM BMD FME BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩⊥⊥DBM ⊥⊥EFM ;⊥DM =EM ;(3)解:过点E 作EF //AB 交CB 的延长线于点F ,⊥⊥DBM =⊥EFM ,⊥DMB =⊥EMF⊥⊥DBM ⊥⊥EFM ,⊥BD :EF =DM :ME ,⊥AB =AC ,⊥⊥ABC =⊥C ,⊥⊥F =⊥ABC ,⊥⊥F =⊥C ,⊥EF =EC ,⊥BD :EC =DM :ME =1:2,⊥MD =12ME . 【点睛】本题主要考查了三角形综合,涉及了等腰三角形性质和判定、全等三角形的判定与性质、相似三角形的判定和性质,利用平行构造全等三角形是解题关键.10.选择(1)(3)证明,证明见解析【解析】【分析】如图(1)延长DE 到F 使得EF=DE,证明△DCE⊥⊥FBE,得到⊥CDE=⊥F,BF=DC,结合题干条件即可得到结论;如图3,过C 点作CF⊥AB 交DE 的延长线于F,得到△ABE⊥⊥FCE,AB=FC,结合题干条件即可得到结论,【详解】如图(1)延长DE 到F 使得EF=DE在△DCE 和△FBE 中,EF DE DEC FEB BE EC =∠=∠=⎧⎪⎨⎪⎩⊥△DCE⊥⊥ FBE (SAS)⊥⊥CDE=⊥F,BF=DC⊥⊥BAE=⊥CDE⊥BF=AB⊥AB= CD如图3,过C 点作CF⊥AB 交DE 的延长线于F在△ABE 和△FCE 中B ECF BE ECBAE F ∠=∠=∠=∠⎧⎪⎨⎪⎩⊥△ABE⊥⊥ FCE(AAS),⊥AB=FC⊥⊥BAE=⊥CDE⊥⊥F=⊥CDE⊥CD=CF⊥AB=CD【点睛】此题考查全等三角形的判定与性质和等腰三角形的性质,解题关键在于利用三角形全等的性质证明。
中考数学专题复习平行线问题骨折型

中考数学专题复习平行线问题骨折型学校:___________姓名:___________班级:___________考号:___________评卷人得分一、填空题1.如图,如果AB∥EF,EF∥CD,则∥1,∥2,∥3的关系式__________.2.如图所示,AB∥CD,∥E=37°,∥C=20°,则∥EAB的度数为__________.3.如图,已知//AB DE,∥ABC=80°,∥CDE=140°,则∥BCD=_____.4.如图,直线MA∥NB,∥A=70°,∥B=40°,则∥P=___________度.5.如图,AB∥CD,则∥1+∥3—∥2的度数等于__________.评卷人得分二、解答题6.(1)如图,AB//CD,CF平分∥DCE,若∥DCF=30°,∥E=20°,求∥ABE的度数;(2)如图,AB//CD,∥EBF=2∥ABF,CF平分∥DCE,若∥F的2倍与∥E的补角的和为190°,求∥ABE的度数.(3)如图,P为(2)中射线BE上一点,G是CD上任一点,PQ平分∥BPG,GN//PQ,GM平分∥DGP,若∥B=30°,求∥MGN的度数.7.已知直线AB∥CD,P为平面内一点,连接P A、PD.(1)如图1,已知∥A=50°,∥D=150°,求∥APD的度数;(2)如图2,判断∥P AB、∥CDP、∥APD之间的数量关系为.(3)如图3,在(2)的条件下,AP∥PD,DN平分∥PDC,若∥P AN+12∥P AB=∥APD,求∥AND的度数.8.如图1,MN∥PQ,点C、B分别在直线MN、PQ上,点A在直线MN、PQ之间.(1)求证:∥CAB=∥MCA+∥PBA;(2)如图2,CD∥AB,点E在PQ上,∥ECN=∥CAB,求证:∥MCA=∥DCE;(3)如图3,BF平分∥ABP,CG平分∥ACN,AF∥CG.若∥CAB=60°,求∥AFB的度数.9.(1)如图1,l1∥l2,求∥A1+∥A2+∥A3=______.(直接写出结果)(2)如图2,l1∥l2,求∥A1+∥A2+∥A3+∥A4=_____.(直接写出结果)(3)如图3,l1∥l2,求∥A1+∥A2+∥A3+∥A4+∥A5=_______.(直接写出结果)(4)如图4,l1∥l2,求∥A1+∥A2+…+∥An=_______.(直接写出结果)10.已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∥BME、∥E、∥END的数量关系为:;(不需要证明)如图2中,∥BMF、∥F、∥FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∥FND,MB平分∥FME,且2∥E+∥F=180°,求∥FME的度数;(3)如图4中,∥BME=60°,EF平分∥MEN,NP平分∥END,且EQ∥NP,则∥FEQ 的大小是否发生变化,若变化,请说明理由,若不变化,求出∥FEQ的度数.11.综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动(1)如图1,//EF MN,点A、B分别为直线EF、MN上的一点,点P为平行线间一点,请直接写出PAF∠、PBN∠和APB∠之间的数量关系;【问题迁移】(2)如图2,射线OM与射线ON交于点O,直线//m n,直线m分别交OM、ON于点A、D,直线n分别交OM、ON于点B、C,点P在射线OM上运动,∥当点P 在A 、B (不与A 、B 重合)两点之间运动时,设ADP α∠=∠,BCP β∠=∠.则CPD ∠,α∠,β∠之间有何数量关系?请说明理由.∥若点P 不在线段AB 上运动时(点P 与点A 、B 、O 三点都不重合),请你画出满足条件的所有图形并直接写出CPD ∠,α∠,β∠之间的数量关系.12.已知AB //CD ,求证:∥B =∥E +∥D13.为更好地理清平行线与相关角的关系,小明爸爸为他准备了四根细直木条AB 、BC ,CD 、DE ,做成折线ABCDE ,如图1,且在折点B 、C 、D 处均可自由转出.(1)如图2,小明将折线调节成50,75,25B C D ∠=︒∠=︒∠=︒,判别AB 是否平行于ED ,并说明理由;(2)如图3,若25C D ∠=∠=︒,调整线段AB 、BC 使得//AB CD ,求出此时B 的度数,要求画出图形,并写出计算过程.(3)若85,25,//C D AB DE ∠=︒∠=︒,求出此时B 的度数,要求画出图形,直接写出度数,不要求计算过程.参考答案:1.∥2+∥3﹣∥1=180°【解析】【分析】根据平行线的性质和平角定义求解即可.【详解】解:∥AB∥EF,EF∥CD,∥∥2+∥BOE=180°,∥3+∥COF=180°,∥∥2+∥3+∥BOE+∥COF=360°,∥∥BOE+∥COF+∥1=180°,∥∥BOE+∥COF=180°﹣∥1,∥∥2+∥3+(180°﹣∥1)=360°,即∥2+∥3﹣∥1=180°.故答案为:∥2+∥3﹣∥1=180°.【点睛】本题考查平行线的性质、平角定义,熟练掌握平行线的性质是解答的关键.2.57°【解析】【分析】根据三角形内角和180°以及平行线的性质:1、如果两直线平行,那么它们的同位角相等;2、如果两直线平行,那么它们的同旁内角互补;3、如果两直线平行,那么它们的内错角相等,据此计算即可.【详解】解:设AE、CD交于点F,∥∥E=37°,∥C=20°,∥∥CFE=180°-37°-20°=123°,∥∥AFD=123°,∥AB∥CD,∥∥AFD+∥EAB=180°,∥∥EAB=180°-123°=57°,故答案为:57°.【点睛】本题主要考查三角形内角和定理以及平行线的性质,熟知平行的性质是解题的关键.3.40︒【解析】【分析】∠,延长ED交BC于M,根据两直线平行,内错角相等证明∥BMD=∥ABC,再求解CMD再利用三角形的外角的性质可得答案.【详解】解:延长ED交BC于M,∥//AB DE,∥∥BMD=∥ABC=80°,∥180100∠=︒-∠=︒;CMD BMD又∥∥CDE=∥CMD+∥C,∥14010040∠=∠-∠=︒-︒=︒.BCD CDE CMD故答案是:40°【点睛】本题考查了平行线的性质.三角形的外角的性质,邻补角的定义,掌握以上知识是解题的关键.4.30【解析】【分析】要求∥P的度数,只需根据平行线的性质,求得其所在的三角形的一个外角,根据三角形的外角的性质进行求解.【详解】解:根据平行线的性质,得∥A的同位角是70°,再根据三角形的外角的性质,得∥P=70°−40°=30°.故答案为30.【点睛】本题考查了平行线的性质以及三角形的一个外角等于和它不相邻的两个内角和,可以牢记此题中的结论:∥P=∥A−∥B.5.180°【解析】【详解】解:∥AB∥CD∥∥1=∥EFD∥∥2+∥EFC=∥3∥EFD=180°-∥EFC∥∥1+∥3—∥2=180°故答案为:180°6.(1)∥ABE=40°;(2)∥ABE=30°;(3)∥MGN=15°.【解析】【分析】(1)过E作EM∥AB,根据平行线的判定与性质和角平分线的定义解答即可;(2)过E作EM∥AB,过F作FN∥AB,根据平行线的判定与性质,角平分线的定义以及解一元一次方程解答即可;(3)过P作PL∥AB,根据平行线的判定与性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义解答即可.【详解】解:(1)过E作EM∥AB,∥AB∥CD,∥CD∥EM∥AB,∥∥ABE=∥BEM,∥DCE=∥CEM,∥CF平分∥DCE,∥∥DCE=2∥DCF,∥∥DCF=30°,∥∥DCE=60°,∥∥CEM=60°,又∥∥CEB=20°,∥∥BEM=∥CEM﹣∥CEB=40°,∥∥ABE=40°;(2)过E作EM∥AB,过F作FN∥AB,∥∥EBF=2∥ABF,∥设∥ABF=x,∥EBF=2x,则∥ABE=3x,∥CF平分∥DCE,∥设∥DCF=∥ECF=y,则∥DCE=2y,∥AB∥CD,∥EM∥AB∥CD,∥∥DCE=∥CEM=2y,∥BEM=∥ABE=3x,∥∥CEB=∥CEM﹣∥BEM=2y﹣3x,同理∥CFB=y﹣x,∥2∥CFB+(180°﹣∥CEB)=190°,∥2(y﹣x)+180°﹣(2y﹣3x)=190°,∥x=10°,∥∥ABE=3x=30°;(3)过P作PL∥AB,∥GM平分∥DGP,∥设∥DGM=∥PGM=y,则∥DGP=2y,∥PQ平分∥BPG,∥设∥BPQ=∥GPQ=x,则∥BPG=2x,∥PQ∥GN,∥∥PGN=∥GPQ=x,∥AB∥CD,∥PL∥AB∥CD,∥∥GPL=∥DGP=2y,∥BPL=∥ABP=30°,∥∥BPL=∥GPL﹣∥BPG,∥30°=2y﹣2x,∥y﹣x=15°,∥∥MGN=∥PGM﹣∥PGN=y﹣x,∥∥MGN=15°.【点睛】此题考查平行线的判定与性质,角平分线的定义,三角形的内角和定理,解题关键在于作辅助线和掌握判定定理.7.(1)∥APD=80°;(2)∥P AB+∥CDP-∥APD=180°;(3)∥AND=45°.【解析】【分析】(1)首先过点P作PQ∥AB,则易得AB∥PQ∥CD,然后由两直线平行,同旁内角互补以及内错角相等,即可求解;(2)作PQ∥AB,易得AB∥PQ∥CD,根据平行线的性质,即可证得∥P AB+∥CDP-∥APD=180°;(3)先证明∥NOD=12∥P AB,∥ODN=12∥PDC,利用(2)的结论即可求解.【详解】解:(1)∥∥A=50°,∥D=150°,过点P作PQ∥AB,∥∥A=∥APQ=50°,∥AB∥CD,∥PQ∥CD,∥∥D+∥DPQ=180°,则∥DPQ=180°-150°=30°,∥∥APD=∥APQ+∥DPQ=50°+30°=80°;(2)∥P AB+∥CDP-∥APD=180°,如图,作PQ∥AB,∥∥P AB=∥APQ,∥AB∥CD,∥PQ∥CD,∥∥CDP+∥DPQ=180°,即∥DPQ=180°-∥CDP,∥∥APD=∥APQ-∥DPQ,∥∥APD=∥P AB-(180°-∥CDP)=∥P AB+∥CDP-180°;∥∥P AB+∥CDP-∥APD=180°;(3)设PD交AN于O,如图,∥AP∥PD,∥∥APO=90°,由题知∥P AN+12∥P AB=∥APD,即∥P AN+12∥P AB=90°,又∥∥POA+∥P AN=180°-∥APO=90°,∥∥POA=12∥P AB,∥∥POA=∥NOD,∥∥NOD=12∥P AB,∥DN平分∥PDC,∥∥ODN=12∥PDC,∥∥AND=180°-∥NOD-∥ODN=180°-12(∥P AB+∥PDC),由(2)得∥P AB+∥CDP-∥APD=180°,∥∥P AB+∥PDC=180°+∥APD,∥∥AND=180°-12(∥P AB+∥PDC)=180°-12(180°+∥APD)=180°-12(180°+90°)=45°,即∥AND=45°.【点睛】本题考查了平行线的性质以及角平分线的定义.注意掌握辅助线的作法,注意掌握数形结合思想的应用.8.(1)证明见解析;(2)证明见解析;(3)120°.【解析】【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∥MCA=∥DAC,∥PBA=∥DAB,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∥、∥CAB+∥ACD=180°,由邻补角定义得到∥ECM+∥ECN=180°,再等量代换即可得解;(3)由平行线的性质得到,∥F AB=120°﹣∥GCA,再由角平分线的定义及平行线的性质得到∥GCA﹣∥ABF=60°,最后根据三角形的内角和是180°即可求解.【详解】解:(1)证明:如图1,过点A作AD∥MN,∥MN∥PQ,AD∥MN,∥AD∥MN∥PQ,∥∥MCA=∥DAC,∥PBA=∥DAB,∥∥CAB=∥DAC+∥DAB=∥MCA+∥PBA,即:∥CAB=∥MCA+∥PBA;(2)如图2,∥CD∥AB,∥∥CAB+∥ACD=180°,∥∥ECM+∥ECN=180°,∥∥ECN=∥CAB∥∥ECM=∥ACD,即∥MCA+∥ACE=∥DCE+∥ACE,∥∥MCA=∥DCE;(3)∥AF∥CG,∥∥GCA+∥F AC=180°,∥∥CAB=60°即∥GCA+∥CAB+∥F AB=180°,∥∥F AB=180°﹣60°﹣∥GCA=120°﹣∥GCA,由(1)可知,∥CAB=∥MCA+∥ABP,∥BF平分∥ABP,CG平分∥ACN,∥∥ACN=2∥GCA,∥ABP=2∥ABF,又∥∥MCA=180°﹣∥ACN,∥∥CAB=180°﹣2∥GCA+2∥ABF=60°,∥∥GCA﹣∥ABF=60°,∥∥AFB+∥ABF+∥F AB=180°,∥∥AFB=180°﹣∥F AB﹣∥FBA=180°﹣(120°﹣∥GCA)﹣∥ABF=180°﹣120°+∥GCA﹣∥ABF=120°.【点睛】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.9.(1)360°;(2)540°;(3)720°;(4)(n-1)180 °【解析】【分析】(1)过点A2作A2B∥l1,根据平行线的性质,即可求解;(2)过点A2作A2B∥l1,过点A3作A3C∥l1,根据平行线的性质,即可求解;(3)根据平行线的性质,即可求解;(4)根据平行线的性质,即可求解.【详解】解:(1)过点A2作A2B∥l1,∥l1∥l2,∥A2B∥l1∥l2,∥∥A1+∥A1A2B=180°,∥A3+∥A3A2B=180°,∥∥A1+∥A1A2A3+∥A3=∥A1+∥A1A2B+∥A3+∥A3A2B=180°+180°=360°,故答案是:360°;(2)过点A2作A2B∥l1,过点A3作A3C∥l1,∥l1∥l2,∥A3C∥A2B∥l1∥l2,∥∥A1+∥A1A2B=180°,∥A4+∥A4A3B=180°,∥BA2A3+∥CA3A2=180°,∥∥A1+∥A1A2A3+∥A2A3A4+∥A4=∥A1+∥A1A2B+∥A4+∥A4A3B+∥BA2A3+∥CA3A2=180°+180°+180°=540°,故答案是:540°;(3)同理可得:∥A1+∥A2+∥A3+∥A4+∥A5=180°+180°+180°+180°=720°,故答案是:720°;(4)同理可得:∥A1+∥A2+…+∥An=(n-1)180 °,故答案是:(n-1)180 °.【点睛】本题主要考查平行线的性质,添加辅助线,构造平行线,是解题的关键.10.(1)∥BME=∥MEN﹣∥END;∥BMF=∥MFN+∥FND;(2)120°;(3)不变,30°【解析】【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∥BME+∥END)+∥BMF-∥FND=180°,可求解∥BMF=60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∥FEQ=12∥BME,进而可求解.【详解】解:(1)过E作EH∥AB,如图1,∥∥BME=∥MEH,∥AB∥CD,∥HE∥CD,∥∥END=∥HEN,∥∥MEN=∥MEH+∥HEN=∥BME+∥END,即∥BME=∥MEN﹣∥END.如图2,过F作FH∥AB,∥∥BMF=∥MFK,∥AB∥CD,∥FH∥CD,∥∥FND=∥KFN,∥∥MFN=∥MFK﹣∥KFN=∥BMF﹣∥FND,即:∥BMF=∥MFN+∥FND.故答案为∥BME=∥MEN﹣∥END;∥BMF=∥MFN+∥FND.(2)由(1)得∥BME =∥MEN ﹣∥END ;∥BMF =∥MFN +∥FND .∥NE 平分∥FND ,MB 平分∥FME ,∥∥FME =∥BME +∥BMF ,∥FND =∥FNE +∥END ,∥2∥MEN +∥MFN =180°,∥2(∥BME +∥END )+∥BMF ﹣∥FND =180°,∥2∥BME +2∥END +∥BMF ﹣∥FND =180°,即2∥BMF +∥FND +∥BMF ﹣∥FND =180°,解得∥BMF =60°,∥∥FME =2∥BMF =120°;(3)∥FEQ 的大小没发生变化,∥FEQ =30°.由(1)知:∥MEN =∥BME +∥END ,∥EF 平分∥MEN ,NP 平分∥END ,∥∥FEN =12∥MEN =12(∥BME +∥END ),∥ENP =12∥END , ∥EQ ∥NP ,∥∥NEQ =∥ENP ,∥∥FEQ =∥FEN ﹣∥NEQ =12(∥BME +∥END )﹣12∥END =12∥BME ,∥∥BME =60°,∥∥FEQ =12×60°=30°. 【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键. 11.(1)360PAF PBN APB ∠+∠+∠=°;(2)∥CPD αβ∠=∠+∠,理由见解析;∥图见解析,CPD βα∠=∠-∠或CPD αβ∠=∠-∠【解析】【分析】(1)作PQ ∥EF ,由平行线的性质,即可得到答案;(2)∥过P 作//PE AD 交CD 于E ,由平行线的性质,得到DPE α∠=∠,CPE β∠=∠,即可得到答案;∥根据题意,可对点P 进行分类讨论:当点P 在BA 延长线时;当P 在BO 之间时;与∥同理,利用平行线的性质,即可求出答案.【详解】解:(1)作PQ ∥EF ,如图:∥//EF MN ,∥////EF MN PQ ,∥180PAF APQ ∠+∠=°,180PBN BPQ ∠+∠=°,∥APB APQ BPQ ∠=∠+∠∥360PAF PBN APB ∠+∠+∠=°;(2)∥CPD αβ∠=∠+∠;理由如下:如图,过P 作//PE AD 交CD 于E ,∥//AD BC ,∥////AD PE BC ,∥DPE α∠=∠,CPE β∠=∠,∥CPD DPE CPE αβ∠=∠+∠=∠+∠;∥当点P 在BA 延长线时,如备用图1:∥PE ∥AD ∥BC ,∴∴EPC=β,∥EPD=α,∥CPDβα∠=∠-∠;当P在BO之间时,如备用图2:∥PE∥AD∥BC,∥∥EPD=α,∥CPE=β,∥CPDαβ∠=∠-∠.【点睛】本题考查了平行线的性质,解题的关键是熟练掌握两直线平行同旁内角互补,两直线平行内错角相等,从而得到角的关系.12.见解析【解析】【分析】过点E作EF∥CD,根据平行线的性质即可得出∥B=∥BOD,根据平行线的性质即可得出∥BOD=∥BEF、∥D=∥DEF,结合角之间的关系即可得出结论.【详解】证明:过点E作EF∥CD,如图∥AB∥CD,∥∥B=∥BOD,∥EF∥CD(辅助线),∥∥BOD=∥BEF(两直线平行,同位角相等);∥D=∥DEF(两直线平行,内错角相等);∥∥BEF=∥BED+∥DEF=∥BED+∥D(等量代换),∥∥BOD=∥E+∥D(等量代换),即∥B=∥E+∥D.【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出相等或互补的角.13.(1)AB∥DE,理由见解析;(2)25°或155°,画图见解析;(3)60°或120°或70°或110°【解析】【分析】(1)过点C作CF∥AB,利用平行线的判定和性质解答即可;(2)分别画图3和图4,根据平行线的性质可计算∥B的度数;(3)分别画图,根据平行线的性质计算出∥B的度数.【详解】解:(1)AB∥DE,理由是:如下图,过点C作CF∥AB,∥∥B=∥BCF=50°,∥∥BCD=75°,∥∥DCF=25°,∥∥D=25°,∥∥D=∥DCF=25°,∥CF∥DE,∥AB∥DE;(2)如下图,∥AB∥CD,∥∥B=∥BCD=25°;如图4:∥AB∥CD,∥∥B+∥BCD=180°,∥∥ABC=180°-25°=155°;(3)由(1)得:∥B=85°-25°=60°;如图5,过C作CF∥AB,则AB∥CF∥CD,∥∥FCD=∥D=25°,∥∥BCD=85°,∥∥BCF=85°-25°=60°,∥AB∥CF,∥∥B+∥BCF=180°,∥∥B=120°;如图6,∥∥C=85°,∥D=25°,∥∥CFD=180°-85°-25°=70°,∥AB∥DE,∥∥B=∥CFD=70°,如图7,同理得:∥B=25°+85°=110°,综上所述,∥B的度数为60°或120°或70°或110°.【点睛】本题主要考查了平行线的性质和三角形内角和的运用,解决问题的关键是作辅助线构造同位角以及内错角,依据平行线的性质及三角形外角性质进行推导计算.。
人教中考数学综合题专题复习【平行四边形】专题解析附详细答案
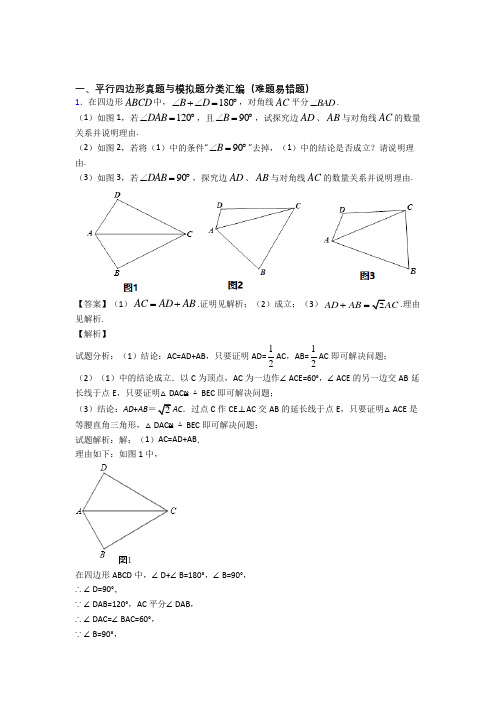
一、平行四边形真题与模拟题分类汇编(难题易错题)1.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB AC +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB =2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD 中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC 平分∠DAB ,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°.∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.在Rt△ACE中,∠CAB=45°,∴AE=245ACACcos︒=∴2AD AB AC+=.2.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)3【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB223BD AD-,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF22AB AF+3.3.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).【答案】(1)作图参见解析;(2)作图参见解析.【解析】试题分析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN即可;(2)根据勾股定理画出图形即可.试题解析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN,如图1所示;(2)等腰直角三角形MON面积是5,因此正方形面积是20,如图2所示;于是根据勾股定理画出图3:考点:1.作图﹣应用与设计作图;2.勾股定理.4.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222106DF CF-=-8.∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH的值为8;迁移拓展:如图,由题意得:A(0,8),B(6,0),C(﹣4,0)∴AB2268+10,BC=10.∴AB=BC,(1)由结论得:P1D1+P1E1=OA=8∵P1D1=1=2,∴P1E1=6 即点P1的纵坐标为6又点P1在直线l2上,∴y=2x+8=6,∴x=﹣1,即点P1的坐标为(﹣1,6);(2)由结论得:P2E2﹣P2D2=OA=8∵P2D2=2,∴P2E2=10 即点P1的纵坐标为10又点P1在直线l2上,∴y=2x+8=10,∴x=1,即点P1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.5.(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在∠的度数为______.点C'处,若42ADB=∠,则DBE(2)小明手中有一张矩形纸片ABCD ,4AB =,9AD =.(画一画)如图2,点E 在这张矩形纸片的边AD 上,将纸片折叠,使AB 落在CE 所在直线上,折痕设为MN (点M ,N 分别在边AD ,BC 上),利用直尺和圆规画出折痕MN (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);(算一算)如图3,点F 在这张矩形纸片的边BC 上,将纸片折叠,使FB 落在射线FD 上,折痕为GF ,点,A B 分别落在点A ',B '处,若73AG =,求B D '的长.【答案】(1)21;(2)画一画;见解析;算一算:3B D '=【解析】【分析】(1)利用平行线的性质以及翻折不变性即可解决问题;(2)【画一画】,如图2中,延长BA 交CE 的延长线由G ,作∠BGC 的角平分线交AD 于M ,交BC 于N ,直线MN 即为所求;【算一算】首先求出GD=9-72033=,由矩形的性质得出AD ∥BC ,BC=AD=9,由平行线的性质得出∠DGF=∠BFG ,由翻折不变性可知,∠BFG=∠DFG ,证出∠DFG=∠DGF ,由等腰三角形的判定定理证出DF=DG=203,再由勾股定理求出CF ,可得BF ,再利用翻折不变性,可知FB′=FB ,由此即可解决问题.【详解】 (1)如图1所示:∵四边形ABCD 是矩形,∴AD∥BC,∴∠ADB=∠DBC=42°,由翻折的性质可知,∠DBE=∠EBC=12∠DBC=21°,故答案为21.(2)【画一画】如图所示:【算一算】如3所示:∵AG=73,AD=9,∴GD=9-72033=,∵四边形ABCD是矩形,∴AD∥BC,BC=AD=9,∴∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,∴∠DFG=∠DGF,∴DF=DG=203,∵CD=AB=4,∠C=90°,∴在Rt△CDF中,由勾股定理得:22222016433 DF CD⎛⎫-=-=⎪⎝⎭,∴BF=BC-CF=9161133-=,由翻折不变性可知,FB=FB′=11 3,∴B′D=DF-FB′=2011333-=.【点睛】四边形综合题,考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题.6.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.7.如图,在正方形ABCD中,点E在CD上,AF⊥AE交CB的延长线于F.求证:AE=AF.【答案】见解析【解析】【分析】根据同角的余角相等证得∠BAF=∠DAE,再利用正方形的性质可得AB=AD,∠ABF=∠ADE=90°,根据ASA判定△ABF≌△ADE,根据全等三角形的性质即可证得AF=AE.【详解】∵AF⊥AE,∴∠BAF+∠BAE=90°,又∵∠DAE+∠BAE=90°,∴∠BAF=∠DAE,∵四边形ABCD是正方形,∴AB=AD,∠ABF=∠ADE=90°,在△ABF和△ADE中,,∴△ABF≌△ADE(ASA),∴AF=AE.【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质等知识点,证明△ABF≌△ADE是解决本题的关键.8.已知点O是△ABC内任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作▱OBFC,连接OF与BC交于点H,再连接EF.(1)如图1,若△ABC为等边三角形,求证:①EF⊥BC;②EF=BC;(2)如图2,若△ABC为等腰直角三角形(BC为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图3,若△ABC是等腰三角形,且AB=AC=kBC,请你直接写出EF与BC之间的数量关系.【答案】(1)见解析;(2)EF⊥BC仍然成立;(3)EF=BC【解析】试题分析:(1)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等边三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(2)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰直角三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(3)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰三角形的性质和AB=AC=kBC得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可.试题解析:(1)连接AH,如图1,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等边三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2,∴AH==BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(2)EF⊥BC仍然成立,EF=BC,如图2,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等腰三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2=(BH)2﹣BH2=BH2,∴AH=BH=BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(3)如图3,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC 是等腰三角形, ∴AB=kBC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2﹣BH 2=(kBC )2﹣(BC )2=(k 2-)BC 2,∴AH=BH=BC ,∵OA=AE ,OH=HF , ∴AH 是△OEF 的中位线, ∴AH=EF ,AH ∥EF , ∴EF ⊥BC ,BC=EF ,∴EF=BC .考点:四边形综合题.9.已知ABC ,以AC 为边在ABC 外作等腰ACD ,其中AC AD =. (1)如图①,若AB AE =,60DAC EAB ∠=∠=︒,求BFC ∠的度数. (2)如图②,ABC α∠=,ACD β∠=,4BC =,6BD =.①若30α=︒,60β=︒,AB 的长为______.②若改变,αβ的大小,但90αβ+=︒,ABC 的面积是否变化?若不变,求出其值;若变化,说明变化的规律.【答案】(1)120°;(2)55【解析】试题分析:(1)根据SAS ,可首先证明△AEC ≌△ABD ,再利用全等三角形的性质,可得对应角相等,根据三角形的外角的定理,可求出∠BFC 的度数;(2)①如图2,在△ABC 外作等边△BAE ,连接CE ,利用旋转法证明△EAC ≌△BAD ,可证∠EBC=90°,EC=BD=6,因为BC=4,在Rt △BCE 中,由勾股定理求BE 即可;②过点B 作BE ∥AH ,并在BE 上取BE=2AH ,连接EA ,EC .并取BE 的中点K ,连接AK ,仿照(2)利用旋转法证明△EAC ≌△BAD ,求得EC=DB ,利用勾股定理即可得出结论. 试题解析:解:(1)∵AE=AB,AD=AC,∵∠EAB=∠DAC=60°,∴∠EAC=∠EAB+∠BAC,∠DAB=∠DAC+∠BAC,∴∠EAC=∠DAB,在△AEC和△ABD中{AE ABEAC BAD AC AD=∠=∠=∴△AEC≌△ABD(SAS),∴∠AEC=∠ABD,∵∠BFC=∠BEF+∠EBF=∠AEB+∠ABE,∴∠BFC=∠AEB+∠ABE=120°,故答案为120°;(2)①如图2,以AB为边在△ABC外作正三角形ABE,连接CE.由(1)可知△EAC≌△BAD.∴EC=BD.∴EC=BD=6,∵∠BAE=60°,∠ABC=30°,∴∠EBC=90°.在RT△EBC中,EC=6,BC=4,∴22EC BC-2264-∴5②若改变α,β的大小,但α+β=90°,△ABC的面积不变化,以下证明:如图2,作AH⊥BC交BC于H,过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK.∵AH⊥BC于H,∴∠AHC=90°.∵BE∥AH,∴∠EBC=90°.∵∠EBC=90°,BE=2AH,∴EC2=EB2+BC2=4AH2+BC2.∵K为BE的中点,BE=2AH,∴BK=AH.∵BK∥AH,∴四边形AKBH为平行四边形.又∵∠EBC=90°,∴四边形AKBH为矩形.∠ABE=∠ACD,∴∠AKB=90°.∴AK是BE的垂直平分线.∴AB=AE.∵AB=AE,AC=AD,∠ABE=∠ACD,∴∠EAB=∠DAC,∴∠EAB+∠EAD=∠DAC+∠EAD,即∠EAC=∠BAD,在△EAC与△BAD中{AB AEEAC BAD AC AD=∠=∠=∴△EAC≌△BAD.∴EC=BD=6.在RT△BCE中,BE=22EC BC-=25,∴AH=12BE=5,∴S△ABC=12BC•AH=25考点:全等三角形的判定与性质;等腰三角形的性质10.(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.小明应用这个结论进行了下列探索活动和问题解决.问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及PQ最小时的值.(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为,当PQ最小时= _____ __;(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时的值;问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图4,若为上任意一点,以,为边作□.试求对角线长的最小值和PQ最小时的值.(2)若为上任意一点,延长到,使,再以,为边作□.请直接写出对角线长的最小值和PQ最小时的值.【答案】问题1:(1)3,;(2)PQ=,=.问题2:(1)=4,.(2)PQ的最小值为..【解析】试题分析:问题1:(1)首先根据条件可证四边形PCBQ是矩形,然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC,从而可求的值.(2)由题可知:当QP⊥AC 时,PQ最小.过点C作CD⊥AB于点D.此时四边形CDPQ为矩形,PQ=CD,在Rt△ABC中,∠C=90°,AC=4,BC=3,利用面积可求出CD=,然后可求出AD=,由AE=nPA可得PE=,而PE=CQ=PD=AD-AP=,所以AP=.所以=.问题2:(1)设对角线与相交于点.Rt≌Rt.所以AD=HC,QH=AP.由题可知:当QP⊥AB时,PQ最小,此时=CH=4,根据条件可证四边形BPQH为矩形,从而QH=BP=AP.所以.(2)根据题意画出图形,当AB 时,的长最小,PQ的最小值为..试题解析:问题1:(1)3,;(2)过点C作CD⊥AB于点D.由题意可知当PQ⊥AB时,PQ最短.所以此时四边形CDPQ为矩形.PQ=CD,DP=CQ=PE.因为∠BCA=90°,AC=4,BC=3,所以AB=5.所以CD=.所以PQ=.在Rt△ACD中AC=4,CD=,所以AD=.因为AE=nPA,所以PE==CQ=PD=AD-AP=.所以AP=.所以=.问题2:(1)如图2,设对角线与相交于点.所以G是DC的中点,作QH BC,交BC的延长线于H,因为AD//BC,所以.所以.又,所以Rt≌Rt.所以AD=HC,QH=AP.由图知,当AB时,的长最小,即=CH=4.易得四边形BPQH为矩形,所以QH=BP=AP.所以.(若学生有能力从梯形中位线角度考虑,若正确即可评分.但讲评时不作要求)(2)PQ的最小值为..考点:1.直角三角形的性质;2.全等三角形的判定与性质;3.平行四边形的性质;4矩形的判定与性质.。
初中数学复习几何模型专题讲解29--- 平行线中和角平分线有关的图形

初中数学复习几何模型专题讲解专题29 平行线中和角平分线有关的图形一、单选题1.在钝角△ABC中,延长BA到D,AE是∠DAC的平分线,AE//BC,则与∠B相等的角有()A.1个B.2个C.3个D.4个【答案】C【分析】依据角平分线的性质和平行线的性质即可求解.【详解】解析:依据角平分线的性质和平行线的性质,可知∠B =∠DAE=∠CAE=∠C故选C.【点睛】此题主要考查角平分线的性质与平行线的性质,解题的关键是熟知角平分线的性质.2.如图,点A、C为∠FBE边上的两点,AD∥BE,AC平分∠BAD,若∠F AD=45°,则∠ACE=()A.45°B.67.5°C.112.5°D.135°【答案】C【分析】先根据平角的定义求出∠BAD,根据角平分线的性质求出∠DAC,再利用平行线的性质,得到∠ACB的度数.最后通过平角求出∠ACE.【详解】解:∵∠F AD=45°,∴∠BAD=180°-45°=135°.∵AC平分∠BAD,∴∠DAC=12BAD∠=67.5°.∵AD∥BE,∴∠ACB=∠DAC=67.5°.∴∠ACE=180°-67.5°=112.5°.故选:C.【点睛】本题考查平行的性质和角平分线的性质,解题关键是运用题目中的条件去求解角的度数,能够从角平分线和平行这两个条件想到图中存在等腰三角形.3.如图,已知BM平分∠ABC,且BM//AD,若∠ABC=70°,则∠A的度数是()A.30°B.35°C.40°D.70°【答案】B【分析】先根据角平分线的性质,求出∠ABC的度数,再由平行线的性质得到∠A的度数.【详解】解:∵BM平分∠ABC,∴∠MBA=12∠ABC=35°.∵BM∥AD,∴∠A=∠MBA=35°.故选:B.【点睛】本题考查的是角平分线的性质,平行线的性质,掌握以上知识是解题的关键.二、解答题4.如图所示,直线AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF、∠DFE 的平分线相交于点K.(1)求∠EKF的度数;(2)如图(2)所示,作∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图(2)中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,……,请直接写出∠K4的度数.【答案】(1)∠EKF=90°;(2)∠K=2∠K1,证明见解析;(3)∠K4=5.625°.【分析】(1)过K作KG∥AB,交EF于G,根据平行于同一条直线的两直线平行可得AB∥KG∥CD,从而得出∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,然后根据角平分线的定义即可求出∠BEK+∠DFK=90°,从而得出结论;(2)根据角平分线的定义可得∠BEK1=∠KEK1,∠KFK1=∠DFK1,结合(1)的结论可得∠BEK1+∠DFK1=45°,从而求出∠K1,即可得出结论;(3)根据(2)中的规律即可得出结论.【详解】(1)如图(1),过K作KG∥AB,交EF于G,∵AB∥CD,∴AB∥KG∥CD,∴∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,∵EK、FK分别为∠BEF与∠EFD的平分线,∴∠BEK=∠FEK,∠EFK=∠DFK,∴2(∠BEK+∠DFK)=180°,∴∠BEK+∠DFK=90°,则∠EKF=∠EKG+∠GKF=90°;(2)∠K=2∠K1,理由为:∵∠BEK、∠DFK的平分线相交于点K1,∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,∴∠BEK+∠KFD=90°,即∠BEK1+∠DFK1=45°,同(1)得∠K1=∠BEK1+∠DFK1=45°,则∠K=2∠K1;(3)如图(3),根据(2)中的规律和推导方法可得:∠K2=12∠K1=22.5°,∠K3=12∠K2=11.25°,∠K4=12∠K3=5.625°.【点睛】此题考查的是平行线的性质及判定,掌握平行线的各个性质定理是解题关键.5.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是;②∵AM∥BN,∴∠ACB=∠;(2)求∠CBD的度数;(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是.【答案】(1)①116,︒②CBN;(2)58︒;(3)不变,:2:1APB ADB∠∠=,理由见解析;(4)29.︒【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;(2)由角平分线的定义可以证明∠CBD=12∠ABN,即可求出结果;(3)不变,∠APB:∠ADB=2:1,证∠APB=∠PBN,∠PBN=2∠DBN,即可推出结论;(4)可先证明∠ABC=∠DBN,由(1)∠ABN=116°,可推出∠CBD=58°,所以∠ABC+∠DBN=58°,则可求出∠ABC的度数.【详解】解:(1)①∵AM//BN,∠A=64°,∴∠ABN=180°﹣∠A=116°,故答案为:116°;②∵AM//BN,∴∠ACB=∠CBN,故答案为:CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣64°=116°,∴∠ABP+∠PBN=116°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=116°,∴∠CBD=∠CBP+∠DBP=58°;(3)不变,∠APB:∠ADB=2:1,∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD =∠CBD+∠DBN∴∠ABC =∠DBN ,由(1)∠ABN =116°,∴∠CBD =58°,∴∠ABC+∠DBN =58°,∴∠ABC =29°,故答案为:29°.【点睛】本题考查了角平分线的定义,平行线的性质等,解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等.6.如图1,在平面直角坐标系中,(,0),(,2)A a C b ,且满足2(2)20a b ++-=,过C 作CB x ⊥轴于B .(1)求ABC ∆的面积.(2)若过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,求AED ∠的度数.(3)在y 轴上存在点P 使得ABC ∆和ACP ∆的面积相等,请直接写出P 点坐标.【答案】(1)4;(2)45︒;(2)(0,3)P 或(0,1)-.【分析】(1)根据非负数的性质易得2a =-,2b =,然后根据三角形面积公式计算; (2)过E 作//EF AC ,根据平行线性质得////BD AC EF ,且1312CAB ∠=∠=∠,1422ODB ∠=∠=∠,所以112()2AED CAB ODB ∠=∠+∠=∠+∠;然后把90CAB ODB ∠+∠=︒ 代入计算即可;(3)分类讨论:设(0,)P t ,当P 在y 轴正半轴上时,过P 作//MN x 轴,//AN y 轴,//BM y 轴,利用4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形可得到关于t 的方程,再解方程求出t ; 当P 在y 轴负半轴上时,运用同样方法可计算出t .【详解】解:(1)2(2)20a b ++-=,20a ∴+=,20b -=,2a ∴=-,2b =,CB AB ⊥(2,0)A ∴-,(2,0)B ,(2,2)C ,ABC ∆∴的面积12442=⨯⨯=; (2)解://CB y 轴,//BD AC ,5CAB ∴∠=∠,又∵590ODB ∠+∠=︒,∴90CAB ODB ∠+∠=︒,过E 作//EF AC ,如图①,//BD AC , ////BD AC EF ∴, 31∴∠=∠,42∠=∠ AE ∵,DE 分别平分CAB ∠,ODB ∠,即:132CAB ∠=∠,142ODB ∠=∠, 112()452AED CAB ODB ∴∠=∠+∠=∠+∠=︒;(3)(0,1)P -或(0,3). 解:①当P 在y 轴正半轴上时,如图②,设(0,)P t , 过P 作//MN x 轴,//AN y 轴,//BM y 轴,4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形, ∴4(2)(2)42t t t t -+---=,解得3t =, ②当P 在y 轴负半轴上时,如图③4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形 ∴4(2)(2)42t t t t -+-+--=,解得1t =-,综上所述:(0,3)P 或(0,1)-.【点睛】本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.构造矩形求三角形面积是解题关键.7.阅读下面材料:彤彤遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED . 求证:∠BED =∠B +∠D .彤彤是这样做的:过点E 作EF //AB ,则有∠BEF =∠B .∵AB //CD ,∴EF//CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D.即∠BED=∠B+∠D.请你参考彤彤思考问题的方法,解决问题:如图乙.已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.(1)如图1,当点B在点A的左侧时,若∠ABC=60°,∠ADC=70°,求∠BED的度数;(2)如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,直接写出∠BED的度数(用含有α,β的式子表示).【答案】(1)65°;(2)11 18022αβ︒-+【分析】(1)如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,∠ADC=70°,参考彤彤思考问题的方法即可求∠BED的度数;(2)如图2,过点E作EF∥AB,当点B在点A的右侧时,∠ABC=α,∠ADC=β,参考彤彤思考问题的方法即可求出∠BED的度数.【详解】(1)如图1,过点E作EF∥AB,有∠BEF=∠EBA.∵AB∥CD,∴EF∥CD.∴∠FED=∠EDC.∴∠BEF+∠FED=∠EBA+∠EDC.即∠BED=∠EBA+∠EDC,∵BE平分∠ABC,DE平分∠ADC,∴∠EBA=12∠ABC=30°,∠EDC=12∠ADC=35°,∴∠BED=∠EBA+∠EDC=65°.答:∠BED的度数为65°;(2)如图2,过点E作EF∥AB,有∠BEF+∠EBA=180°.∴∠BEF=180°﹣∠EBA,∵AB∥CD,∴EF∥CD,∴∠FED=∠EDC.∴∠BEF+∠FED=180°﹣∠EBA+∠EDC.即∠BED=180°﹣∠EBA+∠EDC,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β, ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣12α +12β. 答:∠BED 的度数为180°﹣12α +12β. 【点睛】本题考查了平行线的判定与性质以及角平分线的定义,解决本题的关键是熟练掌握平行线的判定与性质.8.如图,已知//AM BN ,60A ∠=︒,点P 是射线AM 上一动点(与点A 不重合),BC ,BD 分别平分ABP ∠和PBN ∠,分别交射线AM 于点C ,D .(1)求CBD ∠的度数(2)当点P 运动时,:APB ADB ∠∠的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点P 运动到某处时,ACB ABD =∠∠,求此时ABC ∠的度数.【答案】(1)60°;(2)不变,∠APB :∠ADB=2:1;(3)30°【分析】(1)根据角平分线的定义只要证明∠CBD=12∠ABN 即可; (2)不变.可以证明∠APB=∠PBN ,∠ADB=∠DBN=12∠PBN . (3)想办法证明∠ABC=∠CBP=∠DBP=∠DBN 即可解决问题;【详解】解:(1)∵AM∥BN,∴∠ABN=180°-∠A=120°,又∵BC,BD分别平分∠ABP和∠PBN,∴∠CBD=∠CBP+∠DBP=12(∠ABP+∠PBN)=12∠ABN=60°,(2)不变.理由如下:∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,又∵BD平分∠PBN,∴∠ADB=∠DBN=12∠PBN=12∠APB,∴∠APB:∠ADB=2:1.(3)∵AM∥BN,∴∠ACB=∠CBN,又∵∠ACB=∠ABD,∴∠CBN=∠ABD,∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,∴∠ABC=∠CBP=∠DBP=∠DBN,∴∠ABC=14∠ABN=30°,【点睛】本题考查平行线的性质、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9.如图,已知AB∥CD,BE平分∠ABC,交CD于点D,∠CDE=160°,求∠C的度数【答案】140°【分析】先根据邻补角的定义求出∠CDB的度数,再根据平行线的性质及角平分线的定义得出∠ADB及∠ABC的度数,由平行线的性质可得出∠C的度数.【详解】解:∵∠CDE=160°,∴∠CDB=180°-∠CDE=180°-160°=20°,∵AB∥CD,∴∠ABD=∠CDB=20°,∵BE平分∠ABC,∴∠ABC=2∠ABD=2×20°=40°,∴∠C=180°-∠ABC=180°-40°=140°.【点睛】本题考查的是平行线的性质、角平分线的定义及邻补角的性质,熟知平行线的性质是解答此题的关键.10.如图,已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,求证:∠1=∠E.下面是部分推理过程,请你填空或填写理由证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90∘(),∴AD∥EG(),∴∠2=______,( )∠3=______(两直线平行,同位角相等) .又∵AD平分∠BAC(),∴∠2=∠3(),∴∠1=∠E()【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,内错角相等;∠E;已知;角平分线的定义;等量代换【分析】根据平行线的性质和判定以及角平分线的定义证明即可.【详解】证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90°(垂直的定义),∴AD//EG(同位角相等,两直线平行),∴∠2=1,(两直线平行,内错角相等)∠3=∠E(两直线平行,同位角相等) .又∵AD平分∠BAC(已知),∴∠2=∠3(角平分线的定义),∴∠1=∠E(等量代换).【点睛】本题主要考查平行线的性质及判定,角平分线的定义,掌握平行线的性质及判定是解题的关键.AB CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,11.已知直线//CM交AB于点H,过点A作AG⊥AC交CM于点G.(1)如图1,点G在CH的延长线上时,若∠GAB =36°,求∠MCD的度数;(2)如图2,点G在CH上时,试说明:2∠MCD+∠GAB=90°.【答案】(1)63°;(2)见解析【分析】(1)依据AG⊥AC,∠GAB=36°,可得∠CAH的度数,依据角平分线的定义以及平行线的性质,即可得到∠MCD的度数;(2)结合(1)得ACD+∠CAH=180°,再依据角平分线的定义,即可得2∠MCD+∠GAB=90°.【详解】(1)∵AG⊥AC,∠GAB=36°,∴∠CAH=90°-36°=54°,∵AB∥CD,∴∠ACD+∠CAH=180°,∴∠ACD=126°,∵CM是∠ACD的平分线,∴∠ACH=∠DCM=63°;(2)∵∠ACH=∠DCM,∴∠ACD=2∠MCD,由(1)得ACD+∠CAH=180°,∵AG⊥AC,∴∠CAG=90°,∴2∠MCD+90°+∠GAB=180°,∴2∠MCD+∠GAB=90°.【点睛】本题主要考查了平行线的性质,垂直的定义,角平分线的定义,利用两直线平行,同旁内角互补是解决问题的关键.12.阅读理解:我们知道“三角形三个内角的和为180°”,在学习平行线的性质之后,可以对这一结论进行推理论证.请阅读下面的推理过程:如图①,过点A作DE//BC∴∠B=∠EAB,∠C=∠DAC又∵∠EAB+∠BAC+∠DAC=180°∴∠B+∠BAC+∠C=180°即:三角形三个内角的和为180°.阅读反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系.方法运用:如图②,已知AB//DE,求∠B+∠BCD+∠D的度数.(提示:过点C作CF//AB)深化拓展:如图③,已知AB//CD,点C在点D的右侧,∠ADC=70°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,且点E在AB与CD两条平行线之间,求∠BED的度数.【答案】方法运用:360°;深度拓展:65°【分析】方法运用:过C作CF∥AB,根据平行线的性质得到∠D=∠FCD,∠B=∠BCF,然后根据已知条件即可得到结论;深化拓展:过点E作EF∥AB,然后根据两直线平行内错角相等,再利用角平分线的定义和等量代换即可求∠BED的度数.【详解】方法运用:解:过点C作CF∥AB∴∠B=∠BCF∵CF∥AB且AB∥DE∴CF∥DE∴∠D=∠DCF∵∠BCD+∠BCF+∠DCF=360°∴∠B+∠BCD+∠D=360°深化拓展:过点E作EF∥AB∴∠BEF=∠ABE又∵BE平分∠ABC,∠ABC=60°∴∠BEF=∠ABE=12∠ABC=30°∵EF∥AB,AB∥CD∴EF∥CD∴∠DEF=∠EDC又∵DE平分∠ADC,∠ADC=70°∴∠DEF=∠EDC=12∠ADC=35°∴∠BED=∠BEF+∠DEF=30°+35°=65°【点睛】本题主要考查平行线的性质和角平分线的定义,能够作出平行线是解题的关键.13.在综合与实践课上,老师让同学们以“三条平行线m,n,l(即始终满足m∥n∥l)和一副直角三角尺ABC,DEF(∠BAC=∠EDF=90°,∠FED=60°,∠DFE=30°,∠ABC=∠ACB=45°)”为主题开展数学活动.操作发现(1)如图1,展翅组把三角尺ABC的边BC放在l上,三角尺DEF的顶点F与顶点B 重合,边EF经过AB,顶点E恰好落在m上,顶点D恰好落在n上,边ED与n相交所成的一个角记为∠1,求∠1的度数;(2)如图2,受到展翅组的启发,高远组把直线m向下平移后使得两个三角尺的两个直角顶点A、D分别落在m和l上,顶点C恰好落在n上,边AC与l相交所成的一个角记为∠2,边DF与m相交所成的一个角记为∠3,请你说明∠2﹣∠3=15°;结论应用(3)老师在点评高远组的探究操作时提出,在(2)的条件下,若点N是直线n上一点,CN恰好平分∠ACB时,∠2与∠3之间存在一个特殊的倍数关系,请你直接写出它们之间的倍数关系,不需要说明理由.【答案】(1)75°;(2)见解析;(3)∠2=3∠3【分析】(1)利用三角板的度数,求出∠DBC的度数,再利用平行线的性质得到∠BDN的度数,由此得到∠1的度数;(2)过B点作BG∥直线m,利用平行线的性质可得到∠3=DBG和∠LAB=∠ABG,再利用等量代换得到∠3+∠LAB=75°,利用余角性质得到∠LAB=90°-∠2,由此证明结论;(3)结论:∠2=3∠3.利用(2)中结论,结合平行线的性质得到∠2和∠3的度数由此证明结论.【详解】(1)∵直线n∥直线l,∴∠DBC=∠BDN,又∵∠DBC=∠ABC﹣∠ABD=45°﹣30°=15°,∴∠BDN=15°,∴∠1=90°﹣15°=75°.(2)如图所示,过B点作BG∥直线m,∵BG∥m,l∥m,∴BG∥l(平行于同一直线的两直线互相平行),∵BG∥m,∴∠3=DBG,又∵BG∥l,∴∠LAB=∠ABG,∴∠3+∠LAB=∠DBA=30°+45°=75°,又∵∠2和∠LAB互为余角,∴∠LAB =90°﹣∠2,∴∠3+90°﹣∠2=75°,∴∠2﹣∠3=15°.(3)结论:∠2=3∠3.理由:在(2)的条件下,∠2﹣∠3=15°,又∵CN 平分∠BCA ,∴∠BCN =∠CAN =22.5°,又∵直线n ∥直线l ,∴∠2=22.5°,∴∠3=7.5°,∴∠2=3∠3.【点睛】考查平行线的性质并结合了三角板中的特殊角度,学生需要作辅助线利用平行线的传递性将特殊的角的关系联系起来,熟悉掌握平行线之间角的关系是解题的关键. 14.如图,AB CD ∥,点E 、F 分别在直线AB 、CD 上,点O 在直线AB 、CD 之间,100EOF ∠=︒.(1)求BEO DFO ∠+∠的值;(2)如图2,直线MN 交BEO ∠、CFO ∠的角平分线分别于点M 、N ,求EMN FNM∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG n OEG ∠=∠,FK 在DFO ∠内,DFK n OFK ∠=∠.直线MN 交FK 、EG 分别于点M 、N ,若50FMN ENM ∠-∠=︒,则n 的值是__________.【答案】(1)260° ;(2)40°;(3)53【分析】(1)如下图,过点O 作OG AB ,可得出AB OG CD ,然后利用平行的性质进行角度转换可得出答案;(2)如图,过点M 作MK AB ,过点N 作NH CD ∥,然后设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=,利用方程思想进行角度推导,可得出答案;(3)如下图,过点O 作AB 的平行线OQ ,同样利用方程思想进行推导转化,可得出n 的值.【详解】(1)证明:过点O 作OG AB∵AB CD ∥∴AB OG CD∴180BEO EOG ∠+∠=︒,180DFO FOG ∠+∠=︒∴360BEO EOG DFO FOG ︒∠+∠+∠+∠=即360BEO EOF DFO ∠+∠+∠=︒∵100EOF ∠=︒∴260BEO DFO ︒∠+∠=(2)解:过点M 作MK AB ,过点N 作NH CD ∥,∵EM 平分BEO ∠,FN 平分CFO ∠设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=∵260BEO DFO ︒∠+∠=∴21802260BEO DFO x y ︒︒∠+∠=+-=∴40x y -=︒∵MK AB ,NH CD ∥,AB CD ∥ ∴AB MK NH CD∴EMK BEM x ∠=∠=,HNF CFN y ∠=∠=,KMN HNM ∠=∠∴()EMN FNM EMK KMN HNM HNF ∠∠=∠+∠-∠+∠-x KMN HNM y =+∠-∠-40x y ︒=-=(3)如下图,过点O 作AB 的平行线OQ设∠NEO=x ,则∠AEN=nx设∠OFM=y,则∠MFD=ny∵AB∥CD,AB∥OQ∴AB∥OQ∥CD∴∠EOQ=∠AEO=(n+1)x,∠QOF=180°-(n+1)y∵∠EOF=100°∴∠EOQ+∠QOF=100°,化简得:(n+1)(y-x)=80°在△NPE中,∠ENP=180°-x-∠NPE在四边形POFM中,∠PMF=360°-y-100°-∠OPM∵∠PMF-∠ENP=50°∴∠PMF-∠ENP=50=360°-y-100°-∠OPM-(180°-x-∠NPE) ∵∠NPE=∠OPM∴∠PMF-∠ENP化简后得:150°+(y-x)=180°∴y-x=30°∵(n+1)(y-x)=80°∴解得:n=53.【点睛】本题考查平行线的综合应用,解题关键是构造平行线,然后利用方程思想进行角度转化求解.15.如图,已知∠AOB,作∠AOB的平分线OC,将直角尺DEMN如图所示摆放,使EM边与OB边重合,顶点D落在OA边上,DN边与OC交于点P.(1)猜想DOP是三角形;(2)补全下面证明过程:∵OC平分∠AOB∴=∵DN∥EM∴=∴=∴=【答案】等腰,∠DOP,∠BOP,∠DPO,∠BOP,∠DOP,∠DPO,OD,PD,见解析【分析】(1)三角形的种类有多种,从边和角的关系上看常见的有:等腰三角形、等边三角形、直角三角形、观察此三角形即可大体猜想出三角形的类型;(2)根据角平分线的性质和平行线的性质,求得∠DOP=∠DPO,即可判断三角形的形状.【详解】解:(1)我们猜想△DOP是等腰三角形;(2)补全下面证明过程:∵OC平分∠AOB,∴∠DOP =∠BOP ,∵DN ∥EM ,∴∠DPO =∠BOP ,∴∠DOP =∠DPO ,∴OD =PD .故答案为:等腰,∠DOP ,∠BOP ,∠DPO ,∠BOP ,∠DOP ,∠DPO ,OD ,PD .【点睛】本题考查了角平分线的性质和平行线的性质及等腰三角形,解决本题的关键是掌握平行线的性质定理,找到相等的角.16.在小学认识三角形的基础上我们来继续学习三角形.三角形可用符号“”表示. 例:如图1中的三角形可记作“ABC ”;在一个三角形中,如果有两个角相等,我们新定义这个三角形为等角三角形.(1)如图1,ABC ∠的角平分线交AC 于D ,//DE BC 交AB 于E ,①请在图1中依题意补全图形;②判断EBD △是不是等角三角形;(直接写出结论即可).(2)如图2,AF 是GAC ∠的角平分线,//BC AF .判断ABC 是不是等角三角形,并说明理由.(3)如图3,BM ,CM 分别是ABC ∠和ACB ∠的角平分线,请过图中某一点,作一条图中已有线段的平行线,使图中出现一个或两个等角三角形,标出字母,并就出现的一个三角形是等角三角形说明理由.【答案】(1)①见解析;②△EBD 是等角三角形;(2)△ABC 是等角三角形,理由见解析;(3)见解析【分析】(1)①根据题意画出图形即可;②根据角平分线定义可得∠ABD =∠DBC ,根据平行线的性质可得∠EDB =∠DBC ,进而可得∠EBD =∠EDB ,从而可得△EBD 是等角三角形;(2)根据平行线的性质可得∠1=∠B ,∠2=∠C ,再根据角平分线的性质可得∠1=∠2,进而可得结论;(3)过点M 作GH ∥BC ,交AB 于点G ,交AC 于点H ,利用平行线的性质和角平分线定义解答即可.【详解】解:(1)①补全图形如图4所示.②△EBD是等角三角形.理由:∵BD平分∠ABC,∴∠ABD=∠DBC,∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴△EBD是等角三角形;(2)△ABC是等角三角形.理由如下:如图5,∵AF∥BC,∴∠1=∠B,∠2=∠C,∵AF是∠GAC的角平分线,∴∠1=∠2,∴∠B=∠C,∴△ABC是等角三角形.(3)过点M作GH∥BC,交AB于点G,交AC于点H,如图6,出现两个等角三角形分别是:△GBM和△HMC.下面说明△GBM是等角三角形.理由:∵GH∥BC,∴∠1=∠2,∵BM是∠ABC角平分线,∴∠GBM=∠2,∴∠1=∠GBM,所以△GBM是等角三角形.【点睛】此题主要考查了平行线的性质以及角平分线的定义,正确理解题意、熟练掌握平行线的性质是解题的关键.17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠DCE 2的平分线,交点为E 3,…,第n 次操作,分别作∠ABE n ﹣1和∠DCE n ﹣1的平分线,交点为E n .(1)如图①,已知∠ABE=50°,∠DCE=25°,则∠BEC = °;(2)如图②,若∠BEC=140°,求∠BE 1C 的度数;(3)猜想:若∠BEC =α度,则∠BE n C = °.【答案】(1)75;(2)70°;(3)2n α⎛⎫ ⎪⎝⎭【分析】(1)先过E 作EF ∥AB ,根据AB ∥CD ,得出AB ∥EF ∥CD ,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE=75°;(2)先根据∠ABE 和∠DCE 的平分线交点为E 1,运用(1)中的结论,得出∠BE 1C=∠ABE 1+∠DCE 1=12∠ABE+12∠DCE=12∠BEC ; (3)根据∠ABE 1和∠DCE 1的平分线,交点为E 2,得出∠BE 2C=14∠BEC ;根据∠ABE 2和∠DCE 2的平分线,交点为E 3,得出∠BE 3C=18∠BEC ;…据此得到规律∠E n =12n ∠BEC ,最后求得∠BE n C 的度数.【详解】解:(1)如图①,过E 作EF ∥AB ,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE=75°;故答案为:75;(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,∴由(1)可得,∠BE1C=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC;∵∠BEC=140°,∴∠BE1C=70°;(3)如图2,∵∠ABE1和∠DCE1的平分线交点为E2,∴由(1)可得,∠BE 2C=∠ABE 2+∠DCE 2=12∠ABE 1+12∠DCE 1=12∠CE 1B=14∠BEC ; ∵∠ABE 2和∠DCE 2的平分线,交点为E 3,∴∠BE 3C=∠ABE 3+∠DCE 3=12∠ABE 2+12∠DCE 2=12∠CE 2B=18∠BEC ; …以此类推,∠E n =12n ∠BEC , ∴当∠BEC=α度时,∠BE n C 等于2n α⎛⎫ ⎪⎝⎭°. 故答案为:2n α⎛⎫ ⎪⎝⎭. 【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.18.完成下面的证明.如图:BAP ∠与APD ∠互补,BAE CPF ∠=∠,求证:E F ∠=∠.对于本题小明是这样证明的,请你将他的证明过程补充完整.证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴.( )BAP ∴∠= .(两直线平行,内错角相等)BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,(等量代换)即EAP ∠= .∴ .(内错角相等,两直线平行)E F ∴∠=∠.( )19.如图,//AB CD ,点C 在点D 的右侧,ABC ∠,ADC ∠的平分线交于点E (不与B ,D 点重合),70ADC ∠=︒.设BED n ∠=︒.(1)若点B 在点A 的左侧,求ABC ∠的度数(用含n 的代数式表示)(2)将(1)中的线段BC 沿DC 方向平移,当点B 移动到点A 右侧时,请画出图形并判断ABC ∠的度数是否改变.若改变,请求出ABC ∠的度数(用含n 的代数式表示);若不变,请说明理由.【答案】同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【分析】已知∠BAP 与∠APD 互补,根据同旁内角互补两直线平行,可得AB ∥CD ,再根据平行线的判定与性质及等式相等的性质即可得出答案.【详解】证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴(同旁内角互补,两直线平行).BAP ∴∠=APC ∠(两直线平行,内错角相等), BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,即EAP ∠=APF ∠,//AE FP ∴(内错角相等,两直线平行),E F ∴∠=∠(两直线平行,内错角相等). 故答案为:同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【点睛】本题考查了平行线的判定与性质和等式的性质,关键是正确理解与运用平行线的判定与性质.20.如图,AC ∥DE ,BD 平分∠ABC 交AC 于F ,∠ABC=70°,∠E=50°,求∠D ,∠A 的度数.【答案】95,60D A ∠=︒∠=︒【分析】根据BD 平分∠ABC ,∠ABC=70°得出1352ABF DBC ABC ∠=∠=∠=︒,再根据//,50AC CE E ∠=︒得出50∠=°ACB ,从而计算,D A ∠∠.【详解】∵根据BD 平分∠ABC 交AC 于F ,∠ABC=70° ∴1352ABF DBC ABC ∠=∠=∠=︒ 又∵//,50AC CE E ∠=︒∴50∠=°ACB∴180705060A ∠=︒-︒-︒=︒180355095BFC ∠=︒-︒-︒=︒∴95D BFC ∠=∠=︒综上所述:95,60D A ∠=︒∠=︒【点睛】本题考查了三角形的内角和定理以及平行线的性质,转化相关的角度是解题关键. 21.直线AB ∥CD ,直线EF 分别交AB 、CD 于点A 、C ,CM 是ACD ∠的平分线,CM 交AB 于点N .(1)如图①,过点A 作AC 的垂线交CM 于点M ,若55MCD ∠=,求MAN ∠的度数; (2)如图②,点G 是CD 上的一点,连接MA 、MG ,180MGD EAB ∠+∠=,MC 平分AMG ∠.①AMG ∠和EAB ∠满足怎么样的数量关系时EC AM ⊥?②若36AMG ∠=,求ACD ∠的度数.【答案】(1)20°;(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥;②108°【分析】(1)根据角平分线的定义求出∠ACD ,然后根据平行线的性质可得∠EAB=∠ACD=110°,然后根据垂直的定义求出∠MAE=90°,即可求出结论;(2)①当AMG ∠+EAB ∠=180°时,根据平行线的性质可推出∠AMG +∠ACD=180°,然后根据角平分线的定义可得出∠ACM +∠AMC=90°,利用三角形的内角和即可求出∠MAC=90°,从而得出EC AM ⊥;②设∠ACD=x ,根据角平分线的定义可得∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18°,根据平行线的性质可得∠EAB=∠ACD=x ,从而得出∠MGD=180°-x ,然后根据三角形外角的性质列出方程即可求出结论.【详解】解:(1)∵CM 是ACD ∠的平分线,55∠=︒MCD∴∠ACD=2∠MCD=110°∵AB ∥CD ,∴∠EAB=∠ACD=110°∵MA ⊥AC∴∠MAE=90°∴∠MAN=∠EAB -∠MAE=20°(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥ ∵AB ∥CD ,∴∠EAB=∠ACD∴∠AMG +∠ACD=180°∵CM 是ACD ∠的平分线,MC 平分AMG ∠∴∠ACM=12ACD ∠,∠AMC=12∠AMG ∴∠ACM +∠AMC=12ACD ∠+12∠AMG =()12∠∠+ACD AMG =90° ∴∠MAC=180°-(∠ACM +∠AMC )=90° ∴EC AM ⊥;②设∠ACD=x∵CM 是ACD ∠的平分线,MC 平分AMG ∠,36∠=︒AMG∴∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18° ∵AB ∥CD ,∴∠EAB=∠ACD=x∵180MGD EAB ∠+∠=∴∠MGD=180°-x∵∠MGD=∠GCM +∠GMC即180-x=12x +18 解得:x=108即∠ACD=108°【点睛】此题考查的是平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质,掌握平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质是解决此题的关键.22.已知AB//CD,点E是平行线之间一点.(测量发现)连结EA,EC,分别做∠EAB与ECD的角平分线交于点F,通过测量我们发现∠AEC=2∠AFC.(探索新知)如图,若∠EAF=14∠EAB,∠ECF=14∠ECD,试探索∠AFC与∠AEC之间的关系,请说明理由.(合理猜想)若∠EAF=1n∠EAB,∠ECF=1n∠ECD,请猜想∠AFC与∠AEC之间的关系,不必说明理由.【答案】∠AFC=34∠AEC,理由见解析;∠AFC=1nn∠AEC【分析】探索新知:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=14∠EAB,∠ECF=14∠ECD即可证明;合理猜想:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=1n∠EAB,∠ECF=1n∠ECD,即可证明.【详解】探索新知:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=14∠EAB,∠ECF=14∠ECD,∴∠FAB+∠FCD=34∠AEC,∴∠AFC=34∠AEC;合理猜想:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=1n∠EAB,∠ECF=1n∠ECD,∴∠FAB+∠FCD=1nn-∠AEC,∴∠AFC=1nn-∠AEC.【点睛】本题是对平行线性质的考查,熟练掌握平行线的性质定理是解决本题的关键.23.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E.∠ADC=70°.(1)求∠EDC 的度数;(2)若∠ABC=30°,求∠BED 的度数;(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC =n°,请直接写出∠BED 的度数(用含n的代数式表示).【答案】(1)35︒(2)50︒(3)12152n ︒-︒ 【分析】(1)根据角平分线定义即可得到答案;(2)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解;(3)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解.【详解】解:(1)∵DE 平分ADC ∠,70ADC ∠=︒ ∴1352EDC ADC ∠=∠=︒; (2)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,30ABC ∠=︒ ∴1352EDC ADC ∠=∠=︒,1152ABE ABC ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,15FEB ABE ∠=∠=︒∴50BED FED FEB ∠=∠+∠=︒;(3)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,ABC n ∠=︒ ∴1352EDC ADC ∠=∠=︒,1122ABE ABC n ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,11801802FEB ABE n ∠=︒-∠=︒-︒ ∴113518021522BED FED FEB n n ∠=∠+∠=︒+︒-︒=︒-︒. 故答案是:(1)35︒(2)50︒(3)12152n ︒-︒ 【点睛】本题考查了角平分线的定义、平行线的判定和性质以及角的和差,解答本题的关键是作出辅助线,要求同学们掌握平行线的性质,难度中等.24.如图①,BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠,设BAD ∠=α,BCD β∠=.(1)若110αβ+=︒,则MBC NDC ∠+∠= ︒;(2)若BE 与DF 相交于点G ,且25BGD ∠=︒,求α、β所满足的等量关系式,并说明理由;(3)如图②,若αβ=,试判断BE 、DF 的位置关系,并说明理由.【答案】(1)110;(2)50βα-=︒,理由见解析;(3)BE DF ∥,理由见解析【分析】(1)根据四边形的内角和与邻补角的性质即可求解;(2)连接BD ,先得到1()2CBG CDG αβ∠+∠=+,再根据三角形的内角和得到角度的关系即可求解;(3)由(1)有,∠MBC +∠NDC =αβ+,BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ,则∠CBE +∠CDH =12(αβ+),∠CBE +β−∠DHB =12(αβ+),根据α=β,则有∠CBE +β−∠DHB =12(β+β)=β,得到∠CBE =∠DHB ,故可得到BE ∥DF .【详解】解:(1)∵∠ABC +∠ADC =360°−(αβ+)=250°,∴∠MBC +∠NDC =180°−∠ABC +180°−∠ADC =360°-(∠ABC +∠ADC )=αβ+=110°.故答案为:110;(2)50βα-=︒.理由如下:如解图①,连接BD ,由(1)知,MBC NDC αβ∠+∠=+, BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠, ∴12CBG MBC ∠=∠,12CDG NDC ∠= ()1111()2222CBG CDG MBC NDC MBC NDC αβ∴∠+∠=∠+=∠+=+. 在△BCD 中,∠BDC +∠CBD =180°−∠BCD =180°−β, 在△BDG 中,∠GBD +∠GDB +∠BGD =180°,∴∠CBG +∠CBD +∠CDG +∠BDC +∠BGD =180°,∴(∠CBG +∠CDG )+(∠BDC +∠CBD )+∠BGD =180°, ∴12(αβ+)+180°−β+25°=180°, 整理得50βα-=︒;(3)BE DF ∥.理由如下,如解图②所示,延长BC 交DF 于点H ,由(1)、(2)可知,MBC NDC αβ∠+∠=+,1()2CBE CDH αβ∠+∠=+.BCD CDH DHC ∠=∠+∠,CDH BCD DHC DHC β∴∠=∠-∠=-∠,1()2CBE DHC βαβ∴∠+-∠=+. αβ=,1()2CBE DHB ββββ∴∠+-∠=+=, CBE DHB ∴∠=∠,BE DF ∴∥.【点睛】此题考查了平行线的性质及其判定,多边形的内角和公式,利用多边形的内角和公式倒角为解题关键.25.已知AM ∥CN ,点B 为平面内一点,AB ⊥BC 于B(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD=∠C ;(3)如图3,在(2)问的条件下,点E.F 在DM 上,连接BE.BF.CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB+∠NCF=180°,∠ABF=2∠ABE ,求∠EBC 的度数.【答案】(1)90°;(2)详见解析;(3)105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.【详解】解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,即∠ABD+∠ABG=90°,又∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥AM,∴CN∥BG,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,①由AB⊥BC,可得β+β+2α=90°,②由①②联立方程组,解得α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.。
中考数学常考易错点 角、相交线与平行线 专题练习试题合集(含答案解析)

中考数学常考易错点角、相交线与平行线专题练习试题合集(含答案解析)易错清单1.平行线的性质.【例1】(2014·湖北襄阳)如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于().A.35°B.45°C.55°D.65°【解析】利用“直角三角形的两个锐角互余”的性质求得∠A=35°,然后利用平行线的性质得到∠1=∠A=35°.【答案】∵BC⊥AE,∴∠ACB=90°.∴∠A+∠B=90°.又∵∠B=55°,∴∠A=35°.又CD∥AB,∴∠1=∠A=35°.【误区纠错】本题考查了平行线的性质和直角三角形的性质.此题也可以利用垂直的定义、邻补角的性质以及平行线的性质来求∠1的度数.【例2】(2014·广东梅州)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是().A.15°B.20°C.25°D.30°【解析】根据两直线平行,内错角相等求出∠3,再求解即可.【答案】∵直尺的两边平行,∠1=20°,∴∠3=∠1=20°.∴∠2=45°-20°=25°.【误区纠错】误认为∠1与∠2是内错角来解题.【例3】(2014·湖北孝感)如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数().A.46°B.44°C.36°D.22°【解析】根据两直线平行,内错角相等可得∠3=∠1,再根据直角三角形两锐角互余列式计算即可得解.【答案】∵l1∥l2,∴∠3=∠1=44°.∵l3⊥l4,∴∠2=90°-∠3=90°-44°=46°.故选A.【误区纠错】本题考查了平行线的性质,垂线的定义,要熟记性质并准确识图.例外识别∠3与∠1是同位角很重要.2.平行线的判定.【例4】(2014·湖南湘潭)如图,直线a,b被直线c所截,若满足,则a,b平行.【解析】根据同位角相等两直线平行可得∠1=∠2时,a∥b.其他合理答案亦可.【答案】∵∠1=∠2,∴a∥b(同位角相等两直线平行).故可填∠1=∠2.【误区纠错】分不清三线八角,以及平行线的判定方法是解题的误区,本题属条件开放性题.名师点拨1.能记住点、线、面的概念.2.能利用角的概念判断角的大小及角的表示方法;会进行角的换算;能正确区分角的大小;会进行角的和、差运算.3.能区分补角、余角的概念,记住补角、余角的性质.4.掌握角平分线定理和线段垂直平分线定理并能正确使用.5.会画直线的垂线;能区分垂线、垂线段的联系与区别.6.掌握平行的概念,会进行平行线的判断.7.能利用直尺画直线的平行线;会作两平行线间的距离;能确定并准确度量两平行线间的距离.提分策略1.直线平行与垂直的判定及简单应用.计算角度问题时,要注意挖掘图形中的隐含条件(三角形内角和、互为余角或补角、平行性质、垂直)及角平分线知识的应用.【例1】如图,△ABC中,∠A=90°,点D在边AC上,DE∥BC.若∠1=155°,则∠B的度数为.【解析】由∠1=155°,可求得∠BCD=∠CDE=25°,最后求∠B=65°.【答案】65°2.平行线的性质和判定的应用.主要理解和掌握:(1)平行线的性质;(2)平行线的判定.【例2】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD的关系,请你从所得到的关系中任选一个加以证明.【解析】①∠APC=∠PAB+∠PCD;②∠APC=360°-(∠PAB+∠PCD);③∠APC=∠PAB-∠PCD;④∠APC=∠PCD-∠PAB.如证明①∠APC=∠PAB+∠PCD.证明:过点P作PE∥AB,所以∠A=∠APE.又因为AB∥CD,所以PE∥CD.所以∠C=∠CPE.所以∠A+∠C=∠APE+∠CPE.所以∠APC=∠PAB+∠PCD.同理可证明其他的结论.专项训练一、选择题1.(2014·四川峨眉山二模)如图,已知直线AB,CD相交于点O,OE平分∠CPB.若∠BOD=70°,则∠COE的度数是().A.45°B.70°C.55°D.110°(第1题)(第2题)2.(2014·北京平谷区模拟)如图,AB∥CD,O为CD上一点,且∠AOB=90°.若∠B=33°,则∠AOC的度数是().A.33°B.60°C.67°D.57°3.(2014·山东日照模拟)将一副三角板按图中的方式叠放,则∠α等于().A.75°B.60°C.45°D.30°(第3题)(第4题)4.(2013·广东广州海珠区毕业班综合调研)如图,∠1与∠2是同位角,若∠2=65°,则∠1的大小是().A.25°B.65°C.115°D.不能确定5.(2013·浙江温州一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为().A.9B.6C.4D.3(第5题)(第6题)6.(2012·湖北荆门东宝区模拟)如图,已知直线a∥b,∠1=40°,∠2=60°.则∠3等于().A.100°B.60°C.40°D.20°二、填空题7.(2014·广东模拟)将三角板ABC按下图放置,使其三个顶点分别落在三条平行直线上,其中∠CAB=90°,且CF恰好平分∠ACB.若∠CBA=40°,则∠DAC的度数是.(第7题)(第8题)8.(2014·河南鹿邑一模)如图,∠1=∠2,∠3=40°.则∠4= .9.(2014·湖北鄂州二模)如图AB∥CD,∠1=50°,∠2=110°,则∠3= .(第9题)(第10题)10.(2013·湖北孝感模拟)如图,直线AB,CD相交于点E,EF⊥AB于点E,若∠CEF=59°,则∠AED的度数为.三、解答题11.(2014·河南安阳模拟)已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD.探究下列问题:(1)如图(1),当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图(2),当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图(3),当∠ACB变化,且点D与点C位于直线AB的两侧时,求CD的最大值及相应的∠ACB的度数.(第11题)参考答案与解析1.C[解析]2.D[解析]∠AOC=90°-33°=57°.3.A[解析]∠α=45°+(90°-60°)=75°.4.D[解析]两直线平行同位角相等,如果不能确定两直线是平行线则不能确定同位角之间的关系.5.A[解析]首先利用平行线判定两三角形相似,然后利用相似三角形对应边的比等于相似比求得线段BC的长即可.6.A[解析]∠3=∠1+∠2=100°.8.140°[解析]∠4=180°-∠3=140°.9.60°[解析]∠3=180°-(∠1+180°-∠2)=60°.10.149°[解析]∵EF⊥AB于点E,∠CEF=59°,∴∠AEC=90°-∠CEF=90°-59°=31°.∴∠AED=180°-∠AEC=180°-31°=149°.11.(3)以点D为中心,将△DBC逆时针旋转60°,则点B落在点A,点C落在点E.连接AE,CE.∴CD=ED,∠CDE=60°,AE=CB=a.∴△CDE为等边三角形.∴CE=CD.如图(1),当点E,A,C不在一条直线上时,有CD=CE<AE+AC=a+b;如图(2),当点E,A,C在一条直线上时,CD有最大值,CD=CD=a+b.此时∠CED=∠BCD=∠ECD=60°,∴∠ACB=120°.因此当∠ACB=120°时,CD有最大值a+b.(第11题)。
中考数学专项练习相交线与平行线(含解析)

中考数学专项练习相交线与平行线(含解析)一、单选题1.下面四个图形中,∠1与∠2互为对顶角的是()A.B. C.D.2.下列说法:(1)同角的余角相等(2)相等的角是对顶角(3)在同一平面内,不相交的两条直线叫平行线(4)直线外一点与直线上各点连接的所有线段中,垂线段最短中,正确的个数是()A.1B.2C.3D.43.如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°4.如图,AB∥CD,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=()A.10°B.15°C.20°D.30°5.如图,已知直线AB、CD相交于点O,OB平分∠EOD,若∠EOD= 110°,则∠AOC的度数是()A.35°B.55°C.70°D.110°6.如图,在△ABC中,∠CAB=70º,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB, 则∠BAD的度数为()A.30°B.35°C.40°D.50°7.如图所示,在Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于点H,EF⊥AB于点F,则下列结论中,不正确的是()A.ACD=B B.CH=CE=EF C.AC=AF D.CH=HD8.如图,以下推理正确的是()A.若AB∥CD,则∠1=∠2B.若AD∥BC,则∠1=∠2C.若∠B=∠D,则AB∥CDD.若∠CAB=∠ACD,则AD∥BC9.如图,下列说法中,正确的是()A.因为∠A+∠D=180°,因此AD∥BC B.因为∠C+∠D=18 0°,因此AB∥CDC.因为∠A+∠D=180°,因此AB∥CD D.因为∠A+∠C=18 0°,因此AB∥CD10.如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2,AC=3,BC=6,则⊙O的半径是()A.3B.4C.4D.2二、填空题11.填写理由AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?什么缘故?解:BE∥/DF∵AB⊥BC,∠ABC=________即∠3+∠4=________又∵∠1+∠2=90°,且∠2=∠3∴________=________理由是:________∴BE∥DF理由是:________12.如图,a∥b,∠1=65°,∠2=140°,则∠3等于________.13.如图,直角三角尺的直角顶点在直线b上,∠3 = 25°,转动直线a,当∠1=________,时,a∥b14.如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是依照________15.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E=________度.16.如图,在正方体中,与线段AB平行的线段有________.17.如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点.OE ⊥AC于E,OE=2,则点O到AB与CD的距离之和为________.18.已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,O D∥AB交BC于D,OE∥AC交BC于E,若BC=10 cm,则△ODE的周长________cm.三、运算题19.如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.20.如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BA D和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.21.如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.22.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.四、解答题23.如图,直线l1∥l2,∠BAE=125°,∠ABF=85°,则∠1+∠2等于多少度?24.如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.25.已知:如图,a//b,∠1=55°,∠2=40°,求∠3和∠4的度数.五、综合题26.如图,点M(4,0),以点M为圆心,2为半径的圆与x轴交于点A、B,已知抛物线y= x2+bx+c过点A和B,与y轴交于点C.(1)求点C的坐标,并画出抛物线的大致图象.(2)点P为此抛物线对称轴上一个动点,求PC﹣PA的最大值.(3)CE是过点C的⊙M的切线,E是切点,CE交OA于点D,求O E所在直线的函数关系式.答案解析部分一、单选题1.【答案】C【考点】对顶角、邻补角【解析】【解答】解:依照对顶角的定义可知:C中∠1、∠2属于对顶角,故选C.【分析】依照对顶角的定义来判定,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,如此的两个角叫做对顶角.2.【答案】C【考点】余角和补角,对顶角、邻补角,垂线段最短【解析】【解答】解:同角的余角相等,故(1)正确;如图:∠ACD=∠BCD=90°,但两角不是对顶角,故(2)错误;在同一平面内,不相交的两条直线叫平行线,故(3)正确;直线外一点与直线上各点连接的所有线段中,垂线段最短,故(4)正确;即正确的个数是3,故选C.【分析】依照余角定义,对顶角定义,垂线段最短,平行线定义逐个判定即可.3.【答案】C【考点】平面中直线位置关系【解析】【解答】解:如图,∵∠1=∠2,∴a∥b,∴∠3=∠5,∵∠3=40°,∴∠5=40°,∴∠4=180°﹣40°=140°,故答案为:C.【分析】第一依照同位角相等,两直线平行可得a∥b,再依照平行线的性质可得∠3=∠5,再依照邻补角互补可得∠4的度数.4.【答案】B【考点】平行线的性质【解析】【解答】过点P作PM∥AB,∴AB∥PM∥CD,∴∠BAP=∠APM,∠DCP=∠MPC,∴∠APC=∠APM+∠CPM=∠BAP+∠DCP,∴45°+α=(60°-α)+(30°-α),解得α=15°.故选B.【分析】过点P作一条直线平行于AB,依照两直线平行内错角相等得:∠APC=∠BAP+∠PCD,得到关于α的方程,解即可.注意此类题要常作的辅助线,充分运用平行线的性质探求角之间的关系.5.【答案】B【考点】角平分线的定义,对顶角、邻补角【解析】【解答】解:∵∠EOD=110°,OB平分∠EOD,∴∠BOD = ∠EOD=55°,∴∠AOC=∠BOD=55°,故选:B.【分析】依照角平分线定义可得∠BOD= ∠EOD,由对顶角性质可得∠A OC=∠BOD.6.【答案】C【考点】平行线的性质,全等三角形的判定与性质,旋转的性质【解析】【分析】因为△ADE是由△ABC绕点A逆时针旋转得到的,因此△ADE≌△ABC,因此∠CAB=∠EAD=70º,AE=AC,因为EC∥AB,因此∠CAB=∠ECA=70°,因为AE=AC,因此∠AEC=70°,因此∠EAC=180°-70°×2=40°,因此∠CAD=∠EAD-∠EAC=70º-40°=30°,因此∠BAD=∠CAB-∠CAD =70º-30°=40°.【点评】该题是常考题,要紧考查学生对图形旋转的意义,以及对全等三角形性质和角的等量代换的应用。
中考数学相交线与平行线专题训练50题-含答案

中考数学相交线与平行线专题训练50题含答案(单选、填空、解答题)一、单选题1.一副直角三角板如图所示摆放,它们的直角顶点重合于点O,//CO AB,则∠=()BODA.30︒B.45︒C.60︒D.90︒2.∠1与∠2是一组平行线被第三条直线所截的同旁内角,若∠1=50°,则()A.∠2=50°B.∠2=130°C.∠2=50°或∠2=130°D.∠2的大小不一定3.如图,AB//CD,如果∠B=30°,那么∠C为()A.40°B.30°C.50°D.60°4.如图,已知∠1=50°,要使a∠b,那么∠2等于()A.40°B.130°C.50°D.120°5.在同一平面内不重合的三条直线的交点个数()A.可能是0个,1个,2个B.可能是0个,1个,3个C.可能是0个,1个,2个,3个D.可能是0个,2个,3个6.在下图中,1∠是同位角的是()∠和2A .(1)、(2)B .(1)、(3)C .(2)、(3)D .(2)、(4) 7.在平面直角坐标系中,点A (﹣3,2),B (3,5),C (x ,y ),若AC ∥x 轴,则线段BC 的最小值及此时点C 的坐标分别为( )A .6,(﹣3,5)B .6,(3,2)C .3,(3,0)D .3,(3,2) 8.下面四个图形中,1∠与2∠是同位角的是( )A .B .C .D .9.如图,直线l ∠m ,将Rt △ABC (∠ABC =45°)的直角顶点C 放在直线m 上,若∠2=24°,则∠1 的度数为( )A .23︒B .22︒C .21︒D .24︒ 10.如图,已知1130∠=︒,250∠=︒,3115∠=︒,则4∠的度数为( )A .65︒B .60︒C .55︒D .50︒11.如图,直线AB ,CD 被直线EF 所截,则∠AGE 的同位角是( )A .∠BGEB .∠BGFC .∠CHED .∠CHF 12.下列四个选项中不是命题的是( )A .对顶角相等B .过直线外一点作直线的平行线C .三角形任意两边之和大于第三边D .如果a b a c ==,,那么b c =13.如图,直线AB 、直线CD 交于点E ,EF AB ⊥,则CEF ∠与BED ∠的关系是( )A .互余B .相等C .对顶角D .互补 14.下列命题是真命题的是()A .过一点有且只有一条直线与已知直线垂直B .经过一点有且只有一条直线与已知直线平行C .同旁内角互补,两直线平行D .同位角相等15.如图,已知AB =DC ,AD =BC ,E ,F 在DB 上两点且BF =DE ,若∠AEB =120°,∠ADB =30°,则∠BCF = ( )A .150°B .40°C .80°D .90° 16.如图,直线a //b ,∠1=85°,∠2=35°,则∠3的度数为( )A .40°B .45°C .50°D .55° 17.如图,AB CD ∥,直线EF 分别交AB ,CD 于点M ,N ,将一个含有45°角的直角三角尺按如图所示的方式摆放,若80EMB ∠=︒,则PNM ∠等于( )A .15°B .25°C .35°D .45° 18.如图,∠1=∠2=22°,∠C=130°,则∠DAC = ( )A .28°B .25°C .23°D .22° 19.如图,∠ADB =∠ACB =90°,AC 与BD 相交于点O ,且OA =OB ,下列结论:∠AD =BC ;∠AC =BD ;∠∠CDA =∠DCB ;∠CD ∠AB ,其中正确的有( )A .1个B .2个C .3个D .4个 20.一辆汽车在笔直的公路上行驶,两次拐弯后,在与原方向相反的方向上平行行驶,则这两次拐弯的角度应为( )A .第一次向右拐38°,第二次向左拐142°B .第一次向左拐38°,第二次向右拐38°C .第一次向左拐38°,第二次向左拐142°D.第一次向右拐38°,第二次向右拐40°二、填空题a b∠=︒,则∠2=_________.21.如图,已知直线//,17022.如图,AB∠CD,CE∠GF,若∠1=60°,则∠2=_____°.23.如图,直线AC和FD相交于点B,下列判断:∠∠GBD和∠HCE是同位角;∠∠ABD和∠ACH是同位角;∠∠FBC和∠ACE是内错角;∠∠FBC和∠HCE是内错角;∠∠GBC和∠BCE是同旁内角.其中正确的是____.(填序号)24.如图,直线a,b交于点O,若138∠=︒,则2∠=__°.25.如图,四边形ABCD,点E是AB的延长线上的一点.请你添加一个条件,能判定∥.这个条件是______.AD BC26.如图,AB 、BC 是∠O 的弦,OM ∥BC 交AB 于点M ,若∠AOC =100°,则∠AMO =___.27.检验直线与平面平行的方法:(1)______________只能检验直线与水平面是否平行;(2)______________可以检验一般的直线与平面是否垂直;28.如图,AB//CD ,点E 在线段BC 上,若140∠=,230∠=,则3∠的度数是______.29.命题:“两个角的和等于平角时,这两个角互为邻补角”是_____命题(填“真”或“假”)30.如图,AB∠CD .EF∠AB 于E ,EF 交CD 于F ,已知∠1=58°12',则∠2=______.31.如图,直线AB 、CD 相交于点O ,∠AOC=80°,∠1=30°,求∠2的度数解:因为∠DOB=∠______ ( )_________=80° (已知)所以,∠DOB=____°(等量代换)又因为∠1=30°( )所以∠2=∠____- ∠_____ = _____ - _____=_____ °32.把一张宽度相等的纸条按如图所示的方式折叠.图中∠1=100°,则∠2=____°.33.已知,如图,在△ABC 中,BO 和CO 分别平分△ABC 和△ACB ,过O 作DE△BC ,分别交AB 、AC 于点D 、E ,若BD+CE=5,则线段DE 的长为________.34.如图,在四边形ABCD 中,AB ∠CD ,连接AC ,BD .若∠ACB =90°,AC =BC ,AB =BD ,AD =AE 则∠ADC =_____°.35.如图,BE 平分ABC ∠,DE BC ∥,若1=25∠.,则2∠的度数为______.36.在四边形ABCD 中,AD BC ∥,AD BC <,90A ∠=︒,4AB =,3BC =,点E 为BCD ∠的平分线上一点,连接BE ,且3BE =,连接DE ,则CDE 的面积为________.37.如图,将矩形纸片ABCD 沿EF 折叠后,点C 、D 分别落在点C ′、D ′处,若∠AFE=65°,则∠C ′EB =________度.38.已知 ∠1 的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为__. 39.如图,在∠ABC 中,∠ABC 和∠ACB 的平分线交于点D ,过点D 作EF∠BC 交AB 于E ,交AC 于F.若BE=2,CF=3,则线段EF 的长为________.40.如图,在t R ABC ∆中,90︒∠=C ,6AC =,8BC =,点F 在边AC 上,并且2CF =,点E 为边BC 上的动点,将CEF ∆沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是________.三、解答题41.如图,∠A=∠1,∠1=∠2,CD 平分∠ADE ,试说明∠C=∠ADC .42.如图.BA DE ∥,30B ∠=︒,40D ∠=︒,求∠C 的度数.43.如图所示,已知12180,3,B DE ∠+∠=︒∠=∠和BC 平行吗?如果平行,请说明理由.44.如图,点E 、F 分别在AB 、CD 上,AF ∠CE 于点O ,∠1=∠B ,∠A +∠2=90°,求证∠AB ∥CD .请填空.证明∠∠AF ∠CE (已知),∠∠AOE =90°(___)又∠∠1=∠B (已知)∠CE ∥BF (_____),∠∠AFB =∠AOE (___)∠∠AFB =90°(_)又∠∠AFC +∠AFB +∠2=180°(平角的定义)∠∠AFC +∠2=(________)又∠∠A +∠2=90°(已知)∠∠A =∠AFC (_____)∠AB ∥CD (_____)45.如图,在∠ABC 中,AB =BC ,点D 、E 分别在边AB 、BC 上,且DE ∠AC ,AD =DE ,点F 在边AC 上,且CE =CF ,连接FD .(1)求证:四边形DECF是菱形;(2)如果∠A=30°,CE=4,求四边形DECF的面积.46.已知:如图,B、D分别在AC、CE上,AD是∠CAE的平分线,BD∠AE,AB=BC.求证:AC=AE.47.如图,直线AB与CD交于点F,锐角∠CDE=α,∠AFC+α=180°.(1)求证:AB∠DE;(2)若G为直线AB(不与点F重合)上一点,∠FDG与∠DGB的角平分线所在的直线交于点P.∠如图2,α=50°,G为FB上一点,请补齐图形并求∠DPG的度数;∠直接写出∠DPG的度数为(结果用含α的式子表示).48.完成下面的证明.已知:如图,BC∠DE,BE、DF分别是∠ABC、∠ADE的平分线.求证:∠1=∠2.证明:∠BC∠DE,∠∠ABC=∠ADE().∠BE、DF分别是∠ABC、∠ADE的平分线.∠∠3=12∠ABC,∠4=12∠ADE.∠∠3=∠4.∠∠().∠∠1=∠2().49.如图所示,∠ABC∠∠DEF,试说明AB∠DE,BC∠EF.50.(1)填空:如图∠,AB∠CD,猜想∠BPD与∠B,∠D的关系,并说明理由.解:过点P作EF∠AB,如图所示∠∠B+∠BPE=180°(______________________________).∠AB∠CD,AB∠EF∠EF∠CD(如果两条直线都和第三条直线平行,那么(_____________________).∠∠EPD+∠D=180°∠∠B+∠BPE+∠EPD+∠D=________,即∠BPD+∠B+∠D=360°(2)仿照上面的解题方法,观查图∠,已知AB∠CD,猜想图中∠BPD与∠B,∠D的关系,并说明理由.(3)观查图∠和∠,已知AB∠CD,猜想图中∠BPD与∠B,∠D的关系,不需要说明理由.参考答案:1.C【分析】由AB //CO 得出∠BAO =∠AOC ,即可得出∠BOD .【详解】解://AB CO ,60OAB AOC ∴∠=∠=︒6090150BOC ∴∠=︒+︒=︒90AOC DOA DOA BOD ∠+∠=∠+∠=︒60AOC BOD ∴∠=∠=︒故选:C .【点睛】本题考查两直线平行内错角相等的知识点,掌握这一点才能正确解题. 2.B【分析】根据两直线平行,同旁内角互补即可得.【详解】根据题意有:∠1+∠2=180°,∠∠1=50°,∠∠2=130°,故选:B .【点睛】本题主要考查了平行线的性质的知识,掌握两直线平行,同旁内角互补是解答本题的关键.3.B【分析】根据两直线平行内错角相等即可解决.【详解】解://30AB CD B ∠=︒,,30C ∴∠=︒, 故选:B .【点睛】本题主要考查平行线的性质,平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;题目较简单,能正确识别角的类型是解题的关键.4.C【分析】先假设a ∠b ,由平行线的性质即可得出∠2的值.【详解】解:假设a ∠b ,∠∠1=∠2,∠∠1=50°,∠∠2=50°.故选:C.【点睛】本题考查的是平行线的判定定理,即同位角相等,两直线平行.5.C【分析】在同一平面内,两条直线的位置关系有两种,平行和相交,三条直线互相平行无交点,两条直线平行,第三条直线与它相交,有2个交点,三条直线两两相交,最多有3个交点,最少有1个交点.【详解】解:由题意画出图形,如图所示:故选C.【点睛】本题考查了直线的交点个数问题,此类题没有明确平面上三条不重合直线的相交情况,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.6.B【分析】根据同位角的特征:两条直线被第三条直线所截形成的角中,两个角都在两条被截直线的同侧,并且在第三条直线(截线)的同旁,由此判断即可.【详解】解:∠∠1和∠2是同位角;∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共,∠1和∠2不是同位角;∠∠1和∠2是同位角;∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共,∠1和∠2不是同位角.故选:B.【点睛】本题考查三线八角中的某两个角是不是同位角,同位角完全由两个角在图形中的相对位置决定.在复杂的图形中判别同位角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F “形.7.D【分析】由AC x ∥轴,A (-3,2),根据坐标的定义可求得y 值,根据线段BC 最小,确定BC ∠AC ,垂足为点C ,进一步求得BC 的最小值和点C 的坐标.【详解】解:∠AC x ∥轴,A (-3,2),(),C x y ,()3,5B ,∠y =2,当BC ∠AC 于点C 时, 点B 到AC 的距离最短,即:BC 的最小值为:5−2=3, ∠此时点C 的坐标为(3,2),故D 正确.故选:D .【点睛】本题主要考查平面直角坐标系中的点的坐标,根据题意,画出图形,掌握“直线外一点与直线上各个点的连线中,垂线段最短”,是解题的关键.8.D【分析】根据同位角的定义和图形逐个判断即可.【详解】A 、不是同位角,故本选项错误;B 、不是同位角,故本选项错误;C 、不是同位角,故本选项错误;D 、是同位角,故本选项正确;故选:D .【点睛】本题考查了同位角的应用,注意:两条直线被第三条直线所截,如果有两个角在第三条直线的同旁,并且在两条直线的同侧,那么这两个角叫同位角.9.C【分析】过点B 作直线b∠l ,再由直线m∠l 可知m∠l∠b ,得出∠3=∠1,∠2=∠4,由此可得出结论.【详解】解:过点B 作直线b∠l ,如图所示:∠直线m∠l ,∠m∠l∠b ,∠∠3=∠1,∠2=∠4.∠∠2=24°,∠∠4=24°,∠∠3=45°-24°=21°,∠∠1=∠3=21°;故选择:C.【点睛】本题考查的是平行线的性质;熟练掌握平行线的性质,并能进行推理论证与计算是解决问题的关键.10.A【分析】如图,由题意易得a ∠b ,则有∠3+∠5=180°,∠4=∠5,然后问题可求解.【详解】解:如图,∠1130∠=︒,250∠=︒,∠12180∠+∠=︒,∠a ∠b ,∠∠3+∠5=180°,∠3115∠=︒,∠4565∠=∠=︒;故选A .【点睛】本题主要考查平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.11.C【分析】根据同位角的定义进行分析解答即可,两个角都在截线的同旁,又分别处在被截的两条直线同侧,具有这样位置关系的一对角叫做同位角.【详解】解:∠直线AB 、CD 被直线EF 所截,∠只有∠CHE 与∠AGE 在截线EF 的同侧,且在AB 和CD 的同旁,即∠AGE 的同位角是∠CHE .故选:C .【点睛】本题考查同位角概念,解题的关键在于运用同位角的定义正确地进行分析. 12.B【分析】判断一件事情的语句,叫做命题.根据定义判断即可.【详解】解:由题意可知,A 、对顶角相等,故选项是命题;B 、过直线外一点作直线的平行线,是一个动作,故选项不是命题;C 、三角形任意两边之和大于第三边,故选项是命题;D 、如果a b a c ==,,那么b c =,故选项是命题;故选:B .【点睛】本题考查了命题与定理:判断一件事情的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.注意:疑问句与作图语句都不是命题.13.A【分析】根据邻补角的定义由90BEF ∠=︒得到90FEA ∠=︒,即90CEA AEF ∠+∠=︒,再根据对顶角相等得到CEA BED ∠=∠,所以90CEF BED ∠+∠=︒.【详解】解:90BEF ∠=︒,90FEA ∴∠=︒,即90CEA CEF ∠+∠=︒,CEA BED ∠=∠,90CEF BED ∴∠+∠=︒,即CEF ∠与BED ∠互余.故选:A .【点睛】本题考查了对顶角、邻补角:解题的关键是:知道有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角;只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.14.C【分析】根据两直线的位置关系、平行线的性质与判定分别进行判断即可.【详解】A:同一平面内,过一点有且只有一条直线与已知直线垂直,错误;B:过直线外一点有且只有一条直线与已知直线平行,错误;C:平行线的判定:同旁内角互补,两直线平行,正确;D:平行线的性质:两直线平行,同位角相等,错误.故答案选:C【点睛】本题考查两直线的位置关系以及平行线的性质与判定,掌握两直线的位置关系以及平行线的性质与判定是解题关键.15.D【详解】解:∠AB=DC,AD=BC,∠四边形ABCD为平行四边形,∠∠ADE=∠CBF,∠BF=DE,∠∠ADE∠∠CBF,∠∠BCF=∠DAE,∠∠DAE+∠ADB=∠AEB∠∠BCF=∠DAE=∠AEB-∠ADB=90°故选D.16.C【分析】根据平行线的性质可得同位角相等,再根据三角形的外角性质可求出∠3,即可求出结果.a b【详解】解://∴∠=∠︒14=85∠=∠∠,由三角形外角性质知,42+3∠=︒又235∴∠=∠-∠=︒-︒=︒,342853550故选:C.【点睛】本题考查平行线的性质、三角形的外角等知识,是重要考点,难度较易,掌握相关知识是解题关键.17.C【分析】根据平行线的性质得到∠DNM=∠BME=80°,由等腰直角三角形的性质得到∠PND=45°,即可得到结论.【详解】解:∠AB∠CD,∠∠DNM=∠BME=80°,∠∠PND=45°,∠∠PNM=∠DNM-∠DNP=35°,故选:C.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.18.A【详解】因为∠1=∠2=22°,所以AB//CD,所以∠DAC+∠CAB=180°.由于∠C=130°,则︒-︒-︒=︒.故选A.∠DAC=180130222819.D【分析】由△ABC∠∠BAD(AAS),推出AD=BC,AC=BD,故∠∠正确,再证明CO=OD,可得∠CDA=∠DCB,故∠正确,由∠CDO=∠OAB,可得CD∠AB,故∠正确;【详解】解:∠OA=OB,∠∠DAB=∠CBA,∠∠ACB=∠BDA=90°,AB=BA,∠∠ABC∠△BAD(AAS),∠AD=BC,AC=BD,故∠∠正确,∠BC=AD,BO=AO,∠CO=OD,∠∠CDA=∠DCB,故∠正确,∠∠COD=∠AOB,∠∠CDO=∠OAB,∠CD∠AB,故∠正确,故选:D.【点睛】本题考查全等三角形的判定和性质、等腰三角形的判定和性质、平行线的判定等知识,解题的关键是灵活的选择判定方法证明三角形全等.20.B【详解】A. 如图:∠∠1=38°,∠2=142°,∠∠3=180°−∠2=38°,∠∠4=∠1+∠3=76°≠∠1,∠AB与CD不平行;故本选项错误;B. 如图:∠∠1=∠2=38°,∠AB∠CD,且方向相同;故本选项正确;C. 如图:∠∠2=142°,∠∠3=180°−∠2=38°,∠∠1=38°,∠∠1=∠2,∠AB∠CD,但方向相反;故本选项错误;D. 如图:∠∠2=40°,∠∠3=180°−∠2=140°≠∠1,∠AB与CD不平行,故本选项错误.故选:B.21.110°【详解】解:根据a∠b得∠1=∠3=70°,∠∠2+∠3=180°,∠∠2=180°-70°=110°.故答案为110°.22.60【分析】根据AB∠CD得出:∠1=∠CEF,又CE∠GF得出:∠2=∠CEF,根据等量代换∠=∠=︒.即可得出:1260【详解】解:∠AB∠CD,∠∠1=∠CEF,∠CE∠GF,∠∠2=∠CEF,∠∠2=∠1,∠∠1=60°,∠∠2=60°,故答案为:60.【点睛】本题考查平行线的性质,注意两直线平行,内错角相等、同位角相等. 23.∠∠∠【分析】根据同位角、内错角、同旁内角的定义判断即可.【详解】∠中∠GBD 和∠HCE 没有任何关系,故∠错;∠中∠ABD 和∠ACH 是直线FD 与直线CH 被直线AC 所截形成的同位角,故∠对; ∠中∠FBC 和∠ACE 是直线FD 与直线CE 被直线AC 所截形成的内错角,故∠对; ∠中∠FBC 和∠HCE 没有任何关系,故∠错;∠中∠GBC 和∠BCE 是直线BG 与直线CE 被直线AC 所截形成的同旁内角,故∠对; 综上正确的有:∠∠∠.【点睛】本题主要考查同位角、内错角、同旁内角的定义,解题的关键是能够熟练地掌握同位角、内错角、同旁内角的定义即可.24.38【分析】根据对顶角相等进行解答即可.【详解】解:∠图中1∠和2∠是对顶角,138∠=︒,∠2138∠=∠=︒.故答案为:38.【点睛】本题主要考查了对顶角的性质,熟练掌握对顶角相等,是解题的关键. 25.A CBE ∠=∠(答案不唯一)【分析】根据平行线的判定方法结合图形进行补充条件即可.【详解】解:补充:,A CBE由同位角相等,两直线平行可得,AD BC ∥补充:180,A ABC根据同旁内角互补,两直线平行可得,AD BC ∥故答案为:A CBE ∠=∠或180A ABC ∠+∠=︒(任写一个即可)【点睛】本题考查的是平行线的判定,掌握“同位角相等,两直线平行或同旁内角互补,两直线平行”是解本题的关键.26.50°##50度【分析】先由圆周角定理求出∠B 的度数,再根据平行线的性质即可求出∠AMO 的度数【详解】∠∠AOC =2∠B ,∠AOC =100°,∠∠B =50°,∠OM ∥BC ,∠∠AMO =∠B =50°,故答案为50°.【点睛】本题考查了圆周角定理,平行线的性质,熟练掌握圆周角定理,并找到∠AMO 与∠B 的关系,已知角与∠B 的关系,从而求出角的度数.27. 铅垂线 合页型折纸【分析】根据平行线的判定,以及“铅垂线”、“合页型折纸法”、“长方形纸片法”的方法分析判断即可得解.【详解】(1)根据重力学原理,铅垂线垂直于水平面,与铅垂线垂直的直线则与平面平行,故填:铅垂线;(2)合页型折纸其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把折断的两边放到水平面上,可判断折痕与水平面垂直,故填:合页型折纸.【点睛】本题考查了平行线的判定与垂线,利用物理力学原理是最好的检验方法. 28.70【分析】先根据平行线的性质求出C ∠的度数,再由三角形外角的性质即可得出结论.【详解】解:AB//CD ,140∠=,230∠=,C 40∠∴=,3∠是CDE 的外角,3C 2403070∠∠∠∴=+=+=.故答案为70.【点睛】本题考查了平行线的性质,三角形外角的性质,用到的知识点为:两直线平行,内错角相等.29.假.【分析】根据邻补角的定义来分析:既要其和是个平角(或180°),也要满足位置关系.【详解】解:根据邻补角的定义可知,两个角的度数和是180度,且有一条公共边称这两个角互为邻补角,∴如果两个角的和是平角时,那么这两个角不一定是邻补角.故答案为:假.【点睛】本题主要考查了邻补角的概念,比较简单.30.31°48′【分析】先由平行线的性质求出∠3的度数,再由∠AEF=90°,即可求出∠2.【详解】∠AB ∠ CD,∠1=58°12',∠∠3=∠1=58°12',∠EF∠AB,∠∠AEF=90°,∠∠2=90°-∠3=90°-58°12'=31°48′,故答案为31°48′.【点睛】本题考查了平行线的性质、垂线的定义,熟练掌握相关内容是解题的关键. 31.∠AOC,对顶角相等,∠AOC, 80°,已知BOD,1,80°,30°,50【详解】解:因为∠DOB=∠AOC (对顶角相等),∠AOC=80° (已知),所以,∠DOB=80°(等量代换),又因为∠1=30°(已知),所以∠2=∠BOD- ∠1 = 80°-50°=30°,故答案为:∠AOC,对顶角相等,∠AOC,80°,已知,BOD,1,80°,30°,50. 32.50.【详解】试题解析:如图:∠FED,根据折叠得出∠2=∠DEM=12∠是一张宽度相等的纸条,∠AE∠BM,∠1=100°,∠∠FED=∠1=100°,∠∠2=50°考点:1.平行线的性质;2.翻折变换(折叠问题).33.5【详解】∠在△ABC 中,BO 和CO 分别平分∠ABC 和∠ACB , ∠∠DBO=∠OBC ,∠ECO=∠OCB ,∠DE∠BC ,∠∠DOB=∠OBC=∠DBO ,∠EOC=∠OCB=∠ECO ,∠DB=DO ,OE=EC ,∠DE=DO+OE ,∠DE=BD+CE=5.故答案为5.34.105【分析】先根据90,ACB AC BC ∠=︒=判断出ACB ∆是等腰直角三角形,再根据AB BD =,AD DE =利用等腰三角形两底角相等的性质求算.【详解】∠90,ACB AC BC ∠=︒=∠45CAB ∠=︒又∠,AB BD AD AE ==∠,ADE AED BAD BDA ∠=∠∠=∠设=ADE AED x ∠=∠︒∠1802DAE x DAB ADB x ∠=︒-︒∠=∠=︒,∠180245x x ︒-︒+︒=︒∠75x =︒∠75DAB x ∠=︒=︒又∠//AB CD∠18075105ADC ∠=︒-︒=︒故答案为:105【点睛】本题考查平行线、等腰三角形、等腰直角三角形的性质,转化相关的角度是解题关键.35.50.【分析】先由角平分线的定义即可得出∠ABC 的度数,再根据平行线的性质求出∠1的度数.【详解】∠BE 平分∠ABC ,∠∠ABC=2∠1=50°.∠DE∠BC,∠∠ABC=∠2=50°.故答案为50°.【点睛】本题考查的是平行线的性质,解题时注意:两直线平行,同位角相等.36.6【分析】过点D作DF∠BC,连接BD,根据平行线的判定和性质得出DF=AB=4,再由等边对等角确定∠BEC=∠BCE,利用各角之间的关系及平行线的判定及性质得出BE∠DC,∆CED与∆CDB的边CD上的高相等,结合图形求解即可.【详解】解:过点D作DF∠BC,连接BD,如图所示,∠AD∠BC,∠A=90,∠∠ABC=90,∠DF∠BC,∠∠DFB=90,∠DF∠AB,∠四边形ABFD为平行四边形,∠DF=AB=4,∠BE=BC=3,∠∠BEC=∠BCE,∠CE平分∠BCD,∠∠DCE=∠BEC,∠BE∠DC,∠∆CED与∆CDB的边CD上的高相等,∠1·62CDE BCDS S BC DF===,故答案为:6.【点睛】题目主要考查平行四边形的判定和性质,平行线的判定,角平分线的计算,等边对等角等,理解题意,综合运用这些知识点是解题关键.37.50【详解】试题解析:∠AD∠BC∠∠FEC=∠AFE=65°又∠沿EF折叠∠∠C′EF=∠FEC=65°,∠∠C'EB=180°-65°-65°=50°.【点睛】本题考查了翻折变换的知识,解答本题关键是掌握折叠前后图形的对应边和对应角相等,另外要熟练运用平行线的性质,难度一般.38.40°或140°【分析】如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. 根据题意, ∠1=∠2或∠1和∠2互补.【详解】解:根据题意,得∠1=∠2=40°或∠2=180°-∠1=180°-40°=140°故答案为40°或140°.【点睛】本题考查了平行线的性质,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.39.5【分析】利用角平分线和平行可证得∠EBD=∠EDB,∠FDC=∠FCD,可得到DE=BE,DF=FC,可得到EF=BE+FC.【详解】∠BD平分∠ABC,∠∠EBD=∠DBC,∠EF∠BC,∠∠EDB=∠DBC,∠∠EBD=∠EDB,∠DE=BE=2,同理DF=3,∠EF=DE+DF=2+3=5.【点睛】此题主要考查学生对等腰三角形的判定与性质和平行线性质的理解和掌握,解答此题的关键是熟练掌握等腰三角形的两角相等或两边相等.40.1.2【分析】过点F 作FG ∠AB ,垂足为G ,过点P 作PD ∠AB ,垂足为D ,根据垂线段最短,得当PD 与FG 重合时PD 最小,利用相似求解即可.【详解】∠90︒∠=C ,6AC =,8BC =,∠AB =10,∠2CF =,将CEF ∆沿直线EF 翻折,点C 落在点P 处,∠CF =PF =2,AF =AC -CF =6-2=4,过点F 作FG ∠AB ,垂足为G ,过点P 作PD ∠AB ,垂足为D ,根据垂线段最短,得当PD 与FG 重合时PD 最小,∠∠A =∠A ,∠AGF =∠ACB ,∠△AGF ∠△ACB , ∠AF GF AB CB =, ∠4108GF =, ∠FG =3.2,∠PD =FG -PF =3.2-2=1.2,故答案为:1.2.【点睛】本题考查了勾股定理,折叠的性质,三角形相似,垂线段最短,准确找到最短位置,并利用相似求解是解题的关键.41.见解析.【分析】根据平行线的判定可得AD∠BE ,然后求出∠2=∠E ,结合已知条件可证明AC∠DE ,进而得到∠C=∠CDE ,再根据角平分线的定义求出∠ADC=∠CDE ,等量代换即可证明结论.【详解】证明:∠∠A=∠1,∠AD∠BE ,∠∠2=∠E ,∠∠1=∠2,∠∠1=∠E ,∠AC∠DE ,∠∠C=∠CDE ,∠CD 平分∠ADE ,∠∠ADC=∠CDE ,∠∠C=∠ADC.【点睛】本题考查了角平分线的定义以及平行线的判定和性质,灵活运用平行线的判定定理和性质定理是解题的关键.42.70°【分析】过点C 作//CF BA ,根据平行线的性质及可求解;【详解】解:过点C 作//CF BA ,∠30BCF B ∠=∠=︒,∠//BA DE ,∠//CF DE ,∠40FCD D ∠=∠=︒,∠70BCD BCF FCD ∠=∠+∠=︒.【点睛】本题主要考查平行线的性质,掌握平行线的性质是解题的关键.43.DE ∠BC ,理由见解析【分析】由条件可得到∠2+∠DFH =180°,可证得AB//EH ,可得到∠3+∠BDE=180°,结合条件可证明DE//BC【详解】DE ∠BC ,理由如下:∠∠1+∠2=180°,∠1=∠DFH ,∠∠2+∠DFH =180°,∠AB ∠EH ,∠∠3+∠BDE =180°,∠∠B =∠3,∠∠B +∠BDE =180°,∠DE ∠B C .【点睛】本题主要考查平行线的判定,用到的知识点为:同旁内角互补,两直线平行. 44.垂直的定义;内错角相等,两直线平行;两直线平行,同位角相等;等量代换;90°;同角的余角相等;内错角相等,两直线平行.【分析】根据垂直的定义,平行线的判定与性质即可得.【详解】证明∠∠AF ∠CE (已知),∠∠AOE =90°(垂直的定义),又∠∠1=∠B (已知),∠CE BF ∥ (内错角相等,两直线平行),∠∠AFB =∠AOE (两直线平行,同位角相等),∠∠AFB =90°(等量代换),又∠∠AFC +∠AFB +∠2=180°(平角的定义),∠∠AFC +∠2=(90°),又∠∠A +∠2=90°(已知),∠∠A =∠AFC (同角的余角相等),∠AB CD ∥ (内错角相等,两直线平行),故答案为:垂直的定义;内错角相等,两直线平行;两直线平行,同位角相等;等量代换;90°;同角的余角相等;内错角相等,两直线平行.【点睛】本题考查了垂直的定义,平行线的判定与性质,解题的关键是掌握这些知识点. 45.(1)证明见解析;(2)四边形DECF 的面积=8【分析】(1)根据等腰三角形的性质和平行线的性质得到BDE BED ∠=∠,求得BD BE =,推出四边形DECF 是平行四边形,于是得到结论;(2)过点F 作FG BC ⊥交BC 于G ,根据菱形的性质得到4CF =,根据等腰三角形的性质得到A C ∠=∠,根据直角三角形的性质得到122FG FC ==,于是得到结论.【详解】(1)解:AB BC =,A C ∴∠=∠,//DE AC ,BDE A ∴∠=∠,BED C ∠=∠,BDE BED ∴∠=∠,BD BE ∴=,BA BD BC BE ∴-=-,AD CE ∴=,AD DE =,DE EC ∴=,CE CF =,DE CF ∴=,//DE FC ,∴四边形DECF 是平行四边形,CE CF =,∴四边形DECF 是菱形;(2)解:过点F 作FG BC ⊥交BC 于G ,四边形DECF 是菱形,4CE =,4CF ∴=,AB BC =,A C ∴∠=∠,30A ∠=︒,30C ∴∠=︒,90FGC ∠=︒,30C ∠=︒,122FG FC ∴==, ∴四边形DECF 的面积428EC FG ==⨯=.【点睛】本题考查了菱形的判定和性质,平行四边形的判定和性质,等腰三角形的性质,直角三角形的性质,解题的关键是正确的识别图形.46.见解析【分析】根据角平分线和平行线的性质以及等腰三角形的判定解答即可.【详解】证明:∠AD 是∠CAE 的平分线,∠∠BAD =∠DAE ,∠BD ∠AE ,∠∠BDA =∠DAE ,∠∠BAD =∠BDA ,∠AB =BD ,∠AB =BC ,∠BC =BD ,∠∠C =∠CDB ,∠BD ∠AE ,∠∠E =∠CDB ,∠∠C =∠E ,∠AC =AE .【点睛】此题考查等腰三角形的性质与判定,关键是根据角平分线和平行线的性质得出BC=BD .47.(1)见解析;(2)∠见解析,∠DPG =65°;∠(90°﹣12a )或(90°+12a ) 【分析】(1)利用邻补角的意义,得出∠D =∠AFD ,根据内错角相等,两直线平行即可得结论;(2)∠根据题意画出图形结合(1)即可求出∠DPG 的度数;∠结合∠即可写出∠DPG 的度数.【详解】(1)证明:∠∠AFC +∠AFD =180°,∠AFC +α=180°,∠∠AFD =α=∠CDE ,∠AB∠DE;(2)解:∠如图即为补齐的图形,∠∠FDG与∠DGB的角平分线所在的直线交于点P,∠∠FDG=2∠FDP=2∠GDP,∠DGB=2∠DGQ=2∠BGQ,由(1)知AB∠DE,∠∠DFB=180°﹣α=180°﹣50°=130°,∠∠DGB=∠FDG+∠DFG,∠2∠DGQ=2∠GDP+130°,∠∠DGQ=∠GDP+65°,∠∠DGQ=∠GDP+∠DPG,∠∠DPG=65°;∠由∠知∠DPG=12∠DFB=12(180°﹣α)=90°﹣12a.当点G在AF上时,∠DPG=180°﹣(∠GDP+∠DGP)=180°﹣12(∠GDC+∠DGB)=180°﹣12∠DFB=180°﹣12(180°﹣α)=90°+12 a.故答案为:(90°﹣12a)或(90°+12a).【点晴】考查了平行线的判定与性质,解题关键是灵活运用其性质.48.两直线平行,同位角相等;DF;BE;同位角相等,两直线平行;两直线平行,内错角相等.【分析】根据平行线的性质得出∠ABC=∠ADE,根据角平分线定义得出∠3=12∠ABC,∠4=12∠ADE,求出∠3=∠4,根据平行线的判定得出DF∠BE,根据平行线的性质得出即可.【详解】证明:∠BC∠DE,∠∠ABC=∠ADE(两直线平行,同位角相等).∠BE、DF分别是∠ABC、∠ADE的平分线.∠∠3=12∠ABC,∠4=12∠ADE.∠∠3=∠4,∠DF∠BE(同位角相等,两直线平行),∠∠1=∠2(两直线平行,内错角相等),故答案是:两直线平行,同位角相等;DF;BE;同位角相等,两直线平行;两直线平行,内错角相等.【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,能综合运用平行线的性质和判定进行推理是解此题的关键.49.见解析.【分析】根据∠ABC∠∠DEF,得到∠A=∠D,∠1=∠2,根据内错角相等,两直线平行即可判定.【详解】解:证明:∠∠ABC∠∠DEF∠∠A=∠D,∠AB//DE;∠∠ABC∠∠DEF,∠∠1=∠2,∠BC//EF.【点睛】考查全等三角形的性质以及平行线的判定,掌握全等三角形的性质是解题的关键.50.(1)两直线平行,同旁内角互补;这两条直线互相平行;360°(2)∠BPD=∠B+∠D;理由见解析(3)图∠:∠D=∠B+∠BPD;图∠:∠B=∠BPD+∠D【分析】(1)利用平行线的性质解答;(2)作平行线,根据内错角相等可证∠BPD=∠B+∠D;(3)同样作平行线,根据内错角相等可证∠B=∠BPD+∠D.【详解】(1)过点P作EF∥AB,如图所示:∠∠B+∠BPE=180°(两直线平行,同旁内角互补),∠AB∥CD,EF∥AB,∠CD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),∠∠EPD+∠D=180°,∠∠B+∠BPE+∠EPD+∠D=360°,∠∠B+∠BPD+∠D=360°.故答案为:两直线平行,同旁内角互补;这两条直线互相平行;360°.(2)猜想∠BPD=∠B+∠D;理由:过点P作EP∥AB,如图所示:∠EP∥AB,∠∠B=∠BPE(两直线平行,内错角相等),∠AB∥CD,EP∥AB,∠CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),∠∠EPD=∠D,∠∠BPD=∠B+∠D.(3)图∠结论:∠D=∠BPD+∠B,。
中考复习初中数学几何证明经典试题(含答案)
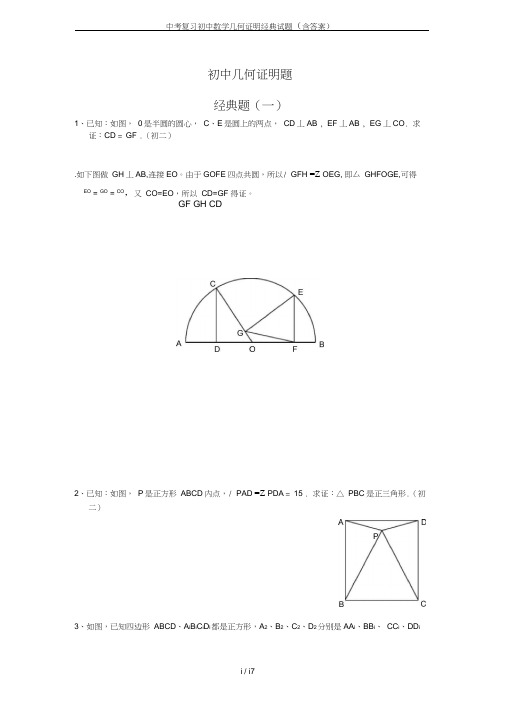
初中几何证明题经典题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB , EF丄AB , EG丄CO. 求证:CD = GF .(初二).如下图做GH丄AB,连接EO。
由于GOFE四点共圆,所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO,又CO=EO,所以CD=GF 得证。
GF GH CD2、已知:如图,P是正方形ABCD内点,/ PAD =Z PDA = 15°. 求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD、A i B i C i D i都是正方形,A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二)3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN P 、Q .4、 1、求证:四边形 A 2B 2C 2D 2是正方形.(初二)已知: 求证: 如图,在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中,AD = BC , M 、N 分别是 AB 、CD 的中点,AD 、BC 于E 、F .经典题(二)已知: (1) 求证:AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 (各边高线的交点),0为外心,且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线,过O 作OA 丄MN 于A ,自A 引圆的两条直线,交圆于DCGN求证:AP = AQ .(初二)ECAM NP4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于 AB 的一半.(初二)经典题(二)1、如图,四边形 ABCD 为正方形, 求证:CE = CF .(初二)2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于F . 求证:AE = AF .(初二)DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)B 、D .求证: AB = DC , BC = AD .(初三)1、已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)AO DB EFC求证:4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数. LiB C经典题(一)1•如下图做GH丄AB,连接E0。
中考数学模拟题汇总《平行线的证明》专项练习(附答案解析)

中考数学模拟题汇总《平行线的证明》专项练习(附答案解析)一、综合题1.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.2.如图,在矩形ABCD中,E是BC边上的点,AE=BC ,DF⊥AE,垂足为F,连接DE。
(1)求证:AB=DF;(2)若CE=1,AF=3,求DF的长。
3.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D在同一直线上,且AB∥DE,连接AE.(1)求证:△ABC≌△DCE.(2)当BC=5,AC=12时,求AE的长.4.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是.(2)猜想论证当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.(3)拓展探究已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使SΔDCF=SΔFDE,请直接写出相应的BF的长.5.如图, ∠1+∠2=180° , ∠DEF=∠A , ∠BED=70° .(1)求证: EF//AB :(2)求∠ACB的度数.6.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.7.在△ABC中,点D在直线AB上,在直线BC上取一点E,连接AE,DE,使得 AE=DE,DE交AC于点G,过点D作DF∥AC,交直线BC于点F,∠EAC=∠DEF.(1)当点E在BC的延长线上,D为AB的中点时,如图1所示.①求证:∠EGC=∠AEC;②若DF=3,求BE的长度;(2)当点E在BC上,点D在AB的延长线上时,如图2所示,若CE=10,5EG=2DE,求AG的长度.8.如图1,在Rt△ABC中,∠C=90°,AC=BC=2√2,点D、E分别在边AC、AB上,AD=DE=12AB,连接DE .将△ADE绕点A顺时针方向旋转,记旋转角为θ .(1)(问题发现)①当θ=0°时,BECD =;②当θ=180°时,BECD=;(2)(拓展研究)试判断:当0°≤θ<360°时,BECD的大小有无变化?请仅就图2的情形给出证明;(3)(问题解决)在旋转过程中,求出BE的最大值.9.如图,已知AB是圆O的直径,F是圆O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.(1)求证:DE是⊙O的切线;(2)若DE=3,CE=2,的值;①求BCAEEG最小值.②若点G为AE上一点,求OG+ 1210.如图,已知在菱形ABCD中,AB=5,cosB=3,点E、F分别在边BC、CD上,AF的延长5∠BAD.线交BC的延长线于点G,且∠EAF=12(1)求证:AE2=EC⋅EG;(2)如果点F是边CD的中点,求S△ABE的值;(3)延长AE、DC交于点H,联结GH、AC,如果△AGH与△ABC相似,求线段BE的长.11.如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心的圆恰好经过A、B、C三点,⌢=CE⌢,连接OA、OF.⊙O交BD于E,交AD于F,且AE(1)求证:四边形ABCD是菱形;(2)若∠AOF=3∠FOE,求∠ABC的度数.,过点C作CD∥AB,点E在边AC上,AE=CD,联结12.在△ABC中,AB=AC=10,sin∠BAC= 35AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.(1)求证:∠ABE=∠CAD.(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.(3)若△DFG是直角三角形,求△CEF的面积.13.在ΔABC中,∠A=90°,AB=8cm,AC=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s 的速度向点C运动(点M不与A,B重合,点N不与A,C重合),设运动时间为xs .(1)求证:ΔAMN∽ΔABC;(2)当x为何值时,以MN为直径的⊙O与直线BC相切?(3)把ΔAMN沿直线MN折叠得到ΔMNP,若ΔMNP与梯形BCNM重叠部分的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?14.如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作CD∥AB,且CD=OB .连接AD,分别交OC,BC于点E,F,与⊙O交于点G,若∠ABC=45∘ .(1)求证:①△ABF∽△DCF;②CD是⊙O的切线.(2)求EF的值.FG15.小东在做九上课本123页习题:“1:√2也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:√2.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.(1)你赞同他的作法吗?请说明理由.(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.①如图3,当点D运动到点A时,求∠CPE的度数.②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.16.在等腰△ABC中,AB=BC,点D,E在射线BA上,BD=DE,过点E作EF//BC,交射线CA于点F.请解答下列问题:(1)当点E在线段AB上,CD是△ACB的角平分线时,如图①,求证:AE+BC=CF;(提示:延长CD,FE交于点M.)(2)当点E在线段BA的延长线上,CD是△ACB的角平分线时,如图②;当点E在线段BA的延长线上,CD是△ACB的外角平分线时,如图③,请直接写出线段AE,BC,CF之间的数量关系,不需要证明;(3)在(1)、(2)的条件下,若DE=2AE=6,则CF=.参考答案与解析1.【答案】(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,∴OE=OC,OC=OF,∴OE=OF(2)解:当O运动到AC中点时,四边形AECF是矩形,∵AO=CO,OE=OF,∴四边形AECF是平行四边形,∵∠ECA+∠ACF= 12∠BCD,∴∠ECF=90°,∴四边形AECF是矩形2.【答案】(1)证明:在矩形ABCD中∴BC=AD AD∥BC,∠B=∠C=90°∴∠DAF=∠AEB∵DF⊥AE,AE=BC,∴∠AFD=90°=∠B,AE=AD∴△ABE≌△DFA,∴AB=DF(2)解:由(1)可得△ABE≌△DFA,∴AF=BE=3,DF=AB=CD∴∠DFE=∠DCE∴△DFE≌△DCE,∴CE=EF=1,AE=4在Rt△ABE中,AB= √42−32 = √73.【答案】(1)证明:∵AB∥DE,∴∠BAC=∠D.在△ABC和△DCE中,{∠B=∠DCE∠BAC=∠DAC=DE∴△ABC≌△DCE(AAS)(2)解:由(1)可得△ABC≌△DCE,∴CE=BC=5,在Rt△ACE中,AE=√AC2+CE2=√122+52=13.4.【答案】(1)DE∥AC;S1=S2(2)解:如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,{∠ACN=∠DCM∠CMD=∠N=90°AC=CD,∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2(3)解:如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF1=S△BDE;过点D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,∵BF1=DF1,∠F1BD= 12∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB= 12×60°=30°,∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,∵在△CDF1和△CDF2中,{DF1=DF2∠CDF1=∠CDF2CD=CD,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD= 12×60°=30°,又∵BD=4,∴BE= 12×4÷cos30°=2÷√32= 4√33,∴BF1= 4√33,BF2=BF1+F1F2= 4√33+ 4√33= 8√33,故BF的长为4√33或8√33.5.【答案】(1)解:∵∠1+∠DFE=180°,∴∠1+∠2=180°.∴∠DFE=∠2,∴EF//AB;(2)解:∵EF//AB , ∴∠DEF=∠BDE. 又∵∠DEF=∠A , ∴∠BDE=∠A , ∴DE//AC , ∴∠ACB=∠DEB. 又∵∠DEB=70°, ∴∠ACB=70°.6.【答案】(1)解:连接OF ;根据切线长定理得:BE=BF ,CF=CG ,∠OBF=∠OBE ,∠OCF=∠OCG ; ∵AB ∥CD ,∴∠ABC+∠BCD=180°, ∴∠OBE+∠OCF=90°, ∴∠BOC=90°(2)解:由(1)知,∠BOC=90°.∵OB=6cm ,OC=8cm ,∴由勾股定理得到:BC= √OB 2+OC 2 =10cm ,∴BE+CG=BC=10cm(3)解:∵OF ⊥BC ,∴∠BFO=∠OFC=90°∵∠BOC=90°∴∠BOF+∠COF=90°,∠COF+∠FCO=90°。
中考数学【相交线与平行线】考点专项复习教案(含例题、习题、答案)

第五章相交线与平行线本章小结小结1 本章概述本章的主要内容是两条直线的位置关系——相交与平行.特别是垂直和平行关系是平面几何所要研究的基本内容之一.这一章的内容是很重要的基本知识,是几何学习的重要阶段,要引起高度重视.教材在给出对顶角、邻补角、垂线、点到直线的距离等概念的基础上又给出了对顶角、邻补角的性质、垂线的基本性质和平行线的判定和性质,最后给出平移的概念、性质以及利用平移绘制图案.小结2 本章学习重难点【本章重点】了解对顶角、余角、补角的概念;掌握等角的余角相等,等角的补角相等;掌握垂线、垂线段的概念;知道两条直线平行,同位角相等以及同位角相等,两直线平行,进一步探索平行线的性质和判定.【本章难点】掌握垂线段最短的性质,体会点到直线的距离的意义;通过具体实例认识平移;能按要求作出简单平面图形平移后的图形,利用平移进行图案设计,认识和欣赏平移在现实生活中的应用.小结3 中考透视中考所考查的内容主要体现在以下几个方面:1. 对顶角、邻补角、垂线、点到直线的距离等概念的理解,对顶角、邻补角以及垂线性质的应用,包括实际应用.2. 同位角、内错角、同旁内角的含义,能由线找出角、由角说出线.3. 平行线的识别与特征,以及在实际问题中的应用.4. 简单命题的证明.知识网络结构图专题总结及应用一、知识性专题专题1 有关基本图形的问题【专题解读】本章中主要考查数图形的个数问题,构造基本图形以及基本图形的组合,如平行线与角平分线的组合,平行线与平行线的组合等.例1 如图5-132所示,直线AB,CD,EF都经过点O,图中共有几对对顶角?分析数基本图形不能重复,不能遗漏.我们知道两条直线相交有两对对顶角,图中有3组两条直线相交,故对顶角有2×3=6(对).解:共有6对对顶角.【解题策略】数图形个数及书写时,应注意顺序性,这样不易例2 如图5-133所示,图中共有几对同旁内角?分析我们知道两条直线被第三条直线所截共形成八个角,其中有两对同旁内角.图形中有两个“三线八角”,即CD,EF被GH所截,形成两对同旁内角,AB,EF被GH所截,又形成两对同旁内角,所以共有4对同旁内角.解:图中共有4对同旁内角.【解题策略】注意观察同旁内角的特点.例3 如图5-134所示,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.分析此图不是我们所学的“三线八角”的基本图形,需添加一些线(辅助线)把它们转化成我们熟悉的基本图形.解:如图5-134所示,过点P作射线PN∥AB.因为AB∥CD(已知),所以PN∥CD(平行于同一条直线的两直线平行),所以∠4=∠2=25°(两直线平行,内错角相等).因为PN∥AB(已知),所以∠3=∠1=32°(两直线平行,内错角相等).所以∠BPC=∠3+∠4=32°+25°=57°.【解题策略】构造基本图形就是将残缺的基本图AB所以GM∥HN(内错角相等,两直线平行).【解题策略】此题考查平行线的性质、判定以及角平分线的综合应用.例5 如图5-136所示,已知AB∥CD,BC∥DE.试说明∠B=∠D.分析条件为直线平行,故可根据平行线的性质说明.解:因为AB∥CD(已知),所以∠B=∠C(两直线平行,内错角相等).因为BC∥DE(已知),所以∠C=∠D(两直线平行,内错角相等).【解题策略】此题重点考查了平行线的性质的应用.例6 如图5-137所示,已知AB∥CD,G为AB上任一点,GE,GF分别交CD于E,F.试说明∠1+∠2+∠3=180°.分析要说明180°问题,想到了“平角”和“两直线平行,同旁内角互补”这两个知识点,故可用它们解决问题.解:因为AB∥CD(已知),所以∠4=∠2,∠3=∠5(两直线平行,内错角相等).因为∠4+∠1+∠5=180°(平角定义),所以∠2+∠1+∠3=180°(等量代换).【解题策略】此题把说明∠2+∠1+∠3=180°转化为说明∠1+∠5+∠4=180°,应用等量代换解决了问题.例7 如图5-138所示,AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC.试说明OE⊥OF解:因为OE,OF分别平分∠AOC与∠BOC(已知),所以∠1=12∠AOC,∠2=12∠BOC(角平分线定义).所以∠1+∠2=12∠AOC+12∠BOC=12(∠AOC+∠BOC).又因为∠AOC+∠BOC=180°(邻补角定义),所以∠1+∠2=1×180°=90°,∠和°可说明∠1+∠2=90°.例9 如图5-140所示,在三角形ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC.试说明∠1=∠2.解:因为CD⊥AB,FG⊥AB(已知),所以∠CDB=∠FGB=90°(垂直定义),所以∠2=∠3(两直线平行,同位角相等).因为DE∥BC(已知),所以∠1=∠3(两直线平行,内错角相等),所以∠1=∠2(等量代换).【解题策略】多次运用平行线的性质说明∠1,∠2,∠3的关系.二、规律方法专题专题2 基本命题的计算与证明【专题解读】基本命题的计算与证明涉及的题型有(1)有关角的计算;(2)有关角相等的判定;(3)判定平行问题;(4)判定垂直问题;(5)判定共线问题.例10 如图5-141所示,已知∠4=70°,∠3=110°,∠1=46°,求∠2的度数.分析由∠3+∠4=180°,知AB∥CD,故∠2=180°-∠1.解:因为∠4=70°,∠3=110°(已知),所以∠4+∠3=180°,所以AB∥CD(同旁内角互补,两直线平行),所以∠2=180°-∠1=180°-46°=134°(两直线平行,同旁内角互补).【解题策略】此题考查由同旁内角互补判定两直线平行,由两直线平行可行同旁内角互补,从而计算相关的角.例11 如图5-142所示,AB∥CD,EB∥DF.试说明∠1=∠2.解:因为AB∥CD(已知),所以∠1+∠3=∠2+∠4(两直线平行,内错角相等).因为EB∥DF(已知),所以∠3=∠4(两直线平行,内错角相等),所以∠1=∠2(等式性质).【解题策略】判定角相等的方法有:(1)同角(等角)的余角相等;(2)同角(等角)的补角相等;(3)对顶角相等;(4)角平分线定义;(5)两直线平行,同位角相等;(6)两直线平行,内错角相等.例12 如图5-143所示,DF∥AC,∠1=∠2.试说明DE=AB.分析要说明DE∥AB,可说明∠1=∠A,而由DF∥AC,有∠2=∠A.又因为∠1=∠2,故有∠1=∠A,从而得出结论.解:因为DF∥AC(已知),所以∠2=∠A(两直线平行,同位角相等).因为∠1=∠2(已知),所以∠1=∠A(等量代换),所以DE∥AB(同位角相等,两直线平行).【解题策略】判定平行的方法有:(1)平行于同一条直线的两直线平行;(2)垂直于同一条直线的两直线平行;(3)同位角相等,两直线平行;(4)内错角相等,两直线平行;(5)同旁内角互补,两直线平行.例13 如图5-144所示,∠1=∠2,CD∥EF.试说明EF⊥AB.分析要说明EF⊥AB,可说明∠2=90°,而由CD∥EF,可得∠1+∠2=180°,又∠1=∠2,所以有∠1=∠2=90°,从而得出结论.解:因为CD∥EF(已知),所以∠1+∠2=180°(两直线平行,同旁内角互补).又因为∠1=∠2(已知),所以∠1=∠2=90°,所以EF⊥AB(垂直定义).【解题策略】判定垂直的方法有:(1)说明两条相交线的一个交角为90°;(2)说明邻补角相等;(3)垂直于平行线中的一条,也必垂直于另一条.例14 如图5-145所示,直线AB,CD相交于点O,OE平分∠AOC,OF平分∠BOD.试说明E,O,F三点在一条直线上.分析要说明E,O,F三点共线,只需说明∠EOF=180°.解:因为AB,CD相交于点O(已知),所以∠AOC=∠BOD(对顶角相等).因为OE,OF分别平分∠AOC与∠BOD(已知),已知的.例15 如图5-146所示,直线AB,CD相交于点O,OD平分∠AOE,且∠COA:∠AOD=7:2,求∠BOE的度数.分析欲求∠BOE,因为∠BOE与∠AOE互为邻补角,所以可先求∠AOE,而∠AOE=2∠AOD,所以只需求∠AOD即可,由已知条件可求得∠AOD.解:∵∠COA+∠AOD=180°,∠COA:∠AOD=7:2,∴∠COA=79×180°=140°,∠AOD=29×180°=40°.∵OD平分∠AOE,∴∠AOE=2∠AOD=2×40°=80°,∴∠BOE=180°-∠AOE=180°-80°=100°.【解题策略】互为邻补角的两个角的和为180°、对顶角相等是在有关求角的大小的问题中常用的两个等量关系,要注意发现图形中的这两种角,它们常隐藏在直线条件的背后.2011中考真题相交线与平行线精选一、选择题1.(2011云南保山2,3分)如图,l1∥l2,∠1=120°,则∠2= .考点:平行线的性质;对顶角、邻补角。
中考数学模拟题汇总《平行线的判定》专项练习(附答案解析)

中考数学模拟题汇总《平行线的判定》专项练习(附答案解析)一、综合题1.已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.(1)求证:BD平分∠ABC;(2)若∠DAC=45°,OA=1,求OC的长.2.已知等腰直角△ABC中,∠BAC=90°,AB=AC,以A为顶点作等腰直角△ADE,其中AD=DE.(1)如图1,点E在BA的延长线上,连接BD,若∠DBC=30°,若AB=6,求BD的值;(2)将等腰直角△ADE绕点A顺时针旋转至图2,连接BE,CE,过点D作DF⊥CE交CE的延长线于F,BE;交BE于M,求证:BM=12(3)如图3,等腰直角△ADE的边长和位置发生变化的过程中,DE边始终经过BC的中点G,连接BE,N 为BE中点,连接AN,当AB=6且AN最长时,连接NG并延长交AC于点K,请直接写出△ANK的面积.3.如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC .(1)求抛物线的解析式;(2)若四边形OABE的面积为14,求S△ECF;(3)是否存在点E,使得△BEF为等腰三角形?若存在,求点E的坐标;若不存在,请说明理由. 4.如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1 = x2 + 2x + 2与y2 = x2 - 2x + 2是“关于y轴对称二次函数”.(1)二次函数y= 2(x + 2)2 + 1的“关于y轴对称二次函数”解析式为;二次函数y = a(x - h)2 + k的“关于y轴对称二次函数”解析式为;(2)如备用图,平面直角坐标系中,记“关于y轴对称二次函数”的图象与y轴的交点为A,它们的两个顶点分别为B,C,且BC=6,顺次连接点A,B,O,C得到一个面积为24的菱形,求“关于y轴对称二次函数”的函数表达式.(3)在第(2)题的情况下,如果M是两个抛物线上的一点,以点A,O,C,M为顶点能否构成梯形. 若能,求出此时M坐标;若不能,说明理由.5.如图1,我们把一副两个三角板如图摆放在一起,其中OA,OD在一条直线上,∠B=45°,∠C=30°,固定三角板ODC,将三角板OAB绕点O按顺时针方向旋转,记旋转角∠AOA'=α(0<α<180°).(1)在旋转过程中,当α为度时,A'B'∥OC,当α为度时,A'B'⊥CD;(2)如图2,将图1中的△OAB以点O为旋转中心旋转到△OA'B'的位置,求当α为多少度时,OB'平分∠COD;(3)当90°<α<120°时,连接A'D,利用图3探究∠B'A'D+∠B'OC+∠A'DC值的大小变化情况,并说明理由.6.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D。
2018届中考数学复习 专题21 平面几何初步(点、线、面、角、相交线与平行线等)试题(B卷,含解析)

平面几何初步一、选择题1. ( 福建福州,3,3分)如图,直线a ,b 被直线c 所截,∠1和∠2的位置关系是A .同位角B .内错角C .同旁内角D .对顶角【答案】B【逐步提示】本题考查了同位角、内错角、同位角和对顶角的识别,解题的关键是认识三线八角,根据内错角的定义可得答案.【详细解答】解:直线a ,b 被直线c 所截,∠1与∠2是内错角,故选择B .【解后反思】三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线. 【关键词】内错角;同位角;同旁内角;对顶角2. ( 甘肃省武威市、白银市、定西市、平凉市、酒泉市、临夏州、张掖市等9市,6,3分)如图,AB ∥CD ,DE ⊥CE ,∠1=34º,则∠DCE 的度数为( )A . 34º B.54º C. 66º D . 56º1BE第6题图【答案】D 【逐步提示】本题考查了平行线的性质,解题的关键是将线的位置关系转化为角的数量关系,应用平行线的性质:两直线平行线内错角相等得出∠EDC 的度数,再利用直角三角形两锐角互余得出∠DCE 的度数. 【详细解答】解:∵AB ∥CD ,∴ ∠EDC =∠1=34°.∵DE ⊥CE ∴ ∠DEC =90°,∴∠EDC +∠DCE =90°.∴∠DCE =90°-34°=56º,故选择D .【解后反思】本题考查了平行线的性质即两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.【关键词】平行线的性质;垂直的定义;直角三角形的性质; 3. ( 甘肃省天水市,5,4分)如图,直线AB ∥CD ,OG 是∠EOB 的平分线,∠EFD =70°,则∠BOG 的度数是( ) A .70° B .20° C .35° D .40°【答案】C【逐步提示】本题考查了平行线的性质和角平分线的定义,解题关键是注意两直线平行,相关的同位角相等、内错角相等及同旁内角互补.要求∠BOG 的度数,关键是先求∠EOB 的度数,这可根据∠EFD =70°,联想到两直线CO A B D E FG平行,同位角相等解决.【详细解答】解:∵AB∥CD,∴∠EOB=∠EFD=70°.又∵OG平分∠EOB,∴∠BOG=12∠EOB=12×70°=35°.故选择C.【解后反思】平行线间的角离不开同位角、同旁内角,及内错角等知识,另外还要和三角形的内角和定理,及外角等于与它不相邻的两内角和知识相联系,只要从这些方面思考,就不难得到解决.【关键词】平行线的性质;角的平分线.4.(广东茂名,5,3分)如图,直线a、b被直线c所截,若a∥b,∠1=60°,那么∠2的度数为()A.120°B.90°C.60°D.30°【答案】C【逐步提示】本题考查了平行线的性质,解题的关键是识别出图中的∠1、∠2是两条平行直线a、b被第三条直线c截出的一组相等的同位角.直接利用“两直线平行,同位角相等”解题即可.【详细解答】解:∵a∥b,∴∠1=∠2. ∵∠1=60°,∴∠2=60°.故选择C .【解后反思】“两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补”这是由直线的位置关系得出角的数量关系,“同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;”这是由角的数量关系得出直线的位置关系,这里体现了数形结合的思想.【关键词】同位角;平行线的性质5.(贵州省毕节市,8,3分)如图,直线a//b,∠1=85°,∠2=35°,则∠3=()(第8题图)A. 85°B. 60°C. 50°D. 35°【答案】C【逐步提示】本题考查平行线的性质,三角形外角和定理,解题的关键是能从图中发现∠3与∠1、∠2的联系.【详细解答】解:如图,∵a//b,∴∠4=∠3.又∵∠1=∠2+∠4,∴∠4=∠1-∠2=85°-35°=50°,∴∠3=50°,故选择C.【解后反思】此类问题容易出错的地方是找不到图形中角与角之间的数量关系.【关键词】平行线的性质;三角形外角和定理6.(河北省,13,2分)如图,将□ABCD沿对角线AC折叠,使点B落在点B’处.若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°【答案】C【逐步提示】根据平行线的性质和折叠的性质得到∠BAC=12∠B’AB=12∠1=22°,再在△ABC中根据三角形内角和定理求得∠B的度数.【详细解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B’AB=∠1=44°.根据折叠的性质可知∠BAC=12∠B’AB=12×44°=22°.又∵∠2=44°,∴∠B=180°-22°-44°=114°,故答案为选项C.【解后反思】折叠问题是属于轴对称变换,折叠后图形的形状和大小不变,三角形折叠后得到的三角形与原三角形全等,对应边和对应角相等.【关键词】平行四边形的性质;平行线的性质;折叠;三角形内角和定理7.(湖北省黄冈市,3,3分)如图,直线a∥b,∠1=550,则∠2= ()A.350B.450C. 550D.650【答案】C【逐步提示】本题考查了平行线的性质“两直线平行,同位角相等”及对顶角的性质“对顶角相等”,解题的关键是能观察出∠1与∠2之间的联系而不走弯路.由图易发现,∠1的对顶角与∠2是同位角,a∥b是沟通∠1与∠2的桥梁.【详细解答】解:如图,∵a∥b,∴∠3=∠2.∵∠3=∠1,∴∠2=∠1=55°,故选择C.【解后反思】此类题主要考查形式为选择或填空,解决此类题型常用的方法是根据平行线的性质:两直线平行同位角相等、两直线平行内错角相等,两直线平行同旁内角互补,结合对顶角相等或邻补角和为180°,直接求出正确答案后做出选择.【关键词】平行线的性质;对顶角。
中考数学一轮复习数学第五章 相交线与平行线试题含答案
中考数学一轮复习数学第五章 相交线与平行线试题含答案一、选择题1.把一张有一组对边平行的纸条,按如图所示的方式析叠,若∠EFB =35°,则下列结论错误的是( )A .∠C 'EF =35°B .∠AEC =120° C .∠BGE =70°D .∠BFD =110° 2.如图,已知AB CD ∕∕,AF 交CD 于点E ,且,40BE AF BED ⊥∠=︒,则A ∠的度数是( )A .40︒B .50︒C .80︒D .90︒3.甲,乙两位同学用尺规作“过直线l 外一点C 作直线l 的垂线”时,第一步两位同学都以C 为圆心,适当长度为半径画弧,交直线l 于D ,E 两点(如图);第二步甲同学作∠DCE 的平分线所在的直线,乙同学作DE 的中垂线.则下列说法正确的是( )A .只有甲的画法正确B .只有乙的画法正确C .甲,乙的画法都正确D .甲,乙的画法都不正确4.已知:如图,直线a ∥b ,∠1=50°,∠2=∠3,则∠2的度数为( )A .50°B .60°C .65°D .75°5.如图,下列能判断AB ∥CD 的条件有 ( )①∠B+∠BCD=180°②∠1 = ∠2 ③∠3 =∠4 ④∠B = ∠5A.1 B.2 C.3 D.46.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为()A.①②③④B.①②④C.①③④D.①②③7.下列命题是假命题的有()①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.A.1个B.2个C.3个D.4个8.如图,直线AB、CD、EF相交于点O,其中AB⊥CD,∠1:∠2=3:6,则∠EOD=()A.120° B.130° C.60° D.150°9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是()A.∠1=50°,∠2=40°B.∠1=50°,∠2=50°C.∠1=∠2=45°D.∠1=40°,∠2=40°⊥于点B,在直线l上取一点C,连接10.如图,A是直线l外一点,过点A作AB lAC,使2=,P在线段BC上,连接AP.若3AC ABAB=,则线段AP的长不可能是()A .4B .5C .2D .5.5二、填空题11.如图,现给出下列条件:①∠1=∠2,②∠B =∠5,③∠3=∠4,④∠5=∠D ,⑤∠B+∠BCD =180°,其中能够得到AD ∥BC 的条件是______(填序号);能够得到AB ∥CD 的条件是_______.(填序号)12.如图,点О为直线AB 上一点,,,135OC OD OE AB ⊥⊥∠=︒.(1)EOD ∠= °,2∠= °;(2)1∠的余角是_ ,EOD ∠的补角是__ .13.如图,已知AB ∥CD ,点E ,F 分别在直线AB ,CD 上点P 在AB ,CD 之间且在EF 的左侧.若将射线EA 沿EP 折叠,射线FC 沿FP 折叠,折叠后的两条射线互相垂直,则∠EPF 的度数为 _____.14.如图, 已知//AB CF ,//CF DE , 90BCD ∠=︒,则D B ∠-∠=_________15.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B 灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是.16.如图,有两个正方形夹在AB与CD中,且AB//CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为________度(正方形的每个内角为90°)17.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.18.如图,已知直线AB,CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠BOD=_________.19.如图,a∥b,∠2=∠3,∠1=40°,则∠4的度数是______度.20.如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为_____.三、解答题21.如图1,在平面直角坐标系中,()()02A a C b ,,,,且满足()240a b a b ++-+=,过C 作CB x ⊥轴于B(1)求三角形ABC 的面积.(2)发过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,若,90()CAB ACB a αββ∠=∠=+=︒,求AED ∠的度数.(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等?若存在,求出P 点坐标;若不存在;请说明理由.22.如图,//AB CD ,EG 平分DEF ∠,FG 平分BFE ∠.(1)求证:90EFG GEF ∠+∠=︒;(2)在(1)问的条件下,过点G 作GH AB ⊥,垂足为H ,FGH ∠的平分线GI 交AB 于点I ,EGH ∠的平分线GJ 交AB 于点J ,求IGJ ∠的度数.23.问题情境:如图1,AB CD ∥,130PAB ∠=︒,120PCD ∠=︒,求APC ∠的度数.小明的思路是:如图2,过P 作PE AB ,通过平行线性质,可得APC ∠=______. 问题迁移:如图3,AD BC ∥,点P 在射线OM 上运动,ADP α∠=∠,BCP β∠=∠.(1)当点P 在A 、B 两点之间运动时,CPD ∠、α∠、β∠之间有何数量关系?请说明理由.(2)如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出CPD ∠、α∠、β∠之间有何数量关系.24.问题情境(1)如图①,已知360B E D ∠+∠+∠=︒,试探究直线AB 与CD 有怎样的位置关系?并说明理由.小明给出下面正确的解法:直线AB 与CD 的位置关系是//AB CD .理由如下:过点E 作//EF AB (如图②所示)所以180B BEF ∠+∠=︒(依据1)因为360B BED D ∠+∠+∠=︒(已知)所以360B BEF FED D ∠+∠+∠+∠=︒所以180FED D ∠+∠=︒所以//EF CD (依据2)因为//EF AB所以//AB CD (依据3)交流反思上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?“依据1”:________________________________;“依据2”:________________________________;“依据3”:________________________________.类比探究(2)如图,当B 、E ∠、F ∠、D ∠满足条件________时,有//AB CD . 拓展延伸(3)如图,当B 、E ∠、F ∠、D ∠满足条件_________时,有//AB CD .25.(1)如图1,已知直线//m n ,在直线n 上取A B 、两点,C P 、为直线m 上的两点,无论点C P 、移动到任何位置都有:ABC S ____________ABP S △(填“>”、“<”或“=”)(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.(3)如图3,王爷爷和李爷爷两家田地形成了四边形DEFG ,中间有条分界小路(图中折线ABC ),左边区域为王爷爷的,右边区域为李爷爷的。
中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图在四边形ABCD中AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是()A.CF=AE B.OE=OFC.△CDE为直角三角形D.四边形ABCD是平行四边形2.如图四边形ABCD中AB∥CD,∥B=∥D点E为BC延长线上一点,连接AE,AE交CD于点H,∥DCE的平分线交AE于点G.若AB=2AD=10,点H为CD的中点,HE=6,则AC的值为()A.9B.√97C.10D.3 √103.如图在Rt∥ABC中∥ACB=90°,分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE,连结DE,CA的延长线交DE于点F,则与线段AF相等的是()A.AC B.AB C.BC D.AB4.如图在菱形ΑΒCD中∠Α=60∘,AD=8,F是ΑΒ的中点.过点F作FΕ⊥ΑD,垂足为Ε.将ΔΑΕF沿点Α到点Β的方向平移,得到ΔΑ′Ε′F ′.设Ρ、Ρ′分别是ΕF、Ε′F ′的中点,当点Α′与点Β重合时,四边形ΡΡ′CD的面积为()A.28√3B.24√3C.32√3D.32√3−85.下列说法中错误的是()A.平行四边形的对角线互相平分B.对角线互相垂直的四边形是菱形C.菱形的对角线互相垂直D.对角线互相平分的四边形是平行四边形6.如图.若要使平行四边形ABCD成为菱形.则需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD7.如图点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∥ABC+∥ADC=120°,则∥A的度数是()A.100°B.110°C.120°D.125°8.如图在∥ABC中AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则∥BED与∥DFC的周长的和为()A.34B.32C.22D.209.如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4),当四边形ABCD 的周长最小时,则m 的值为().A.√2B.32C.2D.310.如图分别在四边形ABCD的各边上取中点E,F,G,H,连接EG,在EG上取一点M,连接HM,过F作FN∥HM,交EG于N,将四边形ABCD中的四边形①和②移动后按图中方式摆放,得到四边形AHM′G′和AF′N′E,延长M′G′,N′F′相交于点K,得到四边形MM′KN′.下列说法中错误的是()A.S四边形MM′KN′=S四边形ABCD B.HM=NFC.四边形MM′KN′是平行四边形D.∠K=∠AHM′11.如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为()A.2B.3C.4D.512.如图P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若S四边形AHPE=3,S四边形PFCG=5,则S∥PBD为()A.0.5B.1C.1.5D.2二、填空题13.如图在平行四边形ABCD中点E,F分别在BC,AD上,请添加一个条件,使四边形AECF是平行四边形(只填一个即可).14.如图在Rt△ABC中AC=2√3,BC=2,点P是斜边AB上任意一点,D是AC的中点,连接PD并延长,使DE=PD.以PE,PC为边构造平行四边形PCQE,则对角线PQ的最小值为.15.如图▱ABCD中∥BAD=120°,E、F分别在CD和BC的延长线上,AE∥BD,EF∥BC,EF=5√3,则AB的长是16.如图在∥ABC中∥ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= 13BD,连接DM、DN、MN.若AB=6,则DN=.17.若AC=10,BD=8,那么当AO=DO=时,四边形ABCD是平行四边形。
【中考冲刺】初三数学培优专题 14 平行线分线段成比例(含答案)(难)

平行线分线段成比例阅读与思考平行线分线段成比例定理是证明比例线段的常用依据之一,是研究比例线段及相似形的最基本、最重要的理论.运用平行线分线段成比例定理解题的关键是寻找题中的平行线.若无平行线,需作平行线,而作平行线要考虑好过哪一个点作平行线,一般是由成比例的两条线段启发而得.此外,还要熟悉并善于从复杂的图形中分解出如下的基本图形:例题与求解【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.(上海市竞赛试题)解题思路:建立含PQ 的比例式,为此,应首先判断PQ 与AD (或BC )的位置关系,关键是从复杂的图形中分解出基本图形,并能在多个成比例线段中建立联系.【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )A .3︰2︰1B .4︰2︰1C .5︰4︰3D .5︰3︰2(“祖冲之杯”邀请赛试题)解题思路:因题设条件没有平行线,故须过M 作BC 的平行线,构造基本图形.A BCDEGH MQA BCDEFP【例3】如图,□ABCD中,P为对角线BD上一点,过点P作一直线分别交BA,BC的延长线于Q,R,交CD,AD于S,T.求证:PQ•PT=P R•PS.(吉林省中考试题)解题思路:要证PQ•PT=P R•PS,需证PQPS=PRPT,由于PQ,PT,P R,PS在同一直线上,故不能直接应用定理,需观察分解图形.【例4】梯形ABCD中,AD//BC,AB=DC.(1)如图1,如果P,E,F分别是BC,AC,BD的中点,求证:AB=PE+PF;(2)如图2,如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.(上海市闵行区中考试题)解题思路:(1)不难证明;对于(2),先假设结论成立,从平行线出发证明AB=PE+PF,即要证明PEAB+PFAB=1,将线段和差问题的证明转化为与成比例线段相关问题的证明.AB CDEFP图2AB CDEFP图1QARBCDSP【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .求证:MN +PQ =2PN .解题思路:考虑延长BA ,EC 构造平行四边形,再利用平行线设法构造有关的比例式.(浙江省竞赛试题)【例6】已知:△ABC 是任意三角形.(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且AM AB =13,AN AC =13,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;(3)如图3,点M ,N 分别在边AB ,AC 上,且P 1,P 2,…,P 2009是边BC 的2010等分点,则∠MP 1N +∠MP 2N +…+∠MP 2009N =____.(济南市中考试题)解题思路:本题涉及的考点有三角形中位线定理、平行四边形的判定、相似三角形的判定与性质.ABCM NP图1A BC MN1P 2P 图2A MNBC1P 2P 2009P 图3QABCDEFGMNP能力训练A 级1.设K =a b c c +-=a b c b -+=a b ca-++,则K =____. (镇江市中考试题)2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____.(杭州市中考试题)4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.(重庆市中考试题)5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则ab 的值为( ) ABCD6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )A .1︰10B .1︰9C .1︰8D .1︰77.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4B .8C .12D .168.如图,EF ∥BC ,FD ∥AB ,BD =35BC ,则BE ︰EA 等于( )A .3︰5B .2︰5C .2︰3D .3︰2A BCD E F 第2题ABCD M N第3题ABCDEFGH 第4题A BCEFG第5题ABCDE F第6题QABCP第7题AB CDEF 第8题9.(1)阅读下列材料,补全证明过程.已知,如图,矩形ABCD 中,AC ,BD 相交于点O ,OE ⊥BC 于E ,连结DE 交OC 于点F ,作FG ⊥BC 于G .求证:点G 是线段BC 的一个三等分点.(2)请你依照上面的画法,在原图上画出BC 的一个四等分点.(要求:保留画图痕迹,不写画法及证明过程)(山西中考试题)10.如图,已知在□ABCD 中,E 为AB 边的中点,AF =12FD ,FE 与AC 相交于G . 求证:AG =15AC .11.如图,梯形ABCD 中,AD ∥BC ,EF 经过梯形对角线的交点O ,且EF ∥AD . (1)求证:OE =OF ; (2)求OE AD +OEBC的值; (3)求证:1AD +1BC =2EF. (宿迁市中考试题)ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题12.如图,四边形ABCD 是梯形,点E 是上底边AD 上的一点,CE 的延长线与BC 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,MB 与AD 交于点N .求证:∠AFN =∠DME .(全国初中数学联赛试题)B 级1.如图,工地上竖立着两根电线杆AB ,CD ,它们相距15cm ,分别自两杆上高出地面4m ,6m 的A ,C 处,向两侧地面上的E ,D 和B ,F 点处,用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD 与BC 的交点P 离地面的高度为____m .(全国初中数学联赛试题)2.如图,□ABCD 的对角线交于O 点,过O 任作一直线与CD ,BC 的延长线分别交于F ,E 点.设BC =a ,CD =b ,CF =c ,则CE =____.(黑龙江省中考试题)3.如图,D ,F 分别是△ABC 边AB ,AC 上的点,且AD ︰DB =CF ︰F A =2︰3,连结DF 交BC 边的延长线于点E ,那么EF ︰FD =____.(“祖冲之杯”邀请赛试题)4.如图,设AF =10,FB =12,BD =14,DC =6,CE =9,EA =7,且KL ∥DF ,LM ∥FE ,MN ∥ED ,则EF ︰FD =____.(江苏省竞赛试题)ABCDEF M NP ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题5.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,那么EF 的值是( ) A .10B .12C .16D .18(全国初中数学联赛试题)6.如图,CE ,CF 分别平分∠ACB ,∠ACD ,AE ∥CF ,AF ∥CE ,直线EF 分别交AB ,AC 于点M ,N .若BC =a ,AC =b ,AB =c ,且c >a >b ,则EM 的长为( )A .2c a- B .2a b- C .2c b- D .2a b c+- (山东省竞赛试题)7.如图,在□ABCD 的边AD 延长线上取一点F ,BF 分别交AC 与CD 于E ,G .若EF =32,GF =24,则BE 等于( )A .4B .8C .10D .12E .16(美国初中数学联赛试题)8.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 是对角线AC 的中点,直线BE 交AD 于点F ,则AF ︰FD 的值是( )A .2B .53C .32D .1(黄冈市竞赛试题)9.如图,P 是梯形ABCD 的中位线MN 所在直线上的任意一点,直线AP ,BP 分别交直线CD 于E ,F .求证:MN NP =1()2AE BFEP FP+. (宁波市竞赛试题)ABCD EFG第7题ABCDE F第8题A BCD E F MNP第9题A BCDE F第5题AB CD E F LKMN第4题AB CDEFM第6题10.如图,在四边形ABCD 中,AC 与BD 相交于O ,直线l 平行于BD 且与AB ,DC ,BC ,AD 及AC 的延长线分别交于点M ,N ,R ,S 和P .求证:PM ·PN =P R ·PS .(山东省竞赛试题)11.如图,AB ⊥BC ,CD ⊥BC ,B ,D 是垂足,AD 和BC 交于E ,EF ⊥BD 于F .我们可以证明:11AB CD +=1EF 成立(不要求证出).以下请回答:若将图中垂直改为AB ∥CD ∥EF ,那么, (1)11AB CD+=1EF 还成立吗?如果成立,请给出证明;如果不成立,请说明理由. (2)请找出S △ABD ,S △BED 和S △BDC 的关系式,并给出证明.(黄冈市竞赛试题)ABCDEF第11题SA R BC DMN OPl第10题12.在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过D点的直线PQ交边AC于点P,交边AB 的延长线于点Q.(1)如图1,当PQ⊥AC时,求证:11AQ AP+;(2)如图2,当PQ不与AD垂直时,(1)的结论还成立吗?证明你的结论;(3)如图3,若∠BAC=60°,其它条件不变,且11AQ AP+=nAD,则n=____(直接写出结果)AQ B CDP图1AQB CDP图2AQB CDP图3专题14 平行线分线段成比例例1aba b+ 提示:由AP DQ a PF QF b ==,推得PQ ∥AD 。
中考数学复习专题之平行四形的性质与判定,考点过关与基础练习题

24.平行四边形➢考点分类考点1平行四边形的性质例1如图所示,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF(2)连接DE,若AD=2AB,求证:DE⟂AF.考点2平行四边形的判定例2如图所示,DE是ABC的中位线,延长DE至F,使EF=DE,连接BF.(1)求证:BF=DC(2)求证:四边形ABFD是平行四边形.考点3平行四边形综合探究例3如图1,在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于F.(1)当∠ABC=90°时,G是EF的中点,联结DB,DG(如图2),请直接写出∠BDG 的度数(2)当∠ABC=120°时,FG∥CE,且FG=CE,分别联结DB、DG(如图3),求∠BDG 的度数.➢真题演练1.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是()A.20B.21C.22D.232.在平行四边形ABCD中,已知∠A+∠C=200°,则∠A=()A.40°B.60°C.80°D.100°3.如图,平行四边形ABCD的对角线AC,BD相交于点O.点E为BC的中点,连接EO 并延长交AD于点F,∠ABC=60°,BC=2AB.下列结论:①S▱ABCD=AB•AC;②AD=4OE;③EF⊥AC;④S△BOE=14S△ABC.其中正确结论的个数是()A.4B.3C.2D.14.如图,在Rt △ABC 中,∠B =90°,BC =4,AC =5,点D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是( )A .3B .6C .8D .105.如图,在▱ABCD 中,AD =BD ,∠ADC =105°,点E 在AD 上,∠EBA =60°,则ED AE的值是( )A .23B .√3C .√32D .√336.如图,⟂ABCD 的对角线AC ,BD 交于点O ,AE 平分⟂BAD ,交BC 于点E ,且⟂ADC =60°,AD =2AB ,连接OE ,下列结论:⟂⟂CAD =30°;⟂OD =AB ;⟂S 平行四边形ABCD =AC •CD ;⟂S 四边形OECD =32S ⟂AOD :⟂OE =14AD .其中成立的个数是( )A .1个B .2个C .3个D .4个7.如图,点O 是平行四边形ABCD 对角线的交点,EF 过点O 分别交AD ,BC 于点E ,F .下列结论:①OE =OF ;②AB =BF ;③∠DOC =∠OCD ;④∠CFE =∠DEF ,其中正确结论的个数是( )A .4个B .3个C .2个D .1个8.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AO=2,BC=5,则AE的长为.9.如图,在平行四边形ABCD中,AD=5,AB=3,∠BAD的平分线AE交BC于E点,则EC的长为.10.如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=3BG,S▱BEPG =1.5,则S▱AEPH=.11.如图,在平行四边形ABCD中,E,F分别是AB,BC的中点,EH⊥AC,垂足为H,与AF交于点G,若AC=24,GF=6√5,则EG的长为.12.在平行四边形ABCD中,∠C=45°,AD=BD,点P为边CD上的动点(点P不与点D重合),连接AP,过点P作EP⊥AP交直线BD于点E.(1)如图①,当点P为线段CD的中点时,求证:P A=PE;(2)如图②,当点P在线段CD上时,求证:DE﹣DA=√2DP.13.已知:如图,▱ABCD 中,F 是AB 中点,连接DF ,DF 延长线交CB 的延长线于点E ,连接AE . 求证:(1)△AFD ≌△BFE ;(2)若BF =BC ,∠EDC =60°,判断四边形AEBD 的形状,并证明你的结论.➢ 课后练习1.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,AE 平分∠BAD ,分别交BC ,BD 于点E 、P .连接OE ,∠ADC =60°,AB =12BC =1,则下列结论: ①∠CAD =30°;②BD =2√3;③S 平行四边形ABCD =AB •AC ; ④AD =4OE .其中结论正确的个数是( )A .1个B .2个C .3个D .4个2.如图,平行四边形ABCD 中,对角线AC 、BD 相交于O ,过点O 作OE ⊥AC 交AD 于点E ,若AE =4,DE =3,AB =5,则AC 的长为( )A .3√2B .4√2C .5√2D .5√223.如图,已知在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列结论正确的有()个.①F A:FB=1:2;②BE:CF=1:2;③AE:BC=1:2;④S△ABE:S△FBC=1:4.A.1个B.2个C.3个D.4个4.如图,在平行四边形ABCD中,CE平分∠BCD,交AB于点E,AE=3,EB=5,ED=4.则CE的长是()A.2√2B.6√2C.5√5D.4√55.如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E 不与A、B重合),连接EF、CF,则下列结论中正确个数是()①∠DCF=12∠BCD;②EF=CF;③S△BEC<2S△CEF;④∠DFE=4∠AEFA.4B.3C.2D.16.如图,在平行四边形ABCD中,E为CD上一点,且CE=BC,AE=DE,AE=4,∠DAE =60°,则下列结论:①∠AEB=90°;②平行四边形ABCD周长是24;③∠ABE=∠EBC=30°;④BE2=48;⑤E为CD中点.正确的结论有()A.2个B.3个C.4个D.5个7.如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于G,交AD延长线于F,若BC=6,DF=4,EF=2AE,则△ABE的面积为.8.如图,在▱ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,BE=1,平行四边形ABCD面积为6√3.则AF=.9.如图,在▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有(填序号).10.如图,在平行四边形ABCD中,AD=12,AB=6,以AD为底边向右作腰长为10的等腰△ADP,Q为边BC上一点,BQ=4,连接PQ,则PQ的最小值为.11.在平面直角坐标系中,O为原点,点A(√3,0),点B(0,1),点E是边AB中点,把△ABO绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为α.(1)如图①,当点D恰好在AB上时,求点D的坐标;(2)如图②,若α=60°时,求证:四边形OECD是平行四边形.12.如图,在▱ABCD中,AE平分∠BAD交对角线BD于点E,CF平分∠DCB交对角线BD 于点F,连接AF,CE.(1)若∠BCF=50°,求∠ADC的度数;(2)求证:四边形AECF为平行四边形.➢冲击A+如图,在△ABC中,AB=BC,AB为⊙O的直径,AC与⊙O相交于点D,过点D做DE⊥BC于点E,CB延长线交⊙O于点F.(1)求证:DE为⊙O的切线;(2)若BE=1,BF=2,求AD的长.。
2018年全国各地中考数学试题《平行四边形》解答题试题汇编(含答案解析)

2018年全国各地中考数学试题《平行四边形》解答题试题汇编(含答案解析)1.(2018•连云港)如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.2.(2018•湘西州)如图,在矩形ABCD中,E是AB的中点,连接DE、CE.(1)求证:△ADE≌△BCE;(2)若AB=6,AD=4,求△CDE的周长.3.(2018•湘潭)如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.(1)求证:△DAF≌△ABE;(2)求∠AOD的度数.4.(2018•泰安)如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.5.(2018•重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E 是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=CG.6.(2018•北京)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B 重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.7.(2018•重庆)如图,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.(1)若BC=12,AB=13,求AF的长;(2)求证:EB=EH.8.(2018•玉林)如图,在▱ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC 与AB上的垂足分别是M,N与M′,N′,连接EF.(1)求证:四边形EFNM是矩形;(2)已知:AE=4,DE=3,DC=9,求EF的长.9.(2018•新疆)如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.(1)求证:△DOE≌△BOF;(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.10.(2018•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.11.(2018•舟山)如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.12.(2018•福建)如图,▱ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.13.(2018•宿迁)如图,在▱ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.14.(2018•张家界)在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.(1)求证:DF=AB;(2)若∠FDC=30°,且AB=4,求AD.15.(2018•盐城)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.16.(2018•吉林)如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.17.(2018•无锡)如图,平行四边形ABCD中,E、F分别是边BC、AD的中点,求证:∠ABF=∠CDE.18.(2018•大连)如图,▱ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE=DF.19.(2018•淮安)已知:如图,▱ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F.求证:AE=CF.20.(2018•临安区)已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:(1)△ADF≌△CBE;(2)EB∥DF.21.(2018•遂宁)如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.22.(2018•巴中)如图,在▱ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.(1)求证:四边形BMDN是平行四边形;(2)已知AF=12,EM=5,求AN的长.23.(2018•郴州)如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.24.(2018•沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O.过点C 作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是.25.(2018•北京)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD 交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,BD=2,求OE的长.26.(2018•曲靖)如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.(1)求证:△AFN≌△CEM;(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.27.(2018•孝感)如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.28.(2018•岳阳)如图,在平行四边形ABCD中,AE=CF,求证:四边形BFDE是平行四边形.29.(2018•乌鲁木齐)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.(1)求证:四边形AECD是菱形;(2)若AB=6,BC=10,求EF的长.30.(2018•南京)如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.31.(2018•衢州)如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.32.(2018•呼和浩特)如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.(1)求证:△ABC≌△DEF;(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.33.(2018•内江)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.求证:(1)△AED≌△CFD;(2)四边形ABCD是菱形.34.(2018•黄冈)如图,在▱ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.(1)求证△ABF≌△EDA;(2)延长AB与CF相交于G.若AF⊥AE,求证BF⊥BC.35.(2018•青岛)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.(1)求证:AB=AF;(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.36.(2018•柳州)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.(1)求菱形ABCD的周长;(2)若AC=2,求BD的长.37.(2018•广西)如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:▱ABCD是菱形;(2)若AB=5,AC=6,求▱ABCD的面积.38.(2018•白银)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≌△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.39.(2018•梧州)如图,在▱ABCD中,对角线AC,BD相交于点O,过点O的一条直线分别交AD,BC于点E,F.求证:AE=CF.40.(2018•大庆)如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.参考答案与试题解析1.(2018•连云港)如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.【分析】(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到CD=FA,再根据CD∥AF,即可得出四边形ACDF是平行四边形;(2)先判定△CDE是等腰直角三角形,可得CD=DE,再根据E是AD的中点,可得AD=2CD,依据AD=BC,即可得到BC=2CD.【解答】解:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠FAE=∠CDE,∵E是AD的中点,∴AE=DE,又∵∠FEA=∠CED,∴△FAE≌△CDE,∴CD=FA,又∵CD∥AF,∴四边形ACDF是平行四边形;(2)BC=2CD.证明:∵CF平分∠BCD,∴∠DCE=45°,∵∠CDE=90°,∴△CDE是等腰直角三角形,∴CD=DE,∵E是AD的中点,∴AD=2CD,∵AD=BC,∴BC=2CD.【点评】本题主要考查了矩形的性质以及平行四边形的判定与性质,要证明两直线平行和两线段相等、两角相等,可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上,通过证明四边形是平行四边形达到上述目的.2.(2018•湘西州)如图,在矩形ABCD中,E是AB的中点,连接DE、CE.(1)求证:△ADE≌△BCE;(2)若AB=6,AD=4,求△CDE的周长.【分析】(1)由全等三角形的判定定理SAS证得结论;(2)由(1)中全等三角形的对应边相等和勾股定理求得线段DE的长度,结合三角形的周长公式解答.【解答】(1)证明:在矩形ABCD中,AD=BC,∠A=∠B=90°.∵E是AB的中点,∴AE=BE.在△ADE与△BCE中,,∴△ADE≌△BCE(SAS);(2)由(1)知:△ADE≌△BCE,则DE=EC.在直角△ADE中,AE=4,AE=AB=3,由勾股定理知,DE===5,∴△CDE的周长=2DE+AD=2DE+AB=2×5+6=16.【点评】本题主要考查了全等三角形的判定和性质,矩形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.3.(2018•湘潭)如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.(1)求证:△DAF≌△ABE;(2)求∠AOD的度数.【分析】(1)利用正方形的性质得出AD=AB,∠DAB=∠ABC=90°,即可得出结论;(2)利用(1)的结论得出∠ADF=∠BAE,进而求出∠ADF+∠DAO=90°,最后用三角形的内角和定理即可得出结论.【解答】(1)证明:∵四边形ABCD是正方形,∴∠DAB=∠ABC=90°,AD=AB,在△DAF和△ABE中,,∴△DAF≌△ABE(SAS),(2)由(1)知,△DAF≌△ABE,∴∠ADF=∠BAE,∵∠ADF+∠DAO=∠BAE+∠DAO=∠DAB=90°,∴∠AOD=180°﹣(∠ADF+DAO)=90°.【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,三角形的内角和定理,判断出△DAF≌△ABE是解本题的关键.4.(2018•泰安)如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.【分析】(1)依据条件得出∠C=∠DHG=90°,∠CGE=∠GED,依据F是AD的中点,FG∥AE,即可得到FG是线段ED的垂直平分线,进而得到GE=GD,∠CGE=∠GDE,利用AAS即可判定△ECG≌△GHD;(2)过点G作GP⊥AB于P,判定△CAG≌△PAG,可得AC=AP,由(1)可得EG=DG,即可得到Rt△ECG≌Rt△GPD,依据EC=PD,即可得出AD=AP+PD=AC+EC;(3)依据∠B=30°,可得∠ADE=30°,进而得到AE=AD,故AE=AF=FG,再根据四边形AECF是平行四边形,即可得到四边形AEGF是菱形.【解答】解:(1)∵AF=FG,∴∠FAG=∠FGA,∵AG平分∠CAB,∴∠CAG=∠FGA,∴∠CAG=∠FGA,∴AC∥FG,∵DE⊥AC,∴FG⊥DE,∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∴∠C=∠DHG=90°,∠CGE=∠GED,∵F是AD的中点,FG∥AE,∴H是ED的中点,∴FG是线段ED的垂直平分线,∴GE=GD,∠GDE=∠GED,∴∠CGE=∠GDE,∴△ECG≌△GHD;(2)证明:过点G作GP⊥AB于P,∴GC=GP,而AG=AG,∴△CAG≌△PAG,∴AC=AP,由(1)可得EG=DG,∴Rt△ECG≌Rt△GPD,∴EC=PD,∴AD=AP+PD=AC+EC;(3)四边形AEGF是菱形,证明:∵∠B=30°,∴∠ADE=30°,∴AE=AD,∴AE=AF=FG,由(1)得AE∥FG,∴四边形AECF是平行四边形,∴四边形AEGF是菱形.【点评】本题属于四边形综合题,主要考查了菱形的判定、全等三角形的判定和性质,线段垂直平分线的判定与性质以及含30°角的直角三角形的性质的综合运用,利用全等三角形的对应边相等,对应角相等是解决问题的关键.5.(2018•重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E 是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=CG.【分析】(1)利用勾股定理即可得出BH的长,进而运用公式得出△ABE的面积;(2)过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,判定△AME≌△BNG(AAS),可得ME=NG,进而得出BE=GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=CG.【解答】解:(1)∵AH=3,HE=1,∴AB=AE=4,又∵Rt△ABH中,BH==,∴S=AE×BH=×4×=;△ABE(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,∵∠ACB=45°,∴∠MAC=∠NGC=45°,∵AB=AE,∴BM=EM=BE,∠BAM=∠EAM,又∵AE⊥BG,∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,∴∠MAE=∠NBG,设∠BAM=∠MAE=∠NBG=α,则∠BAG=∠45°+α,∠BGA=∠GCN+∠GBC=45°+α,∴AB=BG,∴AE=BG,在△AME和△BNG中,,∴△AME≌△BNG(AAS),∴ME=NG,在等腰Rt△CNG中,NG=NC,∴GC=NG=ME=BE,∴BE=GC,∵O是AC的中点,∴OA=OC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠OAF=∠OCE,∠AFO=∠CEO,∴△AFO≌△CEO(AAS),∴AF=CE,∴AD﹣AF=BC﹣EC,即DF=BE,∴DF=BE=CG.【点评】本题主要考查了平行四边形的性质,全等三角形的判定与性质,等腰直角三角形的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造全等三角形以及等腰直角三角形,利用全等三角形的对应边相等得出结论.6.(2018•北京)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B 重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.【分析】(1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt △DFG≌Rt△DCG,可得结论;(2)证法一:如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:EM=AE,得结论;证法二:如图3,作辅助线,构建全等三角形,证明△DAE≌△ENH,得AE=HN,AD=EN,再说明△BNH是等腰直角三角形,可得结论.【解答】证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,∵,∴Rt△DFG≌Rt△DCG(HL),∴GF=GC;(2)BH=AE,理由是:证法一:如图2,在线段AD上截取AM,使AM=AE,∵AD=AB,∴DM=BE,由(1)知:∠1=∠2,∠3=∠4,∵∠ADC=90°,∴∠1+∠2+∠3+∠4=90°,∴2∠2+2∠3=90°,∴∠2+∠3=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,△DEH是等腰直角三角形,∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,∴∠1=∠BEH,在△DME和△EBH中,∵,∴△DME≌△EBH,∴EM=BH,Rt△AEM中,∠A=90°,AM=AE,∴EM=AE,∴BH=AE;证法二:如图3,过点H作HN⊥AB于N,∴∠ENH=90°,由方法一可知:DE=EH,∠1=∠NEH,在△DAE和△ENH中,∵,∴△DAE≌△ENH,∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=HN=AE.【点评】本题考查了正方形的性质,全等三角形的判定定理和性质定理,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.7.(2018•重庆)如图,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.(1)若BC=12,AB=13,求AF的长;(2)求证:EB=EH.【分析】(1)依据BF⊥AC,∠ACB=45°,BC=12,可得等腰Rt△BCF中,BF=sin45°×BC=12,再根据勾股定理,即可得到Rt△ABF中,AF==5;(2)连接GE,过A作AF⊥AG,交BG于P,连接PE,判定四边形APEG是正方形,即可得到PF=EF,AP=AG=CH,进而得出△APB≌△HCE,依据AB=EH,AB=BE,即可得到BE=EH.【解答】解:(1)如图,∵BF⊥AC,∠ACB=45°,BC=12,∴等腰Rt△BCF中,BF=sin45°×BC=12,又∵AB=13,∴Rt△ABF中,AF==5;(2)如图,连接GE,过A作AF⊥AG,交BG于P,连接PE,∵BE=BA,BF⊥AC,∴AF=FE,∴BG是AE的垂直平分线,∴AG=EG,AP=EP,∵∠GAE=∠ACB=45°,∴△AGE是等腰直角三角形,即∠AGE=90°,△APE是等腰直角三角形,即∠APE=90°,∴∠APE=∠PAG=∠AGE=90°,又∵AG=EG,∴四边形APEG是正方形,∴PF=EF,AP=AG=CH,又∵BF=CF,∴BP=CE,∵∠APG=45°=∠BCF,∴∠APB=∠HCE=135°,∴△APB≌△HCE(SAS),∴AB=EH,又∵AB=BE,∴BE=EH.【点评】本题考查了平行四边形的性质,正方形的判定以及全等三角形的判定与性质的运用,解题时注意:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.8.(2018•玉林)如图,在▱ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC 与AB上的垂足分别是M,N与M′,N′,连接EF.(1)求证:四边形EFNM是矩形;(2)已知:AE=4,DE=3,DC=9,求EF的长.【分析】(1)要说明四边形EFNM是矩形,有ME⊥CD.FN⊥CD条件,还缺ME=FN.过点E、F分别作AD、BC的垂线,垂足分别是G、H.利用角平分线上的点到角两边的距离相等可得结论.(2)利用平行四边形的性质,证明直角△DEA,并求出AD的长.利用全等证明△GEA≌△CNF,△DME≌△DGE从而得到DM=DG,AG=CN,再利用线段的和差关系,求出MN的长得结论.【解答】解:(1)证明:过点E、F分别作AD、BC的垂线,垂足分别是G、H.∵∠3=∠4,∠1=∠2,EG⊥AD,EM⊥CD,EM′⊥AB∴EG=ME,EG=EM′∴EG=ME=ME′=MM′同理可证:FH=NF=N′F=NN′∵CD∥AB,MM′⊥CD,NN′⊥CD,∴MM′=NN′∴ME=NF=EG=FH又∵MM′∥NN′,MM′⊥CD∴四边形EFNM是矩形.(2)∵DC∥AB,∴∠CDA+∠DAB=180°,∵,∠2=∠DAB∴∠3+∠2=90°在Rt△DEA,∵AE=4,DE=3,∴AB==5.∵四边形ABCD是平行四边形,∴∠DAB=∠DCB,又∵∠2=∠DAB,∠5=∠DCB,∴∠2=∠5由(1)知GE=NF在Rt△GEA和Rt△CNF中∴△GEA≌△CNF∴AG=CN在Rt△DME和Rt△DGE中∵DE=DE,ME=EG∴△DME≌△DGE∴DG=DM∴DM+CN=DG+AG=AB=5∴MN=CD﹣DM﹣CN=9﹣5=4.∵四边形EFNM是矩形.∴EF=MN=4【点评】本题考查了平行四边形的性质、矩形的判定、角平分线的性质、勾股定理及三角形全等的判定.题目综合性较强,需认真分析.9.(2018•新疆)如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.(1)求证:△DOE≌△BOF;(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.【分析】(1)根据SAS即可证明;(2)首先证明四边形EBFD是平行四边形,再根据对角线相等的平行四边形是矩形即可证明;【解答】(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OE=OF,在△DEO和△BOF中,∴△DOE≌△BOF.(2)解:结论:四边形EBFD是矩形.理由:∵OD=OB,OE=OF,∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.【点评】本题考查平行四边形的性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.10.(2018•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.【分析】(1)证△OAM≌△OBN即可得;(2)作OH⊥AD,由正方形的边长为4且E为OM的中点知OH=HA=2、HM=4,再根据勾股定理得OM=2,由直角三角形性质知MN=OM.【解答】解:(1)∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;(2)如图,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM==2,∴MN=OM=2.【点评】本题主要考查正方形的性质,解题的关键是掌握正方形的四条边都相等,正方形的每条对角线平分一组对角及全等三角形的判定与性质.11.(2018•舟山)如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.【分析】先判断出AE=AF,∠AEF=∠AFE=60°,进而求出∠AFD=∠AEB=75°,进而判断出△AEB≌△AFD,即可得出结论.【解答】解:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°,∵△AEF是等边三角形,∴AE=AF,∠AEF=∠AFE=60°,∵∠CEF=45°,∴∠CFE=∠CEF=45°,∴∠AFD=∠AEB=180°﹣45°﹣60°=75°,∴△AEB≌△AFD(AAS),∴AB=AD,∴矩形ABCD是正方形.【点评】此题主要考查了矩形的性质,等边三角形的性质,全等三角形的判定和性质,正方形的判定,判断出∠AFD=∠AEB是解本题的关键.12.(2018•福建)如图,▱ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.【分析】由四边形ABCD是平行四边形,可得OA=OC,AD∥BC,继而可证得△AOE≌△COF(ASA),则可证得结论.【解答】证明:∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,∴∠OAE=∠OCF,在△OAE和△OCF中,,∴△AOE≌△COF(ASA),∴OE=OF.【点评】此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.13.(2018•宿迁)如图,在▱ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.【分析】利用平行四边形的性质得出AF=EC,再利用全等三角形的判定与性质得出答案.【解答】证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,AD∥BC,∴∠E=∠F,∵BE=DF,∴AF=EC,在△AGF和△CHE中,∴△AGF≌△CHE(ASA),∴AG=CH.【点评】此题主要考查了平行线的性质以及全等三角形的判定与性质,正确掌握平行线的性质是解题关键.14.(2018•张家界)在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.(1)求证:DF=AB;(2)若∠FDC=30°,且AB=4,求AD.【分析】(1)利用“AAS”证△ADF≌△EAB即可得;(2)由∠ADF+∠FDC=90°、∠DAF+∠ADF=90°得∠FDC=∠DAF=30°,据此知AD=2DF,根据DF=AB可得答案.【解答】证明:(1)在矩形ABCD中,∵AD∥BC,∴∠AEB=∠DAF,又∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B,又∵AD=EA,∴△ADF≌△EAB,∴DF=AB.(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,∴∠FDC=∠DAF=30°,∴AD=2DF,∵DF=AB,∴AD=2AB=8.【点评】本题主要考查矩形的性质,解题的关键是掌握矩形的性质和全等三角形的判定与性质及直角三角形的性质.15.(2018•盐城)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.【分析】(1)根据正方形的性质和全等三角形的判定证明即可;(2)四边形AECF是菱形,根据对角线垂直的平行四边形是菱形即可判断;【解答】证明:(1)∵正方形ABCD,∴AB=AD,∴∠ABD=∠ADB,∴∠ABE=∠ADF,在△ABE与△ADF中,∴△ABE≌△ADF(SAS);(2)连接AC,四边形AECF是菱形.理由:∵正方形ABCD,∴OA=OC,OB=OD,AC⊥EF,∴OB+BE=OD+DF,即OE=OF,∵OA=OC,OE=OF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形.【点评】本题考查正方形的性质、全等三角形的判定和性质、菱形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.(2018•吉林)如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.【分析】根据正方形的性质,利用SAS即可证明;【解答】证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,在△ABE和△BCF中,,∴△ABE≌△BCF.【点评】本题考查正方形的性质全等三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.17.(2018•无锡)如图,平行四边形ABCD中,E、F分别是边BC、AD的中点,求证:∠ABF=∠CDE.【分析】根据平行四边形的性质以及全等三角形的性质即可求出答案.【解答】解:在▱ABCD中,AD=BC,∠A=∠C,∵E、F分别是边BC、AD的中点,∴AF=CE,在△ABF与△CDE中,∴△ABF≌△CDE(SAS)∴∠ABF=∠CDE【点评】本题考查平行四边形的性质,解题的关键是熟练运用平行四边形的性质以及全等三角形,本题属于中等题型18.(2018•大连)如图,▱ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE=DF.【分析】只要证明△BEO≌△DFO即可;【解答】证明:∵四边形ABCD是平行四边形,∴OA=OC,OD=OB,∵AE=CF,∴OE=OF,在△BEO和△DFO中,,∴△BEO≌△DFO,∴BE=DF.【点评】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.19.(2018•淮安)已知:如图,▱ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F.求证:AE=CF.【分析】利用平行四边形的性质得出AO=CO,AD∥BC,进而得出∠EAC=∠FCO,再利用ASA求出△AOE≌△COF,即可得出答案.【解答】证明:∵▱ABCD的对角线AC,BD交于点O,∴AO=CO,AD∥BC,∴∠EAC=∠FCO,在△AOE和△COF中,∴△AOE≌△COF(ASA),∴AE=CF.【点评】此题主要考查了全等三角形的判定与性质以及平行四边形的性质,熟练掌握全等三角形的判定方法是解题关键.20.(2018•临安区)已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:(1)△ADF≌△CBE;(2)EB∥DF.【分析】(1)要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为ABCD是平行四边形,得出AD=CB,∠DAF=∠BCE,从而根据SAS推出两三角形全等;(2)由全等可得到∠DFA=∠BEC,所以得到DF∥EB.【解答】证明:(1)∵AE=CF,∴AE+EF=CF+FE,即AF=CE.又ABCD是平行四边形,∴AD=CB,AD∥BC.∴∠DAF=∠BCE.在△ADF与△CBE中,∴△ADF≌△CBE(SAS).(2)∵△ADF≌△CBE,∴∠DFA=∠BEC.∴DF∥EB.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.21.(2018•遂宁)如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.【分析】根据对角线互相垂直的平行四边形是菱形即可证明;【解答】证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵DE=BF,∴AE=CF,∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形.【点评】本题考查平行四边形的性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.22.(2018•巴中)如图,在▱ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.(1)求证:四边形BMDN是平行四边形;(2)已知AF=12,EM=5,求AN的长.【分析】(1)只要证明DN∥BM,DM∥BN即可;(2)只要证明△CEM≌△AFN,可得FN=EM=5,在Rt△AFN中,根据勾股定理AN=即可解决问题;【解答】(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,∵BM⊥AC,DN⊥AC,∴DN∥BM,∴四边形BMDN是平行四边形;(2)解:∵四边形BMDN是平行四边形,∴DM=BN,∵CD=AB,CD∥AB,∴CM=AN,∠MCE=∠NAF,∵∠CEM=∠AFN=90°,∴△CEM≌△AFN,∴FN=EM=5,在Rt△AFN中,AN===13.【点评】本题考查平行四边形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.23.(2018•郴州)如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.【分析】根据平行四边形的性质以及全等三角形的判定方法证明出△DOE≌△BOF,得到OE=OF,利用对角线互相平分的四边形是平行四边形得出四边形EBFD 是平行四边形,进而利用对角线互相垂直的平行四边形是菱形得出四边形BFDE 为菱形.【解答】证明:∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD和△FOB中,,∴△DOE≌△BOF(ASA);∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,∵EF⊥BD,∴四边形BFDE为菱形.【点评】此题主要考查了菱形的判定,平行四边形的性质以及全等三角形的判定与性质等知识,得出OE=OF是解题关键.24.(2018•沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O.过点C 作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是4.【分析】(1)欲证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.【解答】(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°.∵CE∥OD,DE∥OC,∴四边形OCED是平行四边形,又∠COD=90°,∴平行四边形OCED是矩形;(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD是菱形,∴AC=2OC=4,BD=2OD=2,∴菱形ABCD的面积为:AC•BD=×4×2=4.故答案是:4.【点评】考查了矩形的判定与性质,菱形的性质.此题中,矩形的判定,首先要判定四边形是平行四边形,然后证明有一内角为直角.25.(2018•北京)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD 交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,BD=2,求OE的长.【分析】(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA,即可得出结论.【解答】解:(1)∵AB∥CD,∴∠OAB=∠DCA,∵AC为∠DAB的平分线,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD=AB,∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴▱ABCD是菱形;(2)∵四边形ABCD是菱形,∴OA=OC,BD⊥AC,∵CE⊥AB,∴OE=OA=OC,∵BD=2,∴OB=BD=1,在Rt△AOB中,AB=,OB=1,∴OA==2,∴OE=OA=2.【点评】此题主要考查了菱形的判定和性质,平行四边形的判定和性质,角平分线的定义,勾股定理,判断出CD=AD=AB是解本题的关键.26.(2018•曲靖)如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.(1)求证:△AFN≌△CEM;(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.【分析】(1)利用平行线的性质,根据SAS即可证明;(2)利用全等三角形的性质可知∠NAF=∠ECM,求出∠ECM即可;【解答】(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,∴∠AFN=∠CEM,∵FN=EM,AF=CE,∴△AFN≌△CEM(SAS).(2)解:∵△AFN≌△CEM,∴∠NAF=∠ECM,∵∠CMF=∠CEM+∠ECM,∴107°=72°+∠ECM,∴∠ECM=35°,∴∠NAF=35°.【点评】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.27.(2018•孝感)如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.【分析】由AB∥DE、AC∥DF利用平行线的性质可得出∠B=∠DEF、∠ACB=∠F,由BE=CF可得出BC=EF,进而可证出△ABC≌△DEF(ASA),根据全等三角形的性质可得出AB=DE,再结合AB∥DE,即可证出四边形ABED是平行四边形.【解答】证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.∵BE=CF,∴BE+CE=CF+CE,∴BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AB=DE.又∵AB∥DE,∴四边形ABED是平行四边形.【点评】本题考查了平行线的性质、平行四边形的判定以及全等三角形的判定与性质,利用全等三角形的性质找出AB=DE是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018 初三中考数学复习平行线的证明专题复习练习
1. 下列说法正确的是( D )
A.经验、观察或试验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个2. “两条平行直线被第三条直线所截,同位角相等”这句话是( C )
A.定义 B.假命题 C.公理 D.定理
3. 下列语句中,是命题的是( C )
A.直线AB和CD垂直吗B.过线段AB的中点C画AB的垂线C.同旁内角不互补,两直线不平行D.连接A,B两点
4.如图,AB∥CD,CB⊥DB,∠D=65°,则∠ABC的大小是( A ) A.25°B.35°C.50°D.65°
5.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于( B )
A.90°B.100°C.130°D.180°
6.如图,已知△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( A )
A .∠DCE>∠AD
B B .∠ADB>∠DBC
C .∠ADB>∠ACB
D .∠ADB>∠DEC
7.如图,AB ∥CD ,直线EF 交AB 于点E ,交CD 于点F ,EG 平分∠BEF ,交CD 于点G ,∠1=50°,则∠2等于( C )
A .50°
B .60°
C .65°
D .90°
8.如图,已知直线AB ∥CD ,BE 平分∠ABC ,且BE 交CD 于点D ,∠CDE =150°,则∠C 的度数为( C )
A .150°
B .130°
C .120°
D .100°
9.如图,直线a ∥b ,∠A =38°,∠1=46°,则∠ACB 的度数是( C )
A .84°
B .106°
C .96°
D .104°
10.适合条件∠A =12∠B =13∠C 的三角形ABC 是( B )
A .锐角三角形 B. 直角三角形 C .钝角三角形 D .都有可能
11.如图,在折纸活动中,小明制作了一张△ABC 纸片,点D ,E 分别在边AB ,AC 上,将△ABC 沿着DE 折叠压平,A 与A ′重合.若∠A =75°,则∠1+
∠2等于( A )
A.150° B. 210°C.105°D.75°
12.已知直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( B )
A.30° B. 35°C.40°D.45°
13.如图,DAE是一条直线,DE∥BC,则x=__64°__.
14.如图,已知AB∥CD,∠DEF=50°,∠D=80°,∠B的度数是__50°__.
15.如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=__70°__,∠CED=__110°__.
16.已知如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠DAC =100°,则∠BAC=__120°__.
17.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为__22°__.
18.已知等腰三角形的一腰上的高与另一腰的夹角为40°,则这个等腰三角形的顶角为__50°或130°__.
19.如图所示,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A=__10__度.
20.如图,∠C=∠1,∠2和∠D互余,BE⊥FD,求证:AB∥CD.
解:∵∠C=∠1,∴CF∥BE,又BE⊥FD,∴CF⊥FD,∴∠CFD=90°,则∠2+∠BFD=90°,又∠2+∠D=90°,∴∠D=∠BFD,则AB∥CD
21.一天,爸爸带着小刚到建筑工地去玩,看见有如图所示的人字架,爸爸说:“小刚,我考考你,这个人字架的夹角∠1等于130°,你能求出∠3比∠2大多少吗?”小刚马上得到了正确答案,他的答案是多少?请说明理由.
解:50°,因为∠1=130°,所以与∠1相邻的内角为50°,所以∠3-∠2=
50°
22.如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.
解:∵BE∥DF,∴∠ABE=∠D,又AB=FD,∠A=∠F,∴△ABE≌△FDC(ASA),∴AE=FC
23.如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,又∠BDC=∠BCD,且∠1=∠2,求∠3的度数.
解:由∠BAC=90°,∠ABC=∠ACB易求∠ACB=45°,设∠1=x,可得∠BCD=∠2+45°=x+45°=∠3,∴x+(x+45°)+(x+45°)=180°,x=30,则∠3=x+45°=75°
24.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
解:∵∠A+∠B+∠C=180°,∴∠B+∠C=110°,∵∠B=∠DEB,∠C=
∠DFC ,∴∠B +∠DEB +∠C +∠DFC =220°,∵∠B +∠DEB +∠C +∠DFC +∠EDB +∠FDC =360°,∴∠EDB +∠FDC =140°,即∠EDF =180°-140°=40°
25.如图,已知∠1+∠2=180°,∠3=∠B ,试判断∠AED 与∠C 的大小关系,并对结论进行证明.
解:∠AED =∠C.∵∠1+∠2=180°,∠1+∠EFD =180°,∴∠2=∠EFD ,∴AB ∥EF ,∴∠3=∠ADE ,又∵∠3=∠B ,∴∠ADE =∠B ,∴DE ∥BC ,∴∠AED =∠C
26.【问题】如图①,在△ABC 中,BE 平分∠ABC ,CE 平分∠ACB ,若∠A =
80°,则∠BEC =__130°__;若∠A =n °,则∠BEC =__90°+12n °__.
【探究】
(1)如图②,在△ABC 中,BD ,BE 三等分∠ABC ,CD ,CE 三等分∠ACB.若∠
A =n °,则∠BEC =__60°+23n °__;
(2)如图③,O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点,试分析∠BOC
和∠A 有怎样的关系?请说明理由;
(3)如图④,O 是外角∠DBC 与外角∠BCE 的平分线BO 和CO 的交点,则∠BOC 与∠A 有怎样的关系?(只写结论,不需证明)
解:(2)∠BOC =12∠A.理由:∠BOC =∠2-∠1=12∠ACD -12∠ABC =12(∠ACD
-∠ABC)=12∠A
(3)∠BOC =90°-12∠A。
