p-3型分布参数估计
工程水文学第四章 水文统计基本方法

反应系列 总水平
定义模比系数: 则:
Ki
xi x
1
1 n
n i 1
Ki
K1 K2 Kn n
⒉ 均方差σ、变差系数Cv:
反映系列中各变量值集中或离散的程度
n
(xi x)2
i1
n
Cv
n
(Ki 1)2
i 1
n
例4-2: 5, 10, 15 x=10 σ=4.08 995,1000,1005 x=1000 σ=4.08
Cv=0.48 Cv=0.0048
⒊偏态系数(Cs): 反映系列在均值两边对称程度
n
( Ki 1)3
Cs i1 nCv3
正态曲线或正态分布: 密度函数:
密度曲线:
例4-3:计算系列的统计参数均值、变差系数、 偏态系数。
样本 1 2 3 4 5
系列 300 200 185 165 150
例如:
T 1 1 P
当某一洪水的频率为P=1%时,则T=100年,称此洪
水为百年一遇洪水,表示大于等于这样的洪水平均100
年会遇到一次。
对于p=80%的枯水流量,则 T=5 年,称作以五年一
遇枯水流量作为设计来水的标准。表示小于等于这样的
流量平均5年会遇到一次。说明具有80%的可靠程度。
第五节 P—Ⅲ型分布参数估计
经验频率 (5) 9.1 18.2 27.3 36.4 45.5 54.5 63.6 72.7 81.8 90.9
某枢纽年最大洪峰流量经验频率曲线
二、理论频率曲线: 1、皮尔逊Ⅲ型分布曲线( P-Ⅲ)
一端有限,一端无限 的不对称单峰曲线
形状、尺度和 位置参数
可以推证:
4 CS2
P_III型分布频率分析在Excel中的实现及应用_黄继文

PIII 型分布频率分析在 Excel 中的实现及应用
黄继文
( 山东省水利科学研究院 , 山东 济南 250013) 摘 要 : 探讨没有其他专业绘图 软件帮助的情况下 , 在 Excel 中 利用规划求解 、GAMMADIST 和 GAMMAINV 函数 实现用 P -III 型曲线进行水文频率计算 , 为广大基层水 文工作者 提供一个既 简单又便 捷的水文 频率分 析计算 的方法 。 关键词 : Excel ; P -III 型分布 ; 频 率分析 ; GAMMADIST 函数
图 1 GAMMADIST 函数计算示意
5 应用实例
根据 P -III 型分布密度函数和 GAMMADIST 函数的关系 , 在 对某一系列( 降雨 、径流或其他 系列) 采用 适线法 进行频 率分析 时 , 可以在 Excel 中进行 。 现有某站 1960 ~ 2003 年降水量系列资料 , 见表 1 。 试 用 P III 型分布进行适线分析 , 并计算频率为 P =50 %、 P =10 %、 P =1 %、 P =0 . 1 %时的降雨量 。
图 2 相对误差计算示意
( 7)利用 Excel 中的 规 划求 解功 能 优化 配 线 , 反 求 α 、β 、b 值 。 可采取最小二乘法 准则以 偏差平 方和最 小为目 标 , 但 为了 照顾频率值较小的点以相对误 差平方和最小为目标较好 。 调用 Excel 中规划求解功能 , 以 b 、α 、β1 值为变量 , 计算方法见图 3 、图 4 。 如图所示 , 规划求解“ 目标 单元格” 为 相对误差 平方 和 , 目标 值选“ 最小” , 可变单元格为 b 、α 、β1 值 , 然后点 击“ 求 解” 。 最终 求出的结果 b 、α 、β 1 值分别为 167 . 27 、6 . 05 和 77 . 86 。 ( 8) 根据确定的 b 、α 、β1 值利用 GAMMAINV 函 数就可 以计 算出不同频率下的降 水量值 , 计算方法见图 5 。
p-3型分布参数估计

3、理论频率曲线
PⅢ型分布
f(x) (
)xa01e(xa0)
4
C
2 s
2
xCV Cs
a0
x1
2CV Cs
水文计算中,一般需求出指定频率p所对应
的随机变量取值,例如,频率为1%(百年一 遇)的设计洪峰流量。
p p (x x p) ()x p(x a 0 ) 1 e (x a 0 )d x
§7-3 P-Ⅲ型分布参数的估计
一、 P-Ⅲ型分布
在水文频率曲线线型选择上,世界各地差异很大, 常用线型达20多种。我国20世纪60年代以来,通过对洪 水极值资料的验证,认为P-Ⅲ型能较好拟合我国大多数 河流的洪水系列,因此我国水利水电工程水文计算规范 推荐采用该分布。
P-Ⅲ型分布的密度函数: f(x) ()(x a 0) 1e (x a 0)•xa 0
二、 适线法
研究发现:极大似然法用于估计P-Ⅲ型分布 参数时,需要试算,而且有时似然方程无解,因 此,在我国水文计算工作中并不常用。对P-Ⅲ分 布,我国常采用适线法估计其参数。
• 四、现行水文频率计算方法——适线法
用有限的样本观测资料估计总体分布线型
中的参数,如P—Ⅲ型的 x 、Cv、 Cs。
1、P—Ⅲ型的分布参数初估方法
的假定值。估计时,因Cs 的抽样误差太大,
一般不计算Cs,而是根据经验假定 Cs为 Cv的某一 倍数(如 Cs=2Cv)。
(值4),根以据xp假为定纵的坐x标、,Cvp、为C横s,坐查标附,表即4可,得计到算频x率p
曲线。将此线画在绘有经验点据的图上,看与经 验点据配合的情况,若不理想,则修改参数(样 本均值估计误差小,一般不做调整;主要调整 Cv、Cs)再次进行计算。
P—Ⅲ型曲线参数估计方法研究综述

P—Ⅲ型曲线参数估计方法研究综述作者:雷冠军王文川殷峻暹张丽丽来源:《人民黄河》2017年第10期摘要:水文频率分析以概率统计理论为基础,通过建立模型来优化理论频率曲线参数,对经验频率曲线进行延展。
对P-Ⅲ型曲线参数估计的矩法、概率权重矩法、权函数法、线性矩法、优化适线法、加权适线法、数值积分算法、优化适线准则在水文频率参数估计中的研究和应用,以及水文频率参数估计的不确定性研究进行了介绍和阐述,并提出了水文频率参数估计的建议:①加强对水文序列不确定性机理的研究,使水文频率分析的适线结果具有较好的延展性;②应立足于现有的水文频率参数估计的理论基础,针对不同的适线目的和数据精度,选择合适的参数估计结果,提高人机交互水平,将客观信息和主观经验结合起来,为水利设施规划、工程规模的确定提供有力支持;③水文序列存在非一致性,应对水文序列的不确定性和模型参数估计的不确定性加以有效分离和衡量,进一步提高适线精度。
关键词:不确定性;目标函数;适线法;解析法;参数估计;P-Ⅲ型曲线水文频率分析计算以概率统计理论为基础,运用理论频率曲线对水文序列进行展延。
正确的水文频率参数对于确定工程规模、合理规划水利设施、有效利用资金等具有重要的意义和价值。
由于水文序列样本容量有限,加之历史特大洪水的存在、样本点据的精度以及适线的目的不同,因此根据已有的样本点确定理论频率曲线后,在对经验点据进行展延时需要综合考虑各种因素,反复协调试算。
我国水文频率分析计算中规定以P-Ⅲ型曲线为通用线型,均值、变差系数和偏态系数为待定参数。
参数的估计方法可分为解析法和适线法两大类,解析法包括矩法、权函数法、概率权重矩法、线性矩法等,适线法包括目估适线法和优化适线法。
目前在工程实践中频率参数的确定采用的是二者联合运用的方法:运用解析法求出参数初值,根据适线目的、点据的精度和重要性,采用目估适线法或优化适线法进行参数调整,最终确定出最优且合理的频率曲线。
P-Ⅲ型分布在设计潮位中的应用

=
由于 潮位 是随机 变量 , 用频 率分析 法推 求设计 潮位 有 采
均方 误差 盯 。 为了 安全 起见 , 通常 要在设 计 值上加 上均 方误 差 作为安 全修 正值[]均方误 差计 算公式 为 : 5。 - 6
P () ≤ 刮 小a. 争≤ =5 0 9
说 明方 差 一 致 。 : 即 样本 参 数 与 总体 是一 致 的 , 有 较 具
好 的代 表 性 。
4 小 结
根据 验 潮 站六 米 站 、 河 闸和 北 炮 台 l 5 一 l 9 海 9 9 9 2年 的 潮 位 资料 , P 1 型分 布 和 G mbl 分布 设计 潮 位 , —I 由 一1 I u e型 P l I
03 6 样本 方差 O= .8 则统 计 量 n 0 4 .。 显著 水 平 .1 , ' 02 , o s 2 33 取 =
设 计 潮 位 类 型 全 年 汛 期 全 年 汛 期 全 年 汛 期
01
.
O5 . 0 3l - 03 .4
O3 .O
1 O2 .5
型 分布 的拟 合效 果较 优 : 参数 检 验 , — I 频 率曲线 更适 经 P I型 I 于在 潮位 分 布 中的计 算应 用 。 因此 ,—n 型分 布适 宜 应用 于 P l 推 求设计 潮位 。 5 参 考 文献
… 孔 乐 , 娥 . 海 地 区设 计 潮 位 计 算 方 法 探 讨 【J 州职 业 技 术 学 院 1 陈 沿 J. 泰 学 报 ,o 5 5 3 :6 3 . 2 o , ( )3 — 8 【] 世 才 , 月 英 , 文 展 . 2李 彭 魏 设计 潮 位 计 算 的 算 法 设 计 与 应 用 分析 【. J广 】 西 水 利 水 电 ,0 2 1 :5 1. 2 0 ( ) 1— 8 f1 元 芳 , 玉 , 一Ⅲ分 布 参 数 估 计 方 法 的 研 究 叨 . 海 大 学 学 报 : 3陈 侯 P 河 自 然 科 学 版 ,9 2 2 ( )2 — 1 1 9 ,0 3 :4 3 . 【】 4 翁克勤. 海岛 的设计潮位计算【 . J 水运工程 ,9 34 :5 1 ,2 】 t9 ( ) 1— 84 . [】 震 , 有 兴 , 长 宽 . 于 潮 流 数 值 模 拟 的 设 计 潮 位 推 算 方 法 【 . 5王 魏 张 基 J 水 ] 科 学 进 展 ,0 7 1 ( )56 5 9 2 0 ,8 4 :6 — 6 . 【] 松 柏 ..Ⅲ分 布 函数 的概 率 权 重 矩 法 S函 数 计 算 [J 文 ,0 82 6宋 P J. 水 20 ,8
p-ⅲ型曲线参数估计方法研究综述

【P-ⅲ型曲线参数估计方法研究综述】在计量经济学领域,P-ⅲ型曲线参数估计方法一直是一个备受关注的话题。
它是对经济学模型进行参数估计的一种重要方法,能够帮助研究者更深入地理解和分析经济现象。
在本文中,我们将对P-ⅲ型曲线参数估计方法进行综述,并共享一些个人观点和理解。
1. P-ⅲ型曲线参数估计方法简介P-ⅲ型曲线是一种常见的经济曲线类型,通常用来描述两种变量之间的非线性关系。
P-ⅲ型曲线参数估计方法,是通过对P-ⅲ型曲线的数据进行分析和建模,来估计曲线的参数值,以便更好地理解和预测经济现象。
这种方法在经济学研究中有着广泛的应用,例如对失业率和通货膨胀率之间的关系进行分析。
2. P-ⅲ型曲线参数估计方法的研究历程P-ⅲ型曲线参数估计方法的研究始于上世纪,最初是基于经验模型和数据拟合的方法。
随着计量经济学和统计学的发展,研究者们提出了各种不同的参数估计方法,包括OLS(最小二乘法)、MLE(最大似然估计)和GMM(广义矩估计)等。
这些方法在不同的经济领域得到了广泛的应用,为经济学研究提供了重要的工具和思路。
3. P-ⅲ型曲线参数估计方法的优缺点分析在使用P-ⅲ型曲线参数估计方法时,我们需要充分考虑其优缺点。
其中,最小二乘法是最常用的参数估计方法之一,它可以直接给出参数的估计值,并且易于理解和应用。
而最大似然估计方法则更适用于非线性模型的参数估计,可以在概率统计的框架下进行推导和分析。
然而,这些方法在数据样本较小或者模型条件不充分时,可能会出现估计偏差和模型不稳定的情况。
4. P-ⅲ型曲线参数估计方法的发展趋势随着大数据和机器学习等技术的兴起,P-ⅲ型曲线参数估计方法也在不断发展和完善。
一些研究者提出了基于深度学习的参数估计方法,通过神经网络等模型对非线性关系进行建模和预测,取得了一定的成果。
贝叶斯方法、面板数据模型等在P-ⅲ型曲线参数估计上也有着重要的应用前景。
总结回顾通过以上的综述,我们对P-ⅲ型曲线参数估计方法有了更深入的理解。
广义极值分布参数估计方法的对比分析

广义极值分布参数估计方法的对比分析陈子燊;刘曾美;路剑飞【摘要】简介了广义极值分布的3种参数估计方法:极大似然(ML)、线性矩(LM)和间隔最大积(MPS)方法的特点和计算方法,采用历年马口月最大径流量和广州日最大降水量作为广义极值分布不同参数估计方法的实证分析例子.分析结果表明,两实例各自3种参数估计方法得到的3个参数值较为接近,各种拟合优度检验结果表明两实例均服从广义极值分布,但MPS参数估计推算的设计值与观测值拟合更好.【期刊名称】《中山大学学报(自然科学版)》【年(卷),期】2010(049)006【总页数】5页(P105-109)【关键词】广义极值分布;参数估计方法;拟合优度检验;实证分析【作者】陈子燊;刘曾美;路剑飞【作者单位】中山大学水资源与环境系,广东,广州,510275;中山大学水资源与环境系,广东,广州,510275;华南理工大学水利水电工程系,广东,广州,510640;中山大学水资源与环境系,广东,广州,510275【正文语种】中文【中图分类】TV122政府间气候变化专门委员会(IPCC)第一工作组2007年编写的第四份评估报告指出,全球暖化愈趋明显,水文气象极端事件发生的频率可能会增大[1]。
准确地度量极值事件发生的概率及其分位数,预测极值事件可能造成的危害,已经成为工程风险管理、控制和决策研究的重要问题。
通常对水文气象极端事件频率分析采用两种方法:一是选用某些统计分布函数拟合水文气象要素的累积概率及其相应的重现水平,如显示了较大实用性并得到广泛应用的皮尔逊Ⅲ型分布[2-4],但其是根据一定代表性的经验得出的分布曲线,缺乏严格的概率理论依据;另一种方法是应用极值分布理论,分别使用Weibull、Gumbel、Frechet三种极值分布函数之一对水文气象极值序列加以拟合计算[5-9]。
近年来,许多研究人员采用了适用性更强的广义极值分布(generalized extreme-value distribution,简称GEV)理论,解决了只能用一种极值分布函数类型的局限性,广义极值(GEV)分布已经在水文气象极端事件研究领域得到了较多的应用[10-15]。
P—Ⅲ分布求矩适线法MATLAB实现与北海海域设计波高估计

MAT LAB a n d Es t i ma t i o n o f Be i h a i Hy d r o l o g i c a l S t a t i o n’ S De s i g n Wa v e He i g h t
ZHANG Bi n g — we i ,HE We n— l i a n g,Z HOU Ch o n g
第1 1 卷第 5 期
2 0 1 3 年 1 0月
水 利与建 筑 工程 学报
J o u ma l o f Wa t e r R e s o u r c e s a n d A r c h i t e c t ra u l
V0 1 . 1 1 No. 5 0c t..201 3
a n d a r e a d j u s t e d 。 nd a t h e n h t e r e l a t i o n s h i p b e t w e e n C v nd a C s i s d e b u g g e d . n I a c c o r d nc a e w i h t t h e a b s o l u t e v a l u e c r i -
数 和均值 进 行调整 , 然后调试偏态 系数 与 之 间的关系 , 并且按 照绝对 值准则挑 选 出一 组最
P3曲线

曲线做好后,双击曲线,弹出如图对话框,在 “图案”卡片中,选择适合的线形、线宽、颜色 (两理论曲线选择不同的颜色),并在“数据标 记”选择“无”。(这样做出的图更容易辨认)。
完成上述操作后,即可得出如下图 :
20000 19200 18400 17600 16800 16000 15200 14400 13600 12800 12000 11200 10400 9600 8800 8000 7200 6400 5600 4800 4000 3200 2400 1600 800 0
1977 1987 1988
214
1117 761 980
1993
1994 1995
571
1995 1840
(1)将上表中的流量按从大到小的顺序排列; (2)计算以下数值;
序号
① 1 2 3 … 31 ∑
x
m
Km
xm
x
Km 1
( K m 1) 2 ( K m 1) 3 Pm m n 1
在x轴和P轴都是等分分格的坐标纸上, P(X x)
=G(x,,…,)曲线是S形的,不便于配线和外 延,因此,设计了一种专门的坐标纸,它的概率 坐标不是等分的,而是能使(累积)频率曲线画 在上面成为直线,这种坐标纸常称为概率格纸。
水文上常用的是正态概率格纸(又称海森机率格
纸),正态分布函数画在上面成为直线。
§7-3 P-III型分布参数的估计
主要内容: P-III型分布参数的估计方法——
适线法。
学习要求:了解P-III型分布的基本概念,掌握
P-III型分布参数的计算公式,熟练运用适线法
绘制P-III型曲线。
第七章 水文频率计算

§7-3 P-Ⅲ型分布参数的估计
• P-Ⅲ型分布是我国水利水电工程水文计算规范 中推荐采用的分布,我国水文工作者对其参数估 计的方法作了大量研究,现行广泛采用的是适线 法。
一、适线法
适线法不是给出估计量的计算公式,而是由 实测样本直接推求参数的估计值。
(一)适线法的基本原理
设随机变量X的超过制分布函数P( X x) G(x;u10,L ,ul0 ) 的函数类型已知(本书沿用水文上的习惯,采用超过制分布 函数),其中的参数u10 ,L , ul0未知,待估计,又设x1, x2 ,L , xn为 X的一个容量为n的样本,现要利用这个样本通过适线法估计 参数u10 ,L , ul0的值。
基本参数E( X ),CV ,CS表示如下
a0
E(X
)(1
2CV CS
)
4 CS 2
2
E( X )CV CS
X的分布函数为
F(x)
( )
x a0
(
x
a0
)
1
e
(
xa0
)dx
X的超过累积概率为
G(x) P(X x)
( )
x
(
x
a0
)
1
e
(
xa0
)
d
x
令 t x E(X )
则 x t E(X )
记
vk= E(Xk)=gk(u01,…,u02,u0l)
• 从方程组
可解出
•
•
• 以后在不造成混淆的情况下,随机变量与普通变 量不再严格按大小写作区分。
矩 法 例题
• 例:设(X1,X2 , … , Xn )为总体X的一个样本,求总体的 均值a , 及方差σ2的矩估计。
【国家自然科学基金】_p-ⅲ型分布_基金支持热词逐年推荐_【万方软件创新助手】_20140729
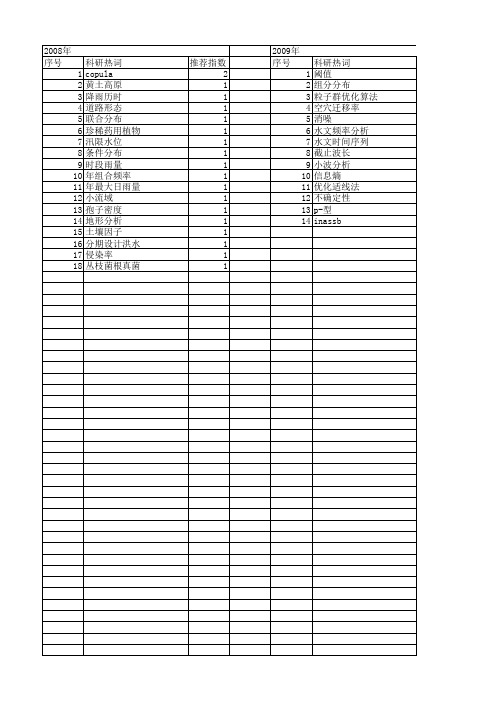
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 copula 黄土高原 降雨历时 道路形态 联合分布 珍稀药用植物 汛限水位 条件分布 时段雨量 年组合频率 年最大日雨量 小流域 孢子密度 地形分析 土壤因子 分期设计洪水 侵染率 丛枝菌根真菌
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
copula函数:条件分布 copula chover型重对数律 am算法
1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 p-ⅲ型分布 非参数核密度 陕北地区 蒙特卡罗试验 自回归马尔可夫模型 自助抽样Байду номын сангаас 矩法 水文频率计算 水文时间序列 概率格纸 概率分布 极大似然法 最大熵法 年径流频率 年径流 干旱极限分析 小波变换 噪声 参数估计 matlab lscv法 copula方法
皮尔逊三型频率曲线的三个统计参数

皮尔逊三型频率曲线是一种统计学上用于描述概率分布的曲线,通常用于表示对称但不一定正态分布的情况。
这个分布具有三个统计参数,它们是:
1.众数(Mode):众数是频率分布中出现频率最高的值,即曲线的高峰点。
在皮尔逊
三型频率曲线中,众数通常处于曲线的中心。
2.中位数(Median):中位数是将频率分布分成两半的值,即50%的观察值在中位数
的左侧,50%在右侧。
在对称的皮尔逊三型频率曲线中,众数和中位数通常相等。
3.平均数(Mean):平均数是所有观察值的总和除以观察值的数量。
在皮尔逊三型频
率曲线中,平均数通常位于曲线的中心。
由于对称性,平均数与众数和中位数相等。
这三个统计参数在描述皮尔逊三型频率曲线的形状和集中趋势时起到关键的作用。
当众数、中位数和平均数相等时,分布呈对称形状,且曲线两侧相对平缓。
当它们不相等时,分布可能具有偏斜或倾斜的形状。
需要注意的是,皮尔逊三型频率曲线并不是正态分布(正态曲线);它在中心附近可能会呈现更加陡峭的形状。
这种曲线形状的特点使得在一些实际应用中更适用于描述非对称分布。
2019-6水文统计-PIII型分布-精选文档

0 l
n
使 L 达到极值时,有u i的极大似然估计值和极大似然估计
量如下:
0 0 ˆ ˆ u u x , x , , x ) i i( 1 2 n
0 0 ˆ ˆ u u X , X , , X ) i i( 1 2 n
i 1
p.178 例6
*矩法和极大似然法的异同
4/41
权函数法 —— 加权矩法” p.187
进一步推导,还有
X M 0; M 1 1 Cv H ( ) ; M 2 2 M 0 M 2 3 R M 2 M 1 2
x
这里的H和R都与Cs有关,可通过查表求出,再计算得到x、 Cv和Cs。
7/41
水文适线方法:
目估适线法(配线法、图解法)—— 以经验频率点据为基础,在一定的适线准则下,求解与经验 点据拟合最优的频率曲线参数,是集线型选配和参数估计“合二 为一”的方法(p.179~p.185) 。 基本步骤: 1)将实测水文系列从大到小排列,用经验频率公式(期望公式)
2 2 1 x
1
x
式中,f(t)和f(x)均为P-III型分布的概率密度函数。
6/41
其中,
1 1 1 t x S ( ) x [ t e dt ] x e dx 1 ( ) ( ) 0 0
x
1 1 t 2 1 x S ( ) x [ t e dt ] x e dx 2 ( ) ( ) 0 0
n 1 2 ˆ2 s (x x ) i n1
ˆ C s
3 ( k 1 ) i 1
n
ˆ 3 nC v
3/41
极大似然法 ——“发生概率最大的事件可能发生”
水文统计PIII型分布

§6 P-III型分布参数估计和经验频率曲线(p.173-196)
6.1 估计理论
参数估计 —— X、Cv、Cs 非参数估计 —— 当没有确切的数学分布时
点估计的思想:假设样本X的分布函数为F(x; u ),u 为未知参数,
构造估计量U=U(X1,X2,…,Xn),若将一个具体样本(x1,x2, …,xn)带入U, 则可以得到u 的估计值为u=u(x1,x2, …,xn)。 区间估计的思想:即估计参数所在的区间,或永一个区间区区估计未 知参数。
Qp=1%=1246×(1+3.33×0.6)=3730m3/s
14/41
三点法 ——
在经验频率曲线上任取3个点(xp1,P)、(xp2,P)、(xp3,P),代入P-III
i 1 n 2 2 ( K 1 ) i i 1 n
C v
n n 1
n
n 1
12/41
3)点绘经验频率曲线(图4-9)
13/41
4)选配理论频率曲线(表4-4)
5)推求百年一遇的设计洪峰流量
由图4-9,查 p=1%对应的流量 Qp=3730m3/s
或用式 x 直接计算,得到 x ( 1 Cv ) p p
0
0 l
n
使 L 达到极值时,有u i的极大似然估计值和极大似然估计
量如下:
0 0 ˆ ˆ u u x , x , , x ) i i( 1 2 n
0 0 ˆ ˆ u u X , X , , X ) i i( 1 2 n
i 1
p.178 例6
*矩法和极大似然法的异同
4/41
权函数法 —— 加权矩法” p.187
n 1 2 ˆ2 s (x x ) i n1
p-3型分布参数估计解读

一、经验频率曲线与理论频率曲线 1. 经验频率计算公式
经验频率曲线由实测资料绘制而成,它是水文频率 计算的基础,具有一定的实用性。 设某水文要素(如年径流量)的实测系列共n项,按 由大到小的次序排列为x1、x2、...、xm、...、xn。经验频 率就是在系列中大于及等于样本xi的出现次数与样本容量 之比值,即
量好,在数理统计中,极大似然法被认为是最
好的方法。
§7-3 P-Ⅲ型分布参数的估计
一、 P-Ⅲ型分布
在水文频率曲线线型选择上,世界各地差异很大, 常用线型达20多种。我国20世纪60年代以来,通过对洪 水极值资料的验证,认为P-Ⅲ型能较好拟合我国大多数 河流的洪水系列,因此我国水利水电工程水文计算规范 推荐采用该分布。 ( x a0 ) 1 e ( x a ) • x a0 P-Ⅲ型分布的密度函数: f ( x) ( )
1 n 均值 x 的无偏估计: x xi n i 1
Cv的无偏估计量:
Cs 的无偏估计量:
Ki
xiห้องสมุดไป่ตู้x
模比系数
2. 现行水文频率计算——适线法 适线法(或称配线法)是以经验频率点据为基础, 在一定的适线准则下,求解与经验点据拟合最优的频 率曲线参数,得到一条理论频率曲线。 目估适线法、优化适线法 目估适线法: (1)将实测资料由大到小排列,计算各项的经验频率, 在频率格纸上点绘经验点据(纵坐标为变量取值,横 坐标为对应的经验频率)。 (2)选定水文频率分布线型(一般选用PⅢ型)。 (3)假定一组参数 x 、Cv、 Cs。为了使假定值大致接 近实际,可用矩法求出3个参数,作为3个参数第一次 的假定值。估计时,因Cs 的抽样误差太大,
3. 统计参数对频率曲线的影响: (1)均值 x 对频率曲线的影响
极端暴雨条件下暴雨频率曲线线型及参数分析

第47卷第4期2021年4月水力发电极端暴雨条件下暴雨频率曲线线型及参数分析彭慧1,郭士红1,龚晶1,公绪英1,彭远2(1.山东省水利勘测设计院,山东济南250014;2.山东省新泰市水利局,山东新泰271200)摘要:为解决极端暴雨条件下频率曲线线型及参数问题,分别采用不同偏变比P-m型以及广义极值分布(GEV)频率曲线分析,并以山东省小清河流域为实例说明了算法适用性#利奇马暴雨在小清河重现期为120-140a,利用=3.5、R”=5和R”=6三种偏变比P-m型频率曲线,以及广义极值分布(GEV)频率曲线拟合1951年~2019年不同历时%最大24、72h)暴雨经验点据,结果表明:上游、中游、下游最大24h暴雨以及上游、中游最大72h暴雨均可采用R”=3.5的P-m型频率曲线;下游最大72h暴雨,GEV与R”=5的P-(型拟合效果佳且二者成果接近,工程设计中可采用R”=5的P-m型频率曲线#关键词:暴雨频率曲线;P-m型;偏变比;广义极值分布;利奇马暴雨Research on Frrquency Curves and Parameters of Extrrme StormPENG Hui1,GUO Shihong1,GONG Jing1,GONG Xuying1,PENG Yuan2(1.Shandong Survey and Design Institute oS Water Conservancy,Jinan250014,Shandong,China;2.Water Conservency Burevu oS Xintai City,Xintai271200,Shandong,China)Abstrach In order to solve the problems oS frequenca curve type and parameter selection for extreme storm research,the P-III and GEV curves are used and applied in Xiaoqing River basin in Shandong Provincc to study the applicability oS different aagoeithms.Theoccu e ence eequencyoOLiqimaeainstoem in XiaoqingRieeeis120-140yeaes,and theeeP-I cueeeswith dferent ratios oS skewnes s to variation(R,=3.5,5and6respectively)and the GEV curve are used to fit the1951-2019 histoeicaadataoomeasueed eainoa a.Theeesuatsindicatethat,(a)thematimum24h dueation eainoa a oouppeeeeach,middae eeach and aoweeeeach and thematimum72h dueation eainoa a oouppeeeeach and middaeeeach couad usetheP-I cueeewith R,=3.5to fit;and(b)the P-II I curve with R,=5and the GEV curve have same better fitting effect for the maximum72h duGation Gainoa a ooaoweGGeach,and theP-I cuGeewith R,=5ispGoposed tobeused in engineeGingdesign.Key Words:rainstorm frequenca curve;P-III curve;ratio oS skewness to variation;generalized extremum distribution;Liqima eainstoem中图分类号:P333.2文献标识码:A文章编号:0559-9342%2021)04-0024-050引言我国暴雨洪水频率曲线一般采用皮尔逊III型。
权函数法在P—Ⅲ型分布中的应用

,
X
对 于频 率 计 算 ,在 线 型 已定 的 情 况 下 ,选 取 量 优 的参 数估 计 方 法是提 高 计 算 精 度 的 根 本 所 在 ,在 数 理 统 计 方法
中即为 改 善求矩 误差 。水 文 计 算 中 的数 理 统 计 用 样 本 矩 来 估 计 总 体 矩 , 而 在 概 率 论 中 对 于 无 限 总 体 ,各 阶 矩 都 是 积 分 式 。 而 数 理 统 计 中 的 样 本 矩 就 是 累 加 求 和 矩 ,是 寄 托 在
维普资讯
4 6 浙 江 水 利 科 技 ・0 2年 ・ 4期 20 第
权 函 数 法 在 P 1 型 分 布 中 的 应 用 一I [
陈 望 春 ,赵 立 锋
( 波 市 水 文站 ,浙 江 宁 波 宁 35 1) 10 6
摘 要 :系统 地 介绍 了权 函数法 ,并 结合 实 测 资料 ,对 权 函数 法进 行 了深 入地 探 讨 ,为 P Ⅲ型分 布 参 数估 计 -
增 加 均 值附近 数 据 在 求 距 时 的作 用 ,降 低 远 离 均 值 处 数 据 的影 响 ,必能 提 高估 计 精度 。权 函数 法 的 实质 正 是 基于 此 ,
收 稿 丑 期 :2 0 -33 0 20 —0 作者 简 介 : 陈 望 春 ( 9 6一 ) 男 , 助 理 工 程 师 , 大 学 本 科 17 , 主要从 事水 文测验 与分 析 工作 。
大 的 结 果 ;同 时 , 由 于 假 定 采 用 某 种 经 验 频 率 公 式 造 成 样 本 矩 偏 小 达 不 到 总 体 全 矩 ,造 成 端 距 误 差 。
、
E () x
要 提 高参 数 估 计 的 精 度 ,唯 有 提 高 求 矩 的 计 算 精 度 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 统计参数对频率曲线的影响: (1)均值 x 对频率曲线的影响
(2)Cv对频率曲线的影响
(3)Cs对频率曲线的影响
二、优化适线法 在一定的适线准则(即目标函数)下,求解 与经验点据拟合最优的频率曲线的统计参数的方 法。
优化适线法准则: 离差平方和最小准则(OLS)(最小二乘法): 使经验点据和同频率的频率曲线纵坐标之差的平 方和达到最小。 离差绝对值和最小准则(ABS)
量好,在数理统计中,极大似然法被认为是最
好的方法。
§7-3 P-Ⅲ型分布参数的估计
一、 P-Ⅲ型分布
在水文频率曲线线型选择上,世界各地差异很大, 常用线型达20多种。我国20世纪60年代以来,通过对洪 水极值资料的验证,认为P-Ⅲ型能较好拟合我国大多数 河流的洪水系列,因此我国水利水电工程水文计算规范 推荐采用该分布。 ( x a0 ) 1 e ( x a ) • x a0 P-Ⅲ型分布的密度函数: f ( x) ( )
则有 X p X (1 cV p )
p( p ) p f ( p , Cs )d
p ( p )
p
f , C s d
该式包含 Cs、P与Φp的关系,查附表4, 由已知的Cs值,查表可得不同P的 Φp值,然 后利用已知的 和Cv值,通过下式即可求出 x 与各种P相应的xp值,从而可绘出理论频率曲 线。
第7章 估计理论
§7-3 P-Ⅲ型分布参数的估计
回顾复习
矩法
点估计
估 计 理 论 参数估计 区间估计 非参数估计
极大似然法
适线法
矩法与极大似然法
矩法的优点是寻求总体数字特征等的估计 量时无须知道随机变量的分布函数,而应用极 大似然法时必须知道总体的概率分布;估计量
质量方面,极大似然估计量的性质要比矩估计
§7-3 P-Ⅲ型分布参数的估计
二、 适线法
研究发现:极大似然法用于估计P-Ⅲ型分布 参数时,需要试算,而且有时似然方程无解,因 此,在我国水文计算工作中并不常用。对P-Ⅲ分 布,我国常采用适线法估计其参数。
• 四、现行水文频率计算方法——适线法 用有限的样本观测资料估计总体分布线 型中的参数,如P—Ⅲ型的 、Cv、 Cs。 x 1、P—Ⅲ型的分布参数初估方法 (1)矩法 用样本矩估计总体矩,并通过矩与参数之 间的关系,来估计频率曲线的参数。
X p X (1 cV p )
• 例3-2 已知某站年最大洪峰流量系列的平均 x=825m3/s,Cv=0.4,Cs=1.0,求p=1%的设计 值。 解:由Cs=1.0,查附表4,得p=1%的 Фp=3.02,则 X p X (1 cV p ) =825×(0.4×3.02+1)=1822
m p 100 % n
当m=n时,p=100%,即样本的末项 xn是总体中的 最小值,显然不符合实际,因为随着观测年数的增多, 总会出现更小的数值。
1
切哥达也夫公式
p
m 0.3 100 % n 0.4
海森公式
m 0.5 p 100 % n
0
一、经验频率曲线与理论频率曲线 1. 经验频率计算公式
经验频率曲线由实测资料绘制而成,它是水文频率 计算的基础,具有一定的实用性。 设某水文要素(如年径流量)的实测系列共n项,按 由大到小的次序排列为x1、x2、...、xm、...、xn。经验频 率就是在系列中大于及等于样本xi的出现次数与样本容量 之比值,即
例如,对于p=90%的枯水流量,则T=10年,称此为十年一 遇枯水流量,表示小于等于这样的流量平均10年会遇到一次。
3、理论频率曲线 PⅢ型分布
x a0 1 e ( xa0 ) f ( x) ( )
4 C s2
2 xCV C s
2CV a 0 x 1 Cs
一般不计算Cs,而是根据经验假定 Cs为 Cv的某一 倍数(如 Cs=2Cv)。 (4)根据假定的 x 、Cv、Cs,查附表4,计算xp值, 以xp为纵坐标,p为横坐标,即可得到频率曲线。 将此线画在绘有经验点据的图上,看与经验点据 配合的情况,若不理想,则修改参数(样本均值 估计误差小,一般不做调整;主要调整 Cv、Cs) 再次进行计算。 (5)最后根据频率曲线与经验点据的配合情况, 从中选择一条与经验点据配合较好的曲线作为采 用曲线。相应于该曲线的参数便看作是总体参数 的估值。 (6)求指定频率的水文变量设计值。
水文计算中,一般需求出指定频率p所对 应的随机变量取值,例如,频率为1%(百年一 遇)的设计洪峰流量。 1 ( x a0 ) p p( x x p ) dx x p ( x a0 ) e ( ) 令
xx xCV
Φ是均值为零,标准差为1的标准化变量 (离均系数)
1 n 均值 x 的无偏估计: x xi n i 1
Cv的无偏估计量:
Cs 的无偏估计量:
Ki
xi x
模比系数
2. 现行水文频率计算——适线法 适线法(或称配线法)是以经验频率点据为基础, 在一定的适线准则下,求解与经验点据拟合最优的频 率曲线参数,得到一条理论频率曲线。 目估适线法、优化适线法 目估适线法: (1)将实测资料由大到小排列,计算各项的经验频率, 在频率格纸上点绘经验点据(纵坐标为变量取值,横 坐标为对应的经验频率)。 (2)选定水文频率分布线型(一般选用PⅢ型)。 (3)假定一组参数 x 、Cv、 Cs。为了使假定值大致接 近实际,可用矩法求出3个参数,作为3个参数第一次 的假定值。估计时,因Cs 的抽样误差太大,
2. 经验频率曲线
水文上常用“重现期”来代替“频率”
1. 当研究暴雨或洪水时(一般p≤50%)
T 1 P
例如,当某一洪水的频率为p=1%时,则T=100年,称此 洪水为百年一遇洪水,表示大于等于这样的洪水平均100年会 遇到一次。 2. 当研究枯水或年径流时(一般p≥50%)
T 1 1 P
