高等数学:5-5 广义积分
高考数学必绝活高等数学广义积分计算方法

高考数学必绝活高等数学广义积分计算方法高考数学必绝活:高等数学广义积分计算方法在高考数学中,广义积分的计算虽然不是常见的考点,但一旦出现,往往能拉开考生之间的差距。
掌握广义积分的计算方法,不仅能在高考中多一份胜算,也为后续的高等数学学习打下坚实的基础。
接下来,让我们一起深入探讨高等数学广义积分的计算方法。
一、广义积分的概念广义积分是定积分的扩展,当积分区间为无穷区间或者被积函数在积分区间内有无穷间断点时,就涉及到广义积分。
对于无穷区间上的广义积分,比如积分区间为 a, +∞),我们可以写成:∫a, +∞) f(x) dx =lim b→+∞ ∫a, b f(x) dx同样,如果积分区间为(∞, b,则广义积分为:∫(∞, b f(x) dx =lim a→∞ ∫a, b f(x) dx而对于被积函数在积分区间内有无穷间断点的广义积分,以区间 a,b 上,x =c 为无穷间断点为例,广义积分为:∫a, b f(x) dx =∫a, c) f(x) dx +∫(c, b f(x) dx其中,∫a, c) f(x) dx =lim ε→0+ ∫a, c ε f(x) d x ,∫(c, b f(x) dx = lim ε→0+ ∫c +ε, b f(x) dx二、常见的广义积分类型及计算方法1、无穷区间上的广义积分(1)形如∫a, +∞) x^n dx (n ≠ -1)对于这种类型的广义积分,我们可以使用幂函数的积分公式:∫ x^n dx =(1/(n + 1)) x^(n + 1) + C则∫a, +∞) x^n dx =lim b→+∞ (1/(n + 1)) b^(n + 1) (1/(n + 1)) a^(n + 1)当 n >-1 时,该广义积分收敛;当n ≤ -1 时,广义积分发散。
(2)形如∫a, +∞) e^(px) dx (p > 0)先对被积函数进行积分:∫ e^(px) dx =(-1/p) e^(px) + C则∫a, +∞) e^(px) dx =lim b→+∞ (-1/p) e^(pb) (-1/p) e^(pa)因为当b → +∞ 时,e^(pb) → 0 ,所以该广义积分收敛,其值为(1/p) e^(pa) 。
定积分求解方式更新丨10分钟掌握高数上定积分求解问题(考研、期末复习均可以用)

定积分求解方式更新丨10分钟掌握高数上定积分求解问题(考研、期末复习均可以用)最近一直没有时间更新知识点,今天抽了点空,继续往下写点东西下面是之前更新的内容,请自取10分钟掌握高等数学上册函数极限求解问题(考研、期末复习均可以用)10分钟掌握高等数学上册导数及微分问题(考研、期末复习均可以用)10分钟掌握高等数学上册函数图像绘制问题(考研、期末复习均可以用)10分钟掌握中值定理相关问题(考研、期末复习均可以用)10分钟掌握高数上不定积分问题(考研、期末复习均可以用)码字不易,观看后的同学请给个赞+关注如果有考研或是期末复习方面问题的话可以随时留言或者私信【答学百科】,更多期末复习资料更多更新内容也可以点击下方链接加入社群--------------分割线---------------正式进入定积分前,先简单说下什么是定积分吧:定积分就是函数 f(x) 与 x=a,x=b 及 x 轴所围成的区域对应的曲面面积,若曲面面积位于x 轴下方,则对应的积分值为负基于以上的描述,下方具体开始讲解一、定积分的定义上述介绍了定积分表示的几何意义,下面利用极限的形式看下定积分的定义:设 y=f(x) 在 [a,b] 上有界①设 a=x_{0}<x_{1}<...<x_{n}=b ,则[a,b]=[x_{0},x_{1}]\cup[x_{1},x_{2}]\cup...\cup[x_{n-1},x_{n}] ,其中 \Delta x_{i}=x_{i}-x_{i-1}(i=1,2,3...)②取 \xi_{i}=\in[x_{i-1},x_{i}] ,则“面积”为f(\xi_{1})\Delta x_{1}+f(\xi_{2})\Deltax_{2}+...+f(\xi_{n})\Deltax_{n}=\sum_{i=1}^{n}{f(\xi_{i})\Delta x_{i}}③取 \lambda=max(\Delta x_{1},\Delta x_{2}...\Deltax_{n}) ,若 \lim_{\lambda \rightarrow0}{\sum_{i=1}^{n}{f(\xi_{i})\Delta x_{i}}} 存在,则称f(x) 在[a,b]上可积分,记为 \int_{a}^{b}f(x)dx ,即\int_{a}^{b}f(x)dx=\lim_{\lambda \rightarrow0}{\sum_{i=1}^{n}{f(\xi_{i})\Delta x_{i}}}注:有的同学会发现一个问题,为何要多引入一个 \lambda 值,令 n\rightarrow\infty 时不就可以了么下面简单看个图像如果仅仅是n\rightarrow\infty,那在区间内进行分段时,完全可以在 [a,c](c<b) 段上进行 \Delta x_{1}-\Deltax_{n-1} 的划分,然后把最后一段 \Delta x_{n} 留给 [c,b] 区段上,这种情况下该段的条形面积f(\xi_{n})\Deltax_{n} 的值就不会等于曲线与数轴之间围成的面积了,所以如果仅仅是n\rightarrow\infty的条件,累计的值并不等于积分值注:(1)极限 \lim_{\lambda \rightarrow0}{\sum_{i=1}^{n}{f(\xi_{i})\Delta x_{i}}} 是否存在,与区间的分法和 \xi 的取值无关( \xi 一般取区间的左右端点)(2)函数 f(x) 在 [a,b] 上有界是函数可积的必要条件,而非充分条件(3)利用定积分可以求解极限题目,之前在讲解极限以及每日一题的时候有提到过相关的原理和操作,下面有链接,此处不再重复:10分钟掌握高等数学上册函数极限求解问题(考研、期末复习均可以用)大学数学每日一题——微积分1208二、定积分的性质1、 \int_{a}^{a}f(x)dx=0 ,\int_{a}^{b}f(x)dx=-\int_{b}^{a}f(x)dx2、若 f(x) 可积,\int_{a}^{b}f(x)dx=\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x) dx3、若 f(x) 可积且f(x)\geq0,则\int_{a}^{b}f(x)dx\geq0 ;若 f(x) 不恒等于 0 时,\int_{a}^{b}f(x)dx>04、若 f(x),g(x) 可积>f(x)\geq g(x),\int_{a}^{b}f(x)dx\geq\int_{a}^{b}g(x)dx ,若 f(x) 不恒等于 g(x) 时, \int_{a}^{b}f(x)dx>\int_{a}^{b}g(x)dx5、若 f(x) 可积,则 \left| \int_{a}^{b}f(x)dx\right|\leq \int_{a}^{b}\left| f(x) \right|dx6、设f(x) 可积,且 m\leq f(x)\leq M ,则 m(b-a)\leq \int_{a}^{b}f(x)dx\leq (b-a)M7、积分中值定理设 f(x) 在 [a,b] 上连续,则存在 \xi\in[a,b] 使得\int_{a}^{b}f(x)dx=(b-a)f(\xi)注:积分中值定理是针对闭区间的定理,当然也有针对开区间的中值定理,下面进行证明例题:设 f(x) 在 [a,b] 上连续,求证存在 \xi\in(a,b)使得 \int_{a}^{b}f(x)dx=(b-a)f(\xi)解答:设 F(x)=\int_{a}^{x}f(t)dt , F'(x)=f(x) ,根据拉格朗日中值定理可知:存在 \xi\in(a,b),使得\frac{F(b)-F(a)}{b-a}=F'(\xi) ,即:\frac{\int_{a}^{b}f(x)dx-\int_{a}^{a}f(x)dx}{b-a}=f(\xi) ,即\int_{a}^{b}f(x)dx=f(\xi)(b-a)大家在进行解题的时候应该注意题目要求的是证明开区间还是闭区间内的中值定理8、柯西不等式f(x),g(x) 在 [a,b] 上连续,则(\int_{a}^{b}f(x)g(x)dx)^{2}\leq\int_{a}^{b}f^{2}(x)dx \int_{a}^{b}g^{2}(x)dx以上8个性质在证明题中均可以直接使用三、定积分求解方法定积分的求解中涉及方法较多,最常见的是牛顿莱布尼兹公式,通过求出原函数来进行求解,除了牛顿,定积分的求解还涉及到很多不需要求解出原函数,而是通过定积分的特殊性质即可求解的情况,下列具体讲解:1、牛顿--莱布尼兹公式设 f(x) 在 [a,b] 上连续,且 F(x) 为 f(x) 的一个原函数,则\int_{a}^{b}f(x)dx=F(b)-F(a)牛顿莱布尼兹公式是求解定积分最基本的方法,其基础是不定积分,忘记的同学请自取:10分钟掌握高数上不定积分问题(考研、期末复习均可以用)例题:求解 \int_{0}^{1}xe^xdx解答:\int_{0}^{1}xe^xdx=\int_{0}^{1}xde^x=[xe^{x}]_{0}^{1}-\int_{0}^{1}e^xdx=e-[e^x]_{0}^{1}=12、定积分的特殊性质(1)对称区间上函数的定积分性质设函数f(x) 在 [-a,a] 上连续,则 \int_{-a}^{a}f(x)dx=\int_{0}^{a}f(x)+f(-x)dx特别的,当 f(x) 为奇函数时, \int_{-a}^{a}f(x)dx=0 ;当 f(x) 为偶函数时, \int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx例题:求解 \int_{-1}^{1}\frac{x}{1+sin^2x}dx解答:设被积函数 f(x)=\frac{x}{1+sin^2x} ,f(-x)=\frac{-x}{1+sin^2x}=-f(x) ,由关系式可知,被积函数为奇函数,故该积分为0例题:求解 \int_{-\pi/2}^{\pi/2}\frac{sin^2x}{1+e^x}dx解答:该积分为对称区间上的积分,所以可以直接用公式:\int_{-a}^{a}f(x)dx=\int_{0}^{a}f(x)+f(-x)dx\int_{0}^{\pi/2}\frac{sin^2x}{1+e^x}+\frac{sin^2x}{1+e^{-x}}dx\int_{0}^{\pi/2}sin^2xdx=\frac{1}{2}\frac{\pi}{2}=\frac{\pi}{4}上述题目两道题目如果用牛顿莱布尼兹公式求解的话着实很难求出原函数,且耗费时间较多,没有必要(2)三角函数定积分性质设 f(x) 在 [0,1] 上连续,则a、\int_{0}^{\pi/2}f(sinx)dx=\int_{0}^{\pi/2}f(cosx)dxb、\int_{0}^{\pi/2}sin^nxdx=\int_{0}^{\pi/2}cos^nxdx=\fra c{n-1}{n}\frac{n-3}{n-2}...\frac{2}{3} ( n 为奇数)c、\int_{0}^{\pi/2}sin^nxdx=\int_{0}^{\pi/2}cos^nxdx=\fra c{n-1}{n}\frac{n-3}{n-2}...\frac{1}{2}\frac{\pi}{2} ( n 为偶数)d、\int_{0}^{\pi}f(sinx)dx=2\int_{0}^{\pi/2}f(sinx)dxe、\int_{0}^{\pi}xf(sinx)dx=\frac{\pi}{2}\int_{0}^{\pi}f( sinx)dx=\pi\int_{0}^{\pi/2}f(sinx)dx以上几个式子的证明过程不在此处进行详说,基本上都是用到二类换元法和分布积分法进行求解的,有兴趣的小伙伴可以自己尝试求解下(3)定积分的特殊性质设 f(x) 是以 T 为周期的可积分函数,则a、 \int_{a}^{a+T}f(x)dx=\int_{0}^{T}f(x)dxb、\int_{0}^{nT}f(x)dx=n\int_{0}^{T}f(x)dx(4)特殊函数积分这里重点说一个大部分人经常遇到的一个积分,即\int_{-\infty}^{+\infty}e^{-x^2}dx初学者遇到该问题时往往会想把原函数给求解出来,但是实际上这个函数是无法求解出原函数的(或者说在高等数学的范畴中是不要求求解出原函数的)没有原函数是不是代表该题目无法解答呢,实际上不是的,该积分题目其实求解的方法还是蛮多样的,接下来介绍两种方法,涉及到二重积分和概率论的解答思路a、利用二重积分进行解答:I=\int_{-\infty}^{+\infty}e^{-x^2}dx=\int_{-\infty}^{+\infty}e^{-y^2}dyI^2=\int_{-\infty}^{+\infty}e^{-x^2}dx\int_{-\infty}^{+\infty}e^{-y^2}dy=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-(x^2+y^2)}dxdy=\int_{0}^{2\pi}d\theta\int_{0}^{+\infty}re^{-r^2}dr=\piI=\sqrt{\pi}b、利用概率论中标准正态分布解法进行解答:标准正态分布概率密度函数如下:f(x)=\frac{1}{\sqrt{2\pi}}e^{\frac{-x^2}{2}} ,根据概率密度函数的在正负无穷上积分等于1的性质可得\int_{-\infty}^{+\infty}f(x)dx=1令 x=\sqrt{2}t ,原式变为 \int_{-\infty}^{+\infty}\frac{\sqrt{2}}{\sqrt{2\pi}}e^{-t^2}dt=\int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}}e^{-t^2}dt=1=\int_{-\infty}^{+\infty} e^{-t^2}dt=\sqrt{\pi}四、变限积分求导法则设 f(x) 在 [a,b] 上连续,则(\int_{\psi(x)}^{\varphi(x)}f(t)dt)'=f(\varphi(x))\var phi'(x)-f(\psi(x))\psi'(x)特别的档 \varphi(x)=x,\psi(x)=0 时,(\int_{a}^{x}f(t)dt)'=f(x)例题1:设 f(x) 在 [a,b] 上连续, F(x)=\int_{0}^{x}(x-t)f(t)dt ,求解 F'(x)解答:F(x)=x\int_{0}^{x}f(t)dt-\int_{0}^{x}tf(t)dtF'(x)=xf(x)+\int_{0}^{x}f(t)dt-xf(x)=\int_{0}^{x}f(t)dt例题2:设 f(x) 在 [a,b] 上连续,F(x)=\int_{0}^{x}f(x-t)dt ,求解 F'(x)解析:题设中的被积函数含有 x,t ,有的同学拿到后会直接利用公式进行求导,即F'(x)=f(0) (常数)但是细想觉得求导后应该为一个函数表达式,不应该为一个常数的确,上述的求法是错误的,正确的解答方法应该将被积函数的 x,t进行分离,分离开后再进行导数计算解答:x-t=k ,当 t=x 时, k=0 ;当 t=0时, k=x ; dt=-dkF(x)=\int_{0}^{x}f(x-t)dt=-\int_{x}^{0}f(k)dk=\int_{0}^{x}f(k)dkF'(x)=f(x)例题3:设 f(x)=\int_{1}^{x}e^{t^2}dt ,求\int_{0}^{1}x^2f(x)dx解答:\int_{0}^{1}x^2f(x)dx=\int_{0}^{1}f(x)d(\frac{1}{3}x^3)=\frac{1}{3}x^3f(x)|_{0}^{1}-\int_{0}^{1}\frac{1}{3}x^3f'(x)dx=-\int_{0}^{1}\frac{1}{3}x^3f'(x)dx=-\int_{0}^{1}\frac{1}{3}x^3e^{x^2}dx=-\frac{1}{6}\int_{0}^{1}x^2e^{x^2}dx^2=-\frac{1}{6}\int_{0}^{1}xe^{x}dx=-\frac{1}{6}\int_{0}^{1}xde^{x}=-\frac{1}{6}xe^x|_{0}^{1}+\int_{0}^{1}\frac{1}{6}e^xdx=-\frac{1}{6}五、广义积分广义积分是相对于正常积分所提出来的一个积分概念,即对于积分上下限为无穷大,或是积分限内含有第二类间断点的积分1、积分区域无穷大的广义积分\int_{a}^{+\infty}f(x)dx,\int_{-\infty}^{0}f(x)dx,\int_{-\infty}^{+\infty}f(x)dx以上三个积分均为积分区域无穷大的广义积分,当该积分的极限存在时,则说明该广义积分收敛,否则称其为发散敛散性判别法:设 \lim_{x \rightarrow \infty}{x^kf(x)dx}=M ( M 为常数),则当 k>1 时极限成立,该广义积分收敛;当 k\leq1 时极限成立,该广义积分发散例题:求解\int_{1}^{+\infty}\frac{1}{x}dx解答:设\lim_{x \rightarrow \infty}{x^kf(x)dx}=\lim_{x\rightarrow \infty}{x^k\frac{1}{x}}=M ,为使该极限成立,可推出 k 的取值为 k\leq1 ,所以根据收敛判别式可知该积分为发散积分2、积分区间上存在无穷断点的广义积分\int_{a}^{b}f(x)dx函数 f(x) 在 x=a 的左邻域或 x=b 的右邻域或 x=a,x=b 的左右邻域内无界,则该积分称之为广义积分,当该积分的极限存在时,则说明该广义积分收敛,否则称其为发散敛散性判别法:(1)设 f(x) 在x=a 的左邻域无界,且\lim_{x\rightarrow a^+}{(x-a)^kf(x)dx}=M ( M 为常数),则当k<1 时极限成立,该广义积分收敛;当 k\geq1 时极限成立,该广义积分发散(2)设 f(x) 在x=b 的右邻域无界,且\lim_{x\rightarrow b^-}{(b-x)^kf(x)dx}=M ( M 为常数),则当k<1 时极限成立,该广义积分收敛;当 k\geq1 时极限成立,该广义积分发散例题:求解\int_{0}^{1}\frac{1}{x}dx解答:被积函数在x=0 处为无界函数,所以设极限 \lim_{x\rightarrow 0}{x^kf(x)dx}=\lim_{x \rightarrow0}{x^k\frac{1}{x}}=M ,为使该极限成立,可推出k 的取值为 k\geq1 ,所以根据收敛判别式可知该积分为发散积分3、积分区间内部存在无穷间断点\int_{a}^{b}f(x)dx被积函数在 x=c(a<c<b) 的去心邻域内无界,则\int_{a}^{b}f(x)dx=\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x) dx ,此处必须将 c 点进行分离考虑,当两个式子的积分极限都存在时方能判断整个式子的极限存在例题:求解\int_{-1}^{1}\frac{1}{x^{2}}dx错误解法:\int_{-1}^{1}\frac{1}{x^{2}}dx=-\frac{1}{x}|_{-1}^{1}=-2 ,该做法错误的地方是未考虑到 x=0 为函数的无穷断点,直接跳过了断点进行积分正确做法:\int_{-1}^{1}\frac{1}{x^{2}}dx=\int_{-1}^{0}\frac{1}{x^{2}}dx+\int_{0}^{1}\frac{1}{x^{2}}dx,将分离后的两个积分进行单独考虑\int_{-1}^{0}\frac{1}{x^{2}}dx 在 x=0 处是无界的,所以考虑 \lim_{x \rightarrow0}{x^kf(x)dx}=\lim_{x \rightarrow0}{x^k\frac{1}{x^2}}=M ,为使该极限成立,可推出k 的取值为 k\geq2 ,所以根据收敛判别式可知该积分为发散积分同理可知\int_{0}^{1}\frac{1}{x^{2}}dx 也是发散积分,所以判断该积分为发散积分六、定积分的应用1、面积(1)设 D 由 y=f(x)\geq0 , x=a 及 x=b(b>a)围成,则D 的面积为 S=\int_{a}^{b}f(x)dx(2)设 D 由 y=f(x) , y=g(x) , x=a 及 x=b(b>a)围成,则 D 的面积为 S=\int_{a}^{b}\left| f(x)-g(x)\right|dx(3)极坐标法的面积 D 求解公式为S=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)d\theta ;当曲线由 r=r_{1}(\theta), r=r_{2}(\theta) 组成,则面积S=\frac{1}{2}\int_{\alpha}^{\beta}[r_{2}^{2}(\theta)-r_{1}^{2}(\theta)]d\theta(4)旋转曲面的面积函数 f(x) 绕 x 轴旋转一周所得到的旋转体侧面的面为S=2\pi\int_{a}^{b}\left| f(x)\right|\sqrt{1+f'^2(x)}dx备注:以上均是利用 y=f(x) 的函数进行面积求解,有的题目未直接给出 y=f(x) 的关系式,而是给出了参数方程的形式( x=\varphi(t),y=\psi(t) ),可以直接将上述式子中的f(x),x,dx 等函数进行替换即可2、体积(1)y=f(x)绕 x 轴旋转后的体积:V=\pi\int_{a}^{b}f^2(x)dx(2)y=f(x)绕 y 轴旋转后的体积:V=2\pi\int_{a}^{b}\left| x \right|\left| f(x)\right|dx3、长度(1)设 L:y=f(x)(a\leq x\leq b) ,则曲线长度为l=\int_{a}^{b}\sqrt{1+f'^2(x)}dx(2)设 L:x=\varphi(t),y=\psi(t)(\alpha\leq t\leq\beta) ,则曲线长度为l=\int_{\alpha}^{\beta}\sqrt{\varphi'^2(t)+\psi'^2(t)} dt(3)设 L:r=r(\theta)(\alpha\leq x\leq \beta) ,则曲线长度为l=\int_{\alpha}^{\beta}\sqrt{r^2(\theta)+r'^2(\theta)} d\theta例题1:求由曲线 y=4-x^2 与 x 轴围成的部分绕直线 x=3旋转一周所成的几何体的体积解答:利用微元法进行求解:取 [x,x+dx]\subset[-2,2] ,则 dv=2\pi(3-x)(4-x^2)dx ,则 V=\int_{-2}^{2}2\pi(3-x)(4-x^2)dx=64\pi例题2:求由曲线 y=4-x^2 与 x 轴围成的部分绕直线 y=-3旋转一周所成的几何体的体积解答:利用微元法进行求解:取 [x,x+dx]\subset[-2,2] ,则dv=[\pi(y+3)^2-\pi(-3)^2]dx ,则 V=\int_{-2}^{2}[\pi(y+3)^2-\pi(-3)^2]dx=\int_{-2}^{2}[\pi(7-x)^2-\pi(-3)^2]dx=\int_{-2}^{2}40\pi+\pi x^2dx=2\int_{0}^{2}40\pi+\pi x^2dx=\frac{496}{3}\pi。
高等数学课件5第四节 反常积分ppt

lim
t b
t a
f
(
x
)
dx
b
a
f (x) 在 [a , b) 上的反常积分(或瑕积分).
这时称反常积分
收敛;
否则, 称反常积分 发散.
定义6. 设函数 f ( x)在[a, b]上除点c (a c b)外连续,
点 c 为f (x)的瑕点.
若 瑕 积 分ac
f
(
解:
原式
1 p
0
td(e
pt
)
1 p
([te
pt
]0
e
0
pt dt )
a
udv
[uv]a
a
vdu
1 p
( lim te t
pt
0
[
1 p
e
pt
]0
)
0
1 p2
( lim e
t
pt
1)
1 p2
.
定义2. 设 f ( x)在(, b)上连续.
b
f
( x) dx
lim
t
tb
f
( x) dx
若极限存在,则称无穷限积分
2
1)3
]13
1
1
lim 3( x 1)3+ 3 3 3 4 lim 3( x 1)3
x1
x1
3(1 3 4 ).
例12.
讨
论
反
常
积
分
1 1
dx x2
的
收
敛
性.
解:
lim
x0
1 x2
,
x
0是
1 x2
的瑕点.
无穷限广义积分的计算

指导教师:陈一虎作者简介:陈雪静(1986-),女,陕西咸阳人,数学与应用数学专业2008级专升本1班.无穷限广义积分的计算陈雪静(宝鸡文理学院 数学系,陕西 宝鸡 721013)摘 要: 文章归纳总结了利用数学分析、复变函数、积分变换、概率论统计理论等知识计算无穷限广义积分的几种方法.在学习中运用这几种方法可开拓视野,激发学习数学的兴趣.关键词: 广义积分;收敛;计算方法广义积分是《高等数学》学习中的一个难点知识,广义积分的概念不仅抽象,而且计算方法灵活,不易掌握.广义积分包括两大类,一类是积分区间无穷型的广义积分,另一类是积分区间虽为有穷,但被积函数在该区间内含有有限个无穷型间断点(瑕点)的广义积分.一般的判别法是对积分区间无穷型的广义积分,先将积分限视为有限的积分区间按常义积分处理,待积分求出原函数后再考查其极限是否存在,在用此极限去判定原积分是否收敛.对于第二类广义积分,我们可将积分区间改动,使被积函数在改动后的积分区间内成为有界函数再按常义积分处理,求出原函数之后考查它在原积分区间上的极限是否收敛.但是有些被积函数的原函数不易求出或无法用初等函数表示,使得广义积分无法用常规方法计算,因此需寻求其它的计算方法.本文主要研究无穷限广义积分的计算方法,主要方法包括利用广义积分定义、参量积分、变量代换、二重积分、留数定理、级数展开、概率论知识以及拉普拉斯变换等方法.1 无穷限广义积分的定义定义1 设函数()f x 在区间[,)a +∞上连续,取t a >.如果极限lim ()d tat f x x →+∞⎰存在,则称此极限为函数()f x 在无穷区间[,)a +∞上的反常积分(也称作广义积分),记作()d af x x +∞⎰,即()d af x x +∞⎰=lim ()d tat f x x →+∞⎰;这时也称反常积分()d a f x x +∞⎰收敛;如果上述极限不存在,函数()f x 在无穷区间[,)a +∞上的反常积分()d af x x +∞⎰就没有意义,习惯上称为反常积分()d af x x +∞⎰发散,这时记号()d af x x +∞⎰不再表示数值了.类似地,设函数()f x 在区间(,]b -∞上连续,取t b <. 如果极限lim ()d btt f x x →-∞⎰存在,则称此极限为函数()f x 在无穷区间(,]b -∞上的反常积分,记作()d b f x x -∞⎰,即()d bf x x -∞⎰=lim ()d btt f x x →-∞⎰;这时也称反常积分()d b f x x -∞⎰收敛;如果上述极限不存在,就称反常积分()d bf x x-∞⎰发散.设函数()f x 在无穷区间(,)-∞+∞内连续,如果广义积分()d cf x x -∞⎰和()d cf x x +∞⎰(c 为常数)都收敛,则称上述两个反常积分之和为函数()f x 在无穷区间(,)-∞+∞内的广义积分,记作()f x dx +∞-∞⎰,即()d f x x +∞-∞⎰=()d cf x x -∞⎰+()d cf x x +∞⎰=lim ()d ctt f x x →-∞⎰+lim ()d tct f x x →+∞⎰这时也称广义积分()d f x x +∞-∞⎰收敛;否则就称反常积分()d f x x +∞-∞⎰发散.上述反常积分统称为积分区间为无穷区间的广义积分或无穷限广义积分.2 无穷限广义积分的计算方法2.1利用广义积分的定义求无穷限广义积分由定义计算可以分两步:1求定积分()d Aaf x x ⎰=()F A .需要说明的是原函数()F A 均指有限形式.2取极限lim ()d AaA f x x →+∞⎰=lim A →+∞()F A .例1[1]计算23121()d 1x x x+∞++⎰解 =23121lim()d 1bb x x x →+∞++⎰231121lim[d d ]1b b b x x x x→+∞=++⎰⎰ 2111lim[2arctan ]2bbb x x →+∞=-211lim[2arctan arctan1]22b b b →+∞=--+ 2π11lim 2arctan lim 222b b b b →+∞→+∞=--+ π122=+ 2.2利用含参量积分的理论求无穷限广义积分含参量积分:10()e d s x s x x +∞--Γ=⎰(0s >)1110(,)(1)d p q p q x x x --B =-⎰ (0,0p q >>)统称为欧拉积分.其中()s Γ称为格马函数.(,)p q B 称为贝塔函数.且有递推公式(1)()s s s Γ+=Γ 及 1(,)(,1)1q p q p q p q -B =B -+-.因此在计算广义积分时看所给广义积分当,,s p q 为何值时对应的欧拉积分,然后用欧拉积分公式直接算出广义积分的值.例2[5] 求220e d n x x x +∞-⎰(n 为正整数)解 此广义积分与表达式相似,因此可用Γ函数法求解.220ed n x x x +∞-⎰=limA →+∞220ed An x x x -⎰2t x =21201lim e d 2A n t A t t --→+∞⎰=12112e d n t t t +∞+--⎰==121()2n Γ+=121[()1]2n Γ-+ =121()2n -1()2n Γ-=121()2n -3()2n -3()2n Γ-17(21)2n n +-注:1()2Γ=2.3利用变量代换法求无穷限广义积分有些函数的原函数不易求出或直接积分不出来,但如果对被积函数施以变量代换,在辅以一定的技巧就可以求出这类积分.作变量带换时,首先要对被积函数的结构进行分析,然后再看积分限与被积函数的关系.变换的方向是求出原函数或求出一个含原积分的方程,从而求得所含广义积分的值.例3[2] 求I=401d 1x x +∞+⎰解 令x=1t ,则I=204d d 11t t x t +∞-+⎰上式加上I=04d 11t t +∞+⎰ 得2I=2401d 1t t t +∞++⎰=202211d 1t t t t +∞++⎰=021d()1()2t t t t +∞--+⎰故2.4利用二重积分理论计算无穷限广义积分.利用二重积分理论计算广义积分时,应分两步: 1把广义积分巧妙的化为一个二重积分.2计算二重积分,从而间接的计算出广义积分的值. 例4[5]计算广义积分2ed x x +∞-⎰解 由于20ed x x +∞-⎰=2e d y y +∞-⎰所以22[ed ]x x +∞-⎰=22ed ed x y x y +∞+∞--⋅⎰⎰而22e d e d x y x y +∞+∞--⋅⎰⎰=22()e d d xy Dx y -+⎰⎰ 其中D=[0,)[0,)∞⨯∞故()22ed x x +∞-⎰=22()e d d x y Dx y -+⎰⎰而22()e d d xy Dx y -+⎰⎰=π42ed x x +∞-⎰=2. 例5[3]计算广义积分I=0sin sin e d pxbx axx x+∞--⎰ 解 因为sin sin bx ax x-=cos()d ba xy y ⎰ 所以I=0sin sin e d px bx ax x x+∞--⎰=0e (cos()d )d bpx axy y x +∞-⎰⎰=0d e cos()d b px ax xy y +∞-⎰⎰=0d e cos()d b px ay xy x +∞-⎰⎰=22d bap y p y +⎰=arctan b p -arctan ap. 2.5积分号下求导法计算无穷限广义积分.收敛因子法:此方法是对被积函数引入一个收敛因子,因子中有一个参数, 对参数(不一定是收敛因子中的参数)求导,有时可求得原积分的值.在此情况下引入的收敛因子加强了原积分的收敛性(如条件收敛的成为绝对收敛,或求导后发散的,变成一致收敛).这样使积分号下求导条件得以满足.一般采用e kx -(k>0)作为收敛因子.例65]求积分0sin d axx x+∞⎰(0a ≥) 解 引入积分因子e px -(p >0)作积分()F p =0sin e d px axx x+∞-⎰ ()F p '=0e cos d px ax x +∞-⎰=22pp a+ 故 ()F p = arctana p +C =arctan ap(显然C =I(0)=0)由此有 0lim arctanp a p +→=π2所以 I=π2 故同样可得 0sin d ax x x +∞⎰=-π2(0)a <2.6积分号下求积分法算无穷限广义积分这种方法是将被积函数中某一因子表为一个适当的积分.于是将原积分化成二次积分.交换这两个积分的顺序,就可求出所给的积分.例7[2]求积分I=2cos d 1xx x β+∞+⎰(0)β> 解 由201e sin d 1xy y y x+∞-=+⎰,于是 I=0cos d e sin d xy x x y y β+∞+∞-⋅⎰⎰=0sin d e cos d xy y y x x β+∞+∞-⋅⎰⎰=22sin d y yy yβ+∞+⎰y t β==2sin d 1t tt t β+∞+⎰由20d sin d d 1I x x x x ββ+∞=-+⎰,有d d I β=I -所以 I =C e β-为了确定C ,令0β=. 得 020d π12x I C x +∞===+⎰故πe 2I β-=.2.7利用复变函数理论中的留数定理计算无穷限广义积分.定理1[5] 设函数()f z 在实轴上处处解析,在上半平面Im 0z >除有限个孤立奇点1,2z z ⋅⋅⋅n z 外处处解析,且存在常数00R >,0M >,0δ>,使得当0z R >,且Im 0z >时, 1()M f z zδ+≤,则1()d 2πi [(),]nk k f x x Res f z z +∞-∞==∑⎰推论 1[5]设()()()P z f z Q z =是有理函数,()P z 与()Q z 为z 的n ,m 次多项,多项式()Q z 的次数比()P z 至少高2次,()Q z 在实轴上没有零点,1,2z z ⋅⋅⋅n z 是()f z 在上半平面Im 0z >的孤立奇点,则1()d 2πi [(),]nk k f x x Res f z z +∞-∞==∑⎰例84]计算广义积分22222d ()()x x x a x b +∞-∞++⎰解 因为22222()()()z f z z a z b =++,显然()f z 满足推论的条件,且1z =i a ,2z =i b 是()f z 在上半平面的孤立奇点,这两个点都是()f z 的一级极点,因此有22222ai Re [(),i]lim[(i)]()()z z s f z a z a z a z b →=-++ 2222i()a ab a -=- 222i()aa b =- 同理Re [(),i]s f z b =222i()bb a - 故22222d ()()x x x a x b +∞-∞++⎰=2πi [222()a i a b -+222()bi b a -] =πa b+ 2.8级数展开法求广义积分利用无穷级数计算广义积分也是常用的一种技巧.常有两种方法. 其一是将被积函数展成级数以求积分;其二是将无穷区间上的广义积分表示成级数的形式以求积分.例92]求积分I=2e cos 2d x bx x +∞-⎰解 利用余弦函数的幂级数展开以及指数函数的展开式0e !nxn x n ∞==∑ (2)!2!(21)!n n n n =⋅-我们有2ecos 2d x bx x +∞-⎰=22200(1)(2)ed (2)!n n x n n b x x n ∞+∞-=-∑⎰=22200(1)(2)e d (2)!n n x nn b x x n ∞+∞-=-∑⎰=0n ∞=20()2!nn b n ∞=-∑2b - 例10[5]计算广义积分1ln d (1)xx x x +∞-⎰. 解 由于1ln d (1)xx x x +∞-⎰=211n n∞=-∑ 而211n n∞=∑=2π6 故原式=-2π6.利用级数展开求积分,展开的仅是被积函数的某个因子,“展开因子”选择应是其展开的级数形式比较简单;展开的级数连同被积函数剩下的因子可逐项积分;这些积分容易求出.因此记住一些常用函数的展开式及一些数项级数的和对积分计算是有益的.2.9利用概率统计知识求无穷限广义积分.例11[5] 计算广义积分I=0sin sin e d pxbx axx x+∞--⎰. 解因为22()x f x -=为标准的正态分布密度函数所以()d f x x +∞-∞⎰= 1.即22d x x +∞--∞⎰=1.所以2201d 2xx +∞-=⎰即22ed x x +∞--∞⎰令222x u -=⇒u =⇒20e d uu +∞-⎰220e d x x +∞-2 2.10用拉普拉斯变换求无穷限广义积分定义2[6] 设()f t 在0t ≥上有定义,且积分0()()e d st F s f t t +∞-=⎰(s 是复变参量)关于某一范围内的s 收敛,则由这个积分确定的函数0()()e d st F s f t t +∞-=⎰称为函数()f t 的拉普拉斯变换.并记做[()]L f t ,即[()]L f t =0()()e d st F s f t t +∞-=⎰,其中的()F s 称为()f t 的像函数,()f t 称为()F s 的像原函数.定理 2[5] (Laplace 变换存在定理) 设函数()f t 在0t ≥的任何有限区间内分段连续,并且当t →+∞时, ()f t 的增长速度不超过某一指数函数,即存在常数0M >,和00s >,使得在[0,]+∞上,0()e s t f t M ≤,则在半平面0Re s s >上,[()]L f t 存在,且()F s =[()]L f t 是s 的解析函数.其中0s 称为()f t 的增长指数.性质1[1](积分性质)若[()]()L f t F p =,则0()[()d ]tF p L f t t p=⎰(p 为复数) (1)性质2[1](终值性质) 若[()]()L f t F p =,且()p F p 的所有奇点全在p 平面的部0lim ()lim ()t p f t p F p →+∞→=⋅ (2)性质3[1] 若[()]()L f t F p =,()F p 在Re 0p >上解析,且0()d n t f t t +∞⎰收敛,则0(1)lim ()n n p F p →-存在,且(1)lim ()()d n nn p F p t f t t +∞→-=⎰(3)证明 [()]()L f t F p = 由微分性知 ()n F p =[()()]n L t f t -[()]n L t f t =(1)()n n F p -由性质1 0(1)()[()d ]n n t nF p L t f t t p-=⎰所以由性质2 00(1)()lim[()d ]lim n n t nt p F p t f t t p→+∞→-=⎰即 0()d n t f t t +∞⎰=0(1)lim ()n n p F p →-特别的,0n =时,有()d lim ()p f t t F p +∞→=⎰. (4)性质4[1](象函数的积分性质)若[()]()L f t F p =,且积分()d F p p ∞⎰收敛()[]()d p f t L F p p t∞=⎰. (5)性质 5[1]设[()]()L f t F p =,且()d F p p ∞⎰与0()d f t t t∞⎰皆收敛,则 0()()d d f t F p p t t∞∞=⎰⎰(6) 证明 由(5)式,()[]()d p f t L F p p t∞=⎰ 由(4)式,()d f t t t∞⎰=0lim ()d p p F p p ∞→⎰()d F p p ∞=⎰例12[4] 求sin ()tf t t =的拉普拉斯变换,并求积分0sin d t t t+∞⎰.解 由定理2,因为0()1e f t ≤⋅,故在s 的实部大于零上, 拉普拉斯变换存在,且esin d stt t ω+∞-⎰=22e [sin cos ]st s t t s ωωωω---+=22s ωω+于是 22[sin ]L t s ωωω=+ (在s 的实部大于零) 那么 2sin 1[]1t L t s =+ 由命题4知 sin []t L t =21d 1s s s +∞+⎰=πarctan 2s -在利用命题5知0sin d t t t +∞⎰=201d 1s s +∞+⎰=π2. 例13[6] 计算下列积分30e sin d t t t t +∞-⎰ 解 21[sin ]1L t s =+, 由微分性质知, 22212[sin ]()1(1)s L t t s s '=-=++ 但是另一方面 0[sin ]sin e st L t t t t dt +∞-=⋅⎰当3s =时,即30e sin d t t t t +∞-⎰=2232(1)s s +=350致谢:本文在写作过程中得到陈一虎老师的指导.在此表示感谢!参考文献:[1] 白水周.无穷限广义积分的几种有效解法[J].开封大学学报,2000,14(1):49-50.[2] 李绍成.论广义积分的计算[J].绵阳农专学报:自然科学版,1996,13(2):65-70.[3] 数学分析.华东师范大学数学系[M].高等教育出版社,2001.[4] 宋叔尼,孙涛.复变函数与积分变换[M].北京:科学出版社,2006.[5] 刘开生,杨钟玄.无穷限广义积分的几种计算方法[J].天水师范学院学报:自然科学版,2002,22(2):9-10.[6] 盖云英,包革军.复变函数与积分变换学习指导[M].科学出版社,2004.Ways of calculating limitless generalized integralCHEN Xue-Jing(Department of Mathematic,Baoji University of Arts and Science Baoji 721013,Shaanxi ,China) Abstract:ways of calculating generlazed integral are given by using maths analysis, complex variable and integral transform, complex function and proabability statistical theroy. In the study the use of these methods can broaden their horizons, stimulate interest in learning mathematics.Key words:generalized integration; convergence; calculation method.。
高等数学@5-4反常积分

( x)dx
发散
.
y f (x)
s
a
b
x
b
定义
b
f ( x)dx lim f ( x)dx .
a a
右端极限存在,
则称 反 广常 义积分
b
f
( x)dx
收敛
,
否则
,
则称
b
f
( x)dx
发散
.
2
f ( x)dx
定义
0
f ( x)dx
F () lim F (x) ; F () lim F (x)
x
x
则有类似牛 – 莱公式的计算表达式 :
a f (x) dx F (x)
F () F (a)
b
f (x) dx F (x)
f (x) dx F (x)
F (b) F () F () F ()
(a 0)
解.
x
3a 是
x 3a2
x
2
的无穷间断点
.
3a x dx
0
3a2 x2
( 3a)
3a2 x2
0
(0 3a) 3a . #
上限 (
3 a)
代入的含义是
lim
x( 3 a)
3a2 x2 .
13
例6.
1 1 1 x
解:
[ arctan x ]|0
[ arctan x ]|
0 22
思考:
分析:
原积分发散 !
高教社2024高等数学第五版教学课件-5.4 反常积分

0
计算反常积分−∞ − 。
0
−∞
−
0 −
→−∞
=
= (− − )|0 = (−1 + − ) = +∞
→−∞
→−∞
0
所以,反常积分−∞ − 发散。
例3
解
+∞ 1
计算反常积分−∞
。
→0+
→0+
1
1
计算反常积分0
。
1− 2
解 因为
1
→1− 1− 2
1
1
0 1− 2
=
= +∞,所以 = 1是瑕点。故有
1−
1
0
2
1−
→0+
=
|1−
0
= = ( 1 − ) =
→0+
2
3
2
2
=
2 1
(
−
1
).
2
,
2
当 → +∞时,其极限就是火箭无限远离地球需作的功.
我们很自然地会把这个极限写作上限为+∞的“积分”:
+∞ 2
2
=
2
→+∞ 2
=
2 1
(
→+∞
1
− ).
1
最后,由机械能守恒定律可求得初速度0 至少应使 0 2
2
用 = 9.81/ 2 , = 6.371 × 106 代入得0 =
高等数学-高等数学-第5章定积分

教学过程教学思路、主要环节、主要内容我们先来看一个实际问题———求曲边梯形的面积。
设曲边梯形是有连续曲线y=f(x)、x轴与直线x=a、x=b所围成。
现在计算它的面积A.我们知道矩形面积的求法,但是此图形有一边是一条曲线,该如何求呢?我们知道曲边梯形在底边上各点处的高f(x)在区间[a,b]上变动,而且它的高是连续变化的,因此在很小的一段区间的变化很小,近似于不变,并且当区间的长度无限缩小时,高的变化也无限减小。
因此,如果把区间[a,b]分成许多小区间,在每个小区间上,用其中某一点的高来近似代替同一个小区间上的窄曲变梯形的变高,我们再根据矩形的面积公式,即可求出相应窄曲边梯形面积的近似值,从而求出整个曲边梯形的近似值。
显然:把区间[a,b]分的越细,所求出的面积值越接近于精确值。
为此我们产生了定积分的概念。
定积分的概念:设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点a=x0<x1<...<x n-1<x n=b 把区间[a,b]分成n个小区间[x0,x1],...[x n-1,x n], 在每个小区间[x i-1,x i]上任取一点ξi(x i-1≤ξi≤x i),作函数值f(ξi)与小区间长度的乘积f(ξi)△x i并作出和,如果不论对[a,b]怎样分法,也不论在小区间上的点ξi怎样取法,只要当区间的长度趋于零时,和S总趋于确定的极限I,这时我们称这个极限I为函数f(x)在区间[a,b]上的定积分,记作。
即:定理(1):设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积。
(2):设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积。
如果我们对面积赋以正负号,在x轴上方的图形面积赋以正号,在x轴下方的图形面积赋以负号,则在一般情形下,定积分的几何意义为:它是介于x轴、函数f(x)的图形及两条直线x = a、x = b之间的各部分面积的代数和。
G5_5反常积分[49页]
![G5_5反常积分[49页]](https://img.taocdn.com/s3/m/6481aaabf90f76c661371aa9.png)
dx
lim
b
b1 0 1 x2 dx
lim arctan
a
x0a
lim arctan
b
x
b
0
lim arctana a
lim arctanb b
2
2
.
退出ห้องสมุดไป่ตู้
高等数学(上)
或者做法如下
dx
1 x2 .
解
1
dx x2
arctan x
出版社 理工分社
lim arctan x lim arctan x
例2
求
0
1
1 x
2
dx.
出版社 理工分社
解
1 0 1 x2 dx
arctan x
0
2
0
2
.
例 3 判断 cos xdx 的 收 敛 性. 0
解
cos xdx sin x .
0
0
由于当 x + 时,sin x 没有极限,所以广义积分 发散 .
退出
高等数学(上)
例 4 计算 0 xexdx.
积分区间有限 常义积分
被积函数有界 推 广
积分区间无限 广义积分
被积函数无界 6.1 无穷区间上的广义积分
出版社 理工分社
退出
高等数学(上)
出版社 理工分社
定义 1 设函数 f (x) 在 [a, + )上连续,取实 数 b > a, 如果极限
b
lim f ( x)dx
b a
存在,则称此极限为函数 f (x) 在无穷区间[a, + )
x
x
2
2
.
y
2013高等数学 C5定积分与不定积分

即
2013
0
2
2
dx 2 f ( x ) dx 2 1 dx
0
2
0
1
0
sin x dx x 2
思考题:
1. 判断下列定积分的大小:
(1) sin dx
2 0 3
( 2) sin dx
2 0 5
( 3) x d x
2 0 3
2. 证明:
1 2 1 2 dx 2 0 3 2 2 x x
2013
问题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ? 事实上由定理1, 存在原函数 . 初等函数在定义区间上连续
初等函数在定义区间上有原函数
2013
注意: 原函数都在函数族 证: 1) 即 ( C 为任意常数 ) 内 .
又知
[( x) F ( x)] ( x) F ( x) f ( x) f ( x) 0
y
y x2
取
则
2013
i2 f (i )xi i2 xi 3 n
o
i n
1x
1 1 f ( i )xi 3 i n(n 1)(2n 1) 1 (1 1 )(2 1 ) n i 1 6 n n n3 6 i 1
2
n
1
n
1 2 x 0
由 x(0) x0 , 得 C2 x0 , 于是所求运动规律为
x(t ) 1 g t 2 v0t x0 2
2013
不定积分性质:
d f ( x)d x f (x) 或 d f ( x)dx f ( x) dx (1) dx
课程教学大纲(高等数学一)

《高等数学一》课程教学大纲一、课程基本信息课程名称:高等数学一英文名称:Advanced Mathematics 1课程性质:专业基础课周学时/学分:5/4适用专业:使用教材:《高等数学》由济大学数学系编,高等数学同济第七版是普通高等教育“十二五”GJJ规划教材,在第6版基础上作了进一步修订。
二、课程简介《高等数学》是高等学校中经济类和理工类专业必修的重要基础理论课。
高等数学是高校不可或缺的一门基础课,为学生学习专业课奠定了基础,对对培养学生严密的思维能力和创新能力起着不可替代的作用。
旨在通过高等数学得学习,进行逻辑思维能力的训练,为其他课程奠定一个坚实的基础。
三、教学基本要求将社会主义核心价值观贯穿始终,使学生树立正确的价值观,培养学生敬业、精益、专注、创新、追求卓越的工匠精神;培养学生将实际问题转化为数学问题以及所学知识去解决实际问题的能力,力求使学生在原有初等数学的基础上,学习与掌握高等数学的思想与方法,并能用高等数学的思想与方法去分析、解决实际问题,让数学成为学生解决实际问题的工具,更好的服务于学生后续专业课程的学习与素质的全面提高,培养面向基层、面向生产、面向管理与服务的一线高技能应用型人才;理解函数极限、连续、导数、微分、不定积分和定积分的概念;熟练掌握函数的极限、导数、积分的计算;能对函数进行连续性的判断,会求最值、切线、平面图形的面积以及旋转体的体积等;在教学过程中结合学校“三考一创”特色,着重对学生考研知识框架内进行学习与指导。
五、考核方式和成绩评定方法1、考核方式:闭卷考2、成绩评定方法:平时、期中、期末成绩分别为20%、20%、60%(平时成绩由作业成绩、课堂讨论成绩、考勤成绩构成)六、教学内容提要第一章函数1、教学目的:1.理解函数、复合函数、分段函数、基本初等函数、初等函数的概念。
2.了解几类特殊的函数。
3.掌握函数的表示方法及求函数的定义域和函数值的方法。
4.了解函数的奇偶性、单调性、周期性和有界性。
高等数学微积分--第五章-一元函数积分学(版本1)

例7 求
x4 dx
1 x2
解:原式
(x2
1)( x2 1 x2
1)
dx
1 1 x2 dx
x3 x arctan x C
3
例8 求
cos2
x 2
dx
解:原式=
1 2
dx
c
os 2
x
dx
1 x 1 sin x C 22
例9 求 tan2 xdx
解:原式=
sec2 xdx dx
1
(kx C) k
2
( 1 x1 ) x
1
3
(ln x ) 1
x
4
( a x ) a x
ln a
5 (e x ) e x
f (x)dx F(x) C
kdx kx C
x dx 1 x1 C( 1)
1
1dx x
ln
x
C
a xdx a x C
ln a
exdx ex C
2xdx x2 C
得曲线簇 y=x2+C, 将x=1,y=3代入,得 C=2 所以 y=x2+2
3.1.2 不定积分的基本公式和运算法则
一、不定积分的基本公式
由不定积分的定义可知,不定积分就是微分运 算的逆运算。因此,有一个导数或微分公式,就 对应地有一个不定积分公式。
基本积分表
序号 F(x) f (x)
例19 求
1
1
dx x
根式代换
解: 考虑到被积函数中的根号是困难所在,故
解: (1) (sinx)'= cos x cosxdx sin x C
(2)
1
x4
x3
高等数学(第五章)定积分

二、定积分的定义
定义 设 f ( x) 在[ a , b ]上有界
(1) 将[ a , b ] 任意分成 n 个小区间 [ x0 , x1 ],[ x1 , x2 ],, [ xi 1 , xi ] ,, [ xn 1 , xn ], x0 a , xn b . xi xi xi 1 (i 1, 2,, n), 为第 i 个小区间的长度 .
f ( )x . 在 x 与 x x 之间 . x 0 , x
定理 2 (变上限的积分求导定理) 设 f ( x) 在[ a , b ] 上连续 , x 则 f (t )dt f ( x) .
a
x a
f (t )dt
f (t)
b a
o a
c1
c2
b
f ( x) dx .
x
根据定积分的几何意义 我们可以计算一些简单的定积分 .
y
yx
例1
b a
1dx b a . ?
ab 1 2 2 x dx ? (b a) (b a ) . 2 2
o
a
b
x
例2
例3
b a
R 0
R x dx
2 2
0
i 1
n
并称极限值为 f ( x) 在[ a , b ]上的定积分.
记为
b a
f ( x)dx
上限
b a
f ( x)dx lim f (i )xi .
0
i 1
n
下限
a 叫积分下限 , b 叫积分上限 ,[ a , b ]叫积分区间. f ( x) 叫被积函数 , x 叫积分变量 . f ( x)dx叫被积表达式 .
高等数学教学资料微积分学广义积分敛散性判别

a
g ( x) d x 收敛 ,
则由 (1) 立即可得出矛盾 :
a
f ( x) d x 收敛 .
定理
(比较判别法的极限形式法)
设 f ( x) , g ( x) 为定义在 [a, ) 上的非负函数 , A [a, ) ,
f ( x) , g ( x) R( [a, A] ) . 若有极限 lim
0 f (t ) d t g (t ) d t ,
a a
x
x
从而, 积分上限函数
F ( x) f (t ) d t 在 [a, ) 上有上界 ,
a x
故积分
a
f ( x) d x 收敛 .
(2) 运用反证法.
如果
a
f ( x) d x 发散时 , 积分
(3) 当 时 , 无穷积分
a
g ( x) d x 发散 , 则
a
例1 解
判别无穷积分
1
arctan x d x 的敛散性. x
因为
arctan x lim x lim arctan x , x x x 2
故无穷积分
b
f ( x) d x lim
b x
x
这样可以利用积分上限 函数来进行有关的讨论 .
定理
设函数 f ( x) C( [a, ) ) , 且 f ( x) 0 .
若积分上限函数 F ( x) f (t ) d t 在 [a, )
a x
上有上界 , 则无穷积分
f ( x), g ( x) R( [a, A] ) , 且满足
第十周周一高等数学の5-定积分在几何物理上的应用广义积分
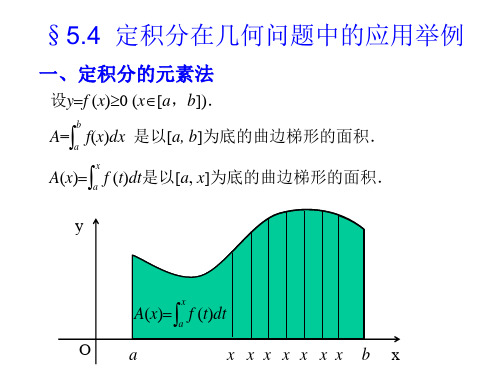
x
设曲线弧由直角坐标方程 yf(x) (axb)给出,其中f(x)在区 间[a,b]上具有一阶连续导数,则
ds 1 y2dx ,s b 1 y2dx . a
讨论:
(1)设曲线弧由参数方程
x
y
(t), (t)
( t )给出,其中
(t)、(t)在[,]上具有连续导数, 问弧长元素ds和弧长 s 各
2
2
1
1a
ab
b2
2(1(1cocso2st2)td)tdt11
a
ab·b·
11
a ab b..
22 0 0
2 2 2 24 4
A 4A1 a b.
2. 极坐标的情形
•曲边扇形及曲边扇形的面积元素:
由曲线r()及射线 , 围成的图形称为曲边扇形.
•曲边扇形的面积元素:
dA 1 [()] 2d .
a2 (1 cos )2 a2 sin 2 d 2a sin d .
2
所求弧长为
s
2 2a sin d
0
2
2a[2
cos
2
]02
8a .
y
2a
O
a
2 a
x
3. 极坐标的情形
设曲线弧由极坐标方程
r = r() ( ) 给出,其中r()在[,]上具有连续导数. 由直角坐标与极坐标的关系可得
是什么?
(2)设曲线弧由极坐标方程r = r() ( )给出,其中r() 在[,]上具有连续导数, 问弧长元素ds和弧长 s 各是什么?
) Ds MO MP ,
ds MP dx2 dy2 ,
直角坐标系下 y f x,
P
O
dy
高等数学(上)第5章.第2节 牛顿-莱布尼兹公式

解
原式
d dx
x
x
cos tdt
a
x a
t
cos
t
dt
x
a cos t dt x cos x x cos x
x
a cos t dt
例 4 设 f ( x)在[0,1]上连续,且 f ( x) 1,
证明:
2
x
x
0
f (t)dt 1在[0,1]上只有一个解.
(x) lim lim f () lim f () f (x)
x x0
x0
x
若 x a ,取 x 0 ,则同理可证 (a) f (a) ; 若 x b ,取 x 0 ,则同理可证 (b) f (b) ;
即
d (x) dx
定理5.4(原函数存在定理)
如果 f ( x) 在[a, b]上连续,则积分上限的函
有一质点在一直线上运动,在这直线上取定原点、正向及长度单位,
使它成一数轴.设时间 t 时物体在位置函数为 s(t) ,速度为 v(t) ,
在时间间隔[T1,T2 ] 上的位移为 s
T2 v(t)dt .
T1
另一方面,该位移又可以通过位移函数 s(t) 在区间[T1, T2] 上的增量 s(T2 ) s(T1) 来表达.
例1
已知
y
x2
sin tdt
,求
0
解
dy sin( x2 )( x2 ) 2 x sin ( x 2 ) dx
例2 已知 y cos x cos( t 2 )dt , 求 dy
sin x
dx
解 dy cos( cos 2 x)(cos x) cos( sin 2 x)(sin x)
北京邮电大学《高等数学教学课件》5-习题课

4 (cos x sin x)dx
0
2(sin x cos x)dx
4
2 2 2.
例5
求
1
2 1
2
[
sin x x8 1
ln2(1 x)]dx.
1
解
原式 0
2 1
ln(1
x)dx
2
0
1
1 ln(1 x)dx
2 ln(1 x)dx
0
2
3 ln 3 ln 1 . 22 2
x
x
x 0 f (u)du 0 uf (u)du
所以
x
0
u 0
f
( x)dxdu
x
( x u) f (u)du .
0
1/ 2
例 设 f ( x ) 在[0,1]可微,且满足 f (1) 2 xf ( x)dx 0
证明:(0,1)使
f ( ) f ( )
0
分析:变形为: f ( ) f ( ) 0, [ xf ( x)] 0
0
1 x
5、 1 dx ;
1
1
1 2x
7、 2
dx
;
1 x 3x2 2x 1
2、 a
dx
;
0 x a2 x2
4、 5 x 2 2x 3 dx ; 2
6、
x 2
dx 4x
; 9
8、
1
dx .
1 x x1
五、设 f ( x)在 0 , 1 上有连续导数, f (0) 0 ,
且0 f ( x) 1,试证:
f (u a2 ) du u 2u
1 a2 21
f (u
a2 ) du uu
第五章 积分 5-4 反常积分

b
1
t (x a) p d x
|
1 1
p
(x
a) 1
p
b
,
t
p1 ,
|
ln
(x
a)
b
,
t
p1
《高等数学》课件 (第五章第四节)
所以
b
1
lim
ta
t
(x a) p d x
1 (b a) 1 p , 1 p ,
p1 p1,
,
p1
所以, 反常积分 (1) 当 p < 1 时收敛, p 1时发散. 类似地, 反常积分 (1) 当 p < 1 时收敛, p 1时发散.
《高等数学》课件 (第五章第四节)
5.4.1 无限区间上的反常积分 y
考虑由直线 x = a, y = 0 和曲线
y = f (x) ( 0) 围成的平面无穷区域
f (x)
的面积 A.
x Oa
视面积 A 为有限区域 0 y f (x), y
a x b 面积 A b
b f ( x) d x 的极限,
xa _
a 为 f (x) 的奇点或暇点. 同样若函数 f (x) 在 a < 0 附近有定义,
且 lim f (x) , 则称 x a 为 f (x) 的奇点或暇点.
xa
定义 5-4 设函数 y = f (x) 在 [a, b) 连续, b 是 f 的奇点, 若
t
lim f ( x) d x
0
解
In
x ne x d x
0
x n d e x
0
| x n e x
n
x n1 e x d x
中国人民大学出版社(第四版)高等数学一第5章课后习题详解

高等数学一第5章课后习题详解课后习题全解习题5-1★★1.利用定积分的定义计算由抛物线21y x =+,直线x a =,x b =()b a >及横轴所围成的图形的面积知识点:定积分的定义及几何意义 思路:根据求定积分的三步骤做 解:将[],a b 分成n 等分,取(1,2,)i i n ξ=为第i 个小区间1[(),()]i ia b a a b a n n-+-+-的右端点,则,i b a x n λ-=∆=,i b aa i nξ-=+ 显然, 0,n λ→⇔→∞于是根据定积分的几何意义,该图形面积lim ()nbi i ai A ydx y x λξ→===∆∑⎰ 21lim [()1]nn i b a b aa in n→∞=--=++∑ 22221()lim [12]n n i b a b a b a a ai i n n n→∞=---=+++∑222211()lim [(1)2]nnn i i b a b a b a n a a i in n n →∞==---=+++∑∑22232()(1)()1lim{()[1(1)(21)]}26n a b a n n b a b a a n n n n n →∞-+-=-+++++221()11()lim[1()(1)(1)(2)]6n b a b a a a b a n n n→∞-=-++-++++ 222()()[1]3b a b a a ab a -=-++-+33().3b a b a -=+- ★★2.利用定积分的定义计算下列积分:知识点:定积分的定义 思路:根据求定积分的三步骤做(1)baxdx ⎰()a b <.解:易见函数[](),f x x C a b =∈,从而可积,将[],a b 分成n 等分,则,i b ax nλ-=∆=于是0,n λ→⇔→∞;取(1,2,)i i n ξ=为第i 个小区间的右端点,则,0,1,2,,1,ib aa ii n nξ-=+=-所以110lim ()lim ()n n bi i an i i b a b axdx f x a in nλξ--→→∞==--=∆=+∑∑⎰1()lim{[(0121)]}n b ab a na n n n→∞-=-+++++-2(1)()lim[]2n b a n n b a a n →∞--=-+1()lim[(1)]2n b a b a a n→∞-=-+-221()()().22b a b a a b a -=-+=-(2)1ln exdx ⎰解:用分点(0,1,,)i ni x e i n ==划分区间[]1,e :11,1,2,,i i nni i i x x x e e i n --∆=-=-=, 取i ξ是区间右端点,则 ,()ln()ln ,i i nnii i i i x e f e nξξξ=====作和,并取极限得:111ln lim ()lim ()i i nnenn i i n n i i i xdx f x e e nξ-→∞→∞===∆=-∑∑⎰111111lim{[()]}i i i nn n n nn i i i i e e e n n n --→∞==-=-+∑∑11111(1)lim lim (1)i nn n n i n e e e e n n e -→∞→∞=-=-=--∑111(1)lim ()1n n e e n e →∞=--- 记()1xx g x e =-,则当0x →时,()g x 是0型的,由洛必达法则, 有 001lim lim 11x xx x x e e →→==---从而,当n →+∞时,有111lim 11n nne →+∞=--,故1ln (1) 1.exdx e e =+-=⎰★3.利用定积分的几何意义,说明下列等式:(1)121xdx =⎰.知识点:定积分的几何意义思路:定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:等式左边为直线2y x =与x 轴和1x =三条直线所围成的面积,该面积等于11212==等式右边. (2)sin 0xdx ππ-=⎰解: 等式左边为正弦曲线sin y x =与x 轴在x π=及x π=-之间所围成的面积,其左右两边面积互为相反数. 则sin ()0xdx A A ππ-=-+==⎰等式右边★★4.用定积分的几何意义求a⎰(0)b >的值.知识点:定积分的几何意义思路:定积分的几何意义为被积函数与边界所形成曲边梯形的面积 解:=是以2a b +为圆心,2b a-为半径的上半圆,其面积为:2221()()2228b a b a S r πππ--===由定积分的几何意义知:2().8ab a π-=⎰★★★5.试将和式的极限112lim p p pp n n n +→∞+++(0)p >表示成定积分.知识点:定积分的定义思路:根据定积分的定义推导过程可知,求和的极限公式可表示为定积分解: 112112limlim [()()()]p p p p pp p n n n n n n n nn +→∞→∞+++=+++11lim ()n pn i i n n→∞==∑设()p f x x =,则用定义求解1()f x dx ⎰为:①、等分[0,1]为n 个小区间:11[,], 1,2,, i i ii n x n nn-=∆=②、求和:取区间1[,]i i n n -上的右端点为i ξ,即i in ξ=,作和:111()n ni i i i i f x nn ξ==∆=⨯∑∑③、求极限:011111lim()lim ()lim ()nnn p pi i n n i i i i i f x nn n n λξ→→∞→∞===∆=⨯=∑∑∑∴1101121lim lim ()p p p n pp p n n i n i x dx n n n+→∞→∞=+++==∑⎰ ★★★6.有一河,宽为200米,从一岸到正对岸每隔20米测量一次水深,测得数据如下:试用梯形公式求此河横截面面积的近似值.知识点:定积分的几何意义思路:由定积分定义知:求定积分(曲边梯形面积)的第二步:用小矩形面积近似代替小曲边梯形面积,即1()()ii x i i x f x f x dx ξ-∆≈⎰,若用小梯形面积近似代替小曲边梯形面积则为:111[()()]()2i i x i i i x f x f x x f x dx --+∆≈⎰。
高等数学:第十一章 广义积分与含参变量的积分

因此积分 dx发散. y
1x
y 1 x
b dx
1x
01
bx
例3. 使两个带电粒子从初始距离a分开到距离b 所需能量由
E
b kq1q2 a r2
dr
给出, 其中q1, q2是电荷的数量, k为常数. 若q1, q2 的单位为库仑(C), a, b是米(m), E的单位为焦耳(J).
k = 9109.
a
X
即当A X时有
A
g(x)dx
g(x)dx
X
X
由已知条件:当x X a时,0 f (x) g(x).
所以 A f (x)dx
A
g(x)dx
g(x)dx
X
X
X
而 g(x)dx收敛,所以当A X时,A f (x)dx有界,因此 f (x)dx收敛。
X
X
X
由于 f (x)dx
一个氢原子由一个质子和一个电子组成, 它们 带有数值为1.610–19 C的相反电荷. 求使氢原子激 发(即使电子从其轨道移动到离质子无穷远处)的 能量. 假设电子和质子之间的初始距离为玻尔半径
RB = 5.310–11m.
解: 因为由初始距离RB移动到最终距离的能 量由广义积分表示为
E
a
例.
判断
2
1 x ln
x
dx(
0,
R) 的敛散性.
解:
当
1时, 2
1 x ln
x
dx
2
1 x ln x
dx
ln
ln
xA 2
.
1
当
1时,x
ln 1
x
1 ln x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
只要有一个发散, 就称
f (x)dx
发散。
说明: 一般来说
f ( x)dx lim
a
f ( x)dx
a a
例如 xdx,由于
xdx 发散,故
0
xdx 发散。
但 a xdx 0, a
a
lim xdx lim 0 0
a a
a
4
★无穷区间上的广义积分的计算 引入记号
F () lim F ( x) ; F () lim F ( x)
x
x
则有类似于牛顿—莱布尼兹公式的计算表达式:
a f ( x)dx F () F (a) F ( x)
b
f
( x) dx
F(b)
F ()
F(x)
f ( x)dx
F()
F ()
F(x)
5
例1.
1 1
2
x2 sin x dx
2
sin
1 x
d(
1) x
cos
1 x
2
1
6
例2.
a
ta t
f (x)dx
这时称广义积分
收敛; 如果上述极限 不存在,
就称广义积分
发散 。
类似地 , 若 f ( x) C [a , b), 点 b 为 f (x) 的 瑕点,
则定义
b
f ( x)dx lim
t
f (x)dx
a
tb a
10
点 c 为 f (x) 瑕点, 则定义
c
b
a f ( x)dx c f ( x)dx
t
b
lim f ( x)dx lim f ( x)dx
tc a
tc t
瑕积分的计算
若a 为瑕点, 则
b
a
f
(
x)dx
F
(b)
F
(a
)
若b 为瑕点, 则
b
a
f
(
x)dx
F(b)ຫໍສະໝຸດ F(a)11
a dx
例4. 计算 0 a 2 x 2
(a 0)
解: x = a 为瑕点
a dx
0 a2 x2
arcsin
0
0
x
如果函数 f (x) 在点 a 的任一邻域内都 无界,
则点 a 称为函数 f (x) 的 瑕点。
9
定义2 设 f ( x) C (a , b], 点 a 为 f (x) 的 瑕点,
取
若极限
存在,
则称此 极限 为函数 f (x) 在 (a , b] 上的 广义积分, 记作
b
b
f ( x)dx lim
x a
|a
0
arcsin1
2
y
y 1
a2x2
1 a
O
ta x
12
例5. 计算 2 03
dx (1 x)2
解:x = 1 为瑕点。 2 dx
0 3 (1 x)2
1 dx 0 (1 x)2 / 3
2 dx 1 (1 x)2 / 3
[3(
x
1)1/
3
]1 0
[3(
x
1)1/
3
]2
p1 p1
因此, 当 p >1 时, 广义积分 收敛, 其值为
a 1 p ;
p1
当 p 1 时, 广义积分 发散. 8
二、无界函数的广义积分(瑕积分)
引例
与 x 轴, y 轴和直线
开口曲边梯形的面积 可记作
y
所围成的
其含义可理解为
y 1 x
1 dx
A lim
0
x
lim
0
2
1
x
A
lim 2(1 ) 2
b dx 1 x2
lim (
b
1 x
)1b
lim (1 1) 1 b b
y
1 x2
A
1
b
2
定义1 设f ( x) C [a , ), 对 t a ,
若
存在,
则称此 极限 为 f (x) 在 [a , +) 的 广义积分, 记作
t
a
f
( x) dx
lim
t
a
f
( x) dx
这时称广义积分
0
1 x p dx
的敛散性
15
[arctan x]
思考:
y
y
1
1 x
2
o
x
分析:
原积分发散 !
注意: 对广义积分, 只有在 收敛的条件下 才有
“偶倍奇零” 的性质。
7
★ 例3. 证明广义 积分
当 p >1 时收敛;
P 1 时发散.
证明: 当 p =1 时
ln
x
a
当p≠1时
x1 p 1 p
a
, a 1 p , p1
第五节 广义积分
一、无穷区间上的广义积分
二、无界函数的广义积分
积分限有限 前面所讲的定积分称为常义积分
推广
被积函数有界
积分区间为无穷区间 广义积分
被积函数无界
1
一、无穷区间上的广义积分
引例 曲线
和直线
及 x 轴所围成的开口
曲边梯形的面积可记作
A
dx 1 x2
其含义可理解为
A lim b
证明: x = a为瑕点
当q = 1时,
ln
x
a
b a
当 q≠1 时
( x a)1q 1q
b
(b
a)1q 1q
a ,
,
q1 q1
★
特例
1 0
1 xq
dx
当 q < 1 时收敛,
q 1 时发散.
14
当同时含两类广义积分时, 需 划分积分区间, 分别讨论相应的广义积分的敛散性。
例7. 讨论
1
3(0 1) 3(1 0) 6
说明:如果有人这样做:
2
0(x
dx 1)2 / 3
[3( x
1)1/ 3 ]02
3[1
(1)]
6
结果虽然对,但方法不对。
例如:1 dx
1 x 2
[
1 x
]11
2
事实上,
1 dx 发散 1 x2
13
例6. 证明广义积分
当 q < 1 时收敛;
q 1 时发散.
a
f
( x) dx
收敛;
如果上述极限 不存在,
就称广义积分 a
f (x)dx
发散 。
类似地 , 若 f ( x) C (, b], 则定义
b f ( x)dx lim
b
f (x)dx
t t
3
若 f ( x) C ( , ), 则定义
f (x)dx
0
f (x)dx
f (x)dx
