基于MATLAB的平面六杆机构运动分析

合集下载

matlab平面连杆结构分析(机械原理课程设计)

优化参数：连杆长度、角度、质量等
优化结果：得到最优的连杆结构设计
感谢观看
汇报人：
平面连杆结构的应用范围
机械工程：用于设计、分析和优化机械设备
生物医学：用于设计、分析和优化假肢、康复设备等
航空航天：用于设计、分析和优化飞机、火箭等航天器
机器人技术：用于设计、分析和优化机器人关节、机械臂等
汽车工业：用于设计、分析和优化汽车底盘、悬挂系统等
建筑工程：用于设计、分析和优化建筑结构、桥梁等
03
平面连杆结构的运动学分析
平面连杆结构的运动学方程
平面连杆结构的运动学方程是描述连杆系统运动状态的数学模型运动学方程包括位移方程、速度方程和加速度方程运动学方程的建立需要知道连杆系统的几何参数和运动参数运动学方程的求解可以通过数值积分方法或解析方法进行
平面连杆结构的运动学特性
运动学方程：描述连杆结构的运动状态运动学参数：包括位移、速度、加速度等运动学约束：限制连杆结构的运动范围运动学仿真：通过计算机模拟连杆结构的运动过程
平面连杆结构的形状优化
优化目标：提高连杆结构的稳定性和刚度
优化方法：有限元分析、拓
扑优化等
优化参数：连杆的长度、宽
度、厚度等
优化效果：提高连杆结构的承载能力和使
用寿命
平面连杆结构的拓扑优化
拓扑优化：通过改变材料的分布和形状，约束条件：结构的刚度、强度、稳定
以实现最优的结构性能
性等性能要求
目标函数：最小化重量或体积，同时满足给定的性能要求
优化方法：遗传算法、粒子群算法、模拟退火算法等
设计变量：材料的分布和形状
应用领域：汽车、航空航天、机械制造等

基于MATLAB的机构运动学分析

1. Movement analysis on materials flowing through a vertical pipe based on MATLAB2. Modeling and simulation of aircraft movement based on matlab/S-function3. Based on matlab electrically operated windshield wiper systems design method4. Optimum design of integral type steering mechanism based on MATLAB5. Analysis of assistant robotic leg on MATLABIEEE International Conference on Mechatronics and Automation, ICMA 2006Database: Compendex3.3 万方数据库3.3.1 检索式题名或关键词=机构运动与题名或关键词=Matlab 2005-20103.3.2 检索年限2003-20123.3.3 检索结果⑴【名称】基于CFD软件的数字船模平面运动机构实验方法【申请（专利）号】CN200810064057.2【申请人】哈尔滨工程大学.【发明人】张赫,李晔,庞永杰,徐玉如,秦再白,苏玉民,万磊,邹劲.【申请日期】2008-3-3【公告日期】2008-8-20【摘要】本发明提供的是一种基于计算流体动力学CFD软件FLUENT的数字船模平面运动机构实验方法。

包括应用FLUENT前处理软件GAMBIT建立研究对象模型及控制域；在模型表面布置三角形网格，进而在控制域内布置非结构化网格；设定边界条件，加入用户自定义函数UDF文件，引入动网格技术，采用基于完全非结构化网格的有限体积法，实现平面运动机构实验进行的纯横荡运动、纯升沉运动、纯摇首运动、纯俯仰运动和纯横滚运动；对FLUENT得到的力与力矩系数应用科学计算软件MATLAB傅立叶展开，EXCEL最小二乘法拟合，无因次化得到垂直面和水平面的水动力系数以及相关的流体动力分析。

基于MATLAB的六杆机构动力学分析与仿真

六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB仿真分析工具箱Simulink对其进行仿真分析。

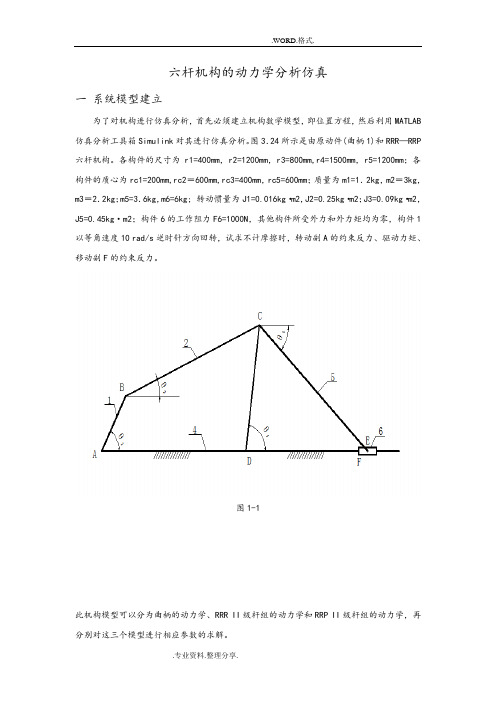
图3．24所示是由原动件(曲柄1)和RRR—RRP六杆机构。

各构件的尺寸为r1=400mm，r2=1200mm，r3=800mm,r4=1500mm，r5=1200mm；各构件的质心为rc1=200mm,rc2＝600mm,rc3=400mm，rc5=600mm；质量为m1=1．2kg，m2＝3kg，m3＝2．2kg；m5=3．6kg，m6=6kg; 转动惯量为J1=0.016kg·m2，J2=0.25kg·m2；J3=0.09kg·m2，J5=0.45kg·m2；构件6的工作阻力F6=1000N，其他构件所受外力和外力矩均为零，构件1以等角速度10 rad/s逆时针方向回转，试求不计摩擦时，转动副A的约束反力、驱动力矩、移动副F的约束反力。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ••=+-s m F R X XB 111y A Im R ••=+-s m F R y yB1111111111111cos )(sin )(cos sin ••=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=•••••••c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=•••••••c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡••••••••••g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ••=++s m R F R XC X XB 2222Im ••=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ••=-+s m R F R XC X XD 3333Im ••=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=•••••••c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=•••••••c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++••••••••••••••••••••••••3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型••=++s m R F R xE x xC Re 55 ••=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ••=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型••=--E m R R F F xE x Re sin 666θ ••=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ•••••••+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ•••••••+++=c c r r s66cos Re θ••••=s E 66sin Im θ••••=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------••••••••••••••••g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

基于MATLAB的平面连杆机构运动分析及动画毕业论文

基于MATLAB的平面连杆机构运动分析及动画摘要建立了平面机构运动分析的数学模型，利用MATLAB进行了编程并设计了计算交互界面进而求解，为解析法的复杂计算提供了便利的方法，此方法也同样适用于复杂平面机构的运动分析，并为以后机构运动分析的通用软件的设计提供了基础。

建立了平面四杆机构运动分析的数学模型，以MATLAB 程序设计语言为平台，将参数化设计与交互式相结合，设计了平面四杆机构仿真软件，该软件具有方便用户的良好界面，并给出界面设计程序，从而使机构分析更加方便、快捷、直观和形象。

设计者只需输入参数就可得到仿真结果，再将运行结果与设计要求相比较，对怎样修改设计做出决策，它为四杆机构设计提供了一种实用的软件与方法。

以一种平面六连杆为例建立了平面多连杆机构的运动分析数学模型，应用MATLAB 软件进行了优化设计和仿真分析，为机构优化设计提供了一种高效、直观的仿真手段，提高了对平面多连杆机构的分析设计能力。

同时，也为其他机构的仿真设计提供了借鉴。

关键词：解析法，平面连杆机构，MATLAB，运动分析，运动仿真Based on the MATLAB Planar Linkage Mechanism MotionAnalysis and AnimationABSTRACTThis article established the kinematical mathematic model of the planar mechanism ,which is programmed and solved with designing the mutual interface of the calculation by MATLAB.This convenient method is provided for the complicated calculation of the analysis and also applicable to the kinematical analysis of the complex planar mechanism.A mathematical model of motion analysis was established in planar four- linkage ,and emulational software was developed. The software adopted MATLAB as a design language. It combined parametric design with interactive design and had good interfacefor user. Thus,it was faster and more convenient to analyse linkage. The emulational result was obtained as soon as input parameters was imported and the devisers can make decision-making of modification by the comparing emulational result with design demand. It provides an applied software and method for linkage.This paper took a planar six-linkage mechanism as a example to set up the mathematics model of planar multi-linkage mechanisms, and made the optimization design and simulation by the MATLAB software. It gave a efficiently and directly method to optimization design of mechanisms, and improved the ability of analyzing and designing the planar multi-linkage mechanisms. At the same time, it also provides a use for reference to the design and simulation for other mechanisms.KEY WORDS: analysis, planar linkage mechanisms, MATLAB, kinematical analysis, kinematical simulation目录1.1 平面连杆机构的研究意义 (1)1.2 平面连杆机构的研究现状 (1)1.3 MATLAB软件介绍 (2)1.3.1 MATLAB简介 (2)1.3.2 MATLAB软件的特点 (4)1.3.3 用MATLAB处理工程问题优缺点 (5)第2章平面机构运动分析的复数矢量解 (6)第3章平面四杆机构运动分析 (8)3.1 铰链四杆机构曲柄存在条件 (8)3.2 平面四杆机构的位移分析 (9)3.3 平面四杆机构的速度分析 (14)3.4 平面四杆机构的加速度分析 (15)第4章基于MATLAB的平面四杆机构运动分析 (17)4.1 基于MATLAB的平面四杆机构运动参数输入界面 (17)4.2 基于MATLAB的平面四杆机构运动参数计算 (21)4.3 基于MATLAB的平面四杆机构运动分析界面 (24)4.4 基于MATLAB的平面四杆机构运动仿真 (26)4.5 基于MATLAB的平面四杆机构运动参数清空及退出 (30)第5章平面六杆机构运动分析 (32)5.1 构建平面六杆机构数学模型 (32)5.2 平面六杆机构的运动分析 (33)5.2.1 曲柄导杆机构的运动分析 (33)5.2.2 摆动滑块机构的运动分析 (36)第6章基于MATLAB的平面六杆机构运动分析 (39)6.1 基于MATLAB的平面六杆机构运动参数输入界面 (39)6.2 基于MATLAB的平面六杆机构运动参数计算 (45)6.3 基于MATLAB的平面六杆机构运动分析界面 (49)6.4 基于MATLAB的平面六杆机构运动仿真 (52)6.5 基于MATLAB的平面六杆机构运动参数清空及退出 (56)结论 (57)参考文献 (59)第1章前言1.1 平面连杆机构的研究意义机构运动分析是不考虑引起机构运动的外力的影响，而仅从几何角度出发，根据已知的原动件的运动规律（通常假设为匀速运动），确定机构其它构件上各点的位移、速度、加速度，或构件的角位移、角速度、角加速度等运动参数。

基于MATLAB的六杆机构动力学分析和仿真

六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB 仿真分析工具箱Simulink对其进行仿真分析。

图3．24所示是由原动件(曲柄1)和RRR—RRP 六杆机构。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ∙∙=+-s m F R X XB 111y A Im R ∙∙=+-s m F R y yB1111111111111cos )(sin )(cos sin ∙∙=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙∙∙∙∙∙∙∙∙∙g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ∙∙=++s m R F R XC X XB 2222Im ∙∙=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ∙∙=-+s m R F R XC X XD 3333Im ∙∙=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型∙∙=++s m R F R xE x xC Re 55 ∙∙=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ∙∙=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型∙∙=--E m R R F F xE x Re sin 666θ ∙∙=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s66cos Re θ∙∙∙∙=s E 66sin Im θ∙∙∙∙=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

机械原理4-23MATLAB平面连杆机构动力学分析

基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数)，滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。

试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。

构件1上的平衡力偶Mb分别对三个构件进行受力分析如图：构件3受力图构件2受力图构件1受力图（1）滑块2：V S2 =L AB W1 ①a s2 = L AB W12②构件3：S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力：F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程：构件3：∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2：∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1：∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程，八个未知数。

归纳出一元八次方程矩阵：1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得：X=A\B。

六杆受力分析

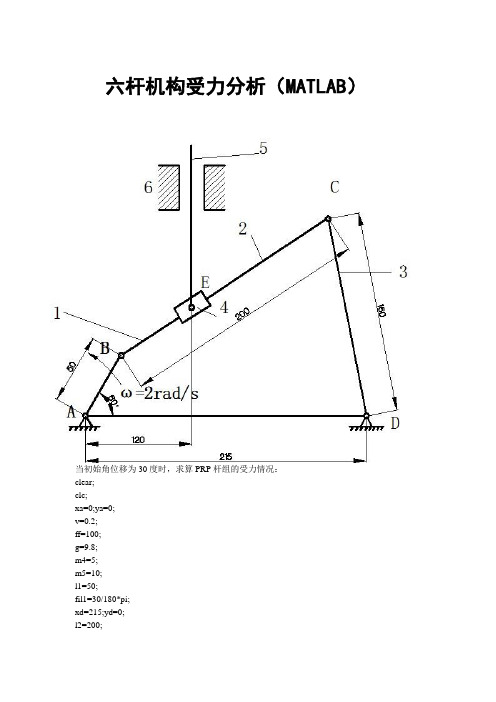
六杆机构受力分析（MATLAB）当初始角位移为30度时，求算PRP杆组的受力情况：clear;clc;xa=0;ya=0;v=0.2;ff=100;g=9.8;m4=5;m5=10;l1=50;fil1=30/180*pi;xd=215;yd=0;l2=200;l3=160;l=120;omigl=2;xb=xa+l1*cos(fil1);yb=ya+l1*sin(fil1);vbx=-omigl*l1*sin(fil1);vby=omigl*l1*cos(fil1);abx=-omigl*omigl*l1*cos(fil1);aby=-omigl*omigl*l1*sin(fil1);h=sqrt((xd-xb).*(xd-xb)+ (yd-yb).*(yd-yb));delta=atan((yd-yb)/(xd-xb));gama=acos((h.*h+l2*l2-l3*l3)/(2.*h.*l2));fil2=gama-delta;xc=xb+l2*cos(fil2);yc=yb+l2*sin(fil2);omigl3=((-vbx).*(xc-xb)+(-vby).*(yc-yb))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd));omigl2=((-vbx).*(xc-xd)+(-vby).*(yc-yd))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd));e=-abx+omigl2*omigl2.*(xc-xb)-omigl3*omigl3.*(xc-xd);f=-aby+omigl2*omigl2.*(yc-yb)-omigl3*omigl3.*(yc-yd);vcx=vbx-l2*omigl2*sin(fil2);vcy=vby+l2*omigl2*cos(fil2);el2=(e.*(xc-xd)+f.*(yc-yd))/((xc-xb).*(yc-yd)-(xc-xd).*(yc-yb));acx=abx-el2.*(yc-yb)-omigl2*omigl2.*(xc-xb);acy=aby+el2.*(xc-xb)-omigl2*omigl2.*(yc-yb);xe=l+0*cos(fil1);ye=l1*sin(fil1)+(l-l1*cos(fil1))*tan(fil2);vex=0+0*cos(fil1);vey=omigl*l1*cos(fil1)+l*omigl2/((cos(fil2))*(cos(fil2)))+omigl*l1*sin(fil1)*tan(fil2)-omigl2*l1 *cos(fil1)/((cos(fil2))*(cos(fil2)));aex=0+0*cos(fil1);aey=-omigl*omigl*l1*sin(fil1)+el2*l/((cos(fil2))*(cos(fil2)))+2*l*omigl2*omigl2*sin(fil2)/((cos( fil2))*(cos(fil2))*(cos(fil2)))+omigl*omigl*l1*cos(fil1)*tan(fil2)+omigl*omigl2*l1*sin(fil1)/((co s(fil2))*(cos(fil2)))-el2*l1*cos(fil1)/((cos(fil2))*(cos(fil2)))+omigl*omigl2*l1*sin(fil1)/((cos(fil2) )*(cos(fil2)))-2*omigl2*omigl2*l1*cos(fil1)*sin(fil2)/((cos(fil2))*(cos(fil2))*(cos(fil2)));A=[1 0 -1 0 0 0;0 1 0 -1 0 0;cos(fil2) sin(fil2) 0 0 0 0;0 0 1 0 -1 0;0 0 0 1 0 -1;0 0 0 0 v -1];B=[0;m4*aey+m4*g;0;0;m5*aey+m5*g;0];C=inv(A)*BC =R24x=-8.3957*1.0e+003R24y=5.1653*1.0e+003R45x=-8.3957*1.0e+003R45y=2.8838*1.0e+003R56x=-8.3957*1.0e+003R56y=-1.6791*1.0e+003当初始角位移为30度时，求算RRR杆组的受力情况：clear;clc;R24x=-8.3957*1.0e+003;R24y=5.1653*1.0e+003;xa=0;ya=0;v=0.2;ff=100;g=9.8;m2=10;js2=0.2;js3=0.2;m3=10;m4=5;m5=10;l1=50;fil1=30/180*pi;xd=215;yd=0;l2=200;l3=160;l=120;omigl=2;xb=xa+l1*cos(fil1);yb=ya+l1*sin(fil1);vbx=-omigl*l1*sin(fil1);vby=omigl*l1*cos(fil1);abx=-omigl*omigl*l1*cos(fil1);aby=-omigl*omigl*l1*sin(fil1);h=sqrt((xd-xb).*(xd-xb)+ (yd-yb).*(yd-yb));delta=atan((yd-yb)/(xd-xb));gama=acos((h.*h+l2*l2-l3*l3)/(2.*h.*l2));fil2=gama-delta;xc=xb+l2*cos(fil2);yc=yb+l2*sin(fil2);omigl3=((-vbx).*(xc-xb)+(-vby).*(yc-yb))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd)); omigl2=((-vbx).*(xc-xd)+(-vby).*(yc-yd))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd)); e=-abx+omigl2*omigl2.*(xc-xb)-omigl3*omigl3.*(xc-xd);f=-aby+omigl2*omigl2.*(yc-yb)-omigl3*omigl3.*(yc-yd);vcx=vbx-l2*omigl2*sin(fil2);vcy=vby+l2*omigl2*cos(fil2);el2=(e.*(xc-xd)+f.*(yc-yd))/((xc-xb).*(yc-yd)-(xc-xd).*(yc-yb));el3=(e.*(xc-xb)+f.*(yc-yb))/((xc-xb).*(yc-yd)-(xc-xd).*(yc-yb));acx=abx-el2.*(yc-yb)-omigl2*omigl2.*(xc-xb);acy=aby+el2.*(xc-xb)-omigl2*omigl2.*(yc-yb);as2x=abx-el2.*(yc-yb)/2-omigl2*omigl2.*(xc-xb)/2;as2y=aby+el2.*(xc-xb)/2-omigl2*omigl2.*(yc-yb)/2;xe=l+0*cos(fil1);ye=l1*sin(fil1)+(l-l1*cos(fil1))*tan(fil2);vex=0+0*cos(fil1);vey=omigl*l1*cos(fil1)+l*omigl2/((cos(fil2))*(cos(fil2)))+omigl*l1*sin(fil1)*tan(fil2)-omigl2*l1 *cos(fil1)/((cos(fil2))*(cos(fil2)));aex=0+0*cos(fil1);aey=-omigl*omigl*l1*sin(fil1)+el2*l/((cos(fil2))*(cos(fil2)))+2*l*omigl2*omigl2*sin(fil2)/((cos( fil2))*(cos(fil2))*(cos(fil2)))+omigl*omigl*l1*cos(fil1)*tan(fil2)+omigl*omigl2*l1*sin(fil1)/((co s(fil2))*(cos(fil2)))-el2*l1*cos(fil1)/((cos(fil2))*(cos(fil2)))+omigl*omigl2*l1*sin(fil1)/((cos(fil2) )*(cos(fil2)))-2*omigl2*omigl2*l1*cos(fil1)*sin(fil2)/((cos(fil2))*(cos(fil2))*(cos(fil2)));fil3=atan((yc-yd)/(xc-xd));as3x=l3/2*el3*cos(fil3)+omigl3*omigl3*l3/2*sin(fil3);as3y=omigl3*omigl3*l3/2*cos(fil3)+l3/2*el3*sin(fil3);A=[1 0 -1 0 0 0;0 1 0 -1 0 0;(yc-yb)/2 (xb-xc)/2 (yc-yb)/2 (xb-xc)/2 0 0;0 0 1 0 -1 0;0 0 0 1 0 -1;0 0 (yd-yc)/2 (xc-xd)/2 (yd-yc)/2 (xc-xd)/2];B=[m2*as2x+R24x;m2*as2y+R24y+m2*g;js2*el2+R24y*(xe-(xb+xc)/2)-R24x*(ye-(yb+yc)/2); m3*as3x;m3*as3y+m3*g;js3*el3];C=inv(A)*BC =R12x=-7.4060*1.0e+003R12y=-5.5947*1.0e+003R23x=3.3282*1.0e+003R23y=-9.7564*1.0e+003R36x=2.9970*1.0e+003R36y=-8.7134*1.0e+003当初始角位移为30度时，求算原动件的受力以及平衡力矩：clear;clc;R12x=-7.4060*1.0e+003;R12y=-5.5947*1.0e+003;xa=0;ya=0;v=0.2;ff=100;g=9.8;m1=5;M=200;m2=10;js2=0.2;js3=0.2;m3=10;m4=5;m5=10;l1=50;omigl=2;fil1=30/180*pi;as1x=l1*omigl*omigl/2*cos(fil1);as1y=l1*omigl*omigl/2*sin(fil1);xd=215;yd=0;l2=200;l3=160;l=120;xb=xa+l1*cos(fil1);yb=ya+l1*sin(fil1);vbx=-omigl*l1*sin(fil1);vby=omigl*l1*cos(fil1);abx=-omigl*omigl*l1*cos(fil1);aby=-omigl*omigl*l1*sin(fil1);h=sqrt((xd-xb).*(xd-xb)+ (yd-yb).*(yd-yb));delta=atan((yd-yb)/(xd-xb));gama=acos((h.*h+l2*l2-l3*l3)/(2.*h.*l2));fil2=gama-delta;xc=xb+l2*cos(fil2);yc=yb+l2*sin(fil2);omigl3=((-vbx).*(xc-xb)+(-vby).*(yc-yb))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd));omigl2=((-vbx).*(xc-xd)+(-vby).*(yc-yd))/((yc-yd).*(xc-xb)-(yc-yb).*(xc-xd));e=-abx+omigl2*omigl2.*(xc-xb)-omigl3*omigl3.*(xc-xd);f=-aby+omigl2*omigl2.*(yc-yb)-omigl3*omigl3.*(yc-yd);vcx=vbx-l2*omigl2*sin(fil2);vcy=vby+l2*omigl2*cos(fil2);el2=(e.*(xc-xd)+f.*(yc-yd))/((xc-xb).*(yc-yd)-(xc-xd).*(yc-yb));el3=(e.*(xc-xb)+f.*(yc-yb))/((xc-xb).*(yc-yd)-(xc-xd).*(yc-yb));acx=abx-el2.*(yc-yb)-omigl2*omigl2.*(xc-xb);acy=aby+el2.*(xc-xb)-omigl2*omigl2.*(yc-yb);as2x=abx-el2.*(yc-yb)/2-omigl2*omigl2.*(xc-xb)/2;as2y=aby+el2.*(xc-xb)/2-omigl2*omigl2.*(yc-yb)/2;xe=l+0*cos(fil1);ye=l1*sin(fil1)+(l-l1*cos(fil1))*tan(fil2);vex=0+0*cos(fil1);vey=omigl*l1*cos(fil1)+l*omigl2/((cos(fil2))*(cos(fil2)))+omigl*l1*sin(fil1)*tan(fil2)-omigl2*l1 *cos(fil1)/((cos(fil2))*(cos(fil2)));aex=0+0*cos(fil1);aey=-omigl*omigl*l1*sin(fil1)+el2*l/((cos(fil2))*(cos(fil2)))+2*l*omigl2*omigl2*sin(fil2)/((cos(fil2))*(cos(fil2))*(cos(fil2)))+omigl*omigl*l1*cos(fil1)*tan(fil2)+omigl*omigl2*l1*sin(fil1)/((co s(fil2))*(cos(fil2)))-el2*l1*cos(fil1)/((cos(fil2))*(cos(fil2)))+omigl*omigl2*l1*sin(fil1)/((cos(fil2) )*(cos(fil2)))-2*omigl2*omigl2*l1*cos(fil1)*sin(fil2)/((cos(fil2))*(cos(fil2))*(cos(fil2)));fil3=atan((yc-yd)/(xc-xd));as3x=l3/2*el3*cos(fil3)+omigl3*omigl3*l3/2*sin(fil3);as3y=omigl3*omigl3*l3/2*cos(fil3)+l3/2*el3*sin(fil3);A=[-1 0 0;0 -1 0;-yb/2 xb/2 1];B=[m1*as1x+R12x;m1*as1y+R12y;-M-yb/2*R12x+xb/2*R12y];C=inv(A)*BC =R16x=0.6973*1.0e+004R16y=0.5345*1.0e+004Mb=-5.6908*1.0e+004每次求算时，需给定初始角位移fil1，对于PRP杆组，只给定初始角位移fil1，就可得出R24x，R24y，R45x，R45y，R56x，R56y；而对于RRR杆组，给定初始角位移fil1后，需将上一步得出的R24x，R24y代入，然后就可以求算出R12x，R12y，R23x，R23y，R36x，R36y；对于原动件，给定初始角位移fil1后，需将上一步得出的R12x，R12y代入，然后就可以求算出R16x，R16y，Mb。

平面连杆机构运动分析&动态静力分析及机械运动方程求解的Matlab语言m文件使用说明及算例

构件上点的运动分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）p_crank.m function [p_Nx,p_Ny]=p_crank(Ax,Ay,theta,phi,l1)v_crank.m function [v_Nx,v_Ny]=v_crank(l1,v_Ax,v_Ay,omiga,theta,phi)a_crank.m function [a_Nx,a_Ny]=a_crank(l1,a_Ax,a_Ay,alpha,omiga,theta,phi)函数中的符号说明函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）p_RRR.m function [cx,cy,theta2,theta3]=p_RRR(bx,by,dx,dy,l2,l3,m)v_RRR.m function [vcx,vcy,omiga2,omiga3]=v_RRR(vbx,vby,vdx,vdy,cx,cy,bx,by,dx,dy)a_RRR.m function [acx,acy,alpha2,alpha3]=a_RRR(abx,aby,adx,ady,cx,cy,bx,by,dx,dy,omiga2,omiga3)函数中的符号说明m =1 m = -1RRR Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）p_RRP.m function [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m)v_RRP.m function [vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3) a_RRP.m function [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3)函数中的符号说明1 1∠BCP < 90︒，∠BC 'P > 90︒，m =1RRP Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）p_RPR.m function [dx,dy,sr,theta3]=p_RPR(bx,by,cx,cy,e,l3,m)v_RPR.m function [vdx,vdy,omiga3,vr]=v_RPR(bx,by,cx,cy,dx,dy,vcx,vcy,vbx,vby,theta3) a_RPR.m function [adx,ady,alpha3,ar]=a_RPR(bx,by,cx,cy,dx,dy,acx,acy,abx,aby,vr,omiga3,theta3)RPR Ⅱ级杆组运动分析实线位置，m =1 虚线位置，m = -1函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）F_RRR.m function [R12x,R12y,R23x,R23y,R34x,R34y]=F_RRR(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,as2,as3,alpha2,alpha3)RRR Ⅱ级杆组力分析R 23xF 2R F 3xR 23函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）F_RRP.m function [R12x,R12y,R23x,R23y,R34x,R34y,lcn]=F_RRP(bxy,cxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,theta3,as2,as3,alpha2,alph3)RRP Ⅱ级杆组力分析R 34函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（输入参数）F_RPR.m function [R12x,R12y,R23x,R23y,R35x,R35y,lcn]=F_RRP(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,R34,theta3,as2,as3,alpha3)RPR Ⅱ级杆组力分析238. 作用有平衡力的构件力分析作用有平衡力的构件力分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）F_Bar.m function [R01x,R01y,Mb]=F_Bar(axy,bxy,s1,m1,Js1,M1,F1,R12,as1,alpha1)函数中的符号说明9. 平面连杆机构运动分析算例例1图示曲柄摇杆机构，已知l 1=150mm ，l 2=220mm ，l 3=250mm ，l 4=300mm ，曲柄以n 1=100r/min 逆时针匀速转动，分析该机构的运动。

基于MATLAB的平面六杆机构运动分析(1)

关键词：六杆机构；运动分析；ＭＡＴＬＡＢ
中图分类号：ＴＨ１１２
文献标识码：Ａ
文章编号：１６７３－１９８０（２００８）０１－００５５－０３
ＭＡＴＬＡＢ是Ｍａｔｈｗｏｒｋｓ公司于１９８２年推出的一套功能强大的工程计算软件，广泛应用于自动控制、机械设计、流体力学和数理统计等工程领域，被誉为巨人肩上的工具。它集数值分析、矩阵运算、信号处理和图形显示于一体，构成了一个方便的、界面友好的用户环境。工程人员通过使用ＭＡＴＬＡＢ提供的工具箱，可以高效求解复杂的工程问题，并可以对系统进行动态仿真，用强大的图形功能对数值计算结果进行显示。
杨春辉：基于ＭＡＴＬＡＢ的平面六杆机构运动分析
ｓｕｂｐｌｏｔ（２，２，１）ｐｌｏｔ（ｓ４５（：，１），ｓ４５（：，３））ｇｒｉｄｘｌａｂｅｌ（＇曲柄转角＇）ｙｌａｂｅｌ（＇滑块位移＇）％－－－－－－－计算滑块５速度ｆｏｒｉ＝１：７２ｅｔ＝（ｉ－１）＊ｄｔｈ；Ｅ＝［－ｌ４＊ｓｉｎ（ｓ４５（ｉ，２）＊ｄｒ）－１；ｌ４＊ｃｏｓ（ｓ４５（ｉ，２）＊ｄｒ）０］；Ｆ＝［ｌ４＊ｖ２３（ｉ，２）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）；－ｌ４＊ｖ２３（ｉ，２）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）］；ｂ＝ｉｎｖ（Ｅ）＊Ｆ；ｂ１＝ｂ（１）；ｂ２＝ｂ（２）；ｂ２３（ｉ，：）＝［ｅｔ／ｄｒｂ１ｂ２］；ｅｎｄ％绘制滑块５的速度线图．．．．．．％— —— —— —— ——计算滑块５的加速度ｆｏｒｉ＝１：７２ｅｕ＝（ｉ－１）＊ｄｔｈ；Ｇ＝［－ｌ４＊ｓｉｎ（ｓ４５（ｉ，２）＊ｄｒ）－１；ｌ４＊ｃｏｓ（ｓ４５（ｉ，２）＊ｄｒ）０］；Ｈ＝［ｌ３＊ａ２３（ｉ，２）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）＋ｌ３＊ｖ２３（ｉ，２）＾２＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）＋ｌ４＊ｂ２３（ｉ，２）＾２＊ｃｏｓ（ｓ４５（ｉ，２）＊ｄｒ）；－ｌ３＊ａ２３（ｉ，２）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）＋ｌ３＊ｖ２３（ｉ，２）＾２＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）＋ｌ４＊ｂ２３（ｉ，２）＾２＊ｓｉｎ（ｓ４５（ｉ，２）＊ｄｒ）］；ｄ＝ｉｎｖ（Ｇ）＊Ｈ；ｄ１＝ｄ（１）；ｄ２＝ｄ（２）；ｄ４５（ｉ，：）＝［ｅｕ／ｄｒｄ１ｄ２］；ｅｎｄ％绘制滑块５加速度ｓｕｂｐｌｏｔ（２，２，３）ｐｌｏｔ（ｄ４５（：，１），ｄ４５（：，２））ｇｒｉｄｘｌａｂｅｌ（＇曲柄转角＇）ｙｌａｂｅｌ（＇连杆角加速度＇）

对缝纫机六杆机构运动的MATLAB分析及UG运动仿真答辩稿

研究背景及意义
(1)连杆机构的研究一般有瞬心法，图解法，分析操作繁
琐，且结果不易验证。
（2）本文采用复数矢量法，借助MATLAB分析编程，
快捷的得出详细运动参数。并用UG进行动态模拟仿真及
输出曲线对结果验证。
（3这种借助计算机软件编程仿真，可大大提高分析效
率及准确性，值得进一步深入研究。
牛头刨床相关曲线
图1 挑线端位移曲线
图2 针头位移曲线
头运动范围
缝纫机速度数据及曲线图
பைடு நூலகம்
挑线端和针头速度数据有图表知挑线端速度 min= - 0.161m/s max=0.176m/s 针头速度 min= - 0.091m/s max=0.091m/s
图1 挑线端速度
图2 针头速度
缝纫机加速度数据及曲线图
图3 挑线端和针头加速度数据由图表知挑线端加速度min=-1.184m/s2 max=1.194m/s2 2 针头加速度min= - 0.531m/s 2 max=0.369m/s
牛头刨床位移曲线对照
牛头刨床速度曲线对照曲线说明各图中的红色曲线为牛头刨床刨刀的运动曲线，可以清晰的看到牛头刨床的急回特性
牛头刨床加速度曲线对照
牛头刨床ug仿真动画
（1）滑杆式挑线机构
（2）连杆式挑线机构
（3）单轴等速转盘挑线机构
（4）滑杆式挑线机构
本文所研究的缝纫机机构
机构简化矢量图
缝纫机位移数据及曲线图挑线端和针头数据有图表知挑线端角位移min27719max31202针头位移min0082mmax0118m差值0036m符合实际针头运动范围缝纫机速度数据及曲线图针头速度挑线端和针头速度数据有图表知挑线端速度min0161msmax0176ms针头速度min0091msmax0091ms缝纫机加速度数据及曲线图挑线端和针头加速度数据由图表知挑线端加速度min1184msmax1194ms针头加速度min0531msmax0369ms1牛头刨床分析显示结果完全符合课本中附属的运动曲线对此分析方法的准确性给以肯定

平面六杆机构的运动分析Matlab代码

平面六杆机构的运动分析Matlab代码平面六杆机构的运动分析M代码%参数赋值clc,clearl0=22;l1=40;l2=55;l3=55;l4=44;l5=35;M=-1;Omiga1=10;Theta1=0:0.01:360;Theta1=Theta1*pi/180;%求解各个构件位移、速度、加速度A=2*l1*l2*sin(Theta1);B=2*l2*(l1*cos(Theta1)-l0);C=l1^2+l2^2+l0^2-l3^2-2*l1*l0*cos(Theta1);E=2*l1*l3*sin(Theta1);F=2*l3*(l1*cos(Theta1)-l0);G=l2^2-l1^2-l3^2-l0^2+2*l1*l0*cos(Theta1);Theta3=2*atan((E+M*sqrt(E.^2+ F.^2- G.^2))./(F-G)); Theta31= Theta3-30;S=l5.*cos(Theta31)-sqrt(-l5^2.* sin(Theta31).^2+l4^2);Theta2=2*atan((A+M*sqrt(A.^2+B.^2-C.^2))./(B-C));Theta4=atan(l5.*sin(Theta31)./(l5.*cos(Theta31)-S));Omiga2=Omiga1*l1*sin(Theta1-Theta3)./(l2*sin(Theta3-Theta2));Omiga3=Omiga1*l1*sin(Theta1-Theta2)./(l3*sin(Theta3-Theta2)); Omiga4=((-l5).*Omiga3.*cos(Theta31))./(l4.*cos(Theta4)); Vf=-l5.*Omiga3.*sin(Theta31)+l4.*Omiga4.*sin(Theta4);Alfa3=(Omiga1^2*l1*cos(Theta1-Theta2)+Omiga2.^2*l2-Omiga3.^2*l3.*cos(Theta3-Theta2))./(l3*sin(Theta3-Theta2));Alfa2=(-Omiga1^2*l1*cos(Theta1-Theta3)+Omiga3.^2*l3-Omiga2.^2*l2.*cos(Theta2-Theta3))./(l2*sin(Theta2-Theta3));Alfa4=(l5.*Alfa3.*cos(Theta31)+l4.*Omiga4.^2.*sin(Theta4)-l5.*Omiga3.^2.*sin(Theta31))./(l4.*cos(Theta4));Af=(-l5).*Omiga3.^2.*cos(Theta31)+l4.*(Omiga4.^2.*cos(Theta4)+Alfa4.*sin(Thet a4))-l5.*Alfa3.*sin(Theta31);%绘图Theta1=Theta1*180/pi;Subplot(3,1,1)plot(Theta1,Theta2),grid on xlabel('曲柄转角(^。

基于MATLAB与SolidWorks的平面六杆机构运动分析及仿真

表3平面六杆机构中预设的部分构件初始参数
3.2平面六杆机构motion运动分析
本部分介绍了利用SolidWorks中的motion插件
进行运动仿真分析以输出平面六杆机构中构件5的
运动图像。首先，利用SolidWorks中的motion功能，将
电机加装在杆*上，设定电机转速恒定为10 r=d・s>#
，X motion 分析中，对构件 5 进行运动分析
终端
发
至
，
回入库
旧管
系统，
资的用，
本:
Research and Design "0 Fixed Network Terminal Inventory Management
U*#=)-
bang bing
(Chongbo Information Technology Researph Institute Ko・HLtd・，Nanjing Jiangs. 211500)
，
输出平面六杆机构中构件 5 的位移、速度、加速度运
动图像⑷(构件5运动图像如图4所示)。
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>1
Ie
>FG
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>2滑块I方
-速度
@
50 100 150 200 250 300 350 400
角度JM
图!平面六杆机构构件4的运动图像
' (" " 789:;<FG*H

平面六杆机构的运动分析Matlab代码

(完整版)在MATLAB环境下开发平面连杆机构运动分析系统毕业设计

在MATLAB环境下开发平面连杆机构运动分析系统摘要建立了铰链四杆机构运动分析的数学模型 ,以MATLAB程序设计语言为平台 ,将参数化设计与交互式相结合 ,设计了铰链四杆机构分析软件 ,该软件具有方便用户的良好界面 ,并给出界面设计程序 ,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到分析结果 ,再将运行结果与设计要求相比较 ,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词：平面四杆机构，MATLAB软件，运动分析，分析THE DEVELOPMENT OF SYSTEM FOR ANALYSIS OF MOTION IN PLANE FOUR BAR MECHANISM BASED ONMATLAB SOFTWAREAbstractA mathematical model of motion analysis was established in planefour - linkage , and analytical software was developed. The software adopted Matlab as a design language. It combined parametric design with interactive design and as input parameters was imported and the devisers can make decision - making of modification by the comparing analytical result with design demand. It provides an applied software and method for linkage.Key words:Plane Four Bar Mechanism, MATLAB, Analysis of Motion, Analyze目录1 绪论 (1)2 平面连杆机构的设计分析 (4)2.1平面四连杆机构的运动分析 (4)2.2 机构的数学模型的建立 (4)2.2.1 建立机构的闭环矢量位臵方程 (5)2.2.2 求解方法 (7)3 基于MATLAB程序设计 (8)3.1 程序流程 (8)3.2M文件编写 (8)3.3程序运行结果输出 (12)4 基于MATLAB图形界面设计 (23)4.1界面设计 (23)4.2代码设计 (24)5 结论.......................................................................................... 错误！未定义书签。

第6章 Matlab平面连杆机构的动力学分析

§6-1 曲柄的动力学仿真模块
由运动学知识可推得：
Re i Re A rcii cos i 2 rcii2 cos i s Im i Im A rcii sin i 2 rcii2 sin i s
§6-1 曲柄的动力学仿真模块
1．曲柄的动力学矩阵表达式曲柄AB复向量的模 ri 为常数、幅角 i 为变量。质心到转动副A的距离为 rci ，质量为 mi ，绕质心的转动惯量为 Ji ，作用于质心上的外力为 Fxi 和 Fyi 、外力矩为M i ，曲柄与机架联接，转动副A的约束反力为 RxA 和 RyA ，驱动力矩为 M 1 。
由理论力学可得：
RxA RxB Fxi mi Re i s
RyA RyB Fyi mi g mi Im i s
M1 M i RxArci sin i RyArci cos i RxB ri rci sin i RyB ri rci cos i J ii
§6-2 RRR II级杆组的动力学仿真模块
2．RRR II级杆组动力学分析M函数
g=9.8; %重力加速度 ri=1; rj=07; %两杆的长度 rci=0.5;rcj=0.35; %质心到铰链B的距离 %质心到铰链D的距离 mi=3; mj=2.2; %两杆的质量 Ji=0.25;Jj=0.09;%两杆的转动惯量 ReddD=0;ImddD=0; Fxi=0;Fyi=0;Mi=O; %i杆的外力和外力矩 a=zeros(6); a(1,1)=1;a(1,3)=1; a(2,2)=1; a(2,4)=1; a(3,1)=rci*sin(x(1)); a(3,2)=-rci*cos(x(1)); a(3,3)=-(ri-rci)*sin(x(1)); a(3,4)=(ri-rci)*cos(x(1)); a(4,3)=-1; a(4,5)=1; a(5,4)=-1; a(5,6)=1; a(6,3)=(rj-rcj)*sin(x(2)); a(6,4)=-(rj-rcj)*cos(x(2)); a(6,5)=rcj*sin(x(2)); a(6,6)=-rcj*cos(x(2));

机械原理3-28MATLAB平面连杆机构运动分析,解三角函数超越方程

根据第一步得到的数据进行数据输入，运行程序计算各速度值。程序如下：
x2=[x1' p(:,2) p(:,3) p(:,4) 10*ones(15,1) 40*ones(15,1) 50*ones(15,1)... 75*ones(15,1) 35*ones(15,1) 70*ones(15,1) p(:,1) 60*ones(15,1)]; q=zeros(4,15); for m=1:15 y2=rrrvel(x2(m,:)); q(:,m)=y2; end q
norm(f); end; y(1)=lA; y(2)=theta2; y(3)=theta3; y(4)=theta4;
再进行数据输入，运行程序进行运算。这里我们根据上面分析的θ1 的极限位置取θ1 的范围为 40°~55°并均分成 15 个元素： clc
clear x1=linspace(40*pi/180,55*pi/180,15); x=zeros(length(x1),11); for n=1:15 x(n,:)=[x1(:,n) pi/6 8*pi/9 2*pi/3 40 50 75 35 70 75 60]; end p=zeros(length(x1),4); for k=1:15 y= rrrposi(x(k,:)); p(k,:)=y; end >> p
% while norm(f)>epsilon
J=[0 -x(6)*sin(theta2) x(7)*sin(theta3) -x(8)*sin(theta4);
0 x(6)*cos(theta2) -x(7)*cos(theta3) x(8)*cos(theta4);
cos(x(1)) 0 0 x(11)*sin(theta4); sin(x(1)) 0 0 -x(11)*cos(theta4)]; dth=inv(J)*(-1.0*f); lA=lA+dth(1); theta2=theta2+dth(2); theta3=theta3+dth(3); theta4=theta4+dth(4);

基于MATLAB的平面六杆机构运动分析

·５６·
ｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））；ｅｌｓｅｉｆｔｈ（１）＜＝２７０＊ｄｒｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））＋ｐｉ；ｅｌｓｅｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））；ｅｎｄｓ３＝（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１））＋ｌ２＊ｃｏｓ（ｔｈ（１）））／（ｓｉｎ（ｔｈ３）＋ｃｏｓ（ｔｈ３））；ｗ（ｉ，：）＝［ｔｈ（１）／ｄｒｔｈ３／ｄｒｓ３］；％矩真ｔｈ（１）＝ｔｈ（１）＋ｄｔｈ；ｅｎｄ％（２） — ——计算导杆３的角速度和滑块２速度ｆｏｒｉ＝１：７２ｃｔ（２）＝（ｉ－１）＊ｄｔｈ；Ａ＝［－ｗ（ｉ，３）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）；ｗ（ｉ，３）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）］；Ｂ＝［－ｌ２＊ｏｍｇ＊ｓｉｎ（ｃｔ（２））；ｌ２＊ｏｍｇ＊ｃｏｓ（ｃｔ（２））］；ｖ＝ｉｎｖ（Ａ）＊Ｂ；％输出角速度矩阵
（１）
其中Ｓ２３为滑块２到Ｃ的位移，它随曲柄转动
而变化。
式（１）在ｘ、ｙ轴的分量等式为
!Ｌ２ｃｏｓ（ π／２）＋Ｌ１ｃｏｓφ＝Ｓ２３ｃｏｓθ
Ｌ２ｓｉｎ（ π／２）＋Ｌ１ｓｉｎφ＝Ｓ２３ｓｉｎθ
（２）
当 Φ在０°￣３６０°作匀速变化时，就可求出对应
的导杆３的转角 θ及滑块２位移Ｓ２３值。
图２滑块５的运动规律
３结语
利用ＭＡＴＬＡＢ强大的科学计算和绘图功能能开发各类机构的运动分析和动画模拟系统，不仅十分方便，可视化的结果还可以分析机构设计中存在的刚性冲击等问题，使用户摆脱了繁琐、复杂的传统设计计算，设计效率大大提高。

基于-MATLAB的六杆机构动力学分析及仿真

图3．24所示是由原动件(曲柄1)和RRR—RRP六杆机构。

图1-1此机构模型可以分为曲柄的动力学、RRR II 级杆组的动力学和RRP II 级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ∙∙=+-s m F R X XB111yA Im R ∙∙=+-s m F R y yB1111111111111cos )(sin )(cos sin ∙∙=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙∙∙∙∙∙∙∙∙∙g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ∙∙=++s m R F R XC X XB2222Im ∙∙=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ∙∙=-+s m R F R XC X XD3333Im ∙∙=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型∙∙=++s m R F R xE x xC Re 55∙∙=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ∙∙=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型∙∙=--E m R R F F xE x Re sin 666θ∙∙=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s66cos Re θ∙∙∙∙=s E 66s i n Im θ∙∙∙∙=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 10sin 0100cos )(sin )(cos sin 011000101θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

基于ADAMS与MATLAB的平面六杆机构运动分析

基于ADAMS与MATLAB的平面六杆机构运动分析作者：***来源：《现代信息科技》2022年第01期摘要：运用解析法对平面六杆机构进行运动规律分析，通过数学模型建立六杆机构的运动方程，进行位移、速度和加速度的分析。

利用MATLAB建立运动分析程序并绘制出运动曲线图。

利用ADAMS建立六杆机构虚拟样机进行运动仿真并获得运动参数曲线图，通过分析两者输出的运动参数图像，发现两者的仿真结果具有一致性。

并且，使用ADAMS仿真对机构进行运动分析可以提高分析的效率，能精确实现对平面六杆机构的运动学精确分析，这对机械系统的运动方案设计结构的优化具有重要的意义。

关键词：平面六杆机构;运动分析;MATLAB仿真;ADAMS仿真中国分类号：TP391.9 文献标识码：A文章编号：2096-4706（2022）01-0100-06Abstract： Analyze the motion rule of plane six-bar mechanism by analytic method， and establish the equation of motion of the six-bar mechanism through the mathematical model， then analyze the displacement， velocity and acceleration. MATLAB is used to establish action analysis procedure and draw the motion curve graphs. ADAMS is used to establish a six- bar mechanism virtual prototype for motion simulation and obtain the motion parameter curve graphs. By analyzing the two deferent motion parameter images， it is found that two deferent results are consistent. Moreover， using ADAMS simulation to analyze the motion of mechanism can improve the efficiency of analysis and realize the accurate kinematic analysis of the plane six-bar mechanism，which is of great significance to the optimization of the scheme design structure of the mechanical system.Keywords： plane six-bar mechanism; motion analysis; MATLAB simulation; ADAMS simulation0 引言机构运动分析是在给定机构尺度及原动件运动规律时分析机构从动件、各运动副运动规律[1] ，从而分析机构运动性能。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（１）
其中Ｓ２３为滑块２到Ｃ的位移，它随曲柄转动
而变化。
式（１）在ｘ、ｙ轴的分量等式为
!Ｌ２ｃｏｓ（ π／２）＋Ｌ１ｃｏｓφ＝Ｓ２３ｃｏｓθ
Ｌ２ｓｉｎ（ π／２）＋Ｌ１ｓｉｎφ＝Ｓ２３ｓｉｎθ
（２）
当 Φ在０°￣３６０°作匀速变化时，就可求出对应
的导杆３的转角 θ及滑块２位移Ｓ２３值。
图２滑块５的运动规律
３结语
利用ＭＡＴＬＡＢ强大的科学计算和绘图功能能开发各类机构的运动分析和动画模拟系统，不仅十分方便，可视化的结果还可以分析机构设计中存在的刚性冲击等问题，使用户摆脱了繁琐、复杂的传统设计计算，设计效率大大提高。
参考文献［１］徐金明．ＭＡＴＬＡＢ实用教程［Ｍ］．北京：清华大学出版社，２００５．［２］孙桓．机械原理［Ｍ］．北京：高等教育出版社，１９９６．［３］陈怀琛．ＭＡＴＬＡＢ及其在理工课程中的应用指南［Ｍ］．西
! "! " －Ｌ４ｓｉｎδ－１Ｌ４ｃｏｓδ０
ａ４ａ５＝
#
２
２
&
ａ$
$ $
３
Ｌ３
ｓｉｎθ＋ω３
Ｌ３
ｃｏｓθ＋ω４
Ｌ４
ｃｏｓδ
’ ’ ’
$ $
２
２
’ ’
（８）
－$$
%
ａ３
Ｌ３
ｃｏｓθ＋ω３
Ｌ３
ｓｉｎθ＋ω４Ｌ４
ｓｉｎδ’’(
２利用ＭＡＴＬＡＢ求解
２．１程序源％平面六杆机构运动分析％（１） — —— —— —— —— ——导杆位置％各杆长度输入ｌ１＝ｉｎｐｕｔ（＇机架长度（ｍｍ）＇）；ｌ２＝ｉｎｐｕｔ（＇曲柄长度（ｍｍ）＇）；ｌ３＝ｉｎｐｕｔ（＇导杆长度（ｍｍ）＇）；ｌ４＝ｉｎｐｕｔ（＇连杆长（ｍｍ）＇）；ｌ５＝ｉｎｐｕｔ（＇滑块５到坐标原点距离（ｍｍ）＇）；ｏｍｇ＝ｉｎｐｕｔ（＇曲柄角速度（ｒａｄ／ｓ）＇）；ｄｒ＝ｐｉ／１８０．０；％角度与弧度的转换％机构的初始位置ｔｈ（１）＝０．０；ｄｔｈ＝５＊ｄｒ；％循环增量％计算导杆的位置角度ｔｈ和滑块的ｓ２３％曲柄０－３６０度转，步长为５度ｆｏｒｉ＝１：７２ｃｔ＝ｉ＊ｄｔｈ；ｉｆｔｈ（１）＜＝９０＊ｄｒ
关键词：六杆机构；运动分析；ＭＡＴＬＡＢ
中图分类号：ＴＨ１１２
文献标识码：Ａ
文章编号：１６７３－１９８０（２００８）０１－００５５－０３
ＭＡＴＬＡＢ是Ｍａｔｈｗｏｒｋｓ公司于１９８２年推出的一套功能强大的工程计算软件，广泛应用于自动控制、机械设计、流体力学和数理统计等工程领域，被誉为巨人肩上的工具。它集数值分析、矩阵运算、信号处理和图形显示于一体，构成了一个方便的、界面友好的用户环境。工程人员通过使用ＭＡＴＬＡＢ提供的工具箱，可以高效求解复杂的工程问题，并可以对系统进行动态仿真，用强大的图形功能对数值计算结果进行显示。
安：西安电子科技大学出版社，２０００．［４］张森，张正亮．ＭＡＴＬＡＢ仿真技术与实例应用教程［Ｍ］．北
第１０卷第１期
重庆科技学院学报（自然科学版）
２００８年２月
基于ＭＡＴＬＡＢ的平面六杆机构运动分析
杨春辉（华东交通大学，南昌３３００１３）
摘要：介绍利用ＭＡＴＬＡＢ语言求解平面六杆机构的运动规律，使其结果可视化，使机构的运动分析直观、简单、精确，
提高机构的设计精度和效率。
假设曲柄做匀角速度 ω运动，即 ω＝ｄφ／ｄｔ是常
数，对式（２）求时间导数，速度Ｖ２３，方程式如下
" #" $% $ －Ｓ２３ｓｉｎθ ｃｏｓθ ω３＝－ ωＬ１ｓｉｎφ
（３）
Ｓ２３ｃｏｓθ ｓｉｎθ Ｖ２３ ωＬ１ｃｏｓφ
对式（３）求时间导数，得到导杆３的角加速度及
滑块２沿导杆３移动的加速度Ｓ２３，方程式如下：
收稿日期：２００７－１０－２０作者简介：杨春辉（１９７２－），男，江西丰城人，讲师，硕士，研究方向为机械设计。
·５５·
杨春辉：基于ＭＡＴＬＡＢ的平面六杆机构运动分析
ｖ１＝ｖ（１）；ｖ２＝ｖ（２）；ｖ２３（ｉ，：）＝［ｃｔ（２）／ｄｒｖ１ｖ２］；％矩阵［曲柄转角导杆角速度滑块速度］ｅｎｄ％（３） — ——导杆３的加速度ａ２＝０；％曲柄等角速度ｆｏｒｉ＝１：７２ｃ（２）＝（ｉ－１）＊ｄｔｈ；Ｃ＝［－ｗ（ｉ，３）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）；ｗ（ｉ，３）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）］；Ｄ（１）＝［－ｌ２＊ｏｍｇ＾２＊ｃｏｓ（ｃ（２））＋２＊ｖ２３（ｉ，２）＊ｖ２３（ｉ，３）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）＋ｗ（ｉ，３）＊ｏｍｇ＾２＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）］；Ｄ（２）＝［－ｌ２＊ｏｍｇ＾２＊ｓｉｎ（ｃ（２））－２＊ｖ２３（ｉ，３）＊ｖ２３（ｉ，２）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）＋ｗ（ｉ，３）＊ｏｍｇ＾２＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）］；ａ＝ｉｎｖ（Ｃ）＊Ｄ＇；ａ１＝ａ（１）；ａ２＝ａ（２）；ａ２３（ｉ，：）＝［ｃ（２）／ｄｒａ１ａ２］；％矩阵［曲柄转角导杆角加速度滑块加速度］ｅｎｄ％（４）－－－－－－－－－－计算滑块５的位移ｆｏｒｉ＝１：７２．．．．．．ｅｎｄ％绘制滑块５的位移
! "! " －Ｓ２３ｓｉｎθ ｃｏｓθ ａ３＝Ｓ２３ｃｏｓθ ｓｉｎθ ａ２３
#２
２
&
－$
$ $
ωＬ１ｃｏｓφ＋２ω３Ｖ２３
ｓｉｎθ＋ω
Ｓ２３
ｃｏｓθ’’ ’
$
’
（４）
$２
２
’
$$ %
ω
Ｌ１
ｓｉｎφ－
２ω３
Ｖ２３
ｃｏｓθ＋ω
Ｓ２３
ｓｉｎθ
’’ (
再对构件３、４、５、６组成的摆动滑块机构进行运
２
Ｌ４－（Ｌ５－ｓｉｎθ））
（６）
.
Ｓ..
/５
＝Ｌ３
ｃｏｓθ＋Ｌ４
ｃｏｓδ
连杆４角速度 ω４和滑块５速度方程
! "! "! " －Ｌ４ｓｉｎδ－１ ω４＝ ω３Ｌ３ｓｉｎθ
（７）
Ｌ４ｃｏｓδ０Ｖ５－ ω３Ｌ３ｃｏｓθ
连杆４角加速度ａ４和滑块５加速度ａ５方程
·５６·
ｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））；ｅｌｓｅｉｆｔｈ（１）＜＝２７０＊ｄｒｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））＋ｐｉ；ｅｌｓｅｔｈ３＝ａｔａｎ（２＊（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１）））／（ｌ２＊ｃｏｓ（ｔｈ（１））））；ｅｎｄｓ３＝（ｌ１＋ｌ２＊ｓｉｎ（ｔｈ（１））＋ｌ２＊ｃｏｓ（ｔｈ（１）））／（ｓｉｎ（ｔｈ３）＋ｃｏｓ（ｔｈ３））；ｗ（ｉ，：）＝［ｔｈ（１）／ｄｒｔｈ３／ｄｒｓ３］；％矩真ｔｈ（１）＝ｔｈ（１）＋ｄｔｈ；ｅｎｄ％（２） — ——计算导杆３的角速度和滑块２速度ｆｏｒｉ＝１：７２ｃｔ（２）＝（ｉ－１）＊ｄｔｈ；Ａ＝［－ｗ（ｉ，３）＊ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）；ｗ（ｉ，３）＊ｃｏｓ（ｗ（ｉ，２）＊ｄｒ）ｓｉｎ（ｗ（ｉ，２）＊ｄｒ）］；Ｂ＝［－ｌ２＊ｏｍｇ＊ｓｉｎ（ｃｔ（２））；ｌ２＊ｏｍｇ＊ｃｏｓ（ｃｔ（２））］；ｖ＝ｉｎｖ（Ａ）＊Ｂ；％输出角速度矩阵
在机械传动系统中，机构的运动分析是机械系统分析的基础。设计者可以根据原动件的运动规律，来求出机构上其它构件和构件上特定点的位移、速度和加速度。平面六杆机构是一种重要的传动装置，在机械工程中有的应用较广，如牛头刨床。本文以曲柄导杆一型移动从动件平面六杆机构为例，利用ＭＡＴＬＡＢ所具有的符号计算、数值计算以及图形可视化处理等功能，对该机构的运动分析，提高了设计的精度和设计效率。
ｓｕｂｐｌｏｔ（２，２，４）ｐｌｏｔ（ｄ４５（：，１），ｄ４５（：，３））ｇｒｉｄｘｌａｂｅｌ（＇曲柄转角＇）ｙｌａｂｅｌ（＇滑块加速度＇）２．２结果可视化程序运行时，输入以下内容：机架长度４０ｍｍ；曲柄长度２５ｍｍ；导杆长度９０ｍｍ；连杆长８０ｍｍ；滑块到坐标原点距离８０ｍｍ；角速度１０ｒａｄ／ｓ。图２为该六杆机构滑块５的位移、速度、加速度及连杆４的角加速度的运动规律。
动分析。首先建立机构位置方程，方程如下：
ｉθ
ｉδ
ｉπ／２
ｉ０
Ｌ３ｅ＋Ｌ４ｅ＝Ｌ５ｅ＋Ｓ５ｅ
（５）
式中Ｓ５为滑块的行程。
按同样的方法可分别得到滑块５的位置、速度、
加速度方程。
连杆４和滑块５位置方程
* ) + ,
２
...δ＝ａｒｃｔａｎ
-
（Ｌ５－Ｌ３ｓｉｎθ）／（－