初中数学竞赛专题复习第二篇平面几何第17章几何不等式与极值问题试题新人教版
数学竞赛——几何不等式

几何不等式一、知识点:1、有关线段不等的性质公理 在连接两点的所有线中线段最短定理1 在同一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边 定理2 在同一个三角形中大角对大边定理3 在两个三角形中,如果有两组对应边分别相等,那么夹角大的对边较大 已知:在ΔABC 和ΔA 'B 'C '中,AB =A 'B ',AC =A 'C ',∠BAC >∠B 'A 'C '. 求证:BC >B 'C '. 分析:将ΔA 'B 'C '平移到ΔABD ,连接CD ,则ΔADC 是等腰三角形,作AE ⊥CD 于E ,交BC 于H ,连接HD .由等腰三角形的轴对称性得HC =HD ,则BC =BH +HC =BH +HD >BD =B 'C '. 从而得证.2、有关角不等的性质定理1 三角形的任一外角大于和它不相邻的任意一个内角 定理2 在同一个三角形中大边对大角定理3 在两个三角形中,如果有两组对应边分别相等,那么第三边所对的角也大 二、例题 例1、已知直线l 上有依次5个点A 、B 、C 、D 、E ,那么到这五个点距离和最小的点( ) A .在线段AE 之外的某个点 B .有无穷多个 C .只能是AE 中点 D .只有1个点 解:选 D例2、如果7条线段的长都是正整数,且任取其中3条都不能组成三角形,则其中最长的线段至少长为( )A .13B .14C .15D .21解:这7条线段长度依次至少为1,1,2,3,5,8,13.即最长的线段至少为13,故选A .延伸:介绍费波那契数列 思考:(1)、若六边形周长等于20,各边长为整数,且以它们的任意三边为边不能构成三角形,这样的六边形( )A 、不存在B 、只有一个C 、有有限个但不止一个D 、有无穷多个 解:选 D(2)、有一根长150厘米的铁丝,现要将其截成n 小段,每段长均为整数,且任意3段都不能构成三角形,求n 的最大值并说明有哪几种不同的截法。
初中数学竞赛专题辅导试题资料下载几何不等式

初中数学竞赛专题辅导几何不等式平面图形中所含的线段长度、角的大小及图形的面积在许多情形下会呈现不等的关系.由于这些不等关系出现在几何问题中,故称之为几何不等式.在解决这类问题时,我们经常要用到一些教科书中已学过的基本定理,本讲的主要目的是希望大家正确运用这些基本定理,通过几何、三角、代数等解题方法去解决几何不等式问题.这些问题难度较大,在解题中除了运用不等式的性质和已经证明过的不等式外,还需考虑几何图形的特点和性质.几何不等式就其形式来说不外乎分为线段不等式、角不等式以及而积不等式三类,在解题中不仅要用到一些有关的几何不等式的基本定理,还需用到一些图形的面积公式.下而先给出几个基本定理.定理1在三角形中,任两边之和大于第三边,任两边之差小于第三边.定理2同一个三角形中,大边对大角,小边对小角,反之亦然.定理3在两边对应相等的两个三角形中,第三边大的,所对的角也大,反之亦然.定理4三角形内任一点到两顶点距离之和,小于另一顶点到这两顶点距离之和.定理5自直线1外一点P引直线1的斜线,射影较长的斜线也较长,反之,斜线长的射影也较长.说明如图2-135所示.PA,PB是斜线,HA和HB分别是PA和PB在1上的射影,若HA>HB,则PA>PB;若PA>PB,则HA>HB.事实上,由勾股定理知PA^HA^PH^PB2-,所以PA」PB2=HA2・HB2.从而定理容易得证.定理6在△ABC中,点P是边BC上任意一点,则有PAWmax(AB»AC),当点P为A或B时等号成立.说明max{AB,AC)表示AB,AC中的较大者,如图2・136所示,若P在线段BH上,则由于PHWBH,由上面的定理5知PAWBA,从而PAWmax{AB,AC).同理,若P在线段HC上,同样有PAWmax(AB,AC).例1在锐角三角形ABC中,AB>AC,AM为中线,P为ZkAMC内一点,证明:PB>PC(图2-137).证在ZkAMB与ZkAMC中,AM是公共边,BM=MC,且AB>AC,由定理3知,ZAMB>ZAMC,所以NA?4CV90°.过点P作PH_LBC,垂足为H,则H必定在线段BM的延长线上.如果H在线段MC内部,贝UBH>BM=MC>HC.如果H在线段MC的延长线上,显然BH>HC,所以PB>PC.例2已知P是ZkABC内任意一点(图2・138).(1)求证:!(a+b+c)<PA+PB+PCVa+b+c:(2)若AABC为正三角形,且边长为1,求证:PA+PB+PCV2.证(1)由三角形两边之和大于第三边得PA+PB>c,PB+PC>a, PC+PA>b.把这三个不等式相加,再两边除以2,便得PA+PB+PC〉!(a+b+c).又由定理4可知PA+PBVa+b,PB+PCVb+c,PC+PAVc+a.把它们相加,再除以2,便得PA+PB+PCVa+b+c.所以:(a+b+c)<PA+PB+PC<a+b+c.(2)过P作DE/7BC交正三角形ABC的边AB,AC于D,E,如图2・138所示.于是PAVmax{AD,AE)=AD,PBVBD+DP,PCVPE+EC,所以PA+PB+PCVAD+BD+DP+PE+EC=AB+AE+EC=2.例3如图2-139.在线段BC同侧作两个三角形ABC和DBC,使得AB=AC,DB>DC,且AB+AC=DB+DC.若AC与BD相交于E,求证:AE>DE.证在DB上取点F,使DF=AC,并连接AF和AD.由已知2DB>DB+DC=AB+AC=2AC,所以DB>AC.由于DB+DC=AB+AC=2AC,所以DC+BF=AC=AB.在Z^ABF中,AF>AB-BF=DC.在Z iADC和AADF中,AD=AD,AC=DF,AF>CD.由定理3,Z1>Z2,所以AE>DE.例4设G是正方形ABCD的边DC上一点,连结AG并延长交BC延长线于K,求证:;(AG+AK)>AC.分析在不等式两边的线段数不同的情况下,一般是设法构造其所对应的三角形,转化为角的不等式,即构造以!(AG+AK)和AC2为边的三角形.证如图2-140,在GK上取一点M,使GM=MK,则:(AG+AK)=AM.在RtAGCK中,CM是GK边上的中线,所以NGCMNMGC.而ZACG=45°,ZMGOZACG,于是ZMGC>45°,所以ZACM=ZACG+ZGCM>90°.囹2-14。
初中数学竞赛专题复习第二篇平面几何第17章几何不等式与极值问题试题新人教版

第17章 几何不等式与极值问题17.1.1★ 一个凸行边形的内角中,恰好有4个钝角,求n 的最大值.解析考虑这个凸行边形的n 个外角,有4n -个角90︒≥,故有()490360n -⨯︒<︒(严格小于是由于4个钝角的外角和大于0︒),因此8n <,n 的最大值是7.易构造这样的例子。
如果恰好有k 个钝角,则n 的最大值是3k +. 17.1.2★ 在ABC △中,A B A C >,P 为BC 边的高AD 上的一点,求证:AB AC PB PC -<-.PCDB A解析易知AB AC PB PC +>+,又2222AB AC BD CD -=- 22PB PC =-,故有AB AC PB PC -<-.评注 读者不妨考虑AD 是角平分线与中线的情况.17.1.3 已知四边形ABCD ,AC 、BD 交于O ,ADO △和BCO △的面积分别为3、12,求四边形ABCD 面积的最小值.CB ODA解析易知ABO BCOADO DCOS S BO S DO S ==△△△△,故36ABO CDO ADO BCO S S S S ⋅=⋅=△△△△.从而12ABO CDO S S +△△≥,且当ABO CDO S S =△△(此时四边形ABCD 为一梯形)时等号成立,所以此时四边形ABCD 面积达到最小值27.17.1.4★ 已知:直角三角形ABC 中,斜边BC 上的高6h =. (1)求证:BC h AB AC +>+; (2)求()()22BC h AB AC ++-. 解析()()22BC h AB AC +-+222222BC h BC h AB AC AB AC =++⋅---⋅,由条件,知242ABC BC h S AB AC ⋅==⋅△,且222AB AC BC +=, 于是()()22236BC h AB AC h +-+==.注意:这同时解决了(1)和(2).17.1.5★ 设矩形ABCD ,10BC =,7CD =,动点F 、E 分别在BC 、CD 上,且4BF ED +=,求AFE △面积的最小值.B FCED A解析设 BF x=,()4DE y x ==-,则()()()117101077022ABF ADE ECF S S S x y x y xy ++=++--=+⎡⎤⎣⎦△△△。
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
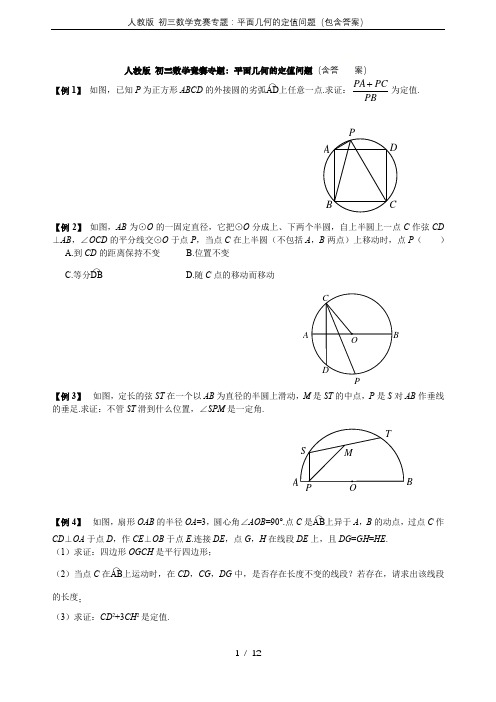
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
全国初中数学竞赛试题汇编---几何解答题及答案

全国初中数学竞赛试题汇编---几何解答题1、如图,圆O 与圆D 相交于,A B 两点,BC 为圆D 的切线,点C 在圆O 上,且AB BC =.(1)证明:点O 在圆D 的圆周上.(2)设△ABC 的面积为S ,求圆D 的的半径r 的最小值.解:(1)连,,,OA OB OC AC ,因为O 为圆心,AB BC =,所以△OBA ∽△OBC ,从而OBA OBC ∠=∠.因为,OD AB DB BC ⊥⊥,所以9090DOB OBA OBC DBO ∠=°−∠=°−∠=∠,所以DB DO =,因此点O 在圆D 的圆周上.(2)设圆O 的半径为a ,BO 的延长线交AC 于点E ,易知BE AC ⊥.设2AC y =(0)y a <≤,OE x =,AB l =,则222a x y =+,()S y a x =+,22222222()2222()aSl y a x y a ax x a ax a a x y=++=+++=+=+=.因为22ABC OBA OAB BDO ∠=∠=∠=∠,AB BC =,DB DO =,所以△BDO ∽△ABC ,所以BD BO AB AC =,即2r a l y =,故2alr y=.所以22223222()4422a l a aS S a Sr y y y y ==⋅=⋅≥,即r ≥其中等号当a y =时成立,这时AC 是圆O 的直径.所以圆D 的的半径r .2、如图,给定锐角三角形ABC ,BC CA <,AD ,BE 是它的两条高,过点C 作△ABC 的外接圆的切线l ,过点D ,E 分别作l 的垂线,垂足分别为F ,G .试比较线段DF 和EG 的大小,并证明你的结论.解法1:结论是DF EG =.下面给出证明.因为FCD EAB ∠=∠,所以Rt △FCD ∽Rt △EAB .于是可得CD DF BE AB =⋅.同理可得CEEG AD AB=⋅.又因为tan AD BEACB CD CE ∠==,所以有BE CD AD CE ⋅=⋅,于是可得DF EG =.解法2:结论是DF EG =.下面给出证明连接DE ,因为90ADB AEB ∠=∠=°,所以A ,B ,D ,E 四点共圆,故CED ABC ∠=∠.又l 是⊙O 的过点C 的切线,所以ACG ABC ∠=∠.所以,CED ACG ∠=∠,于是DE ∥FG ,故DF =EG .3、是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的△ABC ?证明你的结论.解:存在满足条件的三角形.当△ABC 的三边长分别为6=a ,4=b ,5=c 时,B A ∠=∠2.………………5分如图,当B A ∠=∠2时,延长BA 至点D ,使b AC AD ==.连接CD ,则△ACD 为等腰三角形.因为BAC ∠为△ACD 的一个外角,所以2BAC D ∠=∠.由已知,2BAC B ∠=∠,所以D B ∠=∠.所以△CBD 为等腰三角形.又D ∠为△ACD 与△CBD 的一个公共角,有△ACD ∽△CBD ,于是BDCDCD AD =,即cb aa b +=,所以()c b b a +=2.而264(45)=×+,所以此三角形满足题设条件,故存在满足条件的三角形.………………15分说明:满足条件的三角形是唯一的.若B A ∠=∠2,可得()c b b a +=2.有如下三种情形:(i )当b c a >>时,设1+=n a ,n c =,1−=n b (n 为大于1的正整数),代入()c b b a +=2,得()()()21121n n n +=−−,解得5=n ,有6=a ,4=b ,5=c ;(ⅱ)当b a c >>时,设1+=n c ,n a =,1−=n b (n 为大于1的正整数),代入()c b b a +=2,得()n n n 212⋅−=,解得2=n ,有2=a ,1=b ,3=c ,此时不能构成三角形;(ⅲ)当c b a >>时,设1+=n a ,n b =,1−=n c (n 为大于1的正整数),代入()c b b a +=2,得()()1212−=+n n n ,即0132=−−n n ,此方程无整数解.所以,三边长恰为三个连续的正整数,且其中一个内角等于另一个内角的2倍的三角形存在,而且只有三边长分别为4,5,6构成的三角形满足条件.4、△ABC 的三边长,,,,,BC a AC b AB c a b c === 都是整数,且,a b 的最大公约数是2.点G和点I 分别为△ABC 的重心和内心,且90oGIC ∠=,求△ABC 的周长.解:如图,连结GA ,GB ,过G ,I 作直线交BC 、AC 于点E 、F ,作△ABC 的内切圆I ,切BC 边于点D 。
初中数学竞赛辅导2021届人教版初中数学第17章《几何不等式与极值

初中数学竞赛辅导2021届人教版初中数学第17章《几何不等式与极值2021年初中数学竞赛辅导专题讲义第17章几何不等式与极值问题17.1.1★一个凸行边形的内角中,恰好有4个钝角,求n的最大值.解析考虑这个凸行边缘的n个外角,n?四角≥ 90?, 为什么?N4.90?? 360? (严格)小于是由于4个钝角的外角和大于0?),因此n?8,n的最大值是7.易构造这样的例子。
如果恰好有k个钝角,则n的最大值是k?3.17.1.2 ★ 在里面△ ABC,AB?AC,P是BC侧的高ad点。
验证:ab?交流电?PB个人计算机apcbd分析易知ab?ac?pb?pc,又是AB2?ac2?bd2?cd2?pb2?pc2故有ab?ac?pb?pc.评论的读者可能希望考虑AD是角平分线和中线的情况。
17.1.3已知四边形abcd,ac、bd交于o,△ado和△bco的面积分别为3、12,求四边形abcd面积的最小值.adobc解析易懂s△abobos△bco??,故s△abo?s△cdo?s△ado?s△bco?36.s△adodos△dco从而s△abo?s△cdo≥2s△abo?s△cdo?12,什么时候△ 阿布?当s时,等号成立△ CDO(此时,四边形ABCD为梯形),因此四边形ABCD面积达到最小值2717.1.4★已知:直角三角形abc中,斜边bc上的高h?6.(1)求证:bc?h?ab?ac;(2)求?bc?h?-?ab?ac?.解析22? 卑诗省?H2.ab?交流电?2?bc2?h2?2bc?h?ab2?ac2?2ab?ac,一2021年初中数学竞赛辅导专题讲义从情况来看,知道2BC吗?H4s△abc?2ab?AC和AB2?ac2?BC2,那么?卑诗省?Hab?交流电??h2?36注意:这同时解决了(1)和(2).17.1.5 ★ 设置矩形ABCD,BC=10,CD?7.移动点F和E分别位于BC和CD上,BF?预计起飞时间?4.找出△ AFE区域ade22bfc分析设置BF?十、de?y??4?x?,则11秒△abf?s△艾德?s△ecf??7x?10岁??10? 十、7.Y70? xy??22 by XY≤ 12? 十、Y4.因此△ AEF≥ 70 ℃ 70? 4.332当bf?ed?2时达到最小值.17.1.6 ★ 将P设置为固定角度?在a中的某一点,通过P的驱动直线与M和n中的两侧相交△ amn最小,P是Mn的中点mpαaβn解析如图所示,连接AP并设置?地图打盹从…起s△amp?s△anp?s△man,得是美联社?罪一美联社?罪是安辛又左式≥2ap?am?an≥sin??sin?,故s△amn当达到最小值时,s△ 放大器?s△ 所以p是Mn的中点n、ca、ab上,bm?cn?ap?1,17.1.7★正三角形abc的边长为1,p分别在bc、m、二12ap2sin?sin?。
新人教版七年级下册数学竞赛试卷及答案

54D3E 21C B A七年级下册数学竞赛题一、选择题(共10小题,每小题3分,共30分) 1、如右图,下列不能判定AB ∥CD 的条件是( ).A 、︒=∠+∠180BCDB B 、;C、43∠=∠; D 、 5∠=∠B .2、在直角坐标系中,点P(6-2x ,x -5)在第二象限,•则x 的取值范围是( )。
A 、3< x <5B 、x > 5C 、x <3 D、-3< x <5 3、点A (3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B 的坐标为( ) A、(1,-8) B 、(1, -2) C 、(-7,-1)D 、( 0,-1)4、在下列各数:3.1415926、 10049、0.2、π1、7、11131、327、中,无理数的个数( )A、2 B 、3 C 、4 D、5 5、下列说法中正确的是( )A . 实数2a -是负数 B. a a =2 C. a -一定是正数 D .实数a -的绝对值是a6、若a >b,则下列不等式变形错误..的是 A.a +1 > b +1 B. a2 > 错误! C . 3a -4 > 3b -4 D .4-3a > 4-3b7、如图,直线l 1∥l 2,l 3⊥l 4,∠1=44°,那么∠2的度数( )A . 46°B . 44°C. 36°D . 22°8、若方程组⎩⎨⎧-=++=+a y x ay x 13313的解满足y x +>0,则a 的取值范围是( ) A 、a <-1 B 、a <1 C 、a >-1 D、a >19、如图,宽为50 cm的长方形图案由10个全等的小长方形拼成,其小长方形的面积( )A .400 cm 2ﻩB .500 cm 2 ﻩ C.600 c m2 ﻩD.4000 cm210.若不等式组有解,则实数a的取值范围是()A.a<﹣36 B. a≤﹣36 C. a>﹣36ﻩD. a≥﹣36二、填空题(本大题共9小题, 每题3分,共27分)11、16的平方根是_______________12、规定用符号[x]表示一个实数的整数部分,例如[3.69]=3.[]=1,按此规定,[﹣1]=.ﻩ13、已知点A在x轴上方,到x轴的距离是3,到y轴的距离是4,那么点A的坐标是________.14、阅读下列语句:①对顶角相等;②同位角相等;③画∠AOB的平分线OC;④这个角等于30°吗?在这些语句中,属于真命题的是_____ _____(填写序号)15、某次知识竞赛共出了25道题,评分标准如下:答对1题加4分;答错1题扣1分;不答记0分.已知小明不答的题比答错的题多2道,他的总分为74分,则他答对了题.16、如图④,AB∥CD,∠BAE =120º,∠DCE = 30º,则∠AEC = 度。
九年级数学中考典型及竞赛训练专题25平面几何的最值问题2(附答案解析)

九年级数学中考典型及竞赛训练专题25 平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值.求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在RtA ABC中,CB=3, C4=4, M为斜边AB ±一动点.过点M作MD丄AC于点D,过M 作ME丄CB于点E,则线段DE的最小值为__________________ .(四川省竞赛试题)解题思路:四边形CDMF为矩形,连结CM,则DE= CM,将问题转化为求CM的最小值.【例2】如图,在矩形ABCD中,4B=20cm, BC=10cm.若在AC, AB上各取一点M, N,使BM+M/V 的值最小,求这个最小值.(北京市竞赛试题)解题思路:作点8关于&C的对称点连结B'M, B'A,贝'J BM= B'M,从而BM+MN= B'M+MN.要使BM+MN的值最小,只需使FM十M/V的值最小,当B', M, N三点共线且B7V丄AB时,B'M+MN的值最小.【例3】如图,己知DABCD, AB=a, BC=b(a>b), P为边上的一动点,直线DP交CB的延长线于Q.求AP+BQ的最小值. (永州市竞赛试题)解题思路:设AP=x,把AP, BQ分别用x的代数式表示,运用不等式以a2+b2>2ab或a+b》2范 (当且仅当a=b时取等号)来求最小值.【例4]阅读下列材料:问题如图1, 一圆柱的底面半径为5dm,高为5dm, BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到C点的最短路线.小明设计了两条路线:沿AB剪开路线1:侧面展开图中的线段AC.如图2所示.设路线I的长度为/i,则/i2=AC2=AB2 +BC2 =25+(571)2=25+25n2.路线2:高线AB十底面直径BC.如图1所示.设路线 / 的长度为b,则 F = (BCMB)2=(5+10)2 =225.••/I2-/22 = 25+257T2-225=257r2-200=25(7T2-8), /. 42 >/22 , /. h>l2 .所以,应选择路线2.(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1分米,高AB为5分米"继续按前面的路线进行计算.请你帮小明完成下面的计算:路线1:h2=AC2= ____________ :路线2: /22= (AB+BC) 2= __________ .•••/『______ 於,・・・h___ /2(填“〉"或“<"),所以应选择路线__________ (填“1"或"2")较短.(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为门高为h时,应如何选择上面的两条路线才能使蚂蚁从点&出发沿圆柱表面爬行到C点的路线最短. (衢州市中考试题)解题思路:本题考查平面展开一最短路径问题•比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,己知边长为4的正方形钢板,有一个角锈蚀,其中AF=2, BF=1.为了合理利用这块钢板,将在五边形EABCD内截取一个矩形块MD/VP,使点P在AB上,且要求面积最大,求钢板的最大利用率. (中学生数学智能通讯赛试题)解题思路:设DN* PN=y,则S=xy.建立矩形MD/VP的面积S与x的函数关系式,利用二次函数性质求S的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD=DC=1, Z DAB=A DCB=90°, BC, AD 的延长线交于P,求AB& PAB 的最小值.(中学生数学智能通讯赛试题)AR PA解题思路:设PD=x (x>l ),根据勾股定理求出PC,证RtA PCD- RtA PAB,得到 ——=——,求出 P AB,根据三角形的面积公式求出y=AB^P AB .整理后得到y$4,即可求出答案.能力训练A 级1. 如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条 垂直时,菱形的周长有最小值,那么菱形周长的最大值是 ________________ .(烟台市中考试题)2. D 是半径为5cm 的O0内一点,且OD=3cm,则过点0的所有弦中,最短的弦 _______________ cm.(广州市中考试题)3. 如图,有一个长方体,它的长BC=4,宽AB=3,高BBi=5. —*只小虫由A 处出发,沿长方体表面 爬行到G ,这时小虫爬行的最短路径的长度是 ___________ .("希望杯"邀请赛试题)4.如图,Uh ABC 中,AB=1Q, BC=6,经过点C 且与边AB 相切的动圆与CB, CA 分别相交于点E, F,则线段EF 长度的最小值是()(兰州市中考试题)5. 如图,圆锥的母线长04=6,底面圆的半径为2. —小虫在圆锥底面的点&处绕圆锥侧面一周又第1题图A. 4A /2B. 4.75C. 5D. 4.8第4題图回到点则小虫所走的最短距离为()(河北省竞赛试题)A. 12B. 4TIC. 6 VID. 6 羽6. 如图,已知Z MON= 40°, P 是Z MO N 内的一定点,点A, B 分别在射线OM, OA/上移动,当△网3 周长最小时,ZAPB 的值为()(武汉市竞赛试题)A. 80°B. 100°C. 120°D. 140°7. 如图,血是以等边三角形ABC-边AB 为半径的四分之一圆周,P 为AD 上任意一点.若4C=5, 则四边形ACBP 周长的最大值是()(福州市中考试题)A. 15B. 20C. 15+5V2D. 15+5 石交AB 于M,交DC 与N.⑴设AE=x,四边形ADNM 的面积为S,写出S 关于x 的函数关系式. (2)当AE 为何值时,四边形ADNM 的面积最大?最大值是多少?(山东省中考试题)9. 如图,六边形ABCDEF 内接于半径为/•的O0,其中AD 为直径,且AB=CD=DE=FA.(1)当Z BAD=75°时,求处的长; (2)求证:BCII 40II FE :⑶设AB=X t 求六边形ABCDEF 的周长/关于x 的函数关系式,并指出x 为何值时,/取得最大值.10. 如图,已知矩形ABCD 的边长AB=2, BC=3,点P 是AD 边上的一动点(P 异于A 、D ). Q 是BC第6题图&如图,在正方形ABCD 中,AB=2,第8題图E 是AD 边上一点(点E 与点A, D 不重合),BE 的垂直平分线第7題图边上任意一点.连结AQ ,DQ,过P 作PEII DQ 交于AQ 于F,作PF//AQ 交DQ 于F.(1) 求证:△&PE-厶 ADQ ;(2) 设&P 的长为X,试求APEF 的面积关于x 的函数关系式,并求当P 在何处时,取得 最大值?最大值为多少?(3)当Q 在何处时,AADQ 的周长最小?(须给出确定Q 在何处的过程或方法,不必证明)(无锡市中考试题)11. 在等腰AABC 中,AB=AC=5, BC=6.动点M, N 分别在两腰AB, AC 上(M 不与B 重合,N 不与A, C 重合),且M/VII BC.将NAMN 沿M/V 所在的直线折叠,使点A 的对应点为P.(1) 当MN 为何值时,点P 恰好落在BC 上?(2)设MN=x, △ MNP 与等腰NABC 重叠部分的面积为y,试写出y 与x 的函数关系式,当x 为何值时,y 的值最大,最大值是多少?(宁夏省中考试题)B 级1. 己知凸四边形ABCD 中,AB+AC+CD= 16,且S 馳彤MCO =32,那么当AC= _____________________ , BD= 时,四边形4BCD 面积最大,最大值是 _________ .(“华杯赛"试题)2. 如图,已知ZkABC 的内切圆半径为门Z4=60°, BC=2y[3 ,则/■的取值范围是 ___________ •(江苏 省竞赛试题)3. 如图O0的半径为2, O0内的一点P 到圆心的距离为1,过点P 的弦与劣弧金组成一个弓形,则此弓形面积的最小值为 __________4. 如图,A4BC 的面积为 1,点 D, G, E 和 F 分别在边 AB, AC, BC 上,BD<DA, DGII BC, DEWAC,A B第2题图 第3题图第4题图GFIIAB,则梯形DEFG面积的最大可能值为.(上海市竞赛试题)5.已知边长为a的正三角形ABC,两顶点A, B分别在平面直角坐标系的x轴,y轴的正半轴上滑动,点C在第一象限,连结0C,则0C的最大值是____________ •(潍坊市中考试题)6.已知直角梯形ABCD中,ADW BC,丄BC, AD=2, BC=DC=5,点P在BC上移动,则当必+ PD取最小值时,"PD中边AP上的高为()(鄂州市中考试题)D. 3第6題图第7题图第8题图7.如图,正方形&BCD的边长为4cm,点P是BC边上不与点B, C重合的任意一点,连结AP,过点P 作PQ丄&P交DC于点Q.设BP的长为xcm, CQ的长为ycm.(1)求点P在BC上运动的过程中y的最大值;(2)当尸丄cm时,求x的值. (河南省中考试题)4&如图,y轴正半轴上有两点A(0, a), 8(0, b),其中a>b>0.在x轴上取一点C,使乙ACB最大, 求C点坐标. (河北省竞赛试题)9.如图,正方形&BCD的边长为1,点M, /V分别在BC, CD上,使得△ CMN的周长为2.求:(1)Z MAN的大小;(2)△MAN的面积的最小值. (“宇振杯"上海市竞赛试题)10,如图,四边形ABCD中,AD= CD, Z DAB=A ACB=90°,过点D作DE丄AC于F, DE与相交于GFIIAB,则梯形DEFG 面积的最大可能值为 .(上海市竞赛试题)点E.(1) 求证:AB AF=CB ・CD ;(2) 已知AB=15cm, 8C=9cm, P 是射线DE 上的动点,设DP=xcm(x>0),四边形BCDP 的面积为ycm 2. ① 求y 关于x 的函数关系式;② 当x 为何值时,NPBC 的周长最小?求出此时y 的值.(南通市中考试题)11. 如图,己知直线/: y = Rx+2 — 4R 伙为实数).(1) 求证:不论k 为任何实数,直线/都过定点M,并求点M 的坐标;(2) 若直线/与x 轴、y 轴的正半轴交于A, B 两点,求AAOB 面积的最小值.(太原市竞赛试题)12. 如图,在RtA ABC 中,Z C=90°, BC=2, AC=x,点F 在边AB ±,点G, H 在边BC 上,四边形 EFGH 是一个边长为y 的正方形,且AE=AC.(1) 求y 关于x 的函数解析式;(2) 当x 为何值时,y 取得最大值?求出y 的最人值.(上海市竞赛试题)第6题图第9题图专题25 平面几何的最值问题12~5提示:当CM丄AB时,CM值最小,CM =警詈例2如图.蜩+ M/V的最小值为点厅到离B'F, BE= ABBC = 4^5 cm, BB' = 8>/5 cm , AE = ACJ AB'_ BE'= 8>/5cm.在△ABF中,由丄BB,2AB的距•处=丄AB'B'F,得B'F=16cm.故BM + MN的最小值为216旳例3由5DS△呻得話喘’即话畔:.AP+BQ=x+--b. \'x+ — >2jx— = 2y/ab,・••当且仅当x x V x= 俪时,上式等号成立.故当AP=y^b时.AP+BQ最小,其最小值为2他(例5题图)-b.例4⑴£=25 + *, /; =49, /i</2,故要选择路线/较短.(2)/;=//+(〃)',f =(方+ 2r)‘,一g=r[(沪一4”一4/?].当r=斗时,/f = 1},当r> 严厶时,I; > I;,当r<-^—时,/; < 7;. 例 5 设DN=x, PN=y,贝!)S=xy.由厶APQc^^ABF,得=丄_兀__4 _2-(4-x) 2即x=10—2y,代入S=xy 得S=xy=y(10—2y),即S=-2(y-# 25 5+ —.因3<y<4,而)/=空不在自变量y的取值范围内,所以y=仝不是极值点.当y=3时.S(3)=12.当y=4时,S(4)=&故Smax=12.此2时,钢板的最大利用率——j ---------- =80%. 例6设PD=x(x〉l),则PC= ,由RtAPCDcoA42— x2xl2咙得妇警.眉,令FS.则尸敎5如=斜’求y的最小值有时’y有最小值4.②运用基本不等式"弓+占S23222 r-1 2口+心•••当〒=口即当口时宀有最小值丄③借用判别式.去分母’得塔+2 (1—y) x+l+2y=0,由A=4 (1—y) 2—4 (l+2y) =4y (y —4) >0,得y>4, .'.y 的最小值为 4. A 级1. 17提示:当两张纸条的对角重合时,菱形周长最大.2.83. >/744.D5.D6. B7. C 提示:当点P 与点D 重合时.四边形ACBP 的周长最大.& ⑴连结 ME,过N 作 NF 丄ABTF.可证明 R^EBA^Rt^MNF,得 MF=AE=x.\'ME 2=AE 2+AM 2, 故 .即(2-AM) —X+AM, AM=1 一丄x 2,.・.S=人“十xAD=人“十力尸 x2422=AM+AM+MF=2AM+AE=2 (1 一丄F) +/= — 丄x 2+x+2.42(2) S=~- (x 2-2x+l) +-= 一丄(x-1)计?.故当胚=x=l 时,四边形ADNM 的面积最大,2 2 2 2 此时最大值为-.29. (1) BC 长为迥.(2)提示:连结BD (3)过点B 作BM 丄AD T M ・由 ⑵ 知四边形ABCD3AB , x 2,W为等腰梯形.从而 BC=AD-2 AM=2r-2AM.由厶BAM^^DAB,得 AM=・・・BC=2/•—一.AD 2rr最大值6 r.10. (1) Z.APE= Z.ADQ, Z.AEP=Z.AQD.・'.^APE^^ADQ. (2)由厶APE^>^ADQ, 'PDFs'1 1 13 3 3ADQ, S\PEF = — SmPfQf,得 S APEF = — — x~~^~x =—— (x — — ),+—.故当 x=—时,即 P 是 AD 的中点2 3 3 2 4 2 时,Sw 取得最大值.(3)作A 关干直线BC 的对称点A f.连结D 川交BC 干Q,则这个Q 点就是使 △AD0周长最小的点,此时0是BC 的中点.11. (1)点P 恰好在BC 上时,由对称性知MN 是厶4肚 的中位线・・••当MN=^BC=3时,点P 在r"r"x同理.EF=2r- — .l=4x+2 (2 r-—)=--r r r(x-r) 2+6r (0<v<V2 r)..当 x=r^, l 取得(第8題图)5. 卑丄4提示:当04=03时.0C 的长最大.6.CBC 上.( 2)由已知得"BC 底边上的高力=J5L32 =4.①当0<疋3时.如图1,连结AP 并延长交BC 干点D, AD 与MN 交干点0.2 12 1 1由MAWC,得A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17章 几何不等式与极值问题一个凸行边形的内角中,恰好有4个钝角,求n 的最大值.解析考虑这个凸行边形的n 个外角,有4n -个角90︒≥,故有()490360n -⨯︒<︒(严格小于是由于4个钝角的外角和大于0︒),因此8n <,n 的最大值是7.易构造这样的例子。
如果恰好有k 个钝角,则n 的最大值是3k +.在ABC △中,AB AC >,P 为BC 边的高AD 上的一点,求证:AB AC PB PC -<-. 解析 易知AB AC PB PC +>+,又2222AB AC BD CD -=- 22PB PC =-,故有AB AC PB PC -<-.评注 读者不妨考虑AD 是角平分线与中线的情况.17.1.3 已知四边形ABCD ,AC 、BD 交于O ,ADO △和BCO △的面积分别为3、12,求四边形ABCD 面积的最小值.解析 易知ABO BCOADO DCO S S BO S DO S ==△△△△,故36ABO CDO ADO BCO S S S S ⋅=⋅=△△△△.从而12ABO CDO S S +=△△≥,且当ABO CDO S S =△△(此时四边形ABCD 为一梯形)时等号成立,所以此时四边形ABCD 面积达到最小值27.已知:直角三角形ABC 中,斜边BC 上的高6h =. (1)求证:BC h AB AC +>+; (2)求()()22BC h AB AC ++-. 解析()()22BC h AB AC +-+222222BC h BC h AB AC AB AC =++⋅---⋅,由条件,知242ABC BC h S AB AC ⋅==⋅△,且222AB AC BC +=, 于是()()22236BC h AB AC h +-+==.注意:这同时解决了(1)和(2).设矩形ABCD ,10BC =,7CD =,动点F 、E 分别在BC 、CD 上,且4BF ED +=,求AFE △面积的最小值. 解析设 BF x=,()4DE y x ==-,则()()()117101077022ABF ADE ECF S S S x y x y xy ++=++--=+⎡⎤⎣⎦△△△。
由()2144xy x y +=≤。
故 ()170704332AEF S -⨯+=△≥.当2BF ED ==时达到最小值. 设P 是定角A ∠内一定点,过P 作动直线交两边于M 、N ,求证:AMN △面积最小时,P 为MN 的中点. 解析 如图,连结AP ,设MAP α∠=,NAP β∠=,θαβ=+,由 AMP ANP MAN S S S +=△△△,得sin sin sin AM AP AN AP AM AN αβθ⋅⋅+⋅⋅=⋅。
又 左式2AP ≥, 故 212sin sin sin 2sin AMNAP S AM AN αβθθ=⋅⋅△≥。
达到最小值时,须AMP ANP S S =△△,故P 为MN 之中点.正三角形ABC 的边长为1,M 、N 、P 分别在BC 、CA 、AB 上,1BM CN AP ++=,求MNP △的最大面积。
解析 如图,设BM x =,CN y =,AP z =,则0x ≤,y ,1z ≤,1x y z ++=。
()()()1111sin602APN BPM MNC S S S x z y x z y ++=-+-+-︒⎡⎤⎣⎦△△△, 于是问题变为求()()()111x z y x z y -+-+-的最小值,展开后约去()1x y z ++=,即求xz yx zy ++的最大值. 由不等式()21133xy yz zx x y z ++++=≤知,当13x y z ===时,29APN BPM MNC ABC S S S S ===△△△△,此时MNP S △的面积达到最大值。
()max 13MNP ABC S S =△△.设ABC △是边长为l 的正三角形,过顶点A 引直线l ,顶点B 、C 到l 的距离记为1d 、2d ,求12d d +的最大值.解析如图,若l 穿过BC ,则由“直角边小于斜边”知121d d BC +=≤,取到等号时仅当l BC ⊥.若l 不经过BC ,取BC 中点P ,作PQ l ⊥,Q 在l 上,则1222d d PQ AP +==≤号仅当l BC ∥.综上所述,12d d +17.1.9 在数1、12、13、14、15、16、17、18、19、110中,若任找三个数能组成三角形的三边,则称这三个数是“好搭档”,则总共有多少组“好搭档”? 解析 此题可分类讨论。
显然1不可能为边.由于1115910<+,故15⎧⎨⎩,16,17,18,19,110⎫⎬⎭中任三数可构成三角形的三边,一共有6!203!3!=组。
当最大边为12时,次大边只能为13,最小边为14或15,有2组。
当最大边为13时,次大边为14或15.次大边为14时,最小边1113412>-=,故可取11~510;次大边为15时,最小边1123515>-=,可取16与17共有8组.当最大边为14时,次大边为15、16、17.次大边 为15时,最小边1114520>-=,可取11~610;次大边为16时,最小边1114612>-=,可取11~710; 次大边为17时,最小边1134728>-=,可取18和19。
共有11组。
综上所述,总共有41组.设60XOY ∠=︒,A 、B 是OX 上的两个定点,P 是OY 上的一个动点,问当P 在什么位置时,22PA PB +最小?解析 如图,设OA a =,OB b =,OP x =,不妨设a b <。
则 222PA a x ax =+-, 222PB b x bx =+-,故 ()222222PA PB x a b x a b +=-+++()2222248a b a b x a b ++⎛⎫=-++- ⎪⎝⎭。
显然当4a bx +=时,22PA PB +最小。
评注容易验证,此时P 为AB 的中点在OY 上的射影。
设直角ABC △中,90C ∠=︒,求证:24ABC AB S △≤. 解析 如图,作A 关于BC 的对称点A ',连结'A B 、'A C ,则2211sin 244AB B AB =≤. 取等号仅当ABC △为等腰直角三角形。
X 是ABC △的边AB 上一点,P 为ACX △的内心,Q 是BCX △的内心,M 是PQ 的中点,求证:MC MX >.解析如图,连结XP 、XQ 、CP 、CQ ,则90QXP ∠=︒,12MX PQ =,又1902PCQ BCA ∠=∠<︒,故12CM PQ >,于是结论成立。
评注 三角形某边上的中线分别大于、等于、小于该边的充要条件是该边所对内角为锐角、直角或钝角,这是一个常见的结论.已知凸六边形ABCDEF 中,AF CD ∥,AB ED ∥,BC EF ∥, 求证:ACE BDF ABCDEF S S S +△△≥. 解析如图,作ABCD □、QCDE □、EFAR □,于是出现三组全等三角形。
这样便有()2ACE PQR PQR ABCDEF S S S S -+=△△△六边形,即 ()1+2ACE PQR ABCDEFS SS =△△六边形 12ABCDEF S 六边形≥. 同理有 12BDF ABCDEF S S △六边形≥.评注 不破除对称性,此题就比较复杂(当然不是所有的题目都能带给你好运).另外,用这种方法还能证明ACE BDF S S =△△.已知矩形ABCD ,3AB =,5BC =,P 是AD 上一点,CP 、BA 延长后交于M ,直线CQ 垂直于BP ,交BM 于Q ,若Q 为MB 中点,求AP .又条件同上,若BC 的长度不固定,求BC 的最小值. 解析如图,设AP x =,由MBC △∽CDP △,得MB CD BC PD =,代入得155MB x=-。
又APB △∽BQC △,得BQ AP BC AB =,53BQ x =。
由2MB BQ =,得3253x x =-,或221090x x -+=,解得x =若BC 长度不固定,设其为y ,3y MB y x =-,3xyBQ =,故由2MB BQ =得323x y x =-,或22290x yx -+=,由0∆≥得y ≥BC 可取的最小值是P 为AD 中点。
设I 为ABC △的内心,P 是ABC △内部的一点,满足PBA PCA PBC PCB ∠+∠=∠+∠.求证:AP AI ≥,并说明等号成立的充分必要条件是P I =. 解析 易知()12PBC PCB B C IBC ICB ∠+∠=∠+∠=∠+∠, 因此 BPC BIC ∠=∠.故B 、C 、I 、P 四点共圆,即点P 在BCI △的外接圆ω上。
记ABC △的外接圆为Ω,则ω的中心M 为Ω的BC 的中点,即为A ∠的平分线AI 与Ω的交点。
在APM △中,有AP PM AM AI IM AI PM +=+=+≥, 故 AP AI ≥.等号成立的充分必要条件是点P 位于线段AI 上,即P I =.延长一凸四边形形的四边和对角线,得六条直线,任两条直线有一个不大于90︒的夹角(这些线无两条平行),求这些夹角中最小的一个的最大值. 解析 如图,标好各角,则12345612180ACB ABC ∠+∠+∠+∠+∠+∠=∠+∠+∠+∠=︒,故总有一角30︒≤,当ABC △为正三角形,DB AB ⊥、DC AC ⊥时最小角达到最大值30︒ 凸四边形ABCD 中,点M 、P 分别是BC 、CD 的中点,若AM AP a +=,求证:21<2ABCD S a 四边形。
解析 如图,连结AC 、MP ,易知 1142AMP BDC AMCP ABCD S S S S +==△△四边形四边形.又BDC ABCD S S <△四边形,221()1288AM AP AM AP a +⋅=≤≤, 因此 2111248ABCD ABCD S S a <+四边形四边形,即212ABCD S a <四边形.在三角形ABC 中,4AC =,6BC =,2BAC ABC ∠=∠.P 是平面上任意一点,求32PA PB PC ++的最小值. 解析 因为224AB AC AB +=+≥. 下面来求AB .延长BA 至D ,使得DA AC =,连结CD ,则12D DCA BAC ABC ∠=∠=∠=∠,所以DCA △∽DBC △,故DC DABD DC=,所以2DC DA DB =⋅,即364(4)AB =+,故5AB =. 所以,所求的最小值为14. 在锐角三角形ABC 中,求证: cos cos 2sin2A B C +≤. 解析 当B C ∠=∠时,显然有cos cos 2sin2AB C +=.下面不妨设AB AC >. 在AB 上取点F ,使AF AC =.作角平分线AE 、高AD ,则AE 垂直平分CF .又作FH AD ⊥于H ,AD 与CF 交于G ,则2sin cos cos 2A CF FG CG FH CDB C AC FA AC FA AC==+>+=+. ABC △中,点D 为BC 之中点,点E 、F 分别在AC 、AB 上,求证: 2DEF ABC AEF S S S <-△△△.解析 如图,连结BE 、CF ,则由BD CD =,得 2DEF BEF CEF S S S =+△△△.而BEF BCF S S <△△,故BEF CEF BCF CEF ABC AEF S S S S S S +<+=-△△△△△△.于是结论成立. 设a 、b 、c 为三角形三边长,则对任意实数x 、y 、z ,有 22()()()()a x y x z b y z y x --+--2()()0c z x z y +--≥.解析 设x y p -=,y z q -=,则x z p q -=+, 原式222()()a p p q b qp c p q q =+-++ 2222222()()a p a b c pq c q f p =+-++=.它的判别式 22222222()4a b c q a c q ∆=-+-0≤.于是()0f p ≥.已知图中窗框总材料一定,问何时窗的面积最大?(图中6个矩形全等) 解析 设AB x =,AC y =,则总材料为109πl x y x =++(l 为常数),面积为2π62S xy x =+.于是(10π)9l x y -+=,代入,得2220π336l S x x ⎛⎫=-+ ⎪⎝⎭.这个二次函数在240πlx =+时取到极大值,此时x 、y 均有实际意义.取得窗的最大面积为221203πl +.ABCD 和EFGH 都是边长为1的正方形,且AB EF ∥.两个正方形重叠部分的面积为116,求两个正方形中心距离的最小值. 解析 如图,设ABCD 的中心为I ,EFGH 的中心为J ,过I 、J 分别作IK AB ∥,JK BC ∥,IK 、JK 交于K .又设两正方形重叠部分为矩形BMHN ,HM x =,HN y =,则116xy =,11122IK x x ⎛⎫=+-=- ⎪⎝⎭,同理1JK y =-, 所以222(1)(1)IJ x y =-+-277(1)88x y =+-+≥.所以, IJ .当x ,23y 时等号成立.故所求的最小值为4. 在锐角ABC △的边BC 、CA 、AB 上各有一动点D 、E 、F ,求证:DEF △的周长达到最小当且仅当AD 、BE 、CF 为ABC △的三条高.解析 如图,设D 关于AB 、AC 的对称点分别为G 、H ,GD 与AB 交于M ,DH 与AC 交于N ,则DEF△的周长22sin GF FE EH GH MN AD BAC =++==∠≥≥42sin ABCS AD BAC BC'∠=⋅△ 2sin ABCS BAC R∠=△. 这里AD '为ABC △的高,R 为ABC △的外接圆半径.又由对称性,除了AD BC ⊥外,BE 、CF 也分别必须垂直于AC 、AB 时方能达到.直角三角形内切圆半径为1,求其面积的最小值.解析 设该直角三角形直角边长为a 、b ,则易知其内切圆半径为1(12a b +=,整理,得222(2)a b a b +-=+,或2222ab a b =+-≥,此即22)2≥.由于每条直角边均大于内切圆直径22>2积为3+梯形ABCD 高为d ,上底AD a =,对角线交于P ,求用a 、d 表示APD △与BCP △面积之和的最小值.解析 如图,作EPF 与AD 、BC 垂直,垂足分别是E 、F .设BC x =,则PE PF d +=,PE AD aPF BC x ==,解得ad PE a x=+,xd PF a x=+,于是2222111222APD BCPa d x d a x S S d a x a x a x++=⋅+⋅=⋅+++△△.设22a x y a x+=+,则220x yx a ay -+-=有解,故0∆≥,即224()y a ay -≥,即2y a +≥,y 的最小值为1)a ,故最小面积为1)ad .此时1)x a =.设D 是ABC △的边BC 的中点,E 、F 分别在边AB 、AC 上,DE DF ⊥,试比较BE CF +与EF 的大小关系.解析 如图,延长FD 至P 使DP DF =,由BD CD =,知BDP △≌(SAS)CDF △,故CF BP =.又ED 垂直平分PF ,故EF PE =,易见EP BE BP <+,所以EF BE CF <+.一凸六边形ABCDEF 每条边长均为1,求证:AD 、BE 、CF 中至少有一个2≤.解析 如图,由于720A B C D E F ∠+∠+∠+∠+∠+∠=︒,不妨设240A F ∠+∠︒≤,作菱形ABGF ,则60GFE ∠︒≤,1FG FE ==,则GE 是FGE △最小边,1GE ≤,又1BG =,故2BE BG GE +≤≤.在正ABC △内,P 是一动点,求以P 在三边上的射影为顶点的三角形面积的最大值. 解析 如图,ABC △内一点P 在BC 、CA 、AB 的射影分别为D 、E 、F ,则)PD PE PE PF PF PD =⋅+⋅+⋅. 由熟知的不等式21()3ab bc ca a b c ++++≤,及PD PE PF ++为常数(ABC △的高h ),得21144ABC S ==△. 等式成立,仅当PD PE PF ==,此时P 为ABC △的中心.证明:四边形四边的平方和不小于对角线的平方和,等号成立仅当该四边形为平行四边形时.解析 如图,设BD 中点为E ,由中线长公式知 222224AB AD BD AE +=-, 222224BC CD BD CE +=-. 又由基本不等式,有22222()()AE CE AE CE AC ++≥≥,故用中线长公式代入,即得四边形四边平方和的不等式.等号成立时A 、E 、C 共线,且E 为AC 中点,即AC 、BD 互相平分,于是四边形ABCD 为一平行四边形.评注 又由托勒密不等式AD BC AB CD AC BD ⋅+⋅⋅≥,知有222()()()AD BC AB CD AC BD ++++≥,等号成立仅当四边形ABCD 为矩形.设面积为1的锐角ABC △三条边分别是a 、b 、c ,动点P 在AC 上,P 在BC 上的射影是Q ,求BPQ △面积的最大值(用a 、b 、c 表示). 解析 如图,作AR BC ⊥于R .因为cot BQ PQ C BC +=(常数),于是4cot BQ PQ C ⋅⋅= 22()BC BQ CQ --.当BR RC ≤,即AB AC ≤或c b ≤时,Q 可为BC 中点,此时BQ CQ =,从而BPQ S △可得最大值为 22224cos 2()ABC a S a b C a b c ⋅==+-△. 当BR RC >,即c b >时,BQ CQ >.当Q 落在R 上,BQ CQ -达到最小,BQ PQ ⋅达到最大.此时BPQ S △的最大值为22222sin cos cos 22ABR c c a c b S B B B a a +-===△.设D 为定线段AB 上一定点,P 为动点,PD 的长度固定,求PA PB +之最大值. 解析 由斯图沃特定理222PA BD PB AD AD BD AB PD AB ⋅+⋅=⋅⋅+⋅,注意等式右端为定值. 又由柯西不等式(或展开后移项配方)有22211()()PA BD PB AD PA PB BD AD ⎛⎫+⋅+⋅+ ⎪⎝⎭≥, 故222PD AB AB BD AD⋅=+⋅,于是PA PB +的最大值是PA ADPB BD=,PD 为APB ∠的平分线. 直角三角形ABC 的直角顶点C 在直角三角形DEF 的斜边DF 上,而E 在ABC △的斜边AB 上,如AC 、BC 、DE 、EF 分别等于10、15、12、12,求凸四边形ABFD 之面积的最大值.解析 如图,由四边形面积公式,知1115022ABFD AECD EBFC S S S AC DE EF BC =+⋅+⋅=四边形四边形四边形≤.取等号须AC DE ⊥,EF BC ⊥.此时若将点C 位于DF 中点,则由DE 、EF 的值易知E 在ACB ∠平分线上,BC 垂直平分EF ,AC 垂直平分DE ,进而由AC 、BC 之值可知E 在AB 上,满足要求.所以ABFD S 四边形的最大值为150.凸四边形一内点到四个顶点的距离分别是1、2、3、4,求这样的四边形的最大面积.解析 设凸四边形ABCD 内有一点P , {PA ,PB ,PC ,}{1PD =,2,3,4}, 则2125()82PA PC PB PD +++=≤. 等号成立,必须PA PC PB PD +=+,比如1PA =,4PC =,2PB =,3PD =,且A 、P 、C 共线,B 、P 、D 共线,AC BD ⊥,此时,5AC BD ==,ABCD S 四边形取最大值252.面积为1的三角形ABC 中,三条边长a 、b 、c 满足a b c ≤≤,求a b +的最小值. 解析 如图,过C 作直线l AB ∥,又作BE l ⊥于E ,延长一倍至D ,连结CD .则a b AC CD AD +=+≥h BE =.显然有22448c h ch +==≥,于是a b +≥仅当A 、C 、D 共线,即a b ==,且22c h ==时取等号,此时ABC △为等腰直角三角形.三角形两边长分别等于10和15,证明:这两个边的夹角的角平分线小于12. 解析 如图,不妨设15AB =,10AC =,AD 为角平分线.今在AB 上取一点E ,使ED AC ∥,则易知153255ED BD AB AC BC AB AC ====+, 故31065ED =⨯=,又由EAD DAC EDA ∠=∠=∠知6AE ED ==,于是12AD AE ED <+=.显然12是最佳上界.正三角形ABC 边长为1,M 、N 、P 分别在BC 、CA 、AB 上(含顶点),AP AN BP BM MC CN +=+=+,求MNP △的最大周长和最小周长. 解析 如图,易知1AP AN BP BM MC CN +=+=+=.由PN AP AN +≤等知MNP △的周长3AB BC CA ++=≤,达到最大值时M 、N 、P 分别落在ABC △的三个顶点上.又作BAC ∠的平分线AST ,PT 、NS 分别与AST 垂直于T 、S ,由于30PAS NAS ∠=∠=︒,1222AP AN PT SN PN =+=+≤,故12PN ≥,取等号时PN AS ⊥,且P 、N 是AB 、AC的中点,同理有PM ,12MN ≥,故MNP △的周长32≥,取等号仅当M 、N 、P 为各边之中点时.已知面积为T 的梯形ABCD 满足AB CD ∥,E 为边AB 上一点,且满足EC AD ∥,直线AC 、BD 、DE 交出的三角形面积为t .当t T 最大时,求AB CD. 解析 如图,设DE 与AC 交于M ,BD 与AC 交于N ,则MND S t =△. 设CD x =,()AB y x =≥,2ADCE ABCD S xS x y=+梯形,即2ADCExT S x y =+,2()DMC xTS x y =+△,又设AM CM p ==,MN q =,则y AB AN p qx CD CN p q+===-,解出q y xp y x-=+,即2()2()2()DMN y x xT y x xT t S y x x y x y --==⋅=+++△.于是要2()()y x xx y -+达到最大,即21(1)k k -+达最大,其中1y k x =≥.令1112S k ⎛⎫= ⎪+⎝⎭≤,则222111212122(12)(1)2228k S S S S S S k -+-⎛⎫=-=⋅⋅-⋅= ⎪+⎝⎭≤,仅当212S S =-时达到最大,此时3k =.已知ABC △的边AB 、AC 上分别有点D 、E,F 在DE 上,求证: ABC S △,并求等号成立的条件.解析 如图,连结CD 、AF .设1AD k DB =,2AE k CE =,3DFk EF =,则 23111111EFC EFC AFC ADCABC AFC ADC ABCS S S S kS S S S k k k =⋅⋅=⋅⋅+++△△△△△△△△. 同理321321111DFB ABC S k k S k k k =⋅⋅+++△△. 于是31222221231111(1)(1)(1)44464EFC DFB ABC S S k k k S k k k ⋅=⋅⋅⨯⨯=+++△△△≤. 开方即得结论.取等号时1231k k k ===,即DE 是中位线,F 为DE 中点.已知Rt ABC △中,90C ∠=︒,CD AB ⊥于D ,B ∠的平分线交CD 于E ,交CA 于F ,G是EF 的中点,连结CG ,设CFG △、BED △、BFC △的周长分别为1C 、2C 、3C .求123C C C +的最大值.解析 易知1902CFB ABC BED CEF ∠=︒-∠=∠=∠,可得CE CF =,则CG 平分ECF ∠,而90ECF BCD ABC ∠=︒-∠=∠,所以FCG ECG CBF ABF ∠=∠=∠=∠,可推得CFG △∽BFC △∽BED △.因此13C CF C BF =,23C BEC BF =. 设CFx BF =,因为2BE BF GF =-,2CF GF BF =,所以 22121212BE GF CF x BF BF BF ⎛⎫=-⋅=-⋅=- ⎪⎝⎭.因此,221212333199(12)2488C C C C CF BE x x x C C C BF BF +⎛⎫=+=+=+-=--+ ⎪⎝⎭≤,所以,当14x =,即4CF BF =时,123C C C +有最大值98. BE 、CF 是ABC △的中线,且BE CF ⊥,设AC b =,()AB c c b =>. (1)求BC 之长(用b 、c 表示);(2)若ABC △存在,求bc的范围. 解析 (1)设BE 交CF 于G ,则G 为ABC △的重心,故2GF GC =,2GE BG =,设GE x =,GF y =,因FGB △、EGC △、GBC △为直角三角形,于是有: 由①+②得222215()()4x y b c +=+,由③得 2221()5BC b c =+,即BC =(2)如果ABC △存在,则 AB AC BC AB AC +>>-, 于是有:从而2222221()(),51()().5c b b c c b b c ⎧+>+⎪⎪⎨⎪-<+⎪⎩④⑤不等式④恒成立;由不等式⑤得: 241040b b c c ⎛⎫⎛⎫-+< ⎪ ⎪⎝⎭⎝⎭, 解之得:122bc<<. 由于0c b >>,结合不等式⑤的解,得: 112bc<<. 所以,当112bc<<时,ABC △存在. ABC △中,点D 、E 、F 分别在BC 、CA 、AB 上,求证:1min(,,)4AFE BFD CED ABC S S S S △△△△≤,并求等号成立的条件. 解析 如图,222AFE BFD DCE ABC ABC ABC S S S AF AE BF BD CD CE AF BF BD CD CE EAS S S AB AC AB BC BC CA AB BC AC ⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅=⋅⋅⋅⋅⋅△△△△△△.易知221()4AF BF AF BF AB AF BF ⋅⋅=+≤,仅当F 为AB 中点时取等号,同理2BD CD BC ⋅,214CE EA AC ⋅≤,于是记min(,,)AFE BFD CED S S S S =△△△,则33164AFE BFD DCE ABCABC ABC ABC S S S S S S S S ⋅⋅△△△△△△△≤≤. 所以14ABC S S △≤,取等号时仅当D 、E 、F 为各边中点.已知:锐角ABC △中,角平分线AD 、中线BM 、高CH 交于一点P ,证明:45BAC ∠>︒. 解析 如图,若45BAC ∠︒≤,则由于90ACB ∠<︒,得45ABC ∠>︒,故AC BC >,AH BH >.作边AB 上的中线CN ,交BM 于Q ,易知N 在AH 内,于是12AH HP NQ AC CP QC =<=,故在直角三角形AHC 中,60BAC ∠>︒,矛盾,于是45BAC ∠>︒.证明托勒密定理和托勒密不等式:对于凸四边形ABCD ,AB CD AD BC AC BD ⋅+⋅⋅≥,等号成立仅当A 、B 、C 、D 共圆.解析 如图,今在AB 或延长线上取一点M ,在AD 或延长线上取一点N ,使2AB AM AC AD AN ⋅==⋅,连结MC 、NC 、MN .易知ABC △∽ACM △,故AC MC BC AB =⋅,同理,ACNC CD AD=⋅,又ABD △∽ANM △,故2AM BD AC MN BD AD AD AB=⋅=⋅. 由于MN CM CN +≤,上几式代入,得2BD AC AC ACBC CD AD AB AB AD⋅⋅+⋅≤, 去分母,即得托勒密不等式.等式成立的条件是M 、C 、N 共线,此时 180ABC ADC ACM ACN ∠+∠=∠+∠=︒, 即A 、B 、C 、D 共圆.边长为1的正方形内部或边界上有n个点,则必有两点距离3)n =,1(4)n =. 解析 如图(a),先说明一个结果:ABC △中AD 为角平分线,AA '是AD 的反向延长,则由90A AB A AC ''∠=∠>︒,得A B AB '>,A C AC '>.先考虑3n =的情形,假定P 、Q 、R 三点在正方形ABCD (边长1)内或边上.若P 在内,则可用QPR ∠角平分线反向延长,交到正方形某边或顶点为P ',这样P QR '△的每边都不小于PQR △的相应边.于是P 、Q 、R 三点最终都被“调”到正方形ABCD 的边或顶点上.再通过平移,必能使某点落在正方形的顶点上,其余点若在正方形内,再按上述办法继续调,最终三个顶点都落在正方形边界上,且其中至少有一个点的正方形的顶点.不妨设P 落在A 的位置,若Q 在AD 或AB 上,则1PQ <≤于是由对称性,可设Q 在CD 上,而R 在BC 上.如图(b).若AQ >2DQ ,1CQ <,同理1CR <,RQ综上所述结论成立.以下讨论4n =的情形.由于正方形内或边上最远两点距离是正方形对角线长度,故正方形ABCD (边长1)中四点P 、Q 、R 、S 中任两点距离如四点构成凸四边形PQRS ,不妨设90S ∠︒≥,则2222PS SR PR +≤≤,所以PS 、SR 中有一个1≤.如四点中S 位于PQR △内或边上,不妨设12090PSR ∠︒>︒≥,同理得min(,)1PS PS <.设ABC △三边长分别为a 、b 、c ,D 、E 分别在AB 、AC 上,且DE 平分ABC △的面积,求DE 的最值(用a 、b 、c 表示). 解析 如图,设CF 、BH 为中线.设AD x =,AE y =,则由12ADE ABC S S =△△,有12xy bc =.又由余弦定理,222222cos ()2(1cos )()(1cos )DE x y xy A x y xy A x y bc A =+-=-+-=-+-. 因(1cos )bc A -为常数,故DE 的大小取决于||x y -.由于xy 为常数,故x y -是x 的增函数.当||x y -取最大值,x 需最大或最小,x 最大为AB c =(这时y 取最小值2b ),最小为2c(这时y 取最大值b ).因此DE 的最大值是AB 、AC 中短边上的中线.比如当c b ≥时,DE. 记()f x x y =-,若()0f c ≥,02c f ⎛⎫⎪⎝⎭≤,则x y =可取到,于是当122c b ≤≤时,DE 的最=当12c b <或2c b >时,比如2c b >时,x 总不会小于y ,此时2cx =时,||x y -最小,DE 就是CF ,即为AB 、AC 中长边上的中线,所以在2c b >的前提下,DE 最小值是.2b c >时可以类推. 在Rt ABC △中,D 、E 、F 分别为AB 、AC 、BC 的中点,H 为斜边AB 的高的垂足,G 是DH 的中点.设O 为AB 上的任一点,求证:EOF ∠取最大的角便是EGF ∠. 解析 连结CH ,则HF 为Rt CHB △斜边BC 上的中线,故12HF BC FB ==. D 、E 分别为AB 、AC 中点,故DE ==∥12BC ,所以DE HF =,ADE ABC FHB ∠=∠=∠,从而EDG FHG ∠=∠.又DG GH =,故EDG △≌FHG △. 于是有EG GF =,EGD FGH ∠=∠.延长EG 至N ,使GN EG =,连结HN ,易知FGH △≌NGH △.从而FH HN =.结合GF GN =知GH 为线段FN 的垂直平分线.设O 为AB 上任一异于G 的点,则OF ON =,且易知ON OF OE =>(若O 在G 的左边,OF OE >,O 在G 的右边,则OE OF >).从而 OFG ONG OEM ∠=∠∠≤,在OEM △与MGF △中,EMO ∠与FMG ∠为对顶角,于是有: (等号当且仅当点O 与点G 重合时取到). 这就证明了EOF ∠取最大角时便是EGF ∠.设四边形四边依次为a 、b 、c 、d ,则其面积S 中2a b c dp +++=.取到最大值时,仅当四边形内接于圆. 解析 如图,连结AC 、BD ,交于O ,AOB θ∠=,则由四边形的余弦定理(见题,得 22222cos b d a c AC BD θ+--=⋅,又42sin ABCD S AC BD θ=⋅⋅四边形,两式平方后相加,得2222222164()ABCD S AC BD b d a c =⋅-+--四边形,即ABCD S 四边形 由托勒密不等式(参见题17.1.44),有AC BD ac bd ⋅+≤,故由托勒密定理知,仅当ABCD 内接于圆时,面积取最大值.,D 、E 分别是边BC 、AB 上的点,且123∠=∠=∠.如果ABC △、EBD △、ADC △的周长依次为m 、1m 、2m ,求证:1254m m m +≤. 解析因为23∠=∠,所以ED AC ∥,EBD △∽ABC △,1m BDm BC=;又13∠=∠,所以ADC △∽BAC △,2m AC m BC=,设AC b =,BC a =,由ADC △∽BAC △得22AC b DC BC a ==,222b a b BD a a a -=-=,这样,由2212m BD a b m BC a -==,2m AC b m BC a ==,可得2221221551244m m a b b b b b m a a a a a +-⎛⎫⎛⎫=+=-++=--+ ⎪ ⎪⎝⎭⎝⎭≤.当12b a =,即2BC AC =时,等号成立.17.1.50★★★为ABC △内一点,过O 引三条边的平行线DE BC ∥,FG CA ∥,HI AB ∥.D 、E 、F 、G 、H ,I 为各边上的点(如图),记1S 为六边形DGHEFJ 的面积,2S 为ABC △的面积.证明:1223S S ≥.解析 可以从DGO △、OHE △,OIF △的面积与ABC △的面积关系入手. 设BC a =,CA b =,AB c =,FI x =,EH y =,DG z =.易知OIF △∽HOE △∽GDO △∽ABC △,所以,z OD BI c a a ==,y OE FCb a a==, 由此可得1x y z IF FC BIa b c a++++==. 由柯西不等式知: 222222221133OIF OEH OGD S S S x y z x y z S a b c a b c ++⎛⎫=++++= ⎪⎝⎭△△△≥,从而223OHAG OEFC OIBD S S S S ++四边形四边形四边形≤.而四边形OHAG 、OECF 、OIBD 均为平行四边形,所以213AHG CEF BDI S S S S ++△△≤,即1223S S ≥.ABC ,1BC =,90C ∠=︒,30A ∠=︒,P 、Q 、R 分别在AB 、BC 、CA 上,求()max , , PQ QR RP 的最小值.解析 如图,猜想最小值是当PQR △为正三角形时取到.为求此值,不妨设图中的PQR△为正三角形.作QD AC ∥,S 在AB 上.当S 在AP 上时1302PSQ PRQ ∠=︒=∠,故S 、P ,Q 至R 等距,S 在BP 上亦然.于是SR RQ =,SR RQ =,RQ =,而显见SQ +=,故RQ 当37CQ =时,RQ若能证明对一般的动点P 、Q 、R ,有()max , , PQ QR RP 问题就解决了.用反证法,假定PQ ,QR,RP <设ABC △的费马点为F (图中未画出),则120BFA AFC CFB ∠=∠=∠=︒,设FA a =,FB b =,FC c =,则由余弦定理,知①-②,得()()1b c a b c -++=, ②-③,得()()2a b a b c -++=,故a b c >>,22a b b c -=-,32a b c =-,代入②得 2222331b c bc b c bc +-==++,于是224b bc =,2b c =,4a c =,代入上式得c,b =,a =,a b c ++=()12ABC APFR CRPQ BPFQ S S S S PR FA RQ FC PQ FB ==++⋅+⋅+⋅△≤)a b c <++= 因此()max , , PQ QR RP评注PQR △实为费马点的等角共扼点的垂足三角形.a b c ++其实也等于(CD =,ABD △为向外作的正三角形.a b c ,则1a b +、1b c +、1c a +也能.又若a 、b 、c 构成锐角三角形三边长,则1a b +、1b c+、1c a+呢? 解析 不妨设a ≥b ≥c >0,问题归结为:若b c a +>,则111a b c a b c+>+++.证明如下: 1112222b c b c b c>+=+++. 当a 、b 、c 构成锐角三角形时,1a b +、1b c +、1c a+也构成锐角三角形,证明如下(仍设a ≥b ≥c >0): 由于()()()()22112c a a b c a a b +++++≥,下证()()()221a b c a b c >+++即可,此等价于()222b c a bc ab ca+>+++,由于()2222222b c b c bc a bc a bc +=++>+>+,又()()()()2b c b c b c a b c ab ac +=++>+=+,两式相加即得结论.D E F BC CA AB ,若分别记AEF S △、BFD S △、CED S △为1S 、2S 、3S ,证明:DEF S △≥,当且仅当AD 、BE 、CF 共点时等号成立.解析 设1AF BF λ=,2BD CD λ=,3CEAE λ=,则 ()()111311ABCS Sλλλ=++△, ()()222111ABC S S λλλ=++△,()()332311ABC S S λλλ=++△,所以 ()()()1231231111ABC S λλλλλλ+=+++△.又有()()()1231232322123111ABCS S S S λλλλλλ=+++△, 故 223123123DEF ABC DEF ABCABC S S S S S S S S S S S ⎛⎫⋅=⋅⎪⎝⎭△△△△△ ()212312314λλλλλλ+=≥,于是命题得证.仅当1231λλλ=时取等号,由塞瓦逆定理知,此时必有AD 、BE 、CF 共点. ()XOY θ=∠P ,动直线l 过P ,交XOY ∠两边于M 、N ,求OM ON +之最小值(假定POX α=∠,POY β=∠,PO d =).解析如图,由面积得MON MOP NOPS S S =+△△△,即sin sin sin OM ON OM OP ON OP θαβ⋅⋅=⋅⋅+⋅⋅,此式可化为sin sin sin ON OM dαβθ+=. 用柯西不等式(或展开后用平均不等式),可得2≥,故OM ON +的最小值为2sin dθ.等号成立,仅当OM ON =.其与sin sin sin ON OM d αβθ+=联立,可解得)sin sin dOM βθ=,)sin sin d ON αθ=.又作PK OY ∥,与OX 交于K ,则sin sin dOK βθ=⋅,OK OM <,这样的M 、N 的确存在.ABC ,D 、E 、F 分别是BC 、CA 、AB 上的动点,求证:222DE EF FD ++达到最小时,满足GD BC ⊥、GE AC ⊥、GF AB ⊥,及等价的AB AC BCGF GE GD==,此处G 为DEF △重心,并用ABC △三边及面积表示这个最小值.解析 如图,先设E 、F 固定,M 为EF 中点,则2222122DE DF MD EF +=+.当MD 达最小时,应有MD BC ⊥,如对三边作处理,便有GD BC ⊥、GE AC ⊥、GF AB ⊥,此时GFD GED S S =△△,sin sin FG FGD GE EGD ⋅=⋅∠∠,故sin sin FG B GE C ⋅=⋅,sin sin FG GEC B=,同理此值为sin GD A ,此即AB AC BCGF GE GD==.下证此时的DEF △确实达到三边之平方和最小.先求此值,设GF k AB =⋅,GE k AC =⋅,GD k BC =⋅,则()2222ABC k AB BC CA S ++=△.又2222cos DE GE GD GE GD C =++⋅⋅()222222k AC BC AB =+-,同理有另两式,加之,得222212ABCS AB BC CA =++△. 下证对于一般的DEF △,有 212ABC S △≥.找到DEF △重心G ,由中线长,易知有212ABC S △≥.评注 这里用到柯西不等式,不难得出等号成立之条件.此题还包含了另一个问题:三角形内求一点至三边距离平方和最小.ABC △,D 、E 分别在BC 、AB 上,AD 、CE 交于O ,记ACO △、EDO △、BED △的面积分别是1S 、2S 、3S ,求3S 的最小值(假定1s 、2s 已知,用1S 、2S 表示之). 解析 如图,若设AEO S S =△,ODC S S =△′,则由简单的比例知S S ⋅′12S S =⋅,又231S =+,故3S最小值为2S S S =′,即ED AC ∥.ABC △a b c ,其中b 、c 确定,D 为BC 中点,ADC θ=∠,求sin θ的最大值(a 不固定,用b 、c 表示).解析 易知2222cos a b c bc A =+-,()222212cos 4AD l b c bc A ==++(延长AD 一倍至E 并连CE 即知).于是()22222sin 4sin ABC bc A S a l θ==△,下证此式()222224b c bc+≤.这等价于()()22222222224cos sin b c b c A b c A +-+≥,这可由222b c bc +≥及2cos 0A ≥推出,故sin θ的最大值为222bcb c +,仅当90BAC =∠゜或AB AC =时成立.A B ,在介质分界面l 上折射.设C 为l 上一点,直线AC 、BC 与l 所夹锐角分别为1θ、2θ,又设C ′是l 上另一点.求证:当1v 、2v (光线在两种不同介质中的速度)满足 时必有1212AC BC AC BCv v v v ''+>+. 解析 作点B 关于直线l 的对称点1B ,则有 1B C BC =,1B C ′BC =′, 12DCB DCB θ==∠∠.过A 作CA 的垂线,过1B 作1B C 的垂线,两垂线交于点F ,且与l 分别交于E 、D .在DEF △中,EF C ⋅′A DF C +⋅′()12C EF C FD B S S ''>+△△1EF CA DF CB =⋅+⋅.由正弦定理,得2211cos sin sin cos v EF FDE DF FED v θθ===∠∠, 故 2v AC ⋅′11v B C +⋅′211v AC v B C >⋅+⋅, 即 111212B C B CAC AC v v v v ''+>+, 得1212AC BC AC BC v v v v ''+>+. ABC △D ,180ADC ABC +=∠∠゜,CD AB a ==,AC b =.a <b <2a ,求ABC ACD S S -△△的最大值(用a 、b 表示,需分情况讨论).解析 易知90ADC >∠゜.如图,延长AD 至P ,使APC ABC CDP ==∠∠∠,则CP CD AB ==,且A 、B 、P 、C 共圆,于是四边形ABPC 为等腰梯形,因此ABC ACD APC ACD DCP S S S S S -=-=△△△△△.问题归结为求DCP S △的最大值.当然是希望90DCP =∠゜,这样212DCP S a =△.下面来研究DCP ∠的可取范围,设DCP θ=∠.由于AE CE =,DAC DCA ∠≥∠,因此CD AD ≥.在ACP △中,由等腰三角形CDP 知22b a AD AP -=⋅(见题2222sin 2AD AD DP CD CD DP a a a θ=+⋅+⋅=+⋅≤,即221sin 22b a θ-≤.因为b <2a ,故左式<1,θ总有解,下面讨论之. (1)当1ba<θ可取90゜,此时的最大面积正是212a ;(2)2ba<时,取22sin 122b a θ=-,则22sin 22b PD a a a θ==-,DCP S △得最大值为2sin cos 22a θθ=.60O =∠゜,内有一定点P ,OP 平分O ∠,OP d =,过P 作一动直线交O ∠两边于A 、B (OAB ∠、90OBA ∠≤゜),过A 、B 分别作OA 、OB 的垂线交于Q .求四边形AOBQ 面积的最大值,并刻画此时AB 的位置.解析 不妨设OA a =,OB b =,作AD OB ⊥于D ,则cos602a BDb a b =-=-゜,2cos ab ABO AB-=∠,同理 2cos b a OAB AB-=∠. 由正弦定理,sin sin BQ AB BAQ Q =∠,或cos sin 60BQ ABOAB =∠゜,故2b BQ a ⎫=-⎪⎭,2215222422ABQa b a b S BD BQ b a ab ⎫⎫⎛⎫=⋅⋅=--=--⎪⎪⎪⎝⎭⎝⎭⎝⎭△,又OAB S =△,故)224OBQA S ab a b =--. 下面求出a 与b 之间的关系.由AOB AOP BOP S S S =+△△△,得sin30sin30sin60ad bd ab +=゜゜゜,不妨设d a b ab+=.由此得ab ≥4ab ≥. 又()()()()22222466938ab a b ab a b ab ab ab -+=-+=-=--≤. 于是当2a b ==时,OBQAS 一般情况下.当a b=2),此时AB OP ⊥.ABC △BC D ,AD BC ⊥,又在BC 上找一点E ,使BE CD =(E 比D 靠近B ),过E 任作一直线,交AB 于F ,交AC 的延长线于G ,求证:BC FG <.解析1 如图(a ),连结BG 、DG ,显然ABC ∠、ACB ∠均为锐角.由梅氏定理,有1BA FG EC AF GE CB ⋅⋅=,于是欲证结论变成求证1BA EC AF GE ⋅<,或BF GE CEAF CE-<. 作GH BC ⊥于H ,连结AE 、AH ,注意左边为BEG DCG DHG AHG AEG AEG AEG AEG S S S S CH EH CE GE CES S S S CE CE CE --=<===<△△△△△△△△. 于是结论成立.解析2 如图(b ),作FM 、GN 与BC 垂直,垂足为M 、N .由梅氏定理知1AG CE BFGC BE AF⋅⋅=,文档从互联网中收集,已重新修正排版,word 格式支持编辑,如有帮助欢迎下载支持。
