第四讲 运动方程的积分算法
第4讲 典型环节
输出量不失真、无惯性、快速地跟随输入量,两者成 比例关系。
其运动方程为:xo(t)=Kxi(t)
xo(t)、xi(t)——分别为环节的输出量和输入量; K——比例系数,等于输出量与输入量之比。
比例环节的传递函数为: X o ( s) G( s) = =K X i ( s)
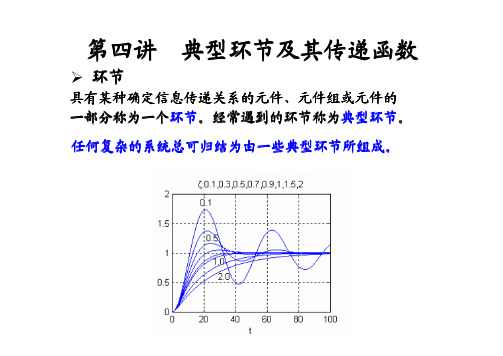
传递函数: G ( s ) = K τ 2 s 2 + 2ξ τs + 1
(
)
式中,τ——时间常数 ξ——阻尼比,对于二阶微分环节, 0<ξ<1 K——比例系数
系统数学模型 第二章 � 积分环节
输出量正比于输入量对时间的积分。 运动方程为: xo (t ) = 1 ∫ t xi (t )dt 0
T
车初始位置距平衡点1.0,则所建立模型如图示。
F c k 系统微分方程 ̇ ̇= − x ̇− x x m m m
若外力输入F=0,仿真所得示 波器窗口小车位移随时间变 化的轨迹如图。
F
为0
初值为1
第二章 系统数学模型
质量—弹簧—阻尼系统
F
F如下图 系统输入 系统输入F
系统输出 x如下图所示 系统输出x
微分环节的输出是输入的导数,即输出反映了 输入信号的变化趋势,从而给系统以有关输入 变化趋势的预告。因此, 微分环节常用来改善 变化趋势的预告。因此,微分环节常用来改善 控制系统的动态性能。
第二章 系统数学模型
� 二阶微分环节 运动方程:
⎡ 2 d2 ⎤ d xo (t ) = K ⎢τ x (t ) + 2ξ τ xi (t ) + xi (t )⎥, 0 < ξ < 1 2 i dt ⎣ dt ⎦
利用积分计算物体运动的位移

通过位移函数计算物体在终点的坐标位置
二维运动下的位移计算
积分计算
将速度函数积分得到位移 函数 利用初末速度计算平均速 度
坐标变换
根据不同坐标系变换坐标 计算物体在不同坐标系下 的位移
二维投影
将二维运动投影到x轴和y 轴上 分解运动的加速度和速度 分量
二维运动的应用
航空航天
● 03
第3章 二维运动下的位移计 算
二维运动的描述
二维运动是指物体在平面上同时具有x轴和y轴 方向上的运动。在二维平面上,物体的运动状态 可以通过坐标系进行描述,从而便于计算。
速度向量
速度方向
描述物体在二维 平面上的运动方
向
速度变化
记录物体速度随 时间变化的规律
速度大小
表示物体在单位 时间内的位移量
景
数学工具
学习更多数学工 具和方法,用于 物体运动位究
积分在科学研究中的重要作用和应用
02 工程设计
工程设计中积分在位移计算中的价值和实用 性
03 生物医学
生物医学领域中积分在位移测量中的应用案 例
感想与收获
感想
通过学习位移计算,深刻 认识到数学在物理中的重 要性 对积分应用于物体运动的 理解更加透彻
物体运动的基本概念
01 位置
物体所在的空间坐标
02 速度
位置变化的快慢
03 加速度
速度变化的快慢
位移的定义
移动距离
物体从一个位置到另一个 位置的距离变化
方向的变化
描述物体在空间中移动的 路径变化
积分在位移计算中的应用
速度函数
描述物体运动的 速度变化
积分计算
通过速度和加速 度函数计算物体
分步积分的计算公式

分步积分的计算公式积分是微积分中的重要概念,它是对函数的反导数运算,可以用来求函数的面积、体积、平均值等。
而分步积分则是一种特殊的积分方法,它可以将一个复杂的积分问题分解成若干个简单的积分问题,然后分别求解,最后将结果合并得到最终的积分结果。
本文将介绍分步积分的计算公式及其应用。
一、分部积分法的基本公式。
分部积分法是求不定积分中的一种常用方法,它的基本公式如下:∫u dv = uv ∫v du。
其中,u和v是待定函数,它们的选择通常是要使得∫u dv或∫v du中的一个积分式子简化。
在实际应用中,我们通常将∫u dv称为“被积函数”,∫v du称为“积分因子”。
二、分步积分的计算公式。
1. 二次函数积分。
对于形如∫x^2 e^x dx的积分,我们可以使用分步积分的方法来求解。
首先,我们选择u=x^2,dv=e^x dx,然后分别求出du和v,得到du=2x dx,v=e^x。
将这些结果代入分部积分的基本公式中,得到:∫x^2 e^x dx = x^2 e^x ∫2x e^x dx。
接下来,我们再次使用分部积分的方法对∫2x e^x dx进行求解,选择u=2x,dv=e^x dx,然后分别求出du和v,得到du=2 dx,v=e^x。
将这些结果代入分部积分的基本公式中,得到:∫2x e^x dx = 2x e^x ∫2 e^x dx。
最终,我们可以得到∫x^2 e^x dx的积分结果为:∫x^2 e^x dx = x^2 e^x 2x e^x + 2 e^x + C。
其中,C为积分常数。
2. 三角函数积分。
对于形如∫sinx e^x dx的积分,我们同样可以使用分步积分的方法来求解。
首先,我们选择u=sinx,dv=e^x dx,然后分别求出du和v,得到du=cosx dx,v=e^x。
将这些结果代入分部积分的基本公式中,得到:∫sinx e^x dx = -cosx e^x ∫(-cosx) e^x dx。
欧拉运动方程及其积分详解

将欧拉运动方程中的时间和空间变量进行傅里叶变换,通过求解变换后的常微分方程得到解析解。
近似积分方法
泰勒级数法
将欧拉运动方程中的非线性项进行泰勒级数展开,通过求解近似线性化的常微分方程得 到近似解。
多项式拟合法
利用已知的初值条件和时间步长,通过多项式拟合的方法逼近物体的运动轨迹,得到近 似解。
发展历程
随着科学技术的不断进步,欧拉运动方程在理论和应用方面得到了不断发展和完 善,对于推动力学和其他学科的发展起到了重要作用。
02
欧拉运动方程的数学表达
位置和速度的表示
位置表示
在二维平面中,物体的位置可以用二维向量表示,例如$r = (x, y)$。在三维空间中,物体的位置可以用三维向量表示, 例如$r = (x, y, z)$。
速度表示
速度是位置对时间的导数,可以用向量表示为$vec{v} = frac{dvec{r}}{dt}$。在二维平面中,速度向量可以表示为 $vec{v} = (v_x, v_y)$;在三维空间中,速度向量可以表示为 $vec{v} = (v_x, v_y, v_z)$。
力和加速度的表示
力表示
力是作用在物体上的外力,可以用向量表示为$vec{F}$。在二维平面中,力向量可以表示为$vec{F} = (F_x, F_y)$;在三维空间中,力向量可以表示为$vec{F} = (F_x, F_y, F_z)$。
04
欧拉运动方程的应用实例
在物理中的应用
01
02
03
刚体动力学
欧拉运动方程可以描述刚 体的旋转和直线运动,是 刚体动力学的基本方程之 一。
陀螺仪
欧拉运动方程在陀螺仪的 应用中非常重要,用于描 述陀螺仪的旋转运动和进 动。
积分方程的数值解法

dy = − 2 g (h − y ) sin β , dt
因此
dt = −
上式两边从 0 到 h 积分,并记
dy . 2 g (h − y ) sin β
2
ϕ ( y) =
就有
1 , sin β
∫
h
0
ϕ ( y) dy = − 2 g f1 (h) . h− y
记- 2 g f1 (h) = f (h) ,最后得到
Abstract : This paper describes two numerical solution methods of integral equations ,namely,successive approximation method and the use of any nuclear degenerate kernel approximation method. This paper is structured as follows.first briefly introduces the basic knowledge of integral equations, then discusses whether the solutions of four common equations exist and how to slove a special kind of equation (Degenerate equation) , finally since for the majority of the integral equations we can not find out their exact analytical solutions,therefore we turn to introducing the two numerical solution methods of integral equations. Key words: integral equation of integral equations equations with degenerate kernel numerical solution
积分的基本公式和法则

积分的基本公式和法则积分公式是普遍用于积分问题的公式方法,有许多同学想了解积分常用公式有哪些?下面是由小编为大家整理的“积分的基本公式和法则”,仅供参考,欢迎大家阅读。
积分的基本公式和法则设是函数f(x)的一个原函数,我们把函数f(x)的所有原函数F(x)+C(C为任意常数)叫做函数f(x)的不定积分,记作,即∫f(x)dx=F(x)+C。
其中∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数,求已知函数不定积分的过程叫做对这个函数进行积分。
积分的运算法则积分的运算法则,别称积分的性质。
积分是线性的。
如果一个函数f可积,那么它乘以一个常数后仍然可积。
如果函数f和g可积,那么它们的和与差也可积。
通常意义:积分都满足一些基本的性质。
以下的I在黎曼积分意义上表示一个区间,在勒贝格积分意义下表示一个可测集合。
线性:积分是线性的。
如果一个函数f可积,那么它乘以一个常数后仍然可积。
如果函数f和g可积,那么它们的和与差也可积。
保号性:如果一个函数f在某个区间上黎曼可积,并且在此区间上大于等于零。
那么它在这个区间上的积分也大于等于零。
如果f勒贝格可积并且几乎总是大于等于零,那么它的勒贝格积分也大于等于零。
作为推论,如果两个I上的可积函数f和g相比,f(几乎)总是小于等于g,那么f 的(勒贝格)积分也小于等于g的(勒贝格)积分。
如果黎曼可积的非负函数f在I上的积分等于0,那么除了有限个点以外,f=0。
如果勒贝格可积的非负函数f在I上的积分等于0,那么f几乎处处为0。
如果F中元素A的测度μ(A)等于0,那么任何可积函数在A上的积分等于0。
函数的积分表示了函数在某个区域上的整体性质,改变函数某点的取值不会改变它的积分值。
对于黎曼可积的函数,改变有限个点的取值,其积分不变。
对于勒贝格可积的函数,某个测度为0的集合上的函数值改变,不会影响它的积分值。
如果两个函数几乎处处相同,那么它们的积分相同。
1.5运动积分

展开上式并交换求和:
s n 1 s n ri ri ri ri 1 n ri 2 q ( mi mi ( ) T ( mi )q )q 2 1 i 1 q q q t 2 i 1 t 1 i 1
E p E p x E p x 2 x1 E p x 2 x1
在这样的条件下,坐标1和2所受的力分别为
E p x E p F1 x1 x x1 x E p E p x E p F2 x 2 x x 2 x
ri 当 0, H T2 T0 V E t ri 当 0, T0 0, T T2 , H T2 V T V E ; t
对于完整的有势系,若L不显含t,且体系受定常约束时, 系统的H(即系统的机械能)能量积分表明系统的机械能守恒; 而L不显含t,但体系受非定常约束时,系统的H广义能量积分.
对于保守系统,动量守恒的条件简化为合外力为零。 若整个力学系统所受合力为零,则其动量守恒。如碰撞过程。
动量守恒实例
• 一质量为m的质点在重力场中运动,取直角坐标x、y、z为广义坐标 拉氏函数为
T 1 2 y 2 z 2 ), m( x 2 L T U 1 2 y 2 z 2 ) mgz m( x 2
参考:运动积分实例
例:圆锥面上质点,质量为m,约束在半顶角为α的圆锥
面上运动,求其运动积分。
解 : 自 由 度 为 2, 约 束 方 程 为 z rctg 取柱坐标 ( r , , z )中 的r ,为 广 义 坐 标 ,
积分的计算方法

积分的计算方法
积分是一种数学运算方法,用于求解函数的面积、曲线的弧长以及各类函数的变换等问题。
下面将介绍一些常见的计算方法。
1. 定积分
定积分是对函数在某一区间上的积分运算。
设函数为f(x),区
间为[a, b],则定积分可以表示为∫[a, b]f(x)dx。
计算定积分的方法有多种,包括基本的定积分法、换元法、分部积分法等。
2. 不定积分
不定积分是求解函数的原函数,也可以理解为对函数的积分运算。
设函数为f(x),则不定积分可以表示为∫f(x)dx。
计算不定
积分的方法包括基本的不定积分法、换元法、分部积分法等。
3. 曲线的弧长
曲线的弧长是指曲线在一段区间上的弧长长度。
设曲线方程为
y = f(x),在区间[a, b]上的弧长可以表示为∫[a, b]√(1 +
[f'(x)]^2)dx。
其中f'(x)表示函数f(x)的导数。
4. 极坐标下的曲线长度
对于极坐标方程r = f(θ),其中r表示极径,θ表示极角。
极坐
标下的曲线长度可以表示为∫[α, β]√(r^2 + [f'(θ)]^2)dθ。
其中f'(θ)表示函数f(θ)的导数。
这些是积分的一些常见计算方法,可以根据具体问题选择相应的方法进行计算。
运动方程怎么求轨迹方程

运动方程怎么求轨迹方程运动方程和轨迹方程是物理学中重要的概念。
在物理学和工程学中,当一个物体运动时,我们常常需要知道物体的运动方程和轨迹方程。
运动方程描述物体的运动状态,有助于我们确定物体的速度、加速度和位移等物理量。
轨迹方程描述物体的运动轨迹,有助于我们预测物体的运动路径,以及对物体进行精密控制。
本文将介绍如何求运动方程和轨迹方程。
一、如何求运动方程运动方程是描述物体在运动中的位置、速度和加速度随时间变化的函数关系。
在一般情况下,运动方程可表示为:s = f(t)v = ds / dta = dv / dt其中,s是物体的位移,t是时间,v是物体的速度,a是物体的加速度。
如果我们知道物体的运动状态,就可以根据上述公式计算出它的运动方程。
以下是一些常见的情况和运动方程的求解方法:1.匀速直线运动如果物体在直线上以匀速运动,那么其位移随时间的变化关系为:s = v*t其中,v是物体的速度,t是时间。
这是一个简单的线性关系,代表了物体在直线上做匀速直线运动的情况。
2.匀加速直线运动如果物体在直线上做匀加速直线运动,那么其位移随时间的变化关系为:s = vt + (1/2)at²其中,v是物体的初速度,a是物体的加速度,t是时间。
这是一个二次关系,描述了物体在直线上做匀加速直线运动的情况。
注意,这里的加速度是常数,并且在正方向和负方向上均有可能。
3.匀速圆周运动如果物体做匀速圆周运动,那么我们可以使用极坐标系来描述物体的位置。
在极坐标系中,物体的位置由径向距离r和极角θ来描述。
在匀速圆周运动的情况下,物体角速度ω是恒定的,我们可以得到以下关系式:r = constantθ = ωt + θ₀其中,r是物体与圆心的距离,ω是物体的角速度,t是时间,θ₀是物体在t=0时位于的角度。
请注意,这里的角速度是恒定的,因此,物体的角度随时间的变化可以用简单的线性函数来表示。
二、如何求轨迹方程轨迹方程是描述物体在运动中路径的函数关系。
加速度的积分公式机器人动力学

加速度的积分公式机器人动力学
机器人动力学是研究机器人运动规律和力学特性的学科,其中涉及到加速度的积分公式。
在机器人动力学中,加速度是机器人运动状态的重要指标之一、加速度描述了系统在单位时间内速度变化的快慢程度。
在求解机器人运动学和动力学问题时,往往需要进行加速度的积分操作。
机器人动力学中常见的加速度的积分公式有以下几种:
1.速度的积分公式
速度是位移的变化率,即 v = ds/dt,其中 v 表示速度,s 表示位移,t 表示时间。
通过对速度进行积分,可以求得位移。
∫ds = ∫v dt
2.位置的积分公式
位置是位移的累积,即p = ∫ds。
通过对位移进行积分,可以求得位置。
3.加速度的积分公式
加速度是速度的变化率,即 a = dv/dt。
通过对加速度进行积分,可以求得速度。
∫dv = ∫a dt
4.位移的二次积分公式
位移的二次积分即是位置,通过对加速度进行两次积分,可以求得位移。
∫∫ds = ∫∫v dt = ∫(∫a dt) dt
需要注意的是,在实际应用中,通常并不会直接进行加速度的积分,
而是通过其他已知的运动规律和力学特性进行求解。
机器人动力学建模中,常常使用拉格朗日动力学方程或牛顿-欧拉动力学方程来描述机器人系统
的运动规律。
这些方程可以表达位移、速度和加速度之间的关系,从而实
现对运动状态的分析和仿真。
总之,加速度的积分公式在机器人动力学中是非常重要的一部分。
通
过对速度、加速度的积分操作,可以求解位移、速度和加速度之间的关系,进而实现机器人运动状态的预测和控制。
直接积分法(课堂PPT)

3
常用的隐式积分法
• 隐式积分归结为求解非线性方程组。但是 从计算效率考虑,在结构动力响应分析中 一般对它的计算过程加以修正提高计算收 敛性和效率,各种改进算法中Newmark β 法和Wilson θ法是结构振动响应分析中最常 用的两种方法。
τ θΔt
18
• 代入结构运力方程式 得到计算 tτ 时刻位移的方程组
19
• 得到位移后进一步得到t+τ加速度,然后内插 得到t+Δt加速度,进一步计算位移和速度。
当θ≧1.37时Wilsonθ法为无条件稳定的计算方法 20
wilsonθ法的计算过程
1. 计算常数
a0
6 τ2
a1
3 τ
a2 2a1
统一表达式
β=1/6 为线性加速度 β=1/4 为平均加速度
12
用增量形式表示
振动方程 位移、速度和加速度增量
这里
13
• 根据上式,得到速度和加速度的增量 • 代入运动方程
14
Newmark β法的收敛性
• 可以证明, Newmark β法当β≥1/4时,
计算是无条件收敛的。
• Newmark β法是工程计算中最常用的方法,
28
• 稳定性好的计算方法并不意味可以用任意大的时间步长 进行积分计算,无条件稳定的计算方法(比如Wilsonθ法) 虽然不会发生数学上的发散现象,但是容易出现早期结果 偏大、后期出现异常振动的计算结果,而且也有可能导致 高频振动的计算结果失真的现象,因此,这种算法一般不 太合适于带有冲击响应的结构计算。对于高次振动成分比 较重要的计算,用非常小的时间步长按显式积分较多。
分步积分的计算公式

分步积分的计算公式在微积分中,积分是一个非常重要的概念,它可以帮助我们求解曲线下面的面积、求解定积分和不定积分等问题。
在实际应用中,我们经常会遇到一些复杂的函数,需要通过分步积分的方法来求解。
分步积分是指将一个复杂的积分问题分解成多个简单的积分问题,然后分别求解这些简单的积分问题,最后将结果合并起来得到最终的积分结果。
在本文中,我们将介绍分步积分的计算公式,并通过一些例题来展示如何应用这些公式来求解积分问题。
1. 分部积分公式。
分部积分公式是分步积分中最常用的公式之一,它可以帮助我们将一个积分问题分解成两个简单的积分问题。
分部积分公式的表达式如下:∫u dv = uv ∫v du。
其中,u和v是可微函数,可以通过对u和v求导得到du和dv。
通过这个公式,我们可以将一个积分问题分解成两个简单的积分问题,然后分别求解这两个简单的积分问题,最后将结果合并起来得到最终的积分结果。
2. 分部积分的应用。
下面我们通过一个例题来展示如何应用分部积分公式来求解积分问题。
考虑如下的积分问题:∫xsin(x)dx。
我们可以将sin(x)看作是u,x看作是dv,然后对u和v求导得到du和dv:u = sin(x), dv = xdx。
du = cos(x)dx, v = (1/2)x^2。
然后我们可以将原来的积分问题转化成两个简单的积分问题:∫xsin(x)dx = sin(x)(1/2)x^2 ∫(1/2)x^2cos(x)dx。
接下来我们可以分别求解这两个简单的积分问题:∫xsin(x)dx = -1/2xcos(x) + 1/2sin(x) + C。
通过这个例题,我们可以看到如何通过分部积分公式将一个复杂的积分问题分解成两个简单的积分问题,然后分别求解这两个简单的积分问题,最后将结果合并起来得到最终的积分结果。
3. 三角代换公式。
三角代换是一种常用的积分方法,它可以帮助我们将一个复杂的积分问题转化成一个简单的三角函数积分问题。
lammps 运动方程积分算法

lammps 运动方程积分算法(实用版)目录MMPS 简介MMPS 的运动方程MMPS 的积分算法MMPS 的应用领域正文MMPS 简介LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)是一款大规模原子/分子并行模拟器,主要用于分子动力学和材料科学研究。
LAMMPS 通过高效的并行计算,可以模拟数百万甚至数千万原子/分子的系统,从而在原子尺度上研究材料的结构和性质。
MMPS 的运动方程LAMMPS 基于牛顿运动定律,模拟原子/分子系统的运动。
其运动方程可以表示为:a = F/m其中,a 是加速度,F 是作用在粒子上的力,m 是粒子的质量。
LAMMPS 考虑了各种相互作用力,如范德华力、库仑力和弹性力等。
通过求解运动方程,LAMMPS 可以获得原子/分子在给定时间内的位移、速度等信息。
MMPS 的积分算法LAMMPS 采用了多种积分算法来求解运动方程,主要包括:- 欧拉算法(Euler):这是一种常用的数值积分方法,通过对速度和加速度进行四阶龙格 - 库塔(龍格 - 库塔)求解,可以获得较为准确的结果。
- 维诺算法(Verlet):该算法通过对位置和速度进行二次龙格 - 库塔求解,时间步长较短时,可以获得较高的精度。
- 高阶龙格 - 库塔算法(High Order Lagrangian):该算法可以提高数值稳定性和精度,适用于较长时间步长的模拟。
MMPS 的应用领域LAMMPS 广泛应用于多个领域,如材料科学、生物物理、化学反应动力学等。
通过模拟原子/分子的运动,研究人员可以深入了解材料的微观结构和性能,进而优化材料设计和制造工艺。
此外,LAMMPS 还可以模拟生物大分子(如蛋白质)的结构和功能,为生物科学研究提供有力支持。
一元一次方程-球赛积分-答案版

球赛积分问题单循环赛:所有参加比赛的队均能相遇一次单循环赛比赛场次:X=N(N-1)÷2,即:队数×(队数—1)÷2例如:8个队参加比赛,比赛总场数是:28双循环赛:所有参加比赛的队均能相遇两次,如果参赛队少,或者创造更多的比赛机会,通常采用双循环的比赛方法。
双循环比赛一般都是属于联赛性质的,任意两支球队都要在自己的主场和对方的主场各交战一回合.双循环赛比赛场次:N 支球队,比赛场数共为N(N-1)场。
1、一份试卷共有25道题,每道题都给出了4个答案,其中只有一个正确答案,每道题选对得4分,不选或错选倒扣1分,如果一个学生得90分,那么他做对了多少道题?解:设他做对了x 道题目,根据题意可列方程:()902514=-⨯-x x解得:x=23答:如果一个学生90分,那么他做对23道题。
2、某企业对应聘人员进行逻辑思维考试,试题由50道选择题组成,评分标准规定:每道题的答案选对得3分,不选得0分,选错倒扣1分。
已知某人有5道题未作,得了103分,则这个人选错了几道题? 解:设回答正确的题目数量为x ,错误题数则为(50-5—x ),即(45—x ),根据题意可列方程: 3x-(45-x)=103解得:x=37答:这个人选错了8题。
3、某学校七年级8个班进行足球友谊赛,采用胜一场得3分,平一场得1分,负一场得0分的记分制.某班与其他7个队各赛1场后,以不败的战绩积17分,那么该班共胜了几场比赛?解:设该班共胜了x 场比赛,则平了(7-x )场,根据题意可列方程:3x+(7-x )×1=17解得:x=5答:该班共胜了5场比赛。
4、在一次12个队参加的足球单循环赛中,规定胜一场记3分,平一场记1分,负一场记0分。
某队在这次循环赛中所胜场数比所负场数多2场,结果共计18分,问该队平几场?解:12个球队进行单循环赛,每个队需要比赛11场,设该队负了x场,则胜了x+2场,平的场数为11-x-(x+2)=9-2x根据题意可列出方程:3×(x+2)+1×(9-2x)+0×x=18解得:x=3,则x+2=5,9-2x=3答:该队平了3场,胜了5场,负了3场。
lammps 运动方程积分算法

lammps 运动方程积分算法
(实用版)
目录
1.引言
mmps运动方程积分算法的原理
mmps运动方程积分算法的步骤
mmps运动方程积分算法的优缺点
5.结论
正文
一、引言
Lammps是一种常用的分子动力学模拟软件,用于模拟原子系统的运动方程。
本文将介绍Lammps运动方程积分算法的原理、步骤、优缺点以及应用场景。
二、Lammps运动方程积分算法的原理
Lammps运动方程积分算法基于牛顿-欧拉法,通过不断迭代求解微分方程来近似模拟系统的运动。
该算法将微分方程转化为差分方程,并使用递推的方式求解,从而实现对系统的模拟。
三、Lammps运动方程积分算法的步骤
1.定义系统的运动方程,并将其转化为差分方程。
2.初始化系统参数,包括原子坐标、势能函数等。
3.迭代求解微分方程,即牛顿-欧拉法。
4.更新系统参数,包括原子坐标、势能函数等。
5.重复步骤3和4,直到满足收敛条件。
四、Lammps运动方程积分算法的优缺点
1.优点:算法简单易懂,易于实现;能够处理复杂的多体相互作用;适用于多种类型的分子动力学模拟。
2.缺点:需要消耗较多的计算资源;收敛速度较慢;对初始条件比较敏感。
五、结论
Lammps运动方程积分算法是一种常用的分子动力学模拟方法,具有简单易懂、易于实现等优点。
第三章 运动方程求解

pd 1 uz μ r z r r r
一、圆管中的轴向稳态层流
θ 分量:
uθ uθ uθ uθ ur uθ uθ ur uz ' θ r r θ r z 2 2 1 u uθ u 1 pd 1 2 θ r ν (ruθ ) 2 2 2 2 ρr θ r θ z r θ r r r
2 uθ 1 p r ρ r
三、旋转黏度计的测量原理
uθ uθ uθ uθ ur uθ uθ ur uz θ r r θ r z 2 2 1 1 1 p 1 uθ 2 ur uθ Xθ ν (ruθ ) 2 2 2 2 ρ r θ r θ z r θ r r r
三、旋转黏度计的测量原理
连续性方程简化
ur 0 , uz 0 1 1 uθ u z (rur ) 0 r r r θ z
uθ 0 θ
运动方程简化
2 ur ur uθ ur uθ ur ur uz θ r r θ r z 2 2 1 u u ur 1 p 1 2 θ r Xr ν (rur ) 2 2 2 2 ρ r r θ z r θ r r r
一、圆管中的轴向稳态层流
pd 0 r
z 分量:
uz uz uθ uz uz ur uz ' θ r r θ z 1 uz 1 pd 1 2u z 2u z ν (r ) 2 2 2 ρ z r θ z r r r
一、圆管中的轴向稳态层流
二、套管环隙中的轴向稳态层流
三、旋转黏度计的测量原理
运动微分方程

运动微分方程弹性体体积V ,表面积S ,密度ρ,单位质量所受的体力为f,体力场为f(x,t),单位向量为n 的面元dS 的面力场为t(n,x,t),x 为原点到受力点的向量,t 为时间。
弹性体在t 时刻的动量P (t)dV v dt ddV f dS t dtdP F f V f m F dVf dS t F F F dVv m v p Vi Vi si ii Vi si i Vi i ⎰⎰⎰⎰⎰⎰=+=⨯=⨯=+=+===ρρρρρ动量定理合力弹性体动量体体面*******************************************************************************散度定理:散度定理是矢量场中体积分与面积分之间的一个转换。
⎰⎰∙=∙∇sVS d F dV F散度:表征矢量场A 产生的体积(三维)或面积(二维)的相对膨胀率,其表达式为▽·A 。
zRy Q x P R Q P z y x F ∂∂+∂∂+∂∂=∙∂∂∂∂∂∂=∙∇),,(),,( ,P,Q ,R 为F 在x,y,z 上的分量。
散度定理的证明:S d F dV F sV∙=∙∇⎰⎰⎰⎰⎰。
令()R Q P F ,,=,假设F =(0,0,R),则需要证明dS n R dV R sVz⎰⎰⎰⎰⎰∙=),0,0( 如下图,投影区为U。
dxdy y x z y x R y x zy x R dxdy dz R dV R Uy x Z y x Z zDz ))],(,,()),(,,([)(),(),(底顶顶底⎰⎰⎰⎰⎰⎰⎰⎰-==S=S 底+S 顶+S 侧面令S 底=S1,S 顶=S2,S 侧面=S3. 对于顶面,则dxdy yZ x Z dS n )1,,(22∂∂-∂∂-=Rdxdy dxdy y Z x Z R dS n R =∂∂-∂∂-=)1,,)(,0,0(),0,0(22dxdy y x z y x R dxdy R dS n R U⎰⎰⎰⎰⎰⎰==)),(,,(),0,0(顶顶顶对于底面,则dxdy yZ x Z dS n )1,,(11-∂∂∂∂=dxdy y x z y x R dxdy R dS n R U⎰⎰⎰⎰⎰⎰=-=)),(,,(-),0,0(底底底对侧面,S3=0。
速率方程的积分形式.

dcA
/
dt
kcA2
1
cA
1
1 cA,0 xA
kt
kt
aA bB 产物
cA,0 1 xA
当a b, cA,0
cB,0
,
dcA dt
kAcA2
dcA dt
kAcAcB
当a
b,
cB,0
/
b
cA,0
/
a,
• 2.5 小结
例题:蔗糖在稀酸水溶液中按下式水解:
C12H O 22 11 H2O H C6H12O6 C6H12O6
葡萄糖
果糖
当催化剂HCl的浓度为0.1mol·l-1,温度为48℃时,其速率常数
k=0.0193min-1。今有体积均为2L,浓度分别为0.200mol·l-1和0.400mol·l-
dc蔗糖 dt
kc水c蔗糖
k种反应物而使反应降为一 级的反应称为准一级反应
1850年Wilhelmy在历史上第一次用旋光仪测定酸催化蔗 糖水解反应,并建立上述速率方程,它是化学动力学中最早经 过定量研究的一个反应
例题:二甲醚的气相分解反应是一级反应
ln cA ~ t呈线性关系,直线斜率为-k k的单位:时间1 半衰期:t1/2 ln 2 / k
(3)应用举例
反应物的浓度随时间呈指数性衰 减。只有当t=∞时,才有cA=0, 即从理论上说一级反应需要无穷 长的时间才能完成
一级反应半衰期与起始浓度无关
放射性元素的蜕变是一级反应。在放射化学中,蜕变速率总是用半
v2 kcA0,2 0.0193min1 0.400mol l1 0.0772mol l1 min1
运动方程、速度

物理学中,把式这样的方程称为质点的运动方程
。其中x(t)、y(t)和z(t)是质点运动方程在坐标轴上 的分量式函数,从中消去参数t便可得到质点运动 的轨迹方程。例如质点平抛运动的运动方程为
x v0t y 1 gt 2
2
消去t得质点轨迹运动方程为
y
g 2v02
x2
4.速度
速度是描述质点运动快慢和方向的物理量。
对于曲线运动:加速度的方向和速度的方向不一 定相同,当两者成锐角时,速率增加;成钝角时, 速率减小;成直角时,速率不变。加速度的方向 总是指向曲线凹的一方,如图所示。
(2)加速度具有瞬时性:运动质点在不同时刻的加 速度可以不同。
(3)加速度具有相对性:在不同的参照系中,同一 质点的加速度可以不同。
注:对加速度概念说明 (1)加速度是矢量,既有大小又有方向,二者
只要有一个变化,加速度就变化;当a=恒量, 物体做匀变速运动;当a不等于恒量,物体做非 匀变速运动。对于直线运动:当物体做加速运 动时,物体加速度方向与速度的方向相同;当 物体做减速运动时,物体加速度方向与速度方 向相反。注意,并不是说加速度为正就是加速 运动,加速度为负就是减速运动。因为加速度 的正负与坐标系坐标轴的方向选择有关。
平均速率,用v表示,即 v
s
t
当t 0时,平均速率的极限值称为质点的瞬时速 率,简称速率,用v表示,即
lim v
s ds
t0 t dt
注:
1.对速度概念的说明
①速度是矢量,既有大小又有方向,二者只要 有—个变化,速度就变化;
②速度具有瞬时性,运动质点在不同时刻的速 度是不同的(匀速直线运动除外);
(4)在SI制中,加速度的单位:m/s2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢erlet算法
速度Verlet算法
Velocity-Verlet算法不仅可以获得相同精度的原 子位置和速度量,给出了显式的速度项,而且在 每步积分中只需要存储一个时刻的状态变量,模 拟稳定性好,允许采用较大的时间步长,计算量 适中,因而在分子动力学方程的积分算法中得到 了最广泛的应用。
正加速度ac(t+ t)。定义预测误差
❖第三步根据加速度的预测误差对各预测量进行修 正:
Gear预测校正法
• 预测-校正法允许的时间步长比其它算法 长两倍以上
• 每个积分步内要计算两次体系势能,以得 到原子间相互作用力。
• 该算法的稳定差,能量波动较大,较verlet 算法占用更多的内存。
时间步长
不存在
MD模拟所研究的所有体系,体系的轨迹穿过相空
间(即对于用由所有粒子坐标和动量所跨过的6N维
空间)时敏感地依赖于初始条件。
这意味着两个初始靠得很近的轨迹随时间的演绎
将会显著分开。
李雅普诺夫不稳定性
MD获得的轨迹在某种意义上与真实的轨迹相接近。 MD的目标并不是精确地预测一个已知初始条件的体系轨迹将会发生什么(卫 星轨道预测)。而对统计预测感兴趣。在MD中,统计预测是足够精确的。
二阶对称算子
➢可以看出原子应力具有“能量密度”的量纲。 ➢包括了原子动量流和原子间作用力的贡献。 ➢是原子的一种力学“活性能”,反应了原子产生运动的潜在能 力。
原子应力
Voronoi几何构形的数学描述
原子应力
Lammps原子应力的定义
原子对势相互作用
原子键作用
键角作用
面弯曲作用
约束作用
二面角作用
节省内 存??
能量守 恒??
积分运动方程的注意点
要想获得允许使用长时间步的算法,必须将 信息存储在粒子坐标的较高阶导数中。结果 是这需要更多的内存。对于一个通常的模拟 来说,这并不是一个严重的缺点。因为除非 处理很大的体系,存储这些导数所需的内存 与即便是在一个通常的工作站上所能获取的 总量相比来说仍是很小。
• 一般来说,在探讨其力学行为时,我们需要研究 一些宏观力学概念的物理量,比如温度、能量、 压强、应力状态等,这就需要我们对分子动力学 计算出来的粒子数据进行分析。
• 统计力学是连接微观层次的物理量和宏观概念物 理量的桥梁,利用统计力学原理我们可以从系统 中单个粒子的运动学状态得到整个粒子系统的一 些性质。
RMS (Reservoir Modeling System保守系统的模拟) Energy deviation
(log/log scale)
时间步长
• 时间步长与研究对象、系统温度、所采用 的数值积分算法及势能函数有关。不存在 一个通用的时间步长值。
• 一般情况下,体系的温度越低,允许采用 的时间步长越大;而模拟较高温度时必须 采取较小的时间步长。
标准Verlet算法
• Verlet提出的Verlet算法在分子动力学中 应用最为广泛。
由Taylor公式展开有:
+
位移
标准Verlet算法
由Taylor公式展开有:
-
速度
不出现在 算法中。
在典型分子动力学模拟中,只有原子的初始位置和初 始速度是给定的,而在verlet算法中,计算下一步的 原子的位置需要前两步的信息。
能量守恒是一个重要的判据,但实际上需要 区分两种能量守恒,即短时间的和长时间的。 复杂的高阶算法通常在短时间内(如在几个 时间步内)有很好的能量守恒性,然而该方 法通常会有所不期望的特征,即时间较长时 总能量漂移。(不一定最好)
积分运动方程的注意点
最好有一个算法能同时在短时间和长时间准确地预
测所有粒子的轨迹。
• 一般认为,时间步长应小于原子振动周期 的十分之一,而通常原子振动周期的数量 级为0.1皮秒(10-12s),即时间步长应选择在 飞秒级(10-15s)。
宏观物理量的计算
• 分子 动 力 学计算最终得到的是系统各个时刻的 相空间轨道(the phase-space trajectory),包括任 意时刻所有原子的坐标和速度,这些都是微观原 子层次的物理量。
第四讲 运动方程的积分算法
黄敏生
积分运动方程的注意点
• 何为一个好的运动方程积分算法?
计算速 度??
但这并不是很贴切,因为花在积分运动方程上 的时间分率(相对于计算相互作用来说)很小, 至少对原子或简单分子体系是这样。
准确度对较大的时间步长来说更重要, 因为所能使用的时间步长越长,单位时 间内力的计算量越少。因此,这意味着 准确度?? 采用允许用长时间步长的成熟算法是有 利的。(然而,保证准确度,不允许发 散)
的定义方式
原子应力
宏观应力
反映了单位面积上作用力的 大小,是关于面积的强度量。
原子应力
离散原子系统的原子应力是 关于体积的强度量。实际上, 原子应力只是形式地沿用了 应力的概念,具有与宏观应 力完全不同的特征。
原子 应 力 表明一个原子与周围原子相互作用的强弱程度
原子应力
动量 势能
Hamilton 自由能
Too short - computation needlessly slow Too long - errors result from approximations
Just right - errors acceptable, maximum speed
时间步长
过长的时间步
时间步长过大,原子的作用 力急剧改变。 误差逐渐累计,导致结果发 散.
两个 Argon (氩)原子 在两个不同时间步长 ts的模拟。 图中画出的是计算模拟值与理论值的差。
误差与时间步长的关系
Circles: Verlet Squares: Gear 4th order Triangles: Gear 5th order Diamonds: Gear 6th order
计算 不 同 热力学状态的总能E和温度,可以得到内 能一温度曲线E(T )。这对于监测相变的发生非常有 用,相变发生时,该曲线会有跳跃。
原子应变
• 应变 是 表 示物体变形大小的测度,可以 有不同的定义方式。
• 应变是一个相对量,反映了物体相对初始 构型的变形程度。
• 应变又是纯几何量,与空间尺度变化无关。 • 因此宏观、纳观尺度下应变可以采用相同
Gear预测校正法
预测校正法是分子动力学模拟中的常用算法之一, 其基本思想是Taylor展开,这种算法包含三个部 分。 第一步,利用泰勒展开预测下一时刻的位置及其一 阶、二阶、三阶导数:
式中v、a、b、c分别是位置矢量r的一阶、二阶、三阶和四阶导数。
Gear预测校正法
❖第二步根据新的原子位子rp,计算受力以及修
Lammps中原子应力没有除于体 积,是能量的量纲。(e.v)
原子应力
原子应力与宏观应力的关系
Lammps中原子应力
• 宏观应力实际上是原子应力在一定程度上的统计平均。 • 如果要计算体系中某个区域(由region定义,可以是整个
模拟盒)所围成的“块”的应力,在Lammps只需将该区 域里的所有原子的单原子应力值加起来,再除以这个区域 的体积即可,无须进行单个原子体积的计算。
那么如何采用verlet算法计算第二个时间步的原子位 置呢?
标准Verlet算法
• 解决方法一是,在第二个时间步中,把该 步力看成常量,且使用普通运动学方程:
ri (t) ri (0) ri (0)t
• 解决方法二是
• 流程
标准Verlet算法
标准Verlet算法
加速度项
Leap-frog算法
• 对标准Verlet算法进行改进而得到的蛙跳 算 法 (Leapfrog methods) 。 相 比 标 准 Verlet算法,它有两个优点。
• 一、包含显式速度项。 • 二、计算量稍小。 • 缺点
原子的位置与速度计算不同步,这就意 味着在确定位置时,不能同时计算体系的 动能,给模拟过程带来不便。
宏观物理量的计算
• 系统 的 物 理性质是系统中粒子坐标和速度 的函数,对于任意一个时刻宏观概念物理 量A,定义为
统计平均
宏观物理量的计算
能量
• 势能 部 分 可以按势函数计算,对于不同的原子势函数表 达式有不同的计算公式。
• 动 能计 算 公式为
温度
温度T直接与粒子动能相关,即著名的均匀分
布公式,每个自由度赋予kBT/2的能量, N个 粒子的总自由度为3N,故动能为
