三角函数诱导公式一览表(打印)
数学三角函数诱导公式大全

数学三角函数诱导公式大全(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用资料,如小学资料、初中资料、高中资料、大学资料、文言文、中考资料、高考资料、近义词、反义词、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this store provides you with various types of practical materials, such as primary school materials, junior high school materials, senior high school materials, university materials, classical Chinese, senior high school examination materials, college entrance examination materials, synonyms, antonyms, other materials, etc. If you want to know different data formats and writing methods, please pay attention!数学三角函数诱导公式大全三角函数是数学考试中一个很重要的知识点,学好三角函数要牢记公式,下面整理了三角函数诱导公式,希望能帮助到大家。
完整版)三角函数诱导公式总结

完整版)三角函数诱导公式总结三角函数诱导公式与同角的三角函数知识点1】诱导公式及其应用诱导公式是指通过一些特定的公式,将三角函数中的某些角度转化为其他角度,从而简化计算。
以下是常用的诱导公式:公式一:sin(-α) = -sinα;cos(-α) = cosα;tan(-α) = -tanα公式二:sin(π+α) = -sinα;cos(π+α) = -cosα;tan(π+α) =tanα公式三:sin(π-α) = sinα;cos(π-α) = -cosα;tan(π-α) = -tanα公式四:sin(2π-α) = -sinα;cos(2π-α) = cosα;tan(2π-α) = -tanα公式五:sin(π/2-α) = cosα;cos(π/2-α) = sinα公式六:sin(π/2+α) = cosα;cos(π/2+α) = -sinα公式七:sin(-π/2-α) = -cosα;cos(-π/2-α) = -sinα公式八:sin(-π/2+α) = -cosα;cos(-π/2+α) = sinα公式九:sin(α+2kπ) = sinα;cos(α+2kπ) = cosα;tan(α+2kπ) = tanα(其中k∈Z)。
以上公式可以总结为两条规律:1.前四组诱导公式可以概括为:函数名不变,符号看象限。
2.公式五到公式八总结为一句话:函数名改变,符号看象限(原函数所在象限)。
另外,还有一个规律是:奇变偶不变,符号看象限。
也就是说,将三角函数的角度全部化成kπ/2+α或是kπ/2-α的形式,如果k是奇数,那么符号要改变;如果k是偶数,符号不变。
例1、求值:(1)cos(2916π)= ________;(2)tan(-855)= ________;(3)sin(-π)= ________。
例2、已知tan(π+α)=3,求:(2cos(-α)-3sin(π+α))/(4cos(-α)+sin(2π-α))的值。
(完整版)三角函数诱导公式大全
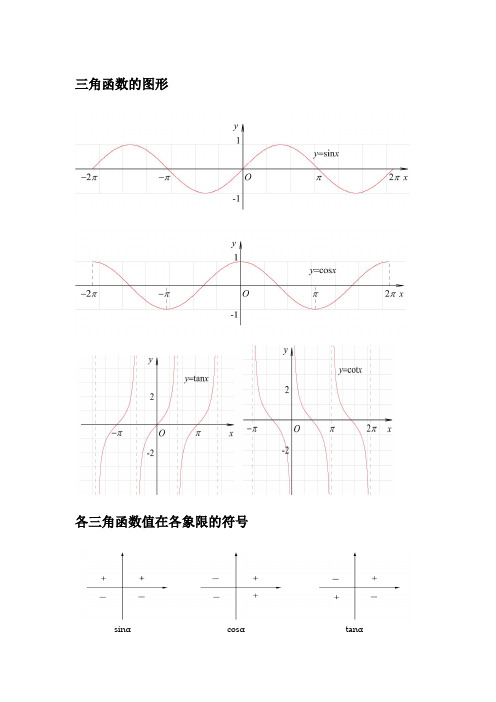
三角函数的图形各三角函数值在各象限的符号sinαcosαtanα三角函数的性质函数y=sinx y=cosx y=tanx定义域R R {x|x∈R且x≠kπ+,k∈Z}2π值域[-1,1]x=2kπ+时2πy max=1x=2kπ-时y min=-12π[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值周期性周期为2π周期为2π周期为π奇偶性奇函数偶函数奇函数单调性在[2kπ-,2kπ+]2π2π上都是增函数;在[2kπ+2π,2kπ+π]上都是减函32数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-,kπ+)2π2π内都是增函数(k∈Z)特殊角的三角函数值表诱导公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα cos (π-α)= -cosα tan (π-α)= -tanα cot (π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα公式六±α及±α与α的三角函数值之间的关系: 2π23πsin (+α)= cosα 2πcos (+α)= -sinα 2πtan (+α)= -cotα 2πcot (+α)= -tanα 2πsin (-α)= cosα2πcos (-α)= sinα 2πtan (-α)= cotα 2πcot (-α)= tanα2πsin (+α)= -cosα23πcos (+α)= sinα23πtan (+α)= -cotα23π3πcot(+α)= -tanα23πsin(-α)= -cosα23πcos(-α)= -sinα23πtan(-α)= cotα23πcot(-α)= tanα2(以上k∈Z)。
三角函数诱导公式大全表格
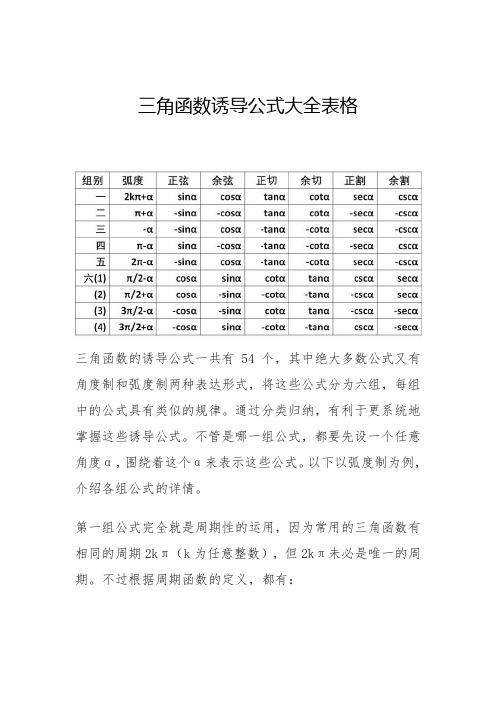
三角函数诱导公式大全表格三角函数的诱导公式一共有54个,其中绝大多数公式又有角度制和弧度制两种表达形式,将这些公式分为六组,每组中的公式具有类似的规律。
通过分类归纳,有利于更系统地掌握这些诱导公式。
不管是哪一组公式,都要先设一个任意角度α,围绕着这个α来表示这些公式。
以下以弧度制为例,介绍各组公式的详情。
第一组公式完全就是周期性的运用,因为常用的三角函数有相同的周期2kπ(k为任意整数),但2kπ未必是唯一的周期。
不过根据周期函数的定义,都有:sin(2kπ+α)=sinα;cos(2kπ+α)=cosα;tan(2kπ+α)=tanα;cot(2kπ+α)=cotα;sec(2kπ+α)=secα;csc(2kπ+α)=cscα。
(k∈Z)第二组公式是π+α的三角函数值与α的三角函数值之间的关系。
一方面正切和余切都以π为最小正周期,所以tan(π+α)=tanα;cot(π+α)=cotα。
另一方面由正弦函数和余弦函数的定义公式,以及它们在坐标平面上的意义,可以推知sin(π+α)=-sinα;cos(π+α)=-cosα,又由正割与余弦的互为倒数关系,以及余割与正弦的互为倒数关系,就可以知道sec(π+α)=-secα;csc(π+α)=-cscα。
在几何意义上,第二组公式表示终边形成平角的两个角的三角函数关系。
第三组公式是互为相反的两个角的三角函数值的关系。
由正弦、正切、余切和余割的奇函数性质,以及余弦、正割的偶函数性质,有:sin(-α)=-sinα;cos(-α)=cosα;tan(-α)=-tanα;cot(-α)=-cotα;sec(-α)=secα;csc(-α)=-cscα.在几何意义上,第三组公式表示终边关于始边对称的两个角的三角函数关系。
第四组公式是π-α和α的三角函数值之间的关系,由第三组公式结合第二组公式推得,即:sin(π-α)=sinα;cos(π-α)=-cosα;tan(π-α)=-tan α;cot(π-α)=-cotα;sec(π-α)=-secα;csc(π-α)=cscα.在几何意义上,第四组公式表示互补的两个角的三角函数关系。
三角函数值诱导公式对应表 三角函数图像表格

sin( 2k ) sin
② .公式(二) : 与
; cos( 2k ) cos
; tan( 2k ) tan
sin sin
③ .公式(三) : 与
; cos cos ; cos cos
;tan ( 2 − ������) =
������
性
函 质
数
y sin x
y cos x
y tan x
图 像
定 义 域 值 域
R
R
x x k , k Z 2
R
1,1
当 x 2 k
1,1
k Z
当 x 2k k Z 时,
; tan tan ; tan tan
sin sin
④ .公式(四) : 与
sin sin
⑤ .公式(五) : 与
; cos cos
; tan tan
2
最 值
时, ymax 1 ; 当 x 2 k
2
k Z
ymax 1 ;当 x 2k
既无最大值也无最小值
时, ymin 1 . 周 期 性 奇 偶 性 在 单 调 性
k Z 时, ymin 1 .
2
2
奇函数
偶函数
奇函数
2k , 2k 2 2
无对称轴
2
; cos
sin cos 2
⑥ .公式(六) : 与
三角函数的诱导公式(精品)

π 5 − cosα 公式 − sin 2 + α
式 公 2
3π sin ( +α) = −cosα 2 诱导公式的变形 诱导公式的变形 3π cos( +α) = sinα 2
公式回顾和总结 sin π −α) = sinα ( cos(π −α) = −cosα tan π −α) = −tanα ( sin(2π −α) = −sinα cos(2π −α) = cosα tan(2π −α) = −tanα
cosα
π
式 公 5
π sin − α 2
sin +α) = cosα ( 2 cos( +α) = −sinα 2
π
诱导公式( 诱导公式(六) 公式
π 3π − α = sin π + − α 因为 sin 2 2
共同点: 共同点: 函数名改变,符号与前面值的正负一至. 函数名改变,符号与前面值的正负一至. 前面值的正负一至
π
π
π
π
记忆方法: ※记忆方法: 奇变偶不变,符号看象限. 奇变偶不变,符号看象限.
说明: 说明:
偶 的 k 奇 性 奇 指 是 中的 偶 ; 2 符 指 是 面 角数 符 ( 象 决 ) 号 的 前 三 函的 号 由 限 定
正弦正切为奇函数、余弦为偶函数!!! 正弦正切为奇函数、余弦为偶函数!!!
因为
sin( −α ) = sin(2π + (− α )) cos( −α ) = cos(2π + (− α )) tan( −α ) = tan(2π + (− α ))
所以
sin 2π −α) = −sinα ( cos(2π −α) = cosα tan 2π −α) = −tanα (
三角函数的诱导公式【六公式】

)/ )
九倍角
sin9A=(sinA*(-3+4*sinA^2 )* ( 64*sinA^6-96*sinA^4+36*sinA^2-3 ))
cos9A=(cosA*(-3+4*cosA^2 )* ( 64*cosA^6-96*cosA^4+36*cosA^2-3 ))
tan9A=tanA* ( 9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8 ) / (1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8 )
例. c^3=c*c^2=c* (1-s^2 ), c^5=c*(c^2 ) ^2=c* ( 1-s^2 ) ^2 )
特殊公式
(sina+sin θ) * ( sina- sin θ) =sin (a+θ) *sin ( a- θ)
证明:(sina+sin θ) *( sina- sin θ) =2 sin[ (θ +a)/2] cos[(a - θ)/2] *2 cos[ (θ +a)/2] sin[(a- θ) /2]
tan (α +β+γ) =(tan α+tan β+tan γ - tan α· tan β· tan γ) / (1- tan α· tan β - tan β· tan γ - tan α· tan γ)
(α +β+γ≠π /2+2k π,α、β、γ≠π /2+2k π)
积化和差的四个公式
sina*cosb=(sin(a+b)+sin(a-b))/2
cosa*sinb=(sin(a+b)-sin(a-b))/2
(完整word)三角函数诱导公式大全,推荐文档

三角函數誘導公式大全三角函数诱导公式常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为:对于k·π/2±α(k∈Z)的个三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)例如:sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
1.3 三角函数的诱导公式

诱导公式(一)
sin( k 360 ) sin
sin( 2k ) sin
cos( k 360 ) cos cos( 2k ) cos tan( k 360 ) tan tan( 2k ) tan 其中 k Z
公式四
公式一~公式六叫做诱导公式
诱导公式记忆口诀 :
奇变偶不变,符号看象限.
说明:
奇偶指的是k 中k的奇偶性; 2 符号指的是化简后三角函数的符号(由已知角的象限决定)
作用: k Z)的三角函数值 k (
2 1 )当k为偶数时ห้องสมุดไป่ตู้等于的同名三角函数值,前面加上 一个把 看作锐角时原三角函数值的符号; 2)当k为奇数时,等于的异名三角函数值,前面加上 一个把 看作锐角时原三角函数值的符号;
3
小结
三角函数的诱导公式
sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα
sin cos , 2 cos sin . 2
cos 2
sin
例4 化简
11 sin 2 cos cos cos 2 2 . 9 cos sin 3 sin sin 2
其中 k Z
实质:终边相同,三角函数值相等
高中三角函数公式大全表格诱导公式

高中三角函数公式大全表格诱导公式高中三角函数公式大全表格包括以下内容:三角函数的基本关系:sinθ = cos(90°- θ)cosθ = sin(90°- θ)tanθ = 1/tan(90°- θ)cotθ = 1/tanθ三角函数的反三角函数:sin^-1x = cos^-1(√(1-x^2))cos^-1x = sin^-1(√(1-x^2))tan^-1x = sin^-1(x/√(1+x^2))cot^-1x = cos^-1(1/x)三角函数的和差公式:sin(α±β) = sinαcosβ±cosαsinβcos(α±β) = cosαcosβ±sinαsinβtan(α±β) = (tanα±tanβ)/(1±tanαtanβ)三角函数的乘除公式:sinαcosβ = (sinαcosβ+cosαsinβ)/2cosαcosβ = (cosαcosβ-sinαsinβ)/2sinα/cosα = tanαcosα/sinα = cotα三角函数的二倍角公式:sin2α = 2sinαcosαcos2α = cos^2α-sin^2αtan2α = (2tanα)/(1-tan^2α)三角函数的诱导公式:sin(nx) = ∑(n为奇数时) (-1)^((n-1)/2)(x^n)/(n!)cos(nx) = ∑(n为偶数时) (-1)^(n/2)(x^n)/(n!)这些公式在学习三角函数时是非常重要的,帮助我们更好地理解和应用三角函数。
诱导公式是一类重要的公式,它可以通过对三角函数的递推来证明。
这些公式可以用来求解三角函数的高阶导数,进而应用到微积分和数学物理中。
三角形诱导公式

三角形诱导公式诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
诱导公式有六组,共54个。
定义常用的诱导公式有以下六组:公式一终边相同的角的同一三角函数的值相等。
设α为任意锐角,弧度制下的角的表示:角度制下的角的表示:sin (α+k·360°)=sinα(k∈Z).cos(α+k·360°)=cosα(k∈Z).tan (α+k·360°)=tanα(k∈Z).cot(α+k·360°)=cotα (k∈Z).sec(α+k·360°)=secα (k∈Z).csc(α+k·360°)=cscα (k∈Z).公式二π+α的三角函数值与α的三角函数值之间的关系。
设α为任意角,弧度制下的角的表示:sin(π+α)=-sinα.cos(π+α)=-cosα.tan(π+α)=tanα.cot(π+α)=cotα.sec(π+α)=-secα.csc(π+α)=-cscα.角度制下的角的表示:sin(180°+α)=-sinα.tan(180°+α)=tanα.cot(180°+α)=cotα.sec(180°+α)=-secα.csc(180°+α)=-cscα.[1]公式三任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinα.cos(-α)=cosα.tan(-α)=-tanα.cot(-α)=-cotα.sec(-α)=secα.csc (-α)=-cscα.公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:弧度制下的角的表示:sin(π-α)=sinα.cos(π-α)=-cosα.tan(π-α)=-tanα.cot(π-α)=-cotα.sec(π-α)=-secα.csc(π-α)=cscα.角度制下的角的表示:sin(180°-α)=sinα.cos(180°-α)=-cosα.tan(180°-α)=-tanα.sec(180°-α)=-secα.csc(180°-α)=cscα.[1]公式五利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:弧度制下的角的表示:sin(2π-α)=-sinα.cos(2π-α)=cosα.tan(2π-α)=-tanα.cot(2π-α)=-cotα.sec(2π-α)=secα.csc(2π-α)=-cscα.角度制下的角的表示:sin(360°-α)=-sinα.cos(360°-α)=cosα.tan(360°-α)=-tanα.cot(360°-α)=-cotα.sec(360°-α)=secα.csc(360°-α)=-cscα.[1]公式六π/2±α 及3π/2±α与α的三角函数值之间的关系:(⒈~⒋)⒈π/2+α与α的三角函数值之间的关系弧度制下的角的表示:sin(π/2+α)=cosα.cos(π/2+α)=-sinα.tan(π/2+α)=-cotα.sec(π/2+α)=-cscα.csc(π/2+α)=secα.[2]角度制下的角的表示:sin(90°+α)=cosα.cos(90°+α)=-sinα.tan(90°+α)=-cotα.cot(90°+α)=-tanα.sec(90°+α)=-cscα.csc(90°+α)=secα.[2]⒉π/2-α与α的三角函数值之间的关系弧度制下的角的表示:sin(π/2-α)=cosα.cos(π/2-α)=sinα.tan(π/2-α)=cotα.cot(π/2-α)=tanα.sec(π/2-α)=cscα.csc(π/2-α)=secα.角度制下的角的表示:sin (90°-α)=cosα.cos (90°-α)=sinα.tan (90°-α)=cotα.cot (90°-α)=tanα.sec (90°-α)=cscα.csc (90°-α)=secα.⒊3π/2+α与α的三角函数值之间的关系弧度制下的角的表示:cos(3π/2+α)=sinα.tan(3π/2+α)=-cotα.cot(3π/2+α)=-tanα.sec(3π/2+α)=cscα.csc(3π/2+α)=-secα.[2]角度制下的角的表示:sin(270°+α)=-cosα.cos(270°+α)=sinα.tan(270°+α)=-cotα.cot(270°+α)=-tanα.sec(270°+α)=cscα.csc(270°+α)=-secα.[2]⒋3π/2-α与α的三角函数值之间的关系弧度制下的角的表示:sin(3π/2-α)=-cosα.cos(3π/2-α)=-sinα.tan(3π/2-α)=cotα.cot(3π/2-α)=tanα.sec(3π/2-α)=-cscα.csc(3π/2-α)=-secα.角度制下的角的表示:sin(270°-α)=-cosα.cos(270°-α)=-sinα.tan(270°-α)=cotα.cot(270°-α)=tanα.sec(270°-α)=-cscα.。
三角函数诱导公式一览表

三角函数诱导公式一览表公式一:设α为任意角,终边相同的角的同一三角函数的值相等:1、sin(2kπ+α)=sinα2、cos(2kπ+α)=cosα3、tan(2kπ+α)=tanα4、cot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:1、sin(π+α)=-sinα2、cos(π+α)=-cosα3、tan(π+α)=tanα4、cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:1、sin(-α)=-sinα2、cos(-α)=cosα3、tan(-α)=-tanα4、cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:1、sin(π-α)=sinα2、cos(π-α)=-cosα3、tan(π-α)=-tanα4、cot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:1、sin(2π-α)=-sinα2、cos(2π-α)=cosα3、tan(2π-α)=-tanα4、cot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:1、sin(π/2+α)=cosα2、cos(π/2+α)=-sinα3、tan(π/2+α)=-cotα4、cot(π/2+α)=-tanα5、sin(π/2-α)=cosα6、cos(π/2-α)=sinα7、tan(π/2-α)=cotα8、cot(π/2-α)=tanα公式七:3π/2±α与α的三角函数值之间的关系:1、sin(3π/2+α)=-cosα2、cos(3π/2+α)=sinα3、tan(3π/2+α)=-cotα4、cot(3π/2+α)=-tanα5、sin(3π/2-α)=-cosα6、cos(3π/2-α)=-sinα7、tan(3π/2-α)=cotα8、cot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
三角函数诱导公式

三角函数诱导公式一.三角函数诱导公式公式一设α为任意角,终边相同的角的同一三角函数的值相等:对于x轴正半轴为起点轴而言弧度制下的角的表示:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)sec(2kπ+α)=secα(k∈Z)csc(2kπ+α)=cscα(k∈Z)角度制下的角的表示:sin (α+k²360°)=sinα(k∈Z)cos(α+k²360°)=cosα(k∈Z)tan (α+k²360°)=tanα(k∈Z)cot(α+k²360°)=cotα(k∈Z)sec(α+k²360°)=secα(k∈Z)csc(α+k²360°)=cscα(k∈Z公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:对于x轴负半轴为起点轴而言弧度制下的角的表示:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsec(π+α)=-secαcsc(π+α)=-cscα角度制下的角的表示:sin(180°+α)=-sinαcos(180°+α)=-cosαtan(180°+α)=tanαcot(180°+α)=cotαsec(180°+α)=-secαcsc(180°+α)=-cscα公式三任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsec(-α)=secαcsc (-α)=-cscα[3]公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:弧度制下的角的表示:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsec(π-α)=-secαcsc(π-α)=cscα角度制下的角的表示:sin(180°-α)=sinαcos(180°-α)=-cosαtan(180°-α)=-tanαcot(180°-α)=-cotαsec(180°-α)=-secαcsc(180°-α)=cscα[3]公式五利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:弧度制下的角的表示:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsec(2π-α)=secαcsc(2π-α)=-cscα角度制下的角的表示:sin(360°-α)=-sinαcos(360°-α)=cosαtan(360°-α)=-tanαcot(360°-α)=-cotαsec(360°-α)=secαcsc(360°-α)=-cscα[3]公式六π/2±α及3π/2±α与α的三角函数值之间的关系:(⒈~⒋)⒈ π/2+α与α的三角函数值之间的关系弧度制下的角的表示:sin(π/2+α)=cosαcos(π/2+α)=—sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsec(π/2+α)=-cscαcsc(π/2+α)=secα角度制下的角的表示:sin(90°+α)=cosαcos(90°+α)=-sinαtan(90°+α)=-cotαcot(90°+α)=-tanαsec(90°+α)=-cscαcsc(90°+α)=secα[3]⒉ π/2-α与α的三角函数值之间的关系弧度制下的角的表示:sin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsec(π/2-α)=cscαcsc(π/2-α)=secα角度制下的角的表示:sin (90°-α)=cosαcos (90°-α)=sinαtan (90°-α)=cotαcot (90°-α)=tanαsec (90°-α)=cscαcsc (90°-α)=secα[3]⒊ 3π/2+α与α的三角函数值之间的关系弧度制下的角的表示:sin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsec(3π/2+α)=cscαcsc(3π/2+α)=-secα角度制下的角的表示:sin(270°+α)=-cosαcos(270°+α)=sinαtan(270°+α)=-cotαcot(270°+α)=-tanαsec(270°+α)=cscαcsc(270°+α)=-secα[3]⒋ 3π/2-α与α的三角函数值之间的关系[1-2]弧度制下的角的表示:sin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsec(3π/2-α)=-cscαcsc(3π/2-α)=-secα角度制下的角的表示:sin(270°-α)=-cosαcos(270°-α)=-sinαtan(270°-α)=cotαcot(270°-α)=tanαsec(270°-α)=-cscαcsc(270°-α)=-secα规律公式一到公式五函数名未改变,公式六函数名发生改变。
诱导公式总结大全

诱导公式1所谓三角函数诱导公式,就就是将角n·(π/2)±α得三角函数转化为角α得三角函数。
公式一: 设α为任意角,终边相同得角得同一三角函数得值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二: 设α为任意角,π+α得三角函数值与α得三角函数值之间得关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三: 任意角α与 -α得三角函数值之间得关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四: 利用公式二与公式三可以得到π-α与α得三角函数值之间得关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五: 利用公式一与公式三可以得到2π-α与α得三角函数值之间得关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六: π/2±α与α得三角函数值之间得关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀奇变偶不变,符号瞧象限。
“奇、偶”指得就是整数n得奇偶,“变与不变”指得就是三角函数得名称得变化:“变”就是指正弦变余弦,正切变余切。
(反之亦然成立)“符号瞧象限”得含义就是:把角α瞧做锐角,不考虑α角所在象限,瞧n·(π/2)±α就是第几象限角,从而得到等式右边就是正号还就是负号。
一全正;二正弦;三两切;四余弦这十二字口诀得意思就就是说: 第一象限内任何一个角得四种三角函数值都就是“+”; 第二象限内只有正弦就是“+”,其余全部就是“-”; 第三象限内只有正切与余切就是“+”,其余全部就是“-”; 第四象限内只有余弦就是“+”,其余全部就是“-”。
(word完整版)三角函数诱导公式一览表

三角函数诱导公式一览表公式一:设α为任意角,终边相同的角的同一三角函数的值相等:1、sin(2kπ+α)=sinα2、cos(2kπ+α)=cosα3、tan(2kπ+α)=tanα4、cot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:1、sin(π+α)=-sinα 2、cos(π+α)=-cosα3、tan(π+α)=tanα4、cot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:1、sin(-α)=-sinα2、cos(-α)=cosα3、tan(-α)=-tanα4、cot(-α)=-cotα公式四:利用公式二和公式三可以得到π—α与α的三角函数值之间的关系: 1、sin(π-α)=sinα 2、cos(π-α)=-cosα3、tan(π-α)=-tanα4、cot(π-α)=-cotα公式五: 利用公式一和公式三可以得到2π—α与α的三角函数值之间的关系:1、sin(2π-α)=-sinα 2、cos(2π-α)=cosα3、tan(2π-α)=-tanα4、cot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:1、sin(π/2+α)=cosα2、cos(π/2+α)=-sinα3、tan(π/2+α)=-cotα4、cot(π/2+α)=-tanα5、sin(π/2-α)=cosα6、cos(π/2-α)=sinα7、tan(π/2-α)=cotα 8、cot(π/2-α)=tanα公式七:3π/2±α与α的三角函数值之间的关系:1、sin(3π/2+α)=-cosα2、cos(3π/2+α)=sinα3、tan(3π/2+α)=-cotα4、cot(3π/2+α)=-tanα5、sin(3π/2-α)=-cosα6、cos(3π/2-α)=-sinα7、tan(3π/2-α)=cotα 8、cot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
三角函数 高中数学诱导公式大全

常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα (k∈Z)cos(2kπ+α)=cosα (k∈Z)tan(2kπ+α)=tanα (k∈Z)cot(2kπ+α)=cotα (k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)注意:在做题时,将a看成锐角来做会比拟好做。
诱导公式记忆口诀规律总结上面这些诱导公式可以概括为:对于π/2xk ±α(k∈Z)的三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
.
三角函数有关诱导公式一览表
公式
)
(
tan
)
2
tan(
cos
)
2
cos(
sin
)
2
sin(
.1Z
k
k
k
k
∈
⎪
⎩
⎪
⎨
⎧
=
+
=
+
=
+
α
α
π
α
α
π
α
α
π
⎪
⎩
⎪
⎨
⎧
=
+
-
=
+
-
=
+
α
α
π
α
α
π
α
α
π
tan
)
tan(
cos
)
cos(
sin
)
sin(
.2
⎪
⎩
⎪
⎨
⎧
-
=
-
=
-
-
=
-
α
α
α
α
α
α
tan
)
tan(
cos
)
cos(
sin
)
sin(
.3
⎪
⎩
⎪
⎨
⎧
-
=
-
-
=
-
=
-
α
α
π
α
α
π
α
α
π
tan
)
tan(
cos
)
cos(
sin
)
sin(
.4
⎪
⎩
⎪
⎨
⎧
=
-
=
-
α
α
π
α
α
π
sin
)
2
cos(
cos
)
2
(
sin
.5
⎪
⎩
⎪
⎨
⎧
-
=
+
=
+
α
α
π
α
α
π
sin
)
2
cos(
cos
)
2
(
sin
.6
⎪
⎩
⎪
⎨
⎧
-
=
-
-
=
-
α
α
π
α
α
π
sin
)
2
3
cos(
cos
)
2
3
(
sin
.7
口诀函数名不变,符号看象限函数名改变,符号看先象限
图形
简记结合图形,7组公式可用口诀概括为:“奇变偶不变,符号看象限”说明
①公式的推导思路:前面4组通过找角的终边
位置关系—坐标关系—三角函数关系而得
出(后面3组通过角的变换,进而借助前面
的有关公式转化得到)
②各组诱导公式都可用含角度的形式
③在应用诱导公式解题时,基本思路是:
“负化正,大化小,化成锐角再求值”。
一定要记清特殊角的三角函数值,根据问题做到准确应用,正确求解。
