超分辨荧光显微技术原理
超分辨显微镜的工作原理和应用

超分辨显微镜的工作原理和应用随着科技的飞速发展,人们对于微小的物体的研究越来越深入。
在过去,显微镜可以提供的最高分辨率为200nm左右,然而很多细胞和物质需要更高的分辨率才能被准确的研究。
超分辨显微镜(deconvolution microscopy)因而被应运而生,它的分辨率可以达到20nm以下,是传统显微镜的10倍以上。
下面,本文将为你介绍超分辨显微镜的工作原理和应用。
一、超分辨显微镜的工作原理超分辨显微镜的工作原理是使样品产生的荧光分子处于暗区域退回到明亮区域,通过这种方法,显微镜能够获取比传统显微镜更清晰的图像。
在超分辨显微镜之前,由于空气折射率的限制,显微镜无法将细胞成像到更高的分辨率。
超分辨显微镜通过不同的方法打破了这个技术障碍。
例如,受到今天最先进的高清电视和摄像机技术的启发,超分辨显微镜使用一种称为激发的荧光分子反转的技术(Stimulated Emission Depletion,简称STED)来实现高分辨率显微成像。
基本上,STED方法是通过在激光束之间使用减少荧光过程的抵消光束来使荧光分子处于暗区域"退回"到明亮区域的。
荧光物质只能在光束中的明亮区域发光,当光束聚焦到小于荧光分子的空间大小时,荧光分子会产生干扰,使得分辨率变得模糊。
为了解决这个问题,STED技术增加了所有光束之间的强烈相互作用,目的是将荧光分子拉回到它们本应该出现的明亮区域。
这使得STED显微镜能够放大高达20nm以下的样品。
二、超分辨显微镜的应用超分辨显微镜的应用涵盖了许多生命科学领域,从细胞核到分子水平都有广泛的应用。
(一)细胞功能研究超分辨显微镜的分辨率可以揭示小分子的扩散、细胞器动力学和蛋白质亚细胞位置,在细胞功能研究中有着重要的应用。
例如,在分子分布的研究中,超分辨显微镜可以帮助研究人员观察受体和离子频繁转位的过程。
该技术还可以用于研究神经元的突触功能,因为它可以检测小型生物分子如神经递质的扩散情况。
超分辨显微技术的原理和应用

超分辨显微技术的原理和应用随着生物学和医学研究的深入,越来越多的问题需要解决,例如细胞和分子结构的研究。
传统显微镜的分辨率受限制,无法同时观察到细胞内的多种分子机器。
因此,生物学家和医学家们需要发展更为先进的显微技术来研究更加复杂的生物结构和过程。
超分辨显微技术应运而生,在生物领域得到了广泛的应用。
本文将介绍超分辨显微技术的原理和应用。
超分辨显微技术的原理在传统显微镜中,光的波长限制了分辨率。
在最好的情况下,传统显微镜的分辨率约为200纳米。
超分辨显微技术则利用各种物理现象或化学反应来提高分辨率。
超分辨显微技术的原始形式是荧光显微镜。
荧光显微镜的原理是受到生物体或化合物吸收的特殊形式的光谱突变,可以使它们发射出可见的荧光光。
这种显微镜可以照射样本并观察荧光的分布。
但是,荧光显微镜分辨率仍然不足以分辨细胞内多种分子结构。
为了克服这个问题,科学家开始使用现代的超分辨显微技术,例如:刺激发射荧光显微镜(STED)、受限制的光学刺激取幅显微学(RESOLFT)、脆性光学限制显微镜(PALM)和单分子光学氧化(SMOX)等技术。
STED是一种使用激光的超分辨显微镜技术。
STED的激光束可以使样本中的分子跳跃到另一种状态。
然后,用另一束激光照射样本,使带有较高能量的分子部分退回最初的状态。
这种技术的分辨率可以达到20 - 30纳米,比荧光显微镜的分辨率要高得多。
RESOLFT技术的原理是在一小部分样本上同时照射两个激光。
一个激光束使样品发生化学反应,并改变其形状。
而另一个激光束可以清楚地观察样本中的分子结构。
与STED类似,RESOLFT的分辨率也达到了20 - 30纳米。
PALM和SMOX技术使用单纯的光学方法来观察细胞和分子结构。
PALM技术涉及到拍摄一系列小的图像,每个图像里只有一部分荧光标记。
这样可以使细胞的所有部分都看到。
用这些图像可以很容易地将所有图像拼接在一起,形成清晰的图像。
SMOX技术则涉及单分子测量。
超分辨显微镜的工作原理与成像技术

超分辨显微镜的工作原理与成像技术超分辨显微镜是一种先进的光学显微镜,具有很高的分辨率和成像能力,可以观察到微观领域中细小的结构和现象。
本文将介绍超分辨显微镜的工作原理和成像技术,以及其在生物医学、材料科学和纳米技术等领域的应用。
一、工作原理超分辨显微镜的工作原理基于曲折规律和波的衍射。
传统光学显微镜由于照明光束的衍射限制,无法分辨出比光的波长还要小的物体细节。
而超分辨显微镜通过使用特殊的技术,克服了这一限制。
1.1 衍射极限传统光学显微镜的分辨率受到衍射极限的限制。
衍射极限(称为耐克斯特准则)是由德国物理学家安德烈亚斯·耐克斯特提出的,规定了光学系统能够分辨物体的最小尺寸,即0.61倍的照明光波长。
超过这个极限,显微镜就无法分辨出物体的细节。
1.2 超分辨技术超分辨显微镜采用了多种技术来突破衍射极限,实现更高的分辨率。
其中最常见的技术包括:1.2.1 利用荧光标记超分辨显微镜可以通过利用荧光标记结合合适的成像技术,将被观察物体的特定部分标记出来,并对其进行成像。
这些标记物在光的刺激下会发出荧光信号,通过检测和分析这种信号,可以实现纳米级的分辨率。
1.2.2 利用近场效应近场光学显微镜利用装载在探针尖端的金属纳米结构,利用探针与样品之间的极短距离来增强照明光的局部电场,从而实现超分辨成像。
这种技术在表面等离子激元共振和原子力显微镜中得到广泛应用。
1.2.3 利用建构性干涉通过将两束光进行干涉,可以在显微镜中形成特定的干涉模式。
这种模式包含了被观察物体的高频细节信息。
运用适当的算法和数学处理,可以从干涉模式中提取出高分辨率的图像。
二、成像技术超分辨显微镜采用多种成像技术来获取高分辨率图像。
以下是几种常用的成像技术:2.1 结构光成像结构光成像利用相干光束通过物体表面,通过记录物体与光束的相互作用,实现高分辨率的三维成像。
利用这种技术,可以获得具有亚微米分辨率的物体表面拓扑图像。
2.2 荧光成像荧光成像是利用带有荧光标记的样品在激发光线照射下发出的荧光信号进行成像。
超分辨荧光显微技术原理

超分辨荧光显微技术原理传统的荧光显微镜受到瑞利准则的限制,即其分辨率受到光学波长和透镜的限制。
超分辨荧光显微技术则通过创新的方法克服了这一限制,实现了超分辨率的荧光成像。
1.非线性显微技术:传统的荧光显微技术采用的是线性成像原理,即通过样品中的荧光物质发射的线性荧光信号来获得图像。
而超分辨荧光显微技术采用非线性成像原理,利用荧光物质的非线性光学效应,提高了分辨率。
例如,通过激光器的脉冲激发,可以使荧光物质在非线性荧光效应下发射高阶谐波信号,从而得到更高分辨率的图像。
2.相干显微技术:传统的荧光显微技术采用的是非相干光源,无法获取相干光的相位信息,从而限制了分辨率的提高。
而超分辨荧光显微技术采用相干光源,如激光光源或可调谐激光器,使得可以获取到样品的相位信息,从而提高了分辨率。
例如,通过在激光束上加入相位调制,可以在信号中提取出相位信息,从而实现更高的分辨率。
3.显微镜改进:传统的荧光显微镜在透镜、光路和探测器等方面都存在一定的限制,无法实现超分辨率成像。
超分辨荧光显微技术通过改进显微镜的设计和构造,例如采用高数值孔径物镜、自适应光学元件和高速探测器等,可以克服这些限制,提高分辨率。
4.数据分析和算法:超分辨荧光显微技术的数据量较大,需要进行大量的图像处理和分析。
通过使用高级算法和计算方法,可以将大量数据进行处理和重建,得到超分辨率的图像。
例如,通过拟合和重建点扩散函数,可以实现超分辨率的成像。
超分辨荧光显微技术的应用非常广泛,涵盖了生物医学、材料科学和纳米技术等领域。
例如,在生物医学领域,超分辨荧光显微技术可以用于观察和研究细胞结构、分子过程和疾病发展等,为生物医学研究提供了重要的工具。
在材料科学领域,超分辨荧光显微技术可以用于材料表征和纳米结构研究,为材料科学的发展和应用提供了有力支持。
总之,超分辨荧光显微技术通过创新的光学方法和图像处理算法,突破了传统荧光显微技术的分辨率限制,实现了超分辨率的荧光成像,为生物医学和材料科学等领域的研究提供了重要工具。
超分辨率荧光显微技术的原理和进展

超分辨率荧光显微技术的原理和进展超分辨率荧光显微技术是一种用于观察细胞和生物分子的显微镜技术,具有比传统荧光显微镜更高的分辨率,可以更清晰地分辨出细胞和生物分子的结构和功能。
其原理基于物理学原理和计算机算法,通过精确的荧光标记和高分辨率成像技术,实现了对生物结构的超分辨率观察。
本文将介绍超分辨率荧光显微技术的原理和进展。
1.超分辨率荧光显微技术的原理抑制光的衍射:传统光学显微镜无法突破维恩衍射极限,限制了其分辨率。
超分辨率荧光显微技术利用光的非线性响应和光学调制技术,使得衍射限制得以突破。
例如,利用单分子荧光显微技术,可以将荧光标记的分子在时间上进行“开关”,只有少数分子发出荧光,可以精确定位每个分子的位置。
利用这种方法,可以获得超分辨率的图像。
图像重建算法:超分辨率荧光显微技术还依赖于一系列图像处理技术,如重建算法和数据解析算法。
这些算法能够在获得低分辨率图像的基础上,通过处理和分析图像数据,恢复出高分辨率的图像。
常见的算法有结构光超分辨率显微镜(SR-SIM)、单分子定位显微镜(SMLM)等。
这些算法通过统计学原理和概率分析等方法,提高图像的分辨率和清晰度。
2.超分辨率荧光显微技术的进展(1)结构光超分辨率显微镜(SR-SIM):这种技术是利用结构光的干涉原理,通过调整光源的相位和频率,实现对样本的超分辨率成像。
SR-SIM技术能够将样本的分辨率提高到约100 nm,从而观察到更细微的结构。
(2)单分子定位显微镜(SMLM):SMLM技术利用荧光标记的分子在时间上进行“开关”,只有少数分子发出荧光,可以精确定位每个分子的位置。
通过收集大量分子的位置信息,可以恢复出高分辨率图像。
SMLM 技术的分辨率可以达到10 nm左右,成为最高分辨率的超分辨率显微技术之一(3)受限激发荧光显微镜(STED):STED技术是一种利用激光束的光强分布来抑制荧光的发射,从而实现超分辨率成像的方法。
STED技术的分辨率可以达到几十纳米,可以观察到更小的细胞结构和分子组装。
超分辨显微技术原理和应用场景

超分辨显微技术原理和应用场景随着科技的不断进步,超分辨显微技术已经成为了现代科学研究中不可或缺的工具。
它可以让我们更加深入地观察和理解生命、物质等领域中的微小细节,为现代科学研究提供更加精确和丰富的数据信息。
一、超分辨显微技术的原理超分辨显微技术是指一系列可以对物质进行高分辨率观察的技术。
这些技术可以让我们在显微镜下看到更加微小的细节,比传统显微技术更加精细。
超分辨显微技术的原理主要有以下几种:1. 结构照明技术结构照明技术通过在样品前加上特殊的光学器件,改变照明光线的传播途径和相位,从而实现更加精细的成像。
2. 荧光共振能量转移技术荧光共振能量转移技术可以用来在单个分子甚至分子集合中的精细定位。
3. 光学斑点技术光学斑点技术是一种通过奇异光束在样品中产生光学斑点的技术。
这种技术可以实现极高的空间分辨率和时间分辨率。
它是超分辨显微技术中最常用的一种。
二、超分辨显微技术的应用超分辨显微技术的应用非常广泛,包括材料科学、生命科学、纳米技术等领域。
下面我们就来看一下超分辨显微技术在不同领域中的应用。
1. 生命科学超分辨显微技术在生命科学中有非常广泛的用途,它们可以让我们更加精细地观察细胞、分子和生物体的内部结构。
其中最广泛使用的超分辨显微技术是荧光显微技术。
荧光显微技术可以用于观察体内特定分子的分布和作用,例如蛋白质、核酸等。
2. 材料科学超分辨显微技术在材料科学中也有广泛的应用。
材料科学中的核心问题之一是探索材料的微观结构和性能,以便更好地设计新型材料。
超分辨显微技术可以提供非常精细的材料结构和性能信息,为材料科学的发展提供了重要的支持。
3. 纳米技术纳米技术是一种基于纳米尺度物质构建和制造的技术。
由于纳米尺度的特殊性质,纳米技术在生物医学、材料科学等领域中有广泛的应用。
超分辨显微技术可以提供非常精细的纳米材料成像,为纳米技术的研究和发展提供重要的支持。
总之,超分辨显微技术的应用和研究已经成为现代科学研究中的重要分支之一。
几种超分辨率显微术原理及对比
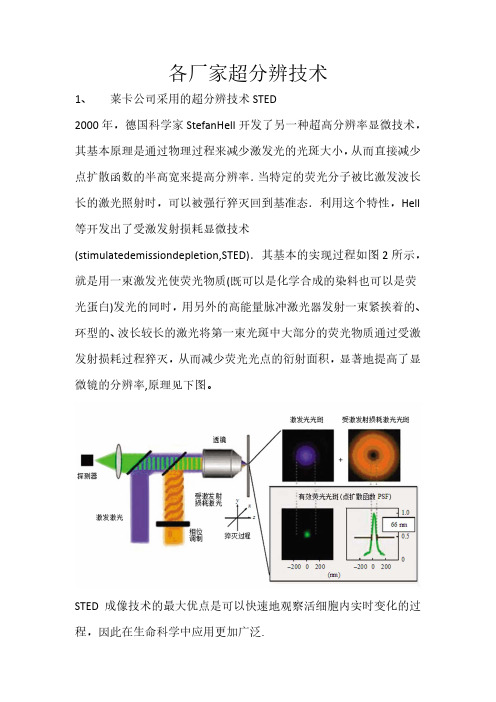
各厂家超分辨技术1、莱卡公司采用的超分辨技术STED2000年,德国科学家StefanHell开发了另一种超高分辨率显微技术,其基本原理是通过物理过程来减少激发光的光斑大小,从而直接减少点扩散函数的半高宽来提高分辨率.当特定的荧光分子被比激发波长长的激光照射时,可以被强行猝灭回到基准态.利用这个特性,Hell 等开发出了受激发射损耗显微技术(stimulatedemissiondepletion,STED).其基本的实现过程如图2所示,就是用一束激发光使荧光物质(既可以是化学合成的染料也可以是荧光蛋白)发光的同时,用另外的高能量脉冲激光器发射一束紧挨着的、环型的、波长较长的激光将第一束光斑中大部分的荧光物质通过受激发射损耗过程猝灭,从而减少荧光光点的衍射面积,显著地提高了显微镜的分辨率,原理见下图。
STED成像技术的最大优点是可以快速地观察活细胞内实时变化的过程,因此在生命科学中应用更加广泛.2、蔡司公司采用的超分辨技术PLAM2002年,Patterson和Lippincott‐Schwartz首次利用一种绿色荧光蛋白(GFP)的变种(PA‐GFP)来观察特定蛋白质在细胞内的运动轨迹.这种荧光蛋白PA‐GFP在未激活之前不发光,用405nm的激光激活一段时间后才可以观察到488nm激光激发出来的绿色荧光.德国科学家EricBetzig敏锐地认识到,应用单分子荧光成像的定位精度,结合这种荧光蛋白的发光特性,可以来突破光学分辨率的极限.2006年9月,Betzig和Lippincott‐Schwartz等首次在Science上提出了光激活定位显微技术(photoactivatedlocalizationmicroscopy,PALM)的概念.其基本原理是用PA‐GFP来标记蛋白质,通过调节405nm激光器的能量,低能量照射细胞表面,一次仅激活出视野下稀疏分布的几个荧光分子,然后用488nm激光照射,通过高斯拟合来精确定位这些荧光单分子.在确定这些分子的位置后,再长时间使用488nm激光照射来漂白这些已经定位正确的荧光分子,使它们不能够被下一轮的激光再激活出来.之后,分别用405nm和488nm激光来激活和漂白其他的荧光分子,进入下一次循环.这个循环持续上百次后,我们将得到细胞内所有荧光分子的精确定位.将这些分子的图像合成到一张图上,最后得到了一种比传统光学显微镜至少高10倍以上分辨率的显微技术,原理如下:PLAM通过定位细微结构乃至单分子,实现 20 nm 的横向分辨率和 50 nm 轴向分辨率。
超分辨荧光显微成像在生命科学中的应用

超分辨荧光显微成像在生命科学中的应用随着科技的不断发展,越来越多的新技术开始被应用于生命科学研究中。
其中,超分辨荧光显微成像技术(super-resolution fluorescence microscopy)是一种非常重要的技术。
本文将介绍超分辨荧光显微成像在生命科学中的应用。
一、超分辨荧光显微成像技术的基本原理传统的荧光显微镜采用的是荧光信号的散射原理,因此其分辨率受到了光学衍射极限的限制。
而超分辨荧光显微成像技术通过各种手段,如利用分子的光物理性质或通过改变荧光分子的环境等,使得分辨率得以超越衍射极限。
常见的超分辨荧光显微成像技术包括结构光照明显微镜(structured illumination microscopy,SIM)、单分子荧光显微镜(single-molecule localization microscopy,SMLM)和受激发发射显微镜(stimulated emission depletion microscopy,STED)等。
二、超分辨荧光显微成像在生命科学中的应用1. 细胞膜和细胞器结构的研究超分辨荧光显微成像技术可以帮助生命科学家们更好地观察细胞膜和细胞器的结构。
例如,在研究膜结构时,超分辨荧光显微成像技术可以帮助生命科学家们观察到细胞膜的细微结构,并支持更准确的图像分析。
同时,荧光标记的细胞器和蛋白质可以使用SMLM技术来定位,以揭示细胞内特定结构的细节。
2. 生命过程的研究超分辨荧光显微成像技术可以用于研究生命中的各种过程,例如细胞核分裂、细胞器运动和分布等。
该技术的高分辨率和高灵敏度可更好地捕获这些过程的细节和动态变化,便于有关知识的进一步研究。
此外,通过该技术,可以装配精细的功能分子探针,以检测特定生物体系中的相关生物分子,从而揭示分子交互和反应的机制。
3. 病毒检测超分辨荧光显微成像技术的应用可以帮助研究人员检测病毒的特定性和结构。
例如,该技术可以用于研究病毒的感染机制和与宿主细胞的相互作用。
超分辨显微成像技术的原理和应用

超分辨显微成像技术的原理和应用超分辨显微成像技术是一种能够突破传统显微技术分辨率限制的一种创新性技术。
它通过在超分辨率显微镜下使用特殊的成像模式和图像处理算法来提高成像精度和分辨能力。
在此文中我将会简要介绍超分辨显微成像技术的原理和应用。
一、超分辨显微成像技术的原理传统的光学显微镜是基于Abbe原理的,它的分辨率受到光学衍射极限的约束。
因为衍射极限所限制的分辨率仅有大约200nm,这个范围内的成像是有限的。
然而,超分辨显微成像技术能够突破这个限制。
超分辨显微成像技术的核心原理基于通过对激光束进行控制来提高成像精度。
Super-resolution optical microscopy (STORM)技术可以使用的荧光染料实际上是由数千个单个荧光发射颗粒组成的。
在这个过程中,首先需要在样品中使用低浓度的荧光染料标记,它们会以随机方式发光。
在这个过程中,观察者将会收集到无序的荧光信号。
其次,由于各种各样的影响因素,这些荧光染料发出的光会以漂移的形式在图像上分散,这会对图像的观察产生严重影响。
通过超分辨显微成像技术,我们可以精确地控制这个过程,在样品中灌注光子,从而定位和确定荧光染料的发射位置。
最后,将所有的荧光信号在计算机上进行整合和分类,并通过算法重新构建出单个荧光粒子的发光图像,从而实现高分辨率的成像。
二、超分辨显微成像技术的应用超分辨显微成像技术的应用非常广泛,主要应用于生命科学和材料科学两个领域。
在生命科学中,人们可以利用这种技术突破Abbe极限,研究生物分子、细胞、组织和器官在分子水平的内部组织结构、物质运移、代谢分子和蛋白质互作等方面的活动行为。
此外,超分辨显微成像技术也可以用于深入研究各种病毒、癌症、脊髓损伤和神经退化等疾病的发病机理。
在材料科学中,超分辨显微成像技术被广泛应用于材料表面和界面结构分析、纳米材料和异质材料界面的研究、材料表面胶体结构的探究和纳米粒子的生物组装研究等领域。
超分辨率显微成像技术

超分辨率显微成像技术,是指利用计算机算法对显微镜所观察的细胞、材料等微观结构进行高分辨率的成像技术。
与传统的显微成像技术相比,能够获得更为清晰和详细的图像信息,有助于科学家更好地理解细胞结构和生命过程、材料物理和化学特性等问题。
本文将介绍的原理、应用场景和发展前景等。
一、原理主要有两种原理:单分子荧光显微镜(SMLM)和结构光显微镜(SLM)。
简单来说,SMLM旨在单独探测位于样品表面的分子,并对分子的位置进行高精度的定位和图像重建;而SLM则采用干涉的原理,通过控制光的相位和波长变化,实现对样品的复杂结构进行高精度成像。
SMLM技术最出名的是PALM(Photoactivated localisation microscopy)和STORM(stochastic optical reconstruction microscopy)两种技术。
这两种技术都利用单分子荧光和光开关技术实现了高分辨率的成像,而STORM还可以通过多层成像技术进一步提高显微成像的分辨率。
SLM技术则主要包括干涉显微镜、相位成像显微镜、光学斑图成像显微镜等。
二、应用场景在生物医学、材料科学、纳米技术等领域都有广泛的应用。
以下是一些具体的应用场景:1. 细胞和分子成像:超分辨率显微技术对于细胞和分子的成像非常有帮助。
例如,用这种技术可以更准确地观察细胞内蛋白质的分布和动态变化,了解分子之间的相互作用和调控机制等。
2. 病毒研究:超分辨率显微技术已经被应用于研究宿主细胞和病原体之间的相互作用机制,例如病毒与感染细胞的相互作用。
这个技术可以清晰地观察到病毒在细胞中的传播、生长和繁殖等过程。
3. 材料研究:超分辨率显微技术可以帮助科学家观察和处理材料中的缺陷、纳米结构和原子级别的表面化学特性等。
4. 纳米器件研究:超分辨率显微技术可以帮助科学家观察和处理纳米器件中的单个颗粒,了解它们的成本、机理和阻力特性等。
三、发展前景已经成为当今科研领域的热点之一。
超分辨荧光显微

随机光学重建显微技术(STORM)
要点一
总结词
要点二
详细描述
STORM是一种基于单分子定位的超分辨技术,通过控制荧 光分子的开关状态,实现高精度单分子定位和超分辨成像 。
STORM技术利用荧光分子在不同开关状态下的光散射性质 不同,通过控制荧光分子的开关状态,实现高精度单分子 定位和超分辨成像。在STORM显微镜中,激光束被聚焦到 样品上,激发荧光分子发光。通过控制荧光分子的开关状 态,可以选择性地激活特定荧光分子并记录其位置信息。 通过大量单分子定位的累积,可以构建出超分辨图像。
未来发展方向
突破光学衍射极限
自动化和智能化
通过发展新型光学器件和技术,突破 光学衍射极限,进一步提高超分辨荧 光显微技术的分辨率。
提高超分辨荧光显微技术的自动化和 智能化水平,使其更易于操作和使用, 降低使用门槛。
多模态成像技术
结合不同成像模态的优势,发展多模 态成像技术,以获得更全面、更准确 的信息。
稀疏光学重构显微技术(SORTIE)
总结词
SORTIE是一种基于光学重构的超分辨技术,通过稀疏采样和光学重构算法,实现高分辨率成像。
详细描述
SORTIE技术利用光学重构的原理,通过稀疏采样和光学重构算法,实现高分辨率成像。在SORTIE显 微镜中,激光束被聚焦到样品上并产生散射光。通过控制散射光的角度和强度,可以对样品进行稀疏 采样。然后利用光学重构算法对采样数据进行处理,实现高分辨率成像。
成熟应用阶段
随着技术的不断完善和优 化,超分辨荧光显微技术 逐渐成为生物学和医学领 域的重要研究工具。
02
超分辨荧光显微技术的基本原 理
荧光物质的激发与发射
荧光物质在特定波长的光激发下,吸 收能量并跃迁至激发态,随后释放能 量回到低能态,并发出特定波长的荧 光。
超分辨显微镜的工作原理及其在生物研究中的应用

超分辨显微镜的工作原理及其在生物研究中的应用超分辨显微镜是一种先进的显微技术,可以提供比传统光学显微镜更高的分辨率和更清晰的成像效果。
它在生物研究领域发挥着重要作用,可以对微观生物结构进行详细观察和研究,帮助科学家们更好地理解生命现象和疾病发生的机制。
一、超分辨显微镜的工作原理超分辨显微镜主要依靠两种技术来提高分辨率:荧光显微镜和近场扫描光学显微镜(NSOM)。
下面将重点介绍这两种技术的工作原理。
1. 荧光显微镜荧光显微镜利用特定物质的荧光素进行成像。
当样本中的目标物质受到激发光的照射时,它们从低能级跃迁到高能级,然后再通过发射能量的方式返回基态。
通过控制激发光的波长和能量,可以使目标物质发射出特定的波长的荧光。
荧光显微镜通过收集和检测这种发射出的荧光信号,再经过图像处理和分析,最终得到高分辨率的显微图片。
2. 近场扫描光学显微镜(NSOM)近场扫描光学显微镜利用很小的光学探针来观察样本表面,并通过探针与样本之间的非接触距离来提高分辨率。
探针与样本之间的非接触距离通常在纳米尺度上,并且具有非线性光学效应。
当探针靠近样本时,探针会捕获和散射光线,然后通过检测和分析这些光线来生成高分辨率的图像。
二、超分辨显微镜在生物研究中的应用超分辨显微镜在生物研究中有广泛的应用。
下面将介绍几个典型的应用领域。
1. 细胞生物学超分辨显微镜可以帮助科学家们观察和研究细胞的结构和功能。
传统光学显微镜的分辨率有限,很难观察到细胞内更小的亚细胞结构。
而超分辨显微镜可以提供更高的分辨率,可以观察到细胞核、线粒体、内质网以及微管等细胞器的详细结构,有助于深入了解细胞的功能和疾病发生的机制。
2. 蛋白质研究蛋白质是生物体内重要的功能分子,超分辨显微镜可以帮助科学家们观察和研究蛋白质的结构和相互作用。
通过荧光标记技术,科学家们可以将特定的蛋白质标记为荧光探针,然后使用超分辨显微镜观察和研究这些蛋白质在细胞内的分布和相互作用。
这对于理解蛋白质的功能以及疾病的发生机制非常重要。
超分辨显微镜技术及其在生物医学中的应用

超分辨显微镜技术及其在生物医学中的应用生物医学领域一直是科技进步的重点之一,随着科技的不断发展,人们对于细胞和组织的表征能力也不断提高。
近年来,超分辨显微镜技术作为新一代显微镜技术,得到了越来越广泛的应用。
本文将介绍超分辨显微镜技术的基本原理和具体应用,并探讨该技术为生物医学研究带来的重大突破。
一、超分辨显微镜技术的基本原理超分辨显微镜技术是一种在可见光微观范围内,突破传统显微镜分辨率极限的显微镜技术。
其基本原理是利用高级别折射率物质(如胶体颗粒、荧光染料等)对光进行调制,借助非常特殊的图案照明和摄影技术,最终达到单分子分辨的目的。
由于超分辨显微镜技术越来越普及,人们可以更好地理解形态、生理学和生物化学方面的基本问题。
二、超分辨显微镜技术在细胞成像中的应用细胞成像是超分辨显微镜技术在生物医学领域中的一个突出应用。
传统显微技术的限制导致了细胞成像无法将不同细胞器之间的空间结构和互动关系呈现出来。
然而,超分辨显微镜技术的应用可以让科学家们通过观察细胞成像图像,更好地理解细胞的构造与功能之间的关系。
其中,荧光重合图谱是一项令人兴奋的技术。
该技术可以同时检测数种不同分子的位置、形态和分布情况。
应用该技术,研究人员发现肝细胞中某些属于酵母菌糖基转移酶家族的蛋白质在细胞内部的转运过程中形成了内含体,在小囊泡形成处它们聚集并被特定的酶加工,此后将被释放到细胞质中完成体内功能。
这项研究不仅为细胞内部运输提供了深入全面的了解,而且为新药物的研究和开发提供了更可靠的信息。
三、超分辨显微镜技术在神经元胶质表面成像中的应用神经元胶质表面成像是另外一个超分辨显微镜技术在生物医学领域中的应用。
神经元胶质表面成像出现的时间比细胞成像更早,是该技术的另外一个突出应用。
超分辨显微镜技术的应用在这个领域有望提供更深入全面的了解,对于对神经系统的基础和临床研究将具有推动作用。
神经元胶质表面成像的脑部表现形式,采用显微技术分辨率的限制使神经元活动无法清晰地展示。
超高分辨率显微镜的工作原理与样品制备技术

超高分辨率显微镜的工作原理与样品制备技术超高分辨率显微镜是一种先进的显微技术,可以在纳米尺度下观察和研究样品的细节。
本文将介绍超高分辨率显微镜的工作原理,并探讨样品制备技术。
一、工作原理超高分辨率显微镜的工作原理基于单分子荧光成像和光学原理。
其主要分为以下几个步骤:1. 激发:通过激光器对样品进行激发,使样品中的荧光标记物进入激发态。
2. 发射:被激发的荧光标记物会发射出一束具有特定波长的荧光光子。
3. 光子检测:利用高灵敏度的光学探测器来检测和记录荧光光子的位置和强度。
4. 定位:通过检测到的荧光光子,利用图像处理算法对其进行定位,从而获得超高分辨率的图像。
二、样品制备技术样品制备是超高分辨率显微镜研究中至关重要的一步。
以下是一些常用的样品制备技术:1. 标记物选择:根据研究目的选择适合的荧光标记物,并通过化学反应将其与待测物相结合。
2. 固定化:将待测物固定在载玻片上,以保持样品的形态结构和稳定性。
常用的固定化方法有化学固定化和凝胶固定化等。
3. 样品清洁:确保样品表面无尘和杂质,以避免影响图像质量。
可以使用超声波清洗等方法进行清洁。
4. 样品切片:对于生物样品,常需要制备薄片以便观察。
切片技术包括常规切片、冷冻切片和超薄切片等。
5. 荧光染色:将样品染色以增加荧光信号的强度和对比度。
常用的荧光染色方法有免疫染色、荧光标记蛋白质等。
6. 抗褪色:荧光信号的褪色是超高分辨率显微镜观察中常见的问题。
为了抵抗荧光信号的褪色,可以使用抗褪色剂。
总结:超高分辨率显微镜通过荧光成像和光学原理实现了对样品细节的高分辨率观察。
样品制备技术在超高分辨率显微镜研究中起到至关重要的作用,包括标记物选择、固定化、样品清洁、样品切片、荧光染色和抗褪色等步骤。
这些技术的应用可以帮助科研人员更准确、高效地研究样品,并为各个领域的科研工作带来更多可能。
超分辨显微镜在生物学研究中的应用

超分辨显微镜在生物学研究中的应用超分辨显微镜是一种相对传统显微镜而言的高级显微镜,这种显微镜可以在很小的区域内获取高质量的图像,帮助生物学家更好地了解生物的结构和功能。
本文将介绍超分辨显微镜的工作原理、分类以及在生物学研究中的应用。
一、工作原理超分辨显微镜是一种新兴的显微技术,工作原理有多种方法:1. STED显微镜STED可刺激发射抑制显微镜是一种抑制荧光现象的技术,它使用激光束的形状和强度来控制荧光蛋白的发射,从而提供更高的空间分辨率。
在STED显微镜中,使用两组激光束,一个用于激发蛋白,另一个用于抑制荧光,可以捕获常规显微镜无法捕获的细微结构。
2. PALM和STORM显微镜PALM和STORM显微镜是一种单分子定位显微镜,可以在细胞分子水平上获得高分辨率的图像。
这种显微镜使用荧光染料来识别单个分子,将其图像组合在一起生成高分辨率图像。
3. SIM和TIRF显微镜结构发射显微镜和全反射显微镜使用超薄光束的原理保持图像的分辨率。
它们在细胞表面附近工作,能够捕获细胞表面和细胞外部分子在细胞分子水平上的高分辨率图像。
二、分类超分辨显微镜可以根据其实现高分辨率的方法进行分类:1. 有阻抑的显微镜(例如STED):使用荧光控制技术来实现高分辨率的图像。
2. 单分子定位显微镜(例如PALM和STORM):通过荧光染料来探测单个分子,再将它们组合在一起生成高分辨率图像。
3. 超薄结构发射显微镜和全反射显微镜(例如SIM和TIRF):它们在细胞表面附近工作,能够捕获细胞表面和细胞外部分子在细胞分子水平上的高分辨率图像。
三、应用超分辨显微镜在生物学研究中的应用非常广泛,以下是一些例子:1. 研究神经元细胞:神经元细胞是非常小的,然而超分辨显微镜能够帮助生物学家观察到它们的内部结构。
2. 研究DNA:PALM和STORM显微镜可以用来研究DNA。
3. 研究蛋白质组装:超分辨显微镜可以用来研究蛋白质的形成和构造,这有助于了解蛋白质在生物体内的作用。
超分辨显微技术的原理与应用

超分辨显微技术的原理与应用近几年,超分辨显微技术(Superresolution Microscopy)在生命科学领域得到了广泛的应用和研究。
相较于传统显微技术,这种技术可以在超过光学分辨率的范围内实现微观结构的观察与研究,从而大大提高了研究的精度和深度。
本文将简要介绍超分辨显微技术的原理以及最常见的应用。
一、超分辨显微技术的原理传统显微技术在观测微观结构时,通常只能观察到与光学分辨率相当或大于它的物体,即大约在200nm以上的物体。
这是因为光学成像的分辨率是有限的,光学系统中所有的物质都有一个理论分辨率限制。
光学分辨度的大小只取决于光波的波长以及物镜的数值孔径,即分辨率等于0.61λ/NA,其中λ为光波长,NA为数值孔径。
因此,光学显微技术在解决微观结构问题上存在局限性。
超分辨显微技术的原理就是利用光学的物理原理以及多种光学技术手段来突破光学分辨率的限制。
例如,受激发射和荧光共振能量转移(FRET)等光学技术可以在生命科学的各个领域中大幅度提高研究的精度和深度。
二、超分辨显微技术的应用(一)荧光重现漫游显微术(STORM)STORM是应用较早的超分辨显微技术之一,也是目前应用最广泛的技术之一。
该技术最早由Eric Betzig等人于2006年开发,并于2008年正式命名为STORM。
STORM使用分子分子标记多个分子,依靠逐渐激光激发单个荧光分子单元,获得分子在三维空间中的位置,并通过多次扫描,将还原出来的图像叠加得到超分辨率的图像。
与传统荧光显微技术相比,STORM可以提高显微镜的空间分辨率,用于生物标记显微领域等。
(二)单分子荧光显微术(SMLM)SMLM是另一种超分辨显微技术,它使用了单分子成像技术。
SMLM的原理是使用由单个光敏分子构成的荧光探针,光子随机地在探针的发光区域中发生发射,使用这种技术可以获得与STORM类似的超分辨率显微镜。
相比于STORM,SMLM的优势在于可以在非生物样品上进行直接成像。
超分辨显微镜的原理及应用

超分辨显微镜的原理及应用超分辨显微镜是一种能够突破传统显微镜分辨极限的高端科技仪器。
其原理是通过使用特定的成像方法,使得显微镜能够在高于传统分辨极限的范围内捕捉细微结构的图像。
这项技术的出现对研究生物学、材料学、化学等领域的微观结构及其相关的科学问题具有非常重要的影响和关键作用。
尤其对于制药、医学和生命科学领域的研究,超分辨显微镜的应用更是得到了广泛的关注。
一、超分辨显微镜的原理传统的显微镜受限于光学分辨率的限制,因此在观察微小的样品时,一定程度上存在画质模糊、细节缺失的问题。
超分辨显微镜通过采用高级的成像技术,使得显微镜能够在高于传统分辨极限的范围内捕捉细微结构的图像,从而解决传统显微镜所存在的问题。
其中比较典型的方法有几种,比如说:1.激光多光子显微镜法多光子显微镜利用非线性光学产生双光子荧光来获得高分辨率的成像。
而双光子荧光是一种非线性物理过程,需要激光的强度大于某个门槛才能发生。
所以,这种方法可以获取在样品内部均匀的质量分布的图像,沿Z轴方向的深度分辨率明显优于普通荧光显微镜。
2.双向激发显微镜法双向激发显微镜是一种适用于单分子荧光的成像技术。
它结合同一波长的双向激发,确定单个分子的位置并使其发出荧光信号,通过这种方式较精确地确定单分子的位置,同时避免了背景干扰。
3.波前调制显微镜法波前调制显微镜是一种超分辨率成像技术,它通过使用可以自主调整成像质量的可编程液晶屏幕,将波前调制器导向不同点的光强,以获取高分辨率成像。
与其他超分辨技术比较,波前调制显微镜优点在于可实现高分辨率、高对比度的成像,且不需要复杂精确的调整。
二、超分辨显微镜的应用超分辨显微镜在生命科学、物理学、化学学等领域都有着广泛应用。
不同成像技术可以适用于不同的研究对象,甚至在同一领域中,也可能需要多种不同的成像技术的协同组合。
尤其对于细胞学和生物医学领域,超分辨显微镜的应用价值更为突出。
这是因为在这些领域中,研究对象都是亚细胞级别的微观结构。
超分辨显微镜的原理和应用

超分辨显微镜的原理和应用超分辨显微镜是一种现代光学仪器,能够生成尺寸比传统显微镜所观察的物体小得多的图像。
它的出现革命性地改变了生物和化学领域的研究方法,极大地拓宽了科学家们的视野。
本文将详细介绍超分辨显微镜的原理及其应用。
一、超分辨显微镜的原理以常用的STED超分辨显微镜为例,它的原理主要基于荧光共振能量转移和饱和吸收的作用。
STED超分辨显微镜的基本原理是:在荧光激发下,样品中的荧光分子会产生荧光,这种荧光会在显微镜上形成图像。
但是,荧光分子之间的光子也会互相干扰,导致图像不清晰或无法分辨。
STED超分辨显微镜通过在样品周围产生一个特定的激光束,该激光束能够使荧光分子在光子共振能量转移后失去荧光的能力,从而实现图像的超分辨。
与传统的荧光显微镜不同,STED超分辨显微镜可以将样品切片成非常小的形状,并让光走过各个分片,这样就可以记录下每个分片发出的荧光,并再次组合成更清晰的高分辨率图像。
二、超分辨显微镜的应用1. 生命科学超分辨显微镜在生命科学领域的应用非常广泛。
它可以帮助科学家们更细致地分析细胞、细胞器、分子以及生物大分子的组成和结构。
超分辨显微镜还可以用于研究具有复杂功能的生物大分子或者是作为治疗疾病的作用靶点的蛋白质,从而在生命科学领域取得更大的进展。
2. 化学在化学领域,超分辨显微镜可以用来研究高分子材料、纳米复合材料和表面化学反应。
这些研究对于探索新型工业催化剂、为新型纳米材料设计制造方法以及开发具有高效催化性能的生物燃料电池等方面都是非常重要的。
3. 材料科学在材料科学领域,超分辨显微镜可以用于研究材料缺陷、微观结构和界面结构,发现材料的微观构造和性质之间的关系,从而为新材料的合成和加工提供重要的理论和技术支持。
4. 环境超分辨显微镜还可以用于环境监测,例如,研究海洋中微型生物的种类和数量,更好地了解和预测全球气候变化的趋势,监测和评估各种污染源对环境的影响。
总之,超分辨显微镜的应用领域极其广泛,它不仅扩展了科研的视野,也为人们解决各种实际问题提供了便利。
超分辨显微镜技术及其应用前景

超分辨显微镜技术及其应用前景显微镜是一种重要的科学工具,它可以让我们观察微观世界中的物质结构和功能。
然而,传统的显微镜在分辨率上受到了严重限制,这限制了我们对很多物质的观察和研究。
超分辨显微镜技术的出现在一定程度上解决了这个问题,它可以使我们观察到比传统显微镜更小的物质结构和功能。
本文将详细介绍超分辨显微镜技术的原理和应用前景。
一、超分辨显微镜技术的原理超分辨显微镜技术是指一种能够绕过传统显微镜分辨率极限的技术,因而可以获得更高的分辨率。
这种技术包括基于单独分子或单光子的方法和各种近场扫描显微镜方法。
其中的单独分子或单光子的方法是通过在荧光显微镜中使用特定的荧光染料来实现的。
这些荧光染料具有“可开关”特性,在开启时可以黏在蛋白质表面的单个分子上,从而可以通过图像分析探测物质分子和聚集的比普通光学分辨率细小得多的小团簇。
这种方法广泛应用于生物学和凝聚态物理学。
另外,近场扫描显微镜方法是通过在样品和探头之间产生一个很小的间隙,从而制备一个高分辨率成像光学盲区。
数据可以在扫描点之间上传到计算机,从而形成高分辨率图像。
这种方法已成功地应用于人类头发、激光等微观结构的研究。
二、超分辨显微镜技术的应用前景超分辨显微镜技术的应用前景也是非常广泛的。
以下是这种技术在各个领域的应用:1.生物学领域超分辨显微镜技术是生物学领域中一个非常有前途的研究工具。
它可以解决传统显微镜无法观察的微观结构和功能。
超分辨显微镜技术在细胞生物学、毒理学以及癌症学研究方面都已经取得了一定的进展,例如可以帮助观察蛋白质、细胞器、膜的移动或者结构内部微观的变化。
2.纳米科技领域超分辨显微镜技术可以用于多种纳米材料结构的探测,如纳米粒子、碳纳米管、量子点等的表面结构和物理化学性质分析。
这可以为材料化学、开发和优化纳米诊断工具,带来一定的帮助。
3.物理学领域超分辨显微镜技术也可以在物理学领域应用。
例如,广泛应用于材料科学、催化剂表观实时探测以及半导体器件等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014 年的诺贝尔理综奖颁发给了“超分辨荧光显微技术”。
也许接下来的几天,媒体会关注 Stefan Hell、Eric Betzig 二人的传奇经历,或者另一名华人女科学家与该奖项失之交臂的遗憾。
但是八卦之外,这项成果背后的科学本身也非常有意思。
这里面有三个关键词:“超分辨”、“荧光”和“显微技术”,我希望能够解释清楚以下几个问题,尤其是后两个问题:1. 为什么需要(光学)显微技术?2. 为什么光学显微镜的分辨率存在理论极限?3. 用怎样的方法可以突破这个理论极限以达到“超分辨”?为什么这个理论极限可以被突破?5. 为什么非得是荧光显微技术,而非普通的明场(透射光)显微技术?1. 采样定理与显微镜我们用肉眼观察或者用相机拍摄一个物体时,物体上的每一个细微的点都会在眼睛的视网膜或是相机的感光芯片上成像。
那么我们为什么不能看到细菌等微小的东西,为什么不能把照片无限放大以看清远处树木上面的每一片叶子呢?这个问题的答案比较简单:因为组成视网膜的每一个感光细胞(视杆细胞和视锥细胞)、相机芯片上的每一个感光元件(CCD、CMOS等)都是有大小的。
比如视网膜中央凹区域的视锥细胞直径平均约为 5 微米。
而由于奈奎斯特-香农采样定理的限制,视网膜上能分清的两个相邻像点的距离是视锥细胞直径的两倍,即 10 微米。
再结合眼球的构造,大致可以推断出,在距离眼睛 25 厘米的位置,我们能分辨物体上相距为 80 微米的两个点,换算成点阵密度就是大约 320 ppi,这也是苹果所谓“视网膜屏”分辨率的来历。
如果要观察小于 80 微米的物体,比如细菌,就需要先将物体放大,再用眼睛或者相机观察。
现代光学显微镜的构造其实非常简单,样品放置在物镜的焦点处,从样品上发射或散射的光经过物镜变成平行(准直)光,再经过一个结像透镜,然后会聚到相机的感光芯片上成像。
按照前面的方法来推算,要区分物体上相距为 200 纳米的两个点,如果使用科研级相机,比如最近火起来的 sCMOS 相机(每个感光像素尺寸为 6.5 微米),只需要使用放大倍率为 65 倍的物镜就足够了。
那么是否可以通过提高物镜的放大倍率来观察低于 200 纳米的物体,比如细胞里面微管呢?答案是不可以。
2. 光学衍射极限由于光是一种电磁波,具有衍射和干涉的特性。
图 1. 光学显微镜简化示意图如上面的简图所示,紫色箭头表示的物体 PQ 经过物镜等之后在相机上成像为P'Q'。
由于光的衍射,物体上的点如 P、Q,在相机上并不是单独的点,而是一个个有一定大小的斑,被称为夫琅禾费衍射斑(或称艾里斑),如右侧的同心圆所示。
那么,当 P'、Q' 相距太近的时候,两个斑会叠加导致难以分辨。
这就要求物体上的 P、Q 要相距一定的距离。
1873 年,德国物理学家、卡尔蔡司公司的恩斯特·阿贝(Ernst Abbe)首次推算出衍射导致的分辨率极限。
根据瑞利判据——“当一个像斑的中心落到另一个像斑的边缘时,就算这两个像刚好能被分辨”,显微镜能分辨的物体上两点 P、Q 的最小距离 h 为:这个公式就是光学显微镜的分辨率公式,或称为光学衍射极限。
(注意此处的分辨率与通常说的显示器分辨率含义不同)其中,为光的波长,n 为物方的折射率,为物体与物镜边缘连线和光轴的夹角。
如上图所示。
为方便起见,其中的通常称为数值孔径,简写为 NA。
摄影领域常用 f/# 或称光圈值来描述镜头,光圈值与数值孔径可以相互换算。
对于一枚光圈为 2.0 的镜头来说,数值孔径为 0.25,其分辨能力约 1.2 微米。
目前常用的高倍物镜 NA 最大为1.49,可以算出,对于可见光,比如波长 500 纳米的绿光,显微镜的分辨率约为 200 纳米。
所以,即使再提高物镜的放大倍率,也不能提高显微镜的分辨率。
而 200 纳米这个数值也就通常被称作衍射极限。
2.5. 光学衍射极限的动态范围从上面的公式可以看到,光学衍射极限其实并不是一个具体的数值,如果改变上述公式中的参数,是可以有效提高分辨率的。
(1) 光的波长可见光波长范围是400~760 nm,如果使用更短波长的光,比如紫外线,理论上可以提高分辨率。
但是紫外线能量高,易损伤样品,而且透射能力低,很难透过物镜。
人们想到了使用高能电子束代替光束,比如 200 keV 的电子对应的的布罗意波长为 0.0025 纳米(2.5 * 米)。
虽然 NA 相对较小(约为10°),依然可以达到0.1 纳米的理论分辨率。
这就是电子显微镜的基本原理。
严格的说,电镜的分辨率依然限制在光学衍射极限的范围内。
只不过这里的“光学”是“电子光学”。
(2) 物方折射率 n空气折射率为 1,水的折射率 1.33,玻璃折射率 1.58。
目前主要的物镜都是玻璃材质,并在物镜与样品之间用与玻璃折射率一致的油来浸润,以提高分辨率。
2012 年 Olympus 发布了一款 NA 高达 1.7 的物镜,光学部分使用蓝宝石(折射率约 1.76)制作,并搭配高折射率的镜油(目测成分应该是二碘甲烷Methylene iodide)。
也许在未来能发明比玻璃更好的材料,折射率更高、易于制作透镜、并且能找到高折射率的油,这样就能进一步提高分辨率。
比如用钻石(折射率大约2.42)打造一枚土豪物镜,并找到同样折射率的透明液体,分辨率可以提高到 1.5 倍。
当然,由于成本及工艺因素,目前尚不现实。
(3) 孔径角看起来的最大值是 90°,但是如果在样品的上下两面都放置物镜,相机同时收集这两个物镜中的光呢?这种方法就是 Stephen Hell 在 1991 年发明的 4 Pi 显微技术。
此时衍射极限的公式稍有变化,分辨率能提高一倍。
简单理解,限制分辨率的一个原因是从物体上向四面八方发射的光线在经过透镜时,由于透镜大小(孔径)的限制,所以很多光线没有经过物体,其承载的物体的“信息”丢失了。
而 4 Pi 其实是通过两个物镜收集了更多的光及“信息”。
每个高 NA 的物镜离物体都非常近,所以几乎能收集到各个角度的光,这也是 4 Pi 这个名称的来历——一个以物体为球心的球体其立体角的大小就是。
另一种“结构照明显微技术(SIM)”很聪明地通过类似摩尔纹的原理,获取到更多“信息”,也可以将分辨率提高一倍。
解释原理需要用到傅里叶光学,在此就不详述了。
它由已故的 Mats Gustafsson 教授于 2000 年发明。
那么问题来了,是否还有办法“真正”突破衍射极限,使之并不受限于这个公式呢?3. 突破光学衍射极限前面的公式推导过程中,有两个隐含条件。
第一个隐含条件是需要用到夫琅禾费衍射,而它也是有条件的,它要求物体与像平面之间的距离远远大于光的波长。
这个条件称为远场条件。
如果离物体足够近,衍射极限便不遵循上述公式。
研究波长以内光传播特性的领域叫近场光学。
Eric Betzig 在 1986 年发明的近场扫描光学显微技术(NSOM)就是使用距离物体远小于波长的光学探针来扫描物体,以达到超分辨的显微图像。
4. 超分辨荧光成像另一个条件则非常隐蔽。
这也是为什么本次诺奖会颁发给几乎没做过超分辨显微技术的 William Moerner 的原因。
首先简单插播一下荧光成像的原理:荧光分子(如获得 2008 年的诺贝尔理综奖的绿色荧光蛋白 GFP)在吸收一个高能量的短波长(如蓝光,称为激发光)跃迁到高能态之后,很快会发射一个低能量的长波长(如绿光,称为发射光)光子回到基态能级。
所以我们可以用蓝光照射样品上标记的 GFP,而接收其发射的绿光,来对物体进行成像。
这样的一个好处就是图像对比度会非常高,只有带有 GFP 的部位会被成像,其它部位都是黑色。
每个荧光分子的发光是完全独立的。
William Moerner 的工作就是推动了对单个分子的成像等研究。
回到前面说的第二个隐藏条件,它假定了图 1 中的物体上的两点 P、Q 同时发光,所以二者的衍射斑才会叠加在一起导致难以区分。
但如果 P、Q 是在不同的时间分别发光,那么可以(通过点扩散函数拟合或者去卷积的方法)精确地定位到每个衍射斑的中心点位置 P'、Q'。
那么也就不存在这样的衍射极限了,理论上即使 P、Q 相距再近都可以被分别定位而加以区分。
更进一步,广义地来说,只要是 P、Q 两点处在可以探测到的不同状态或是不同特征,那么就可以超越衍射极限。
分辨率并不仅仅是关于波的,而且是关于不同状态的!"Resolution is about waves and states." -- by Stefan Hell意识到了这一点,就可以发明很多种真正突破衍射极限的显微技术了。
比如:(1) 区分荧光分子的不同构象/能态荧光分子处在不同构象或能态时,可以发射不同波长的光子,或者不发光。
受激发射耗损显微术(STED):激发光周围套上一圈耗损光,使中心区域的荧光分子处于激发态发光,周围的分子处于耗损态不发光。
这样可以使图 1 中的同心圆表示的衍射斑变小,以此来区分两个相距在衍射极限以内的分子。
这个方法由 Stefan Hell 在 1994 年发明。
随机光学重构显微术(STORM)、光活化定位显微术(PALM)、荧光活化定位显微术(fPALM):它们的共同特征是使样品中每次仅有少量随机、离散的单个荧光分子发光,通过拟合,找出每个荧光分子中心点的位置。
重复拍摄多张图片之后,就可以把所有荧光分子的中心点位置叠加起来形成整幅图像。
这些技术是由庄小威、Eric Betzig 等人在 2006 分别独立发明的。
图 2. 庄小威发明的 STORM 超分辨光学成像效果图。
a, b 为传统光学显微镜拍摄,c, d 为相同区域经 STORM 技术拍摄并重构。
b, d 为 a, c 的局部放大。
图中的结构是细胞内的支架——微管蛋白。
图片来自Nikon MicroscopyU。
RESOLFT:由于 STED 中,耗损光需要很强的亮度,激光器造价昂贵,而且对样品损伤较大,如果借鉴 STORM/PALM/fPALM 的原理,不需要使周围分子处于“耗损态”,而是采用类似于 STORM 等的特殊荧光分子,用较弱的光强使其处于其它能态,也可以实现超分辨。
这也是 Stefan Hell 发明的。
(2) 荧光分子闪烁的不同周期SOFI:有些荧光分子在持续的激发光照射下,并不是持续发光,而是会闪烁。
由于每个荧光分子随机闪烁的时间不一样,可以通过连续拍摄一段录像,分析比较图像中每个像素点记录到的荧光强度在这段时间内的闪烁情况,来区分不同的荧光分子,实现超分辨。
2009 年发明。
(3) 荧光分子的极性/朝向不同SPoD/ExPAN:荧光分子都是偶极子,可以理解成有着不同的朝向。
