上海中考数学二模23题合集
2024年上海市中考数学徐汇区二模卷和参考答案

2023学年第二学期徐汇区学习能力诊断卷初三数学 试卷 2024.4(时间100分钟 满分150分)考生注意∶1.本试卷含三个大题,共25题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的】 1.下列实数中,有理数是(A )3; (B )4; (C )5; (D )6. 2.下列单项式中,与单项式322b a 是同类项的是(A )4ab −; (B )232b a ; (C )233a b ; (D )c b a 222−. 3.已知一次函数b kx y +=的图像经过第一、二、四象限,那么直线k bx y +=经过 (A )第二、三、四象限; (B )第一、二、三象限; (C )第一、二、四象限; (D )第一、三、四象限.4.如表1,记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (A )甲; (B )乙; (C )丙; (D )丁. 5.如图,□ABCD 的对角线AC 、BD 相交于点O ,如果添加一个条件使得□ABCD 是矩形,那么下列添加的条件中正确的是 (A )︒=∠+∠90ADO DAO ; (B )ACD DAC ∠=∠; (C )BAC DAC ∠=∠; (D )ABC DAB ∠=∠. 6.如图,一个半径为cm 9的定滑轮由绳索带动重物上升,如果该定滑轮逆时针旋转了︒120,假设绳索(粗细不计)与滑轮之间没有滑动,那么重物上升的高度是 (A )π5 cm ; (B )π6 cm ; (C )π7cm ; (D )π8cm .表1 甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差统计表BOACD(第5题图)(第6题图)二、填空题(本大题共12题,每题4分,满分48分) 7.方程012=−−x x 的根是___▲___. 8.不等式组⎩⎨⎧>−−>−1)3(23,312x x x 的解集是___▲___.9.方程组⎩⎨⎧=−=+02,522y x y x 的解是____▲____.10.关于x 的一元二次方程012=−−mx x 根的情况是:原方程__▲___实数根.11.如果二次函数1422+−=x x y 的图像的一部分是上升的,那么x 的取值范围是▲_.12.如果反比例函数xy 4−=的图像经过点)2,(t t A −,那么t 的值是____▲_____. 13.如果从长度分别为2、4、6、7的四条线段中任意取出三条,那么取出的三条线段能构成三角形的概率是__▲__.14.小杰沿着坡比4.2:1=i 的斜坡,从坡底向上步行了130米,那么他上升的高度是▲米. 15.某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查, 每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如图1、图2所示的两幅不完整的统计图.如果该校共有2000名学生,那么可以估计该校对手机持“严格管理”态度的家长有__▲__人.16.如图,梯形ABCD 中,AD BC //,CD AB =,AC 平分BAD ∠,如果AB AD 2=,a AB=,b AD =,那么AC 是_▲_(用向量a 、b 表示). 17.如图,在ABC ∆中,6==AC AB ,4=BC . 已知点D 是边AC 的中点,将ABC ∆沿直线BD 翻折,点C 落在点E 处,联结AE ,那么AE 的长是_▲__. 18.如图,点A 是函数)0(8<−=x x y 图像上一点,联结OA 交函数)0(1<−=x xy 图像于 点B ,点C 是x 轴负半轴上一点,且AO AC =,联结BC ,那么ABC ∆的面积是_▲_.(第16题图)D AB C(第17题图)AB C (第15题图1)不管询问 管理(第15题图2) 25℅ 从来 不管 严格 管理稍加 询问三、(本大题共7题,第19—22题每题10分;第23、24题每题12分;第25题14分;满分78分) 19.(本题满分10分)计算:212218−+−−π.20.(本题满分10分)解方程:21416222+=−−−+x x x x . 21.(本题满分10分)如图,⊙1O 和⊙2O 相交于点A 、B ,联结AB 、21O O 、2AO ,已知48=AB ,5021=O O ,302=AO .(1)求⊙1O 的半径长;(2)试判断以21O O 为直径的⊙P 是否经过点B ,并说明理由. 22.(本题满分10分)A 市“第××届中学生运动会”期间,甲校租用两辆小汽车(设每辆车的速度相同)同时出发送8名学生到比赛场地参加运动会,每辆小汽车限坐4人(不包括司机),其中一辆小汽车在距离比赛场地15千米的地方出现故障,此时离截止进场的时刻还有42分钟,这时唯一可利用的交通工具是另一辆小汽车.已知这辆车的平均速度是每小时60千米,人步行的平均速度是每小时5千米(上、下车时间忽略不计).(1)如果该小汽车先送4名学生到达比赛场地,然后再回到出故障处接其他学生,请你判断他们能否在截止进场的时刻前到达?并说明理由;(2)试设计一种运送方案,使所有参赛学生能在截止进场的时刻前到达比赛场地,并说明方案可行性的理由. 23.(本题满分12分) 如图,在菱形ABCD 中,点E 、G 、H 、F 分别在边AB 、BC 、CD 、DA 上,AF AE =,CH CG =,AE CG ≠. (1)求证:GH EF //; (2)分别联结EG 、FH ,求证:四边形EGHF 是等腰梯形.(第23题图)E A B C DFGH (第21题图)AB1O 2O24.(本题满分12分)如图,在平面直角坐标系xOy 中,抛物线)0(442>+−=a ax ax y 与x 轴交于点)0,1(A 和点B ,与y 轴交于点C .(1)求该抛物线的表达式及点B 的坐标;(2)已知点),0(m M ,联结BC ,过点M 作BC MG ⊥,垂足为G ,点D 是x 轴上的动点,分别联结GD 、MD ,以GD 、MD 为边作平行四边形GDMN .① 当23=m 时,且□GDMN 的顶点N 正好落在y 轴上,求点D 的坐标; ② 当0≥m 时,且点D 在运动过程中存在唯一的位置,使得□GDMN 是矩形,求m 的值.25.(本题满分14分)如图,在扇形OAB 中, 26==OB OA ,︒=∠90AOB ,点C 、D 是弧AB 上的动点(点C 在点D 的上方,点C 不与点A 重合,点D 不与点B 重合),且︒=∠45COD . (1)①请直接写出弧AC 、弧CD 和弧BD 之间的数量关系;②分别联结AC 、CD 和BD ,试比较BD AC +和CD 的大小关系,并证明你的结论; (2)联结AB 分别交OC 、OD 于点M 、N .①当点C 在弧AB 上运动过程中, BM AN ⋅的值是否变化,若变化请说明理由;若不变,请求BM AN ⋅的值;②当5=MN 时,求圆心角DOB ∠的正切值.(第25题图)BA CDO2023学年第二学期徐汇区初三年级数学学科学习能力诊断卷参考答案和评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.D ; 4.A ; 5.D ; 6.B . 二.填空题:(本大题共12题,满分48分) 7.1=x ; 8.2>x ; 9.⎩⎨⎧==1,2y x 或⎩⎨⎧−=−=1,2y x ; 10.有两个不相等的;11.1≥x ; 12.2±; 13.21; 14.50; 15.400;16.b a21+; 17.171710; 18.228−.三、(本大题共7题,第19、20、21、22题每题10分,第23、24题每题12分,第25题14分,满分78分)19. 解:原式21)12(22−+−−=1122++−=2=.20.解:去分母,得216)2(2−=−+x x ;化简,得01032=−+x x ; 解得 51−=x ,22=x ; 经检验,2=x 是原方程的增根;所以,原方程的根是5−=x .21.解:(1)联结1AO ,设21O O 与AB 的交点为C . ∵⊙1O 和⊙2O 相交于点A 、B ,∴2421==AB AC ,AB O O ⊥21; 在2ACO Rt ∆中,︒=∠902ACO ,∴182430222222=−=−=AC AO CO ;∴3218502211=−=−=CO O O CO ;在1ACO Rt ∆中,︒=∠901ACO , ∴402432222211=+=+=AC CO AO ;即⊙1O 的半径长为40.(2)以21O O 为直径的⊙P 经过点B .∵535030212==O O AO ,53301822==AO CO ; ∴22212AO CO O O AO =,又A O O C AO 212∠=∠; ∴21O AO ∆∽2ACO ∆;∴︒=∠=∠90221ACO AO O ; 取21O O 的中点P ,联结AP 、BP .∴1PO AP =; 又21O O 垂直平分AB ,1PO AP BP ==; ∴以21O O 为直径的⊙P 经过点B .22.解:(1)他们不能在截止进场的时刻前到达比赛场地.∵单程送达比赛场地的时间是:)(15)(25.06015分钟小时==÷; ∴送完另4名学生的时间是:)(42)(45315分钟分钟>=⨯:∴他们不能在截止进场的时刻前到达比赛场地. (2)方案不唯一.如:先将4名学生用车送达比赛场地,另外4名学生同时步行前往比赛场地, 汽车到比赛场地后返回到与另外4名学生的相遇处再载他们到比赛场地.(用 这种方案送这8名学生到达比赛场地共需时间约为4.40分钟).理由如下:先将4名学生用车送达比赛场地的时间是:)(15)(25.06015分钟小时==÷ 此时另外4名学生步行路程是:25,125,05=⨯(千米);设汽车与另外4名学生相遇所用时间为t 小时.则25.115605−=+t t ;解得5211=t (小时)13165=(分钟); 从相遇处返回比赛场地所需的时间也是13165(分钟);所以,送这8名学生到达比赛场地共需时间为:4.4021316515≈⨯+(分钟); 又424.40<;所以,用这种方案送这8名学生能在截止进场的时刻前到达比赛场地.23.证明:(1)联结BD .∵四边形ABCD 是菱形, ∴CD BC AD AB ===;又AF AE =,CH CG =,∴AD AF AB AE =,CDCHCB CG =; ∴BD EF //,BD GH //; ∴GH EF //.(2)∵BD EF //,∴AB AEBD EF =; ∵BD GH //,∴BCCGBD GH =;又AE CG ≠,∴GH EF ≠; 又GH EF //,∴四边形EGHF 是梯形; ∵AF AD AE AB −=−,即DF BE =; 又CH CD CG BC −=−,即DH BG =; ∵四边形ABCD 是菱形,∴D B ∠=∠; ∴DHF BGE ∆≅∆;∴FH EG =; ∴梯形EGHF 是等腰梯形.24.解:(1)由题意,得044=+−a a ;解得34=a ;∴抛物线的表达式为4316342+−=x x y ; ∵抛物线的对称轴是直线2=x ,∴点)0,3(B . (2)①由题意,得)4,0(C 、)23,0(M ,∴25=CM ; ∵四边形GDMN 是平行四边形,∴NM GD //; 又点N 在y 轴上,∴OD NM ⊥;∴OD GD ⊥; 在BOC Rt ∆中。
上海市2024年黄浦区中考数学二模试卷

上海市2024年黄浦区中考数学二模试卷考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.多项式的因式分解与整式乘法是互逆的.在整式乘法中,“单项式乘以多项式”所对应的互逆因式分解方法是(▲)(A)提取公因式法:(B)公式法;(C)十字相乘法;(D)分组分解法.2.已知第二象限内点P到x轴的距离为2,到y轴的距离为3,那么点P的坐标是(▲)(A)(-2,3);(B)(-3,2);(C)(2,-3);(D)(3,-2).3.如图1,一个3×5的网格,其中的12个单位正方形已经被2张“L”型和1张“田字”型纸片互不重叠地占据了.下列有4个均由4个单位正方形所组成的纸片,依次记为型号1、型号2、型号3和型号4.将这4个型号的纸片做平移、旋转,恰能将图1中3个未被占据的单位正方形占据,并且与已有的3张纸片不重叠的是(▲)(A)型号1;(B)型号2;(C)型号3;(D)型号4.4.对于数据:2、2、2、4、5、6、8、8、9、100,能较好反映这组数据平均水平的是(▲)(A)这组数据的平均数;(B)这组数据的中位数;(C)这组数据的众数;(D)这组数据的标准差.5.反比例函数=1的图像有下述特征:图像与x轴没有公共点且与x轴无限接近.下列说明这一特征的理由中,正确的是(▲)(A)自变量x≠0且x的值可以无限接近0;(B)自变量x≠0且函数值y可以无限接近0;(C)函数值y≠0且x的值可以无限接近0;(D)函数值y≠0且函数值y可以无限接近0.6.小明在研究梯形的相似分割问题,即如何用一条直线将一个梯形分割成两个相似的图形.他先从等腰梯形开始进行探究,得到下面两个结论.结论1:存在与上、下底边相交的直线,能将等腰梯形分割成两个相似的图形;结论2:不存在与两腰相交的直线,能将等腰梯形分割成两个相似的图形.对这两个结论,你认为(▲)(A)结论1、结论2都正确;(B)结论1正确、结论2不正确;(C)结论1不正确、结论2正确;(D)结论1、结论2都不正确.二、填空题:(本大题共12题,每题4分,满分48分)7.100的平方根是▲.8.计算:−X²=.9.方程=+2的解是▲.10.已知关于x的方程.W+B−1=0,判断该方程的根的情况是▲.11.将直线y=2x向上平移2个单位,所得直线与x轴、y轴所围成的三角形面积是▲.12.一副52张的扑克牌(无大、小王)被任意打乱后背面朝上放在桌上,小华先从中抽取1张,取得的是黑桃A.然后小王从剩下的牌中再任意抽取1张,他恰好抽到A的概率是▲.13.小黄对学校提供午餐中的主食、荤菜、蔬菜和汤,开展了一次满意度调查.他利用中午休息时间,随机对学校中50名学生做了问卷调查,汇总数据如下表.如果学校共有1400名学生,那么全校对午餐中主食满意的学生约有▲名.类别主食荤菜蔬菜汤满意人数16520814.现有一张矩形纸片,其周长为36厘米,将纸片的四个角各剪下一个边长为2厘米的正方形,然后沿虚线(如图2所示)将纸片折成一个无盖的长方体.如果所得的长方体的体积是48立方厘米,设原矩形纸片的长是x厘米,那么可列出方程为▲.15.如图3,D、E分别是△ABC边AB、AC上点,满足,A=2A,∠A=∠Bu记B = ,B = ,那么向量B =¯(用向量a、b表示).16.如图4,正六边形MNPQRS位于正方形ABCD内,它们的中心重合于点O,且.M‖B.已知正方形ABCD的边长为a,正六边形MNPQRS的边长为b,那么点P到边CD的距离为▲.(用a、b 的代数式表示)17.如图5,由4个全等的直角三角形拼成一个大正方形ABCD,内部形成一个小正方形MNPQ.如果正方形MNPQ的面积是正方形ABCD面积的一半,那么.∠ABM的正切值是▲.18.如图6,D是等边△ABC边BC上点,BD:CD=2:3,作AD的垂线交AB、AC分别于点E、F,那么AE:AF=▲.三、解答题:(本大题共7题,满分78分)19.(本题满分10分)+2024−20240.计算:|1−tan60∘|20.(本题满分10分)解不等式组:−5≤0,+1−23<021.(本题满分10分).如图7,D是△ABC边AB上点,已知∠BCD=∠A,AD=5,BD=4.(1)求边BC的长;(2)如果△ACD∽△CBD(点A、C、D对应点C、B、D),求∠ACB的度数.网络平台上有一款代金券,主打的广告语是“满80团1张”.规则如下:在平台可以花75元团购一张80元代金券,一张代金券在平台商城内可以抵80元消费额,每笔消费可用于抵扣的代金券数量不限,但不找零.(1)在平台商城一笔375元的消费,如果使用4张代金券,实际共支付了多少元?(2)在充分使用代金券的情况下,在平台商城一笔x元的消费与实际总支付y元间存在着依赖关系,当320<x<375时,写出y关于x的函数关系式;(3)广告语是“满80团1张”.如果在平台商城一笔消费未满80元,那么是不是就一定没必要“团”哪?说说你的理由.23.(本题满分12分)如图8,M、N分别是平行四边形ABCD边AD、BC的中点,对角线BD交AN、CM分别于点P、Q.(1)求证:P=13A;(2)当四边形ANCM是正方形时,试从内角大小和邻边的数量关系的角度探究平行四边形ABCD的形状特征.问题:已知抛物线L:=W−2u抛物线W的顶点在抛物线L上(非抛物线L的顶点)且经过抛物线L的顶点.请求出一个满足条件的抛物线W的表达式.(1)解这个问题的思路如下:先在抛物线L上任取一点(非顶点),你所取的点是①;再将该点作为抛物线W的顶点,可设抛物线W的表达式是②;然后求出抛物线L的顶点是③;再将抛物线L的顶点代入所设抛物线W的表达式,求得其中待定系数的值为④;最后写出抛物线W的表达式是⑤.(2)用同样的方法,你还可以获得其他满足条件的抛物线W,请再写出一个抛物线W的表达式.(3)如果问题中抛物线L和W在x轴上所截得的线段长相等,求抛物线W的表达式.25.(本题满分14分)的中点分别为M、N,MN与AB、OA、已知:如图10,△B是圆O的内接三角形,B=B,弧B、BAC分别交于点P、T、Q.(1)求证:B⊥M;(2)当△B是等边三角形时,求A A的值;(3)如果圆心O到弦BC、MN的距离分别为7和15,求线段PQ的长.。
2019年上海各区初三二模数学试卷23题专题汇编(教师版)

2019年上海各区初三二模数学试卷23题专题汇编(教师版)崇明23.(本题满分12分,每小题满分各6分)如图7,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,对角线AC 、BD 相交于点O . 过点D 作DE BC ⊥,交AC 于点F . (1)联结OE ,若BE AOEC OF=,求证:OE CD ∥; (2)若AD CD =且BD CD ⊥,求证:AF DFAC OB=. 23.(本题满分12分,每小题满分各6分) 证明(1)∵90ABD ∠=︒,BC DE ⊥∴//AB DE ………………………………………………………………(1分) ∴AO BOOF OD=………………………………………………………………(2分) ∵BE AOEC OF =∴AO BEOF EC=……… ………………………………………………………(2分) ∴//OE CD …………………………………………………………………(1分) (2)∵BC AD //,//AB DE ,∴四边形ABED 为平行四边形 又∵90ABD ∠=︒∴四边形ABED 为矩形 ……………………………………………………(1分) ∴AD BE =,90ADE ∠=︒ 又∵CD BD ⊥∴90BDC BDE CDE ∠=∠+∠=︒︒=∠+∠=∠90BDE ADB ADE∴CDE ADB ∠=∠ …………………………………………………………(1分)AD CD =∴DCA DAC ∠=∠∴()A S A CDF ADO ..∆≅∆…………………………………………………(1分) ∴OD DF =DE AB //ABCDOE F图7∴AF BE ADAC BC BC==…………………………………………………………(1分) ∵BC AD //∴BODFBO OD BC AD ==…………………………………………………………(1分) ∴AF DFAC OB=…………………………………………………………………(1分) 奉贤23.(本题满分12分,每小题满分各6分)已知:如图8,正方形ABCD ,点E 在边AD 上,AF ⊥BE ,垂足为点F ,点G 在线段BF 上,BG=AF .(1)求证:CG ⊥BE ;(2)如果点E 是AD 的中点,联结CF ,求证:CF=CB .23.证明:(1)∵四边形ABCD 是正方形,∴AB BC =.90ABC. ··········· (1分) ∵AF ⊥BE ,∴90FAB FBA ∠+∠=︒.∵90FBA CBG ∠+∠=︒,∴FAB CBG ∠=∠. ································ (1分) 又∵AF BG =,∴△AFB ≅△BGC . ············································· (2分)∴AFB BGC ∠=∠. ······································································· (1分) ∵90AFB ∠=︒,∴90BGC ∠=︒,即CG ⊥BE . ······························· (1分) (2)∵ABF EBA ∠=∠,90AFB BAE ∠=∠=︒,∴△AEB ∽△FAB .∴AE AFAB BF=. ················································· (3分) ∵点E 是AD 的中点,AD AB =,∴12AE AB =.∴12AF BF =.··················· (1分) ∵AF BG =,∴12BG BF =,即FG BG =.············································ (1分) ∵CG ⊥BE ,∴CF CB =. ······························································· (1分)ABCD FG E 图8闵行(本题共2小题,每小题6分,满分12分)如图,已知四边形ABCD 是菱形,对角线BD AC 、相交于点O ,AC BD 2=,过点A 作CD AE ⊥,垂足为点E ,AE 与BD 相交于点F ,过点C 作AC CG ⊥,与AE 的延长线相交于点G . 求证:(1)DOA ACG ∆∆≌;(2)AG DE BD DF ⋅=⋅223.证明:(1)在菱形ABCD 中,AD = CD ,AC ⊥BD ,OB = OD .∴ ∠DAC =∠DCA ,∠AOD = 90°.……………………………(1分) ∵ AE ⊥CD ,CG ⊥AC ,∴ ∠DCA +∠GCE = 90°,∠G +∠GCE = 90°.∴ ∠G =∠DCA .…………………………………………………(1分) ∴ ∠G =∠DAC .…………………………………………………(1分) ∵ BD = 2AC ,BD = 2OD ,∴ AC = OD . ……………………(1分) 在△ACG 和△DOA 中,∵ ∠ACG =∠AOD ,∠G =∠DAC ,AC = OD ,∴ △ACG ≌△DOA . ……………………………………………(2分) (2)∵ AE ⊥CD ,BD ⊥AC ,∴ ∠DOC =∠DEF = 90°.…………(1分) 又∵ ∠CDO =∠FDE ,∴ △CDO ∽△FDE .…………………(1分)∴ CD OD DF DE=.即得 OD DF DE CD ⋅=⋅. ……………………(2分) ∵ △ACG ≌△DOA ,∴ AG = AD = CD . ……………………(1分)又∵ 12OD BD =,∴ 2DF BD DE AG ⋅=⋅.…………………(1分)嘉定23.(本题满分12分,第(1)小题6分、第(2)小题6分)如图6,在矩形ABCD 中,点E 是边AB 的中点,△EBC 沿直线EC 翻折,使B 点落在矩形ABCD 内部的点P 处,联结AP 并延长AP 交CD 于点F ,联结BP 交CE 于点Q . (1)求证:四边形AECF 是平行四边形; (2)如果PE PA =,求证:△APB ≌△EPC .23.(1)证明:由翻折得:EC 垂直平分BP ………………1分∴EQ BQ = ………………1分 ∵点E 为AB 的中点,∴EB AE = ………………1分 ∴EQ 是△ABP 的中位线,∴EC ∥AF ,……………1分 ∵四边形ABCD 是矩形∴AE ∥FC ………………1分 ∴四边形AECF 是平行四边形. ………………1分(2)∵AE ∥FC ,∴EQB APB ∠=∠ ………………1分由翻折得: ︒=∠90EQB ,︒=∠90EPC∴︒=∠=∠90EPC APB ………………1分 由翻折得:EB PE =,BEC PEC ∠=∠∵PE PA =,EB AE = ∴AE PE PA ==∴△AEP 是等边三角形,∴︒=∠=∠60AEP PAB …………1分 ∵︒=∠+∠+∠180BEC PEC AEP∴︒=∠60PEC ………………1分AB DCF PEQ图6∴PEC PAB ∠=∠ ………………1分 ∵PE PA =,∴△APB ≌△EPC ………………1分 黄埔23.(本题满分12分)如图6,已知四边形ABCD ,AD ∥BC ,对角线AC 、BD 交于点O ,DO =BO ,过点C 作CE ∥AC ,交BD 的延长线于点E ,交AD 的延长线于点F ,且满足DCE ACB ∠=∠. (1)求证:四边形ABCD 是矩形; (2)求证:DE ADEF CD=.23. 证明:(1)∵AD ∥BC ,∴AD DOBC BO=, ∵DO =BO ,∴AD BC =,--------------------(2分)∴四边形ABCD 是平行四边形. ------------------------------------------------------------------------(1分) ∵CE ⊥AC ,∴90ACD DCE ∠+∠=︒,∵DCE ACB ∠=∠,∴90ACB ACD ∠+∠=︒,即90BCD ∠=︒,------------------------(2分) ∴四边形ABCD 是矩形. --------------------------------------------------------------------------------------(1分)(2)∵四边形ABCD 是矩形,∴AC BD =,90ADC ∠=︒---------------------------------------(2分)∵AD ∥BC ,∴DE EFBD FC=.--------------------------------------------------------------------------------(1分) ∴DE EFAC FC =,------------------------------------------------------------------------------------------------(1分) ∴DE AC EF FC=,∵90ADC ACF ∠=∠=︒, ∴cot AC ADDAC FC CD∠==,----------------------------------------------------------------------------------(1分) ∴DE AD EF CD =.--------------------------------------------------------------------------------------------------(1分)ABC DEF图6OA B CDO E H F 第23题图金山22. 已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若DBC CAD ∠=∠.(1)求证:ABCD 是正方形.(2)E 是OB 上一点,CE DH ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OF OE =.23.(1)证明:∥四边形ABCD 是菱形,∥BC AD //,DAC BAD ∠=∠2,DBC ABC ∠=∠2; (2分) ∥180=∠+∠ABC DAB ; (1分) ∥DBC CAD ∠=∠;∥ABC BAD ∠=∠, (1分) ∥1802=∠BAD ; ∥90=∠BAD ; (1分) ∥四边形ABCD 是正方形. (1分) (2)证明:∥四边形ABCD 是正方形;∥BD AC ⊥,BD AC =,AC CO 21=,BO DO 21=; (1分) ∥90=∠=∠DOC COB ,DO CO =; (1分) ∥CE DH ⊥,垂足为H ;∥90=∠DHE ,90=∠+∠DEH EDH ; (1分) 又∥90=∠+∠DEH ECO ;∥EDH ECO ∠=∠; (1分) ∥ECO ∆≌FDO ∆; (1分) ∥OF OE =. (1分)普陀23.(本题满分12分)已知:如图10,在四边形ABCD 中,AD BC <,点E 在AD 的延长线上, ACE BCD ∠=∠,EC ED EA =⋅2. (1)求证:四边形ABCD 为梯形; (2)如果EC ABEA AC=,求证:AB ED BC =⋅2.23.证明:(1)∵ ACE BCD ∠=∠,∴DCE BCA ∠=∠. ········································· (1分)∵EC ED EA =⋅2,∴ED ECEC EA=. ······················································ (1分) 又∵E ∠是公共角,∴△EDC ∽△ECA . ·············································· (1分) ∴DCE CAE ∠=∠. ········································································· (1分) ∴BCA CAE ∠=∠.∴AD ∥BC . ·················································································· (1分) ∵AD BC <,∴AB 与CD 不平行.∴四边形ABCD 是梯形. ····································································· (1分) (2)∵△EDC ∽△ECA .∴EC CDEA AC =. ∵EC AB EA AC=,∴AB DC =.··························································· (1分) ∴四边形ABCD 是等腰梯形. ···························································· (1分) ∴B DCB ∠=∠. ··········································································· (1分) ∵AD ∥BC .∴EDC DCB ∠=∠.图10A BCD E∴EDC B ∠=∠.∵ECD ACB ∠=∠,∴△EDC ∽△ABC . ········································ (1分) ∴ED DCAB BC=. ··············································································· (1分) ∴AB ED BC =⋅2. ······································································ (1分) 徐汇22. (本题满分(12分),第(1)题满分6分,第(2)小题满分6分) 如图,已知梯形ABCD 中,E AC AB BC AD ,,=∥是边BC 上的点,且CAD AED ∠=∠,DE 交AC 于点F(1) 求证:DAF ABE ∽△△(2) 当EC AE FC AC ⋅=⋅时,求证:BE AD = 23. :(1)BC AD // ACB CAD ∠=∠∴ AC AB = ACB B ∠=∠∴ 又CAD AED ∠=∠CAD AED ACB B ∠=∠=∠=∠∴ 又CED AED BAE B ∠+∠=∠+∠ CED BAE ∠=∠∴又BC AD // CED ADF ∠=∠∴ ADF BAE ∠=∠∴ CAD ABE ∠=∠ ABE ∆∴相似于DAF ∆(2)由(1)知ABE ∆∴相似于DAF ∆AF BE AD AB =∴AFADBE AB =∴ BC AD // FC AF EC AD =∴FCECAF AD =∴ FC ECBE AB =∴ 由(1)知:CED BAE CED B ∠=∠∠=∠,ABE ∆∴相似于ECF ∆ FC BE EC AB =∴ FCEC BE AB =∴ EC AE FC AC ⋅=⋅ FCECAE AC =∴AEAC BE AB =∴ 又AC AB = AE BE =∴ BAE B ∠=∠∴又AED B ∠=∠ AED BAE ∠=∠∴DE AB //∴ 又BC AD //∴四边形ABED 是平行四边形 BE AD =∴杨浦1、 (本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在ABC 中,AB=BC ,∠ABC=90°,点D 、E 分别是AB 、BC 的中点,点F 、G 是边AC 的三等分点,DF 、EG 的延长线相交于H ,联结HA 、HC 求证:(1)四边形FBGH 是菱形 (2)四边形ABCH 是正方形23.证明(1):∵点F 、G 是边AC 的三等分点,∴F 、G 分别是AG 、CF 的中点, ∵点D 是AB 的中点,∴DF //BG ,即FH //BG . ........................ (2分)同理: GH // BF . ........................................................................... (1分) ∴四边形FBGH 是平行四边形. .................................................. (1分) ∵AB =BC ,∴∠BAC =∠ACB .∵点F 、G 是边AC 的三等分点,∴AF =CG .∴△ABF ≌△CBG . ∴BF =BG. .................................................... (1分) ∴平行四边形FBGH 是菱形. ....................................................... (1分)证明(2)联结BH ,交FG 于点O ,∵四边形FBGH 是平行四边形,∴OB =OH ,OF =OG . ............ (2分) ∵AF =CG ,∴OA =OC . ................................................................. (1分) ∴四边形ABCH 是平行四边形. .................................................. (1分) ∵∠ABC =90°,∴平行四边形ABCH 是矩形. .......................... (1分)∵AB =BC ,∴矩形ABCH 是正方形. (1分)长宁23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图5,平行四边形ABCD 的对角线BD AC 、交于点O ,点E 在边CB 的延长线上,且︒=∠90EAC ,EC EB AE ⋅=2. (1)求证:四边形ABCD 是矩形;(2)延长AE DB 、交于点F ,若AC AF =,求证:BF AE =.23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵EC EB AE ⋅=2 ∴AEEB EC AE =又 ∵CEA AEB ∠=∠ ∴AEB ∆∽CEA ∆ (2分) ∴EAC EBA ∠=∠∵︒=∠90EAC ∴︒=∠90EBA (1分) 又 ∵︒=∠+∠180CBA EBA ∴︒=∠90CBA (1分) ∵四边形ABCD 是平行四边形∴四边形ABCD 是矩形 (1分)(2)∵ AEB ∆∽CEA ∆ ∴ AC AB AE BE = 即 ACAE AB BE = , ECA EAB ∠=∠ (2分)∵四边形ABCD 是矩形 ∴BD AC =又 ∵BD OB 21=, AC OC 21= ∴OC OB = ∴ECA OBC ∠=∠ 又 ∵OBC EBF ∠=∠ ECA EBA ∠=∠ ∴EAB EBF ∠=∠又∵F F ∠=∠ ∴EBF ∆∽BAF ∆ (3分)∴AB BE AF BF = ∴ACAEAF BF =(1分) ∵AC AF = ∴AE BF = (1分)图5AB CDE FO宝山23.(本题满分12分,第(1)、第(2)小题满分各6分)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,联结AP 并延长AP 交CD 于F 点, (1)求证:四边形AECF 为平行四边形;(2)如果P A=PC ,联结BP ,求证:∥APB ≅∥EPC .第23题图23.(1)证明:由折叠得到EC 垂直平分BP , ………………1分 设EC 与BP 交于Q ,∥BQ=EQ ………………1分 ∥E 为AB 的中点, ∥AE =EB , ………………1分 ∥EQ 为∥ABP 的中位线,∥AF ∥EC , ………………2分 ∥AE ∥FC , ∥四边形AECF 为平行四边形; ………………1分 (2)∥AF ∥EC ,∥∥A PB =∥EQB =90° ………………1分由翻折性质∥E PC =∥EBC =90°,∥PEC =∥BEC ………………1分 ∥E 为直角∥APB 斜边AB 的中点,且AP =EP ,∥∥AEP 为等边三角形 , ∥BAP =∥AEP =60°, ………………1+1分︒=︒-︒=∠=∠60260180CEB CEP ………………1分 在∥ABP 和∥EPC 中, ∥BAP =∥CEP ,∥APB=∥E PC ,AP =EP ∥∥ABP ∥∥EPC (AAS ), ………………1分松江23.(本题满分12分,每小题各6分)如图,已知□ABCD 中,AB=AC ,CO ⊥AD ,垂足为点O ,延长CO 、BA 交于点E ,联结DE . (1)求证:四边形ACDE 是菱形;(2)联结OB ,交AC 于点F ,如果OF=OC ,求证:22AB BF BO =⋅.23.证明:(1)∵四边形ABCD 是平行四边形∴AB ∥DC ,AB=DC ………………………………………………………………(1分) ∵AB=AC ,∴AC=DC ……………………………………………………………(1分) ∵CO ⊥AD ,∴AO=DO …………………………………………………………(1分) ∵EO AOCO DO=,∴EO=CO ………………………………………………………(1分) ∴四边形ACDE 是平行四边形……………………………………………………(1分) ∵AC=DC ,∴四边形ACDE 是菱形……………………………………………(1分) (2)∵ OF=OC ,∴∠OFC=∠OCF ……………………………………………(1分) ∵AE=AC ,∴∠OCF=∠BEO∵∠OFC=∠BF A ,∴∠BF A=∠BEO …………………………………………(1分) ∵∠ABF=∠OBE …………………………………………………………………(1分) ∴△BF A ∽△BEO ,∴AB BFBO BE=………………………………………………(1分) ∴AB ·BE=BF ·BO ,∵AE=AC=AB ,∴BE=2AB ………………………………(1分) ∴22AB BF BO =⋅………………………………………………………………(1分)(第23题图)OECBA静安22.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)已知:如图5,在矩形ABCD 中,过AC 的中点M 作EF ⊥AC , 分别交AD 、BC 于点E 、F . (1)求证:四边形AECF 是菱形; (2)如果2CD BF BC =⋅,求∠BAF 的度数.22.(本题满分10分,第(1)小题5分,第(2)小题5分) 证明:(1)∵四边形ABCD 为矩形,∴AD //BC , ∴∠1=∠2...........................................(1分)∵点M 为AC 的中点,∴AM =CM .在△AME 与△CMF 中,12AM CM AME CMF ∠=∠⎧⎪=⎨⎪∠=∠⎩..............................................(1分) ∴△AME ≌△CMF ...........................................(1分) ∴AE =CF .∴四边形AECF 为平行四边形. ·································································· (1分) 又∵EF ⊥AC ,∴平行四边形AECF 为菱形. ····································································· (1分) (2)∵2CD BF BC =⋅,∴CD BC BF CD =.又∵四边形ABCD 为矩形,∴AB =CD ,∴AB BC BF AB =. ··········································································· (1分)又∵∠ABF =∠CBA ,∴△ABF ∽△CBA . ·················································································· (1分) ∴∠2=∠3. ···························································································· (1分) ∵四边形AECF 为菱形,∴∠1=∠4,即∠1=∠3=∠4. ····································································· (1分) ∵四边形ABCD 为矩形, ∴∠BAD =∠1+∠3+∠4=90°,∴即∠1=30°. ······················································································· (1分)图5CFEDA BM图5CF EDA B M 124323.(本题满分12分,第(1)小题满分8分,第(2)小题满分4分)已知:如图6,△ABC 内接于⊙O ,AB ﹦AC ,点E 为弦AB 的中点,AO 的延长线交BC 于点D ,联结ED .过点B 作BF ⊥DE 交AC 于点F .(1)求证:∠BAD ﹦∠CBF ; (2)如果OD ﹦DB .求证:AF =BF .证明:(1)∵AB ﹦AC , ∴AB AC =. ........................(1分)∵直线AD 经过圆心O , ..................................................(1分) ∴AD ⊥BC ,BD=CD . ....................................................(1分) ∵点E 为弦AB 的中点, ∴DE 是△ABC 的中位线. ∴DE ∥AC . ......................................................................(1分) ∵BF ⊥DE ,∴∠1=90°, ∴∠2=90°.......................................................................(1分) ∴∠CBF +∠ACB ﹦90°.∵AB ﹦AC ,∴∠ABC ﹦∠ACB , .....................................(1分)∴∠CBF +∠ABC ﹦90°..................................................(1分)又∵AD ⊥BC ,∴∠BAD +∠ABC ﹦90°,∴∠BAD ﹦∠CBF ..............................................................(1分)(2)联结OB .∵AD ⊥BC ,OD ﹦DB ,∴△ODB 是等腰直角三角形........................................................................................................(1分)∴∠BOD ﹦45°. ∵OB=OA ,∴∠OBA ﹦∠OAB .∵∠BOD ﹦∠OBA +∠OAB ,∴∠BAO=12∠BOD=22.5°. .....................................................................................................(1分)∵AB=AC ,且AD ⊥BC , ∴∠BAC=2∠BAO=45°. ∵∠2=90°,即BF ⊥AC ,∴在△ABF 中,∠ABF =180904545--=,................................................................................(1分)图6BCDEF OA· 图6 B C DE F O A·12OE第23题图 C A B D F∴∠ABF =∠BAC ,∴AF =BF ..........................................................................................................................................(1分) 虹口23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,在□ABCD 中,AC 与BD 相交于点O ,过点B 作BE ∥AC ,联结OE 交BC 于点F ,点F 为BC 的中点.(1)求证:四边形AOEB 是平行四边形;(2)如果∠OBC =∠E ,求证:=BO OC AB FC ⋅⋅.23.(1)证明:∵BE ∥AC ∴OC CFBE BF=∵点F 为BC 的中点 ∴CF=BF ∴OC=BE ∵四边形ABCD 是平行四边形 ∴AO=CO ∴AO=BE∵BE ∥AC ∴四边形AOEB 是平行四边形(2)证明:∵四边形AOEB 是平行四边形 ∴∠BAO =∠E ∵∠OBC =∠E ∴∠BAO =∠OBC∵∠ACB =∠BCO ∴△COB ∽△CBA ∴BO BC AB AC =∵四边形ABCD 是平行四边形 ∴AC =2OC ∵点F 为BC 的中点 ∴BC =2FC ∴BO FC AB OC= 即=BO OC AB FC⋅⋅青浦23.(本题满分12分,第(1)、(2)小题,每小题6分)已知:如图9,在菱形ABCD 中,AB =AC ,点E 、F 分别在边AB 、BC 上,且AE =BF ,CE 与AF 相交于点G . (1)求证:∠FGC =∠B ;(2)延长CE 与DA 的延长线交于点H ,求证:.23.证明:(1)∵四边形ABCD 是菱形, ∴AB =BC . ··········································································· (1分)∵AB =AC ,∴AB =BC =AC ,∴∠B =∠BAC =60°. ··························· (1分) 在△EAC 与△FBA 中,∵EA =FB ,∠EAC =∠FBA ,AC =BA , ∴△EAC ≌△FBA , ································································ (1分) ∴∠ACE =∠BAF ,·································································· (1分) ∵∠BAF+∠F AC =60°,∴∠ACE +∠F AC =60°,∴∠FGC =60°, ······· (1分) ∴∠FGC =∠B . ····································································· (1分) (2)∵四边形ABCD 是菱形,∴∠B =∠D ,AB =DC ,AB //DC , ················································ (1分) ∴∠BEC =∠HCD , ································································· (1分) ∴△BEC ∽△DCH , ······························································· (1分)∴=BE ECDC CH, ····································································· (1分) ∴⋅=⋅BE CH EC DC .∵AB =AC ,∴CD =AC , ··························································· (1分) ∵△EAC ≌△FBA , ∴EC =F A ,∴⋅=⋅BE CH AF AC . ························································· (1分)BE CH AF AC ⋅=⋅GF EDA BC图9。
2019上海数学初三二模第23题汇编

证明题专题1.如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,联结AP 并延长AP 交CD 于F 点, (1)求证:四边形AECF 为平行四边形;(2)如果PA PC =,联结BP ,求证:APC EPC ∆≅∆第23题图【答案】(1)由折叠得到EC 垂直平分BP , ………………1分 设EC 与BP 交于Q ,∴BQ EQ = ………………1分 ∵E 为AB 的中点, ∴AE EB =, ………………1分 ∴EQ 为△ABP 的中位线,∴AF ∥EC , ………………2分 ∵AE ∥FC , ∴四边形AECF 为平行四边形; ………………1分 (2)∵AF ∥EC ,∴90APB EQB ∠=∠=︒ ………………1分 由翻折性质90EPC EBC ∠=∠=︒,PEC BEC ∠=∠ ………………1分 ∵E 为直角△ABP 斜边AB 的中点,且=AP EP ,∴△AEP 为等边三角形 , 60BAP AEP ∠=∠=︒, ………………1+1分︒=︒-︒=∠=∠60260180CEB CEP ………………1分在△ABP 和△EPC 中, BAP CEP ∠=∠, APB EPC ∠=∠,AP EP = ∴APC EPC ∆≅∆(AAS ), ………………1分 2.如图7,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,对角线AC 、BD 相交于点O .过点D 作DE BC ⊥,交AC 于点F . (1)联结OE ,若BE AOEC OF=,求证:OE CD ∥; (2)若AD CD =且BD CD ⊥,求证:AF DFAC OB=.【答案】(1)∵90ABD ∠=︒,BC DE ⊥∴//AB DE ………………………………………………………………(1分)∴AO BOOF OD = ………………………………………………………………(2分) ∵BE AOEC OF =∴AO BEOF EC =……… ………………………………………………………(2分)∴//OE CD …………………………………………………………………(1分) (2)∵BC AD //,//AB DE , ∴四边形ABED 为平行四边形 又∵90ABD ∠=︒∴四边形ABED 为矩形 ……………………………………………………(1分) ∴AD BE =,90ADE ∠=︒ 又∵CD BD ⊥∴90BDC BDE CDE ∠=∠+∠=︒ ︒=∠+∠=∠90BDE ADB ADE∴CDE ADB ∠=∠ …………………………………………………………(1分)AD CD =Q∴DCA DAC ∠=∠∴()A S A CDF ADO ..∆≅∆…………………………………………………(1分) ∴OD DF =DE AB //Θ∴AF BE ADAC BC BC ==…………………………………………………………(1分) ∵BC AD //∴BO DFBO OD BC AD ==…………………………………………………………(1分) ∴AF DFAC OB =…………………………………………………………………(1分) 3.如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若DBC CAD ∠=∠.(1)求证:ABCD 是正方形.(2)E 是OB 上一点,CE DH ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OF OE =.【答案】(1)证明:∵四边形ABCD 是菱形,∴BC AD //,DAC BAD ∠=∠2,DBC ABC ∠=∠2………………………………..(2分)∴ο180=∠+∠ABC DAB …………………………………….(1分) ∵DBC CAD ∠=∠;∴ABC BAD ∠=∠……………………………(1分)∴ο1802=∠BAD ; ∴ο90=∠BAD ……………………………………1分) ∴四边形ABCD 是正方形………………………………………(1分) (2)证明:∵四边形ABCD 是正方形;∴BD AC ⊥,BD AC =,AC CO 21=,BO DO 21=…………………………………(1分)∴ο90=∠=∠DOC COB ,DO CO =………………………………………(1分) ∵CE DH ⊥,垂足为H ;∴ο90=∠DHE ,ο90=∠+∠DEH EDH ……………………………………………(1分)又∵ο90=∠+∠DEH ECO ;∴EDH ECO ∠=∠……………………………………………(1分) ∴ECO ∆≌FDO ∆………………………………………………(1分) ∴OF OE =……………………………………………(1分)4.已知:如图6,在直角梯形ABCD 中,AD BC P ,DC BC ⊥,AB AD =,AM BD ⊥,垂足为点M ,联结CM 并延长,交线段AB 于点N 求证:(1)ABD BCM ∠=∠ (2)..BC BN CN DM = 【答案】(1)∵AB AD =,AM BD ⊥∴M 是BD 中点,ABD ADB ∠=∠ ∵DC BC ⊥ ∴BM CM DM == ∴MBC MCB ∠=∠ ∵AD BC P ∴ADB DBC ∠=∠ ∴ABD BCM ∠=∠(2)∵ABD BCM ∠=∠,BNM BNM ∠=∠∴BNM CNB ∆∆: ∴BC CNBM BN=∵DM BM = ∴BC CNDM BN=∴..BC BN CN DM =5.已知:如图8,正方形ABCD ,点E 在边AD 上,AF BE ⊥,垂足为点F ,点G 在线段BF 上,BG AF =.(1)求证:CG BE ⊥;(2)如果点E 是AD 的中点,联结CF ,求证:CF CB =.【答案】(1)∵四边形ABCD 是正方形,∴AB BC =.90ABC??. ········· (1分) ∵AF ⊥BE ,∴90FAB FBA ∠+∠=︒.∵90FBA CBG ∠+∠=︒,∴FAB CBG ∠=∠. ······························ (1分) 又∵AF BG =,∴△AFB ≅△BGC . ············································ (2分) ∴AFB BGC ∠=∠. ····································································· (1分) ∵90AFB ∠=︒,∴90BGC ∠=︒,即CG ⊥BE . ····························· (1分) (2)∵ABF EBA ∠=∠,90AFB BAE ∠=∠=︒,∴△AEB ∽△FAB .∴AE AFAB BF=. ··············································· (3分) ABCDFG E图8∵点E 是AD 的中点,AD AB =,∴12AE AB =.∴12AF BF =. ················ (1分) ∵AF BG =,∴12BG BF =,即FG BG =.·········································· (1分) ∵CG ⊥BE ,∴CF CB =. ····························································· (1分)6. 如图5,平行四边形ABCD 的对角线BD AC 、交于点O ,点E 在边CB 的延长线上,且︒=∠90EAC ,EC EB AE ⋅=2. (1)求证:四边形ABCD 是矩形;(2)延长AE DB 、交于点F ,若AC AF =,求证:BF AE =.【答案】证明:(1)∵EC EB AE ⋅=2 ∴AEEB EC AE =又 ∵CEA AEB ∠=∠ ∴AEB ∆∽CEA ∆ (2分) ∴EAC EBA ∠=∠∵︒=∠90EAC ∴︒=∠90EBA (1分)又 ∵︒=∠+∠180CBA EBA ∴︒=∠90CBA (1分) ∵四边形ABCD 是平行四边形∴四边形ABCD 是矩形 (1分)(2)∵ AEB ∆∽CEA ∆ ∴ AC AB AE BE = 即 ACAE AB BE = , ECA EAB ∠=∠ (2分)∵四边形ABCD 是矩形 ∴BD AC = 又 ∵BD OB 21=, AC OC 21= 图5AB CDEF O∴OC OB = ∴ECA OBC ∠=∠ 又 ∵OBC EBF ∠=∠ ECA EBA ∠=∠ ∴EAB EBF ∠=∠又 ∵F F ∠=∠ ∴EBF ∆∽BAF ∆ (3分) ∴AB BE AF BF = ∴ACAEAF BF =(1分) ∵AC AF = ∴AE BF = (1分)7.如图,已知梯形ABCD 中,AD BC P , AB AC =,E 是边BC 上的点,且AED CAD ∠=∠, DE 交AC 于点F .(1) 求证:ABE DAF ∆∆:;(2) 当..AC FC AE EC =时,求证:AD BE =.【答案】(1)∵AD ∥BC ,∴∠CAD =∠ACB .∵AB =AC ,∴∠B =∠ACB ,∴∠CAD =∠B ∵∠AED =∠CAD ,∴∠B =∠AED∵∠AEC =∠B +∠BAE ,即∠AED +∠DEC =∠B +∠BAE , ∴∠BAE =∠DEC .BE(第23题图)在△AEB 与△EFC 中,B ACEBAE DEC∠=∠⎧⎨∠=∠⎩,∴AEB EFC ∆∆:.∵AD ∥BC ,∴DAF EFC ∆∆: ∴ABE DAF ∆∆:.(2) ∵AEB EFC ∆∆:,∴AB BEEC CF=即AB CF EC BE ⋅=⋅ ∵=AC CF AE EC AB AC ⋅=⋅且,∴AE=BE . ∴∠B =∠BAE∵∠BAE =∠FEC ,∴∠B =∠FEC . ∴AB ∥DE∵AD ∥BC ,∴四边形ABED 是平行四边形 ∴AD =BE .8.如图,已知□ABCD 中,AB=AC ,CO ⊥AD ,垂足为点O ,延长CO 、BA 交于点E ,联结DE .(1)求证:四边形ACDE 是菱形;(2)联结OB ,交AC 于点F ,如果OF=OC , 求证:22AB BF BO =⋅.【答案】证明:(1)∵四边形ABCD 是平行四边形∴AB ∥DC ,AB=DC ………………………………………………………………(1分) ∵AB=AC ,∴AC=DC ……………………………………………………………(1分)∵CO ⊥AD ,∴AO=DO …………………………………………………………(1分) ∵EO AOCO DO=,∴EO=CO ………………………………………………………(1分) ∴四边形ACDE 是平行四边形……………………………………………………(1分) ∵AC=DC ,∴四边形ACDE 是菱形……………………………………………(1分) (2)∵ OF=OC ,∴∠OFC=∠OCF ……………………………………………(1分) ∵AE=AC ,∴∠OCF=∠BEO∵∠OFC=∠BF A ,∴∠BF A=∠BEO …………………………………………(1分) ∵∠ABF=∠OBE …………………………………………………………………(1分) ∴△BF A ∽△BEO ,∴AB BFBO BE=………………………………………………(1分) ∴AB ·BE=BF ·BO ,∵AE=AC=AB ,∴BE=2AB ………………………………(1分) ∴22AB BF BO =⋅………………………………………………………………(1分)9.已知:如图10,在四边形ABCD 中,AD BC <,点E 在AD 的延长线上, ACE BCD ∠=∠,EC ED EA =⋅2. (1)求证:四边形ABCD 为梯形;(2)如果EC ABEA AC=,求证:AB ED BC =⋅2.【答案】(1)∵ ACE BCD ∠=∠,∴DCE BCA ∠=∠. ····························· (1分)图10A BCD E∵EC ED EA =⋅2,∴ED ECEC EA=. ···················································· (1分) 又∵E ∠是公共角,∴△EDC ∽△ECA . ············································ (1分) ∴DCE CAE ∠=∠. ······································································· (1分) ∴BCA CAE ∠=∠.∴AD ∥BC . ················································································ (1分) ∵AD BC <,∴AB 与CD 不平行.∴四边形ABCD 是梯形. ··································································· (1分) (2)∵△EDC ∽△ECA .∴EC CDEA AC=. ∵EC ABEA AC=,∴AB DC =. ························································· (1分) ∴四边形ABCD 是等腰梯形. ·························································· (1分) ∴B DCB ∠=∠. ········································································· (1分) ∵AD ∥BC .∴EDC DCB ∠=∠. ∴EDC B ∠=∠.∵ECD ACB ∠=∠,∴△EDC ∽△ABC . ······································ (1分) ∴ED DCAB BC=. ············································································· (1分) ∴AB ED BC =⋅2. ···································································· (1分)10.如图6,在矩形ABCD 中,点E 是边AB 的中点,△EBC 沿直线EC 翻折,使B 点落在矩形ABCD 内部的点P 处,联结AP 并延长AP 交CD 于点F ,联结BP 交CE 于点Q .(1)求证:四边形AECF 是平行四边形; (2)如果PE PA =,求证:△APB ≌△EPC .【答案】(1)证明:由翻折得:EC 垂直平分BP ………………1分∴EQ BQ = ………………1分∵点E 为AB 的中点,∴EB AE = ………………1分 ∴EQ 是△ABP 的中位线,∴EC ∥AF ,……………1分 ∵四边形ABCD 是矩形∴AE ∥FC ………………1分 ∴四边形AECF 是平行四边形. ………………1分(2)∵AE ∥FC ,∴EQB APB ∠=∠ ………………1分由翻折得: ︒=∠90EQB ,︒=∠90EPC∴︒=∠=∠90EPC APB ………………1分 由翻折得:EB PE =,BEC PEC ∠=∠∵PE PA =,EB AE =ABD CFP E Q图6 ABD CFP E Q图6∴AE PE PA ==∴△AEP 是等边三角形,∴︒=∠=∠60AEP PAB …………1分 ∵︒=∠+∠+∠180BEC PEC AEP∴︒=∠60PEC ………………1分 ∴PEC PAB ∠=∠ ………………1分 ∵PE PA =,∴△APB ≌△EPC ………………1分11.如图,在□ABCD 中,AC 与BD 相交于点O ,过点B 作BE ∥AC ,联结OE 交BC 于点F ,点F 为BC 的中点.(1)求证:四边形AOEB 是平行四边形;(2)如果∠OBC =∠E ,求证:=BO OC AB FC ⋅⋅.【答案】(1)证明:∵BE ∥AC ∴OC CFBE BF=∵点F 为BC 的中点 ∴CF=BF ∴OC=BE ∵四边形ABCD 是平行四边形 ∴AO=CO ∴AO=BE∵BE ∥AC ∴四边形AOEB 是平行四边形(2)证明:∵四边形AOEB 是平行四边形 ∴∠BAO =∠E ∵∠OBC =∠E ∴∠BAO =∠OBC∵∠ACB =∠BCO ∴△COB ∽△CBA ∴BO BCAB AC =∵四边形ABCD 是平行四边形 ∴AC =2OC ∵点F 为BC 的中点 ∴BC =2FC ∴BO FCAB OC= 即=BO OC AB FC⋅⋅12.已知:如图6,△ABC 内接于⊙O ,AB ﹦AC ,点E 为弦AB 的中点,AO 的延长线交BC 于点D ,联结ED .过点B 作BF ⊥DE 交AC 于点F .(1)求证:∠BAD ﹦∠CBF ; (2)如果OD ﹦DB .求证:AF =BF .【答案】证明:(1)∵AB ﹦AC , ∴»»AB AC =. ........................(1分) ∵直线AD 经过圆心O , ..................................................(1分) ∴AD ⊥BC ,BD=CD . ....................................................(1分) ∵点E 为弦AB 的中点,图6BCDEF OA·BCDEFO A· 12∴DE是△ABC的中位线.∴DE∥AC.......................................................................(1分)∵BF⊥DE,∴∠1=90°,∴∠2=90°.......................................................................(1分)∴∠CBF+∠ACB﹦90°.∵AB﹦AC,∴∠ABC﹦∠ACB, .....................................(1分)∴∠CBF+∠ABC﹦90°..................................................(1分)又∵AD⊥BC,∴∠BAD+∠ABC﹦90°,∴∠BAD﹦∠CBF..............................................................(1分)(2)联结OB.∵AD⊥BC,OD﹦DB,∴△ODB是等腰直角三角形...................................................................(1分)∴∠BOD﹦45°.∵OB=OA,∴∠OBA﹦∠OAB.∵∠BOD﹦∠OBA+∠OAB,∠BOD=22.5°.............................................................(1分)∴∠BAO=12∵AB=AC,且AD⊥BC,∴∠BAC=2∠BAO=45°.∵∠2=90°,即BF⊥AC,o o o o,..........................................................(1分)∴在△ABF中,∠ABF=180904545--=∴∠ABF=∠BAC,∴AF=BF.......................................................................................................(1分)13.如图6,已知四边形ABCD ,AD ∥BC ,对角线AC 、BD 交于点O ,DO =BO ,过点C作CE ⊥AC ,交BD 的延长线于点E ,交AD 的延长线于点F ,且满足DCE ACB ∠=∠.(1)求证:四边形ABCD 是矩形;(2)求证:DE ADEF CD=.【答案】证明:(1)∵AD ∥BC ,∴AD DOBC BO=, ∵DO =BO ,∴AD BC =,---(2分) ∴四边形ABCD 是平行四边形. ---------------------------------------------------------------(1分) ∵CE ⊥AC ,∴90ACD DCE ∠+∠=︒,∵DCE ACB ∠=∠,∴90ACB ACD ∠+∠=︒,即90BCD ∠=︒,-------------------(2分) ∴四边形ABCD 是矩形. -----------------------------------------------------------------------(1分)(2)∵四边形ABCD 是矩形,∴AC BD =,90ADC ∠=︒-----------------------(2分) ∵AD ∥BC ,∴DE EFBD FC=.------------------------------------------------------------(1分) ∴DE EFAC FC=,------------------------------------------------------------------------------(1分) ∴DE ACEF FC=,∵90ADC ACF ∠=∠=︒, ∴cot AC ADDAC FC CD∠==,-----------------------------------------------------------(1分) ∴DE ADEF CD=.----------------------------------------------------------------------------(1分)14.已知:如图,在△ABC 中,AB =BC ,∠ABC =90°,点D 、E 分别是边AB 、BC 的中点,点F 、G 是边AC 的三等分点,DF 、EG 的延长线相交于点H ,联结HA 、HC . 求证:(1)四边形FBGH 是菱形; (2)四边形ABCH 是正方形.【答案】证明(1):∵点F 、G 是边AC 的三等分点,∴F 、G 分别是AG 、CF 的中点, ∵点D 是AB 的中点,∴DF //BG ,即FH //BG . ........................ (2分)同理: GH // BF . ........................................................................... (1分) ∴四边形FBGH 是平行四边形. .................................................. (1分) ∵AB =BC ,∴∠BAC =∠ACB .∵点F 、G 是边AC 的三等分点,∴AF =CG .∴△ABF ≌△CBG . ∴BF =BG. ...................................................... (1分) ∴平行四边形FBGH 是菱形. ....................................................... (1分)证明(2)联结BH ,交FG 于点O ,∵四边形FBGH 是平行四边形,∴OB =OH ,OF =OG . ............ (2分) ∵AF =CG ,∴OA =OC . ................................................................. (1分) ∴四边形ABCH 是平行四边形. .................................................. (1分)(第23题图)ADHECFG∵∠ABC =90°,∴平行四边形ABCH 是矩形. ............................ (1分) ∵AB =BC ,∴矩形ABCH 是正方形. ........................................... (1分)15.如图,已知四边形ABCD 是菱形,对角线AC 、BD 相交于点O ,BD = 2AC .过点A 作AE ⊥CD ,垂足为点E ,AE 与BD 相交于点F .过点C 作CG ⊥AC ,与AE 的延长线相交于点G .求证:(1)△ACG ≌△DOA ;(2)2DF BD DE AG ⋅=⋅.【答案】证明:(1)在菱形ABCD 中,AD = CD ,AC ⊥BD ,OB = OD .∴ ∠DAC =∠DCA ,∠AOD = 90°.……………………………(1分) ∵ AE ⊥CD ,CG ⊥AC ,∴ ∠DCA +∠GCE = 90°,∠G +∠GCE = 90°.∴ ∠G =∠DCA .…………………………………………………(1分) ∴ ∠G =∠DAC .…………………………………………………(1分) ∵ BD = 2AC ,BD = 2OD ,∴ AC = OD . ……………………(1分) 在△ACG 和△DOA 中,∵ ∠ACG =∠AOD ,∠G =∠DAC ,AC = OD ,∴ △ACG ≌△DOA . ……………………………………………(2分)ABCDOE GF (第23题)(2)∵ AE ⊥CD ,BD ⊥AC ,∴ ∠DOC =∠DEF = 90°.…………(1分) 又∵ ∠CDO =∠FDE ,∴ △CDO ∽△FDE .…………………(1分)∴CD ODDF DE=.即得 OD DF DE CD ⋅=⋅. ……………………(2分) ∵ △ACG ≌△DOA ,∴ AG = AD = CD . ……………………(1分) 又∵ 12OD BD =,∴ 2DF BD DE AG ⋅=⋅.…………………(1分) 16.已知:如图9,在菱形ABCD 中,AB =AC ,点E 、F 分别在边AB 、BC 上,且AE =BF ,CE 与AF 相交于点G . (1)求证:∠FGC =∠B ;(2)延长CE 与DA 的延长线交于点H ,求证:.【答案】证明:(1)∵四边形ABCD 是菱形,∴AB =BC . ······································································ (1分)∵AB =AC ,∴AB =BC =AC ,∴∠B =∠BAC =60°. ······················ (1分) 在△EAC 与△FBA 中,∵EA =FB ,∠EAC =∠FBA ,AC =BA ,∴△EAC ≌△FBA , ····························································· (1分) ∴∠ACE =∠BAF ,····························································· (1分) ∵∠BAF+∠F AC =60°,∴∠ACE +∠F AC =60°,∴∠FGC =60°, ·· (1分) ∴∠FGC =∠B . ································································ (1分) (2)∵四边形ABCD 是菱形,BE CH AF AC ⋅=⋅GF EDA BC图9∴∠B =∠D ,AB =DC ,AB //DC , ··········································· (1分) ∴∠BEC =∠HCD , ···························································· (1分) ∴△BEC ∽△DCH , ·························································· (1分) ∴=BE ECDC CH, ································································ (1分) ∴⋅=⋅BE CH EC DC .∵AB =AC ,∴CD =AC , ······················································ (1分) ∵△EAC ≌△FBA , ∴EC =F A ,∴⋅=⋅BE CH AF AC . ···················································· (1分)。
上海中考数学二模23题合集
1.已知正方形ABCD的对角线相交于点O,CAB∠的平分线分别交BD、BC于点E、F,作BH AF⊥,垂足为H,BH的延长线分别交AC、CD于点G、P.(1)求证:;(第23题图)B C F2. 已知:如图,梯形ABCD 中,DC ∥AB ,AD=BC=DC ,AC 、BD 是对角线,E 是AB 延长线上一点,且∠BCE =∠ACD ,联结CE . (1)求证:四边形DBEC 是平行四边形; (2)求证:2AC AD AE =⋅.第23题图EDCBA3. 如图,在四边形ABCD 中,AB ∥DC ,E 、F 为对角线BD 上两点,且BE DF =, AF ∥EC .(1)求证:四边形ABCD 是平行四边形;(2)延长AF ,交边DC 于点G ,交边BC 的延长线 于点H ,求证:AD DC BH DG =.A BCEF第23题图DG H4. 如图5,在ABC ∆中,D 、E 分别是AC 、BC 边上的点,AE 与BD 交于点O ,且CD =CE ,12∠=∠.(1)求证:四边形ABED 是等腰梯形;(2)若EC =2,BE =1,21AOD ∠=∠,求AB 的长.图5 AB C DO E125. 如图6,BD 是平行四边形ABCD 的对角线,若∠DBC =45°,DE ⊥BC 于E ,BF ⊥CD 于F ,DE 与BF 相交于H ,BF 与AD 的延长线相交于G . 求证:(1)CD =BH ;(2)AB 是AG 和HE 的比例中项.A图66. 如图, BD是△ABC的角平分线, 点E、F分别在BC、AB上, 且DE∥AB, ∠DEF=∠A. (1)求证: BE=AF ;(2)设BD与EF交于点M, 联结AE, 交BD于点N,求证: BN·MD=BD·ND.M AFB E CD(静安)23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF =DE ,AE 的延长线与DF 相交于点G . (1)求证:∠CDF =∠DAE ;(2)如果DE =CE ,求证:AE =3EG .(闵行)23.(本题满分12分,其中每小题各6分)如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅.(普陀)23.(本题满分12分)如图7,已知在四边形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF ∥AB 分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;(2)设AC AB ⊥,求证:AC OE AB EF =.(第23题图)EDCGFA B(第23题图)AB CDE FGOH(松江)23.(本题满分12分,每小题满分各6分)如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E . (1)求证:∠CAD =∠ECB ;(2)点F 是AC 的中点,联结DF ,求证:BD 2=FC ·BE .(徐汇)23.(本题满分12分)如图7,在ABC ∆中,AC AB =,点D 在边AC 上,DE BD AD ==,联结BE ,︒=∠=∠72DBE ABC .(1)联结CE ,求证:BE CE =;(2)分别延长CE 、AB 交于点F ,求证:四边形DBFE 是菱形.(杨浦)23.(本题满分12分,每小题各6分)已知:如图,在直角梯形纸片ABCD 中,DC //AB ,AB CD AD >>,∠A =90°,将纸片沿过点D 的直线翻折,使点A 落在边CD 上的点E 处,折痕为DF ,联结EF 并展开纸片. (1)求证:四边形ADEF 为正方形;(2)取线段AF 的中点G ,联结GE ,当BG =CD 时, 求证:四边形GBCE 为等腰梯形. CB ADEF(第23题图) (第23题图)图7ABC DE(第23题图)(闸北)23.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.(1)求证:四边形AECD为平行四边形;(2)在CD边上取一点F,联结AF、AC、EF,设AC与EF交于点G,且∠EAF=∠CAD.求证:△AEC∽△ADF;(3)在(2)的条件下,当∠ECA=45°时.求:FG:EG的比值.(浦东)23.(本题满分12分,第(1)、(2)小题各6分)如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA = ∠D.(1)求证:∆EAC∽∆ECB;(2)若DF = AF,求AC︰BC的值.(第23题图)AB CEDFG。
2024年中考数学二模试卷(上海卷)(全解全析)

2024年中考第二次模拟考试(上海卷)数学·全解全析第Ⅰ卷一、选择题(本大题共6个小题,每小题4分,共24分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.在下列图形中,为中心对称图形的是()A .等腰梯形B .平行四边形C .正五边形D .等腰三角形【答案】B【分析】根据中心对称与轴对称的概念和各图形的特点即可求解.【详解】中心对称图形,即把一个图形绕一个点旋转180°后能和原来的图形重合,A 、C 、D 都不符合;是中心对称图形的只有B .故选B .2.下列方程有实数根的是A .4x 20+=B 2x 21-=-C .2x +2x −1=0D .x 1x 1x 1=【答案】C【详解】A .∵x 4>0,∴x 4+2=0无解,故本选项不符合题意;B .∵22x -≥0,∴22x -=−1无解,故本选项不符合题意;C .∵x 2+2x −1=0,∆=8>0,方程有实数根,故本选项符合题意;D .解分式方程1x x -=11x -,可得x =1,经检验x =1是分式方程的增根,故本选项不符合题意.故选C .3.计算:AB BA += ()A .AB ;B .BA ;C .0 ;D .0.【答案】C【分析】根据零向量的定义即可判断.【详解】AB BA += 0 .故选C .4.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是()A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠BAC=∠BCDC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC【答案】C【分析】根据正方形的判定:对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案.【详解】解:A,不能,只能判定为矩形,不符合题意;B,不能,只能判定为平行四边形,不符合题意;C,能,符合题意;D,不能,只能判定为菱形,不符合题意.故选C.5.下列命题中,假命题是()A.如果一条直线平分弦和弦所对的一条弧,那么这条直线经过圆心,并且垂直于这条弦;B.如果一条直线平分弦所对的两条弧,那么这条直线经过圆心,并且垂直于这条弦;C.如果一条直线经过圆心,并且平分弦,那么该直线平分这条弦所对的弧,并且垂直于这条弦;D.如果一条直线经过圆心,并且垂直弦,那么该直线平分这条弦和弦所对的弧.【答案】C【分析】利用垂径定理及其推论逐个判断即可求得答案.【详解】A.如果一条直线平分弦和弦所对的一条弧,那么这条直线经过圆心,并且垂直于这条弦,正确,是真命题;B.如果一条直线平分弦所对的两条弧,那么这条直线一定经过圆心,并且垂直于这条弦,正确,是真命题;C.如果一条直线经过圆心,并且平分弦,那么该直线不一定平分这条弦所对的弧,不一定垂直于这条弦,例如:任意两条直径一定互相平分且过圆心,但不一定垂直.错误,是假命题;D.如果一条直线经过圆心,并且垂直弦,那么该直线平分这条弦和弦所对的弧,正确,是真命题.故选C.【点睛】本题考查了垂径定理及其推论,对于一个圆和一条直线来说如果一条直线具备下列,①经过圆心,②垂直于弦,③平分弦(弦不是直径),④平分弦所对的优弧,⑤平分弦所对的劣弧,五个条件中的任何两个,那么也就具备其他三个.6.如图,已知∠POQ=30°,点A、B在射线OQ上(点A在点O、B之间),半径长为2的⊙A与直线OP 相切,半径长为5的⊙B与⊙A内含,那么OB的取值范围是()A .4<OB <7B .5<OB <7C .4<OB <9D .2<OB <7【答案】A 【分析】作⊙A 半径AD ,根据含30度角直角三角形的性质可得4OA =,再确认⊙B 与⊙A 相切时,OB 的长,即可得结论.【详解】解:设⊙A 与直线OP 相切时的切点为D ,∴AD OP ⊥,∵∠POQ =30°,⊙A 半径长为2,即2AD =,∴24OA AD ==,当⊙B 与⊙A 相切时,设切点为C ,如下图,∵5BC =,∴4(52)7OB OA AB =+=+-=,∴若⊙B 与⊙A 内含,则OB 的取值范围为47OB <<.故选:A .【点睛】本题主要考查了圆与圆的位置关系、切线的性质、含30度角的直角三角形的性质等知识,熟练掌握圆与圆内含和相切的关系是解题关键.二、填空题(本大题共12个小题,每小题4分,共48分)7.分解因式:2218m -=.【答案】()()233m m +-/()()233m m -+【分析】原式提取2,再利用平方差公式分解即可.【详解】解:2218m -=2(m 2-9)=2(m +3)(m -3).故答案为:2(m +3)(m -3).【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.8.2x x +=-的解是.【答案】x =﹣1.【分析】把方程两边平方后求解,注意检验.【详解】把方程两边平方得x +2=x 2,整理得(x ﹣2)(x +1)=0,解得:x =2或﹣1,经检验,x =﹣1是原方程的解.故本题答案为:x =﹣1.【点睛】本题考查无理方程的求法,注意无理方程需验根.9.函数2x y x =-中自变量x 的取值范围是.【答案】0x ≥且2x ≠【分析】根据二次根式中被开方数大于等于0及分母不为0即可求解.【详解】解:由题意可知:020x x ≥⎧⎨-≠⎩,解得:0x ≥且2x ≠,故答案为:0x ≥且2x ≠.【点睛】本题考查的是函数自变量的取值范围的确定,掌握二次根式的被开方数是非负数、分母不为0是解题的关键.10.△ABC 中,AD 是中线,G 是重心,,AB a AD b == ,那么BG =(用a b 、表示).【答案】23a b -+ .【详解】试题分析:∵在△ABC 中,点G 是重心,AD b = ,∴23AG b =,又∵BG AG AB =- ,AB a = ,∴2233BG b a a b =-=-+ ;故答案为23a b -+ .考点:1.平面向量;2.三角形的重心.11.有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图案,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是.【答案】13【详解】解:列树状图得共有12种情况,两张图案一样的有4种情况,所以概率是13.12.在方程224404x x x x +-+=中,如果设y=x 2﹣4x ,那么原方程可化为关于y 的整式方程是.【答案】2430y y ++=【分析】先把方程整理出含有x 2-4x 的形式,然后换成y 再去分母即可得解.【详解】方程2234404x x x x +-+=-可变形为x 2-4x+214x x -+4=0,因为24y x x =-,所以340y y++=,整理得,2430y y ++=13.如果⊙O 1与⊙O 2内含,O 1O 2=4,⊙O 1的半径是3,那么⊙O 2的半径r 的取值范围是.【答案】7r >/7r<【分析】由题意,⊙O 1与⊙O 2内含,则可知两圆圆心距d r r <-小大,据此代入数值求解即可.【详解】解:根据题意,两圆内含,故34r ->,解得7r >.故答案为:7r >.【点睛】本题主要考查了两圆位置关系的知识,熟练掌握由数量关系判断两圆位置关系是解题关键.14.某单位10月份的营业额为100万元,12月份的营业额为200万元,假设该公司11、12两个月的增长率都为x ,那么可列方程是.【答案】100(1+x )2=200【分析】根据题意,设平均每月的增长率为x ,依据10月份的营业额为100万元,12月份的营业额为200万元,即可列出关于x 的一元二次方程.故答案为:100(1+x )2=200【详解】设平均每月的增长率为x ,根据题意可得:100(1+x )2=200.故答案为:100(1+x )2=200.【点睛】此题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出方程是解题关键.15.菱形ABCD 中,已知AB =4,∠B :∠C =1:2,那么BD 的长是.【答案】43【分析】根据题意画出示意图(见详解),由菱形的性质可得BO =12BD ,BD ⊥AC ,在Rt △ABO 中,由cos ∠ABO 即可求得BO ,继而得到BD 的长.【详解】解:如图,∵四边形ABCD 为菱形,∴AB CD ∥,∴∠ABC +∠BCD =180°,∵∠ABC :∠BCD =1:2,∴∠ABC =60°,∴∠ABD =12∠ABC =30°,BO =12BD ,BD ⊥AC .在Rt △ABO 中,cos ∠ABO =BO AB =32,∴BO=AB⋅cos∠ABO=4×32=23.∴BD=2BO=43.故答案为:43.【点睛】本题考查菱形的性质,熟知菱形的对角线互相垂直,利用垂直构造直角三角形,再利用三角函数求解线段长度是解题的关键.16.如图,已知在⊙O中,半径OC垂直于弦AB,垂足为点D.如果CD=4,AB=16,那么OC=.【答案】10【分析】根据垂径定理求出AD的长,设半径OC=OA=r,则OD=r-4,再根据勾股定理列出关于r的方程,解出即可得出OC的长.【详解】设半径OC=OA=r,则OD=OC-CD=r-4半径OC垂直于弦AB,垂足为点D,AB=16∴AD=12AB=8,在Rt△AOD中,OD2+AD2=OA)即(r-4)2+82=r2解得:r=10故答案为10.【点睛】本题考查了垂径定理,勾股定理,熟练掌握定理是解题的关键.17.新定义:有一组对角互余的凸四边形称为对余四边形.如图,已知在对余四边形ABCD中,10AB=,12BC=,5CD=,3tan4B=,那么边AD的长为.【答案】9【分析】连接AC,作AE BC⊥交BC于E点,由3tan4B=,10AB=,可得AE=6,BE=8,并求出AC的长,作CF AD ⊥交AD 于F 点,可证B DCF ∠=∠,最后求得AF 和DF 的长,可解出最终结果.【详解】解:如图,连接AC ,作AE BC ⊥交BC 于E 点,3tan 4B =,10AB =,∴3tan 4AE B BE ==,设AE=3x ,BE=4x ,∴222AE BE AB +=,则()()2223425100x x x +==,解得x=2,则AE=6,BE=8,又 12BC =,∴CE=BC-BE=4,∴22213AC AE CE =+=,作CF AD ⊥交AD 于F 点,+=90B D ∠∠︒,90D DCF ∠+∠=︒,∴B DCF ∠=∠,3tan 4B ==tan DCF ∠=DF CF ,又 5CD =,∴同理可得DF=3,CF=4,∴226AF AC CF =-=,∴AD=AF+DF=9.故答案为:9.【点睛】本题考查四边形综合问题,涉及解直角三角形,勾股定理,有一定难度,熟练掌握直角三角形和勾股定理知识点,根据题意做出正确的辅助线是解决本题的关键.18.如图,在Rt ∆ABC 中,∠ACB =90°,BC =4,AC =3,⊙O 是以BC 为直径的圆,如果⊙O 与⊙A 相切,那么⊙A 的半径长为.【答案】132±【分析】分两种情况:①如图,A 与O 内切,连接AO 并延长交A 于E ,根据AE AO OE =+可得结论;②如图,A 与O 外切时,连接AO 交A 于E ,同理根据AE OA OE =-可得结论.【详解】解:有两种情况,分类讨论如下:①如图1,A 与O 内切时,连接AO 并延长交O 于E ,O 与A 相内切,E ∴为切点,122OE BC ∴==,90ACB ∠=︒ ,根据勾股定理得:22222313OA OC AC =+=+=,132AE OA OE ∴=+=+;即A 的半径为132+;②如图2,A 与O 外切时,连接AO 交O 于E ,同理得132AE AO OE =-=-,即A 的半径为132-,综上,A 的半径为132+或132-.故答案为:132±.【点睛】本题考查了相切两圆的性质、勾股定理,解题的关键是通过作辅助线得出AE 是A 的半径.第Ⅱ卷三、解答题(本大题共7个小题,共78分.解答应写出文字说明,证明过程或演算步骤)19.(10()()()20220118cot 45233sin 30π--︒+-+--︒.【答案】223+【分析】先化简各式,然后再进行计算即可解答.【详解】解:20220118(cot 45)|23|(3)(sin 30)π-+-︒+-+--︒20221132(1)321()2-=+-+-+-3213212=++-+-223=+.【点睛】本题考查了实数的运算,零指数幂,负整数指数幂、绝对值,特殊角的三角函数值,解题的关键是准确熟练地化简各式.20.(10分)如图,AH 是△ABC 的高,D 是边AB 上一点,CD 与AH 交于点E .已知AB =AC =6,cos B =3,AD ∶DB =1∶2.(1)求△ABC 的面积;(2)求CE ∶DE .【答案】解:(1)85;(2)31.【详解】试题分析:(1)根据题意和锐角三角函数可以求得BH 和AH 的长,从而可以求得△ABC 的面积;(2)根据三角形的相似和题意可以求得CE :DE 的值.试题解析:解:(1)∵AB =AC =6,cos B =23,AH 是△ABC 的高,∴BH =4,∴BC =2BH =8,AH =226425-=,∴△ABC 的面积是;2BC AH ⋅=8252⨯=85;(2)作DF ⊥BC 于点F .∵DF ⊥BH ,AH ⊥BH ,∴DF ∥AH ,∴AD HF CE CH AB HB DE HF ==,.∵AD :DB =1:2,BH =CH ,∴AD :AB =1:3,∴13HF HB =,∴31CE CH BH DE HF HF ===,即CE :DE =3:1.点睛:本题考查了解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.(10分)如图,在平面直角坐标系xOy 中,点A 是反比例函数y =x的图象与正比例函数y =kx 的图象在第一象限内的交点,已知点A 的纵坐标为2.经过点A 且与正比例函数y =kx 的图象垂直的直线交反比例函数y =k x的图象于点B (点B 与点A 不是同一点).(1)求k的值;(2)求点B的坐标.【答案】(1)2 (2)(4,12)【分析】(1)根据题意得到22kk=,解方程求得k=2;(2)先求得A的坐标,根据正比例函数的解析式设直线AB的解析式为y12=-x+b,把A的坐标代入解得b52=,再与反比例函数的解析式联立成方程组,解方程组即可求得点B的坐标.【详解】(1)解:∵点A是反比例函数ykx=的图象与正比例函数y=kx的图象在第一象限内的交点,点A的纵坐标为2,∴22k k=,∴2k=4,解得k=±2,∵k>0,∴k=2;(2)∵k=2,∴反比例函数为y2x=,正比例函数为y=2x,把y=2代入y=2x得,x=1,∴A(1,2),∵AB⊥OA,∴设直线AB的解析式为y12=-x+b,把A 的坐标代入得2112=-⨯+b ,解得b 52=,解21522y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩得12x y =⎧⎨=⎩或412x y =⎧⎪⎨=⎪⎩,∴点B 的坐标为(4,12).【点睛】本题是反比例函数与一次函数的交点问题,考查了一次函数、反比例函数图象上点的坐标特征,待定系数法求一次函数的解析式,解题的关键是求出直线AB 的解析式,本题属于中等题型.22.(10分)图1是某区规划建设的过街天桥的侧面示意图,等腰梯形ABCD 的上底BC 表示主跨桥,两腰AB ,CD 表示桥两侧的斜梯,A ,D 两点在地面上,已知AD =40m ,设计桥高为4m ,设计斜梯的坡度为1:2.4.点A 左侧25m 点P 处有一棵古树,有关部门划定了以P 为圆心,半径为3m 的圆形保护区.(1)求主跨桥与桥两侧斜梯的长度之和;(2)为了保证桥下大货车的安全通行,桥高要增加到5m ,同时为了方便自行车及电动车上桥,新斜梯的坡度要减小到1:4,新方案主跨桥的水平位置和长度保持不变.另外,新方案要修建一个缓坡MN 作为轮椅坡道,坡道终点N 在左侧的新斜梯上,并在点N 处安装无障碍电梯,坡道起点M 在AP 上,且不能影响到古树的圆形保护区.已知点N 距离地面的高度为0.9m ,请利用表中的数据,通过计算判断轮椅坡道的设计是否可行.表:轮椅坡道的最大高度和水平长度坡度1:201:161:121:101:8最大高度(m )1.200.900.750.600.30水平长度(m )24.0014.409.00 6.002.40【答案】(1)主跨桥与桥两侧斜梯的长度之和为26.6m(2)轮椅坡道的设计不可行,理由见解析【分析】(1)根据斜坡AB的坡度以及天桥的高度可求出AE,由勾股定理求出AB,进而求出EF=BC的长,再计算主跨桥与桥两侧斜梯的长度之和;(2)根据坡度的定义求出新方案斜坡A B''的水平距离A E'进而求出点M到点G的最大距离,再由表格中轮椅坡道的最大高度和水平长度的对应值进行判断即可.【详解】(1)解:如图,作直线AD,则AD过点A'和点D',过点B、C分别作BE⊥AD,CF⊥AD,垂足为E、F,延长EB,延长FC,则射线EB过点B',射线FC过点C',由题意得,BE=CF=4m,AP=25m,B'E=5m,∵斜坡AB的坡度为1:2.4,即BEAE=1:2.4,∴AE=4×2.4=9.6(m),又∵四边形ABCD是等腰梯形,∴AE=DF=9.6m,∴BC=AD﹣AE﹣DF=5.8(m),AB=22AE BE+=229.64+=10.4(m)=CD,∴主跨桥与桥两侧斜梯的长度之和为AB+BC+CD=10.4+5.8+10.4=26.6(m),答:主跨桥与桥两侧斜梯的长度之和为26.6m.(2)解:∵斜坡A B''的坡度为1:4,即B EA E''=1:4,∴A'E=5×4=20(m),∴A A'=20﹣9.6=11.4(m),A'G=4NG=4×0.9=3.6(m),∴AG=11.4﹣3.6=7.8(m),点M到点G的最多距离MG=25﹣7.8﹣3=14.2(m),∵14.2<14.4,∴轮椅坡道的设计不可行.【点睛】本题主要考查了解直角三角形的应用,根据坡度和坡角构造直角三角形,然后分别用解直角三角形的知识坡道的水平距离是解答本题的关键.23.(12分)已知:如图,在梯形ABCD 中,//AD BC ,90B Ð=°,E 是AC 的中点,DE 的延长线交边BC 于点F.(1)求证:四边形AFCD 是平行四边形;(2)如果22AE AD BC =⋅,求证四边形AFCD 是菱形.【答案】(1)见解析;(2)见解析【分析】(1)由平行四边形的性质可知DAE FCE =∠∠,ADE CFE ∠=∠.再由E 是AC 中点,即AE =CE .即可以利用“AAS ”证明AED CEF ≌,得出AD CF =,即证明四边形AFCD 是平行四边形.(2)由22AE AD BC =⋅和E 是AC 中点,即可推出AE AD CB AC=.又因为DAE FCE =∠∠,即证明ADE CAB ∽△△,即可推出DF AC ⊥.即四边形AFCD 是菱形.【详解】(1)∵//AD BC ,∴DAE FCE =∠∠,ADE CFE ∠=∠.又∵E 是AC 中点,∴AE =CE ,∴在AED △和CEF △中ADE CFE DAE FCE AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AED CEF AAS ≌,∴AD CF =,∴四边形AFCD 是平行四边形.(2)∵//AD BC ,∴DAE FCE =∠∠.∵22AE AD BC =⋅,∴AE AC AD BC ⋅=⋅,∴AE AD CB AC=,∴ADE CAB ∽△△,∴90AED ABC ∠=∠=︒,即DF AC ⊥.∴四边形AFCD 是菱形.【点睛】本题考查梯形的性质,平行四边形的判定,菱形的判定,全等三角形的判定和性质以及相似三角形的判定和性质.掌握特殊四边形的判定方法是解答本题的关键.24.(12分)在平面直角坐标系中,抛物线235y x bx c =-++与y 轴交于点(0,3)A ,与x 轴的正半轴交于点(5,0)B ,点D 在线段OB 上,且1OD =,联结AD ,将线段AD 绕着点D 顺时针旋转90︒,得到线段DE ,过点E 作直线l x ⊥轴,垂足为H ,交抛物线于点F .(1)求抛物线的表达式;(2)联结DF ,求cot ∠EDF 的值;(3)点P 在直线l 上,且∠EDP =45°,求点P 的坐标.【答案】(1)2312355y x x =-++;(2)cot 2EDF ∠=;(3)(4,6)或3(4,)2-.【分析】(1)利用待定系数法即可解决问题;(2)证明()OAD HDE AAS ∆∆≌,再根据全等三角形的性质得1EH OD ==,3DH OA ==,可得(4,1)E ,(4,3)F ,求出3FH DH ==,则45DFH ∠=︒,32DF =,过点E 作EK DF ⊥于K ,根据等腰直角三角形的性质可得2KF KE ==,则22DK DF KF =-=,在Rt DKE ∆中,根据余切的定义即可求解;(3)分两种情形①点P 在点E 的上方时;②点P 在点E 的下方时,根据相似三角形的判定和性质即可解决问题.【详解】(1)解:把点(0,3)A ,点(5,0)B 代入235y x bx c =-++,得:15503b c c -++=⎧⎨=⎩,解得:1253b c ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为2312355y x x =-++;(2)解:如图:90AOD ADE DHE ∠=∠=∠=︒ ,90ADO OAD ∴∠+∠=︒,90ADO EDH ∠+∠=︒,OAD EDH ∴∠=∠,AD DE = ,()OAD HDE AAS ∴∆∆≌,1EH OD ∴==,3DH OA ==,(4,1)E ∴,过点E 作直线l x ⊥轴,垂足为H ,交抛物线2312355y x x =-++于点F .(4,3)F ∴,3FH ∴=,3FH DH ∴==,90DHE ∠=︒ ,45DFH ∴∠=︒,32DF =,过点E 作EK DF ⊥于K ,312EF =-= ,2KF KE ∴==,22DK DF KF ∴=-=,在Rt DKE ∆中,22cot 22DK EDF KE ∠===;(3)解:①当点P 在点E 的上方时,45EDP DFH ∠=∠=︒ ,DEP ∠是公共角,EDF EPD ∴∆∆∽,∴EF ED ED EP=,2ED EF EP ∴=⋅,设(4,)P y ,则1EP y =-,又2EF = ,223110ED =+=,102(1)y ∴=-,解得6y =,∴点P 的坐标为(4,6);②当点P 在点E 的下方时,45EDP DFP ∠=∠=︒ ,DPF ∠是公共角,PED PDF ∴∆∆∽,∴PE DP PD FP=,2DP PE PF ∴=⋅,设(4,)P y ,则1EP y =-,3FP y =-,223DP y =+,29(1)(3)y y y ∴+=--,解得32y =-,∴点P 的坐标为3(4,)2-;综上所述,当45EDP ∠=︒时,点P 的坐标为(4,6)或3(4,)2-.【点睛】本题是二次函数综合题,考查二次函数的应用、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是熟练掌握二次函数的图象及性质,三角形相似的判定及性质.25.(14分)如图,半径为1的⊙O 与过点O 的⊙P 相交,点A 是⊙O 与⊙P 的一个公共点,点B 是直线AP 与⊙O 的不同于点A 的另一交点,联结OA ,OB ,OP .(1)当点B 在线段AP 上时,①求证:∠AOB =∠APO ;②如果点B 是线段AP 的中点,求△AOP 的面积;(2)设点C 是⊙P 与⊙O 的不同于点A 的另一公共点,联结PC ,BC .如果∠PCB =α,∠APO =β,请用含α的代数式表示β.【答案】(1)①见解析;②74(2)β=60°﹣23β【分析】(1)①利用圆的半径相等可得∠OAB =∠OBA =∠AOP ,则∠AOB =∠APO ;②首先利用△AOB ∽△APO ,得OA AB AP OA=,可得AP 的长,作AH ⊥PO 于点H ,设OH =x ,则PH =2﹣x ,利用勾股定理列方程求出OH的长,从而得出AH,即可求得面积;(2)联结OC,AC,利用圆心角与圆周角的关系得∠ACB=12∠AOB=12β,∠ACO=12∠APO=12β,再利用SSS说明△OAP≌△OCP,得∠OAP=∠OCP,从而解决问题.【详解】(1)①证明:∵OA=OB,∴∠OAB=∠OBA,∵PA=PO,∴∠BAO=∠POA,∴∠OAB=∠OBA=∠AOP,∴∠AOB=∠APO;②解:∵∠AOB=∠APO,∠OAB=∠PAO,∴△AOB∽△APO,∴OA AB AP OA=,∴OA2=AB•AP=1,∵点B是线段AP的中点,∴AP=2,作AH⊥PO于点H,设OH=x,则PH=2﹣x,由勾股定理得,12﹣x2=(2)2﹣(2x-)2,解得x=2 4,∴OH=2 4,21由勾股定理得,AH =2221()4-=144,∴△AOP 的面积为11142224OP AH ⨯⨯=⨯⨯=74;(2)解:如图,联结OC ,AC ,∵∠AOB =∠APO ,∴∠AOB =β,∴∠ACB =12∠AOB =12β,∠ACO =12∠APO =12β,∴∠OCP =β+α,∵OA =OC ,AP =PC ,OP =OP ,∴△OAP ≌△OCP (SSS ),∴∠OAP =∠OCP =β+α,在△OAP 中,2(α+β)+β=180°,∴β=60°﹣23β.【点睛】本题是圆的综合题,主要考查了圆的性质,圆心角与圆周角的关系,相似三角形的判定与性质,全等三角形的判定与性质等知识,求出大圆半径是解题的关键.。
上海中考二模数学试题及答案

上海中考二模数学试题及答案一、选择题1. 若集合A = {1, 2, 3, 4, 5, 6, 7},B = {2, 4, 6, 8,10},则A ∩ B = ()A. {2, 4, 6}B. {1, 2, 3}C. {8, 10}D. {1, 3, 5, 7}2. 已知直线l与x轴交于点A,直线l与y轴交于点B,则下列说法中正确的是()A. 点(0, 0)在l上B. 点(0, 1)在l上C. A与B的横坐标之积小于0D. A、B的横坐标之积大于03. 方程(x-2)²-4 = 0的根是()A. 0B. 2C. 4D. 64. a1, a2, a3, ...是等差数列,若a1+a9=28,a5+a11=24,则该数列首项为()A. 1B. 2C. 3D. 45. 在Rt△ABC中,AB=12,AC=16,则BC的长度为()A. 4B. 8C. 12D. 16答案:1. A 2. D 3. B 4. C 5. B二、填空题1. 若a:b=2:3,且a:b:c=3:5:7,求c。
2. 设二次函数f(x)=-2x²+3x+4,若f(x)的图像与x轴交于点A、B,且AB=4,则A、B的横坐标分别为___。
3. 已知平行四边形ABCD中,AB=2a,AD=a+3,AC=4a-3,则BD 等于___。
4. 已知函数y=f(x)的图像关于原点对称,则f(-x)=___。
5. 若函数y=f(x)=ax²+x-1在区间[0, 1]上是增函数,则a的取值范围是___。
答案:1. 7 2. (-1, 3) 3. 2a-3 4. f(x) 5. a>0三、解答题1. 已知等差数列S的首项为a,公差为d,且S1 + S2 + S3 = 15,求S6的值。
解答:设等差数列的第n项是Sn,则有Sn = a + (n-1)d。
根据等差数列和公式,可以得到:S1 = aS2 = a + dS3 = a + 2dS6 = a + 5d给出条件S1 + S2 + S3 = 15,代入上面的式子可以得到:a + (a + d) + (a + 2d) = 153a + 3d = 15再考虑到S6 = a + 5d,将3a + 3d = 15带入可以得到:3a + 3d = 153(a + d) = 15a + d = 5将a + d = 5带入S6 = a + 5d:S6 = 5 + 5dS6 = 5(d + 1)所以S6的值为5(d + 1)。
2024年上海市长宁区中考数学二模试卷及答案解析

2024年上海市长宁区中考数学二模试卷一、选择题(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸相应题号的选项上用2B铅笔正确填涂]1.(4分)下列是最简二次根式的是()A.B.C.D..2.(4分)关于一元二次方程x2+x﹣3=0根的情况,正确的是()A.有两个相等的实数根B.有两个不相等的实数根C.有且只有一个实数根D.没有实数根3.(4分)下列函数中,函数值y随自变量x的值增大而增大的是()A.y=2x2B.C.y=﹣2x D.y=2x+14.(4分)为了解某公司的收入水平,随机挑选五人的月工资进行抽样调查,月工资(单位:元)分别是3000,4000,5000,6000,50000,那么能够较好的反映他们收入平均水平的是()A.中位数B.标准差C.平均数D.众数.5.(4分)如图,已知点A、B、C、D都在⊙O上,OB⊥AC,BC=CD,下列说法错误的是()A.B.∠AOD=3∠BOC C.AC=2CD D.OC⊥BD6.(4分)下列命题是假命题的是()A.对边之和相等的平行四边形是菱形B.一组邻边上的高相等的平行四边形是菱形C.一条对角线平分一组对角,另一条对角线平分一个内角的四边形是菱形D.被一条对角线分割成两个等腰三角形的平行四边形是菱形二、填空题(本大题共12题,每题4分,满分48分)7.(4分)计算:2﹣2=.8.(4分)截至2023年底,全国高铁营业里程约为45000公里,这个数45000用科学记数法表示为.9.(4分)函数的定义域为.10.(4分)方程的解是.11.(4分)已知方程,如果设,那么原方程转化为关于y的整式方程为.12.(4分)如果二次函数y=x2+m的图象向右平移3个单位后经过原点,那么m的值为.13.(4分)在1,2,3中任取两个不重复的数字组成一个两位数,那么这个两位数是素数的概率是.14.(4分)为了解某校六年级300名学生来校的方式,随机调查了该校六年级50名学生同一天来校的方式,并绘制了如图所示的饼状图,那么估计该校六年级300名学生中这一天步行来学校的共有_____名.15.(4分)如图,在△ABC中,点D在边AB上,且BD=2AD,点E是AC的中点,联结DE,设向量,,如果用、表示,那么=.16.(4分)如图,正方形ABCD中,点E在对角线BD上,点F在边CD上(点F不与点C重合),且∠EAF=45°,那么的值为.17.(4分)在Rt△ABC中,∠ACB=90°,AC>BC,将△ABC绕着点C旋转,点A、点B的对应点分别是点D、点E,如果点A在DE的延长线上,且CE∥AB,那么∠CAE的余弦值为.18.(4分)我们把以三角形的重心为圆心的圆叫做该三角形的重心圆.如图,在△ABC中,AB=AC=10,BC=16,如果△ABC的重心圆与该三角形各边的公共点一共有4个,那么它的半径r的取值范围是.三、解答题(本大题共7题,满分78分)[将下列各题的解答过程,做在答题纸的相应位置上] 19.(10分)计算:.20.(10分)解方程组:.21.(10分)如图,⊙O经过平行四边形ABCD的顶点B,C,D,点O在边AD上,AO=3,OD=5.(1)求平行四边形ABCD的面积;(2)求∠D的正弦值.22.(10分)春节期间甲乙两家商店各自推出优惠活动商店优惠方式甲所购商品按原价打八折乙所购商品按原价每满300元减80元设顾客在甲乙两家商店购买商品的原价都为x元,请根据条件回答下列问题:(1)如果顾客在甲商店购买商品选择优惠活动后实际付款y元,求y关于x的函数解析式(不必写出函数定义域);(2)购买原价在500元以下的商品时,如果分别选择甲商店的优惠活动和乙商店的优惠活动后,实际付款金额相等,求x的值;(3)顾客购买原价在900元以下的商品时,如果选择乙商店的优惠活动比选择甲商店的优惠活动更合算,求x的取值范围.23.(12分)已知:在梯形ABCD中,AD∥BC,BD⊥AD,点E在边AD上(点E不与点A、D重合),点F在边CD上,且∠ABD=∠EBF=∠C.(1)求证:;(2)联结EF,与BD交于点G,如果BG=EG,求证:四边形BEDF为等腰梯形.24.(12分)在平面直角坐标系xOy中,已知抛物线y=ax2+2x+c与x轴分别交于点A、B(点A在点B左侧),与y轴交于点C(0,6),其对称轴为直线x=2.(1)求该抛物线的表达式;(2)点F是上述抛物线上位于第一象限的一个动点,直线AF分别与y轴、线段BC交于点D、E.①当CF=DF时,求CD的长;②联结AC,如果△ACF的面积是△CDE面积的3倍,求点F的坐标.25.(14分)已知在△ABC中,CA=CB,AB=6,cos∠CAB=,点O为边AB上一点,以点O为圆心,OA为半径作⊙O,交边AC于点D(点D不与点A、C重合).(1)当AD=4时,判断点B与⊙O的位置关系,并说明理由;(2)过点C作CE⊥OD,交OD延长线于点E.以点E为圆心,EC为半径作⊙E,延长CE,交⊙E 于点C′.①如图1,如果⊙O与⊙E的公共弦恰好经过线段EO的中点,求CD的长;②联结AC′、OC,如果AC′与△BOC的一条边平行,求⊙E的半径长.2024年上海市长宁区中考数学二模试卷参考答案与试题解析一、选择题(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸相应题号的选项上用2B铅笔正确填涂]1.【分析】根据最简二次根式的定义进行解题即可.【解答】解:A、=,故不符合题意;B、==,故不符合题意;C、是最简二次根式,符合题意;D、==5,故不符合题意;故选:C.【点评】本题考查最简二次根式,熟练掌握相关的知识点是解题的关键.2.【分析】先计算出根的判别式的值,然后根据根的判别式的意义对各选项进行判断.【解答】解:∵Δ=12﹣4×(﹣3)=13>0,∴方程有两个不相等的实数根.故选:B.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.3.【分析】根据反比例函数的性质、一次函数的性质及正比例函数的性质、二次函数的性质对各选项进行逐一分析即可.【解答】解:A、函数y=2x2中,当x<0时y随x的增大而减小,不符合题意;B、函数y=﹣中,在每一象限内y随x的增大而增大,不符合题意;C、函数y=﹣2x中,y随x的增大而减小,不符合题意;D、函数y=2x+1中,y随x的增大而增大,符合题意.故选:D.【点评】本题考查的是反比例函数的性质、一次函数的性质及正比例函数的性质、二次函数的性质,熟知以上知识是解题的关键.4.【分析】利用平均数,中位数、众数和给出的数据分别进行分析,即可得出答案.【解答】解:根据给出的数据可得,中位数根据能够较好的反映他们收入平均水平.故选:A.【点评】此题考查了平均数、众数、中位数和标准差,众数是指一组数据中出现次数最多的数据;将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.5.【分析】分别根据垂径定理,圆心角、弧、弦的关系,三角形三边的关系和线段的垂直平分线的判定判断即可.【解答】解:A、∵OB⊥AC,∴=,故不符合题意;B、∵=,∴∠AOB=∠COB,∵BC=CD,∴∠BOC=∠DOC,∴∠AOD=3∠BOC,故不符合题意;C、∵∠AOB=∠BOC=∠DOC,∴∠AOC=∠BOD,∴AC=BD,∵BD<BC+CD=2CD,∴AC<2CD,故符合题意;D、∵OB=OC,BC=DC,∴OC⊥BD,故不符合题意;故选:C.【点评】本题考查圆周角定理、垂径定理、圆心角、弧、弦的关系、三角形三边的关系和线段的垂直平分线的判定,解答本题的关键是明确题意,利用数形结合的思想解答.6.【分析】根据菱形的判定定理判断即可.【解答】解:A、∵平行四边形的对边相等,∴对边之和相等舒,邻边线段,∴平行四边形是菱形,故本选项命题是真命题;B、根据菱形的面积公式可知:一组邻边上的高相等的平行四边形是菱形,故本选项命题是真命题;C、一条对角线平分一组对角,另一条对角线平分一个内角的四边形是菱形,是真命题,不符合题意;D、有一条对角线与一组邻边构成等腰三角形的平行四边形不一定是菱形,故被一条对角线分割成两个等腰三角形的平行四边形是菱形是假命题,符合题意;故选:D.【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.二、填空题(本大题共12题,每题4分,满分48分)7.【分析】根据负整数指数幂法则进行解题即可.【解答】解:2﹣2=.故答案为:.【点评】本题考查负整数指数幂,掌握运算法则是解题的关键.8.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n 是正整数,当原数绝对值<1时,n是负整数.【解答】解:45000=4.5×104.故答案为:4.5×104.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.9.【分析】根据分式的分母不为零列出不等式,解不等式得到答案.【解答】解:由题意得:x﹣2≠0,解得:x≠2,故答案为:x≠2.【点评】本题考查的是函数自变量的取值范围的确定,熟记分式的分母不为零是解题的关键.10.【分析】方程两边平方得出x﹣1=9,求出方程的解,再进行检验即可.【解答】解:,方程两边平方,得x﹣1=9,解得:x=10,经检验:x=10是原方程的解.故答案为:x=10.【点评】本题考查了解无理方程,能把无理方程转化成有理方程是解此题的关键.11.【分析】设,则原方程转化为y﹣=2,再方程两边都乘3y即可.【解答】解:,设,则原方程转化为:y﹣=2,方程两边都乘3y,得3y2﹣1=6y,即3y2﹣6y﹣1=0.故答案为:3y2﹣6y﹣1=0.【点评】本题考查了用换元法解分式方程,能正确换元是解此题的关键.12.【分析】求出函数图象向右平移3个单位后的函数解析式,再由函数图象过原点即可得出m的值.【解答】解:二次函数y=x2+m的图象向右平移3个单位后的解析式为y=(x﹣3)2+m,∵二次函数y=x2+m的图象向右平移3个单位后经过原点,∴(0﹣3)2+m=0,解得m=﹣9.故答案为:﹣9.【点评】本题考查的是二次函数的图象与几何变换,熟知“左加右减”的法则是解题的关键.13.【分析】列表可得出所有等可能的结果数以及这个两位数是素数的结果数,再利用概率公式可得出答案.【解答】解:列表如下:123112132212333132共有6种等可能的结果,其中这个两位数是素数的结果有:13,23,31,共3种,∴这个两位数是素数的概率为=.故答案为:.【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.14.【分析】总人数乘以样本中步行人数所占比例即可.【解答】解:估计该校六年级300名学生中这一天步行来学校的共有300×(1﹣12%﹣32%﹣26%)=90(名),故答案为:90.【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.15.【分析】首先由向量的知识,得到与的值,即可得到的值.【解答】解:在△ABC中,,,则=﹣=﹣.∵BD=2AD,点E是AC的中点,∴==,==﹣,∴=+=+﹣=﹣.故答案为:﹣.【点评】此题考查向量的知识.解题的关键是注意数形结合思想的应用.16.【分析】通过证明△BAE∽△CAF,可得.【解答】解:∵四边形ABCD是正方形,∴AC=AB,∠ABD=∠ACD=45°,∠BAC=∠EAF=45°,∴∠BAE=∠CAF,∴△BAE∽△CAF,∴,故答案为:.【点评】本题考查了正方形的性质,相似三角形的判定和性质,证明三角形相似是解题的关键.17.【分析】由△ABC绕着点C旋转,点A、点B的对应点分别是点D、点E,点A在DE的延长线上,且CE∥AB,得∠ACE=∠BAC=D=x°,得3x+90=180,得∠CAE=x=30°,得∠CAE的余弦值为.【解答】解:由△ABC绕着点C旋转,点A、点B的对应点分别是点D、点E,点A在DE的延长线上,且CE∥AB,得∠ACE=∠BAC=∠D=x°,由△ADC中,∠ACB=90°,得3x+90=180,得∠CAE=x=30°,得∠CAE的余弦值为.故答案为:.【点评】本题主要考查了旋转的性质,解题关键是正确应用旋转的性质.18.【分析】当⊙O与AB、AC相切时(切点是M、N),⊙O与△ABC的三边有4个公共点,连接OM,由△AOM∽△ABH,得到OM:BH=AO:AB,即可求出OM=3.2,当⊙O′与AB、AC分别有一个公共点,与BC有两个公共点时(⊙O′不过B、C两点),△ABC的重心圆与该三角形各边的公共点一共有4个,于是得到当4<r<2时,△ABC的重心圆与该三角形各边的公共点一共有4个,即可得到答案.【解答】解:如图,过A作AH⊥BC于H,∵AB=AC=10,∴HB=HC=BC=×16=8,∴AH==6,设O是△ABC的重心,∴AO=AH=4,当⊙O与AB、AC相切时(切点是M、N),⊙O与△ABC的三边有4个公共点,连接OM,∴OM⊥AB,∴∠AMO=∠AHB=90°,∵∠OAM=∠BAH,∴△AOM∽△ABH,∴OM:BH=AO:AB,∴OM=8=4:10,∴OM=3.2,∴重心圆的半径r=3.2时,△ABC的重心圆与该三角形各边的公共点一共有4个,如图,过作AK⊥BC于K,∵∵AB=AC=10,∴KB=KC=BC=×16=8,∴AK==6,设O′是△ABC的重心,∴AO′=AH=4,∴KO′=6﹣4=2,∴BO′==2,当⊙O′与AB、AC有一个公共点,与BC有两个公共点时(⊙O′不过B、C两点),△ABC的重心圆与该三角形各边的公共点一共有4个,∴当4<r<2时,△ABC的重心圆与该三角形各边的公共点一共有4个,∴重心圆的半径r=3.2或4<r<2时,△ABC的重心圆与该三角形各边的公共点一共有4个,故答案为:r=3.2或4<r<2.【点评】本题考查直线与圆的位置关系,三角形的重心,等腰三角形的性质,相似三角形的判定和性质,关键是要分两种情况讨论.三、解答题(本大题共7题,满分78分)[将下列各题的解答过程,做在答题纸的相应位置上] 19.【分析】先化简各式,然后再进行计算即可解答.【解答】解:原式=2+(﹣+3)﹣2+=2﹣=4.【点评】本题考查了实数的运算,零指数幂,准确熟练地化简各式是解题的关键.20.【分析】把②变形为(x﹣2y)(x﹣3y)=0,可得x﹣2y=0或x﹣3y=0,故原方程组相当于和,分别解两个二元一次方程组可得原方程组的解.【解答】解:由②得:(x﹣2y)(x﹣3y)=0,∴x﹣2y=0或x﹣3y=0,∴原方程组相当于和,分别解两个二元一次方程组可得原方程组的解为和.【点评】本题考查解二元二次方程组,解题的关键是用因式分解法“降次“,把二元二次方程组变形为两个二元一次方程组.21.【分析】(1)过O点作OE⊥BC,如图,先根据平行四边形的性质得到BC=AD=8,AD∥BC,再利用垂径定理得到BE=CE=4,接着利用勾股定理计算出OE=3,然后利用平行四边形的面积公式求解;(2)先证明四边形OECF为矩形得到CF=OE=3,OF=CE=4,所以DF=1,再利用勾股定理计算出CD,然后根据正弦的定义求解.【解答】解:(1)过O点作OE⊥BC,如图,∵四边形ABCD为平行四边形,∴BC=AD=3+5=8,AD∥BC,∵OE⊥BC,∴BE=CE=4,在Rt△OEC中,OE===3,∴平行四边形ABCD的面积=8×3=24;(2)∵OF∥CE,OE⊥CE,CF⊥OF,∴四边形OECF为矩形,∴CF=OE=3,OF=CE=4,∴DF=OD﹣OF=5﹣4=1,在Rt△CDF中,CD===,∴sin D===.【点评】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了平行四边形的性质、圆周角定理和解直角三角形.22.【分析】(1)根据甲商店实际付款是原价的0.8倍列出函数解析式;(2)根据题意可知300≤x<500,然后按活动价列出等式,解方程即可;(3)分当300≤x<600和600≤x<900两种情况列出不等式,解不等式即可.【解答】解:(1)根据题意得:y=0.8x,∴y关于x的函数解析式为y=0.8x;(2)若x<300,则甲商店按原价打八折,乙商店按原价,此时实际付款金额不可能相等,∴300≤x<500,∴0.8x=x﹣80,解得x=400;(3)当300≤x<600时,x﹣80<0.8x,解得x<400,∴300≤x<400;当600≤x<900时,x﹣160<0.8x,解得x<800,∴600≤x<800,综上所述,x的取值范围为300≤x<400或600≤x<800.【点评】本题考查一次函数和一元一次不等式的应用,关键是列出函数解析式和不等式.23.【分析】(1)由AD∥BC,BD⊥AD,得∠ADB=∠DBC=90°,而∠ABD=∠EBF=∠C,可推导出∠ABE=∠DBF,∠A=∠BDF,进而证明△ABE∽△DBF,则=;(2)将=,变形为=,因为∠ABD=∠EBF,所以△ABD∽△EBF,得∠ADB=∠EFB,再证明△BGF∽△EGD,得===1,则BF=ED,FG=DG,所以∠GDF=∠GFD,由∠BGE =2∠GEB=2∠GFD,证明∠GEB=∠GFD,则BE∥DF,所以四边形BEDF为等腰梯形.【解答】(1)证明:∵AD∥BC,BD⊥AD,∴∠ADB=∠DBC=90°,∵∠ABD=∠EBF=∠C,∴∠ABD﹣∠DBE=∠EBF﹣∠DBE,∴∠ABE=∠DBF,∵∠A+∠ABD=90°,∠BDF+∠C=90°,∴∠A=∠BDF,∴△ABE∽△DBF,∴=.(2)证明:联结EF,与BD交于点G,∵=,∴=,∵∠ABD=∠EBF,∴△ABD∽△EBF,∴∠ADB=∠EFB,∵∠BGF=∠EGD,∠GFB=∠GDE,BG=EG,∴△BGF∽△EGD,∠GBE=∠GEB,∴===1,∴BF=ED,FG=DG,∴∠GDF=∠GFD,∵∠BGE=∠GBE+∠GEB=2∠GEB,∠BGE=∠GDF+∠GFD=2∠GFD,∴2∠GEB=2∠GFD,∴∠GEB=∠GFD,∴BE∥DF,∴四边形BEDF为等腰梯形.【点评】此题重点考查平行线的判定与性质、相似三角形的判定与性质、三角形的一个外角等于与它不相邻的两个内角的和等知识,证明△ABE∽△DBF及△ABD∽△EBF是解题的关键.24.【分析】(1)由待定系数法即可求解;(2)①当CF=DF时,则点F在CD的中垂线上,则(6﹣m+6)=﹣m2+2m+6,即可求解;②证明△EMD∽△FNA,得到DE:AF=DM:AN=1:3,则=(m+2),即可求解.【解答】解:(1)由题意得:,解得:,则抛物线的表达式为:y=﹣x2+2x+6;(2)由抛物线的表达式得,点A(﹣2,0)、C(0,6),设点F(m,﹣m2+2m+6),由点A(﹣2,0)、F的坐标得,直线AF的表达式为:y=﹣(m﹣6)(x+2),则点D(0,6﹣m),①当CF=DF时,则点F在CD的中垂线上,则(6﹣m+6)=﹣m2+2m+6,解得:m=0(舍去)或5,则CD=6﹣(6﹣m)=m=5;②由点B、C的坐标得,直线BC的表达式为:y=﹣x+6,联立上式和AF的表达式得:﹣x+6=﹣(m﹣6)(x+2),解得:x==DM,由点F的坐标得,AN=m+2,∵△ACF的面积是△CDE面积的3倍,则DE:AF=1:3过点D作DM∥x轴,作EM⊥DM,过点F作FN⊥x轴,则△EMD∽△FNA,则DE:AF=DM:AN=1:3,则=(m+2),解得:m=﹣4(舍去)或4,即点F(4,6).【点评】本题考查的是二次函数综合运用,涉及到一次函数的基本性质、待定系数法求函数表达式、三角形相似、中垂线的性质等,有一定的综合性,难度适中.25.【分析】(1)借助垂径定理,利用cos A表示出AO和BO,通过比较AO和BO的大小确定点与圆的位置关系;(2)①需要紧扣∠CDE=∠A,结合连心线和公共弦的性质可以发现圆E和圆O是等圆,借助相似三角形的性质或锐角三角函数,用含k的代数式表示出CD、AD,从而求解;②当AC′∥CB时,过点C′作C′N⊥AD,证明出∠C′AD=∠C′DA,在Rt△C′NC中,cos∠C'CN==,得到,解得,则;当AC′∥OC,延长OE交AC′延长线于点F,由AC′∥OC,得到,解得或5(舍去),则CE=4k=.【解答】解:(1)点B在⊙O内;理由如下:过点O作OH⊥AC,垂足为点H,∵OH过圆心,OH⊥AD,∴,∵OH⊥AC,∴∠AHO=90°,在Rt△AOH中,,∴,∵AB=6,∴,∵OB<AO,∴点B在⊙O内;(2)过点C作CM⊥AB,垂足为M,如图2,∵AC=BC,CM⊥AB,∴,在Rt△ACM中,,∴AC=5,∵OA=OD,∴∠CAB=∠ODA,又∵∠ODA=∠CDE,∴∠CAB=∠CDE,∵,在Rt△CDE中,∠CED=90°,,设DE=3k,CD=5k,则,∴AD=5﹣k,①两圆的交点记为P、Q,连接PE,PO,如图3,⊙O与⊙E相交,PQ是公共弦,∴OE垂直平分PQ,即OE⊥PQ,∵PQ经过OE的中点,∴PQ垂直平分OE,∴PE=PO,即CE=AO,,在Rt△AHO中,∠AHO=90°,∴,∵,∴,解得,∴;②由于点A在直线AB上,∴AC′不可能与OB平行,则当AC′∥CB时,过点C′作C′N⊥AD,如图4,∵AC=CB,∴∠CAB+∠B+∠ACB=180°,∴∠ACB=180°﹣2∠CAB,∵AC′∥CB,∴∠C′AD=∠ACB=180°﹣2∠CAB,∵DE⊥CC′,CE=C′E,∴DC′=DC,∴∠CDE=∠C′DE,∵∠C′DA+∠C′DE+∠CDE=180°,∴∠C′DA=180°﹣2∠CDE,∵∠CAB=∠CDE,∴∠CAD=∠CDA,∵C′N⊥AD,∴,∴,在Rt△C′NC中,,∴,∴,∴;当AC∥OC,延长OE交AC延长线于点F,如图5,∵AC′∥OC,∴,∴OE=EF,∴,DE=3k,∴,∴,∴,∵AC′∥OC,∴,∴,解得或5(舍去),∴,综上:或.【点评】本题考查了圆和三角形相结合的问题,锐角三角函数,点与圆的位置关系,相交两圆的性质,相似三角形的判定与性质,添加适当的辅助线,构造直角三角形,并灵活运用勾股定理是解答本题的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
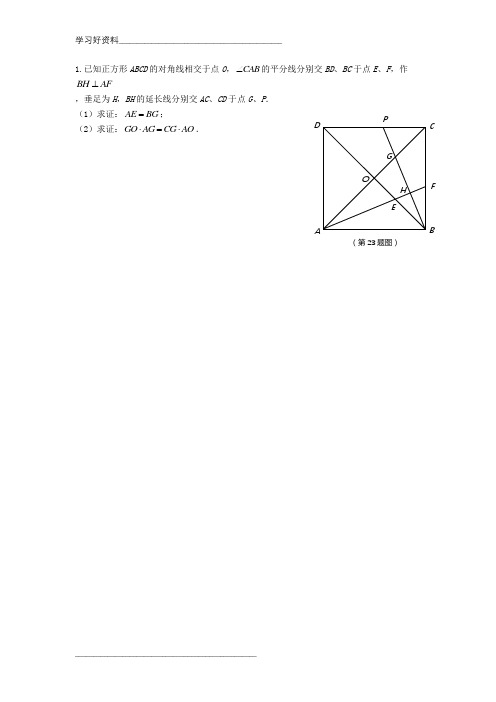
1.已知正方形ABCD的对角线相交于点O,CAB
∠的平分线分别交BD、BC于点E、F,作BH AF
⊥
,垂足为H ,BH的延长线分别交AC、CD于点G、P.
(1)求证:
;
(第23题图)B C F
2. 已知:如图,梯形ABCD 中,DC ∥AB , AD=BC=DC ,AC 、BD 是对角线,E 是AB 延长线上一点,且∠BCE =∠ACD ,联结CE . (1)求证:四边形DBEC 是平行四边形; (2)求证:2AC AD AE =⋅.
第23题图
E
D
C
B
A
3. 如图,在四边形ABCD 中,AB ∥DC ,E 、F 为对角线BD 上两点,
且BE DF =, AF ∥EC .
(1)求证:四边形ABCD 是平行四边形;
(2)延长AF ,交边DC 于点G ,交边BC 的延长线 于点H ,求证:AD DC BH DG =g g .
A B
C
E
F
第23题图
D
G H
4. 如图5,在ABC ∆中,D 、E 分别是AC 、BC 边上的点,AE 与BD 交于点O ,且CD =CE ,12∠=∠.
(1)求证:四边形ABED 是等腰梯形;
(2)若EC =2,BE =1,21AOD ∠=∠,求AB 的长.
图5 A
B C D
O E
1
2
5. 如图6,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.
求证:(1)CD=BH;
(2)AB是AG和HE的比例中项.
G
E
图6
6. 如图, BD是△ABC的角平分线, 点E、F分别在BC、AB上, 且DE∥AB, ∠DEF=∠A. (1)求证: BE=AF ;
(2)设BD与EF交于点M, 联结AE, 交BD于点N,
求证: BN·MD=BD·ND.
M A
F
B E C
D
(静安)23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)
已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF =DE ,AE 的延长线与DF 相交于点G . (1)求证:∠CDF =∠DAE ;
(2)如果DE =CE ,求证:AE =3EG .
(闵行)23.(本题满分12分,其中每小题各6分)
如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅.
(普陀)23.(本题满分12分)
如图7,已知在四边形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF ∥AB 分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;
(2)设AC AB ⊥,求证:AC OE AB EF =g g .
(第23题图)
E
D
C
G
F
A B
(第23题图)
A
B C
D
E F
G
O
H
O
F
E
D
C
B
A
图7
(松江)23.(本题满分12分,每小题满分各6分)
如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E . (1)求证:∠CAD =∠ECB ;
(2)点F 是AC 的中点,联结DF ,求证:BD 2=FC ·BE .
(徐汇)23.(本题满分12分)
如图7, 在ABC ∆中,AC AB =,点D 在边AC 上,DE BD AD ==,联结BE ,︒=∠=∠72DBE ABC .
(1)联结CE ,求证:BE CE =;
(2)分别延长CE 、AB 交于点F ,求证:四边形DBFE 是菱形.
(杨浦)23.(本题满分12分,每小题各6分)
已知:如图,在直角梯形纸片ABCD 中,DC //AB , AB CD AD >>,∠A =90°,将纸片沿过点D 的直线翻折,使点A 落在边CD 上的点E 处,折痕为DF ,联结EF 并展开纸片. (1)求证:四边形ADEF 为正方形;
(2)取线段AF 的中点G ,联结GE ,当BG =CD 时, 求证:四边形GBCE 为等腰梯形. C
B A
D
E
F
(第23题图) (第23题图)
图7
A
B
C D
E
(第23题图)
(闸北)23.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 如图,直角梯形ABCD 中,∠B=90°,AD ∥BC ,BC=2AD ,点E 为边BC 的中点. (1)求证:四边形AECD 为平行四边形;
(2)在CD 边上取一点F ,联结AF 、 AC 、 EF ,设AC 与EF 交于点G ,且∠EAF=∠CAD .求证:△AEC ∽△ADF ;
(3)在(2)的条件下,当∠ECA=45°时.求:FG:EG 的比值.
(浦东)23.(本题满分12分,第(1)、(2)小题各6分)
如图,已知:四边形ABCD 是平行四边形, 点E 在边BA 的延长线上,CE 交AD 于点F ,∠ECA = ∠D .
(1)求证:∆EAC ∽∆ECB ; (2)若DF = AF ,求AC ︰BC 的值.
(第23题图)
A
B
C
E
D F G。
