2018届广东省韶关市高三调研试题(二)文科数学试题 及答案
2018年广东省高考数学二模试卷(文科)(解析版)
3. (5 分)已知 x∈R,集合 A={0,1,2,4,5},集合 B={x﹣2,x,x+2},若 A∩B={0, 2},则 x=( A.﹣2 ) B.0 C.1 D.2
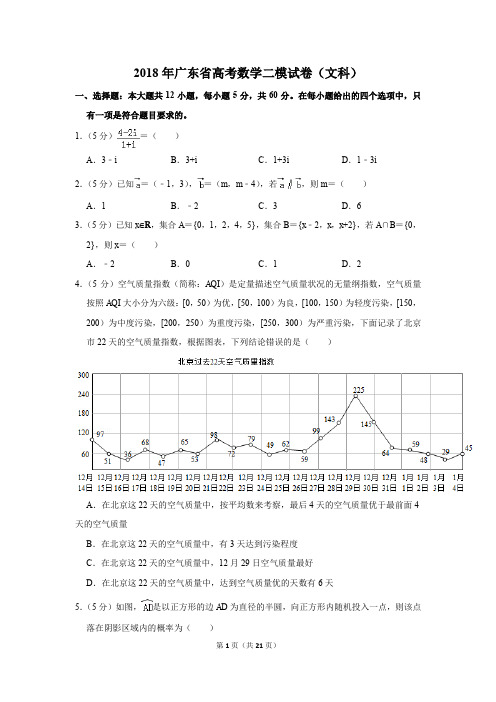
4. (5 分)空气质量指数(简称:AQI)是定量描述空气质量状况的无量纲指数,空气质量 按照 AQI 大小分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150, 200)为中度污染,[200,250)为重度污染,[250,300)为严重污染,下面记录了北京 市 22 天的空气质量指数,根据图表,下列结论错误的是( )
线的两条渐近线互相垂直,则该双曲线的方程为( A. =1
B.
C.
=1
D.
=1 或
=1 )
8. (5 分)已知某几何体的三视图如图所示
B.6π+6
C.8π+12
第 2 页(共 21 页)
D.6π+12
9. (5 分)在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人﹣﹣宰相宰相西萨 •班•达依尔. 国王问他想要什么, 他对国王说: “陛下, 请您在这张棋盘的第 1 个小格里, 赏给我 1 粒麦子,在第 2 个小格里给 2 粒,第 3 小格给 4 粒,以后每一小格都比前一小 格加一倍.请您把这样摆满棋盘上所有的 64 格的麦粒,都赏给您的仆人吧! ”国王觉得 这要求太容易满足了, 就命令给他这些麦粒. 当人们把一袋一袋的麦子搬来开始计数时, 国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那 么,宰相要求得到的麦粒到底有多少粒?下面是四位同学为了计算上面这个问题而设计 的程序框图,其中正确的是( )
第 1 页(共 21 页)
落在阴影区域内的概率为(
普通高等学校2018届高三招生全国统一考试模拟试题(二)数学(文)试题word含答案

普通高等学校2018届高三招生全国统一考试模拟试题(二)数学(文)试题word含答案普通高等学校招生全国统一考试模拟试题——文科数学(二)本试卷满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题纸上。
2.回答选择题时,选出每小题答案后,用铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题纸上,写在本试卷上无效。
3.考试结束后,将本试卷和答题纸一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 $A=\{x|x-\frac{1}{2}<0\}$,$B=\{x|x-\frac{(2a+8)}{a(a+8)}<0\}$,若 $A\cap B=A$,则实数 $a$ 的取值范围是A。
$(-4,-3)$B。
$[-4,-3]$C。
$(-\infty,-3)\cup(4,+\infty)$D。
$(-3,4)$2.已知复数 $z=\frac{3+i}{2-3i}$,则 $z$ 的实部与虚部的和为A。
$-\frac{2}{5}+\frac{1}{5}i$B。
$-\frac{2}{5}-\frac{1}{5}i$C。
$\frac{2}{5}+\frac{1}{5}i$D。
$\frac{3}{5}+\frac{2}{5}i$3.某景区管理部门为征求游客对景区管理方面的意见及建议,从景区出口处随机选取 $5$ 人,其中 $3$ 人为跟团游客,$2$ 人为自驾游散客,并从中随机抽取 $2$ 人填写调查问卷,则这 $2$ 人中既有自驾游散客也有跟团游客的概率是A。
$\frac{2}{3}$B。
$\frac{1}{5}$C。
$\frac{2}{5}$D。
$\frac{3}{5}$4.已知双曲线 $E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ 的离心率为$\frac{\sqrt{10}}{3}$,斜率为 $-\frac{3}{2}$ 的直线 $l$ 经过双曲线的右顶点 $A$,与双曲线的渐近线分别交于 $M$,$N$ 两点,点 $M$ 在线段$AN$ 上,则 $\frac{AN}{AM}$ 等于A。
【韶关二模】广东省韶关市高三第二次调研考试数学文试题 Word版含答案.pdf

韶关市2013届高三年级第一次调研(期末)测试 数学文试题 本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟. 注意事项: 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上; 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分; 3.考试结束,考生只需将答题卷交回. 4. 参考公式: 锥体的体积公式,其中是锥体的底面积,是锥体的高. 正棱锥的侧面积公式:,是底面周长,是斜高. 一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设全集U={,1,2,3,4,5},集合A={2,4},B=,则集合 A.{0,4,5,2} B.{,4,5} C.{2,4,5} D.{1,3,5}=( )A -B -1CD 1 3.设,则这四个数的大小关系是( ) A. B . C. D. 4.若方程表示双曲线,则k的取值范围是( ) A. B. C. D. 或 5.某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是两个全等等腰三角形)根据图中标出的数据,可得这个几何体的表面积为( ) A. B. C. D.12 6.已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )A.=1.23x+4B.=1.23x+5 C.=1.23x+0.08 D.=0.08x+1.23 7. 设不等式组表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于的概率是( ) A. B. C. D. 8. 中,角、、所以的边为、、, 若,,面积,则( ) A. B. C. D. 9.设{an}(n∈N*)是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( ) A.d<0B.a7=0C.S9>S5D.S6与S7均为Sn的最大值 10.已知, 四个函数中,当时, 满足不等式的是 二.填空题:本大题共5小题,每小题5分,满分20分. 11. 若向量满足条件,则= 13. 平面上有条直线, 这条直线任意两条不平行, 任意三条不共点, 记这条直线将平面分成部分, 则___________,时,_________________.)(用表示). 14.(几何证明选讲选做题)AB、CD是圆的两条弦,AB与CD交于, , AB是线段CD的中垂线.若AB=6,CD=,则线段AC的长度为 . 15.(坐标系与参数方程选做题) 在直角坐标系中,圆的参数方程为(为参数);在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点为极点,以轴的正半轴为极轴)中,圆的方程为,则与的位置关系是______(在“相交、相离、内切、外切、内含”中选择一个你认为正确的填上). 三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分12分) 函数 ()的部分图像如右所示. (1)求函数的解析式; (2)设,且,求的值. 17.(本小题满分12分) 高(1)成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题 ()高(1)及分数在之间的频数并计算频率分布直方图中 间的矩形的高; (若要从分数在之间求至少在之间的概率. 本小题⊙所在的平面,是⊙的直径,,C是⊙上一点,且,. (1) 求证:; (2) 求证:; (3)当时,求三棱锥的体积. 19.(本小题的离心率为,两焦点分别为,点M是椭圆C上一点,的周长为16,设线段MO(O为坐标原点)与圆交于点N,且线段MN长度的最小值为. (1)求椭圆C以及圆O的方程; (2)当点在椭圆C上运动时,判断直线与圆O的位置关系. 20.(本小题已知. ()奇偶性, 并求函数的单调区间; ()若有,求实数的取值范围本小题的公差,等比数列公比为,且,, (1)求等比数列的公比的值; (2)将数列,中的公共项按由小到大的顺序排列组成一个新的数列,是否存在正整数(其中)使得和都构成等差数列?若存在,求出一组的值;若不存在,请说明理由. 韶关市2013届高三年级第一次调研(期末)测试 数学试题(文科)参考答案 说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如 果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数. 2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容 和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半; 如果后继部分的解答有较严重的错误,就不再给分. 3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分. DCBAB CDDCA 二、填空题:本大题主要考查基本知识和基本运算.本大题共小题,每小题5分. 12. 13. (2分),(3分) 14. 15. 内切 三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. ()的部分图像如右所示. (1)求函数的解析式; (2)设,且,求的值 解:(1)∵ 由图可知:函数的最大值为, ………2分 且 ∴,最小正周期………………………………………………………4分 ∴ 故函数的解析式为. …………………………………6分 (2),………………………………………………………8分 ∴ ,∵ , ∴ ,…………………………………………………………10分 ∴ …………………………………………………………………12分 17.(本题满分12分) 高(1)成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题 ()高(1)及分数在之间的频数并计算频率分布直方图中 间的矩形的高; (若要从分数在之间求至少在之间的概率. ()分数在之间的频数为,频率为, 高(1)为.所以分数在之间的频数为 频率分布直方图中间的矩形的高为.()至少在之间将之间的编号为,之间的编号为,在之间的任取两的基本事件为:,,,, ,,,,,,,共个………………………………………………………………………………………………..9分 其中,至少有一个在之间的基本事件有个………………………………………11分 答:至少在之间的概率本小题⊙所在的平面,是⊙的直径,C是⊙上一点,且,. (1) 求证: ; (2) 求证:; (3)当时,求三棱锥的体积. 解: (1)证明:在三角形PBC中, 所以 EF//BC, ………………………………………………………………………4分 (2) 又是⊙的直径,所以 ……………………………………………7分 所以, ………………………………………………………8分 因 EF//BC ,所以 因为, 所以. ……………………………………………10分 (3) 在中, = 当时,是中点.为中点 ……… 12分 ……………………………………14分 19.(本题满分14分) 椭圆的离心率为,两焦点分别为,点M是椭圆C上一点,的周长为16,设线段MO(O为坐标原点)与圆交于点N,且线段MN长度的最小值为. (1)求椭圆C以及圆O的方程; (2)当点在椭圆C上运动时,判断直线与圆O的位置关系. 解:(1)设椭圆C的半焦距为c,则,即① ………………………1分 又②………………………………3分 联立①②,解得,所以. 所以椭圆C的方程为.………………………………………………………5分 而椭圆C上点与椭圆中心O的距离为 ,等号在时成立………7分, 而,则的最小值为,从而,则圆O的方程为.………………………………………………………………………………9分 (2)因为点在椭圆C上运动,所以.即. 圆心O到直线的距离.……………12分 当,,则直线l与圆O相交. …………………… ……………14分 20.(本题满分14分) 已知. ()奇偶性, 并求函数的单调区间; ()若有,求实数的取值范围定义域在数轴上关于原点对称, 且,所以是偶函数……………………2分 当时, , 由 , , 解得: 所以在是增函数; 由 , , 解得: .所以在是减函数. ………4分 因为是偶函数, 图象关于轴对称,所以, 当时, 在是减函数, 在是增函数. 所以, 的单调区间,;单调区间,,.………6分 (2) 由,得 , 令………………………………………………………………………8分 当时, ,当, , 在是增函数; 当, , 在是减函数, 所以, 当时,极小值是…………………………………11分 因为是奇函数,所以, 当时, 极大值是 所以 , 即, 函数有零点. ………………………14分 21.(本题满分14分) 设等差数列的公差,等比数列公比为,且,, (1)求等比数列的公比的值; (2)将数列,中的公共项按由小到大的顺序排列组成一个新的数列,是否存在正整数(其中)使得和都构成等差数列?若存在,求出一组的值;若不存在,请说明理由. 解:(1)设=,由题意 即不合题意………………………3分 故,解得 (5) (2)答:不存在正整数(其中)使得和均构成等差数列 证明:假设存在正整数满足题意 设=且,故 ,又 - 即…………………………………………7分 -……………………8分 令,则 ……………………………………………………………………10分 若存在正整数满足题意,则 ,又 又, ----------------------12分 又在R上为增函数,,与题设矛盾, 假设不成立 故不存在满足题意.------------------------ --------------------14分 n=n+2 输出n 结束 是 开始=0,n=1 S>25 否=+n。
韶关市2018届高三第一次调研考试数学(附答案)

韶关市2021届高三第一次调研考试数学试题第一局部选择题〔共50分〕一、选择题:本大题共10小题,每题5分,共50分.在每题给出的四个选项中,只有一项符合题目要求的.〔答案1-10BDAADCDDDC〕〔1〕在正项等比数列a n中,a318,那么a5a6a7的值为,a92A.4B.8C.16D.64〔2〕不等式(x3)|x2|0的解集为A.(3,)B.(,3)(2,)C.(3,2)D.(3,2)(2,) 3〕sin2cos3tan4的值A.小于零B.大于零C.等于零D.不确定〔4〕设定义在R上不恒为0的函数f(x)满足f(x)f(y)f(x y),那么f(x)是A.奇函数B.既是奇函数又是偶函数C.偶函数D.既不是奇函数又不是偶函数〔5〕假设指数函数f ()ax(0且a1)的局部对应值如下表:x ax-202 f(x)1那么不等式f1(|x|)<0的解集为()A.1,1B.1,0C.0,1D.1,00,1〔6〕设集合M=xx m0,N {y|y2x,x},那么实数m的取R,假设M∩N=值范围是:〔〕A.m0B.m0C.m0D.m0〔7〕数列a n 的前n项和S n lg(n1),那么a10a11a999A.1B.-1C.2D.-2〔8〕一次函数 f(x)存在反函数,且满足f(2)1,f(x)f 1(x).那么f(0)A .0B .1C .2D .3〔9〕数列{a n }中,a 1=1,前n项和为 S n ,对任意n≥ 2,总有3S n 4 ,a n ,23S n1成等差数列,那么limS n (D)2n124A .C .13B .D .33〔10〕设定义域为 D 的函数f(x)满足以下条件:①对任意x D,f(x)f( x) 0;②对任意x ,x2[1,a] ,当xx时,有f(x)f(x) 0 .那么以下不等式不一定成立的是 1212 1.....A .f(a)f(0)B .f(1a) f( a)2C .f(13a)f(3)D .f(13a) f(a)1 a1a二、填空题〔11〕函数y2π 的最小正周期是______________.cos (x)4〔12〕设函数f(x)a(x21) x(aR),命题P :x[1,1];命题Q :方程f(x)0有2 2解.那么命题Q 是命题P 的______________条件.〔必要但不充分〕〔13 〕设正方形 ABCD 的边长为2点 P 从点 A 出发,按 A →B →C →D的路径在正方形 ABCD,的边上移动,以 x表示点 P走过的路程, f(x)表示三角形APDP 在CD 边上的面积,当点时,f(x)____________;其中f(x)的定义域是_______________.〔14 〕等差数列{a n }中,a 1 0,前n项和为S n ,且a 2005a 20060,a 2005a 20060,当S n 最大时,n____________;〔2021〕当S n0时,n 的最大值是____________.〔4010〕三、解答题〔15 〕求函数f(x)sinx[cosx sin(x)]的最大值和最小值.解:f(x)sinx[cosx sin(x)] sinx(cosx sinx) sinxcosxsin 2x4分1(sin2x2sin 2x)1(sin2x coa2x1)1(sin2xcos2x)1 7分22222sin(2x) 110分242当x k8(k Z),f(x)max21,2当x k 3(k Z),f(x)min21⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分82.〔16〕不等式x ab的解集是x1x2,求不等式ax2x b0的解集.解:不等式x a b的解是b a x b a,依得b a1解个方程得a 1,b3b a222可知不等式ax2x b01x2x30即x22x3022解得1x3,故不等式ax2xb0的解集是x1x3.〔17〕公比q(q0,q1)的等比数列b n与数列a n足b n3a n,n N*〔1〕判断a n是何种数列,并出明;〔2〕假设13求值og312 a8a m,:l(bb b20)解〔1〕b n3a n,3a1q n13a n a n a1(n1)log3q所以a n是以log3q公差的等差数列.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分〔2〕a8a13m所以由等差数列性得a1a20a8a13ma1a2a20(a1a20)2010m b1b2b203a1a2a20310m 2故log3(b1b2b20)10m⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14分〔18〕某厂生某种品的固定本钱2500元,每生x件的品需要再增大可本钱G(x)200x3x2(元),假设生出的品都能以每件500元售出,要使利最大,厂生多少件种品?最大利是多少?解:厂生x件厂品的利y元,:y500x(200x3x2)2500⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分300x3x22500(x0)3(x50)25000⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分所以当x50,y取得最大,ymax5000⋯⋯⋯⋯11分答:要使利最大,厂生50件种品,最大利 5000元⋯⋯12分〔19〕定点M 〔1,0〕作曲c:y x p (其中x (0,),pN *,p1,p 为常数)的切切点Q ,Q 点在x 上的投影是点R ,又点P 作曲c 的切切点Q ,Q 在111122x 上的投影是R 2⋯,依此下去,得到一系列点Q 1,Q 2,⋯,Q n ,⋯,点Q n 的横坐a n〔1〕求:数列 a n 是等比数列;〔2〕T1 2n 1 n ,比T 与p 2的大小(写出推程)na 1 a 2 an1a nn(3)求:a n1 np ;1明〔1〕y' px p1,假设切点是py a n p pa n p 1(x a n )Q n (a n ,a n ) ,切方程是当n=1,切点P 〔1,0〕即0a 1p pa 1p 1(1 a 1),得a 1p ;⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2分p 1当n>1,切点p n 1(a n1,0)即0a ppa p1(a1a)nnn n得a np ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分an1p 1n所以数列a n 是首p p ,公比 p p 的等比数列,a n pp ,n N *111⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分(2) ∵T n1 2n 1 na 1 a 2a na n1p1T n1 2 n 1 n 两式相减,⋯⋯⋯⋯⋯⋯7分pa 2 a 3a n a n 1得(1p1)S n1 11 n1 1 1 ,⋯⋯⋯⋯8分pa 1 a 2 a na n1 a 1 a 2a np 1 ( p 1n ]1T np [1 p )2 2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔 10分〕p p 1 T n p p pp1 1p(3)a n (p )n (1 1 )np 1 p 1c n 0 c n 11 1c n 2( 1 )2 c n n ( 1 )n ⋯⋯⋯⋯⋯12分p p 1p 1011n〔14分〕c n c n p11p1法二.用数学归纳法证明酌情处理〔20〕函数f(x)ax21(a0)存在极值.x1〔Ⅰ〕如果函数f(x)在区间(1,)上单调递增,求实数a的取值范围;2〔Ⅱ〕设函数f(x)的极小值为g(a),证明:2g(a)1.解:〔Ⅰ〕f(x)a(x21)a1a(x1)a1 x1x1f(x)a a11)2(x当0a1时,f(x)0,函数f(x)在定义域区间(,1)和(1,)上分别为增函数,不存在极值〔或:当0a1时,f(x)0,函数f(x)不存在极值〕,与题设不符;故a 1.法1:当x 1时,f(x)aa1aa13a404(x1)21a2(2321)法2:令f(x)aa10解得xa11或xa11 2a a(x1)故当a1时,函数f(x)的增区间为(,a11),(a11,) a a要函数f(x)在区间(1,)上单调递增,有a111,解这个不等式得a4,2a2314 a3〔Ⅱ〕由〔Ⅰ〕知,a 1.当x(a11,1)(1,a11)时,a af(x)0,函数f(x)的减区间为(a11,1),(1,a11),a a故函数f(x)只在区间(1,)上有一个极小值.当x(1,)时,f(x)a(x1)a1a(x1)a12a2a(a1)2ax1x1a 1 a(a11)21g(a) 2 a(a 1) 2a 〔或g(a)f(a2a(a1)2a 〕a1)a 1a法1:g(a)2a(a 1)2a2 a 2a 1a1 aaa又a 1 , g(a)2 a2a 1aa1 a2 g(x)1.法2:g(a) 2a(a 1) 2a (a (a 1)) 2a 1另一方面,g(a)2 a(a1) 2a 2a(1a 1)aa1 1a 1 a 1aa ag(a)2a(1 a 12a(1a 12))aa2g(x)1.法3:令a sec 2(0),那么2g(a)2sec (tansec2(sin 1) 2(sin1)2) cos 21sin21 sin0 sin11 112 1 sin2 g(a)1.法4:分析法〔略〕精品推荐 强力推荐 值得拥有。
精品解析:广东省2018届高三下学期模拟考试(二)数学(文)试题(解析版)

2018年普通高等学校招生全国统一考试广东省文科数学模拟试卷(二)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. ()A. B. C. D.【答案】D【解析】分析:本题利用复数的除法法则进行求解.详解:.故选D.点睛:复数的除法法则涉及的公式比较难记忆,搞清其实质(分子、分母同乘以分母的共轭复数)是解题的关键.2. 已知,,若,则()A. B. C. D.【答案】A【解析】分析:利用“若,且,则”得到关于的方程,再通过解方程求得值.详解:由题意,得,解得.故选A.点睛:涉及平面向量的共线(平行)的判定问题主要有以下两种思路:(1)若且,则存在实数,使成立;(2)若,且,则.3. 已知,集合,集合,若,则()A. B. C. D.【答案】B【解析】分析:先利用得到,由此得到值,再验证是否成立进行取舍. 详解:因为,,且,所以或,若时,,(舍);若时,,;即.故选B.点睛:本题的易错点是由得到或后,就直接得到错误答案(或),忘记验证是否成立.4. 空气质量指数(简称:)是定量描述空气质量状况的无量纲指数,空气质量按照大小分为六级:为优,为良,为轻度污染,为中度污染,为重度污染,为严重污染.下面记录了北京市天的空气质量指数,根据图表,下列结论错误的是()A. 在北京这天的空气质量中,按平均数来考察,最后天的空气质量优于最前面天的空气质量B. 在北京这天的空气质量中,有天达到污染程度C. 在北京这天的空气质量中,12月29日空气质量最好D. 在北京这天的空气质量中,达到空气质量优的天数有天【答案】C【解析】分析:通过题目所提供的图表得出22个数据,研究在各区间上的数据个数,对选项逐一验证得到答案.详解:因为,所以在北京这天的空气质量中,按平均数来考察,最后天的空气质量优于最前面天的空气质量,即选项A正确;不低于100的数据有3个:,所以在北京这天的空气质量中,有天达到污染程度,即选项B正确;因为12月29日的为225,为重度污染,该天的空气质量最差,即选项C错误;在的数据有6个:,即达到空气质量优的天数有天,即选项D正确.故选C.点睛:本题考查频率分布表的识别和应用,属于基础题,本题的技巧是判定选项A时,仅从各数据的大小关系上进行判定,避免了不必要的运算.5. 如图,是以正方形的边为直径的半圆,向正方形内随机投入一点,则该点落在阴影区域内的概率为()A. B. C. D.【答案】D【解析】分析:先由圆的对称性得到图中阴影部分的面积,再用几何概型的概率公式进行求解.详解:连接,由圆的对称性得阴影部分的面积等于的面积,易知,由几何概型的概率公式,得该点落在阴影区域内的概率为.故选D..点睛:本题的难点是求阴影部分的面积,本解法利用了圆和正方形的对称性,将阴影部分的面积转化为求三角形的面积.6. 已知等比数列的首项为,公比,且,则()A. B. C. D.【答案】B【解析】分析:先根据得到值,再利用等比数列的通项公式进行求解.详解:因为,所以,又因为,所以.故选B.点睛:本题考查了等比数列的基本运算,在记忆等比数列的通项公式时,既要熟记,还要注意的应用.7. 已知双曲线的一个焦点坐标为,且双曲线的两条渐近线互相垂直,则该双曲线的方程为()A. B. C. D. 或【答案】A【解析】分析:先利用双曲线的渐近线相互垂直得出该双曲线为等轴双曲线,再利用焦点位置确定双曲线的类型,最后利用几何元素间的等量关系进行求解.详解:因为该双曲线的两条渐近线互相垂直,所以该双曲线为等轴双曲线,即,又双曲线的一个焦点坐标为,所以,即,即该双曲线的方程为.故选D.点睛:本题考查了双曲线的几何性质,要注意以下等价关系的应用:等轴双曲线的离心率为,其两条渐近线相互垂直.8. 已知某几何体的三视图如图所示,则该几何体的表面积为()A. B. C. D.【答案】B【解析】分析:先利用三视图得到该组合体的结构特征,再分别利用球的表面积公式、圆柱的侧面积公式求出各部分面积,再求和即可.详解:由三视图可得该几何体是由圆柱的一半(沿轴截面截得,底面半径为1,母线长为3)和一个半径为1的半球组合而成(部分底面重合),则该几何体的表面积为.点睛:处理几何体的三视图和表面积、体积问题时,往往先由三视图判定几何体的结构特征,再利用相关公式进行求解.9. 在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人——宰相宰相西萨•班•达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍.请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王觉得这要求太容易满足了,就命令给他这些麦粒.当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那么,宰相要求得到的麦粒到底有多少粒?下面是四位同学为了计算上面这个问题而设计的程序框图,其中正确的是()A. B. C. D.【答案】C【解析】分析:先分析这个传说中涉及的等比数列的前64项的和,再对照每个选项对应的程序框图进行验证.详解:由题意,得每个格子所放麦粒数目形成等比数列,且首项,公比,所设计程序框图的功能应是计算,经验证,得选项B符合要求.故选B.学。
广东省韶关市高三数学第二次调研考试试题 文

数学试题(文科)本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟. 注意事项:1. 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;2. 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分;3.考试结束,考生只需将答题卷交回. 4. 参考公式:(1)锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. (2)样本数据12,,,n x x x 的方差,2211()n i i s x x n ==-∑,其中x 是这组数据的平均数.一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数(1)i ai ⋅+是纯虚数,则实数a 的值是( )A.1B.1-C.0D.0或1-2.已知R 是实数集,{}2|20M x x x =->,N 是函数y x =的定义域,则R C NM =( ) A. (1,2)B. [0,2]C. ∅D. [1,2]3.设25025..12,25,()2.a b c ===,则,,a b c 的大小关系是( )A .a c b >>B .c a b >>C . a b c >>D .b a c >>4.设0x 是方程3log 3x x =-的根,且0(,1)x k k ∈+,则k =( )A .(0,1)B .(1,3)C .(3,4)D .(4,+∞) 5.以抛物线y 2=4x 的焦点为圆心,且过坐标原点的圆的方程为( ) A. 22(1)1x y -+= B. 22(1)1x y ++=C. 22(1)1x y +-=D. 22(1)1x y ++=6. 已知直线l ⊥平面α,直线m ⊂平面β,给出下列四个命题:①m l ⊥⇒βα//②m l //⇒⊥βα;③βα⊥⇒m l //;④βα//⇒⊥m l .其中正确的命题有( )个A .1个B .2个C .3个D .4个 7.函数22()cos ()cos ()44f x x x ππ=--+(R x ∈)是( )A. 周期为π的奇函数B. 周期为π的偶函数C. 周期为π2的奇函数D. 周期为π2的偶函数 8.已知,x y 满足约束条件5000x y x y y ++⎧⎪-⎨⎪⎩≥≤≤,则24z x y =+的最小值是( )A. 15-B. 16-C. 17-D. 18-9.执行如图1所示的程序框图后,输出的值为5,则P 的取值范围( ) A .715816P <≤ B .1516P > C .715816P ≤< D .3748P <≤10.定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,设111sgn()1sgn()122()()22x x f x f x -+-+=⋅+2()f x ⋅,[0,1]x ∈,若1()f x =12x +, 2()f x ⋅=2(1)x -, 则()f x 的最大值等于()A. 2B. 1C. 34D. 12[来二.填空题:本大题共5小题,每小题5分,满分20分.11.已知A 是单位圆上的点,且点A 在第二象限,点B 是此圆与x 轴正半轴的交点,记AOB α∠=, 若点A 的纵坐标为35.则sin α=_____________; tan 2α=_______________.12. 已知向量(1,1)a =,)2,1(=b ,且()()ka b b a -⊥+,则实数k 的值为13.下列四个判断:①某校高三一班和高三二班的人数分别是,m n ,某次测试数学平均分分别是,a b ,则这两个班的数学平均分为2a b+; ②从总体中抽取的样本12221111(,),(,),,(,),,n nn n i i i i x y x y x y x x y y n n ====∑∑若记,则回归直线y =bx a +必过点(,x y )③10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有b a c >>;④绘制频率分布直方图时,各个小长方形的面积等于相应各组的频率. 其中正确的序号是_______________(注意:14、15题是选做题,只能做其中一个,两题全答只计前一题得分)14.(几何证明选讲选做题)如图,AB 是圆O 的直径,DE AD =,6,8==BD AB ,则DEAC= ; 15.(坐标系与参数方程选择题)已知直线l 的方程为11x ty t =+⎧⎨=-⎩,,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为1ρ=,则圆C 上的点到直线l 的最短距离等于 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分12分)数列{}n a 对任意*N n ∈ ,满足11n n a a , 32a =.(1)求数列{}n a 通项公式;(2)若1()3n an b n =+,求{}n b 的通项公式及前n 项和.17.(本题满分12分)某中学在校就餐的高一年级学生有440名,高二年级学生有460名,高三年级学生有500名;为了解学校食堂的服务质量情况,用分层抽样的方法从中抽取70名学生进行抽样调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表(服务满意度为x ,价格满意度为y ).(1)求高二年级共抽取学生人数;(2)求“服务满意度”为3时的5个“价格满意度”数据的方差;(3)为提高食堂服务质量,现从3<x 且42<≤y 的所有学生中随机抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.18.(本题满分14分)如图(1)在等腰ABC ∆中,D 、E 、F 分别是AB 、AC 、BC 边的中点,现将ACD ∆沿CD 翻折,使得平面ACD ⊥平面BCD .(如图(2)) (1)求证://AB 平面DEF ; (2)求证:BD AC ⊥;(3)设三棱锥A BCD -的体积为1V 、多面体ABFED 的体积为2V ,求12:V V 的值.19. (本题满分14分)在ΔABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,其中2c =, 且cos 3cos A b B a == (1)求证:ΔABC 是直角三角形;(2)设圆O 过A ,B ,C 三点,点P 位于劣弧AC ︿上,PAB θ∠=,用θ的三角函数表示三角形PAC ∆的面积,并求PAC ∆面积最大值.20.(本题满分14分)已知函数()ln f x x x =. (1)求函数()f x 的极值;(2)设函数()()(1)g x f x k x =--,其中k R ∈,求函数()g x 在区间[1,e]上的最大值.21.(本题满分14分)在直角坐标系xOy 中,动点P 与定点(1,0)F 的距离和它到定直线2x =,设动点P 的轨迹为1C ,Q 是动圆2222:C x y r +=(12)r <<上一点.(1)求动点P 的轨迹1C 的方程,并说明轨迹是什么图形;(2)设曲线1C 上的三点1122(,),(1,(,)2A x yBC x y 与点F 的距离成等差数列,若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k ;(3)若直线PQ 与1C 和动圆2C 均只有一个公共点,求P 、Q 两点的距离PQ 的最大值.2012届高考模拟测试数学试题(文科)参考答案和评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一.选择题:CBCCA BAAAB 二.填空题:11. 35(2分) 247-(3分)12. 85 13.②④ 14. 431三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分14分) 解:(1)由已知得11nna a 数列{}n a 是等差数列,且公差1d = ……………2分又32a =,得10a =,所以 1n a n =-……………………………………………………………4分(2)由(1)得,11()3n n b n -=+, 所以111(11)(2)()33n n S n -=++++⋅⋅⋅++211111(123)333n n -=+++⋅⋅⋅+++++⋅⋅⋅+…………………………………………………………………………………………………6分111()(1)33(1)3.122213nn n n n n n S --+-+=+=+-……………………………12分 17.(本题满分12分)解:(1)共有1400名学生,高二级抽取的人数为23701400460=⨯(人)…………3分 (2)“服务满意度为3”时的5个数据的平均数为3788465++++=,……………4分所以方差()()()()4.4564682676322222=-+-+-+-=s………………6分(3)符合条件的所有学生共7人,其中“服务满意度为2”的4人记为d c b a ,,, “服务满意度为1”的3人记为z y x ,,. ……………………8分 在这7人中抽取2人有如下情况:()()()()()()z a y a x a d a c a b a ,,,,,,,,,,,()()()()()z b y b x b d b c b ,,,,,,,,,()()()()z c y c x c d c ,,,,,,,()()()z d y d x d ,,,,,()()()z y z x y x ,,,,,共21种情况. ……………………9分其中至少有一人的“服务满意度为1”的情况有15种. ……………………11分 所以至少有一人的“服务满意度”为1的概率为752115==p ……………………12分18(本题满分14分)(1)证明:如图:在△ABC 中,由E 、F 分别是AC 、BC 中点,得EF //AB ,又AB ⊄平面DEF ,EF ⊂平面DEF ,∴AB ∥平面DEF .………………4分 (2)∵平面ACD ⊥平面BCD 于CDAD ⊥CD , 且AD ⊂平面ACD∴AD ⊥平面BCD ,又BD ⊂平面BCD ,∴AD BD ⊥……………………7分 又∵CD BD ⊥,且AD CD D =∴BD ⊥平面ACD ,又AC ⊂平面ACD∴BD AC ⊥.………………………………………………………………9分 (3)由(2)可知AD ⊥平面BCD ,所以AD 是三棱锥A BCD -的高∴113BCD V AD S =⋅⋅……………………………………11分 又∵E 、F 分别是AC 、BC 边的中点,∴三棱锥E CDF -的高是三棱锥A BCD -高的一半三棱锥E CDF -的底面积是三棱锥A BCD -底面积的一半∴三棱锥E CDF -的体积114E CDF V V -=…………………………………12分∴211111344E CDF V V V V V V -=-=-=…………………………………13分∴12:4:3.V V =…………………………………14分 19.(本题满分14分) (1)证明:由正弦定理得cos sin cos sin A B B A=,整理为sin cos sin cos A A B B =,即sin2A =sin2B ∴2A =2B 或2A +2B =π,即A =B 或A +B =π2∵3b a =,∴A =B 舍去. 由A +B =π2可知c =π2,∴ΔABC 是直角三角形…………………6分(2)由(1)及2c =,得3a =,1b =…………………………………………………………7分在Rt ΔPAB 中,cos 2cos PA AB θθ=⋅= 所以,11sin()2cos 3sin()3cos sin()26266PAC S PA AC πππθθθθθ∆=⋅⋅-=⋅⋅⋅⋅-=⋅⋅-………………………………………………………………………………………………………9分313cos (sin cos )2θθθ=⋅-⋅ 33(3sin 2cos 2)44θθ=-+ 3sin(2)26πθ=-34-,62ππθ<<………………………………………………12分 因为62ππθ<<,所以,52666ππθπ<-< 当262ππθ-=,即 3πθ=时,PAC S ∆最大值等于34.………………………………12分 20.(本题满分14分)(1)()ln 1(0)f x x x '=+>. …………………………………………………………1分 令()0f x '≥,得1ln 1ln x e -≥-=,11ln x ee-≥=; 令()0f x '≤,得10,x e⎛⎤∈ ⎥⎝⎦.…………………………………………………………3分()f x ∴的单调递增区间是1,e ⎡⎫+∞⎪⎢⎣⎭,单调递减区间是10,e ⎛⎤ ⎥⎝⎦,min 11()f x f e e ⎛⎫==- ⎪⎝⎭.()f x 无极大值………………………………………………………………………5分(2)()g x =ln (1)x x k x --,则()ln 1g x x k '=+-,由()0g x '=,得1ek x -=,所以,在区间1(0,e)k -上,()g x 为递减函数,在区间1(e ,)k -+∞上,()g x 为递增函数.……………………………………………………………………………………8分 当1e1k -≤,即1k ≤时,在区间[1,e]上,()g x 为递增函数,所以,()g x 最大值为()g e e ke k =-+. …………………10分 当11<e<e k -,即12k <<时,()g x 的最大值是(1)g 或()g e(1)g =()g e ,得1e k e =- 当11ek e <<-时,()0(1)g e e ek k g =-+>=,()g x 最大值为()g e e ke k =-+当21ek e ≤<-时,()0(1)g e e ek k g =-+<=,()g x 最大值为(1)0g = ………………………………………………………………………………12分 当1ee k -≥,即2k ≥时,在区间[1,e]上,()g x 为递减函数,所以()g x 最大值为(1)0g =.综上,当1e k e <-时,()g x 最大值为e ke k -+; 当1e k e ≥-时,()g x 的最大值是0 ……………………………………………………………………………14分21.(本题满分14分)解:(1=2分.将两边平方,并化简得2212x y +=,……………………………………………………4分.故轨迹1C 的方程是2212x y +=,它是长轴、短轴分别为2的椭圆………………4分.(2)由已知可得1)AF x =-,1)BF =-,2)CF x =-,因为2BF AF CF =+,所以1(2)2x -2)2x +-21)2=⨯-, 即得122x x +=, ① ……………………………………………………5分. 故线段AC 的中点为12(1,)2y y +,其垂直平分线方程为121212(1)2y y x x y x y y +--=---, ② ……………………………………………………………………………………………6分.因为,A C 在椭圆上,故有221112x y +=,222212x y +=,两式相减,得:2222121202x x y y -+-= ③ 将①代入③,化简得12121212122()x x y y y y y y x x -+-==+-+, ④ ………………………7分.将④代入②,并令0y =得,12x =,即T 的坐标为1(,0)2。
【高三数学试题精选】2018年韶关市高三数学4月高考模拟试题(文附答案)

,
所以所求的线性回归方程为.
(Ⅲ)当时,;当时,;当时,;当时,;当时,;当时,.
与销售数据对比可知满足(1,2,…,6)的共有3个“好数据”、、.
从6个销售数据中任意抽取2个的所有可能结果有种,
其中2个数据中至少有一个是“好数据”的结果有种,
于是从抽得2个数据中至少有一个销售数据中的产品销量不超过80的概率为.
因为,所以.
(Ⅱ)如图,不妨设,,则,,
,
所以,即,时,最大值是.
23解(Ⅰ)由于
的最大值为,故
(Ⅱ)∵,且,,
∴,
当且仅当,即,等号成立.
Hale Waihona Puke 所以52018年韶关市高三数学4月高考模拟试题(文附答案)
5
5不等式选讲
已知函数的最大值().
(Ⅰ)求的值;
(Ⅱ)若(,),试比较与的大小.
10 11、12
二、填空题
13 143112 15 163
三、解答题
17解(Ⅰ)由正弦定理,又由已知,
所以,,
因为,所以.
(Ⅱ)由已知,则是等腰三角形,,设,
,
由已知的面积为,得,,
20解(Ⅰ)设点的坐标为,因为定点在定直线的右侧,
且动点到定直线的距离比到定点的距离大,
所以且,
化简得,即,
轨迹的方程为.
(Ⅱ)设,(),则,,
∵,,三点共线,
∴,
∴,
又,∴,
直线的方程为,令,得.
同理可得.
所以以为直径的圆的方程为,
即.
将代入上式,可得,
令,即或,
故以为直径的圆被轴截得的弦长为定值4.
21解(Ⅰ)∵,
∴,且,
又在点处的切线方程为,
广东省韶关市高三数学第二次调研考试试题 文(韶关二模)新人教A版

韶关市2013届高三年级第一次调研(期末)测试数学文试题本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟. 注意事项:考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分;3.考试结束,考生只需将答题卷交回. 4. 参考公式:锥体的体积公式13V Sh=,其中S 是锥体的底面积,h 是锥体的高. 正棱锥的侧面积公式:'12S ch=,c 是底面周长,'h 是斜高.一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U={0,1,2,3,4,5},集合A={2,4},B={}0,2,则集合()()A B =痧A .{0,4,5,2}B .{0,4,5}C .{2,4,5}D .{1,3,5}2.已知为虚数单位,则2(1)11i i ++-=( )A -B -1CD 13.设0.320.30.3log 2,log 3,2,0.3a b c d ====,则这四个数的大小关系是( )A .a b c d <<<B . b a d c <<< C. b a c d <<< D.d c a b <<<4.若方程22111x y k k -=+-表示双曲线,则k 的取值范围是( )A. 11k -<<B. 0k >C. 0k ≤D.1k >或1k <-5.某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是两个全等等腰三角形)根据图中标出的数据,可得这个几何体的表面积为( )A.4+ B.4+ C .83 D .126.已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( ) A.y ∧=1.23x +4 B.y ∧=1.23x +5ED CB AC .y ∧=1.23x +0.08D .y ∧=0.08x +1.237. 设不等式组002x y x y ≥⎧⎪≥⎨⎪+≤⎩表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点)A . 4πB .22π- C . 6πD .44π-8. ABC ∆中,角A 、B 、C 所以的边为a 、b 、c , 若3a =,120C =,ABC ∆面积ABC S ∆=c =( )A.5B. 6C. D.79.设{an }(n ∈N*)是等差数列,Sn 是其前n 项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( ) A .d <0 B .a7=0 C .S9>S5 D .S6与S7均为Sn 的最大值10.已知122123412(),(),(),()log x f x x f x x f x e f x x====, 四个函数中,当120x x <<时,满足不等式1212()()()22f x f x x xf ++<的是.A 121()f x x = .B 22()f x x = .C 3()xf x e = .D 412()log f x x=二.填空题:本大题共5小题,每小题5分,满分20分.11. 若向量(1,1),(2,5),(3,)a b c x ===,满足条件(8)30a b c -⋅=,则x = 12. 下图是某算法的程序框图,则程序运行后输出的结果是 .13. 平面上有n 条直线, 这n 条直线任意两条不平行, 任意三条不共点, 记这n 条直线将平面分成()f n 部分, 则(3)f =___________, 4n ≥时,()f n =_________________.)(用n 表示). 14.(几何证明选讲选做题)如图,AB、CD是圆的两条弦,AB与CD交于E, AE EB>, AB是线段CD的中垂线.若AB=6,CD=52,则线段AC的长度为.15.(坐标系与参数方程选做题)在直角坐标系xoy中,圆1C的参数方程为cos1sinxyαα=⎧⎨=+⎩(α为参数);在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴的正半轴为极轴)中,圆2C的方程为4sinρθ=,则1C与2C的位置关系是______(在“相交、相离、内切、外切、内含”中选择一个你认为正确的填上).三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分12分)函数()sin()4f x A xπω=-(0,0Aω>>)的部分图像如右所示.(1)求函数()f x的解析式;(2)设(0,)2πα∈,且6()285fαπ+=,求tanα的值.17.(本小题满分12分)高一(1)班参加校生物竞赛学生成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求高一(1)班参加校生物竞赛人数及分数在[)80,90之间的频数,并计算频率分布直方图中[)80,90间的矩形的高;(2)若要从分数在[]80,100之间的学生中任选两人进行某项研究,求至少有一人分数在[]90,100之间的概率.18.(本小题满分14分)如图,已知⊥PA ⊙O 所在的平面,AB 是⊙O 的直径,4AB =,C 是⊙O 上一点,且PA =BC AC =,PE PFPC PB λ==.(1) 求证:ABC EF 面//; (2) 求证:EF ⊥AE ;(3)当12λ=时,求三棱锥A CEF -的体积.19.(本小题满分14分)椭圆2222:1(0)x y C a b a b +=>>的离心率为35,两焦点分别为12,F F ,点M 是椭圆C 上一点,12F F M ∆的周长为16,设线段MO (O 为坐标原点)与圆222:O x y r +=交于点N ,且线段MN 长度的最小值为154.(1)求椭圆C 以及圆O 的方程; (2)当点000(,)(0)M x y x ≠在椭圆C 上运动时,判断直线00:1l x x y y +=与圆O 的位置关系.20.(本小题满分14分) 已知函数2()ln f x x x =.(1)判断()f x 奇偶性, 并求出函数)(x f 的单调区间; (2)若函数()()1g x f x kx =-+有零点,求实数k 的取值范围.21.(本小题满分14分) 设等差数列}{n a 的公差0≠d ,等比数列}{n b 公比为q ,且11a b =,33b a =,57b a =(1)求等比数列}{n b 的公比q 的值;(2)将数列}{na,}{nb中的公共项按由小到大的顺序排列组成一个新的数列}{nc,是否存在正整数,,λμω(其中λμω<<)使得,,λμω和,,c c cλμωλμω+++都构成等差数列?若存在,求出一组,,λμω的值;若不存在,请说明理由.韶关市2013届高三年级第一次调研(期末)测试数学试题(文科)参考答案说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.DCBAB CDDCA二、填空题:本大题主要考查基本知识和基本运算.本大题共5小题,考生作答4小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.11. 412. 1113. 7(2分),222n n++(3分)14.15. 内切三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分12分)函数()sin()4f x A xπω=-(0,0Aω>>)的部分图像如右所示.(1)求函数()f x的解析式;(2)设(0,)2πα∈,且6()285fαπ+=,求tanα的值解:(1)∵由图可知:函数()f x的最大值为2,………2分且34824 Tπππ=-=∴2A=,最小正周期Tπ=………………………………………………………4分∴22Tπω==故函数()f x的解析式为()2sin(2)4f x xπ=-. …………………………………6分(2)6()2sin285fαπα+==,………………………………………………………8分∴3sin5α=,∵2πα<<,∴4cos5α==,…………………………………………………………10分∴sin3tancos4ααα==…………………………………………………………………12分17.(本题满分12分)高一(1)班参加校生物竞赛学生成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求高一(1)班参加校生物竞赛人数及分数在[)80,90之间的频数,并计算频率分布直方图中[)80,90间的矩形的高;(2)若要从分数在[]80,100之间的学生中任选两人进行某项研究,求至少有一人分数在[]90,100之间的概率.解.(1)分数在[)50,60之间的频数为2,频率为0.008100.08⨯=,∴高一(1)班参加校生物竞赛人数为2250.08=.………2分所以分数在[)80,90之间的频数为25271024----=………4分频率分布直方图中[)80,90间的矩形的高为4100.01625÷=.………6分(2)设至少有一人分数在[]90,100之间为事件A将[)80,90之间的4人编号为1,2,3,4,[]90,100之间的2人编号为5,6, 在[]80,100之间的任取两人的基本事件为:()1,2,()1,3,()1,4,()1,5,()1,6()2,3,()2,4,()2,5,()2,6,()3,4,()3,5,()3,6,()4,5,()4,6. 共15个………………………………………………………………………………………………..9分 其中,至少有一个在[]90,100之间的基本事件有9个……………………………………10分 根据古典概型概率计算公式,得93()155P A ==………………………………………11分答:至少有一人分数在[]90,100之间的概率35 ………………………………………12分18.(本小题满分14分)如图,如图,已知⊥PA ⊙O 所在的平面,AB 是⊙O 的直径,C 是⊙O 上一点,且PA =BC AC =,PE PFPC PB λ==.(1) 求证: ABC EF 面//; (2) 求证:EF ⊥AE ;(3)当12λ=时,求三棱锥A CEF -的体积.解: (1)证明:在三角形PBC 中,PE PFPC PB λ==所以 EF//BC ,ABC,EF ABC,面面⊄⊂BCABC //面EF ∴ ………………………………………………………………………4分(2)⇒⎩⎨⎧⊂⊥ABC BC ABCPA 面面PA BC ⊥ 又AB 是⊙O 的直径,所以AC BC ⊥ ……………………………………………7分 所以,PAC 面⊥BC ………………………………………………………8分 因 EF//BC PAC BC 面⊥,所以PAC EF 面⊥因为AE ⊂PAC 面, 所以EF ⊥AE . ……………………………………………10分(3) 在Rt ABC ∆中,4AB = ∴ PA =BC AC ==当12λ=时,E 是PC 中点.F 为PC 中点 ∴12EF BC ==11111222222EAC PAC S S PA AC ∆∆==⨯⋅=⨯⨯=……… 12分EF PAC⊥面11233A CEF F ACE ACE V V S EF --∆===⨯=……………………………………14分19.(本题满分14分)椭圆2222:1(0)x y C a b a b +=>>的离心率为35,两焦点分别为12,F F ,点M 是椭圆C 上一点,12F F M ∆的周长为16,设线段MO (O 为坐标原点)与圆222:C x y r +=交于点N ,且线段MN 长度的最小值为154.(1)求椭圆C 以及圆O 的方程; (2)当点000(,)(0)M x y x ≠在椭圆C 上运动时,判断直线00:1l x x y y +=与圆O 的位置关系.解:(1)设椭圆C 的半焦距为c ,则35c a =,即35c a= ① ………………………1分 又1212||||||2216MF MF F F a c ++=+=②………………………………3分联立①②,解得5,3a c ==,所以4b ==. 所以椭圆C 的方程为2212516x y +=.………………………………………………………5分而椭圆C 上点00(,)M x y 与椭圆中心O 的距离为||4MO ===≥,等号在00x =时成立………7分,而||||MN MO r =-,则||MN 的最小值为4r -,从而14r =,则圆O 的方程为22116x y +=.………………………………………………………………………………9分(2)因为点00(,)M x y 在椭圆C 上运动,所以220012516x y +=.即2200161625y x =-.圆心O 到直线00:1l x x y y +=的距离d ==.……………12分当00x ≠,14d r <==,则直线l 与圆O 相交. …………………… ……………14分20.(本题满分14分) 已知函数2()ln f x x x =.(1)判断()f x 奇偶性, 并求出函数)(x f 的单调区间; (2)若函数()()1g x f x kx =-+有零点,求实数k 的取值范围.解(1) ()f x 定义域{}|0x x ≠在数轴上关于原点对称,且22()ln()ln ()f x x x x x f x -=--==,所以()f x 是偶函数……………………2分当0x >时, ()2ln f x x x =, '()2(1ln )f x x =+由 '()0f x >, 1ln 0x +>, 解得:1x e >所以()f x 在1(,)e +∞是增函数;由 '()0f x <, 1ln 0x +<, 解得:10x e <<.所以()f x 在1(0,)e 是减函数. ………4分因为()f x 是偶函数, 图象关于y 轴对称,所以, 当0x <时, ()f x 在1(,)e -∞-是减函数, 在1(,0)e -是增函数.所以, )(x f 的单调增区间是1(,)e +∞,1(,0)e -;单调减区间是1(0,)e ,1(,)e -∞-,.………6分(2) 由()0g x =,得2ln 10x x kx ⋅-+=,2ln 1x x k xx ⋅=+令()h x =2ln 1x x xx ⋅+………………………………………………………………………8分 当0x >时,'221()x h x x -=,当12x >, '()0h x >, ()h x 在1(,)2+∞是增函数;当102x <<, '()0h x <, ()h x 在1(0,)2是减函数,所以, 当0x >时,()h x 极小值是1()22ln 22h =-…………………………………11分 因为()h x 是奇函数,所以, 当0x <时, ()h x 极大值是1()2ln 222h -=-所以 ()(22ln 2,)(,2ln 22)h x ∈-+∞-∞-,即(22ln 2,)(,2ln 22)k ∈-+∞-∞-, 函数()g x 有零点. ………………………14分21.(本题满分14分) 设等差数列}{n a 的公差0≠d ,等比数列}{n b 公比为q ,且11a b =,33b a =,57b a =(1)求等比数列}{n b 的公比q 的值;(2)将数列}{n a ,}{n b 中的公共项按由小到大的顺序排列组成一个新的数列}{n c ,是否存在正整数,,λμω(其中λμω<<)使得,,λμω和,,c c c λμωλμω+++都构成等差数列?若存在,求出一组,,λμω的值;若不存在,请说明理由. 解:(1)设11a b ==,a ,由题意⎪⎩⎪⎨⎧+=+=d a aq d a aq 6242 即⎪⎩⎪⎨⎧=-=-da aq d a aq 62420,d ≠∴1q =±不合题意………………………3分故311142=--q q ,解得22=q 2±=∴q …………………………………………………-5分 (2)答:不存在正整数,,λμω(其中λμω<<)使得,,λμω和,,c c c λμωλμω+++均构成等差数列证明:假设存在正整数,,λμω满足题意设11a b ==,a 且m n b a =,故 1)1(-=-+m aq d n a ,又a a aq d =-=22 2ad =∴-1)2(211-±=-+∴m n 即2112)1(1+-±=+m m n …………………………………………7分*1N n ∈+ 1(1)0m -∴±> 1221-=∴+m n m 为奇数,且-……………………8分令)(12*N k k m ∈-=,则2111(2k k m b a a ---=⋅=⋅a c n n 12-=∴ ……………………………………………………………………10分 若存在正整数,,λμω满足题意,则11122(2)(2)(2)a a a μλωμλωμλω---=+⎧⎨⋅+=⋅++⋅+⎩11222μλω--∴=+,又112222("")λωλωλω+--+≥===当且仅当时取 又λμ≠,1122222λωμλω+--∴=+> ----------------------12分 又x y 2=在R 上为增函数,2λωμ+∴>,与题设2λωμ+=矛盾,∴假设不成立故不存在,,λμω满足题意.--------------------------------------------14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省韶关市2018届高三高考模拟(二模)数学试题(文科)本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟. 注意事项: 1.考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上; 2.选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分; 3.考试结束,考生只需将答题卷交回.4. 参考公式:圆柱侧面积公式 2S rl π=侧,其中r 底面半径,l 为圆柱的母线.一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知集合{1,2,3,4}U =,集合={2,3}A ,={3,4}B ,则() U A B = ð A .{1,2,4} B .{2,4} C .{3} D .{1} 2.i 是虚数单位, 复数21=i z i-,则复数z 在复平面内对应的点在 A .第一象限 B .第二象限 C .第三象限 D .第四象限3. 在某次测量中得到的A 样本数据如下:82、84、84、86、86、86、88、88、88、88.若B 样本数据恰好是A 样本数据每一个数都加2后所得数据,则A 、B 两个样本的下列数字特征对应相同的是A .众数B .平均数C .中位D .方差4.设()24x f x x =+-,则函数()f x 的零点位于区间 A .(-1,0) B .(0,1) C .(1,2) D .(2,3)5.执行如图所示的程序框图,若输出的结果是 16,条件是A .6n >?B .7n ≥?C .8?n >D .9?n > 6.由于工业化城镇化的推进,大气污染日益加重,空气质量脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如右的列联表:问有多大的把握认为是否患心脏病与性别有关. 答:. A .95% B .99% C .99.5% D .99.9%参考临界值表:(参考公式:()()()()()22n ad bc K a b c d a c b d -=++++ 其中n = a + b + c + d ).7.某个几何体的三视图如右上图(其中正视图中的圆 弧是半圆)所示,则该几何体的表面积为A .9214π+B .8214π+C .9224π+D .8214π+8. 等差数列{}n a 中,133a =,4d =-,若前n 项和n S 取得最大,则n =A.9B. 10C. 11D. 129. 给出如下四个判断:①00,e 0x x ∃∈≤R ;②2,2x x x ∀∈>+R ;③设,a b 是实数,1,1a b >>是1ab >的充要条件 ; ④命题“若p 则q ”的逆否命题是若q ⌝,则p ⌝.其中正确的判断个数是:A .1B .2C .3D .410.已知函数()222,02,0x x x f x x x x ⎧+≥=⎨-<⎩,若()()2(1)f a f a f -+≤,则实数a 的取值范围是A .[1,0)-B .[]0,1C .[]1,1-D .[]2,2-二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分.(一)必做题(11~13题)ODCBAP11. 已知向量(1,3)=a ,(,21)m m =-b .若向量a 与b 共线,则实数m =_______________12.抛物线22x y =上的点M 到其焦点F 的距离52MF =,则点M 的坐标是_____________13.一只艘船以均匀的速度由A 点向正北方向航行,如图,开始航行时,从A 点观测灯塔C 的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B 点观测灯塔C 的方位角为75°,则A 到C 的距离是__________海里.(二)选做题(14、15题,考生只能从中选做一题)14. (坐标系与参数方程选做题)曲线C 极坐标方程为06sin 4cos 42=+--θρθρρ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,直线l 的参数方程为⎩⎨⎧+=--=ty t x 2322(t 为参数),则曲线C 上的点到直线l 的距离的最小值为 .15.(几何证明选讲选做题) 如图,AB 是半径为3的⊙O 的直径,CD 是弦,BA ,CD 的延长线交于点P ,4,5PA PD ==,则=∠CBD .三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分12分)已知函数.cos 22sin 3)(2x x x f +=CBA75°45°(1)求)34(πf 的值; (2)已知⎥⎦⎤⎢⎣⎡∈2,0πx ,求函数)(x f 的值域.17. (本题满分12分)为调查民营企业的经营状况,某统计机构用分层抽样的方法从A 、B 、C 三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)(1)求x 、y 的值;(2)若从城市A 与B 抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A 的概率.18.(本题满分14分如图1,直角梯形FBCE 中, 四边形ADEF 是正方形,2AB AD ==,4CD =.将正方形沿AD 折起,得到如图2所示的多面F EDCBA MF 1E 1DCBA体,其中面11ADE F ⊥面ABCD ,M 是1E C 中点.(1) 证明:BM ∥平面11ADE F ; (2) 求三棱锥1D BME -的体积.图1图219.(本题满分14分)已知椭圆 的离心率为e =,过1C 的左焦点1F 的直线:20l x y -+=被圆2222:(3)(3)(0)C x y r r -+-=>截得的弦长为(1)求椭圆1C 的方程;(2)设1C 的右焦点为2F ,在圆2C 上是否存在点P ,满足2122a PF PF b=,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.20.(本题满分14分)已知正项数列{}n a 中,其前n 项和为n S ,且1n a =. (1)求数列{}n a 的通项公式; (2)设22n n na b +=,123n n T b b b b =++++ ,求证:352n T ≤<; (3)设c 为实数,对任意满足成等差数列的三个不等正整数,,m k n ,不等式m n k S S cS +>都成立,求实数c 的取值范围.21.(本题满分14分)已知函数32()f x x x b =-++,()ln g x a x =. (1)若()f x 的极大值为427,求实数b 的值; (2)若对任意[]1,x e ∈,都有2()(2)g x x a x -++≥恒成立,求实数a 的取值范围;(3)若函数f (x )满足:在定义域内存在实数x 0,使f (x 0+k )=f (x 0)+ f (k )(k 为常数),则称“f (x )关于k 可线性分解”. 设0b =,若2()()()af x F x g x x =+关于实数a 可线性分解,求a 取值范围.广东省韶关市2018届高三4月高考模拟(二模)数学(文科)参考答案与评分标准一.选择题: DADCC CAAAC1. 解析:{}2,3,4A B = ,()U A B ð{}1=,选D.2. 解析:21=2,i z i i-=+z 对应点在第一象限 , 选A. 3. 解析:由方差意义可知,选D. 4. 解析:(1)10,(2)20f f =-<=> ,选C.5. 解析:第一次循环,1,3S n ==,不满足条件,循环。
第二次循环,134,5S n =+==,不满足条件,循环。
第三次循环,459,7S n =+==,不满足条件,循环。
第四次循环,9716,9S n =+==,满足条件,输出。
所以判断框内的条件是8n >,选C. 6.解析:()()()()()()222502015510258.333252530203n ad bc K a b c d a c b d -⨯-⨯===≈++++⨯⨯⨯ ,又 ()27.7890.0050.5%P K ≥==,所以我们有 99.5%的把握认为患心脏病与性别有关系. 选C.7. 解析: 三视图表示的几何体是由长方体和“半圆柱”组成的几何体,其中,长方体的上底面与“半圆柱”轴截面重合.21(1620)22022592142S πππ=+⨯++⨯+⨯⨯⨯=+,选A. 8. 解析: 由得到0n a ≥ 374n ≤,n 是正整数,9n =,选A. 9. 解析:任意,0x x R e ∈>,①不正确;2x =时,22x x =,②不正确;1ab >不能得到1,1a b >>,③不正确;④正确. 选A.10. 解析: 由偶函数定义可得()f x 是偶函数,故()()f a f a -=,原不等式等价于()(1)f a f ≤,又根据偶函数定义,()()f a f a =(1)f ≤,函数ODCBAP()f x 在(0,)+∞单调递增,1a ≤,[1,1]a ∈-.或利用图象求a 范围.选C.二.填空题:11.1- ; 12. (2,2),(2,2)- ;13. ;; 15. 6π11.解析:由a b λ=可得,1m =-12.解析: 设点(,)M x y ,曲线准线12y =-,再抛物线定义,15()22y --=,2y =,所以224,2x y x ===±13. 解析: 105,30ABC C ∠=∠= ,ABC ∆中,由正弦定理,sin sin AB ABCAC C⋅∠==∠60sin105sin 30⋅=14.解析:曲线C 直角坐标方程 22(2)(2)2x y -+-=,直线l :10x y +-= 最小圆心到直线距离d =所以,曲线C 上点到l 的距离的15. 解析:由割线定理知8=⇒⋅=⋅PD PD PC PB PA ,∴3=CD ,3π=∠COD ,得.6CBD π∠=三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分12分)解:(1)12cos 2sin 3cos 22sin 3)(2++=+=x x x x x f 1)62sin(2++=πx (2)分∴1617sin 21)638sin(2)34(+=++=ππππf 165sin 2+=π 4分 216sin2=+=π6分(2)12cos 2sin 3cos 22sin 3)(2++=+=x x x x x f 1)62sin(2++=πx⎥⎦⎤⎢⎣⎡∈2,0πx ,∴⎥⎦⎤⎢⎣⎡∈+67,662πππx 8分∴1)62sin(21≤+≤-πx , 10分 ∴31)62sin(20≤++≤πx ,即)(x f 的值域是[].3,0 12分17.(本题满分12分) 解:(1)由题意得288446x y ==,………………………………………………4分 所以56x =,2y =……………………………………………………………………6分(2)记从城市A 所抽取的民营企业分别为1234,,,a a a a ,从城市B 抽取的民营企业分别为12,b b . 则从城市A 、B 抽取的6个中再随机选2个进行跟踪式调研的基本事件有12(,)a a ,13(,)a a ,14(,)a a ,11(,)a b ,12(,)a b ,23(,)a a ,24(,)a a ,21(,)a b ,22(,)a b , 34(,)a a ,31(,)a b ,32(,)a b ,41(,)a b ,42(,)a b ,12(,)b b 共15个………………………………8分其中,来自城市A: 12(,)a a ,13(,)a a ,14(,)a a ,23(,)a a ,24(,)a a ,34(,)a a 共6个………10分 因此62()155P X ==.故这2个都来自城市A 的概率为25.………12分N MF 1E 1D CBA18. (本题满分14分)(1)证明:取DE 中点N ,连结,MN AN .在△EDC 中,,M N 分别为,EC ED 的中点,所以MN ∥CD12MN CD =.由已知AB ∥CD ,12AB CD =,所以MN ∥AB ,且MN AB =.所以四边形ABMN为平行四边形,所以BM ∥AN .………3分又因为AN ⊂平面ADEF ,且BM ⊄平面ADEF , 所以BM ∥平面ADEF .…………………4分 (2)面11ADE F ⊥面ABCD ,1E D ⊂面11ADE F , 面11ADE F 面ABCD AD =,1E D AD ⊥,1E D ⊥面ABCD 又BC ⊂面ABCD ,1E D ⊥BC …………………6分梯形ABCD 中,2AB AD ==,4CD =,90A ∠=,BC BD ==所以,222BD BC CD +=, 90CDB ∠= ,BC BD ⊥1BD DE D = ,所以, BC ⊥平面1BDE …………………8分又BC ⊂平面1BCE ,所以,平面1BCE ⊥平面1BDE作DG ⊥1BE ,则DG ⊥平面1BCE ,DG 是所求三棱锥高…………………10分111111332D BME BE M BCE V DG S DG S -∆∆=⋅=⋅在直角三角形1BDE中,由面积关系可得DG =,又1BCE S ∆=所以,143D BME V -=……………………………………14分 另解:AB ∥CD ,AB ⊄面1CDE ,CD ⊄面1CDE ,AB ∥平面1CDE , ,A B 两点到平面1CDE 距离相等…………………7分因为翻折后垂直关系不变,所以AD ⊥平面1CDE ,AD 是三棱锥1B DME -高……9分面11ADE F ⊥面ABCD ,1E D ⊂面11ADE F ,面11ADE F 面ABCD AD =,1E D AD ⊥,1E D ⊥面ABCD ,1E D CD ⊥, 1CDE 是直角三角形………………11分111111111142243323223D BME B DME DME CDE V V AD S AD S --∆∆==⋅=⋅⋅=⨯⨯⨯⨯⨯=…14分19.(本题满分14分)解:因为直线l 的方程为:20l x y -+=,令0y =,得2x =-,即1(2,0)F -………………………………1分∴2c = ,又∵c e a==, ∴ 26a = , 2222b a c =-=∴ 椭圆1C 的方程为221:162x y C +=.………………………………………4分(2)∵ 圆心2(3,3)C 到直线:20l x y -+=的距离为d ==,又直线:20l x y -+=被圆222:66310C x y x y m +--++=截得的弦长为∴由垂径定理得2r ===,故圆2C 的方程为222:(3)(3)4C x y -+-=.………………………………8分设圆2C 上存在点(,)P x y ,满足2122a PF PF b=即123PF PF =,且12,F F 的坐标为12(2,0),(2,0)F F -,= 整理得2259()24x y -+=,它表示圆心在5(,0)2C ,半径是32的圆。
