假设检验案例集
t检验经典案例集

1.某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量,结果如下表:某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数男360 4.66 0.58 4.84(1012/L)女255 4.18 0.29 4.33血红蛋白男360 134.5 7.1 140.2(g/L)女255 117.6 10.2 124.7*实用内科学(1976年)所载均数(转为法定单位)请就上表资料:(1)说明女性的红细胞数与血红蛋白的变异程度何者为大?(2)计算男性两项指标的抽样误差。
(3)试估计该地健康成年女性红细胞数的均数。
(4)该地健康成年男、女血红蛋白含量是否不同?(5)该地男性两项血液指标是否均低于上表的标准值(若测定方法相同)?2.一药厂为了解其生产的某药物(同一批次)之有效成份含量是否符合国家规定的标准,随机抽取了该药10片,得其样本均数为103.0mg,标准差为2.22mg。
试估计该批药剂有效成份的平均含量。
3.通过以往大量资料得知某地20岁男子平均身高为1.68米,今随机测量当地16名20岁男子,得其平均身高为1.72米,标准差为0.14米。
问当地现在20岁男子是否比以往高?4.为了解某一新降血压药物的效果,将28名高血压病患者随机分为试验组和对照组,试验组采用新降压药,对照组则用标准药物治疗,测得治疗前后的舒张压(mmHg)如下表。
问:(1)新药是否有效?(2)要比较新药和标准药的疗效是否不同,请用下述两种不同方式分别进行检验:I仅考虑治疗后的舒张压;II考虑治疗前后舒张压之差。
您认为两种方法各有何优缺点?何种方法更好?两种药物治疗前后的舒张压(mmHg)药治疗前102 100 92 98 118 100 102 116 109 116 92 108 102 100 治疗后90 90 85 90 114 95 86 84 98 103 88 100 88 86标准药病人号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 治疗前98 103 110 110 110 94 104 92 108 110 112 92 104 90 治疗后100 94 100 105 110 96 94 100 104 109 100 95 100 855.某医师观察某新药治疗肺炎的疗效,将肺炎病人随机分为新药组和旧药组,得两组的退热天数如下表。
二项分布的有关假设测验课件

在临床试验中,研究人员将患者随机分为实验组和对照组,分别接受不同的治疗。通过观察两组患者的疗效,可 以评估新药或治疗方法的疗效。二项分布假设测验用于分析试验结果,判断疗效是否显著,从而为新药或治疗方 法的有效性提供科学依据。
案例二:市场调查数据分析
总结词
详细描述
案例三:遗传学研究数据分析
样本量较小的影响
假设检验的误判风险
第一类错误(拒真错误)
第二类错误(纳伪错误)
假设检验的适用范围和限制条件
假设检验仅适用于可量化、可比较的数据,对于不可量化或不可比较的数 据,假设检验可能不适用。
假设检验要求数据来源可靠、样本代表性高,否则可能导致错误的结论。
假设检验不适用于小样本数据或极端值较多的数据集,因为这些情况下统 计推断可能不准确。
二项分布的参数估计方法
01
最大似然估计
矩估计
02
03Байду номын сангаас
贝叶斯估计
最大似然估计是寻找使得样本观 察结果出现的概率最大的参数值。
矩估计是利用样本数据的矩(如 均值、方差等)来估计总体参数。
贝叶斯估计是基于先验信息和样 本数据,通过贝叶斯定理来推断 总体参数的后验概率分布。
参数估计的步骤和流程
01
收集样本数据
• 二项分布的简介 • 二项分布的假设测验 • 二项分布的参数估计
二项分布的定义
二项分布在统计学中的重要性
二项分布在统计学中的重要性在于它 描述了一类具有独立性和等可能性的 试验中成功的次数,是概率论和统计 学中研究的重要对象。
二项分布在现实生活中的应用
假设测验的基本概念
假设
1
假设检验
2
双侧检验
假设检验在质量管理中的应用.

假设检验在质量管理中的应用摘要:随着市场的不断完善,假设检验理论在质量管理中的重要性与日俱增,作为一种由样本信息推断总体特征的数理统计方法,在生产的各个方面都得到了广泛的应用。
本文从实际出发,对国内外研究现状进行了简要的综述,阐述了假设检验理论的基本原理,具体的实施步骤,以及在应用中需要注意的问题,同时将假设检验应用到实际的产品质量控制当中,对相关产品的质量做出合理的结论,为管理者进行改进产品质量的决策提供一定的依据。
关键词:假设检验应用质量管理Hypothesis Testing in the Application ofQuality ManagementAbstract: With the developing of the market,hypothesis testing plays an more important role in quality management.As a mathematical statistical method to make statistical inference in total population from the sample information,it is widely used in many aspects of product.This article summarizes the status of the foreign and domestic explorations.It also introduces the hypothesis testing theory,its steps ,the problems that we should pay attention to and apply it into real product quality control.It can make some conclusion of correlative product.It also can provide basis for the manager to make decision on improving product quality.Key Words: hypothesis testing application quality management在现实的生产生活中,为了取得更好的经济和社会效益,企业单位会在产品生产的各个阶段进行控制,以便达到生产预期效果,达到计划目标。
【解决】用假设检验方法解决实际问题

【关键字】解决案例名:对饮酒对工作能力是否有显著的影响的假设检验分析姓名:范晓维班级:人力031学号:07提交时间:用假设检验方法解决实际问题一:假设检验实际案例:任选19个工人分成两组,让他们每人做一件同样的工作,测得他们的完工时间(单位:分钟)如下:饮酒者 30 46 51 34 48 45 39 61 58 67 未饮酒者 28 22 55 45 39 35 42 38 20 问:饮酒对工作能力是否有显著的影响?(显著水平α=0.05)二:就案例中所面临的问题进行分析随是社会科学的快速发展,各种设施越发齐全,饮酒给大家带来快乐的同时也经常给大家带来不少的困扰和麻烦,甚至危急生命!本案例就饮酒是否对工作能力有影响做了一个假设检验的案例。
这个案例的特点是先提出了一个假设,然后要求从样本出发检验它是否成立,这就是假设检验问题。
假设检验的基本步骤:1:根据问题的性质和要求,提出零假设H0和备择假设H12:构造一个合适的统计量Q,它必须与假设有关,并且在H0成立的情况下,统计量Q的分布是已知的3:给定显著性水平α,确定H0的拒绝域W4:由样本观测值计算出统计量Q的值Q05:对假设H0做出判断:若统计量的值Q0落如拒绝域W内,则拒绝H0,否则接受H0对上题求解:解设两组工人的完工时间分别为总体ε~N(μ1,σ12)和η~N (μ2 ,σ22),其中σ1,σ2 未知,但假设以知有σ1=σ2,问题相当于要检验H0: μ1 = μ2是否成立。
m=10, =47.9,Sx2=125.29,n=9, =36.0, Sy2=112.00,Sω===11.5323T=(- )=2.2458对α=0.05,m+n-2=17,查t分布表,可得由于=2.2458>2.1098,因此拒绝H0: μ1 = μ2,从检验得出的结论是:饮酒对工作能力有显著的影响。
用SPSS的方法:Independent-Samples T Test 过程Analyze-Compare means-Indepant Samples T test附页:数理统计学及其应用领域数理统计学是“数学的一个分支学科。
假设检验的案例与应用

假设检验的案例与应用摘要假设检验又称显著性检验,是统计推断的重要组成部分,其目的是在一定假设的基础上,用样本推断总体,检验实验组与对照组之间是否存在差异,差异是否显著。
在工程实践中,为了保证系统和部件的可靠性,需要建立相应的数学模型,采用概率分布和假设检验的方法进行必要的计算。
本文总结了假设检验处理检验数据的过程,并举例说明了该过程的应用。
本文首先分析了假设检验的基本思想、步骤、检验原理以及假设检验的方法等,重点讨论了假设检验在生产实践中的使用状况,丰富了假设检验在生活中的应用方面的结果。
关键词:假设检验;参数分析;实例验证1引言目前,在日常生活中,假设检验对生活和工作有着至关重要的作用,人们面对问题经常会使用假设检验进行思考,这样就可以降低人们自身因素带来的偏差,从而最大程度避免结果的不确定性给人们生活带来的影响。
通过实例的调查,可以进而拓展对假设检验的理论研究。
在现实生活中,建立的模型和解法被讨论,模型被完全讨论。
这些原则为将来假设检验在多个行业的应用提供了思路。
通常假设检验多是用在有针对性的解决问题,对问题进入深入的探讨,方案的制定等等方面。
所以,科学技术的发展,以及当前社会生活的进步都离不开假设检验。
从当前学术界关于假设检验的相关研究来看,研究成果十分丰富。
潘素娟等人[1]分别介绍了参数假设检验和非参数假设检验两种方法,并通过案例分析了假设检验理论的应用,对抽样的数据进行推断分析,为以后的实际应用提供理论依据。
缪海斌和周炳海[2]在对具体案例进行研究时发现,制造产品过程中的问题,可以引用假设检验来进行测试,从而以最短的时间找到解决的办法。
从产品在生产过程中的众多输入因素中,选出问题存在的深层次原因。
对于原因的查找需要采用假设检验的方法展开统计,从而可以探知真正的问题所在,并使用实验设计等工业工程和六西格玛改善工具对根本原因进行改进,最终显著改善了产品的质量。
张淑贵[3]指出假设检验亦称显著性检验,是统计推断的重要内容。
假设试验相关知识简介

案例四:社会科学中的假设试验
总结词
社会科学中的假设试验主要用于测试社会现象和人类行 为的假设和理论。
详细描述
在社会科学中,假设试验被广泛应用于测试社会现象和 人类行为的假设和理论。例如,社会学家可能会进行实 验来测试不同政策对人们行为的影响,或者心理学家可 能会进行实验来了解人类认知和行为的机制。
进行试验
实施试验
严格按照试验方案进行试验,确保试验 的可靠性。
VS
数据记录
在试验过程中,及时准确地记录所有的数 据,包括观察到的现象和收集到的数据。
分析结果
数据处理
对收集到的数据进行处理和分析,提取有用的信息。
结果解释
根据数据处理的结果,对假设进行验证,解释结果的意义。
撰写报告
撰写报告
将研究过程和结果整理成报告,以供同行评 议和发表。
假设试验的种类
01
02
03
实验室实验
在受控的实验室环境中, 对实验对象进行操作或干 预,以观察其反应和结果 。
现场试验
在现实生活或实际工作环 境中,对研究对象进行操 作或干预,以观察其反应 和结果。
案例研究
对特定个体、群体或组织 进行深入、细致的研究, 以了解其特征、行为和问 题等。
假设试验的应用领域
自然科学
用于探究自然现象、物理现象 、化学反应等,如探究化学反
应的条件和机制等。
社会科学
用于探究社会现象、人类行为 、心理过程等,如探究教育、 经济、政治等领域的问题。
医学科学
用于探究人类疾病的原因、治 疗方法和效果等,如临床试验 和药物研发等。
工程科学
用于探究工程问题的解决方案 、新技术的可行性和效果等, 如机械试验和电子工程实验等
假设检验-单样本检验
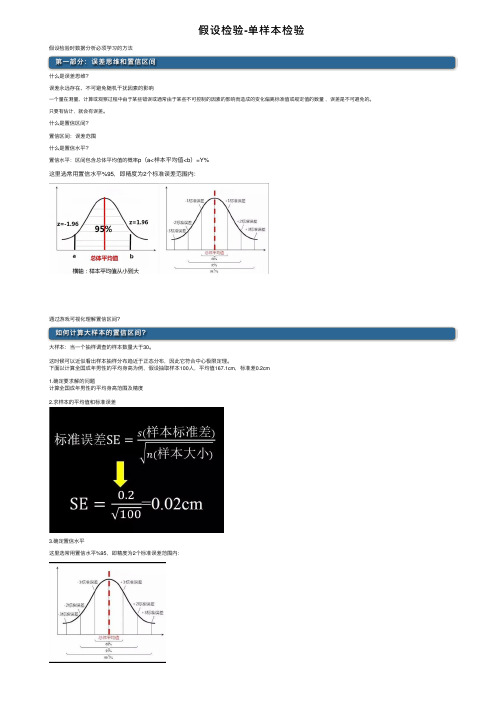
假设检验-单样本检验假设检验时数据分析必须学习的⽅法第⼀部分:误差思维和置信区间什么是误差思维?误差永远存在、不可避免随机⼲扰因素的影响⼀个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响⽽造成的变化偏离标准值或规定值的数量,误差是不可避免的。
只要有估计,就会有误差。
什么是置信区间?置信区间:误差范围什么是置信⽔平?置信⽔平:区间包含总体平均值的概率p(a<样本平均值<b)=Y%这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:通过游戏可视化理解置信区间?如何计算⼤样本的置信区间?⼤样本:当⼀个抽样调查的样本数量⼤于30。
这时候可以近似看出样本抽样分布趋近于正态分布,因此它符合中⼼极限定理。
下⾯以计算全国成年男性的平均⾝⾼为例,假设抽取样本100⼈,平均值167.1cm,标准差0.2cm 1.确定要求解的问题计算全国成年男性的平均⾝⾼范围及精度2.求样本的平均值和标准误差3.确定置信⽔平这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:4.求出置信区间上下限的值(1)由于选⽤的样本⼤⼩为100⼤于30符合正态分布,先求出如下图中两块红⾊区域⾯积(概率):(2)通过查z表格查出标准分Z=-1.96(3)求出a和b的值的⽅法:(4)根据中⼼极限定理,样本平均值约等于总体平均值,最终求出a和b的值:结论:当我们选⽤置信⽔平为%95时,求得置信区间为[167.0608,167.1392],即在两个标准误差范围内,全国成年男性的平均⾝⾼为167.0608cm到167.1392cm之间。
5.常⽤置信⽔平及其对应Z值(标准分)如何计算⼩样本的置信区间?⼩样本:当⼀个抽样调查的样本数量⼩于30。
这时候抽样分布符合t分布:在概率论和统计学中,t-分布(t-distribution)⽤于根据⼩样本来估计呈正态分布且⽅差未知的总体的均值。
如果总体⽅差已知(例如在样本数量⾜够多时),则应该⽤正态分布来估计总体均值。
第8章假设检验

24
6.假设检验的统计结论是根据原假设进行阐述的,
要么拒绝原假设,要么不拒绝原假设 • 当我们不能拒绝原假设时,我们不能说“接受 原假设”,因为我们没有证明原假设是真(如 果用“接受”则意味证明了原假设是正确的), 只不过我们没有足够的证据拒绝原假设,因此 不能拒绝原假设。当我们拒绝原假设时,得出 结论是清楚的。
拒绝原假设
小概率原理:小概率事件在一次试验中几乎不会发生 小概率的标准:与一个显著性水平a 有关, 0<a <1
13
四、假设检验的过程
提出假设 确定适当的检验统计量 规定显著性水平 计算检验统计量的值 作出统计决策
14
五、 原假设和备则假设
15
五、 原假设和备择假设
(一)原假设(null hypothesis)
我认为这种新药比原有 的药物更有效!
总体参数包括总体均 值、比例、方差等 分析之前必需陈述
如 产品合格率在80%以 上等。
9
二、什么是假设检验?
1.
2.
3.
一个假设的提出总是以一定的理由为基础,但 这些理由是不是完全充分的,要进行检验,即 进行判断。如在某种新药的研发中,研究者要 判断新药是否比原有药物更有效;海关人员对 进口货物进行检验,判断该批货物的属性是否 与申报的相一致。 假设检验就是先对总体的参数提出某种假设(原 假设和备择假设),然后利用样本信息判断假设 是否成立的过程 逻辑上运用反证法,统计上依据小概率原理
绝的却是一个真实的假设,采取的是错误行为。
31
二、显著性水平a
(significant level)
1.
2.
3.
4.
计量经济学Eviews操作案例集

在“Objects”菜单中点击“New Objects”,在“New Objects”对话框中选“Group”,并
5
在“Name for Objects”上定义文件名,点击“OK”出现数据编辑窗口。 若要将工作文件存盘,点击窗口上方“Save”,在“SaveAs”对话框中给定路径和文件名, 再点击“ok”,文件即被保存。
Monthly (月度)
Undated or irreqular (未注明日期或不规则的)
在本例中是截面数据,选择“Undated or irreqular”。并在“Start date”中输入开始时间
或顺序号,如“1”在“end date”中输入最后时间或顺序号,如“31”点击“ok”出现“Workfile
案例分析一 关于计量经济学方法论的讨论
问题:利用计量经济学建模的步骤,根据相关的消费理论,刻画我国改革开放以来的边际 消费倾向。
第一步:相关经济理论。首先了解经济理论在这一问题上的阐述,宏观经济学中,关于消 费函数的理论有以下几种:①凯恩斯的绝对收入理论,认为家庭消费在收入中所占的比例取 决于收入的绝对水平。②相对收入理论,是由美国经济学家杜森贝提出的,认为人们的消费 具有惯性,前期消费水平高,会影响下一期的消费水平,这告诉我们,除了当期收入外,前 期消费也很可能是建立消费函数时应该考虑的因素。关于消费函数的理论还有持久收入理 论、生命周期理论,有兴趣的同学可以参考相应的参考书。毋庸置疑,收入和消费之间是正 相关的。
2中国ipo抑价率多因素回归模型在股票发行初级市场中针对ipo的超额收益率设定新股抑价率为arptp0p0构建多因素回归模型跟前文相对应我们先设定两个回归元的回归模型假定ar跟股票的发行规模有关在本例中我们用其发行规模的对数值来替代设定为lgipo除此之外还有股票的中签率有关则设定一个简单的三变量回归模型为arlgiporat月120只上海证券交易所上市的新股数据
12and13假设检验与t检验

第12章分布类型的检验本章将涉及统计学分析中最为主要的理论之一:假设检验,它是分析统计数据、构建统计模型进行决策支持的基石。
12.1假设检验的基本思想12.1.1问题的提出12.1.2假设检验的基本步骤1.小概率事件在讨论假设检验的基本思想之前,首先需要明确小概率事件这一概念。
衡量一个事件发生与否可能性的标准是概率大小,通常概率大的事件容易发生,概率小的事件不容易发生。
习惯上将发生概率很小,如P<=0.05的事件称为小概率事件,表示在一次实验或观察中该事件发生的可能性很小,因此,如果只进行一次试验,可以视为不会发生。
这里需要澄清一个事实:注意上面的表述是“一次试验中小概率事件不应当发生”,这并不表示小概率事件不可能发生,也就是说,这里有一个前提:只进行一次试验,结果应当不会是小概率事件。
如果进行多次(可能无穷多)试验,那么小概率事件就肯定会发生,或者说,小概率事件在一次试验中不大可能发生,然而在大量试验中几乎是必然发生的。
2.小概率反证法假设检验的基本思想是统计学的“小概率反证法”原理:对于一个小概率事件而言,其对立面发生的可能性显然要大大高于这一小概率事件,可以认为,小概率事件在一次试验中不应当发生。
因此可以首先假定需要考察的假设是成立的,然后基于此进行推导,来计算一下在该假设所代表的总体中进行抽样研究得到当前样本(及更极端样本)的概率是多少。
如果结果显示这是一个小概率事件,则意味着如果假设是成立的,则在一次抽样研究中竟然就发生了小概率事件!这显然违反了小概率原理,因此可以按照反证法的思路推翻所给出的假设,认为它们实际上是不成立的,这就是小概率反证法原理。
假设检验的基本逻辑:先成立一个与H1相对立的H0。
各种假设检验方法都是根据H0来成立抽样分布,然后求出H0是正确的可能性。
如果我们能证明H0是对的可能性很小,那么就可以据此排除抽样误差的说法,认为H1可能是对的。
简言之,假设检验的基本原则是直接检验H0因而间接地检验H1,目的是排除抽样误差的可能性。
概率论与数理统计教案假设检验

概率论与数理统计教案-假设检验一、教学目标1. 理解假设检验的基本概念和原理;2. 学会使用假设检验方法对样本数据进行推断;3. 掌握假设检验的类型、步骤和判断准则;4. 能够运用假设检验解决实际问题。
二、教学内容1. 假设检验的基本概念和原理假设检验的定义假设检验的目的是什么假设检验的基本原理2. 假设检验的类型单样本检验双样本检验配对样本检验3. 假设检验的步骤建立假设选择检验统计量确定显著性水平计算检验统计量的值做出判断4. 假设检验的判断准则拒绝域和接受域检验的拒绝准则检验的接受准则5. 假设检验的应用实例应用假设检验解决实际问题实例分析与解答三、教学方法1. 讲授法:讲解假设检验的基本概念、原理、类型、步骤和判断准则;2. 案例分析法:分析实际问题,引导学生运用假设检验方法解决问题;3. 互动教学法:提问、讨论、解答学生提出的问题,促进学生理解和掌握知识;4. 练习法:布置课后作业,让学生巩固所学知识,提高运用能力。
四、教学准备1. 教案、教材、课件等教学资源;2. 投影仪、电脑等教学设备;3. 课后作业及答案。
五、教学过程1. 导入新课:回顾上一节课的内容,引入假设检验的基本概念和原理;2. 讲解假设检验的基本概念和原理,阐述其目的是什么;3. 讲解假设检验的类型,引导学生了解各种类型的假设检验;4. 讲解假设检验的步骤,让学生掌握进行假设检验的方法;5. 讲解假设检验的判断准则,使学生明白如何做出判断;6. 分析实际问题,引导学生运用假设检验方法解决问题;7. 布置课后作业,让学生巩固所学知识;8. 课堂小结,总结本节课的主要内容和知识点。
教学反思:在教学过程中,要注意引导学生理解和掌握假设检验的基本概念、原理和步骤,并通过实际问题让学生学会运用假设检验方法。
要关注学生的学习反馈,及时解答他们提出的问题,提高他们的学习兴趣和积极性。
六、教学评估1. 评估方式:课后作业、课堂练习、小组讨论、个人报告2. 评估内容:学生对假设检验基本概念的理解学生对假设检验类型和步骤的掌握学生对假设检验判断准则的应用学生解决实际问题的能力七、课后作业1. 完成教材后的练习题2. 选择一个实际问题,运用假设检验方法进行分析和解答3. 总结本节课的主要内容和知识点,写下自己的学习心得八、课堂练习1. 例题解析:分析教材中的例题,理解假设检验的步骤和判断准则2. 小组讨论:分组讨论课后作业中的问题,共同解决问题,交流学习心得3. 个人报告:选取一个实际问题,进行假设检验的分析和解题过程报告九、教学拓展1. 假设检验的扩展知识:学习其他类型的假设检验方法,如非参数检验、方差分析等2. 实际应用案例:搜集更多的实际问题,进行假设检验的分析和解答3. 软件操作实践:学习使用统计软件进行假设检验,提高数据分析能力十、教学计划1. 下一节课内容预告:介绍假设检验的扩展知识和实际应用案例2. 学习任务布置:预习下一节课的内容,准备相关问题和建议3. 课后自学计划:鼓励学生自主学习,深入了解假设检验的方法和应用教学反思:在完成本节课的教学后,要关注学生的学习情况,及时解答他们提出的问题,并提供必要的辅导。
两个系数相等的假设检验的stata命令

一、概述假设检验是统计学中一种常用的方法,用于判断统计数据是否支持某一假设。
在实际应用中,我们经常会遇到需要判断两个系数是否相等的情况。
在本文中,我们将探讨如何使用stata软件进行两个系数相等的假设检验,并介绍具体的stata命令。
二、背景知识在统计学中,两个系数相等的假设检验通常使用t检验或者F检验进行。
t检验适用于两组独立样本,用于判断两组样本均值是否相等;F检验适用于多组样本,用于判断多组样本均值是否相等。
在stata软件中,我们可以使用特定的命令来进行这些假设检验。
三、使用stata进行两个系数相等的假设检验在stata中,我们可以使用test命令来进行两个系数相等的假设检验。
具体步骤如下:1. 加载数据:我们需要加载我们要进行假设检验的数据集。
2. 进行回归分析:使用regress命令进行回归分析,得到我们要比较的系数的估计值和标准误差。
3. 使用test命令进行假设检验:在回归分析的结果中,使用test命令进行两个系数相等的假设检验。
具体命令为:test coef1 = coef2其中,coef1和coef2分别为我们要比较的两个系数。
执行该命令后,stata将给出相应的假设检验结果,包括t统计量、p值等。
四、示例为了更好地理解如何使用stata进行两个系数相等的假设检验,以下给出一个简单的示例:假设我们有一组数据,其中y为因变量,x1和x2为自变量。
我们想比较x1和x2对y的影响是否相等。
具体步骤如下:1. 加载数据:我们需要加载我们的数据集,假设为mydata。
2. 进行回归分析:使用regress命令进行回归分析,得到x1和x2对y的系数估计值和标准误差。
3. 使用test命令进行假设检验:在回归分析结果中,使用test命令进行两个系数相等的假设检验。
具体命令为:test _b[x1] = _b[x2]其中,_b[x1]和_b[x2]分别为x1和x2的系数估计值。
执行该命令后,stata将给出假设检验结果,我们可以根据p值判断x1和x2对y的影响是否相等。
方差分析案例

“地域”与“抑郁”朱平辉改编自西南财大网(案例分析者刘玲同学)一、案例简介美国人作了一项调查,研究地理位置与患抑郁症之间的关系。
他们选择了60个65岁以上的健康人组成一个样本,其中20个人居住在佛罗里达,20个人居住在纽约、20个人居住在北卡罗来纳。
对中选的每个人给出了测量抑郁症的一个标准化检验,搜集到表1中的资料,较高的得分表示较高的抑郁症水平。
研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系,这些慢性病诸如关节炎、高血压、心脏失调等。
这种身体状况的人也选出60个组成样本,同样20个人居住在佛罗里达,20个人居住在纽约、20个人居住在北卡罗来纳。
这个研究记录央视主持人崔永元对外公开其患有抑郁症后,使人们对这种精神疾病有了更多的关注。
通过对以上两个数据集统计分析,你能从中看出什么结论?你对该疾病有什么认识?二、抑郁症的相关知识抑郁症有两种含义,广义的抑郁症包括情感性精神病、抑郁性神经症、反应性抑郁症、更年期抑郁症等;狭义的则仅指情感性精神病抑郁症。
抑郁症在国外是一种十分常见的精神疾病,据报告,其患病率最高竟占人群的10%左右,而且社会经济情况较好的阶层,患病率越高。
世界卫生组织预测,抑郁症将成为21世纪人类的主要杀手。
全世界患有抑郁症的人数在不断增长,而抑郁症患者中有10—15%面临自杀的危险……引起抑郁症的原因有很多,为了了解地理位置对抑郁症是否有影响,我们做如下的案例分析:三、地理位置与患抑郁症之间是否有关系作为对65岁以上的人长期研究的一部分,在纽约洲北部地区的Wentworth医疗中心的社会学专家和内科医生进行了一项研究,以调查地理位置与患抑郁症之间的关系。
选择了60个相当健康的人组成一个样本,其中20人居住在佛罗里达,20人居住在纽约,20人居住在北卡罗米纳。
对中选的人给出了测量抑郁症的一个标准化实验,搜集到表1中的资料,较高的分表示较高的抑郁症水平。
研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系,这些慢性病诸如关节炎、高血压、心脏失调等。
假设检验案例集

案例一:假设检验设备判断中的应用1例如:某公司想从国外引进一种自动加工装置..这种装置的工作温度X服从正态分布μ;52;厂方说它的平均工作温度是80度..从该装置试运转中随机测试16次;得到的平均工作温度是83度..该公司考虑;样本结果与厂方所说的是否有显著差异厂方的说法是否可以接受类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题;就是假设检验的问题..我们把任一关于单体分布的假设;统称为统计假设;简称假设..上例中;可以提出两个假设:一个称为原假设或零假设;记为H0:μ=80度;另一个称为备择假设或对立假设;记为H1 :μ≠80度这样;上述假设检验问题可以表示为:H0:μ=80H1:μ≠80原假设与备择假设相互对立;两者有且只有一个正确;备择假设的含义是;一旦否定原假设H0;备择假设H1备你选择..所谓假设检验问题就是要判断原假设H0是否正确;决定接受还是拒绝原假设;若拒绝原假设;就接受备择假设..应该如何作出判断呢如果样本测定的结果是100度甚至更高或很低;我们从直观上能感到原假设可疑而否定它;因为原假设是真实时; 在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的;而现在竟然出现了;当然要拒绝原假设H0..现在的问题是样本平均工作温度为83度;结果虽然与厂方说的80度有差异;但样本具有随机性;80度与83度之间的差异很可能是样本的随机性造成的..在这种情况下;要对原假设作出接受还是拒绝的抉择;就必须根据研究的问题和决策条件;对样本值与原假设的差异进行分析..若有充分理由认为这种差异并非是由偶然的随机因素造成的;也即认为差异是显著的; 才能拒绝原假设;否则就不能拒绝原假设..假设检验实质上是对原假设是否正确进行检验;因此;检验过程中要使原假设得到维护;使之不轻易被否定;否定原假设必须有充分的理由;同时;当原假设被接受时;也只能认为否定它的根据不充分;而不是认为它绝对正确..编辑案例二:假设检验在卷烟质量判断中的应用2在卷烟生产企业经常会遇到如下的问题:卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%;现从一批产品中随机抽取50支卷烟进行检验;发现有2支不合格品;问此批产品能否放行按照一般的习惯性思维:50支中有2支不合格品;不合格品率就是4%;超过了原来设置的3%的不合格品率;因此不能放行..但如果根据假设检验的理论;在α=0.05的显著性水平下;该批产品应该可以放行..这是为什么呢最关键的是由于我们是在一批产品中进行抽样检验;用抽样样本的质量水平来判别整批的质量水平;这里就有一个抽样风险的问题..举例来说;我们的这批产品共有10000支卷烟;里面有4支不合格品;不合格品率是0.04%;远低于3%的合格放行不合格品率..但我们的检验要求是随机抽样50支;用这50支的质量水平来判别整批 10000支的质量水平..如果在50支中恰好抽到了2支甚至更多的不合格品;简单地用抽到的不合格品数除以50来作为不合格品率来判断;那我们就会对这批质量水平合格的产品进行误判..如何科学地进行判断呢这就要用到假设检验的理论..步骤1:建立假设要检验的假设是不合格品率P是否不超过3%;因此立假设H0:P≤0.03这是原假设;其意是:与检验标准一致..H1:P>0.03步骤2:选择检验统计量;给出拒绝域的形式若把比例P看作n=1的二项分别b1;p中成功的概率;则可在大样本场合一般n≥25获得参数p的近似μ的检验;可得样本统计量:近似服从N0;1其中=2/50=0.04;p=0.03;n=50步骤3:给出显著性水平α;常取α=0.05..步骤4:定出临界值;写出拒绝域W..根据α=0.05及备择假设知道拒绝域W为步骤5:由样本观测值;求得样本统计量;并判断..结论:在α=0.05时;样本观测值未落在拒绝域;所以不能拒绝原假设;应允许这批产品出厂..假设检验中的两类错误..进一步研究一下这个例子;在50个样品中抽到多少个不合格品;就要拒绝入库呢我们仍取α=0.05;根据上述公式;得出;解得x>3.48;也就是在50个样品中抽到4个不合格品才能判整批为不合格..而如果我们改变α的取值;也就是我们定义的小概率的取值;比如说取α=0.01;认为概率不超过0.01的事件发生了就是不合理的了; 那又会怎样呢还是用上面的公式计算;则得出;解得x>4.30;也就是在50个样品中抽到5个不合格品才能判整批为不合格..检验要求是不合格品率 P不能超过3%;而现在根据α=0.01;算出来50个样品中抽到5个不合格品才能判整批为不合格;会不会犯错误啊假设检验是根据样本的情况作的统计推断;是推断就会犯错误;我们的任务是控制犯错误的概率..在假设检验中;错误有两类:第一类错误拒真错误:原假设H0为真批产品质量是合格的;但由于抽样的随机性抽到过多的不合格品;样本落在拒绝域W内;从而导致拒绝H0根据样本的情况把批质量判断为不合格..其发生的概率记为α;也就是显著性水平..α控制的其实是生产方的风险;控制的是生产方所承担的批质量合格而不被接受的风险..第二类错误取伪错误:原假设H0不真批产品质量是不合格的;但由于抽样的随机性抽到过少的不合格品;样本落在W外;从而导致接受H0根据样本的情况把批质量判断为合格..其发生的概率记为β..β控制的其实是使用方的风险;控制的是使用方所承担的接受质量不合格批的风险..再回到刚刚计算的上例的情况;α由0.05变化为0.01;我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个;批质量是合格的而不被接受的风险就小了;犯第一类错误的风险小了;也就是生产方的风险小了;但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个;批质量是不合格的而被接受的风险大了;犯第二类错误的风险大了;也就是使用方的风险大了.. 在相同样本量下;要使α小;必导致β大;要使β小;必导致α大;要同时兼顾生产方和使用方的风险是不可能的..要使α、β皆小;只有增大样本量;这又增加了质量成本..因此综上所述;假设检验可以告诉我们如何科学地进行质量合格判定;又告诉我们要兼顾生产方和使用方的质量风险;同时考虑质量和成本的问题..。
假设检验的基本思想和有关概念的教学设计

㊀㊀㊀㊀㊀假设检验的基本思想和有关概念的教学设计假设检验的基本思想和有关概念的教学设计Һ魏满满1㊀李石虎2∗㊀周㊀勤2㊀(1.江苏师范大学科文学院,江苏㊀徐州㊀221116;2.江苏师范大学数学与统计学院,江苏㊀徐州㊀221116)㊀㊀ʌ摘要ɔ本文主要探究了假设检验的基本思想和有关概念的教学设计.首先,通过 女士品茶 的故事引入,提炼出假设检验的基本思想;其次,通过分析项链含金量这一实际案例总结出假设检验的基本步骤,并介绍了假设检验的两类错误和p值的概念;最后,融入思政的元素,丰富了课堂教学内容.ʌ关键词ɔ假设检验;教学设计ʌ基金项目ɔ江苏师范大学课程思政专项研究(KCSZY17);江苏师范大学数学与统计学院思政示范课程(XYKCSZ01)一㊁引㊀言概率论与数理统计课程是各个高校理工科的基础必修课,它在理工科及经管类各专业被广泛应用.假设检验是概率论与数理统计中的重要知识点,是统计推断的主要方法之一,在概率统计的理论研究与实际应用中都占有极其重要的地位.2019年3月18日,在学校思想政治理论课教师座谈会上,习近平总书记明确提出[1]:要坚持灌输性和启发性相统一,注重启发性教育,引导学生发现问题㊁分析问题㊁思考问题,在不断启发中让学生水到渠成得出结论.近年来,各大高校都十分重视思政建设,通过教师培训㊁专家讲座㊁示范课程等多种方式来加深教师对课程思政的理解.教师是高校的 第一主角 ,作为专业课教师,也有责任和义务认真挖掘所授课程的 思政元素 .例如,2021年,李晨和陈丽萍[2]在研究概率统计的思政元素时,以概率学者的文化素养和科学治学精神为切入点,通过多个实际案例剖析全概率公式的应用,潜移默化地引入诸多思政元素来激发学生的学习兴趣.受此启发,本文着重从概率论与数理统计课程中 假设检验 这一角度思考,通过教学设计来探索课程思政理念进概率统计课堂的实践方法,目的就是同大家交流如何上好 假设检验 这一知识点的教学课.首先,我们通过 女士品茶 这一广为流传且富有趣味性的故事引入,启发学生思考,从中提炼出假设检验的基本思想.其次,我们通过分析项链含金量这一实际案例总结出假设检验的基本步骤.接着,我们介绍假设检验的两类错误和p值的概念,并介绍假设检验的一些应用.最后,我们融入思政的元素,以我国著名数学家严加安院士的‘悟道诗“为结尾,阐述了概率统计的基本思想,同时激励学生向老一辈科学家学习,树立正确的价值观,从而丰富了课堂教学内容.二㊁教学过程(一)问题引入首先,我们从一个经典故事出发,来体会假设检验的基本思想.例1[3]㊀(女士品茶试验)故事发生在英国剑桥大学,那是20世纪20年代,一群大学精英们正在品茶.该茶是由牛奶和茶水混合而成的.在品茶过程中,一位女士宣称:先加入牛奶还是先加入茶,不同的顺序会使茶的口感不同.周围人都认为这位女士简直是在胡言乱语,这是不可能的啊!然而在场的统计学家Fisher却对这个话题很感兴趣,他请人端来10杯调制好的茶让该女士品尝,其中有的是先加的牛奶,有的是先加的茶.结果,这位女士正确地鉴别出每一杯茶的制作顺序.该如何判断该女士是否有鉴别能力呢?Fisher的想法:假设该女士没有鉴别能力,这个时候她只能靠猜,从而她猜对的概率为12.因此,她能同时判断出10杯茶的概率为2-10<0.001,这个概率非常非常小,仅仅做一次试验是几乎不会发生的,可是,它却发生了!这表明原假设不恰当,应予以拒绝,认为该女士有鉴别能力!假设检验的基本思想:小概率反证法思想.先提出假设,然后设计试验,在原假设成立的条件下计算概率,依据小概率原理来判断是否拒绝原假设.那么多大的概率属于小概率呢?对于不同的问题,会有不同的标准,在统计学中,这个小概率称为显著性水平,常取0.05或0.01.接下来,我们就通过生活中的一个实际案例来探索一下假设检验的奥秘.(二)实例分析在生活中,经常会遇到一组数据,我们来看下面的例子.例2[4]㊀质检部门接到投诉后,对某金店进行调查,从标有18K的一批项链中抽取20条,测得其含金量如下:表1㊀某金店项链含金量数据单位:K17.618.117.918.318.017.417.518.617.317.817.317.818.117.417.618.017.218.318.317.5∗通信作者:李石虎,男,讲师,博士,就职于江苏师范大学,研究方向为概率论与数理统计.联系方式:江苏省徐州市江苏师范大学泉山校区数学与统计学院;电话邮编:221116;E-mail:shihuli@jsnu.edu.cn.㊀㊀㊀㊀㊀㊀问:如何判断这批项链有没有达到标准呢?(显著性水平α=0.05)分析:观察表1中的数据,我们可以发现:有的含金量大于18K,有的含金量小于18K,还有的恰好等于18K.那么我们能否直接说和标准值18K有显著差别呢?根据所学的统计学思想方法,我们已经了解到答案是否定的,因为这里看到的只是样本数据,我们无法直接做出判断.那么应该如何判断呢?我们的思路如下:首先,计算出这20条项链含金量的平均值为17.8,它与标准值18存在0.2的差值.这0.2的差值是由抽样引起的误差,还是有本质的差别?我们利用上述思想来检验一下.令ξ表示这批项链的含金量,由中心极限定理可知ξ ㊃N(μ,σ2),我们要检验均值是否为μ=18,具体步骤如下:1.建立假设.原假设H0:μ=18,表示这批项链符合标准;与之对立的备择假设H1:μʂ18,表示这批项链不符合标准.2.在H0成立时,由Fisher定理可知统计量T= x-μSnnt(n-1)=t(19).3.由T分布图像(如图1)可以看出:T的取值集中在零点附近.这表明:|T|越大,对应的概率就越小.从而存在临界值C,使得|T|大于或等于C是一个小概率事件,则C要满足P(|T|ȡC|H0成立)=α,再由T分布图像的对称性可知C=t0.975(19)ʈ2.093.图1㊀T分布图像从而,当|T|ȡ2.093时,非常小的概率事件在此就发生了,只能拒绝原假设H0.我们将W={(ξ1,ξ2, ,ξn)||T|ȡ2.093}这一集合称为拒绝域,如果样本的观测值落到W中,则原假设应被拒绝.4.代入样本均值和样本标准差进行计算,得到所观测的样本统计量t的值:|t|=|17.8-18|0.4039320ʈ2.214>2.093,其落到拒绝域W中,因此原假设被拒绝,故这批项链没有达到标准.为了更直观地理解拒绝域的含义,同学们可以参考T分布图像.小结㊀本案例利用假设检验思想得出了该金店项链的含金量不符合标准的结论,启发我们对待任何事情都不要抱有侥幸心理,不要弄虚作假,要诚信做人做事,方能赢得大家的信任.项链含金量不达标可能只是使消费者金钱方面的利益受损.试想一下:如果是某大型婴儿奶粉企业检测出质量不达标的产品呢?再或者是婴儿霜经检测含有毒物质呢?抑或是我们服用的某种药物检测出有危害健康的成分呢?这些案例都不是捕风捉影,均上过各大网站热搜,引起了消费者的恐慌.利用假设检验这个工具,有助于我们全面地认识这类事件,既可以让我们避免无谓的损失,又可以帮助我们找到有利的取舍依据.(三)假设检验的基本步骤通过对上述案例的分析,我们可以归纳出求解假设检验的基本步骤:第一步:从要研究的实际问题引入,先提出一个假设,一般称之为原假设,记为H0,与其对立的假设称为备择假设,记为H1.例如,在上述案例中,原假设为 这批项链符合标准 ,备择假设为 这批项链不符合标准 .第二步:依据所研究总体服从的分布,我们来构造合适的检验统计量,并通过所学知识来确定统计量服从的分布.第三步:接下来,我们需要确定检验的拒绝域W使得P((ξ1,ξ2, ,ξn)ɪW|H0成立)ɤα.第四步:根据样本数值计算统计量所对应的观测值.如果计算所得观测值落进了W中,则说明原假设不当,应予以拒绝,否则原假设不可以被拒绝.(四)假设检验的两类错误在 女士品茶 的例子中,如果该女士本来就没有鉴别能力,但是她运气好,每次都猜对了,这时候我们的推断就出错了.事实上,在假设检验问题中,我们由样本提供的信息来推断总体信息,由于样本只包含总体的一部分信息,这就不可能保证从来不会犯错误.假设检验可能犯的错误有如下两类:(Ⅰ)是否在 拒绝假设H0 时用了 小概率原理 .注意小概率事件并非不可能事件,如果原假设本为真,但由于样本值落进了拒绝区域内而得出 拒绝 的结论,这里犯的错误为弃真错误,通常称为第一类错误,记为α,即P(拒绝H0|H0为真)=α.(Ⅱ)反之,如果原假设H0本来是不成立的,却由于样本值未落进拒绝区域而得出 不能拒绝 的结论.这里的错误是纳伪错误,一般称为第二类错误,记作β,即P(接受H0|H0不真)=β.根据检验法则知:当H0成立时,拒绝H0的概率小于或等于显著性水平α,但是显著性水平α取得越小越好,因为㊀㊀㊀㊀㊀此时拒绝域也会相应地减小,从而导致犯第二类错误的概率增大.这是一个矛盾的双方,类似于区间估计时的做法,我们需要先固定显著性水平α,再选择合理的检验统计量来适当地减小β的值.下面我们再结合一个实际例子来理解两类错误:在新冠肺炎疫情发生初期,新闻报道中时常会出现 假阳 的检测结果.我们可以从假设检验的两类错误的角度来理解:事实上,任何检验方法都会存在犯错误的可能性,理想的试剂应是 假阴 和 假阳 出现的概率都越小越好,但当样本量有限㊁检测技术没有明显优化提升时,一类错误概率的减少必会导致另一类错误概率的增加,因此处理原则是:人为限定犯第一类错误的概率α,为降低犯第二类错误的概率,我们可以增大样本容量.所以,从统计学的观点看,新闻报道中的 假阴 假阳 患者出现并不奇怪.启发:小概率事件虽然在一次试验中不易发生,但绝非不可能事件,重复次数多了,发生的可能性也就增大了.这说明做任何事情都不要存在投机取巧的心理,俗话说 常在河边走,哪有不湿鞋 勿以恶小而为之,勿以善小而不为 .反之,再困难的事情,只要我们持之以恒,总是可以成功的,正所谓 锲而不舍,金石为开 !(五)假设检验的p值可以看出,显著性水平α变小,对应的拒绝域也会变小;当显著性水平α取得足够小时,使得样本值不落在相应的拒绝域中,从而在此显著性水平α下不能拒绝假设H0.当显著性水平α由上述足够小的值不断增大时,对应的拒绝域也会变大,当显著性水平α大到一定程度时,便可以使样本值落入相应的拒绝域中,从而在此显著性水平α下可以拒绝假设H0.对于一个确定的样本值,存在一个实数p(0<p<1),当显著性水平α=p时可以拒绝H0,而当α<p时原假设H0不可以被拒绝.可见,p是使依据给定样本数值做出 拒绝H0 的最小的那个显著性水平,我们称之为检验的p值.在例2中,我们也可以通过统计软件计算t统计量的值和p值:表2㊀某金店项链含金量检验结果检验值=18tdfp值均值差值项链含金量-2.214190.039-0.20000给定显著性水平α为0.05,由表2可知p值0.039<0.05,原假设应被拒绝,认为项链含金量与18K之间有显著的统计差异,从而得出 项链不符合标准 的结论.(六)课堂小结与思政本节课我们主要通过 女士品茶 的案例引入假设检验的基本思想,通过分析项链含金量这一实际案例总结出假设检验的基本步骤,也给出了假设检验的两类错误和p值的含义,这为接下来进一步学习不同类型的㊁具体的假设检验打下了必要的基础.假设检验不仅是一种重要的统计方法,更是一种思维方式,告诉我们用数据来说话,理性地看待问题.正因为如此,假设检验在我们的现实生活中有着十分重要的应用.比如,专家利用假设检验,结合临床数据分析不同采样点㊁人群㊁年龄的新冠病毒核酸检测的结果,给有关部门的决策提供参考.假设检验的理论方法不仅被广泛应用于医学检验㊁生物制药等诸多领域,在我们的生产生活,特别是工业产品的质量判断中也有着十分广泛的应用[5],因为在工厂的实际生产过程中,产品的尺寸总是左右浮动的,存在一定的误差,那么如何判断这些误差是否在允许的范围内?这就要用到假设检验的思想方法.不仅如此,假设检验的理论还可应用于文学研究.例如,东南大学韦博成教授在2009年[6]利用假设检验的理论方法分析了‘红楼梦“前80回与后40回的某些文风差异,得到的结论是 这两部分内容在写作风格方面存在明显的差异 ,给关于‘红楼梦“作者的论断提供了一个强有力的证据.在现实生活中,数据是无处不在的,学习假设检验的思想方法有助于我们正确地挖掘数据背后的规律,做出更客观的判断.如今,我们身处一个大数据时代,通过学习假设检验,更重要的是培养透过现象看本质这一统计思维.这里,调查得来的数据是现象,规律是从数据中探索出来的本质属性.我们需要借助数学模型,并结合统计方法来寻找这其中的规律和随机性,在潜移默化中培养统计思维.正如我国著名的数学家严加安院士在‘悟道诗“中所题:随机非随意,概率破玄机;无序隐有序,统计解迷离.注:课后同学们若想进一步了解统计学的发展历程,可以读一读‘20世纪统计怎样变革了科学:女士品茶“[7]这一科普著作.ʌ参考文献ɔ[1]习近平主持召开学校思想政治理论课教师座谈会[N].新华社,2019-03-18,20:57.[2]李晨,陈丽萍.概率论与数理统计课程教学中思政元素的挖掘与实践[J].大学教育,2021(9):104-106.[3]茆诗松,程依明,濮晓龙.概率论与数理统计教程:第3版[M].北京:高等教育出版社,2019.[4]朱元泽,李贤彬.概率论与数理统计[M].上海:上海交通大学出版社,2015.[5]乔静.假设检验在工业产品质量判断中的应用[J].机电信息,2020(27):142-143.[6]韦博成.‘红楼梦“前80回与后40回某些文风差异的统计分析(两个独立二项总体等价性检验的一个应用)[J].应用概率统计,2009(4):441-448.[7]萨尔斯伯格.20世纪统计怎样变革了科学:女士品茶[M].北京:中国统计出版社,2004.。
Hypothesis Testing

假设检定
Null Hypothesis(Ho)
统计性解释 : 工程 A 和 B 的母集团的平均是一样 . 实际性解释 : 两个工程间的收率 差异是没有 . 既 , 改善工程的收率比 原有工程比提高了 . 母集团的平均是不一样 . 实际性解释 : 工程 B 的平均收率 工程 A 的平均收率不一样 .
84.5
Analyze – 假设检定 - 16
假设检定 例
实际性的提问 : 改善工程 B 的收率比原有工程 A 的收率有变化吗 ?
• • • • •
想知道什么 ? 怎样知道呢 ? 怎样使用道具 ? 需要什么数据 ? 怎样收集数据 ?
统计性的提问 :
工程 B 的平均 (85.54) 和工程 A 的平均 (84.24) 差异按统计性 是否 有有意的差异 ? 平均的差异是否只是时间变动的差异 ?
假设检定
假设检定的两个错误
事实 ( 实值 ) H0 H0 不可以弃却 正确的决定 H1
第 2 种 错误
判断
H0 弃却 第 1 种 错误 正确的决定
第 1 种 错误 (TypeⅠError) : 不顾 Null Hypothesis“H0”, 真实 . 弃却 Null Hypothesis 的错误 把良品判断为不良的时候 α ( − Risk ) 既 , 可以说生产者危险 第 2 种 错误 (TypeⅡError) : 不顾 Null Hypothesis“H0” 假的 . 不弃却 Null Hypothesis 的错误 不良品当成良品的时候 即 , 可以说消费者危险 β ( − Risk )
算术平均数代表性的衡量几种假设检验的方法

第26卷第6期江苏理工学院学报JOURNAL OF JIANGSU UNIVERSITY OF TECHNOLOGY Vo l.26,No.6 Dec.,20202020年12月1问题的提出人们会经常遇到这样的问题:甲乙两个学习小组,甲组10名同学的英语平均分为82分,标准差为40分,乙组10名同学的英语平均分为76分,标准差为38分,问哪组的平均分更有代表性?对于上述问题的解决,在现有的“统计学”教科书中,所提供的方法是采用比较离散系数的大小,即:计算甲组的离散系数v s甲=S甲-X甲=4082=0.49;计算乙组的离散系数v s乙=S乙-X乙=3876=0.50。
由于v s甲<v s乙,所以,可以认为甲组的平均分更有代表性。
如果上述两个离散系数的值相差非常大,则作这样的简单比较,可以说明问题。
但仅就上述例子而言(事实上,并不仅仅限于上述例子),两个离散系数的值相差不大时,用比较离散系数法衡量算术平均数代表性问题就显得不足。
假设检验的方法,不仅为差异比较提供了可靠的方法,而且也为差异的比较提供了一定的范式。
因此,对于算术平均数代表性的衡量,特别是两个离散系数的值相差不大时,有必要将其置于假设检验中,通过检验v s甲与v s乙之间是否有差异,其差异是否具有统计意义而加以完成。
基于此,笔者提出了利用假设检验衡量算术平均数的代表性的三种方法:t检验、F检验和将v s甲与v s乙视作两个比率的t检验。
2衡量算术平均数的代表性:t检验要说明哪组的平均分更有代表性,对于假设检验来说,就是要检验v s甲与v s乙之间是否有差异。
而其关键在于检验统计量的构造,其核心是变量的数学期望和方差的求得。
2.1变量v s甲、v s乙的数学期望和方差设甲总体X∼N(μx,σ2x),乙总体Y∼N(μy,σ2y),分别从甲总体X和乙总体Y中抽取容量为n的样本为x1,x2,…,x n;y1,y2,…,y n;则x∼N(μx,σ2xn),y∼N(μy,σ2yn)[1]。
重视统计思想、融入思政元素的假设检验教学

㊀㊀㊀㊀数学学习与研究㊀2021 12重视统计思想融入思政元素的假设检验教学重视统计思想、融入思政元素的假设检验教学Һ张㊀瑜㊀范梓淼㊀徐刚刚㊀(新疆农业大学数理学院,新疆乌鲁木齐㊀830000)㊀㊀ʌ摘要ɔ假设检验是统计学中一个十分重要的概念,蕴含着十分重要的统计思想,也是衡量是否真正理解统计学的试金石.文章提出了采用案例教学的方式深入浅出地介绍假设检验的思想㊁原理,降低新知识的抽象性,并在重视统计思想讲授的同时把课程思政元素融入整个教学过程中的教学改革.实践表明,这样不仅能使学生更容易理解假设检验的思想,还能培养学生严密的逻辑思维,同时也能以润物细无声的方式对学生进行思想政治教育.ʌ关键词ɔ假设检验;思政元素;统计思想ʌ基金项目ɔ2018年新疆维吾尔自治区级普通教改项目(2018JG13)1㊀引言假设检验是数理统计部分一个十分重要的内容,蕴含着丰富的统计思想.由于教师在授课的过程中往往重视概念㊁法则的介绍及问题的解答,忽略了对统计思想的剖析讲授,因此学生在学习的过程中觉得概念㊁法则难以理解,对问题的分析没有头绪.假设检验虽然很重要,但是它所蕴含的统计思想更为重要,学生只有深刻地理解假设检验的统计思想,才能够真正地掌握统计推断的精髓.习近平总书记在全国高校思想政治工作会议中指出: 要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程. 专业课程同思想政治教育相结合,可以将思政元素潜移默化地融入专业知识,这样学生既可以显性地学到专业知识,又能够隐性地受到良好的思想政治教育.2㊀案例引入,降低新知识的抽象性很多概率论与数理统计教材在介绍假设检验的内容时,都是直接引入假设检验的相关概念及法则,这使得初学者只了解其定义但并不清楚其原理和思想,因此没有对其产生学习兴趣.所以教师在讲授这部分内容时,可以以例题引入,即以问题作为教学的出发点,这样可以激发学生的求知欲,使其主动思考问题,进而顺利接受新的思想.引例[女士品茶]一种奶茶由牛奶和茶按照一定比例混合而成,可以先倒茶后倒奶(TM),也可以反过来(MT).某女士声称她可以鉴别是TM还是MT,周围品茶的人对此产生了议论, 这怎么可能呢? 她在胡言乱语. 不可想象. 在场的费希尔也在思索这个问题,他提议做一项试验来检验如下假设(命题)是否可以被接受.假设H:该女士无此种鉴别能力.他准备了10杯调制好的奶茶,TM和MT都有.该女士一杯一杯地品尝,然后说出是TM还是MT,结果那位女士竟然正确地分辨出10杯奶茶中每一杯的调制顺序.这时该如何对此作出判断呢?引入例题可以激发学生的学习兴趣,共同讨论可以引导学生探索发现假设检验的反证法思想和小概率原理.这样学生不仅学习了假设检验的基本概念及法则,还培养了利用假设检验策略解决实际问题的思维.图1㊀实例引入示意图图2㊀理论联系生活示意图教师引入假设检验的相关理论后,可以举一个生活中的例子,使学生感受生活中的统计思想.将抽象的知识具体化,不仅加深了学生对抽象知识的理解,还让学生感受到这些知识离自己并不遥远,从而提高学生的学习兴趣.比如,某个同学去买橘子,老板说橘子很甜,这时这名学生该怎么判断?通过图2展示该问题中的假设检验思想.通过理论和实际相结合,使学生认识到假设检验的应用价值,进而提高学生思考问题的积极性.3㊀融入思政元素,促进学生全面发展假设检验是数理统计中重要的统计推断方法,其中蕴含着深刻的统计思想.习近平总书记在2016年12月召开的. All Rights Reserved.㊀㊀㊀㊀㊀数学学习与研究㊀2021 12全国高校思想政治工作会议中指出: 要用好课堂教学这个主渠道.各类课程都要与思想政治理论课同向而行,形成协同效应. 因此教师在授课的过程中要融入思政元素,深化教书育人的内涵,提升学生的思想政治觉悟和道德修养,进而达到知识创收和育人的双重目的.3.1㊀小概率原理假设检验的重要原理为小概率原理,小概率原理即小概率事件在一次试验中几乎不会发生.教师在介绍小概率原理时,可以向学生介绍购买彩票的案例,购买彩票中一等奖实际上就是小概率事件.小概率事件虽然发生的概率很小,但也有可能发生.小概率事件的发生也可能造成很严重的后果,比如 9㊃11事件 .通过举例增强学生的忧患意识.忧患意识是中华民族的重要品质,也是防范各种风险的思维方式.新冠疫情的防控再次印证了忧患意识的重要性.3.2㊀概率反证法假设检验所使用的逻辑推理的方法是概率反证法,例题的练习,不仅可以培养学生的统计思维,还能让学生在面对错综复杂的问题时换位思考㊁反向思考,遇到困难不轻言放弃.3.3㊀假设检验的两类错误由于假设检验是根据样本推断总体,推断的结论是 肯定的 还是 否定的 是根据概率而言的,因此就会不可避免地出现两类错误:弃真错误和纳伪错误,这两类错误是一种此消彼长的关系.教师在教学的过程中不能一味地强调如何去避免这两类错误,而是要引导学生了解假设检验是带有一定可靠程度的推断.绝对否定或绝对肯定的事情是很少的,因此学生要用联系的㊁发展的眼光看待问题,避免思想上的极端.在进行假设检验时,通常要根据原假设和备选假设的建立,结合实际,把产生较严重后果的假设作为原假设.比如医学中判断药品是否有毒时,原假设应该为 该药品有毒 ,这时弃真错误为该药品有毒却做出无毒的判断,产生这样的后果是很严重的,我们把它作为第一类错误,因为这类错误是可以控制的.通过理论结合实际,学生能更加理解假设检验的两类错误.同时,融合思政元素,旨在告诉学生事有轻重缓急,在处理问题时要抓住问题的主要矛盾,在做决定时一定要清楚做这件事情可能导致什么样的后果,这个后果是不是在自己可以承受的范围内.4㊀加入实践教学,促进能力发展学生如果已经掌握假设检验的基本思想以及原理,那么便可以利用理论知识解决一些简单的实际问题.另外,在假设检验的教学过程中加入实践教学,要根据学情融入不同的统计软件,比如SPSS.利用统计软件处理教学中的理论例题,让学生自己进行比较㊁分析,这样既可以加深学生对理论知识的理解,也能提高学生解决实际问题的能力.5㊀理论结合实际,促进学科交叉假设检验在实际生活中有着广泛的应用.教师在授课时可以采用课堂翻转的方式,学生搜集假设检验在本专业学科中的应用的相关资料并在课堂分享交流.比如工科的学生可以介绍假设检验在水利水电工程方面的应用;经济类的学生可以介绍假设检验在财务中的相关应用;农科的学生可以介绍假设检验在生物统计中的应用.在课堂翻转的过程中,学生自主分组,课后搜集相关热点难点问题,小组讨论后,以PPT的形式将讨论的结果和收获分享给班里其他学生,这样不仅加深了学生对理论知识的学习和理解,而且拓宽了学生的知识面,锻炼了学生的思考问题和研究问题的能力,同时也提高了学生利用理论知识解决实际问题的能力.6㊀总结数理统计这一学科所特有的研究手段为从数据出发进行归纳和推断,而假设检验作为统计推断的基本手段,在数理统计部分具有重要的作用.假设检验中蕴含着重要的统计思想,学生只有真正理解假设检验的统计思想,才能掌握统计推断的精髓.同时假设检验的思想中又蕴含着很多人生哲理,这些人生哲理能帮助学生树立正确的人生观㊁价值观和世界观.因此教师在授课过程中应该更加注重统计思想的传播,同时融入思政元素,关注假设检验在学生所学专业方面的应用,使学生真正理解所学内容,并能够利用所学内容解决实际问题,进而促进学生的全面发展.ʌ参考文献ɔ[1]茆诗松,程依明,濮晓龙.概率论与数理统计教程(第二版)[M].北京:高等教育出版社,2004.[2]周影,高鹤,刘海东,王化琨,张继民.了解知识背景㊁重视统计思想的概率统计教学[J].高师理科学刊,2014,34(05):88-90.[3]金小梅,毛本清.课程思政在概率统计教学中的探索与实践[J].教育教学论坛,2020(18):106-107.[4]黄昱,李双瑞.课程思政理念下概率论与数理统计教学改革[J].教育现代化,2018,5(53):109-111,124.[5]李玉超.基于水利水电工程质量监督数理统计学的假设检验应用研究[J].水利技术监督,2020(02):24-27.[6]张淑贵.假设检验在工程实践中的应用研究[J].中国设备工程,2019(10):121-122.[7]武淑琴,李灵珊,陶宏娟.参数检验在企业财务预算编制中的应用[J].统计与决策,2020,36(15):185-188.. All Rights Reserved.。
医学论文中常见统计学错误案例分析

医学论文中常见统计学错误案例分析一、概述在医学研究领域,统计学方法的应用至关重要,它有助于科研人员对复杂数据进行深入的分析与解读,从而得出科学的结论。
由于统计学知识的复杂性和多样性,医学论文中常常会出现各种统计学错误。
这些错误不仅可能影响研究结果的准确性和可靠性,还可能误导读者对研究的理解和评价。
本文旨在通过分析医学论文中常见的统计学错误案例,揭示其产生原因和可能带来的后果,以提高医学科研人员和论文作者在统计学应用方面的准确性和规范性。
常见的医学论文统计学错误包括但不限于样本量计算不当、数据分布误判、统计方法选择错误、假设检验理解偏差、多重共线性问题以及P值解读不当等。
这些错误往往源于对统计学基本概念和方法理解不深入,或是忽视了对数据特征和实际研究问题的综合考量。
通过案例分析,我们可以更直观地了解这些错误在实际研究中的表现形式和潜在影响。
每个案例都将详细剖析错误发生的具体原因,并指出正确的处理方法或避免策略。
这将有助于医学科研人员和论文作者在今后的研究中更加谨慎地应用统计学方法,提高研究质量和学术水平。
本文还将强调加强统计学知识和技能的培训在医学科研中的重要性。
只有具备扎实的统计学基础,才能更好地理解和运用各种统计方法,避免或减少统计学错误的发生。
医学科研人员和论文作者应不断学习和更新统计学知识,提高自己在统计学应用方面的能力和素养。
1. 医学论文中统计学的重要性在医学研究中,统计学扮演着至关重要的角色。
它是确保研究设计合理性、数据收集和分析准确性以及结论可靠性的基石。
通过运用统计学方法,医学研究人员能够系统地评估治疗方法的疗效、疾病的发病机制和预后因素,从而为临床实践和政策制定提供科学依据。
统计学在医学论文中有助于确保研究的内部和外部有效性。
通过运用适当的统计学方法,研究人员可以控制潜在的混杂变量和偏倚,从而提高研究的准确性和可靠性。
这有助于避免由于研究设计不当或数据分析错误而导致的误导性结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例一:假设检验设备判断中的应用[1]
例如:某公司想从国外引进一种自动加工装置。
这种装置的工作温度X服从正态分布(μ,52),厂方说它的平均工作温度是80度。
从该装置试运转中随机测试16次,得到的平均工作温度是83度。
该公司考虑,样本结果与厂方所说的是否有显著差异?厂方的说法是否可以接受?
类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题,就是假设检验的问题。
我们把任一关于单体分布的假设,统称为统计假设,简称假设。
上例中,可以提出两个假设:一个称为原假设或零假设,记为H0:μ=80(度);另一个称为备择假设或对立假设,记为H1 :μ≠80(度)这样,上述假设检验问题可以表示为:
H0:μ=80H1:μ≠80
原假设与备择假设相互对立,两者有且只有一个正确,备择假设的含义是,一旦否定原假设H0,备择假设H1备你选择。
所谓假设检验问题就是要判断原假设H0是否正确,决定接受还是拒绝原假设,若拒绝原假设,就接受备择假设。
应该如何作出判断呢?如果样本测定的结果是100度甚至更高(或很低),我们从直观上能感到原假设可疑而否定它,因为原假设是真实时,在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的,而现在竟然出现了,当然要拒绝原假设H0。
现在的问题是样本平均工作温度为83度,结果虽然与厂方说的80度有差异,但样本具有随机性,80度与83度之间的差异很可能是样本的随机性造成的。
在这种情况下,要对原假设作出接受还是拒绝的抉择,就
必须根据研究的问题和决策条件,对样本值与原假设的差异进行分析。
若有充分理由认为这种差异并非是由偶然的随机因素造成的,也即认为差异是显著的,才能拒绝原假设,否则就不能拒绝原假设。
假设检验实质上是对原假设是否正确进行检验,因此,检验过程中要使原假设得到维护,使之不轻易被否定,否定原假设必须有充分的理由;同时,当原假设被接受时,也只能认为否定它的根据不充分,而不是认为它绝对正确。
[编辑]
案例二:假设检验在卷烟质量判断中的应用[2]
在卷烟生产企业经常会遇到如下的问题:卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%,现从一批产品中随机抽取50支卷烟进行检验,发现有2支不合格品,问此批产品能否放行?按照一般的习惯性思维:50支中有2支不合格品,不合格品率就是4%,超过了原来设置的3%的不合格品率,因此不能放行。
但如果根据假设检验的理论,在α=0.05的显著性水平下,该批产品应该可以放行。
这是为什么呢?
最关键的是由于我们是在一批产品中进行抽样检验,用抽样样本的质量水平来判别整批的质量水平,这里就有一个抽样风险的问题。
举例来说,我们的这批产品共有10000支卷烟,里面有4支不合格品,不合格品率是0.04%,远低于3%的合格放行不合格品率。
但我们的检验要求是随机抽样50支,用这50支的质量水平来判别整批10000支的质量水平。
如果在50支中恰好抽到了2支甚至更多的不合格品,简单地用抽到的不合格品数除以50来作为不合格品率来判断,那我们就会对这批质量水平合格的产品进行误判。
如何科学地进行判断呢?这就要用到假设检验的理论。
步骤1:建立假设
要检验的假设是不合格品率P是否不超过3%,因此立假设
H0:P≤0.03
这是原假设,其意是:与检验标准一致。
H1:P>0.03
步骤2:选择检验统计量,给出拒绝域的形式
若把比例P看作n=1的二项分别b(1,p)中成功的概率,则可在大样本场合(一般n≥25)获得参数p的近似μ的检验,可得样本统计量:近似服从N(0,1) 其中=2/50=0.04,p=0.03,n=50
步骤3:给出显著性水平α,常取α=0.05。
步骤4:定出临界值,写出拒绝域W。
根据α=0.05及备择假设知道拒绝域W为
步骤5:由样本观测值,求得样本统计量,并判断。
结论:在α=0.05时,样本观测值未落在拒绝域,所以不能拒绝原假设,应允许这批产品出厂。
假设检验中的两类错误。
进一步研究一下这个例子,在50个样品中抽到多少个不合格品,就要拒绝入库呢?我们仍取α=0.05,根据上述公式,得出,解得x>3.48,也就是在50个样品中抽到4个不合格品才能判整批为不合格。
而如果我们改变α的取值,也就是我们定义的小概率的取值,比如说取α=0.01,认为概率不超过0.01的事件发生了就是不合理的了,那又会怎样呢?还是用上面的公式计算,则得出,解得x>4.30,也就是在50个样品中抽到5个不合格品才能判整批为不合格。
检验要求是不合格品率P不能超过3%,而现在根据α=0.01,算出来50个样品中抽到5个不合格品才能判整批为不合格,会不会犯错误啊!假设检验是根据样本的情况作的统计推断,是推断就会犯错误,我们的任务是控制犯错误的概率。
在假设检验中,错误有两类:
第一类错误(拒真错误):原假设H0为真(批产品质量是合格的),但由于抽样的随机性(抽到过多的不合格品),样本落在拒绝域W内,从而导致拒绝H0(根据样本的情况把批质量判断为不合格)。
其发生的概率记为α,也就是显著性水平。
α控制的其实是生产方的风险,控制的是生产方所承担的批质量合格而不被接受的风险。
第二类错误(取伪错误):原假设H0不真(批产品质量是不合格的),但由于抽样的随机性(抽到过少的不合格品),样本落在W外,从而导致接受
H0(根据样本的情况把批质量判断为合格)。
其发生的概率记为β。
β控制的其实是使用方的风险,控制的是使用方所承担的接受质量不合格批的风险。
再回到刚刚计算的上例的情况,α由0.05变化为0.01,我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个,批质量是合格的而不被接受的风险就小了,犯第一类错误的风险小了,也就是生产方的风险小了;但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个,批质量是不合格的而被接受的风险大了;犯第二类错误的风险大了,也就是使用方的风险大了。
在相同样本量下,要使α小,必导致β大;要使β小,必导致α大,要同时兼顾生产方和使用方的风险是不可能的。
要使α、β皆小,只有增大样本量,这又增加了质量成本。
因此综上所述,假设检验可以告诉我们如何科学地进行质量合格判定,又告诉我们要兼顾生产方和使用方的质量风险,同时考虑质量和成本的问题。
如有侵权请联系告知删除,感谢你们的配合!。
