密码学课程设计论文
《密码学》课程直播教学设计与反思—以AES密码算法为例

《密码学》课程直播教学设计与反思—以AES密码算法为例摘要:为顺利开展疫情期间教学工作,根据密码学学科特点和高校教学安排,对《密码学》课程开展线上直播教学。
本文以AES密码算法为例,进行直播教学设计及教学反思,便于今后更好开展教学工作。
关键词:直播教学;密码学;教学设计一、引言2019年12月以来,湖北省武汉市陆续发现了多例新型冠状肺炎病例,为了防止疫情进一步扩散,2020年1月26日,国务院新闻发布会要求各地大、中、小学2020年春季学期推迟开学[1]。
为了进一步保障教学工作按时完成,教育部1月29日发出倡议:利用网络平台,展开“停课不停学”[2]。
各个高校为响应“听课不停学”政策,纷纷采取了多种教学方式,如:线上直播、电视教学、学生自学等。
作者根据《密码学》课程的学科特点,并结合当前疫情的形势和教学安排,充分利用网络资源开展线上直播教学。
本文以《密码学》课程中的AES密码算法为例,对开展直播教学的工作进行阐述与反思,为今后的教学工作提供经验借鉴。
二、AES密码算法课程设计(一)教学目标学生通过学习本节课的内容,掌握AES密码算法的数学基础、设计思想和算法流程,为后序的密码学实验课程打下理论基础。
同时增强学生的信息保密意识和保密责任感,为今后从事密码学相关工作打下基础。
(二)教学设计AES密码算法由于涉及到一些数论的基本知识且加解密流程较为复杂,因此在课程安排上采用4个学时分别对AES密码的数学基础知识、算法的由来及框架、轮函数及密钥生成算法、思考题探讨与分析进行讲解。
1.数学基础知识(1)十六进制加法学习AES密码的数学基础知识,可以采用回顾旧知识,引入新课的方法。
首先需要同学们回忆一下我们之前学的数的进制。
我们最常用的是几进制数呢?答:十进制。
除了十进制数,我们还学过哪几个进制?答:二进制、八进制和十六进制。
AES密码算法主要涉及十六进制的加法和乘法运算,下面我们首先来看十六进制的加法运算。
密码学课程设计报告01 人人文库

密码学课程设计报告01 人人文库一、引言密码学是一门研究如何保护信息的学科,主要包括加密、解密和信息鉴别等方面。
随着互联网的快速发展以及网络安全问题的日益突出,密码学的重要性也日益凸显。
本次课程设计旨在学习密码学的基本理论和常用算法,以及设计一个简单的密码学系统进行实践。
二、理论基础1.加密与解密加密是将明文通过密码算法转换成密文,解密则是将密文通过相同的密码算法还原成明文。
常见的加密算法有对称密钥算法和非对称密钥算法。
对称密钥算法使用相同的密钥进行加密和解密。
常见的对称密钥算法有DES、AES等。
对称密钥算法具有加密速度快的优点,但是密钥的分发和管理比较困难。
非对称密钥算法则使用不同的密钥进行加密和解密。
常见的非对称密钥算法有RSA、DSA等。
非对称密钥算法具有安全性高的优点,但是加密速度较慢。
2.密钥管理密钥管理是密码学中非常重要的一环。
密钥的选择、生成、分发和存储等都对密码算法的安全性产生重要影响。
一般来说,密钥越长越难破解,但是加密和解密的时间也会更长。
三、设计实现本次课程设计选择使用对称密钥算法AES进行实现。
设计一个简单的密码学系统,包括密钥的生成、加密和解密等功能。
1.密钥的生成首先,选择合适的密钥长度。
一般来说,128位的密钥已经足够安全。
然后,使用随机数生成算法生成一个随机的密钥。
2.加密加密过程中,将明文通过AES算法转换成密文。
AES算法是一种分组密码算法,将明文分成多个长度相同的块,然后对每个块进行加密。
加密过程中使用的密钥与解密时使用的密钥应保持一致。
3.解密解密过程中,将密文通过AES算法转换成明文。
解密的步骤与加密的步骤相反。
使用相同的密钥对密文进行解密,得到原始的明文。
四、实验结果与对比使用实验中设计的密码学系统,选择一个明文进行加密和解密,得到相应的密文和明文。
通过比对原始明文与解密结果,验证系统的正确性。
在对称密钥算法AES中,选择不同的密钥长度,比较不同密钥长度对加密速度和安全性的影响。
密码学课程设计

随着计算机网络技术和通讯技术的迅猛发展,大量的敏感信息常常通过计算机网络进行交换,在这些信息的传输与处理的过程中,如何保护信息安全使之不被非法窃取或篡改,成为人们关注的问题。因此计算机密码学就成为信息安全中的一个重要的研究领域。密码体制的分类方法有很多,常用的几种分类方法如下:根据加密与解密算法中使用密钥是否相同,将其分为对称密钥密码体制和非对称密钥密码体制。
非对称密码体制的由来
在公开的计算机网络上安全地传送和保管密钥是一个严峻的问题。正是由于对称密码学中双方都使用相同的密钥,因此无法实现数据签名和不可否认性等功能。20世纪70年代以来,一些学者提出了公开密钥体制,即运用单向函数的数学原理,以实现加、解密密钥的分离。加密密钥是公开的,解密密钥是保密的。密钥对的工作是可以任选方向的。这提供了"数字签名"的基础,如果要一个用户用自己的私人密钥对数据进行了处理,别人可以用他提供的公共密钥对数据加以处理。由于仅仅拥有者本人知道私人密钥,这种被处理过的报文就形成了一种电子签名----一种别人无法产生的文件。 数字证书中包含了公共密钥信息,从而确认了拥有密钥对的用户的身份。
从对称密码到非对称密码
对称密码算法计算开销小,算法简单,加密速度快,是目前用于信息加密的主要算法。但它在进行安全通信前需要以安全方式进行密钥交换。这一步骤,在某些情况下会非常困难,甚至无法实现。例如,某一贸易方有几个贸易关系,他就要维护几个专用密钥且没法鉴别贸易发起方或贸易最终方,因为贸易的双方的密钥相同。另外,由于对称加密系统仅能用于对数据进行加解密处理,提供数据的机密性,不能用于数字签名。因而人们迫切需要寻找新的密码体制。
在谈到加密的时候,最新的不一定是最好的。应该选择那种合适的、已经被大量公开分析和测试过的加密算法,因为在密码学领域是没有机会去尝试一个新算法的。
信息安全专业中密码学课程的教学研究论文

信息安全专业中密码学课程的教学研究论文信息安全专业中密码学课程的教学研究论文摘要:密码学作为一门数学、计算机科学与通信的交叉学科,是信息安全专业的核心课程,也是数学在信息科学中的重要应用。
该文从密码学的特点出发,对密码学课程目前所存在的问题进行分析,并从教材选择、理论教学和实验教学的角度给出自己的几点建议。
关键词:密码学;信息安全;理论教学;实验教学;教学方法中图分类号:G642.3文献标识码:A文章编号:1009-3044(2017)26-0138-02随着计算机网络的广泛应用和深入发展,电子商务和电子政务以及网络银行和各种移动支付已经成为人们生活的一部分。
在方便人们生活的同时,也带来越来越多的信息安全问题。
因此,信息安全受到社会各界的高度重视,已成为信息社会急需解决的问题。
密码技术作为信息安全的核心技术,获得越来越多的关注。
密码学已成为各类高校信息安全专业的核心课程。
目前,我国有80多所高校开设信息安全专业,100多所高校开设密码学课程[1]。
由于密码学是一门集数学,计算机科学与通信科学等于一身的交叉学科,不同专业、不同学科,在教材的选择、教学内容以及教学方法等诸多方面的认识很难统一,给密码学课程的教学造成诸多困难,同时也是密码学课程教学中值得关注和探讨的问题。
1密码学课程的特点1)密码学所涉及的知识面广,数学基础要求高。
密码学课程前期需要学习信息论、计算复杂度和一些数学知识[2]。
其中数学除高等数学和线性代数以外,还包括数论、抽象代数、代数编码、概率论、有限域等相关内容,这些数学知识的难度也相对较大。
2)理论教学和实验教学的侧重点难以把握。
由于密码学是一门交叉学科,对于不同专业的学生,学习的侧重点也是不一样的。
例如数学科学学院应用数学专业的学生,大多数侧重理论教学,主要讲授密码算法的理论计算,对数学基础要求比较高。
而对于计算机学院信息安全专业的学生,又是以实验教学为主,对编程语言和计算复杂度要求较高。
密码学论文——精选推荐

通过这个学期对应用密码学的学习,我深刻地体会到应用密码学的魅力,也认识到随着科学的发展,密码学越来越成为一个国家不可缺少的一项科学技术。
密码学是研究编制密码和破译密码的技术科学。
研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。
密码是通信双方按约定的法则进行信息特殊变换的一种重要保密手段。
依照这些法则,变明文为密文,称为加密变换;变密文为明文,称为脱密变换。
密码在早期仅对文字或数码进行加、脱密变换,随着通信技术的发展,对语音、图像、数据等都可实施加、脱密变换。
密码学是在编码与破译的斗争实践中逐步发展起来的,并随着先进科学技术的应用,已成为一门综合性的尖端技术科学。
它与语言学、数学、电子学、声学、信息论、计算机科学等有着广泛而密切的联系。
它的现实研究成果,特别是各国政府现用的密码编制及破译手段都具有高度的机密性。
密码学主要经历了三个阶段:古代加密方法、古代密码和近代密码。
首先,古代加密方法处于手工阶段,其源于应用的无穷需求总是来推动技术发明和进步的直接动力。
存于石刻或史书中的记载表明,许多古代文明,包括埃及人、希伯来人、亚述人都在实践中逐步发明了密码系统。
从某种意义上说,战争是科学技术进步的催化剂。
人类自从有了战争,就面临着通信安全的需求,密码技术源远流长。
古代加密方法大约起源于公元前440年出现在古希腊战争中的隐写术。
当时为了安全传送军事情报,奴隶主剃光奴隶的头发,将情报写在奴隶的光头上,待头发长长后将奴隶送到另一个部落,再次剃光头发,原有的信息复现出来,从而实现这两个部落之间的秘密通信。
公元前 400 年,斯巴达人就发明了“塞塔式密码” ,即把长条纸螺旋形地斜绕在一个多棱棒上,将文字沿棒的水平方向从左到右书写,写一个字旋转一下,写完一行再另起一行从左到右写,直到写完。
解下来后,纸条上的文字消息杂乱无章、无法理解,这就是密文,但将它绕在另一个同等尺寸的棒子上后,就能看到原始的消息。
公钥密码学原理及应用信息安全论文大学论文

郑州工业应用技术学院课程设计(论文)题目:公钥密码学原理及应用指导教师: __________ 职称:无学生姓名: ___________ 学号:2—专业:14级通信工程院(系):信息工程学院2017年1月2摘要公开密钥密码体制是现代密码学最重要的发明,也可以说是密码学发展史上最伟大的革命。
一方面,公开密钥密码与之前的密码不同,其算法不是基于替代和置换而是基于数学函数;另一方面,与使用一个密钥的传统对称密钥密码不同,公开密钥密码是非对称的,使用两个独立的密钥。
公开密钥密码体制对保护信息传递的机密性和信息发送人和接收人的真实身份的验证、事后对所发出或接收信息的不可抵赖性以及保障数据的完整性这两个方面都给出了出色的答案。
本文主要就公开密钥密码的理论基础、安全性及应用等方面做出了分析介绍,重点分析了其与电子商务支付安全实践结合产生的应用技术。
1目录摘要.......................................................................... 1..1、信息安全概况............................................................... 3.2、公开密钥理论基础.......................................................... 4..2.1公钥密码系统基本思想和要求................................................ 4.2.2公开密钥密码通信模型........................................................ 4.2.3公开密钥密码的核心思想..................................................... 5.3、公开密钥密码............................................................... 6..3.1 Diffie-Hellman 密钥交换算法 (6)3.2 RSA密码算法 .............................................................. 6.3.3其他公钥密码.............................................................. 7..4、公钥密码安全性分析...................................................... 8.4.1公钥密码学中的攻击形式..................................................... 8.4.2安全性要求................................................................. 8..5、电子支付中公钥技术的应用 (10)5.1PKI/CA身份认证技术。
密码学论文(网络安全期末)

密码学是一门古老而深奥的学科,从古代的加密军书到如今的手机解锁,密码研究已有数千年的历史。
密码学也经历了从古典密码学到现代密码学的演变,虽然密码学的科技在不断地进步,古典密码的难度已经不足一提,但是古老的密码学思想奠定了密码学发展的基础,至今仍然被广泛使用。
密码学是信息安全的一门科学,密码技术是信息安全的核心,现代密码学所涉及的学科很广,包括信息论、概率论、数论、计算复杂性理论、近世代数、离散数学、代数几何学和数字逻辑等。
密码学主要包括两大分支,一是密码编码学,二是密码分析学。
密码学是对这两门分支学进行综合分析、系统研究的科学,是保护信息安全最主要的手段之一。
编码学与分析学是相互对立、相互依存,正是因为这种对立统一的关系,才推动了密码学自身的发展,下面将对这两门学科分别进行介绍。
1.密码编码学密码编码学是研究密码体制的设计的一门学问,主要内容是对信息进行编码密码,以实现对信息的加密。
密码编码技术的主要任务是寻求产生安全性高的有效密码算法和协议,以满足对消息进行加密或认证的要求。
2.密码分析学密码分析学是研究如何破解被加密信息的一门学问,即通过破译密码,来获取到所加密的信息。
经历了多个发展阶段。
密码分析技术的主要任务是破译密码或伪造认证信息,实现窃取机密信息或进行诈骗破坏活动。
密码学的基本思想是通过改变原有信息的顺序或者用不同的字母、数字、汉字等字符去替换原有字符,使原始信息变成混乱无章的乱码,保证了即使被非法获得信息后,也无法了解传送双方在信息中想表达的含义。
由于传送双方在事先进行了约定,接收方会根据某种规则,通过乱码来恢复出原始的信息含义。
伴随着信息科技不断地发展,现如今的密码学应用领域也不仅仅局限于信息的加密,也扩展到了对身份的识别和电子的认证等方面,比如日常所使用的手机指纹识别、解锁图案等,都属于密码学的范畴。
综上所述,密码学思想主要分为加密和解密两大部分,常用的方法有顺序法则和替代法则。
计算机密码学期末论文

《计算机密码学》期末论文学院:计算机科学与技术专业:计算机科学与技术班级:学号:姓名:教师:2016年月日密码学在网络通信加密中的应用摘要:介绍了网络加密方式,分析了DES、RSA等基本的安全技术。
关键词:Internet DES RSA 加密随着科技的发展,Internet的有关技术越来越成熟,现在,Internet在我们的生活中扮演了重要的角色。
Internet对我们的生活越来越重要,人们已经离不开Internet。
随着它的迅猛发展,全球经济和社会生活都产生了巨大变化。
Internet的应用领域极其广阔,如许多高等学校,公司等都已建立自己局域网并与Internet相连。
作为获得信息的重要途径,商业界也在积极地建立企业内部网络并通过Internet向公众提供种类繁多的信息服务,其中最引人注目的当属电子商务,电子商务正是在Internet快速发展的浪潮下应运而生的,它是信息时代社会生产与社会消费之间发生的一次革命。
Internet在为人们带来无限商机的同时,也引起了许多安全问题。
如何保证各种网络应用的安全性,成了我们必须考虑的问题。
例如:电子商务中网上购物是在线付款,用户的信用卡号等许多信息都是敏感信息,而这些网上传输的敏感数据和存放敏感信息的站点正是网络黑客的重点攻击对象。
因此,人们在开展各种网络业务时,首先考虑的是这种网络业务是否能够保证安全,如果不能保证安全,人们也就不会接受这种业务。
网络通信的数据加密包括以下几个方面:(1)数据传输的安全性。
数据传输的安全性即是要保证在公网上传输的数据不被第三方窃。
(2)数据的完整性。
对数据的完整性需求是指数据在传输过程中不被篡改。
通常情况下,网络通信中所采用的安全技术主要有防火墙技术、数据加密技术和身份认证技术等。
本文讨论的重点是数据加密技术在网络通信安全策略中的应用。
一. 开放系统互联参考模型和TCP/ IP分层模型1.1开放系统互连参考模型开放系统互连参考模型(Open System Interconnect 简称OSI)是国际标准化组织(ISO)和国际电报电话咨询委员会(CCITT)联合制定的开放系统互连参考模型,为开放式互连信息系统提供了一种功能结构的框架。
密码学论文

传统加密技术论文软件学院计算机科学与技术07999222李文龙网络信息的飞速发展给人类社会带来巨大的推动与冲击,同时也产生了网络系统安全问题。
计算机网络的安全问题越来越受到人们的重视。
密码技术是保护计算机信息安全的主要手段之一,使用密码技术可以保证信息的机密性,还可以保证信息的完整性和确定性,防止信息被篡改、伪造和假冒。
说道密码技术,以下先了解什么是加密技术。
加密技术包括两个元素:算法和密钥。
算法是将普通的文本(或者可以理解的信息)与一串数字(密钥)的结合,产生不可理解的密文的步骤,密钥是用来对数据进行编码和解码的一种算法。
在安全保密中,可通过适当的密钥加密技术和管理机制来保证网络的信息通讯安全。
密钥加密技术的密码体制分为对称密钥体制和非对称密钥体制两种。
相应地,对数据加密的技术分为两类,即对称加密(私人密钥加密)和非对称加密(公开密钥加密)。
对称加密以数据加密标准(DES,Data Encryption Standard)算法为典型代表,非对称加密通常以RSA(Rivest Shamir Ad1eman)算法为代表。
对称加密的加密密钥和解密密钥相同,而非对称加密的加密密钥和解密密钥不同,加密密钥可以公开而解密密钥需要保密。
对称密码是一种加密使用相同密钥的密码体制,也称为传统密码算法。
对称密码利用密钥和加密算法将明文变成密文。
运用相同的密钥和解密算法,而已从密文恢复出明文。
对密码的两种攻击方法是基于密码算法性质的密码分析和基于穷举密钥的穷举攻击。
传统对称密码(计算机出现前)使用代换和/或置换技术。
代换技术。
代换技术将明文元素(字符、比特)映射为密文元素,置换技术将明文元素的位置进行系统的置换。
转轮技术是计算机出现前使用代换技术的复杂硬件设备。
隐写技术是一种将秘密信息隐藏于其他更大信息中的一种技术,是得其他人无法区分它的存在或隐藏信息的内容。
传统经典加密主要采用了两种加密技术:替代技术和置换技术。
密码学论文(1)

密码学论文(1)密码学论文班级:统计学(金融数学方向)姓名:鲁亚婷学号:110444061密码学论文在我们的生活中有许多的秘密和隐私,我们不想让其他人知道,更不想让他们去广泛传播或者使用。
对于我们来说,这些私密是至关重要的,它记载了我们个人的重要信息,其他人不需要知道,也没有必要知道。
为了防止秘密泄露,我们当然就会设置密码,保护我们的信息安全。
更有甚者去设置密保,以防密码丢失后能够及时找回。
我们要为信息添加安全锁,设置密码,那么密码到底是干什么的呢?其实,密码就是为了防止未被允许进入的陌生人进入你的“账户”、“系统”等读写你的文件和数据。
很简单的理解,就和门要上锁一样,如果不上锁,那别人去你的家就和去自己的家一样了。
有此可知,密码在生活中的重要性。
“密码”一词对人们来说并不陌生,人们可以举出许多有关使用密码的例子。
如保密通信设备中使用“密码”,个人在银行取款使用“密码”,在计算机登录和屏幕保护中使用“密码”,开启保险箱使用“密码”,儿童玩电子游戏中使用“密码”等等。
这里指的是一种特定的暗号或口令字。
现代的密码已经比古代有了长远的发展,并逐渐形成一门科学,吸引着越来越多的人们为之奋斗。
从专业上来讲,密码是通信双方按约定的法则进行信息特殊变换的一种重要保密手段。
依照这些法则,变明文为密文,称为加密变换;变密文为明文,称为脱密变换。
密码在早期仅对文字或数码进行加、脱密变换,随着通信技术的发展,对语音、图像、数据等都可实施加、脱密变换。
为了研究密码所以就有了密码学。
密码学是研究编制密码和破译密码的技术科学。
研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。
密码学是在编码与破译的斗争实践中逐步发展起来的,并随着先进科学技术的应用,已成为一门综合性的尖端技术科学。
它与语言学、数学、电子学、声学、信息论、计算机科学等有着广泛而密切的联系。
密码学论文写作论文

密码学论⽂写作论⽂密码学论⽂写作范例论⽂ 随着⽹络空间竞争与对抗的⽇益尖锐复杂,安全问题以前所未有的深度与⼴度向传统领域延伸。
随着移动互联⽹、下⼀代互联⽹、物联⽹、云计算、命名数据⽹、⼤数据等为代表的新型⽹络形态及⽹络服务的兴起,安全需求⽅式已经由通信双⽅都是单⽤户向⾄少有⼀⽅是多⽤户的⽅式转变。
如果你想深⼊了解这⽅⾯的知识,可以看看以下密码学论⽂。
题⽬:数学在密码学中的应⽤浅析 摘要:密码学作为⼀门交叉学科,涉及学科⼴泛,其中应⽤数学占很⼤⽐例,其地位在密码学中也越来越重要,本⽂简单介绍密码学中涉及数学理论和⽅法计算的各种算法基本理论及应⽤,并将密码学的发展史分为现代密码学和传统密码学,列举⼆者具有代表性的明⽂加密⽅法,并分别对其中⼀种⽅法进⾏加密思想的概括和阐述。
关键词:密码学应⽤数学应⽤ 随着信息时代的⾼速发展,信息的安全越来越重要,⼩到个⼈信息,⼤到国家安全。
信息安全主要是将计算机系统和信息交流⽹络中的各种信息进⾏数学化的计算和处理,保护信息安全,⽽密码学在其中正是处于完成这些功能的技术核⼼。
在初期的学习当中,⾼等数学、线性代数、概率论等都是必须要学习的基础学科,但是涉及密码学的实际操作,数论和近世代数的'数学知识仍然会有不同程度的涉及和应⽤,本⽂在这⼀基础上,讨论密码学中⼀些基本理论的应⽤。
⼀、密码学的含义及特点 密码学是由于保密通信所需从⽽发展起来的⼀门科学,其保密通讯的接受过程如下:初始发送者将原始信息(明⽂)进⾏⼀定⽅式转换(加密)然后发送,接受者收到加密信息,进⾏还原解读(脱密) ,完成保密传输信息的所有过程,但是由于传输过程是经由有线电或⽆线电进⾏信息传输,易被窃取者在信息传输过程中窃取加密信息,在算法未知的情况下恢复信息原⽂,称为破译。
保密信息破译的好坏程度取决于破译者的技术及经验和加密算法的好坏。
实际运⽤的保密通信由两个重要⽅⾯构成:第⼀是已知明⽂,对原始信息进⾏加密处理,达到安全传输性的效果;第⼆是对截获的加密信息进⾏信息破译,获取有⽤信息。
学术论文:【毕业论文】加密和密码学的(AES加密算法)

【毕业论文】加密和密码学的(AES加密算法)本科毕业论文〔设计〕题目::加密和密码学 (AES加密算法)姓名:邓小明第一章绪论1.1 AES高级加密标准随着Internet的迅猛开展,基于Internet的各种应用也日新月异,日益增长。
但是,由于Internet是一个极度开放的环境,任何人都可以在任何时间、任何地点接入Internet获取所需的信息,这也使得在Internet上信息传输及存储的平安问题成为影响Internet应用开展的重要因素。
正因为如此,信息平安技术也就成为了人们研究Internet应用的新热点。
信息平安的研究包括密码理论与技术、平安协议与技术、平安体系结构理论、信息对抗理论与技术、网络平安与平安产品等诸多领域。
在其中,密码算法的理论与实现研究是信息平安研究的根底。
而确保数据加密算法实现的可靠性和平安性对于算法理论应用到各种平安产品中起到了至关重要的作用。
对各类电子信息进行加密,以保证在其存储,处理,传送以及交换过程中不会泄露,是对其实施保护,保证信息平安的有效措施。
1977年1月数据加密标准DES(Data Encryption Standard)正式向社会公布,它是世界上第一个公认的实用分组密码算法标准。
但DES在经过20年的实践应用后,现在已被认为是不可靠的。
1997年1月2日NIST发布了高级加密标准(AES-FIPS)的研发方案,并于同年9月12日正式发布了征集候选算法公告,NIST希望确定一种保护敏感信息的公开、免费并且全球通用的算法作为AES,以代替DES,用以取代DES的商业应用。
在征集公告中,NIST对算法的根本要求是:算法必须是私钥体制的分组密码,支持128bits分组长度和128,192,256bits密钥长度。
经过三轮遴选,Rijndael最终胜出。
2000年10月2日,NIST宣布采用Rijndael算法作为新一代高级加密标准。
Rijndael的作者是比利时的密码专家Joan Daemon博士和Vincent Rijmen博士。
密码学原理及应用的小论文

密码学原理及应用的小论文引言密码学是研究通信安全和信息安全的学科,它涉及到使用密码算法来保障数据的机密性、完整性和可用性。
随着互联网的快速发展,密码学变得越来越重要,它不仅应用于日常的网络通信,还广泛应用于金融、电子商务、军事等领域。
本文将介绍密码学的基本原理以及其在现实生活中的应用。
密码学的基本原理密码学的基本原理主要包括对称密码和非对称密码两种方式。
对称密码对称密码也称为私钥密码,它使用相同的密钥进行加密和解密。
发送方使用密钥对明文进行加密,并将密文传输给接收方,接收方再使用相同的密钥对密文进行解密。
常见的对称密码算法包括DES(Data Encryption Standard)、AES (Advanced Encryption Standard)等。
对称密码的优点是加解密速度快,适合对大量数据进行加密。
然而,由于发送和接收方需要共享同一个密钥,导致密钥管理变得困难,容易引发安全问题。
非对称密码非对称密码也称为公钥密码,它使用两个密钥:公钥和私钥。
发送方使用接收方的公钥对明文进行加密,并将密文传输给接收方。
接收方使用自己的私钥对密文进行解密。
常见的非对称密码算法包括RSA(Rivest-Shamir-Adleman)、DSA (Digital Signature Algorithm)等。
非对称密码的优点是密钥管理方便,安全性较高。
然而,加解密速度比对称密码慢,适合对少量数据进行加密。
密码学的应用网络通信安全网络通信安全是密码学应用的主要领域之一。
在网络通信中,不同的实体通过公网进行数据传输,为了保障数据的机密性和完整性,使用密码学进行加密是必要的。
例如,在网上购物中,消费者使用网银进行支付,需要通过密码学保障交易数据的安全性,防止被黑客篡改或窃取。
数字签名数字签名是密码学在数据完整性验证方面的一个重要应用。
使用私钥对数据进行签名,然后接收方使用发送方的公钥对签名进行验证。
如果验证通过,则说明数据完整且未被篡改。
密码学论文

密码学论文RSA加密算法解析摘要:描述了RSA算法,给出了RSA加密解密的算法原理并用一个实例进行详细描述,以及它的抗攻击能力和常见攻击方式,还有RSA算法的优缺点,最后进行(在VS2019下)RSA算法实现以及演示结果。
关键词:RSA;加密解密;攻击能力;攻击方法;安全性;算法优缺点;RSA实现简介:RSA加密算法是最常用的非对称加密算法,CFCA在证书服务中离不了它。
RSA是第一个比较完善的公开密钥算法,它既能用于加密,也能用于数字签名。
RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名,这个算法经受住了多年深入的密码分析,虽然密码分析者既不能证明也不能否定RSA的安全性,但这恰恰说明该算法有一定的可信性,目前它已经成为最流行的公开密钥算法。
RSA的安全基于大数分解的难度。
其公钥和私钥是一对大素数(100到200位十进制数或更大)的函数。
从一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积。
RSA的公钥、私钥的组成,以及加密、解密的公式可见于下表:一、什么是“素数”?素数是这样的整数,它除了能表示为它自己和1的乘积以外,不能表示为任何其它两个整数的乘积。
例如,15=3*5,所以15不是素数;又如,12=6*2=4*3,所以12也不是素数。
另一方面,13除了等于13*1以外,不能表示为其它任何两个整数的乘积,所以13是一个素数。
素数也称为“质数”。
二、什么是“互质数”(或“互素数”)?定义:“公约数只有1的两个数,叫做互质数。
”这里所说的“两个数”是指自然数。
判别方法主要有以下几种:(1)两个质数一定是互质数。
例如,2与7、13与19。
(2)一个质数如果不能整除另一个合数,这两个数为互质数。
例如,3与10、5与26。
(3)1不是质数也不是合数,它和任何一个自然数在一起都是互质数。
如1和9908。
(4)相邻的两个自然数是互质数。
成都东软学院毕业设计(论文)范例
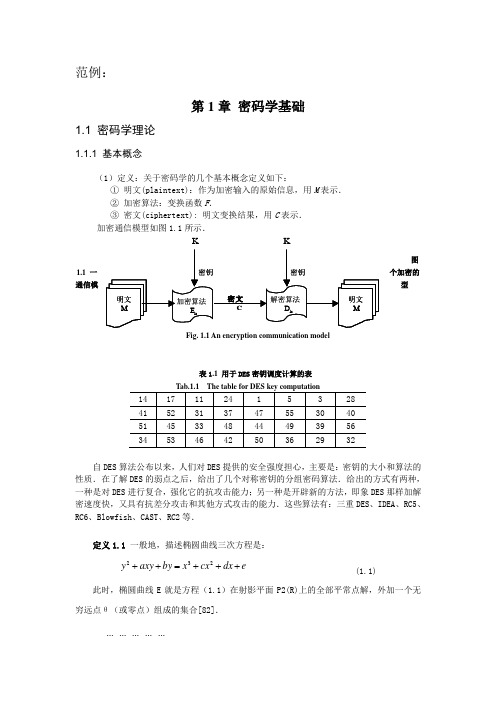
范例:第1章 密码学基础1.1 密码学理论1.1.1 基本概念(1)定义:关于密码学的几个基本概念定义如下:① 明文(plaintext):作为加密输入的原始信息,用M 表示. ② 加密算法:变换函数F .③ 密文(ciphertext): 明文变换结果,用C 表示. 加密通信模型如图1.1所示.图1.1 一个加密的通信模型Fig. 1.1 An encryption communication model表1.1 用于DES 密钥调度计算的表自DES 算法公布以来,人们对DES 提供的安全强度担心,主要是:密钥的大小和算法的性质.在了解DES 的弱点之后,给出了几个对称密钥的分组密码算法.给出的方式有两种,一种是对DES 进行复合,强化它的抗攻击能力;另一种是开辟新的方法,即象DES 那样加解密速度快,又具有抗差分攻击和其他方式攻击的能力.这些算法有:三重DES 、IDEA 、RC5、RC6、Blowfish 、CAST 、RC2等.定义1.1 一般地,描述椭圆曲线三次方程是:e dx cx x by axy y +++=++232(1.1)此时,椭圆曲线E 就是方程(1.1)在射影平面P2(R)上的全部平常点解,外加一个无穷远点θ(或零点)组成的集合[82].… … … … …KK参考文[1] 戴建华,尹华伟,张洪均,吴令安. 混沌在信息加密中的应用[J]. 科学通报,1996[2] Bruce Schneier 著,吴世钟,祝世雄等译. 应用密码学—协议、算法与C程序[M], 第二版,北京:机械工业出版社,2001[3] 许榕生,蒋文葆编著. 电子商务安全与保密[M], 北京:中国电力出版社,2001。
[整理版]密码学论文
![[整理版]密码学论文](https://img.taocdn.com/s3/m/0cb5815fc950ad02de80d4d8d15abe23482f0378.png)
学院:计算机科学与教育软件学院专业:软件工程班级:软工075姓名:tangelyou密码学论文00一、密码学的定义和作用00密码学是主要研究通信安全和保密的学科,他包括两个分支:密码编码学和密码分析学。
密码编码学主要研究对信息进行变换,以保护信息在传递过程中不被敌方窃取、解读和利用的方法,而密码分析学则于密码编码学相反,它主要研究如何分析和破译密码。
这两者之间既相互对立又相互促进。
密码的基本思想是对机密信息进行伪装。
一个密码系统完成如下伪装:加密者对需要进行伪装机密信息(明文)进行伪装进行变换(加密变换),得到另外一种看起来似乎与原有信息不相关的表示(密文),如果合法者(接收者)获得了伪装后的信息,那么他可以通过事先约定的密钥,从得到的信息中分析得到原有的机密信息(解密变换),而如果不合法的用户(密码分析者)试图从这种伪装后信息中分析得到原有的机密信息,那么,要么这种分析过程根本是不可能的,要么代价过于巨大,以至于无法进行。
0二、密码学的发展历程人类有记载的通信密码始于公元前400年。
密码学的起源的确要追溯到人类刚刚出现,并且尝试去学习如何通信的时候,为了确保他们的通信的机密,最先是有意识的使用一些简单的方法来加密信息,通过一些(密码)象形文字相互传达信息。
接着由于文字的出现和使用,确保通信的机密性就成为一种艺术,古代发明了不少加密信息和传达信息的方法。
例如我国古代的烽火就是一种传递军情的方法,再如古代的兵符就是用来传达信息的密令。
就连闯荡江湖的侠士,都有秘密的黑道行话,更何况是那些不堪忍受压迫义士在秘密起义前进行地下联络的暗语,这都促进了密码学的发展。
事实上,密码学真正成为科学是在19世纪末和20世纪初期,由于军事、数学、通讯等相关技术的发展,特别是两次世界大战中对军事信息保密传递和破获敌方信息的需求,密码学得到了空前的发展,并广泛的用于军事情报部门的决策。
太平洋战争中,美军破译了日本海军的密码机,读懂了日本舰队司令官山本五十六发给各指挥官的命令,在中途岛彻底击溃了日本海军,导致了太平洋战争的决定性转折,而且不久还击毙了山本五十六。
密码学课程设计论文

密码学课程设计论文课程设计一、课程设计的内容运用C语言、C++面向对象、数据结构以及刚学习的密码学等知识,在认真学习古典密码的理论知识之后,通过编程进行各类古典密码的算法的实现,并产生界面友好。
二、课程设计的要求与数据论文摘要包括,摘要正文和关键词,课程设计正文(绪论(说明做这个课题的意义)、理论部分(相关的理论)、代码的实现部分、总结)三、课程设计应完成的工作各类古典密码算法的编写程序MFC的关联论文的撰写(目录的自动生成)四、应收集的资料及主要参考文献论文摘要:本文主要对古典密码中的移位密码(凯撒密码),仿射密码,维吉利亚(Vigenere)密码以,单表代换密码,置换密码和周期置换密码进行算法设计,最后用C++方法实现友好界面。
通过对这几个古典密码的算法分析,更加系统的掌握其中的原理和应用。
关键词凯撒密码、置换密码、算法、MFC关联、代码目录第1章绪论 (3)第2章理论部分 (3)2.1:移位密码 (4)2.2:仿射密码 (4)2.3:维吉利亚密码 (4)2.4:一般的单表代换密码 (4)2.5:列置换密码 (4)2.6:周期置换密码 (4)第3章代码的实现 (5)3.1:程序主界面: (5)3.2 移位密码: (5)3.3 仿射密码 (6)3.4 维吉利亚密码 (9)3.5 单表代换密码 (12)3.6 置换密码 (15)3.7 周期置换密码 (16)第4章总结 (18)第5章参考文献 (19)第1章绪论密码学包括两部分,即密码编码学和密码分析学,这两个部分即对立又统一,正是由于其对立性才促进了密码学的发展。
一个密码系统的安全性只有通过对该系统抵抗当前各类攻击能力的考查和全面分析才能做出定论。
密码体制的安全性分析是一个相当复杂的问题,但有一点是清楚的,那就是掌握现有的分析方法并使用这些方法对相应的体制进行分析以考察其安全强度。
在密码编码体制中,有两种最基本也是最古老的编码体制一直沿用至今,它们是代换密码和置换密码,由于历史悠久并且是现代密码体制的基本组成部分,因而在密码学中占有重要的地位。
密码学教学实践应用分析论文(共6篇)

密码学教学实践应用分析论文(共6篇)本文从网络收集而来,上传到平台为了帮到更多的人,如果您需要使用本文档,请点击下载按钮下载本文档(有偿下载),另外祝您生活愉快,工作顺利,万事如意!第1篇:浅析密码学在信息安全中的应用随着人们生活水平的快速提高和现代电子信息技术的发展,互联网开始走进千家万户,不断改变着人们的生活和工作方式。
与此同时,也给人们的个人信息和隐私带来了极大的安全隐患。
相关的恶性事件也多次被新闻媒体曝光,对网络信息安全提出了巨大的挑战。
因此,密码学逐渐被业内人士发现并进行深入研究后,被广泛应用到网络信息安全中来,以确保网络信息达到真正意义上的安全。
1密码学技术主要的分类加密技术使确保网络信息安全的重要手段,工作原理就是将网络信息转化为密文,然后通过网络突进进行传送,即使被不法分子捕获,也无法识别其中的有效信息,在输出时,再将信息转化为人们交流使用的明文。
通过这种方式来确保网络信息的安全。
加密目前有两种主要的分类即专用密钥加密和非对称加密。
专用密钥加密或对称加密方法专用密钥加密或对称加密主要的特点就是加密密钥和解密密钥是同一种密钥,大大简化了对信息加密的过程。
传输双方要想获得有用的信息只需要共享就可以得到,不需要再进行交换彼此的算法[1]。
但是这种方法有一定的缺陷,就是在信息传输过程中无法识别信息的发起方和信息的最终方,而且只能是一一对应的映射方式。
专用密钥加密的密钥总共是56位,在传统的DES 加密技术的基础上,进一步优化改进成三重DES,大大加大了信息的安全性。
并且RCZ和RC4加密技术也逐渐被广泛应用,这种算法的密钥长度是可以改变的,可以根据不同的情况使用不同长度的密钥。
非对称加密或公共密钥加密方法在加密过程中,密钥被进一步分解成一对密钥,这一对密钥中的任何一个密钥都可以作为公开的密钥被大量使用,但是为确保信息安全必须把另外一把密钥保存起来,由一方单独掌握。
非对称密钥常用的加密方法就是RSA算法,它有一个明显的缺点就是运算的速度非常的缓慢[2]。
加密解密论文毕业设计(论文)word格式

目录摘要 (II)Abstract (II)第一章概论 (1)1.1 课题背景 (1)1.2 课题意义 (2)第二章 DES算法设计简介及方案论述 (3)2.1 设计简介 (3)2.2 设计方案 (3)2.2.1 DES的加密过程 (4)2.2.1 DES的解密过程 (5)第三章 DES算法详细设计 (6)3.1 子密钥的产生 (6)3.2 初始值换IP (7)3.3 加密函数 (7)3.4 逆初始值换1IP (9)第四章设计结果及分析 (10)4.1 设计结果 (10)4.2 设计结果分析 (12)总结 (13)致谢 (14)参考文献 (15)附录主要程序代码 (15)摘要DES(Data Encryption Standard)算法是美国国家标准局(NIST)于1977年公布由IBM公司研制的一种加密算法,并且批准它作为非机要部门使用的数据加密标准。
自从公布以来,它一直超越国界,成为国际上商用保密通信和计算机通信的最常用的加密算法。
DES也是曾被广泛使用的分组密码,遍及世界的政府,银行和标准化组织把DES 作为安全和论证通信的基础。
DES算法公开是密码学史上里程碑式的事件。
DES算法是分组密钥,每次处理64位的明文数据,形成64位的密文。
DES也是一个对称算法,加密解密使用相同的算法和密钥,密钥长度为56位,可以为任意的56位的数,且随时可更换。
此次设计主要是对DES数据加密标准原理和流程的描述,D从初始变换、DES的迭代过程、密钥变换和逆置换等四个方面开始研究的,并且用Visual C ++语言实现了它的模拟应用。
关键词:加密;解密;DES算法;Visual C++AbstractDES (Data Encryption Standard) algorithm is that National institute of standards and technology (NIST) announced a kind of encryption algorithm developed by IBM in 1977,and approve for it as whether datum that confidential developments use encrypt standard. Since announcing, it has been surmounting the national boundaries all the time, and has been come the most frequently used of encryption algorithm in the communication of commercial secret and computer in the world .DES block ciphers that enjoys widespread use too, spread all over the government of the world, the bank and standardization tissue regarded DES as the foundation to prove safe and communication to organize. It is a milestone incident in the cryptography history that DES algorithm is disclosed.The key that DES algorithm divides into groups, data are encrypted in 64-bit block each time, form the cipher texts of 64. DES is a symmetrical algorithm too. The same steps, with the same key, are used to reverse the encryption, the key length is 56-bit, and can be the numbers of 56 wanton, and can change at any time. This text is mainly description that encrypts the standard principle and process to the data of DES,and analyses the basic principle of DES encryption algorithm, separately from four parts etc to research that is initial permutation, the DES ‘s iteration course, key permutation and Inverse initial permu tation, and has realized its simulation application with Visual C++language.Keywords:Encrypt;Decrypt;DES algorithm;VC++programming第一章概论本章主要介绍了课题《DES对称密码的算法的设计与实现》的设计背景和意义,提出在当今的信息化时代,信息安全是至关重要的,密码技术更是确保信息安全的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计一、课程设计的内容运用C语言、C++面向对象、数据结构以及刚学习的密码学等知识,在认真学习古典密码的理论知识之后,通过编程进行各类古典密码的算法的实现,并产生界面友好。
二、课程设计的要求与数据论文摘要包括,摘要正文和关键词,课程设计正文(绪论(说明做这个课题的意义)、理论部分(相关的理论)、代码的实现部分、总结)三、课程设计应完成的工作各类古典密码算法的编写程序MFC的关联论文的撰写(目录的自动生成)四、应收集的资料及主要参考文献论文摘要:本文主要对古典密码中的移位密码(凯撒密码),仿射密码,维吉利亚(Vigenere)密码以,单表代换密码,置换密码和周期置换密码进行算法设计,最后用C++方法实现友好界面。
通过对这几个古典密码的算法分析,更加系统的掌握其中的原理和应用。
关键词凯撒密码、置换密码、算法、MFC关联、代码目录第1章绪论 (3)第2章理论部分 (3)2.1:移位密码 (4)2.2:仿射密码 (4)2.3:维吉利亚密码 (4)2.4:一般的单表代换密码 (4)2.5:列置换密码 (4)2.6:周期置换密码 (4)第3章代码的实现 (5)3.1:程序主界面: (5)3.2 移位密码: (5)3.3 仿射密码 (6)3.4 维吉利亚密码 (9)3.5 单表代换密码 (12)3.6 置换密码 (15)3.7 周期置换密码 (16)第4章总结 (18)第5章参考文献 (19)第1章绪论密码学包括两部分,即密码编码学和密码分析学,这两个部分即对立又统一,正是由于其对立性才促进了密码学的发展。
一个密码系统的安全性只有通过对该系统抵抗当前各类攻击能力的考查和全面分析才能做出定论。
密码体制的安全性分析是一个相当复杂的问题,但有一点是清楚的,那就是掌握现有的分析方法并使用这些方法对相应的体制进行分析以考察其安全强度。
在密码编码体制中,有两种最基本也是最古老的编码体制一直沿用至今,它们是代换密码和置换密码,由于历史悠久并且是现代密码体制的基本组成部分,因而在密码学中占有重要的地位。
古典密码是密码学发展的一个阶段,也是近代密码学产生的渊源,尽管古典密码大多比较简单,一般可用手工或机械方式实现其加密和解密过程,破译也比较简单,目前已经很少采用,但了解它们的设计原理,有助于理解、设计和分析现代密码。
日常生活中,在大多数的情况下,我们不用担心别人偷听,因为即使被人偷听到了他也无法用偷听到的信息做什么坏事。
但当我们谈论某些比较敏感的话题时,被别人偷听到的话可能会产生一些负面的影响,对当事人很不利。
在文字交流中,一些重要的信息,比如重要决定,人事变动和秘密情报等,当事人是不希望别人看到的,但如何进行交流呢?一个简单的办法就是采用文字编码。
例如,将英文中的每个字母固定地换成它后面第5个字母,A换成F,B换成G,…,V换成A,W换成B,…,最后Z换成E。
字母编码如下表所示:原文 A B C D …V W X Y Z密文 F G H I … A B C D E 因此,消息I love you就变成了n qtaj dtz,消息有明确的信息,而编码后的字符串却是一串乱码,信息隐藏在其中,达到了保密的效果。
对于古典密码体制而言,我们有如下的约定:加密解密时忽略空格和标点符号,这可能让人不太适应,但是经过解密后,几乎总是可以正确的还原明文中的这些空缺。
如果保留这些空缺,密文会保持明文的结构特点,为攻击者提供便利。
本文主要是通过对各类型的古典密码进行算法设计,通过编写程序来深层掌握古典密码的算法技术,通过对各类型古典密码进行详细的分析,分工讨论,在实现系统掌握这些密码算法的同时,也对C语言和C++面向对象进行了复习,有效的巩固了以前的知识,也培养了对专业密码学的学习兴趣。
第2章理论部分代换是古典密码中用到的最基本的处理技巧,它在现代密码学中得到了广泛的应用,内容非常的丰富,人们采用代换密码进行加密时并没有固定的模式。
按照一个明文字母是否总是被一个固定的字母代换进行划分时,代换密码可以分为两大类:(1)单表代换密码:对明文消息中出现的同一个字母,在加密时都用同一个固定的字母来代换,不管它出现在什么地方。
移位密码和仿射密码都属于单表代换密码。
(2)多表代换密码:明文消息中出现的同一个字母,在加密时不是完全被同一个固定的字母代换,而是根据其出现的位置次序,用不同的字母代换,如维吉利亚密码和Playfair密码。
2.1:移位密码明文空间P与密文空间C都是26个英文字母的集合,密钥空间K={0,1,2,…,25}。
在实际进行加密解密运算时,把26个字母依次与0,1,2,…,25对应。
因而也可以说P=C=K={0,1,…,25}=Z。
E={e:Z->Z,e(x)=x+k(mod 26)},即对每个K∈Z,相应的加密变换为ek(m)=m+k(mod 26),其中m∈Z为明文。
D={d:Z->Z,d(x)=x-k(mod 26)},即对密钥k,解密变换为dk(y)=y-k(mod 26),其中y∈Z为密文。
解密之后要把Z中的元素再变换为英文字母。
2.2:仿射密码明、密文空间与移位密码相同,密钥空间为K={(k1,k2)|k1,k2∈Z,其中gcd(k1,26=1)} gcd表示两个数的最大公因子,gcd(k1,26)=1,即表示k1还 26互素。
对任意的k=(k1,k2)∈K,加密变换为e(m)=k1*m+k2*(mod 26).相应的解密变化为d(c)=k1^(-1)*(c-k2)(mod 26),其中:k1*k1^(-1)=1(mod 26).2.3:维吉利亚密码该密码有一个参数n。
在加解密时同样把英文字母用数字代替进行运算,并按n 个字母一组进行变换。
明、密文空间及密钥空间都是n长的字母串的集合,因此可以表示P=C=K=Z^(26).加密变换如下:设密钥k=(k1,k2,…,kn),明文P=(m1,m2,…,mn),加密函数为e(p)=(c1,c2,…,cn),其中Ci=(mi+ki)(mod 26),i=1,2,…,n。
对密文c=(m1,m2,…,mn),密钥k=(k1,k2,…,kn),解密变换为:e(c)=(m1,m2,…,mn),其中m1=(c1-k1)(mod 26),i=1,2,…,n。
其中mi=(ci-ki)(mod 26),i=1,2,…,n。
2.4:一般的单表代换密码单表代换密码的原理是:以26个字母的集合上的一个置换∏为密钥对明文消息中的每个字母依次进行变换,变换的方法是把明文中的每个字母用它在置换∏下的像去替换。
解密时用∏的逆置换进行替换。
可描述为P=C={0,1,2,…,25}=Z,K={∏:Z->Z|∏是置换}。
密钥∏对应的加密变换e(x)= ∏(x),解密变换为d(y)= ∏^(-1)(y).前面描述的移位密码和仿射密码都是单表代换密码,而维吉利亚密码不是单表代换密码。
2.5:列置换密码置换密码是把明文中各字符的位置次序重新排列来得到密文的一种密码体制。
列置换密码的加密方法如下:把明文字符以固定的宽度m(分组长度)水平地(按行)写在一张纸上,按1,2,3,…,m的一个置换∏交换列的次序位置,再按垂直方向(按列)读出即得密文。
解密就是就是将密文按照相同的宽度m垂直的写在纸上,按置换∏的逆置换交换列的位置次序,然后水平的读出得到明文,置换∏就是密钥。
2.6:周期置换密码周期置换密码是将明文字符按照一定长度m分组,把每组中的字符按1,2,…,m 的一个置换∏重排位置次序来得到密文的一种加密方法。
其中的密钥就是置换∏,在∏的描述中包含了分组长度的信息。
解密时,对密文字符按长度m分组,并按∏的逆置换∏^(-1)把每组字符重排位置次序来得到明文。
第3章代码的实现3.1:程序主界面:3.2 移位密码:部分代码实现:void kaisa::Onjiami(){// TODO: Add your control notification handler code hereint i;char b;this->UpdateData();if (m_mingwen.IsEmpty())MessageBox("要加密的文字不能为空!");m_jiami=m_mingwen;int n=m_jiami.GetLength();for( i=0;i<n;i++){b=m_jiami.GetAt(i);if('a' <= b && b <= 'z')m_jiami.SetAt(i,'a'+(b-'a'+m_k)%26);elseif('A' <= b && b <= 'Z')m_jiami.SetAt(i,'A'+(b-'A'+m_k)%26);else{m_jiami="";this->MessageBox("输入明文只能为大、小写字母或空格!");}}this->UpdateData(false);}void kaisa::Onjiemi(){// TODO: Add your control notification handler code here this->UpdateData();int i;m_jiemi=m_jiami;int n=m_jiemi.GetLength();for(i=0;i<n;i++){char b=m_jiemi.GetAt(i);if('a' <= m_jiami.GetAt(i) && m_jiami.GetAt(i) <= 'z') m_jiemi.SetAt(i,'a'+(b-'a'-m_k+26)%26);if('A' <= b && b <= 'Z')m_jiemi.SetAt(i,'A'+(b-'A'-m_k+26)%26);}this->UpdateData(false);}void kaisa::Onclose(){// TODO: Add your control notification handler code here CDialog::OnOK();}3.3 仿射密码部分代码如下:fangshe::fangshe(CWnd* pParent /*=NULL*/): CDialog(fangshe::IDD, pParent){//{{AFX_DATA_INIT(fangshe)m_mingwen = _T("");m_k1 = 0;m_k2 = 0;m_jiami = _T("");m_jiemi = _T("");//}}AFX_DATA_INIT}void fangshe::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(fangshe)DDX_Text(pDX, IDC_EDIT1, m_mingwen);DDX_Text(pDX, IDC_EDIT2, m_k1);DDX_Text(pDX, IDC_EDIT3, m_k2);DDX_Text(pDX, IDC_EDIT4, m_jiami);DDX_Text(pDX, IDC_EDIT5, m_jiemi);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(fangshe, CDialog)//{{AFX_MSG_MAP(fangshe)ON_BN_CLICKED(IDCANCEL, Onjiami)ON_BN_CLICKED(IDOK, Onjiemi)ON_BN_CLICKED(IDC_BUTTON1, Onclose)//}}AFX_MSG_MAPEND_MESSAGE_MAP()//////////////////////////////////////////////////////////////////////// /////// fangshe message handlersint gcd(int a, int b) /*辗转相除法求a,b的最大公因数*/{int k = 0;do{k = a%b;a = b;b = k;}while(k!=0);return a;}int Ni(int a, int b) /*求a相对于b的逆*/{int i = 0;while(a*(++i)%b!=1);return i;}void fangshe::Onjiami(){// TODO: Add your control notification handler code hereint i;this->UpdateData();if (m_mingwen.IsEmpty())MessageBox("要加密的文字不能为空!");m_jiami=m_mingwen;int n=m_jiami.GetLength();char b;for( i=0;i<n;i++){b=m_jiami.GetAt(i);// if('a' <= b && b <= 'z')if(gcd(m_k1,26)==1){if('a' <= b && b <= 'z')m_jiami.SetAt(i,'a'+(m_k1*(b-'a')+m_k2)%26);elseif('A' <= b && b <= 'Z')m_jiami.SetAt(i,'A'+(m_k1*(b-'A')+m_k2)%26);elseif(b==' '){m_jiami.SetAt(i,NULL);}else{m_jiami="";this->MessageBox("输入明文只能为大、字母或空格!");}}else{m_jiami="";this->MessageBox("请输入一个和26互素的正整数作为密钥!");}}this->UpdateData(false);}void fangshe::Onjiemi(){// TODO: Add your control notification handler code herethis->UpdateData();int i;m_jiemi=m_jiami;int n=m_jiemi.GetLength();for(i=0;i<n;i++){char b=m_jiemi.GetAt(i);if('a' <= b && b <= 'z')m_jiemi.SetAt(i,'a'+(Ni(m_k1,26)*(b-'a'-m_k2+26))%26);if('A' <= b && b <= 'Z')m_jiemi.SetAt(i,'A'+(Ni(m_k1,26)*(b-'A'-m_k2+26))%26);}this->UpdateData(false);}void fangshe::Onclose(){// TODO: Add your control notification handler code hereCDialog::OnOK();3.4 维吉利亚密码部分代码:void Vigenere::OnButton1(){// TODO: Add your control notification handler code hereCDialog::OnOK();}void Vigenere::Onjiami(){// TODO: Add your control notification handler code hereint i,j,k;int pos=0,tag;this->UpdateData();if (m_mingwen.IsEmpty())MessageBox("要加密的文字不能为空!");if (m_k.IsEmpty())MessageBox("密钥不能为空!");int n=m_mingwen.GetLength();//求输入内容的长度int m=m_k.GetLength();//密钥长度m_jiami=m_mingwen;for( i=0,j=0;i<n;i++)//把明文中非空格的元素存在数组B中。
