固体与半导体物理(第七章)
半导体物理学第七章知识点

半导体物理学第七章知识点第7章⾦属-半导体接触本章讨论与pn 结特性有很多相似之处的⾦-半肖特基势垒接触。
⾦-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之⼀:§7.1⾦属半导体接触及其能级图⼀、⾦属和半导体的功函数1、⾦属的功函数在绝对零度,⾦属中的电⼦填满了费⽶能级E F 以下的所有能级,⽽⾼于E F 的能级则全部是空着的。
在⼀定温度下,只有E F 附近的少数电⼦受到热激发,由低于E F 的能级跃迁到⾼于E F 的能级上去,但仍不能脱离⾦属⽽逸出体外。
要使电⼦从⾦属中逸出,必须由外界给它以⾜够的能量。
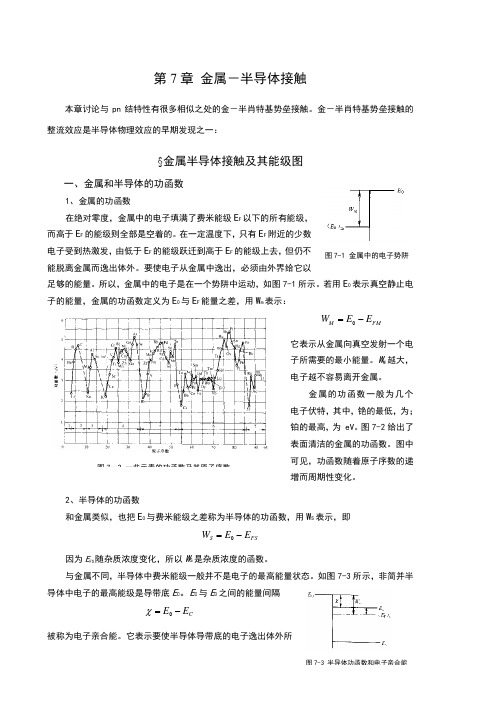
所以,⾦属中的电⼦是在⼀个势阱中运动,如图7-1所⽰。
若⽤E 0表⽰真空静⽌电⼦的能量,⾦属的功函数定义为E 0与E F 能量之差,⽤W m 表⽰:FM M E E W -=0它表⽰从⾦属向真空发射⼀个电⼦所需要的最⼩能量。
W M 越⼤,电⼦越不容易离开⾦属。
⾦属的功函数⼀般为⼏个电⼦伏特,其中,铯的最低,为1.93eV ;铂的最⾼,为5.36 eV 。
图7-2给出了表⾯清洁的⾦属的功函数。
图中可见,功函数随着原⼦序数的递增⽽周期性变化。
2、半导体的功函数和⾦属类似,也把E 0与费⽶能级之差称为半导体的功函数,⽤W S 表⽰,即FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与⾦属不同,半导体中费⽶能级⼀般并不是电⼦的最⾼能量状态。
如图7-3所⽰,⾮简并半导体中电⼦的最⾼能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电⼦亲合能。
它表⽰要使半导体导带底的电⼦逸出体外所需要的最⼩能量。
利⽤电⼦亲合能,半导体的功函数⼜可表⽰为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费⽶能级与导带底的能量差。
图7-1 ⾦属中的电⼦势阱图7-2 ⼀些元素的功函数及其原⼦序数图7-3 半导体功函数和电⼦亲合能表7-1 ⼏种半导体的电⼦亲和能及其不同掺杂浓度下的功函数计算值⼆、有功函数差的⾦属与半导体的接触把⼀块⾦属和⼀块半导体放在同⼀个真空环境之中,⼆者就具有共同的真空静⽌电⼦能级,⼆者的功函数差就是它们的费⽶能级之差,即W M -W S =E FS -E FM 。
半导体物理与器件-第七章 pn结

7.1 pn结的基本结构
冶金结:P区和n区的交界面
突变结 突变结-均匀分布,交界处突变
5
7.1 pn结的基本结构
PN结的形成
Space charge region
空间电荷区=耗尽区(没有可自由移动的净电荷,高阻区)
6
pn结的形成
Байду номын сангаас.2 零 偏
pn结能带图
7.2.1内建电势差
当两块半导体结合成pn结时,按费米能级的意义,电子将 从费米能级高的n区向费米能级低的p区,空穴则从p区流向n区 ,因而FFn不断下移,且EFp不断上移,直至时FFn = EFp为止;这 时pn结中有统一的费米能级EF,pn结处于热平衡状态。
4、对单边突变结,空间电荷区的宽度W取决于轻掺杂一侧杂质的浓度。
7.2零偏
7.2.3空间电荷区宽度
7.3 反 偏
7.3.1空间电荷区宽度与电场
反偏
与内建电场方向相同
外加偏置电压VR(以P端相对于N端电压为定义方向) 正偏:P端接正;
反偏:P端接负。
EF不再统一
n
16
7.3反偏
V=Vbi+VR
第7章 pn结
本章内容
第7章 pn结 7.1 pn结的基本结构 7.2零偏 7.3反偏 *7.4非均匀掺杂pn结 7.5小结
2
引言
PN结是几乎所有半导体器件的基本单元。除金属-半导体接触器 件外,所有结型器件都由PN结构成。PN结本身也是一种器件-整 流器。PN结含有丰富的物理知识,掌握PN结的物理原理是学习其 它半导体器件器件物理的基础。正因为如此, PN结一章在半导 体器件物理课的64学时的教学中占有16学时,为总学时的四分之 一。
半导体物理 第七章 电荷转移器件 图文

国家级精品课程——半导体器件物理与实验
第七章 电荷转移器件
§7.1 电荷转移
❖ 小结:
体表面形成由电离受主构成的负的空间电荷区。空间电荷区为耗
尽层。由于不是处于热平衡状态,耗尽层不受热平衡时的最大厚
度的限制,而直接由栅压VG的大小来决定。这时表面势也不受形 成强反型层时ψs=2φf的限制,也直接由VG 的大小来决定。在深 耗尽状态,耗尽层厚度Xd>Xdm,表面势ψs>2φf ,所以称之为深 耗尽状态。
CTD的核心是MOS电容的有序阵列(arrays)加上输 入与输出部分。在栅电极加上时钟脉冲电压时,在 半导体表面就形成了能存储少数载流子的势阱。用 光或电注入的方法把代表信号的少数载流子注入势 阱中。通过时钟脉冲的有规律变化,使势阱的深度 发生相应的变化,从而使注入势阱中的少数载流子 在半导体表面内作定向运动,再通过对少数载流子 的收集和再生得到信号的输出。
国家级精品课程——半导体器件物理与实验
第七章 电荷转移器件
§7.1 电荷转移
二、电荷耦合器件——CCD
图7-2 三相CCD动作, p+扩散用来限制沟道 1. 若在图7-2a中,电极2偏置在10V,比它附近两个电极的偏置电压(5V)高,
这样就建立了用虚线描绘的势阱,电荷存储在这个电极下边。 2. 现在让电极3偏置在15V,在电极3下边于是就建立起一个更深的势阱
第七章 电荷转移器件
Charge-Transfer Devices—CTD
黄昆 固体物理 讲义 第七章

+
K =k ⋅
m
K p
)unk K
K (r )
=
[En
K (k )
−
K =2k 2 2m
]unk
K (r )
,同时利用周期性函数解的条件,即
可以得到电子的全部能量 En (k ) 。
K k
⋅
K p
微扰法的中心思想:如果已知
K k0
处的解,利用微扰法则可以得到
K k
的解,即原则上布里渊区其
它任一点的解 u K 可以用 u K 来表示。
§7.2 半导体中的杂质 理想的半导体材料是没有缺陷或没有杂质,半导体中的载流子只能是激发到导带中的电子和价带中 的空穴。
对纯的半导体材料掺入适当的杂质,也能提供载流子。因此实际的半导体中除了与能带对应的电子 共有化状态以外,还有一些电子可以为杂质或者缺陷原子所束缚,束缚电子具有确定的能级,杂质 能级位于带隙中接近导带的位置,在一般温度下即可被激发到导带中,从而对半导体的导电能力产 生大的影响。 设想一个第 IV 族元素 Ge(4 价元素)被一个第 V 族元素 As(5 价元素)所取代的情形,As 原子和 近邻的 Ge 原子形成共价键后尚剩余一个电子。如图 XCH007_000_01~02 所示。
)2
有效质量的计算
——
K k
⋅
K p
微扰法
晶体中电子的波函数可以写成布洛赫波:ψ nk
=
e ikK⋅rK
unk
(
K r
)
电子的布洛赫波满足:
[
K p
2
2m
+V
K (r
)]e
ikK⋅rK
unk
K (r )
固体与半导体物理(第七章)

qV f / k BT
− 1)
V f ↑ ,J f 指数式 ↑
= J S (e
Vf ↑
qV f / k BT
− 1)
势垒高度 ↓
扩散运动 ↑
Jf ↑
(二)反向偏压下p-n结的特性 反向偏压下p 非子的产生 -扩散 -抽取 1.P- 1.P-n结势垒的变化 在反偏下 Vr 与ε同向 势垒区加宽 势垒高度增高 漂移运动大于扩散运动 2.少子的抽取 2.少子的抽取 边界处的少子扫向对方, 边界处的少子扫向对方,体内补充 少子的抽取
2.电势能-qV(x) 电势能- 电势能 势垒区内任一点x 势垒区内任一点x处的电势能
qVD − qV ( x)
E ( x) = −qv( x)
比n区电子的电势能高
−qV (x) − (−qVD ) = qVD − qV (x)
3.势垒区内载流子分布 3.势垒区内载流子分布 (1)势垒区内x处的电子浓度 势垒区内x
A:扩散区长度 A:扩散区长度 ≠ 扩散长度 Lp或Ln B:在该区完成了少子扩散电流 B:在该区完成了少子扩散电流 与多子漂移电流的转换 (3)中性区 (3)中性区 载流子浓度接近平衡值 主要是多子的漂移电流 通过任一截面 电子电流和空穴电流不相等 电流连续性原理 通过任一截面的总电流相等
J = Jn + J p
3.正向 -n结能带图 正向p- 结能带图 正向
平衡p 平衡p-n结能带图
正向偏压下p 正向偏压下p-n结能带图
(1)势垒区和扩散区存在非子 n (1)势垒区和扩散区存在非子 EF ≠ EFp (2)中性区非子基本复合完毕 n (2)中性区非子基本复合完毕 EF = EFp
半导体物理第七章金属和半导体的接触

半导体的导电性能介于金属和绝缘体 之间。其内部存在一个或多个能隙, 使得电子在特定条件下才能跃迁到导 带。常见的半导体材料有硅、锗等。
接触的物理意义
01
金属和半导体的接触在电子器件 中具有重要应用,如接触电阻、 欧姆接触等。
02
理解金属和半导体的接触性质有 助于优化电子器件的性能,如减 小接触电阻、提高器件稳定性等 。
03
肖特基结模型适用于描述金属 和p型半导体之间的接触。
06
金属和半导体的接触实验 研究
实验设备和方法
实验设备
高真空镀膜系统、电子显微镜、 霍尔效应测量仪等。
实验方法
制备金属薄膜,将其与半导体材 料进行接触,观察接触表面的形 貌、电子输运特性等。
实验结果分析
接触表面的形貌分析
通过电子显微镜观察接触表面的微观结构, 了解金属与半导体之间的相互作用。
详细描述
当金属与半导体相接触时,由于金属和半导体的功函数不同,会产生电子的转移。这种电子的转移会 导致在接触区域形成一个势垒,阻碍电子的流动,从而产生接触电阻。接触电阻的大小与金属和半导 体的性质、接触面的清洁度、温度等因素有关。
热导率
总结词
热导率是指材料传导热量的能力,金属 和半导体的热导率差异较大,这会影响 它们之间的热交换效率。
详细描述
欧姆接触的形成需要满足一定的条件,包括金属与半导体之间要有良好的化学相容性和冶金相容性,以及半导体 内部载流子浓度要足够高。欧姆接触在集成电路和电子器件中具有广泛应用。
隧道结
总结词
隧道结是指金属和半导体之间形成的 具有隧道传输特性的结,当外加电压 达到一定阈值时,电流可以通过隧道 效应穿过势垒。
2
这个接触势垒会影响金属和半导体之间的电流传 输和热传导,进而影响电子器件的性能。
半导体物理第七章总结复习_北邮分析

第七章一、基本概念1.半导体功函数: 半导体的费米能级E F 与真空中静止电子的能量E 0的能量之差。
金属功函数:金属的费米能级E F 与真空中静止电子的能量E 0的能量之差2.电子亲和能: 要使半导体导带底的电子逸出体外所需的最小能量。
3. 金属-半导体功函数差o: (E F )s-(E F )m=Wm-Ws4. 半导体与金属平衡接触平衡电势差: q W W V sm D -=5.半导体表面空间电荷区 : 由于半导体中自由电荷密度的限制,正电荷分布在表面相当厚的一层表面层内,即空间电荷区。
表面空间电荷区=阻挡层=势垒层6.电子阻挡层:金属功函数大于N 型半导体功函数(Wm>Ws )的MS 接触中,电子从半导体表面逸出到金属,分布在金属表层,金属表面带负电。
半导体表面出现电离施主,分布在一定厚度表面层内,半导体表面带正电。
电场从半导体指向金属。
取半导体内电位为参考,从半导体内到表面,能带向上弯曲,即形成表面势垒,在势垒区,空间电荷主要有带正电的施主离子组成,电子浓度比体内小得多,因此是是一个高阻区域,称为阻挡层。
【电子从功函数小的地方流向功函数大的地方】7.电子反阻挡层:金属功函数小于N 型半导体功函数(Wm<Ws )的MS 接触,电子从金属流向半导体,半导体表面带负电,金属表面带正电,电场方向指向半导体。
从半导体内到表面,能带下弯曲,半导体表面电子浓度比体内高(N 型反阻挡层)。
8.半导体表面势垒(肖特基势垒)高度:s m s D W W qV qV -=-=9.表面势垒宽度:10.半导体表面势: 取半导体体内为参考电位,半导体表面的势能Vs 。
11 .表面态: 在半导体表面处的禁带中存在着表面态,对应的能级称为表面能级。
表面态一般分为施主型和受主型两种。
若能级被电子占据时呈中性,施放电子后呈正电性,成为施主型表面态;若能级空着的时候为电中性,接收电子后带负电,则成为受主型表面态。
《半导体物理》胡礼中第七章 半导体的接触现象

第七章 半导体的接触现象半导体的接触现象主要有半导体与金属之间的接触(肖特基结和欧姆接触)、半导体与半导体之间的接触(同质结和异质结)以及半导体与介质材料之间的接触。
这一章主要介绍前两种接触现象。
§7-1 外电场中的半导体无外加电场时,均匀掺杂半导体中的空间电荷处处等于零。
当施加外电场时,在半导体中引起载流子的重新分布,从而产生密度为)(r ρ的空间电荷和强度为)(r ∈的电场。
载流子的重新分布只发生在半导体的表面层附近,空间电荷将对外电场起屏蔽作用。
图7-1a 表示对n 型半导体施加外电场时的电路图。
在图中所示情况下,半导体表面层的电子密度增大而空穴密度减小(见图7-1b 、c ),从而产生负空间电荷。
这些空间电荷随着离开样品表面的距离的增加而减少。
空间电荷形成空间电场s ∈,在半导体表面s ∈达到最大值0s ∈(见图7-1d )。
空间电场的存在将改变表面层电子的电势和势能(见图7-1e 、f ),从而改变样品表面层的能带状况(见图7-1g )。
电子势能的变化量为)()(r eV r U -=,其中)(r V 是空间电场(也称表面层电场)的静电势。
此时样品的能带变化为)()(r U E r E c c += (7-1a ))(r E v =)(r U E v + (7-1b )本征费米能级变化为 )()(r U E r E i i += (7-2a )杂质能级变化为 )()(r U E r E d d += (7-2b )由于半导体处于热平衡状态,费米能级处处相等。
因此费米能级与能带之间的距离在表面层附近发生变化。
无外电场时这个距离为(f c E E -)和(v f E E -) (7-3)而外场存在时则为[]f c E r U E -+)( 和-f E [)(r U E v +] (7-4)比较(7-3)和(7-4)式则知,如果E c 和E f 之间的距离减少)(r U ,E f 与E v 之间的距离则增加)(r U 。
半导体物理与器件第七章1

②单边突变结的空间电荷区宽度随低掺杂一边的杂质浓度的增加而 下降,而且内建电势差主要分配在这一区域
当施加外电压时,可推广为:
W
(Vbi
V
)( 2s
e
)(
Na Nd Na Nd
)
7.3 PN结反偏特性
成结后:
电子由n型材料 向p型材料扩散
空穴由p型材料 向n型材料扩散
P区
N区
n区处留下带正 电的施主杂质
p区处留下带负 电的受主杂质
空间电荷区 内建电场
在pn结附近,n区一侧电离施
主形成正电荷区,P区一侧电离受
P
N
主形成负电荷区,两者统称为空 间电荷区,所带电荷为空间电荷
由于空间电荷区中的可动载流
dEFi dx
)
本征费米能级 EFi 与电子的附加电势能 -e(x) 变化一致,即:
dEFi e d(x) eE
dx
dx
则
Jn
nqn
E
1 q
( dEF dx
dEFi dx
)
Jn
nn
dEF dx
同理:
Jp
p p
dEF dx
以上两式说明通过pn结的电流密度与费米能级的变化
有关,对于平衡p-n结,Jn、Jp应均为零
E
子基本处于耗尽状态,因此空
成结后各电流成分:
间电荷区也称作耗尽区。
载流子扩散流:
(J p )扩
eDp
dp(x) dx
(Jn )扩
eDn
dn(x) dx
内建电场导致的漂移电流: (J p )漂 p(x)e p E
半导体物理学第七章

J = J m → s + J s →m
qφns qV = A T exp(− )[exp( ) − 1] k0T k0T
∗ 2
qV = J sT [exp( ) − 1] k0T
与扩散理论得到的J-V形式上是一样的,所不同的是JsT与外加电压无 关,却是一个更强烈依赖于温度的函数。
3、镜像力和隧道效应的影响
接触电阻定义为零偏压下的微分电阻,即
∂I Rs = ∂V V =0
−1
下面估算一下以隧道电流为主时的接触电阻。讨论金属和n型半导体接触的 势垒贯穿问题。将导带底选为电势能的零点。
qN D V ( x) = − ( x − d0 )2 2ε r ε 0
电子的势垒为:
q2 ND −qV ( x) = ( x − d0 )2 2ε r ε 0
2
半导体内电场为零,因而
E ( xd ) = − dV dx
x = xd
=0
金属费米能级除以-q作为电势零点,则有 势垒区中
V (0) = −φns
dV ( x) qN D E ( xd ) = − = ( x − xd ) dx ε rε 0 1 2 V ( x) = ( xxd − x ) − φns ε rε 0 2 qN D
2、接触电势差
设想有一块金属和n型半导体, 它们有共同的真空静止能级。 假定
Wm > Ws
接触前,未平衡的能级
平衡状态的能级
q(Vs' − Vm ) = Wm − Ws Ws − Wm Vms = Vm − V = q
' s
接触电势差
紧密接触
忽略间隙 当 Vms 很小时,接触电势差绝大部分 落在空间电荷区。 金属一边的势垒高度是
半导体物理作业(七)答案

第七章金属和半导体的接触1. 基本概念1)什么是金属的功函数?答:金属费米能级的电子逸出到真空中所需要的能量,即()m F m E E W −=0。
其中E 0:真空中电子的静止能量,(E F )m :金属的费米能。
随着原子序数的递增,金属的功函数呈周期性变化。
2)什么是半导体的电子亲和能?答:半导体导带底的电子逸出到真空中所需要的能量,即C 0E E −=χ。
其中E 0:真空中电子的静止能量,E C :半导体导带底的能量。
3)以金属-n 型半导体接触为例,如果金属的功函数大于半导体的功函数,即W m >W s ,则半导体表面的空间电荷、电场和表面势垒具有什么特点?如果W m >W s ,又如何呢?答:金属-n 型半导体接触,如果W m >W s ,电子从半导体流向金属。
半导体表面形成正的空间电荷区,电场方向由体内指向表面,形成表面势垒。
在势垒区,空间电荷主要由电离施主形成,电子浓度比体内低很多,为高阻区域,称为阻挡层。
如果W m <W s ,电子从金属流向半导体,势垒区电子浓度比体内大很多,为高电导区,称为反阻挡层。
4)什么是表面态对势垒的钉扎?答:表面态密度存在时,即使不与金属接触,表面也会形成势垒。
高的表面态密度,可以屏蔽金属接触的影响,使半导体势垒高度几乎与金属的功函数无关,即势垒高度被高的表面态密度钉扎(pinned )5)为什么金属-n 型半导体接触器件具有整流作用?答:外加电压V ,如果使金属的电势升高,由于n 型半导体高阻挡层为高阻区,外压V 将主要降落在阻挡层,则势垒下降,电阻下降。
反之,如果金属的电势下降,则势垒增高,势垒区电子减少(多子),电阻更高。
因此阻挡层具有类似于pn 结的整流作用。
6)以金属-n 型半导体接触为例,写出势垒宽度大于电子的平均自由程时,其扩散电流密度与电压的关系。
与pn 结的电流密度-电压关系比较,各自具有什么相同和不同的特点?答:金属-n 型半导体接触,扩散电流为⎟⎟⎠⎞⎜⎜⎝⎛−=1kT qV sD e J J ,()T k qVr D D sD D e V V qN J 02/102−⎭⎬⎫⎩⎨⎧−=εεσ 与pn 结的电流密度-电压关系比较,二者均具有单向性的特征;所不同的是,金属-n 型半导体接触的反向电流随外加电压增加呈1/2次方增加,而pn 结的反向电流不随电压变化。
固体物理与半导体物理智慧树知到课后章节答案2023年下浙江大学

固体物理与半导体物理智慧树知到课后章节答案2023年下浙江大学浙江大学第一章测试1.半导体电阻率的范围通常为()Ω·cmA:B:>10C:D:>>10答案:2.半导体的特性包括()A:导通特性B:温度敏感性C:光敏感性D:杂质敏感性答案:温度敏感性;光敏感性;杂质敏感性3.随着温度升高,半导体的电阻率一定升高()答案:错4.半导体材料的电阻率,跨越了非常大的范围,使得我们能够通过各种效应来对它们进行调制,比如,我们可以通过掺杂改变半导体的电阻率()A:对 B:错答案:对5.摩尔定律,是指单位面积的集成电路上晶体管数目,或者说集成电路的集成度,每18个月要增加一倍。
()A:错 B:对答案:对第二章测试1.半导体材料最常见的晶体结构不包括()A:纤锌矿型结构B:闪锌矿型结构C:金刚石型结构D:密堆积结构答案:密堆积结构2.描述晶体结构的最小体积重复单元的是()A:原胞B:晶胞D:基矢答案:原胞3.正四面体的对称操作有()个A:24B:32C:16D:8答案:244.晶体结构的基本特点不包括()A:周期性B:重复性C:各向异性D:单一性答案:各向异性;单一性5.各向异性不是晶体的基本特性之一。
()A:对 B:错答案:错第三章测试1.每个布里渊区的体积均相等,都等于倒格子()的体积。
A:单胞B:原胞C:晶胞D:晶体答案:原胞2.周期性边界条件决定了电子的波矢K在第()布里渊区内可取值数量与晶体的初基元胞数N相等。
A:三B:二C:四D:一答案:一3.布里渊区的特点不包括 ( )A:各个布里渊区的形状都不相同B:各布里渊区经过适当的平移,都可移到第一布里渊区且与之重合C:每个布里渊区的体积都不相等D:晶体结构的布喇菲格子虽然相同,但其布里渊区形状却不会相同答案:每个布里渊区的体积都不相等;晶体结构的布喇菲格子虽然相同,但其布里渊区形状却不会相同4.对于一定的布喇菲晶格,基矢的选择是不唯一的,但是对应的倒格子空间是唯一的。
半导体物理学第七章知识点
第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处的金-半肖特基势垒接触。
金-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之一:§金属半导体接触及其能级图一、金属和半导体的功函数1、金属的功函数在绝对零度,金属中的电子填满了费米能级E F 以下的所有能级,而高于E F 的能级则全部是空着的。
在一定温度下,只有E F 附近的少数电子受到热激发,由低于E F 的能级跃迁到高于E F 的能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够的能量。
所以,金属中的电子是在一个势阱中运动,如图7-1所示。
若用E 0表示真空静止电子的能量,金属的功函数定义为E 0与E F 能量之差,用W m 表示: FM M E E W -=0它表示从金属向真空发射一个电子所需要的最小能量。
W M 越大,电子越不容易离开金属。
金属的功函数一般为几个电子伏特,其中,铯的最低,为;铂的最高,为 eV 。
图7-2给出了表面清洁的金属的功函数。
图中可见,功函数随着原子序数的递增而周期性变化。
2、半导体的功函数和金属类似,也把E 0与费米能级之差称为半导体的功函数,用W S 表示,即FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与金属不同,半导体中费米能级一般并不是电子的最高能量状态。
如图7-3所示,非简并半导体中电子的最高能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电子亲合能。
它表示要使半导体导带底的电子逸出体外所图7-1 金属中的电子势阱图7-2 一些元素的功函数及其原子序数图7-3 半导体功函数和电子亲合能需要的最小能量。
利用电子亲合能,半导体的功函数又可表示为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费米能级与导带底的能量差。
表7-1 几种半导体的电子亲和能及其不同掺杂浓度下的功函数计算值 (eV)二、有功函数差的金属与半导体的接触把一块金属和一块半导体放在同一个真空环境之中,二者就具有共同的真空静止电子能级,二者的功函数差就是它们的费米能级之差,即W M -W S =E FS -E FM 。
半导体物理学第七章知识点
第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处得金-半肖特基势垒接触。
金-半肖特基势垒接触得整流效应就是半导体物理效应得早期发现之一:§7、1金属半导体接触及其能级图一、金属与半导体得功函数1、金属得功函数在绝对零度,金属中得电子填满了费米能级E F 以下得所有能级,而高于E F 得能级则全部就是空着得。
在一定温度下,只有E F 附近得少数电子受到热激发,由低于E F 得能级跃迁到高于E F 得能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够得能量。
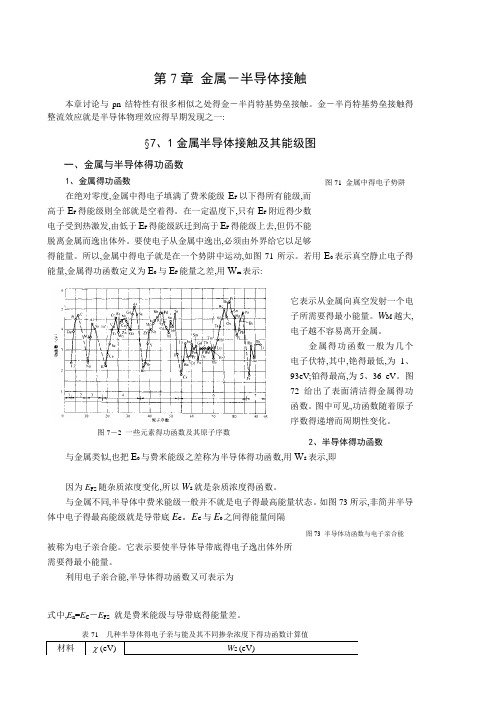
所以,金属中得电子就是在一个势阱中运动,如图71所示。
若用E 0表示真空静止电子得能量,金属得功函数定义为E 0与E F 能量之差,用W m 表示:它表示从金属向真空发射一个电子所需要得最小能量。
W M 越大,电子越不容易离开金属。
金属得功函数一般为几个电子伏特,其中,铯得最低,为1、93eV;铂得最高,为5、36 eV 。
图72给出了表面清洁得金属得功函数。
图中可见,功函数随着原子序数得递增而周期性变化。
2、半导体得功函数与金属类似,也把E 0与费米能级之差称为半导体得功函数,用W S 表示,即因为E FS 随杂质浓度变化,所以W S 就是杂质浓度得函数。
与金属不同,半导体中费米能级一般并不就是电子得最高能量状态。
如图73所示,非简并半导体中电子得最高能级就是导带底E C 。
E C 与E 0之间得能量间隔被称为电子亲合能。
它表示要使半导体导带底得电子逸出体外所需要得最小能量。
利用电子亲合能,半导体得功函数又可表示为式中,E n =E C -E FS 就是费米能级与导带底得能量差。
表71 几种半导体得电子亲与能及其不同掺杂浓度下得功函数计算值 材料 (eV) W S (eV)图71 金属中得电子势阱图7-2 一些元素得功函数及其原子序数 图73 半导体功函数与电子亲合能二、有功函数差得金属与半导体得接触把一块金属与一块半导体放在同一个真空环境之中,二者就具有共同得真空静止电子能级,二者得功函数差就就是它们得费米能级之差,即W M-W S =E FS-E FM。
半导体物理学第七章知识点
第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处的金-半肖特基势垒接触。
金-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之一:§7.1金属半导体接触及其能级图一、金属和半导体的功函数1、金属的功函数在绝对零度,金属中的电子填满了费米能级E F 以下的所有能级,而高于E F 的能级则全部是空着的。
在一定温度下,只有E F 附近的少数电子受到热激发,由低于E F 的能级跃迁到高于E F 的能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够的能量。
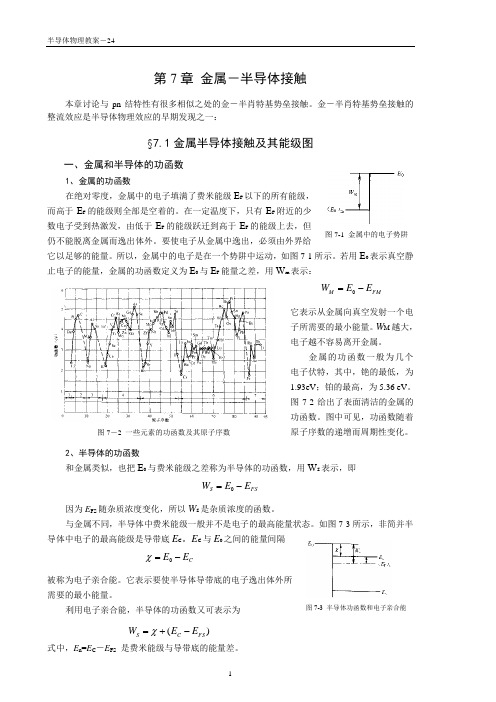
所以,金属中的电子是在一个势阱中运动,如图7-1所示。
若用E 0表示真空静止电子的能量,金属的功函数定义为E 0与E F 能量之差,用W m 表示:FM M E E W -=0它表示从金属向真空发射一个电子所需要的最小能量。
W M 越大,电子越不容易离开金属。
金属的功函数一般为几个电子伏特,其中,铯的最低,为1.93eV ;铂的最高,为5.36 eV 。
图7-2给出了表面清洁的金属的功函数。
图中可见,功函数随着原子序数的递增而周期性变化。
2、半导体的功函数和金属类似,也把E 0与费米能级之差称为半导体的功函数,用W S 表示,即FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与金属不同,半导体中费米能级一般并不是电子的最高能量状态。
如图7-3所示,非简并半导体中电子的最高能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电子亲合能。
它表示要使半导体导带底的电子逸出体外所需要的最小能量。
利用电子亲合能,半导体的功函数又可表示为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费米能级与导带底的能量差。
图7-1 金属中的电子势阱图7-2 一些元素的功函数及其原子序数图7-3 半导体功函数和电子亲合能表7-1 几种半导体的电子亲和能及其不同掺杂浓度下的功函数计算值二、有功函数差的金属与半导体的接触把一块金属和一块半导体放在同一个真空环境之中,二者就具有共同的真空静止电子能级,二者的功函数差就是它们的费米能级之差,即W M -W S =E FS -E FM 。
31_半导体物理学(第四版)第七章(教材)

–若
,金属和n型半导体接触可形成反阻挡层;
–
时,金属和p型半导体接触也能形成反阻挡层,
反阻挡层没有整流作用,可实现欧姆接触
– 实际生产中利用隧道效应的原理,把半导体一侧重掺杂 形成金属—n+n或金属—p+p结构,从而得到理想的欧姆 接触
27
28
29
30
31
pn结一般为0.7V
7.3 少数载流子的注入和欧姆接触
23
24
欧姆接触应满足一下三点: 1.伏安特性近似为线性,且是对称的 2.接触引入的电阻很小 3. 在接触区附近,载流子浓度等于热 平衡的值,即,没有少子注入
25
欧姆接触
• 欧姆接触
– 不产生明显的附加阻抗,而且不会使半导体内部的平衡 载流子浓度发生显著的改变,为非整流接触
10
表面态密度极高,半导体和 金属接触时,只转移表面态 中的电子就可以使整个系 统达到平衡. 即接触前后,半导体一侧的 空间电荷不发生变化,表面 势垒不变,称为钉扎效应或 锁定效应
11
12
7.2 M—S接触的整流理论
13
14
15
16
17
极管的比较
第七章金属和半导体的接触
7.1 M—S接触的势垒模型 7.2 M—S接触的整流理论 7.3 少数载流子的注入和欧姆接触
本章重点: 势垒模型, 整流理论的概念 欧姆接触的性质及特点
1
为什么研究金属与半导体接触? 什么是M-S接触?
2
7.1 M—S接触的势垒模型
3
E0:真空能级
4
5
6
7
8
9
• 相同点
– 单向导电性
• 不同点
– 正向导通时,pn结正向电流由少数载流子的扩散运动 形成,而肖特基势垒二极管的正向电流由半导体的多数 载流子发生漂移运动直接进入金属形成,因此后者比前 者具有更好的高频特性
固体与半导体物理(第七章)

(五)P-n结的载流子分布 P区电势低于n区电势 1.电势V(x) p区: V ( xp ) 0 n区: V ( xn ) VD 势垒区中任一点x的电势V(x)为正值
2.电势能-qV(x) 势垒区内任一点x处的电势能
qVD qV ( x)
E ( x) qv( x)
比n区电子的电势能高
qVD EFn EFp
1 VD ( EFn EFp ) q
k BT nn 0 ln q np0
利用np0 pp0 ni2
VD
注意np0 pn0 ni2
kBT nn 0 p po ln q ni2
常温下,杂质全电离
nn 0 N D
VD
pp0 N A
kBT N D N A ln பைடு நூலகம் ni2
能带在交界面处不连续有一个突变导带底在交界面处的突变价带顶在交界面处的突变而且对所有突变异质结都适用分别称为导带阶和价带阶重要的物理量n型半导体的导带底在界面处形成一向上的尖峰p型半导体的导带底在界面处形成一向下的凹口qvqvqv对于反型异质结交界面两边都是耗尽层2突变np异质结形成突变np异质结之前的能带图形成突变np异质结之后的平衡能带图突变同型异质结能带图1突变nn异质结形成突变nn异质结之前的能带图形成突变nn异质结之后的平衡能带图禁带宽度小的n型半导体一边形成电子的积累层禁带宽度大的n型半导体一边形成电子的耗尽层2突变pp异质结一边是空穴积累层一边是空穴耗尽层二
n
J
1.雪崩击穿
碰撞电离引起载流子倍增
反偏压很大 势垒区电场很强
碰撞电离使载流子浓度急剧增加的效应为载流子倍增效应
2.隧道击穿(齐纳击穿) 在强电场作用下,发生隧道效应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x处的势能比n区势能高0.1ev
室温下:kBT 0.026ev
qVD qV ( x) 0.1ev
n0 ( x) nn 0e0.1/0.026
nn 0 50
(2) qV ( x) 0.6ev
p0 ( x) p p 0e0.6/0.026 1010 p p 0
结区的载流子浓度很小,已经耗尽。-耗尽区
n
J
1.雪崩击穿
碰撞电离引起载流子倍增
反偏压很大 势垒区电场很强
碰撞电离使载流子浓度急剧增加的效应为载流子倍增效应
2.隧道击穿(齐纳击穿) 在强电场作用下,发生隧道效应
A: 势垒高度↑↑ B: 能带很倾斜 C: P区价带顶比n区导带底高 D: A点电子能量和B点电子能量相等 E: p区A点电子有一定几率 穿过禁带进入n区导带的B点 F: x 短到一定程度,大量电子从p区 价带通过隧道穿透,进入n区导带 G: 反向电流↑↑,p-n结发生隧道击穿
三.表面电场效应 1.表面电场 (1)表面态与体内电子态之间交换电子 (2)金属-半导体接触 (3)MOS结构和MIS结构
SiO2
sio2
2.空间电荷层及表面势 (1)EF EF
S
S EF
EF
n型
P型
A:电子从体内转移到表面态 -表面受主态 B:正空间电荷层
C:表面势为 VS
VS 0
D:空间电荷层能带弯曲 电子势垒 空穴势阱
电子从n区到p区,空穴从p区到n区的净扩散流
构成从p区到n区的正向电流
2.载流子在势垒区外的运动 (1)非子的注入
在 x 处存在电子的积累,成为p区的非平衡少数载流子
p
在 xn 处存在空穴的积累,成为n区的非平衡少数载流子 外加电压,使非平衡载流子进入半导体的过程 非子电注入 (2)扩散区
A:扩散区长度 扩散长度 Lp或Ln
p0 ( x) NV e
p0 ( x p ) p p 0
{ EF [ Evp qV ( x )]}/ k BT
p p 0 e qV ( x )/ kBT
p0 ( xn ) pn 0 p p 0 e qVD / kBT
4.估算势垒区内某一处的载流子浓度 (1)假如
qVD 0.7ev
雪崩击穿为主 隧道击穿为主
x 1 (ND )
1 2
{7.2 半导体表面
外 表 面
内 表 面
表面状态的变化会影响半导体器件的稳定性、可靠性 利用表面效应可制作MOS器件、CCD器件、表面发光器件等
一.纯净表面和实际表面 纯净表面 没有杂质吸附层和氧化层的理想表面
(1)超高真空下解理 (2)高温加热 (3)离子轰击 实际表面J r J s [1 e qVr / kB ] Vr
J s -反向饱和电流密度
Jr Js
(三)理想p-n结的电流-电压公式 1.小注入 2.突变耗尽层 3.忽略势垒区中载流子的产生和复合 4.载流子分布满足玻尔兹曼分布
J J s [e
qV / kB
1]
二.表面态 (1)从能带角度
当晶体存在表面,在垂直表面方向成了半无限周期势场
表面存在而产生的附加电子能级 -表面能级 对应的电子能态 -表面态
(2)从化学键角度 表面是原子周期排列终止的地方 未饱和键-悬挂键 纯净表面的表面态密度为 1015 cm2
实际表面的表面态密度 1011 ~ 1013 cm2
J n ( xn )=J n ( x p )
Jn (xp ) q Dn n( x p ) Ln
n( x p ) -x p处非平衡少子电子的浓度
计算J p ( xn )和J n ( x p )归结为计算p( xn )和n( x p )
n( x p )=n p n p 0
平衡p-n结 正向偏压下
3.反向p-n结的能带图
综合正、反偏压下p-n结的能带图
(1)势垒区和扩散区存在非子 正偏
n P EF EF
n P 这两个区 EF EF
n P EF EF
反偏
n P (2) EF 和EF 在扩散区变化
正偏 反偏
n 0, P 0 n 0, P 0
扩散区存在少子注入 扩散区存在少子抽取
q( n p 0 Dn Ln pn 0 D p Lp )(e
qV f / k BT
1)
V f ,J f 指数式
J S (e
Vf
qV f / kBT
1)
势垒高度
扩散运动
Jf
(二)反向偏压下p-n结的特性
非子的产生 -扩散 -抽取
1.P-n结势垒的变化 在反偏下 Vr 与同向 势垒区加宽 势垒高度增高 漂移运动大于扩散运动 2.少子的抽取 边界处的少子扫向对方,体内补充 少子的抽取
正偏
反偏
2.扩散电容
发生在扩散区
扩散区的电荷数量随 外加电压的变化所产生的电容效应
3.说明 (1)电容值随外加电压变化 可变电容 (2)反偏时,势垒电容为主,扩散电容很小 正偏时,既有势垒电容,也有扩散电容 (3)势垒电容效应明显,扩散电容效应不明显
四.p-n结击穿
VB -击穿电压
J n qnn
B:在该区完成了少子扩散电流 与多子漂移电流的转换
(3)中性区
载流子浓度接近平衡值
主要是多子的漂移电流 通过任一截面 电子电流和空穴电流不相等 电流连续性原理 通过任一截面的总电流相等
J Jn J p
3.正向p-n结能带图
平衡p-n结能带图
正向偏压下p-n结能带图
n (1)势垒区和扩散区存在非子 EF EFp
qVD EFn EFp
1 VD ( EFn EFp ) q
k BT nn 0 ln q np0
利用n p 0 p p 0 ni2
VD
注意n p 0 pn 0 ni2
k BT nn 0 p po ln q ni2
常温下,杂质全电离
nn 0 N D
VD
pp0 N A
第七章 半导体器件物理基础
P-n结 金属-半导体接触
{7.1
P-n结
P-n结的形成 单向导电性 同种材料形成的P-n结 -同质结 不同种材料形成的P-n结 -异质结 一.平衡P-n结 (一) P-n结的杂质分布
pn
p n Ge Ge p n Si Si p n Ge Si
Ga As Ga P
n p 0 nn 0e qVD / kBT
势垒从qVD q(VD V f )
n p nn e
[ q (VD V f )]/ k BT
nn 0e qVD / kBT e
nn nn 0 nn
qV f / k BT
忽略nn
qV f / k BT
nn nn 0
nn 0e[ qVD qV ( x )]/ kBT
V ( xn ) VD
n0 ( xn ) nn 0
n0 ( x) nn 0e[ qVD qV ( x )]/ kBT
V ( xp ) 0
n0 ( x p ) n p 0 nn 0e qVD / kBT
(2)势垒区内x处的空穴浓度
VD
qVD EFn EFp
势垒区
空间电荷区
结区
同为一区域
VD 与哪些因素有关?
( E E )/ k T n区平衡电子浓度 nn 0 NC e C Fn B
P区平衡电子浓度 n p 0 N C e ( EC EFp )/ kBT
nn 0 ( E E )/ k T e Fn Fp B np0 nn 0 1 ln ( EFn EFp ) n p 0 k BT
n p n p 0e
n( x p )=n p n p 0 n p 0 [e qV
f
/ k BT
1]
同样
p( xn ) pn 0 [eqV
f
/ k BT
1]
J f J n ( x p ) J p ( xn )
Dp Dn qV f / k BT qV / k T q n p 0 (e 1) q pn 0 (e f B 1) Ln Lp
V V f 0 J J f 0 从p区流向n区的正向电流
V Vr 0 J J r 0 从n区流向p区的反向电流
实际p-n结的电流-电压公式与理想有较大的偏差
三.p-n结电容 “存”“放”电荷的特性 1.势垒电容 发生在势垒区
势垒区的空间电荷数量随 外加电压的变化所产生的电容效应
比n区电子的电势能高
qV ( x) (qVD ) qVD qV ( x)
3.势垒区内载流子分布 (1)势垒区内x处的电子浓度
Ecn [ qVD qV ( x )] EF / k BT
n0 ( x) NC e
NC e[ Ecn EF ]/ kBT e[ qVD qV ( x )]/ kBT
二.非平衡p-n结
正向
反向
P-n结的伏安特性
P-n结的单向导电性是因为势垒的存在 (一)正向偏压下p-n结的特性
非子的注入 -扩散 -复合
1.p-n结势垒的变化
外加正向偏压V f 与自建场 反向
势垒高度降低 qVD q(VD V f )
势垒宽度变窄
载流子的扩散运动大于漂移运动
n型 (2)EF EF
S
P型
n型
P型
A:电子从表面态转移到体内 -表面施主态 B:负空间电荷层 C:表面势
VS 0
D:电子势阱 空穴势垒
电子 势阱
