黄金分割法编程
大智慧黄金分割线主图指标公式编程思路破译和风险提示

大智慧黄金分割线主图指标公式编程思路破译和风险提示DRAWGBKLAST(成交量(手)>1,STRIP(自定色,自定色,0))输出AH:HHVALL(最高价)输出 AL:LLVALL(最低价)AHL赋值:AH-AL输出A19:AL+AHL*0.191,COLORAAAAAA输出A38:AL+AHL*0.382,COLOR00AAAA输出A50:AL+AHL*0.500,线宽为1,POINTDOT,画绿色输出A61:AL+AHL*0.618,COLOR00AAAA输出A80:AL+AHL*0.809,COLORAAAAAAY赋值:999DRAWTEXTREL(0,0,'100% '+AH),COLORAAAAAA DRAWTEXTREL(0,Y*0.191,'0.809% '+A80),COLORAAAAAA DRAWTEXTREL(0,Y*0.382,'0.618% '+A61),COLOR00AAAA DRAWTEXTREL(0,Y*0.500,'0.50% '+A50),COLOR00AAAA DRAWTEXTREL(0,Y*0.618,'0.382% '+A38),COLOR00AAAA DRAWTEXTREL(0,Y*0.809,'0.191% '+A19),COLORAAAAAA DRAWTEXTREL(0,Y-30,'最高 '+AH),COLORAAAAAA DRAWTEXTREL(900,0,'100% '+AH),COLORAAAAAA DRAWTEXTREL(900,Y*0.191,'0.809% '+A80),COLORAAAAAA DRAWTEXTREL(900,Y*0.382,'0.618% '+A61),COLOR00AAAA DRAWTEXTREL(900,Y*0.500,'0.50% '+A50),COLOR00AAAA DRAWTEXTREL(900,Y*0.618,'0.382% '+A38),COLOR00AAAA DRAWTEXTREL(900,Y*0.809,'0.191% '+A19),COLORAAAAAA DRAWTEXTREL(900,Y-30,'最高 '+AH),COLORAAAAAAW赋值:上次DISPSTATUS=1距今天数P赋值:若DISPSTATUS=2则将最近W/2+1周期置为1 VERTLINE(P上穿0.5,4),COLOR889999 DRAWTEXTREL(500,0,'最高' ),画红色DRAWTEXTREL(500,900+76,'最低'),COLOR00FF00DRAWTEXTREL(500,0.50*(900+76),'0.5'),COLOR0099FFDRAWTEXTREL(500,0.191*(900+76),'0.809'),画黄色DRAWTEXTREL(500,0.382*(900+76),'0.618'),画黄色DRAWTEXTREL(500,0.618*(900+76),'0.382'),画黄色DRAWTEXTREL(500,0.809*(900+76),'0.191'),画黄色RSV赋值:(((收盘价 - 13日内最低价的最低值) / (13日内最高价的最高值 - 13日内最低价的最低值)) * 100)K赋值:RSV的3日[1日权重]移动平均D赋值:K的3日[1日权重]移动平均J赋值:((3 * K) - (2 * D))RSV24赋值:(((收盘价- 55日内最低价的最低值) / (55日内最高价的最高值 - 55日内最低价的最低值)) * 100)K24赋值:RSV24的3日[1日权重]移动平均D24赋值:K24的3日[1日权重]移动平均J24赋值:((3 * K24) - (2 * D24))压力位赋值:如果J24上穿J,返回最高价,否则返回上次J24上穿J 距今天数日前的最高价支撑位赋值:如果J上穿J24,返回最低价,否则返回上次J上穿J24距今天数日前的最低价TJ赋值:如果(收盘价-1日前的收盘价)/1日前的收盘价>0.025,返回1,否则返回0YL赋值:如果收盘价>上次TJ=1距今天数日前的开盘价,返回上次TJ=1距今天数日前的开盘价,否则返回0FT赋值:上次YL距今天数YLX赋值:FT日前的YLBT赋值:如果收盘价<OPENANDREF(收盘价,1)>1日前的开盘价,返回1日前的收盘价,否则返回0XFT赋值:上次BT距今天数XYLX赋值:XFT日前的BT平台调下赋值:XYLX上穿收盘价平台突破赋值:收盘价上穿YLXVAR2赋值:1日前的最低价VAR3赋值:最低价-VAR2的绝对值的13日[1日权重]移动平均/最低价-VAR2和0的较大值的13日[1日权重]移动平均*100 VAR4赋值:如果收盘价*1.2,返回VAR3*13,否则返回VAR3/13的13日指数移动平均VAR5赋值:34日内最低价的最低值VAR6赋值:34日内VAR4的最高值VAR7赋值:如果56日内最低价的最低值,返回1,否则返回0VAR8赋值:如果最低价<=VAR5,返回(VAR4+VAR6*2)/2,否则返回0的3日指数移动平均/618*VAR7主力进场赋值:VAR8>1日前的VAR8进场赋值:1日前的主力进场当满足条件进场AND平台突破时,在最低价*0.97位置书写文字,ALIGN1,COLOR0000FF当满足条件进场AND平台突破时,在最低价*0.94位置书写文字,ALIGN1,COLOR0000FF当满足条件进场AND平台突破ANDL=支撑位时,在最低价*0.93位置画1号图标,ALIGN1,VALIGN2风险提示该公式包含未来函数:BACKSET。
黄金分割法python代码

黄金分割法python代码黄金分割法是一种古老而神秘的比例,它可以在许多不同的领域中发挥作用。
在数学上,它是一种简单而优美的比例,被广泛用于建筑、绘画和美学等领域。
在计算机科学中,黄金分割法也被用于优化算法的设计,特别是在搜索和排序方面。
本文将介绍黄金分割法的定义、性质和应用,并提供Python代码实现。
1. 黄金分割法的定义黄金分割法是指将一条线段分割成两部分,使其中一部分与整条线段的比例等于另一部分与这部分的比值相等,即A/B = B/(A+B)。
这个比例被称为黄金比例,也被称为“神圣的比例”。
黄金比例的近似值是1.61803398875,它是一个无限不循环的小数,也是一个无理数。
黄金比例的近似值可以通过求解方程x^2=x+1来得到,其中x是黄金比例的值。
这个方程的正根就是黄金比例的值。
2. 黄金分割法的性质黄金分割法有许多有趣的性质,其中一些包括:(1)黄金比例的平方等于黄金比例加1,即φ^2=φ+1;(2)黄金比例的倒数等于黄金比例减1,即1/φ=φ-1;(3)黄金比例是一种最优比例,它可以使得两个部分的比例在视觉上感觉最为和谐和美丽。
3. 黄金分割法的应用黄金分割法在建筑、绘画、美学等领域中有广泛的应用。
例如,在建筑中,黄金分割法可以用来设计建筑物的比例和比例关系,以创造出最美丽的效果。
在绘画中,黄金分割法可以用来设计画面的比例和构图,以创造出最和谐的效果。
在美学中,黄金分割法可以用来评估和设计美的标准。
在计算机科学中,黄金分割法也有着广泛的应用。
特别是在搜索和排序算法中,黄金分割法被用于优化算法的设计。
例如,在二分查找算法中,可以将搜索区间按照黄金比例分割,以减少搜索次数和时间复杂度。
在排序算法中,可以将数组按照黄金比例分割成多个子数组,然后使用递归算法进行排序,以减少排序时间和空间复杂度。
4. Python代码实现以下是使用Python实现黄金分割法的代码,其中使用了递归算法来计算黄金比例的近似值。
黄金分割法C程序源代码

t=(t1+t2)/2; b=t2;
t2=t1; f2=f1; t1=a+b-t2;
f1=f(t1); }
else { a=t1; t1=t2; f1=f2; t2=a+beta*(b-a); f2=f(t2); } } k++;
} t=(t1+t2)/2; printf("\nt=%lf",t); return t; }
*a=t<t1?t:t1; *b=t>t1?t:t1; break; } } t1=t0+h; f1=f(t1); } }
double hjfg() { double beta,t1,t2,t; double f1,f2; double a=0,b=0; double *c,*d; int k=0; c=&a,d=&b; sb(c,d); printf("\n[a,b]=[%lf,%lf]",a,b);
#include<stdio.h> #include<math.h> #define f(t) (8*pow(t,3)-2*pow(t,2)-7*t+3) #define eps pow(10,-6)
void sb(doቤተ መጻሕፍቲ ባይዱble *a,double *b) { double t0,t1,t,h,alpha,f0,f1; int k=0; printf("请输入初始点 t0="); scanf("%lf",&t0); printf("\n 请输入初始步长 h="); scanf("%lf",&h); printf("\n 请输入加步系数 alpha(需大于 1)="); scanf("%lf",&alpha); f0=f(t0); t1=t0+h; f1=f(t1); while(1) {
内蒙古科技大学进退发黄金分割法二次插值法编程

进退法试用进退法确定函数f(x)=3x2+8x+9的初始单峰区间,设定给定的初始值x0=0,初始步长h=0.1。
#include <math.h>#include <stdlib.h>#include <stdio.h>main(){float x0=0,x1,x2;float h=0.1;double f1,f2;printf("请输入初始点,初始步长。
\n");/*scanf("%f%f\n",&x0,&h);*/x1=x0;x2=x1+h;printf("%f,%f\n",x1,x2);f1=3*pow(x1,2)-8*x1+9;f2=3*pow(x2,2)-8*x2+9;printf("%f,%f\n",f1,f2);if(f1>f2) {ss:h=2*h;x2=x2+h;f1=f2;f2=3*pow(x2,2)-8*x2-9;if(f2>f1)printf("区间是%f,%f\n",x1,x2);else {x1=x2-h;if(f1==f2)printf("区间是%f,%f\n",x1,x2);else goto ss;}}else{if(f2==f1)printf("区间是%f,%f\n",x1,x2);else{h=-h/4;kk: x1=x1+h;f2=f1;f1=3*pow(x1,2)-8*x1-9;if(f2<f1)printf("区间是%f,%f\n",x1,x2);else{x2=x1-h;if(f1=f2)printf("区间是%f,%f\n",x1,x2);else{h=2*h;goto kk;}}}}}输出正确结果:(0.7,3.1)黄金分割法试用黄金分割法求一元函数minf(x)=x2+6x+9的最优解。
黄金分割法求极小的MATLAB程序

end
end
error('iteration exceeds the limitation');
Fibonacci法求极小的MATLAB程序
function [x,y] = Fibo(f,a,b,n)
% F2=round(sqrt(5)*(0.5*(1+sqrt(5)))^(n+1)*0.2);F1=round(sqrt(5)*(0.5*(1+sqrt(5)))^(n)*0.2);
***[JimiSoft: Unregistered Software ONLY Convert Part Of File! Read Help To Know How To Register.]***
y=yd; % 其函数值yd作为x点的函数值。
else %当离a 较近点x的函数值y小于离b较近的点d的函数值yd时。去掉含
% 端点b的一段区间,得区间 [a,d], 但由于现在x离 d点较近,所以
b=a; %令a 为端点b
a=d; 令d为端点a
F1=.44721359549995793928*1.6180339887498949025^n; F2=F1*1.6180339887498949025;
F1=round(F1); F2=round(F2);
h=(b-a)/F2; % 均分区间
x=b-h*F1; % x 是离端点 a 较近的试探点
PAGE 1
x=b-(b-a)*golden; % x是离端点a较近的试探点
y=feval(f,x); % 求x的函数值y
for k=1:maxsearch % 作最大叠代次数为maxsearch的循环。
最优化方法三分法+黄金分割法+牛顿法

最优化⽅法三分法+黄⾦分割法+⽜顿法最优化_三等分法+黄⾦分割法+⽜顿法⼀、实验⽬的1. 掌握⼀维优化⽅法的集中算法;2. 编写三分法算法3. 编写黄⾦分割法算法4. 编写⽜顿法算法⼆、系统设计三分法1.编程思路:三分法⽤于求解单峰函数的最值。
对于单峰函数,在区间内⽤两个mid将区间分成三份,这样的查找算法称为三分查找,也就是三分法。
在区间[a,b]内部取n=2个内等分点,区间被分为n+1=3等分,区间长度缩短率=1 3 .各分点的坐标为x k=a+b−an+1⋅k (k=1,2) ,然后计算出x1,x2,⋯;y1,y2,⋯;找出y min=min{y k,k=1,2} ,新区间(a,b)⇐(x m−1,x m+1) .coding中,建⽴left,mid1,mid2,right四个变量⽤于计算,⽤新的结果赋值给旧区间即可。
2.算法描述function [left]=gridpoint(left,right,f)epsilon=1e-5; %给定误差范围while((left+epsilon)<right) %检查left,right区间精度margin=(right-left)/3; %将区间三等分,每⼩段长度=marginm1=left+margin; %left-m1-m2-right,三等分需要两个点m2=m1+margin; %m2=left+margin+marginif(f(m1)<=f(m2))right=m2; %离极值点越近,函数值越⼩(也有可能越⼤,视函数⽽定)。
else %当f(m1)>f(m2),m2离极值点更近。
缩⼩区间范围,逼近极值点left=m1; %所以令left=m1.endend %这是matlab的.m⽂件,不⽤写return.黄⾦分割法1.编程思路三分法进化版,区间长度缩短率≈0.618.在区间[a,b]上取两个内试探点,p i,q i要求满⾜下⾯两个条件:1.[a i,q i]与[p i,b i]的长度相同,即b i−p i=q i−a i;2.区间长度的缩短率相同,即b i+1−a i+1=t(b i−a i)]2.算法描述⾃⼰编写的:function [s,func_s,E]=my_golds(func,left,right,delta)tic%输⼊: func:⽬标函数,left,right:初始区间两个端点% delta:⾃变量的容许误差%输出: s,func_s:近似极⼩点和函数极⼩值% E=[ds,dfunc] ds,dfunc分别为s和dfunc的误差限%0.618法的改进形式:每次缩⼩区间时,同时⽐较两内点和两端点处的函数值。
黄金分割法

黄金分割法学习目标➢理解单谷函数及其性质➢理解黄金分割法的基本原理➢掌握黄金分割法的步骤➢编程实现黄金分割法黄金分割法也叫0.618法,属于区间收缩方法。
首先找出包含极小点的初始搜索区间,然后按黄金分割点通过对函数值的比较不断缩小搜索区间。
当然,要保证极小点始终在搜索区间内,当区间长度小到精度范围之内时,可以粗略地认为区间中点为极小点的近似值。
黄金分割法适用于单谷函数,即在某一区间中存在唯一极小点的函数。
f (x )O a 1 x * b 1 x一、单谷函数及其性质定义1设单变量函数f(x)在区间a 1,b 1内存在唯一的极小点x ∗,x ∗∈a 1,b 1,且f(x)在x ∗点的左侧严格下降,在x ∗点的右侧严格上升,则称f(x)在区间a 1,b 1上是单谷函数或者下单峰函数,a 1,b 1为f(x)的单谷区间,见图1。
图1 单谷区间与单谷函数单谷函数具有一个重要的消去性质(I) 若f(a) < f(b), x *∈[a1,b]f(x)xa 1b 1(I) 消去[b, b 1]x *b a (II )若f(a)≥f(b),x *∈[a,b 1]f(x)xa 1b 1(II) 消去[a 1, a ]x *a b单谷区间与单谷函数有如下性质:若f(x)是单谷区间a1,b1上的单谷函数,极小点为x∗,在a1,b1任取两点a和b,且a<b,计算这两点的函数值f(a)和f(b),则:(1)当f a<f(b)时,x∗∈a1,b。
(2)当f a≥f(b)时,x∗∈a,b1。
由单谷函数的性质可知:➢在单谷区间a1,b1内任取两点a和b都可以求得一个相对更小的单谷区间。
➢这个过程可以一直重复下去,如果某个单谷区间的长度足够小,该区间的中点就可以作为极小点的近似。
二、黄金分割法的基本原理设计思路:反复使用单谷函数的消去性质,不断缩小包含极小点的搜索区间,直到满足精度为止。
设计原则:(1)迭代公式简单;(2)消去效率高;(3)对称性:a−a1=b1−b;(4)保持缩减比,即保留的区间长度与原区间长度之比保持不变。
黄金分割法及程序设计求解
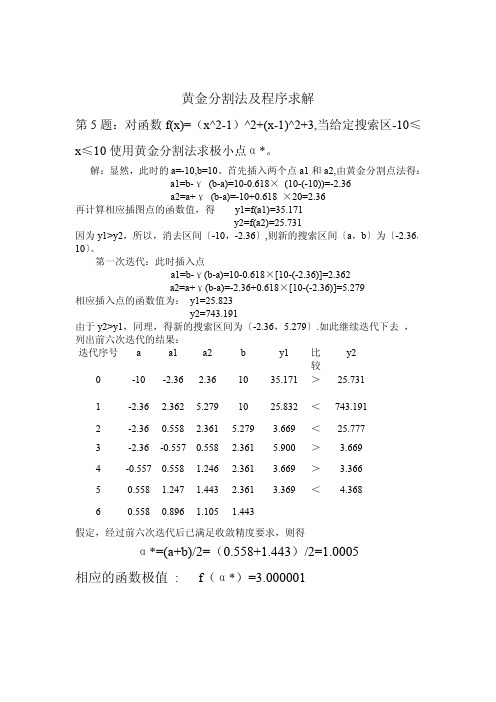
黄金分割法及程序求解第5题:对函数f(x)=(x^2-1)^2+(x-1)^2+3,当给定搜索区-10≤x≤10使用黄金分割法求极小点α*。
解:显然,此时的a=-10,b=10。
首先插入两个点a1和a2,由黄金分割点法得:a1=b-γ(b-a)=10-0.618×(10-(-10))=-2.36a2=a+γ(b-a)=-10+0.618×20=2.36再计算相应插图点的函数值,得y1=f(a1)=35.171y2=f(a2)=25.731因为y1>y2,所以,消去区间〔-10,-2.36〕,则新的搜索区间〔a,b〕为〔-2.36,10〕。
第一次迭代:此时插入点a1=b-γ(b-a)=10-0.618×[10-(-2.36)]=2.362a2=a+γ(b-a)=-2.36+0.618×[10-(-2.36)]=5.279相应插入点的函数值为:y1=25.823y2=743.191由于y2>y1,同理,得新的搜索区间为〔-2.36,5.279〕.如此继续迭代下去,列出前六次迭代的结果:y2迭代序号a a1a2b y1比较0-10-2.36 2.361035.171>25.7311-2.36 2.362 5.2791025.832<743.1912-2.360.558 2.361 5.279 3.669<25.7773-2.36-0.5570.558 2.361 5.900> 3.6694-0.5570.558 1.246 2.361 3.669> 3.36650.558 1.247 1.443 2.361 3.369< 4.36860.5580.896 1.105 1.443假定,经过前六次迭代后已满足收敛精度要求,则得α*=(a+b)/2=(0.558+1.443)/2=1.0005相应的函数极值:f(α*)=3.000001运用MATLB程序求解:建立m文件:function[x,minf]=minHJ(f,a,b,k) format long;if nargin==3eps=0.000001;enda1=b-0.618*(b-a);a2=a+0.618*(b-a);k=1;tol=b-a;while tol>eps&&k<100000fa1=subs(f,findsym(f),a1);fa2=subs(f,findsym(f),a2);if fa1>fa2a=a1;a1=a2;a2=a+0.618*(b-a);else b=a2;a2=a1;a1=b-0.618*(b-a);endk=k+1;tol=abs(b-a);endif k==100000disp('找不到最小值');x=NaN;minf=NaN;return;endkx=(a+b)/2minf=subs(f,findsym(f),x)format short函数文件:syms x;f=(x^2-1)^2+(x-1)^2+3;[x,minf]=minHJ(f,-10,10);运行结果:k=36k=36x=1.000004289112507 minf=3.000000000091983。
黄金分割法进退法求极小值matlab程序

%%%%%%%%%%%%%%%%%%%%%%%%%%-----进退法求合适区间-------%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear;syms x; %创建一个符号变量h=diff(f(x),x); %求对x的一阶导数x0=10;g=subs(h,x0); %在x0处h的值%%%%%%%%---------初始值在极小值点左侧的时候-------%%%%%%%%%%%%%%%%%%%%%%%%%%%%%if g<0step=10;x1=x0+step;if f(x1)<=f(x0)step=2*step;x2=x1+step;while f(x1)>f(x2)x0=x1;x1=x2;step=2*step;x2=x1+step;endelsestep=0.5*step;x2=x1-step;while f(x0)>f(x2)x0=x0+0.5*step;x2=x2+step;endenda=x0;b=x2;disp(['f(x)极小值点所在区间为(',num2str(a),',',num2str(b),')']);end%%%%%%%%%%%%%%%%%%%%当极小值点在初始点右侧时%%%%%%%%%%%if g>0step=6;x1=x0-step;%以下方法仅仅适用于初始值在极小值点右侧的时候if f(x1)<=f(x0)step=2*step;x2=x1-step;while f(x1)>f(x2)x0=x1;x1=x2;step=2*step;x2=x1-step;endstep=0.5*step;x2=x1+step;while f(x0)>f(x2)x0=x0-0.5*step;x2=x2-step;endenda=x2;b=x0;disp(['f(x)极小值点所在区间为(',num2str(a),',',num2str(b),')']);end%%%%%%%%%%%%%%%%%%%%----------当极小值点就是初始点时---------------%%%%%%%%%%%if g==0xm=x0;fm=f(x0);disp(['使用黄金分割法可得到f(x)在xm=',num2str(xm),'处取最小值fm=',num2str(fm)]);end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%-----黄金分割法求极值-------%%%%%%%%%%%%%%%%%%%%%%%%%%%%%e=10^(-6);x2=a+0.618*(b-a);f2=f(x2);x1=a+0.382*(b-a);f1=f(x1);while abs(b-a)>eif f1<f2b=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);f1=f(x1);else if f1==f2a=x1;b=x2;x2=a+0.618*(b-a);f2=f(x2);x1=a+0.382*(b-a);f1=f(x1);elsea=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);f2=f(x2);endendxm=0.5*(b+a);fm=f(xm);disp(['使用黄金分割法可得到f(x)在xm=',num2str(xm),'处取最小值fm=',num2str(fm)]);自定义函数程序为:function y=f(x)y=3*x^2+2*x+5;%y=10*x^2+15*x+7;运行结果为:f(x)极小值点所在区间为(-8,10)使用黄金分割法可得到f(x)在xm=-0.33334处取最小值fm=4.6667。
优化算法之黄金分割算法-Matlab

优化算法之黄金分割算法-Matlab黄金分割算法适用于一元函数f(x)在给定区间[a, b]内搜索极小点的问题。
其基本原理为: 按照黄金分割比例原则逐步缩小搜索区间, 可类比二分法, 二分法是取a和b的中点逐渐缩小搜索空间, 而黄金分割算法是取a和b的黄金分割点。
一、Matlab脚本文件在此文件进行相应修改,然后运行即可。
% 1.设置要求的目标函数和搜索区间syms x; %定义x为自变量y = (x-1)^2 + 1; %要求的目标函数a = 0.1;b = 2; %a,b为搜索区间epsilon = 1e-3; %epsilon为收敛精度% 2.调用黄金分割算法函数求解[best_x, best_y] = golddiv(y, x, a, b,epsilon)二、黄金分割算法的函数文件function [best_x, best_y] = golddiv(y, x,a, b, epsilon)% 本函数实现黄金分割算法% y是目标函数, x是自变量, a,b为区间范围, epsilon为精度% best_x为黄金分割算法找到的最优点% best_y为最优点处的函数值if nargin == 4 %如果输入参数没有精度要求epsilon=0.001; %设置默认的epsilonendx1 = a + 0.382 * (b - a); %根据黄金分割比例确定搜索点f1 = subs(y, x, x1); %函数y在x1处的值x2 = a + 0.618 * (b - a); %根据黄金分割比例确定搜索点f2 = subs(y, x, x2); %函数y在x2处的值while(abs(b - a) > epsilon)if f1 < f2="">b = x2; %b为新的右边界x2 = x1; %更新x2值f2 = f1;x1 = a + 0.382 * (b - a); %更新x1值f1 = subs(y, x, x1);elsea = x1;x1 = x2;f1 = f2;x2 = a + 0.618 * (b - a);f2 = subs(y, x, x2);endendbest_x = (a + b) / 2; %最优的x值取a 和b的平均值best_y = subs(y, x, best_x); %最优的函数值end。
黄金分割法求最优解

printf("经过%d次迭代后:\n在给定区间内,最优解为x=%lf,f(x)=%lf",n,x,fun(x,k,i));
getch();
return 0;
}
double fun(double x,double k[],int m)
{
double sum=0,y;
int i=0,j,flag=1;
{
double k[S]={60,-6,4,-5,1};
double a,b,c,x,x1,x2,y1,y2,e=0.618;
int i,j,n=0;
printf("黄金分割法求最优解by lin\n");
printf("函数的最高阶次为几次?");
scanf("%d",&i);
for(j=i;j>=0;j--)
y2=fun(x2,k,i);
do
{
if(y1>=y2)
{
a=x1;x1=x2;y1=y2;
x2=a+e*(b-a);y2=fun(x2,k,i);
}
else
{
b=x2;x2=x1;y2=y1;
x1=b-e*(b-a);y1=fun(x1,k,i);
}
n+Biblioteka ;}while(abs((b-a)/b)>=c||abs((y2-y1)/y2)>=c);
for(i=0;i<=m;i++)
sum=sum+k[i]*pow(x,i);
return sum;
}
求解课本P2591-(2)题:
机械优化黄金分割法程序设计

机械优化黄金分割法程序设计机械优化黄金分割法程序设计1.黄金分割法介绍黄金分割法适用于[a,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
因此,这种方法的适应面非常广。
黄金分割法也是建立在区间消去法原理基础上的试探方法,即在搜索区间[a,b]内适当插入两点a1,a2,并计算其函数值。
a1,a2将区间分成三段,应用函数的单谷性质,通过函数值大小的比较,删去其中一段,是搜索区间得以缩小。
然后再在保留下来的区间上作同样的处理,如此迭代下去,是搜索区间无限缩小,从而得到极小点的数值近似解。
1.1黄金分割法原理一维搜索是解函数极小值的方法之一,其解法思想为沿某一已知方向求目标函数的极小值点。
一维搜索的解法很多,这里主要采用黄金分割法(0.618法)。
该方法用不变的区间缩短率0.618代替斐波那契法每次不同的缩短率,从而可以看成是斐波那契法的近似,实现起来比较容易,也易于人们所接受。
黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。
它是优化计算中的经典算法,以算法简单、收敛速度均匀、效果较好而著称,是许多优化算法的基础,但它只适用于一维区间上的凸函数[6],即只在单峰区间内才能进行一维寻优,其收敛效率较低。
其基本原理是:依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。
具体步骤是:在区间[a,b]内取点:a1 ,a2 把[a,b]分为三段。
如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+r*(b-a);如果f(a1)黄金分割法:黄金分割法适用于确定区间上的任何单谷函数求极小值的问题。
对函数除要求“单谷”之外没有任何其他要求。
1. 给出初始搜索区间,及收敛精度将其赋以0.618。
2. 计算a1和a2,并计算起对应的函数值y1,y2。
3. 根据期间消去法原理缩短搜索区间,为了能用原来的坐标点计算公式,需进行区间名称的代换,并在保留区间中计算一个新的试验点及其函数值。
第三章—黄金分割法

黄金分割法迭代次数与精度研究function [ x,fval,iter] = gold_section_method(a,b,d) %黄金分割法主程序%x 极致点%fval 函数极值%iter 迭代次数%a b 搜索区间%d 精度iter=0;while abs(b-a)>diter = iter+1;x1=a+0.382*(b-a);x2=a+0.618*(b-a);f1=Function1(x1);f2=Function1(x2);if f1>f2a=x1;elseb=x2;endendx=(a+b)/2;fval = Function1(x);end算例函数fval = x^3-1;fval = x^4-1;fval = x^5-1;结果分析:表一算例结果表一为算例计算结果,通过查表可知:1.计算精度越小,迭代次数越多。
2.在相同精度、搜索区间条件下,仅修改算例对迭代次数无影响。
3.计算精度减小10倍,迭代次数增加5次左右。
这种收敛表现与黄金分割法的缩小区间比例有关。
下面为对特点3进行简单的推导:迭代一次,区间长度由l变为0.618l,当取精度为ε,计算迭代次数为k,此时的条件为:b a ε-<此时对精度进行调节'0.1εε=则迭代次数需增加p ,使得:()(0.618)0.1p b a ε-⨯<又 b a ε-<p ⇒≈5上述推导过程证明了黄金分割法的迭代次数与精度关系,同时也说明黄金分割法的收敛速度是均匀的。
黄金分割法子程序

附录Ⅱ黄金分割法子程序int golden(double a,double b,double e,double x[1],double y[1])/*返回区间消去的次数:初始区间[a,b],收敛精度e,最优点x,最优解y*/{int k=0;double x1,x2,y1,y2; /*黄金分割点及其函数值*/x1=a+0.382*(b-a);y1=func(x1);x2=a+0.618*(b-a);y2=func(x2);for(;;) /*区间消去的计算循环*/{k=k+1; /*区间消去的次数*/if(y1<y2){ /*消去右边*/b=x2;x2=x1;y2=y1;/*原右分割点为右端点,原左分割点为新的右分割点*/ x1=a+0.382*(b-a); /*计算新的左分割点及其目标函数值*/y1=func(x1);}else /*消去左边*/{a=x1;x1=x2;y1=y2; /*原左分割点为左端点,原右分割点为新的左分割点*/x2=a+0.618*(b-a); /*计算新的右分割点及其目标函数值*/y2=func(x2);fprintf(fp,"\nNew golden point2 %12.5e %12.5e",x2,y2);}if((b-a)<e) /*如果达到收敛精度要求则结束寻优*/{x[0]=0.5*(a+b);y[0]=func(x[0]);if(y[0]>y1){x[0]=x1;y[0]=y1;}if(y[0]>y2){x[0]=x2;y[0]=y2;}return(k);}}/*结束区间消去大循环*/}/*结束一维黄金分割法子程序*/int main()/*主程序*/{int i,j,k=0;double x[3],y[3],h,e,a,b,x_=0,y_=0;/*区间的三点及其目标函数值,初始步长,收敛精度值e,区间端点a、b,最优点、解*/x[0]=-1; /*初始点*/h=0.1; /*初始步长*/k=JT(x,h);/*进退法确定区间子程序(返回计算目标函数值的次数)*/e=0.02; /*收敛精度值*/a=x[0]; b=x[2];k=golden(a,b,e,x_,y_);/*黄金分割法子程序(返回区间消去的次数)*/printf("\n区间消去次数k=%4d 最优点为%12.5e 最优解为%12.5e",k,x_,y_);}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 本题中需要注意的地方:1.度需要转化为弧度
• (3)讨论
• 黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于 另一部分与这部分之比。其比值是一个无理数,用分数表示为(√5-1)/2,取 其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此 称为黄金分割,也称为中外比。这个分割点就叫做黄金分割点。 • 黄金比例的求法如下: 设一条线段AB的长度为a,C点在靠近B点的黄金分割点上,且AC为b,则a 比b就是黄金数
• 黄金分割法是用于一元函数f(x)在给定初始区间,[a,b] 内搜索极小点xmin的一种方法。它是优化计算中的经 典算法,以算法简单、收敛速度均匀、效果较好而著 称,是许多优化算法的基础,但它只适用于一维区间 上的单谷或单峰函数,即只在单谷或单峰区间内才能 进行一维寻优,其收敛效率较低。 • 其基本原理是:依照“去劣存优”原则、对称原则、 以及等比收缩原则来逐步缩小搜索区间。
Golden section method
Golden section method
• Problem: • Minimize f(x)=-sin(x)*cos(x) • x=[40° ,50°] d=0.13° • (1)Program • (2)Example solution,report • (3)Discussion(discuss the any significant aspects of the problem,characteristics of golden section method,and your own understanding of project)
• • • • • • • • • • • • • •
x1=a; x2=b; a=x2-0.618*(x2-x1); b=x1+0.618*(x2-x1); else f1<f2 x2=b; b=a; a=x2-0.618*(x2-x1); end k=k+1 %迭代次数 end %迭代到满足条件就停止迭代 w=(x2+x1)/2; %计算平均值 fmin=-sin(w)*cos(w) %得出函数的极小值 &本程序可以直接用来求不同 x1,x2,d的最小值。
• (1)M文件程序:
• function fmin=gold(x1,x2,d) %建立函数文件 • d=0.13/180*pi; %将度转换为弧度 • x1=40/180*pi; • x2=50/180*pi; • x=x1:d:x2; • f=-sin(x).*cos(x); • plot(x,f,'r') %画出函数图形 • title('黄金分割法求函数最小值-1304卢贵兵') • xlabel('x') • ylabel('f') • axis tight
• a=x2-0.618*(x2-x1); %用黄金分割法求出两个黄金分割点的值 • b=x1+0.618*(x2-x1); • k=0; • while (x2-x1)>=d %while条件循环 • f1=-sin(a)*cos(a) %计算黄金分割点对应的函数值 • f2=-sin(b)*cos(b) • if f1>f2 %if条件控制,对f1,f2大小进行比较 • x1=a; %满足条件,把a赋值给x1 • a=b; %把b赋值给a • b=x1+0.618*(x2-x1); %用黄金分割法计算新的b • elseif f1==f2
• 以下是对单谷函数求最小值做简单分析: • 具体步骤是:在区间[a,b]内取点:a1 ,a2 把[a,b]分为三段。 ① 如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+0.618*(b-a); ② 如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=b-0.618*(b-a); ③如果f(a1)==f(a2),令a=a1,b=a2, a1=b-0.618*(b-a); a2=a+0.618*(b-a); (可分为两种情况,简化程序) 如果|(b-a)/b|和|(y1-y2)/y2|都大于收敛精度ε重新开始循环。 因为[a,b]为单谷或单峰区间,这样每次可将搜索区间缩小0.618倍, 处理后的区间都将包含极小点的区间缩小,然后在保留下来的区间 上作同样的处理,如此迭代下去,将使搜索区[a,b]逐步缩小,直到 满足预先给定的精度时,即获得一维优化问题的近似最优解 k=
•
• •
10
fmin = -0.5000
函数图像:
• • • • • • • • • • • • •
运行程序后可以明显的看见函数的最小值fmin=-0.5000,迭代次数k=10 次和每次迭代循环过程中得出的f1,f2的值,并且画出函数图像用来和 计算得出的最小值做对照。 本题中if条件控制部分分了三部分,分别是f1>f2,f1<f2,f1==f2. 实际上f1==f2可以归纳到f1>f2,f1<f2中任意一个,如下 if f1>f2 %if条件控制,对f1,f2大小进行比较 x1=a; %满足条件,把a赋值给x1 a=b; %把b赋值给a b=x1+0.618*(x2-x1); %用黄金分割法计算新的b else f1<f2 x2=b; b=a; a=x2-0.618*(x2-x1); end 运行程序可以得到相同的结果
(2)报告(结果):
运行程序得: • f1 = • -0.4996 • f2 = • -0.4996 • ans = • 1 • k = • 1 • f1 = • -0.4979 • f2 = • -0.4996 • k = • 2
•
f1 =
•
• • • • • •
-0.4996
f2 = -0.5000 k= 3 …… ……
