91公因数和最大公因数_1
最大公因数、最小公倍数练习题

一、填空:1、如果自然数A除以自然数B商是17,那么A与B的最大公因数是〔〕, 最小公倍数是〔〕.2、最小质数与最小合数的最大公因数是〔〕,最小公倍数是〔〕.3、能被5、7、16整除的最小自然数是〔〕.4、〔1〕〔7、8〕最大公因数〔〕,最小公倍数〔〕(2)〔25, 15〕最大公因数〔〕,最小公倍数〔〕(3)〔140, 35〕最大公因数〔〕最小公倍数〔〕(4)〔24, 36〕最大公因数〔〕最小公倍数〔〕(5)〔3, 4, 5〕最大公因数〔〕最小公倍数〔〕(6)〔4, 8, 16〕最大公因数〔〕最小公倍数〔〕5、5和12的最小公倍数减去〔〕就等于它们的最大公因数.91和13的最小公倍数是它们最大公因数的〔〕倍.6、两个互质数的最小公倍数是153,这两个互质数是〔〕和〔〕.7、甲数=2X3X5X7,乙数=2X3X 11,甲乙两数的最大公因数是〔〕,最小公倍数是〔〕.8、3个连续自然数的最小公倍数是60,这三个数是〔〕、〔〕和〔〕.9、被2、3、5除,结果都余1的最小整数是〔〕,最小三位整数是〔〕.10、一筐苹果4个4个拿,6个6个拿,或者8个8个拿都正好拿完,这筐苹果最少有〔〕个.11、三个连续偶数的和是42,这三个数的最大公因数是〔〕.12、三个不同质数的最小公倍数是105,这三个质数是〔〕、〔〕和〔〕.13、自然数m和n,n= m+1,m和n的最大公因数是〔〕,最小公倍数是〔〕.14、把自然数a与b分解质因数,得到a=2x 5X7Xm, b=3X5Xm,如果a与b 的最小公倍数是2730,那么m = 〔〕015、〔273, 231, 117〕最大公因数〔〕,[273, 231, 117]最小公倍数〔〕16、三个数的和是312,这三个数分别能被7、8、9整除,而且商相同.这三个数分别是〔〕、〔〕和〔〕.17、〔A, 40〕 =8, [A, 40]=80,那么A=〔〕.18、找一个与众不同的数〔三个方法〕并说明理由〕:1、2、3、5、7、9、151:选,由于2:选,由于3:选,由于19、按要求写互质数两个都是质数〔〕和〔〕;两个都是合数〔〕和〔〕;一个质数和一个奇数〔〕和〔〕;一个偶数和一个合数〔〕和〔〕;一个质数和一个合数〔〕和〔〕;一个偶数和一个合数〔〕和〔〕.二、解决以下的问题:1、有一行数:1 , 1, 2, 3, 5, 8, 13, 21 , 34, 55……,从第三个数开始,每个数都是前两个数的和,在前100个数中,偶数有多少个?2、一个长方形的长和宽都是自然数,面积是36平方米,这样的形状不同的长方形共有多少种?3、一种长方形的地砖,长24厘米,宽16厘米,用这种砖铺一个正方形,至少需多少块砖?有一个长80厘米,宽60厘米,高115厘米的长方体储冰容器,往里面装入大小相同的立方体冰块,这个容器最少能装多少数量冰块?某小学六年级学生超过100人,而缺乏140人.将他们按每组12人分组, 多3人;按每组8人分,也多3人.这个学校六年级学生多少?有四个小朋友,他们的年龄一个比一个大一岁,四个人的年龄的乘积是360.他们中年龄最大是多少岁?7、汽车站内每隔3分钟发一辆公交车,4分钟发一辆中巴车,1小时共发了几辆汽车?其中有几辆中巴车?8、一块长方形铁皮,长96厘米,宽80厘米,要把它剪成同样大小的正方形且没有剩余,这种正方形的边长是多少?被剪成几块?9、王老师把25本作文和39本数学分别平均分给第一组的同学, 结果作文本多1本,数学本多3本,第一组最多有几位同学?10、一张长方形纸长16厘米,宽12厘米,把它裁成大小一样的正方形,而没有剩余,最少可以裁成多少个正方形?每个正方形的边长是多少?11、某班同学,排成7排多3人,排成8排少4人,这个班至少多少人?12、五〔1〕班同学做操,排成8排少1人,排成10排也少1人,这个班至少多少人?13、有一个自然数,被6除余1,被5除余1,被4除余1,这个自然数最小是几?2〕把长120厘米,宽80厘米的铁板裁成面积相等,最大的正方形而且没有剩余, 可以裁成多少块?3〕把长132厘米,宽60厘米,厚36厘米的木料锯成尽可能大的,同样大小的正方体木块,锯后不能有剩余,能锯成多少块?4〕一盒钢笔可以平均分给2、3、4、5、6个同学,这盒钢笔最小有多少枝?5〕用96朵红花和72朵白花做成花束,如果各花束里红花的朵数相同,白花的朵数也相同,每束花里最少有几朵花?6〕从小明家到学校原来每隔50米安装一根电线杆,加上两端的两根一共是55 根电线杆,现在改成每隔60米安装一根电线杆,除两端的两根不用移动外,中途还有多少根不必移动?7〕每筐梨,按每份2个梨分多1个,每份3个梨分多2个,每份5个梨分4个, 那么筐里至少有多少个梨?8〕现在有香蕉42千克,苹果112千克,桔子70千克,平均分给幼儿园的几个班,每班分到的这三种水果的数量分别相等, 那么最多分给了多少个班?每个班至少分到了三种水果各多少千克?9〕有三根铁丝,一根长54米,一根长72米,一根长36米,要把它们截成同样长的小段,不许剩余,每段最长是多少米?10.有一级茶叶96克,二级茶叶156克,三级茶叶240克,价值相等.现将这三种茶叶分别等分装袋〔均为整数克〕,每袋价值相等,要使每袋价值最低应如何装袋?a、b两数的最大公因数是12,a有8个因数,b有9个因数,求a与b.两个数的积是6912,最大公因数是24,求它们的最小公倍数?甲、乙、丙三个学生定期向某老师求教,甲每4天去一次,乙每6天去一次,丙每9天去一次,如果这一次他们三人是3月23日都在这个老师家见面,那么下一次三人都在这个老师家见面的时间是几月几日?求被5除余2,被6除余3,被7除4的大于1000、小于1500的所有自然数.1、一张长方形纸,长96厘米,宽60厘米,如果把它裁成同样大小且边长为整厘米的最大正方形,且保持纸张没有剩余,每个正方形的边长是几厘米?每个正方形的面积是多少?可以裁多少个这样的正方形?2、有一块长方形纸板,长24厘米,宽15厘米,将这块纸板裁成同样大小的正方形,不能有剩余,每块小正方形的边长是最长是多少?可以裁成多少块?3、王师傅找到一块长72厘米,宽60厘米,高48厘米的长方体木料,王师傅把它锯成同样大小的正方体木块,木块的体积最大,不能有剩余,算一算,可以锯成多少块?4、五〔1〕班给每个同学买了1个练习本,共花去9.30元钱,每个练习本的价钱比学生人数少,五〔1〕班共有多少个学生?5、张林、李强都爱在图书馆看书,张林每4天去一次,李强每6天去一次,有一次他们两人在图书馆相遇,至少再过多少天他们又可以在图书馆相遇?6、有一包奶糖,无论分给6个小朋友,8个小朋友,还是10个小朋友,都正好分完,这包糖至少有多少块?7、某公共汽车站有三条不同线路,1路车每隔6分钟发一辆,2路车每隔10分钟发一辆,3路车每隔12分钟发一辆,三路车在早上8点同时发车后,至少再到什么时候又可以同时发车?8、一个班缺乏50人,上体育课站队时,无论每行站16人,还是每行站24人, 都正好是整行,这个班有多少人?9、用一个数去除52,余4,再用这个数去除40,也余4,这个数最大是多少?把19支钢笔和23个软面抄平均奖给几个三好学生,结果钢笔多出了3支,软面抄也多出了3三,得奖的学生最多有几人?11、一个自然数,去除22少2,去除34也少2,这个自然数最大是几?12、一个数除73余1,除98余2,除147余3,这个数最大应是多少?13、有一批作业本,无论是平均分给10个人,还是12个人,都剩余4本,这批作业本至少有多少本?14、有一箱卡通书,把它平均分给6个小朋友,多出1本;平均分给8个小朋友, 也多出1本;平均分给9个小朋友,还是多1本,这箱卡通书最少有多少本?15、五年级同学参加社区效劳活动,人数在40和50之间,如果分成3人一组, 4人一组或6人一组都正好缺一人,五年级参加活动的一共有多少人?16、有一篮鸡蛋,两个两个去数,余1个;三个三个去数,余2个;四个四个去数,余3个,这篮鸡蛋至少有多少个?17、有两根钢管,一根长25米,一根长20米,把它们锯成同样长的小段,使每根不许有剩余,每段最长几米?一共要锯几次?18、李老师要把84本语文课本,70本数学课本,56本自然课本,平均分为假设干堆,每堆中这三种课本的数量分别相等,那么最多可以分成多少堆?每堆中有语文、数学、自然课本各多少本?19、缝纫店有一块长40分米,宽25分米的布料,现在顾客要求把它裁成正方形小布块〔不能有剩余〕,块数又要求最少,那么裁成的正方形不布块面积有多大? 20、一盒铅笔,可以平均分给4,5,6个小朋友,都没有剩余,这盒铅笔最少有多少只?21、某学校暑假期间安排王老师生4天值一次班,李老师每6天值一次班,张老师每8天值一次班,如果7月1日他们三人同一天值班,下一次他们三人同一天值班是几月几日?22、开学初,学校准备了96个黑板擦,72把扫帚,48个纸篓,平均分给各个班每一种物品的个数都对应相等,最多可分给多少个班?每种物品各几个?从运动场的一端到另一端全长120米,从一端起到另一端每隔4米插一面小红旗, 现在要改成每隔6米插一面小红旗,最多有多少面小红旗不必移动?24、某市有一个三角形公园,三边长分别为498米,612米,528米.方案在公园周围每隔假设干米植一棵樟树,并且每两棵之间的距离最远,每两棵树相隔多远?25爸爸拿了216元钱去买一种书,正好把钱用完,如果每本书降价1元钱,那么可以多买3本,钱也正好用完,爸爸一共买了多少本书?26、有一堆苹果,每8千克一份,9千克一份,或10千克一份,都会多出3千克,这堆苹果至少有多少千克?27、五〔1〕班和五〔2〕班两个班的同学去野炊,吃饭时,他们3人一个菜碗, 4人一个汤碗,他们共用了28个碗,这两个班参加野炊的同学共有多少人?28、学校合唱队排练时,如果7人一排就差2人,8人一排也差2人,合唱队至少有多少人?29、甲、乙、丙三人早晨在体育场跑步,甲跑完一圈要3分钟,乙跑完一圈要7 分钟,内跑完一圈要6分钟,三人同时从起点出发,经过多长时间三人再次在起点处相遇?30、把37支钢笔和38本书,平均奖给几个学习成绩优秀的学生, 结果钢笔多出一支,书还缺2本,最多有几个学习成绩优秀的同学?1、有三根钢筋,分别长12分米,18分米、30分米,把它们都截成同样长的小段〔整分米〕,不许有剩余,每小段最长是多少分米?2、有50个梨、75个苹果和100个桔子,要把这些水果平均分给几个小组,并且每个小组分得的三种水果的个数也相同,最多可以分给几个小组?每组中每样水果各几个?3、一块长45厘米,宽30厘米的长方形木板,把它锯成假设干块相同的正方形而没有剩余,所锯成的正方形的边长〔整厘米数〕最长是多少厘米?共能锯成多少块?4、甲、乙两数的最大公因数是9,最小公倍数是90,甲数是18,乙数是多少?5、某市1路、2路和8路公交车都从南站出发,1路车每隔10分钟发出一辆车,2 路车每隔12分钟发出一辆车,8路车每隔15分钟发出一辆车,当这三种路线的车同时发车后,至少要经过多少分钟又同时发车?希望对你能有所帮助.1 .都是自然数,如果,的最大公因数是〔〕,最小公倍数是〔〕.2 .甲,乙,甲和乙的最大公因数是〔〕X〔〕=〔〕,甲和乙的最小公倍数是〔〕X〔〕X〔〕X〔〕 = 〔〕.3.所有自然数的公因数为〔〕.4.如果m和n是互质数,那么它们的最大公因数是〔〕,最小公倍数是〔〕.5.在4、9、10和16这四个数中,〔〕和〔〕是互质数,〔〕和〔〕是互质数, 〔〕和〔〕是互质数6 .用一个数去除15和30,正好都能整除,这个数最大是〔〕.子*7 .两个连续自然数的和是21,这两个数的最大公因数是〔〕,最小公倍数是〔〕.*8 .两个相邻奇数的和是16,它们的最大公因数是〔〕,最小公倍数是〔〕.**9.某数除以3、5、7时都余1,这个数最小是〔〕.10.根据下面的要求写出互质的两个数.〔1〕两个质数〔〕和〔〕.〔2〕连续两个自然数〔〕和〔〕.〔3〕 1和任何自然数〔〕和〔〕.〔4〕两个合数〔〕和〔〕.〔5〕奇数和奇数〔〕和〔〕.〔6〕奇数和偶数〔〕和〔〕.二 .判断题.1 .互质的两个数必定都是质数.〔〕2 .两个不同的奇数一定是互质数.〔〕3 .最小的质数是所有偶数的最大公约数.〔〕4 .有公约数1的两个数,一定是互质数.〔〕5 .a是质数,b也是质数,,一定是质数.〔〕三 .直接说出每组数的最大公约数和最小公倍数.26 和13 ( ) 13 和6 ( ) 54 和6 ( ) 5 和9 ( ) 29 和87 ( ) 30 和15 ()13 和26 ()四.求下面每组数的最大公因数和最小公倍数.(三个数的只求最小公倍数)45 和60 3660 27 和7276 和80 42105 和5624、36 和48五 .动脑筋,想一想:学校买来40支圆珠笔和50本练习本,平均奖给四年级三好学生,结果圆珠笔多4支,练习本多2本,四年级有多少名三好学生,他们各得到什么奖品?。
[转载]求N个数的最大公因数(算法)
![[转载]求N个数的最大公因数(算法)](https://img.taocdn.com/s3/m/b102b06000f69e3143323968011ca300a6c3f647.png)
[转载]求N个数的最⼤公因数(算法)在⼀般的程序设计书⾥⾯,都有关于求两个数的最⼤公因数的算法(或者叫做最⼤公约数)。
求两个数的最⼤公约数算法⽤的最多的是辗转相除法。
基本思路就是1 getCommonMutiple(a,b){ //这⾥假定a 是较⼤的数,实际编码时要先判断谁⼤谁⼩;23 r = a%b;45if(r != 0){67 a = b;89 b = r;1011 getCommonMutiple(a ,b);1213 }1415return b;1617 }但是如何求N个数的最⼤公因数呢?(N > 1)在初等数学⾥,有这么⼏个定理1、任何⼀个整数,都可以分解为素数因⼦的乘积⽐如24 = 2* 2* 2 * 3;26 = 2 * 13;分解时应该从2开始分解起2、若⼲个数的最⼤公因数是共同素数因⼦的乘积⽐如求 48 60 72 的最⼤公因数48 = 2*2*2*2*360 = 2*2*3*572 = 2*2*2*3*3共同的素数因⼦为 2 * 2 * 3 = 12 所以他们的最⼤公因数就是12有了这两个知识点之后,我们开始写程序详见代码1/**2 *Aug 25, 20133 *Copyright(c)JackWang4 *All rights reserve5 *@Author <a href="mailto:wangchengjack@">JackWang</a>6*/7package com.example.blog;89import java.util.ArrayList;10import java.util.List;1112/**13 * 计算机⾥求最⼤公因数的⽅法通常是辗转相除法14 * 但是这个⽅法的缺陷在与⼀次只能求两个数的最⼤公因数15 * 如果需要求若⼲个数的最⼤公因数呢?16 * 需求:设计⼀个算法,可以求出若⼲个整数的最⼤公因数17 * @author Administrator18 *19*/20public class CommonMutiple {21public static void main(String[] args) {22int[] data1 = {26,13};23int[] data2 = {735000,421160,238948};24int[] data3 = {1008,1260,882,1134};2526int result1 = getCommonMutiple(data1);27int result2 = getCommonMutiple(data2);28int result3 = getCommonMutiple(data3);2930 System.out.println(result1);31 System.out.println(result2);32 System.out.println(result3);33 }34/**35 * 得到最⼤公倍数的⽅法36 * @param data1 传⼊数组37 * @return返回最⼤公倍数38*/39private static int getCommonMutiple(int[] data1) {40 List<List<Integer>> divisorList = new ArrayList<>();41for(int data :data1){42 divisorList.add(getDivisors(data));43 }44return getResult(divisorList);45 }46/**47 * 得到⼀个数的全部素数因⼦48 * @param data 传⼊⼀个整数49 * @return返回素数因⼦50*/51private static List<Integer> getDivisors(int data) {52 List<Integer> primeList = new ArrayList<>();53int k = Math.abs(data);54int sum = 1;55if(!isPrime(data)){ //如果这个数是素数的话,直接返回56int len = (int)Math.sqrt(Math.abs(data));57for(int i = 2; i <= len; i++){ //任何⼀个数都可以分解为素数因⼦的乘积58if(isPrime(i)){59while(data % i == 0){60 sum *= i;61if(sum <= k){62 primeList.add(i);63 }64 data = data / i;65if(isPrime(data)){66 primeList.add(data);67 sum *= data;68break;69 }70 }71if(sum == k)72break;73 }74 }75 }else {76 primeList.add(data);77 }78return primeList;79 }8081private static boolean isPrime(int data) {82for(int i = 2;i <= Math.sqrt(Math.abs(data)); i++){83if (data % i == 0)84return false;85 }86return true;87 }8889/**90 * 通过将各个数的素数因⼦传⼊该⽅法,得到最⼤公因数91 * 实际就是求⼀组数的交集92 * 如果这组数存在最⼤公因数,则最⼤公因数必定在素数因⼦最⼩的集合⾥93 * @param divisorList94 * @return95*/96private static int getResult(List<List<Integer>> divisorList) {97int result = 1; //存储最终结果,如果返回是1的话,则说明不存在最⼤公因数 98for(int element :divisorList.get(0)){99boolean flag = true;100for(int j = 1;j < divisorList.size();j++){101if(!divisorList.get(j).contains(element)){102 flag = false;103break;104 }105 divisorList.get(j).remove(divisorList.get(j).indexOf(element)); 106 }107if (flag) {108 result *= element;109 }110 }111112113114// int k = divisorList.get(0).size();115// int j = 0; //记录最⼩元素数的脚标116// for(int i = 1 ; i < divisorList.size(); i++){117// if (divisorList.get(i).size() <= k) {118// k = divisorList.get(i).size();119// j = i;120// }121// }122//123// for(List<Integer> list :divisorList){124// divisorList.get(j).retainAll(list);125// }126//127// for (int i = 0; i <divisorList.get(j).size() ; i++) {128// System.out.println(divisorList.get(j).get(i));129//130// }131//132// if(divisorList.get(j).size() != 0){133// for (int r : divisorList.get(j)) {134// result = result * r;135// }136// }137return result;138 }139 }这⾥两个较为重要的算法是1、如何将⼀个整数分解为素数因⼦的乘积2、如何找出若⼲个素数因⼦中共同的素数因⼦对于第⼀个算法,对应的代码为1private static List<Integer> getDivisors(int data) {2 List<Integer> primeList = new ArrayList<>();3int k = Math.abs(data);4int sum = 1;5if(!isPrime(data)){ //如果这个数是素数的话,直接返回6int len = (int)Math.sqrt(Math.abs(data));7for(int i = 2; i <= len; i++){ //任何⼀个数都可以分解为素数因⼦的乘积 8if(isPrime(i)){9while(data % i == 0){10 sum *= i;11if(sum <= k){12 primeList.add(i);13 }14 data = data / i;15if(isPrime(data)){16 primeList.add(data);17 sum *= data;18break;19 }20 }21if(sum == k)22break;23 }24 }25 }else {26 primeList.add(data);27 }28return primeList;29 }思路为:先判断传⼊的数据是否为素数,如果是素数直接加到list中返回即可,否则从素数2开始分解,如果能整除2,则说明2是⼀个素因⼦,继续整除2,如果不能整除了先要判断这个已经是不是⼀个素数了,如果是的话就要加到list⾥,这是⾮常容易忽略的地⽅,我也是⽤26这个数据做测试的时候才发现(26 = 2* 13)在判断过程中,要将素数因⼦乘积存到sum变量⾥,因为当sum = data时就应该已经分解完成了。
精品拓展教案——最大公因数与最小公倍数(可用)
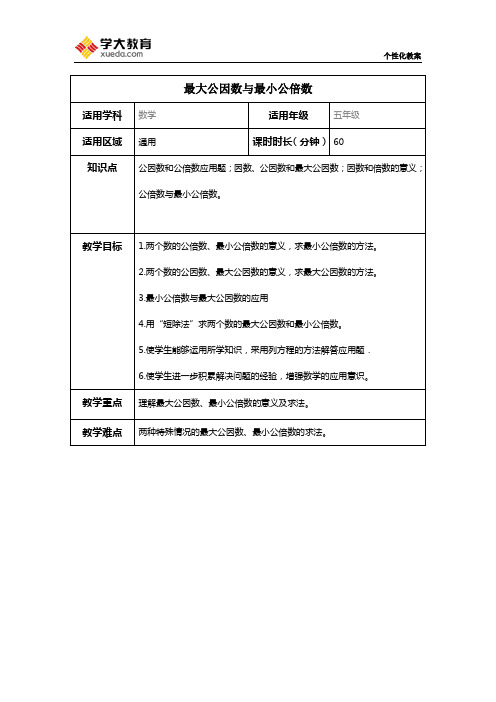
最大公因数与最小公倍数适用学科数学适用年级五年级适用区域通用课时时长(分钟)60知识点公因数和公倍数应用题;因数、公因数和最大公因数;因数和倍数的意义;公倍数与最小公倍数。
教学目标 1.两个数的公倍数、最小公倍数的意义,求最小公倍数的方法。
2.两个数的公因数、最大公因数的意义,求最大公因数的方法。
3.最小公倍数与最大公因数的应用4.用“短除法”求两个数的最大公因数和最小公倍数。
5.使学生能够运用所学知识,采用列方程的方法解答应用题.6.使学生进一步积累解决问题的经验,增强数学的应用意识。
教学重点理解最大公因数、最小公倍数的意义及求法。
教学难点两种特殊情况的最大公因数、最小公倍数的求法。
教学过程一、复习预习1、什么是倍数①一个整数能够把另一整数整除,这个整数就是另一整数的倍数。
如15能够被3或5整除,因此15是3的倍数,也是5的倍数。
②一个数除以另一数所得的商。
如a÷b=c,就是说a是b的c倍,a是b的倍数。
③一个因数能让它的积整除,那么,这个数就是因数,它的积就是倍数。
例如: 3 × 5 = 15↑↑↑因数1 因数2 倍数A÷B=C,就可以说A是B的C倍④一个数的倍数(0除外)有无数个,也就是说一个数的倍数的集合为无限集.注意:不能把一个数单独叫做倍数,只能说谁是谁的倍数。
2、什么是因数:整数A能被整数B整除,A叫做B的倍数,B就叫做A的因数或素数,(在自然数的范围内)例:6÷2=3 ,1、2、3和6就是6的因数。
6的因数有:1、2、3、610的因数有:1、2、5、1015的因数有:1、3、5、15二、知识讲解1、一个数最小的因数是1,最大的因数是它本身,一个数因数的个数是有限的。
一个数最小的倍数是它本身,没有最大的倍数。
一个数倍数的个数是无限的。
一个数最大的因数等于这个数最小的倍数。
2、几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。
12短除法求最大公因数 (3)

1
2
3
4
9
6
12
你知道吗? 利用分解质因数的方法,可以比较简 便地求出两个数的最大公因数。
例如:求24和36的最大公因数?
24 = 2×2×2×3 36 = 2×2×3×3
24 和 36 的最大公因数 = 2×2×3 = 12。
1、甲=2×3×5,乙=2×3×7,甲 和乙的最大公因数是( ).
2、甲数=2×3×5,乙数=7×1 1×13,甲数和乙数的最大公因数 是( )。
88和11
(倍数关系)
(一般关系) (互质关系)
42和28
(一般关系)
5和9
13和91
14和21
9和16
(互质关系) (一般关系)
88和121
(一般关系)
(倍数关系) (互质关系)
求下列各组数的最大公因数。
13和39
42和34
15和16
4. 选出正确答案的编号填在横线上。 A. 1 A. 4 B. 3 B. 6 C. 4 C. 8
书第64页9题
A (1) 9 和 16 的最大公因数是______ 。
D. 9 D. 16
D (2) 16 和 48 的最大公因数是______ 。
(3) 甲数是乙数的倍数,甲、乙两数的最大
C 公因 数是______ 。
A. 1
B. 甲数
பைடு நூலகம்C. 乙数
D. 甲、乙两数的积
(1) 自然数a除以b商是15,那么a和b的最 b 。 大公因数______ (2)m和n是相邻的两个不为零的自然数,
书第61页做一做2
学号是 12 的因数而不是 18 的因数的同学 站左边,是 18 的因数而不是 12 的因数的
苏教版五年级最大公因数及最小公倍数

9 10 19 20 29 30 39 40 49 50 59 60 69 70 79 80 89 90 99 100
个位上是____ 0 或____ 5 的数,是 5 的倍数。
下面哪些数是 2 的倍数? 哪些数是 5 的倍数? 哪些数既是 2 的倍数也是 5 的倍数?
24 35 67 90 99 15 60 75 106 130 521 280
3 13 23 33 43 53 63 73 83 93
4 14 24 34 44 54 64 74 84 94
5 15 25 35 45 55 65 75 85 95
6 16 26 36 46 56 66 76 86 96
7 17 27 37 47 57 67 77 87 97
8 18 28 38 48 58 68 78 88 98
偶数: 98、988、0、3 678、1 000、5 656。
5 的倍数的特征
学号是 5 的倍数 的同学请举手。
哪些数是 5 的倍数?
在下表中找出 5 的倍数,并涂上颜色。看看有
什么规律。
1 11 21 31 41 51 61 71 81 91
2 12 22 32 42 52 62 72 82 92
可能是 7,14, 21,42。
我知道了, 是____ 42 。
( 2)
我的最大因 数和最小倍 数都是 18。
18
( 3)
1
我的最小 倍数是 1。
14 是 7 的倍数,21 是 7 的倍数。
14 和 21 的和是 7 的倍数吗?
18 是 9 的倍数,27 也是 9 的倍
数。18 和 27 的和是 9 的倍数吗?
你有什么发现?
2. 2、5、3 的
公因数与最大公因数(练习)

例2、有一張長6公分,寬4公分的長方形色紙, 要將它剪成相同大小的正方形且不浪費紙,那 么这样的正方形边長最大几公分?
解:
(6,4) =2 6÷ 2 =3(长可剪成3个) 4÷ 2 =2(寬可剪成2个)
2 6 3 4 2
答: 正方形的边长最大是2公分.
1.8只大闸蟹与12小丑鱼混在一起分组, 每组中大闸蟹的数量相等,小丑鱼的 数量也相等 ,全部分完,可以怎么分?
5
除到两个商是互质数为止
18和30的最大公因数是 2×3=6
求两个数的最大公因数, 先用这两个数公有的质因数 连续去除(一般从最小的开 始),一直除到所得的商是 互质数为止,然后把所有的 除数连乘起来.
1 )
• 18和30的最大公因数是( 6 ), 它们所有的公因数有( ) 1,2,3 , 6
想一想,填一填
• 甲数=3×5×7,乙数=5×7×17, 甲乙两数的最大公因数是( 35 ) • A=2×2×5×7,B=2×2×5×11 • A、B两数的最大公因数是( 20 )
9.* 小巧匠。
要把它们截成同样长的小 棒,不能有剩余,每根小
例1 求18和30的最大公因数: 解一:18的因数有:1、2、3、6、9、18; 30的因数有:1、2、3、5、6、10、 15、30; 公因数有:1、2、3、6,最大公因数是6.
解二:18=2×3×3 30=2×3×5 公有质因数有2和3, 最大公因数=2×3=6
用短除法求48和60的最大公因数:
公因数与最大公因数 (练习)
一、填空 1、甲=2×3×5,乙=2×3×7,甲和乙 的最大公约数是( 6 ). 2, 2, 3 2、36和60相同的质因数有( ), 它们的积是(12 ),也就是36和60的 最大公因数). ( 3、( )的两个数,叫做互质数. 4、自然数a除以自然数b,商是15,那么 a和b的最大公因数是( b ).
公因数、最大公因数、公倍数和最小公倍数

公因数、最大公因数、公倍数和最小公倍数公因数、最大公因数、公倍数和最小公倍数在数学中,我们常常需要求出多个数的公因数、最大公因数、公倍数和最小公倍数。
掌握这些概念和求法是非常重要的。
最大公因数是几个数公有的因数中最大的那个,可以用列举法、观察法和短除法等方法求得。
例如,求8和6的最大公因数,我们可以先列出它们的因数,然后找出它们的公因数,最后找出它们的最大公因数,即2.观察法可以应用于特殊情况,例如两个数具有倍数关系时,它们的最大公因数就是其中较小的数;两个数是互质数时,它们的最大公因数就是1.如果两个数不是倍数和互质关系,我们可以用小数缩小法,即把较小的数缩小,每次缩小后看得到的商是不是另一个数的因数,直到所得的商是另一个数的因数为止。
短除法是一般情况下求最大公因数的常用方法。
我们可以用这两个数除以它们的公因数,一直除到所得的两个商只有公因数1为止。
然后把最后所有的除数连乘,就得到了二个数最大公因数。
除了最大公因数,我们还需要掌握最小公倍数的求法。
最小公倍数是几个数公有的倍数中最小的那个,可以用列举法、分解质因数法和公式法等方法求得。
例如,求6和8的最小公倍数,我们可以先列出它们的倍数,然后找出它们的公倍数,最后找出它们的最小公倍数,即24.最后,我们需要学会如何解有关最大公因数和最小公倍数的应用题,例如求某些数的最大公因数或最小公倍数,或者求某些数的倍数关系等。
通过练,我们可以更好地掌握这些知识点,并在实际问题中灵活运用。
12和24的最大公因数是4,可以表示为(12,24)=4.互质数是指公因数只有1的两个数,例如1和任何自然数都是互质数,相邻两个自然数如2和3、8和9也是互质数。
两个质数一定是互质数,而两个合数可能是互质数,例如8和9、25和49.2和所有奇数都是互质数,质数与比它小的合数也是互质数。
需要注意的是,质数是对一个数来说,而互质数是对两个数的关系来说的。
在练中,需要判断每组数是不是互质关系或倍数关系,并求出它们的最大公因数。
《公因数和最大公因数》评课稿

《公因数和最大公因数》评课稿
我觉得本节课有三个亮点:
1、谷老师的个人魅力和学生的表现值得我学习。
谷老师思路清晰、语言简炼、教态大方,学生读题、发言声音洪亮、充满自信,可见平时谷老师对学生的指导到位、训练有素。
2、找公因数和最大公因数的四种方法逐步呈现(列举法、韦恩图法、筛选法、短除法),体现了了解决问题策略的多样化,同时也尊重了学生的差异、体现了学生的主体地位。
3、本节课的练习设计很有层次,我在听课的过程中能够感受到通过由浅入深、由易到难的练习学生对知识的理解一步步加深、解决问题的能力也在逐步提升。
同时,我也有两点不太成熟的思考或者说是困惑的地方:
1、找公因数的方法很多,需不需要进行优化,让学生重点理解和掌握其中的一种方法?
2、学生汇报完短除法后,老师是不是应该借助分解质因数的知识对“为什么把除数相乘得到公因数”的道理加以解释?以便学生对这一简便方法理解的更加透彻。
苏教版五年级下册数学最大公因数最小公倍数易错题和重点题型

一、知识点整理:1、一个数最小的因数是1,最大的因数是它本身,一个数因数的个数是有限的.一个数最小的倍数是它本身,没有最大的倍数.一个数倍数的个数是无限的.一个数最大的因数等于这个数最小的倍数.2、几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,用符号,表示.几个数的公倍数也是无限的.3、两个数公有的因数,叫做这两个数的公因数,其中最大的一个,叫做这两个数的最大公因数,用符号, .两个数的公因数也是有限的.4、两个素数的积一定是合数.举例:3×5=15,15是合数.5、两个数的最小公倍数一定是它们的最大公因数的倍数.举例:6,8=24,6,8=2,24是2的倍数.6、求最大公因数和最小公倍数的方法:倍数关系的两个数,最大公因数是较小的数,最小公倍数是较大的数.举例:15和5,15,5=15,15,5=5素数关系的两个数,最大公因数是1,最小公倍数是它们的乘积.举例:3,7=21,3,7=1一个素数和一个合数,最大公因数是1,最小公倍数是它们的乘积.5,8=40,5,8=1相邻关系的两个数,最大公因数是1,最小公倍数是它们的乘积.9,8=72,9,8=1特殊关系的数两个都是合数,一个是奇数,一个是偶数,但他们之间只有一个公因数1,比如4和9、4和15、10和21,最大公因数是1,最小公倍数是它们的乘积.一般关系的两个数,求最大公因数用列举法或短除法,求最小公倍数用大数翻倍法或短除法.二、经典例题:例1,写出每组数的最大公因数7和9 5和25 10和4写出每组数的最小公倍数8和10 51和3 5和4例2:有一批地砖,每块长45厘米、宽30厘米,至少要用多少块这样的地砖才能铺成一个正方形在一张长40厘米,宽32厘米的长方形红纸上裁出同样大小,面积最大的正方形,并且没有剩余.一共可以裁出多少个这样的正方形例3:五1班学生人数不超过50人,在分小组做游戏时,可以分为每组6人或者每组8人,两种分法都刚好分完.这个班的学生可能有多少人例4:甲、乙两人到图书馆去借书,甲每4天去一次,乙每5天去一次,如果7月1日他们两人在图书馆相遇,那么他们下一次同时到图书馆是几月几日三、课堂练习1,暑假期间,小华,小明和小芳都去图书馆借书,小华每3天去一次,小明每4天去一次,小芳每6天去一次,8月1日他们都去借了书,那么小芳每次去借书的那天也去了,三人同一天去借书的时间是.2、一个数的最大因数是13,这个数的最小倍数是.3、两个自然数a、b的最大公因数是1,它们的最小公倍数是.4、如果A=2×2×3,B=2×3×3,那么它们的最大公因数是,最小公倍数是.5、一个数是3的倍数,又是5的倍数,还有因数7.这个数最小是.6、一个数既是30的因数、又是45的因数,最大的是.7、如果两个数的最大公因数是1,它们最小公倍数是91,那么这两个数的和最大是.8、任何两个奇数的和是.A、奇数B、合数C、偶数9、12是的最大公因数.A、1和12B、12和24C、3和410、任何两个自然数的的个数是无限的.A、公倍数B、公因数C、倍数11、A是B倍数,那么它们的最小公倍数是.A、ABB、AC、B12、两个数的最大公因数是15,最小公倍数是90,这两个数一定不是.A、15和90B、45和90C、45和30用短除法求出每组数的最大公因数和最小公倍数.32和612和1872和4813,在周长是400米的椭圆形跑道上插彩旗,原来每间隔8米插一面彩旗,现在改为每隔10米插一面彩旗,如果以其中的一面彩旗为起点不改变,那么一共需要移动多少面彩旗14、把两根长度分别是45厘米和60厘米的铁丝,截成长度相等的小段,每根都不能有剩余.每小段最长多少厘米可以剪成多少段15、李刚和李强是兄弟,两人都在外地工作.李刚隔6天回家一次,李强隔8天回家一次,十月一日这天他们同时回家,再过多少天他们才能再一次见面16,把48米,60米的两根钢管锯成长度一样的钢管且没有剩余.(1),锯好的钢管每段最长是多少米2,如果每锯一次需要2分钟,一共需要锯多少分钟17、在一根长100厘米的木棍上,自左至右每隔6厘米染一个红点,同时自右至左每隔5厘米染一个蓝点,有多少个点同时染了红色和蓝色18、植树节那天,园林工人在一段公路的一边每隔4米栽一棵树,一共栽了40棵,现在改成每隔5米栽一棵树,那么有多少棵树不用移动四:课堂检测1、两个数的最大公因数是1,最小公倍数是21,这两个数分别是和,或者和2、已知A=5B,则A,B=,A,B=3、已知a=b+2,则a,b=4、a是一个素数,则a的倍数有个A、1个B、2个C、无数个5、如果b是一个整数,那么2b一定是A、合数B、偶数C、素数写出每组数的最小公倍数和最大公因数.4和155和790和306、甲,乙两人到图书馆借书,甲每4天去一次,乙每6天去一次,如果3月16日他们两人到图书馆相遇,那么下一次都到图书馆是几月几日7、有一包糖果.如果平均分给8个小朋友,正好分完;如果平均分给10个小朋友,也正好分完.这包糖果至少有多少块8、有两根彩带,一根长45厘米,另一根长30厘米.现在要把它们剪成长度一样的短彩带且没有剩余,每根短彩带最长是多少厘米9、在一张长60厘米的纸条上,从左端起,先每隔3厘米画一个红点,再从左端起,每隔4厘米画一个红点.纸条的两端都不画.最后,纸条上共有多少个红点五、课后作业1、如果A=2×3×7,B=2×5×7,那么A和B的最大公因数是,最小公倍数是.2、要使601□既是2的倍数,又是3的倍数,那么□里可以填.3、如果a÷b=4a、b为整数那么a和b的最大公因数是4.4、一个数最小的倍数与它最大的因数相等.5、任何一个自然数的因数至少有2个.6、1和任何自然数0除外都没有公因数.7、写出每组数的最大公因数7和9 5和25 10和48、写出每组数的最小公倍数8和10 51和3 5和49、a与b的最大公因数是6,最小公倍数是72,a是18,b是多少10、从小明家到学校原来每隔5米安装一根电线杆,加上两端的两根一共是25根电线杆,现在改成每隔6米安装一根电线杆,除两端的两根不需要移动外,中间有多少根不必移动。
公因数和公倍数知识点

公因数和公倍数【知识点回顾】1、公因数(1)互素数:公因数只有1的两个自然数叫做互素数。
(2)简分数:分子、分母是互素数的分数叫做简分数。
(3)求最大公因数的方法:分解素因数法和短除法。
2、公倍数求最小公倍数的方法:分解素因数和短除法,即用最大公因数×各自独有的因数。
3、求两个数的最大公因数和最小公倍数,有3种基本情况,区别如下:4、求最大公因数和最小公倍数的方法:一、特殊情况:(1)倍数关系的两个数,最大公因数是较小的数,最小公倍数是较大的数。
(如;6和12的最大公因数是6,最小公倍数是12。
)(2)互质关系的两个数,最大公因数是1,最小公倍数是它们的乘积。
(如,5和7的最大公因数时1,最小公倍数是5×7=35)二、一般情况:(1)求最大公因数:列举法、单列举法、分解质因数法、短除法、除法算式法。
①列举法:如,求18和27的最大公因数先找出两个数的所有因数18的因数有:1、2、3、6、9、1827的因数有:1、3、9、27再找出两个数的公因数:18的因数有:1、2、3、6、9、1827的因数有:1、3、9、271、3、9最后找出最大公因数:9②单列举法:如,求18和27的最大公因数先找出其中一个数的因数:18的因数有:1、2、3、6、9、18再找这些因数中那些又是另一个数的因数:1、3、9又是27的因数最后找出最大公因数:9③短除法:3 18 273 6 92 3除到商是互质数为止,最后把所有的除数相乘3×3=9④除法算式法:用这两个数同时除以公因数,除到最大公因数为止。
18÷9就是18和27的最大公因数27(2)求最小公倍数:列举法、单列举法、大数翻倍法、分解质因数法或短除法。
①列举法:如,求18和12的最小公倍数先按从小到大的顺序找出这两个数的倍数:18的倍数:18、36、54、7212的倍数:12、24、36、48 再找出两个数的最小公倍数:18的倍数:18、36、54、7212的倍数:12、24、36、48②单列举法:如,求18和12的最小公倍数先找出一个数的倍数:18的倍数有:18、36、54、72再按从小到大的顺序找这些倍数中那个又是另一个数的倍数,找出最小公倍数:36 ③大数翻倍法:如,求18和12的最小公倍数把较大的数翻倍(2倍开始),每次翻倍后看结果是不是另一个数的倍数,直到找到最小公倍数为止。
最大公因数和最小公倍数

第八讲最大公因数与最小公倍数知识平台:1.定义(1)几个数公有的因数,叫做这几个数的公因数;其中最大的一个,叫做这几个数的最大公因数。
(2)几个数公有的因数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
2.性质(1)两个数的最大公因数的因数,都是这两个数的公因数。
(2)两个数分别除以它们的最大公因数,所得的商一定是互质的。
(3)两个自然数的最大公因数与最小公倍数的乘积等于这两个数的乘积。
3.特殊关系数的最大公因数和最小公倍数。
(1)两数互质,最大公因数是1,最小公倍数是两数之和。
(2)两数成倍数关系,最大公因数是较小数,最小公倍数是较大数。
范例点击例1 在一个长30米,宽12米的长方形池塘的四角和四条边上种树,若相邻两棵树之间的距离相等,最小要种多少棵树?每相邻两棵树之间的距离是多少米?分析与解答要使种树棵数最少,则使每相邻两树之间的距离最大,就是求长和宽的最大公因数。
30和12的最大公因数是6。
30÷6=5,12÷6=2树的棵数是:5×2+2×2=14棵每相邻两棵树之间的距离是6米。
练习将一个长325厘米,宽175厘米,高75厘米的长方体木块锯成相等的正方体小木块,最少可锯多少块?分析与解答要使小木块的块数最小,则小正方体的棱长是长方体的长、宽、高的最大公因数。
325,175,75的最大公因数是25,所以,小正方体木块有:(325÷25)×(17525)×(75÷25)=273例2 甲、乙、丙三人在少年宫分别参加了不同的兴趣小组,甲每4天去参加一次活动,乙每5天去参加一次活动,丙每6天去参加一次活动。
某一个星期日,他们三人去参加活动时相遇,问至少要多少天,他们才会再次相遇?相遇时是星期几?分析与解答距再次相遇的天数应是4、5、6的公倍数,而且是最小公倍数。
所以:4、5、6的最小公倍数是60,60÷7=8…4 至少要过60天他们才会再次相遇,相遇时是星期四。
六年级同步第2讲:分解素因数 - 教师版

分解素因数是六年级数学上学期第一章第二节内容,主要包含素数、合数的概念以及分解素因数,公因数与最大公因数,公倍数与最小公倍数这三大块内容,这节课主要讲解前面两大块内容,重点是素数与合数的概念以及分解素因数,难点是求2个整数或者是3个整数的最大公因数.通过这节课的学习一方面为我们后面学习公倍数和最小公倍数奠定基础,另一方面用所学知识解决实际问题,加强学生对数学学习的兴趣.1、素数与合数(1)素数:一个正整数,如果只有1和它本身两个因数,则叫做素数,也叫做质数;(2)合数:一个正整数,如果除了1和它本身以外还有别的因数,则叫做合数;(3)1既不是素数,也不是合数;正整数可分为:1、素数和合数三类.分解素因数知识结构模块一:素数与合数知识精讲内容分析1 / 1例题解析【例1】判断37,39,47和49是素数还是合数.【难度】★【答案】37和47是素数,39和40是合数.【例2】下列各数中,哪些是素数?哪些是合数?6,13,18,31,51,67,87,120.【难度】★【答案】13,31,67是素数;6,18,51,87,120是合数.【例3】根据要求填空:在1,2,9,21,43,51,59,64这八个数中:(1)是奇数又是素数的数是();(2)是奇数不是素数的数是();(3)是素数而不是奇数的数是();(4)是合数而不是偶数的数是().【难度】★【答案】(1)43,59 ;(2)1,9,21,51 ;(3)2;(4)9,21,51.【例4】已知字母p、q分别代表一个素数,并且p + q = 99,你能知道p、q这两个数相乘的积是多少吗?【难度】★★【答案】194【解析】99是一个奇数和一个偶数的和,且这两个数都是素数,所以这两个数是2和97,积是194.【总结】2是最小的素数,也是唯一的偶素数.【例5】判断题(若是正确的,请说明理由;若是错误的,请把它改正确).(1)所有的偶数是合数,所有的奇数是素数;(2)某数是3的倍数,这个数一定是合数;(3)一个合数至少有3个因数;(4)在所有的素数中,只有2是偶数,其余的素数都是奇数;(5)一个自然数,如果不是素数,就一定是合数;(6)两个素数的和一定是合数;(7)大于2的合数都是偶数;3 / 3(8) 一个大于1的自然数,如果有小于本身的因数,那么这个数一定是合数.【难度】★★【答案】(1)×;(2)×;(3)√;(4)√;(5)×;(6)×;(7)×;(8)×.【例6】用10以内的质数组成一个三位数,使它能同时被3、5整除,这个数最小和最大分别是多少? 【难度】★★ 【答案】375和735.【例7】一个两位质数,交换个位与十位上的数字,所得的两位数仍是质数,这个数是多少? 【难度】★★【答案】11,13,17,31,37,71,73,79,97.【解析】两位质数中,十位数字是2、4、5、6、8的,不满足条件,剩余的有:11,13,17,19,31,37,53,59,71,73,79,97,其中满足条件的有:11,13,17,31,37,71,73,79,97.【总结】本题主要查对质数概念的理解和运用.【例8】已知一个长方形的长和宽都是质数厘米,并且周长是36厘米.问这个长方形的面积至多是多少个平方厘米? 【难度】★★★ 【答案】77平方厘米【解析】由周长是36厘米可得:长+宽=18,由于长和宽都是质数, 所以18只能写成5+13或7+11.所以这个长方形的面积最大为:7×11=77平方厘米 答:这个长方形的面积至多是77平方厘米. 【总结】本题是利用质数解决实际问题.师生总结1、 最小的素数是几?最小的合数是几?2、 最小的偶素数是几?3、 如何判断一个正整数是不是素数?【例9】三个素数的和是100,这三个素数的积最大是多少? 【难度】★★★ 【答案】4514【解析】由三个素数和为100且2是素数中唯一的偶数,所以2是其中一个素数, 即:另两个素数的和是98. 又:98=19+79=31+67=37+61所以这三个数的乘积最大是:2×37×61=4514. 答:这三个素数的积最大是4514.【总结】偶数与偶数的和是偶数,偶数与奇数的和是奇数,2是唯一的偶素数.【例10】若三个素数的乘积恰好等于它们的和的11倍,那么这三个素数各是几? 【难度】★★★【答案】2、11、13或3、7、11.【解析】设这三个质数为a 、b 、c ,可得等式:11()abc a b c =++, 又11也是质数,所以a ,b ,c 中必有一个数是11, 设a =11,即11bc =11(11+b +c ),所以11bc b c =++. ①当b 、c 中含有质数2时,不妨令b =2 2c =11+2+c ,解得c =13,符合题意.②当b 、c 中不含有质数2,即b c 都是奇数时, 不妨令:b =2M +1,c =2N +1,有: (2M +1)(2N +1)=11+2M +1+2N +1. 即4MN =12,MN =3. 显然只能是M =3,N =1.此时b =2×3+1=7,c =1×2+1=3,符合题意. 综上,这三个质数可以是:2、11、13或3、7、11.【总结】本题是一道综合性非常强的题目,要求学生要充分理解其中的假设法.1、分解素因数每个合数都可以写成几个素数相乘的形式,其中每个素数都是这个合数的因数,叫做这个合数的素因数.知识精讲模块二:分解素因数5 / 5把一个合数用素因数相乘的形式表示出来,叫做分解素因数. 2、口算法分解素因数例如:728922233=⨯=⨯⨯⨯⨯. 3、短除法分解素因数形如右图,这种在左侧写除数,下方写商的除法格式叫做“短除法”. 用短除法分解素因数的步骤如下:(1)先用一个能整除这个合数的素数(通常从最小的开始)去除;(2)得出的商如果是合数,再按照上面的方法继续除下去,直到得出的商是素数为止; (3)然后把各个除数和最后的商按从小到大的顺序写成连乘的形式.【例11】把24分解素因数的正确算式是( )A .24234=⨯⨯B .242223=⨯⨯⨯C .2412223=⨯⨯⨯⨯D .24226=⨯⨯【难度】★ 【答案】B【解析】A 、D 选项中有合数,C 选项中有1,1既不是素数,也不是合数. 【总结】每个合数都可以写成几个素数相乘的形式,叫做分解素因数.【例12】在等式462223n ⨯==⨯⨯⨯中,4和6都是n 的( ),2和3都是n 的( )A .素因数B .素数C .因数D .合数【难度】★ 【答案】C 、A 【解析】略【总结】本题主要考察素数和素因数的区别. 【例13】把以下各数分解素因数:35,72,105,108,238.【难度】★【答案】35=5×7; 72=2×2×2×3×3; 105=3×5×7; 108=2×2×3×3×3;238=2×7×17.【解析】略【总结】本题主要考查如何将一个合数分解素因数.例题解析355 7【例14】请把2、3、5、7、14、15这六个数分成两组,使每组数的乘积相等. 【难度】★★【答案】3、5、14和2、7、15.【解析】因为14=2×7,所以14和2、7分在两组;因为15=3×5,所以15和3、5分在两组;故:3、5、14一组,2、7、15一组. 【总结】本题主要是对分解素因数的综合运用.【例15】如果a <>表示全部素因数的和,如6235<>=+=,试求3510<>-<>的值. 【难度】★★ 【答案】7【解析】由已知得:<35>=5+7=14,<10>=2+5=7, 所以<35>-<10>=7. 【总结】本题类似于阅读理解题,要对a <>所表示的概念准确理解.【例16】下面的算式里,□里数字各不相同,求这四个数字的和.□□×□□=1995.【难度】★★ 【答案】20【解析】因为1995=3×5×7×19=35×57,所以这四个数分别是3、5、5、7, 和是:3+5+5+7=20.【总结】本题主要是对分解素因数的综合运用.【例17】有168颗糖,平均分成若干份,每份不得少于10颗,也不能多于50颗.共有多少种分法? 【难度】★★ 【答案】5种【解析】由因为168=1×168=2×84=3×56=4×42=6×28=8×21=12×14;所以168的因数有:1,2,3,4,6,8,12,14,21,28,42,56,84,168.师生总结1、 分解素因数的方法有哪些?2、归纳总结短除法分解素因数的步骤.因为每份不得少于10颗,也不能多于50颗,所以满足条件的因数有:12、14、21、28、42.所以共有5种分法.【总结】本题主要是利用因数的概念解决实际问题.【例18】把一篮苹果分给4人,使四人的苹果数一个比一个多2,且他们的苹果个数之积是1920.这篮苹果共有多少个?【难度】★★【答案】28个【解析】因为1920=2×2×2×2×2×2×2×3×5=4×6×8×10,所以四个小朋友分别分到4、6、8、10个苹果,4+6+8+10=20(个) 答:这篮苹果共有20个.【总结】本题是一道应用题,主要是还是利用分解素因数的思想进行求解.【例19】有a个人都属鸡,而且生日都是3月20日.某年,他们的年龄数的乘积为207025,他们的年龄数之和是102.则a等于几?【难度】★★★【答案】6【解析】因为207025=5×5×7×7×13×13=1×13×13×25×49,又这几个人的生肖相同,所以他们的年龄是49,25,13,13,1,因为49+25+13+13=100,所以102-100=2.所以有2人年龄为1,有2人年龄为13,有1人年龄为25,有1人年龄为49,共6人,即a=6.【总结】本题是一道非常综合的题目,主要还是利用分解素因数的方法,找到原数的因数,从而求出适合题意的解来.模块三:公因数和最大公因数知识精讲1、公因数几个数公有的因数,叫做这几个数的公因数.2、最大公因数7 / 7几个数的公因数中,最大的一个叫做这几个数的最大公因数.3、两个数互素如果两个整数只有公因数1,那么称这两个数互素.4、求最大公因数求几个数的最大公因数,只要把它们所有公有的素因数连乘,所得的积就是它们的最大公因数.例题解析【例20】求出下列各组数的最大公因数.(1)14和42;(2)121和44;(3)28和56;(4)17和9.【难度】★【答案】(1)14;(2)11;(3)28;(4)1.【例21】指出下列哪组中的两个数互素.(1)3和5;(2)6和9;(3)14和15;(4)18和1.【难度】★【答案】(1)(3)(4).【解析】如果两个整数只有公因数1,那么称这两个数互素.【总结】互素两数的几种常见类型:(1)两个数都是素数;(2)一个素数,一个合数;(3)1和其它的任意正整数.【例22】找出下列各数的公因数与最大公因数.(1)84、28、60;(2)12、16、20.【难度】★【答案】(1)公因数:1、2、4,最大公因数:4;(2)公因数:1、2、4,最大公因数:4.【例23】下列说法中,正确的个数有()个①2是4和16的一个公因数;②12是24和36的最大公因数;③如果两个数互素,那么这两个数一定都是素数;④1和任何正整数互素.A.0 B.1 C.2 D.3【答案】D9 / 9【例24】已知m n p 、、都为自然数,且2n p ÷=,12m n ÷=,那么m n p 、、的最大公因数是多少? 【难度】★★ 【答案】p【解析】m 是n 的倍数,n 是p 的倍数,因此m 是p 的倍数;所以最大公因数是p . 【总结】若三个数都是倍数关系,则它们的最大公因数是最小的那个数.【例25】已知两个数的积是5766,它们的最大公因数是31,求这两个数. 【难度】★★【答案】31、168或62、93.【解析】设这两个数是31a ,31b (a 、b 互素), 则:31a ×31b =5766 ∴ab =6① a =1,b =6时,两个数是31、168; ②a =2,b =3时,两个数是62、93.【总结】本题是一道综合题,综合运用了最大公因数和因数的概念.【例26】将长、宽、高分别是120厘米,90厘米,60厘米的长方体木料锯成同样大小的正方体木块,而没有剩余,锯成的木块棱长最长是多少?共可以锯成多少块? 【难度】★★ 【答案】30厘米,9块【解析】120、90、60的最大公因数是30,所以棱长最长为30厘米. (120+90+60)÷30=9(块)答:锯成的木块棱长最长是30厘米,共可以锯成9块.【例27】学校买来40支圆珠笔和50本练习本,平均奖给四年级三好学生,结果圆珠笔多4支,练习本多2本,四年级有多少名三好学生,他们各得到什么奖品? 【难度】★★【答案】(1)12名,3支圆珠笔,4本练习本;(2)6名,6支圆珠笔,8本练习本. 【解析】40-4=36(支),50-2=48(本),36与48的最大公因数是12. 12=1×12=2×6=3×4.(1)若12名,每人3支圆珠笔,4本练习本; (2)若6名,每人6支圆珠笔,8本练习本; (3)若4名或2名,圆珠笔可分完,与题意矛盾; 【总结】本题是利用最大公因数的思想解决实际问题.【例28】幼儿园一个班买书,如买35本,平均分给每个小朋友差一本,如买56本,平均分给每个小朋友后还剩2本,如买69本,平均分给每个小朋友则差3本.这个班的小朋友最多有几人?【难度】★★★【答案】18人【解析】35+1=36本,56-2=54本,69+3=72本,36、54、73的最大公因数是18.答:这个班的小朋友最多有18人.【总结】本题是利用最大公因数的思想解决实际问题.师生总结1、两个整数的最大公因数的方法有哪些?2、互素的两个整数具有什么样的特征?【习题1】下列说法中,正确的个数有()个①一个自然数,不是质数就是合数;②任何一个自然数至少有2个因数;③90分解素因数是90=5⨯2⨯9;④两个素数的和一定是偶数;A.0 B.1 C.2 D.3【难度】★【答案】A【习题2】将20写成两个质数之和,这两个质数最大乘积是多少?【难度】★【答案】91【解析】因为20可以写成3+17或7+13的两个质数的和,所以积最大是:7×13=91.【习题3】下列各数中是否含有相同的公因数,若含有请指出,并求出最大公因数.(1)6和9;(2)27和51;(3)28、42和56.【难度】★【答案】(1)含有,最大公因数:3;(2)含有,最大公因数:3;(3)含有,最大公因数:14.【习题4】已知两个数的和是107,它们的乘积是1992,这两个数分别是多少?【难度】★★【答案】24和83【解析】1992=2×2×2×3×83=24×83,所以这两个数是24和83.【总结】本题主要是考查分解素因数在数字求和中的运用.【习题5】两个正整数的和是50,他们的最大公因数是5,这两个数的差的最大值是几?【难度】★★【答案】40【解析】设这两个数是5a,5b(a、b互素),则:5a+5b=50.所以a+b=10 .①a=1,b=9时,两个数是5、45;45-40=5;②a=3,b=7时,两个数是15、35.35-15=20;所以这两个数的差的最大值是40.【总结】本题主要考查素数在数字计算中的运用.【习题6】王老师带领一班同学去植树,学生恰好分成4组.如果王老师和学生每人植树一样多,那么他们一共植了539棵.这个班有多少个学生?每人植树多少棵?【难度】★★【答案】48个,11棵【解析】因为539=7×7×11=49×11,所以学生数是48人,每人植树11棵.【总结】本题是对分解素因数的综合运用.【习题7】某农副食品店销售三级别的大米,已知一级大米150斤,二级大米180斤,三级大米210斤的价格都是450元,现需将这三种大米分别按整斤数装袋,要求每袋的价格都相等,那么每袋的价格最低是多少元?【难度】★★【答案】15元【解析】因为150、180、210的最大公因数是30,所以每种大米最多分30小份,11 / 11即每份最低:450÷30=15元.答:每袋的价格最低是15元.【总结】本题是利用最大公因数的思想解决实际问题.【习题8】 “九九重阳节敬老节”将至,幸福小区组织一批老年人决定分乘若干辆至多可乘44人的大巴前去郊游.如果打算每辆车坐22个人,就会有1个人没有座位;如果少开一辆车,那么,这批老人刚好平均分乘余下的大巴.那么有多少个老人?原有多少辆大巴?【难度】★★★【答案】529个,24辆.【解析】22+1=23人,因23是质数,所以把这23人,只能平均分到23个车里. 所以原来的车数是:23+1=24(辆),24×22+1=529(个).答:有529个老人,原有24辆大巴.【总结】本题的综合性比较强,解题是注意对本题中的“23”这个素数的准确理解.【习题9】 甲乙两人射箭,规定每射一箭得到的环数是0~10这10个数中的一个整数,他们各射5靶,每人得到的环数之积刚好都是1764,但是甲的总环数比乙少4环,求甲、乙各自的总环数.【难度】★★★【答案】24环,28环.【解析】因为1764=2×2×3×3×7×7,所以每人都有两个7环.剩余三个环数可能为:2、2、9; 3、3、4; 2、3、6; 1、4、9; 1、6、6. 和分别为:13,10,11,14,13.因为甲的总环数比乙少4环,所以甲另外三环的和应是10环,乙另外三环的和应是14环.所以甲的环数为:14+10=24环,乙的环数为:14+14=28环.【总结】本题依旧是考查分解素因数在实际问题中的应用.【习题10】 有a b c d 、、、四个数,已知a b 、的最大公因数是60,c d 、的最大公因数是96,这四个数的最大公因数是多少?【难度】★★★【答案】12【解析】由已知得:a 、b 是60的倍数,c 、d 是96的倍数,因此60和96的最大公因数即是a b c d 、、、四个数的最大公因数.而60和96的最大公因数是12.13 / 13 答:这四个数的最大公因数是12.【总结】本题主要是考查学生对最大公因数的概念的准确理解和运用.【作业1】 求出下列每组数的最大公因数.(1)48和72;(2)104和182; (3)13和52; (4)160和185. 【难度】★【答案】(1)24;(2)26;(3)13;(4)5.【解析】(1)短除法得: 48与72的最大公因数是24;(2)短除法得:104与182的最大公因数是26;(3)13和52是倍数关系,最大公因数是较小数,13与52的最大公因数是13;(4)短除法得:160与185的最大公因数是5.【总结】本题主要是考查求两个数的最大公因数.【作业2】 已知四个小于10的自然数,它们的积是360.已知这四个数中只有一个是合数,求这四个数.【难度】★【答案】3、3、5、8【解析】因为360=2×2×2×3×3×5,又四个数中只有一个合数,且小于10,所以只能是8.所以这四个数是3、3、5、8;【总结】本题还是考查分解素因数的运用.【作业3】 已知:235A =⨯⨯,335B =⨯⨯,则A 和B 的公因数有哪些,最大公因数是几?【难度】★【答案】公因数:3、5、15;最大公因数:15.【解析】略【总结】求最大公因数的方法:①枚举法;②短除法;③分解素因数法.【作业4】 将下列各数分解素因数.36,81,143,437,663【难度】★★ 课后作业【答案】36=2×2×3×3;81=3×3×3×3;143=11×13;663=3×13×17.【解析】略【总结】本题主要是考查如何将一个正整数分解素因数.【作业5】两个数的和为90,两个数的最大公因数是15,求这两个数.【难度】★★【答案】15,75【解析】设这两个数是15a,15b(a、b互素),则:15a+15b=90,所以a + b = 6 .因为这两个数的最大公因数是15,所以a=1,b=5.所以这两个数是15、75.【总结】本题已知两数和和两数的最大公因数,在求这两个数时注意方法的选用.【作业6】已知两个数的和被5除余1,它们的积是2924,那么它们的差等于多少?【难度】★★【答案】25【解析】2924=2×2×17×43=1×2924=2×1462=4×731=17×172=34×86=43×68因为和被5除余1,所以这两个数是:43、68,68-43=25,答:它们的差是25.【总结】本题是利用求一个数的因数的方法求出满足条件的两个数.【作业7】用一个数去除18、24、60都能整除,这个数最大是多少?【难度】★★【答案】6【解析】18、24、60的最大公因数是6,所以这个数最大是6.【总结】本题主要考查求三个数的最大公因数.【作业8】288人参加团体操,分成人数相等的若干队,每队人数在15至35之间.有哪些分法?【难度】★★【答案】3种分法:(1)每队16人,共18队;(2)每队18人,共16队;(3)每队24人,共12队.【解析】因为288=2×2×2×2×2×3×3 =2×144=3×76=4×72=6×48=8×36=12×24=16×18,而每队人数在15至35之间,故有3种分法:16人,18队;18人,16队;24人,12队;【总结】本题是利用求一个数的因数的方法求出满足条件的两个数.【作业9】有三根绳子,一根长36米,一根长16米,一根长24米.要把它们剪成同样长的小段做跳绳,每小段要尽量长,一共能剪成多少根跳绳?【难度】★★★【答案】19根【解析】因为36、16、24的最大公因数是4,所以一共能剪成:(36+16+24)÷4=19根.【总结】本题主要是考查利用三个数的最大公因数解决实际问题.【作业10】从一块正方形的木板上锯下宽为3分米的一个木条后,剩下木板的面积是108 平方分米,则锯下的木条面积是多少平方分米?【难度】★★★【答案】36平方分米【解析】108=2×2×3×3×3=12×9,则原来木板边长12分米.12×3=36平方分米.答:锯下的木条面积是36平方分米.【总结】本题综合性较强,解题时注意对题意的准确理解.15 / 15。
《最大公因数》(同步练习)五年级下册数学人教版

《最大公因数》(同步练习)五年级下册数学人教版一、单选题1.16和24的最大公因数是()A.4B.8C.16D.482.12和24的公因数有()个。
A.4B.5C.63.有一个比20小的偶数,有因数3,又是4的倍数,这个数是()A.18B.12C.8D.64.李婷家客厅长4.8米,宽4.2米,选用边长()分米的方砖铺地不需要切割。
A.4B.5C.65.14和28的公倍数()。
A.有无数个B.只有1个C.一定比28小D.是286.6是下列哪一组数的最大公因数()A.24和30B.16和24C.18和20D.12和157.3a=b,(a、b都是非0自然数),a和b的最大公因数是()。
A.1B.a C.b D.b+a8.a=2×3×7 ,b=3×7×11 ,a和b的最大公约数是()。
A.3B.7C.6D.219.刘师傅为一间长50分米,宽30分米的书房铺设方砖,要想方砖没有剩余,方砖的边长最长是()分米。
A.5B.10C.15D.3010.在a与b两个整数中,a的所有质因数2、3、5、7、11,b的所有质因数是2、3、13,那么a与b的最大公因数是()A.210B.6C.55D.4211.a、b的最大公因数是10,a、b的公因数有()个。
A.1B.4C.3D.512.两个数最大公因数是4,最小公倍数是24,如果其中一个数是12,那么另一个数是()A.4B.8C.16D.24二、判断题13.m和n是两个大于0的自然数,m是n的5倍,那么m和n的最大公因数是n()14. 能被2、3、5、6同时整除的最小的一个数是60.()15.最小的合数和最小的质数这两个数的公因数只有1.()16.两个质数没有最大公因数。
()17.两个数的积一定比这两个数的最小公倍数大。
()18.如果甲数是乙数的2倍(甲、乙两数均为非0的自然数),那么甲数和乙数的最大公因数就是2。
()三、填空题19.一个自然数的最大因数与他的最小倍数的关系是。
最大公因数

第四讲 最大公因数由于一个数的因数个数是有限的而且最大的因数是这个数本身,最小的因数都是1.因此,几个数公共的因数也只考虑其最大的公共因数,而不考虑最小的公共因数。
例如:12、16、18的最大公因数12的因数有:1、2、3、4、6、1216的因数有:1、2、4、8、16 18的因数有:1、2、3、6、9、18因此12、16、18的最大的公共因数即最大公因数是:2一、填空1、甲=2×3×5,乙=2×3×7,甲和乙的最大公因数是( ).2、36和60相同的质因数有( ),它们的积是( ),也就是36和60的(). 3、( )的两个数,叫做互质数.4、自然数a 除以自然数b ,商是15,那么a 和b 的最大公因数是( )5、按要求,使填出的两个数成为互质数.①质数( )和合数( ),②质数( )和质数( ),③合数( )和合数( ),④奇数( )和奇数( ),⑤奇数( )和偶数().6、两个数为互质数,这两个数的最大公因数是( ).7、所有自然数的公因数为( ).8、8与9的最大公因数是( );48、12和16的最大公约数是( );6、30和45的最大公约数是( );150和25的最大公约数是( ).二、判断(对的打“√”,错的打“×” ).1、互质数是没有公因数的两个数.( )2、成为互质数的两个数,一定是质数.( )3、只要两个数是合数,那么这两个数就不能成为互质数.( )4、两个自然数分别除以它们的最大公因数,商是互质数.( )5、因为 15÷3=5,所以15和3的最大公因数是5.( )6、30 、15和5的最大公因数是30.( )7、最小的合数和最小的质数这两个数不是互质数.( )8两个数的公因数的个数是有限的. ( )公共得因数有:1、29、1和任意非零自然数的最大公因数是1. ()三、选择题1、成为互质数的两个数().①没有公因数②只有公因数1 ③两个数都是质数④都是质因数2、下列各数中与18互质的数是().①21 ②40 ③25 ④183、下列各组数中,两个数互质的是().①17和51 ②52和91 ③24和25 ④ 11和224、甲数的质因数里有1个7,乙数的质因数里没有7,它们的最大公因数的质因数里应该().①有1个7 ②没有7 ③不能确定5、甲、乙两数的最大公因数是7,甲数的3倍与乙数的5倍的最大公因数()①肯定是7 ②肯定不是7 ③不能肯定6、甲数是乙数的倍数,甲乙两数的最大公因数是()① 1 ②甲数③乙数④甲乙两数的积四、用短除法求下列各组数的最大公约数.1、 56和422、 225和153、 84和1054、 54、72和905、 60、90和120五、应用题1、用96朵红花和72朵白花做花束,如果每个花束里的红花朵数都相等,每个花束里的白花的朵数也都相等.每个花束里最少有几朵花?2、五年级同学参加劳动,男同学有54名,女同学有60名。
最小公因数

最小公因数
1、最小公因数就是两个数同时可以除以的最小的数。
公因数,亦称“公约数”。
它是一个能同时整除若干整数的整数。
2、如果一个整数同时是几个整数的因数,称这个整数为它们的“公因数”,公因数中最大的称为最大公因数,最小的即是最小公因数。
任何两个不为零正整数的最小公因数均为1。
最大公因数的求法:质因数
分解法:把每个数分别分解质因数,再把各数中的全部公有质因数提取出来连乘,所得的积就是这几个数的最大公约数。
短除法:短除法求最大公约数,先
用这几个数的公约数连续去除,一直除到所有的商互质为止,然后把所有的除
数连乘起来,所得的积就是这几个数的最大公约数。
最大公因数,也称最大公约数、最大公因子,指两个或多个整数共有约数
中最大的一个。
a,b的最大公约数记为(a,b),同样的,a,b,c的最大公约数记为(a,b,c),多个整数的最大公约数也有同样的记号。
求最大公约数有多种方法,常见的有质因数分解法、短除法、辗转相除法、更相减损法。
与
最大公约数相对应的概念是最小公倍数,a,b的最小公倍数记为[a,b]。
最大和最小公因数怎样找
1.用短除法
把两个数同时除以共有的因数.
最小公因数当然是1,最大的是把左边的数乘起来.
2.分解质因数
如:80和60
80=2×2×2×2×5
60=2×2×3×5
最小公因数是1,
最大公因数是2×2×5=20。
455 68 的最大公因数

455 68 的最大公因数最大公因数,也叫最大公约数,是指两个或多个整数共有的约数中最大的一个。
在这里,我们要求455和68的最大公因数是多少。
我们可以列举出455的约数:1, 5, 7, 13, 35, 65, 91, 455。
然后,我们列举出68的约数:1, 2, 4, 17, 34, 68。
观察这两个数的约数,可以发现它们的公约数有:1和17。
其中最大的一个是17,因此455和68的最大公因数是17。
最大公因数在数学中有很多应用。
例如,我们可以利用最大公因数来简化分数。
将分子和分母同时除以最大公因数,可以得到一个分数的最简形式。
最大公因数还可以用来求解整数的倍数关系。
当两个整数的最大公因数为1时,我们称这两个数互质。
互质的两个数的倍数关系具有一些特殊的性质。
最大公因数还可以应用在代数中的因式分解问题中。
通过找出多项式中的最大公因式,可以将多项式分解为更简单的因式。
最大公因数还与质因数分解有密切关系。
每个正整数都可以唯一地表示为一串质数的乘积,这就是质因数分解。
最大公因数可以通过求取两个数的质因数分解,再取两者中相同质因数的乘积得到。
除了最大公因数,还有一个相关的概念是最小公倍数。
最小公倍数是指两个或多个整数的公倍数中最小的一个。
最小公倍数在解决整数倍数关系、分数加减法、有理数运算等问题中有重要应用。
在实际生活中,寻找最大公因数和最小公倍数也有很多应用。
例如,在设计家具布局时,需要考虑到家具尺寸的公约数和公倍数,以便合理摆放。
在电子产品的设计中,寻找最大公因数和最小公倍数有助于优化电路布局和减少电路元件的数量。
最大公因数是一个数学中常见且有重要应用的概念。
通过寻找最大公因数,我们可以简化分数、解决倍数关系、进行因式分解等问题。
在实际生活中,最大公因数和最小公倍数也有很多应用。
希望通过本文的介绍,读者对最大公因数有更深入的了解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.把15和20的因数、公因数分 别填在圈内,再找出它们的最 大公因数。
15的因数 1 5
20的因数 1 5 2 4
3
15
10 20
15的因数
3
20的因数 1
5
2
10
4
20
15
15和20的公因数
2.先在空格里画“√”,再 填空。
√√ √ √√ √ √ √
√√ √√
√
√
8和10的公因数有 1,2 。 最大公因数是 2 。 8和20的公因数有1,2,4 。 最大公因数是 4 。 10和20的公因数有1,2, 5,10 。 最大公因数是 10 。
12÷1=12
18÷1=18
边长1厘米的正方形纸 片正好能铺满。
边长1厘米、2厘米或 3厘米的正方形纸片都 能正好铺满。
只要边长的厘米数既 是12的因数,又是18的 因数,就能正好铺满。
1,2,3和6既是12的因数, 又是18的因数,它们是12和 18的公因数。
4是12和18的公因数吗?为什么?
12的因数有1,2,3, 4,6,12; 42的因数有1,2,3, 6,7,14,21,42; 12和42的公因数有1, 2 ,3 ,6 ; 最大的公因数是6。
用同样的方法找 出16和24的公因数。
4虽然是12的因数,但不是 18的因数 (18÷4=4···2 ),所以 说4不是12和18的公因数。
8和12的公因数有哪些?最 大的公因数是几?
先独立解答,然后 在小组内交流。
分别写出8和12的所有因数, 再找一找。 8的因数:1,2,4,8。 12的因数:1,2,3,4, 6,12。 8和12的公因数有1,2,4, 最大的公因数是4。
12
8和12的的公因数
在18的因数上画“△”,在 30的因数上画“○”。 1 ○ 2 ○ 3 4 ○○ 5 △ 6 7 8 △ 9 ○ 10 △ △ △ ○ 11 12 13 14 ○ 15 16 17 △ 18 19 20
21 22 23 24 25 26 27 28 29 30
○
18和30的公因数有 1,2,3,6, 最大公因数是 6 。
边长6厘米的正方形纸 片正好能铺满。
12÷4=3
18÷4=4··2
边长4厘米的正方形纸 片不能正好铺满。
还有哪些边长是整厘米数 的正方形纸片也能正好铺满 这个长方形?有什么规律呢边长3厘米的正方形纸 片正好能铺满。
12÷2=6
18÷2=9
边长2厘米的正方形纸 片正好能铺满。
苏教版五年级数学下册
公因数和最大公因数
学习目标
1、 理解公因数、最大公因数的概念,能运
用所学概念判断两个数是不是互质数。
2、认识公因数和最大公因数,会在集合图中
分别表示两个数的因数和它们的公因数。
分别用边长6厘米和4厘米的正 方形纸片铺下面的长方形。
哪种纸片能将长方形正好铺满?
12÷6=2
18÷6=3
先找8的因数,再从8的 因数中找出12的因数。 8的因数有1,2,4,8。 其中1,2,4也是12的因数。 8和12的公因数有1,2,4, 最大的公因数是4。
8和12的公因数中最大的 一个是4,4就是8和12的最 大公因数。
我们可以用下图表示8和12 的公因数。 8的因数 12的因数
8 1 2 4 3 6
