高中数学必修4第一章_三角函数知识点

合集下载

高中数学必修四第一章三角函数 1.4.2.1 周期函数

7 2
-4
, 即��
7 2
= ��
-
1 2
.
又当 x∈(-1,0)时,f(x)=2x+1,
∴��
7 2
= ��
-
1 2
=2×
-
1 2
+ 1 = 0.
题型一题型二题型三题型四
反思1.解答此类题目的关键是利用化归的思想,借助周期函数的定义把待求问题转化到已知区间上,代入求值即可.
π 6
+ 2π = 2(�� + π) − π6,
∴f(x+π)=sin
2(��
+
π)-
π 6
=sin
2��-
π 6
+
2π
= sin
2��-
π 6
= ��(��).
∴T=π.
本节结束，谢谢大家！
题型一题型二题型三题型四
题型二求三角函数的周期
【例 2】求下列函数的周期:
(1)f(x)=sin
1 4
��
+
π 3
(��∈R);
(2)y=|sin x|(x∈R).
分析:对于(1),可结合周期函数的定义求解;对于(2),可通过画函
数图象求周期.
题型一题型二题型三题型四
(2)函数 y=sin
��
+
π 4
(��
>
0)的周期是
2π 3
,
则��
=
_____.

高中数学必修4《三角函数》知识点与易错点归纳

高中数学必修4《三角函数》知识点与易错点归纳知识点（一）任意角和弧度制1．与θ终边相同的角的集合是；第一或第三象限角的集合是；x 轴上的角的集合是；2.若α是锐角，则πα-是第象限角；πα+是第象限角；2πα-是第象限角；α-是第象限角；32πα-是第象限角；2πα+是第象限角。

3.180°=π；1°= 弧度； 1弧度= ；圆心角α弧度数的绝对值||α= ；扇形面积公式S = 。

4.角ααcos 2=-，则2α角是象限角。

知识点二．任意角的三角函数1.任意角的三角函数的定义：设α是任意一个角，(,)P x y 是α的终边上的任意一点（异于原点），它与原点的距离是0r =>，那么sin α= ，cos α= ,tan α= 。

2.如图，三角函数线：正弦线是、余弦线是、正切线是；4.已知角α的终边经过点(3,4)P -，则sin tan αα+的值为； 5．函数sin cos tan |sin ||cos ||tan |y αααααα=++的值域是； 6．sin cos θθ<⇔ ；sin cos θθ>⇔ 。

知识点三．同角三角函数的基本关系式及诱导公式1.平方关系：22sin cos αα+= ；商数关系：tan α= ；2.已知tan 2α=，则ααααcos sin cos 3sin +-＝；sin cos αα⋅＝；4.1419costan()34ππ+-的值为； 5.化简23sin (180)cos(360)sin(270)cos (180)cos(90)tan(180)αααααα+⋅-⋅-=--⋅+⋅+ 。

yTA xα B SO M P知识点四．正弦、余弦、正切公式及倍角公式1.基本公式及变式()()22222sin sin cos cos sin sin 22sin cos 1sin 2(sin cos )cos cos cos sin sin cos2cos sin 2cos 112sin t αβαβαβαβαβαααααααβαβαβααααα==±=±−−−→=⇒±=±±=−−−→=-=-=-↓↓令令　()222tan tan 2tan 1+cos21cos2an tan 2cos sin 1tan tan 1tan 22αβααααβααααβα±-±=→=- ＝　,＝变式：1tantan tan tan()(1tan tan),tan()1tan4απαβαβαβαα++=+⋅-⋅=+-；sin cos ),sin 2sin(cos 2sin()436πππθθθθθθθθθ±=±±=±±=±2.4411111212cos sin ππ-= ；sin163sin 223sin 253sin313+= ； 3.在ABC ∆中，53sin ,cos 135A B ==,则cos C = ； 4.在直角ABC ∆中，sin sin A B ⋅的最大值为；5.已知等腰三角形的一个底角的正弦值为13，则这个三角形的顶角的余弦值是。

高一数学人教A版必修4第一章(三角函数)本章小结课件

1-(-
5 5
)2
=
-
2
5 5
.
6. 用 cosa 表示 sin4a-sin2a+cos2a.
解: sin4a-sin2a+cos2a = sin2a(sin2a-1)+cos2a = sin2a(-cos2a)+cos2a = cos2a(1-sin2a) = cos4a.
7. 求证:
(1) 2(1-sina)(1+cosa) = (1-sina+cosa)2; (2) sin2a+sin2b-sin2a·sin2b+cos2a·cos2b =1.
6. 终边位置确定三角函数值的正负
y
y
y
++ -o - x
-+
ox
-+
-+
ox
+-
sina
cosa
tana
正弦上正下负, 余弦右正左负, 正切一三正二四负.
7. 同角三角函数的关系
sin2a+cos2a=1,
sina cosa
=
tana
.
常用的变形:
sin2a=1-cos2a. cos2a=1-sin2a.
解: 由已知得 sin2x=4cos2x, 1-cos2x=4cos2x,
解得 cos x =
5 5
.
又由已知得 tanx =2,
则 x 是第一、第三象限角.
当 x 是第一象限角时,
cos x =
5 5
,
sin x =
1-(
5 5
)2=
2
5 5
;
当 x 是第三象限角时,

必修4 数学三角函数1

高中数学必修4——三角函数1【知识归纳】1、象限角：第一象限角的集合为第二象限第三象限第四象限2、与角α终边相同的角的集合为{}360,k k ββα=⋅+∈Z3、弧度制与角度制的换算公式：2360π=，1180π=，180157.3π⎛⎫=≈ ⎪⎝⎭． 4、定义：设α是一个任意大小的角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()0r r =>，则sin y r α=，cos x r α=，()tan 0yx xα=≠． 5、三角函数在各象限的符号：一全二正弦，三切四余弦6、三角函数线：sin α=MP ，cos α=OM ，tan α=AT ．7、同角三角函数的基本关系：()221sin cos 1αα+= ()sin 2tan cos ααα=8、三角函数的诱导公式：（口诀：奇变偶不变，符号看象限．）9、函数sin y x =的图象上所有点向左（右）平移ϕ个单位长度，得到函数sin y x =+的图象；再将函数()sin y x ϕ=+的图象上所有点的横坐标缩短（ω>1）（伸长ω<1）到原来的ω倍（纵坐标不变），得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象． 10.函数()()sin 0,0y x ωϕω=A +A >>的性质： ①振幅：A ；②周期：2πωT =；③频率：12f ωπ==T ；④相位：x ωϕ+；⑤初相：ϕ．11、正弦函数、余弦函数和正切函数的图象与性质：sin y x = cos y x =tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1- []1,1-R函数性质最值当22x k ππ=+()k ∈Z 时，max 1y =；当22x k ππ=-()k ∈Z 时，min 1y =-．当()2x k k π=∈Z 时，max 1y =；当2x k ππ=+()k ∈Z 时，min 1y =-．既无最大值也无最小值周期性 2π2ππ奇偶性奇函数偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数；在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数．在[]()2,2k k k πππ-∈Z 上是增函数；在[]2,2k k πππ+()k ∈Z 上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z ⎪⎝⎭对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴【类型题】1．已知A={第一象限角},B={锐角},C={小于90°的角},那么A.B.C 的关系是( ) A ．B=A ∩C B ．B ∪C=C C ．A C D ．A=B=C 2．下列各组角中，终边相同的角是（） A ．π2k与)(2Z k k ∈+ππ B ．)(3k3Z k k ∈±πππ与 C ．ππ)14()12(±+k k与 )(Z k ∈ D ．)(66Z k k k ∈±+ππππ与4. 已知)20(παα<<的正弦线与余弦线相等,且符号相同,那么α的值为（）A ．ππ434或 B ．ππ4745或 C ．ππ454或 D ．ππ474或 5. 已知sin 2cos 5,tan 3sin 5cos ααααα-=-+那么的值为（）A ．－2B ．2C ．1623D ．－1623变：已知21tan -=x ，则1cos sin 3sin 2-+x x x = .6、已知34tan =x ,且x 在第三象限，则=x cos ( )A.54B. 54-C. 53D.53-8. 设角则,635πα-=)(cos )sin(sin 1)cos()cos()sin(222απαπααπαπαπ+--+++--+的值等于（） A ．33B ．－33 C ．3 D ．－39. 函数)4sin(π+=x y在下列哪个区间为增函数（）A ．]4,43[ππ-B ．]0,[π-C ．]43,4[ππ-D ．]2,2[ππ-10. 函数)42sin(log 21π+=x y的单调减区间为（）A ．)(],4(Z k k k ∈-πππ B ．)(]8,8(Z k k k ∈+-ππππC ．)(]8,83(Z k k k ∈+-ππππD ．)(]83,8(Z k k k ∈++ππππ11. 函数)252sin(π+=x y的图象的一条对称轴方程是（）A ．2π-=xB ．4π-=xC ．8π=xD ．π45=x13、要得到函数)32cos(2π+=x y 的图像。

必修四第一章诱导公式、三角函数图像及其性质复习

学生教案教师姓名学生姓名填写时间年级高一学科数学上课时间第（）次课阶段基础（ √ ）提高（）强化（1、熟记诱导公式及其运用； 2、熟悉三角函数的图像及其单调性；）课时计划共（）次课教学目标3、熟悉 y  Asin(x   )( A  0，  0) 的图像及其变化1、重难点 2、诱导公式及三角函数的关系；三角函数图像的变化与三角函数的关系；课后作业：教师评语及建议：科组长签名学生教案诱导公式可用十个字概括为“奇变偶不变，符号看象限” 。

诱导公式一： sin(  2k )  sin  ，诱导公式二： sin(180   )   sin  ；诱导公式三： sin( )   sin  ；诱导公式四： sin(180   )  sin  ；诱导公式五： sin(360   )   sin  ；－ sin cos －sin  cos cos(  2k )  cos  ，其中 k  Zc o s ( 1 8 0  )c o s cos( )  cos cos(180   )   cos c o s ( 3 6 0  )  cos2  －sin  cos  sin  －cos  －cos  －sin 2k   k  Z cos  sin 2cos  sin （1）要化的角的形式为 k 180   （ k 为常整数）；（2）记忆方法： “函数名不变，符号看象限” ；知识点一、诱导公式的的直接运用用诱导公式可将任意角的三角函数化为锐角的三角函数，其一般步骤是什么？ ①化负角的三角函数为正角的三角函数； ②化大于 2 π 的正角的三角函数为 0～ 2 π 内的三角函数； ③化 0～ 2 π 内的三角函数为锐角的三角函数．1 例 1、：已知  是第三象限的角且 sin    ，求 sin( π   ) ， sin(  π) 3变式 1、cos150 °的值为（）2、下列各数中，与 cos1030 °相等的是（A ． cos50 ° B ． -cos50 °） C ． sin50 ° D ． -sin50 °3、学生教案4、5、诱导公式 tan （ n π - α ） = （A ． -tan α C ． ± tan α）（其中 n∈ Z） B ． tan α D．与 n 的值为奇偶数有关6、例 2、、已知 cos  , 且 1 32   0, 求sin(   )  sin(2   ) 的值 cos( )  tan变式练习 1、2、例题 3、变式练习 1、学生教案2、3、配凑角例题 4、已知 sin(π 1 5π   )  ，求 sin(   ) 的值. 6 3 6变式练习1、2、汇总练习 1 选择题（1） 1  sin 2 678 =（（A）sin42° （2）计算（A）0 （3）cos( π +α )= A.  ）（C）sin21° ）（C）-1 （D）2 ) D.  （D）cos21°（B）cos42° sin(  )  sin() 的值为（ tan(  )（B）11 3π  α  2 π ，则 sin(2 π -α )等于( ， 2 2B.3 23 2C.1 23 2学生教案cos(  ) sin 2 (  3) （4）化简的结果是（ tan(  4) tan(  ) cos3 (  )（A）1 （5）已知α ∈  （B）0 （C）－1）（D）1 2）3  π 3π  ,  , tan(α -9 π )=- ,则 sin α +cosα 等于（ 4 2 2 B．-A．-1 53 5C．1 5D．±1 52、计算 tan 37π 55π  35π   46π  的值． tan  sin    cos 6 6  6   3 3、化简：sin(5400  x) 1 cos(3600  x)   sin( x) tan( 9000  x) tan(4500  x) tan( 8100  x)正弦、余弦、正切函数的图象和性质函数正弦函数余弦函数正切函数图象定义域值域周期性奇偶性R [-1，1] 周期为 2π 奇函数R [-1，1] 周期为 2π 偶函数    x | x   k , k  Z  2  R 周期为π 奇函数学生教案在每一个闭区间在每一个闭区间    － 2  2k , 2  2k  上都  是增函数；单调性在每一个闭区间3    2  2k , 2  2k  上都  （k  Z）是减函数 2k－1），（ 2k 上都是增在每一个开区间函数；在每一个闭区间    －  k ,  k  上都是 2  2 （k  Z）增函数2k（ , 2k＋ 1 ）  上都是减（k  Z）函数当 x    2k , k  Z 时，y2当 x  2k , k  Z 时， y取得最大值 1；当无最大值，也无最小值取得最大值 1；当最值x2 2k , k  Z 时， x    2k , k  Z 时，y取得最小值-1．既是中心对称图形，对称中y 取得最小值-1．既是中心对称图形，对称中心为 k ,0, (k  Z ) ；又是对称性轴对称图形，对称轴为直线  心为    k ,0 , (k  Z ) ； 2 又是轴对称图形，对称轴为是中心对称图形，对称中心为 k ,0, (k  Z )x2 k , ( k  Z )x  k , (k  Z )2．图象画法：①“几何描点法”——借助三角函数线；②“五点作图法”――抓住五个关键点． 3．周期函数定义：一般地，对于函数 f(x)，如果存在一个非零常数．．．．T，使得当 x 取定义域内的每一个值时，都有 f(x＋T)＝f(x)，那么函数 f(x)就叫做周期函数，非零常数 T 叫做这．．．个函数的周期．对于一个周期函数 f(x)，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做 f(x)的最小正周期．学生教案知识点 1 正弦、余弦图像、正切图形例题 1、变式练习 1 、已知 a 是实数，则函数 f （ x ） =acosax 的图象可能是（）A．B．C．D．2 、已知函数 f （ x ） =x 2 sinx ，则 f （ x ）在 [-2 π ， 2 π ] 上的大致图象是（）A．B．C．D．3、学生教案例题变式练习1 、函数 y=1+cosx 的图象（ A．关于 x 轴对称） B．关于 y 轴对称 D ．关于直线 x= C．关于原点对称π 2对称）2、已知 a 是实数，则函数 f （ x ） =acosax 的图象可能是（A．B．C．D．知识点二正余弦图像性质(正切图像对图像进行分析主要突出定义域和单调区间的不同) 三角函数周期例题 1、变式练习1、D． A． 4π B． 2π C． ππ 22、函数 y=sin3x 的最小正周期是（）学生教案3、例题 2、变式练习1、2、函数 f （ x ） =Asin （ ω x+ θ ）（ A ＞ 0 ， ω ＞ 0 ）的部分图象如图所示，则 f （ 1 ）+f （ 2 ） + „ +f （ 2011 ）的值为（）三角函数奇偶性例题 1、函数 y=-sin2x ， x ∈ R 是（ A．最小正周期为 π 的奇函数 B．最小正周期为 π 的偶函数 C．最小正周期为 2π 的奇函数 D．最小正周期为 2π 的偶函数）学生教案例题 2变式练习 1 、2 、三角函数定义域与值域例题 1、若三角方程 sinx=0 与 sin2x=0 的解集分别为 E ， F ，则（A． E⊊F B． E⊋F C ． E=F ） D ． E ∩ F= ∅变式练习 1、值域例题 1、函数 y=sinx 的最大值是（ A ． -1 B． 0 ） C． 1 D． 2变式 2、3、 4、学生教案三角函数的单调性例题 1、1、2、下列函数中在区间（ 0 ， + ∞ ）上单调递增的是（A ． y=sinx B ． y=-x 2 C ． y=e - x） D ． y=x 33、4、5、学生教案6、对称性例题 1、变式练习 1 、复合函数求单调性、最值、等问题例题 1、变式 1、求上式子的最值及其对应的 x，对称轴、对称中心、变式 2、学生教案变式 3变式 4、变式 5提高例 2、变式1、学生教案2、3、4、函数 y  Asin(x   )( A  0，  0) 的图象要点归纳 1．函数 y  Asin(x   )( A  0，  0) 的相关概念： A——振幅， T＝2——周期， f＝1 ——频率， x   ——相位，  ——初相 T2．函数 y  Asin(x   )( A  0，  0) 的图象： 3 （1）五点作图法：令 x    0，，，， 2 从而得到 x、y 的值进而找出关键点． 2 2知识点一、五点做函数图像学生教案例 1、例2变式练习 1 、2、学生教案知识点二、图像的变化（通过简单作图分析 A 、  、  对图像的影响）（2）图象变换法 y=sinx x  [0,2 ]向左(φ>0)或向右(φ<0)平移|φ|个单位横坐标不变，纵坐标变为原来的 A 倍y=sin(x+φ) x  [ ,2   ]纵坐标不变，横坐标变为原来的y=sin(ωx+φ)x  [1倍 2   , ]  y=Asin(ωx+φ) 2   x  [ , ]  扩展(每次平移2个单位长度)y=Asin(ωx+φ) x∈ R例题1 、变式1、学生教案4、5、6、提高学生教案知识点三观察图像求解析式例题 1、例2、变式练习 1、2、学生教案2、3、4、学生教案5、6、7、提高备注：请加封面。

(完整版)高一数学必修4三角函数知识点及典型练习

第一、任意角的三角函数一：角的概念：角的定义，角的三要素，角的分类（正角、负角、零角和象限角），正确理解角，与角终边相同的角的集合}{|2,k k z ββπα=+∈ ，弧度制，弧度与角度的换算，弧长lr α=、扇形面积21122s lr r α==，二：任意角的三角函数定义：任意角α的终边上任意取一点p 的坐标是（x ，y ），它与原点的距离是22r x y =+(r>0)，那么角α的正弦r y a =sin 、余弦r x a =cos 、正切xya =tan ，它们都是以角为自变量，以比值为函数值的函数。

三角函数值在各象限的符号：三：同角三角函数的关系式与诱导公式： 1. 平方关系：22sincos 1αα+= 2. 商数关系：sin tan cos ααα=3．诱导公式——口诀：奇变偶不变，符号看象限。

正弦余弦正切4. 两角和与差公式：()()()sin sin cos cos sin cos cos cos sin sin tan tan tan 1tan tan αβαβαβαβαβαβαβαβαβ⎧⎪±=±⎪⎪±=⎨⎪±⎪±=⎪⎩m m5.二倍角公式：22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα⎧⎪=⎪=-=-=-⎨⎪⎪=-⎩余弦二倍角公式变形： 222cos1cos2,2sin 1cos2αααα=+=-第二、三角函数图象和性质基础知识:1、三角函数图像和性质2、熟练求函数sin()y A x ωϕ=+的值域，最值，周期，单调区间，对称轴、对称中心等，会用五点法作sin()y A x ωϕ=+简图：五点分别为：、、、、。

3、图象的基本变换：相位变换：sin sin()y x y x ϕ=⇒=+ 周期变换：sin()sin()y x y x ϕωϕ=+⇒=+ 振幅变换：sin()sin()y x y A x ωϕωϕ=+⇒=+ 4、求函数sin()y A x ωϕ=+的解析式：即求A 由最值确定，ω有周期确定，φ有特殊点确定。

高中数学必修4第一章_三角函数知识复习

1第一章三角函数知识点1、角的定义：⎧⎪⎪⎨⎪⎪⎩正角:按逆时针方向旋转形成的角任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角2、角α的顶点与原点重合，角的始边与x 轴的非负半轴重合，终边落在第几象限，则称α为第几象限角。

第一象限角的集合为22,2k k k παπαπ⎧⎫<<+∈Z ⎨⎬⎩⎭第二象限角的集合为22,2k k k παπαππ⎧⎫+<<+∈Z ⎨⎬⎩⎭第三象限角的集合为322,2k k k παππαπ⎧⎫+<<+∈Z ⎨⎬⎩⎭第四象限角的集合为3222,2k k k παπαππ⎧⎫+<<+∈Z ⎨⎬⎩⎭终边在x 轴上的角的集合为{},k k ααπ=∈Z 终边在y 轴上的角的集合为,2k k πααπ⎧⎫=+∈Z ⎨⎬⎩⎭终边在坐标轴上的角的集合为,2k k παα⎧⎫=∈Z ⎨⎬⎩⎭3、与角α终边相同的角的集合为{}2,k k ββπα=+∈Z4、已知α是第几象限角，确定()*n nα∈N 所在象限的方法：先把各象限均分n 等份，再从x 轴的正半轴的上方起，依次将各区域标上一、二、三、四，则α原来是第几象限对应的标号即为nα终边所落在的区域。

5、长度等于半径长的弧所对的圆心角叫做1弧度。

6、半径为r 的圆的圆心角α所对弧的长为l ，则角α的弧度数的绝对值是l rα=。

7、弧度制与角度制的换算公式：180********.3180πππ⎛⎫===≈ ⎪⎝⎭，，8、若扇形的圆心角为()αα为弧度制，半径为r ，弧长为l ，周长为C ，面积为S ，则l r α=，2C r l =+，21122S lr r α==。

9、设α是一个任意大小的角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()0r r =>，则sin yrα=，cos x r α=，()tan 0y x x α=≠。

10、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正。

必修四-第一章-三角函数知识点及例题详解

第一章三角函数知识点详列一、角的概念及其推广正角：一条射线绕着端点以逆时针方向旋转形成的角1、任意角零角：射线不做任何旋转形成的角负角：一条射线绕着端点以顺时针方向旋转形成的角记忆法则：第一象限全为正,二正三切四余弦.ααcsc sin 为正全正ααcot tan 为正ααsec cos 为正例1、（1）判断下列各式的符号： ①,265cos 340sin∙ ②,423tan 4sin ⎪⎭⎫⎝⎛-∙π③)cos(sin )sin(cos θθ其中已知)0tan ,cos cos (<-=θθθ且答案：+ — —2、象限角：角α的顶点与原点重合，角的始边与x 轴的非负半轴重合，终边落在第几象限，则称α为第几象限角．第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k k α⋅+<⋅+∈Z第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z 第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z3、终边相同的角：一般地，所有与α角终边相同的角连同α在内（而且只有这样的角），cot α<0tan α<0cos α>0sin α<0cot α>0tan α>0cos α<0sin α<0cot α<0tan α<0cos α<0sin α>0sin α>0tan α>0cot α>0cos α>0可以表示为.,360Z k k∈+∙α4、特殊角的集合：（1）终边在X 轴非负半轴上的角的集合为{};,2Z k k ∈=παα（2）终边在X 轴非正半轴上的角的集合为(){};,12Z k k ∈+=πα （3）终边在X 轴上的角的集合为{};,Z k k ∈=παα（4）终边在Y 轴非负半轴上的角的集合为;,22⎭⎬⎫⎩⎨⎧∈+=Z k k ππαα （5）终边在Y 轴非正半轴上的角的集合为;,22⎭⎬⎫⎩⎨⎧∈-=Z k k ππαα（6）终边在Y 轴上的角的集合为;,2⎭⎬⎫⎩⎨⎧∈+=Z k k ππαα （7）终边在坐标轴上角的集合为;,2⎭⎬⎫⎩⎨⎧∈=Z k k παα（8）终边在一、三象限角平分线上的角的集合为;,4⎭⎬⎫⎩⎨⎧∈+=Z k k ππαα （9）终边在二、四象限角平分线上的角的集合为.,4⎭⎬⎫⎩⎨⎧∈-=Z k k ππαα 二、弧度1、定义：长度等于半径长的弧所对的圆心角叫做1弧度2、弧度制与角度制的换算公式：2360π=，1180π=，180157.3π⎛⎫=≈ ⎪⎝⎭． 3、半径为r 的圆的圆心角α所对弧的长为l ，则角α的弧度数的绝对值是lrα= 4、两个公式：若扇形的圆心角为()αα为弧度制，半径为r ，弧长为l ，周长为C ，面积为S ，则l r α=，2C r l =+，21122S lr r α==．三、三角函数1.设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ）则P 与原点的距离02222>+=+=y x yx r2.比值r y 叫做α的正弦记作： r y =αsin 比值r x 叫做α的余弦记作： r x =αcos比值x y 叫做α的正切记作： x y =αtan比值y x叫做α的余切记作： yx =αcot比值x r 叫做α的正割记作： x r =αsec 比值y r叫做α的余割记作： yr =αcsc 以上六种函数，统称为三角函数.2．同角三角函数的基本关系式：（1）倒数关系：tan cot 1αα⋅=；（2）商数关系：sin cos tan ,cot cos sin αααααα==；（3）平方关系：22sin cos 1αα+= ．3．诱导公式，奇变偶不变，符号看象限．()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭．口诀：正弦与余弦互换，符号看象限．例2．化简（1）sin()cos()44ππαα-++；（2）已知32,cos(9)5παπαπ<<-=-，求11cot()2πα-的值． ry)(x,αP解：（1）原式sin()cos[()]424πππαα=-++-sin()sin()044ππαα=---=．（2）3cos()cos(9)5απαπ-=-=-，∴3cos 5α=，∵2παπ<<，∴4sin 5α=-，sin 4tan cos 3ααα==，∴1134cot()cot()tan 223ππααα-=--=-=．例3 确定下列三角函数值的符号(1)cos250° （2）)4sin(π-（3）tan （－672°） (4))311tan(π解：(1)∵250°是第三象限角 ∴cos250°＜0(2)∵4π-是第四象限角，∴0)4sin(<-π(3)tan （－672°）＝tan （48°－2×360°）＝tan48°而48°是第一象限角，∴tan （－672°）＞0(4) 35tan)235tan(311tanππππ=+= 而35π是第四象限角，∴0311tan<π. 例4 求值：sin(-1320°)cos1110°+cos(-1020°)sin750°+tan495°．解：原式=sin(-4×360°+120°)·cos(3×360°+30°)+cos(-3×360°+60°)sin(2×360°+30°)+tan(360°+135°) =sin120°·cos30°+cos60°·sin30°+tan135°=21212323⨯+⨯-1=0 题型一象所在象限的判断例5（1）如果α为第一象限角，试问2α是第几象限角？（2）如果α为第二象限角，试问：απαπα+--,,分别为第几象限角？答案：（1）第一或者第三；（2）第三，第一，第四。

高中数学必修4三角函数知识点归纳总结【经典】

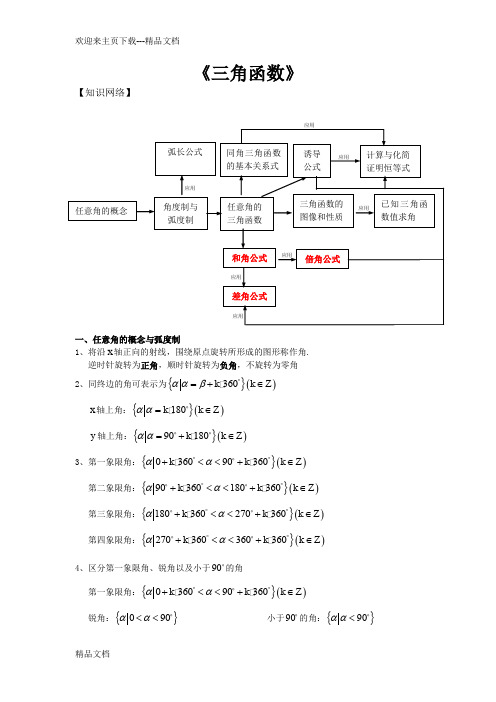
《三角函数》【知识网络】一、任意角的概念与弧度制1、将沿x 轴正向的射线，围绕原点旋转所形成的图形称作角. 逆时针旋转为正角，顺时针旋转为负角，不旋转为零角2、同终边的角可表示为{}()360k k Z ααβ︒=+∈x 轴上角：{}()180k k Z αα=∈ y 轴上角：{}()90180k k Z αα=+∈3、第一象限角：{}()036090360k k k Z αα︒︒+<<+∈第二象限角：{}()90360180360k k k Z αα︒︒+<<+∈第三象限角：{}()180360270360k k k Z αα︒︒+<<+∈第四象限角：{}()270360360360k k k Z αα︒︒+<<+∈4、区分第一象限角、锐角以及小于90的角第一象限角：{}()036090360k k k Z αα︒︒+<<+∈锐角：{}090αα<< 小于90的角：{}90αα<任意角的概念弧长公式角度制与弧度制同角三角函数的基本关系式诱导公式计算与化简证明恒等式任意角的三角函数三角函数的图像和性质已知三角函数值求角和角公式倍角公式差角公式应用应用应用应用应用应用应用5、若α为第二象限角，那么2α为第几象限角？ ππαππk k 222+≤≤+ππαππk k +≤≤+224,24,0παπ≤≤=k ,2345,1παπ≤≤=k所以2α在第一、三象限6、弧度制：弧长等于半径时，所对的圆心角为1弧度的圆心角，记作1rad .7、角度与弧度的转化：01745.01801≈=︒π 815730.571801'︒=︒≈︒=π8、角度与弧度对应表：角度 0︒ 30︒ 45︒ 60︒90120︒ 135︒ 150︒ 180︒ 360︒弧度6π 4π 3π 2π 23π 34π 56π π2π9、弧长与面积计算公式弧长：l R α=⨯；面积：21122S l R R α=⨯=⨯，注意：这里的α均为弧度制.二、任意角的三角函数1、正弦：sin y r α=；余弦cos x r α=；正切tan yxα=其中(),x y 为角α终边上任意点坐标，22r x y =+.2、三角函数值对应表：3、三角函数在各象限中的符号口诀：一全正，二正弦，三正切，四余弦.（简记为“全s t c ”）度0 30 45 60 90 120 135 150 180︒270360弧度6π 4π 3π 2π 23π 34π 56π π32π 2πsin α 01222 32132 22121 0cos α132 2212 012- 22- 32- 1- 0 1tan α 0 3313无 3-1-33-无ry)(x,αPsin α tan α cos α 第一象限：0,0.>>y x sin α>0,cos α>0,tan α>0, 第二象限：0,0.><y x sin α>0,cos α<0,tan α<0, 第三象限：0,0.<<y x sin α<0,cos α<0,tan α>0, 第四象限：0,0.<>y x sin α<0,cos α>0,tan α<0,4、三角函数线设任意角α的顶点在原点O ，始边与x 轴非负半轴重合，终边与单位圆相交与P (,)x y ，过P 作x 轴的垂线，垂足为M ；过点(1,0)A 作单位圆的切线，它与角α的终边或其反向延长线交于点T.由四个图看出：当角α的终边不在坐标轴上时，有向线段,OM x MP y ==，于是有sin 1y y y MP r α====， c o s 1x x x OM r α====， tan y MP ATAT x OM OAα====．我们就分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线。

(完整版)人教高中数学必修四第一章三角函数知识点归纳

三角函数一、随意角、弧度制及随意角的三角函数1．随意角(1)角的观点的推行①按旋转方向不一样分为正角、负角、零角．正角 : 按逆时针方向旋转形成的角随意角负角: 按顺时针方向旋转形成的角零角 : 不作任何旋转形成的角②按终边地点不一样分为象限角和轴线角．角的极点与原点重合，角的始边与 x 轴的非负半轴重合，终边落在第几象限，则称为第几象限角．第一象限角的会合为 k 360ok 360o 90o , k第二象限角的会合为 k 360o 90o k 360o 180o , k第三象限角的会合为 k 360o 180o k 360o 270o , k第四象限角的会合为k 360o 270ok 360o360o , k终边在 x 轴上的角的会合为 k 180o , k终边在 y 轴上的角的会合为 k 180o 90o , k终边在座标轴上的角的会合为k 90o ,k(2)终边与角 α同样的角可写成 α＋ k ·360 °(k ∈ Z)．终边与角同样的角的会合为k 360o, k(3)弧度制① 1 弧度的角：把长度等于半径长的弧所对的圆心角叫做1 弧度的角．②弧度与角度的换算： 360°＝ 2π弧度； 180°＝ π弧度．③ 半径为 r 的圆的圆心角所对弧的长为 l ，则角的弧度数的绝对值是lr④ 若扇形的圆心角为为弧度制，半径为 r ，弧长为 l ，周长为 C ，面积为 S ，则 lr，C2r l ，S1 lr 1 r2 ． 222 ．随意角的三角函数定义设 α是一个随意角，角 α的终边上随意一点P(x ， y)，它与原点的距离为 r rx 2 y 2 ，那么角 α的正弦、余弦、rrx（三角函数值在各象限的符号规律归纳为：一全正、二正弦、三正切分别是： sin α＝ y ， cos α＝ x ， tan α＝ y．正切、四余弦）3．特别角的三角函数值角度030456090120135150180270360函数角 a 的弧度0π /6π/4π /3π /22π /33π /45π/6π3π /22πsina01/2√ 2/2√ 3/21√ 3/2√ 2/21/20-10 cosa1√ 3/2√ 2/21/20-1/2-√ 2/2-√ 3/2-101 tana0√ 3/31√ 3-√ 3-1-√ 3/300二、同角三角函数的基本关系与引诱公式A.基础梳理1．同角三角函数的基本关系(1)平方关系： sin2α＋ cos2α＝ 1；（在利用同角三角函数的平方关系时，若开方，要特别注意判断符号）sin α(2)商数关系：＝tanα.（3）倒数关系：tan cot 1cos α2．引诱公式公式一： sin( α＋ 2kπ)＝sin α， cos(α＋ 2kπ)＝cos_α，tan(2k )tan此中 k∈Z .公式二： sin( π＋α)＝－ sin_α， cos( π＋α)＝－ cos_α， tan( π＋α)＝ tan α.公式三： sin( π－α)＝ sin α， cos( π－α)＝－ cos_α，tan tan．公式四： sin( －α)＝－ sin_α， cos(－α)＝ cos_α，tan tan .ππ公式五： sin －α＝ cos_α， cos－α＝ sin α.22ππ公式六： sin 2＋α＝ cos_α， cos2＋α＝－ sin_α.π口诀：奇变偶不变，符号看象限．此中的奇、偶是指π引诱公式可归纳为 k· ±α的各三角函数值的化简公式．的奇数22倍和偶数倍，变与不变是指函数名称的变化．假如奇数倍，则函数名称要变( 正弦变余弦，余弦变正弦 ) ；假如偶数倍，则函数名称不变，符号看象限是指：把πα当作锐角时，依据 k· ±α在哪个象限判断原三角函数值的符号，最后作为结．．．．2．．．果符号．B. 方法与重点一个口诀1、引诱公式的记忆口诀为：奇变偶不变，符号看象限．2、四种方法在求值与化简时，常用方法有：sin α(1)弦切互化法：主要利用公式tan α＝化成正、余弦．cos α(2)和积变换法：利用 (sin θ±cos θ)2＝1 ±2sin θcos θ的关系进行变形、转变．（ sin cos、sin cos、sin cos三个式子知一可求二）(3)巧用 “1”的变换： 1＝ sin 2θ＋ cos 2θ= sinπ＝tan 42（4）齐次式化切法：已知 tank ，则 a sinbcos a tan b ak bm sinn cos m tan n mk n三、三角函数的图像与性质学习目标：1 会求三角函数的定义域、值域2 会求三角函数的周期：定义法，公式法，图像法（如y sin x 与 y cosx 的周期是）。

(完整版)高中必修四三角函数知识点总结

§04。

三角函数知识要点1. ①与α(0°≤α＜360°）终边相同的角的集合（角α与角β的终边重合):{}Z k k ∈+⨯=,360|αββ②终边在x 轴上的角的集合： {}Z k k ∈⨯=,180|ββ ③终边在y 轴上的角的集合：{}Z k k ∈+⨯=,90180|ββ ④终边在坐标轴上的角的集合：{}Z k k ∈⨯=,90| ββ ⑤终边在y =x 轴上的角的集合：{}Z k k ∈+⨯=,45180| ββ⑥终边在x y -=轴上的角的集合：{}Z k k ∈-⨯=,45180| ββ⑦若角α与角β的终边关于x 轴对称，则角α与角β的关系：βα-=k 360 ⑧若角α与角β的终边关于y 轴对称,则角α与角β的关系：βα-+= 180360k ⑨若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180⑩角α与角β的终边互相垂直,则角α与角β的关系： 90360±+=βαk2. 角度与弧度的互换关系：360°=2π 180°=π 1°=0。

01745 1=57。

30°=57°18′ 注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.、弧度与角度互换公式： 1rad ＝π180°≈57。

30°=57°18ˊ． 1°＝180π≈0。

01745（rad ）3、弧长公式：rl ⋅=||α。

扇形面积公式:211||22s lr r α==⋅扇形4、三角函数：设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y)P与原点的距离为r,则 ry =αsin ； rx =αcos ； =αtan yx=αcot ； xr =αsec ；。

yr=αcsc 。

5、三角函数在各象限的符号：（一全二正弦，三切四余弦）正切、余切余弦、正割正弦、余割6、三角函数线正弦线：MP ；余弦线：OM; 正切线： AT.SIN \COS 三角函数值大小关系图1、2、3、4表示第一、二、三、四象限一半所在区域16. 几个重要结论:8、同角三角函数的基本关系式：αααtan cos sin = αααcot sin cos = 1cot tan =⋅αα 1sin csc =α⋅α 1cos sec =α⋅α1cos sin 22=+αα 1tan sec 22=-αα 1cot csc 22=-αα9、诱导公式：2k παα±把的三角函数化为的三角函数，概括为： “奇变偶不变，符号看象限"公式组二公式组三(完整版)高中必修四三角函数知识点总结x x k x x k x x k x x k cot )2cot(tan )2tan(cos )2cos(sin )2sin(=+=+=+=+ππππ x x x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=-=--=- 公式组四公式组五公式组六xx x x x x xx cot )cot(tan )tan(cos )cos(sin )sin(=+=+-=+-=+ππππ xx x x x x xx cot )2cot(tan )2tan(cos )2cos(sin )2sin(-=--=-=--=-ππππ xx x x xx xx cot )cot(tan )tan(cos )cos(sin )sin(-=--=--=-=-ππππ（二）角与角之间的互换公式组一公式组二 βαβαβαsin sin cos cos )cos(-=+ αααcos sin 22sin =βαβαβαsin sin cos cos )cos(+=- ααααα2222sin 211cos 2sin cos 2cos -=-=-= βαβαβαsin cos cos sin )sin(+=+ ααα2tan 1tan 22tan -=βαβαβαsin cos cos sin )sin(-=- 2cos 12sinαα-±= βαβαβαtan tan 1tan tan )tan(-+=+ 2cos 12cos αα+±=βαβαβαtan tan 1tan tan )tan(+-=- 公式组三公式组四公式组五2tan 12tan2sin 2ααα+= 2tan 12tan 1cos 22ααα+-= 2tan 12tan2tan 2ααα-=42675cos 15sin -== ,42615cos 75sin +== ，3275cot 15tan -== ，3215cot 75tan +== 。

高中数学必修4《第一章三角函数》精品课件：1.1.1任意角

S={α|α=45°＋k·180°，k∈Z}.
S={ －315°，-135°，45°，225°， 405°，585°}
课堂小结
Office组件之word2007
1.角的概念推广正角、负角、零角、象限角
2.终边相同的角
3.终边在x轴、y轴上的角的表示
4.终边在各个象限上的角的表示
Office组件之word2007
思考2：终边在x轴上的角的集合表示
终边在x轴上：S={α|α=k·180°，k∈Z}；
新课教学
Office组件之word2007
思考3：终边在y轴非正半轴、非负半轴
上的角分别如何表示？
y轴非负半轴:α= 90°＋k·360°，k∈Z ； y轴非正半轴:α= 270°＋k·360°，k∈Z .
思考4：终边在y轴上的角的集合表示
y
x o
知识探究（三）：终边相同的角 Office组件之word2007
思考1：－32°，328°，－392°是第几象限的角？这些角有什么内在联系？
y
328° o
－392° x
－32°
新课教学
Office组件之word2007
思考2：与－32°角终边相同的角有多少个？这些角与－32°角在数量上相差多少？
Office组件之word2007
1.1.1 任意角
知识探究（一）：角的概念的推广
Office组件之word2007
复习：角的定义角是由平面内一条射线绕其端点从
一个位置旋转到另一个位置所组成的图形（如图）.
B
始边
终边
A O
顶点
新课教学
Office组件之word2007
思考1：你认为将一条射线绕其端点按逆时针方向旋

人教版数学必修4第一章1.2.1《任意角的三角函数》课件

公式作用：可以把求任意角的三角函数值，
转化为求 0 到 2 或 0 到角3 的三 6 角函0数值 .
例3 求下列三角函数值：
（1） cos9
4
（2） tan( 11)
6
解：（1）co 9 4 sco 4 s 2 ( ) co 4 s2 2
（2）ta 1 n )1 ( ta n 2 ) (ta n ta n 3
A.4 3
B.4 3
C.4 3
D. 3
例2、已知角的终边经过点P0(3,4)，求角
的正弦、余弦和正切值 .
解：由已知可得：
rx2y2 3 2 ( 4 )2 5
于是，sin y 4 r5
cosx 3 r5
tan y 4 x3
合作演练
变式1、已知角的终边过点 P1,2 5 ，
求的三个三角函数值.
规律： “一全正、二正弦正、三正切正、四余弦正”
“一全二正弦，三切四余弦”
例1 确定下列三角函数值的符号：
（1）co2s50（2）tan(67)2（3）sin
4
解：（1）因为 250是第三象限角，所以co 2s5 0 0；
（2）因为 tan(67)2= ta 2 n 3 ( 6 4 ) 0 8 ta 4 ，n 8
r
第二象限： x 0 ,r 0 ,故 r x 为负值； o
x
第三象限： x 0 ,r 0 ,故 x 为负值； r
第四象限： x 0 ,r 0 ,故 x 为正值； r
三角函数在各象限内的符号：
交叉正负
第 3一、象正限切：函 x 数 0 ,值 y t0 a,n 故 y 为 x y 正值； y x

高一下册数学必修四第一章三角函数.知识点及同步练习

巩固练习
1、在直角坐标系中，若角α与角β的终边关于x轴对称，则α与β的
关系一定是（）
A．α=－β B．α+β=k·360°(k∈Z) C．α－β=k·360°(k∈Z)
D．以上答案都不对
2、圆内一条弦的长等于半径，这条弦所对的圆心角是
（）
A．等于1弧度 B．大于1弧度 C．小于1弧度
D．无法
判断
（2）角α + k·720 °与角α终边相同，但不能表示与角
α终边相同的所有角．例4．写出终边在y轴上的角的集合(用0°到360°的角表示) ．例5．写出终边在上的角的集合S,并把S中适合不等式－ 360°≤β＜720°的元素β写出来．思考题：已知α角是第三象限角，则α/2，α/3，α/4各是第几象限角？
D．｛α∣－270°＋k·360°<α<－180°＋k·360°，k∈Z｝
11、下列命题是真命题的是（）
Α．三角形的内角必是一、二象限内的角 B．第一象限的角必是
锐角
C．不相等的角终边一定不同
D．=
12、已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、
C关系是（）
A．B=A∩C B．B∪C=C
度记做1rad．在实际运算中，常常将rad单位省略．
3．思考：
（1）一定大小的圆心角所对应的弧长与半径的比值是否是确
定的？与圆的半径大小有关吗？
弧度制的性质：
①半圆所对的圆心角为
②整圆所对的圆心角为
③正角的弧度数是一个正数．
④负角的弧度数是一
个负数．
⑤零角的弧度数是零．
⑥角α的弧度数的绝
对值|α|=
始边终边顶点 A O B

高中数学必修4(人教A版)第一章三角函数1.6知识点总结含同步练习及答案

21 24 7.9 11.1
经长期观察，函数 y = f (t) 的图象可以近似地看成函数 y = k + A sin (ωt + φ) 的图象．下面的函数中，最能近似表示表中数据间对应关系的函数是 ( A．y = 11 + 3 sin (
)
π π t + ) , t ∈ [0, 24] 12 2 π B．y = 11 + 3 sin ( t + π) , t ∈ [0, 24] 6 π C．y = 11 + 3 sin t , t ∈ [0, 24] 12 π D．y = 11 + 3 sin t , t ∈ [0, 24] 6
π π t + ) ， t ∈ [0, 24] 12 2 π B． y = 11 + 3 sin ( t + π) ， t ∈ [0, 24] 6 π C． y = 11 + 3 sin t ， t ∈ [0, 24] 6 π D． y = 11 + 3 sin t ， t ∈ [0, 24] 12
3. 某城市一年中 12 个月的平均气温与月份的关系可近似地用三角函数 y = a + A cos
π (x − 6) ( 6
x = 1, 2, 3, ⋯ , 12 ) 来表示，已知 6 月份的月平均气温最高，为 28∘ C ， 12 月份的月平均气温最
低，为 18∘ C ，则 10 月份的平均气温值为
B．[1, 7]
D．[0, 1] 和 [7, 12]
2π π π 弧度，从而经过 t 秒转了 = t 弧度． 12 6 6 1 √3 π 而 t = 0 时，点 A ( , ．经过 t 秒后点 A 的纵坐标为 ) ，则 ∠xOA = 2 2 3