MATLAB二分法
matlab二分法

matlab二分法MATLAB二分法是一种常用的求解非线性方程的数值解法,它通过不断地将定义域分成若干个子区间,从而找到近似解。
与梯形法和牛顿迭代法相比,MATLAB 二分法又称为“分治法”,是一种简单、直观、快速和有效的求解非线性方程的数值解法。
1. 二分法原理MATLAB 二分法是根据“分而治之”的思想来求解非线性方程的数值解的。
它的基本思想是,将定义域分成两个子区间,其中一个子区间的函数值的符号一定是固定的,另一个子区间的函数值的符号也是固定的,只有当它们的符号相反时,才能确定解存在于这两个子区间之间。
然后,再对缩小的子区间重复以上操作,进而确定非线性方程的近似解,也就是所谓的“黄金分割法”。
2. MATLAB 二分法的步骤(1)始条件首先,要将定义域分成两个子区间,在每一个子区间内,假定函数值的符号是固定的;确定迭代初值 $x_0,比如$x_0=0.5;(2)代计算求出迭代第二值 $x_1,即 $x_1=x_0+frac{b-x_0}{2},计算出$x_1$值,计算函数值的符号;(3)晕条件当求得的函数值的符号与定义域中一边的函数值的符号相反时,认为解存在于此子区间之间,继续将所取得的子区间继续缩小,直到定义域中的某两个端点接近,或者函数值的绝对值小于指定的误差范围,此时称为收敛;(4)的输出将收敛时的根 $x_n$ 作为解的输出。
3. MATLAB 二分法的优缺点(1) MATLAB 二分法的优点MATLAB 二分法具有简单、直观、快速和有效的特点,只要能够确定函数在定义域中的一边的函数值的符号,就可以求出近似解。
(2) MATLAB 二分法的缺点MATLAB 二分法容易收敛到局部极小值,而无法收敛到全局最优值;同时,它也不适用于函数值在定义域内不连续或周期变化的情况。
4. MATLAB 二分法的应用MATLAB 二分法在实际工程中广泛应用,主要用于求解非线性方程、解决二次规划问题、求解非线性最小化问题、结构优化问题等。
MATLAB计算方法迭代法牛顿法二分法实验报告

完美WORD格式姓名实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理 (1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2a b x -=。
否则,继续判断是否0)()(<∙x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 7.0软件四、 结果预测(1)11x =0.09033 (2)5x =0.09052 (3)2x =0,09052 五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x的近似根。
要求误差不超过3105.0-⨯。
借助Matlab使用二分法求解方程的根
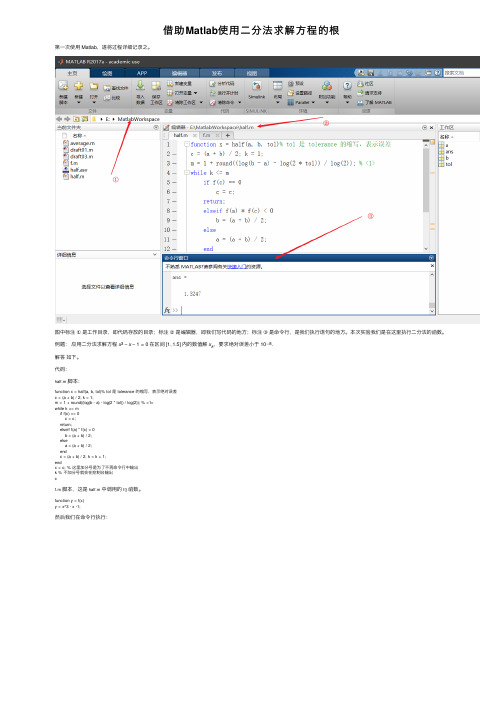
借助Matlab使⽤⼆分法求解⽅程的根第⼀次使⽤ Matlab,遂将过程详细记录之。
图中标注①是⼯作⽬录,即代码存放的⽬录;标注②是编辑器,即我们写代码的地⽅;标注③是命令⾏,是我们执⾏语句的地⽅。
本次实验我们是在这⾥执⾏⼆分法的函数。
例题:应⽤⼆分法求解⽅程x3−x−1=0 在区间 [1,1.5] 内的数值解x k,要求绝对误差⼩于 10−8.解答如下。
代码:half.m脚本:function x = half(a, b, tol)% tol 是 tolerance 的缩写,表⽰绝对误差c = (a + b) / 2; k = 1;m = 1 + round((log(b - a) - log(2 * tol)) / log(2)); % <1>while k <= mif f(c) == 0c = c;return;elseif f(a) * f(c) < 0b = (a + b) / 2;elsea = (a + b) / 2;endc = (a + b) / 2; k = k + 1;endx = c; % 这⾥加分号是为了不再命令⾏中输出k % 不加分号就会在控制台输出cf.m脚本,这是half.m中调⽤的f()函数。
function y = f(x)y = x^3 - x -1;然后我们在命令⾏执⾏:可以看出,最后求解得到的x=1.3247,即输出的ans,迭代次数k=27.关于代码half.m中的标注<1>,有如下解释:注意,在 Matlab 中,log()函数的底是e.补充例题(感兴趣的朋友可以⾃⾏测试):Processing math: 100%。
二分法matlab

二分法matlab二分法是一种常用的数值计算方法,也被称为二分查找或折半查找。
它通过将搜索范围逐渐缩小一半来快速定位目标值。
在MATLAB中,我们可以利用二分法来解决一些数值计算问题,下面将介绍二分法的原理和应用。
二分法的基本思想是将搜索范围一分为二,然后确定目标值位于左半部分还是右半部分,然后继续将该部分一分为二。
重复这个过程直到找到目标值或者确定目标值不存在。
二分法的核心就是不断将搜索范围缩小一半。
首先,我们需要确定搜索范围的初始值。
通常情况下,我们会选择数组或者有序列表的首尾元素作为搜索范围的边界。
然后,我们计算出搜索范围的中间位置,并将中间位置的值与目标值进行比较。
如果中间位置的值等于目标值,那么我们就找到了目标值;如果中间位置的值大于目标值,那么目标值可能在左半部分;如果中间位置的值小于目标值,那么目标值可能在右半部分。
根据比较结果,我们可以缩小搜索范围,重复上述步骤直到找到目标值或者确定目标值不存在。
二分法在MATLAB中的应用非常广泛。
下面以两个例子来说明二分法在MATLAB中的使用。
第一个例子是求解方程的根。
假设我们需要求解方程f(x)=0的根,其中f(x)是一个连续函数。
我们可以利用二分法来逼近方程的根。
首先,我们需要确定一个初始搜索范围[a, b],使得f(a)和f(b)的符号不同。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到一个近似的根。
第二个例子是查找有序列表中的某个元素。
假设我们有一个有序列表A,我们需要查找其中的某个元素x。
我们可以利用二分法来快速确定x是否在列表中,并返回其索引位置。
首先,我们需要确定初始搜索范围的左右边界。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到x或者确定x不存在于列表中。
二分法是一种常用的数值计算方法,在MATLAB中也有广泛的应用。
通过将搜索范围一分为二,二分法可以快速定位目标值,解决方程的根或者查找有序列表中的元素。
熟练掌握二分法的原理和应用,对于解决一些数值计算问题非常有帮助。
二分法及其matlab程序-经典

避免数值不稳定性
对于涉及大量计算或迭代的过程,要注意数值稳定性问题, 采取适当的算法或技巧,如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法,其基本思想是通过不断将区间一分为二,逐步缩小求解范围, 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根,可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时,可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建:对于n阶矩阵A,构建特征多项式f(λ) = |A - λI|。 • 初始区间选择:确定包含特征值的初始区间[a, b]。 • 二分迭代:取中点c = (a + b) / 2,计算f(c)。若f(c) == 0,则c为特征值;否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢,需要多次迭代才能得 到精确解,且对于多峰函数或者复杂函数可 能无法找到全局最优解。
matlab二分法代码

在MATLAB中,可以编辑一个函数脚本文件(例如:`bisection_method.m`)来实现二分法(bisection method)。
二分法是一种求解非线性方程在某区间内根的数值方法。
以下是一个简单的实现:% bisection_method.mfunction [root, n_iterations] = bisection_method(func, a, b, tol, max_iterations)% func: 要求解的非线性方程的函数句柄% a: 区间的左端点% b: 区间的右端点% tol: 容差,当相邻两次迭代的结果小于容差时停止迭代% max_iterations: 最大迭代次数if nargin < 5max_iterations = 100;endif nargin < 4tol = 1e-6;endfa = func(a);fb = func(b);if sign(fa) == sign(fb)error('区间两端点上函数值的符号相同,请检查输入的区间。
');endn_iterations = 0;while (b - a) / 2 > toln_iterations = n_iterations + 1;if n_iterations > max_iterationserror('已达到最大迭代次数,但仍未满足容差要求。
');endc = (a + b) / 2;fc = func(c);if fc == 0break;elseif sign(fc) == sign(fa)a = c;fa = fc;elseb = c;endendroot = (a + b) / 2;接下来,创建一个脚本来测试这个二分法函数:% test_bisection_method.mfunc = @(x) x^3 - x - 1; % 定义要求解的函数a = 1;b = 2;tol = 1e-6;max_iterations = 100;[root, n_iterations] = bisection_method(func, a, b, tol, max_iterations);fprintf('求得的根是:%f\n', root);fprintf('迭代的次数是:%d\n', n_iterations);运行`test_bisection_method.m`脚本,你将得到二分法求解的根和迭代次数。
matlab_examples(数值分析)

Experiments in Finding Root of Equation
计算方法课程组
华中科技大学数学与统计学院
1
方程求根 —二分法
一、实验目的
1) 熟悉Matlab编程 ; 2) 应用 Matlab实现二分法,牛顿迭代法等求根算法 ;
二、二分法
基本思想: 二分法通过不断搜索有根区间,最终收缩为一 点。算法简单、容易且保证算法收敛。
答案: x=1.3247
f(x)=-7.6580e-005
5
作
业
参看范例代码(.m文件) 独立完成如下编程内容:
6
2
方程求根 —二分法
function [xvect,xdif,fx,nit]=bisect(fun,a,b,toll,nmax)
% % % % % % % % % % 求根算法:二分法 [xvect,xdif,fx,nit]=bisect(fun,a,b,toll,nmax) fun 求根函数名 [a,b] 最初的有根区间的范围 toll 精度,默认为10e-5 nmax 最大迭代次数 xvect 返回所得根 xdif 返回缩小的根区间的长度 fx 返回函数值 nit 返回满足要求的迭代次数
bisect _main.m
x=1:0.01:2;
y=x.^3-x-1; plot(xห้องสมุดไป่ตู้y);hold on;
运行结果:
plot(x,zeros(size(x)),'r-.');
fun=inline('x^3-x-1');
[xvect,xdif,fx,nit]=bisect(fun,1,2,0.005,100);
disp((['
matlab中bisection函数用法

matlab中bisection函数用法
在MATLAB中,bisection函数是一种用于实现二分法的数值计算方法,用于求解方程的根。
该方法的基本思路是将函数图像的两侧区域进行二分,不断缩小目标区域的范围,最终获得方程的近似解。
在MATLAB中,可以使用以下代码实现bisection函数:
```matlab
% 定义函数
function y = f(x)
y = x^2 - 2;
% 定义bisection方法
function (root, n) = bisection(a, b, tol)
fa = f(a);
fb = f(b);
if sign(fa) == sign(fb)
disp('两端点函数值异号');
else
c = (a + b)/2;
fc = f(c);
if abs(fc) <= tol
root = c;
n = n + 1;
else
if sign(fa) == sign(fc)
b = c;
else
a = c;
end
end
end
```
其中,f 为待求解的函数,a 和 b 分别为函数图像两侧的端点,tol 为误差限。
bisection 函数返回的 root 即为方程的根,n 为二分的次数。
如果你想了解更多关于bisection函数的信息,请提供更多上下文或给出具体的问题。
数学实验二(matlab中二分法求解方程)

云南大学数学与统计学实验教学中心实验报告
数学实验(二)
一、实验目的:练习用数值迭代逼近法解非线性方程。
1.区间迭代法:对分法和黄金分割法
2.点的迭代法:简单迭代法
二、实验内容:用二分法(即对分法)编程求解方程。
0123=---x x x
三、实验环境:MATLAB.
四.实验方法:
程序代码:
function X=fan(a,b)
e=1e-2;
ep=1;
x0=a;
xn=b;
x=0;
k=0;
N=100;
while (ep>e)
x=(x0+xn)/2;
f1=x^3-x^2-x-1;
f2=x0^3-x0^2-x0-1;
f3=xn^3-xn^2-xn-1;
if f1*f2<0
x0=a;
xn=x;
elseif f1*f3<0
x0=x;
xn=b;
end
ep=abs(f1);
k=k+1;
if k>N
break;
end
x
ep
实验结果:
fan(a,b)
x =
1.8572
ep =
0.0993
五、实验过程
1实验步骤
2 关键代码及其解释
3 调试过程
六、实验总结
1.遇到的问题及解决过程
2.产生的错误及原因分析
3.体会和收获。
计算方法matlab实验报告

计算方法matlab实验报告计算方法MATLAB实验报告引言:计算方法是一门研究如何用计算机来解决数学问题的学科。
在计算方法的学习过程中,MATLAB作为一种强大的数值计算软件,被广泛应用于科学计算、工程计算、数据分析等领域。
本实验报告将介绍在计算方法课程中使用MATLAB 进行的实验内容和实验结果。
一、二分法求方程根在数值计算中,求解非线性方程是一个常见的问题。
二分法是一种简单而有效的求解非线性方程根的方法。
在MATLAB中,可以通过编写函数和使用循环结构来实现二分法求解方程根。
实验步骤:1. 编写函数f(x),表示待求解的非线性方程。
2. 设定初始区间[a, b],满足f(a) * f(b) < 0。
3. 利用二分法迭代求解方程根,直到满足精度要求或迭代次数达到预设值。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个非线性方程的根。
例如,对于方程f(x) = x^3 - 2x - 5,我们通过二分法迭代了5次,得到了方程的一个根x ≈ 2.0946。
二、高斯消元法解线性方程组线性方程组的求解是计算方法中的重要内容之一。
高斯消元法是一种常用的求解线性方程组的方法,它通过矩阵变换将线性方程组化为上三角矩阵,从而简化求解过程。
在MATLAB中,可以利用矩阵运算和循环结构来实现高斯消元法。
实验步骤:1. 构建线性方程组的系数矩阵A和常数向量b。
2. 利用高斯消元法将系数矩阵A化为上三角矩阵U,并相应地对常数向量b进行变换。
3. 利用回代法求解上三角矩阵U,得到线性方程组的解向量x。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个线性方程组。
例如,对于线性方程组:2x + 3y - z = 13x - 2y + 2z = -3-x + y + 3z = 7经过高斯消元法的计算,我们得到了方程组的解x = 1,y = -2,z = 3。
三、数值积分方法数值积分是计算方法中的重要内容之一,它用于计算函数在给定区间上的定积分。
二分法matlab

二分法matlab二分法是一种常见的数值计算方法,也称为折半查找法。
它的主要思想是将一个区间分成两个部分,判断目标值在哪个部分,然后继续对该部分进行二分处理,直到最后找到目标值为止。
在Matlab中,可以用以下代码实现二分法:function [x] = binary_search(f, a, b, tol)% f: 待求解函数% a,b: 初始区间% tol: 精度要求while abs(b-a) > tolx = (a + b) / 2;if f(x) == 0return;elseif f(x) * f(a) < 0b = x;elsea = x;endendx = (a + b) / 2;其中,f表示待求解的函数,a和b表示初始的区间,tol表示精度要求。
在每次循环中,先计算出当前区间的中点x,并判断f(x)与0的大小关系。
如果f(x)=0,则直接返回x;如果f(x)*f(a)<0,则说明目标值在左半部分区间内,则将右端点b更新为x;否则说明目标值在右半部分区间内,则将左端点a更新为x。
循环直到满足精度要求为止。
下面是一个简单的例子:假设我们要求解方程sin(x)=0.5在[0, pi/2]内的一个近似解。
可以定义函数f(x)=sin(x)-0.5,然后调用binary_search函数求解。
function [x] = f(x)x = sin(x) - 0.5;endx = binary_search(@f, 0, pi/2, 1e-6);最终得到的近似解为x=0.523599。
二分法是一种简单而有效的数值计算方法,在Matlab中也很容易实现。
它可以用于求解方程、寻找极值等问题,是数值计算中常用的基本工具之一。
二分法程序代码【matlab源码】

毕业论文(设计)题目学院学院专业学生姓名学号年级级指导教师教务处制表二分法程序代码一、程序说明本团队长期从事matlab编程与仿真工作,擅长各类毕业设计、数据处理、图表绘制、理论分析等,程序代做、数据分析具体信息联系二、程序示例主程序:function [k,x,wuca,yx]=erfenfa(a,b,tol)%a、b为区间左右端点值,tol是精度,k为计算次数,x为使用k次二分法得到的小区间[ak,bk]的中点值,y(x)为x的函数值,wuca=|ak-bk|/2。
a1=a; b1=b;ya=fun(a1); yb=fun(b1); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), returnendmax1=-1+ceil((log(b1-a1)- log(tol))/ log(2)); % ceil是上取整for k=1: max1+1ya=fun(a1);yb=fun(b1);x=(a1+b1)/2;yx=fun(x);wuca=abs(b1-a1)/2;k=k-1;[k,a,b,x,wuca,ya,yb,yx];if yx==0a1=x; b1=x;elseif yb*yx>0b1=x;yb=yx;elsea1=x;ya=yx;endif b1-a1< tol , return, endendk=max1;x;wuca;yx=fun(x);End、分程序:function y1=fun(x)y1=sqrt(x^2+1)-tan(x);end结果:[k,x,wuca,yx]=erfenfa(0,pi/2,10^-5)k =17x =0.9415wuca =5.9921e-06yx =-2.6595e-06。
二分法、简单迭代法的matlab代码实现

实验一非线性方程的数值解法(一)信息与计算科学金融崔振威201002034031一、实验目的:熟悉二分法和简单迭代法的算法实现。
二、实验内容:教材P40 2.1.5三、实验要求1 根据实验内容编写二分法和简单迭代法的算法实现2 简单比较分析两种算法的误差3 试构造不同的迭代格式,分析比较其收敛性(一)、二分法程序:function ef=bisect(fx,xa,xb,n,delta)% fx 是由方程转化的关于x 的函数,有fx=0 。
% xa 解区间上限% xb 解区间下限% n 最多循环步数,防止死循环。
%delta 为允许误差x=xa;fa=eval(fx);x=xb;fb=eval(fx);disp('[ n xa xb xc fc ]'); for i=1:nxc=(xa+xb)/2;x=xc;fc=eval(fx);X=[i,xa,xb,xc,fc];disp(X),if fc*fa<0xb=xc;else xa=xc;endif (xb-xa)<delta,break,endend(二)、简单迭代法程序:function [x0,k]=iterate (f,x0,eps,N)if nargin<4N=500;endif nargin<3ep=1e-12;endx=x0;x0=x+2*eps;k=0;while abs(x-xO)>eps &k<NxO=x;x=feval(f,xO);k=k+1;endx0=x;if k==Nend解:a、g(x)=x5-3x3-2x2+2二分法求方程:(1)、在matlab的命令窗口中输入命令:>>fplot('[x A5-3*x A3-2*x A2+2]',[-3,3]);grid 得下图:由上图可得知:方程在[-3,3]区间有根。
(2 )、二分法输出结果>>f='xA5-3*xA3-2*xA2+2'f =xA5-3*xA3-2*xA2+2>>bisect(f,-3,3,20,10A(-12))2.0000 -3.0000 0 -1.5000 0.03133.0000 -3.0000 -1.5000 -2.2500 -31.61824.0000 -2.2500 -1.5000 -1.8750 -8.43015.0000 -1.8750 -1.5000 -1.6875 -2.96326.0000 -1.6875 -1.5000 -1.5938 -1.21817.0000 -1.5938 -1.5000 -1.5469 -0.53828.0000 -1.5469 -1.5000 -1.5234 -0.24059.0000 -1.5234 -1.5000 -1.5117 -0.101510.0000 -1.5117 -1.5000 -1.5059 -0.034311.0000 -1.5059 -1.5000 -1.5029 -0.001412.0000 -1.5029 -1.5000 -1.5015 0.015013.0000 -1.5029 -1.5015 -1.5022 0.006814.0000 -1.5029 -1.5022 -1.5026 0.002715.0000 -1.5029 -1.5026 -1.5027 0.000716.0000 -1.5029 -1.5027 -1.5028 -0.000317.0000 -1.5028 -1.5027 -1.5028 0.000218.0000 -1.5028 -1.5028 -1.5028 -0.000119.0000 -1.5028 -1.5028 -1.5028 0.000120.0000 -1.5028 -1.5028 -1.5028 -0.00002、迭代法求方程:迭代法输出结果:>>f=inlin e('x A5-3*x A3-2*x A2+2');>> [x0,k]=iterate(fun1,2)x0 =>> [x0,k]=iterate(fun1,1.5)x0 =NaNk =6 >> [x0,k]=iterate(fun1,2.5)x0 =NaN k =5(3)、误差分析:由二分法和迭代法输出结果可知,通过定点迭代法得出方程的解误差比二分法大,而利用二分法求出的结果中,可以清楚看出方程等于零时的解,其误差比迭代法小。
matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码用二4224min ()f t t t t =--[,.]t ∈内的极小值点,要求准1.function [t d]=erfenfa(a,b)k=1; %记录循环次数 while abs(a-b)>0.0005c=(a+b)/2;C(k)=c; %存储每次循环中点c 的值if ff(c)<0a=c;endif ff(c)==0t1=c;break ;endif ff(c)>0b=c;endk=k+1;endt=(a+b)/2; %最终符合要求的值d=f(t); %最优解Ckfunction y=f(t)y=t^4-2*t^2-4*t;function y=ff(t)y=4*t^3-4*t-4;运行结果>> [t d]=erfenfa(1,1.5)C =Columns 1 through 91.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252Column 101.3247k =11t =1.3250d =-5.72902.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3],收敛精度0.5 function [t,f]=huangjinfenge(a,b)m=1-(sqrt(5)-1)/2;t2=a+m*(b-a)f2=g(t2);t1=a+b-t2f1=g(t1);while abs(t1-t2)>0.5if f1<f2< bdsfid="121" p=""></f2<>a=t2;t2=t1f2=f1;t1=a+b-t2f1=g(t1);elseb=t1;t1=t2f1=f2;t2=a+m*(b-a)f2=g(t2);endendt=(t1+t2)/2;f=g(t);function y=g(t)y=t^3-2*t+1;运行结果> [t,f]=huangjinfenge(0,3)t2 =1.1459t1 =1.8541t1 =1.1459t2 =0.7082t =0.9271f =-0.0574>>3. 用牛顿法求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [t1,d]=Newton(t0)t=t0-ff(t0)/fff(t0);k=1;%记录迭代次数T(1)=t;%存储迭代点while abs(t-t0)>0.000005t0=t;t=t0-ff(t)/fff(t);k=k+1;T(k)=t;endt1=t0;d=f(t1);kTfunction y=f(x)y=9*x^2-sin(x)-1;function y=ff(x)y=18*x-cos(x);function y=fff(x)y=18+sin(x);运行结果>> [t1,d]=Newton(0.4)k =3T =0.0586 0.0555 0.0555t1 =0.0555d =-1.0277>>4. 最速下降法验证课本上的例题求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [G,g,X,F]=zuisu(X0)F(1)=f(X0);%存储x 点处的值G(:,1)=h(X0); %存储梯度向量g(1)=norm(G(:,1));%存储梯度模长X(:,1)=X0; %存储x 值A=[2,0;0,8];for j=1:2X(:,j+1)=X(:,j)-(G(:,j)'*G(:,j))/(G(:,j)'*A*G(:,j))*G(:,j);F(j+1)=f(X(:,j+1));G(:,j+1)=h(X(:,j+1));g(j+1)=norm(G(:,j+1));endif (G(:,2)'*G(:,1)<1E-10& G(:,3)'*G(:,2)<1E-10)disp(['相邻两搜索方向是正交的'])endfunction y=f(X)y=X(1)^2+4*X(2)^2;function n=h(X)n=[2*X(1),8*X(2)]';运行结果>> [G,g,X,F]=zuisu(X0)相邻两搜索方向是正交的G =2.0000 1.4769 0.2215 8.0000 -0.3692 0.8862g =8.2462 1.5224 0.9134X =1.0000 0.7385 0.1108 1.0000 -0.0462 0.1108F =5.0000 0.5538 0.0613 >>。
二分法,不动点迭代法,艾特肯加速迭代法,牛顿切线法的matlab程序及举例

§2.1.1 二分法的MATLAB主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), returnendmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是向∞+方向取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b);x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);§2.1.2 不动点迭代法的MATLAB主程序function[k,piancha,xdpiancha,xk,yk]=diedai2(x0,tol,ddm ax)x(1)=x0;for i=1: ddmaxx(i+1)=fun(x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) piancha xdpiancha xk yk]if (piancha<tol)|(xdpiancha< tol)k=i-1; xk=x(i);return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i);yk=fun(x(i));[(i-1) piancha xdpiancha xk yk];return;endP=[(i-1),piancha,xdpiancha,xk,yk]'; §2.1.3 艾特肯加速迭代法的MATLAB主程序function [k,xk,yk,p]= Aitken (x0,tol, ddmax) x(1)=x0;for i=1: ddmaxx1(i+1)=fun(x(i));x2(i+1)=fun(x1(i+1));x(i+1)=x2(i+1)-(x2(i+1)-x1(i+1))^2/(x2(i+1)-2*x1(i+1)+ x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1; xk=x(i);yk=fun(x(i));if(piancha<tol)|(xdpiancha<tol)k=i-1; xk=x(i);yk=fun(x(i));m=[0,1:i-1];p=[m',x1',x2',x'];return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i); yk=fun(x(i));m=[0,1:i-1]; p=[m',x1',x2',x'];return;endm=[0,1:i-1]; p=[m',x1',x2',x'];§2.1.4 牛顿切线法的MATLAB主程序function[k,xk,yk,piancha,xdpiancha]=newtonqx(x0,tol,ft ol,gxmax)x(1)=x0;for i=1: gxmaxx(i+1)=x(i)-fun(x(i))/(dfun(x(i))+eps);piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps); i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) xk yk piancha xdpiancha]if(abs(yk)<ftol)&((piancha<tol)|(xdpiancha< tol))k=i-1; xk=x(i);[(i-1) xk yk piancha xdpiancha]return;endendif i>gxmaxdisp('请注意:迭代次数超过给定的最大值gxmax。
