大学物理化学知识点归纳
物理化学知识点(全)
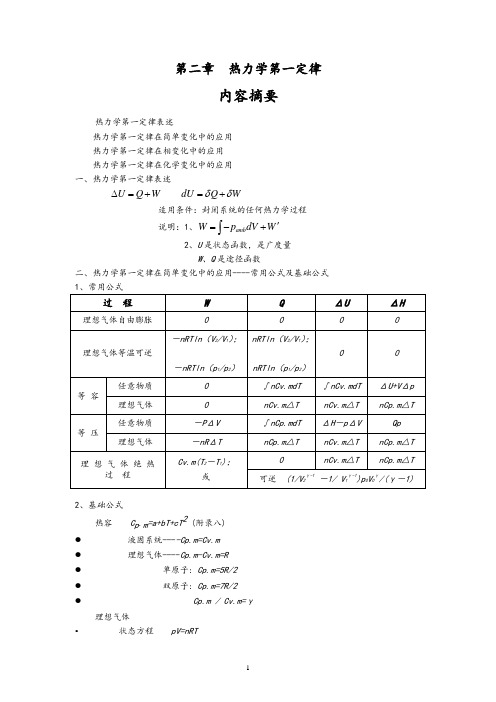
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件:封闭系统的任何热力学过程 说明:1、amb W p dV W '=-+⎰2、U 是状态函数,是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆-nRTln (V 2/V 1); -nRTln (p 1/p 2) nRTln (V 2/V 1);nRTln (p 1/p 2)0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质-P ΔV ∫nCp.mdT ΔH -p ΔV Qp 理想气体-nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2-T 1);或nCv.m △TnCp.m △T可逆 (1/V 2γ-1-1/ V 1γ-1)p 0V 0γ/(γ-1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m - p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = -Δ蒸发H m (T)Δ凝固H m (T) = -Δ熔化H m (T) Δ凝华H m (T) = -Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点: 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
物理化学的知识点总结

物理化学的知识点总结一、热力学1. 热力学基本概念热力学是研究能量转化和传递规律的科学。
热力学的基本概念包括系统、环境、热、功、内能、焓、熵等。
2. 热力学第一定律热力学第一定律描述了能量守恒的原理,即能量可以从一个系统转移到另一个系统,但总能量量不变。
3. 热力学第二定律热力学第二定律描述了能量转化的方向性,熵的增加是自然界中不可逆过程的一个重要特征。
4. 热力学第三定律热力学第三定律表明在绝对零度下熵接近零。
此定律是热力学的一个基本原理,也说明了热力学的某些现象在低温下会呈现出独特的特性。
5. 热力学函数热力学函数是描述系统状态和性质的函数,包括内能、焓、自由能、吉布斯自由能等。
二、化学热力学1. 热力学平衡和热力学过程热力学平衡是指系统各个部分之间没有宏观可观察的能量传输,热力学过程是系统状态发生变化的过程。
2. 能量转化和热力学函数能量转化是热力学过程中的一个重要概念,热力学函数则是描述系统各种状态和性质的函数。
3. 热力学理想气体理想气体是热力学研究中的一个重要模型,它通过状态方程和理想气体定律来描述气体的性质和行为。
4. 热力学方程热力学方程是描述系统热力学性质和行为的方程,包括焓-熵图、温度-熵图、压力-体积图等。
5. 反应焓和反应熵反应焓和反应熵是化学热力学研究中的重要参数,可以用来描述化学反应的热力学过程。
三、物质平衡和相平衡1. 物质平衡物质平衡是研究物质在化学反应和物理过程中的转化和分配规律的一个重要概念。
2. 相平衡相平衡是研究不同相之间的平衡状态和转化规律的一个重要概念,包括固相、液相、气相以及其之间的平衡状态。
3. 物质平衡和相平衡的研究方法物质平衡和相平衡的研究方法包括热力学分析、相平衡曲线的绘制和分析、相平衡图的绘制等。
四、电化学1. 电解质和电解电解质是能在水溶液中发生电离的化合物,电解是将电能转化为化学能或反之的过程。
2. 电化学反应和电势电化学反应是在电化学过程中发生的化学反应,电势是描述电化学系统状态的一个重要参数。
《大学物理化学》知识点总结

第一章 理想气体1、理想气体:在任何温度、压力下都遵循PV=nRT 状态方程的气体。
2、分压力:混合气体中某一组分的压力。
在混合气体中,各种组分的气体分子分别占有相同的体积(即容器的总空间)和具有相同的温度。
混合气体的总压力是各种分子对器壁产生撞击的共同作用的结果。
每一种组分所产生的压力叫分压力,它可看作在该温度下各组分分子单独存在于容器中时所产生的压力B P 。
P y P B B =,其中∑=BBB B n n y 。
分压定律:∑=BB P P道尔顿定律:混合气体的总压力等于与混合气体温度、体积相同条件下各组分单独存在时所产生的压力的总和。
∑=BB V RT n P )/(3、压缩因子ZZ=)(/)(理实m m V V 4、范德华状态方程 RT b V V ap m m=-+))((2 nRT nb V Van p =-+))((225、临界状态(临界状态任何物质的表面张力都等于0)临界点C ——蒸气与液体两者合二为一,不可区分,气液界面消失; 临界参数:(1)临界温度c T ——气体能够液化的最高温度。
高于这个温度,无论如何加压 气体都不可能液化;(2)临界压力c p ——气体在临界温度下液化的最低压力; (3)临界体积c V ——临界温度和临界压力下的摩尔体积。
6、饱和蒸气压:一定条件下,能与液体平衡共存的它的蒸气的压力。
取决于状态,主要取决于温度,温度越高,饱和蒸气压越高。
7、沸点:蒸气压等于外压时的温度。
8、对应状态原理——处在相同对比状态的气体具有相似的物理性质。
对比参数:表示不同气体离开各自临界状态的倍数 (1)对比温度c r T T T /= (2)对比摩尔体积c r V V V /= (3)对比压力c r p p p /= 9、rr r c r r r c c c T Vp Z T V p RT V p Z =⋅=10、压缩因子图:先查出临界参数,再求出对比参数r T 和r p ,从图中找出对应的Z 。
《物理化学》知识点汇总

《物理化学》知识点汇总热力学系统:热力学系统是指热力学研究的对象,是物质或物质的集合体。
状态:状态是指热力学系统中物质的宏观性质及其变化的状态。
热力学第一定律:能量守恒定律在热力学中的表现形式,它说明能量不能被创造或消失,只能从一种形式转化为另一种形式。
能量守恒:能量既不能被创造也不能被消失,它只能从一种形式转化为另一种形式。
热力学第二定律:热力学中描述自然过程方向性的定律,它表明,在一个封闭系统中,自发过程总是向熵增加的方向进行。
熵增:在封闭系统中,自发过程总是向熵增加的方向进行,也就是说,系统总是朝着更大的混乱状态发展。
相平衡:在热力学中,相平衡是指不同物相之间达到的平衡状态。
化学平衡:在化学反应中,反应物和生成物之间达到的平衡状态。
化学动力学:研究化学反应速率以及反应机制的科学。
表面化学:研究表面吸附、表面反应等表面现象的化学分支。
胶体分散系:由一种或多种物质在另一种物质中分散而成的系统。
以上是《物理化学》中的一些重要知识点,这些知识点是理解物理化学概念和应用的基础。
在学习过程中,需要不断巩固和深化对这些知识点的理解,以更好地掌握物理化学这门学科。
《经济法基础》是会计专业技术资格考试中的一门科目,主要考察考生对经济法相关知识的掌握程度和应用能力。
考试内容涉及广泛,包括经济法的基本概念、市场主体、市场秩序、宏观调控、劳动法等。
考试形式为闭卷、笔试,考试时间为90分钟。
经济法的基本概念:经济法的定义、特征、原则等。
市场主体:各类企业、个体工商户、农村承包经营户等市场主体的设立、变更和终止的相关法律规定。
市场秩序:市场竞争、市场准入、市场退出等方面的法律规定。
宏观调控:产业政策、财税政策、货币政策等宏观调控手段的法律规定。
劳动法:劳动者的权利和义务,劳动合同的签订和履行,劳动安全卫生、社会保险等方面的法律规定。
经济法涉及的法律法规众多,需要考生具备较为扎实的法律基础。
考试内容涉及面广,考生需要全面掌握各个方面的知识。
物理化学知识点总结大一

物理化学知识点总结大一一、导言大一的物理化学是一门基础性科学课程,为了让大家更好地掌握相关知识点,下面将对大一物理化学的重要知识点进行总结与归纳,希望对大家的学习有所帮助。
二、热力学1. 热力学基本概念:系统、界面、状态函数、过程函数等。
2. 热力学第一定律:能量守恒定律,内能变化等于对外界做功与传热的代数和。
3. 热力学第二定律:热力学不可逆性、熵增原理、卡诺循环等。
4. 热力学第三定律:绝对零度的存在性及应用。
三、化学平衡1. 平衡常量与平衡常数:反应物与产物的浓度及其对平衡常数的影响。
利用平衡常数判断反应方向。
2. 离子的溶解度与溶度积:离子在溶液中的溶解度及其对溶度积的影响。
3. 化学反应速率与速率方程:反应速率、速率常数、速率方程、反应级数等相关概念。
4. 反应动力学:表达反应速率的等式推导与实验确定方法。
四、电化学1. 电池与电解池:电化学反应的基本概念、标准电极电势、电池电动势等。
2. 电解质溶液与电解质离子浓度:电解质溶液中离子的浓度计算及其对电解过程的影响。
3. 法拉第定律与电解定律:法拉第电解定律的推导与应用,电解产物的选择性。
4. 化学电源与蓄电池:干电池、燃料电池、锂离子电池等。
五、化学热力学1. 火焰温度与燃烧热:火焰温度的计算,燃烧反应的焓变及其应用。
2. 燃烧热与键能:键能的概念,燃烧反应中键能的变化。
3. 化学反应焓变:化学反应焓变的定义、测定及其应用。
4. 化学反应熵变:化学反应熵变的定义、计算及其与焓变的关系。
六、物理化学实验1. 基本实验器材:量筒、分液漏斗、溶液容器等基本器材的使用与注意事项。
2. 量的测量及误差分析:物质的质量、体积、浓度等量的测量以及误差的计算和分析。
3. 溶解度测定与曲线拟合:溶解度的测定方法及曲线拟合分析。
4. 酸碱中和反应的滴定:滴定的原理、影响滴定结果的因素以及滴定曲线的解析。
七、总结与展望大一的物理化学涉及的知识点较多,以上只是其中一部分。
物理化学大一知识点归纳

物理化学大一知识点归纳物理化学是研究物质的物理性质和化学性质的一门学科。
大一是学习物理化学的起点,掌握基础知识对以后的学习非常重要。
本文将对大一物理化学的知识点进行归纳总结,帮助同学们更好地理解和记忆物理化学的基础知识。
1. 基本概念物理化学涉及的基本概念包括物质、质量、物质的量、分子、原子等。
物质是构成宇宙的基本要素,可以分为纯物质和混合物。
质量是物质的一个属性,可以通过称量进行测量。
物质的量用摩尔表示,是指含有物质粒子数的数量关系。
2. 物质的性质物质的性质分为物理性质和化学性质。
物理性质是指物质在不改变其化学组成的情况下的性质,如密度、熔点、沸点等。
化学性质是指物质在与其他物质发生作用时的性质,如酸碱性、氧化性等。
3. 热力学热力学是研究热能转化和能量守恒的科学。
其中,热力学第一定律是能量守恒定律,表明能量可以转化但不能消失;热力学第二定律是热力学过程方向性的规律,表明热能只能从高温物体流向低温物体。
4. 化学平衡化学平衡是指化学反应达到动态平衡的状态。
平衡常数是衡量反应平衡程度的指标,反应物和生成物浓度的比值与平衡常数之间存在关系。
平衡常数的大小可以预测反应的进行方向和平衡位置。
5. 气体状态方程气体状态方程是描述气体性质的数学表达式,常见的有理想气体状态方程和范德瓦尔斯方程。
理想气体状态方程是描述理想气体性质的理论模型,其中PV = nRT,P是气体压强,V是体积,n是物质的量,R是气体常数,T是温度。
范德瓦尔斯方程是修正理想气体行为的方程。
6. 化学动力学化学动力学是研究化学反应速率的科学。
影响化学反应速率的因素包括温度、浓度、催化剂等。
速率方程描述了反应速率与反应物浓度之间的关系。
活化能是化学反应必须克服的能垒。
7. 酸碱理论酸碱理论包括布朗斯特德酸碱理论和伦琴酸碱理论。
布朗斯特德酸碱理论认为酸是能提供H+离子的物质,碱是能提供OH-离子的物质。
伦琴酸碱理论将酸碱定义为电子对的供体和受体。
物理化学知识点总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程:1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功) 等压热:Q p =ΔH (封闭系统不作其他功) 焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p 热容与温度的关系:C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ; 利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学重要知识点总结及其考点说明

物理化学重要知识点总结及其考点说明
一、化学热力学
1、化学热力学的定义:化学热力学是研究化学反应中物质的热量及能量变化的学科。
2、热力学三定律:第一定律:能量守恒定律;第二定律:热力学第二定律确定有序
能可以被有度能转化;第三定律:热力学第三定律始终指出热力学反应的可能性和温度有关。
3、焓的概念:焓是衡量物质的热力学状态的量,它是物质的热力学特性连续变化的
测量,是物质拥有的热量能量,也可以视为物质拥有的有序能。
4、热力学平衡:热力学平衡是指在不变的温度、压力和其他条件下,恒定的化学反
应发生,直至反应物和生成物的物质形式和化学结构保持不变,热量吸积也变得稳定,这
种状态称为热力学平衡。
二、物理化学
1、物理化学的概念:物理化学是一门融合了物理学和化学的学科,通过应用物理方法,来研究化学性质的变化和分子间的作用及反应,其研究具有多学科的性质。
2、气体的特性:气体的物理性质有很多,如压强、体积、温度、熵、焓等。
质量和
体积的关系为:在一定温度下,气体的质量和体积都成正比。
3、溶质的溶解度:溶解度是衡量溶质溶解在溶剂中的性质,它是指在一定温度、压
力下,溶质在溶剂中的最高溶解量。
溶质的溶解度与温度,压强及溶剂特性有关。
4、化学均衡:化学均衡是指在特定温度和压强下,混合物中物质的各种浓度比例,
产物与原料之间的反应紊乱程度,变化状态的一种稳定平衡状态。
大一物理化学知识点总结

大一物理化学知识点总结大一是每个大学新生迈入大学生活的重要一年,在这一年中,大多数学生都需要学习物理和化学等基础科学知识。
物理化学作为一门重要的交叉学科,涵盖了物质的性质、结构、变化以及相关的物理原理和化学反应等内容。
下面将对大一物理化学的一些重要知识点进行总结。
一、物理学基础知识:1.力学:包括质点运动学、力学中的牛顿定律、能量和动量等的计算、弹性碰撞及碰撞动量定理等。
2.热学:理想气体状态方程、内能、热量传递及传导定律、热力学第一、第二定律等。
3.电磁学:库仑定律、电场与电势、电容和电路等的基本概念,电磁感应、电磁波、光的干涉、衍射等。
二、化学基础知识:1.物质的组成:原子结构、元素周期表的基本规律、分子与物质的宏观性质等。
2.化学反应:化学反应的基本类型,如氧化还原、酸碱中和、置换反应等,以及化学反应速率与平衡等。
3.溶液与溶解:溶解度、溶液的浓度计算、溶解过程中的物理化学变化等。
4.热力学:标准生成焓与标准反应焓、熵、自由能等。
三、物理化学实验基础:1.实验室安全与仪器使用:正确使用实验室仪器设备、了解实验室化学品的性质与安全措施。
2.实验技巧与数据处理:实验中的常见技巧,如称量、操作、数据的测量、记录、处理与分析等。
四、物理化学的应用与拓展:1.能源与环境:燃烧、电池及燃料电池等能源转化及利用,环境污染与治理等。
2.材料科学:结构与性质关系、合金与晶体的结构特性、纳米材料等。
以上只是大一物理化学知识点的基本概述。
在学习这些知识点的过程中,重要的是理解概念、掌握基本原理,并通过实际例子和应用案例加深理解。
此外,积极参加实验课程及实际操作,能够帮助学生将理论知识与实际应用相结合。
同时,物理化学领域也是一个不断发展的领域,随着科学技术的进步和应用的需求,新的物理化学原理和应用正在不断涌现,因此,大一物理化学知识只是物理化学学习的起点。
学生们应该继续深入学习,不断拓展自己的知识面,培养科学研究的兴趣和能力。
大学课程《物理化学》各章节知识点汇总

第一定律的数学表达式
U Q W
对微小变化: dU Q W
等容热效应
dU Q W W pdV 0
dU QV
CV
QV
dT
U T
V
U QV ,
U nB
S ,V ,n j B
H nB
S, p,nj B
F nB
T ,V ,n j B
B
G nB
T , p,n j B
n B
S ,V ,n j B
F f (T ,V , n1, n2 )
H f (S, p, n1, n2 )
组成可变系统的热力学基本关系式:
dU TdS pdV BdnB
Q和W都不是状态函数,其数值与变化途径有关。
§1-4 可逆过程和体积功
一、体积功
因系统的体积变化而引起的系统与环境之间交换的功称
为体积功。 pe
W Fedl ( pe A)dl
ped ( Al) pedV
A
dl
pi
二、功与过程
功不是状态函数,其数值与过程有关。系统由同一始态 经不同的过程变化到同一终态,则体统对环境或环境对 体系所作的功不同。
p2 dp
压缩
p1
p1
p2 , V2
p1, V1
p2
V1
V2
W
V1 V2
pedV
( p V1
V2
i
dp)dV
V1 V2
pi dV
三、可逆过程
某系统经一系列的过程后,如果系统回到初始状态叫做 系统的复原;环境在经历一些的变化后,如果既没有功 的得失也没有热的得失就叫做环境的复原。
厦门大学 物理化学 (上) 各章 知识点 总结

第1章第零定律与物态方程一、基本要点公式及其适用条件1.系统的状态和状态函数及其性质系统的状态—就是系统物理性质和化学性质的综合表现,它采用系统的宏观性质来描述系统的状态,系统的宏观性质,也称为系统的"状态函数"。
系统的宏观性质(状态函数)—就是由大量(摩尔级)的分子、原子、离子等微观粒子组成的宏观集合体所表现出的集团行为,简称"热力学性质"或“热力学函数”如p、V、T、U、H、S、A、G 等。
Z=f(x,y)表示一定量、组成不变的均相系统,其任意宏观性质(Z)是另两个独立宏观性质(x,y)的函数。
状态函数Z具有五个数学特征:(1),状态函数改变量只决定于始终态,与变化过程途径无关。
(2),状态函数循环积分为零,这是判断Z是否状态函数的准则之一。
(3),系Z的全微分表达式(4),系Z的Euler 规则,即微分次序不影响微分结果。
(5),系Z、x、y满足循环式,亦称循环规则。
2.热力学第零定律即热平衡定律:当两个物态A和B分别与第三个物体C处于热平衡,则A和B之间也必定彼此处于热平衡。
T =t+273.15,T是理想气体绝对温标,以"K"为单位。
t是理想气体摄氏温标,以"℃"为单位。
绝对温标与摄氏温标在每一度大小是一样的,只是绝对温标的零度取在摄氏温标的-273.15℃处,可以看出,有了绝对温标的概念后,只需确定一个固定参考点(pV)0p=0,依国际计量大会决定,这个参考点选取在纯水三相点,并人为规定其温度正好等于273.16K。
3.理想气态方程及其衍生式为:;式中p、V、T、n单位分别为Pa、m3、K、mol;R=8.314J〃mol-1〃K-1,V m为气体摩尔体积,单位为m3〃mol-1,ρ 为密度单位kg〃m-3,M 为分子量。
此式适用于理想气或近似地适用于低压气。
4.理想混合气基本公式(1)平均摩尔质量;式中M B和y B分别为混合气中任一组份B 的摩尔质量与摩尔分数。
大学物理化学知识点归纳

大学物理化学知识点归纳一、物理化学的基本概念物理化学是研究物质的性质和变化规律的学科,它融合了物理学和化学的理论与方法,对于理解和探索物质世界具有重要意义。
二、物理化学的热力学1. 热力学基本概念:热力学研究物质在不同温度、压力和组成条件下的能量转化和热效应。
2. 热力学第一定律:能量守恒定律,描述了物质的内能和热交换之间的关系。
3. 热力学第二定律:能量的不可逆性原理,描述了自然界中能量转化的方向和过程的规律。
4. 熵的概念:熵是衡量系统混乱程度的物理量,与物质的排列和有序程度相关。
5. 自由能与平衡:自由能是描述系统稳定性和反应方向的指标,平衡状态下自由能取最小值。
三、物理化学的动力学1. 动力学基本概念:动力学研究物质内部结构与变化之间的关系,以及反应速率和反应机理等问题。
2. 反应速率与速率常数:反应速率描述了反应速度的快慢,速率常数与反应机理密切相关。
3. 反应平衡与化学平衡常数:反应平衡是指在一定条件下反应物与生成物浓度保持不变的状态,化学平衡常数决定了反应的平衡位置。
4. 反应机理与活化能:反应机理描述了反应的详细步骤和中间产物,活化能是指反应过程中所需的最小能量。
四、物理化学的量子化学1. 量子化学基本概念:量子化学研究微观粒子(如电子)在原子和分子尺度下的性质和行为。
2. 波粒二象性:微观粒子既具有波动性又具有粒子性,具体表现为波粒二象性。
3. 波函数与薛定谔方程:波函数是描述微观粒子状态的数学函数,薛定谔方程描述了波函数的演化和微观粒子的运动规律。
4. 量子力学的应用:量子力学提供了解释原子和分子结构、光谱学和化学键性质等的理论基础。
五、物理化学的电化学1. 电化学基本概念:电化学研究物质在电解质溶液中的电荷转移和电极反应等现象。
2. 电解与电解质:电解是指将化学物质转化为离子的过程,电解质是能够在溶液中导电的化合物。
3. 电流与电解质溶液:电流是指电荷流动的物理现象,电解质溶液中的电流与离子在电场中的迁移相关。
物理化学大一知识点笔记

物理化学大一知识点笔记一、热力学1. 热力学基本概念- 系统与环境- 状态函数与过程函数- 热力学第一定律2. 理想气体状态方程- 环境压强与气体压强- 环境温度与气体温度- 理想气体状态方程及其推导3. 内能、焓和焓变- 内能的定义和性质- 焓的定义和性质- 焓变与热量的关系4. 熵和熵变- 熵的定义和性质- 熵增原理- 熵变与热量的关系5. 等温、绝热过程- 等温过程的性质和示意图- 绝热过程的性质和示意图- 理想气体的等温、绝热过程公式6. 热力学循环- 闭合系统的热力学循环- 热机效率和制冷系数- 卡诺循环和卡诺定理二、化学反应动力学1. 反应速率与反应级数- 反应速率的定义和表达式- 反应级数与反应速率的关系- 零级、一级和二级反应速率方程2. 碰撞理论- 碰撞理论的基本思想- 反应物分子碰撞的能量、角动量要求- 碰撞理论与反应速率的关系3. 简单化学反应动力学公式- 推导简单化学反应速率方程- 求解反应速率常数和反应级数- 缓慢反应和快速反应的判断4. 温度对反应速率的影响- 温度对反应速率的影响规律- 阿伦尼乌斯方程及其应用- 活化能和反应速率常数的关系5. 反应速率与浓度的关系- 工程级数和动力学级数的定义与区别- 工程级数和动力学级数的计算方法- 浓度对反应速率的影响规律6. 反应平衡和化学平衡常数- 反应平衡的条件- 平衡常数的定义和性质- 平衡常数与反应热力学的关系三、电化学1. 电化学基本概念- 电解质与非电解质- 电解和电极- 电池和电解槽2. 电解过程- 电解过程的基本方程- 电解过程的质量和电荷关系- 电解过程的电动势和电压3. 电池和电池电势- 电池的基本构成和工作原理- 电池的电动势和电动势方程- 电池电势和标准氢电极的关系4. 氧化还原反应- 氧化还原反应的基本概念- 氧化还原反应的电子转移和离子转移- 氧化还原反应的电子转移系数5. 电化学动力学- 过电位和极化现象- 极化曲线和电解过程的动力学- 电化学反应的速率方程和电流效率6. 腐蚀与防护- 金属腐蚀的基本机理- 腐蚀速率与电流密度的关系- 防腐涂层和电阻涂层的应用以上是物理化学大一知识点的笔记,涵盖了热力学、化学反应动力学和电化学三个方面的基础概念和公式。
大学物理化学总结.ppt

=0
不可逆 可逆
(dS )U.V 0
> 0 不可逆,自发过程 = 0 可逆,达到平衡
用熵判据判断过程是否为自发过程,一定要用
隔离系统。
(2). Helmholts自由能判据
<0
(dA)T ,V ,Wf 0 0
=0
不可逆,自发过程 可逆,达到平衡
自发变化向着Helmholts自由能减小的方向进行
Qp 与 QV 之间的关系
1. 对凝聚相反应 Qp QV 2. 对有气相参与的反应 Qp QV nRT
标准摩尔反应焓
r
H
m
B
f
H
m
(B)
B
C
H
m
(
B
)
B
B
Kirchhoff定律
从一个温度下的反应焓变,去计算另一温度 下的反应焓变
3 热力学第二定律
1.热力学第二定律
4.气体化学势
单种理想气体化学势
(T , p) (T ) RT ln p
理想气体混合物化学势
p
B (T ,
p)
B
(T )
RT
ln
pB p
B* (T, p) RT ln xB
大学物理化学知识点归纳

第一章气体的pvT关系一、理想气体状态方程pV=(m/M)RT=nRT(1.1)或pVm=p(V/n)=RT(1.2)式中p、V、T及n的单位分别为P a 、m3、K及mol。
Vm=V/n称为气体的摩尔体积,其单位为m3·mol。
R=8.314510J·mol-1·K-1称为摩尔气体常数。
此式适用于理想,近似于地适用于低压下的真实气体。
二、理想气体混合物1.理想气体混合物的状态方程(1.3)pV=nRT=(∑BBn)RTpV=mRT/Mmix(1.4)式中Mmix为混合物的摩尔质量,其可表示为Mmix def ∑BBy M B(1.5)Mmix=m/n=∑BBm/∑BBn(1.6)式中MB为混合物中某一种组分B的摩尔质量。
以上两式既适用于各种混合气体,也适用于液态或固态等均匀相混合系统平均摩尔质量的计算。
2.道尔顿定律pB=nBRT/V=yBp(1.7)P=∑BBp(1.8)理想气体混合物中某一种组分B的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。
而混合气体的总压即等于各组分单独存在于混合气体的温度、体积条件下产生压力的总和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
3.阿马加定律V B *=nBRT/p=yBV(1.9)V=∑VB*(1.10)VB*表示理想气体混合物中物质B 的分体积,等于纯气体B在混合物的温度及总压条件下所占有的体积。
理想气体混合物的体积具有加和性,在相同温度、压力下,混合后的总体积等于混合前各组分的体积之和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
三、临界参数每种液体都存在有一个特殊的温度,在该温度以上,无论加多大压力,都不可能使气体液化,我们把这个温度称为临界温度,以Tc 或tc表示。
我们将临界温度Tc时的饱和蒸气压称为临界压力,以pc表示。
在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积,以Vm,c 表示。
大学课程《物理化学》各章节知识点汇总

1. 自由膨胀过程(即外压等于零):
W pedV
W
V2 V1
pedV
0
5
2. 恒定外பைடு நூலகம்膨胀(压缩)过程
a. 一次膨胀过程
p2
p2
膨胀
p1, V1
p2 , V2
p1
W
V2 V1
pedV
p2
p2 (V2 V1)
V1
V2
a ' .一次压缩过程
p1 p1
p2 , V2
压缩
p1, V1 p1
W
A (p1V1)
p
D
A S1(等 温)C S2 (等容) B
S
S1
S2
nR ln
p1
T
T
T
V1
p2
可逆相变过程的熵变
S Qr Qp H TT T
20
变温过程中熵变的计算
Q CdT
dS Q C dT
T
T
等容过程:
dT dS CV T
或
S
C T2
T1 V
dT T
等压过程:
dS
Cp
dT T
或
S
C T2
T1 p
dT T
压力、体积、温度都发生 变化的过程
U QV
T2 T1
CV
dT
等压热效应(p1 p2 pe ) U Q W
U U2 U1 Qp pe (V2 V1)
(U2 p2V2 ) (U1 p2V2 ) Qp
H2 H1 H Qp
dH Qp
Cp
Qp
dT
H T
p
pH Qp
T2 T1
C
大学物理化学笔记总结

⼤学物理化学笔记总结第⼀章物理化学的定义,相变化(物质在熔点沸点间的转化)物理化学的基本组成:1化学热⼒学(⽅向限度)2化学动⼒学(速率与机理)3结构化学物理化学的研究⽅法、热⼒学⽅法、动⼒学⽅法、量⼦⼒学⽅法系统、环境的定义。
系统的分类:开放系统,封闭系统,隔离系统系统的性质:强度性(不可加),⼴延性(可加)。
系统的状态状态函数及其性质:1单值函数2仅取决于始末态3全微分性质。
热⼒学能、热和功的定义热分:潜热,显热。
功分:膨胀功、⾮膨胀功。
热⼒学第⼀定律的两类表述:1第⼀类永动机不可制成。
2封闭体系:能量可从⼀种形式转变为另⼀种形式,但转变过程中能量保持不变。
、恒容热、恒压热,焓的定义。
PV U H def+≡恒容热:①封闭系统② W f =0 ③W e =0 恒压热:①封闭系统②W f =0 ③d p =0 理想⽓体的热⼒学能和焓是温度的函数。
C, C V , C V,m , C P , C P,m 的定义。
△u =n C V,m (T 2-T 1) △H=n C P,m (T 2-T 1) C V,m =a+bT+cT 2+…/ a+bT -1+cT -2+… 单原⼦分⼦C V,m =23R C P,m =25R 双原⼦分⼦C V,m =25R C P,m =27R γ单=35 γ双=57 C P,m - C V,m =R R=·mol -1·k-1可逆过程定义及特点:①阻⼒与动⼒相差很⼩量②完成⼀个循环⽆任何功和热交换③膨胀过程系统对环境做最⼤功,压缩过程环境对系统做最⼩功可逆过程完成⼀个循环△u=0 ∑=0W ∑=0QW 、 Q 、△u 、△H 的计算①等容过程:W=0 Q=△u △u=n C V,m (T 2-T 1) △H=n C P,m (T 2-T 1)②等压过程:W=-Pe(V 2-V 1) Q=△H △u=n C V,m (T 2-T 1) △H=n C P,m (T 2-T 1) ③等温过程:W=-nRTln 12V V Q=-W △u=△H=0④绝热可逆过程:W=n C V,m (T 2-T 1) /??---1112111γγv v v p Q=0 △u=n C V,m (T 2-T 1)△H=n C P,m (T 2-T 1) 21p p =(12v v )γ 21T T =(12v v )1-γ 21T T=(21p p )γγ1-相变化过程中△H 及△u 的计算△u=△H-P △V=△H-nRT 见书1-10 化学计量系数ν化学反应进度??=BνBn ?(必与指定的化学反应⽅程对应)化学反应热效应定义,盖斯定律:⼀个化学反应,不管是⼀步完成或是经数步完成,反应的总标准摩尔焓变是相同的,即盖斯定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章气体的pvT关系一、理想气体状态方程pV=(m/M)RT=nRT(1.1)或pV m=p(V/n)=RT(1.2)式中p、V、T及n的单位分别为P a、m3、K及mol。
V m=V/n称为气体的摩尔体积,其单位为m3·mol。
R=8.314510J·mol-1·K-1称为摩尔气体常数。
此式适用于理想,近似于地适用于低压下的真实气体。
二、理想气体混合物1.理想气体混合物的状态方程(1.3)pV=nRT=(∑BBn)RTpV=mRT/M mix(1.4)式中M mix为混合物的摩尔质量,其可表示为M mix def∑BBy M B(1.5)M mix=m/n=∑BBm/∑BBn(1.6)式中M B为混合物中某一种组分B的摩尔质量。
以上两式既适用于各种混合气体,也适用于液态或固态等均匀相混合系统平均摩尔质量的计算。
2.道尔顿定律p B=n B RT/V=y B p(1.7)P=∑BBp(1.8)理想气体混合物中某一种组分B的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。
而混合气体的总压即等于各组分单独存在于混合气体的温度、体积条件下产生压力的总和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
3.阿马加定律V B*=n B RT/p=y B V(1.9)V=∑V B*(1.10)V B*表示理想气体混合物中物质B 的分体积,等于纯气体B在混合物的温度及总压条件下所占有的体积。
理想气体混合物的体积具有加和性,在相同温度、压力下,混合后的总体积等于混合前各组分的体积之和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
三、临界参数每种液体都存在有一个特殊的温度,在该温度以上,无论加多大压力,都不可能使气体液化,我们把这个温度称为临界温度,以T c或t c表示。
我们将临界温度T c时的饱和蒸气压称为临界压力,以p c表示。
在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积,以V m,c表示。
临界温度、临界压力下的状态称为临界状态。
四、真实气体状态方程1.范德华方程(p+a/V m2)(V m-b)=RT (1.11)或(p+an2/V2)(V-nb)=nRT (1.12)上述两式中的a和b可视为仅与气体种类有关而与温度无关的常数,称为范德华常数。
a的单位为Pa·m6·mol,b的单位是m3mol.-1。
该方程适用于几个兆帕气压范围内实际气体p、V、T的计算。
2.维里方程Z(p,T)=1+Bp+Cp+Dp+…(1.13)或Z(V m, ,T)=1+B/V m+C / V m2 +D/ V m3 +…(1.14)上述两式中的Z均为实际气体的压缩因子。
比例常数B’,C’,D’…的单位分别为Pa-1,Pa-2,Pa-3…;比例常数B,C,D…的单位分别为摩尔体积单位[V m]的一次方,二次方,三次方…。
它们依次称为第二,第三,第四……维里系数。
这两种大小不等,单位不同的维里系数不仅与气体种类有关,而且还是温度的函数。
该方程所能适用的最高压力一般只有一两个MPa,仍不能适用于高压范围。
五、对应状态原理及压缩因子1.压缩因子的对应式Z def PV/(nRT) =pV m/(RT) (1.15)压缩因子Z是个量纲为1的纯数,理想气体的压缩因子恒为1。
一定量实际气体的压缩因子不仅与气体的T,P 有关,而且还与气体的性质有关。
在任意温度下的任意实际气体,当压力趋于零时,压缩因子皆趋于1。
此式适用于纯实际气体或实际气体混合系统在任意T,p下压缩因子的计算。
2.对应状态原理P r=p/p c(1.16)V r=V m/V m,c(1.17)T=T/T c(1.18)p r、V r、T c分别称为对比压力、对比体积和对比温度,又统称为气体的对比参数,三个量的量纲均为1。
各种不同的气体,只要有两个对比参数相同,则第三个对比参数必定(大致)相同,这就是对应状态原理。
第二章热力学第一定律一、热力学基本概念1.状态函数状态函数,是指状态所持有的、描述系统状态的宏观物理量,也称为状态性质或状态变量。
系统有确定的状态,状态函数就有定值;系统始、终态确定后,状态函数的改变为定值;系统恢复原来状态,状态函数亦恢复到原值。
2.热力学平衡态在指定外界条件下,无论系统与环境是否完全隔离,系统各个相的宏观性质均不随时间发生变化,则称系统处于热力学平衡态。
热力学平衡须同时满足平衡(△T=0)、力平衡(△p=0)、相平衡(△μ=0)和化学平衡(△G=0)4个条件。
二、热力学第一定律的数学表达式1.△U=Q+W或dU=ΔQ+δW=δQ-p amb dV+δW`规定系统吸热为正,放热为负。
系统得功为正,对环境做功为负。
式中p amb为环境的压力,W`为非体积功。
上式适用于封闭系统的一切过程。
2.体积功的定义和计算系统体积的变化而引起的系统和环境交换的功称为体积功。
其定义式为:δW=-p amb dV(1)气体向真空膨胀时体积功所的计算W=0(2)恒外压过程体积功W=p amb(V1-V2)=-p amb△V对于理想气体恒压变温过程W=-p△V=-nR△T(3)可逆过程体积功W r=⎰21pVVdV(4)理想气体恒温可逆过程体积功W r=⎰21pVVdV=-nRTln(V1/V2)=-n RTln(p1/p2)(5)可逆相变体积功W=-pdV三、恒热容、恒压热,焓 1.焓的定义式H def U + p V 2.焓变(1)△H=△U+△(pV) 式中△(pV)为p V 乘积的增量,只有在恒压下△(pV)=p(V 2-V 1)在数值上等于体积功。
(2)△H=⎰21,T T m p dT nC此式适用于理想气体单纯p VT 变化的一切过程,或真实气体的恒压变温过程,或纯的液、固态物质压力变化不大的变温过程。
3. 内能变 (1)△U=Qv式中Qv 为恒热容。
此式适用于封闭系统,W`=0、dV=0的过程。
△ U=⎰21,v T T m dT nC =)(12,v T -T m nC 式中m C ,v 为摩尔定容热容。
此式适用于n 、C V,m 恒定,理想气体单纯p 、V 、T 变化的一切过程。
4. 热容 (1) 定义当一系统由于加给一微小的热容量δQ 而温度升高dT 时,δQ/dT 这个量即热容。
(2) 摩尔定容热容C V ,mC V ,m =C V /n=(TU mаа)V (封闭系统,恒容,W 非=0)(3)摩尔定压热容C p,mC p,m ==n p C P⎪⎭⎫⎝⎛T H m аа (封闭系统,恒压,W 非=0)(4) C p, m 与 C V ,m 的关系 系统为理想气体,则有C p, m —C V ,m=R系统为凝聚物质,则有C p, m —C V ,m ≈0(5)热容与温度的关系,通常可以表示成如下的经验式C p, m =a+bT+cT 2 或C p, m =a+b`T+c`T -2式中a 、b 、c 、b`及c`对指定气体皆为常数,使用这些公式时,要注意所适用的温度范围。
(6)平均摩尔定压热容C p,mC p,m =⎰21,T T m p dT nC (T 2-T 1)四、理想气体可逆绝热过程方程()Cm V ,12TT ()RV V 12=1()C m p ,12TT ()Rp p -12=1()12pp ()Γ12V V =1上式γ=m C ,p /m C ,v ,称为热容比(以前称为绝热指数),以上三式适用于m C ,v 为常数,理想气体可逆绝热过程,p,V,T 的计算。
五、反应进度 ξ=△n B /v B上式适用于反应开始时的反应进度为零的情况,△n B =n B -n B ,0,n B ,0为反应前B 的物质的量。
νB 为B 的反应计算数,其量纲为1。
ξ的单位为mol 。
六、热效应的计算 1.不做非体积功的恒压过程Q p =△H=⎰21,T Tm p dT nC2.不做非体积功的恒容过程Q v =△U=⎰21,v T Tm dT nC3.化学反应恒压热效应与恒容热效应关系Q p - Q v =(△n)RT4.由标准摩尔生成焓求标准摩尔反应焓变ΘmrH △=∑ΘBm f B )(H v B △5由标准摩尔燃烧焓求标准摩尔反应焓变Θm rH △=—∑ΘBm C )(H B v B △6. m rH △与温度的关系 基希霍夫方程的积分形式Θm rH △(T 2)= Θm rH △(T 1)+⎰Θ21)(,T T m p dT B rC △基希霍夫方程的微分形式 d Θm rH △=△rΘmp,C dT=∑ΘBmpBvBC)(,七、节流膨胀系数的定义式μJ-T=(аT/аp)HμJ-T又称为焦耳—汤姆逊系数第三章热力学第二定律一、卡诺循环1.热机效率η=-W/Q1=(Q1+Q2)/Q1=(T1-T2)/T1式中Q1和Q2分别为工质在循环过程中从高温热源T1吸收热量和向低温热源T2放出热量这两个过程的可逆热。
此式适用于在两个不同的温度之间工作的热机所进行的一切可逆循环。
2.卡诺循环所有工作于两个确定温度之间的热机,以可逆热机效率最大。
η1rηr即是Q1/T1+Q2/T2≤0⎪⎪⎭⎫⎝⎛=<可逆循环不可逆循环式中T1、T2为高低温热源的温度。
可逆时等于系统的温度。
二、热力学第二定律1.克劳修斯说法“不可能把热从低温物体传到高温物体而不产生其他影响。
”2.开尔文说法“不可能从单一热源吸取热量使之完全转变为功而不产生其他影响。
”三、熵1.熵的定义d S defδQ r/T式中Q r为系统与环境交换的可逆热,T为可逆热δQ r时系统的温度。
2.克劳修斯不等式dS⎭⎬⎫⎩⎨⎧>=,不可逆过程δ,可逆过程δTQTQ//3.熵判据△S iso =△S sys +△S amb ⎭⎬⎫⎩⎨⎧=>,可逆不可逆0,0式中iso 、sys 和amb 分别代表隔离系统、系统和环境。
在隔离系统中,不可逆过程即自发过程。
可逆,即系统内部及系统与环境之间处于平衡态。
在隔离系统中,一切自动进行的过程都是向熵增大的方向进行,这称为熵增原理。
此式只适用于隔离系统。
四、熵变的计算 1.单纯的PVT 变化过程中无相变化和化学变化,W`=0,可逆。
△S=⎰21T Q rδ=⎰+21T pdV dU =⎰+21T Vdp dH 理想气体系统 △S=nC V,m ln12T T +nRln 12V V= nC p,m ln12T T - nRln 12p p= n C p ,m l n12V V + n C V ,m ln 12p p 恒温(T 1=T 2)△S= nRln12V V =- nRln12p p 恒压(p 1=p 2)△S= nC p,m ln12T T = n C p ,m l n12V V 恒容(V 1=V 2)△S= nC V,m ln12T T = n C V ,m ln12p p 凝聚相系统 △S=⎰21TQ rδ 恒容△S =T,v 21dT nC m T T ⎰恒压△S=⎰21T,T T m p dT nC恒温△S=δQ r /T 2.相变化可逆变化βα△S=βα△H/T不可逆相变,通常设计一条要包括可逆相变步骤在内的可逆途径,此可逆途径的热温熵才是该不可逆过程的熵变。
