系统动力学预测模型
系统动力学模型

系统动力学模型什么是系统动力学系统动力学是一种研究系统行为的方法和工具,它主要关注系统结构形成的动力学过程。
它可用于预测系统变化的趋势和影响,以及设计改变系统行为的政策。
系统动力学是一种模拟性思维工具,用于解决涉及许多互相联系的因素的复杂问题,例如企业管理、城市规划、环境保护、流行病传播等。
系统动力学建立在一系列原理之上,包括动态、非线性、复杂性和反馈。
它将系统看作一个有机整体,受到内部和外部因素的相互作用和影响。
系统动力学的核心是建立一个结构模型,该模型基于特定系统的组成部分,系统变量和它们之间的动态关系。
系统动力学模型的基本组成部分一个典型的系统动力学模型包括以下四个主要部分:构建系统结构图系统结构图是系统动力学模型的核心。
它包括不同变量之间的关系,变量可以是数量、资料、质料、阈值或事件。
结构图可以通过新陈代谢循环、储备、增值、流动和调控来定义系统变量和它们的依赖关系。
确定变量因素每个系统变量都受多种因素的影响,并与其他变量相互影响。
变量因素可能是外部因素,如市场需求、公司预算、环境限制等,也可能是内部因素,如员工行为、财务报告、产品质量等。
定义动态性系统动力学模型是建立在动态性基础上的。
变量不断变化,相互作用和影响会产生系统行为和性能的变化。
动态模型可以从时间维度中展现出来,当然还要考虑到周期性和规律性。
分析政策通过模型的分析,会得出许多新见解,从而制定出需要采取的具体政策和措施。
可以评估不同政策的影响,从而制定最佳的决策方案。
系统动力学模型的使用系统动力学模型非常适合用于下列场景:多变量和相互影响如果一个问题涉及许多因素和相互的影响,系统动力学模型是一种非常有效的解决方案。
它允许解决复杂的问题,包括环境、制造、管理、公共政策等。
长期影响系统动力学模型还可以用于评估政策和措施的长期效果,以及它们及其组合可能产生的复杂后果。
它可以帮助预测趋势和影响,为政策制定提供依据。
数据不足当您对一个系统缺少足够的信息时,使用系统动力学模型可以预测未来的变化趋势,并识别最重要的变量和因素。
系统动力学模型

如:
用
表示。
系统动力学的建模步骤
例1:建立“一阶库存管理系统”的系统动力学模型,并分析系统 的
动态趋势。
例2,: 建立“二阶库存管理系统”的系统动力学模型,并分析系统 的
动态趋势。
思考题
• 物流系统的系统动力学模型构建
• 决策变量(又称流率)(r):
描述系统物质流动或信息流动积累效应变化快慢的变 量,其具有瞬时性的特征。
——反映单位时间内物质流动或信息流量的增加或 减少的量
——相对量、速度、微积分中的变化率等
决策变量符号表示:
注 意:
(3) 常数:描述系统中不随时间而变化的量,
用
表示。
如:
(4) 辅助变量:从信息源到决策变量之间,起到辅助表达信息反 馈决策作用的变量。
——流图能反映出物质ห้องสมุดไป่ตู้积累值和积累效应变化快慢的区别
2. 流图 :
流图确定反馈回路中变量状态发生变化的机制,明确表 示系统各元素间的数量关系,反映物质链与信息链的区 别,能够反映物质的积累值及积累效应变化快慢的区别。
(1). 物质链与信息链
物质链:系统中流动的实体,连接状态变量 是不使状态值变化的守恒流。
物质链符号表示:要素A→要素B
• 信息链:连接状态和变化率的信息通道,是与因果关系相连 的信息传输线路。
信息链符号表示:A O···→B
(2)状态变量与决策变量
• 状态变量(又称流位)(x):
描述系统物质流动或信息流动积累效应的变量,表 征系统的某种属性,有积累或积分过程的量
—— 绝对量、位移、微积分中的积分量等
1. 因果关系图: 2. 因果链:
3. 反馈回路:
综合“因果关系图”:
系统动力学模型

系统动力学模型系统动力学模型是指它是一种分析和模拟物理系统及其动力学过程的数学技术。
它可以用来研究运动学,控制系统,流体动力学,形式力学,电学,冲击学和弹性动力学等领域的数学模型,并可用于实际的工程问题的解决。
系统动力学模型基于物理系统的动力学处理和控制问题,用来研究物体的运动行为。
例如,系统动力学模型可以用来探讨汽车的运动性,即汽车在不同条件下的行驶特性,以确定汽车行驶性能的最佳状态。
此外,系统动力学模型还可以模拟任意静力学,力学,流体力学或热力学系统的运动模式。
系统动力学模型的建立要求具备完备的物理基础知识,形成一个系统模型的首要任务是了解物理系统的特性和行为,因此必须确定物理系统的运动方程和力学特征,物理量的表达式在构建模型时必须明确。
模式构建完成后,需要求解模型,并将模型运用到实际问题中,用以求解物理过程及其动力学运行状态。
为此,我们可以使用计算机模拟技术来求解模型,用以检验结果的正确性和准确性。
系统动力学模型在很多领域中都发挥着重要的作用,例如机械系统的设计,控制系统的调整,电子电气系统的设计,机器人的控制,航空航天技术,建筑工程设计等。
例如,在机器人技术中,系统动力学模型可以模拟机器人的运动特性,帮助机器人决定如何完成任务。
此外,系统动力学模型在工程设计中也有广泛应用,可用于分析和解决工程设计问题,以便改善工程性能。
例如,系统动力学模型可以帮助分析和解决结构物振动问题,提高结构物的稳定性和耐久性,以及改善系统的可靠性。
此外,系统动力学模型也可以帮助优化控制系统的性能,以提高系统的功率和可靠性。
综上所述,系统动力学模型是一个强大的工具,可以帮助我们研究和分析物理系统及其动力学过程,从而有效地改善工程性能。
它在机械,控制,电子,航空航天等各个领域都有广泛的应用,并被广泛用来分析和解决工程设计问题。
《系统动力学模型》课件
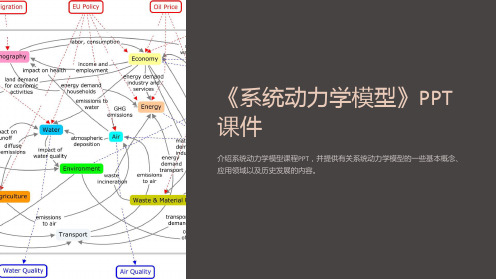
3 交通拥堵问题
利用系统动力学模型分析 交通系统中的关键影响因 素,提出拥堵缓解策略。
总结
系统动力学模型的优 点
能够综合考虑各种因素的复杂 相互关系,揭示潜在的系统行 为规律。
系统动力学模型的局 限性
构建和验证模型需要大量的数 据和计算资源,并且容易受到 参数估计误差的影响。
系统动力学模型的未 来发展
3
1 972 年
《The Limits to Growth》的发表使系统动力学模型成为一个热门研究领域。
系统动力学基本理论
系统动力学图形符号、流量与库存的关系以及系统动力学中的反馈思想是构建系统动力学模型的基本理论。
系统动力学模型的构建
步骤一:制定概念模 型
定义系统的边界和范围,确定 系统中的因素。
步骤二:建立定量模 型
全面考虑建模元素,建立动态 模型方程。
步骤三:模型验证和 仿真
模型验证的用案例
1 企业资源分配问题
通过系统动力学模型优化 企业的资源配置方案,提 高经济效益。
2 环境污染问题
应用系统动力学模型预测 环境污染的发展趋势,制 定相应的环境保护措施。
复杂性分析
适用于复杂问题,帮助发现问题背后的潜在因果 关系。
系统动力学模型的应用领域
商业与管理 公共政策 能源与资源管理
环境与可持续发展 社会科学 健康与医疗
系统动力学模型的历史发展
1
1940年代
系统动力学的基本概念和方法首先由Jay W. Forrester提出。
2
1960年代
MIT的Jay W. Forrester开始使用计算机来构建和模拟系统动力学模型。
(完整版)系统动力学模型案例分析
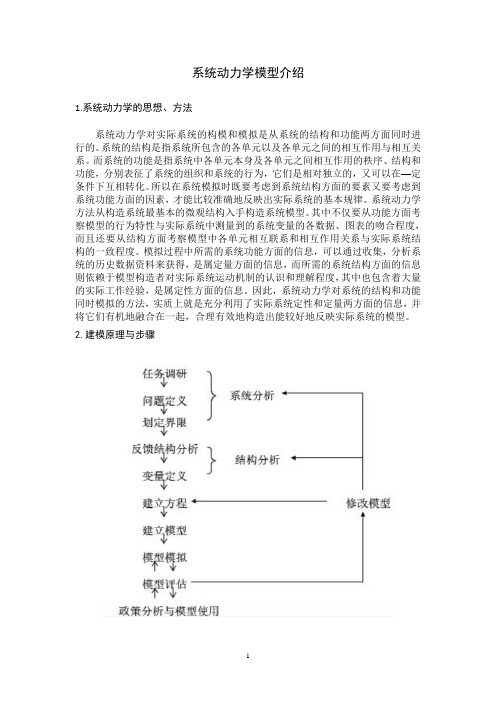
系统动力学模型介绍1.系统动力学的思想、方法系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。
系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。
而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了系统的组织和系统的行为,它们是相对独立的,又可以在—定条件下互相转化。
所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素,才能比较准确地反映出实际系统的基本规律。
系统动力学方法从构造系统最基本的微观结构入手构造系统模型。
其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度,而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。
模拟过程中所需的系统功能方面的信息,可以通过收集,分析系统的历史数据资料来获得,是属定量方面的信息,而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度,其中也包含着大量的实际工作经验,是属定性方面的信息。
因此,系统动力学对系统的结构和功能同时模拟的方法,实质上就是充分利用了实际系统定性和定量两方面的信息,并将它们有机地融合在一起,合理有效地构造出能较好地反映实际系统的模型。
2.建模原理与步骤(1)建模原理用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。
系统动力学认为系统具有整体性、相关性、等级性和相似性。
系统内部的反馈结构和机制决定了系统的行为特性,任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。
系统动力学模型的系统目标就是针对实际应用情况,从变化和发展的角度去解决系统问题。
系统动力学构模和模拟的一个最主要的特点,就是实现结构和功能的双模拟,因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。
与其它模型一样,系统动力学模型也只是实际系统某些本质特征的简化和代表,而不是原原本本地翻译或复制。
系统动力学9种模型

系统动力学9种模型系统动力学是一种系统分析和建模方法,通过对系统的结构和行为进行建模,研究系统内部的相互作用和反馈机制,从而预测其未来的发展趋势。
在系统动力学中,有9种常见的模型,分别是增长模型、衰退模型、饱和模型、振荡模型、周期性波动模型、滞后效应模型、优化模型、风险分析模型和政策评估模型。
1. 增长模型增长模型是最基本的系统动力学模型之一。
它描述了一个系统在没有外界干扰的情况下,如何随着时间推移而不断增长。
这种增长可以是线性的也可以是非线性的。
例如,在经济领域中,GDP随着时间推移而不断增加。
2. 衰退模型衰退模型与增长模型相反,它描述了一个系统在没有外界干扰的情况下如何随着时间推移而逐渐减少。
例如,在生态学领域中,物种数量会随着时间推移而逐渐减少。
3. 饱和模型饱和模型描述了一个系统在达到某个极限之后停止增长或减少。
例如,在市场经济学中,销售量可能会在达到一定数量之后停止增长。
4. 振荡模型振荡模型描述了一个系统在内部反馈机制的作用下如何产生周期性变化。
例如,在经济领域中,经济周期的波动就是一种典型的振荡模型。
5. 周期性波动模型周期性波动模型是振荡模型的一种特殊形式,它描述了一个系统在内部反馈机制的作用下如何产生固定频率的周期性变化。
例如,在天文学中,月相变化就是一种周期性波动模型。
6. 滞后效应模型滞后效应模型描述了一个系统在外界干扰下,其响应速度比干扰发生速度慢的现象。
例如,在宏观经济学中,货币政策对经济增长的影响可能需要几个季度或几年才能显现出来。
7. 优化模型优化模型描述了一个系统如何通过最大化或最小化某个目标函数来达到最佳状态。
例如,在工业领域中,企业可能会通过优化生产流程和降低成本来提高利润率。
8. 风险分析模型风险分析模型描述了一个系统在面临不确定性和风险的情况下如何进行决策。
例如,在金融领域中,投资者可能会使用风险分析模型来评估不同投资方案的风险和回报。
9. 政策评估模型政策评估模型描述了一个系统在政策干预下如何变化。
系统动力学模型特点

系统动力学模型特点
系统动力学模型是一种应用于系统分析和控制的模型技术。
具有一系列的特点:
1. 长期决策分析
系统动力学模型的主要应用是进行长期决策分析,根据系统的历史数据进行预测,指导长期决策。
例如,全球气候变化、人口增长、经济增长等问题。
2. 重视非线性因素
系统动力学模型认为,许多系统间的关系都是非线性的,线性模型不能完全的反映真实情况。
因此,它们采用非线性方法,更好的建立出系统间的关系来。
3. 从整合的角度构建模型
在系统动力学模型中,单一因素的影响并不是最终的因素,而是所有影响因素之间相互作用的结果,模型综合了所有相关因素,从而更准确地预测和控制系统的运行和行为。
4. 强调时间因素
系统动力学模型认为,时间是最重要的因素之一,而且时间是不可逆转的。
因此,模型建立在时间因素的考虑上,可以更好地预测未来的变化。
5. 迭代与反馈
系统动力学模型逐步演化、重复检验,并通过反馈修正模型,以更准确地反映实际情况。
这种迭代和反馈的过程可以保证模型的准确性,并能更好地控制系统。
6. 多维复杂度的考虑
系统动力学模型具有很强的可扩展性和可复用性,在处理多维复杂的问题时显得尤为重要。
这种模型可以更好地应对不同方向上的数据和来源,并更加准确的预测和控制系统。
综上所述,系统动力学模型认为时间、整合、迭代和反馈是建立复杂系统模型的重要组成部分。
因此,它们不断优化,提高了可预测性和可控性,为长期决策提供了有力的支持。
基于系统动力学的人口预测

3.2基于系统动力学的人口预测21世纪是人类面临三大问题:第一是人口膨胀,第二是就业困难,第三是环境污染,这三大问题的焦点在于人口。
因此,如何对未来的人口进行预测和控制,一直是人们关心的重要领域。
本课题是在宋健人口模型的基础上,考虑到上海作为一个开放城市,改良建立了双线性开放/动态人口模型。
采用上述基于人口结构模型,预测上海2010—2050年的人口年龄、性别结构。
为了更准确地研究人口系统,我们将人口按0-4岁、5-9岁、10-14岁、…、95-99岁、100岁及以上分群,分为21个群,并假设女性的生育时间以不同的概率分布在15-49岁之间。
然后以政策系数和生育时间的分布概率为政策参数进行仿真分析和政策试验。
3.2.1系统模拟的一些基本假设●人口分年龄数据2000年人口普查的数据上海常住人口总数为1640万,而根据上海统计年鉴2000年上海常住人口总数为1608万。
因为后续计算都是采用上海统计年鉴上的数据,所以按上海统计年鉴的常住人口总数1608万对2000年人口普查的数据进行了同比例调整。
通过《上海统计年鉴》、《上海市2000年人口普查资料》、《2005年上海市1%人口抽样调查资料》等文献的搜索,得2000年上海市分年龄段的男、女人数数据见表1。
表1 上海市2000年分年段男、女人数(单位:万人)第五次普查(2000年) 第五次普查(2000年)年龄段合计男女年龄段合计男女0~4岁49 25.7 23.3 55~59岁66.61 34.3 32.315~9岁58.67 30.53 28.14 60~64岁57.73 28.54 29.1910~14岁93.42 47.95 45.48 65~69岁68.31 32.25 36.0615~19岁129.51 64.9 64.62 70~74岁53.13 24.37 28.7620~24岁135.3 69.72 65.57 75~79岁36.71 15.94 20.7725~29岁135.4 72.09 63.31 80~84岁19.39 7.67 11.7330~34岁139.48 76.16 63.32 85~89岁7.9 2.71 5.1935~39岁150.65 81.27 69.38 90~94岁 2.16 0.61 1.5540~44岁170.02 88.98 81.04 95~99岁0.42 0.11 0.3245~49岁159.15 82.89 76.26 100岁及以上0.03 0.004 0.0250~54岁107.8 56.33 51.46●妇女生育时间根据人口生育的一般规律可知,对出生有贡献的只有15-49岁的女性人口。
系统动力学模型构建方法总结

系统动力学模型构建方法总结系统动力学是一种描述系统行为和相互作用的建模方法。
它通过对系统的各个组成部分进行建模与分析,探索因果关系和反馈环路之间的相互影响,以更好地理解系统的演化和预测系统的未来行为。
系统动力学模型可以应用于各种领域,如经济学、管理学、环境科学和社会科学等,用于研究复杂系统的行为和决策。
构建系统动力学模型是一个有序且有迭代过程的任务。
下面将总结步骤和方法以帮助读者更好地理解和应用系统动力学模型。
1. 确定研究目标和问题:在构建系统动力学模型之前,我们需要明确研究目标和问题。
通过明确目标和问题,可以帮助我们选择适当的系统边界、变量和关系,从而建立具有可解释性和可预测性的模型。
2. 确定系统边界和变量:系统边界定义了模型所要研究的系统的范围,而变量则是描述系统状态和行为的要素。
在确定系统边界和变量时,我们应该考虑到其实际意义和对研究问题的影响。
3. 构建因果关系和反馈回路:因果关系和反馈回路是系统动力学模型的核心。
因果关系描述了变量之间的因果关系,而反馈回路则探索了变量与自身之间的相互影响。
构建因果关系和反馈回路时,我们可以借助系统动力学模型中的积分方程、差分方程和代数方程等数学工具。
4. 估计参数和校准模型:为了使模型能够更好地描述实际系统,我们需要估计模型中的参数,并进行校准。
参数的估计可以通过历史数据、专家知识和实证研究等途径来进行。
而模型的校准则是通过与实际观测数据对比来调整模型的参数和结构,从而提高模型的预测能力。
5. 模型验证和敏感性分析:模型验证是指利用新的数据验证模型的准确性和预测能力。
敏感性分析则是用于评估模型对输入参数的响应程度。
通过模型验证和敏感性分析,可以帮助我们评估模型的可靠性和稳健性,从而增加对模型结果的信任度。
6. 模型应用和政策决策:最后,根据模型的设计目标和研究问题,我们可以利用模型进行政策决策和行动规划。
模型的应用可以帮助决策者更好地理解系统行为和影响因素,预测未来趋势,并通过制定合理的政策来优化系统的性能。
系统动力学模型

系统动力学模型系统动力学模型是一种旨在评估和预测系统行为的工具。
它可以量化系统的状态改变,以及它们之间的相互作用。
系统动力学模型是一种有用的工具,可以用来研究复杂系统,了解系统是如何处理不同类型的信息,并预测它们的未来行为。
系统动力学模型是一种基于理论的系统分析方法,它的基本假设是系统的行为可以用一组模型来表示。
模型可以是相互作用的系统元素,也可以是连接系统元素的联系。
系统动力学模型的目的是使用这些模型来研究系统的结构、属性和行为,并预测系统的未来发展。
系统动力学模型采用了一种基于计算机的技术,称为差分方程式方法,来描述和解释系统的动力学变化。
差分方程式方法使用动力学变量,如速度、位置、电位、势能等,来描述系统的运动。
这种方法可以用来模拟并预测复杂系统的行为。
系统动力学模型还应用于行为学领域,用于模拟人类行为的动态变化的过程。
行为学中的系统动力学模型可以用来理解社会行为中的复杂性和模糊性,以及行为的有机变化。
在行为学中,系统动力学模型的一个重要应用是可以用来计算不同行为的不稳定性,并预测行为的发展趋势。
系统动力学模型有助于分析和预测复杂系统的行为,它可以用来理解和描述系统的内在振荡机制,以及两个或多个系统之间的互动关系。
它还可以用来分析行为学中的行为变化,并预测行为的趋势。
系统动力学模型的广泛应用使它成为一种重要的工具,用于研究复杂系统的运作和行为,以及理解行为的动态变化。
综上所述,系统动力学模型是一种用于评估和预测系统行为的有用工具。
它可以使用模型来描述系统的结构、属性和行为,并利用差分方程式方法来模拟复杂系统的行为,为行为学提供有用的工具。
系统动力学模型的应用范围广泛,可以用来研究复杂系统的内部机制,以及行为的发展趋势。
系统动力学模型

第10章系统动力学模型系统动力学模型(System Dynamic)是社会、经济、规划、军事等许多领域进行战略研究的重要工具,如同物理实验室、化学实验室一样,也被称之为战略研究实验室,自从问世以来,可以说是硕果累累。
1 系统动力学概述2 系统动力学的基础知识3 系统动力学模型第1节系统动力学概述1.1 概念系统动力学是一门分析研究复杂反馈系统动态行为的系统科学方法,它是系统科学的一个分支,也是一门沟通自然科学和社会科学领域的横向学科,实质上就是分析研究复杂反馈大系统的计算仿真方法。
系统动力学模型是指以系统动力学的理论与方法为指导,建立用以研究复杂地理系统动态行为的计算机仿真模型体系,其主要含义如下:1 系统动力学模型的理论基础是系统动力学的理论和方法;2 系统动力学模型的研究对象是复杂反馈大系统;3 系统动力学模型的研究内容是社会经济系统发展的战略与决策问题,故称之为计算机仿真法的“战略与策略实验室”;4 系统动力学模型的研究方法是计算机仿真实验法,但要有计算机仿真语言DYNAMIC的支持,如:PD PLUS,VENSIM等的支持;5 系统动力学模型的关键任务是建立系统动力学模型体系;6 系统动力学模型的最终目的是社会经济系统中的战略与策略决策问题计算机仿真实验结果,即坐标图象和二维报表;系统动力学模型建立的一般步骤是:明确问题,绘制因果关系图,绘制系统动力学模型流图,建立系统动力学模型,仿真实验,检验或修改模型或参数,战略分析与决策。
地理系统也是一个复杂的动态系统,因此,许多地理学者认为应用系统动力学进行地理研究将有极大潜力,并积极开展了区域发展,城市发展,环境规划等方面的推广应用工作,因此,各类地理系统动力学模型即应运而生。
1.2 发展概况系统动力学是在20世纪50年代末由美国麻省理工学院史隆管理学院教授福雷斯特(JAY.W.FORRESTER)提出来的。
目前,风靡全世界,成为社会科学重要实验手段,它已广泛应用于社会经济管理科技和生态灯各个领域。
系统动力学9种模型

系统动力学9种模型引言系统动力学是一种研究动态系统行为的方法论,它通过构建系统模型来分析系统的各种因果关系和变化规律。
在系统动力学中,有9种基本模型被广泛应用于各种领域的问题分析和解决。
本文将对这9种模型进行全面、详细、完整且深入地探讨。
1. 积累模型积累模型是系统动力学中最基本的模型之一,它描述了一个变量或者一组变量的积累过程。
例如,当我们考虑人口增长的问题时,可以使用积累模型来描述人口数量随时间的变化。
积累模型通常使用微分方程表示。
1.1. 特点 - 变量之间存在流入和流出的关系; - 变量之间的积累是连续的; - 流入量和流出量可以是恒定的或者变化的。
1.2. 应用示例积累模型在生态学、经济学、工程管理等领域得到了广泛的应用。
例如,在生态学中,可以使用积累模型来研究物种数量的变化;在经济学中,可以使用积累模型来研究货币的流通和储蓄;在工程管理中,可以使用积累模型来研究项目进展和资源分配。
1.3. 示例方程dP/dt = b*P - d*P其中,P表示人口数量,t表示时间,b表示出生率,d表示死亡率。
2. 流动模型流动模型描述了一个变量或者一组变量之间的流动过程。
它通常用来研究物质、能量、信息等在系统中的传递和传播。
例如,在物流管理中,可以使用流动模型来研究物料的流动和分配。
2.1. 特点 - 变量之间存在流动的关系; - 流动可以是单向的或者双向的; -流动可以是连续的或者离散的。
2.2. 应用示例流动模型在供应链管理、信息传输、能量传递等领域具有广泛的应用。
例如,在供应链管理中,可以使用流动模型来优化物料的流动和库存的控制;在信息传输中,可以使用流动模型来研究信息的传播和处理;在能量传递中,可以使用流动模型来分析能量的转化和利用。
2.3. 示例方程dQ/dt = f - k*Q其中,Q表示物料的数量,t表示时间,f表示流入量,k表示流失率。
3. 动力平衡模型动力平衡模型描述了一个变量或者一组变量在达到平衡状态时的行为。
系统动力学模型

系统动力学模型系统动力学模型是研究各种动力学运动的概念模型。
它是一种描述力学系统的行为的解析方法,可以精确地描述物体的运动,并预测其未来的行为及其变化趋势。
系统动力学模型可以用于描述各种动力学系统,包括化学反应、生物运动、工业流程以及经济系统等,是许多应用科学领域的核心技术。
系统动力学模型可以分为四种类型:常规系统动力学模型、非线性系统动力学模型、时滞系统动力学模型和混沌系统动力学模型。
常规系统动力学模型是一种基本的动力学模型,它表示一定的力学系统满足特定的初始条件,描述其时间变化。
非线性系统动力学模型是一种比常规模型更为复杂的动力学模型,它可以考虑更多的变量和更多的外部输入变量。
时滞系统动力学模型的特点是反应外部力的变化的反应可能会有一定的滞后期,使得系统的变化更为复杂。
最后,混沌系统动力学模型是一种考虑系统的复杂性的模型,它可以描述系统内部的复杂性而产生的不可预测的行为。
系统动力学模型是一种抽象的概念,它可以帮助人们更好地理解动力学系统的行为。
它有助于分析系统中的关系,识别输入和输出之间的依赖关系,确定系统中的参数,预测其未来行为等。
这种方法不仅可以描述一个已知的动力学系统,而且可以预测未来的系统行为。
此外,系统动力学模型也可以用于研究动力学系统的外部环境,以及外部环境对动力学系统的影响。
它可以帮助我们了解系统的外部环境,并为我们把握系统的概况提供见解。
另外,它还可以帮助我们针对不同的外部环境给出最合适的解决方案。
系统动力学模型是有用的工具,它可以帮助我们更好地理解系统的行为,并预测它们未来的发展趋势。
它不仅可以帮助我们研究动力学系统,而且可以帮助我们研究系统的外部环境,并给出有效的解决方案。
它的重要性不言而喻,是未来应用科学领域不可忽视的核心技术。
总之,系统动力学模型是研究各种动力学运动的概念模型,可以用于描述各种动力学系统,并帮助我们理解系统、研究系统的外部环境、预测未来的系统行为以及给出有效的解决方案。
系统动力学的9种模型解析

系统动力学的9种模型解析标题:系统动力学的9种模型解析引言:系统动力学是一种研究动态复杂系统行为的数学方法,广泛应用于经济学、生态学、管理学等领域。
本文将深入探讨系统动力学的9种常见模型,并分析其理论基础和应用领域。
通过对这些模型的解析,旨在帮助读者更深入地理解系统动力学及其在实践中的作用。
第一部分:系统动力学概述在介绍具体的模型之前,有必要先了解系统动力学的基本概念和原理。
系统动力学着重于分析系统内部各个组成部分之间的相互关系,通过建立微分方程等数学模型来描述系统的演化过程。
这一方法注重动态演化和非线性特性,在解决复杂问题时具有独特的优势。
第二部分:9种系统动力学模型1. 常微分方程模型:系统动力学的基础,用于描述动态系统的变化过程。
2. 资源流模型:关注系统内资源的流动和变化,适用于生态学、能源管理等领域的研究。
3. 增长模型:研究系统中因子的增长和衰减,可应用于经济学、人口学等领域。
4. 循环模型:探讨系统中的循环过程,如经济周期的波动,可应用于宏观经济研究。
5. 积聚模型:研究系统中积聚和堆积的过程,如资本积累,适用于经济学和企业管理等领域。
6. 信息流模型:研究系统中信息传递和决策的影响,可用于管理学和组织行为学的研究。
7. 优化模型:优化系统中某些指标的值,如最大化效益或最小化成本,适用于运筹学等领域。
8. 非线性模型:考虑系统中的非线性效应,如混沌和复杂性的产生,广泛应用于自然科学和社会科学。
9. 策略模型:研究系统中不同决策对结果的影响,适用于战略管理和政策制定等领域。
第三部分:系统动力学的理论与实践系统动力学的理论基础包括建模、仿真和分析等方法。
通过系统动力学模型,我们可以深入研究系统的行为、寻找潜在问题,并基于模型结果做出合理的决策。
在实践中,系统动力学可应用于企业管理、政策制定、环境保护等领域,为问题解决提供了一种全面和系统的方法。
第四部分:总结与回顾通过对系统动力学的9种模型的解析,我们可以看到系统动力学对于复杂问题的分析和理解具有重要意义。
系统动力学模型课件

系统动力学模型的基本概念
,咔 (
1 贯彻 C
系统动力学模型的基本概念
IR
匆ly navbars work on " fellow 那一天空
系统动力学模型的基本概念
ohist.小时 Institution -ance
系统动力学模型的基本概念
锦
Institution.O沪深 theism by -m G
市场预测
在商业领域,系统动力学模型可以用于预测市场变化,帮助企业制定营销策略 和调整生产计划。例如,预测市场需求、竞争态势、产品生命周期等。
优化决策
资源分配
系统动力学模型可以帮助决策者优化资源分配,提高资源利用效率。例如,在有 限的预算下,合理分配资金、人力、物资等资源,实现效益最大化。
决策支持
系统动力学模型可以为决策者提供决策支持,帮助其分析不同方案的可能影响。 通过模拟不同方案的效果,决策者可以更好地权衡利弊,做出更明智的决策。
详细描述
供应链管理模型通过模拟供应链中供应商、制造商、分销商和零售商等各环节的动态行为,优化供应链的性能, 提高企业的竞争力。该模型可以用于制定采购、生产、物流等方面的策略,降低成本、提高效率。
人口增长模型
总结词
人口增长模型是系统动力学中用于模拟人口增长过程的模型 。
详细描述
人口增长模型通过模拟人口出生率、死亡率、迁移率等动态 因素,预测未来人口数量和结构的变化。该模型可以用于制 定人口政策、资源分配和经济发展等方面的策略,促进人口 与环境的协调发展。
要点二
详细描述
在设定参数与初始条件时,需要依据实际情况和可获取的 数据,为模型中的参数和初始条件进行合理的赋值。这些 参数和初始条件将直接影响模型的模拟结果,因此需要谨 慎选择和验证。
生态系统动力学模型与预测

生态系统动力学模型与预测在我们的日常生活中,生态系统扮演着至关重要的角色,它们是我们赖以生存的基础。
生态系统的复杂性使得预测其未来发展变得十分困难,但是生态系统动力学模型的出现为我们提供了一个理解和预测生态系统变化的重要工具。
生态系统动力学模型是一种数学模型,通过模拟生态系统内各个组成部分(如生物种群、物种互动、环境变量)之间的相互作用和反馈机制来预测生态系统的行为。
这些模型基于对已知生态学原理和规律的理解,并利用数学方程来描述生态系统中的各种变化。
通过模拟不同的场景和假设,研究人员可以预测生态系统的演化趋势和对外界变化的响应。
一个生态系统动力学模型的建立首先需要从实地观测数据中获取参数和初始条件。
这些数据可以包括物种的丰度、生物种群的生命周期、各种环境因素如温度、气候变化等。
通过分析这些数据,研究人员可以建立数学方程,以描述不同因素之间的相互作用和反馈机制。
这些方程可以是线性的或非线性的,它们可以是离散的或连续的,取决于所研究的生态系统的特点。
一旦模型建立完毕,它可以用来预测生态系统在不同条件下的演变过程。
例如,我们可以利用模型来研究生物种群的生命周期,以及它们对环境变化的响应。
这些模型还可以用来研究生态系统的稳定性,以及不同因素对生态系统稳定性的影响。
通过提出不同的假设和场景分析,我们可以预测生态系统在不同的干扰下的响应和适应能力。
生态系统动力学模型不仅可以帮助我们理解生态系统的整体行为,还可以为我们制定保护和管理策略提供有益的建议。
例如,在考虑到不同干扰和变化的情况下,我们可以利用模型来评估不同的保护措施和管理方法的效果。
通过模拟不同的管理方案和政策,我们可以选择最优的方案来维持生态系统的健康和稳定。
尽管生态系统动力学模型在预测生态系统行为和响应方面具有很大的潜力,但它们仍然有一些局限性。
首先,生态系统是非常复杂和动态的,模型必须包括大量的变量和参数,这使得建模过程十分复杂。
其次,我们对生态系统的理解仍然有限,存在很多未知的因素和未解决的问题。
anylogic系统动力学建模案例

anylogic系统动力学建模案例AnyLogic系统动力学建模是一种基于系统动力学原理的建模方法,通过对系统内部结构和变化规律的分析,模拟系统中各种因素之间的相互作用,从而帮助决策者更好地理解系统的运行机制,预测系统的未来发展趋势,优化决策方案。
下面将列举一些基于AnyLogic 系统动力学建模的案例。
1. 疾病传播模型利用AnyLogic系统动力学建模,可以模拟疾病在人群中的传播过程。
通过设定各种参数,如感染率、治愈率、接触率等,可以模拟不同传染病在不同人群中的传播情况,帮助卫生部门制定防控策略,减少疫情的蔓延。
2. 环境污染模型利用AnyLogic系统动力学建模,可以模拟工厂排放的污染物在大气中的扩散过程。
通过设定风向、风速、排放量等参数,可以评估不同排放源对周围环境的影响程度,为环保部门提供科学依据,制定减排措施。
3. 市场竞争模型利用AnyLogic系统动力学建模,可以模拟不同企业在市场中的竞争关系。
通过设定市场需求、价格弹性、广告投入等参数,可以模拟企业之间的价格竞争、产品创新等策略,帮助企业制定市场营销策略,提升市场竞争力。
4. 交通拥堵模型利用AnyLogic系统动力学建模,可以模拟城市交通系统中车辆的流动情况。
通过设定道路容量、信号灯时长、车辆速度等参数,可以评估不同交通管理政策对交通拥堵的影响,为交通部门提供优化交通流量的建议。
5. 供应链模型利用AnyLogic系统动力学建模,可以模拟供应链中各个环节的运作情况。
通过设定生产周期、库存水平、订单量等参数,可以评估不同供应链管理策略对供应链效率的影响,帮助企业优化供应链设计,降低成本。
6. 金融风险模型利用AnyLogic系统动力学建模,可以模拟金融市场中不同资产的价格波动情况。
通过设定利率、市场情绪、政策变化等参数,可以评估不同投资组合的风险水平,帮助投资者制定风险管理策略,保护资产安全。
7. 人力资源规划模型利用AnyLogic系统动力学建模,可以模拟企业人力资源的供需关系。
系统动力学模型在医疗领域的应用

系统动力学模型在医疗领域的应用随着信息技术的迅速发展,医疗领域的数据也愈加丰富。
借助于数据科学手段,可预测性医疗得到了广泛关注。
其中,系统动力学模型 (System dynamics model) 是一种建模方法,它通过对环境中因果关系的理解和描述,可以预测未来的结果,为解决诸如疾病流行、医疗资源配置等问题带来了新路径。
下面,我们将着重介绍系统动力学模型在医疗领域的应用。
首先,系统动力学模型在疾病流行中的应用。
在疾病流行期间,疫情的扩散速度和范围是一个非常复杂的系统问题,它受到多种因素的影响,例如感染力、隔离措施、物流等等。
在这种情况下,系统动力学模型可以充分考虑这些因素的相互作用,建立了一个更加完整的模型。
以新冠肺炎为例,研究人员可以通过系统动力学模型,将不同的因素纳入其中,来预测疫情的发展趋势。
通过这种预测,医疗系统可以更好地安排资源,以更为高效的方式进行疫情防控。
同时,系统动力学模型在医疗资源利用方面也有广泛的应用。
在许多医疗机构中,医疗资源的分配并不完全依赖于实际的病情,也存在着其他的因素影响,例如资金和技术的不平衡分配。
这种情况下,研究人员可以通过系统动力学模型优化医疗资源的分配计划,使其更加公平和高效。
例如,通过将资源分配与人口的分布、经济状况等因素相结合,建立系统动力学模型,医疗机构可以更合理的分配其资源,实现更为平衡地服务。
此外,系统动力学模型还能够为医疗改革提供支持。
诸如医疗保障、医疗服务改革等方案,其长期影响往往较难预测。
通过使用系统动力学模型,可以将医疗体系视为一个系统,充分考虑其内部和外部因素间的关系。
并通过预测不同方案对于该系统的影响,医疗系统可以良性发展,建立更优的医疗体系。
然而,系统动力学模型的应用在医疗领域中也存在着一些挑战。
首先,大多数医疗问题是十分复杂的,参考因素过多,建立系统动力学模型必须涵盖各种因素。
除此以外,医疗数据的质量和完整性也是该模型的局限之一。
对于医疗体系中的复杂问题,系统动力学模型的建立也需要相应的数据分析人员、医疗领域专家的支持。
(完整版)系统动力学模型SD3

Fox
Population
fox births
fox deaths
Rabbit
fox rabbit rabbit deaths Population consumption
rabbit births
fox birth rate
init ial fox population
average fox life
把某变量定义为状态变量? 1. 积累量:即首先取决于是否能把这个量看作为某种对时间变 化的积累过程。 2. 根据积分过程的时间常数来判断:
时间常数很大时→常数项; 时间常数很小时→辅助变量; 一般情况→状态变量。
5.1.2 速率(变化率)方程
速率方程的功用:把影响系统状态的诸因素——来自系统内外 的信息、计划与决策,转化成改变系统状态的行动。
(10) fox food requirements = 25 Units: Rabbit/Year/Fox
(11) fox mortality lookup ([(0,0)-(2,20)],(0,20),(0.5,2),(1,1),(2,0.5) ) Units: Dmnl
(12) Fox Population = INTEG (fox births-fox deaths, initial fox population) Units: Fox
(05) FINAL TIME = 50 Units: Year The final time for the simulation.
(06) fox birth rate = 0.25 Units: 1/Year
(07) fox births = Fox Population * fox birth rate Units: Fox/Year
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统动力学的建模步骤
例1:建立“一阶库存管理系统”的系统动力学模型,并分析系统 的动态趋势。
例2,: 建立“二阶库存管理系统”的系统动力学模型,并分析系统 的 动态趋势。
思考题
• 物流系统的系统动力学模型构建
1. 因果关系图: 2. 因果链:
3. 反馈回路:
综合“因果关系图”:
例1:建立牧场“种草与养羊”的多种经营的因果关系图
要素:养羊 —— 羊总数、羊繁殖率、羊死亡数 种草 —— 草总数、草繁植率、草消亡数 因果关系图:
注 意:
因果关系图简洁明了地反映了要素之间的因果反馈回路关系。 但: 10· 不足以反映物质链和信息链的差别; 20· 也不能反映出物质的积累值和积累效应变化快慢的区别。
描述系统物质流动或信息流动积累效应变化快慢的变 量,其具有瞬时性的特征。 —— 反映单位时间内物质流动或信息流量的增加或 减少的量 ——相对量、速度、微积分中的变化率等 决策变量符号表示:
(3) 常数:描述系统中不随时间而变化的量, 如: 用 表示。
(4) 辅助变量:从信息源到决策变量之间,起到辅助表达信息反 馈决策作用的变量。
•
信息链:连接状态和变化率的信息通道,是与因果关系相连 的信息传输线路。 信息链符号表示:A O· · · →B
(2)状态变量与决策变量
• 状态变量(又称流位)(x):
描述系统物质流动或信息流动积累效应的变量,表 征系统的某种属性,有积累或积分过程的量 —— 绝对量、位移、微积分中的积分量等
• 决策变量(又称流率)(r):
———系统动力学模拟时间可长可短,尤长为好, 尤其适用中长期预测预报,这一特性对具有 大惯性的社会经济系统的模拟尤为珍贵。
系统动力学探讨的问题具备的特征:
第一:动态 第二:反馈
系统动力学研究问题的基本阶段
• • • • • • 问题定义 模型概念化 模型数学表达 仿真 评价 政策分析。
模型的表示方法
——流图能反映出物质的积累值态发生变化的机制,明确表 示系统各元素间的数量关系,反映物质链与信息链的区 别,能够反映物质的积累值及积累效应变化快慢的区别。
(1). 物质链与信息链
物质链:系统中流动的实体,连接状态变量 是不使状态值变化的守恒流。 物质链符号表示:要素A→要素B
第四章 系统动力学模型
什么是系统动力学?
系统动力学又称系统动态学(System Dynamics)——简称SD
◆ 系统动力学的理论基础:反馈控制理论 ◆ 系统动力学的技术手段:计算机技术 ◆ 系统动力学的研究对象:擅长研究复杂社会经济大系统
◆ 系统动力学的研究方法:从系统内部微观结构入手,建立SD数学模型。 运用计算机技术,并按时间步长(足够小)法 模拟上机运行。根据前一时刻系统状态,估算 出下一时刻系统状态,一步步展现系统动态演 变过程。
