届全国中学生数理化学科能力竞赛
第三届全国中学生数理化学科能力展示活动 北京赛区获奖名单

韦钧天 七年级 数学 清华附中 二等奖
代家麟 七年级 数学 北京四中初中部 二等奖
冯纪元 七年级 数学 北京五中分校 二等奖
冯曦林 七年级 数学 北京八中 二等奖
宁小芾 七年级 数学 北京四中初中部 二等奖
乔文锐 七年级 数学 清华附中 二等奖
仲顗宸 七年级 数学 北京五中分校 二等奖
任思怡 七年级 数学 北京景山学校 二等奖
伞擎杨 七年级 数学 北京八中 二等奖
关艾 七年级 数学 北京八中 二等奖
关吉正 七年级 数学 北京市二中分校 二等奖
刘云婷 七年级 数学 北京景山学校 二等奖
刘心然 七年级 数学 北京五中分校 二等奖
何知闲 七年级 数学 清华附中 一等奖
何逸 七年级 数学 清华附中 一等奖
吴承羽 七年级 数学 北京市文汇中学 一等奖
吴浛 七年级 数学 清华附中 一等奖
吴楠 七年级 数学 清华附中 一等奖
张之微 七年级 数学 北京景山学校 一等奖
张宇佳 七年级 数学 北京景山学校 一等奖
任卓林 七年级 数学 学而思 一等奖
刘亦卓 七年级 数学 清华附中 一等奖
刘柏瑞 七年级 数学 高思教育 一等奖
刘洪麟 七年级 数学 清华附中 一等奖
刘家玮 七年级 数学 清华附中 一等奖
刘浩辰 七年级 数学 高思教育 一等奖
刘梦佳 七年级 数学 北京三帆中学 一等奖
马逸婷 七年级 数学 北京景山学校 二等奖
丰明远 七年级 数学 北京四中初中部 二等奖
孔繁浩 七年级 数学 北京市一七一中学 二等奖
毛治齐 七年级 数学 高思教育 二等奖
首届全国中学生数理化学科能力竞赛--数学初赛试题(七八九年级)

首届全国中学生数理化学科能力竞赛 七年级数学学科能力解题技能初赛试题试卷说明:1、本试卷共计15题,满分为120分2、考试时间为120分钟一、选择题(共6小题,每题5分,共30分)1、北京奥运期间,体育场馆要对观众进行安全检查.设某体育馆在安检开始时已有若干名观众在馆外等候安检,安检开始后,到达体育馆的观众人数按固定速度增加.又设各安检人员的安检效率相同.若用3名工作人员进行安检,需要25分钟才能将等候在馆外的观众检测完,使后来者能随到随检;若用6名工作人员进行安检,时间则缩短为10分钟.现要求不超过5分钟完成上述过程,则至少要安排 名工作人员进行安检.A. 9B. 10C. 11D. 122、2008年9月25日,中国国家主席胡锦涛在酒泉卫星发射中心“问天阁”为执行神州7号飞行任务的航天员壮行.3天后,神州7号巡天归来,在太空中留下了中国人骄人的足迹.根据这些事实和数据,我们发现有可能存在这样的等式: 神州7号问天×3 = 问天神州7号上述等式中,每个汉字代表从0到9中的不同自然数(其中7已经被使用).要使得等式成立,则神州7号 = .A. 2075B. 3075C. 3076D. 30783、若“学”、“科”、“能”、“力”这四个汉字中每个汉字分别代表一个非零的个位数,对于运算符号“∆”有:学科能力∆1=科学能力;学科能力∆2=能力科学,那么1234∆1∆2 = D .A. 4312B. 3421C. 4321D. 34124、一个数学玩具的包装盒是正方体,其表面展开图如下.现在每方格内都填上相应的数字.已知将这个表面展开图沿虚线折成正方体后,相对面上的两数之和为“0 ”,则填在A 、B 、C 内的三个数依次是 .A. 0,-2,1B. 0,1,-2C. 1,0,-2 D. -2,0,15、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划.该球拍每只售价为人民币60元,购买者同时获赠1张奖券;积累3张奖券可兑换1只球拍.由此可见,1张奖券价值为 元.A. 20B. 15C. 18D. 126、10个同学藏在10个谜宫里面.男同学的谜宫门前写的是一个正数,女同学的谜宫门前写的是一个负数,这10个迷宫门前的数字依次为8200823(5)(1)83(2008),,0.1,,,2008,2,,4(2),51,(25)20081997(3)a ---+---⨯-⨯---- 则谜宫里面的男同学、女同学的人数分别为 .A. 4人、6人B. 6人、4人C. 3人、7人D. 7人、3人二、填空题:(共6小题,每题5分,共30分)7、若(x -2y )2+(y +2)2=0,则y -x = .8、由6条长度均为2 cm 的线段可构成边长为2 cm 的n 个正三角形,则n 的最大值为 .9、在△ABC 中,点D 为边BC 的中点,点E 为线段AD 上一点,且满足AE =2ED ,则△ABC 与△BDE 的面积之比为 .10、某校A 、B 、C 三名同学参加全国中学生数理化学科能力竞赛,其指导教师赛前预测:“A 获金牌;B 不会获金牌;C 不会获铜牌.”结果出来后,三人之中,一人获金牌,一人获银牌,一人获铜牌,指导教师的预测只有一个与结果相符.由此可以推论: 获得银牌.11、已知2x y +(其中,x y 都是整数)能被9整除,则2(584)x y --被9除的余数为 -8或1 .12、从2008,2009,2010,…, 2028这些数中,任取两个数,使其和不能写成三个连续自然数的和,则有 种取法.三、解答题(每小题20分,共60分)13、鲁西西开始研究整数的特征.她发现:4=22-02,12=42-22,20=62-42. 4,12,20这些正整数都能表示为两个连续偶数的平方差,她称这些正整数为“和谐数”.现在请你在鲁西西研究的基础上,进一步探究下列问题:(1) 判断28、2008是否为“和谐数”.(2) 根据上述判断,请你推广你的结论,指出判断一个正整数是否为“和谐数”的标准.(3) 更进一步探究:两个连续奇数的平方差(取正数)是“和谐数”吗?为什么?14、已知2008=1(xyx ,其中x,y为正整数,求x+y的最大值和最小值.15、《歌词古体算题》记载了中国古代的一道在数学史上名扬中外的“勾股容圆”名题,其歌词为:十五为股八步勾,内容圆径怎生求?有人算得如斯妙,算学方为第一筹.当中提出的数学问题是这样的:已知直角三角形的两直角边边长分别为15步,8步,试求其内切圆的直径.请你尝试完成上述任务,如果时光倒流,看看你是否算得上古代中国的一流数学家.(温馨提示:直角三角形的三边存在这样的数量关系:斜边的平方等于两直角边的平方和.)首届全国中学生数理化学科能力竞赛八年级数学学科能力解题技能初赛试题试卷说明:1、本试卷共计15题,满分为120分2、考试时间为120分钟一、 选择题(每题5分,合计30分)1、如果“学”、“科”、“能”、“力”这四个汉字中每个汉字分别代表一个非零个位数,对于运算符号“∆”有:学科能力∆1=科学能力;学科能力∆2=能力科学,那么1234∆1∆2=( ).A .4312B .3421C .4321D .34122、已知点P 关于原点对称点1P 的坐标是(-2,3),则点P 关于y 的对称点2P 的坐标是( ).A .(-3,-2)B .(2,-3)C .(-2,-3)D .(-2,3)3、方程组36x y x y z +=⎧⎨+=⎩的非负整数解有( )个.A .1B .2C .3D .无数4、由6条长度均为2 cm 的线段可构成边长为2 cm 的n 个等边三角形,则n 的最大值为( ). A .4 B .3 C .2 D .15、已知三角形的三条边长分别8x 、x 2、84,其中x 是正整数,这样的互不全等的三角形共有( )个.A .5B .6C .7D .86、已知=++++++++2008200813312211112222( )A .1B .20072008C .20092008D .20082009二、 填空题(每题5分,合计30分)7、北京奥运期间,体育场馆要对观众进行安全检查.设某体育馆在安检开始时已有若干名观众在馆外等候安检,安检开始后,到达体育馆的观众人数按固定速度增加.又设各安检人员的安检效率相同.若用3名工作人员进行安检,需要25分钟才能将等候在馆外的观众检测完,使后来者能随到随检;若用6名工作人员进行安检,时间则缩短为10分钟.现要求不超过5分钟完成上述过程,则至少要安排 名工作人员进行安检.8、已知,a b 均为质数,且满足213aa b +=,则2ba b += .9、如图,在△ABC 中,点D 为边B C 的中点,点E 为线段A D 上一点,且满足2A E E D =,则△ABC 与△BDE 的面积之比为___ _____.10、已知2x y +(其中,x y 都是整数)能被9整除,则2(584)x y --被9除的余数为 .11、某班学生共有50人,会游泳的有27人,会体操的有18人,游泳、体操都不会的有15人,那么既会游泳又会体操的有 人.12、当x 分别等于2008,2007,2006,,2,1,21,,20061,20071,20081 时,计算代数式221xx+的值,再把所得的结果全部加起来.则这个总和为_____________.三、 解答题(每题20分,合计60分)13、求方程2008=++xy y x 的正整数解.14、 如图,在△ABC 中,点D 是边A B 延长线上的一点,点F 是边A C 上的一点,D F 交B C 于点E ,并已知,B D C F D E E F ==,∠A =58°,求∠C 的值.15、已知05224224=++++-nnm m m ,且m 、n 均为正整数,求m 、n 的值.参考答案1-6 B C C C C D 7、11; 8、17; 9、6:1; 10、1; 11、10; 12、2007.5;13、x=6,y=286;x=286,y=6;x=40,y=48;x=48,y=40; 14、∠C=610;(提示:在EC 上取EG=BE ,连结FG ) 15、m =3,n=2;首届全国中学生数理化学科能力竞赛九年级数学学科能力解题技能初赛试题试卷说明:1、本试卷共计15题,满分为120分2、考试时间为120分钟一、选择题(每小题5分,共30分)1.若152525+-++=N ,则N =( )A .1B .2C .3D .42.一个完全平方数的最前两位数为19,最末两位数为99,则这样的完全平方数( )A .不存在B .只有一个C .有两个D .有两个以上3.已知三角形的三条边长分别8x 、x 2、84,其中x 是正整数,这样的互不全等的三角形共有( )个.A .5B .6C .7D .84.如图,在△ABC 中,D 是AB 上一点,且2A CA D AB =⋅,则 ( )A .△ADC ∽△ACB B .△BDC ∽△BCA C .△ADC ∽△CDBD .无相似三角形5.运算符号∆的含义是,,a a ba b b a b ≥⎧∆=⎨<⎩,则方程(1)(12)5x x +∆-=的所有根之和为( )A .2-B .0C .2D .46.《歌词古体算题》记载了中国古代的一道在数学史上名扬中外的“勾股容圆”名题,其歌词为:“十五为股八步勾,内容圆径怎生求?有人算得如斯妙,算学方为第一筹.”当中提出的数学问题是这样的:今有股长15步,勾长8步的直角三角形,试求其内切圆的直径.正确的答案是( ) A .3步B .4步C .5步D .6步二、填空题(每小题5分,共30分)7.当x 分别等于2008,2007,2006,,2,1,21,,20061,20071,20081 时,计算代数式221xx+的值,再把所得的结果全部加起来.则这个总和为____________.8.某班学生共有50人,会游泳的有27人,会体操的有18人,游泳、体操都不会的有15人,那么既会游泳又会体操的有 人.9.已知,a b 均为质数,且满足213aa b +=,则2ba b += .10.设a ,b ,c 是从1到9的互不相同的整数,则abcc b a ++的最大值为 .11.高斯记号[]x 表示不超过实数x 的最大整数,如[]1.232-=-,[]1.231=.若1x =,则([])([]1)x x x x ----= .12.如图,D ,E 是等边△ABC 两边上的两个点,且AE=CD ,连结BE ,与AD 交于点P ,过点B 作BQ ⊥AD 于Q , 那么,BP :PQ = .三、解答题(每小题20分,共60分)13.设a ,b 为整数,且方程012=++bx ax的两个不同的正数根都小于1,求a 的最小值.14.已知正六边形ABCDEF的边长为1,QR是正六边形内平行于AB的任意线段,求以QR为底边的内接于正六边形ABCDEF的△PQR的最大面积.15.对满足221+=的一切实数,t s,不等式t s222++->-++恒成立,求实数m的取值范围.(2)2(21)(21)2m t s t s t m。
首届全国中学生数理化学科能力竞赛数学学科能力解题技能初赛试题(高二)

则集 合 C的元素 个数 为 (
A 2。;
C 8 ;
) 。
B 4;
D 16
[ 丢- 3 贝而1 jl 一 ]一 I 十丽1 ] 2 J [ + 1 ]… [ -+ t 1 丽] - 一
-
三 、 答 题 解
2曲 =i( 1+ 。( . 线y s 等+ ) c 等+1的 轴之 n s ) 对称
当 m ≥ 5时 ,
间距离 的 最小值 为 (
A 1:
C 3:
1. 本小 题满 分 2 3( O分 ) 在 数 列 { 中 , 知 a — 1, 1ห้องสมุดไป่ตู้2 n— 1 a) 已 1 口+— n + .
(I) 数 列 { 的 通 项 公 式 ; 求 口} (I) 一 n ” , { 的 前 n项 和 为 S 求 I设 a + 且 b) ,
f( 口 tb > _( ) 厂( ) 成 立 , n 与 一 b 的 大 小 2- ) 厂口 + - 6恒 则
首届全国中学生数理化学科能力竞赛 数学学科能力解题技能初赛试题( 高二)
关 系 是—
—
.
1 . 知 函 数 厂( 同 时 满 足 以 下 3个 条 件 : 1已 z) ( ) 在 反 函 数 f ( ) 1存 - ; z ( ) ( 1 在 函 数 ,( 的 图 象 上 ; 2 点 1, ) z) ( ) 数 厂( 3函 z+ 1 的 反 函 数 为 厂 一 1 . ) ( )
B 3 : 1;
D 4 :1
4 如 果 关 于 z 的 方 程 4 一 a ・2 + n 一 3 0至 少 有 一 . —
个 实 根 , 实 数 n的 取 值 范 围是 ( 则
全国中学生数理化学科能力竞赛

全国中学生数理化学科能力竞赛简介全国中学生数理化学科能力竞赛是面向全国中学生的一项富有挑战性和指导性的学科竞赛活动。
该竞赛旨在通过比赛形式,提高中学生的数理化学学科素养和综合应用能力,激发学生对数理化学科的兴趣和热爱,培养科学精神和创新意识。
竞赛内容全国中学生数理化学科能力竞赛主要涵盖数学、物理和化学三个学科的内容。
竞赛题目旨在考察学生对基础知识的理解和掌握程度,以及解决实际问题的能力和创新思维。
题型一般为选择题、填空题和解答题,难度逐渐递增,旨在对学生的数理化综合能力进行全面考核。
竞赛组织全国中学生数理化学科能力竞赛由教育行政部门主办,各地区教育部门和学校共同组织。
竞赛分为初赛和决赛两个阶段。
初赛由各地区学校自行组织,决赛则由教育行政部门统一安排。
初赛采取校内选拔形式,决赛则是在特定场地进行的综合性考试。
竞赛意义全国中学生数理化学科能力竞赛对于中学生的成长和发展具有重要意义。
首先,通过竞赛的形式,可以激发学生学习数理化学科的兴趣和热爱,培养科学精神和创新意识。
其次,竞赛能够全面考核学生的数理化综合能力,提高学生解决实际问题的能力和创新思维。
此外,竞赛还能够促进学生相互之间的交流和竞争,激发学生的学习动力,推动学生的个人发展。
竞赛影响全国中学生数理化学科能力竞赛在教育领域具有广泛的影响。
一方面,竞赛有助于提高中学生的数理化学学科素养,培养创新精神和实践能力,为高等教育的发展提供源源不断的人才支持。
另一方面,竞赛活动也为学校和教育部门提供了一个对教育教学质量进行评估和提升的平台,有助于推动教育教学改革。
总结全国中学生数理化学科能力竞赛是一项有益于中学生综合能力发展的活动。
通过参加竞赛,学生可以提高数理化学科的学习兴趣和热爱,培养科学精神和创新意识。
同时,竞赛也为学校和教育部门提供了一个评估和提升教育质量的平台。
全国中学生数理化学科能力竞赛的影响正逐渐扩大,对于推动中学生素质教育的发展起到积极的促进作用。
全国中学生数理化竞赛试题

(数学部分)第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分数学建模论文示范论文首届全国中学生数理化学科能力竞赛化学学科笔试部分竞赛大纲(2013年试验稿)为了提高广大青少年走进科学、热爱科学的兴趣,培养和发现创新型人才,团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”(以下简称“竞赛”)。
竞赛由北京师范大学《高中数理化》杂志社承办。
为保证竞赛活动公平、公正、有序地进行,现将数学学科笔试部分竞赛大纲颁布如下:1 命题指导思想和要求根据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求,着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题力及创新能力。
命题吸收各地高考和中考的成功经验,以能力测试为主导,体现新课程标准对能力的要求,注意数学知识中蕴涵的丰富的思维素材,强调知识点间的内在联系;注重考查数学的通法通则,注重考查数学思想和方法。
激发学生学科学的兴趣,培养实事求是的科学态度和创新能力,促进新课程标准提出的“知识与技能”、“过程与方法”、“情感与价值观”三维目标的落实。
总体难度把握上,要追求“源于教材,高于教材,略高于高考”的原则。
并提出以下三个层面上的命题要求:1)从宏观上看:注意对知识点和能力点的全面考查,注意对数学基本能力(空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力)的考查,注意对数学思想和方法方面的考查,注意考查通则通法。
2)从中观上看:注意各个主要知识块的重点考查,注意对主要数学思维方法的考查。
3)从微观上看:注意每个题目的基础性(知识点)、技能性(能力点)、能力性(五大基本能力为主)和思想性(四种思想为主),注意考查大的知识块中的重点内容(如:代数中的函数的单调性、奇偶性、周期性),注意从各个知识点之间的交汇命题,注意每个题目的通则通法使用的同时也适度引进必要的特技,注意题目编拟中一些题目的结构特征对思路形成的影响。
首届全国中学生数理化学科能力竞赛.doc

首届全国中学生数理化学科能力竞赛数学学科笔试部分竞赛大纲(2008年试验稿)为了提高广大青少年走进科学、热爱科学的兴趣,培养和发现创新型人才,团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”(以下简称“竞赛”)。
竞赛由北京师范大学《高中数理化》杂志社承办。
为保证竞赛活动公平、公正、有序地进行,现将数学学科笔试部分竞赛大纲颁布如下:1 命题指导思想和要求根据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求,着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题力及创新能力。
命题吸收各地高考和中考的成功经验,以能力测试为主导,体现新课程标准对能力的要求,注意数学知识中蕴涵的丰富的思维素材,强调知识点间的内在联系;注重考查数学的通法通则,注重考查数学思想和方法。
激发学生学科学的兴趣,培养实事求是的科学态度和创新能力,促进新课程标准提出的“知识与技能”、“过程与方法”、“情感与价值观”三维目标的落实。
总体难度把握上,要追求“源于教材,高于教材,略高于高考”的原则。
并提出以下三个层面上的命题要求:1)从宏观上看:注意对知识点和能力点的全面考查,注意对数学基本能力(空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力)的考查,注意对数学思想和方法方面的考查,注意考查通则通法。
2)从中观上看:注意各个主要知识块的重点考查,注意对主要数学思维方法的考查。
3)从微观上看:注意每个题目的基础性(知识点)、技能性(能力点)、能力性(五大基本能力为主)和思想性(四种思想为主),注意考查大的知识块中的重点内容(如:代数中的函数的单调性、奇偶性、周期性),注意从各个知识点之间的交汇命题,注意每个题目的通则通法使用的同时也适度引进必要的特技,注意题目编拟中一些题目的结构特征对思路形成的影响。
2 命题范围依据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求,初赛和决赛所考查的知识点范围,不超出相关年级在相应的时间段内的普遍教学进度。
首届全国中学生数理化学科能力竞赛数学学科模拟题(高二)

6 1 2_ 3 + … + 2 . 十 } ㈣
A C 2; 6;
) .
二 、 空 题 :每 题 9分 。 5 填 ( 共 4分 )
7 对 于 函数 ( ) . 一 n + 6 存 在 一 个 正 数 b 使 得 T! z, , f( 的 定 义 域 和 值 域 相 同 , 非 零 实 数 n 的 值 为 z) 则
● 特策 别划
8 集 合 X 中 的 元 素 是 正 整 数 , 有 性 质 : 3∈ X , . 且 若 2 则 1 一 z∈ x , 样 的 集 合 x 共 有 — 2 这
c os( 4z + )一
— —
—
个.
9 已 知 实 数 z, 满 足 ( z+ ) . 3 十 十 4 + 一 0 则 ,
7 a一 一 4 . . 1 . 2 1 .
8 6 . 3个 . 9 1 . .
1 . 一 √2 0 .
_ 6
37 ’
1 .2 ̄3. 2 /
1 锐 , 至 . 为 角 要 圭 设 一
一
√ si n a — c ) a r (S
, 百 : , 一 F
) .
≥ z .; ≥ ) '
数 列 { , 6 的 值 . 6 )求 z
,
sn l 叶 一 os a c
则 .. , 的 大 小 顺 序 为 ( . r y
将 拒 谏 则 英 雄散 , 不从 则 谋 士 叛. 一 策
黄石 公
● 特策 别划
首 届 全 国 中 学 生 数 理 化 学 科 能 力 竞 赛 数 学 学 科 模 拟 题 ( 二 ) 考 答 案 高 参
1 A. . 2. D. 3. A . 4. B. 5. C . 6. D .
首届全国中学生数理化学科能力竞赛化学学科能力解题技能初赛试题(高二)

高 压 下 , 激 光 器 加 热 到 1 8 0 K, 们 成 功 地 制 得 了 用 0 人
原 子 晶体干 冰.
( ) TV《 技 博 览 》 道 , 0 4年 3月 中 科 院 2 CC 科 2 5 1时 1 分 神 七 发 射 成 功 , 舟 0 神 七 号 圆 满 完 成 中 国 航 天 员 出 舱 等 四 大 科 学 试 验 , 下 创
1 3 5g 时 , 转 移 电 子 2 mo 0 . 则 l
7 在 恒 温 、 容 的 密 闭 容 器 中 , 生 反 应 . 恒 发
3 ( A g)+ B( . - ̄ g)- - xC ( . - - g)
D 2 e ・F Oz F [ e ] FO e , e F O2 2
2 中 和 一 定 量 的 某 醋 酸 溶 液 时 , 耗 氢 氧 化 钠 m . . 消 g 如 果 先 向 该 醋 酸 溶 液 中 加 入 少 量 的 醋 酸 钠 , 后 N- 然 用 氢氧化 钠 中和 , 时 可 消 耗 氢 氧 化 钠 ng 则 m 与 n 此 .
3 ( B) 一 ( )+ 3 ; A
) .
4 长 期 使 用 的 锅 炉 底 部 会 形 成 一 层 锅 垢 , 是 由 一 . 它
种 难 溶 性 的盐 和 一 种 难 溶 性 的 碱 组 成 的 , 列 可 能 属 下 于锅垢 成分 的一 组物质 是 ( ) .
A Ca 0H) ( 2和 M g CO ̄ B Ca O ̄和 Mg( ; S OH) ; 2
错 选 不 得 分 .)
化 学 能 解 技垡赛璧(二 首 全 中 题 能 试 赛 学科力 初 题高 )
暑
过程 中, 已 乙 醇 和 乙 酰 乙醇 、 乙酰丙酮混合液、四
第五届全国中学生数理化学科能力竞赛高一物理初赛试题及解答

/ 1 8k m h W
的速度 . 假设行驶过程中电能转化为机械能 的 效 率 为 1 0 0% ,
6 ) 百公里耗电 1 度 ( 3 . 6×1 0 J
) 0 . 0 7 ( )根据表中提供的参量计算正常行驶时电动车的额定 1 ,最大行程s ; m= ( )在匀速行驶过程中 , 电动车受到的总阻力 ( 摩擦阻力 2 和空 气 阻 力 ) 是车重( 包 括 载 重) 的 k 倍, 请 推 算 出 k= 功率 P=
1
力 FN 的大小变化情况是 ( A F 减小 , FN 不变 ; C F 不变 , FN 增大 ;
如 果 仅 使 其 中 的 一 个 力 大 小 逐 渐 减 小 到 零, 然 4.一个物体在多个力的作用下处于 静 止 状 态 . , 后又从零逐渐恢复到原来的大小 ( 此力的方向始终未变 ) 在该过程中其余各力均不变 . 那么下 列各图中 , 能正确描述该过程中物体速度变化情况的是 ( ) .
该滑轮 , 细线两端 各 拴 一 个 质 量 相 等 的 砝 码 m1 和 m2 .
固定在竖直平面内的光滑圆环的最高点有一 3.如 右 图 所 示 , 个光滑的小孔 . 质量为 m 的小球套在圆环上 . 一根细线的下端 系着小球 , 上端穿过小孔用手拉住 . 现拉动细线 , 使小球沿圆环 缓慢上移 . 在移动过 程 中 手 对 线 的 拉 力 F 和 轨 道 对 小 球 的 弹 高一物理试卷 共6页 第 1页
4
面顶端的轻滑轮 , 滑轮与转轴之间的摩擦不计 , 斜面固定在水平桌面上 , 如图所示 . 第一次 , m1
次, 将 m1 和 m2 位置互换 , 使 m2 悬 空 , 发 现 m1 自 m1 放 在 斜 面 上 ,
m2 之比 .
全国中学生数理化学科能力竞赛高一化学学科能力解题技能全国总决赛试题

首届全国中学生数理化学科能力竞赛 高一化学学科能力解题技能全国总决赛试题试题说明:1.本试卷满分为100分. 2.考试时间为120分钟. 3. 相对原子质量 H —1 C —12 N —14 O —16 Na —23 Mg —24 S —32 Cl —35.5 K —39 Ca —40 Mn —55 Cu —64 Ba —137 La —138.9 一、选择题(本题包括7个小题,每小题3分,共21分.每小题只有1个选项符合题意.) 1、 2008年9月27日,中国航天员首次在太空成功回收了暴露试验的固体润滑材料。
这些搭载于“神七”飞船的材料共分为4大类15种,这是中国首次暴露于太空环境并成功回收的空间材料试验样品。
经过太空的试验以后,以肉眼观察,发现两类产品变化很大,一类是银与银合金的薄膜材料,经过原子氧和紫外光的辐照以后,其表面变花或者变暗;另一类是二硫化钼润滑薄膜产品,表面变得更为粗糙。
下列有关说法正确的是( ) A .原子氧比氧气化学性质活泼,二者互为同素异形体 B .银与银合金的薄膜材料化学性质活泼 C .原子氧和紫外光的辐照对二硫化钼润滑薄膜产品没有影响 D .二硫化钼润滑薄膜产品不适合用作航天器的润滑剂 2、毛泽东同志曾写下许多伟大光辉的诗篇,其中一篇中有两句为“赤橙黄绿青蓝紫,谁持彩练当空舞”。
根据下列物质的颜色,按“赤橙黄绿青蓝紫”的顺序编组的是( ) ①溴水 ②CuSO 4 ③KMnO 4 ④CuO ⑤AgI ⑥FeSO 4 ·7H 2O ⑦CuSO 4·5H 2O ⑧HgO ⑨CuS A .①②③④⑤⑥⑦ B .⑧①⑤⑥④⑦③ C .⑧⑨⑤⑥②③①D .⑧①⑤⑥④②③3、为了使鸡蛋保鲜,可在蛋壳表面上涂一层水玻璃溶液,这是利用了水玻璃的( )A .氧化性B .还原性C .稳定性D .水解性4、下列物质长时间存放在敞口瓶里,会发生变质的是( )①碳酸钠晶体;②亚硫酸钠溶液 ③五氧化二磷 ;④碳铵;⑤碱石灰;⑥石灰水A .①②③⑤B .①②④⑥C .②③④⑤D .①②③④⑤⑥5、干燥剂的干燥性能可用干燥效率(1 m 3空气中实际余留水蒸气的质量)来衡量。
第二届全国中学生数理化学科能力竞赛

16
• 3、材料组织 、 • 整理组织你所学到的关于该课题的所有知识,在这一 整理组织你所学到的关于该课题的所有知识, 步骤中你应该通过把思想集中在某个范围内来慢慢确定 你的假设。 你的假设。 • 4、制定一个时间表 、 • 选定一个不仅仅使你感兴趣,而且可以再你所有的时间 选定一个不仅仅使你感兴趣, 内完成的课题,用一个日历标出完成的日期。为调查、 内完成的课题,用一个日历标出完成的日期。为调查、 实验或收集资料留出充足的时间, 实验或收集资料留出充足的时间,并且要留出时间来具 体撰写论文。 体撰写论文。
二、怎样写好论文 1、题目 、 将题目居中,将你的名字、学校、 将题目居中,将你的名字、学校、指导教师及联 系方式写在右下角,论文题目应该尽可能短, 系方式写在右下角,论文题目应该尽可能短, 但要意思完整。题目应反映主要观点、 但要意思完整。题目应反映主要观点、主题或 围绕其开展的研究。 围绕其开展的研究。 2、问题的提出或前言 、 先总体介绍一下研究对象的背景, 先总体介绍一下研究对象的背景,并对你研究 动机的解释以及你想要达到的目的。 动机的解释以及你想要达到的目的。
小论文的形成过程
• • • • • 选题 数据获取 计算和分析 问题解决 对解决方法进一步思考
解题技能展示 考核学生的基础知识与基本技能
论文写作与答辩 考核学生应用知识解决问题的素 养
创新实践能力
学科信息技术 学科综合能力
考核学生计算机与
北京大学张海霞教授做主题报告
建模论文写作须知 一、如何准备你的论文资料 1、选择一个研究对象(可以是一种现象、一种物 、选择一个研究对象(可以是一种现象、 体或一个事件等) 体或一个事件等) 2、初步确定课题 、 选择完研究对象后,可到图书馆、 选择完研究对象后,可到图书馆、网络等查询 相关信息,收集资料,若有条件, 相关信息,收集资料,若有条件,可与该领域 的专家进行沟通
第四届全国中学生数理化学科能力展示活动获创新能力一二三等奖名单
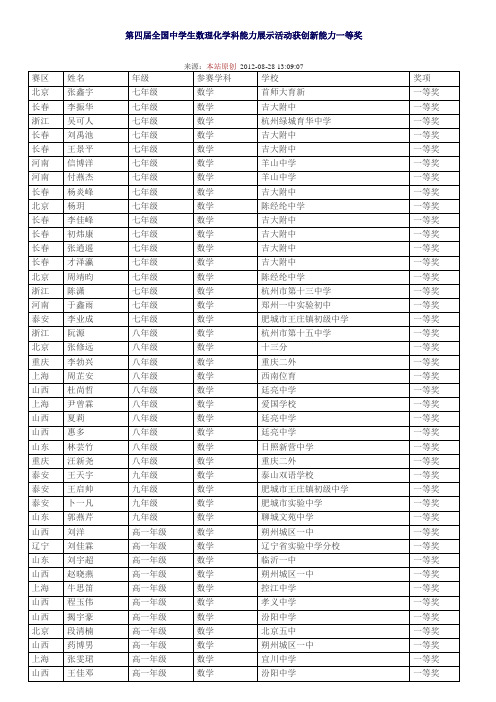
北京
胡哲遒
七年级
数学
首师大育新
二等奖
北京
王子墨
七年级
数学
陈经纶中学
二等奖
重庆
冉开
七年级
数学
重庆二外
二等奖
北京
刘懿
七年级
数学
首师大育新
二等奖
天津
刘逸群
七年级
数学
南开中学
二等奖
北京
陈雪
七年级
数学
清华附中
二等奖
北京
张鑫宇
七年级
数学
首师大育新
二等奖
北京
陈雨乔
七年级
数学
五中分校
二等奖
长春
李振华
七年级
数学
吉大附中
二等奖
长春
孙滢雪
七年级
数学
二等奖
上海
潘依韵
七年级
数学
新华初级中学
二等奖
辽宁
赵碧宁
七年级
数学
辽宁省实验中学北校
二等奖
重庆
甘凤
七年级
数学
重庆二外
二等奖
广东
箫志豪
七年级
数学
深圳市高级中学
二等奖
广东
李元峰
七年级
数学
广州第二中学应元学校
二等奖
浙江
吴可人
七年级
数学
杭州绿城育华中学
二等奖
辽宁
尹鑫
七年级
数学
一等奖
泰安
苏晓楠
九年级
化学
新泰市汶城中学
一等奖
北京
姚远
高一年级
化学
北京八中
第一届全国中学生数理化学科能力竞赛物理赛题

(物理部分)第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分物理实验报告方法及示范报告首届全国中学生数理化学科能力竞赛物理学科笔试部分竞赛大纲(2008年试验稿)为了提高广大青少年走进科学、热爱科学的兴趣,培养和发现创新型人才,团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”(以下简称“竞赛”)。
竞赛由北京师范大学《高中数理化》杂志社承办。
为保证竞赛活动公平、公正、有序地进行,现将物理学科笔试部分竞赛大纲颁布如下:一、命题指导思想和对能力的要求根据教育部《全日制义务教育物理课程标准》和《全日制普通高级中学物理课程标准》的要求,着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题的能力及创新能力。
命题吸收各地高考和中考的成功经验,以能力测试为主导,体现新课程标准对能力的要求,注重对物理知识和物理规律的理解,强调知识点间的内在联系;注重考查应用语言文字、数学方法准确表述物理思想与物理过程的能力;注重理论联系实际,注意科学技术和社会、经济发展的联系,注重物理知识在生产生活中的广泛应用,激发学生学科学的兴趣,培养实事求是的科学态度和创新能力,促进新课程标准提出的“知识与技能”、“过程与方法”、“情感、态度与价值观”三维目标的落实。
初三组和高一组中涉及初中内容的命题,把“注重学生发展,改变学科本位;从生活走向物理,从物理走向社会;注重科学探究,提倡学习方式多样化;注重学科渗透,关心科技发展,构建新的评价体系”作为命题的最重要的指导思想。
高中竞赛组则把对理解能力、推理能力、综合分析能力、创新能力、应用数学处理物理问题的能力和实验与探究能力的考查作为命题的最重要的指导思想。
二、竞赛对学科能力考查的说明(一)初三组和高一组考查初中部分知识时对学科能力的考查要求⒈科学探究能力科学探究能力的考查,在内容上可以是《全日制义务教育物理课程标准》所要求的科学内容,也可以是与《全日制义务教育物理课程标准》科学内容有关的学科交叉的内容;在形式上可以是实验探究,也可以是问题研究、调查分析等学习活动。
第三届“全国中学生数理化学科能力展示活动”总决赛数学获奖学生名单
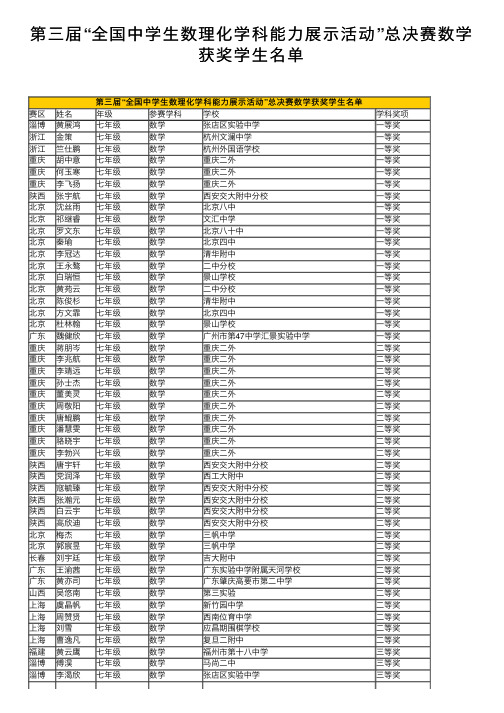
第三届“全国中学⽣数理化学科能⼒展⽰活动”总决赛数学获奖学⽣名单第三届“全国中学⽣数理化学科能⼒展⽰活动”总决赛数学获奖学⽣名单赛区姓名年级参赛学科学校学科奖项淄博黄展鸿七年级数学张店区实验中学⼀等奖浙江⾦策七年级数学杭州⽂澜中学⼀等奖浙江竺仕鹏七年级数学杭州外国语学校⼀等奖重庆胡中意七年级数学重庆⼆外⼀等奖重庆何⽟寒七年级数学重庆⼆外⼀等奖重庆李飞扬七年级数学重庆⼆外⼀等奖陕西张宇航七年级数学西安交⼤附中分校⼀等奖北京沈丝⾬七年级数学北京⼋中⼀等奖北京祁继睿七年级数学⽂汇中学⼀等奖北京罗⽂东七年级数学北京⼋⼗中⼀等奖北京秦瑜七年级数学北京四中⼀等奖北京李冠达七年级数学清华附中⼀等奖北京王永骜七年级数学⼆中分校⼀等奖北京⽩瑞恒七年级数学景⼭学校⼀等奖北京黄苑云七年级数学⼆中分校⼀等奖北京陈俊杉七年级数学清华附中⼀等奖北京⽅⽂霏七年级数学北京四中⼀等奖北京杜林翰七年级数学景⼭学校⼀等奖⼴东魏健欣七年级数学⼴州市第47中学汇景实验中学⼀等奖重庆蒋朋岑七年级数学重庆⼆外⼆等奖重庆李兆航七年级数学重庆⼆外⼆等奖重庆李靖远七年级数学重庆⼆外⼆等奖重庆孙⼠杰七年级数学重庆⼆外⼆等奖重庆董美灵七年级数学重庆⼆外⼆等奖重庆周敬阳七年级数学重庆⼆外⼆等奖重庆唐鲲鹏七年级数学重庆⼆外⼆等奖重庆潘慧雯七年级数学重庆⼆外⼆等奖重庆骆晓宇七年级数学重庆⼆外⼆等奖重庆李勃兴七年级数学重庆⼆外⼆等奖陕西唐宇轩七年级数学西安交⼤附中分校⼆等奖陕西党润泽七年级数学西⼯⼤附中⼆等奖陕西寇毓臻七年级数学西安交⼤附中分校⼆等奖陕西张瀚元七年级数学西安交⼤附中分校⼆等奖陕西⽩云宇七年级数学西安交⼤附中分校⼆等奖陕西⾼欣迪七年级数学西安交⼤附中分校⼆等奖北京梅杰七年级数学三帆中学⼆等奖北京郭宸昱七年级数学三帆中学⼆等奖长春刘宇廷七年级数学吉⼤附中⼆等奖⼴东王渝茜七年级数学⼴东实验中学附属天河学校⼆等奖⼴东黄亦司七年级数学⼴东肇庆⾼要市第⼆中学⼆等奖⼭西吴悠南七年级数学第三实验⼆等奖上海虞晶帆七年级数学新⽵园中学⼆等奖上海周赞贤七年级数学西南位育中学⼆等奖上海刘雪七年级数学应昌期围棋学校⼆等奖上海曹逸凡七年级数学复旦⼆附中⼆等奖福建黄云鹰七年级数学福州市第⼗⼋中学三等奖淄博傅淏七年级数学马尚⼆中三等奖淄博李渴欣七年级数学张店区实验中学三等奖淄博赵⾬洁七年级数学张店区实验中学三等奖淄博舒正彦七年级数学张店区实验中学三等奖淄博吴浩源七年级数学张店区实验中学三等奖淄博赵奇志七年级数学张店区实验中学三等奖淄博刘锐七年级数学⼭东淄博桓台县实验学校三等奖泰安邢⼦铭七年级数学泰⼭博⽂中学三等奖重庆王浩宇七年级数学重庆⼆外三等奖重庆黄晶星七年级数学重庆⼆外三等奖重庆易⼒七年级数学重庆⼆外三等奖重庆任翔渝七年级数学重庆⼆外三等奖重庆唐⼦钦七年级数学重庆⼆外三等奖重庆周孝倩七年级重庆⼆外三等奖重庆李祎七年级重庆⼆外三等奖重庆陈曦七年级重庆⼆外三等奖重庆叶林七年级重庆⼆外三等奖陕西李⼦贤七年级西⼯⼤附中三等奖陕西常恩浦七年级西⼯⼤附中三等奖陕西李浩民七年级西安交⼤附中分校三等奖陕西张亦驰七年级西安交⼤附中分校三等奖陕西范家豪七年级西安交⼤附中分校三等奖陕西曹宇⾠七年级西安交⼤附中分校三等奖陕西史晨阳七年级西安交⼤附中分校三等奖北京朱⼦溪七年级景⼭学校三等奖北京王如萱七年级⼆中分校三等奖北京刘若伦七年级景⼭学校三等奖长春张栩熙七年级吉⼤附中三等奖长春周智⽂七年级吉⼤附中三等奖⼴东邱成聪七年级⼴东四会市四会中学三等奖⼴东李活⽂七年级⼴东肇庆⾼要市第⼆中学三等奖⼴东余和格七年级⼴东肇庆⾼要市第⼆中学三等奖⼴东洪嘉利七年级⼴州市⼴外附设外语学校三等奖⼴东纪颖仪七年级⼴东四会市四会中学三等奖⼴东梁秋雄七年级⼴东四会市四会中学三等奖⼴东赖宇坤七年级⼴州市⼴外附设外语学校三等奖⼭西靳⼦轩七年级平阳中学三等奖上海姚逸磊七年级爱国学校三等奖上海⾦嘉颖七年级浦东交中初级三等奖上海周亦翀七年级应昌期围棋学校三等奖上海林舒莹七年级迅⾏中学三等奖上海陈哲远七年级迅⾏中学三等奖上海陆悦诗七年级爱国学校三等奖淄博任筱仪⼋年级⼭东淄博桓台县实验学校⼀等奖泰安张兆刚⼋年级泰⼭博⽂中学⼀等奖重庆董⼜铭⼋年级重庆⼆外⼀等奖重庆罗汉⼋年级重庆⼆外⼀等奖陕西岳天溦⼋年级西安交⼤附中分校⼀等奖陕西刘梓航⼋年级西安交⼤附中分校⼀等奖北京赵伯杨⼋年级⼈⼤附中⼀等奖北京张泽宇⼋年级清华附中⼀等奖北京王正⼋年级⼈⼤附中⼀等奖北京杨林⼋年级⽂汇中学⼀等奖北京刘丰铭⼋年级五中分校⼀等奖北京项梁⼋年级师⼤实验⼀等奖长春谢禹睿⼋年级师⼤附中⼀等奖长春谢岩峰⼋年级师⼤附中⼀等奖长春陈浩翔⼋年级省实验中学⼀等奖上海贺⼦唯兰⽣复旦⼀等奖湖南张鹏⼋年级北师⼤株洲附校⼆等奖淄博王秋实⼋年级张店区实验中学⼆等奖淄博张尚熹⼋年级张店区实验中学⼆等奖浙江麦炜琦⼋年级杭州锦绣中学⼆等奖重庆谭智敏⼋年级重庆⼆外⼆等奖重庆钟樱琪⼋年级重庆⼆外⼆等奖济南刘贻鑫⼋年级微⼭夏镇⼀中西校⼆等奖陕西安明杰⼋年级西安交⼤附中分校⼆等奖陕西⽥鑫⾬⼋年级庆安中学⼆等奖北京闫天润⼋年级五中分校⼆等奖北京王宇⼋年级⾸师⼤育新⼆等奖北京韦祎⼋年级五中分校⼆等奖北京王则林⼋年级三帆中学⼆等奖北京童梓轩⼋年级北京五中分校⼆等奖北京陈家⾔⼋年级景⼭学校⼆等奖长春张天衡⼋年级吉⼤附中⼆等奖上海贾盛杰⼋年级新⽵园中学⼆等奖上海吴⾠渝⼋年级兰⽣复旦⼆等奖上海叶⽂谦⼋年级彭浦初级中学⼆等奖上海邹⼀⼋年级迅⾏中学⼆等奖上海邱天⼋年级新北郊初级中学⼆等奖湖南李科磊⼋年级邵阳⼗中三等奖湖南邓海亮⼋年级湖南⼤学附属中学三等奖淄博聂楚阳⼋年级马尚⼆中三等奖淄博⽥⼤有⼋年级张店区实验中学三等奖淄博张良⼋年级张店区实验中学三等奖淄博牟建学⼋年级⼭东淄博桓台县实验学校三等奖重庆詹启鹏⼋年级重庆⼆外三等奖重庆朱彦松⼋年级重庆⼆外三等奖济南程允浩⼋年级嘉祥县萌⼭初级中学三等奖陕西李泽豪⼋年级西安交⼤附中分校三等奖陕西赵霁恺⼋年级西安交⼤附中分校三等奖陕西杨潇弘⼋年级西安交⼤附中分校三等奖陕西胡⼀帆⼋年级西安交⼤附中分校三等奖北京张乐临⼋年级⼈⼤附中三等奖北京华易⼋年级清华附中三等奖长春丁笑维⼋年级省⼆实验三等奖⼴东裴⼦晏⼋年级⼴州市第⼋⼗六中学分校三等奖⼴东钱锶煌⼋年级⼴州市第⼋⼗六中学分校三等奖⼴东林家全⼋年级⼴州市第⼋⼗六中学分校三等奖⼴东林伟峰⼋年级深圳市宝安东⼭书院三等奖⼴东胡其骁⼋年级⼴州市第75中学三等奖⼴东冼圣杰⼋年级⼴东肇庆⾼要市第⼆中学三等奖⼴东郑东哲⼋年级⼴东实验中学附属天河学校三等奖⼭西刘丁豪⼋年级平阳中学三等奖⼭西李冉⼋年级第三实验三等奖⼭西于光辉⼋年级平阳中学三等奖⼭西柴瑛桢⼋年级平阳中学三等奖⼭西闫青松⼋年级联盛中学三等奖上海黄家祺⼋年级迅⾏中学三等奖上海陆凯铭⼋年级迅⾏中学三等奖上海宋浩博⼋年级兰⽣复旦三等奖上海章祎鹏⼋年级兰⽣复旦三等奖上海章承宇⼋年级迅⾏中学三等奖上海乔慕⼋年级爱国学校三等奖上海⽑诗炜⼋年级爱国学校三等奖上海朱逸刚⼋年级爱国学校三等奖北京张⼦璐九年级北京⼋中⼀等奖上海王歆哲九年级教科实验⼀等奖湖南彭昊程九年级湖南⼤学附属中学⼆等奖淄博郑海明九年级⼭东淄博桓台县实验中学⼆等奖北京王昊翔九年级北京铁⼆中⼆等奖福建杨陈健九年级福州市屏东中学三等奖淄博姜肖九年级⼭东淄博桓台县实验中学三等奖北京赵琛九年级北京铁⼆中三等奖长春孙逸凡九年级吉⼤附中三等奖济南孙宇新⾼⼀年级临沂⼀中⼀等奖河北杨泽⾼⼀年级河北师⼤附中⼀等奖河北王卫玮⾼⼀年级河北师⼤附中⼀等奖北京陈政道⾼⼀年级北京⼋中⼀等奖北京周晓磊⾼⼀年级北京156中⼀等奖长春梁久阳⾼⼀年级师⼤附中⼀等奖⼴东林恩润⾼⼀年级⼴东⼴雅中学⼀等奖⼭西胡瑞⾼⼀年级太原市实验中学⼀等奖⼭西武⽂霞⾼⼀年级孝义中学⼀等奖⼭西任祚民⾼⼀年级孝义中学⼀等奖⼭西郑世豪⾼⼀年级太原市实验中学⼀等奖⼭西闫宁⾼⼀年级⼤同⼆中⼀等奖上海苏佳琪⾼⼀年级华师⼤⼆附中⼀等奖上海万成城⾼⼀年级交⼤附中⼀等奖上海刘怡圣⾼⼀年级西南位育中学⼀等奖湖南易煌辉⾼⼀年级长沙县⼀中⼆等奖湖南王培能⾼⼀年级双峰⼀中⼆等奖湖南王花⼀⾼⼀年级双峰⼀中⼆等奖浙江胡韩晟⾼⼀年级台州⼀中⼆等奖泰安钟瑞玥⾼⼀年级泰安⼆中⼆等奖济南陈⼀⾼⼀年级临沂⼀中⼆等奖河南李牵⾼⼀年级偃师⾼中⼆等奖北京⾦雅晴⾼⼀年级北京铁⼆中⼆等奖长春刘桐⾼⼀年级省实验⼆等奖⼴东麦俊杰⾼⼀年级⼴东⼴雅中学⼆等奖⼴东曾兆⽣⾼⼀年级⼴州市西关外国语学校⼆等奖⼴东陈卓均⾼⼀年级⼴州市番禺象贤中学⼆等奖⼴东赵家希⾼⼀年级⼴东⼴雅中学⼆等奖⼴东卢佑聪⾼⼀年级⼴东⼴雅中学⼆等奖⼭西王泽超⾼⼀年级⼤同⼆中⼆等奖⼭西师云柯⾼⼀年级阳⾼⼀中⼆等奖⼭西魏泽彤⾼⼀年级曲沃中学⼆等奖⼭西姚鹏宇⾼⼀年级⼴灵⼀中⼆等奖上海储⽅蕙⾼⼀年级市⼆中学⼆等奖湖南沈路铭⾼⼀年级长沙市明德中学三等奖湖南徐运培⾼⼀年级长沙市明德中学三等奖湖南尹洪东⾼⼀年级洞⼝⼀中三等奖湖南李克⾼⼀年级长沙县⼀中三等奖湖南王佑天⾼⼀年级北师⼤株洲附校三等奖湖南胡冠明⾼⼀年级北师⼤株洲附校三等奖湖南韩素⾼⼀年级双峰⼀中三等奖湖南徐泽宇⾼⼀年级浏阳⼀中三等奖陕西思磊⾼⼀年级横⼭中学三等奖陕西李国霏⾼⼀年级西安市第83中学三等奖陕西徐浩隽⾼⼀年级西安市第89中学三等奖陕西雷婧⾼⼀年级横⼭中学三等奖陕西王浩泽⾼⼀年级西安市第89中学三等奖陕西任童洲⾼⼀年级西安市第89中学三等奖陕西付彭升⾼⼀年级横⼭中学三等奖河北苑琳⾼⼀年级河北师⼤附中三等奖河北路泽阳⾼⼀年级河北师⼤附中三等奖⼴东钟昀霖⾼⼀年级⼴东惠州市第⼀中学三等奖⼴东张梓麟⾼⼀年级⼴东⼴雅中学三等奖⼴东⽅泽伦⾼⼀年级⼴东⼴雅中学三等奖⼴东张⼒⾼⼀年级⼴东⼴雅中学三等奖⼭西曹聪⾼⼀年级阳⾼⼀中三等奖⼭西马昕⾼⼀年级孝义中学三等奖⼭西杜⼩娇⾼⼀年级阳⾼⼀中三等奖⼭西王向乾⾼⼀年级孝义中学三等奖⼭西崔泽亮⾼⼀年级长治市六中三等奖⼭西马震宇⾼⼀年级曲沃中学三等奖⼭西赵卿皓⾼⼀年级长治市六中三等奖⼭西施昱鹏⾼⼀年级李林中学三等奖⼭西⾼伟鹏⾼⼀年级曲沃中学三等奖⼭西郭恺恺⾼⼀年级⼴灵⼀中三等奖上海杨彦博⾼⼀年级南模中学三等奖上海马嘉⽂⾼⼀年级西南位育中学三等奖福建郭志罡⾼⼆年级福清市第⼀中学⼀等奖湖南周泽军⾼⼆年级益阳市箴⾔中学⼀等奖湖南杨依⾼⼆年级湖南省地质中学⼀等奖湖南舒含奇⾼⼆年级溆浦⼀中⼀等奖湖南黄添琦⾼⼆年级湖南省地质中学⼀等奖长春傅睿⾼⼆年级师⼤附中⼀等奖⼴东区⾄豪⾼⼆年级⼴州市协和中学⼀等奖⼴东唐晓琨⾼⼆年级⼴东⼴雅中学⼀等奖⼭西杨学博⾼⼆年级孝义中学⼀等奖⼭西杨云龙⾼⼆年级经纬中学⼀等奖上海吴逸飞⾼⼆年级西南位育中学⼀等奖福建林国樑⾼⼆年级⼤⽥⼀中⼆等奖湖南刘丰⾼⼆年级宁乡⼀中⼆等奖湖南郭耀⾼⼆年级宁远⼀中⼆等奖湖南万容均⾼⼆年级宁乡⼀中⼆等奖湖南周芃⾼⼆年级宁乡⼀中⼆等奖湖南柳栋梁⾼⼆年级长沙县实验中学⼆等奖济南李耀祖⾼⼆年级章丘⼀中⼆等奖北京陈凌欣⾼⼆年级北京⼋中⼆等奖⼴东谭梓祺⾼⼆年级⼴州市西关外国语学校⼆等奖⼴东韦⼒⾼⼆年级⼴东省实验中学⼆等奖⼴东钟卓睿⾼⼆年级⼴东⼴雅中学⼆等奖⼭西闫思淼⾼⼆年级清徐中学⼆等奖⼭西马泽昆⾼⼆年级经纬中学⼆等奖上海倪佳峰⾼⼆年级交⼤附中⼆等奖福建郑钊⾼⼆年级⼤⽥⼀中三等奖福建林达栋⾼⼆年级⼤⽥⼀中三等奖湖南黄鑫⾼⼆年级郴州资兴市⽴中学三等奖湖南张琳⾼⼆年级溆浦⼀中三等奖湖南吴源波⾼⼆年级长沙县实验中学三等奖陕西刘星泽⾼⼆年级澄城中学三等奖北京曹⼼睿⾼⼆年级景⼭学校三等奖⼴东彭⼒恒⾼⼆年级⼴州市西关外国语学校三等奖⼴东梁题⾼⼆年级⼴东⼴雅中学三等奖⼴东罗⼦云⾼⼆年级⼴东⼴雅中学三等奖⼴东陶然⾼⼆年级⼴州市⼴外附设外语学校三等奖⼭西刘宝源⾼⼆年级成成中学三等奖⼭西郭⾬晴⾼⼆年级阳⾼⼀中三等奖⼭西管璞⾼⼆年级怀仁⼀中云东校区三等奖⼭西⾼鹏昕⾼⼆年级怀仁⼀中云东校区三等奖⼭西程曦⾼⼆年级清徐中学三等奖上海陈卓超⾼⼆年级市北中学三等奖上海费翔⾼⼆年级交⼤附中三等奖上海许兆伟⾼⼆年级风华中学三等奖上海邓颖康⾼⼆年级市⼆中学三等奖。
全国中学生数理化学科能力竞赛(高二年级数学竞赛试题)

本题得分 评卷人 本题得分 评卷人首届全国中学生数理化学科能力竞赛高二数学学科能力解题技能初赛试题试卷说明:1、本试卷共计15题,满分为120分2、考试时间为120分钟一、选择题(每小题5分,共30分)1.已知{}{}{}2,,A x N x B x x A C x x B =∈<=⊆=⊆,则集合C 的元素个数为( )(A )82 (B )4 (C )8 (D )162.曲线sin(1)3cos(1)33xx y ππ=+++的对称轴之间距离的最小值为( )(A )1 (B )2 (C )3 (D )43.设点P 为△ABC 的边BC 上的一点,且满足1344AP AB CA =-,则△ABP 与△APC 的面积之比为( )(A ) 1:3 (B ) 3:1 (C ) 1:4 (D ) 4:14.如果关于x 的方程24230x x a a -⨯+-=至少有一个实根,则实数a 的取值范围是( )(A )[2,2]- (B )(3,2] (C )(3,2]- (D )[3,2]- 5.设实数y x ,满足条件⎪⎩⎪⎨⎧≤--≤--≥+-033022042y x y x y x ,则y x y x y x f 22),(22+++=的最大值为( )(A )23 (B )25 (C )23 (D )56.已知)(x f 对于任意的R y x ∈、,有633)()()(++=-y x xy f y f x f ,则=)2008(f ( )(A )2008 (B )2009 (C) 2010 (D )2011总分本题得分 评卷人二、填空题(每小题5分,共30分)7.已知,a b 均为质数,且满足213a a b +=,则2b a b += .8.已知△ABC 的三边长分别为13,14,15. 有4个半径同为r 的圆O 、1O 、2O 、3O 放在△ABC 内,并且圆1O 与边AB 、AC 相切,圆2O 与边BA 、BC 相切,圆3O 与边CB 、CA 相切,圆O 与圆1O 、2O 、3O 相切,则=r . 9.若不等式n a n n1)1(2)1(+-+<⋅-对任意正整数n 恒成立,则实数a 的取值范围是 .10.函数()f x 在R 是减函数,且不等式(2)(2)()()f a b f a b f a f b +++>+恒成立,则a 与b -的大小关系是 .11.已知函数()f x 同时满足以下三个条件:(1)存在反函数1()f x -;(2)点(1,1)在函数()f x 的图象上;(3)函数(1)f x +的反函数为1(1)f x --.则1()(1)f n f n ⎧⎫⎨⎬+⎩⎭的前n 项和n T = . 12.若[]x 表示不超过x 的最大整数(如[]11.31,234⎡⎤=-=-⎢⎥⎣⎦等),则1212⎡⎤+⎢⎥-⨯⎣⎦ 111323434200920082009⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥-⨯-⨯-⨯⎣⎦⎣⎦⎣⎦=____________________. 三、解答题13.(本小题满分20分) 在数列{}n a 中,已知111,21n n a a a n +==+-.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2,n n b na n =+且{}n b 的前项n 和为n S ,求证:126n n S S +≥+.14.(本小题满分20分)已知,,x y z 是一个三角形的三个内角,求三元方程2cos 2cos 2cos 3x y z ++=的所有解.15.(本小题满分20分)有一个m n p ⨯⨯的长方体盒子,另有一个(2)(2)(2)m n p +⨯+⨯+的长方体盒子, 其中,,m n p 均为正整数(m n p ≤≤),并且前者的容积是后者一半,求p 的最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
届全国中学生数理化学科能力竞赛
七年级数学学科能力解题技能初赛试题
试卷说明:1、本试卷共计15题,满分为120分
2、考试时间为120分钟
一、选择题(共6小题,每题5分,共30分)
1、北京奥运期间,体育场馆要对观众进行安全检查.设某体育馆在安检开始
时已有若干名观众在馆外等候安检,安检开始后,到达体育馆的观众人数按
固定速度增加.又设各安检人员的安检效率相同.若用3名工作人员进行安
检,需要25分钟才能将等候在馆外的观众检测完,使后来者能随到随检;
若用6名工作人员进行安检,时间则缩短为10分钟.现要求不超过5分钟完
成上述过程,则至少要安排 名工作人员进行安检.
A. 9
B. 10
C. 11
D. 12
2、2008年9月25日,中国国家主席胡锦涛在酒泉卫星发射中心“问天阁”
为执行神州7号飞行任务的航天员壮行.3天后,神州7号巡天归来,在太
空中留下了中国人骄人的足迹.根据这些事实和数据,我们发现有可能存在
这样的等式: 神州7号问天×3 = 问天神州7号
上述等式中,每个汉字代表从0到9中的不同自然数(其中7已经被使
用).要使得等式成立,则神州7号 = .
A. 2075
B. 3075
C. 3076
D. 3078
3、若“学”、“科”、“能”、“力”这四个汉字中每个汉字分别代表一个非零
的个位数,对于运算符号“∆”有:学科能力∆1=科学能力;学科能力∆2
=能力科学,那么1234∆1∆2 = .
A. 4312
B. 3421
C. 4321
D. 3412
4、一个数学玩具的包装盒是正方体,其表面展开图如下.现在每方格内都填
上相应的数字.已知将这个表面展开图沿虚线折成正方
体后,相对面上的两数之和为“0 ”,则填在A 、B 、C
内的三个数依次是 .
A. 0,-2,1
B. 0,1,-2
C. 1,0,-2
D. -2,0,1
5、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划.该球拍每只售价为人民币60
元,购买者同时获赠1张奖券;积累3张奖券可兑换1只球拍.
由此可见,1张奖券价值为
元.
A. 20
B. 15
C. 18
D. 12
6、10个同学藏在10个谜宫里面.男同学的谜宫门前写的是一个正数,女同学的谜宫门前写的是一个负数,这10个迷宫门前的数字依次为
8200823(5)(1)83(2008),,0.1,,,2008,2,,4(2),51,(25)20081997(3)
a ---+---⨯-⨯---- 则谜宫里面的男同学、女同学的人数分别为 .
A. 4人、6人
B. 6人、4人
C. 3人、7人
D. 7人、3人
二、填空题:(共6小题,每题5分,共30分)
7、若(x -2y )2+(y +2)2=0,则y -x = .
8、由6条长度均为2 cm 的线段可构成边长为2 cm 的n 个正三角形,
则n 的最大值为 .
9、在△ABC 中,点D 为边BC 的中点,点E 为线段AD 上一点,且满
足AE =2ED ,则△ABC 与△BDE 的面积之比为 .
10、某校A 、B 、C 三名同学参加全国中学生数理化学科能力竞赛,其指导教师赛前预测:“A 获金牌;B 不会获金牌;C 不会获铜牌.”结果出来后,三人之中,一人获金牌,一人获银牌,一人获铜牌,指导教师的预测只有一个与结果相符.由此可以推论: 获得银牌.
11、已知2x y +(其中,x y 都是整数)能被9整除,则2(584)x y --被9除的余数为 .
12、从2008,2009,2010,…, 2028这些数中,任取两个数,使其和不能写成三个连续自然数的和,则有 种取法.
三、解答题(每小题20分,共60分)
13、鲁西西开始研究整数的特征.她发现:4=22-02,12=42-22,20=62-42
. 4,12,20这些正
整数都能表示为两个连续偶数的平方差,她称这些正整数为“和谐数”.现在请你在鲁西西研究的基础上,进一步探究下列问题:
(1) 判断28、2008是否为“和谐数”.
(2) 根据上述判断,请你推广你的结论,指出判断一个正整数是否为“和谐数”的标准.
(3) 更进一步探究:两个连续奇数的平方差(取正数)是“和谐数”吗?为什么?
14、已知2008=)1
(x y x ,其中x ,y 为正整数,求x +y 的最大值和最小值.
15、《歌词古体算题》记载了中国古代的一道在数学史上名扬中外的“勾股容圆”名题,其歌词为:
十五为股八步勾,内容圆径怎生求?
有人算得如斯妙,算学方为第一筹.
当中提出的数学问题是这样的:已知直角三角形的两直角边边长分别为
15步,8步,试求其内切圆的直径.
请你尝试完成上述任务,如果时光倒流,看看你是否算得上古代中国的
一流数学家.(温馨提示:直角三角形的三边存在这样的数量关系:斜边的
平方等于两直角边的平方和.)。
