中考数学填空选择最后一题
中考数学选择填空最后一题汇总
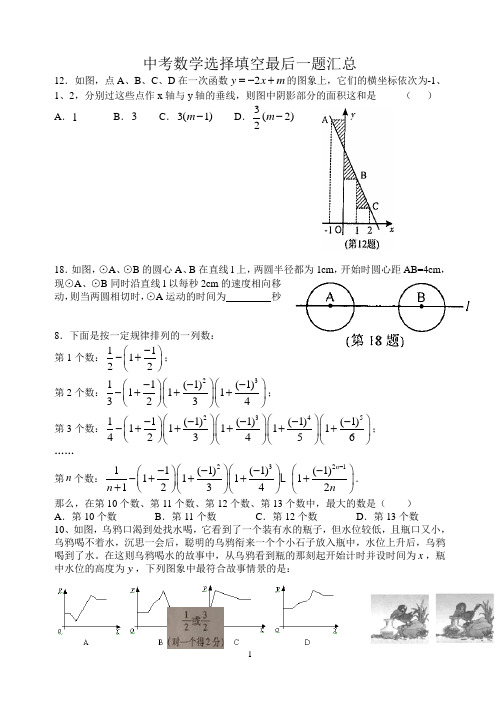
中考数学选择填空最后一题汇总12.如图,点A 、B 、C 、D 在一次函数2y x m =-+的图象上,它们的横坐标依次为-1、1、2,分别过这些点作x 轴与y 轴的垂线,则图中阴影部分的面积这和是 ( )A .1B .3C .3(1)m -D .3(2)2m -18.如图,⊙A 、⊙B 的圆心A 、B 在直线l 上,两圆半径都为1cm ,开始时圆心距AB=4cm ,现⊙A 、⊙B 同时沿直线l 以每秒2cm 的速度相向移动,则当两圆相切时,⊙A 运动的时间为 秒8.下面是按一定规律排列的一列数: 第1个数:11122-⎛⎫-+ ⎪⎝⎭; 第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭; 第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭; ……第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭.那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )A .第10个数B .第11个数C .第12个数D .第13个数10、如图,乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水。
在这则乌鸦喝水的故事中,从乌鸦看到瓶的那刻起开始计时并设时间为x ,瓶中水位的高度为y ,下列图象中最符合故事情景的是:12、B 18、 8、A 10.D18、若将4根木条钉成的矩形木框变形为平行四边形形状,并使面积为矩形面积的一半,则这个平行四边形的一个最小内角是______度。
10.如图,等腰△ABC 中,底边a BC =,︒=∠36A ,ABC ∠的平分线交AC 于D ,BCD ∠的平分线交BD 于E ,设215-=k ,则=DE ( ▲ )A .a k 2B .a k 3C .2k aD .3k a16.如图,在直角坐标系中,已知点)0,3(-A ,)4,0(B ,对△OAB 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 ▲ .12.已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,请你在图中任意画一条抛物线,问所画的抛物线最多能经过81个格点中的多少个?( ) A .6 B .7 C .8 D .9ADC EB (第10题)(第12题)B18、30 10.A 16.(360),12、C18.如图,已知Rt ABC △,1D 是斜边AB 的中点, 过1D 作11D E AC ⊥于E 1,连结1BE 交1CD 于2D ; 过2D 作22D E AC ⊥于2E ,连结2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…,如此继续,可以依次得到点45D D ,,…,n D ,分别记112233BD E BD E BD E △,△,△,…,n n BD E △的面积为123S S S ,,,…n S .则n S =________ABC S △(用含n 的代数式表示).10、如图4,矩形纸片ABCD 中,AB=4,AD=3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则AG 的长为( ) A .1B .34C .23D .210.若不等式组0,122x a x x +⎧⎨->-⎩≥有解,则a 的取值范围是( )(A)a >-1. (B)a ≥-1. (C)a ≤1. (D)a <1.18.如图,正方形ABCD 边长为1,动点P 从A 点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2009时,点P 所在位置为______;当点P 所在位置为D 点时,点P的运动路程为______(用含自然数n 的式子表示).C图418.()211n +10、C10、c10、A 18.点B ;4n +3(录入者注:填4n-1(n 为正整数)10、A10.如图,已知△ABC 中,∠ABC =90°,AB =BC ,三角形的顶点在相互平行的三条直线l 1,l 2,l 3上,且l 1,l 2之间的距离为2 , l 2,l 3之间的距离为3 ,则AC 的长是 A .172 B .52 C .24 D .716.如图,图①是一块边长为1,周长记为P 1的正三角形纸板,沿图①的底边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第n (n ≥3)块纸板的周长为P n ,则P n -P n-1= ▲ .10、如图5,AB 是⊙O 的直径,且AB=10,弦MN 的长为8,若弦MN 的两端在圆上滑动时,始终与AB 相交,记点A 、B 到MN 的距离分别为h 1,h 2,则|h 1-h 2| 等于( ) A 、5 B 、6 C 、7 D 、8 16、如图7所示,P 1(x 1,y 1)、P 2(x 2,y 2),……P n (x n ,y n )在函数y=x9(x >0)的图象上,△OP 1A 1,△P 2A 1A 2,第18题图 BD A (P )C(第10题)l 1l 2l 3ACB (第16题)…① ② ③ ④△P 3A 2A 3……△P n A n -1A n ……都是等腰直角三角形,斜边OA 1,A 1A 2……A n-1A n ,都在x 轴上,则y 1+y 2+…y n = 。
2024年浙江九年级中考数学最后一卷答案

2024年浙江中考最后一卷数学解析及参考答案一、单选题1.D【分析】此题考查了实数的大小比较法则:正数大于零,零大于负数,两个负数绝对值大的反而小,据此判断.【详解】∵510−<−<<故选:D .2.D【分析】根据各个选项中的式子可以计算出正确的结果,本题得以解决.【详解】解:∵3a ﹣2a =a ,故选项A 错误;∵2a 2+4a 2=6a 2,故选项B 错误;∵(x 3)2=x 6,故选项C 错误;∵x 8÷x 2=x 6,故选项D 正确;故选D .【点睛】本题考查整式的混合运算,解答本题的关键是明确整式混合运算的计算方法.3.B【分析】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a ×的形式,其中110a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值10≥时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】解:80.16亿98.01610×,故选:B .4.B【分析】本题考查立体几何的三视图.根据题意,逐项判断即可.【详解】解:A.主视图为长方形,此项不符合题意;B.主视图为三角形,此项符合题意;C.主视图为圆,此项不符合题意;D.主视图为长方形,此项不符合题意.故选:B .5.C【分析】先解不等式,求出解集,然后在数轴上表示出来.【详解】解:不等式x ﹣2≤0,得:2x ≤ ,把不等式的解集在数轴上表示出来为:.故选:C【点睛】本题主要考查了解不等式,并在数轴上表示解集,解题的关键是熟练掌握解不等式的步骤,不等式的解集在数轴表示时空心圈不包含该点,实心圈包含该点.6.D【分析】本题为统计题,考查众数与中位数的意义,根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按从小到大依次排列,处于中间位置的两个数的平均数即为中位数.【详解】有45辆自动驾驶汽车参与了这次测试,45个分数,按大小顺序排列最中间的数据是第23个数:85,故得分的中位数是85(分),得80分的人数最多,有16人,故众数为80,故选D .7.A【分析】本题考查了垂径定理和勾股定理的应用,根据垂径定理求出AE 的长是解此题的关键.连接OA ,根据垂径定理求出AE ,再根据勾股定理求出OA ,最后根据线段的和差求解即可.【详解】解:如图,连接OA ,线段CD 是O 的直径,CD AB ⊥于点E ,∴12AE AB =,8AB =, ∴4AE =,3OE =,∴5OA ,∴5OC OA ==,∴8CE OC OE =+=,故选:A .8.A【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是设每头牛、每只羊分别值金x 两、y 两,根据“5头牛,2只羊,值金10两;2头牛,5只羊,值金8两”列出方程组即可得答案.【详解】解:设每头牛值金x 两,每只羊值金y 两,则可列方程组为5210258x y x y += +=, 故选A .9.B【分析】本题考查了菱形的性质、二次函数图象上点的坐标特征,根据二次函数图象上点的坐标性质得出BD 的长是解题关键.连接BC 交OA 于D ,如图,根据菱形的性质得BC OA ⊥,60OBD ∠=°,利用含30度的直角三角形三边的关系得OD =,设BD t =,则OD =,()B t ,利用二次函数图象上点的坐标特征得2=,得出14BD =,OD =C 点坐标. 【详解】解:连接BC 交OA 于D ,如图,四边形OBAC 为菱形,BC OA ,120ABO ∠=° ,60OBD ∴∠=°,OD ∴,设BD t =,则OD =,()B t ∴,把()B t 代入2y =,得2=,解得10t =(舍去), 214t =,14BD ∴=,OD =故C 点坐标为:14 − .故答案为:B .10.C【分析】本题考查的是矩形的性质、翻折的性质及相似多边形性质,熟练应用矩形和相似多边形性质是解题关键,设CD x =,则()1,1EC x CG x x =-=--,根据两矩形相似求出即可.【详解】解:在矩形ABCD 中,设CD x =,则ABCD x ==,1AD BC ==, 由翻折得,90AB AF x AFE B BAF ==∠=∠=∠=︒,∴四边形ABEF 是正方形,同理,四边形DFHG 是正方形,,1BE AB x DF DG x ∴====-,()1,121CE x CG x x x ∴=-=--=-,矩形HECG ∽矩形ABCD ,EC CG BC CD∴=,即1211x x x --=,解得:x =,经检验,xCD ∴ 故选:C .二、填空题11.()()22t t t +−【分析】本题考查了因式分解,先提取公因式,再利用公式法即可求解,熟练掌握提公因式法及公式法分解因式是解题的关键.【详解】解:()()()324422t t t t t t t −=−=+−,故答案为:()()22t t t +−.12.14/0.25 【分析】本题考查了概率公式的应用,用到的知识点为:概率所求情况数与总情况数之比.全部情况的总数是四种,符合条件的情况的是一种,二者的比值就是其发生的概率.【详解】由于概率为所求情况数与总情况数之比,而抽取卡片为“特区精神”的情况数只有一种,从暗箱随机抽取一张的情况数为四种,故抽取卡片为“特区精神”的概率为14, 故答案为14. 13.0(答案不唯一)【分析】本题主要考查了二次根式有意义的条件,分式有意义的条件,根据二次根式有意义的条件的条件是被开方数大于等于0,分式有意义的条件是分母不为0进行求解即可.∴10x −>,解得1x <.∴x 的值可以是0,故答案为:0(答案不唯一).14.100°/100度【分析】本题考查的是已知弧长与半径求解弧所对的圆心角,熟记弧长公式是解本题的关键.直接利用弧长公式计算即可.【详解】解: 设“弓”所在的圆的弧长圆心角度数是n °, 则1.2π2π1803n =, 解得:100n =,故答案为:100°.15.0.5−【分析】本题考查了反比例函数k 值的几何意义,熟练掌握k 值的几何意义是解答本题的关键.根据反比例函数k 值的几何意义进行解答即可.【详解】AB x ⊥ 轴于点B ,CD x ⊥轴,∴AB CD ,又 AD BC ,∴四边形ABCD 是平行四边形,过点作AM y ⊥轴,则四边形ABOM 是矩形, ∴0.5,ABOMABCD S S k ===矩形平行四边形∵反比例函数图象在第二象限,0.5k ∴=−,故答案为:0.5−.16.23、54【分析】本题考查了折叠的性质,正方形的性质,勾股定理,圆的定义;分三种情况讨论,设O 的半径为r ,分别根据勾股定理,即可求解.【详解】设O 的半径为r ,当O 经过A O ′的中点,即经过AO 的中点, ∴1233r AB =,当O 经过OD 的中点,则12r OB OD ==, ∴2OD r =,2AO AB OB r =−=−, 在Rt AOD 中,222AD AO OD +=∴()()222222r r +−=解得:r = 当O 经过A D ′的中点,即经过AD 的中点,设AD 的中点为M ,∴2,1,AO r AM OM r =−== ∴()22221r r −+= 解得:54r =综上所述,半径为23、54故答案为:23、54 三、解答题17.(1)5(2)222m mn −+【分析】此题考查了实数的运算以及整式的混合运算,熟练掌握运算法则是解本题的关键.(1)原式利用零指数幂、绝对值的代数意义以及负整数指数幂法则计算即可求出值;(2)根据平方差公式和完全平方公式化简,再合并同类项即可.【详解】(1)解:原式159=-+5=;(2)原式()22222n m m mn n =−−−+22222n m m mn n =−−+−222m mn =−+18.(1)图见解析(2)【分析】本题考查作图-轴对称变换,旋转变换,以及求弧长,熟练掌握相关作图方法是解题关键; (1)根据点关于y 轴对称的性质分别找到对应的点1A ,1B ,1C ,然后进一步连接即可;(2)利用旋转变换的性质分别作出A ,B ,C 的对应点2A ,2B ,2C ,再顺次连接即可,利用弧长公式求得点C 经过的路径长.【详解】(1)解:如图,111A B C △即为所求;(2)如图,222A B C △即为所求,由题意可知,OC∴点C 旋转到点2C =. 19.(1)6,40(2)1120 (3)全校学生一周内平均读书时间23t ≤<(答案不唯一)【分析】本题考查了扇形统计图,样本估计总体等知识.(1)由等级得到学生总数,即可得出a ,再求C 等级的占比即可;(2)用样本估计总体即可得出结果;(3)根据表格可题建议合理即可.【详解】(1)解:由等级D 得到学生总数1530%50÷=人, ∴504201556a −−−−,()%2050100%40%m =÷×=,40m =,故答案为:6,40.(2)1552800112050+×=人, 故该校2800名学生每周读书时间至少3小时的人数为1120人.故答案为:1120.(3)根据表格可建议:全校学生一周内平均读书时间23t ≤<.20.(1)是;222AB BD AD +=,由勾股定理的逆定理可知AB BC ⊥.(2).【分析】本题考查的勾股定理的逆定理的应用,解直角三角形的应用,理解题意是解本题的关键. (1)利用勾股定理的逆定理判断即可;(2)先画图,利用三角函数再计算BE=BF =,从而可得答案. 【详解】(1)解:是, 理由:由测量结果可知得 1.5m BD =, 2.5m AD =,而2m AB =,∴2226.25AB BD AD +==,∴90ABD ,∴AB BC ⊥.故答案是:是;222AB BD AD +=,由勾股定理的逆定理可知AB BC ⊥.(2)如图,由题意可得:90ABC ∠=°,2AB =,30AFB ∠=°,60AEB ∠=°,∴tan tan 60AB AEB BE∠=°=,∴BE =, 同理:tan tan 30AB AFBBF ∠=°=,∴BF =,∴FE BF BE =−==. 21.(1)证明见解析(2)6【分析】(1)依据平行线的性质以及矩形的性质,即可得到∠AFE =∠AEF ,进而得出AE =AF .(2)设BE =x ,则AE =EC =8-x ,在Rt △ABE 中,根据勾股定理可得方程,即可得到BE 的长,再根据三角形面积计算公式求解.【详解】(1)证明:∵四边形ABCD 矩形,∴AD ∥BC ,∴∠AFE =∠FEC ,由折叠的性质得:∠AEF =∠FEC ,∴∠AFE =∠AEF ,∴AE =AF .(2)解:根据折叠的性质可得AE =EC ,设BE =x ,则AE =EC =8-x ,在Rt △ABE 中,根据勾股定理可得:222AB BE AE +=,即()22248x x +=−,解得:x =3,∴BE =3,∴ABE S = 12AB •BE =12×4×3=6. 【点睛】本题主要考查了折叠问题以及矩形的性质的运用,解题的方法是设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.22.(1)220y x =−+ (2)5种(3)当转运A 种脐橙的车4辆,转运B 种脐橙的车12辆,转运C 种脐橙的车4辆时,利润最大为140800元【分析】(1)根据题意列式:()20651040x x y y −−=++,整理后即可得到220y x =−+; (2)根据装运每种水果的车辆数都不少于4辆,4x ≥,2204x −+≥,解不等式组即可;(3)设利润为W 元,则()480016000048W x x =−+≤≤,根据一次函数的增减性求解即可. 【详解】(1)根据题意,装运A 种水果的车辆数为x ,装运B 种水果的车辆数为y ,∴装运C 种水果的车辆数为()20x y −−,∴()20651040x x y y −−=++, 整理得220y x =−+. (2)由(1)知,装运A ,B ,C 三种水果的车辆数分别为x ,220x −+,x ,由题意得2204x −+≥,解得8x ≤,∵4x ≥,∴48x ≤≤.∵x 为整数,∴x 的值为4,5,6,7,8,∴安排方案共有5种.(3)设利润为W 元,∴()612005220160041000W x x x =×+−+×+× 4800160000x =−+,因为48000−<,且x 的值为4,5,6,7,8,∴W 的值随x 的增大而减小,∴当4x =时,销售利润最大.当装运A 种水果4车,B 种水果12车,C 种水果4车,销售获利最大.最大利润48004160000140800W =−×+=(元).【点睛】主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意要根据自变量的实际范围确定函数的最值.23.(1)2(0,0)P ,3(1,1)P ,4(2,2)P(2)①AC =BC =AB =ABC 是直角三角形,理由见解析【分析】本题考查了二次函数的图象与性质、勾股定理以及勾股定理逆定理:(1)根据“梦之点”的定义判断这几个点是否在矩形的内部或者边上即可得到答案;(2)①根据“梦之点”的定义求出A ,B 的坐标,再求出顶点的坐标,计算出AC ,AB ,BC 的长; ②根据勾股定理逆定理,即可求解.【详解】(1)解:∵矩形ABCD 的顶点坐标分别是(1,2)A −,(1,1)B −−,(3,1)C −,(3,2)D ,∴矩形ABCD 的“梦之点”(),x y 满足2,131x y −−≤≤≤≤,∴点2(0,0)P ,3(1,1)P ,4(2,2)P 是矩形ABCD 的“梦之点”,1(2,2)P −−不是矩形的“梦之点”.故答案为:2(0,0)P ,3(1,1)P ,4(2,2)P(2)解:①A 、B 是抛物线21922y x x =−++上的“梦之点”, ∴21922x x x =−++, 解得:123,3x x ==−,当3x =时,3y =,当3x =−时,=3y −,∴()()3,3,3,3A B −−, ∵()2219115222y x x x =−++=−−+, ∴顶点坐标为()1,5C ,∴AC =BC =AB =; ②ABC 是直角三角形,理由如下:∵AC =BC =AB =∴((2222280AB AC BC +=+==, ∴ABC 是直角三角形.24.(1)证明见解析(2)证明见解析(3)①EF =253CF =【分析】本题考查了圆的性质,等腰三角形的判定与性质,相似三角形的判定与性质,锐角三角函数等知识,掌握相关知识是解题的关键.(1)利用勾股和锐角三角函数求得AC BC =即可证明;(2)连接,OA OB ,延长CO 交AD 于点M ,交AB 于点N ,先证明CO 是ACB ∠的角平分线,再证明ANM CDM ∽即可得出结论;(3)①过O 点作OH BC ⊥交BC 于点H ,点E 是OC 上一动点,EF AB ∥交BC 于点F ,先证明CHO CFB ∽,设EF x =3x =即可求解,②要使OEF 的面积与CEF △的面积差最大,必须使EF 和()CE OE −最大,当E 点与O 点重合时,EF 最大,CE OE OC −=最大,先求得EF =即可求出CF . 【详解】(1)证明:∵AD 是∴90ADC ADB ∠=∠=°, ∵9AD =,12CD =,∴15AC ===,∵tan 3ABD ∠=, ∴tan 3AD ABD BD∠==, ∴3BD =, ∴31215BC BD CD =+=+=, ∴AC BC =,∴ABC 是等腰三角形.(2)证明:连接,OA OB ,延长CO 交AD 于点M ,交AB 于点N ,如图:∵AC BC =,∴CAB CBA ∠=∠, ∵OA OB =,∴OAB OBA ∠=∠, ∴CAO CBO ∠=∠, ∵OA OC =,∴CAO ACO ∠=∠, ∵OB OC =,∴BCO CBO ∠=∠, ∴ACO BCO ∠=∠, ∴CO 是ACB ∠的角平分线, 又∵ AC BC =,∴CN AB ⊥,∴90ANC BNC ∠=∠=°, ∴90MDC ANE ∠=∠=°, 又∵AMN CMD ∠=∠, ∴ANM CDM ∽,∴DCM NAM ∠=∠, ∴BCO BAD ∠=∠. (3)解:①过O 点作OH BC ⊥交BC 于点H ,点E 是OC 上一动点,EF AB ∥交BC 于点F ,如图:∵,,15OB OC OH BC BC =⊥=, ∴17.52CH BC ==,90CHO CFB ∠=∠=°, ∴CHO CFB ∽,∴COH CBF ∠=∠, ∵tan 3ABD ∠=, ∴tan tan 3CH COH CBF OH∠=∠==, ∴ 2.5OH =,∴OC =, ∵EF AB ∥,90BNC ∠=°, ∴CEF CNB ∽,∴90CEF CNB ∠=∠=°, 设EF x =,∴tan tan 3CE CE CFE CBN EF x∠=∠===, ∴3CE x =,∵OEF ADB ∽,∴OE EF AD BD=, ∵OEOC CE =−,3x =, 解得:x =∴EF ②∵90CEF ∠=°,即EF OC ⊥, ∴12CEF S CE EF =⋅ ,12OEF S OE EF =⋅ , ∴()111222CEF OEF S S CE EF OE EF EF CE OE −=⋅−⋅=⋅− , 由题知,要使OEF 的面积与CEF △的面积差最大,必须使EF 和()CE OE −最大,∴当E 点与O 点重合时,EF 最大,CE OE OC −=最大,如图:∵EF AB ∥,∴CEF CNB ∽,∴CFE CBN ∠=∠,CE OC ==,∴tan tan 3CE CFE CBN EF ∠=∠==,∴EF∴253CF =.。
2024年安徽省宿州市宿城第一初级中学中考模拟最后一卷数学试题

2024年安徽省宿州市宿城第一初级中学中考模拟最后一卷数学试题一、单选题1.如果a的相反数是2,那么a等于()A.2-B.2 C.12D.12-2.华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为().A.7710⨯﹣B.80.710⨯﹣C.8710⨯﹣D.9710⨯﹣3.关于x的不等式3x-2≥2x+1的解集是()A.x≤3B.x<-3 C.x≥-3 D.x≥341在数轴上的对应点可能是()A.A点B.B点C.C点D.D点5.如图,菱形ABCD的的边长为6,60ABC∠=︒,对角线BD上有两个动点E、F(点E 在点F的左侧),若EF=2,则AE+CF的最小值为()A.B.C.6 D.86.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是()A .12B .13C .14 D .157.如图,二次函数:2(0)y ax bx c a =++≠与一次函数:y =mx +n (m ≠0)的图象交于A ,B 两点,则一元二次方程2ax bx c mx n ++=+的解为( )A .121x x ==-B .11x =,22x =C .11x =-,22x =D .122x x == 8.化简21211x x ---的结果是( ) A .1x x - B .1x x + C .11x + D .1x x+ 9.如图,在平面直角坐标系中,Rt ABC V 的顶点A C 、的坐标分别为(0,5)、(5,0),90ACB ∠=︒,2AC BC =,函数(0,0)ky k x x=>>的图象经过点B ,则k 的值为( )A .754B .758C .252D .2510.如图,在平面直角坐标系中,点A 在一次函数y位于第一象限的图象上运动,点B 在x 轴正半轴上运动,在AB 右侧以它为边作矩形ABCD ,且AB =AD =1,则OD 的最大值是( )AB C D.二、填空题11.若分式12xx-+的值为0.则x=.12.函数y=x的取值范围是.13.计算:11|2sin452-⎛⎫+-=⎪⎭︒⎝.14.某中学规定学生的学期体育成绩满分为100,其中体育课外活动占30%,期末考试成绩占70%,小彤的这两项成绩依次是90,80.则小彤这学期的体育成绩是.15.如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:①AF的长为10;②△BGH的周长为18;③BGGF=23;④GH的长为5,其中正确的结论有.(写出所有正确结论的番号)三、解答题16.先化简,再求值:2213222x xxx x-+⎛⎫÷--⎪++⎝⎭,请从-2,-1,0,1,中选择一个合适的值代入求值.17.在新冠疫情防控期间,某医疗器械商业集团新进了40台A型电子体温测量仪,60台B 型电子体温测量仪,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种测量仪每台的利润(元)如下表:设集团调配给甲连锁店x台A型测量仪,集团卖出这100台测量仪的总利润为y(元).(1)求y关于x的函数关系式,并求出x的取值范围:(2)为了促销,集团决定仅对甲连锁店的A型测量仪每台让利a元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大18.某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题(1)表中m=,n=;(2)扇形统计图中,A部分所对应的扇形的圆心角是°,所抽取学生对丁雾霾了解程度的众数是;(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?19.如图,在平面直角坐标系中,将△ABC进行位似变换得到△A1B1C1.(1)△ABC与△A1B1C1的位似比是.(2)画出△ABC绕点O逆时针旋转180°得到的△A2B2C2.(3)若点P(a,b)为△ABC内一点,求点P在△A2B2C2内的对应点P2的坐标.20.(2017山东省威海市)图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:如图2,AB BC ⊥,垂足为点B ,EA AB ⊥,垂足为点A ,CD AB ∥,10cm CD =,120cm DE =,FG DE ⊥,垂足为点G .(1)若3750θ∠=︒',则AB 的长约为cm ;(参考数据:sin3750061.︒'≈,cos3750079.︒'≈,tan3750078.︒'≈)(2)若30cm FG =,60θ∠=︒,求CF 的长.21.如图,AB 是⊙O 的直径,点C 为⊙O 上一点,CN 为⊙O 的切线,OM ⊥AB 于点O ,分别交AC 、CN 于D 、M 两点.(1)求证:MD =MC ;(2)若⊙O 的半径为5,ACMC 的长.22.为了缓解我市新型冠状肺炎护目镜需求,两江新区某护目镜生产厂家自正月初三起便要求全体员工提前返岗.在接到单位的返岗任务后,员工们都毫无怨言,快速回到了自己的工作岗位,用努力工作的行动践行着自己的社会责任感与社会担当.已知该厂拥有两条不同的护目镜加工生产线A、B.原计划A生产线每小时生产护目镜400个,B生产线每小时生产护目镜500个.(1)若生产线A、B共工作12小时,且生产护目镜总数量不少于5500个,则B生产线至少生产护目镜多少小时?(2)原计划A、B生产线每天均工作8小时,但现在为了尽快满足我市护目镜的需求,两条生产线每天均比原计划多工作了相同的小时数,但因为机器损耗及人员不足原因,A生产线每增加1小时,该生产线实际工作时每小时的产量均减少10个,B生产线每增加1小时,该生产线每小时的产量均减少15个,这样一天生产的护目镜将比原计划多3300个,求该厂实际每天生产护目镜的时间.23.如图1,矩形ABCD的对角线AC与BD相交于点O,将矩形沿对角线AC折叠,折叠后点B落在点E处,CE交AD于点F,连接DE.AC DE;(1)求证://(2)当AB与BC满足什么数量关系时,四边形AODE是菱形?请说明理由;(3)将图1中的矩形ABCD改为平行四边形ABCD,其它条件不变,如图2,若AB=∠ABC=30°,点E在直线AD上方,试探究:△AED是直角三角形时,BC的长度是多少.24.如图,已知二次函数213y x bx c =-++的图像与x 轴交于A 、B 两点,与y 轴交于点C ,其中点A 的坐标为(30)-,,对称轴是直线12x =. (1)求该二次函数的表达式;(2)如图,连接AC ,若点P 是该抛物线上一点,且12PAB ACO ∠=∠,求点P 的坐标;(3)如图,点P 是该抛物线上一点,点Q 为射线CB 上一点,且P 、Q 两点均在第四象限内,线段AQ 与BP 交于点M ,当PBQ AQB ∠∠=,且△ABM 与△PQM 的面积相等时,请问线段PQ 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.。
2024年福建莆田中考数学试题及答案(1)
2024年福建莆田中考数学试题及答案一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.下列实数中,无理数是( )A .3-B .0C .23D 2.据《人民日报》3月12日电,世界知识产权组织近日公布数据显示,,全球PCT (《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69610用科学记数法表示为( )A .696110´B .2696.110´C .46.96110´D .50.696110´3.如图是由长方体和圆柱组成的几何体,其俯视图是( )A .B .C .D .4.在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD ^DE )按如图方式摆放,若AB P CD ,则1Ð的大小为( )A .30°B .45°C .60°D .75°5.下列运算正确的是( )A .339a a a ×=B .422a a a ¸=C .()235a a =D .2222a a -=6.哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是( )A .14B .13C .12D .237.如图,已知点,A B 在O e 上,72AOB Ð=°,直线MN 与O e 相切,切点为C ,且C 为»AB 的中点,则ACM Ð等于( )A .18°B .30°C .36°D .72°8.今年我国国民经济开局良好,市场销售稳定增长,社会消费增长较快,第一季度社会消费品零售总额120327亿元,比去年第一季度增长4.7%,求去年第一季度社会消费品零售总额.若将去年第一季度社会消费品零售总额设为x 亿元,则符合题意的方程是( )A .()1 4.7%120327x +=B .()1 4.7%120327x -=C .1203271 4.7%x=+D .1203271 4.7%x=-9.小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案.如图,其中OAB V 与ODC V 都是等腰三角形,且它们关于直线l 对称,点E ,F 分别是底边AB ,CD 的中点,OE OF ^.下列推断错误的是( )A .OB OD ^B .BOC AOBÐ=ÐC .OE OF =D .180BOC AOD Ð+Ð=°10.已知二次函数()220y x ax a a =-+¹的图象经过1,2a A y æöç÷èø,()23,B a y 两点,则下列判断正确的是( )A .可以找到一个实数a ,使得1y a >B .无论实数a 取什么值,都有1y a >C .可以找到一个实数a ,使得20y <D .无论实数a 取什么值,都有20y <二、填空题:本题共6小题,每小题4分,共24分.11.因式分解:x 2+x = .12.不等式321x -<的解集是 .13.学校为了解学生的安全防范意识,随机抽取了12名学生进行相关知识测试,将测试成绩整理得到如图所示的条形统计图,则这12名学生测试成绩的中位数是 .(单位:分)14.如图,正方形ABCD 的面积为4,点E ,F ,G ,H 分别为边AB ,BC ,CD ,AD 的中点,则四边形EFGH 的面积为 .15.如图,在平面直角坐标系xOy 中,反比例函数ky x=的图象与O e 交于,A B 两点,且点,A B 都在第一象限.若()1,2A ,则点B 的坐标为 .16.无动力帆船是借助风力前行的.下图是帆船借助风力航行的平面示意图,已知帆船航行方向与风向所在直线的夹角PDA Ð为70°,帆与航行方向的夹角PDQ Ð为30°,风对帆的作用力F 为400N .根据物理知识,F 可以分解为两个力1F 与2F ,其中与帆平行的力1F 不起作用,与帆垂直的力2F 仪可以分解为两个力1f 与21,f f 与航行方向垂直,被舵的阻力抵消;2f 与航行方向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大小,据此,建立数学模型:400F AD ==,则2f CD == .(单位:N )(参考数据:sin400.64,cos400.77°=°=)三、解答题:本题共9小题,共86分。
中考数学---几何选择填空压轴题精选1

中考数学---几何选择填空压轴题精选1一.选择题:1.如下图1,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为()①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HE•HB.A. 1个B. 2个C. 3个D. 4个2、如上图2,梯形ABCD中,AD∥BC,,∠ABC=45°,AE⊥BC于点E,BF⊥AC于点F,交AE于点G,AD=BE,连接DG、CG.以下结论:①△BEG≌△AEC;②∠GAC=∠GCA;③DG=DC;④G为AE中点时,△AGC的面积有最大值.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个3.如上图3,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论:①EC=2DG;②∠GDH=∠GHD;③S△CDG=S▭DHGE;④图中有8个等腰三角形.其中正确的是()A.①③ B.②④ C.①④ D.②③4.如下图1,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交BD于点02,同样以AB,AO2为两邻边作平行四边形ABC2O2.…,依此类推,则平行四边形ABC2009O2009的面积为()A.B. C. D.5、如上图2,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,BN=PC.其中正确的个数是()A.1个 B.2个 C.3个 D.4个6.Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下图1,下列结论:①(BE+CF)=BC;②S△AEF ≤S△ABC;③S四边形AEDF=AD•EF;④AD≥EF;⑤AD与EF可能互相平分,其中正确结论的个数是()A.1个B.2个C.3个D.4个7.如上图2,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连接GF.下列结论①∠ADG=22.5°;②tan∠AED=2;③S△AGD =S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有()A.①④⑤B.①②④C.③④⑤D.②③④8.如上图3,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE 交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤.其中正确的结论是()A.①②③B.①②④C.①②⑤D.②④⑤9.如下图1,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有()A.①②③B.①②④C.①③④D.①②③④10.正方形ABCD、正方形BEFG和正方形RKPF的位置如上图2所示,点G在线段DK上,正方形BEFG 的边长为4,则△DEK的面积为()A. 10B. 12C. 14D. 16二.填空题1.如下图1,观察图中菱形的个数:图1中有1个菱形,图2中有5个菱形,图3中有14个菱形, 图4中有30个菱形…,则第6个图中菱形的个数是 个.2.如下图2,在△ABC 中,∠A=α.∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1; ∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2; …;∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012,得∠A 2012,则∠A 2012= .3.如下图1,已知Rt △ABC 中,AC=3,BC=4,过直角顶点C 作CA 1⊥AB ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去,得到了一组线段CA 1,A 1C 1,C 1A 2,…,则CA 1= ,= .4、如上图2,点A 1,A 2,A 3,A 4,…,A n 在射线OA 上,点B 1,B 2,B 3,…,B n ﹣1在射线OB 上, 且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ﹣1B n ﹣1,A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n ﹣1,△A 1A 2B 1,△A 2A 3B 2,…,△A n ﹣1A n B n ﹣1为阴影三角形,若△A 2B 1B 2,△A 3B 2B 3的面积分别为1、4,则△A 1A 2B 1的面为 ; 面积小于2011的阴影三角形共有 个. 5、如下图1,已知点A 1(a ,1)在直线l :上,以点A 1为圆心,以为半径画弧,交x 轴于点B 1、B 2,过点B 2作A 1B 1的平行线交直线l 于点A 2,在x 轴上取一点B 3,使得A 2B 3=A 2B 2,再过点B 3作A 2B 2的平行线交直线l 于点A 3,在x 轴上取一点B 4,使得A 3B 4=A 3B 3,按此规律继续作下去, 则①a= ;②△A 4B 4B 5的面积是 .6、如下图,在梯形ABCD中,AD∥BC,EA⊥AD,M是AE上一点,F、G分别是AB、CM的中点,且∠BAE=∠MCE,∠MBE=45°,则给出以下五个结论:①AB=CM;②A E⊥BC;③∠BMC=90°;④EF=EG;⑤△BMC是等腰直角三角形.上述结论中始终正确的序号有.7、如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为.8、如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于.9.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD =15cm2,S△BQC=25cm2,则阴影部分的面积为cm2.中考数学---几何选择填空压轴题精选1答案一.选择题:1、解:作EJ⊥BD于J,连接EF①∵BE平分∠DBC ∴EC=EJ,∴△DJE≌△ECF ∴DE=FE∴∠HEF=45°+22.5°=67.5°∴∠HFE==22.5°∴∠EHF=180°﹣67.5°﹣22.5°=90°∵DH=HF,OH是△DBF的中位线∴OH∥BF ∴OH=BF②∵四边形ABCD是正方形,BE是∠DBC的平分线,∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,∵CE=CF,∴Rt△BCE≌Rt△DCF,∴∠EBC=∠CDF=22.5°,∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,∵OH是△DBF的中位线,CD⊥AF,∴OH是CD的垂直平分线,∴DH=CH,∴∠CDF=∠DCH=22.5°,∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故②正确;③∵OH是△BFD的中位线,∴DG=CG=BC,GH=CF,∵CE=CF,∴GH=CF=CE∵CE<CG=BC,∴GH<BC,故此结论不成立;④∵∠DBE=45°,BE是∠DBF的平分线,∴∠DBH=22.5°,由②知∠HBC=∠CDF=22.5°,∴∠DBH=∠CDF,∵∠BHD=∠BHD,∴△DHE∽△BHD,∴=∴DH=HE•HB,故④成立;所以①②④正确.故选C.(第5题图)2、解:根据BE=AE,∠GBE=∠CAE,∠BEG=∠CEA可判定①△BEG≌△AEC;用反证法证明②∠GAC≠∠GCA,假设∠GAC=∠GCA,则有△AGC为等腰三角形,F为AC的中点,又BF⊥AC,可证得AB=BC,与题设不符;由①知△BEG≌△AEC 所以GE=CE 连接ED、四边形ABED为平行四边形,∵∠ABC=45°,AE⊥BC于点E,∴∠GED=∠CED=45°,∴△GED≌△CED,∴DG=DC;④设AG为X,则易求出GE=EC=2﹣X 因此,S△AGC =SAEC﹣SGEC=﹣+x=﹣(x2﹣2x)=﹣(x2﹣2x+1﹣1)=﹣(x﹣1)2+,当X取1时,面积最大,所以AG等于1,所以G是AE中点,故G为AE中点时,GF最长,故此时△AGC的面积有最大值.故正确的个数有3个.故选C.3、解:∵DF=BD,∴∠DFB=∠DBF,∵AD∥BC,DE=BC,∴∠DEC=∠DBC=45°,∴∠DEC=2∠EFB,∴∠EFB=22.5°,∠CGB=∠CBG=22.5°,∴CG=BC=DE,∵DE=DC,∴∠DEG=∠DCE,∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°,∠DGE=180°﹣(∠BGD+∠EGF)=180°﹣(∠BGD+∠BGC),=180°﹣(180°﹣∠DCG)÷2=180°﹣(180°﹣45°)÷2=112.5°,∴∠GHC=∠DGE,∴△CHG≌△EGD,∴∠EDG=∠CGB=∠CBF,∴∠GDH=∠GHD,∴S△CDG =S▭DHGE.故选D.4、解:∵矩形ABCD的对角线互相平分,面积为5,∴平行四边形ABC1O1的面积为,∵平行四边形ABC1O1的对角线互相平分,∴平行四边形ABC2O2的面积为×=,…,依此类推,平行四边形ABC2009O2009的面积为.故选B.5、解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,∴PM=BC,PN=BC,∴PM=PN,正确;②在△ABM与△ACN中,∵∠A=∠A,∠AMB=∠ANC=90°,∴△ABM∽△ACN,∴,正确;③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,∴∠ABM=∠ACN=30°,在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°,∵点P是BC的中点,BM⊥AC,CN⊥AB,∴PM=PN=PB=PC,∴∠BPN=2∠BCN,∠CPM=2∠CBM,∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,∴∠MPN=60°,∴△PMN是等边三角形,正确;(见上图)④当∠ABC=45°时,∵CN⊥AB于点N,∴∠BNC=90°,∠BCN=45°,∴BN=CN,∵P为BC边的中点,∴PN⊥BC,△BPN为等腰直角三角形;∴BN=PB=PC,正确.故选D.6、解:∵Rt△ABC中,AB=AC,点D为BC中点,∴∠C=∠BAD=45°,AD=BD=CD,∵∠MDN=90°,∴∠ADE+∠ADF=∠ADF+∠CDF=90°,∴∠ADE=∠CDF.在△AED与△CFD中,∵,∴△AED≌△CFD(ASA),∴AE=CF,在Rt△ABD中,BE+CF=BE+AE=AB==BD=BC.故①正确;设AB=AC=a,AE=CF=x,则AF=a﹣x.∵S△AEF =AE•AF=x(a﹣x)=﹣(x﹣a)2+a2,∴当x=a时,S△AEF有最大值a2,又∵S△ABC =×a2=a2,∴S△AEF≤S△ABC.故②正确;EF2=AE2+AF2=x2+(a﹣x)2=2(x﹣a)2+a2,∴当x=a时,EF2取得最小值a2,∴EF≥a(等号当且仅当x=a时成立),而AD=a,∴EF≥AD.故④错误;由①的证明知△AED≌△CFD,∴S四边形AEDF =S△AED+S△ADF=S△CFD+S△ADF=S△ADC=AD2,∵EF≥AD,∴AD•EF≥AD2,∴AD•EF>S四边形AEDF故③错误;当E、F分别为AB、AC的中点时,四边形AEDF为正方形,此时AD与EF互相平分.故⑤正确.综上所述,正确的有:①②⑤,共3个.故选C.7、解:∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG=∠ADO=22.5°,故①正确.∵tan∠AED=,由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE<AB,∴tan∠AED=>2,故②错误.∵∠AOB=90°,∴AG=FG>OG,△AGD与△OGD同高,∴S△AGD >S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF=OG,∴BE=EF=×OG=2OG.故⑤正确.∴其中正确结论的序号是:①④⑤.故选:A.8、解:①由∠ABC=90°,△BEC为等边三角形,△ABE为等腰三角形,∠AEB+∠BEC+∠CEH=180°,可求得∠CEH=45°,此结论正确;②由△EGD≌△DFE,EF=GD,再由△HDE为等腰三角形,∠DEH=30°,得出△HGF为等腰三角形,∠HFG=30°,可求得GF∥DE,此结论正确;③由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD此结论不正确;④如图,过点G作GM⊥CD垂足为M,GN⊥BC垂足为N,设GM=x,则GN=x,进一步利用勾股定理求得GD=x,BG=x,得出BG=GD,此结论不正确;⑤由图可知△BCE和△BCG同底不等高,它们的面积比即是两个三角形的高之比,由④可知△BCE的高为(x+x)和△BCG的高为x,因此S△BCE :S△BCG=(x+x):x=,此结论正确;故正确的结论有①②⑤.故选C.9、解:(1)连接FC,延长HF交AD于点L,∵BD为正方形ABCD的对角线,∴∠ADB=∠CDF=45°.∵AD=CD,DF=DF,∴△ADF≌△CDF.∴FC=AF,∠ECF=∠DAF.∵∠ALH+∠LAF=90°,∴∠LHC+∠DAF=90°.∵∠ECF=∠DAF,∴∠FHC=∠FCH,∴FH=FC.∴FH=AF.(上图2)(2)∵FH⊥AE,FH=AF,∴∠HAE=45°.(3)连接AC交BD于点O,可知:BD=2OA,(上图3)∵∠AFO+∠GFH=∠GHF+∠GFH,∴∠AFO=∠GHF.∵AF=HF,∠AOF=∠FGH=90°,∴△AOF≌△FGH.∴OA=GF.∵BD=2OA,∴BD=2FG.(4)延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,根据△MEC≌△CIM,(见下图2)可得:CE=IM,同理,可得:AL=HE,∴HE+HC+EC=AL+LI+IM=AM=8.∴△CEH的周长为8,为定值.故(1)(2)(3)(4)结论都正确.故选D.10、解:如下图1,连DB,GE,FK,则DB∥GE∥FK,在梯形GDBE中,S△DGE =S△GEB(同底等高的两三角形面积相等),同理S△GKE=S△GFE.∴S阴影=S△DGE+S△GKE=S△GEB+S△GEF=S正方形GBEF=4×4=16 故选D.二.填空题:1、解:观察图形,发现规律:图1中有1个菱形,图2中有1+22=5个菱形,图3中有5+32=14个菱形,图4中有14+42=30个菱形,则第5个图中菱形的个数是30+52=55,第6个图中菱形的个数是55+62=91个.故答案为91.2、解:∵∠ABC与∠ACD的平分线交于点A1,∴∠A1BC=∠ABC,∠A1CD=∠ACD,根据三角形的外角性质,∠A+∠ABC=∠ACD,∠A1+∠A1BC=∠A1CD,∴∠A1+∠A1BC=∠A1+∠ABC=(∠A+∠ABC),整理得,∠A1=∠A=,同理可得,∠A2=∠A1=×=,…,∠A2012=.故答案为:.3、解:在Rt△ABC中,AC=3,BC=4,∴AB=,又因为CA1⊥AB,∴AB•CA1=AC•BC,即CA1===.∵C4A5⊥AB,∴△BA5C4∽△BCA,∴,∴==.所以应填和.4、解:由题意得,△A2B1B2∽△A3B2B3,∴==,==,又∵A1B1∥A2B2∥A3B3,∴===,==,∴OA1=A1A2,B1B2=B2B3继而可得出规律:A1A2=A2A3=A3A4…;B1B2=B2B3=B3B4…又△A2B1B2,△A3B2B3的面积分别为1、4,∴S△A1B1A2=,S△A2B2A3=2,继而可推出S△A3B3A4=8,S△A4B4A5=32,S△A5B5A6=128,S△A6B6A7=512,S△A7B7A8=2048,故可得小于2011的阴影三角形的有:△A1B1A2,△A2B2A3,△A3B3A4,△A4B4A5,△A5B5A6,△A6B6A7,共6个.故答案是:;6.5、解:如图所示:①将点A1(a,1)代入直线1中,可得,所以a=.②△A1B1B2的面积为:S==;因为△OA1B1∽△OA2B2,所以2A1B1=A2B2,又因为两线段平行,可知△A1B1B2∽△A2B2B3,所以△A2B2B3的面积为S1=4S;以此类推,△A4B4B5的面积等于64S=.6、解:∵梯形ABCD中,AD∥BC,EA⊥AD,∴AE⊥BC,即②正确.∵∠MBE=45°,∴BE=ME.在△ABE与△CME中,∵∠BAE=∠MCE,∠AEB=∠CEM=90°,BE=ME,∴△ABE≌△CME,∴AB=CM,即①正确.∵∠MCE=∠BAE=90°﹣∠ABE<90°﹣∠MBE=45°,∴∠MCE+∠MBC<90°,∴∠BMC>90°,即③⑤错误.∵∠AEB=∠CEM=90°,F、G分别是AB、CM的中点,∴EF=AB,EG=CM.又∵AB=CM,∴EF=EG,即④正确.故正确的是①②④.7、解:连接DB,∵四边形ABCD是菱形,∴AD=AB.AC⊥DB,∵∠DAB=60°,∴△ADB是等边三角形,∴DB=AD=1,∴BM=,∴AM==,∴AC=,同理可得AC1=AC=()2,AC2=AC1=3=()3,按此规律所作的第n个菱形的边长为()n﹣1故答案为()n﹣1.8、解:∵∠1=∠2,∠3=∠4,∴∠2+∠3=90°,∴∠HEF=90°,(见上图3)同理四边形EFGH的其它内角都是90°,∴四边形EFGH是矩形.∴EH=FG(矩形的对边相等);又∵∠1+∠4=90°,∠4+∠5=90°,∴∠1=∠5(等量代换),同理∠5=∠7=∠8,∴∠1=∠8,∴Rt△AHE≌Rt△CFG,∴AH=CF=FN,又∵HD=HN,∴AD=HF,在Rt△HEF中,EH=3,EF=4,根据勾股定理得HF=,∴HF=5,又∵HE•EF=HF•EM,∴EM=,又∵AE=EM=EB(折叠后A、B都落在M点上),∴AB=2EM=,∴AD:AB=5:=.故答案为:.9、解:如图,连接EF;∵△ADF与△DEF同底等高,∴S△ADF =S△DEF即S△ADF﹣S△DPF=S△DEF﹣S△DPF,即S△APD =S△EPF=15cm2,同理可得S△BQC=S△EFQ=25cm2,∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2.故答案为40.。
2024年江苏省徐州市中考考前数学最后一卷+答案解析

2024年江苏省徐州市中考考前数学最后一卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.“坎宁安数”是以英国数学家坎宁安的名字命名的,能写成形式的数字,2024是一个坎宁安数,因为下列各数中均含有“2024”,其中最小的是()A.2024B.C.D.2.下列图形中,既是轴对称图形又是中心对称图形的是()A. B.C.D.3.在单词数学中字母“a ”出现的频率是()A.B.C.D.4.下列运算正确的是()A. B.C.D.5.以下是小李记录的自己一周内每天校外锻炼的时间单位:分钟,,则下列关于小李该周每天校外锻炼时间的描述,正确的是()A.众数为62分钟B.中位数为62分钟C.平均数为70分钟D.方差为06.分式是刻画数量关系和变化规律的一类重要的代数式,我们学习了分式的概念、基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是()A.归纳思想 B.类比思想C.数学抽象D.数形结合思想7.将二次函数的图象先向上平移3个单位长度,再向右平移2个单位长度后得到的图象的顶点坐标是()A.B.C.D.8.中,,,,将绕点A旋转得到,连接CD、CE,在旋转过程中,面积的最大值是()A. B. C.15 D.18二、填空题:本题共10小题,每小题3分,共30分。
9.因式分解:__________.10.第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数字218000000用科学记数法表示为_____.11.如果,则的值为_____.12.如图,CE,CF是正六边形的两条对角线,则的大小为_______.13.已知关于x的分式方程的解为正数,则m的取值范围是___________.14.如图,在中,,点D为AB边的中点,于E,若,则AC的长为_________.15.如图,点A,B,C,D在上,,,则________.16.黄金分割比是让无数科学家、数学家、艺术家为之着迷的数字.黄金矩形的长宽之比为黄金分割比,即矩形的短边为长边的倍.黄金分割比能够给画面带来美感,令人愉悦,在很多艺术品以及大自然中都能找到它.比如蜗牛壳的螺旋中就隐藏了黄金分割比.如图,用黄金矩形ABCD框住整个蜗牛壳,之后作正方形ABFE,得到黄金矩形CDEF,再作正方形DEGH,得到黄金矩形CFGH……,这样作下去,我们以每个小正方形边长为半径画弧线,然后连接起来,就是黄金螺旋.已知,则阴影部分的面积为_____.17.如图,矩形OABC的顶点A在反比例函数的图象上,顶点B、C在第一象限,对角线轴,交y轴于点若矩形OABC的面积是16,,则__________.18.如图,在矩形ABCD中,点E是边AD上一点,连接BE,过点E作BC的垂线,垂足为F,的角平分线分别交EF,EC于点G,若,,,则GH的长为_______.三、计算题:本大题共2小题,共12分。
江苏省2024年中考数学最后一卷(含解析)

2024年江苏中考最后一卷数学注意事项:1.本试卷共有三个大题,分为单项选择题、填空题、解答题,满分130分,考试时间120分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上,答在试卷上的答案无效。
一、单选题(本大题共8小题,每小题3分,共24分)1.2024的倒数是()A.2024B.C.D.2.若,则的补角的度数是( )A.B.C.D.3.“一片甲骨惊天下”,甲骨文是迄今为止中国发现的年代最早的成熟文字系统,是汉字的头和中华优秀传统文化的根脉.下面四个选项分别是用甲骨文书写的虎、牛、龙、兔,其中是轴对称图形的是()A.B.C.D.4.下列运算正确的是( )A.(a+b)2=a2+b2B.(3a2)3=9a6C.50÷5﹣2=D.=﹣35.分式有意义的条件是()A.B.C.D.6.如图,桌面上有3张卡片,1张正面朝上.任意将其中1张卡片正反面对调一次后,这3张卡片中出现2张正面朝上的概率是()A.1B.C.D.7.如图,正五边形内接于,P为上一点,连接,,则的度数为()A.B.C.D.8.如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B 点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )A.2-2B.4﹣2C.2﹣D.-1二、填空题(本大题共8小题,每小题3分,共24分)9.全球最大的水陆两栖飞机—中航工业AG600大型灭火飞机最大起飞重量53500千克,数据53500用科学记数法表达为.10.若分式方程的解是,则.11.分解因式:.12.正方形的边长为1,其面积记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为,…按此规律继续下去,则的值为 13.根据如图所示的统计图,回答问题:该超市年月的水果类销售额月的水果类销售额(填“”“”或“”).14.将直线平移,使之经过点,则平移后的函数解析式为.15.2022年冬奥会吉祥物“冰墩墩”意喻敦厚,健康,可爱,活泼,某零售店“冰墩墩”的销售日益火爆,销售期间发现,每天的销售利润(元)与售价(元)之间的函数解析式是,且售价的范围是,则销售“冰墩墩”每天的最大利润是.16.如图,中,,,射线从射线开始绕点C逆时针旋转角,与射线相交于点D,将沿射线翻折至处,射线与射线相交于点E.若是等腰三角形,则的度数为.三、解答题(本大题共11小题,共82分)(共82分)17.(本题5分)计算:.18.(本题5分)解不等式组,并写出该不等式组的整数解.19.(本题6分)已知点回答下列问题:(1)点在轴上,求出点的坐标;(2)点在第二象限,且它到轴、轴的距离相等,求的值20.(本题6分)已知,如图,某长方形广场的四角都有一块边长为x米的正方形草地.若长方形的长为a米,宽为b米.(1)请用代数式表示阴影部分的面积;(2)若长方形广场的长为米,宽为米,正方形的边长为米,求阴影部分的面积.21.(本题6分)某气球内充满了一定量的气体,当温度不变时,气球内气体的压强是气体体积的反比例函数,其图像如图所示.(1)求这一函数的表达式;(2)当气体压强为时,求V的值.22.(本题8分)为了考查某校学生的体重,对某班45名学生的体重记录如下(单位:千克):48,48,42,50,61,44,43,51,46,46,51,46,50,45,52,54,51,57,55,48,49,48,53,48,56,55,57,42,54,49,47,60,51,51,44,41,49,53,52,49,61,58,52,54,50(1) 这个问题中的总体、个体、样本、样本容量分别是多少?(2) 请用简单的随机抽样方法,将该班45名学生体重分别选取含有6名学生体重的两个样本和含有15名学生体重的两个样本.23.(本题8分)如图,的对角线,相交于点,过点且与,分别相交于点,.连接,.(1)求证:四边形是平行四边形;(2)若,周长是18,则的周长是多少.24.(本题8分)郑州大观音寺,始建于唐代,辉煌于明清,某校课外兴趣小组为测量大殿高度,进行了一系列测量,如图,地面上C,D两处的距离为,,求大殿的高度.(结果保留整数.参考数据:)25.(本题10分)从图所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.具体定义如下:如图,在四边形中,,,我们把这种两组邻边分别相等的四边形叫做“筝形”.()结合图,通过观察、测量、折纸,可以猜想“筝形”具有诸如“平分和”这样的性质,请结合图形,再写出两条“筝形”的性质.①____________________________.②____________________________.()从你写出的两条性质中,任选一条“筝形”的性质给出证明.26.(本题10分)如图①,已知是的直径,过点A作射线,点P为l上一个动点,点C为上异于点A的一点,且,过点B作的垂线交的延长线于点D,连接.(1)求证:为的切线;(2)若,求的值;(3)如图②,过点C作于点E,交于点F,当点P在运动过程中,试探究是否为定值,如果是,请求出该定值;如果不是,请说明理由.27.(本题10分)如图,在平面直角坐标系中,,点B的坐标为.抛物线经过A、B两点.(1)求抛物线的解析式;(2)点P是直线上方抛物线上的一点,过点P作垂直x轴于点D,交线段于点E,使①求点P的坐标;②在直线上是否存在点M,使为等腰三角形?若存在,求出符合条件的所有点M 的坐标;若不存在,请说明理由.2024年江苏中考最后一卷数学参考答案一、单选题1.C【分析】本题考查了倒数,掌握倒数的定义是解答本题的关键.根据乘积是1的两数互为倒数解答即可.【详解】解:2024的倒数是;故选:C.2.C【分析】本题主要考查了求一个角的补角度数,根据度数之和为180度的两个角互补进行求解即可.【详解】解:∵,∴的补角的度数是,故选:C.3.B【分析】本题考查了轴对称图形:如果一个图形沿着某条直线对折后,直线两旁的部分能够重合,则称这个图形是轴对称图形,这条直线叫做对称轴;根据这个概念判断即可.【详解】解:从四个选项的甲骨文看,只有选项B中的甲骨文能找到一条直线,使直线两旁的部分能够重合,而其余甲骨文则不具备这样的特性;故选:B.4.D【分析】根据实数运算法则化简各式子即可.【详解】解:(A)原式=a2+2ab+b2,故A错误;(B)原式=27a6,故B错误;(C)原式=1÷()2=25,故C错误;(D)原式=2﹣5=﹣3,故D正确;故选D.【点睛】本题考查实数运算和整式运算,熟练掌握运算法则是解题关键.5.D【分析】本题考查的是分式有意义的条件,根据分式有意义的条件可得,从而可得答案.【详解】解:∵分式有意义,∴,∴,故选D6.B【分析】本题考查了简单概率的计算,明确题意,知道只有对调反面朝上的2张卡片才能使3张卡片中出现2张正面朝上,是解答本题的关键.任意将其中1张卡片正反面对调一次,有3种对调方式,其中只有对调反面朝上的2张卡片才能使3张卡片中出现2张正面朝上,据此即可作答.【详解】解:∵任意将其中1张卡片正反面对调一次,有3种对调方式,其中只有对调反面朝上的2张卡片才能使3张卡片中出现2张正面朝上,∴,故选:B.7.B【分析】本题考查的是正多边形和圆,掌握正多边形的中心角的计算公式是解题的关键.【详解】解:连接、,∵是圆内接五边形,∴,∴,故选B.8.A【分析】在BC上截取BE=BD,根据等腰直角三角形的性质求得BA和BE,再由旋转的性质证明△BDP'≌△BEP,从而可得到PE=P'D,再由等腰直角三角形的性质求得PE,从而求得DP′的最小值.【详解】解:如图,在BC上截取BE=BD,∵∠ACB=90°,AC=BC=4,CD⊥AB,∴BA=4,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2=BE,∵旋转∴BP=BP',∠PBP'=45°,∵BE=BD,∠ABC=∠PBP'=45°,BP=BP'∴△BDP'≌△BEP(SAS)∴PE=P'D∴当PE⊥CD时,PE有最小值,即DP'有最小值,∵PE⊥CD,∠BCD=45°,∴CE=PE=BC﹣BE=4﹣2∴P'D =PE=2﹣2故选A.【点睛】本题考查了旋转的性质,等腰直角三角形的性质及全等三角形的判定和性质,熟练掌握其性质并能熟练应用是解题的关键.二、填空题9.【分析】本题考查科学记数法,科学记数法的一般形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.据此求解即可.【详解】解:数据53500用科学记数法表达为,故答案为:.10.【分析】此题考查了分式方程的解,需注意在任何时候都要考虑分母不为0.分式方程去分母转化为整式方程,将1代入整式方程即可求出的值.【详解】解:分式方程去分母得:,由分式方程的解为,代入整式方程得:,解得:,故答案为:.11.【分析】本题考查了提公因式法运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.提公因式分解即可解答.【详解】解:.故答案为:.12.【分析】本题考查图形规律探究,等腰直角三角形、正方形的性质,勾股定理,总结归纳出规律是解题的关键.根据题意表示出,,的值,找到规律,根据规律计算即可.【详解】解:由题意可知,面积为的正方形的边长为1,,面积为的正方形的边长为,,面积为的正方形的边长为,,面积为的正方形的边长为,,.一般规律为:,则.故答案为:.13.【分析】本题主要考查条形统计图与折线图的综合运用,掌握统计图的信息的关系是解题的关键,根据销售总额与占比计算出相应的量进行比较即可求解.【详解】解:某超市月的销售总额为万元,水果类销售额占比为,∴某超市月水果类的销售额为:万元;某超市月销售总额为万元,水果类销售额占比为,∴某超市月水果类的销售额为:万元;∵,故答案为:.14.【分析】本题考查了一次函数的平移,待定系数法求函数解析式,先设平移后的函数解析式为,再将代入函数解析式,求解即可.【详解】设平移后的函数解析式为,把代入函数解析式,得,解得,∴平移后的函数解析式为,故答案为:.15.900元【分析】本题考查二次函数的实际应用.熟练掌握二次函数的图象和性质是解题关键.将二次函数一般式改为顶点式.再结合题意可知当时,y有最大值,求出最大值即可.【详解】解:∵,且,又∵售价x的范围是,∴当时,y有最大值,最大值为900,∴最大利润是900元.故答案为:900元.16.或或【分析】分情况讨论,利用折叠的性质知,,再画出图形,利用三角形的外角性质列式计算即可求解.【详解】解:由折叠的性质知,,当时,,由三角形的外角性质得,即,此情况不存在;当时,,,由三角形的外角性质得,解得;当时,,∴,由三角形的外角性质得,解得;当时,,∴,∴;综上,的度数为或或.故答案为:或或.【点睛】本题考查了折叠的性质,三角形的外角性质,等腰三角形的性质,画出图形,数形结合是解题的关键.三、解答题17.【分析】本题考查了立方根,算术平方根以及实数的混合运算,根据相应的运算法则计算即可.【详解】.18.整数解有【分析】本题考查了解一元一次不等式组,先分别解几个不等式,然后把它们的解集的公共部分作为原不等式的解集;按照“同大取大,同小取小,大于小的小于大的取中间,大于小的小于大的为空集”,是解题的关键;分别解出两不等式的解集,再根据大于小的小于大的取中间得到不等式组的解集即可求解.【详解】解:解不等式得解不等式得,则不等式组的解集为:,不等式组的整数解有:19.(1)(2)【分析】本题主要考查平面直角坐标系内点的坐标特点以及绝对值;(1)根据轴上点的特点作答即可;(2)根据点到轴和轴相等列出,再结合第二象限点的特点求出,代入即可.【详解】(1)在轴上解得:(2)点到轴和轴距离相等在第二象限解得:20.(1)(2)平方米【分析】本题考查列代数式及代数式求值.(1)阴影部分的面积=长方形广场面积正方形草地,据此即可列出代数式;(2)将,,代入即可求解.【详解】(1)解:阴影部分的面积(2)解:当,,时,代入(1)得到的式子,得(平方米).答:阴影部分的面积为59600平方米21.(1)(2)2【分析】(1)根据题意可知P与V的函数的表达式为,利用待定系数法即可求得函数解析式;(2)直接把代入解析式计算即可.【详解】(1)解:设P与V的函数关系式为,则,解得,∴函数关系式为.(2)解:将代入中,得,解得,∴当气球内的气压为时,气球的体积为2立方米.【点睛】本题考查了反比例函数的应用,掌握反比例函数的图像及性质是解题的关键.22.(1) 总体是学生体重的全体,个体是每个学生的体重,样本是45名学生的体重,样本容量是45.(2)见解析.【分析】(1) 根据总体、个体、样本、样本容量的定义可以得出,这个问题的总体是某校学生体重的全体,个体是每个学生的体重,样本是45名学生的体重,样本容量是45.(2) 样本的抽取要有代表性.就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.【详解】(1)这个问题的总体是某校学生体重的全体,个体是每个学生的体重,样本是45名学生的体重,样本容量是45.(2)将本班45名学生的体重依次编号,从中抽取6名学生的体重,像这样连续做两遍,选出的两个样本为:①48,42,50,61,53,48和49,53,42,54,49,50;将本班45名学生的体重,依次编号从中抽取15名学生的体重,像这样连续做两遍,选出的两个样本为:①42,50,61,48,53,54,56,55,60,44,49,53,52,61,57;②48,50,44,43,45,54,51,49,48,53,51,47,60,54,50.【点睛】要根据体、个体、样本、样本容量的定义来确定第一小题的答案;第二小题要注意本的抽取要有代表性.23.(1)详见解析(2)36【分析】本题主要考查了平行四边形的性质与判定,菱形的性质与判定,全等三角形的性质与判定:(1)先由平行四边形的性质得到,,再由平行线的性质得到,,进而证明,得到,据此可证明结论;(2)证明四边形是菱形,得到,进而得到,则的周长是36.【详解】(1)证明:在中,,,,又,,,又,四边形是平行四边形(2)解;四边形是平行四边形,四边形是菱形,,,即,即,,即的周长是36.24.大殿的高度为【分析】本题主要考查了解直角三角形的相关计算,设,根据题意可知,,以为等量关系列出关系x的一元一次方程求解,最后再根据求出即可.【详解】解:设,∵,即,又∵,∴,即,解得:,∴.答:大殿的高度为.25.()①.②,.()见解析【分析】(1)①一组对角相等,∠ABC=∠ADC;②AC垂直平分BD,OB=OD,BD⊥AC;(2)证明∠ABC=∠ADC,由已知条件不难证明△ABC≌△ADC,即可证明∠ABC=∠ADC.【详解】解:(1)①一组对角相等,∠ABC=∠ADC;②AC垂直平分BD,OB=OD,BD⊥AC.(2)证明:∠ABC=∠ADC,证:在△ABC和△ADC中,,∴△ABC≌△ADC(SSS),∴∠ABC=∠ADC.【点睛】本题考查四边形综合.关键结合全等三角形的判定与性质解题.26.(1)见解析(2);(3).【分析】(1)连接,证明,求得,据此即可证明为的切线;(2)过点作,设,求得,,利用勾股定理求得,再求得,据此求解即可;(3)连接并延长交的延长线于点,利用切线长定理求得,,由,得到,,利用相似三角形的性质即可求得.【详解】(1)证明:连接,∵是的直径,过点A作射线,∴,∵,,,∴,∴,即,∵是的半径,∴为的切线;(2)解:过点作,垂足为点,设,∴,∵,∴为的切线,∵、、为的切线,∴,,∴,∵射线,,,∴,∴四边形是矩形,∴,,∴,在中,,∴,在中,,∴;(3)解:,理由如下,连接并延长交的延长线于点,∵,∴,∵,,∴,∴,∵,∴,∴,∵,∴,∴,∵,,∴,∴,,∴,,∴,∴.【点睛】本题考查了切线长定理,切线的判定和性质,相似三角形的判定和性质,勾股定理,解直角三角形,正确引出辅助线解决问题是解题的关键.27.(1)(2)①;②存在,点M的坐标为:或或或或【分析】(1)根据条件求出,,根据待定系数法求解即可;(2)先求出的解析式,然后表示出,,根据即可求解;分情况讨论,分别求出,根据等腰三角形的定义求解即可.【详解】(1)解:∵,∴,∵,∴,在中,,∴,∴,把代入.得:解得:∴抛物线的解析式为:(2)①设的解析式为:,∵,,所以解得,所以的解析式为:,设,则,∵∴解得:(舍)或,∴;②∵M在直线上,且,设,∴分三种情况:i)当时,∴解得:∴ii)当时,∴解得:或iii )当时,∴解得:或∴或综上,点M的坐标为:或或或或【点睛】此题是二次函数的综合题,考查了待定系数法求二次函数的解析式,勾股定理的运用,等腰三角形的性质等知识.此题难度适中,解题的关键是注意方程思想与分类讨论思想的应用.。
江苏省无锡地区中考数学选择填空压轴题专题1代数式的求值问题(含答案)62

专题06四边形的综合问题例1.如图,△APB中,AB=22,∠APB=90°,在AB的同侧作正△ABD、正△APE和△BPC,那么四边形PCDE面积的最大值是__________.同类题型:如图,△APB中,AP=4,BP=3,在AB的同侧作正△ABD、正△APE和正△BPC,那么四边形PCDE面积的最大值是___________.同类题型:如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延伸CB交AE于点G,点G在点A、E之间,连结CE、CF,EF,那么以下四个结论必定正确的选项是〔〕①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE.A.只有①② B.只有①②③C.只有③④ D.①②③④同类题型:如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延伸线上一点,以下结论:①BE均分∠CBF;②CF均分∠DCB;③BC=FB;④PF =PC.此中正确的有______________.〔填序号〕同类题型:如图,在□ABCD中,∠DAB的均分线交CD于点E,交BC的延伸线于点G,∠ABC的均分线交CD于点F,交AD的延伸线于点H,AG与BH交于点O,连结BE,以下结论错误的选项是〔〕A.BO=OH B.DF=CE C.DH=CG D.AB=AE例2.图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成〔不重叠、无空隙〕.图乙中AB6=,EF=4cm,上下两个暗影三角形BC72,其内部菱形由两组距离相等的平行线交错获得,那么该菱的面积之和为54cm形的周长为____________.同类题型:如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速挪动〔到点B为止〕,点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,那么t的值为____________.同类题型:如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折获得△A′MN,连结A′C,那么A′C长度的最小值是____________.同类题型:如图,在菱形ABCD中,边长为10,∠A=60°.按序连结菱形ABCD各边中点,可得四边形A1B1C1D1;按序连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;按序连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律持续下去,那么四边形A2021B2021C2021D2021的周长是______________.例3.如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连结CF〔AD>AE〕,以下结论:①∠AEF=∠BCE;②S△CEF=S△EAF+S△CBE;③AF+BC>CF;④假定BC3=,那么△CEF≌△CDF.此中正确的结论是CD2____________.〔填写全部正确结论的序号〕同类题型:如图,在矩形ABCD中,AD=2AB,∠BAD的均分线交BC于点E,DH⊥AE于点H,连结BH并延伸交CD于点F,连结DE交BF于点O,以下结论:①AED=∠CED;②AB=HF,③BH=HF;④BC-CF=2HE;⑤OE=OD;此中正确结论的序号是____________.同类题型:如图,在矩形ABCD中,BC=2AB,∠ADC的均分线交边BC于点E,AH⊥DE于点H,连结CH并延伸交AB边于点F,连结AE交CF于点O,给出以下命题:1AD=DE②DH=22EH③△AEH∽△CFB④HO=2AE此中正确命题的序号是________________〔填上全部正确命题的序号〕同类题型:如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,那么tan∠BDE的值是〔〕2112A.4B.4C.3D.3例4.:如图,在正方形ABCD外取一点E,连结AE,BE,DE.过点A作AE的垂线AP交DE于点P.假定AE=AP=1,PB=6,以下结论:①△APD≌△AEB;②点B到直线AE的距离为2;③EB⊥ED;④S△APD+S△APB=1+6.⑤S正方形ABCD=4+6.此中正确结论的序号是___________________.同类题型:如图,正方形ABCD的边长为2,将长为2的线段QR的两头放在正方形的相邻的两边上同时滑动.假如点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止.点N是正方形ABCD内任一点,把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,那么P=〔〕4-ππ1π-1A.4B.4C.4D.4同类题型:如图,边长为2的正方形ABCD中,AE均分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连结AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=12AF;⑤EG=FG﹒DG,此中2正确结论的个数为〔〕A.2B.3C.4D.5同类题型:如图,边长为1的正方形ABCD的对角线AC、BD订交于点O.有直角∠MPN,使直角极点P与点O重合,直角边PM、PN分别与OA、OB重合,而后逆时针旋转∠MPN,旋转角为θ〔0°<θ<90°〕,PM、PN分别交AB、BC于E、F两点,连结EF交OB于点G,那么以下结论中正确的选项是______________.〔1〕EF=2OE;〔2〕S四边形OEBF:S正方形ABCD=1:4;〔3〕BE+BF=2 OA;〔4〕在旋转过程中,当△BEF与△COF的面积之和最大时,AE=3224;〔5〕OG﹒BD=AE+CF.同类题型:如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连结EF,设EF的中点为G,那么当点P从点C运动到点D时,点G挪动的路径长为_____________.参照答案例1.如图,△APB中,AB=22,∠APB=90°,在AB的同侧作正△ABD、正△APE和△BPC,那么四边形PCDE面积的最大值是__________.解:如图,延伸EP交BC于点F,∵∠APB=90°,∠APE=∠BPC=60°,∴∠EPC=150°,∴∠CPF=180°-150°=30°,PF均分∠BPC,又∵PB=PC,PF⊥BC,设Rt△ABP中,AP=a,BP=b,那么CF=1CP=1b,a2+b2=8,∴22∴∵△APE和△ABD都是等边三角形,AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,12 ∴△EAD ≌△PAB 〔SAS 〕,3 ED =PB =CP ,4 同理可得:△APB ≌△DCB 〔SAS 〕,5 EP =AP =CD ,6 ∴四边形CDEP 是平行四边形,1∴四边形CDEP 的面积=EP ×CF =a ×2b =2ab , 又∵〔a -b 〕2=a 2-2ab +b 2≥0, 2ab ≤a 2+b 2=8,1 2ab ≤2,即四边形PCDE 面积的最大值为2.同类题型:如图,△APB 中,AP =4,BP =3,在AB 的同侧作正△ABD 、正△APE 和正△BPC ,那么四边形PCDE 面积的最大值是___________.解:∵△APE 和△ABD 是等边三角形,AE =AP =4,AB =AD ,∠EAP =∠DAB =60°,∴∠EAD =∠PAB =60°-∠DAP , 在△EAD 和△PAB 中 AE =AP∠EAD =∠PAB AD =AB∴△EAD ≌△PAB 〔SAS 〕, DE =BP ,同理△DBC ≌△ABP ,DC=AP,∵△APE和△BPC是等边三角形,EP=AP,BP=CP,DE=CP=3,DC=PE=4,∴四边形PCDE是平行四边形,当CP⊥EP时,四边形PCDE的面积最大,最大面积是3×4=12.同类题型:如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延伸CB交AE于点G,点G在点A、E之间,连结CE、CF,EF,那么以下四个结论必定正确的选项是〔〕①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE.A.只有①②B.只有①②③ C.只有③④D.①②③④解:∵△ABE、△ADF是等边三角形FD=AD,BE=ABAD=BC,AB=DCFD=BC,BE=DC∵∠B=∠D,∠FDA=∠ABE∴∠CDF=∠EBC∴△CDF≌△EBC,故①正确;∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+〔180°-∠CDA〕=300°-∠CDA,FDC=360°-∠FDA-∠ADC=300°-∠CDA,∴∠CDF=∠EAF,故②正确;同理可得:∠CBE=∠EAF=∠CDF,∵BC=AD=AF,BE=AE,∴△EAF≌△EBC,∴∠AEF=∠BEC,∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,∴∠FEC=60°,∵CF=CE,∴△ECF是等边三角形,故③正确;在等边三角形ABE中,∵等边三角形顶角均分线、底边上的中线、高和垂直均分线是同一条线段∴假如CG⊥AE,那么G是AE的中点,∠ABG=30°,∠ABC=150°,题目缺乏这个条件,CG⊥AE不可以求证,故④错误.选B.同类题型:如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延伸线上一点,以下结论:①BE均分∠CBF;②CF均分∠DCB;③BC=FB;④PF=P C.此中正确的有______________.〔填序号〕解:证明:∵BC=EC,∴∠CEB=∠CBE,∵四边形ABCD是平行四边形,DC∥AB,∴∠CEB=∠EBF,∴∠CBE=∠EBF,∴①BE均分∠CBF,正确;BC=EC,CF⊥BE,∴∠ECF=∠BCF,∴②CF均分∠DCB,正确;DC∥AB,∴∠DCF=∠CFB,∵∠ECF=∠BCF,∴∠CFB=∠BCF,BF=BC,∴③正确;∵FB=BC,CF⊥BE,B点必定在FC的垂直均分线上,即PB垂直均分FC,PF=PC,故④正确.答案为①②③④.同类题型:如图,在□ABCD中,∠DAB的均分线交CD于点E,交BC的延伸线于点G,∠ABC的均分线交CD于点F,交AD的延伸线于点H,AG与BH交于点O,连结BE,以下结论错误的选项是〔〕A.BO=OH B.DF=CE C.DH=CG D.AB=AE∴解:∵四边形ABCD是平行四边形,∴∴∴∴∴∴∴∴∴∴∴AH∥BG,AD=BC,∴∴∠H=∠HBG,∴∵∠HBG=∠HBA,∴∴∠H=∠HBA,∴AH=AB,同理可证BG=AB,∴AH=BG,∵AD=BC,∴DH=CG,故C正确,∴AH=AB,∠OAH=∠OAB,∴∴OH=OB,故A正确,∴DF∥AB,∴∴∠DFH=∠ABH,∴∵∠H=∠ABH,∴∴∠H=∠DFH,∴DF=DH,同理可证EC=CG,∵DH=CG,DF=CE,故B正确,没法证明AE=AB,选D .例2.图甲是小明设计的带菱形图案的花边作品. 该作品由形如图乙的矩形图案拼接而成〔不重叠、无空隙〕.图乙中AB6 =,EF =4cm ,上下两个暗影三角形BC72 ,其内部菱形由两组距离相等的平行线交错获得,那么该菱的面积之和为54cm形的周长为____________.解:如图乙,H 是CF 与DN 的交点,取CD 的中点G ,连结HG ,,设AB =6a cm ,那么BC =7a cm ,中间菱形的对角线HI 的长度为x cm , ∵BC =7a cm ,MN =EF =4cm ,∴CN = 7a +4,2GH ∥BC , GHDG∴ =,2 CNDC 37a -x 4 17a +4=2,2∴x =a -2〔1〕;∵上下两个暗影三角形的面积之和为 2,54cm∴6a ﹒〔7a -x 〕÷2=54,∴a〔7a-x〕=18〔2〕;由〔1〕〔2〕,可得a=2,x=5,∴CD=6×2=12〔cm〕,CN=7a+47×2+4,2=2=9(cm)DN=122+92=15〔cm〕,又∵DH=2227×2-52=〔cm〕,DG+GH=6+()2HN=15-=〔cm〕,∵AM∥FC,KNMN44∴===,HKCM9-4552525HK=4+5×=6(cm),2650∴该菱形的周长为:6×4=3〔cm〕.同类题型:如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速挪动〔到点B为止〕,点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,那么t的值为____________.解:延伸AB至M,使BM=AE,连结FM,∵四边形ABCD是菱形,∠ADC=120°AB=AD,∠A=60°,∵BM=AE,AD=ME,∵△DEF为等边三角形,∴∠DAE=∠DFE=60°,DE=EF=FD,∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°-∠A=120°,∴∠MEF=∠ADE,∴在△DAE和△EMF中,AD=ME∠MEF=∠ADEDE=EF∴△DAE≌EMF〔SAS〕,AE=MF,∠M=∠A=60°,又∵BM=AE,∴△BMF是等边三角形,BF=AE,AE=t,CF=2t,BC=CF+BF=2t+t=3t,∵BC=4,3t=4,4∴t=3.同类题型:如图,在边长为2的菱形ABCD 中,∠A =60°,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折获得△A ′MN ,连结A ′C ,那么A ′C 长度的最小值是____________.解:以下列图:∵MA ′是定值,A ′C 长度取最小值时,即 A ′在MC 上时,1 过点M 作MF ⊥DC 于点F ,2 ∵在边长为2的菱形ABCD 中,∠A =60°,M 为AD 中点, 32MD =AD =CD =2,∠FDM =60°,∴∠FMD =30°, 1FD =2MD =2, 32FM =DM ×cos30°=2, 3 2MC =FM +CF =7,A ′C =MC -MA ′=7-1.同类题型: 如图,在菱形ABCD 中,边长为10,∠A =60°.按序连结菱形ABCD 各边中点,可得四边形A 1B 1C 1D 1;按序连结四边形A 1B 1C 1D 1各边中点,可得四边形ABCD ;按序连结四边形ABCD 各边中点,可得四边形 2 2222222A 3B 3C 3D 3;按此规律持续下去,那么四边形A 2021B 2021C 2021D2021的周长是______________.解:∵菱形ABCD中,边长为10,∠A=60°,按序连结菱形ABCD各边中点,∴△AAD是等边三角形,四边形ABCD是菱形,1122221A1D1=5,C1D1=2AC=53,A2B2=C2D2=C2B2=A2D2=5,111同理可得出:A3D3=5×2,C3D3=2C1D1=2×53,111A5D5=5×〔2〕2,C5D5=2C3D3=〔2〕2×53,5+53.∴四边形A2021B2021C2021D2021的周长是:21007例3.如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连结CF〔AD>AE〕,以下结论:①∠AEF=∠BCE;②S△=S△+S△;③CEF EAF CBEAF+BC>CF;④假定BC3=,那么△CEF≌△CDF.此中正确的结论是CD2____________.〔填写全部正确结论的序号〕解:延伸CB,FE交于点G,∵∠AEF+∠BEC=90°,∠BEC+∠BCE=90°,∴∠AEF=∠BCE,①正确;在△AEF和△BEG中,∠FAE=∠GBE=90°AE=BE,∠AEF=∠BEG∴△AEF≌△BEG〔ASA〕,AF=BG,EF=EG,∵CE⊥EG,S△CEG=S△CEF,CG=CF,S△CEF=S△EAF+S△CBE,②正确;AF+BC=BG+BC=CG=CF,③错误;BC3∵=,CD2∴∠BCE=30°,∴∠FCE=∠FCD=30°,在△CEF和△CDF中,∠D=∠FEC=90°∠DCF=∠ECF,CF=CF∴△CEF≌△CDF〔AAS〕,④正确.同类题型:如图,在矩形ABCD中,AD=2AB,∠BAD的均分线交BC于点E,DH⊥AE于点H,连结BH并延伸交CD于点F,连结DE交BF于点O,以下结论:①AED=∠CED;②AB=HF,③BH=HF;④BC-CF=2HE;⑤OE=OD;此中正确结论的序号是____________.解:∵在矩形ABCD中,AE均分∠BAD,∴∠BAE=∠DAE=45°,∴△ABE是等腰直角三角形,AE=2AB,AD=2AB,∴AE=AD,BAE=∠DAE在△ABE和△AHD中,∠ABE=∠AHD=90°,AE=AD∴△ABE≌△AHD〔AAS〕,BE=DH,AB=BE=AH=HD,1∴∠ADE=∠AED=2〔180°-45°〕=°,∴∠CED=180°-45°-°=°,∴∠AED=∠CED,故①正确;1∴∵∠AHB=〔180°-45°〕=°,∠OHE=∠AHB〔对顶角相等〕,2∴∴∠OHE=∠AED,∴OE=OH,∴∵∠DOH=90°-°=°,∠ODH=°-45°=°,∴∴∠DOH=∠ODH,∴OH=OD,OE=OD=OH,故⑤正确;∵∠EBH=90°-°=°,∴∠EBH=∠OHD,又∵BE=DH,∠AEB=∠HDF=45°∠EBH=∠OHD在△BEH和△HDF中BE=DH∠AEB=∠HDF∴△BEH≌△HDF〔ASA〕,∴BH=HF,HE=DF,故③正确;由上述①、②、③可得CD=BE、DF=EH=CE,CF=CD-DF,BC-CF=〔CD+HE〕-〔CD-HE〕=2HE,因此④正确;∵AB=AH,∠BAE=45°,∴△ABH不是等边三角形,AB≠BH,∴即AB≠HF,故②错误;综上所述,结论正确的选项是①③④⑤.同类题型:如图,在矩形ABCD中,BC=2AB,∠ADC的均分线交边BC于点E,AH⊥DE于点H,连结CH并延伸交AB边于点F,连结AE交CF于点O,给出以下命题:1AD=DE②DH=22EH③△AEH∽△CFB④HO=2AE此中正确命题的序号是________________〔填上全部正确命题的序号〕∵解:在矩形ABCD中,AD=BC=2AB=2CD,∵D E均分∠ADC,∴∠ADE=∠CDE=45°,AD⊥DE,∴△ADH是等腰直角三角形,AD=2AB,AH=AB=CD,∵△DEC是等腰直角三角形,DE=2CD,AD=DE,∴∠AED=°,∴∠AEB=180°-45°-°=°,∴∠AED=∠AEB,AD∥BC,∴∠DAE=∠AEB,∴∠DAE=∠AED,AD=DE,故①正确;设DH=1,那么AH=DH=1,AD=DE=2,HE=2,22HE=22≠1,故②错误;∵∠AEH=°,∴∠EAH=°,∵DH=CD,∠EDC=45°,∴∠DHC=°,∴∠OHA=°,∴∠OAH=∠OHA,OA=OH,∴∠AEH=∠OHE=°,OH=OE,1OH=2AE,故④正确;∵AH=DH,CD=CE,在△AFH与△CHE中,∠AHF=∠HCE=°∠FAH=∠HEC=45°,AH=CE∴△AFH≌△CHE,∴∠AHF=∠HCE,AO=OH,∴∠HAO=∠AHO,∴∠HAO=∠BCF,∵∠B=∠AHE=90°,∴△AEH∽△CFB,故③正确.答案为:①③④.同类题型:如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,那么tan∠BDE的值是〔〕2112A.4B.4C.3D.3∴解:∵四边形ABCD是矩形,∴A D=BC,AD∥BC,12∵点E是边BC的中点,3 1BE=2BC=2AD,∴△BEF∽△DAF,EF BE1∴==,AF AD21EF=2AF,1EF=3AE,∵点E是边BC的中点,∴由矩形的对称性得:AE=DE,12EF=3DE,设EF=x,那么DE=3x,3 2DF=DE-EF=22x,EF x2∴tan∠BDE===;DF22x4选A.例4.:如图,在正方形ABCD外取一点E,连结AE,BE,DE.过点A作AE 的垂线AP交DE于点P.假定AE=AP=1,PB=6,以下结论:①△APD≌△AEB;②点B到直线AE的距离为2;③EB⊥ED;④S+S=1+6.⑤S=4+6.△APD△APB正方形ABCD此中正确结论的序号是___________________.解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=∠PAD,又∵AE=AP,AB=AD,∵在△APD和△AEB中,AE=AP∠EAB=∠PAD,AB=AD∴△APD≌△AEB〔SAS〕;故此选项建立;③∵△APD≌△AEB,∴∠APD=∠AEB,∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,∴∠BEP=∠PAE=90°,EB⊥ED;故此选项建立;②过B作BF⊥AE,交AE的延伸线于F,∵AE=AP,∠EAP=90°,∴∠AEP=∠APE=45°,又∵③中EB⊥ED,BF⊥AF,∴∠FEB=∠FBE=45°,22又∵BE=BP-PE=2,BF=EF=2,故此选项正确;④如图,连结BD,在Rt△AEP中,AE=AP=1,∴EP=2,又∵PB=6,BE=2,∵△APD≌△AEB,PD=BE=2,111 S△ABP+S△ADP=S△ABD-S△BDP=2S正方形ABCD-2×DP×BE=2×〔4+166〕-2×2×2=2.故此选项不正确.⑤∵EF=BF=2,AE=1,2222,∴在Rt△ABF中,AB=〔AE+EF〕+BF=5+2∴S22,=AB=5+2正方形ABCD故此选项不正确.答案为:①②③.同类题型:如图,正方形ABCD的边长为2,将长为2的线段QR的两头放在正方形的相邻的两边上同时滑动.假如点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止.点N是正方形ABCD内任一点,把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,那么P=〔〕4-ππ1π-1A.4B.4C.4D.4解:依据题意得点M到正方形各极点的距离都为1,点M所走的运动轨迹为以正方形各极点为圆心,以1为半径的四个扇形,∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积.290π×1而正方形ABCD的面积为2×2=4,4个扇形的面积为4×360=π,∴点M所经过的路线围成的图形的面积为4-π,∴把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,那么P=4-π.4选:A.同类题型:如图,边长为2的正方形ABCD中,AE均分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连结AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=12AF;⑤EG=FG﹒DG,此中2正确结论的个数为〔〕A.2B.3C.4D.5解:①②如图1,∵四边形ABCD是正方形,AB=AD,∠B=∠D=90°,∠BAD=90°,∵AE均分∠DAC,∴∠FAD=∠CAF=°,∵BH=DF,∴△ABH≌△ADF,AH=AF,∠BAH=∠FAD=°,∴∠HAC=∠FAC,HM=FM,AC⊥FH,∵AE均分∠DAC,DF=FM,FH=2DF=2BH,应选项①②正确;③在Rt△FMC中,∠FCM=45°,∴△FMC是等腰直角三角形,∵正方形的边长为2,AC=22,MC=DF=22-2,FC=2-DF=2-〔22-2〕=4-22,1S△AFC=2CF﹒AD≠1,因此选项③不正确;222+(224-22,④AF=AD+DF=22-2)=2∵△ADF∽△CEF,ADAF∴=,CEFC224-22∴=4-2,CE2∴CE=4-22,1CE=2AF,应选项④正确;⑤延伸CE和AD交于N,如图2,AE⊥CE,AE均分∠CAD,∴CE=EN,EG∥DN,CG=DG,在Rt△FEC中,EG⊥FC,2∴EG2∴EG FG﹒CG,FG﹒DG,应选项⑤正确;本题正确的结论有4个,应选C.同类题型:如图,边长为1的正方形ABCD的对角线AC、BD订交于点O.有直角∠MPN,使直角极点P与点O重合,直角边PM、PN分别与OA、OB重合,而后逆时针旋转∠MPN,旋转角为θ〔0°<θ<90°〕,PM、PN分别交AB、BC于E、F两点,连结EF交OB于点G,那么以下结论中正确的选项是______________.〔1〕EF=2OE;〔2〕S四边形OEBF:S正方形ABCD=1:4;〔3〕BE+BF=2 OA;〔4〕在旋转过程中,当△BEF与△COF的面积之和最大时,322AE=4;〔5〕OG﹒BD=AE+CF.解:〔1〕∵四边形ABCD是正方形,OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,∴∠BOF+∠COF=90°,∵∠EOF=90°,∴∠BOF+∠COE=90°,∴∠BOE=∠COF,在△BOE和△COF中,∠BOE=∠COFOB=OC,∠OBE=∠OCF∴△BOE≌△COF〔ASA〕,OE=OF,BE=CF,EF=2OE;故正确;〔2〕∵1∴S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=4S正方形ABCD,S四边形OEBF:S正方形ABCD=1:4;故正确;〔3〕∴BE+BF=BF+CF=BC=2OA;故正确;124〕过点O作OH⊥BC,∵BC=1,3 1OH=2BC=2,设AE=x,那么BE=CF=1-x,BF=x,∴错误!,1∵a=-2<0,1∴当x=4时,S△BEF+S△COF最大;1即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=4;故错误;5〕∵∠EOG=∠BOE,∠OEG=∠OBE=45°,∴△OEG∽△OBE,∴OE:OB=OG:OE,2∴OG﹒OB=OE,12OB=2BD,OE=2EF,2∴OG﹒BD=EF,222∵在△BEF中,EF=BE+BF,2=2+2,∴2EFAECF3 2OG﹒BD=AE+CF.故正确.故答案为:〔1〕,〔2〕,〔3〕,〔5〕.同类题型:如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连结EF,设EF的中点为G,那么当点P从点C运动到点D时,点G挪动的路径长为_____________.解:如图,设KH的中点为S,连结PE,PF,SE,SF,PS,∵E为MN的中点,S 为KH的中点,∴A,E,S共线,F为QR的中点,S为KH的中点,∴B、F、S共线,由△AME∽△PQF,得∠SAP=∠FPB,ES∥PF,PNE∽△BRF,得∠EPA=∠FBP,∴PE∥FS,那么四边形PESF为平行四边形,那么G为PS的中点,∴G 的轨迹为△CSD的中位线,∵CD=AB-AC-BD=6-1-1=4,1∴点G挪动的路径长2×4=2.。
2024年浙江中考数学最后一卷终极押题卷及答案

2024年浙江中考最后一卷数学注意事项:1.本试卷共有三个大题,分为单项选择题、填空题、解答题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上,答在试卷上的答案无效。
一、单选题(本大题共有10小题,每小题3分,共30分)1.下列各数中最大的数是()A.5−B.0 C.1−D2.下面计算正确的是()A.3a﹣2a=1 B.2a2+4a2=6a4C.(x3)2=x5D.x8÷x2=x63.今年春节电影《热辣滚烫》《飞驰人生2》《熊出没•逆转时空》《第二十条》在网络上持续引发热议,根据国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录.其中数据80.16亿用科学记数法表示为()A.8×80.16108.01610×B.9C.10×80.1610×D.100.8016104.下列立体图形中,主视图是三角形的是()A.B.C.D.5.在数轴上表示不等式x﹣2≤0的解集,正确的是()A.B.C .D .6.随着自动驾驶技术的不断发展,某知名汽车制造公司近期对研发的自动驾驶汽车进行了一次大规模的路测,有45辆自动驾驶汽车参与了这次测试.测试结束后,技术部门对每辆汽车的性能进行评估(车辆的自动驾驶技术、安全性、反应速度等综合表现),得分如下:得分(分) 75 80 85 90车辆(辆) 5 16 14 10得分的中位数和众数分别是( )A .80,80B .82.5,80C .80,85D .85,807.如图,线段CD 是O 的直径,CD AB ⊥于点E ,若8AB =,3OE =,则CE 的长是( )A .8B .7C .6D .58.《九章算术》中曾记载:“今有牛五羊二,直金十两;牛二羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?若设每头牛值金x 两,每只羊值金y 两,则可列方程组为( )A .5210258x y x y += +=B .2510528x y x y += +=C .51058x y x y += +=D .21028x y x y += +=9.二次函数2y =的图象如图所示,点O 为坐标原点,点A 在y 轴的正半轴上,点B ,C 在函数图象上,四边形OBAC 为菱形,且120ABO ∠=°,则点C 的坐标为( )A .14 −B .14 −C . −D .(− 10.如图,四边形ABCD 是一张矩形纸片.折叠该矩形纸片,使AB 边落在AD 边上,点B 的对应点为点F ,折痕为AE ,展平后连接EF ;继续折叠该纸片,使FD 落在FE 上,点D 的对应点为点H ,折痕为FG ,展平后连接HG .若矩形HECG ∽矩形ABCD ,1AD =,则CD 的长为( ).A .0.5B 1−C D二、填空题(本大题共有6小题,每小题4分,共24分)11.因式分解: 34t t −=12.实现中国梦,必须弘扬中国精神.在如图所示除正面图案不同外,其余无差别的四张不透明卡片上分别写有“红船精神”、“长征精神”、“延安精神”、“特区精神”,将卡片置于暗箱摇匀后随机抽取一张,则所抽取卡片为“特区精神”的概率为 .13x 的值可以是 .(写出一个即可) 14.如图,《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕塑,掷铁饼者张开的双臂与肩宽可以近似看像一张拉满弦的弓,若弧长为2π3米,“弓”所在圆的半径1.2米,则“弓”所对的圆心角θ的度数为 .15.如图,点A 为反比例函数(0,0)k y k x x=<<的图象上一点,AB x ⊥轴于点B ,点C 是y 轴正半轴上一点,连接BC ,AD BC ∥交y 轴于点D ,若0.5ABCD S =四边形,则k 的值为 .16.如图,正方形ABCD 的边长为2,以AB 边上的动点O 为圆心,OB 为半径作圆,将AOD △沿OD 翻折至A OD ′ ,若O 过A OD ′ 一边上的中点,则O 的半径为 .三、解答题(本大题共有8小题,共66分)(共66分)17.(本题6分)计算或化简:(1)()201253π− +−−+−; (2)()()()2m n n m m n +−−−.18.(本题6分)如图,在平面直角坐标系中,ABC 的顶点坐标分别为()2,4A ,()3,1B ,()5,3C .(1)作ABC 关于y 轴对称的111A B C △;(2)将ABC 绕原点O 顺时针旋转90°,得到222A B C △,作出222A B C △并求点C 旋转到点2C 所经过的路径长.19.(本题6分)2023年全国教育工作会议提出要把开展读书活动作为一件大事来抓.引导学生爱该书.读好书,善读书,贵阳市某校为了推进这项工作,对全校学生一周内平均读书时间进行抽样调查.将调查结果的数据分成A 、B 、C 、D 、E 五个等级并绘制成表格和扇形统计图如下.等级 周平均读书时间t (单位:小时) 人数A01t ≤< 4 B12t ≤< a C23t ≤< 20 D34t ≤< 15 E 4t ≥5 每个等级人数扇形统计图(1)求统计图表中=a ______,m =______.(2)已知该校共有2800名学生,试估计该校每周读书时间至少3小时的人数为______.(3)请写出一条你对读书的建议.20.(本题8分)我国是世界上最早发明历法的国家之一,《周礼》中记载:垒土为圭,立木为表,测日影,正地中,定四时,如图1,圭是地面上一根水平标尺,指向正北,表是一根垂直于地面的杆,正午,表的日影(即表影)落在圭上,根据表影的长度可以测定节气.在一次数学活动课上,要制作一个圭表模型,如图2,地面上放置一根长2米的杆AB ,向正北方向画一条射线BC ,在BC 上取点D ,测得 1.5m BD =, 2.5m AD =.(1)判断:这个模型中AB 与BC 是否垂直.答:______(填“是”或“否”);你的理由是:______.(2)利用这个圭表模型,测定某市冬至正午阳光与日影夹角30°,夏至正午阳光与日影夹角为60°,请求出这个模型中该市冬至与夏至的日影的长度差(结果保留根号).21.(本题8分)如图,在矩形ABCD 中,沿EF 将矩形折叠,使A 、C 重合,AC 与EF 交于点H .(1)求证:AE =AF ;(2)若AB =4,BC =8,求△ABE 的面积.22.(本题10分)我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售.按计划,20辆车都要装运,每辆汽车只能装运同一种脐橙.且必须装满,根据下表组织的信息,解答以下问题.脐橙品种A B C 每辆汽车运载量(吨) 6 5 4每吨脐橙获利(元) 1200 1600 1000(1)设转运A 种脐橙的车辆数为x ,转运B 种脐橙的车辆数为y ,求y 与x 的函数表达式;(2)如果转运每种脐橙的车辆数都不少于4,那么车辆的安排方案有几种?(3)若要使此次销售获利最大,应采用哪种安排方案?并求出此时最大利润的值.23.(本题10分)定义:平面直角坐标系xOy 中,当点N 在图形M 的内部,或在图形M 上,且点N 的横坐标和纵坐标相等时,则称点N 为图形M 的“梦之点”.(1)如图①,矩形ABCD 的顶点坐标分别是(1,2)A −,(1,1)B −−,(3,1)C −,(3,2)D ,在点1(2,2)P −−,2(0,0)P ,3(1,1)P ,4(2,2)P 中,是矩形ABCD “梦之点”的是________;(2)如图②,已知A 、B 是抛物线21922y x x =−++上的“梦之点”,点C 是抛物线的顶点: ①求出AC ,AB ,BC 三条线段的长度;②判断ABC 的形状,并说明理由.24.(本题12分)如图,ABC 内接于圆O ,AD 是ABC 的高线,9AD =,12CD =,tan 3ABD ∠=,连接OC .(1)求证:ABC 是等腰三角形;(2)求证:BCO BAD ∠=∠;(3)若点E 是OC 上一动点,EF AB ∥交BC 于点F .①若OEF 与ABD △相似,求EF 的长;②当OEF 的面积与CEF △的面积差最大时,直接写出此时CF 的长.2024年浙江中考最后一卷数学解析及参考答案一、单选题1.D【分析】此题考查了实数的大小比较法则:正数大于零,零大于负数,两个负数绝对值大的反而小,据此判断.【详解】∵510−<−<<故选:D .2.D【分析】根据各个选项中的式子可以计算出正确的结果,本题得以解决.【详解】解:∵3a ﹣2a =a ,故选项A 错误;∵2a 2+4a 2=6a 2,故选项B 错误;∵(x 3)2=x 6,故选项C 错误;∵x 8÷x 2=x 6,故选项D 正确;故选D .【点睛】本题考查整式的混合运算,解答本题的关键是明确整式混合运算的计算方法.3.B【分析】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a ×的形式,其中110a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值10≥时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】解:80.16亿98.01610×,故选:B .4.B【分析】本题考查立体几何的三视图.根据题意,逐项判断即可.【详解】解:A.主视图为长方形,此项不符合题意;B.主视图为三角形,此项符合题意;C.主视图为圆,此项不符合题意;D.主视图为长方形,此项不符合题意.故选:B .5.C【分析】先解不等式,求出解集,然后在数轴上表示出来.【详解】解:不等式x ﹣2≤0,得:2x ≤ ,把不等式的解集在数轴上表示出来为:.故选:C【点睛】本题主要考查了解不等式,并在数轴上表示解集,解题的关键是熟练掌握解不等式的步骤,不等式的解集在数轴表示时空心圈不包含该点,实心圈包含该点.6.D【分析】本题为统计题,考查众数与中位数的意义,根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按从小到大依次排列,处于中间位置的两个数的平均数即为中位数.【详解】有45辆自动驾驶汽车参与了这次测试,45个分数,按大小顺序排列最中间的数据是第23个数:85,故得分的中位数是85(分),得80分的人数最多,有16人,故众数为80,故选D .7.A【分析】本题考查了垂径定理和勾股定理的应用,根据垂径定理求出AE 的长是解此题的关键.连接OA ,根据垂径定理求出AE ,再根据勾股定理求出OA ,最后根据线段的和差求解即可.【详解】解:如图,连接OA ,线段CD 是O 的直径,CD AB ⊥于点E ,∴12AE AB =,8AB =, ∴4AE =,3OE =,∴5OA ,∴5OC OA ==,∴8CE OC OE =+=,故选:A .8.A【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是设每头牛、每只羊分别值金x 两、y 两,根据“5头牛,2只羊,值金10两;2头牛,5只羊,值金8两”列出方程组即可得答案.【详解】解:设每头牛值金x 两,每只羊值金y 两,则可列方程组为5210258x y x y += +=, 故选A .9.B【分析】本题考查了菱形的性质、二次函数图象上点的坐标特征,根据二次函数图象上点的坐标性质得出BD 的长是解题关键.连接BC 交OA 于D ,如图,根据菱形的性质得BC OA ⊥,60OBD ∠=°,利用含30度的直角三角形三边的关系得OD =,设BD t =,则OD =,()B t ,利用二次函数图象上点的坐标特征得2=,得出14BD =,OD =C 点坐标. 【详解】解:连接BC 交OA 于D ,如图,四边形OBAC 为菱形,BC OA ,120ABO ∠=° ,60OBD ∴∠=°,OD ∴,设BD t =,则OD =,()B t ∴,把()B t 代入2y =,得2=,解得10t =(舍去), 214t =,14BD ∴=,OD =故C 点坐标为:14 − .故答案为:B .10.C【分析】本题考查的是矩形的性质、翻折的性质及相似多边形性质,熟练应用矩形和相似多边形性质是解题关键,设CD x =,则()1,1EC x CG x x =-=--,根据两矩形相似求出即可.【详解】解:在矩形ABCD 中,设CD x =,则ABCD x ==,1AD BC ==, 由翻折得,90AB AF x AFE B BAF ==∠=∠=∠=︒,∴四边形ABEF 是正方形,同理,四边形DFHG 是正方形,,1BE AB x DF DG x ∴====-,()1,121CE x CG x x x ∴=-=--=-,矩形HECG ∽矩形ABCD ,EC CG BC CD∴=,即1211x x x --=,解得:x =,经检验,xCD ∴ 故选:C .二、填空题11.()()22t t t +−【分析】本题考查了因式分解,先提取公因式,再利用公式法即可求解,熟练掌握提公因式法及公式法分解因式是解题的关键.【详解】解:()()()324422t t t t t t t −=−=+−,故答案为:()()22t t t +−.12.14/0.25 【分析】本题考查了概率公式的应用,用到的知识点为:概率所求情况数与总情况数之比.全部情况的总数是四种,符合条件的情况的是一种,二者的比值就是其发生的概率.【详解】由于概率为所求情况数与总情况数之比,而抽取卡片为“特区精神”的情况数只有一种,从暗箱随机抽取一张的情况数为四种,故抽取卡片为“特区精神”的概率为14, 故答案为14. 13.0(答案不唯一)【分析】本题主要考查了二次根式有意义的条件,分式有意义的条件,根据二次根式有意义的条件的条件是被开方数大于等于0,分式有意义的条件是分母不为0进行求解即可.∴10x −>,解得1x <.∴x 的值可以是0,故答案为:0(答案不唯一).14.100°/100度【分析】本题考查的是已知弧长与半径求解弧所对的圆心角,熟记弧长公式是解本题的关键.直接利用弧长公式计算即可.【详解】解: 设“弓”所在的圆的弧长圆心角度数是n °, 则1.2π2π1803n =, 解得:100n =,故答案为:100°.15.0.5−【分析】本题考查了反比例函数k 值的几何意义,熟练掌握k 值的几何意义是解答本题的关键.根据反比例函数k 值的几何意义进行解答即可.【详解】AB x ⊥ 轴于点B ,CD x ⊥轴,∴AB CD ,又 AD BC ,∴四边形ABCD 是平行四边形,过点作AM y ⊥轴,则四边形ABOM 是矩形, ∴0.5,ABOMABCD S S k ===矩形平行四边形∵反比例函数图象在第二象限,0.5k ∴=−,故答案为:0.5−.16.23、54【分析】本题考查了折叠的性质,正方形的性质,勾股定理,圆的定义;分三种情况讨论,设O 的半径为r ,分别根据勾股定理,即可求解.【详解】设O 的半径为r ,当O 经过A O ′的中点,即经过AO 的中点, ∴1233r AB =,当O 经过OD 的中点,则12r OB OD ==, ∴2OD r =,2AO AB OB r =−=−, 在Rt AOD 中,222AD AO OD +=∴()()222222r r +−=解得:r = 当O 经过A D ′的中点,即经过AD 的中点,设AD 的中点为M ,∴2,1,AO r AM OM r =−== ∴()22221r r −+= 解得:54r =综上所述,半径为23、54故答案为:23、54 三、解答题17.(1)5(2)222m mn −+【分析】此题考查了实数的运算以及整式的混合运算,熟练掌握运算法则是解本题的关键.(1)原式利用零指数幂、绝对值的代数意义以及负整数指数幂法则计算即可求出值;(2)根据平方差公式和完全平方公式化简,再合并同类项即可.【详解】(1)解:原式159=-+5=;(2)原式()22222n m m mn n =−−−+22222n m m mn n =−−+−222m mn =−+18.(1)图见解析(2)【分析】本题考查作图-轴对称变换,旋转变换,以及求弧长,熟练掌握相关作图方法是解题关键; (1)根据点关于y 轴对称的性质分别找到对应的点1A ,1B ,1C ,然后进一步连接即可;(2)利用旋转变换的性质分别作出A ,B ,C 的对应点2A ,2B ,2C ,再顺次连接即可,利用弧长公式求得点C 经过的路径长.【详解】(1)解:如图,111A B C △即为所求;(2)如图,222A B C △即为所求,由题意可知,OC∴点C 旋转到点2C =. 19.(1)6,40(2)1120(3)全校学生一周内平均读书时间23t ≤<(答案不唯一)【分析】本题考查了扇形统计图,样本估计总体等知识.(1)由等级得到学生总数,即可得出a ,再求C 等级的占比即可;(2)用样本估计总体即可得出结果;(3)根据表格可题建议合理即可.【详解】(1)解:由等级D 得到学生总数1530%50÷=人, ∴504201556a −−−−,()%2050100%40%m =÷×=,40m =,故答案为:6,40.(2)1552800112050+×=人, 故该校2800名学生每周读书时间至少3小时的人数为1120人.故答案为:1120.(3)根据表格可建议:全校学生一周内平均读书时间23t ≤<.20.(1)是;222AB BD AD +=,由勾股定理的逆定理可知AB BC ⊥.(2).【分析】本题考查的勾股定理的逆定理的应用,解直角三角形的应用,理解题意是解本题的关键. (1)利用勾股定理的逆定理判断即可;(2)先画图,利用三角函数再计算BE=BF =,从而可得答案. 【详解】(1)解:是, 理由:由测量结果可知得 1.5m BD =, 2.5m AD =,而2m AB =,∴2226.25AB BD AD +==,∴90ABD ,∴AB BC ⊥.故答案是:是;222AB BD AD +=,由勾股定理的逆定理可知AB BC ⊥.(2)如图,由题意可得:90ABC ∠=°,2AB =,30AFB ∠=°,60AEB ∠=°,∴tan tan 60AB AEB BE∠=°=,∴BE =, 同理:tan tan 30AB AFBBF ∠=°=,∴BF =,∴FE BF BE =−==. 21.(1)证明见解析(2)6【分析】(1)依据平行线的性质以及矩形的性质,即可得到∠AFE =∠AEF ,进而得出AE =AF .(2)设BE =x ,则AE =EC =8-x ,在Rt △ABE 中,根据勾股定理可得方程,即可得到BE 的长,再根据三角形面积计算公式求解.【详解】(1)证明:∵四边形ABCD 矩形,∴AD ∥BC ,∴∠AFE =∠FEC ,由折叠的性质得:∠AEF =∠FEC ,∴∠AFE =∠AEF ,∴AE =AF .(2)解:根据折叠的性质可得AE =EC ,设BE =x ,则AE =EC =8-x ,在Rt △ABE 中,根据勾股定理可得:222AB BE AE +=,即()22248x x +=−,解得:x =3,∴BE =3,∴ABE S = 12AB •BE =12×4×3=6. 【点睛】本题主要考查了折叠问题以及矩形的性质的运用,解题的方法是设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.22.(1)220y x =−+ (2)5种(3)当转运A 种脐橙的车4辆,转运B 种脐橙的车12辆,转运C 种脐橙的车4辆时,利润最大为140800元【分析】(1)根据题意列式:()20651040x x y y −−=++,整理后即可得到220y x =−+; (2)根据装运每种水果的车辆数都不少于4辆,4x ≥,2204x −+≥,解不等式组即可;(3)设利润为W 元,则()480016000048W x x =−+≤≤,根据一次函数的增减性求解即可. 【详解】(1)根据题意,装运A 种水果的车辆数为x ,装运B 种水果的车辆数为y ,∴装运C 种水果的车辆数为()20x y −−,∴()20651040x x y y −−=++, 整理得220y x =−+. (2)由(1)知,装运A ,B ,C 三种水果的车辆数分别为x ,220x −+,x ,由题意得2204x −+≥,解得8x ≤,∵4x ≥,∴48x ≤≤.∵x 为整数,∴x 的值为4,5,6,7,8,∴安排方案共有5种.(3)设利润为W 元,∴()612005220160041000W x x x =×+−+×+× 4800160000x =−+,因为48000−<,且x 的值为4,5,6,7,8,∴W 的值随x 的增大而减小,∴当4x =时,销售利润最大.当装运A 种水果4车,B 种水果12车,C 种水果4车,销售获利最大.最大利润48004160000140800W =−×+=(元).【点睛】主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意要根据自变量的实际范围确定函数的最值.23.(1)2(0,0)P ,3(1,1)P ,4(2,2)P(2)①AC =BC =AB =ABC 是直角三角形,理由见解析【分析】本题考查了二次函数的图象与性质、勾股定理以及勾股定理逆定理:(1)根据“梦之点”的定义判断这几个点是否在矩形的内部或者边上即可得到答案;(2)①根据“梦之点”的定义求出A ,B 的坐标,再求出顶点的坐标,计算出AC ,AB ,BC 的长; ②根据勾股定理逆定理,即可求解.【详解】(1)解:∵矩形ABCD 的顶点坐标分别是(1,2)A −,(1,1)B −−,(3,1)C −,(3,2)D ,∴矩形ABCD 的“梦之点”(),x y 满足2,131x y −−≤≤≤≤,∴点2(0,0)P ,3(1,1)P ,4(2,2)P 是矩形ABCD 的“梦之点”,1(2,2)P −−不是矩形的“梦之点”.故答案为:2(0,0)P ,3(1,1)P ,4(2,2)P(2)解:①A 、B 是抛物线21922y x x =−++上的“梦之点”, ∴21922x x x =−++, 解得:123,3x x ==−,当3x =时,3y =,当3x =−时,=3y −,∴()()3,3,3,3A B −−, ∵()2219115222y x x x =−++=−−+, ∴顶点坐标为()1,5C ,∴AC =BC =AB =; ②ABC 是直角三角形,理由如下:∵AC =BC =AB =∴((2222280AB AC BC +=+==,∴ABC 是直角三角形.24.(1)证明见解析(2)证明见解析(3)①EF =253CF =【分析】本题考查了圆的性质,等腰三角形的判定与性质,相似三角形的判定与性质,锐角三角函数等知识,掌握相关知识是解题的关键.(1)利用勾股和锐角三角函数求得AC BC =即可证明;(2)连接,OA OB ,延长CO 交AD 于点M ,交AB 于点N ,先证明CO 是ACB ∠的角平分线,再证明ANM CDM ∽即可得出结论;(3)①过O 点作OH BC ⊥交BC 于点H ,点E 是OC 上一动点,EF AB ∥交BC 于点F ,先证明CHO CFB ∽,设EF x =3x =即可求解,②要使OEF 的面积与CEF △的面积差最大,必须使EF 和()CE OE −最大,当E 点与O 点重合时,EF 最大,CE OE OC −=最大,先求得EF =即可求出CF . 【详解】(1)证明:∵AD 是ABC 的高线,∴90ADC ADB ∠=∠=°, ∵9AD =,12CD =,∴15AC ===,∵tan 3ABD ∠=, ∴tan 3AD ABD BD∠==, ∴3BD =,∴31215BC BD CD =+=+=, ∴AC BC =,∴ABC 是等腰三角形.(2)证明:连接,OA OB ,延长CO 交AD 于点M ,交AB 于点N ,如图:∵AC BC =,∴CAB CBA ∠=∠, ∵OA OB =,∴OAB OBA ∠=∠, ∴CAO CBO ∠=∠, ∵OA OC =,∴CAO ACO ∠=∠, ∵OB OC =,∴BCO CBO ∠=∠, ∴ACO BCO ∠=∠, ∴CO 是ACB ∠的角平分线, 又∵ AC BC =,∴CN AB ⊥,∴90ANC BNC ∠=∠=°, ∴90MDC ANE ∠=∠=°, 又∵AMN CMD ∠=∠, ∴ANM CDM ∽,∴DCM NAM ∠=∠, ∴BCO BAD ∠=∠. (3)解:①过O 点作OH BC ⊥交BC 于点H ,点E 是OC 上一动点,EF AB ∥交BC 于点F ,如图:∵,,15OB OC OH BC BC =⊥=, ∴17.52CH BC ==,90CHO CFB ∠=∠=°, ∴CHO CFB ∽,∴COH CBF ∠=∠, ∵tan 3ABD ∠=, ∴tan tan 3CH COH CBF OH∠=∠==, ∴ 2.5OH =,∴OC =, ∵EF AB ∥,90BNC ∠=°, ∴CEF CNB ∽,∴90CEF CNB ∠=∠=°, 设EF x =,∴tan tan 3CE CE CFE CBN EF x∠=∠===, ∴3CE x =,∵OEF ADB ∽,∴OE EF AD BD=, ∵OEOC CE =−, 3x =, 解得:x =∴EF ②∵90CEF ∠=°,即EF OC ⊥, ∴12CEF S CE EF =⋅ ,12OEF S OE EF =⋅ , ∴()111222CEF OEF S S CE EF OE EF EF CE OE −=⋅−⋅=⋅− , 由题知,要使OEF 的面积与CEF △的面积差最大,必须使EF 和()CE OE −最大,∴当E 点与O 点重合时,EF 最大,CE OE OC −=最大,如图:∵EF AB ∥,∴CEF CNB ∽,∴CFE CBN ∠=∠,CE OC ==,∴tan tan 3CE CFE CBN EF ∠=∠==,∴EF∴253CF =.。
浙江省2021年中考真题汇编专题1:选择填空压轴题(含解析)
2021年浙江省中考真题汇编专题1:选择填空压轴题1.(2021·绍兴)如图,中,,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使,连结CE,则的值为()A. B. C. D. 22.(2021·绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是()A. 用3个相同的菱形放置,最多能得到6个菱形B. 用4个相同的菱形放置,最多能得到15个菱形C. 用5个相同的菱形放置,最多能得到27个菱形D. 用6个相同的菱形放置,最多能得到41个菱形3.(2021·金华)如图,在中,,以该三角形的三条边为边向形外作正方形,正方形的顶点都在同一个圆上.记该圆面积为,面积为,则的值是()A. B. C. D.4.(2021·杭州)已知和均是以为自变量的函数,当时,函数值分别是和,若存在实数,使得,则称函数和具有性质P。
以下函数和具有性质P的是()A. 和B. 和C. 和D. 和5.(2021·嘉兴)已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是()A. ≤B. ≥C. ≥D. ≤6.(2021·宁波)如图是一个由5张纸片拼成的,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为,另两张直角三角形纸片的面积都为,中间一张矩形纸片的面积为,与相交于点O.当的面积相等时,下列结论一定成立的是()A. B. C. D.7.(2021·温州)由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.过点作的垂线交小正方形对角线的延长线于点,连结,延长交于点.若,则的值为()A. B. C. D.8.(2021·湖州)已知抛物线与轴的交点为A(1,0)和B(3,0),点P1(,),P2(,)是抛物线上不同于A,B的两个点,记△P1AB的面积为S1,△P2AB的面积为S2,。
【压轴卷】中考数学试题(带答案)(1)

【压轴卷】中考数学试题(带答案)(1)一、选择题1.如图所示,已知A (12,y 1),B(2,y 2)为反比例函数1y x =图像上的两点,动点P(x ,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是( )A .(12,0) B .(1,0) C .(32,0) D .(52,0) 2.在数轴上,与表示6的点距离最近的整数点所表示的数是( ) A .1B .2C .3D .43.阅读理解:已知两点1122,,()(),M x y N x y ,则线段MN 的中点(),K x y 的坐标公式为:122x x x +=,122y y y +=.如图,已知点O 为坐标原点,点()30A -,,O e 经过点A ,点B 为弦PA 的中点.若点(),P a b ,则有,a b 满足等式:229a b +=.设(),B m n ,则,m n 满足的等式是( )A .229m n +=B .223922m n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭C .()()222323m n ++=D .()222349m n ++=4.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:接力中,自己负责的一步出现错误的是( )A .只有乙B .甲和丁C .乙和丙D .乙和丁5.如图,矩形纸片ABCD 中,4AB =,6BC =,将ABC V 沿AC 折叠,使点B 落在点E 处,CE 交AD 于点F ,则DF 的长等于( )A .35B .53C .73D .546.今年我市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个.假设今年每个项目平均投资是x 万元,那么下列方程符合题意的是( ) A .1069605076020500x x -=+B .5076010696020500x x -=+ C .1069605076050020x x-=+D .5076010696050020x x -=+ 7.某服装加工厂加工校服960套的订单,原计划每天做48套.正好按时完成.后因学校要求提前5天交货,为按时完成订单,设每天就多做x 套,则x 应满足的方程为( ) A .96096054848x -=+ B .96096054848x +=+ C .960960548x-= D .96096054848x-=+ 8.“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x 万平方米,则下面所列方程中正确的是( ) A .606030(125%)x x-=+ B .606030(125%)x x-=+C .60(125%)6030x x ⨯+-=D .6060(125%)30x x⨯+-= 9.如图中的几何体是由一个圆柱和个长方体组成的,该几何体的俯视图是( )A .B .C .D .10.如图,P 为平行四边形ABCD 的边AD 上的一点,E ,F 分别为PB ,PC 的中点,△PEF ,△PDC ,△PAB 的面积分别为S ,1S ,2S .若S=3,则12S S +的值为( )A .24B .12C .6D .311.均匀的向一个容器内注水,在注水过程中,水面高度h 与时间t 的函数关系如图所示,则该容器是下列中的( )A .B .C .D .12.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( ) A .B .C .D .二、填空题13.如图,△ABC 的三个顶点均在正方形网格格点上,则tan ∠BAC =_____________.14.中国的陆地面积约为9 600 000km 2,把9 600 000用科学记数法表示为 . 15.当直线()223y k x k =-+-经过第二、三、四象限时,则k 的取值范围是_____. 16.3x +x 的取值范围是_____.17.“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车.“复兴号”的速度比原来列车的速度每小时快40千米,提速后从北京到上海运行时间缩短了30分钟,已知从北京到上海全程约1320千米,求“复兴号”的速度.设“复兴号”的速度为x 千米/时,依题意,可列方程为_____. 18.分解因式:2x 2﹣18=_____.19.从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是_____.20.在学校组织的义务植树活动中,甲、乙两组各四名同学的植树棵数如下,甲组:9,9,11,10;乙组:9,8,9,10;分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵数为19的概率______.三、解答题21.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?22.某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名;(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数;(3)如果要在这个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).23.已知关于x的方程220++-=.x ax a(1)当该方程的一个根为1时,求a的值及该方程的另一根;(2)求证:不论a取何实数,该方程都有两个不相等的实数根.24.修建隧道可以方便出行.如图:A ,B 两地被大山阻隔,由A 地到B 地需要爬坡到山顶C 地,再下坡到B 地.若打通穿山隧道,建成直达A ,B 两地的公路,可以缩短从A 地到B 地的路程.已知:从A 到C 坡面的坡度1:3i =,从B 到C 坡面的坡角45CBA ∠=︒,42BC =公里.(1)求隧道打通后从A 到B 的总路程是多少公里?(结果保留根号)(2)求隧道打通后与打通前相比,从A 地到B 地的路程约缩短多少公里?(结果精确到0.012 1.414≈3 1.732) 25.解方程:3x x +﹣1x=1.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】求出AB 的坐标,设直线AB 的解析式是y=kx+b ,把A 、B 的坐标代入求出直线AB 的解析式,根据三角形的三边关系定理得出在△ABP 中,|AP-BP|<AB ,延长AB 交x 轴于P′,当P 在P′点时,PA-PB=AB ,此时线段AP 与线段BP 之差达到最大,求出直线AB 于x 轴的交点坐标即可. 【详解】 ∵把A (12,y 1),B (2,y 2)代入反比例函数y=1x 得:y 1=2,y 2=12, ∴A (12,2),B (2,12), ∵在△ABP 中,由三角形的三边关系定理得:|AP-BP|<AB , ∴延长AB 交x 轴于P′,当P 在P′点时,PA-PB=AB , 即此时线段AP 与线段BP 之差达到最大,设直线AB 的解析式是y=kx+b , 把A 、B 的坐标代入得:122122k b k b ⎧+⎪⎪⎨⎪+⎪⎩==, 解得:k=-1,b=52, ∴直线AB 的解析式是y=-x+52, 当y=0时,x=52, 即P (52,0), 故选D . 【点睛】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用,解此题的关键是确定P 点的位置,题目比较好,但有一定的难度.2.B解析:B 【解析】 【分析】6的大小,即可得到结果. 【详解】46 6.25<<Q ,26 2.5∴<<,6的点距离最近的整数点所表示的数是2, 故选:B . 【点睛】此题考查了实数与数轴,以及算术平方根,熟练掌握各自的性质是解本题的关键.3.D解析:D 【解析】 【分析】根据中点坐标公式求得点B 的坐标,然后代入,a b 满足的等式进行求解即可. 【详解】∵点()30A -,,点(),P a b ,点(),B m n 为弦PA 的中点, ∴32a m -+=,02b n +=, ∴23,2a m b n =+=,又,a b 满足等式:229a b +=, ∴()222349m n ++=, 故选D . 【点睛】本题考查了坐标与图形性质,解题的关键是理解中点坐标公式.4.D解析:D 【解析】【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断.【详解】∵22211x x x x x-÷--=2221·1x x x x x --- =()2212·1x x x x x---- =()()221·1x x x x x ---- =()2x x --=2x x-, ∴出现错误是在乙和丁,故选D .【点睛】本题考查了分式的乘除法,熟练掌握分式乘除法的运算法则是解题的关键.5.B解析:B 【解析】 【分析】由折叠的性质得到AE=AB ,∠E=∠B=90°,易证Rt △AEF ≌Rt △CDF ,即可得到结论EF=DF ;易得FC=FA ,设FA=x ,则FC=x ,FD=6-x ,在Rt △CDF 中利用勾股定理得到关于x 的方程x 2=42+(6-x )2,解方程求出x 即可.【详解】∵矩形ABCD 沿对角线AC 对折,使△ABC 落在△ACE 的位置, ∴AE=AB ,∠E=∠B=90°, 又∵四边形ABCD 为矩形, ∴AB=CD , ∴AE=DC , 而∠AFE=∠DFC , ∵在△AEF 与△CDF 中,AFE CFD E DAE CD ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△AEF ≌△CDF (AAS ), ∴EF=DF ;∵四边形ABCD 为矩形, ∴AD=BC=6,CD=AB=4, ∵Rt △AEF ≌Rt △CDF , ∴FC=FA ,设FA=x ,则FC=x ,FD=6-x ,在Rt △CDF 中,CF 2=CD 2+DF 2,即x 2=42+(6-x )2,解得x =133, 则FD =6-x=53. 故选B . 【点睛】考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应边相等.也考查了矩形的性质和三角形全等的判定与性质以及勾股定理.6.A解析:A 【解析】试题分析:∵今后项目的数量﹣今年的数量=20,∴1069605076020500x x-=+.故选A .考点:由实际问题抽象出分式方程.7.D解析:D 【解析】解:原来所用的时间为:96048,实际所用的时间为:96048x +,所列方程为:96096054848x -=+.故选D .点睛:本题考查了由实际问题抽象出分式方程,关键是时间作为等量关系,根据每天多做x 套,结果提前5天加工完成,可列出方程求解.8.C解析:C 【解析】分析:设实际工作时每天绿化的面积为x 万平方米,根据工作时间=工作总量÷工作效率结合提前 30 天完成任务,即可得出关于x 的分式方程.详解:设实际工作时每天绿化的面积为x 万平方米,则原来每天绿化的面积为125%x+万平方米,依题意得:606030125%x x-=+,即()60125%6030x x⨯+-=. 故选C .点睛:考查了由实际问题抽象出分式方程.找到关键描述语,找到合适的等量关系是解决问题的关键.9.D解析:D 【解析】 【分析】根据从上边看得到的图形是俯视图,可得答案. 【详解】解:从上边看是一个圆形,圆形内部是一个虚线的正方形. 故选:D . 【点睛】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.10.B解析:B 【解析】 【分析】 【详解】过P 作PQ ∥DC 交BC 于点Q ,由DC ∥AB ,得到PQ ∥AB , ∴四边形PQCD 与四边形APQB 都为平行四边形, ∴△PDC ≌△CQP ,△ABP ≌△QPB , ∴S △PDC =S △CQP ,S △ABP =S △QPB , ∵EF 为△PCB 的中位线, ∴EF ∥BC ,EF=12BC , ∴△PEF ∽△PBC ,且相似比为1:2,∴S△PEF:S△PBC=1:4,S△PEF=3,S S =12.∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=12故选B.11.D解析:D【解析】【分析】由函数图象可得容器形状不是均匀物体分析判断,由图象及容积可求解.【详解】根据图象折线可知是正比例函数和一次函数的函数关系的大致图象;切斜程度(即斜率)可以反映水面升高的速度;因为D几何体下面的圆柱体的底圆面积比上面圆柱体的底圆面积小,所以在均匀注水的前提下是先快后慢;故选D.【点睛】此题主要考查了函数图象,解决本题的关键是根据用的时间长短来判断相应的函数图象.12.B解析:B【解析】分析:根据轴对称图形与中心对称图形的概念求解即可.详解:A.是轴对称图形,不是中心对称图形;B.是轴对称图形,也是中心对称图形;C.是轴对称图形,不是中心对称图形;D.是轴对称图形,不是中心对称图形.故选B.点睛:本题考查了中心对称图形和轴对称图形的知识,关键是掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.二、填空题13.【解析】分析:在图形左侧添加正方形网格分别延长ABAC连接它们延长线所经过的格点可构成直角三角形利用正切的定义即可得出答案详解:如图所示由图形可知∴tan∠BAC=故答案为点睛:本题考查了锐角三角函解析:13【解析】分析:在图形左侧添加正方形网格,分别延长AB 、AC ,连接它们延长线所经过的格点,可构成直角三角形,利用正切的定义即可得出答案. 详解:如图所示,由图形可知,90AFE ∠=︒,3AF AC =,EF AC =, ∴tan ∠BAC =133EF AC AF AC ==. 故答案为13. 点睛:本题考查了锐角三角函数的定义. 利用网格构建直角三角形进而利用正切的定义进行求解是解题的关键.14.6×106【解析】【分析】【详解】将9600000用科学记数法表示为96×106故答案为96×106解析:6×106. 【解析】 【分析】 【详解】将9600000用科学记数法表示为9.6×106. 故答案为9.6×106. 15.【解析】【分析】根据一次函数时图象经过第二三四象限可得即可求解;【详解】经过第二三四象限∴∴∴故答案为:【点睛】本题考查一次函数图象与系数的关系;掌握一次函数与对函数图象的影响是解题的关键解析:13k <<. 【解析】 【分析】根据一次函数y kx b =+,k 0<,0b <时图象经过第二、三、四象限,可得220k -<,30k -<,即可求解;【详解】()223y k x k =-+-经过第二、三、四象限,∴220k -<,30k -<,∴1k >,3k <, ∴13k <<, 故答案为:13k <<. 【点睛】本题考查一次函数图象与系数的关系;掌握一次函数y kx b =+,k 与b 对函数图象的影响是解题的关键.16.x≥﹣3【解析】【分析】直接利用二次根式的定义求出x 的取值范围【详解】解:若式子在实数范围内有意义则x+3≥0解得:x≥﹣3则x 的取值范围是:x≥﹣3故答案为:x≥﹣3【点睛】此题主要考查了二次根式解析:x ≥﹣3【解析】 【分析】直接利用二次根式的定义求出x 的取值范围. 【详解】.在实数范围内有意义, 则x +3≥0, 解得:x ≥﹣3,则x 的取值范围是:x ≥﹣3. 故答案为:x ≥﹣3. 【点睛】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.17.【解析】【分析】设复兴号的速度为x 千米/时则原来列车的速度为(x-40)千米/时根据提速后从北京到上海运行时间缩短了30分钟列出方程即可【详解】设复兴号的速度为x 千米/时则原来列车的速度为(x ﹣40解析:13201320304060x x -=-. 【解析】 【分析】设“复兴号”的速度为x 千米/时,则原来列车的速度为(x-40)千米/时,根据提速后从北京到上海运行时间缩短了30分钟列出方程即可. 【详解】设“复兴号”的速度为x 千米/时,则原来列车的速度为(x ﹣40)千米/时, 根据题意得:13201320304060x x -=-. 故答案为:13201320304060x x -=-. 【点睛】本题主要考查由实际问题抽象出分式方程,解题的关键是理解题意,找到题目蕴含的相等关系.18.2(x+3)(x﹣3)【解析】【分析】原式提取2再利用平方差公式分解即可【详解】原式=2(x2﹣9)=2(x+3)(x﹣3)故答案为:2(x+3)(x﹣3)【点睛】此题考查了提公因式法与公式法的综合解析:2(x+3)(x﹣3)【解析】【分析】原式提取2,再利用平方差公式分解即可.【详解】原式=2(x2﹣9)=2(x+3)(x﹣3),故答案为:2(x+3)(x﹣3)【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.19.【解析】【分析】列表得出所有等可能结果从中找到积为大于-4小于2的结果数根据概率公式计算可得【详解】列表如下: -2 -1 1 2 -2 2 -2 -4 -1 2 -1 -2 1 -2 -解析:1 2【解析】【分析】列表得出所有等可能结果,从中找到积为大于-4小于2的结果数,根据概率公式计算可得.【详解】列表如下:∴积为大于-4小于2的概率为612=12,故答案为12.【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.20.【解析】【分析】【详解】画树状图如图:∵共有16种等可能结果两名同学的植树总棵数为19的结果有5种结果∴这两名同学的植树总棵数为19的概率为解析:5 16.【解析】【分析】【详解】画树状图如图:∵共有16种等可能结果,两名同学的植树总棵数为19的结果有5种结果,∴这两名同学的植树总棵数为19的概率为5 16.三、解答题21.(1)6月份出售这种蔬菜每千克的收益是2元.(2)5月份出售这种蔬菜,每千克的收益最大.(3)4月份的销售量为4万千克,5月份的销售量为6万千克.【解析】分析:(1)找出当x=6时,y1、y2的值,二者作差即可得出结论;(2)观察图象找出点的坐标,利用待定系数法即可求出y1、y2关于x的函数关系式,二者作差后利用二次函数的性质即可解决最值问题;(3)求出当x=4时,y1﹣y2的值,设4月份的销售量为t万千克,则5月份的销售量为(t+2)万千克,根据总利润=每千克利润×销售数量,即可得出关于t的一元一次方程,解之即可得出结论.详解:(1)当x=6时,y1=3,y2=1,∵y1﹣y2=3﹣1=2,∴6月份出售这种蔬菜每千克的收益是2元.(2)设y1=mx+n,y2=a(x﹣6)2+1.将(3,5)、(6,3)代入y1=mx+n,3563m n m n +=⎧⎨+=⎩,解得:237m n ⎧=-⎪⎨⎪=⎩, ∴y 1=﹣23x+7; 将(3,4)代入y 2=a (x ﹣6)2+1, 4=a (3﹣6)2+1,解得:a=13, ∴y 2=13(x ﹣6)2+1=13x 2﹣4x+13. ∴y 1﹣y 2=﹣23x+7﹣(13x 2﹣4x+13)=﹣13x 2+103x ﹣6=﹣13(x ﹣5)2+73. ∵﹣13<0, ∴当x=5时,y 1﹣y 2取最大值,最大值为73, 即5月份出售这种蔬菜,每千克的收益最大.(3)当t=4时,y 1﹣y 2=﹣13x 2+103x ﹣6=2.设4月份的销售量为t 万千克,则5月份的销售量为(t+2)万千克, 根据题意得:2t+73(t+2)=22, 解得:t=4, ∴t+2=6.答:4月份的销售量为4万千克,5月份的销售量为6万千克.点睛:本题考查了待定系数法求一次(二次)函数解析式、二次函数的性质以及一元一次方程的应用,解题的关键是:(1)观察函数图象,找出当x=6时y 1﹣y 2的值;(2)根据点的坐标,利用待定系数法求出y 1、y 2关于x 的函数关系式;(3)找准等量关系,正确列出一元一次方程.22.(1)280名;(2)补图见解析;108°;(3)0.1. 【解析】 【分析】(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“C”与“E”的情况数,即可求出所求的概率. 【详解】解:(1)56÷20%=280(名),答:这次调查的学生共有280名;(2)280×15%=42(名),280﹣42﹣56﹣28﹣70=84(名),补全条形统计图,如图所示,根据题意得:84÷280=30%,360°×30%=108°,答:“进取”所对应的圆心角是108°;(3)由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩”用列表法为:A B C D EA(A,B)(A,C)(A,D)(A,E)B(B,A)(B,C)(B,D)(B,E)C(C,A)(C,B)(C,D)(C,E)D(D,A)(D,B)(D,C)(D,E)E(E,A)(E,B)(E,C)(E,D)共20种情况,恰好选到“C”和“E”有2种,∴恰好选到“进取”和“感恩”两个主题的概率是0.1.23.(1)12,32;(2)证明见解析.【解析】试题分析:(1)根据一元二次方程根与系数的关系列方程组求解即可.(2)要证方程都有两个不相等的实数根,只要证明根的判别式大于0即可.试题解析:(1)设方程的另一根为x1,∵该方程的一个根为1,∴1111{211a x a x +=--⋅=.解得132{12x a =-=. ∴a 的值为12,该方程的另一根为32-.(2)∵()()222241248444240a a a a a a a ∆=-⋅⋅-=-+=-++=-+>, ∴不论a 取何实数,该方程都有两个不相等的实数根.考点:1.一元二次方程根与系数的关系;2. 一元二次方程根根的判别式;3.配方法的应用. 24.(1)隧道打通后从A 到B 的总路程是(434)+公里;(2)隧道打通后与打通前相比,从A 地到B 地的路程约缩短2.73公里. 【解析】 【分析】(1)过点C 作CD ⊥AB 于点D ,利用锐角三角函数的定义求出CD 及AD 的长,进而可得出结论.(2)由坡度可以得出A ∠的度数,从而得出AC 的长,根据AC CB AB +-即可得出缩短的距离. 【详解】(1)作CD AB ⊥于点D ,在Rt BCD ∆中,∵45CBA ∠=︒,42BC =, ∴4CD BD ==. 在Rt ACD ∆中, ∵1:3CDi AD==, ∴343AD CD ==, ∴()434AB =+公里.答:隧道打通后从A 到B 的总路程是()434+公里.(2)在Rt ACD ∆中, ∵3CDi AD==, ∴30A ∠=︒,∴2248AC CD ==⨯=,∴8AC CB +=+∵4AB =,∴84 2.73AC CB AB +-=+≈(公里).答:隧道打通后与打通前相比,从A 地到B 地的路程约缩短2.73公里. 【点睛】本题考查的是解直角三角形的应用-坡度问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,需要熟记坡度和锐角三角函数的定义. 25.分式方程的解为x=﹣34. 【解析】【分析】方程两边都乘以x (x+3)得出方程x ﹣1+2x=2,求出方程的解,再代入x (x+3)进行检验即可.【详解】两边都乘以x (x+3),得:x 2﹣(x+3)=x (x+3), 解得:x=﹣34, 检验:当x=﹣34时,x (x+3)=﹣2716≠0, 所以分式方程的解为x=﹣34. 【点睛】本题考查了解分式方程,熟练掌握解分式方程的方法与注意事项是解题的关键.。
天津市和平区2024届中考考前最后一卷数学试卷含解析

天津市和平区2024届中考考前最后一卷数学试卷含解析一、选择题(每题3分,共18分)下列运算正确的是( )A. 3a+2b=5abB. a6÷a2=a3C. (a+b)2=a2+b2D. a2⋅a3=a6下列说法中,正确的是( )A. 两点之间的所有连线中,线段最短B. 相等的角是对顶角C. 两条直线被第三条直线所截,同位角相等D. 若 a>b,则 a2>b2下列函数中,y是x的反比例函数的是( )A. y=x+12B. y=2xC. y=x2D. y=x2下列图形中,既是轴对称图形又是中心对称图形的是( )A. 等边三角形B. 平行四边形C. 正方形D. 梯形若关于x的方程2x−3=0与关于y的方程3y−2k=0的解互为相反数,则k的值为( ) A. −23 B. 23 C. −29 D. 29在平面直角坐标系中,点P(2,−3)关于x轴对称的点的坐标是( )A. (−2,−3)B. (2,3)C. (−2,3)D. (3,−2)二、填空题(每题3分,共12分)计算:9−∣2−2∣+(31)−1= _______。
若扇形的圆心角为120∘,半径为3,则该扇形的弧长为_______。
若关于x的一元二次方程x2−2x+m=0有两个不相等的实数根,则m的取值范围是_______。
在△ABC中,∠A=50∘,∠B=60∘,则∠C= _______。
三、解答题(共70分)(8分)计算:(1) −32+∣1−3∣−(−2)3(2) xx2−1÷(x−x2x−1)(10分)解方程:(1) 2x2−4x−1=0(配方法)(2) x−2x+1=2−x3(10分)先化简,再求值:(x2−1x−x+11)÷x−11,其中x=2−1。
(10分)已知一次函数y=kx+b的图象经过点(2,−1)和点(−1,2)。
(1) 求这个一次函数的解析式;(2) 求这个一次函数图象与x轴、y轴的交点坐标。
2023年海南省中考数学真题试卷及答案

海南省2023年初中学业水平考试数学(全卷满分120分,考试时间100分钟)一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的,请在答题卡上把你认为正确的答案的字母代号按要求用2B 铅笔涂黑.1. 如图,数轴上点A 表示的数的相反数是( )A. 1B. 0C. 1-D. 2- 2. 若代数式2x +的值为7,则x 等于( )A. 9B. 9-C. 5D. 5- 3. 共享开放机遇,共创美好生活.2023年4月10日至15日,第三届中国品博览会在海南省海口市举行,以“打造全球消费精品展示交易平台”为目标,进场观众超32万人次,数据320000用科学记数法表示为( )A. 43.210⨯B. 53.210⨯C. 63.210⨯D. 43210⨯ 4. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的俯视图是( )A. B. C. D. 5. 下列计算中,正确的是( )A. 235a a a ⋅=B. ()235a a =C. ()55210a a =D. 448a a a += 6. 水是生命之源.为了倡导节约用水,随机抽取某小区7户家庭上个月家里的用水量情况(单位:吨),数据为:7,5,6,8,9,9,10.这组数据的中位数和众数分别是( )A. 9,8B. 9,9C. 8.5,9D. 8,9 7. 分式方程115x =-的解是( )A. 6x =B. 6x =-C. 5x =D. 5x =- 8. 若反比例函数k y x=(0k ≠)的图象经过点2,1,则k 的值是( ) A. 2 B. 2- C. 12 D. 12- 9. 如图,直线m n ∥,ABC 是直角三角形,90B,点C 在直线n 上.若150∠=︒,则2∠的度数是( )A. 60°B. 50°C. 45°D. 40°10. 如图,在ABC ∆中,40C ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径画弧,两弧相交于M N ,两点,作直线MN ,交边AC 于点D ,连接BD ,则ADB ∠的度数为( )A. 40︒B. 50︒C. 80︒D. 100︒11. 如图,在平面直角坐标系中,点A 在y 轴上,点B 的坐标为()6,0,将ABO ∆绕着点B 顺时针旋转60︒,得到DBC △,则点C 的坐标是( )A. ()B. (C. ()6,3D. ()3,6 12. 如图,在ABCD 中,8AB =,60ABC ∠=︒,BE 平分ABC ∠,交边AD 于点E ,连接CE ,若2AE ED =,则CE 的长为( )A. 6B. 4C.D.二、填空题(本大题满分12分,每小题3分)13. 因式分解:mx my -=________.14. 设n 为正整数,若1n n <<+,则n 的值为_______. 15. 如图,AB 为O 的直径,AC 是O 的切线,点A 是切点,连接BC 交O 于点D ,连接OD ,若40C ∠=︒,则AOD ∠=________度.16. 如图,在正方形ABCD 中,8AB =,点E 在边AD 上,且4AD AE =,点P 为边AB 上的动点,连接PE ,过点E 作EF PE ⊥,交射线BC 于点F ,则EF PE=______.若点M 是线段EF 的中点,则当点P 从点A 运动到点B 时,点M 运动的路径长为_______.三、解答题(本大题满分72分)17. (1)计算:21332-÷-(2)解不等式组:122113x x ->⎧⎪⎨+≥⎪⎩①② 18. 2023年5月10日,搭载天舟六号货运飞船的长征七号遥七运载火箭,在我国文昌航天发射场点火发射成功.为了普及航空航天科普知识,某校组织学生去文昌卫星发射中心参观学习.已知该校租用甲,乙两种不同型号的客车共15辆,租用1辆甲型客车需600元,1辆乙型客车需500元,租车费共8000元.问甲,乙两种型号客车各租多少辆?19. 某中学为了了解学生最喜欢的课外活动,以便更好开展课后服务.随机抽取若干名学生进行了问卷调查.调查问卷如下:根据统计得到的数据,绘制成下面的两幅不完整的统计图.请根据统计图提供的信息,解答下面的问题:(1)本次调查采用的调查方式为 (填写“普查”或“抽样调查”);(2)在这次调查中,抽取的学生一共有 人;扇形统计图中n 的值为 ;(3)已知选择“科技”类课外活动的50名学生中有30名男生和20名女生.若从这50名学生中随机抽取1名学生座谈,且每名学生被抽到的可能性相同,则恰好抽到女生的概率是;(4)若该校共有1000名学生参加课外活动,则估计选择“文学”类课外活动的学生有 人. 20. 如图,一艘轮船在A 处测得灯塔M 位于A 的北偏东30︒方向上,轮船沿着正北方向航行20海里到达B 处,测得灯塔M 位于B 的北偏东60︒方向上,测得港口C 位于B 的北偏东45︒方向上.已知港口C 在灯塔M 的正北方向上.(1)填空:AMB ∠= 度,BCM ∠= 度;(2)求灯塔M 到轮船航线AB 的距离(结果保留根号);(3)求港口C 与灯塔M 的距离(结果保留根号).21. 如图1,在菱形ABCD 中,对角线AC ,BD 相交于点O ,6AB =,60ABC ∠=︒,点P 为线段BO 上的动点(不与点B ,O 重合),连接CP 并延长交边AB 于点G ,交DA 的延长线于点H .(1)当点G 恰好为AB 的中点时,求证:AGH BGC ≌;(2)求线段BD 的长;(3)当APH 为直角三角形时,求HP PC的值; (4)如图2,作线段CG 的垂直平分线,交BD 于点N ,交CG 于点M ,连接NG ,在点P 的运动过程中,CGN ∠的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.22. 如图1,抛物线2y x bx c =++交x 轴于A ,()3,0B 两点,交y 轴于点()0,3C-.点P 为抛物线上一动点.(1)求该抛物线的函数表达式;(2)当点P 的坐标为()1,4-时,求四边形BACP 的面积;(3)当动点P 在直线BC 上方时,在平面直角坐标系是否存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形?若存在,请求出点Q 的坐标;若不存在,请说明理由;(4)如图2,点D 是抛物线的顶点,过点D 作直线DH y ∥轴,交x 轴于点H ,当点P 在第二象限时,作直线PA ,PB 分别与直线DH 交于点G 和点I ,求证:点D 是线段IG 的中点.海南省2023年初中学业水平考试数学参考答案一,选择题1. A2. C3. B4. C5. A6. D7. A8. B9. D10. C11. B解:过点C 作CE OB ⊥,如下图:则90CEB ∠=︒由题意可得:60OBC ∠=︒,6OB OC == ∴30BCE ∠=︒ ∴132BE BC ==∴CE ==3OE OB BE =-=∴C 点的坐标为(故选:B12. C 解:四边形ABCD 是平行四边形60D ABC ∴∠=∠=︒,8CD AB ==,AD BC ∥ AEB CBE ∴∠=∠BE 平分ABC ∠ABE CBE ∴∠=∠ABE AEB ∴∠=∠8AE AB ∴==2AE ED =4DE ∴=如图,过点E 作EF CD ⊥于点F则90EFC EFD ∠=∠=︒90906030DEF D ∴∠=︒-∠=︒-︒=︒ 122DF DE ∴==EF ∴===826CF CD DF =-=-=CE ∴===故选:C . 二、填空题13. ()m x y -14. 115. 10016. ①. 4 ①. 16解:过F 作FK AD ⊥交AD 延长线于点K则四边形ABFK 为矩形,90A K ∠=∠=︒ ∴8AB FK == 由题意可得:124AE AD == ∵EF PE ⊥∴90AEP KEF PEF ∠+∠=∠=︒又∵90PEA APE ∠∠+=︒∴APE KEF ∠=∠∴AEP KFE ∆∆∽ ∴4EF FK PE AE== 过M 作GH AD ⊥交AD 于点G ,交BC 于点H ,如下图∵AD CB ∥,GH AD ⊥∴GH BC ⊥在EGM ∆和△FHM 中MGE MHF EMG FMH ME MF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS EGM FHM ∆∆≌∴MG MH =故点M 的运动轨迹是一条平行于BC 的线段 当点P 与A 重合时,12BF AE ==当点P 与B 重合时,22190BEF F EBF ∠=∠+∠=︒,1190BEF EBF ∠+∠=︒ ∴21F BEF ∠=∠∵12190EF F EF B ∠=∠=︒∴121EF B F F E ∽ ∴11112BF EF EF F F =,即12288F F = 解得1232F F =∵1M ,2M 分别为1EF ,2EF 的中点∴12M M 是12EF F 的中位线 ∴12121162M M F F ==,即点M 运动的路径长为16 故答案为:4,16三、解答题17. (1)2;(2)3x >.18. 甲型号客车租5辆,乙型号客车租10辆 19. (1)抽样调查(2)200,22 (3)25 (4)35020. (1)30,45(2)灯塔M 到轮船航线AB的距离为 (3)港口C 与灯塔M的距离为)101海里 21. (1)见解析 (2)(3)2 (4)CGN ∠的度数是定值,30︒【小问1详解】 证明:四边形ABCD 是菱形AD BC ∴∥HAB ABC ∴∠=∠点G 是AB 的中点AG BG ∴=AGH BGC ∠=∠()AAS AGH BGC ∴∆∆≌;【小问2详解】 解:四边形ABCD 是菱形,6AB =,60ABC ∠=︒AO CO ∴=,BO DO =,AC BD ⊥,1302ABD ABC ∠=∠=︒ 90AOB ∴∠=︒132AO AB ∴==BO ∴===2BD BO ∴==【小问3详解】解:APH ∆为直角三角形AP AD ∴⊥90DAP ∴∠=︒四边形ABCD 是菱形60ABC ADC ∴∠=∠=︒,1302ADB ADC ∠=∠=︒,6AD AB ==,AD BC ∥12AP PD ∴=222AP AD PD +=,即222162PD PD ⎛⎫+= ⎪⎝⎭PD ∴=AP =//AD BC ,60ABC ∠=︒180********BAD ABC ∴∠=︒-∠=︒-︒=︒1209030BAP BAD PAD ABP ∴∠=∠-∠=︒-︒=︒=∠BP AP ∴==//AD BCBPC DPH ∴∆∆∽DP HP BP PC∴=2HP PC ∴==; 【小问4详解】解:CGN ∠的度数是定值如图,取BC 的中点H ,连接OH ,HM ,NCMN 是CG 的垂直平分线GN CN ∴=,GM CM =NGC GCN ∴∠=∠点H 是BC 的中点,GM CM =A MHB ∴∥四边形ABCD 是菱形AO CO ∴=,AC BD ⊥,1230C CBO AB ∠=∠=︒ 点H 是BC 的中点,AO CO =OH AB ∴∥∴点M ,点H ,点O 三点共线点H 是BC 的中点,AC BD ⊥HO HB CH ∴==30CBO BOH ∴∠=∠=︒90COB NMC ∠=∠=︒180CON NMC ∴∠+∠=︒∴点O ,点C ,点M ,点N 四点共圆30BOH NCM ∴∠=∠=︒30CGN NCM ∴∠=∠=︒.22. (1)2=23y x x --(2)9 (3)在平面直角坐标系内存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形,此时点Q 的坐标为()5,2-或5122⎛⎫+- ⎪ ⎪⎝⎭ (4)证明过程见解析【小问1详解】解:由题意可得,3093c b c=-⎧⎨=++⎩ 解得23b c =-⎧⎨=-⎩∴抛物线的解析式为2=23y x x --;【小问2详解】解:连接OP ,过点P 作PE AB ⊥于点E ,如图∵点P 的坐标为()1,4-∴4PE =,1OE =令0y =,则2230x x --=解得3x =或1x =∴()1,0A -∴1OA =∵()0,3C -,()3,0B∴3OC =,3OB = ∴OAC OCP OBPBACP S S S S =++四边形 111=222OA OC OC OE OB PE ⋅+⋅+⋅ 111133134222=⨯⨯+⨯⨯+⨯⨯ 9=;【小问3详解】解:在平面直角坐标系内存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形,理由如下:如图,当BC 为边时,四边形BCQP 为符合条件的矩形,PB 交y 轴于点E ,CQ 交x 轴于点F ,连接EF ,过点P 作PM y ⊥轴于点M ,过点Q 作QN x ⊥轴于点N∵3OC OB ==∴45OBC OCB ∠=∠=︒∵四边形BCQP 为矩形∴==90PBC QCB ∠∠︒∴45OBE OCF ∠=∠=︒∴OBE △和OCF ∆为等腰直角三角形∴====3OB OC OE OF∵四边形BCFE 为正方形∴CF BE =,90EFC BEF ∠=∠=︒∴四边形EFQP 为矩形∴QF PE =∵==45MEP BEO ∠∠︒,==45QFN OFC ∠∠︒∴PME △和QNF △为全等的等腰直角三角形∴===NF QN PM ME∵3OE =∴()0,3E设直线BE 的解析式为()0y kx n k =+≠∴303k n n +=⎧⎨=⎩∴13k n =-⎧⎨=⎩ ∴直线BE 的解析式为3y x =-+联立方程组得2323y x y x x =-+⎧⎨=--⎩解得30x y =⎧⎨=⎩或25x y =-⎧⎨=⎩ ∴()2,5P -∴2PM =∴==2QN NF∴==32=5ON OF NF ++∴()5,2Q -;如图,当BC 为对角线时,四边形BPCQ 为矩形,过点Q 作QD x ⊥轴于点D ,PE x ⊥轴于点E则90PEB BDQ ∠=∠=︒,90PBQ ∠=︒∵90PBE EPB PBE DBQ ∠+∠=∠+∠=︒∴EPB DBQ ∠=∠①BEP QDB ∆∆∽ ①PE BE DB DQ= 设点P 的坐标为:()()2,2303t t t t t --或,()Q Q Q x y ,①()0,3C -,()3,0B①3Q x t =-,22Q y t t =-+①()23,2Q t t t --+∴22DQ t t =-,BD t =-,223EP t t =-++,3BE t =- ∴222332t t t t t t-++-=-- 整理得:324230t t t -++=分解因式得:()()2310t t t ---=解得:13t =(舍去),23t =<(舍去),30t =<①此时点Q 的坐标为:51,22⎛+- ⎝⎭. 综上所述,在平面直角坐标系内存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形,此时点Q 的坐标为()5,2-或5122⎛+- ⎝⎭; 【小问4详解】证明:∵()222314y x x x =--=--∴抛物线2=23y x x --的顶点D 的坐标为()1,4-,对称轴为直线1x = 设()2,23P m m m --,直线PB 的解析式为()=0y cx d c +≠ ∴22330cm d m m c d ⎧+=--⎨+=⎩∴133c m d m =+⎧⎨=--⎩∴直线PB 的解析式为()=133y m x m +--当1x =时,22y m =--∴()1,22I m --∴()=224=22ID m m -----+设直线PA 的解析式为()=0y ex f e +≠∴2230em f m m e d ⎧+=--⎨-+=⎩∴33e mf m =-⎧⎨=-⎩ ∴直线PA 的解析式为()33y m x m =-+-当1x =时,26y m =-∴()1,26G m -∴()=426=22DG m m ----+∴=ID DG∴点D 是线段IG 的中点.。
吉林省通化市2024届中考数学考前最后一卷含解析

吉林省通化市2024届中考数学考前最后一卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分) 1.在平面直角坐标系中,点P (m ﹣3,2﹣m )不可能在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.已知:如图是y =ax 2+2x ﹣1的图象,那么ax 2+2x ﹣1=0的根可能是下列哪幅图中抛物线与直线的交点横坐标( )A .B .C .D .3.下列各式计算正确的是( ) A .2223a a +=B .()236b b -=- C .235c c c ⋅=D .()222m n m n -=-4.三角形的两边长分别为3和6,第三边的长是方程x 2﹣6x +8=0的一个根,则这个三角形的周长是( ) A .9B .11C .13D .11或135.已知A 样本的数据如下:72,73,76,76,77,78,78,78,B 样本的数据恰好是A 样本数据每个都加2,则A ,B 两个样本的下列统计量对应相同的是( ) A .平均数B .标准差C .中位数D .众数6.如图,△ABC 是⊙O 的内接三角形,AD ⊥BC 于D 点,且AC=5,CD=3,BD=4,则⊙O 的直径等于( )A .5B .C .D .77.如图,点M 为▱ABCD 的边AB 上一动点,过点M 作直线l 垂直于AB ,且直线l 与▱ABCD 的另一边交于点N .当点M 从A→B 匀速运动时,设点M 的运动时间为t ,△AMN 的面积为S ,能大致反映S 与t 函数关系的图象是( )A .B .C .D .8.2016年底安徽省已有13个市迈入“高铁时代”,现正在建设的“合安高铁”项目,计划总投资334亿元人民币.把334亿用科学记数法可表示为( ) A .0.334B .C .D .9.如图,AB 是O 的直径,弦CD AB ⊥,CDB 30∠=,CD 23=,则阴影部分的面积为( )A .2πB .πC .π3D .2π 310.下列各组数中,互为相反数的是( ) A .﹣2 与2B .2与2C .3与13D .3与3二、填空题(共7小题,每小题3分,满分21分)11.如图,正方形ABCD 和正方形OEFG 中, 点A 和点F 的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是_________.12.已知直线m∥n,将一块含有30°角的直角三角板ABC按如图方式放置,其中A、B两点分别落在直线m、n上,若∠1=20°,则∠2=_____度.13.若式子x2-在实数范围内有意义,则x的取值范围是.14.化简11x-÷211x-=_____.15.函数32xyx=-中,自变量x的取值范围是______16.已知AB=AC,tanA=2,BC=5,则△ABC的面积为_______________.17.计算:.三、解答题(共7小题,满分69分)18.(10分)下表中给出了变量x,与y=ax2,y=ax2+bx+c之间的部分对应值,(表格中的符号“…”表示该项数据已丢失)x ﹣1 0 1ax2 (1)ax2+bx+c 7 2 …(1)求抛物线y=ax2+bx+c的表达式(2)抛物线y=ax2+bx+c的顶点为D,与y轴的交点为A,点M是抛物线对称轴上一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求B点坐标;(3)在(2)的条件下,设线段BD与x轴交于点C,试写出∠BAD和∠DCO的数量关系,并说明理由.(5分)如图,在建筑物M的顶端A处测得大楼N顶端B点的仰角α=45°,同时测得大楼底端A点的俯角为β=30°.已19.知建筑物M的高CD=20米,求楼高AB为多少米?(3≈1.732,结果精确到0.1米)20.(8分)图1是某市2009年4月5日至14日每天最低气温的折线统计图.图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;在这10天中,最低气温的众数是____,中位数是____,方差是_____.请用扇形图表示出这十天里温度的分布情况.21.(10分)2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:(1)分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;(2)分别求出这两个投资方案的最大年利润;(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?22.(10分)已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:坡顶A到地面PO的距离;古塔BC的高度(结果精确到1米).23.(12分)已知二次函数y=mx2﹣2mx+n的图象经过(0,﹣3).(1)n=_____________;(2)若二次函数y=mx2﹣2mx+n的图象与x 轴有且只有一个交点,求m 值;(3)若二次函数y=mx2﹣2mx+n的图象与平行于x 轴的直线y=5 的一个交点的横坐标为4,则另一个交点的坐标为;(4)如图,二次函数y=mx2﹣2mx+n的图象经过点A(3,0),连接AC,点P 是抛物线位于线段AC 下方图象上的任意一点,求△PAC 面积的最大值.24.(14分)如图,AB是⊙O的直径,点C在⊙O上,CE^ AB于E,CD平分ÐECB,交过点B的射线于D,交AB于F,且BC=BD.(1)求证:BD是⊙O的切线;(2)若AE=9,CE=12,求BF的长.参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、A【解题分析】分点P的横坐标是正数和负数两种情况讨论求解.【题目详解】①m-3>0,即m>3时,2-m<0,所以,点P(m-3,2-m)在第四象限;②m-3<0,即m<3时,2-m有可能大于0,也有可能小于0,点P(m-3,2-m)可以在第二或三象限,综上所述,点P不可能在第一象限.故选A.【题目点拨】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).2、C【解题分析】由原抛物线与x 轴的交点位于y 轴的两端,可排除A 、D 选项;B 、方程ax 2+2x ﹣1=0有两个不等实根,且负根的绝对值大于正根的绝对值,B 不符合题意;C 、抛物线y =ax 2与直线y =﹣2x +1的交点,即交点的横坐标为方程ax 2+2x ﹣1=0的根,C 符合题意.此题得解. 【题目详解】∵抛物线y =ax 2+2x ﹣1与x 轴的交点位于y 轴的两端, ∴A 、D 选项不符合题意;B 、∵方程ax 2+2x ﹣1=0有两个不等实根,且负根的绝对值大于正根的绝对值, ∴B 选项不符合题意;C 、图中交点的横坐标为方程ax 2+2x ﹣1=0的根(抛物线y =ax 2与直线y =﹣2x +1的交点), ∴C 选项符合题意. 故选:C . 【题目点拨】本题考查了抛物线与x 轴的交点以及二次函数的图象与位置变化,逐一分析四个选项中的图形是解题的关键. 3、C 【解题分析】解:A .2a 与2不是同类项,不能合并,故本选项错误; B .应为()236b b -=,故本选项错误;C .235·c c c =,正确;D .应为()2222m n m n mn -=+-,故本选项错误. 故选C . 【题目点拨】本题考查幂的乘方与积的乘方;同底数幂的乘法. 4、C 【解题分析】试题分析:先求出方程x 2-6x +8=0的解,再根据三角形的三边关系求解即可. 解方程x 2-6x +8=0得x=2或x=4当x=2时,三边长为2、3、6,而2+3<6,此时无法构成三角形 当x=4时,三边长为4、3、6,此时可以构成三角形,周长=4+3+6=13 故选C.考点:解一元二次方程,三角形的三边关系点评:解题的关键是熟记三角形的三边关系:任两边之和大于第三边,任两边之差小于第三边.5、B【解题分析】试题分析:根据样本A,B中数据之间的关系,结合众数,平均数,中位数和标准差的定义即可得到结论:设样本A中的数据为x i,则样本B中的数据为y i=x i+2,则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差2,只有标准差没有发生变化.故选B.考点:统计量的选择.6、A【解题分析】连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB,∠ADC=90°,利用勾股定理求得AD=,,再证明Rt△ABE∽Rt△ADC,得到,即2R==.【题目详解】解:如图,连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB;∵AD⊥BC于D点,AC=5,DC=3,∴∠ADC=90°,∴AD=,∴在Rt△ABE与Rt△ADC中,∠ABE=∠ADC=90°,∠AEB=∠ACB,∴Rt△ABE∽Rt△ADC,∴,即2R = =;∴⊙O 的直径等于.故答案选:A. 【题目点拨】本题主要考查了圆周角定理、勾股定理,解题的关键是掌握辅助线的作法. 7、C 【解题分析】分析:本题需要分两种情况来进行计算得出函数解析式,即当点N 和点D 重合之前以及点M 和点B 重合之前,根据题意得出函数解析式.详解:假设当∠A=45°时,2AB=4,则MN=t ,当0≤t≤2时,AM=MN=t ,则S=212t ,为二次函数;当2≤t≤4时,S=t ,为一次函数,故选C .点睛:本题主要考查的就是函数图像的实际应用问题,属于中等难度题型.解答这个问题的关键就是得出函数关系式. 8、B 【解题分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解:334亿=3.34×1010 “点睛”此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值. 9、D 【解题分析】分析:连接OD ,则根据垂径定理可得出CE =DE ,继而将阴影部分的面积转化为扇形OBD 的面积,代入扇形的面积公式求解即可. 详解:连接OD , ∵CD ⊥AB , ∴13,2CE DE CD === (垂径定理), 故OCEODESS,=即可得阴影部分的面积等于扇形OBD 的面积,又∵30CDB ∠=︒,∴60COB ∠= (圆周角定理), ∴OC =2,故S 扇形OBD =260π22π3603⨯=,即阴影部分的面积为2π3. 故选D.点睛:考查圆周角定理,垂径定理,扇形面积的计算,熟记扇形的面积公式是解题的关键. 10、A 【解题分析】根据只有符号不同的两数互为相反数,可直接判断. 【题目详解】-2与2互为相反数,故正确;2与2相等,符号相同,故不是相反数; 3与13互为倒数,故不正确; 3与3相同,故不是相反数. 故选:A. 【题目点拨】此题主要考查了相反数,关键是观察特点是否只有符号不同,比较简单.二、填空题(共7小题,每小题3分,满分21分) 11、(1,0);(﹣5,﹣2). 【解题分析】本题主要考查位似变换中对应点的坐标的变化规律.因而本题应分两种情况讨论,一种是当E 和C 是对应顶点,G 和A 是对应顶点;另一种是A 和E 是对应顶点,C 和G 是对应顶点.【题目详解】∵正方形ABCD 和正方形OEFG 中A 和点F 的坐标分别为(3,2),(-1,-1),∴E (-1,0)、G (0,-1)、D (5,2)、B (3,0)、C (5,0),(1)当E 和C 是对应顶点,G 和A 是对应顶点时,位似中心就是EC 与AG 的交点,设AG 所在直线的解析式为y=kx+b (k≠0),∴231k b b =+⎧⎨-=⎩,解得11b k =-⎧⎨=⎩. ∴此函数的解析式为y=x-1,与EC 的交点坐标是(1,0);(2)当A 和E 是对应顶点,C 和G 是对应顶点时,位似中心就是AE 与CG 的交点,设AE 所在直线的解析式为y=kx+b (k≠0),320k b k b +=⎧⎨-+=⎩,解得1212k b ⎧=⎪⎪⎨⎪=⎪⎩, 故此一次函数的解析式为1122y x =+…①, 同理,设CG 所在直线的解析式为y=kx+b (k≠0),501k b b +=⎧⎨=-⎩,解得151k b ⎧=⎪⎨⎪=-⎩, 故此直线的解析式为115y x =-…② 联立①②得1122115y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩解得52x y =-⎧⎨=-⎩,故AE 与CG 的交点坐标是(-5,-2). 故答案为:(1,0)、(-5,-2).12、1【解题分析】根据平行线的性质即可得到∠2=∠ABC+∠1,据此进行计算即可.【题目详解】解:∵直线m ∥n ,∴∠2=∠ABC+∠1=30°+20°=1°,故答案为:1.【题目点拨】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.13、x 2≥.【解题分析】根据二次根式被开方数必须是非负数的条件,x 20x 2-≥⇒≥.故答案为x 2≥14、x+1【解题分析】分析:根据根式的除法,先因式分解后,把除法化为乘法,再约分即可.详解:解:原式=11x -÷1(1)(1)x x +- =11x -•(x+1)(x ﹣1) =x+1,故答案为x+1.点睛:此题主要考查了分式的运算,关键是要把除法问题转化为乘法运算即可,注意分子分母的因式分解.15、x≠1【解题分析】 解:∵32x y x =-有意义, ∴x -1≠0,∴x ≠1;故答案是:x ≠1.16258【解题分析】作CD ⊥AB ,由tanA=2,设AD=x,CD=2x,根据勾股定理,则BD=x ),然后在Rt △CBD 中BC 2=BD 2+CD 2,即52=4x 2+2x ⎡⎤⎣⎦),解得x 2S△ABC=12AB CD⨯=215252x x x⨯⨯==25255+88【题目详解】如图作CD⊥AB,∵tanA=2,设AD=x,CD=2x,∴AC=5x,∴BD=5-1x(),在Rt△CBD中BC2=BD2+CD2,即52=4x2+25-1x⎡⎤⎣⎦(),x2=25+558,∴S△ABC=12AB CD⨯=215252x x x⨯⨯==25255+88【题目点拨】此题主要考查三角函数的应用,解题的关键是根据题意作出辅助线进行求解.17、3+【解题分析】本题涉及零指数幂、负指数幂、绝对值、特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【题目详解】原式=2×+2﹣+1,=2+2﹣+1,=3+.【题目点拨】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、特殊角的三角函数、绝对值等考点的运算三、解答题(共7小题,满分69分)18、(1) y=x2﹣4x+2;(2) 点B的坐标为(5,7);(1)∠BAD和∠DCO互补,理由详见解析.【解题分析】(1)由(1,1)在抛物线y=ax2上可求出a值,再由(﹣1,7)、(0,2)在抛物线y=x2+bx+c上可求出b、c的值,此题得解;(2)由△ADM和△BDM同底可得出两三角形的面积比等于高的比,结合点A的坐标即可求出点B的横坐标,再利用二次函数图象上点的坐标特征即可求出点B的坐标;(1)利用二次函数图象上点的坐标特征可求出A、D的坐标,过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,根据点B、D的坐标利用待定系数法可求出直线BD的解析式,利用一次函数图象上点的坐标特征可求出点N的坐标,利用两点间的距离公式可求出BA、BD、BN的长度,由三者间的关系结合∠ABD=∠NBA,可证出△ABD∽△NBA,根据相似三角形的性质可得出∠ANB=∠DAB,再由∠ANB+∠AND=120°可得出∠DAB+∠DCO=120°,即∠BAD和∠DCO互补.【题目详解】(1)当x=1时,y=ax2=1,解得:a=1;将(﹣1,7)、(0,2)代入y=x2+bx+c,得:,解得:,∴抛物线的表达式为y=x2﹣4x+2;(2)∵△ADM和△BDM同底,且△ADM与△BDM的面积比为2:1,∴点A到抛物线的距离与点B到抛物线的距离比为2:1.∵抛物线y=x2﹣4x+2的对称轴为直线x=﹣=2,点A的横坐标为0,∴点B到抛物线的距离为1,∴点B的横坐标为1+2=5,∴点B的坐标为(5,7).(1)∠BAD和∠DCO互补,理由如下:当x=0时,y=x2﹣4x+2=2,∴点A的坐标为(0,2),∵y=x2﹣4x+2=(x﹣2)2﹣2,∴点D的坐标为(2,﹣2).过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,如图所示.设直线BD的表达式为y=mx+n(m≠0),将B(5,7)、D(2,﹣2)代入y=mx+n,,解得:,∴直线BD的表达式为y=1x﹣2.当y=2时,有1x﹣2=2,解得:x=,∴点N的坐标为(,2).∵A(0,2),B(5,7),D(2,﹣2),∴AB=5,BD=1,BN=,∴==.又∵∠ABD=∠NBA,∴△ABD∽△NBA,∴∠ANB=∠DAB.∵∠ANB+∠AND=120°,∴∠DAB+∠DCO=120°,∴∠BAD和∠DCO互补.【题目点拨】本题是二次函数综合题,考查了待定系数法求二次函数和一次函数解析式、等底三角形面积的关系、二次函数的图像与性质、相似三角形的判定与性质.熟练掌握待定系数法是解(1)的关键;熟练掌握等底三角形面积的关系式解(2)的关键;证明△ABD∽△NBA是解(1)的关键.19、楼高AB为54.6米.【解题分析】过点C作CE⊥AB于E,解直角三角形求出CE和CE的长,进而求出AB的长.【题目详解】解:如图,过点C作CE⊥AB于E,则AE=CD=20,∵CE=AEtanβ=20tan30=333tan45°33∴3(米),答:楼高AB为54.6米.【题目点拨】此题主要考查了仰角与俯角的应用,根据已知构造直角三角形利用锐角三角函数关系得出是解题关键.20、(1)作图见解析;(2)7,7.5,2.8;(3)见解析.【解题分析】(1)根据图1找出8、9、10℃的天数,然后补全统计图即可;(2)根据众数的定义,找出出现频率最高的温度;按照从低到高排列,求出第5、6两个温度的平均数即为中位数;先求出平均数,再根据方差的定义列式进行计算即可得解;(3)求出7、8、9、10、11℃的天数在扇形统计图中所占的度数,然后作出扇形统计图即可.【题目详解】(1)由图1可知,8℃有2天,9℃有0天,10℃有2天,补全统计图如图;(2)根据条形统计图,7℃出现的频率最高,为3天,所以,众数是7;按照温度从小到大的顺序排列,第5个温度为7℃,第6个温度为8℃,所以,中位数为12(7+8)=7.5;平均数为110(6×2+7×3+8×2+10×2+11)=110×80=8,所以,方差=110[2×(6﹣8)2+3×(7﹣8)2+2×(8﹣8)2+2×(10﹣8)2+(11﹣8)2],=110(8+3+0+8+9),=110×28,=2.8;(3)6℃的度数,210×360°=72°,7℃的度数,310×360°=108°,8℃的度数,210×360°=72°,10℃的度数,210×360°=72°,11℃的度数,110×360°=36°,作出扇形统计图如图所示.【题目点拨】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数、众数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.给定一组数据,出现次数最多的那个数,称为这组数据的众数.21、(1)y1=(120-a)x(1≤x≤125,x为正整数),y2=100x-0.5x2(1≤x≤120,x为正整数);(2)110-125a(万元),10(万元);(3)当40<a<80时,选择方案一;当a=80时,选择方案一或方案二均可;当80<a<100时,选择方案二.【解题分析】(1)根据题意直接得出y1与y2与x的函数关系式即可;(2)根据a的取值范围可知y1随x的增大而增大,可求出y1的最大值.又因为﹣0.5<0,可求出y2的最大值;(3)第三问要分两种情况决定选择方案一还是方案二.当2000﹣200a>1以及2000﹣200a<1.【题目详解】解:(1)由题意得:y1=(120﹣a)x(1≤x≤125,x为正整数),y2=100x﹣0.5x2(1≤x≤120,x为正整数);(2)①∵40<a<100,∴120﹣a>0,即y1随x的增大而增大,∴当x=125时,y1最大值=(120﹣a)×125=110﹣125a(万元)②y2=﹣0.5(x﹣100)2+10,∵a=﹣0.5<0,∴x=100时,y2最大值=10(万元);(3)∵由110﹣125a>10,∴a<80,∴当40<a<80时,选择方案一;由110﹣125a=10,得a=80,∴当a=80时,选择方案一或方案二均可;由110﹣125a<10,得a>80,∴当80<a<100时,选择方案二.考点:二次函数的应用.22、(1)坡顶A到地面PQ的距离为10米;()2移动信号发射塔BC的高度约为19米.【解题分析】延长BC交OP于H.在Rt△APD中解直角三角形求出AD=10.PD=24.由题意BH=PH.设BC=x.则x+10=24+DH.推出AC=DH=x﹣14.在Rt△ABC中.根据tan76°=BCAC,构建方程求出x即可.【题目详解】延长BC交OP于H.∵斜坡AP的坡度为1:2.4,∴512 ADPD=,设AD=5k,则PD=12k,由勾股定理,得AP=13k, ∴13k=26,解得k=2,∴AD=10,∵BC⊥AC,AC∥PO,∴BH⊥PO,∴四边形ADHC是矩形,CH=AD=10,AC=DH, ∵∠BPD=45°,∴PH=BH,设BC=x,则x+10=24+DH,∴AC=DH=x﹣14,在Rt△ABC中,tan76°=BCAC,即14xx-≈4.1.解得:x≈18.7,经检验x≈18.7是原方程的解.答:古塔BC的高度约为18.7米.【题目点拨】本题主要考查了解直角三角形,用到的知识点是勾股定理,锐角三角函数,坡角与坡角等,解决本题的关键是作出辅助线,构造直角三角形.23、(2)-2;(2)m=﹣2;(2)(﹣2,5);(4)当a=32时,△PAC的面积取最大值,最大值为278【解题分析】(2)将(0,-2)代入二次函数解析式中即可求出n值;(2)由二次函数图象与x轴只有一个交点,利用根的判别式△=0,即可得出关于m的一元二次方程,解之取其非零值即可得出结论;(2)根据二次函数的解析式利用二次函数的性质可找出二次函数图象的对称轴,利用二次函数图象的对称性即可找出另一个交点的坐标;(4)将点A的坐标代入二次函数解析式中可求出m值,由此可得出二次函数解析式,由点A、C的坐标,利用待定系数法可求出直线AC的解析式,过点P作PD⊥x轴于点D,交AC于点Q,设点P的坐标为(a,a2-2a-2),则点Q 的坐标为(a,a-2),点D的坐标为(a,0),根据三角形的面积公式可找出S△ACP关于a的函数关系式,配方后即可得出△PAC面积的最大值.【题目详解】解:(2)∵二次函数y=mx2﹣2mx+n的图象经过(0,﹣2),∴n=﹣2.故答案为﹣2.(2)∵二次函数y=mx2﹣2mx﹣2的图象与x轴有且只有一个交点,∴△=(﹣2m)2﹣4×(﹣2)m=4m2+22m=0,解得:m2=0,m2=﹣2.∵m≠0,∴m=﹣2.(2)∵二次函数解析式为y=mx2﹣2mx﹣2,∴二次函数图象的对称轴为直线x=﹣-2m2m=2.∵该二次函数图象与平行于x轴的直线y=5的一个交点的横坐标为4,∴另一交点的横坐标为2×2﹣4=﹣2,∴另一个交点的坐标为(﹣2,5).故答案为(﹣2,5).(4)∵二次函数y=mx2﹣2mx﹣2的图象经过点A(2,0),∴0=9m﹣6m﹣2,∴m=2,∴二次函数解析式为y=x2﹣2x﹣2.设直线AC的解析式为y=kx+b(k≠0),将A(2,0)、C(0,﹣2)代入y=kx+b,得:3k+b=0 {b=-3,解得:k=1{b=-3,∴直线AC的解析式为y=x﹣2.过点P作PD⊥x轴于点D,交AC于点Q,如图所示.设点P的坐标为(a,a2﹣2a﹣2),则点Q的坐标为(a,a﹣2),点D的坐标为(a,0),∴PQ=a﹣2﹣(a2﹣2a﹣2)=2a﹣a2,∴S△ACP=S△APQ+S△CPQ=12PQ•OD+12PQ•AD=﹣32a2+92a=﹣32(a﹣32)2+278,∴当a=32时,△PAC的面积取最大值,最大值为278.【题目点拨】本题考查了待定系数法求一次(二次)函数解析式、抛物线与x轴的交点、二次函数的性质以及二次函数的最值,解题的关键是:(2)代入点的坐标求出n值;(2)牢记当△=b2-4ac=0时抛物线与x轴只有一个交点;(2)利用二次函数的对称轴求出另一交点的坐标;(4)利用三角形的面积公式找出S△ACP关于a的函数关系式.24、(1)证明见解析;(2)1.【解题分析】试题分析:(1)根据垂直的定义可得∠CEB=90°,然后根据角平分线的性质和等腰三角形的性质,判断出∠1=∠D,从而根据平行线的判定得到CE∥BD,根据平行线的性质得∠DBA=∠CEB,由此可根据切线的判定得证结果;(2)连接AC,由射影定理可得,进而求得EB的长,再由勾股定理求得BD=BC的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC∽△BFD,再由相似三角形的性质得出结果.试题解析:(1)证明:∵,∴.∵CD平分,BC=BD,∴,.∴.∴∥.∴.∵AB是⊙O的直径,∴BD是⊙O的切线.(2)连接AC,∵AB是⊙O直径,∴.∵,可得.∴在Rt△CEB中,∠CEB=90°,由勾股定理得∴.∵,∠EFC =∠BFD,∴△EFC∽△BFD.∴.∴.∴BF=1.考点:切线的判定,相似三角形,勾股定理。
2023年广东省广州市数学中考预测定心卷(最后一卷)及参考答案

2023广州数学中考预测定心卷(最后一卷)考试范围:初中考试时间:120分钟第I卷(选择题)一、选择题(本大题共10小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1. 我们把MM={1,3,xx)叫集合MM,其中1,3,xx叫做集合MM的元素.集合中的元素具有确定性(如xx必然存在),互异性(如xx≠1,xx≠3),无序性(即改变元素的顺序,集合不变).若集合NN={xx,1,3},我们说MM=NN.已知集合AA={0,|xx|,yy},集合BB={xx,xxyy,�xx−yy},若AA=BB,则xx+yy 的值是( )A. 4B. 2C. 0D. −22. 若有理数aa,bb,cc在数轴上的位置如图所示,则化简|aa+cc|+|bb−aa|−|bb−cc|的结果是( )A. −2bbB. −2aa−2ccC. −2bb+2ccD. 2aa−2bb3. 关于xx的方程xx+1xx=aa+1aa的两个解为xx1=aa,xx2=1aa,xx+2xx=aa+2aa的两个解为xx1=aa,xx2=2aa,xx+3xx=aa+3aa的两个解为xx1=aa,xx2=3aa,则关于xx的方程xx+10xx+1=aa+10aa+1的两个解为( )A. xx1=aa,xx2=10aaB. xx1=aa,xx2=10aa+1C. xx1=aa,xx2=11−aa aa+1D. xx1=aa,xx2=9−aa aa+14. 下列运算结果正确的是( )A. xx2+xx3=xx5B. (−aa−bb)2=aa2+2aabb+bb2C. aa2÷aa×1aa=aa2D. (3xx3)2=6xx65. 已知AA(xx1,yy1)、BB(xx2,yy2)两点在反比例函数yy=1+|kk|xx(xx>0)的图象上,下列三个命题:其中真命题个数是( )①若xx1=xx2,则yy1=yy2;②若xx1=2019,xx2=2020,则yy1>yy2;③过AA、BB两点的直线与xx轴、yy轴分别交于CC、DD两点,连接OOAA、OOBB,则SS△AAAAAA=SS△BBAABB,A. 0B. 1C. 2D. 36.如图所示,电路连接完好,且各元件工作正常.随机闭合开关SS1,SS2,SS3中的两个,能让两个小灯泡同时发光的概率是( )A. 12B. 13C. 14D. 167. 如图,可变四边形AABBCCDD中,AABB=5,∠AA=∠BB=90°,EE是AABB上的动点(不与端点重合),DDEE:CCEE:CCDD=3:4:5,OO为AABB的中点,OOOO⊥CCDD于OO.下列结论错误的是( )A. △AADDEE与△BBEECC一定相似B. 以点OO为圆心,OOAA长为半径作⊙OO,则CCDD与⊙OO可能相离C. OOOO的最大值是52D. 当OOOO最大时,CCDD=125248. 设二次函数yy=aaxx2+cc(aa,cc是常数,aa<0),已知函数的图象经过点(−2,pp),(√ 10,0),(4,qq),设方程aaxx2+cc+2=0的正实数根为mm,( )A. 若pp>1,qq<−1,则2<mm<√ 10B. 若pp>1,qq<−1,则√ 10<mm<4C. 若pp>3,qq<−3,则2<mm<√ 10D. 若pp>3,qq<−3,则√ 10<mm<49. 如图,△AABBCC中,∠AABBCC=90°,tan∠BBAACC=12,DD是AABB中点,PP是以AA为圆心,以AADD为半径的圆上的动点,连接PPBB、PPCC,则PPBB PPCC的最大值为( )A. √ 103B. 3√ 1010C. √ 13−14D. √ 13+1410. 如图,在正方形AABBCCDD中,点OO是对角线AACC,BBDD的交点,过点OO作射线OOMM,OONN分别交BBCC,CCDD于点EE,FF,且∠EEOOFF=90°,OOCC与EEFF交于点GG.下列结论中:①△OOEEFF是等腰直角三角形;②四边形CCEEOOFF的面积为正方形AABBCCDD面积的14;③OOCC=EEFF;④DDFF2+CCFF2=EEFF2.正确的有( )A. ①③④B. ②③C. ①②③④D. ①②④第II卷(非选择题)二、填空题(本大题共6小题,共18.0分)11. 若一元二次方程xx2−xx+mm=0有两个不相等的实数根xx1和xx2,则xx1+xx2=______ .12. 若一个四位正整数的十位数字比个位数字大5,千位数字比百位数字大5,则称这样的四位正整数为“尚善数”.一个四位正整数mm是尚善数,记PP(mm)为mm的百位数字和个位数字依次组成两位数与mm的千位数字和十位数字依次组成两位数的和,记QQ(mm)为mm的千位数字和百位数字依次组成两位数与mm的十位数字和个位数字依次组成的两位数的差.若�PP(mm)−QQ(mm)为一个正整数,则满足条件中mm的最大值是______ .13. “通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方,如:解方程xx−√xx=0,就可以利用该思维方式,设√xx=yy,将原方程转化为:yy2−yy=0这个熟悉的关于yy的一元二次方程,解出yy,再求xx,这种方法又叫“换元法”,请你用这种思维方式和换元法解方程:xx2+4xx+4√xx2+4xx−5=0.方程的解为.14. 如图,已知AABB//CCDD,CCEE,BBEE的交点为EE,现作如下操作:第一次操作,分别作∠AABBEE和∠DDCCEE的平分线,交点为EE1,第二次操作,分别作∠AABBEE1和∠DDCCEE1的平分线,交点为EE2,第三次操作,分别作∠AABBEE2和∠DDCCEE2的平分线,交点为EE3,…第nn次操作,分别作∠AABBEE nn−1和∠DDCCEE nn−1的平分线,交点为EE nn.若∠EE nn=1°,那∠BBEECC等于______ °.15. 已知如图:正方形AABBCCDD中,EE为CCDD上一点,延长BBCC至点FF,使CCFF=CCEE,BBEE交DDFF于点GG,若GGFF=2,DDGG=3,则BBGG=______.16. 如图,在平面直角坐标系中,矩形AABBOOCC的边OOBB,OOCC分别在xx轴、yy轴的正半轴上,点AA的坐标为(8,6),点PP在矩形AABBOOCC的内部,点EE在BBOO边上,且满足△PPBBEE∽△CCBBOO,当△AAPPCC是等腰三角形时,点PP的坐标为______ .三、计算题(本大题共1小题,共4.0分)17. 解方程组:(1)�2yy−3xx=1xx=yy−1.(2)�3xx−2yy=112xx+3yy=16.四、解答题(本大题共8小题,共68.0分。
中考数学试题及答案初一

中考数学试题及答案初一一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. -1B. 0C. 1D. 2答案:C2. 如果一个数的平方等于9,那么这个数是:A. 3B. -3C. 3或-3D. 9答案:C3. 一个直角三角形的两条直角边分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 8答案:A4. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 0答案:C5. 一个数的倒数是1/2,这个数是:A. 2B. 1/2C. 1D. -1答案:A二、填空题(每题1分,共5分)6. 一个数的平方根是2,这个数是______。
答案:47. 如果一个数的立方是-8,则这个数是______。
答案:-28. 一个数的1/4等于5,那么这个数是______。
答案:209. 一个数加上它的相反数等于______。
答案:010. 如果一个数除以2等于3,那么这个数是______。
答案:6三、计算题(每题5分,共10分)11. 计算下列表达式的值:(3x - 2) / (x + 1),当x = 4时。
答案:(3*4 - 2) / (4 + 1) = 10 / 5 = 212. 解下列方程:2x + 5 = 3x - 2。
答案:2x - 3x = -2 - 5-x = -7x = 7四、解答题(每题15分,共30分)13. 一个直角三角形的斜边长为13,一条直角边长为5,求另一条直角边的长度。
答案:设另一条直角边为a,根据勾股定理,有 a^2 + 5^2 =13^2。
a^2 = 13^2 - 5^2 = 169 - 25 = 144a = √144 = 1214. 一个班级有40名学生,其中1/3的学生是男生,剩余的学生是女生。
求班级中男生和女生的人数。
答案:男生人数= 40 * (1/3) = 40 / 3 ≈ 13.33(取整数为13)女生人数 = 40 - 13 = 27结束语:本试题涵盖了初一数学的主要知识点,包括数的基本概念、代数运算、几何问题等。
2024北京中考数学二轮复习 专题一 选择、填空压轴题 (含答案)

2024北京中考数学二轮复习专题一选择、填空压轴题类型一分析统计图(表)1.根据国家统计局2019—2023年中国普通本专科、中等职业教育及普通高中招生人数的相关数据,绘制统计图如下:2019—2023年普遍本专科、中等职业教育及普遍高中招生人数第1题图下面有四个推断:①2019—2023年,普通本专科招生人数逐年增多;②2023年普通高中招生人数比2019年增加约4%;③2019—2023年,中等职业教育招生人数逐年减少;④2019年普通高中招生人数约是中等职业教育招生人数的1.4倍.所有合理推断的序号是()A.①④ B.②③ C.①②④D.①②③④2.为了解某校学生每周课外阅读时间的情况,随机抽取该校a 名学生进行调查,获得的数据整理后绘制成统计表如下:每周课外阅读时间x (小时)0≤x <22≤x <44≤x <66≤x <8x ≥8合计频数817b 15a 频率0.080.17c 0.151表中4≤x <6组的频数b 满足25≤b ≤35.下面有四个推断:①表中a的值为100;②表中c的值可以为0.31;③这a名学生每周课外阅读时间的中位数一定不在6~8之间;④这a名学生每周课外阅读时间的平均数不会超过6.所有合理推断的序号是()A.①②B.③④C.①②③D.②③④3.密云水库是首都北京重要水源地,水源地生态保护对保障首都水源安全及北京市生态和城市可持续发展具有不可替代的作用.以下是1986—2023年密云水库水体面积和年降水量变化图.1986—2023年密云水库水体面积和年降水量变化图第3题图(以上数据来源于《全国生态气象公报(2023年)》,部分年份缺数据)对于现有数据有以下结论:①2004年的密云水库水体面积最小,仅约为20km2;②2015—2023年,密云水库的水体面积呈持续增加趋势.表明水资源储备增多;③在1986—2023年中,2023年的密云水库水体面积最大,约为170km2;④在1986—2023年中,密云水库年降水量最大的年份,水体面积也最大.其中结论正确的是()A.②③B.②④C.①②③D.③④4.某公司计划招募一批技术人员,他们对25名面试合格人员又进行了理论知识和实践操作测试,其中25名入围者的面试成绩排名,理论知识成绩排名与实践操作成绩的排名情况如图所示第4题图下面有3个推断:①甲的理论知识成绩排名比面试成绩排名靠前;②甲的实践操作成绩排名与理论知识成绩排名相同;③乙的理论知识成绩排名比甲的理论知识成绩排名靠前.其中合理的是()A.①B.①②C.①③D.①②③5.多年来,北京市以强有力的措施和力度治理大气污染,空气质量持续改善,主要污染物的年平均浓度值全面下降.下图是1998年至2019年二氧化硫(SO2)和二氧化氮(NO2)的年平均浓度值变化趋势图.第5题图下列说法错误的是()A.1998年至2019年,SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数B.1998年至2019年,SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数C.1998年至2019年,SO2的年平均浓度值的方差小于NO2的年平均浓度值的方差D.1998年至2019年,SO2的年平均浓度值比NO2的年平均浓度值下降得更快6.“实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为A,B两组,从A,B组各抽取10位客户的电动汽车的实际平均续航里程数据整理成图.其中“⊙”表示A组的客户,“*”表示B组的客户.第6题图下列推断不正确的是()A.A组客户的电动汽车的“实际平均续航里程”的最大值低于B组B.A组客户的电动汽车的“实际平均续航里程”的方差低于B组C.A组客户的电动汽车的“实际平均续航里程”的平均值低于B组D.这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组7.某种预防病虫害的农药即将于三月15日之前喷洒,需要连续三天完成,又知当最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度时药物效果最佳,为此农广站工作人员查看了三月1—15日的天气预报,请你结合气温图给出一条合理建议,药剂喷洒可以安排在________日开始进行.1—15日天气情况第7题图类型二分析与判断函数图象1.如图,一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同.用t 表示小球滚动的时间,v 表示小球的速度.下列图象中,能表示小球在斜坡上时v 与t 的函数关系的图象大致是()第1题图2.某农科所响应“乡村振兴”号召,为某村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗先在农科所的温室中生长,平均高度长到大约20cm 时,移至该村的大棚内继续生长.研究表明,60天内,这种瓜苗的平均高度y (cm)与生长时间x (天)的函数关系的图象如图所示.当这种瓜苗长到大约80cm 时,开始开花结果,此时瓜苗在该村大棚内生长的天数是()第2题图A.10天B.18天C.33天D.48天3.有一圆形苗圃如图①所示,中间有两条交叉过道AB ,CD ,它们为苗圃⊙O 的直径,且AB ⊥C D.入口K位于AD ︵中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为t ,与入口K 的距离为S ,表示S 与t 的函数关系的图象大致如图②所示,则该园丁行进的路线可能是()第3题图A.A →O →DB.C →A →O →BC.D →O →CD.O →D →B →C4.(2023通州区一模)为满足人民对美好生活的向往,造福子孙后代,环保部门要求相关企业加强污水治理能力,污水排放未达标的企业要限期整改.甲、乙两个企业的污水排放量W 与时间t 的关系如图所示,我们用W t表示t时刻某企业的污水排放量,用-Wt1-Wt2t1-t2的大小评价在t1至t2这段时间内某企业污水治理能力的强弱.已知甲、乙两企业在整改期间排放的污水排放量与时间的关系如下图所示.第4题图给出下列四个结论:①在t1≤t≤t2这段时间内,甲企业的污水治理能力比乙企业强;②在t1时刻,乙企业的污水排放量高;③在t3时刻,甲、乙两企业的污水排放量都已达标;④在0≤t≤t1,t1≤t≤t2,t2≤t≤t3这三段时间中,甲企业在t2≤t≤t3的污水治理能力最强.其中所有正确结论的序号是()A.①②③B.①③④C.②④D.①③5.(2023房山区一模)在平面直角坐标系xOy中,若函数图象上任意两点P(x1,y1),Q(x2,y2)均满足(x1-x2)(y1-y2)>0.下列四个函数图象中,所有正确的函数图象的序号是()第5题图A.①②B.③④C.①③D.②④类型三代数类问题1.(2023西城区期末)现有函数y +4(x <a ),2-2x (x ≥a ),如果对于任意的实数n ,都存在实数m ,使得当x =m 时,y =n ,那么实数a 的取值范围是()A.-5≤a ≤4 B.-1≤a ≤4 C.-4≤a ≤1D.-4≤a ≤52.在平面直角坐标系xOy 中,对于自变量为x 的函数y 1和y 2,若当-1≤x ≤1时,都满足|y 1-y 2|≤1成立,则称函数y 1和y 2互为“关联的”.下列函数中,不与y =x 2互为“关联的”函数是()A.y =x 2-1B.y =2x 2C.y =(x -1)2D.y =-x 2+13.(2023人大附中模拟)在数轴上有三个互不重合的点A ,B ,C ,它们代表的实数分别为a ,b ,c ,下列结论中:①若abc >0,则A ,B ,C 三点中,至少有一个点在原点右侧;②若a +b +c =0,则A ,B ,C 三点中,至少有一个点在原点右侧;③若a +c =2b ,则点B 为线段AC 的中点;④O 为坐标原点且A ,B ,C 均不与O 重合,若OB -OC =AB -AC ,则bc >0.所有正确结论的序号是()A.①② B.③④ C.①②③D.①②③④4.(2023西城区二模)从1,2,3,4,5中选择四个数字组成四位数abcd ,其中a ,b ,c ,d 分别代表千位、百位、十位、个位数字.若要求这个四位数同时满足以下条件:①abcd 是偶数;②a >b >c ;③a +c =b +d ,请写出一个符合要求的数________.5.(2023燕山区期末)在实数范围内定义一种运算“*”,其运算法则为a *b =a 2-a b.根据这个法则,下列结论中错误的是________.(把所有错误结论的序号都填在横线上)①2*3=2-6;②若a +b =0,则a *b =b *a ;③(x +2)*(x +1)=0是一元二次方程;④方程(x +2)*1=3的根是x 1=-3-52,x 2=-3+52.6.(2023丰台区一模)京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系xOy 中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G .点A ,B ,C ,D 分别是图形G 与坐标轴的交点,已知点D 的坐标为(0,-3),AB 为半圆的直径,且AB =4,半圆圆心M 的坐标为(1,0).关于图形G 给出下列四个结论,其中正确的是________(填序号).①图形G 关于直线x =1对称;②线段CD 的长为3+3;③图形G 围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点);④当-4≤a ≤2时,直线y =a 与图形G 有两个公共点.第6题图7.(2023石景山区二模)在平面直角坐标系xOy 中,A (0,1),B (1,1),有以下4种说法:①一次函数y =x 的图象与线段AB 无公共点;②当b <0时,一次函数y =x +b 的图象与线段AB 无公共点;③当k >1时,反比例函数y =k x的图象与线段AB 无公共点;④当b >1时,二次函数y =x 2-bx +1的图象与线段AB 无公共点.上述说法中正确的是________.8.(2023一七一中学模拟)小聪用描点法画出了函数y =x (x ≥0)的图象F ,如图所示.结合旋转的知识,他尝试着将图象F 绕原点逆时针旋转90°得到图象F 1,再将图象F 1绕原点逆时针旋转90°得到图象F 2,如此继续下去,得到图象F n .在尝试的过程中,他发现点P (4,2)在图象________上(写出一个正确的即可);若点P (a ,b )在图象F 2021上,则a =________(用含b 的代数式表示).第8题图9.如图,A (0,1),B (1,5),曲线BC 是双曲线y =k x(k ≠0)的一部分,曲线AB 与BC 组成图形G ,由点C 开始不断重复图形G 形成一线“波浪线”,若点P (2023,m ),Q (x ,n )在该“波浪线”上,则m 的值为________.n 的最大值为________.第9题图类型四几何类问题1.(2023海淀区一模)如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR 边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是()第1题图A.AB和CDB.AB和EFC.CD和GHD.EF和GH2.程老师制作了如图①所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动.图②是操作学具时,所对应某个位置的图形的示意图.第2题图有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ;②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ;③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ;④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ.其中所有正确结论的序号是()A.②③B.③④C.②③④D.①②③④3.(2021东城区二模)数学课上,李老师提出如下问题:已知:如图,AB是⊙O的直径,射线AC交⊙O于C.求作:弧BC的中点D.同学们分享了如下四种方案:第3题图①如图①,连接BC,作BC的垂直平分线,交⊙O于点D;②如图②,过点O作AC的平行线,交⊙O于点D;③如图③,作∠BAC的平分线,交⊙O于点D;④如图④,在射线AC上截取AE,使AE=AB,连接BE,交⊙O于点D.上述四种方案中,正确的方案的序号是________.4.(20231大兴区一模)如图,在▱ABCD中,AD>AB,E,F分别为边AD,BC上的点(E,F 不与端点重合).对于任意▱ABCD,下面四个结论中:①存在无数个四边形ABFE,使得四边形ABFE是平行四边形;②至少存在一个四边形ABFE,使得四边形ABFE是菱形;③至少存在一个四边形ABFE,使得四边形ABFE是矩形;④存在无数个四边形ABFE,使得四边形ABFE的面积是▱ABCD面积的一半.所有正确结论的序号是________.第4题图5.(2021西城区期末)如图,在平面直角坐标系xOy中,P(4,3),⊙O经过点P.点A,点B 在y轴上,PA=PB,延长PA,PB分别交⊙O于点C,点D,设直线CD与x轴正方向所夹的锐角为α.(1)⊙O的半径为________;(2)tanα=________第5题图参考答案类型一分析统计图(表)1.C【解析】由题图知2019—2023年,普通本专科招生人数逐年增多,故①正确;2023年普通高中招生人数比2019年增加约876-839×100%≈4%,故②正确;从2019—2018839年,中等职业教育招生人数逐年减少,从2019—2023年,中等职业教育招生人数在增加,故③错误;2019年普通高中招生人数约是中等职业教育招生人数的839÷600≈1.4倍,故④正确.2.A【解析】①8÷0.08=100,故表中a的值为100,是合理推断;②25÷100=0.25,35÷100=0.35,1-0.08-0.17-0.35-0.15=0.25,1-0.08-0.17-0.25-0.15=0.35,故表中c的值为0.25≤c≤0.35,表中c的值可以为0.31,是合理推断;③∵表中4≤x<6组的频数b满足25≤b≤35,∴8+17+25=50,8+17+35=60,∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.3.A【解析】由题图知①2004年的水体面积超过60km2,不符合题意;②2015—2023年,密云水库的水体面积呈持续增加趋势,表明水资源储备增多,符合题意;③在1986—2023年中,2023年的密云水库水体面积最大,约为170km2,符合题意;④水体面积最大的年份是2023年,但年降水量不是最大,不符合题意.4.D【解析】由题图知,甲的面试成绩排名为11,理论知识成绩排名为8,实践操作成绩排名为8;乙的面试成绩排名为7,实践操作成绩排名为15,理论知识成绩排名为5,故①②③都合理,故选D.5.C【解析】由题图可得,A.2000年至2019年,SO2的年平均浓度值都在NO2的年平均浓度值以下,由此可得SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数,此选项正确,不合题意;B.2000年至2019年,SO2的年平均浓度值都在NO2的年平均浓度值以下,由此可得SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数,此选项正确,不合题意;C.根据图中两折线中点的离散程度可得SO2的年平均浓度值的方差大于NO2的年平均浓度值的方差,此选项错误,符合题意;D.1998年至2019年,根据图中两折线的起止点可得SO2的年平均浓度值比NO2的年平均浓度值下降得更快,此选项正确,不合题意.6.C 【解析】由图象可得,A 组客户的电动汽车的“实际平均续航里程”的最大值在350左右,B 组客户的电动汽车的“实际平均续航里程”的最大值在450左右,故A 选项不符合题意;A 组客户的电动汽车的“实际平均续航里程”的数据波动比B 组客户的电动汽车的“实际平均续航里程”的数据波动小,即A 组客户的电动汽车的“实际平均续航里程”的方差比B 组客户的电动汽车的“实际平均续航里程”的方差小,故B 选项不符合题意;A 组客户的电动汽车的“实际平均续航里程”的平均值不一定低于B 组,故C 选项符合题意;这20位客户的电动汽车的“实际平均续航里程”按从大到小排序,第10位,第11位均在B 组,故D 选项不符合题意.7.3或12(任写一个即可)【解析】由题图可知,3日、4日、5日最低温度分别是1摄氏度、2摄氏度、0摄氏度,且昼夜温差分别是8-1=7摄氏度,4-2=2摄氏度,9-0=9摄氏度,最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度,可以药剂喷洒,12日、13日、14日最低温度分别是6摄氏度、7摄氏度、8摄氏度,且昼夜温差分别是12-6=6摄氏度,16-7=9摄氏度,14-8=6摄氏度,最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度,可以药剂喷洒.类型二分析与判断函数图象1.D 【解析】∵一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同,∴v t为定值,∴v 与t 是正比例函数的关系.∴选项D 符合题意.2.B 【解析】当15<x ≤60时,设y =kx +b (k ≠0),k +b =20,k +b =170,=103,=-30,∴y =103x -30.当y =80时,103x -30=80,解得x =33,33-15=18(天),∴开始开花结果,此时瓜苗在该村大棚内生长的天数是18天.3.B 【解析】若按A →O →D 路线,图象应呈现对称性,故A 错误;若按C →A →O →B ,则从C →A 距离逐渐减少,A →O →B 距离先减少,再增大,符合题图中函数图象的大致走势,故B 正确;C 、D 中,起始点处S 值小于终点处S 值,由题图可知在起点和终点时,S 值最大且相等,故C 、D 错误.4.D 【解析】①在t 1≤t ≤t 2这段时间内,甲企业的图象比乙企业的图象倾斜角度大,故①正确;②在t 1时刻,甲企业的污水排放量高,故②错误;③在t 3时刻,甲、乙两企业的污水排放量在达标量以下,故③正确;④在0≤t ≤t 1,t 1≤t ≤t 2,t 2≤t ≤t 3这三段时间中,甲企业在t 1≤t ≤t 2的图象倾斜角度最大,即治理污水能力最强,故④错误.5.D 【解析】由题意中(x 1-x 2)(y 1-y 2)>0可知,x 1-x 2>0,y 1-y 2>0或x 1-x 2<0,y 1-y 2<0,即当x 1>x 2时,y 1>y 2或当x 1<x 2时,y 1<y 2.故函数中y 随着x 的增大而增大,故②④正确.类型三代数类问题1.A 【解析】如解图,由图象可知,当-5≤a ≤4时,对于任意的实数n ,都存在实数m ,使得当x =m 时,函数y =n .第1题解图2.C 【解析】A .∵|y 1-y 2|=|x 2-(x 2-1)|=1≤1,故A 选项与y =x 2互为“关联的”函数;B .∵|y 1-y 2|=|x 2-2x 2|=x 2,又∵-1≤x ≤1,∴x 2≤1,故B 选项与y =x 2互为“关联的”函数;C .∵|y 1-y 2|=|x 2-(x -1)2|=|2x -1|,又∵-1≤x ≤1,∴|2x -1|≤3,故C 选项不与y =x 2互为“关联的”函数;D .∵|y 1-y 2|=|x 2-(-x 2+1)|=|2x 2-1|,又∵-1≤x ≤1,∴|2x 2-1|≤1,故D 选项与y =x 2互为“关联的”函数.3.D 【解析】若全在原点的左侧,则a <0,b <0,c <0,与abc >0矛盾,∴三点中至少有一个在原点的右侧,故①正确;若全在原点的左侧,则a <0,b <0,c <0,∴a +b +c <0.又∵a ,b ,c 不全为0,与a +b +c =0矛盾,∴至少有一个点在原点右侧,故②正确;∵a +c =2b ,∴b =a +c 2,∴B 为AC 的中点,故③正确;由绝对值的意义:OB =|b |,OC =|c |,AB =|b -a |,AC =|c -a |,|b |-|c |=|b -a |-|c -a |,∴A 在最左或最右时,上面等式的右边=b -c 或c -b ,∴|b |-|c |=b -c ,∴b >0,c >0,∴bc >0,|b |-|c |=c -b ,∴b <0,c <0,∴bc >0,故④正确.4.4312(答案不唯一)【解析】∵abcd 是偶数,∴d =2或4.∵a >b >c ,a +c =b +d ,∴a =4,b =3,c =1,d =2,或a =5,b =4,c =1,d =2,或a =5,b =3,c =2,d =4,或a =5,b =2,c =1,d =4,∴abcd =4312或5412或5324或5214.5.③④【解析】根据题中的定义得:2*3=(2)2-2×3=2-6,①正确,不符合题意;若a +b =0,则有a =-b ,a *b =a 2-ab =b 2+b 2=2b 2,b *a =b 2-ab =b 2+b 2=2b 2,即a *b =b *a ,②正确,不符合题意;已知等式变形得:(x +2)2-(x +2)(x +1)=0,即x 2+4x +4-x 2-3x -2=0,合并得:x +2=0,是一元一次方程,③错误,符合题意;④方程变形得:(x +2)2-(x +2)=3,整理得:x 2+4x +4-x -2-3=0,即x 2+3x -1=0,∵a =1,b =3,c =-1,∴x =-b ±b 2-4ac 2a =-3±132,解得x 1=-3+132,x 2=-3-132,④错误,符合题意.6.①②【解析】由半圆M 可知A (-1,0),B (3,0),M (1,0),且点A ,B 在抛物线上,∴图形G 关于直线x =1对称,故①正确;如解图,连接CM ,第6题解图在Rt △MOC 中,∵OM =1,CM =2,∴OC =22-12= 3.又∵D (0,-3),∴OD =3,∴CD =OC +OD =3+3,故②正确;根据题图得,图形G 围成区域内(不含边界)恰有13个整点(即横、纵坐标均为整数的点),故③错误;由题意得A (-1,0),B (3,0),当a =-4时,直线y =-4与图形G 有一个公共点,当a =2时,直线y =2与图形G 有一个公共点,故④错误.综上所述,正确的有①②.7.②③【解析】一次函数y =x 图象经过点B (1,1),即一次函数y =x 的图象与线段AB 有公共点,故①错误;一次函数y =x 图象刚好经过点B (1,1),向下平移直线y =x ,此时b <0,直线y =x +b 与线段AB 无公共点,故②正确;反比例函数y =1x的图象刚好经过点B (1,1),当k >1时,反比例函数y =k x的图象沿着y =x 向远离原点的方向平移,与线段AB 无公共点,故③正确;二次函数y =x 2-bx +1的图象一定经过A (0,1),即二次函数的图象与线段AB 有公共点,故④错误.8.F 4,-b 【解析】根据旋转的规律得,F 1的解析式为y =x 2,其图象位于第二象限;F 2的解析式为y =--x ,其图象位于第三象限;F 3的解析式为y =-x 2,其图象位于第四象限;F 4的解析式为y =x ,其图象位于第一象限;…则2021÷4=505……1,即F 2021的图象位于第二象限,该图象的函数解析式是y =x 2.∵P (4,2)位于第一象限,∴点P 所在的图象是F 4.∵点P (a ,b )在图象F 2021上,∴b =a 2,∴a =-b .9.1,5【解析】∵B (1,5)在y =k x 的图象上,∴k =1×5=5.当x =5时,y =55=1.∴C (5,1).又∵2023÷5=404,∴m =1.∵Q (x ,n )在该“波浪线”上,∴n 的最大值是5.类型四几何类问题1.D 【解析】如解图,连接OQ ,则∠POQ =45°,sin 45°=cos 45°=22,当点M 在AB 和CD 上时,α<45°,则sin α<cos α,当点M 在EF 和GH 上时,α>45°,sin α>cos α.第1题解图2.C 【解析】①当∠PAQ =30°,PQ =6时,以P 为圆心,6为半径画弧,与射线AM 有两个交点,则△PAQ 的形状不能唯一确定,故①错误;②当∠PAQ =30°,PQ =9时,以P 为圆心,9为半径画弧,与射线AM 有两个交点,但左边位置的Q 不符合题意,∴Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故②正确;③当∠PAQ =90°,PQ =10时,以P 为圆心,10为半径画弧,与射线AM 有两个交点,但此时两个三角形全等,Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故③正确;④当∠PAQ =150°,PQ =12时,以P 为圆心,12为半径画弧,与射线AM 有两个交点,左边的Q 不符合题意,∴Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故④正确,故选C .3.①②③④【解析】①如题图①,由作图可知,BC 的垂直平分线经过圆心O ,∵OD⊥BC ,∴点D 是BC ︵的中点;②如解图①,连接BC ,∵AB 是⊙O 的直径,∴∠ACB =90°.∵OD ∥AC ,∴OD ⊥BC ,∴点D 是BC ︵的中点;③如题图③,∵∠BAD =∠CAD ,∴点D 是BC ︵的中点;④如解图②,连接AD ,∵AB 是⊙O 的直径,∴∠ADB =90°.∵AE =AB ,∴∠BAD =∠CAD ,∴点D 是BC ︵的中点.图①图②第3题解图4.①②④【解析】只要满足AB ∥EF ,则四边形ABFE 是平行四边形,这样的EF 有无数条,故①正确;∵AD >AB ,∴在AD 上截取AE =AB ,再满足AB ∥EF ,就能使得四边形ABFE 是菱形,故②正确;∵∠B 不是直角,∴矩形ABFE 不存在,故③错误;只要当EF 经过▱ABCD 对角线交点时,四边形ABFE 的面积是▱ABCD 面积的一半,这样的EF 有无数条,故④正确.5.(1)5;(2)43【解析】(1)如解图,连接OP ,∵P (4,3),∴OP =32+42=5;(2)如解图,设CD 交x 轴于点J ,过点P 作PT ⊥AB 交⊙O 于点T ,交AB 于点E ,连接CT ,DT ,OT ,∵P (4,3),∴PE =4,OE =3.在Rt △OPE 中,tan ∠POE =PE OE =43,∵OE ⊥PT ,OP =OT ,∴∠POE =∠TOE ,∴∠PDT =12∠POT =∠POE ,∵PA =PB ,PE ⊥AB ,∴∠APT =∠DPT ,∴TC ︵=DT ︵,∴∠TDC =∠TCD ,∵PT ∥x 轴,∴∠CJO =∠CKP ,∵∠CKP =∠TCK+∠CTK ,∠CTP =∠CDP ,∠PDT =∠TDC +∠CDP ,∴∠TDP =∠CJO ,∴∠CJO =∠POE ,∴tan α=tan ∠CJO =tan ∠POE =43.第5题解图。
2020年中考数学试题(及答案)

2020年中考数学试题(及答案)一、选择题1.华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ). A .7710⨯﹣ B .80.710⨯﹣C .8710⨯﹣D .9710⨯﹣ 2.预计到2025年,中国5G 用户将超过460 000 000,将460 000 000用科学计数法表示为( )A .94.610⨯B .74610⨯C .84.610⨯D .90.4610⨯3.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( ) A .众数B .方差C .平均数D .中位数4.三张外观相同的卡片分别标有数字1,2,3,从中随机一次性抽出两张,则这两张卡片上的数字恰好都小于3的概率是( ) A .19B .16C .13D .235.点 P (m + 3,m + 1)在x 轴上,则P 点坐标为( ) A .(0,﹣2)B .(0,﹣4)C .(4,0)D .(2,0)6.如图,直线l 1∥l 2,将一直角三角尺按如图所示放置,使得直角顶点在直线l 1上,两直角边分别与直线l 1、l 2相交形成锐角∠1、∠2且∠1=25°,则∠2的度数为( )A .25°B .75°C .65°D .55°7.在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x 个队参赛,根据题意,可列方程为() A .()11362x x -= B .()11362x x += C .()136x x -= D .()136x x +=8.甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次性降价30%.则顾客到哪家超市购买这种商品更合算( ) A .甲 B .乙C .丙D .一样9.下列计算错误的是( )A .a 2÷a 0•a 2=a 4 B .a 2÷(a 0•a 2)=1 C .(﹣1.5)8÷(﹣1.5)7=﹣1.5D .﹣1.58÷(﹣1.5)7=﹣1.510.下列长度的三根小木棒能构成三角形的是( )A .2cm ,3cm ,5cmB .7cm ,4cm ,2cmC .3cm ,4cm ,8cmD .3cm ,3cm ,4cm 11.二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy ++=在同一坐标系内的图象大致为( )A .B .C .D .12.an30°的值为( ) A .B .C .D .二、填空题13.已知关于x 的方程3x n22x 1+=+的解是负数,则n 的取值范围为 . 14.如图,在平面直角坐标系中,菱形OABC 的面积为12,点B 在y 轴上,点C 在反比例函数y =k x的图象上,则k 的值为________.15.当直线()223y k x k =-+-经过第二、三、四象限时,则k 的取值范围是_____.16.如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC 与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M ,绕中点M 转动上面的三角尺ABC ,使其直角顶点C 恰好落在三角尺A′B′C′的斜边A′B′上.当∠A =30°,AC =10时,两直角顶点C ,C′间的距离是_____.17.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .18.如图,一张三角形纸片ABC ,∠C=90°,AC=8cm ,BC=6cm .现将纸片折叠:使点A 与点B 重合,那么折痕长等于 cm .19.3x +在实数范围内有意义,则x 的取值范围是_____. 32x-2三、解答题21.如图,某地修建高速公路,要从A地向B地修一座隧道(A、B在同一水平面上),为了测量A、B两地之间的距离,某工程师乘坐热气球从B地出发,垂直上升100米到达C处,在C处观察A地的俯角为39°,求A、B两地之间的距离.(结果精确到1米)(参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81)22.在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小吉从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为奇数的概率.23.如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.(1)求线段AD的长度;(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.24.解不等式组3415122x xxx≥-⎧⎪⎨--⎪⎩>,并把它的解集在数轴上表示出来25.距离中考体育考试时间越来越近,某校想了解初三年级1500名学生跳绳情况,从中随机抽查了20名男生和20名女生的跳绳成绩,收集到了以下数据:男生:192、166,189,186,184,182,178,177,174,170,188,168,205,165,158,150,188,172,180,188女生:186,198,162,192,188,186,185,184,180,180,186,193,178,175,172,166,155,183,187,184.根据统计数据制作了如下统计表:个数x150≤x<170170≤x<185185≤x<190x≥190男生5852女生38a3两组数据的极差、平均数、中位数、众数如表所示:(1)请将上面两个表格补充完整:a =____,b =_____,c =_____;(2)请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分(185个及以上)的同学大约能有多少人?(3)体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好,请你结合统计数据,写出支持江老师观点的理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】由科学记数法知90.000000007710-=⨯; 【详解】解:90.000000007710-=⨯; 故选:D . 【点睛】本题考查科学记数法;熟练掌握科学记数法10n a ⨯中a 与n 的意义是解题的关键.2.C解析:C 【解析】 【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n 是正数;当原数的绝对值小于1时,n 是负数. 【详解】460 000 000=4.6×108. 故选C . 【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.3.D【解析】【分析】根据中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)的意义,9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.【详解】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.故本题选:D.【点睛】本题考查了统计量的选择,熟练掌握众数,方差,平均数,中位数的概念是解题的关键.4.C解析:C【解析】【分析】画出树状图即可求解.【详解】解:画树状图得:∵共有6种等可能的结果,而两张卡片上的数字恰好都小于3有2种情况,∴两张卡片上的数字恰好都小于3概率=13;故选:C.【点睛】本题考查的是概率,熟练掌握树状图是解题的关键.5.D解析:D【解析】【分析】根据点在x轴上的特征,纵坐标为0,可得m+1=0,解得:m=-1,然后再代入m+3,可求出横坐标.【详解】解:因为点P(m + 3,m + 1)在x轴上,所以m+1=0,解得:m=-1,所以m+3=2,所以P点坐标为(2,0).故选D.【点睛】6.C解析:C【解析】【分析】依据∠1=25°,∠BAC=90°,即可得到∠3=65°,再根据平行线的性质,即可得到∠2=∠3=65°.【详解】如图,∵∠1=25°,∠BAC=90°,∴∠3=180°-90°-25°=65°,∵l1∥l2,∴∠2=∠3=65°,故选C.【点睛】本题考查的是平行线的性质,运用两直线平行,同位角相等是解答此题的关键.7.A解析:A【解析】【分析】共有x个队参加比赛,则每队参加(x-1)场比赛,但2队之间只有1场比赛,根据共安排36场比赛,列方程即可.【详解】解:设有x个队参赛,根据题意,可列方程为:1x(x﹣1)=36,2故选:A.【点睛】此题考查由实际问题抽象出一元二次方程,解题关键在于得到比赛总场数的等量关系.8.C解析:C【解析】试题分析:设商品原价为x,表示出三家超市降价后的价格,然后比较即可得出答案.解:设商品原价为x,甲超市的售价为:x(1﹣20%)(1﹣10%)=0.72x;乙超市售价为:x(1﹣15%)2=0.7225x;丙超市售价为:x(1﹣30%)=70%x=0.7x;故到丙超市合算.考点:列代数式.9.D解析:D 【解析】分析:根据同底数幂的除法法则,同底数幂的乘法的运算方法,以及零指数幂的运算方法,逐项判定即可.详解:∵a 2÷a 0•a 2=a 4, ∴选项A 不符合题意; ∵a 2÷(a 0•a 2)=1, ∴选项B 不符合题意; ∵(-1.5)8÷(-1.5)7=-1.5, ∴选项C 不符合题意; ∵-1.58÷(-1.5)7=1.5, ∴选项D 符合题意. 故选D .点睛:此题主要考查了同底数幂的除法法则,同底数幂的乘法的运算方法,以及零指数幂的运算方法,同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a 可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.10.D解析:D 【解析】 【详解】A .因为2+3=5,所以不能构成三角形,故A 错误;B .因为2+4<6,所以不能构成三角形,故B 错误;C .因为3+4<8,所以不能构成三角形,故C 错误;D .因为3+3>4,所以能构成三角形,故D 正确. 故选D .11.D解析:D 【解析】 【分析】根据二次函数图象开口向上得到a>0,再根据对称轴确定出b ,根据二次函数图形与x 轴的交点个数,判断24b ac -的符号,根据图象发现当x=1时y=a+b+c<0,然后确定出一次函数图象与反比例函数图象的情况,即可得解. 【详解】∵二次函数图象开口方向向上, ∴a >0,∵对称轴为直线02bx a=->,二次函数图形与x 轴有两个交点,则24b ac ->0, ∵当x =1时y =a +b +c <0,∴24y bx b ac =+-的图象经过第二四象限,且与y 轴的正半轴相交,反比例函数a b cy x++=图象在第二、四象限, 只有D 选项图象符合. 故选:D. 【点睛】考查反比例函数的图象,一次函数的图象,二次函数的图象,掌握函数图象与系数的关系是解题的关键.12.D解析:D 【解析】 【分析】直接利用特殊角的三角函数值求解即可. 【详解】 tan30°=,故选:D .【点睛】本题考查特殊角的三角函数的值的求法,熟记特殊的三角函数值是解题的关键.二、填空题13.n <2且【解析】分析:解方程得:x=n ﹣2∵关于x 的方程的解是负数∴n﹣2<0解得:n <2又∵原方程有意义的条件为:∴即∴n 的取值范围为n <2且解析:n <2且3n 2≠- 【解析】 分析:解方程3x n22x 1+=+得:x=n ﹣2, ∵关于x 的方程3x n22x 1+=+的解是负数,∴n ﹣2<0,解得:n <2. 又∵原方程有意义的条件为:1x 2≠-,∴1n 22-≠-,即3n 2≠-. ∴n 的取值范围为n <2且3n 2≠-. 14.-6【解析】因为四边形OABC 是菱形所以对角线互相垂直平分则点A 和点C 关于y 轴对称点C 在反比例函数上设点C 的坐标为(x)则点A 的坐标为(-x)点B 的坐标为(0)因此AC=-2xOB=根据菱形的面积等解析:-6 【解析】设点C 的坐标为(x ,k x ),则点A 的坐标为(-x ,k x ),点B 的坐标为(0,2k x ),因此AC=-2x,OB=2K X,根据菱形的面积等于对角线乘积的一半得:()OABC 122122kS x x=⨯-⨯=菱形,解得 6.k =-15.【解析】【分析】根据一次函数时图象经过第二三四象限可得即可求解;【详解】经过第二三四象限∴∴∴故答案为:【点睛】本题考查一次函数图象与系数的关系;掌握一次函数与对函数图象的影响是解题的关键解析:13k <<. 【解析】 【分析】根据一次函数y kx b =+,k 0<,0b <时图象经过第二、三、四象限,可得220k -<,30k -<,即可求解; 【详解】()223y k x k =-+-经过第二、三、四象限,∴220k -<,30k -<, ∴1k >,3k <, ∴13k <<, 故答案为:13k <<. 【点睛】本题考查一次函数图象与系数的关系;掌握一次函数y kx b =+,k 与b 对函数图象的影响是解题的关键.16.5【解析】【分析】连接CC1根据M 是ACA1C1的中点AC=A1C1得出CM=A1M=C1M=AC=5再根据∠A1=∠A1CM=30°得出∠CMC1=60°△MCC1为等边三角形从而证出CC1=CM解析:5 【解析】 【分析】连接CC 1,根据M 是AC 、A 1C 1的中点,AC=A 1C 1,得出CM=A 1M=C 1M=12AC=5,再根据∠A 1=∠A 1CM=30°,得出∠CMC 1=60°,△MCC 1为等边三角形,从而证出CC 1=CM ,即可得出答案. 【详解】解:如图,连接CC 1,∵两块三角板重叠在一起,较长直角边的中点为M , ∴M 是AC 、A 1C 1的中点,AC=A 1C 1, ∴CM=A 1M=C 1M=12AC=5, ∴∠A 1=∠A 1CM=30°, ∴∠CMC 1=60°, ∴△CMC 1为等边三角形,∴CC1长为5.故答案为5.考点:等边三角形的判定与性质.17.3【解析】试题解析:根据概率公式摸出黑球的概率是1-02-05=03考点:概率公式解析:3.【解析】试题解析:根据概率公式摸出黑球的概率是1-0.2-0.5=0.3.考点:概率公式.18.cm【解析】试题解析:如图折痕为GH由勾股定理得:AB==10cm由折叠得:AG=BG=AB=×10=5cmGH⊥AB∴∠AGH=90°∵∠A=∠A∠AGH=∠C=90°∴△ACB∽△AGH∴∴∴G解析:cm.【解析】试题解析:如图,折痕为GH,由勾股定理得:AB==10cm,由折叠得:AG=BG=AB=×10=5cm,GH⊥AB,∴∠AGH=90°,∵∠A=∠A,∠AGH=∠C=90°,∴△ACB∽△AGH,∴,∴,∴GH=cm.考点:翻折变换19.x≥﹣3【解析】【分析】直接利用二次根式的定义求出x 的取值范围【详解】解:若式子在实数范围内有意义则x+3≥0解得:x≥﹣3则x 的取值范围是:x≥﹣3故答案为:x≥﹣3【点睛】此题主要考查了二次根式解析:x ≥﹣3【解析】【分析】直接利用二次根式的定义求出x 的取值范围.【详解】.在实数范围内有意义,则x +3≥0,解得:x ≥﹣3,则x 的取值范围是:x ≥﹣3.故答案为:x ≥﹣3.【点睛】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.20.【解析】【分析】根据解分式方程的步骤即可解答【详解】方程两边都乘以得:解得:检验:当时所以分式方程的解为故答案为【点睛】考查了解分式方程解分式方程的基本思想是转化思想把分式方程转化为整式方程求解解分解析:x 1=【解析】【分析】根据解分式方程的步骤,即可解答.【详解】方程两边都乘以x 2-,得:32x 2x 2--=-,解得:x 1=,检验:当x 1=时,x 21210-=-=-≠,所以分式方程的解为x 1=,故答案为x 1=.【点睛】考查了解分式方程,()1解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解().2解分式方程一定注意要验根.三、解答题21.123米.【解析】【分析】在Rt △ABC 中,利用tan BC CAB AB∠=即可求解. 【详解】解:∵CD∥AB,∴∠CAB=∠DCA=39°.在Rt△ABC中,∠ABC=90°,tanBC CABAB∠=.∴100123tan0.81BCABCAB==≈∠.答:A、B两地之间的距离约为123米.【点睛】本题考查解直角三角形,选择合适的锐角三角函数是解题的关键.22.49.【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次抽取的卡片上数字之和是奇数的情况,再利用概率公式即可求得答案即可.【详解】解:画树状图得:∵共有9种等可能的结果,两次抽取的卡片上数字之和是奇数的有4种情况,∴两次两次抽取的卡片上数字之和是奇数的概率为49.【点睛】本题考查列表法与树状图法.23.(1)AD=95;(2)当点E是AC的中点时,ED与⊙O相切;理由见解析.【解析】【分析】(1)由勾股定理易求得AB的长;可连接CD,由圆周角定理知CD⊥AB,易知△ACD∽△ABC,可得关于AC、AD、AB的比例关系式,即可求出AD的长.(2)当ED与 O相切时,由切线长定理知EC=ED,则∠ECD=∠EDC,那么∠A和∠DEC就是等角的余角,由此可证得AE=DE,即E是AC的中点.在证明时,可连接OD,证OD⊥DE即可.【详解】(1)在Rt△ACB中,∵AC=3cm,BC=4cm,∠ACB=90°,∴AB=5cm;连接CD,∵BC为直径,∴∠ADC=∠BDC=90°;∵∠A=∠A,∠ADC=∠ACB,∴Rt△ADC∽Rt△ACB;∴,∴;(2)当点E是AC的中点时,ED与⊙O相切;证明:连接OD,∵DE是Rt△ADC的中线;∴ED=EC,∴∠EDC=∠ECD;∵OC=OD,∴∠ODC=∠OCD;∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°;∴ED⊥OD,∴ED与⊙O相切.【点睛】本题考查了圆周角定理、切线的判定、相似三角形的判定与性质,熟练掌握该知识点是本题解题的关键. 24.-1<x≤1【解析】【分析】分别解两个不等式,然后根据数轴或“都大取大,都小取小,大小小大取中间,大大小小无解了”求解不等式组.【详解】解:341 {5122x xxx≥--->①②解不等式①可得x≤1,解不等式②可得x>-1在数轴上表示解集为:所以不等式组的解集为:-1<x≤1.【点睛】本题考查了解不等式组,熟练掌握计算法则是解题关键.25.(1)a=6,b=179,c=188;(2)600;(3)详见解析.【解析】【分析】(1)依据中位数以及众数的定义即可将上面两个表格补充完整;(2)依据样本中能得满分(185个及以上)的同学所占的比例,即可估计该校初三年级学生中考跳绳成绩能得满分的人数;(3)依据两组数据的极差和平均数的大小,即可得到结论.【详解】(1)满足185≤x<190的数据有:186,188,186,185,186,187.∴a=6,20名男生的跳绳成绩排序后最中间的两个数据为178和180,∴b=(178+180)=179,20名男生的跳绳成绩中出现次数最多的数据为188,∴c=188,故答案为:6;179;188;(2)∵20名男生和20名女生的跳绳成绩中,185个及以上的有16个,∴该校初三年级学生中考跳绳成绩能得满分(185个及以上)的同学大约能有1500×=600(人);(3)理由:初三年级的女生跳绳成绩的极差较小,而平均数较大.【点睛】本题考查了用样本估计总体,中位数,众数,正确的理解题意是解题的关键.一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考填空选择习题
不管是中考数学最后一题还是其他题,都一样的:从题目条件入手,一般来说最后一问可能会难一点,前两问尤其是第一问从条件出发稍微推理下就能得出答案。
做不出来时,再读一遍题目,留意给的每一个条件,就像我们从一个地方到另一个地方不知道具体的路怎么走,但是我们可以根据路边的提示慢慢的往前摸索,终究能到达终点。
如果题目条件不会运用,那就说明可能是你基础还有问题,初中知识点不是很多,把基础打牢,才能灵活运用。
要坚信:一分耕耘,一分收获!
1. 如图,在Rt ⊿ABC 中,AB=3,BC=4,∠ABC=90°,过B 作BA 1⊥AC ,过A 1作A 1B 1⊥BC ,得阴影Rt ⊿A 1B 1B ;再过B 1作B 1A 2⊥AC ,过A 2作A 2B 2⊥BC ,得阴影Rt ⊿A 2B 2B 1;……如此下去,请猜测这样得到的所有阴影三角形的面积之和为( ) 9
A. 1625
B. 9625
C. 5441
D. 96
41
2. 如图△ABC 中,∠A CB =90°,BC =6 cm ,AC =8cm ,动点P 从A 出发,以2 cm / s 的速度沿AB 移动到B ,则点P 出发 s 时,△BCP 为等腰三角形.
3.如图,Rt △ABC 的直角边BC 在x 轴正半轴上,斜边AC 上的中线BD
的反向延长线交y 轴负半轴于点E,双曲线x
k
y =(x >0)的图像经过
点A ,若8=∆EBC S 则k =_____________
4.【改编】如图,E 、F 分别是
B C D 的边AB 、CD 上 的点,AF 与DE 相交于点P ,
BF 与CE 相交于 点Q ,若S △APD 15=2
cm ,S △BQC 25=2
cm , 则阴影部分的面积为 2
cm 。
5. 如图,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE =60°,BD =3,
第4题 A
B
C
E
6.已知一直线过点(1,a )且与直线y=3x-6平行,与二次函数y=ax 2只有 一个公共点,则a 的值是__________。
7. 如图,点C 、D 是以线段AB 为公共弦的两条圆弧的中点,AB =4,点E 、F 分别是线段
CD ,AB 上的动点,设AF =x ,AE 2-FE 2=y ,则能表示y 与x 的函数关系的图象是( )
8. 如图,把正△ABC 的外接圆对折,使点A 落在弧BC 的中点F 上,若BC=5,则折痕在△ABC 内的部分DE 长为_______。
9. 正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置.
点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y kx b =+(k >0) 和x 轴上,已知点B 1(1,1),B 2(3,2), 则B n 的坐标是_______________.
10. 如图,直线4
3
y x =
与双曲线()0k y x x =>交于点A ,将直线
43y x =
向右平移92个单位后,与双曲线()0k
y x x
=>交于点B ,
与x 轴交于点C . 若2OA
BC
=,则=k 。
15 11.如图6,
,过
上到点
的距离分别为
的点作
的垂线
与
相交,得到并标出一组黑色梯形,它们的面
积分别为.观察图中的规律,求出第10
个黑色梯形的面积
( ).
A.32
B.54
C.76
D.86
12.如图,AC 是O ⊙的直径,P A ,PB 是O ⊙的切线,A ,B 为切点,AB =6,P A =5.则O ⊙的半径____________.16
13. 如图,直线y =2x +3与x 轴交于点A ,与y 轴交于点B 。
过B 点作直线BP 与x 轴交于点P ,且使OP =2OA ,则△ABP 的面积为 。
14、如图,点P 为△ABC 的内心,延长AP 交△ABC 的外接圆于D ,过D 作DE//BC ,交AC 的延长线于E 点。
①则直线DE 与⊙O 的位置关系是 ;②若AB=4,AD=6,CE=3,则DE= 。
15.设0<k <2,关于x 的一次函数2(1)y kx x =+-,当1≤x ≤2时的最大值是( )
(A )22k - (B )1k - (C )k (D )1k +
16. 一名模型赛车手遥控一辆赛车,先前进1m ,然后,原地逆时针方向旋转角a(0°<α<180°)。
被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )
(A) 7 2° (B )108°或14 4° (C )144° (D ) 7 2°或144° 17. 双曲线x 10
y =
与x
6y =在第一象限内的图象依次是M 和N ,设点P 在图像M 上,PC 垂直于X 轴于点C 交图象N 于点A 。
PD 垂直于Y 轴于D 点,交图象N 于点B ,则四边
形PAOB 的面积为( )
(A) 8 (B) 6 (C)4 (D) 2
18.已知二次函数y = 2
y ax bx c =++的图像如图所示,令M=︱4a-2b+c ︱+︱a+b+c ︱- ︱2a+b ︱+︱2a-b ︱,则以下结论正确的是………………………………………………( )
A.M <0
B.M >0
C.M=0
D.M 的符号不能确定
19.若【x 】表示不超过x 的最大整数(如【∏】=3,【2
23
-】=-3等),
则【
】+
【】+…+
【】
= .
C
(第12题)
E
D
C B
A
20. 如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y 轴上,OA=10cm ,OC=6cm 。
P 是线段OA 上的动点,从点O 出发,以1cm/s 的速度沿OA 方向作匀速运动,点Q 在线段AB 上。
已知A 、Q 两点间的距离是O 、P 两点间距离的a 倍。
若用(a ,t )表示经过时间t(s)时,△OCP 、△PAQ 、△CBQ 中有两个三角形全等
况 .19
21. 如图,在矩形ABCD 中,BC=8,AB=6,经过点B 和点D 的两个
动圆均与AC 相切,且与AB 、BC 、AD 、DC 分别交于点G 、H 、E 、F ,则EF+GH 的最小值是( )
A .6
B .8
C .9.6
D .10
22.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的面积为 .
23.如图,正方形ABCD 中,E 是BC 边上一点,以E 为圆心,EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则tan
∠EAB 的值是( ) 24.边长为1的正方形OA 1B 1C 1的顶点A 1在X 轴的正半轴上,如图将
(第20题) 第21题
正方形OA 1B 1C 1绕顶点O 顺时针旋转75°得正方形OABC ,使点B 恰好落在函数y=ax
2
(a<0)的图像上,则a 的值为___________. 25.(6分)(根据杭州启正中学2010学年第二学期九下期初摸底卷第14题改编)已知关于
x 的函数2(1)4y k x x k =-++的图像与坐标轴只有2个交点,求k 的值.。
