基于MATLAB进行控制系统的滞后-超前校正设计
基于MATLAB进行控制系统的滞后-超前校正设计要点

计算机控制技术------滞后-超前校正控制器设计系别:电气工程与自动化专业:自动化班级:B110411学号:B11041104姓名:程万里目录一、 滞后-超前校正设计目的和原理 (1)1.1 滞后-超前校正设计目的......................................................... 1 1.2 滞后-超前校正设计原理......................................................... 1 二、滞后-超前校正的设计过程 (3)2.1 校正前系统的参数 (3)2.1.1 用MATLAB 绘制校正前系统的伯德图................................. 3 2.1.2 用MATLAB 求校正前系统的幅值裕量和相位裕量.................. 4 2.1.3 用MATLAB 绘制校正前系统的根轨迹................................. 5 2.1.4 对校正前系统进行仿真分析.............................................5 2.2 滞后-超前校正设计参数计算 (6)2.2.1 选择校正后的截止频率c ω............................................. 6 2.2.2 确定校正参数β、2T 和1T (6)2.3 滞后-超前校正后的验证 (7)2.3.1 用MATLAB 求校正后系统的幅值裕量和相位裕量..................7 2.3.2 用MATLAB 绘制校正后系统的伯德图.................................8 2.3.3 用MATLAB 绘制校正后系统的根轨迹.................................9 2.3.4 用MATLAB 对校正前后的系统进行仿真分析 (10)三、前馈控制3.1 前馈控制原理..................................................................... 12 3.2控制对象的介绍及仿真......................................................... 12 四、 心得体会.............................................................................. 16 参考文献.......................................................................................17 附录 (18)一、滞后-超前校正设计目的和原理1.1 滞后-超前校正设计目的所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足给定的性能指标。
用MATLAB进行控制系统的滞后-超前校正设计

课程设计任务书学生姓名: 专业班级:指导教师: 程 平 工作单位: 自动化学院 题 目: 用MATLAB 进行控制系统的滞后-超前校正设计 初始条件:已知一单位反馈系统的开环传递函数是)102.0)(11.0()(++=s s s Ks G要求系统的静态速度误差系数150-≥S v K , 40≥γ,s rad w c /10≥。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、MATLAB 作出满足初始条件的最小K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
2、前向通路中插入一相位滞后-超前校正,确定校正网络的传递函数。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、用Matlab 对校正前后的系统进行仿真分析,画出阶跃响应曲线5、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日串联滞后-超前校正兼有滞后校正和超前校正的优点,即已校正系统的响应速度较快,超调量较小,抑制高频噪声的性能也较好。
当校正系统不稳定,且要求校正后系统的响应速度,相角裕度和稳态精度较高时,以采用串联滞后-超前校正为宜。
其基本原理是利用滞后-超前网络的超前部分来增大系统的相角裕度,同时利用滞后部分来改善系统的稳态性能。
此次课程设计就是利用MATLAB对一单位反馈系统进行滞后-超前校正。
通过运用MATLAB的相关功能,绘制系统校正前后的伯德图、根轨迹和阶跃响应曲线,并计算校正后系统的时域性能指标。
关键字:超前-滞后校正 MATLAB 伯德图时域性能指标1 滞后-超前校正设计目的和原理 (1)1.1 滞后-超前校正设计目的 (1)1.2 滞后-超前校正设计原理 (1)2 滞后-超前校正的设计过程 (3)2.1 校正前系统的参数 (3)2.1.1 用MATLAB绘制校正前系统的伯德图 (4)2.1.2 用MATLAB求校正前系统的幅值裕量和相位裕量 (4)2.1.3 用MATLAB绘制校正前系统的根轨迹 (5)2.1.4 对校正前系统进行仿真分析 (6)2.2 滞后-超前校正设计参数计算 (7) (8)2.2.1 选择校正后的截止频率c2.2.2 确定校正参数 (8)2.3 滞后-超前校正后的验证 (9)2.3.1 用MATLAB求校正后系统的幅值裕量和相位裕量 (9)2.3.2 用MATLAB绘制校正后系统的伯德图 (10)2.3.3 用MATLAB绘制校正后系统的根轨迹 (11)2.3.4 用MATLAB对校正前后的系统进行仿真分析 (12)3 心得体会 (14)参考文献 (16)用MATLAB进行控制系统的滞后-超前校正设计1 滞后-超前校正设计目的和原理1.1 滞后-超前校正设计目的所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足给定的性能指标。
用MATLAB进行控制系统的超前设计

题 目: 用MATLAB 进行控制系统的超前校正设计 初始条件:已知一单位反馈系统的开环传递函数是)5.01)(05.01()(s s s Ks G ++=要求系统跟随2r/min 的斜坡输入产生的最大稳态误差为2°, 45≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、用MATLAB 作出满足初始条件的最小K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
2、在系统前向通路中插入一相位超前校正,确定校正网络的传递函数。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:任务 时间(天)审题、查阅相关资料1 分析、计算2 编写程序 2 撰写报告 2 论文答辩0.5指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日控制系统的超前校正设计1校正简介以及超前校正的原理方法 1.1校正简介所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足所给定的性能指标。
校正环节的形式及其在系统中的位置称为校正方案。
一般有:串联校正,并联校正,反馈校正,以及前馈校正,本次课设就是用的串联校正中的超前校正。
1.2超前校正及其特性超前校正就是在前向通道中串联传递函数为:()()()111G c ++⋅==Ts aTs a s R s C s 式中:1221>+=R R R a C R R R R T 2121+=通常 a 为分度系数,T 叫时间常数,由式(2-1)可知,采用无源超前网络进行串联校正 时,整个系统的开环增益要下降 a 倍,因此需要提高放大器增益交易补偿. 如果对无源超前网络传递函数的衰减由放大器增益所补偿,则()11++=Ts aTs s aG c上式称为超前校正装置的传递函数。
无源超前校正网络的对数频率特性如图1。
滞后-超前校正

目录摘要 (1)引言 (2)1 滞后-超前校正设计目的和原理 (2)1.1滞后-超前校正设计目的 (2)1.2滞后-超前校正设计原理 (2)2 滞后-超前校正的设计过程 (4)2.1校正前系统的参数 (4)2.1.1 用MATLAB绘制校正前系统的伯德图 (4)2.1.2 用MATLAB求校正前系统的幅值裕量和相位裕量 (5)2.1.3 用MATLAB绘制校正前系统的根轨迹 (6)2.1.4 对校正前系统进行仿真分析 (7)2.2滞后-超前校正设计参数计算 (8)ω (8)2.2.1 选择校正后的截止频率c2.2.2确定校正参数β、2T和1T (8)2.3滞后-超前校正后的验证 (9)2.3.1 用MATLAB求校正后系统的幅值裕量和相位裕量 (9)2.3.2 用MATLAB绘制校正后系统的伯德图 (10)2.3.3 用MATLAB绘制校正后系统的根轨迹 (11)2.3.4 用MATLAB对校正前后的系统进行仿真分析 (12)结束语 (14)参考文献 (15)用MATLAB进行控制系统的滞后-超前校正设计摘要自动控制技术的应用日益广泛,除了在国防、空间科技等尖端领域里成为不可或缺的重要技术之外,在机电工程、冶金、化工、轻工、交通管理、环境保护、农业等领域中,自动控制技术的作用也日显突出。
自动控制技术的运用大大提高了劳动生产率和产品质量,同时,也改善了劳动条件,在改善人类的居住环境和提高生活质量方面也发挥了非常重要的作用。
今天的社会生活中,自动化装置已经无所不在,为人类文明进步做出了重要的贡献。
自动控制系统的课程设计是检验我们学过知识扎实程度的好机会,也让我们的知识体系更加系统,更加完善。
在不断学习新知识的基础上得到了动手能力的训练,启发创新思维及独立解决实际问题的能力,提高设计、装配、调试能力。
关键词:滞后超前校正伯德图 MATLAB 校正参数引言如果系统设计要求满足的性能指标属频域特征量,则通过采用频域校正方法。
用MATLAB进行控制系统的滞后校正设计
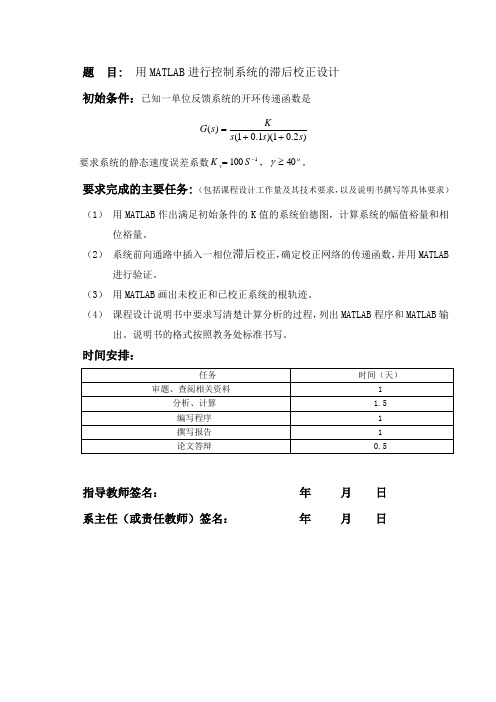
题 目: 用MATLAB 进行控制系统的滞后校正设计 初始条件:已知一单位反馈系统的开环传递函数是)2.01)(1.01()(s s s Ks G ++=要求系统的静态速度误差系数1100-=S K v ,ο40≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1) 用MATLAB 作出满足初始条件的K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
(2) 系统前向通路中插入一相位滞后校正,确定校正网络的传递函数,并用MATLAB进行验证。
(3) 用MATLAB 画出未校正和已校正系统的根轨迹。
(4) 课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日用MATLAB 进行控制系统的滞后校正设计1滞后校正特性及校正方法1.1滞后校正特性滞后校正就是在前向通道中串联传递函数为)(s G c 的校正装置来校正控制系统,)(s G c 的表达式如下所示。
1,11)(<++=a TsaTss G c 其中,参数a 、T 可调。
滞后校正的高频段是负增益,因此,滞后校正对系统中高频噪声有削弱作用,增强了抗干扰能力。
可以利用滞后校正的这一低通滤波所造成的高频衰减特性,降低系统的截止频率,提高系统的相位裕度,以改善系统的暂态性能。
滞后校正的基本原理是利用滞后网络的高频幅值衰减特性使系统截止频率下降,从而使系统获得足够的相位裕度。
或者,是利用滞后网络的低通滤波特性,使低频信号有较高的增益,从而提高了系统的稳态精度。
可以说,滞后校正在保持暂态性能不变的基础上,提高开环增益。
也可以等价地说滞后校正可以补偿因开环增益提高而发生的暂态性能的变化。
1.2滞后校正设计的一般步骤与方法(1)按稳态性能指标要求的开环放大系数绘制未校正系统的伯德图。
用MATLAB进行控制系统的超前校正设计

012111136023学号:2课程设计用MATLAB进行控制系统的超前校正题目设计学院自动化学院专业自动化班级自动化11班姓名指导教师谭思云2013年12月25日课程设计任务书学生姓名: 刘嘉雯 专业班级:自动化1102班指导教师: 谭思云 工作单位: 自动化学院题 目: 用MATLAB 进行控制系统的超前校正设计。
初始条件:已知一单位反馈系统的开环传递函数是)3.01)(1.01()(s s s K s G ++= 要求系统的静态速度误差系数 456v ≥≤γ,K 。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、用MATLAB 作出满足初始条件的K 值的系统伯德图,计算系统的幅值裕度和相位裕度。
2、在系统前向通路中插入一相位超前校正,确定校正网络的传递函数,并用MATLAB 进行验证。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:1、课程设计任务书的布置,讲解 (半天)2、根据任务书的要求进行设计构思。
(半天)3、熟悉MATLAB 中的相关工具(一天)4、系统设计与仿真分析。
(三天)5、撰写说明书。
(二天)6、课程设计答辩(半天)指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 01课程设计目的 (1)2设计条件及任务要求 (1)2.1设计条件 (1)2.2设计任务要求 (1)3设计基本原理 (2)3.1超前校正 (2)3.2根轨迹法 (4)4设计过程 (5)4.1基本思路及步骤 (5)4.2校正前系统分析 (5)4.2.1开环增益 (5)4.2.2相位裕度和幅值裕度 (6)4.2.3伯德图 (7)4.2.4根轨迹 (8)4.3超前校正系统设计 (9)4.3.1 理论分析 (9)4.3.2参数计算 (10)4.3.3编程设计 (11)4.4校正后系统分析 (12)4.4.1伯德图 (12)4.4.2根轨迹 (13)5结果对比与分析 (14)5.1校正前后阶跃响应曲线 (14)5.2结果分析 (15)6总结 (17)参考文献 (18)摘要在自动控制理论中,超前校正是相当重要的一环,对于系统的优化有很重要的意义。
用MATLAB进行控制系统的滞后-超前校正设计

课程设计任务书学生姓名: 李 超 专业班级: 电气 1001班 指导教师: 刘志立 工作单位: 自动化学院 题 目: 用MATLAB 进行控制系统的滞后-超前校正设计 初始条件:已知一单位反馈系统的开环传递函数是)2)(1()(++=s s s K s G 要求系统的静态速度误差系数110-≥S K v ,ο45≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 MATLAB 作出满足初始条件的最小K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
2、前向通路中插入一相位滞后-超前校正,确定校正网络的传递函数。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、用Matlab 对校正前后的系统进行仿真分析,画出阶跃响应曲线,计算其时域性能指标。
5、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日MATLAB是一个包含大量计算算法的集合。
其拥有600多个工程中要用到的数学运算函数,可以方便的实现用户所需的各种计算功能。
函数中所使用的算法都是科研和工程计算中的最新研究成果,而前经过了各种优化和容错处理。
在通常情况下,可以用它来代替底层编程语言,如C和C++。
在计算要求相同的情况下,使用MATLAB的编程工作量会大大减少。
MATLAB的这些函数集包括从最简单最基本的函数到诸如矩阵,特征向量、快速傅立叶变换的复杂函数。
函数所能解决的问题其大致包括矩阵运算和线性方程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和其他初等数学运算、多维数组操作以及建模动态仿真等。
此次课程设计就是利用MATLAB对一单位反馈系统进行滞后-超前校正。
用MATLAB进行控制系统的滞后校正课程设计

附件2:课程设计任务书学生姓名: 专业班级: 指导教师: 工作单位:题 目: 用MATLAB 进行控制系统的滞后校正设计。
初始条件:已知一单位反馈系统的开环传递函数是)2.01)(1.01()(s s s Ks G ++=要求系统的静态速度误差系数1100-=S K v , 40≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、用MATLAB 作出满足初始条件的K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
2、系统前向通路中插入一相位滞后校正,确定校正网络的传递函数。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日目录1 滞后校正系统的设计系统滞后校正设计方案 (2)1.1 设计原理 (2)1.2 设计步骤 (3)2 设计串联滞后校正 (4)2.1 校正前参数确定 (4)3 系统前向通路中插入一相位滞后校正 (5)3.1 确定校正网络的传递函数 (5)3.2 应用MATLAB进行验证 (7)3.3 波特图的理论绘制 (8)3.4 用MATLAB进行设计 (9)4 画出未校正和已校正系统的根轨迹 (11)4.1 用MATLAB画出未校正系统和已校正系统的根轨迹114.2 根轨迹的理论作图步骤 (12)5 设计总结 (13)6 收获与体会 (14)参考文献 (15)1 滞后校正系统的设计系统滞后校正设计方案1.1设计原理所谓校正,就是在系统中加入一些其参数可以根据需要而改变的机构或装置,使系统整个特性发生变化,从而满足给定的各项性能指标。
系统校正的常用方法是附加校正装置。
按校正装置在系统中的位置不同,系统校正分为串联校正、反馈校正和复合校正。
按校正装置的特性不同,又可分为超前校正、滞后校正和滞后-超前校正、PID校正。
用MATLAB进行控制系统的滞后校正设计

题 目: 用MATLAB 进行控制系统的滞后校正设计 初始条件:已知一单位反馈系统的开环传递函数是)2.01)(1.01()(s s s Ks G ++=要求系统的静态速度误差系数1100-=S K v ,ο40≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1) 用MATLAB 作出满足初始条件的K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
(2) 系统前向通路中插入一相位滞后校正,确定校正网络的传递函数,并用MATLAB进行验证。
(3) 用MATLAB 画出未校正和已校正系统的根轨迹。
(4) 课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日用MATLAB 进行控制系统的滞后校正设计1滞后校正特性及校正方法1.1滞后校正特性滞后校正就是在前向通道中串联传递函数为)(s G c 的校正装置来校正控制系统,)(s G c 的表达式如下所示。
1,11)(<++=a TsaTss G c 其中,参数a 、T 可调。
滞后校正的高频段是负增益,因此,滞后校正对系统中高频噪声有削弱作用,增强了抗干扰能力。
可以利用滞后校正的这一低通滤波所造成的高频衰减特性,降低系统的截止频率,提高系统的相位裕度,以改善系统的暂态性能。
滞后校正的基本原理是利用滞后网络的高频幅值衰减特性使系统截止频率下降,从而使系统获得足够的相位裕度。
或者,是利用滞后网络的低通滤波特性,使低频信号有较高的增益,从而提高了系统的稳态精度。
可以说,滞后校正在保持暂态性能不变的基础上,提高开环增益。
也可以等价地说滞后校正可以补偿因开环增益提高而发生的暂态性能的变化。
1.2滞后校正设计的一般步骤与方法(1)按稳态性能指标要求的开环放大系数绘制未校正系统的伯德图。
自动控制原理MATLAB课程设计--滞后-超前校正

滞后-超前校正——课程设计一、设计目的:1. 了解控制系统设计的一般方法、步骤。
2. 掌握对系统进行稳定性的分析、稳态误差分析以及动态特性分析的方法。
3. 掌握利用MATLAB 对控制理论内容进行分析和研究的技能。
4. 提高分析问题解决问题的能力。
二、设计内容与要求:设计内容:1. 阅读有关资料。
2. 对系统进行稳定性分析、稳态误差分析以及动态特性分析。
3. 绘制根轨迹图、Bode 图、Nyquist 图。
4. 设计校正系统,满足工作要求。
设计条件:1、被控制对象的传递函数是m m 1m 2012mn sn 1n 2012nb s b s b s b ()a s a a s a G S ----+++⋯+=+++⋯+(n≥m)2、参数a0,a1,a2,...an和b0,b1,b2,...bm因小组而异。
设计要求:1. 能用MATLAB 解复杂的自动控制理论题目。
2. 能用MATLAB 设计控制系统以满足具体的性能指标。
3. 能灵活应用MATLAB 的CONTROL SYSTEM 工具箱和SIMULINK 仿真软件,分析系统的性能。
三、设计步骤:1、自学MATLAB软件的基本知识,包括MATLAB的基本操作命令。
控制系统工具箱的用法等,并上机实验。
2、基于MALAB用频率法对系统进行串联校正设计,使其满足给定的领域性能指标。
要求程序执行的结果中有校正装置传递函数和校正后系统开环传递函数,校正装置的参数T,α等的值。
已知开环传递函数为G(S)= 0(2)(40)k s s s ++,使用频率法设计串联滞后—超前校正装置,使系统的相角裕度大于等于40°,静态速度误差系数等于20。
校正前根据上式可化简G(S)= 00.0125(0.51)(0.0251)k s s s ++,所以公式G(S)=20(0.51)(0.0251)s s s ++,所以=1,则c w = 6.1310,相角裕度γ为9.3528。
用MATLAB进行控制系统的超前校正设计

用MATLAB进行控制系统的超前校正设计超前校正是一种用于控制系统设计的技术,它通过提前预测系统的动态性质,并校正输出信号,以改善系统的性能和稳定性。
在MATLAB中,我们可以使用控制系统工具箱来进行超前校正的设计。
超前校正的设计步骤如下:1. 确定系统的传递函数模型:首先,我们需要确定待控制系统的数学模型,通常使用传递函数表示。
在MATLAB中,我们可以使用`tf`函数定义传递函数。
例如,如果系统的传递函数为G(s) = (s + 2)/(s^2 + 5s + 6),可以用以下命令定义该传递函数:```matlabG = tf([1 2], [1 5 6]);```2.确定要求的超前时间常数和相位余量:超前校正的目标是在系统的低频区域增加相位余量,以提高系统的稳定性和性能。
我们需要根据应用需求确定所需的超前时间常数和相位余量。
一般来说,相位余量取值在30到60度之间较为合适。
3.计算所需的超前网络增益:根据所需的超前时间常数和相位余量,可以使用以下公式计算所需的超前网络增益:```matlabKc = 1 / sqrt(phi) * abs(1 / evalfr(G, j * w_c))```其中,phi为所需的相位余量,w_c为所需的截止角频率,evalfr函数用于计算传递函数在复频域上的值。
4. 设计超前校正网络:超前校正网络通常由一个增益项和一个零点组成,用于提高低频响应的相位余量。
使用`leadlag`函数可以方便地设计超前校正网络。
例如,以下命令可以设计一个零点在所需截止频率处的超前校正网络:```matlabw_c=1;%所需的截止角频率phi = 45; % 所需的相位余量Gc = leadlag(w_c, phi);```5. 计算开环传递函数和闭环传递函数:使用`series`函数可以计算超前校正网络和原系统传递函数的乘积,得到开环传递函数。
而使用`feedback`函数可以根据需要计算闭环传递函数。
基于MATLAB的滞后-超前校正器的设计

2009级自动化专业《计算机控制技术》课程设计任务书
论文
题目
基于MATLAB的滞后-超前校正器的设计
设计类型
导师姓名
主要内容及目标
滞后-超前校正设计的基本原理是利用网络的超前部分来增大系统的相角裕度,同时利用滞后部分来改善系统的稳态性能。这种校正方法兼有滞后校正和超前校正的优点,即已校正系统响应速度较快,超调量较小,抑制高频噪声的性能也较好。当待校正系统不稳定,且要求校正后系统的响应速度、相角裕度和稳态精度较高时,采用滞后-超前校正比较适合。
滞后-超前校正器的传递函数可表示为: 其中: . =1, >1,. <1, 为网络的滞后部分, 为网络的超前部分。。
具有的设计条件
1.PC机一台,教学实验箱一台;,
计划学生数及任务
3人
(1):明确课题功能。
(2):把复杂问题分解为若干模块,确定各模块处理方法。
(3):编制程序,根据流程图来编制源程序
(5):调试和修改,直到程序运行结果正确为止。
计划设计进程
一、总体方案设计
二、控制系统的建模和数字控制器设计
三、软件设计
四、编写课程设计说明书,绘制完整的校正前后的Bode图和系统的阶跃响应曲线图。
参考文献
1.于海生计算机控制技术[M]北京:机械工业出版社,2007.6
2、王素青.基于MATLAB的滞后-超前校正器的设计[J].微计算机信息,2009,25(6-1)
滞后-超前校正

目录摘要 (1)引言 (2)1 滞后-超前校正设计目的和原理 (2)1.1滞后-超前校正设计目的 (2)1.2滞后-超前校正设计原理 (2)2 滞后-超前校正的设计过程 (4)2.1校正前系统的参数 (4)2.1.1 用MATLAB绘制校正前系统的伯德图 (4)2.1.2 用MATLAB求校正前系统的幅值裕量和相位裕量 (5)2.1.3 用MATLAB绘制校正前系统的根轨迹 (6)2.1.4 对校正前系统进行仿真分析 (7)2.2滞后-超前校正设计参数计算 (8)ω (8)2.2.1 选择校正后的截止频率c2.2.2确定校正参数β、2T和1T (8)2.3滞后-超前校正后的验证 (9)2.3.1 用MATLAB求校正后系统的幅值裕量和相位裕量 (9)2.3.2 用MATLAB绘制校正后系统的伯德图 (10)2.3.3 用MATLAB绘制校正后系统的根轨迹 (11)2.3.4 用MATLAB对校正前后的系统进行仿真分析 (12)结束语 (14)参考文献 (15)用MATLAB进行控制系统的滞后-超前校正设计摘要自动控制技术的应用日益广泛,除了在国防、空间科技等尖端领域里成为不可或缺的重要技术之外,在机电工程、冶金、化工、轻工、交通管理、环境保护、农业等领域中,自动控制技术的作用也日显突出。
自动控制技术的运用大大提高了劳动生产率和产品质量,同时,也改善了劳动条件,在改善人类的居住环境和提高生活质量方面也发挥了非常重要的作用。
今天的社会生活中,自动化装置已经无所不在,为人类文明进步做出了重要的贡献。
自动控制系统的课程设计是检验我们学过知识扎实程度的好机会,也让我们的知识体系更加系统,更加完善。
在不断学习新知识的基础上得到了动手能力的训练,启发创新思维及独立解决实际问题的能力,提高设计、装配、调试能力。
关键词:滞后超前校正伯德图 MATLAB 校正参数引言如果系统设计要求满足的性能指标属频域特征量,则通过采用频域校正方法。
用MATLAB进行控制系统的滞后校正设计

题 目: 用MATLAB 进行控制系统的滞后校正设计 初始条件:已知一单位反馈系统的开环传递函数是)2.01)(1.01()(s s s Ks G ++=要求系统的静态速度误差系数1100-=S K v , 40≥γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1) 用MATLAB 作出满足初始条件的K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
(2) 系统前向通路中插入一相位滞后校正,确定校正网络的传递函数,并用MATLAB进行验证。
(3) 用MATLAB 画出未校正和已校正系统的根轨迹。
(4) 课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:任务 时间(天)审题、查阅相关资料1 分析、计算 1.5 编写程序 1 撰写报告 1 论文答辩0.5指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日用MATLAB 进行控制系统的滞后校正设计1滞后校正特性及校正方法1.1滞后校正特性滞后校正就是在前向通道中串联传递函数为)(s G c 的校正装置来校正控制系统,)(s G c 的表达式如下所示。
1,11)(<++=a TsaTss G c 其中,参数a 、T 可调。
滞后校正的高频段是负增益,因此,滞后校正对系统中高频噪声有削弱作用,增强了抗干扰能力。
可以利用滞后校正的这一低通滤波所造成的高频衰减特性,降低系统的截止频率,提高系统的相位裕度,以改善系统的暂态性能。
滞后校正的基本原理是利用滞后网络的高频幅值衰减特性使系统截止频率下降,从而使系统获得足够的相位裕度。
或者,是利用滞后网络的低通滤波特性,使低频信号有较高的增益,从而提高了系统的稳态精度。
可以说,滞后校正在保持暂态性能不变的基础上,提高开环增益。
也可以等价地说滞后校正可以补偿因开环增益提高而发生的暂态性能的变化。
用MATLAB进行滞后—超前校正器的设计

【 ywo d 】 L g1 dc ret r u cinflge d Ke r s a . a orco ;F nt r la ;Co ue ie ein e o a mp tr d dd s a g
超前校正 的作 用是使 响应 加快 ,使系统的稳 定性 增加 。 滞后校 正的作用则是改善 系统 的稳态精确度 ,但将减慢 响应 速度 。如果要 同时改善 瞬态响应和稳态 响应 ,则需要采 用滞
(
GI =Kc () G()
f
=∞\
0 P 1
0 B f . e
确定增 益 ,使其满足稳态 误差系数 的要 求。
() 用 已经确 定 的增 益 ,画出未校 正 的系统 G( 的 2利 ) j 伯德 图
() 定校 正后 的穿越 频率 。, 得滞后. 前校正器在 穿越频 率 处 产 生的相 位超 前角 超 就等于 系统的相 位裕度 }。 ,
考 虑图2 所示 的控制 系统 ,
采用式() 1表示 的滞 后一 超
式( 中 > ,右端第一 项分式为滞 后一 1 ) 1 超前校 正器 的超
前 部分( 含7的部分) 包 , ,它改变 了频率响应 曲线 ,这是 因为 它 增加了相 位超 前角 ,并且增加 了相位裕度 ;右端第二项 分 式为滞后一 超前校 正器的滞后部 分( 包含 的部分) ,它在穿越 频 率附近引起响应的衰减 ,因此,它允许在低频 范围内增 加 增 益 ,从而改善系统 的稳态特性 。
图1当 = 时式() l 1给出 的滞序 超前校正器的乃魁斯特图
当 = 时 ,滞 后一 1 超前校 正器 的乃魁斯 特 图( q i)1 Ny us  ̄ t1
图1 所示 ,由图1 以看 出 ,当0 < 可 < 肘 ,该校 正器作为一 个 滞后校正 器 ;当 ,6< 。 ,该校正器 作为 一个超前校 <3 。 时
基于MATLAB进行控制系统的滞后-超前校正设计

目录1 滞后-超前校正设计目的和原理 (1)1.1 滞后-超前校正设计目的 ............................................................................... 1 1.2 滞后-超前校正设计原理 ............................................................................... 1 2 滞后-超前校正的设计过程 .. (2)2.1 校正前系统的参数 (2)2.1.1 用MATLAB 绘制校正前系统的伯德图 .............................................. 3 2.1.2 用MATLAB 求校正前系统的幅值裕量和相位裕量 .......................... 3 2.1.3 用MATLAB 绘制校正前系统的根轨迹 .............................................. 4 2.1.4 对校正前系统进行仿真分析 ............................................................. 5 2.2 滞后-超前校正设计参数计算 .. (6)2.2.1 选择校正后的截止频率c ω ................................................................ 6 2.2.2 确定校正参数β、2T 和1T ................................................................. 6 2.3 滞后-超前校正后的验证 . (7)2.3.1 用MATLAB 求校正后系统的幅值裕量和相位裕量 .......................... 7 2.3.2 用MATLAB 绘制校正后系统的伯德图 .............................................. 8 2.3.3 用MATLAB 绘制校正后系统的根轨迹 .............................................. 9 2.3.4 用MATLAB 对校正前后的系统进行仿真分析 .. (10)3 心得体会.................................................................................................................. 12 参考文献 . (13)用MATLAB进行控制系统的滞后-超前校正设计1 滞后-超前校正设计目的和原理1.1 滞后-超前校正设计目的所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足给定的性能指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机控制技术------滞后-超前校正控制器设计系别:电气工程与自动化专业:自动化班级:B110411学号:B********姓名:***目录一、 滞后-超前校正设计目的和原理 (1)1.1 滞后-超前校正设计目的......................................................... 1 1.2 滞后-超前校正设计原理......................................................... 1 二、滞后-超前校正的设计过程 (3)2.1 校正前系统的参数 (3)2.1.1 用MATLAB 绘制校正前系统的伯德图................................. 3 2.1.2 用MATLAB 求校正前系统的幅值裕量和相位裕量.................. 4 2.1.3 用MATLAB 绘制校正前系统的根轨迹................................. 5 2.1.4 对校正前系统进行仿真分析.............................................5 2.2 滞后-超前校正设计参数计算 (6)2.2.1 选择校正后的截止频率c ω............................................. 6 2.2.2 确定校正参数β、2T 和1T (6)2.3 滞后-超前校正后的验证 (7)2.3.1 用MATLAB 求校正后系统的幅值裕量和相位裕量..................7 2.3.2 用MATLAB 绘制校正后系统的伯德图.................................8 2.3.3 用MATLAB 绘制校正后系统的根轨迹.................................9 2.3.4 用MATLAB 对校正前后的系统进行仿真分析 (10)三、前馈控制3.1 前馈控制原理..................................................................... 12 3.2控制对象的介绍及仿真......................................................... 12 四、 心得体会.............................................................................. 16 参考文献.......................................................................................17 附录 (18)一、滞后-超前校正设计目的和原理1.1 滞后-超前校正设计目的所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足给定的性能指标。
校正方案主要有串联校正、并联校正、反馈校正和前馈校正。
确定校正装置的结构和参数的方法主要有两类:分析法和综合法。
分析法是针对被校正系统的性能和给定的性能指标,首先选择合适的校正环节的结构,然后用校正方法确定校正环节的参数。
在用分析法进行串联校正时,校正环节的结构通常采用超前校正、滞后校正和滞后-超前校正这三种类型。
超前校正通常可以改善控制系统的快速性和超调量,但增加了带宽,而滞后校正可以改善超调量及相对稳定度,但往往会因带宽减小而使快速性下降。
滞后-超前校正兼用两者优点,并在结构设计时设法限制它们的缺点。
1.2 滞后-超前校正设计原理滞后-超前校正RC网络电路图如图1所示。
图1 滞后-超前校正RC网络下面推导它的传递函数:()()()()()2221121*********21111221111111)(s C R C R s C R C R C R s C R s C R sC R sC R sC R sC R s E s M s G c ++++++=++++==令1,,,21221121222111>++=+==βββC R C R C R T T C R T C R T ,则()()()()s T s T s T s T s G c 21211111ββ+⎪⎪⎭⎫⎝⎛+++=其中1T 为超前部分的参数,2T 为滞后部分的参数。
滞后-超前校正的频域设计实际是超前校正和滞后校正频域法设计的综合,基本方法是利用滞后校正将系统校正后的穿越频率调整到超前部分的最大相角处的频率。
具体方法是先合理地选择截止频率c ω,先设计滞后校正部分,再根据已经选定的β设计超前部分。
应用频率法确定滞后超前校正参数的步骤: 1、根据稳态性能指标,绘制未校正系统的伯德图; 2、选择校正后的截止频率c ω; 3、确定校正参数β; 4、确定滞后部分的参数2T ; 5、确定超前部分的参数1T ;6、将滞后部分和超前部分的传递函数组合在一起,即得滞后-超前校正的传递函数;7、绘制校正后的伯德图,检验性能指标。
二、 滞后-超前校正的设计过程2.1 校正前系统的参数根据初始条件,调整开环传递函数:()()()s s s Ks G 5.0115.0++=当系统的静态速度误差系数110-=S K v 时,v K K =5.0。
则120-=s K满足初始条件的最小K 值时的开环传递函数为()()()s s s s G 5.01110++=2.1.1 用MATLAB 绘制校正前系统的伯德图程序:num=[10];den=[0.5,1.5,1,0]; bode(num,den) grid得到的伯德图如图2所示。
图2 校正前系统的伯德图2.1.2 用MATLAB 求校正前系统的幅值裕量和相位裕量用命令margin(G)可以绘制出G 的伯德图,并标出幅值裕量、相位裕量和对应的频率。
用函数[kg,r,wg,wc]=margin(G)可以求出G 的幅值裕量、相位裕量和幅值穿越频率。
程序:num=[10];den=[0.5,1.5,1,0]; G=tf(num,den); margin(G)[kg,r,wg,wc]=margin(G)得到的幅值裕量和相位裕量如图3所示。
图3 校正前系统的幅值裕量和相位裕量运行结果: kg=0.3000 r=-28.0814wg=1.4142 wc=2.4253即幅值裕量dB h 5.103.0lg 20-==,相位裕量β=-28.0814o。
2.1.3 用MATLAB 绘制校正前系统的根轨迹MATLAB 中专门提供了绘制根轨迹的有关函数。
[p,z]=pzmap(num,den)的功能是绘制连续系统的零、极点图。
[r,k]=rlocus(num,den)的功能是绘制∞→=0k 部分的根轨迹。
程序:num=[10];den=[0.5,1.5,1,0]; rlocus(num,den)得到校正前系统的根轨迹如图4所示。
图4 校正前系统的根轨迹2.1.4 对校正前系统进行仿真分析Simulink 是可以用于连续、离散以及混合的线性、非线性控制系统建模、仿真和分析的软件包,并为用户提供了用方框图进行建模的图形接口,很适合于控制系统的仿真。
仿真后得到的结果如图5和图6所示。
图5 校正前系统的仿真图图6 校正前系统仿真的阶跃响应曲线2.2 滞后-超前校正设计参数计算2.2.1 选择校正后的截止频率c ω若性能指标中对系统的快速性未提明确要求时,一般对应()︒-=∠180ωj G 的频率作为c ω。
从图3中得,c ω=1.5。
这样,未校正系统的相位裕量为0o,与要求值仅差+45o,这样大小的超前相角通过简单的超前校正是很容易实现的。
2.2.2 确定校正参数β、2T 和1Tβ由超前部分应产生超前相角ϕ而定,即ϕϕβsin 1sin 1-+=。
在本题中,︒=︒+︒=50545ϕ,因此55.750sin 150sin 1≈︒-︒+=β取c T ω15112=,以使滞后相角控制在-5o 以内,因此1.012=T ,滞后部分的传递函数为01.01.0++s s 。
过()()ccj G ωωlg 20,-,作20dB/dec 直线,由该直线与0dB 线交点坐标1T β确定1T 。
未校正系统的伯德图在c ω=1.5处的增益是13dB 。
所以过点(1.5,-13)画一条20dB/dec 的直线,与0dB 线的交点确定转折频率。
经计算得,转折频率89.011=T ,另一转折频率为7.61=T β。
所以超前部分的传递函数为7.689.0++s s 。
将滞后校正部分和超前校正部分的传递函数组合在一起,得滞后-超前校正的传递函数为()01.01.07.689.0++++=s s s s s G c系统校正后的传递函数为()()()()()()()()01.07.615.011.089.010++++++=s s s s s s s s G s G c2.3 滞后-超前校正后的验证由于校正过程中,多处采用的是近似计算,可能会造成滞后-超前校正后得到的系统的传递函数不满足题目要求的性能指标。
所以需要对滞后-超前校正后的系统进行验证。
下面用MATLAB 求已校正系统的相角裕量和幅值裕量。
2.3.1 用MATLAB 求校正后系统的幅值裕量和相位裕量程序:num=[10,9.9,0.89];den=[0.5,4.855,11.0985,6.8055,0.067,0]; G=tf(num,den);margin(G)[kg,r,wg,wc]=margin(G)得到的校正后系统的幅值裕量和相位裕量如图7所示。
1010101010101010P h a s e (d e g )Bode DiagramGm = 15.4 dB (at 3.68 rad/sec) , P m = 47.6 deg (at 1.21 rad/sec)Frequency (rad/sec)-150-100-50050100150M a g n i t u d e (d B )图7 校正后系统的幅值裕量和相位裕量运行结果: kg=5.9195 r=47.6239wg=3.6762 wc=1.2072即校正后系统的相位裕量︒=6239.47γ,()10lim 0==→s sG K s v 满足指标。
假设验证结果不满足指标,重新选择校正后的截止频率,重复上述过程,直到满足性能指标为止。
2.3.2 用MATLAB 绘制校正后系统的伯德图程序:num=[10,9.9,0.89];den=[0.5,4.855,11.0985,6.8055,0.067,0]; bode(num,den) grid得到的伯德图如图8所示。
