流函数势函数-第一章
流函数和势函数公式

流函数和势函数公式流函数与势函数是描述流体运动的两个重要概念,在流体力学中被广泛应用。
本文将介绍流函数和势函数的基本概念、性质以及求解方法。
1.流函数的概念和性质流函数是描述在二维定常流动中,各个流线上速度矢量的旋转情况的函数。
对于二维流动,假设流体流动的速度场为V(x,y),则流函数Ψ(x,y)定义为:V=∇Ψ=(∂Ψ/∂x,∂Ψ/∂y)其中,∇Ψ是流函数Ψ的梯度向量。
流函数的性质如下:1)斜率定理:沿着流线的方向,流函数的局部斜率等于流体的速度分量。
2)流线定理:流线上的流函数值保持不变,即Ψ为常数。
3)流函数的连续性:在空间中的流函数是连续的,除非在相应的流体内有边界。
4)流函数的耗散性:流函数对时间是线性的,即流函数在时间方向上是耗散的。
2.势函数的概念和性质势函数是描述流体在无旋力场中流动时所具备的性质的函数。
无旋力场是指速度场的旋度等于零。
对于二维流动,假设流体流动的速度场为V(x,y),则势函数φ(x,y)定义为:V=∇φ=(∂φ/∂x,∂φ/∂y)其中,∇φ是势函数φ的梯度向量。
势函数的性质如下:1)势函数的梯度向量是速度向量。
2)势流是不可压缩的,即∇·V=0。
3)势函数满足拉普拉斯方程,即∇²φ=0。
4)由于速度场的旋度等于零,势函数是无旋的。
3.流函数和势函数的关系在二维流动中,流函数和势函数之间存在一种特殊的关系,称为流函数-势函数耦合关系。
根据流函数和势函数的定义,可以得到流函数和势函数的关系:Ψ = ∫(∂φ/∂y)dx + f(y)φ = ∫(∂Ψ/∂x)dy + g(x)其中,f(y)和g(x)是任意常数函数。
根据流函数-势函数耦合关系可以求解流体的速度场,并且满足连续性方程和运动方程。
4.求解流函数和势函数的方法求解流函数和势函数的方法有多种,常用的方法有分离变量法、解析法和数值法。
4.1分离变量法分离变量法是将流函数和势函数分解为各自的变量函数,并通过解偏微分方程的边值问题来确定这些变量函数。
流函数和势函数公式(一)

流函数和势函数公式(一)资深创作者列举流函数和势函数公式的相关公式,并进行例解释。
流函数公式二维空间中的流函数公式在二维空间中,流函数用于描述流体的运动状态。
对于二维流动,在直角坐标系下,流函数的公式可以表示为:ψ = ∫(Vx dy - Vy dx)其中,Vx和Vy分别表示流体在x和y方向的速度分量。
ψ表示流函数。
举例:假设在二维平面内,某个点(x, y)的速度分量分别为Vx = x*y和Vy = x^2。
那么该点处的流函数可以计算如下:ψ = ∫(x*y dy - x^2 dx)三维空间中的流函数公式在三维空间中,流函数的公式稍有不同。
在直角坐标系下,流函数可以表示为:ψ = ∫(Vx dy dz - Vy dx dz + Vz dx dy)其中,Vx、Vy和Vz分别表示流体在x、y和z方向的速度分量。
ψ表示流函数。
Vx = x^2,Vy = y^2和Vz = z^2。
那么该点处的流函数可以计算如下:ψ = ∫(x^2 dy dz - y^2 dx dz + z^2 dx dy)势函数公式二维空间中的势函数公式在二维空间中,势函数用于描述流体的势能分布。
对于二维流动,在直角坐标系下,势函数的公式可以表示为:φ = ∫(Vx dx + Vy dy)其中,Vx和Vy分别表示流体在x和y方向的速度分量。
φ表示势函数。
举例:假设在二维平面内,某个点(x, y)的速度分量分别为Vx = 2x和Vy = 3y。
那么该点处的势函数可以计算如下:φ = ∫(2x dx + 3y dy)三维空间中的势函数公式在三维空间中,势函数的公式稍有不同。
在直角坐标系下,势函数可以表示为:φ = ∫(Vx dx + Vy dy + Vz dz)其中,Vx、Vy和Vz分别表示流体在x、y和z方向的速度分量。
φ表示势函数。
Vx = x^2,Vy = y^2和Vz = z^2。
那么该点处的势函数可以计算如下:φ = ∫(x^2 dx + y^2 dy + z^2 dz)总结:•流函数公式和势函数公式分别用于描述流体的运动状态和势能分布。
南信大流体力学第一章4讲

是某一函数全微分的充分必要条件为
∂v ∂y = ∂(− u ) ∂x 。该充要条件又恰好满足上述无辐散流条件,
即(1-75)式可改写成某一函数 ψ
( x, y , t )
的全微分,即
dψ ( x , y , t ) = v ( x, y , t )dx − u ( x , y , t )dy = 0
(1-94)
另外,有流函数和速度势函数后,还可以引入复速度势 的概念。对于定常无旋无辐散条件,可组成一个复速度势函数
F ( z ) (简称复势)如下:
F ( z ) = ϕ ( x, y ) + iψ ( x, y )
− dF dz = u − iv
(1-95)
(1-104)
四、流动的分类 1.一般流动; 2.无旋流动; 3.无辐散流动; 4.纯平移流动; 5.拉普拉斯流动; 6.无形变流动; 7.声振动流动; 8.流体无运动或流体静力学。
对于某确定时刻t,取速度势函数等于某常数值,即
(1-70)
ϕ ( x, y , z , t )
=常数
(1-71)
则上式所表达的空间几何图象为一空间曲面,称作 等势函数面――等位势面。
根据梯度的定义可知,速度矢与等势面相垂直,且从高位势 流向低位势,等势面彼此紧密之处流速值越大;等位势面彼此疏 远之处,流速值越小。然后对上述速度场取散度,即
1 ∂v ∂u ωz = − = 0 ,即 2 ∂x ∂y
∂v ∂u − =0 ∂x ∂y
,将
u = −
∂ψ ∂ψ ,v = ∂y ∂x
在势流条件下,流函数 代入上式,整理得 满足拉普拉斯方程,为调和函数。
ψ
∂ 2ψ ∂ 2ψ + = 0 2 2 ∂x ∂y
流函数与势函数

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。
所谓平面流动是指流场中各点的流速都平行于某一固定平面,并且各物理量在此平面的垂直方向上没有变化。
由不可压缩流体的平面流动的连续方程得平面流动的流线微分方程为式(1)是式(2)成为某一函数的全微分的必要且充分的条件,即于是很显然,在流线上dψ=0或ψ=C。
每条流线对应一个常数值,所以称函数ψ为流函数。
对于不可压缩流体的平面流动,用极坐标表示的连续方程、流函数的微分和速度分量分别为:流函数具有明确的物理意义:平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。
在流函数ψ的定义中,为保证流函数变化值dψ与流量增量值dq v 同号,规定绕B点逆时针方向穿过曲线AB的流量为正,反之为负,这是指通过z方向为单位高度的柱面的体积流量。
里的流量qv通过A点的流线的流函数值ψ1,通过B点的流线的流函数值ψ2,则通过AB柱面的体积流量为在引出流函数这个概念时,既没有涉及流体是粘性的还是非粘性的,也没有涉及流体是有旋的还是无旋的。
所以,无论是理想流体还是粘性流体,无论是有旋流动还是无旋流动,只要是不可压缩流体的平面流动,就存在流函数,对于xoy平面内的无旋流动,有 z=0,即:也可得即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程,也是调和函数。
对于极坐标系,该满足拉普拉斯方程为二、速度势函数对于无粘性(理想)流体的无旋流动而言,由斯托克斯定理可知,沿流场中任意封闭周线的速度线积分,即速度环量均为零。
对于无旋流动,该封闭周线所包围的速度环量为零,有对于理想流体无旋流动,从参考点A到另一点B的速度线积分与点A 至点B的路径无关,上式中ds表示连接点A与点B的任意微元曲线。
也就是说,速度线积分仅仅取决于B点相对于A点的位置,具有单值势函数的特征。
由无旋流动的充要条件可知即:上式是成为某一函数的全微分的必要且充分条件。
函数成为速度势函数,简称速度势。
流函数与势函数.docx

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。
所谓平面流动是指流场中各点的流速都平行于某一固定平面,并且各物理量在此平面的垂直方向上没有变化。
由不可压缩流体的平面流动的连续方程得du dv--- =—―dx dy平面流动的流线微分方程为吗一血" ⑵式(1)是式(2)成为某一函数的全微分的必要且充分的条件,即于是很显然,在流线上(1屮二0或屮二C。
每条流线对应一个常数值, 所以称函数屮为流函数。
对于不可压缩流体的平面流动,用极坐标表示的连续方程、流函数的微分和速度分量分别为:(1)dr dddy/流函数具有明确的物固愿契:平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。
在流函数屮的定义中,为保证流函数变化值(1屮与流量增量值dq、同号,规定绕B点逆时针方向穿过曲线AB的流量为正,反之为负,这里的流量4,.是指通过z方向为单位高度的柱面的体积流量。
通过A点的流线的流函数值屮1 ,通过B点的流线的流函数值屮2 ,则通过AB柱面的体积流量为¥ r w 辛q v = \V -dZ = J \u cos(n7 x) +v cos(再y)](SA A["字 + v(-务问二j (T -vdx)AB\(1屮=屮2_屮\A在引出流函数这个概念时,既没有涉及流体是粘性的还是非粘性的,也 没有涉及流体是有旋的还是无旋的。
所以,无论是理想流体还是粘性流 体,无论是有旋流动还是无旋流动,只要是不可压缩流体的平面流动, 就存在流函数,dv du .----- —=0对于xoy 平面内的无旋流动,有CO Z =0,即:去Oy口2 才屮 d 2i// 门VV=—r + —r=0也可得dx创即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程,也是调和 函数。
对于极坐标系,该满足拉普拉斯方程为d 2u/ 1 du/ 1 d 2u/ c+ -- +——^=0 dr 2 r dr r 2 d02二、速度势函数屮】对于无粘性(理想)流体的无旋流动而言,由斯托克斯定理可知, 沿流场中任意封闭周线的速度线积分,即速度环量均为零。
流函数势函数
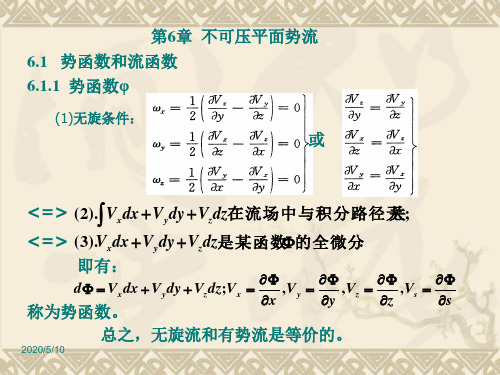
(1)无旋条件:
或
<=> ( 2). Vx dx V y dy Vz dz在 流 场 中 与 积 分 路 径 关 无; <=> ( 3).Vx dx V y dy Vz dz是 某 函 数 的 全 微 分 . 即有:
d Vx dx V y dy Vz dz;Vx ,V y ,Vz ,Vs x y z s
称为势函数。 总之,无旋流和有势流是等价的。
2015-6-8
6.1.2 平面流的流函数ψ
(1)
<=> ( 2). V y dx Vx dy在 流 场 中 与 积 分 路 径 关 无; <=> ( 3). V y dx Vx dy是 某 函 数 的 全 微 分 . 称为流函数。
2015-6-8
Vy
2.两点流函数值之差6 .1 .4 势函数方程和流函数方程——拉普拉斯方程
2015-6-8
6 .1 .5 等势线和等流线的正交性
2015-6-8
y
即有: d V dx V dy;V ,V y x x y
x
适用条件:二维连续流动,有旋流/无旋流均适用。 6.1.3 流函数ψ的性质 1. 等流函数线就是流线
Vx 若 C d V y dx Vx dy 0 为流线 dy dx
流函数势函数-第一章

0
对于无旋流动,必定存在一个函数 x, y, z, t 满足如:
V
或 V grad
无旋流动,其速度矢总可以用函数 的梯度来表示,把函数 x, y, z, t 叫做速度的(位)势函数,可以用这个函数来表 示无旋流动的流场。 通常将无旋流动称为有势流动或势流。
u
A
A
Q dy dx Q B A 或 A y x 表明:经过两点为端点的任何曲线的流体通量,决定于该 两点的流函数差,而与曲线的长度和形状无关。
B
用流函数可以来方便地表征无辐散场的流体通量。
曲线法向方向的单位矢量定义为:
dl n k dl 而: dl i dx j dy
A
B
Chen Haishan NIM NUIST
,v y x 引用流函数,并考虑: dl n k (dyi dxj ) / dl dl B B Q V n dl Vndl
Chen Haishan NIM NUIST
(3)表征流体涡度
v u 由涡度的定义 x y ,可得到用流函数来表
示的涡度表达式:
2 2 2 2 x y
可见,对流函数取拉普拉斯运算即可得到流体的涡度。 同样,求解流函数的方法为: (1)已知涡度,直接求解泊松(Poisson)方程; (2)已知速度场,先求出涡度,然后求解泊松方程。
Chen Haishan NIM NUIST
④ 势函数的求解 u v w D 假如流体的散度为: x y z 根据势函数的定义有: 2 D
2 2 2 其中, 2 2 2 2 为三维拉普拉斯算子。 x y z
流体力学2011-第一章作业讲解4

Vy dy dx V C x
Chen Haishan NIM NUIST
等势线和等流函数线在点(x,y ) 的斜率乘积
dy dy Vx V y 1 dx dx V y Vx C C
u ,v x y
u ,v y x
Chen Haishan NIM NUIST
方法二: 等势函数线是指
C
的曲线 ,沿等势线 , d 0
即
d dx dyVx dxVy dy0 x y
d dx dy(V )dx(V )dy0 x y x y
u ,v y x
Chen Haishan NIM NUIST
流函数和势函数都是调和函数(满足二维拉普拉斯方程)
2 2 2 2 y x 2 2 x 2 y 2 D
2 2 2 2 0 y x 2 2 2 0 2 y x
Chen Haishan NIM NUIST
习题1-6-2 请问是否存在既满足无辐散条件又满足无 旋条件的流动?如存在,请举例说明。 解: 满足无辐散条件又满足无旋条件,即:
V 0
V 0
u at, v 0, w 0
Chen Haishan NIM NUIST
由上式,可得到等势线在流场中任意点(x,y)的斜率
dy Vx dx V C y
Chen Haishan NIM NUIST
等流函数是指 C 的曲线,即流线,沿等流函数, d 0 即
d dx dy Vy dxVx dy0 x y
流函数与势函数

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。
所谓平面流动是指流场中各点的流速都平行于某一固定平面,并且各物理量在此平面的垂直方向上没有变化。
由不可压缩流体的平面流动的连续方程得平面流动的流线微分方程为式(1)是式(2)成为某一函数的全微分的必要且充分的条件,即于是很显然,在流线上dψ=0或ψ=C。
每条流线对应一个常数值,所以称函数ψ为流函数。
对于不可压缩流体的平面流动,用极坐标表示的连续方程、流函数的微分和速度分量分别为:流函数具有明确的物理意义:平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。
在流函数ψ的定义中,为保证流函数变化值dψ与流量增量值dq v 同号,规定绕B点逆时针方向穿过曲线AB的流量为正,反之为负,这是指通过z方向为单位高度的柱面的体积流量。
里的流量qv通过A点的流线的流函数值ψ1,通过B点的流线的流函数值ψ2,则通过AB柱面的体积流量为在引出流函数这个概念时,既没有涉及流体是粘性的还是非粘性的,也没有涉及流体是有旋的还是无旋的。
所以,无论是理想流体还是粘性流体,无论是有旋流动还是无旋流动,只要是不可压缩流体的平面流动,就存在流函数,对于xoy平面内的无旋流动,有 z=0,即:也可得即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程,也是调和函数。
对于极坐标系,该满足拉普拉斯方程为二、速度势函数对于无粘性(理想)流体的无旋流动而言,由斯托克斯定理可知,沿流场中任意封闭周线的速度线积分,即速度环量均为零。
对于无旋流动,该封闭周线所包围的速度环量为零,有对于理想流体无旋流动,从参考点A到另一点B的速度线积分与点A至点B的路径无关,上式中ds表示连接点A与点B的任意微元曲线。
也就是说,速度线积分仅仅取决于B点相对于A点的位置,具有单值势函数的特征。
由无旋流动的充要条件可知即:上式是成为某一函数的全微分的必要且充分条件。
函数成为速度势函数,简称速度势。
流函数势函数

大气中充沛的水汽和水汽持续的输送是 形成强降水的必需条件,丁一汇等[3 ] 分 析了1998 年中国大洪水时期的全球水汽 背景,得到中国大洪水时期部分水汽收支 图像,揭示了水汽循环的一些规律。 由于2003 年强降水发生的区域和大环境 与1998 年不尽相同,分析对应时期的大范 围的水汽输送特征对理解2003 年江淮流 域暴雨洪涝的形成和维持也是有必要 的。
[4 ] 丁一汇. 天气动力学中的诊断分析方法. 北京:科学出版 社,1989 ,293pp [5 ] 周玉淑. 梅雨锋系的空间结构特征、形成机理及湿位涡 异常的研究. 中国科学院大气物理研究所博士学位论 文,2002 ,189pp [6 ] Gao Shouting ,Zhou Yushu ,Lei Ting. The structure features of the Meiyu front system. Acta MeteorologicSinica ,2002 ,16 :195~204
流函数、势函数的计算
1、对于无旋运动一定存在一个速度势 ,也称
势函数,该运动在任意方向的分速度即在此方 向的微分,对于x,y两个方向应有:
u
(1)
v
x y
只要找到势函数场,则与其对应 的无旋运动场的特点就清楚了。
2 2 u v D ( 2 2 ) 2 x y x y
(8)
实际工作中,常先规定一个误差标准值 运用(9)、(10)、(11)式反复迭代:
R =
n i,j
0
n i+1,j
in1, j in, j 1 2 2 ( 2 2 )in, j Di , j (9) 2 x y 2 x y
n i,j+1
流函数势函数

2
( x2
2 y2 ) 2
(2)
2、对于无辐散运动,一定存在一个流函数 ,
无辐散运动在x,y方向的分速度为:
u
(3)
v
y
x
只要找到流函数场,则与其对 应的无辐散运动的速度分布的特点
就清楚了。
v u 2
x y
(7)
(6)、(7)相减,整理得:
1 i,
j
0 i,
j
R0 i,j
11
2( x2 + y2 )
(8)
实际工作中,常先规定一个误差标准值 0
运用(9)、(10)、(11)式反复迭代j
in1,
= x2
j
n
i,j+1
in,
y 2
j
1
2 (x2
2
y2 )in, j
Di , j
(9)
in, j1 , in j
Rin, j 11
(10)
2( x2 + y2 )
当 n N 时,对于所有 i, j 如都满足
0
Rn i,j
(11)
则此时的解 iN, j ,即为近似解。
超张弛法的迭代公式稍有修改,目的是加 快收敛速度,其公式为:
流函数、势函数的计算
王咏青 南京信息工程大学
流函数、势函数的计算
1、对于无旋运动一定存在一个速度势 ,也称
势函数,该运动在任意方向的分速度即在此方 向的微分,对于x,y两个方向应有:
(1)
u x
v
y
只要找到势函数场,则与其对应 的无旋运动场的特点就清楚了。
第14讲势流理论1

∇2ϕ = 0
z y
o V (t)
x
x0
(2)边界面有大球表面(外边界)和小球表面(内边界)。内边界 就是小球的表面,其方程为:
F = (x − x0 )2 + y2 + z 2 − a2
t
∫ (x0 =
V (t)dt)
t0
由内边界方程可得:
y (2) 平面点源和点汇
设从源注入流场的体积流量为m,称m 为平面点源的强度。m>0,是点源;m<0, 是点汇。
r
x
如图取极坐标系,点源位于原点,则
流场中只有径向速度vr。
ψ = 常数
ϕ = 常数
由质量守恒定律,单位时间内流过半径为r的单位厚度柱面的流体体
积等于源强:
m = 2π rvr
则平面点源的速度场为:
第14讲 势流理论(1)
(Potential Flow Theory)
主要内容: 1.势流问题的基本方程和边界条件 2.复势 3.平面势流的基本解
1 势流问题的基本方程和边界条件
(1) 势流问题
势流:不可压、理想流体的无旋流动称为势流。势流即无源、无旋的 流动,其势函数满足拉普拉斯方程
势流问题:势流流场对物体的作用力 势流问题的求解思路:
① 物体表面(船体表面,鱼身体表面); ② 互不渗透的两种流体边界(海面); ③ 无穷远边界面。
物面边界条件
理想流体中不存在剪应力,流体质点可以沿物面滑动,但不能穿越物 面,即理想流体在物面上满足不可穿透条件:
v ⋅n = vb ⋅n
∂ϕ
∂n
=
vb ⋅n
也就是说,流体和物面在物面法向的速度相同。根据梯度的概念,物面的 单位外法向量可用物面方程表示:
速度势函数和流函数

拉普拉斯流动
满足以下条件的为【拉普拉斯流动】: ① 两维平面运动(u,v 不为零,w=0 ) ② 理想流体(不考虑粘性, 0 = μ) ③ 无辐散流(D=0 );无旋流
18
拉普拉斯流的特点:
特点一: 势函数和流函数都是调和函数 特点二:等势线与等流函数线垂直
19
证明:
因为:矢量与本身的叉乘恒为零,则: 而拉普拉斯流动无旋无辐散,则速度矢:
由无辐散条件 ,可以找到一个函数与速度矢对应,我们把这个函 数写成ψ ,ψ 的全微分为:
8
流函数:
(1.77)中
为二维矢量微商符
上面的ψ就是流函数, (1.77 )就是流函数与速度矢的关系。
9
流函数与流线的关系
根据流线方程的求法,(* )的流线方程为:
(1.75 )可积的充要条件是无辐散,与(1.76 )对比,发现是一 样的。对(1.76 )积分,得:
上面两个图中,标量场是黑白的,黑色表示大的数值,而其相应的梯度用蓝 色箭头表示。
2
势函数
无旋运动时,其速度矢
是可以由函数
的
梯度来表示的,这个函数
就称为速度矢
的
【(位)势函数】。
可见,用一个标量函数就把三维的速度矢都表示出来了,减少了 未知量。
3
等(位)势面:
取t 为一固定时刻,若有
此时
11
流函数与体积通量:
图中自南向北的4 条线是流线(等流函数线),任取AB曲线,在 该线上任一点的速度矢是 ,法向单位矢是 ,曲线单位矢是
上式表明,两点的流函数值之差等于过这两点的任何曲线的流体 的体积通量(体积流量)值,跟曲线的形状、长短无关。
12
流函数讲义
7
【例4-3】 有一不可压流体平面流动的速度分布 为 u 4x,v 4y 。①该平面流动是否存在流函数和速度 势函数;②若存在,试求出其表达式;③若在流场中A (1m,1m)处的绝对压强为1.4×105Pa,流体的密度 1.2kg/m3,则B(2m,5m)处的绝对压强是多少?
【解】 (1)由不可压流体平面流动的连续性方程
3
二、流函数的性质
(1)对于不可压缩流体的平面流动,流函数Ψ 永远 满足连
续性方程。
2
2
yx xy
(2)对于不可压缩流体的平面势流,流函数Ψ满足拉普拉斯 方程,流函数也是调和函数。
对于平面无旋流动 z 0
v u 0 x y
2
x 2
2
y2
在两流线间任一曲线AB,则 通过单位厚度的体积流量为
y2
x2
y2
x2
qV
udy
y1
v(dx)
x1
y1
y
dy
x1
x
dx
x2 , y2
d 2 1
( x1 , y1 )
平面流动中两条流线间通过的 流量等于这两条流线上的流函 数之差。
5
三、 和 的关系
10
(3)由于 V 2 u 2 v2,因此,A和B处的速度分别为
VA2 (4 1)2 (4 1)2 32(m2 s 2 )
VB2 (4 2)2 (4 5)2 464 (m2 s2 )
由伯努里方程
可得
pA
1 2
VA2
pB
1 2
VB2
pB
pA
122《高等渗流力学》—势函数部分

y xa
y , θ 2 = arctg x+a
y y y y ' arctg = arctg x a x + a = C 0 θ 1 θ 2 = arctg xa x+a y2 1+ (x a )(x + a )
直角 坐标
y y x a x + a = C '' 0 y2 1+ (x a )(x + a )
4,无限大地层等产量一源一汇的渗流场
红色—流线 蓝色—等势线 X轴 —流线 Y轴 —等势线
6,等势线方程
( x a)2 + y 2 rB = = C0 为任意常数 令 2 2 rA ( x + a) + y
( x a ) + y C0 [( x + a ) + y ] = 0
2 2 2 2 2
1 + C02 2 2aC0 2 2 (x ) +y =( ) 2 2 1 C0 1 C0
x0
R
圆的方程……
6,等势线方程
1 + C02 2 2aC0 2 2 (x ) +y =( ) 2 2 1 C0 1 C0
x0
R
C0 = 1时,x0 → ∞, R → ∞, rA = rB
同理,可得流线方程为
整理
x +y
2 2
2a C0
''
y a2 = 0
配方,整理
a 2 x + y '' C0
2
'' 2 a 1 + C0 = '' C0
2
它是一个圆心都在y轴上的圆族方程,其圆心坐标为:
流函数和势函数公式

流函数和势函数公式一、流函数的公式流函数是描述二维流动中速度分布情况的数学函数。
在笛卡尔坐标系下,流函数的公式可以表示为:Ψ(x,y)=Ψ(x(x,y),y(x,y))其中,(x,y)表示流体的位置坐标,Ψ表示流函数。
流函数的物理意义是沿着流线的流体质点速度分量的积分,即在流体的其中一位置,流函数的数值表示沿着该位置流线的任一质点在单位时间内浸入或流出以单位长度为界的穿过该位置的流线的质量。
在极坐标系下,流函数的公式为:Ψ(r,θ)=Ψ(r(r,θ),θ(r,θ))其中,(r,θ)表示流体的极坐标,Ψ表示流函数。
流函数具有以下性质:1.流函数是速度场的偏微分方程的解;2.流函数在各处连续可微,即满足流函数的充要条件为满足连续性方程的速度场。
二、势函数的公式势函数是描述速度场的另一种数学函数。
在二维流动中,势函数的公式可以表示为:φ(x,y)=φ(x(x,y),y(x,y))其中,(x,y)表示流体的位置坐标,φ表示势函数。
势函数的物理意义是在流体中任意一点,流速的大小等于该点的势函数的梯度的模,即V=∇φ。
在极坐标系下,势函数的公式为:φ(r,θ)=φ(r(r,θ),θ(r,θ))其中,(r,θ)表示流体的极坐标,φ表示势函数。
势函数具有以下性质:1.势函数是速度场的偏微分方程的解;2.势函数在各处连续可微,即满足势函数的充要条件为满足无旋条件的速度场。
三、流函数和势函数的关系υ=r∂Ψ/∂rυ=−1/r∂φ/∂θ其中,υ表示速度场的极坐标下的径向速度分量。
根据以上关系,可以得出以下推论:1.如果流函数为常数,则速度场满足旋度为零,即速度场满足无旋条件;2.如果势函数为常数,则速度场满足收敛性条件,即速度场满足连续性方程。
因此,流函数和势函数可以分别用于描述无旋的速度场和无散的速度场。
总结起来,流函数和势函数是描述二维流动中速度场的重要数学函数。
流函数描述流体沿流线方向的速度分布情况,势函数描述速度的梯度与流速的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当取 常值时,也可以得到 dx / u dy / v
试问两式是否等价?请说明理由?
本节总结
§6速度势函数和流函数 (概念、理解) ①速度势函数的定义、存在条件、表示流体运动的方法; ②流函数的定义、存在条件、表示流体运动的方法; ③速度势函数、流函数表示二维流动。
其流线方程为: dx dy 或vdx udy 0 uv
根据格林积分公式(平面曲线积分与路径无关的条件)可 知,满足无辐散条件下:
vdx udy 0
d x, y, t vx, y, t dx ux, y, tdy 0
流速与该函数满足: u , v y x
矢量形式:
V k
(2)如已知速度场,可以先求出D,然后再求解泊松方 程,最终得到势函数。
二、速度流函数
①定义及存在条件 引入流体散度的概念之后,可将流体运动分为:
流体运动
无辐散流 辐散流
•V 0
•V 0
考虑二维无辐散流动,即满足:
w0
u ux, y, t , v vx, y, t
u / x v / y 0
v x
u y
0
D
u xv y0 NhomakorabeaV V V
①②
①无辐散涡旋流 ②无旋辐散流
V V
•V 0
V 0
•V •V
V k
V
2
x
2
2
y 2
2
x
2
2
y 2
D
V k
u
y x v
x y
上式为大气动力学中广泛采用的形式。
课 后习 题
习题1-6-1 已知二维流速场为:
(1)减少表征流动的变量
(2)表征流体通量
在流体中任取一条有向曲线A B,顺着该有向曲线
流体自右侧向左侧的通量Q:
B
B
Q
V • n dl
A
A Vn dl
流速在曲线法向方向上的分量
曲线法向n方向k的单d位l 矢量定义为:
A
B
dl
而: dl i dx jdy
u ,v
引用流函数,并考虑:n
由流速场与势函数的关系可知:V
流速矢与等位势面相垂直,由高位势流向低位势,等位势 面紧密处,位势梯度大,相应的流速大;等位势面稀疏处 ,位势梯度小,相应的流速小。
例1-6-1 已知流体作无旋运动,对应的等势函数线分布如
图所示(其中,0 < 1< 2 )的,请判断并在图
中标出A、B两处流体速度的方向,并比较A、B 两处流速的大小。
第六节 速度势函数和流函数
速度势函数 速度流函数 二维流动的表示
一、速度势函数
① 定义(速度势函数的引入及存在条件)
如果在流体域内涡度为零,即: V 0
无旋流动;
否则,则称之为涡旋流动:V 0
流体运动
无旋流动 涡旋流动
据矢量分析知识,任意一函数的梯度,取旋度恒等于零:
0 对于无旋流动,必定存在一个函数 x, y, z, t 满足如:
积分以上的全微分形式,可以得到:
=常数 x, y, t
对某一固定的时刻:一空间曲线--流线方程积分曲线。
流速与该函数的关系---曲线的切线方向与流速矢 的方向是相吻合的。
上式所描述的曲线就是流线,当然,它也是函数 的等
值线。
将以上引进的函数 称之为流函数,而流线也就是等流函
数线。
②引入流函数的优点
kdyl
x
(dyi
dxj )
/
dl
dl
B
B
Q
V • n dl
A
A Vn dl
Q
B A
y
dy
x
dx
或
Q B A
表明:经过两点为端点的任何曲线的流体通量,决定于该
两点的流函数差,而与曲线的长度和形状无关。
用流函数可以来方便地表征无辐散场的流体通量。
(3)表征流体涡度
V
或
V grad
无旋流动,其速度矢总可以用函数 的梯度来表示,把函数
x, y, z, t 叫做速度的(位)势函数,可以用这个函数来表
示无旋流动的流场。 通常将无旋流动称为有势流动或势流。
②引入势函数的优点
流速矢描述流体运动 需要给定三个变量
含有三个变量; 刻画流体的运动情况。
而引进了势函数后:
①
u ax by v cx dy
u (2a x) y
②
v
b( x2
y2)
分别求势函数和流函数存在的条件。
习题1-6-2 请问是否存在既满足无辐散条件又满足无 旋条件的流动?如存在,请举例说明。
习题1-6-3 请证明无辐散的平面无旋流动:(1)流函 数和势函数都是调和函数(满足二维拉普拉斯方程) (2)等势函数线和等流函数线正交。
由涡度的定义
v x
u y
,可得到用流函数来表
示的涡度表达式: 2 2 x2 y2
可见,对流函数取拉普拉斯运算即可得到流体的涡度。
同样,求解流函数的方法为: (1)已知涡度,直接求解泊松(Poisson)方程; (2)已知速度场,先求出涡度,然后求解泊松方程。
三、二维流动
一般二维流动,既不满足无旋条件,也不满足无辐 散条件,流动是有旋有辐散的。此时,其涡度和散度均 不为零,即满足:
V ui vj wk
u ,v , w
x
y
z
只要一个变量(势函数)就可以来描述流体运动,
大大地减少了描写流体运动所需的变量,简化了问题。
③用势函数来描述流体运动
对于某一固定时刻
x, y, z, t =常数
为一空间曲面,称为等势函数面或者等位势面。
上式取不同常数 不同的等位势面 等位势面族。
④ 势函数的求解 假如流体的散度为:D u v w x y z
根据势函数的定义有:2 D
其中, 2
2 x 2
2 y 2
2 z 2
为三维拉普拉斯算子。
可以看出,如果给定D,通过求解泊松(Poisson)方 程,即可求得势函数。
求解势函数的具体方法(仅考虑二维的情况):
(1)如已知D,直接求解泊松(Poisson)方程,可得势函数。
