吉林大学工程流体力学第5章 孔口出流
合集下载
水力学课件——第五章:孔口、管嘴出流

10 ×10−3 Q= = 3.049m3 /s 32.8
A dC 8 ε = C = = = 0.64 A d 10
2
2
由薄壁孔口出流的计算公式,可得流量系数
Q 3.049 ×10−5 µ= = =0.62 2 A 2 gH 0.25 × 3.14 × 0.01 × 2 × 9.8 × 2
(3)保证管嘴正常工作的条件 ) 从前面的分析可知,收缩断面的真空度和作用水头成正比。作用水头越大, 真空度越大,流量越大。 但是,流量并不能无限制地增大。当真空度大于7m水柱时,由于收缩断面 处真空度过大,气体会从出口处吸入管嘴,真空环境被破坏,出口流动不 再为满管流动,此时管嘴出流近似为孔口出流,流量反而减小。 因此,要保证管嘴正常工作,要求收缩断面真空度小于7m,则
流速系数 又因为
0.62 ϕ = µ /ε = = 0.97 0.64 1 1 1 可得 ζ = ϕ= −1 = − 1 = 0.063 2 2 1+ ζ 0.97 ϕ
5.2 液体经管嘴的恒定出流
(1)定义、分类及流动特点: )定义、分类及流动特点:
管嘴实际上是以某种方式连接于孔口上的具有一定长度的短管 实际上是以某种方式连接于孔口上的具有一定长度的短管。 管嘴实际上是以某种方式连接于孔口上的具有一定长度的短管。 液体经由容器外壁上安装的长度约( 液体经由容器外壁上安装的长度约(3~4)倍管径的短管出流,或容器壁 )倍管径的短管出流, 的厚度为( 管嘴出流。 的厚度为(3~4)孔径的孔口出流,称为管嘴出流。 )孔径的孔口出流,称为管嘴出流 管嘴出流也可以分为恒定和非恒定出流,自由和淹没出流。 管嘴出流也可以分为恒定和非恒定出流,自由和淹没出流。 管嘴出流的流动特点是:水流进入管嘴之前的流动情况和孔口出流相同, 管嘴出流的流动特点是:水流进入管嘴之前的流动情况和孔口出流相同, 进入管嘴后, 先形成收缩断面,在收缩断面附近水流与管壁分离, 进入管嘴后, 先形成收缩断面,在收缩断面附近水流与管壁分离,形成 漩涡区,之后水流逐渐扩大,直至完全充满整个管面。 漩涡区,之后水流逐渐扩大,直至完全充满整个管面。管嘴出口断面上为 满管流。 满管流。 因为管长很小,沿程损失可以忽略,因此管嘴出流的水头损失主要来源于 因为管长很小,沿程损失可以忽略,因此管嘴出流的水头损失主要来源于 孔口的局部水头损失和水流断面扩大所引起的局部水头损失, 孔口的局部水头损失和水流断面扩大所引起的局部水头损失,即
《流体力学》第五章孔口管嘴管路流动
2 Av A
2g
P0
2 AvA
2g
H
p0
当淹没出流时:
H 0 (Z A Z B ) H' p0 p0 ' pa
A
A
H'
2 2 A v A B vB
H
B
C
2g
2 2 A v A B vB
2g
§5.2 孔口淹没出流
C
1 孔口 vc 2 gH 0 Q A 2 gH 0 A 2 gH 0 自由 c 1 2 出流 pA pC AvA H 0 ( Z A ZC ) 2g
§5.3 管嘴出流
从局部阻力系数图423中查得锐缘进口 ζ=0.5
管嘴真空现象及真空值通过C-C与B-B断面列 能量方程得到证明: 2 2 pC C vC pB B vB hl 2g 2g
2 l vB hl=突扩损失+沿程损失 ( m ) d 2g
A 1 vc vB vB Ac
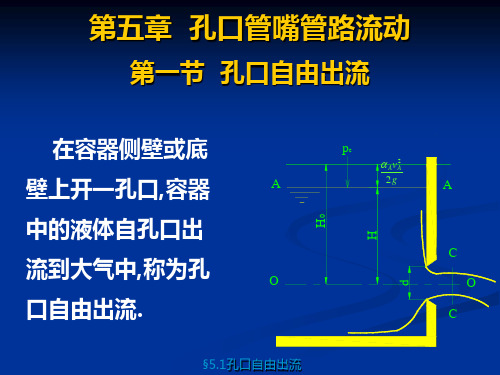
第五章
孔口管嘴管路流动
孔口自由出流
pc
2 Av A
第一节
在容器侧壁或 底壁上开一孔口,容
A
2g
A
器中的液体自孔口
出流到大气中,称为
O
H0
H
C O C
孔口自由出流.
§5.1孔口自由出流
d
pc
2 Av A
A
2g
A
H0
H
C O O C
收缩断面:C-C断面 薄壁孔口:出流流股与孔口壁接触仅是一条周线, 这种条件的孔口称为薄壁孔口。 厚壁孔口(管嘴):若孔壁厚度和形状促使流股 收缩后又扩开,与孔壁接触形成面而不是线,这 种孔口称为厚壁孔口或管嘴。
工程流体力学课件5孔口、管嘴出流及有压管流

H
0v02 2g
v2 2g
hw
忽略管嘴沿程损失,且令
H0
H
0v02
2g
则管嘴出口速度
v 1
2gH0 n 2gH0
Q vA n A 2gH0 n A 2gH0
其中ζ为管嘴的局部阻力系数,取0.5;则
流速系数 流量系数
n
1
1 0.82 <孔口 0.97 ~ 0.98 1 0.5
说明管嘴过流能力更强
l1, l2 ,1, 2 , n, 1, 2 , 3
求 泄流量Q, 画出水头线
3
Rd 4
R, n
C
1 n
1
R6
8g C2
1, 3 H
1
2 l1
2
l2
v
1
2gH
1
l d
1
2
1
出口断面由A缩小为A2
出口流速
v2
管内流速
v2
A2 A
3
新增出口局部损失 3
v2
2gH
13
(
l d
1
2
)
A2 A
2
= =
H+h 0
h
v2
l v2
v2
( )
2g
d 2g
2g
1
用3-3断面作 下游断面
O1
H
v
23
h O 出口水头损失
按突扩计算 23
( z1
p1
1v12
2g
) (z3
p3 )
3v32
2g
h f 12
h j12 h j23
= = = = =
H+h
工程流体力学第五章 孔口、管嘴和有压管流

通过水泵叶轮转动的作用,在水泵进口端形成真空,使 水流在池面大气压作用下沿吸水管上升,流经水泵时从水泵 获得能量,从而输入压力管,再流入水塔。
水泵进口处的真空不能太大,否则会导致水泵汽蚀,降 低水泵的吸水性能,甚至破坏水泵叶轮。所以进口处的真空 值必须满足水泵铭牌上的最大允许吸上真空高度。
【例5-1】用虹吸管由井向集水池输水。虹吸管长 l = lAB+ lBC = 30 + 40 = 70 m,直径d = 200 mm。井与集水 池之间的水位差为 H = 1.60 m。如果管道沿程损失系数为
第五章 孔口、管嘴和有压管路
5.1薄壁孔口恒定出流
液体经容器壁上孔口流出的水力现象称为孔口出流。
孔口形心的淹没深度。
1.孔口分类:
⑴按孔口的相对孔径分:孔口的孔径。
大孔口 H/d<10
小孔口 H/d≥10
⑵按流动的形式分:
恒定出流和非恒定出流;
⑶按出流形式分:
自由出流和淹没出流;
对于淹没出流无所 谓大孔口和小孔口
4.小孔口的收缩系数及流量系数
Q A 2gH
实验证明,不同形状(三角形、圆形、矩形等)小孔口的 流量系数差别不大,但孔壁的厚度对收缩系数会有影响,薄壁
孔口的收缩系数ε最小,圆边孔口收缩系数ε较大,甚至等于1。 孔口在壁面上的位置,对收缩系数ε有直接影响 ,不完善收缩 孔口、部分收缩孔口的流量系数μ大于完善收缩孔口的流量系 数μ。
L
2 水泵
2 1
h V 2 l V 2 58000 2g d 2g
h 58000 V 2 l V 2 5.75m 2g d 2g
⑵对 1-1 和 3-3 截面列伯努利方程
水力学第五章 有压管流与孔口、管嘴出流

(图5-1)
5
5-1 有压管路水力计算
– 自由出流计算公式 • 计算图式——图5-1a • 公式推导方法——列1-1、2-2断面能量方程
H
0 0v2
2g
0 0 v2
2g
hw
H0
H
0v02
2g
v2
2g
hw
(5-1)
hw
hfi
hji
i
l1 d
v2 2g
i
v2 2g
c
v2 2g
c
1 c
1
l d
i
(5-4c)
μc—自由出流流量系数
7
5-1 有压管路水力计算
– 淹没出流计算公式 • 计算图式——图5-1b • 公式推导方法——列1-1和2-2断面能量方程
H 0 0 0 0 0 hw
H0 H hw hf hj
H0
l d
i
v2 2g
c
v2 2g
水可头有线恒呈定阶流A梯与状非沿恒14程定下流d降,2,的均折匀线流。与非d均,流p之分 。pa
2
5-1 有压管路水力计算
• 类型 – 按管路组成分类 • 简单管路——管径沿程不变的管路 • 复杂管路——两根以上管道 组成的管路 – 串联管路——管段首尾串接的管路 – 并联管路——多根管段首尾并接的管路 – 管网——多种管路组合而成的管系(其组成又可有技状或环状两 类)
3
4
• 4 1 c s
9
5-1 有压管路水力计算
• 短管水力计算(简单管路) – 作用水头 H0 计算比较 • 自由出流 – H0 起算零点——水管出口中心 • 淹没出流 – H0 起算零点——下游水面
10
5
5-1 有压管路水力计算
– 自由出流计算公式 • 计算图式——图5-1a • 公式推导方法——列1-1、2-2断面能量方程
H
0 0v2
2g
0 0 v2
2g
hw
H0
H
0v02
2g
v2
2g
hw
(5-1)
hw
hfi
hji
i
l1 d
v2 2g
i
v2 2g
c
v2 2g
c
1 c
1
l d
i
(5-4c)
μc—自由出流流量系数
7
5-1 有压管路水力计算
– 淹没出流计算公式 • 计算图式——图5-1b • 公式推导方法——列1-1和2-2断面能量方程
H 0 0 0 0 0 hw
H0 H hw hf hj
H0
l d
i
v2 2g
c
v2 2g
水可头有线恒呈定阶流A梯与状非沿恒14程定下流d降,2,的均折匀线流。与非d均,流p之分 。pa
2
5-1 有压管路水力计算
• 类型 – 按管路组成分类 • 简单管路——管径沿程不变的管路 • 复杂管路——两根以上管道 组成的管路 – 串联管路——管段首尾串接的管路 – 并联管路——多根管段首尾并接的管路 – 管网——多种管路组合而成的管系(其组成又可有技状或环状两 类)
3
4
• 4 1 c s
9
5-1 有压管路水力计算
• 短管水力计算(简单管路) – 作用水头 H0 计算比较 • 自由出流 – H0 起算零点——水管出口中心 • 淹没出流 – H0 起算零点——下游水面
10
流体力学 水力学 孔口和管嘴出流与有压管流.ppt

20
Zs Z
虹吸管是一种压力管,顶部弯曲且其高程高于 上游供水水面。其顶部的真空值一般不大于7-8m
水柱高。虹吸管安装高度Zs越大,顶部真空值越大。
虹吸管的优点在于能跨越高地,减少挖方。 虹吸管长度一般不长,故按短管计算。
2020/8/10
21
例5 4:虹吸管长l lAB lBC 20m 30m 50m, 直径d 200mm。两水池水位差H 1.2m,已知:
不含1,但淹没中两断面间又多了一个由管口进入下
游水池的局部水头损失,而这个水头损失系数ξ=1,
故
c。 c
2020/8/10
17
二、短管水力计算实例
(一)虹吸水力计算
Zs Z
虹吸管是一种压力管,顶部弯曲且其高程高于 上游供水水面。其顶部的真空值一般不大于7-8m
水柱高。虹吸管安装高度Zs越大,顶部真空值越大。
管道比阻。它也是n和d的函数,也可用表5-4查得。
由于
H
Q2 K2
l
S0lQ 2
故
S0K 2 1
2020/8/10
38
(三) 紊流过渡区的水力计算
当V<1.2m/s时,长管中的液体流动属过渡粗糙区,
H(hf)与V不是平方关系,而是1.8次方的关系。为 使上述两法能用于处于紊流过渡区的长管水力计
算,我们引入一修正系数k,即
当管中局部水头损失和流速水头相对于沿程水头损 失而言较小而可以被忽略的管道称为长管。当管道 较长时,沿程水头损失hf占总水头损失hw的绝大部 分,因而可把hj忽略,故长管的水力计算较简单:
H
hf
l d
V2 2g
, V
l 2gH
d
, Q A l 2gH
Zs Z
虹吸管是一种压力管,顶部弯曲且其高程高于 上游供水水面。其顶部的真空值一般不大于7-8m
水柱高。虹吸管安装高度Zs越大,顶部真空值越大。
虹吸管的优点在于能跨越高地,减少挖方。 虹吸管长度一般不长,故按短管计算。
2020/8/10
21
例5 4:虹吸管长l lAB lBC 20m 30m 50m, 直径d 200mm。两水池水位差H 1.2m,已知:
不含1,但淹没中两断面间又多了一个由管口进入下
游水池的局部水头损失,而这个水头损失系数ξ=1,
故
c。 c
2020/8/10
17
二、短管水力计算实例
(一)虹吸水力计算
Zs Z
虹吸管是一种压力管,顶部弯曲且其高程高于 上游供水水面。其顶部的真空值一般不大于7-8m
水柱高。虹吸管安装高度Zs越大,顶部真空值越大。
管道比阻。它也是n和d的函数,也可用表5-4查得。
由于
H
Q2 K2
l
S0lQ 2
故
S0K 2 1
2020/8/10
38
(三) 紊流过渡区的水力计算
当V<1.2m/s时,长管中的液体流动属过渡粗糙区,
H(hf)与V不是平方关系,而是1.8次方的关系。为 使上述两法能用于处于紊流过渡区的长管水力计
算,我们引入一修正系数k,即
当管中局部水头损失和流速水头相对于沿程水头损 失而言较小而可以被忽略的管道称为长管。当管道 较长时,沿程水头损失hf占总水头损失hw的绝大部 分,因而可把hj忽略,故长管的水力计算较简单:
H
hf
l d
V2 2g
, V
l 2gH
d
, Q A l 2gH
工程流体力学 第5章 管路管嘴

以0-0作为基准面,写出1-1和2-2断面的总流 伯努利方程 2 2 p a 1 v1 pa 2 v2 H 0 hl 2g 2g 上式中, v1
0
因为是长管,忽略局部阻力
2 2
2v h r 和速度水头 , 则 hl h f ,故 2g H hf (5.1)
5.1.2 长管的水力计算
对于一般输水管道,常取y =1/6,即曼宁公 式 1 1 c R6 (5.5) n 管壁的粗糙系数值随管壁材料、内壁加工 情况以及铺设方法的不同而异。一般工程 初步估算时可采用表5.1数值。
5.1.2 长管的水力计算
序号 1 壁面种类及状况 安装及联接良好的新制清洁铸铁 管及钢管;精刨木板
5.1.1 短管的水力计算
水泵的吸水管、虹吸管、液压传动系统的输油管 等,都属于短管,它们的局部阻力在水力计算时 不能忽略。短管的水力计算没有什么特殊的原则, 主要是如何运用前一章的公式和图表。
[例题5.1] 水泵管路如图5.1所示, 铸铁管直径d=150mm,管长 l=180m ,管路上装有吸水网(无 底阀)一个,全开截止阀一个,管 半径与曲率半径之比为 r/R=0.5 的 弯头三个,高程h=100m,流量 Q=225m3/h,水温为20℃。试求水 泵的输出功率。
5.2.2 并联管路
根据连续性方程,有 Q Q1 Q2 Q3 (5.11) 根据式(5.10)和式(5.11)可以解决并联管路水 力计算的各种问题。 强调 :虽然各并联管路的水头损失相等,但这只说 明各管段上单位重量的液体机械能损失相等。由 于并联各管段的流量并不相等,所以各管段上全 部液体重量的总机械能损失并不相等,流量大的 管段,其总机械能损失也大。
吉林大学工程流体力学第5章 孔口出流
2p
1 1
2 gH Cv 2 gH
qv Av Cv A 2 gH Cq A 2 gH
5.2.2 厚壁孔口出流系数
收缩系数 C c : Cc 1
1
1
阻力系数 :
2 3
0.5
流速系数 Cv : Cv
流量系数 Cv :
1 1
0.82 0.82
M
Fl F l l3 v2 Fl
力的比例尺
力矩比例尺
压强(应力)比例尺
p
A F 2 v F A A
F
动力粘度比例尺
v v l v v
P l v P l2 v3 P t
1. 厚壁孔口只有内收缩而无外
l 2 4 d
收缩,此时CC=1
2. 总局部阻力系数包括三部分:a) 入口系数(相当于薄壁孔口 出流;b) c-c断面后扩张阻力系数(可按突扩计算),c) 后半段 l 上的沿程当量系数。 ( e ) 2d
5.2.1 厚壁孔口出流的速度和流量
v
1 1
虑在孔口射流断面上各点的水头、压强、速度沿孔口高度的 变化,这时的孔口称为大孔口。 小孔口(small orifice ):当孔口直径d(或高度e)与 孔口形心以上的水头高度H的比值小于0.1,即d/H<0.1时,可 认为孔口射流断面上的各点流速相等, 且各点水头亦相等, 这时的孔口称为小孔口。
2.根据出流条件的不同,可分为自由出流和淹没出流
qV 比较(1)、(2)两式: Cq q T
可见,只要测得 qV,测得H和A就可以得到Cq 。
工程流体力学-第五章

……………………
三、Π定理
对于某个物理现象或过程,如果存在有n个变量互为函数关
系, f(a1,a2, …an)=0 而这些变量含有m个基本量纲,可把这n个变量转换成为有 (n-m)=i个无量纲量的函数关系式
F(1,2, … n-m)=0
这样可以表达出物理方程的明确的量间关系,并把方程中的 变量数减少了m个,更为概括集中表示物理过程或物理现 象的内在关系。
之间函数关系的一种方法,也可以得出相似准
则。
量纲分析法有两种:瑞利法和π定理
瑞利法
解题步骤:首先找出影响流动的物理量,并用它们
写出假拟的指数方程; 然后以对应的量纲代替方程中的物理量本身,并 根据量纲和谐性原理求出各物理量的指数,整理 出最后形式。
例题a:自由落体运动的位移s与时间t、重力加速度g有关。 试求位移s的表达式。
实验研究 发展流体 力学理论 验证流体 力学假说 解释流 动现象 解决流体 力学问题
流体力学的研究方法中实验研究既是理论分析 的依据,同时也是检验理论的准绳,具有很重要的 作用。 本章将探讨其理论基础: 量纲分析 相似理论
直接实验法 物理规律 理论分析法 模型研究法 相似理论
从相似的概念入手,引入相似准数; 从相似原理和量纲分析出发导出相似准数的结 构; 分析实际问题与实验模型相似的条件;
[B]=MLT
4 基本量 导出量
一个物理问题中诸多的物理量分成基本物理量(基本量:
具有独立性、唯一性)和其他物理量(导出量),后者可由前 者通过某种关系到除,前者互为独立的物理量。基本量个数取 基本量纲个数,所取定的基本量必须包括三个基本量纲在内, 这就是选取基本量的原则。 流速 密度 力 压强 dimv=LT-1 dimρ=ML-3 dimF=MLT-2 dim p=M L-1 T-2
三、Π定理
对于某个物理现象或过程,如果存在有n个变量互为函数关
系, f(a1,a2, …an)=0 而这些变量含有m个基本量纲,可把这n个变量转换成为有 (n-m)=i个无量纲量的函数关系式
F(1,2, … n-m)=0
这样可以表达出物理方程的明确的量间关系,并把方程中的 变量数减少了m个,更为概括集中表示物理过程或物理现 象的内在关系。
之间函数关系的一种方法,也可以得出相似准
则。
量纲分析法有两种:瑞利法和π定理
瑞利法
解题步骤:首先找出影响流动的物理量,并用它们
写出假拟的指数方程; 然后以对应的量纲代替方程中的物理量本身,并 根据量纲和谐性原理求出各物理量的指数,整理 出最后形式。
例题a:自由落体运动的位移s与时间t、重力加速度g有关。 试求位移s的表达式。
实验研究 发展流体 力学理论 验证流体 力学假说 解释流 动现象 解决流体 力学问题
流体力学的研究方法中实验研究既是理论分析 的依据,同时也是检验理论的准绳,具有很重要的 作用。 本章将探讨其理论基础: 量纲分析 相似理论
直接实验法 物理规律 理论分析法 模型研究法 相似理论
从相似的概念入手,引入相似准数; 从相似原理和量纲分析出发导出相似准数的结 构; 分析实际问题与实验模型相似的条件;
[B]=MLT
4 基本量 导出量
一个物理问题中诸多的物理量分成基本物理量(基本量:
具有独立性、唯一性)和其他物理量(导出量),后者可由前 者通过某种关系到除,前者互为独立的物理量。基本量个数取 基本量纲个数,所取定的基本量必须包括三个基本量纲在内, 这就是选取基本量的原则。 流速 密度 力 压强 dimv=LT-1 dimρ=ML-3 dimF=MLT-2 dim p=M L-1 T-2
流体力学第五章 孔口及管嘴ppt课件

3.孔口在壁面上的位置对μ 的影响 孔口在壁面上的位置对
收缩系数有直接的影响,如 图
全部收缩孔口〔full contrastive orifice〕:当 孔口的全部边境都不与相邻 的容器底边和侧边重合时, 孔口出流时的周围流线都发 生收缩,这种孔口称为全部 收缩孔口 (如A, B) 。
全部收缩孔口又分完善收缩和不完善收缩。 完善收缩〔perfect contraction〕:凡孔 口与相邻壁面的间隔大于同方向孔口尺寸的3 倍〔L>3a或L>3b〕,孔口出流的收缩不受距 壁面远近的影响,这就是完善收缩(如
2.知Q及管路情况,求作用水头H。——直接用公 式。
3.知H, Q及部分管路情况,求d。〔d需规格化〕
第五节 管路的串联和并联
一、串联管道 串联管道〔pipes in series):由直径不同的几段管
段依次衔接而成的管道称为串联管道。
1. 串联管道流量计算的根本公式 1〕能量方程
〔5-20〕
式中: n——管段的总数目, m——部分阻力的总数 目。
三. 厚壁孔口出流
厚壁孔口出流与薄壁孔口
出流的差别在于收缩系数和
边壁性质有关,留意到收缩
A
系数定义中的A为孔口外侧 面积,容易看出孔边修圆
Ac
Ac
后,收缩减小,收缩系数和
流量系数都增大。
第二节 管嘴出流
管嘴出流〔nozzle discharge〕 :在孔口周边衔接 一长为3~4倍孔径的短管,水经过短管并在出口断 面满管流出的水力景象,称为管嘴出流。
图5-14
〔2〕节点的延续性方程
或 量分出
2. 串联管道水力计算根本类型
1〕知Q,d,求H
由Q、d
v
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.根据孔口水头变化情况,出流可分为:恒定出流、非恒定出流
恒定出流(steady discharge):当孔口出流时,水箱中水量如能得到 源源不断的补充,从而使孔口的水头不变,此时的出流称为恒定出流。
非恒定出流(unsteady discharge):当孔口出流时,水箱中水量得不 到补充,则孔口的水头不断变化,此时的出流称为非恒定出流。
的物理量的换算关系也就都可以确定了。 实物和模型大多是处于同样的地心引力范围,因此
单位质量重力的比例尺一般等于1,即:
g 1
5.5.2 相似准则
1)、弗劳德(Froude)数
代表惯性力与重力之比。
v v gl g l
2 2
弗劳德数
v Fr gl
2
2)、欧拉数
代表压力与惯性力之比。
t v l t t l v v
v 2 a t v v a a v t l t
l
加速度比例尺
流量比例尺
qv l3 q 3t l2 v qv l t t
l3
运动粘度比例尺
l2 v v 2 t l v v l 2 t t
或
F F 2 2 2 2 v L v L
欧拉模型法用于自动模型区的管中流动、风洞实验及气 体绕流等情况。
2p
2p
Cv
2p
Cv 2 gH (1)
2 gH
(2)
vc 比较(1)、(2)两式: Cv vT
流速系数的测定
应注意到:孔口出流进入大气后即成平抛运动。
流量系数 C q : 实际流量与理想流量之比。 流量为:qV Cq A
2p
Cq A 2 gH
(1)
而理想流量: q A 2p A 2 gH (2) T
v v gl g l
2 2
同时
p p 2 v v 2
几何相似
一般模型流动与实物流动中的重力加速度是相同的,于是
2 v v 2 l l
2
或
v l
1
2
此式说明在弗劳德模型法中,速度比例尺可以不再作为需 要选取的基本比例尺。 弗劳德模型法在水利工程上应用甚广,大型水利工程设计 必须首先经过模型实验的论证而后方可投入施工。
自由出流(free discharge):若经孔口流出的水流直接进入空气中, 此时收缩断面的压强可认为是大气压强,即pc=pa,则该孔口出流称为孔 口自由出流。
淹没出流(submerged discharge):若经孔口流出的水流不是进入空 气,而是流入下游水体中,致使孔口淹没在下游水面之下,这种情况称 为淹没出流。
第五章 孔口出流
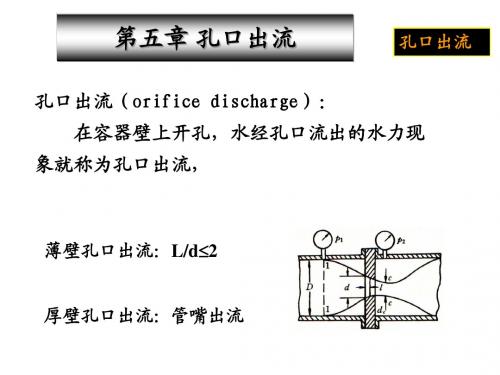
孔口出流(orifice discharge):
孔口出流
在容器壁上开孔,水经孔口流出的水力现
象就称为孔口出流,
薄壁孔口出流:L/d2
厚壁孔口出流:管嘴出流
一、分类
1.根据d/H的比值:大孔口、小孔口 大孔口(big orifice) :当孔口直径d(或高度e)与孔 口形心以上的水头高H的比值大于0.1,即d/H>0.1时,需考
d 所以,v1 Cc vc,pc p2,代入伯努利方程,整 理得 D
vc 1 d 1 Cc2 D
4
2
2p
d (1)对于小孔口: D,有 0 d D
4
1 出流速度 vc 简化为: vc 1
2p
Cv
Reynolds number
Mach number Froude number
Strouhal number
Prandtl number Nusselt number
Grashov number
5.5.3 近似模型法
不能保证全面力学相似的模型设计方法叫近似模型法。
1)弗劳德模型法
在水利工程及明渠无压流动中,处于主要地位的力是重 力。用水位落差形式表现的重力是支配流动的原因,重力是 水工结构中的主要矛盾。粘性力有时不起作用,有时作用不 甚显著,因此可用弗劳德模型法解决此类问题 :
p p 2 v v 2
欧拉数
p Eu 2 v
3)、雷诺数
代表惯性力与粘性力之比。
vl vl
雷诺数
vl
Re
总结以上可见,如果两个流动成力学相似,则
它们的弗劳德数、欧拉数、雷诺数必须各自相等。
Fr Fr
Eu Eu Re Re
称为不可压缩流体定常流动的力学相似准则。可 据此判断两个流动是否相似。
3 2
功率的比例尺
无量纲系数的比例尺
c 1
在相似的实物流动与模型流动之间存在着一切无
量纲系数皆对应相等的关系,这提供了在模型流动上
测定实物流动中的流速系数、流量系数、阻力系数等 等的可能性。 所有力学相似的比例尺中,基本比例尺l、v
、
ρ是各自独立的,基本比例尺确定后,其它一切物理
量的比例尺都可确定,模型流动与实物流动之间一切
l 长度比例尺: l l
A l2 面积比例尺: A 2 l2 A l
V l3 3 体积比例尺: V 3 l V l
2)运动相似:即实物流动与模型流动的流线应该几何相似, 而且对应点上的速度成比例。
速度比例尺
v V v
时间比例尺
M
Fl F l l3 v2 Fl
力的比例尺
力矩比例尺
压强(应力)比例尺
p
A F 2 v F A A
F
动力粘度比例尺
v v l v v
P l v P l2 v3 P t
C q Cv
5.3 几种孔口出流性能比较
出口面积和器壁上的面 积不等时,Cq的大小并不代表流量大 小。
为什么厚壁孔口流量大于薄壁孔口流量?
5.4 机械中的气穴现象
5.4.1 气穴概念
气穴产生的条件:局部地区的高速和低压。
5.4.2 节流气穴
5.4.3 泵进口处的气穴
防止泵前气穴的方法: 1. 降低吸水高度; 2. 降低吸水管、吸油管的局部沿程阻力; 3. 加大管径以降低流速;4.减少进水管输送长度。
l2
角速度比例尺
l v v l
l
v
3)动力相似:即实物流动与模型流动应受同种外力作
用,而且对应点上的对应力成比例。
密度比例尺
质量比例尺
m V m l3 m V
F ma F m a l2 v2 F ma
qV 比较(1)、(2)两式: Cq q T
可见,只要测得 qV,测得H和A就可以得到Cq 。
收缩系数 C c : C c
Cq Cv
0.64
阻力系数
1 : 2 1 Cv
0.06
流量系数 C q :
qV Cq qT
0.62
流速系数 C v
0.97
5.2 厚壁孔口出流 厚壁孔口: 特点:
二、管嘴出流:在孔口周边连接一长为3~4倍孔径的短管,水 经过短管并在出口断面满管流出的水力现象,称为管嘴出流。
圆柱形外管嘴:先收缩后扩大到整满管。
圆锥形扩张管嘴:较大过流能力,较低出口流速。 引射器,水轮机尾水管,人工降雨设备。
流线形外管嘴:无收缩扩大,阻力系数最小。水坝泄流
圆锥形收缩管嘴:较大出口流速。水力挖土机喷嘴,消防用喷嘴。
虑在孔口射流断面上各点的水头、压强、速度沿孔口高度的 变化,这时的孔口称为大孔口。 小孔口(small orifice ):当孔口直径d(或高度e)与 孔口形心以上的水头高度H的比值小于0.1,即d/H<0.1时,可 认为孔口射流断面上的各点流速相等, 且各点水头亦相等, 这时的孔口称为小孔口。
2.根据出流条件的不同,可分为自由出流和淹没出流
2p
1 1
2 gH Cv 2 gH
qv Av Cv A 2 gH Cq A 2 gH
5.2.2 厚壁孔口出流系数
收缩系数 C c : Cc 1
1
2 3
阻力系数 :
1
0.5
流速系数 Cv : Cv
流量系数 Cv :
1 1
0.82 0.82
型区时,雷诺准则失去判别相似的作用。
这也就是说,研究雷诺数处于自动模型区时的粘性流 动不满足雷诺准则也会自动出现粘性力相似。因此设计模 型时,粘性力的影响不必考虑了;如果是管中流动,或者
是气体流动,其重力的影响也不必考虑;这样我们只需考
虑代表压力和惯性力之比的欧拉准则就可以了。
即:
p p 2 2 v v
3)欧拉模型法
粘性流动中有一种特殊现象,当雷诺数增大到一定界
限以后,惯性力与粘性力之比也大到一定程度,粘性力的
影响相对减弱,此时继续提高雷诺数,也不再对流动现象 和流动性能发生质和量的影响,此时尽管雷诺数不同,但 粘性效果却是一样的。这种现象叫做自动模型化,产生这 种现象的雷诺数范围叫做自动模型区,雷诺数处在自动模
4
Cq A 2 gH
流量系数
Cq CcCv
Cc
2 d 1 Cc D 4
5.1.2 孔口出流系数
一、流速系数 C v: 实际流速与理想流速之比, 孔口阻力系数越大,实际流速越小,流速系数也就越小。
1 v 出流速度 : c 1
而理想流速为 :vT
相似准则不但是判别相似的标准,而且也是设计
