解直角三角形及其应用-课件ppt
合集下载
《解直角三角形及其应用》ppt导学课件

义务教育教科书(人教版)九年级数学下册
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
结束语Biblioteka 学习知识要善于思考,思考,再思考。
《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
结束语Biblioteka 学习知识要善于思考,思考,再思考。
《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
《解直角三角形及其应用》实用课件 (PPT优 秀课件 ) 《解直角三角形及其应用》实用课件 (PPT优 秀课件 )
解直角三角形的应用ppt课件

(结果保留一位小数).
(参考数据:sin63°≈0.9,cos63°≈0.5,
tan63°≈2.0, ≈1.73)
26.4 解直角三角形的应用
解:(1)∵MC=AB=10 cm,∠ACM=63°,
重 ∴AM=MC·tan∠ACM=MC·tan63°≈10×2.0=20(cm).
难
题 答:AM 的长为 20 cm;
直接测量的物体高度或长度
26.4 解直角三角形的应用
归纳总结
考
点
(1)仰角和俯角是视线相对于水平视线而言的,可巧记
清
单 为“上仰下俯”;(2)实际问题中遇到仰角或俯角时,要
解
读 放在直角三角形或转化到直角三角形中运用,注意确定水平
视线;(3)在解有关俯角、仰角的问题中,常作水平线或
铅垂线来构造直角三角形.
,
∴tan30°=
=
−
+
=
,解得
x=60 +90,经检验
x=60 +90 是原方程的解且符合题意,∴AB=(60 +90) m
,
26.4 解直角三角形的应用
变式衍生 3 某中学依山而建,校门 A 处有一坡角
重
难
题 α=30°的斜坡 AB,长度为 30 m,在坡顶 B 处测得教学
26.4 解直角三角形的应用
(2)如答案图,过点 D 作 DH⊥AB,垂足为点 H,则
重
难
题 DG=BH=30 m,DH=BG.设 BC=x m,
型
在 Rt△ABC 中,∠ACB=45°,
突
破
∴AB=BC·tan45°=x m,
∴AH=AB-BH=(x-30) m,
(参考数据:sin63°≈0.9,cos63°≈0.5,
tan63°≈2.0, ≈1.73)
26.4 解直角三角形的应用
解:(1)∵MC=AB=10 cm,∠ACM=63°,
重 ∴AM=MC·tan∠ACM=MC·tan63°≈10×2.0=20(cm).
难
题 答:AM 的长为 20 cm;
直接测量的物体高度或长度
26.4 解直角三角形的应用
归纳总结
考
点
(1)仰角和俯角是视线相对于水平视线而言的,可巧记
清
单 为“上仰下俯”;(2)实际问题中遇到仰角或俯角时,要
解
读 放在直角三角形或转化到直角三角形中运用,注意确定水平
视线;(3)在解有关俯角、仰角的问题中,常作水平线或
铅垂线来构造直角三角形.
,
∴tan30°=
=
−
+
=
,解得
x=60 +90,经检验
x=60 +90 是原方程的解且符合题意,∴AB=(60 +90) m
,
26.4 解直角三角形的应用
变式衍生 3 某中学依山而建,校门 A 处有一坡角
重
难
题 α=30°的斜坡 AB,长度为 30 m,在坡顶 B 处测得教学
26.4 解直角三角形的应用
(2)如答案图,过点 D 作 DH⊥AB,垂足为点 H,则
重
难
题 DG=BH=30 m,DH=BG.设 BC=x m,
型
在 Rt△ABC 中,∠ACB=45°,
突
破
∴AB=BC·tan45°=x m,
∴AH=AB-BH=(x-30) m,
18、解直角三角形及其应用PPT课件

中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
6
已知条件 已知两直角边(a,b) 已知斜边和一条直角边(c,a)
图形
解法 c= a2+b2,由 tanA=ab求∠A,∠ B=90°-∠A b= c2-a2,由 sinA=ac求∠A,∠ B=90°-∠A
202X权威 · 预测
第一部分 教材同步复习
12
(2)∵∠ABE=90°,AB=6,sinA=45=BAEE, ∴设 BE=4x,则 AE=5x,得 AB=3x, ∴3x=6,得 x=2,∴BE=8,AE=10, ∴tanE=ABBE=68=CDDE=D4E, 解得,DE=136, ∴AD=AE-DE=10-136=134,即 AD 的长是134.
第一部分 教材同步复习
4
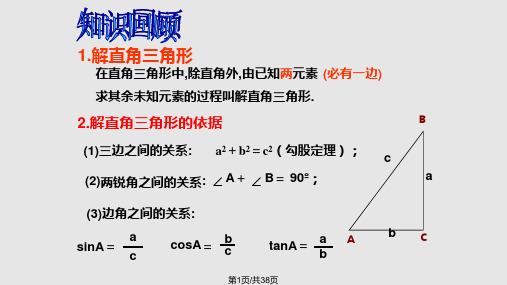
►知识点二 解直角三角形
1.解直角三角形的定义及依据 (1)定义:在直角三角形中,除直角外,由已知元素求未知元素的过程就是解直 角三角形; (2)依据:在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c, 则①边角关系:sinA=ac,cosA=bc,tanA=ab;②三边之间的关系:a2+b2=c2;③锐 角之间的关系:∠A+∠B=∠C; 1 (3)面积公式:S△ABC=12ab=①__2_c_h_____.(h 为斜边 c 上的高)
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
11
【思路点拨】 本题考查解直角三角形.(1)要求BC的长,只要求出BE和CE的 长即可,由题意可以得到BE和CE的长,本题得以解决;(2)要求AD的长,只要求出 AE和DE的长即可,根据题意可以得到AE、DE的长,本题得以解决.
解直角三角形应用举例PPT课件
2 2
cm
2
(根号保留).
第14页/共38页
当堂反馈
5.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基
间的水平距离BD为100m,塔高CD为 (100 3 50)m,
则下面结论中正确的是( C )
3
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形; 3.得到数学问题的答案; 4.得到实际问题的答案.
第16页/共38页
新人教版九年级数学(下册)第二十八章
§28.2 解直角三角形(3)
第17页/共38页
在进行观察或测量时,
仰角和俯角
从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.
A
C
D
B
第10页/共38页
2、在山脚C处测得山顶A的仰角为450。问题如下:
变式: 沿着坡角为30 °的斜坡前进300米到达D 点,在D点测得山顶A的仰角为600 ,求山高AB。
A
D xF
30°
C
Ex B
第11页/共38页
3、在山顶上处D有一铁塔,在塔顶B处测得地面上一 点A的俯角α=60o,在塔底D测得点A的俯角β=45o, 已知塔高BD=30米,求山高CD。
y/km A
O
北
东
C x/km
第27页/共38页
B 图12
解:(1) B(100 3,100 3) C(100 3,200 100 3)
(2)过点C作 CD OA于点D,如图2,则 CD 100 3
26.4 解直角三角形的应用 - 第1课时仰角、俯角、方位角问题课件(共23张PPT)

解:如图,α = 30° , β= 60°,AD=120. ∵ , ∴BD=AD·tanα=120×tan30︒, =120× =40 . CD=AD·tanβ=120×tan60︒, =120× =120 . ∴BC=BD+CD=40 +120 =160 ≈277(m).答:这栋楼高约为277m.
例1 如图,小明在距旗杆4.5 m的点D处,仰视旗杆顶端A,仰角(∠AOC)为50°;俯视旗杆底部B,俯角(∠BOC)为18°.求旗杆的高.(结果精确到0.1 m)
例题示范
知识点2 方向角方位角:由正南或正北方向线与目标方向线构成的锐角叫做方位角.如下图中的目标方向OA,OB,OC,OD的方向角分别表示________60°,________45°(或__________),_________80°及_________30°.
拓展提升
1.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
分析:如图,α=30°,β=60°.在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
第二十六章 解直角三角形
26.4 解直角三角形的应用
第1课时 仰角、俯角、方位角问题
学习目标
学习重难点
重点
难点
1.巩固解直角三角形有关知识,了解仰角、俯角、方向角的概念.2.运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.
回顾复习
例1 如图,小明在距旗杆4.5 m的点D处,仰视旗杆顶端A,仰角(∠AOC)为50°;俯视旗杆底部B,俯角(∠BOC)为18°.求旗杆的高.(结果精确到0.1 m)
例题示范
知识点2 方向角方位角:由正南或正北方向线与目标方向线构成的锐角叫做方位角.如下图中的目标方向OA,OB,OC,OD的方向角分别表示________60°,________45°(或__________),_________80°及_________30°.
拓展提升
1.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
分析:如图,α=30°,β=60°.在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
第二十六章 解直角三角形
26.4 解直角三角形的应用
第1课时 仰角、俯角、方位角问题
学习目标
学习重难点
重点
难点
1.巩固解直角三角形有关知识,了解仰角、俯角、方向角的概念.2.运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.
回顾复习
解直角三角形的应用举例课件

1 直角三角形的两条直角边相互垂直。 2 直角三角形的斜边是直角边的对边。 3 直角三角形的两条直角边的和等于斜边的长。
直角三角形的边和角的关系
1 正弦定理:sin(边/邻边
2 余弦定理:cos(A) =
邻边/斜边,cos(B) = 对边/斜边,cos(C) = 对边/邻边
解直角三角形的应用举例 ppt课件
直角三角形是一种特殊的三角形,它具有很多实用的应用。本课件将介绍直 角三角形的定义、特点、边和角的关系,以及直角三角形在测量、几何图形 和实际生活中的常见应用举例。
直角三角形的定义
1 对于一个三角形来说,如果有一个角是直角(90°角),则该三角形是直角三角形。
直角三角形的特点
直角三角形在实际生活中的应用举例
航海导航
用直角三角形的海图与经纬线相交确定位置。
建筑施工
用直角三角形测量建筑物的角度和比例,确保施 工的准确性。
飞行导航
用直角三角形计算飞机航线、飞行高度、地平线 角度等。
摄影测量
使用直角三角形测量物体的距离和高度,帮助摄 影师选择拍摄的角度和位置。
3
测量斜率
直角三角形可以用来测量地面的斜率, 帮助工程师确定在不同地形上的施工方 法。
直角三角形在几何图形中的应用举例
图形拼接
将多个直角三角形拼接在一起, 可以创建各种几何图形,例如正 方形、长方形和平行四边形。
金字塔
金字塔是由多个直角三角形堆叠 而成,是古代建筑中常见的形式 之一。
三棱柱
三棱柱的两个底面都是直角三角 形,是几何学中常见的立体图形。
直角三角形的特性被电路设计 师用于计算电阻、电流和电压 的关系,对电路的分析和设计 提供了便利。
直角三角形在测量中的应用举例
直角三角形的边和角的关系
1 正弦定理:sin(边/邻边
2 余弦定理:cos(A) =
邻边/斜边,cos(B) = 对边/斜边,cos(C) = 对边/邻边
解直角三角形的应用举例 ppt课件
直角三角形是一种特殊的三角形,它具有很多实用的应用。本课件将介绍直 角三角形的定义、特点、边和角的关系,以及直角三角形在测量、几何图形 和实际生活中的常见应用举例。
直角三角形的定义
1 对于一个三角形来说,如果有一个角是直角(90°角),则该三角形是直角三角形。
直角三角形的特点
直角三角形在实际生活中的应用举例
航海导航
用直角三角形的海图与经纬线相交确定位置。
建筑施工
用直角三角形测量建筑物的角度和比例,确保施 工的准确性。
飞行导航
用直角三角形计算飞机航线、飞行高度、地平线 角度等。
摄影测量
使用直角三角形测量物体的距离和高度,帮助摄 影师选择拍摄的角度和位置。
3
测量斜率
直角三角形可以用来测量地面的斜率, 帮助工程师确定在不同地形上的施工方 法。
直角三角形在几何图形中的应用举例
图形拼接
将多个直角三角形拼接在一起, 可以创建各种几何图形,例如正 方形、长方形和平行四边形。
金字塔
金字塔是由多个直角三角形堆叠 而成,是古代建筑中常见的形式 之一。
三棱柱
三棱柱的两个底面都是直角三角 形,是几何学中常见的立体图形。
直角三角形的特性被电路设计 师用于计算电阻、电流和电压 的关系,对电路的分析和设计 提供了便利。
直角三角形在测量中的应用举例
解直角三角形及其应用精选教学PPT课件

第24讲┃ 回归教材
中考变式
[2012·扬州] 如图24-7,一艘巡逻艇航行至海面B处 时,得知正北方向上距B处20海里的C处有一渔船发 生故障,就立即指挥港口A处的救援艇前往C处营救. 已知C处位于A处的北偏东45°的方向上,港口A处 位于B处的北偏西30°的方向上. 求A、C两处之间的 距离.(结果精确到0.1 海里. 参考数据:≈1.41, ≈1.73)
你已经可以为自己的幸运 烧香拜佛了
还有什么是真爱呢 真正的爱情
年少时站在校园里期待的那种爱情 早已
在尘世中消失离别的时候 每一句话都是那么重
缓缓地扣击着我们的心灵 窗被敲开了
我们诉说着回忆中的快乐 回想著一张张可爱的笑脸
院子里,操场上 充满了甜甜的空气
离别的时候 每一句话都是那么轻 轻轻地说着离别时的感言 轻轻的拉着彼此的手 轻轻地在耳际说声对不起
第24讲┃ 归类示例
有关解直角三角形的实际问题,一般需要利用方向 角等构造直角三角形解决.
第24讲┃ 归类示例
► 类型之三 利用直角三角形解决坡度问题 命题角度: 1. 利用直角三角形解决坡度问题; 2. 将实际问题转化为直角三角形问题.
例3 [2013·衡阳]如图24-5,一段河坝的横断面为梯形 ABCD,试根据图中的数据,求出坝底宽AD.(i=CE∶ED, 单位:m)
图24-6
第24讲┃ 回归教材
解:如图所示,由题意知,∠CAD=27°,∠CBD=40°,AB=50 m,
点A、B、D在一条直线上,CD⊥AD.设BD=x m,CD=h m,
在Rt△ACD中,
tan27°=50h+
, x
h=(50+x)·tan 27°.①
在Rt△BCD中,
解直角三角形的应用(19张ppt)课件

选择合适的解法
根据实际情况选择合适的解法,如近似计算、 精确计算等。
注意单位统一
在实际应用中,要注意单位统一,避免计算 错误。
考虑多解情况
在某些情况下,解直角三角形可能存在多个 解,需要全面考虑。
06
练习与巩固
基础练习题
总结词
掌握基本概念和公式
直角三角形中的角度和边长关系
理解直角三角形中锐角、直角和钝角之间 的关系,以及边长与角度之间的勾股定理 。
利用三角函数定义求解
总结词
通过已知角度和邻边长度,求对边或 斜边长度。
详细描述
根据三角函数定义,已知一个锐角和它 所对的边,可以通过三角函数求出其他 两边。例如,已知∠A=30°和a=1,可 以通过三角函数sin(30°)求出对边b。
利用勾股定理求解
总结词
通过已知两边的长度,求第三边长度。
详细描述
向。
确定建筑物的角度
在建筑设计中,通过解直角三角形, 可以确定建筑物的角度和方向。
确定建筑物的长度
在建筑设计中,通过解直角三角形, 可以确定建筑物的长度和方向。
物理问题中的运用
确定物体的运动轨迹
在物理问题中,通过解直角三角形,可以确定物体的运动轨 迹和方向。
确定物体的受力情况
在物理问题中,通过解直角三角形,可以确定物体的受力情 况和方向。
04
实际应用案例
测高问题
01
02
03
测量山的高度
通过测量山脚和山顶的仰 角,利用解直角三角形的 知识,可以计算出山的高 度。
测量楼的高度
利用解直角三角形的知识, 通过测量楼底和楼顶的仰 角,可以计算出楼的高度。
测量树的高度
通过测量树底部和树顶部 的仰角,利用解直角三角 形的知识,可以计算出树 的高度。
新人教版九年级下册数学 28.2 解直角三角形及其应用参考课件(共30张PPT)

2.如图,沿AC方向开山修路,为了加快施工进度,要在小山的 另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m, ∠d=50°,那么开挖点E离D多远正好能A,C,E使成一直线,(精 确到0.1m)?
例5.如图,一般海轮位于灯塔P的北偏东65°方向,距离灯 塔80海里的A处,它沿正南方向航行一段时间后,到达位于 灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距 离灯塔P有多远(结果取整数)?
问题 要想使人平安地攀上斜靠在墙面上的梯子的顶 端,梯子与地面所成的角α,一般要满足50°≤α≤75°. 现有一个长6m的梯子.问
(1)使用这个梯子最高可以平安攀上多高的墙(精确到0.1m)
对于问题(1),当梯子与地面成的角α为75°时,梯子顶 端与地面的距离是使用这个梯子所以攀到的最大高度.
问题(1)可以归结为:在Rt△ABC中,己知∠A=75°,斜边 AB=6,求∠A的对边BC的长.
(1)坡度α和β; (2)坝顶宽AD和斜坡AB的长(精确到0.1m)
利用解直角三角形的知识解决实际问题的一般过程是: (1)将实际问题抽象为数学问题(画出平面图形,转化为解直角 三角形问题); (2)根据条件的特点,适中选用锐角三角函数等去解直角三角形; (3)得到数学问题的答案; (4)得到实际问题的答案.
例3 2022年6月18日,“神舟〞九号载人航天飞船与“天宫〞 一号目标飞行器成功实现交会对接.“神舟〞九号与“天宫〞一 号的组合体当在离地球外表343km的圆形轨道上运行.如图,当组 合体运行到地球外表上P点的正上方时,从中能直接看到的地球 外表最远的点在什么位置?最远点与P点的距离是多少?(地球半 径约为6 400 km,π取3.142,结果取整数)?
解 : 如图在RtAPC中
解直角三角形的应用ppt课件

为点E、 F,由题意可知BE=CF=23m , EF=BC=6m.
在Rt△ABE中,
∵=
= ,
∴ = 3 = 3 × 23 = 69(m)
在Rt△DCF中,同理可得 =
=
.
∴ = 2.5 = 2.5 × 23 = 57.5(m)
∴ = + + = 69 + 6 + 57.5 = 132.5(m)
在Rt△ABE中,由勾股定理可得
∴ = 2 + 2 = 692 + 232 ≈ 72.7(m)
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
例2 如图,在山坡上种树,要求株距(相邻
两树间的水平距离)是5.5米,测得斜坡的坡
角是30°,求斜坡上相邻两树间的坡面距
离是多少米?(结果精确到0.01m)
(2)坡面与水平面的夹角 叫坡角
2.坡度与坡角 的关系
h
i tan
l
显然,坡度越大,坡角
就越大,坡面就越
水库
五、课后作业
1、课本60练习1,2
2.习题2.5 1-12
B
C
30°
(
5.5
A
解:由题意得
AC=5.5m,∠A=30°,
∠C=90°
在Rt △ ABC中, C 90
AC 5.5
3
cos A
AB AB
2
11 3
AB
6.35 m
3
∴相邻两颗树之间的坡面距离约为6.35m。
三、课堂练习
1.如图,在东西方向的海岸线上有A,B两个港口,甲货船
在Rt△ABE中,
∵=
= ,
∴ = 3 = 3 × 23 = 69(m)
在Rt△DCF中,同理可得 =
=
.
∴ = 2.5 = 2.5 × 23 = 57.5(m)
∴ = + + = 69 + 6 + 57.5 = 132.5(m)
在Rt△ABE中,由勾股定理可得
∴ = 2 + 2 = 692 + 232 ≈ 72.7(m)
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
例2 如图,在山坡上种树,要求株距(相邻
两树间的水平距离)是5.5米,测得斜坡的坡
角是30°,求斜坡上相邻两树间的坡面距
离是多少米?(结果精确到0.01m)
(2)坡面与水平面的夹角 叫坡角
2.坡度与坡角 的关系
h
i tan
l
显然,坡度越大,坡角
就越大,坡面就越
水库
五、课后作业
1、课本60练习1,2
2.习题2.5 1-12
B
C
30°
(
5.5
A
解:由题意得
AC=5.5m,∠A=30°,
∠C=90°
在Rt △ ABC中, C 90
AC 5.5
3
cos A
AB AB
2
11 3
AB
6.35 m
3
∴相邻两颗树之间的坡面距离约为6.35m。
三、课堂练习
1.如图,在东西方向的海岸线上有A,B两个港口,甲货船
九年级数学下册28.2 《解直角三角形及其应用》PPT课件

解:设登到B处,视线BC在C点与地球相切,也就是 看C点,AB就是“楼”的高度,
在Rt△OCB中,∠O
AC OC
180
4.5 ,
OB
OC cos∠O
6370 cos 4.5
6389km,
∴ AB=OB-OA=6389-6370=19(km). 即这层楼至少要高19km,即1900m. 这是不存在 的.
例1 2012年6月18日,“神州”九号载人航天飞船与“天宫”一号
目标飞行器成功实现交会对接. “神州”九号与“天宫”一号的
组合体在离地球表面343km的圆形轨道上运行. 如图,当组
合体运行到离地球表面P点的正上方时,从中能直接看到的
地球表面最远的点在什么位置?最远点与P点的距离是多少
(地球半径约为6 400km,取3.142,结果取整数)?
个角), 其中∠C=90°.
B
(1) 三边之间的关系:a2+b2=__c_2__;
c a
(2) 锐角之间的关系: ∠A+∠B=__9_0_°_;
A
a
bC
b
(3) 边角之间的关系:sinA=__c___,cosA=__c___,
a
tanA=___b__.
讲授新课
一 已知两边解直角三角形
合作探究
在图中的Rt△ABC中,
三 已知一锐角三角函数值解直角三角形
例3 如图,在Rt△ABC 中,∠C=90°,cosA = 1,
3
BC = 5, 试求AB的长.
解: C 90,cos A 1, AC 1 . 3 AB 3
设 AB x, AC 1 x,
B
解直角三角形及其应用ppt课件

形
例1 在△ABC中,∠C为直角,∠A、∠B、∠C所
对的边分别为a、b、c,且b= 2 ,a= 6 ,解这 个三角形.
解:∵tanA=
a b
=____62___=
3
∴∠A=60°
∴∠B=__9_0_°__-_∠=A30°
∴AB=2AC=___2__2___
研读课文
解 知直 识角 点三 二角
形
例2 在Rt△ABC中, ∠B =35度,b=20,解这个
B
∴AC= 6
归纳小结
1、直角三角形ABC中,∠C=90°,a、b、c、 ∠A、∠B这五个元素间的等量关系:
(1)三边之间的关系:___a2_+_b_2_=_c_2__________
(2)两锐角之间的关系:_∠_A_+_∠_B=_9_0°__________ (3)边角之间的关系: ___si_n _A_ __A斜的_边_对_边_=_ac___co_s_A___A斜的_边_邻_边_=_bc___t_an_A___AA_的的_对邻_边边__=_ba_ 2、根据直角三角形的____2_个_____元素(至少有一 个边),可求出其余所有元素的过程,叫 __解__直__角__三__角__形_____. 3、学习反思:______________________________ ____________________________________。
强化训练
1、在Rt△ABC中, ∠C=90°,已知tanB= 5 ,则
2
cosA等于( D )
5
5
25
2
A. 2
B. 3
C. 5
D. 3
2、在Rt△ABC中,∠C=90°,a=35,c= 35 2
例1 在△ABC中,∠C为直角,∠A、∠B、∠C所
对的边分别为a、b、c,且b= 2 ,a= 6 ,解这 个三角形.
解:∵tanA=
a b
=____62___=
3
∴∠A=60°
∴∠B=__9_0_°__-_∠=A30°
∴AB=2AC=___2__2___
研读课文
解 知直 识角 点三 二角
形
例2 在Rt△ABC中, ∠B =35度,b=20,解这个
B
∴AC= 6
归纳小结
1、直角三角形ABC中,∠C=90°,a、b、c、 ∠A、∠B这五个元素间的等量关系:
(1)三边之间的关系:___a2_+_b_2_=_c_2__________
(2)两锐角之间的关系:_∠_A_+_∠_B=_9_0°__________ (3)边角之间的关系: ___si_n _A_ __A斜的_边_对_边_=_ac___co_s_A___A斜的_边_邻_边_=_bc___t_an_A___AA_的的_对邻_边边__=_ba_ 2、根据直角三角形的____2_个_____元素(至少有一 个边),可求出其余所有元素的过程,叫 __解__直__角__三__角__形_____. 3、学习反思:______________________________ ____________________________________。
强化训练
1、在Rt△ABC中, ∠C=90°,已知tanB= 5 ,则
2
cosA等于( D )
5
5
25
2
A. 2
B. 3
C. 5
D. 3
2、在Rt△ABC中,∠C=90°,a=35,c= 35 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)若某坡面的坡角为 45,则坡度 i=1:1 ; (2)若某坡面的坡度为 1: 3 ,则坡角是 30 。
坡度
如图,拦水坝的横断面为梯形 ABCD ,根据图中的数据, 求坝顶宽 AD 和斜坡 AB 的长。
坡度
解:依题意,得 DE 1 。
EC 3
Q DE AF 6 m ,
EC 1(8 m) 。
角是_____1_பைடு நூலகம்___。
仰角、俯角
如图,某航天飞船在地球表面点 P的正上方 A处, 从A 处观测到地球上的最远点 Q,若QAP ,地球
半径为 R ,则航天飞船距离地球表面的最近距离 AP
是( B )
A. R
sin
C.
R +R
sin
B. R R
sin
D.
R R
cos
方向角
1.方向角是表示方向的角;以__正__北______和 ___正__南_____方向为基准,来描述物体所处的方向;
迎水坡坡角BAC 30 ,则 AB的长为 16m 。
坡度
3.(1)坡度 i 是指__竖__直__高__度__与__水__平__距__离__的比,
这个值与坡角的____正__切____值相等;
(2)坡度 i 一般写成 1:m 的形式,坡度 i 的值
越大,表明坡角越____大______,即坡越陡。 4.填空:
解直角三角形及其应用
仰角、俯角
如图,在进行高度测量时,视线与水平线所成的角 中,视线在水平线上方的是___仰__角_____,视线在水平线 下方的是___俯__角_____。
仰角、俯角
如图,C=DEB=90 ,FB P AC ,从 A 点看 D 点的仰角是____2__,从 B 点看 D 点的俯角是___F_B_D__, 从 A 点看 B 点的_____仰__角是____B_A_C___,从 D 点看 B 点的____仰____角是_____3___,从 B点看 A 点的___俯___
航行到灯塔的正东方向 B 处,那么海轮航行的距离 AB
的长是( C )
A. 10海里
C. 10 cos 50 海里
B. 10sin 50 海里 D. 10 tan 50 海里
坡度
1. 一个人从山底沿30°的山坡登上山顶,他走
了 500m ,则这座山的高度是 250m。 2. 某河堤的横断面如图所示,河堤高 BC 8 m ,
2.描述方向角时,一般先叙述北或南,再叙 述偏东或偏西。(注意几个方向的角平分线按日 常习惯,即东北,东南,西北,西南。 )
方向角
3. 如图,点 A 位于点 O 的_北__偏__西__6_5_°_的方向上。
方向角
如图,一艘海轮位于灯塔 P 的北偏东50°方向,
距离灯塔 P为10海里的点 A 处,如果海轮沿正南方向
依题意,得
AF BF
1 1.5
,
Q AF 6m ,
BF (9 m)。
AD EF 30 9 18 (3 m),
AB AF 2 BF 2 =3 1(3 m)。
谢谢
坡度
如图,拦水坝的横断面为梯形 ABCD ,根据图中的数据, 求坝顶宽 AD 和斜坡 AB 的长。
坡度
解:依题意,得 DE 1 。
EC 3
Q DE AF 6 m ,
EC 1(8 m) 。
角是_____1_பைடு நூலகம்___。
仰角、俯角
如图,某航天飞船在地球表面点 P的正上方 A处, 从A 处观测到地球上的最远点 Q,若QAP ,地球
半径为 R ,则航天飞船距离地球表面的最近距离 AP
是( B )
A. R
sin
C.
R +R
sin
B. R R
sin
D.
R R
cos
方向角
1.方向角是表示方向的角;以__正__北______和 ___正__南_____方向为基准,来描述物体所处的方向;
迎水坡坡角BAC 30 ,则 AB的长为 16m 。
坡度
3.(1)坡度 i 是指__竖__直__高__度__与__水__平__距__离__的比,
这个值与坡角的____正__切____值相等;
(2)坡度 i 一般写成 1:m 的形式,坡度 i 的值
越大,表明坡角越____大______,即坡越陡。 4.填空:
解直角三角形及其应用
仰角、俯角
如图,在进行高度测量时,视线与水平线所成的角 中,视线在水平线上方的是___仰__角_____,视线在水平线 下方的是___俯__角_____。
仰角、俯角
如图,C=DEB=90 ,FB P AC ,从 A 点看 D 点的仰角是____2__,从 B 点看 D 点的俯角是___F_B_D__, 从 A 点看 B 点的_____仰__角是____B_A_C___,从 D 点看 B 点的____仰____角是_____3___,从 B点看 A 点的___俯___
航行到灯塔的正东方向 B 处,那么海轮航行的距离 AB
的长是( C )
A. 10海里
C. 10 cos 50 海里
B. 10sin 50 海里 D. 10 tan 50 海里
坡度
1. 一个人从山底沿30°的山坡登上山顶,他走
了 500m ,则这座山的高度是 250m。 2. 某河堤的横断面如图所示,河堤高 BC 8 m ,
2.描述方向角时,一般先叙述北或南,再叙 述偏东或偏西。(注意几个方向的角平分线按日 常习惯,即东北,东南,西北,西南。 )
方向角
3. 如图,点 A 位于点 O 的_北__偏__西__6_5_°_的方向上。
方向角
如图,一艘海轮位于灯塔 P 的北偏东50°方向,
距离灯塔 P为10海里的点 A 处,如果海轮沿正南方向
依题意,得
AF BF
1 1.5
,
Q AF 6m ,
BF (9 m)。
AD EF 30 9 18 (3 m),
AB AF 2 BF 2 =3 1(3 m)。
谢谢
