高中数学选修一第3章 导数及其应用课件ppt3.1.3
合集下载
(人教版)高中数学选修1-1课件:第3章 导数及其应用3.3.3

数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(3)函数f(x)在闭区间[a,b]上图象连续不断,是f(x)在闭区 间[a,b]上有最大值与最小值的充分条件而非必要条件.
(4)函数在其定义区间上的最大值、最小值最多各有一个, 而函数的极值可能不止一个,也可能一个也没有,函数的最大 值一定不小于它的最小值.
函数在闭区间上的最值可在端点处取 ③×
得,也可以在内部取得 ④ × 单调函数在开区间(a,b)内无最值
答案: A
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.函数f(x)=x3-3x2-9x+k在区间[-4,4]上的最大值为
10,则其最小值为( )
A.-10
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(2)若 a<0,当 x 变化时,f′(x),f(x)的变化情况如下表:
x
[-1,0)
0
(0,2]
f′(x)
-
0
+
f(x)
极小值
所以当 x=0 时,f(x)取得最小值, 所以 f(0)=b=-29.
数学 选修1-1
x
-3 (-3,-1) -1 (-1,0) 0 (0,1)
f′(x)
+
0
-
0+
f(x)
-60
极大 值4
极小 极大 值3 值4
∴当 x=-3 时,f(x)取最小值-60;
1 (1,2) 2 0-
- 5
高中数学新人教B版选修1-1第三章导数及其应用3.1.3导数的几何意义课件

第三章 §3.1 导 数
3.1.3 导数的几何意义
学习目标
XUEXIMUBIAO
1.了解导函数的概念,理解导数的几何意义. 2.会求简单函数的导函数. 3.根据导数的几何意义,会求曲线上某点处的切线方程. 4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
内容索引
NEIRONGSUOYIN
解析 设点 P(x0,2x20+4x0),
则 f′(x0)= lim Δx→0
fx0+Δx-fx0 Δx
= lim Δx→0
2Δx2+4Δx0x·Δx+4Δx=4x0+4,
令4x0+4=16,得x0=3,∴P(3,30).
12345
课堂小结
KETANGXIAOJIE
1.导数 f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处切线的斜率,即 k=
线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在 切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
∴x0=2,∴P(2,8+a). 将x=2,y=8+a代入到8x-y-15=0中,
得a=-7.
反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线 的倾斜角的大小确定数据的大小.
f2-f1 跟踪训练 4 (1)已知函数 f(x)在 R 上可导,其部分图象如图所示,设
2-1
=a,则下列不等式正确的是
则12a-23a·|a3|=16, 解得a=±1.
核心素养之直观想象
HEXINSUYANGZHIZHIGUANXIANGXIANG
求切线倾斜角的范围
典例 已知点 P 在曲线 y=x3-x+32上,直线 l 为曲线在 P 点处的切线,求直 线 l 的倾斜角的取值范围.
3.1.3 导数的几何意义
学习目标
XUEXIMUBIAO
1.了解导函数的概念,理解导数的几何意义. 2.会求简单函数的导函数. 3.根据导数的几何意义,会求曲线上某点处的切线方程. 4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
内容索引
NEIRONGSUOYIN
解析 设点 P(x0,2x20+4x0),
则 f′(x0)= lim Δx→0
fx0+Δx-fx0 Δx
= lim Δx→0
2Δx2+4Δx0x·Δx+4Δx=4x0+4,
令4x0+4=16,得x0=3,∴P(3,30).
12345
课堂小结
KETANGXIAOJIE
1.导数 f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处切线的斜率,即 k=
线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在 切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
∴x0=2,∴P(2,8+a). 将x=2,y=8+a代入到8x-y-15=0中,
得a=-7.
反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线 的倾斜角的大小确定数据的大小.
f2-f1 跟踪训练 4 (1)已知函数 f(x)在 R 上可导,其部分图象如图所示,设
2-1
=a,则下列不等式正确的是
则12a-23a·|a3|=16, 解得a=±1.
核心素养之直观想象
HEXINSUYANGZHIZHIGUANXIANGXIANG
求切线倾斜角的范围
典例 已知点 P 在曲线 y=x3-x+32上,直线 l 为曲线在 P 点处的切线,求直 线 l 的倾斜角的取值范围.
(人教版)高中数学选修1-1课件:第3章 导数及其应用3.1.3

切线方程为y-__f_(_x0_)_=__f′_(_x_0)_(_x-__x_0_)_____.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
函数y=f(x)的导函数
确定
导数
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
合作探究 课堂互动
高效测评 知能提升
答案: x+y-2=0
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
过点P的切线
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
(1)求曲线在点P处的切线的斜率; (2)求曲线在点P处的切线方程.
[思路点拨]
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
标.
(3)求切线的斜率f′(x0); (4)由斜率间的关系列出关于x0的方程,解方程求x0; (5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0得切点坐
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
函数y=f(x)的导函数
确定
导数
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
合作探究 课堂互动
高效测评 知能提升
答案: x+y-2=0
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
过点P的切线
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
(1)求曲线在点P处的切线的斜率; (2)求曲线在点P处的切线方程.
[思路点拨]
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修1-1
第三章 导数及其应用
标.
(3)求切线的斜率f′(x0); (4)由斜率间的关系列出关于x0的方程,解方程求x0; (5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0得切点坐
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
高中数学人教A版选修1-1课件:3.1.3《导数的几何意义》

x x0
x0
x
所以,斜率为 k f (2) y |x2 2 2 4 .
故点 A(2, 4) 处切线方程为: y 4 4(x 2) ,即 4x y 4 0 .
变式训练 2 求过点 P(3,5) 且与曲线 y x2 相切的直线方程.
[错解] y lim y lim (x x)2 x2 2x .
记作: f (x) 或 y ,即: f (x) y lim f (x x) f (x) .
x0
x
注:函数 f (x) 在 x0 处的导数 f (x0 ) 就是函数 f (x) 的导(函)
数 f (x) 在 x0 处的函数值.
h
l0 l1
O
t0
t1
t2
t
l2
图3.1 3
解:我们用曲线h t 在t0 , t1 , t2 处的切线,刻画曲 线h t 在上述三个时刻附近的变化情况.
导数的几何意义
提出问题
动画演示02:50-03:40
y
y fx
/edu/ppt/
ppt_playVideo.action?mediaVo.
resId=54800cd9956ed1ed6016a
1c2 y
y fx
P1 T
P2 T
P
O
x
O
x
1
2
y
y fx
[正解] 法一: y lim y lim (x x)2 x2 2x .
x x0
x0
x
设所求切线的切点为 A(x0, y0 ) .
点 A 在曲线 y x2 上, y0 x02 . 又 A 是切点,过点 A 的切线的斜率 y |xx0 2x0 . 所求切线方程为 y x02 2x0 (x x0 ) , 将点 P(3,5) 代入切线方程得 x0 1或5 . 切点坐标为 (1,1) 或 (5, 25) ,
高中数学(人教版选修1-1)配套课件:第3章 导数及其应用3.3.1

又∵x>0,∴0<x< 33.
∴f(x)的单调递增区间为(
33,+∞),单调递减区间为(0,
3 3 ).
解析答案
(4) f(x)=x3-3tx. 解 f′(x)=3x2-3t. 令f′(x) >0,得3x2-3t>0,即x2>t, ∴当t≤0时,f′(x)>0恒成立,函数的增区间是(-∞,+∞); 当 t>0 时,解 x2>t 得 x> t或 x<- t;
导数
单调递_增__
f′(x) ≥0
单调递_减__
f′(x)≤0
常函数
f′(x)=0
思考 在区间(a,b)内,函数f(x)单调递增是f′(x)>0的什么条件? 答案 必要不充分条件.
答案
知识点二 利用导数求函数的单调区间 求可导函数单调区间的基本步骤: (1)确定定义域; (2)求导数f′(x); (3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间; (4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间.
返回
题型探究
题型一 利用导数判断函数的单调性
例1 证明
证明:函数 f(x)=sinx x在区间π2,π上单调递减.
f′(x)=xcos
x-sin x2
x ,又
x∈π2,π,
则cos x<0,∴xcos x-sin x<0,
∴f′(x)<0,∴f(x)在π2,π上是减函数.
12345
解析答案
12345
2.f′(x)是函数y=f(x)的导函数,若y=f′(x)的图象如图所示,则函数 y=f(x)的图象可能是( D )
解析 由导函数的图象可知,当x<0时,f′(x)>0,即函数f(x)为增函数; 当0<x<2时,f′(x)<0,即f(x)为减函数; 当x>2时,f′(x)>0,即函数f(x)为增函数.观察选项易知D正确.
高中数学(人教版选修1-1)配套课件:第3章 导数及其应用3.1.1~3.1.2

解析答案
题型二 物体运动的瞬时速度 例2 一辆汽车按规律s=2t2+3(时间的单位:s,位移的单位:m)做直线 运动,求这辆汽车在t=2 s时的瞬时速度. 解 设在t=2 s附近的时间增量为Δt, 则位移的增量Δs=[2(2+Δt)2+3]-(2×22+3)=8Δt+2(Δt)2. 因为ΔΔst=8+2Δt,Δlit→m0 ΔΔst=Δlit→m0 (8+2Δt)=8, 所以这辆汽车在t=2 s时的瞬时速度为8 m/s.
,即 f′(x0)=lim Δx→0
Δy Δx
= lim Δx→0
fx0+ΔΔxx-fx0.
答案
返回
题型探究
重点突破
题型一 平均变化率
例1 已知函数h(x)=-4.9x2+6.5x+10.
(1)计算从x=1到x=1+Δx的平均变化率,其中Δx的值为①2;②1;
③0.1;④0.01. 解 ∵Δy=h(1+Δx)-h(1)=-4.9(Δx)2-3.3Δx,∴ΔΔyx=-4.9Δx-3.3. ①当 Δx=2 时,ΔΔyx=-4.9Δx-3.3=-13.1; ②当 Δx=1 时,ΔΔyx=-4.9Δx-3.3=-8.2; ③当 Δx=0.1 时,ΔΔyx=-4.9Δx-3.3=-3.79; ④当 Δx=0.01 时,ΔΔyx=-4.9Δx-3.3=-3.349.
人教版七年级上册Unit4 Where‘s my backpack?
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
lim
题型二 物体运动的瞬时速度 例2 一辆汽车按规律s=2t2+3(时间的单位:s,位移的单位:m)做直线 运动,求这辆汽车在t=2 s时的瞬时速度. 解 设在t=2 s附近的时间增量为Δt, 则位移的增量Δs=[2(2+Δt)2+3]-(2×22+3)=8Δt+2(Δt)2. 因为ΔΔst=8+2Δt,Δlit→m0 ΔΔst=Δlit→m0 (8+2Δt)=8, 所以这辆汽车在t=2 s时的瞬时速度为8 m/s.
,即 f′(x0)=lim Δx→0
Δy Δx
= lim Δx→0
fx0+ΔΔxx-fx0.
答案
返回
题型探究
重点突破
题型一 平均变化率
例1 已知函数h(x)=-4.9x2+6.5x+10.
(1)计算从x=1到x=1+Δx的平均变化率,其中Δx的值为①2;②1;
③0.1;④0.01. 解 ∵Δy=h(1+Δx)-h(1)=-4.9(Δx)2-3.3Δx,∴ΔΔyx=-4.9Δx-3.3. ①当 Δx=2 时,ΔΔyx=-4.9Δx-3.3=-13.1; ②当 Δx=1 时,ΔΔyx=-4.9Δx-3.3=-8.2; ③当 Δx=0.1 时,ΔΔyx=-4.9Δx-3.3=-3.79; ④当 Δx=0.01 时,ΔΔyx=-4.9Δx-3.3=-3.349.
人教版七年级上册Unit4 Where‘s my backpack?
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
lim
高中数学(人教版选修1-1)配套课件:第3章 导数及其应用3.1.3

人教版七年级上册Unit4 Where‘s my backpack?
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
自主学习
知识点一 导数的几何意义
函数y=f(x)在点x=x0处的导数的几何意义是曲线y=f(x)在点P(x0,f(x0))处 的切线的 斜率 .也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是 f′(x0) .相应地,切线方程为 y-f(x0)=f′(x0)(x-x0) .
知识点二 函数的导函数
当x=x0时,f′(x0)是一个确定的数,则当x变化时,f′(x)是x的一个函数,
称f′(x)是f(x)的导函数(简称导数).f′(x)也记作y′,
fx+Δx-fx
即 f′(x)=y′=lim Δ重点突破
题型一 已知过曲线上一点求切线方程
例1 若曲线y=x3+3ax在某点处的切线方程为y=3x+1,求a的值.
高效学习模型-内外脑模型
2
内脑-思考内化
思 维 导 图 &超 级 记 忆 法 &费 曼 学 习 法
1
外脑-体系优化
知 识 体 系 &笔 记 体 系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆规律
记忆前
选择记忆的黄金时段 前摄抑制:可以理解为先进入大脑的信息抑制了后进 入大脑的信息
后摄抑制:可以理解为因为接受了新的内容,而把前 面看过的忘记了
x0+1 ΔΔxx-x10=-x120,
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
自主学习
知识点一 导数的几何意义
函数y=f(x)在点x=x0处的导数的几何意义是曲线y=f(x)在点P(x0,f(x0))处 的切线的 斜率 .也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是 f′(x0) .相应地,切线方程为 y-f(x0)=f′(x0)(x-x0) .
知识点二 函数的导函数
当x=x0时,f′(x0)是一个确定的数,则当x变化时,f′(x)是x的一个函数,
称f′(x)是f(x)的导函数(简称导数).f′(x)也记作y′,
fx+Δx-fx
即 f′(x)=y′=lim Δ重点突破
题型一 已知过曲线上一点求切线方程
例1 若曲线y=x3+3ax在某点处的切线方程为y=3x+1,求a的值.
高效学习模型-内外脑模型
2
内脑-思考内化
思 维 导 图 &超 级 记 忆 法 &费 曼 学 习 法
1
外脑-体系优化
知 识 体 系 &笔 记 体 系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆规律
记忆前
选择记忆的黄金时段 前摄抑制:可以理解为先进入大脑的信息抑制了后进 入大脑的信息
后摄抑制:可以理解为因为接受了新的内容,而把前 面看过的忘记了
x0+1 ΔΔxx-x10=-x120,
高中数学第三章导数及其应用3.1.3导数的几何意义课件新人教A版选修1_1

• (2)导数的几何意义:函数f(x)在x=x0处的导数
f(x0+Δ x)-f(x0)
就 是 切 线 PT 的 斜 率 Δkx , 即 k =
____________________= f′(x0).
• 2.导函数的概念 f′(x)
• (1)定义:当x变化时,_____便是x的一个函数,
f(x+Δ x)-f(x)
所以 2x30-3x20+1=(x0-1)2(2x0+1)=0, 解得 x0=1 或 x0=-12.(6 分) 第二步,求切点横坐标 故所求直线斜率为 k=3x20-3=0 或 k=3x20-3=-94, 于是 y-(-2)=0·(x-1)或 y-(-2)=-94(x-1), 即 y=-2 或 y=-94x+14.(10 分) 故过点 P(1,-2)的切线方程为 y第=三-步2 ,或求y=过-P的94x切+线14.(方12程分)
• (1)与导数的几何意义相关的题目往往涉及解 析几何的相关知识,如直线的方程、直线间的 位置关系等,因此要综合应用所学知识解题.
• (2)与导数的几何意义相关的综合问题解题的 关键是函数在某点处的导数,已知切点可以求 斜率,已知斜率也可以求切线,切点的坐标是 常设的未知量.
◎变式训练 • 3.设函数f(x)=x3+ax2-9x-1(a<0),若曲线 y=f(x)的斜率最小的切线与直线12x+y=6平行, 求a的值.
即 f′(x0)=3x20+2ax0-9=3x0+a32-9-a32. 当 x0=-a3时,f′(x0)取最小值-9-a32. ∵斜率最小的切线与 12x+y=6 平行, ∴该切线斜率为-12.∴-9-a32=-12. 解得 a=±3.又 a<0,∴a=-3.
短板补救案·核心素养培优
人教A版高中数学选修1-1课件:3.1.3导数的几何意义 (共19张PPT)
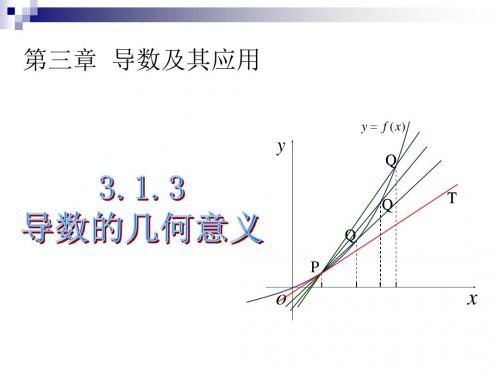
第三章 导数及其应用
y f ( x)
y
Q Q Q P T
o
x
1.平均变化率定义是什么?几何意义 是什么?
2.函数y=f(x)在x=x0时的瞬时变化率是什么? 瞬时变化率又叫什么?几何意义又是什么 呢?
y
y f ( x)
相交
o
P
x
再来一次
直线PQ的斜率为
k PQ ( y0 y) y0 y xQ xP ( x0 x) x0 x yQ yP
PQ无限靠近切线PT
k PT lim k PQ
x 0
y lim x 0 x
1.割线PPn的斜率kn与切线PT的斜率k有什么关系? fxn-fx0 提示:割线PPn的斜率是kn= ,当点Pn沿着曲 xn-x0 线无限趋近于点P时,kn无限趋近于切线PT的斜率k.
2.本节定义的切线与以往学习的切线的定义有什么不 同? 提示:这里是利用极限思想,即用割线的极限位置定 义曲线的切线.这种定义曲线切线的方法适用于各种曲 线.hl0源自l1ot4 t3 t0
t1
t2
l2
1.导数的几何意义是指:曲线y=f(x)在点(x0,y0)处的 切线的斜率就是函数y=f(x)在x=x0处的导数,而切线的斜 率就是切线倾斜角的正切值. 2.由导数值判断函数在某点的变化情况:当f′(x)>0 时,函数图象应是上升的,f′(x)越大,图象上升越快,越 “陡峭”;当f′(x)<0时,函数图象是下降的,且k越小, 下降越快.
【例 2】
1 3 4 已知曲线 y=3x +3.
(1)求曲线在点 P(2,4)处的切线方程; (2)求曲线过点 P(2,4)的切线方程.
曲线y=x3-3x2+1在点P处的切线平行于直线y=9x- 1,则切线方程为( A.y=9x C.y=9x+26 ) B.y=9x-26 D.y=9x+6或y=9x-26
y f ( x)
y
Q Q Q P T
o
x
1.平均变化率定义是什么?几何意义 是什么?
2.函数y=f(x)在x=x0时的瞬时变化率是什么? 瞬时变化率又叫什么?几何意义又是什么 呢?
y
y f ( x)
相交
o
P
x
再来一次
直线PQ的斜率为
k PQ ( y0 y) y0 y xQ xP ( x0 x) x0 x yQ yP
PQ无限靠近切线PT
k PT lim k PQ
x 0
y lim x 0 x
1.割线PPn的斜率kn与切线PT的斜率k有什么关系? fxn-fx0 提示:割线PPn的斜率是kn= ,当点Pn沿着曲 xn-x0 线无限趋近于点P时,kn无限趋近于切线PT的斜率k.
2.本节定义的切线与以往学习的切线的定义有什么不 同? 提示:这里是利用极限思想,即用割线的极限位置定 义曲线的切线.这种定义曲线切线的方法适用于各种曲 线.hl0源自l1ot4 t3 t0
t1
t2
l2
1.导数的几何意义是指:曲线y=f(x)在点(x0,y0)处的 切线的斜率就是函数y=f(x)在x=x0处的导数,而切线的斜 率就是切线倾斜角的正切值. 2.由导数值判断函数在某点的变化情况:当f′(x)>0 时,函数图象应是上升的,f′(x)越大,图象上升越快,越 “陡峭”;当f′(x)<0时,函数图象是下降的,且k越小, 下降越快.
【例 2】
1 3 4 已知曲线 y=3x +3.
(1)求曲线在点 P(2,4)处的切线方程; (2)求曲线过点 P(2,4)的切线方程.
曲线y=x3-3x2+1在点P处的切线平行于直线y=9x- 1,则切线方程为( A.y=9x C.y=9x+26 ) B.y=9x-26 D.y=9x+6或y=9x-26
高中数学第三章导数及其应用3.1.3导数的几何意义课件新人教A版选修1-1

2.函数 y=f(x)在点 x0 处的导数 f′(x0)的几何意义是曲线 y=f(x)在点 P(x0, f(x0))处__切__线__的__斜__率___,在点 P 的切线方程为__y_-__f_(x_0_)=__f_′(_x_0_)(_x_-__x_0)____.
判断(正确的打“√”,错误的打“×”) (1)直线与曲线相切则直线与已知曲线只有一个公共点.( ) (2)过曲线上的一点作曲线的切线,这点一定是切点.( ) (3)若 f′(x0)不存在,则曲线 y=f(x)在点(x0,f(x0))处无切线.( ) 【答案】 (1)× (2)× (3)×
=y′=__Δl_ixm_→_0 ______Δ_x_________.
判断(正确的打“√”,错误的打“×”) (1)函数 f(x)在点 x0 处的导数 f′(x0)与导函数 f′(x)之间是有区别的.( ) (2)导函数 f′(x)的定义域与函数 f(x)的定义域相同.( ) (3)函数 f(x)=x2 的导数是 f′(x)=2x.( ) (4)函数 f(x)=0 没有导函数.( ) 【答案】 (1)√ (2)× (3)√ (4)×
求切点坐标
过曲线 y=x2 上哪一点的切线满足下列条件? (1)平行于直线 y=4x-5; (2)垂直于直线 2x-6x+5=0; (3)倾斜角为 135°. 【精彩点拨】 本题考查曲线的切线的有关问题.解题的关键是设出切点 的坐标,求出切线的斜率.
解答此类题目时,所给的直线的倾斜角或斜率是解题的关键,由这些信息 得知函数在某点处的导数,进而可求此点的横坐标.解题时要注意解析几何知 识的应用,如直线的倾斜角与斜率的关系,平行,垂直等.
导数几何意义的应用
[小组合作型]
如图 3-1-3,点 A(2,1),B(3,0),E(x,0)(x≥0),过点 E 作 OB 的 垂线 l.记△AOB 在直线 l 左侧部分的面积为 S,则函数 S=f(x)的图象为下图中的 ()
判断(正确的打“√”,错误的打“×”) (1)直线与曲线相切则直线与已知曲线只有一个公共点.( ) (2)过曲线上的一点作曲线的切线,这点一定是切点.( ) (3)若 f′(x0)不存在,则曲线 y=f(x)在点(x0,f(x0))处无切线.( ) 【答案】 (1)× (2)× (3)×
=y′=__Δl_ixm_→_0 ______Δ_x_________.
判断(正确的打“√”,错误的打“×”) (1)函数 f(x)在点 x0 处的导数 f′(x0)与导函数 f′(x)之间是有区别的.( ) (2)导函数 f′(x)的定义域与函数 f(x)的定义域相同.( ) (3)函数 f(x)=x2 的导数是 f′(x)=2x.( ) (4)函数 f(x)=0 没有导函数.( ) 【答案】 (1)√ (2)× (3)√ (4)×
求切点坐标
过曲线 y=x2 上哪一点的切线满足下列条件? (1)平行于直线 y=4x-5; (2)垂直于直线 2x-6x+5=0; (3)倾斜角为 135°. 【精彩点拨】 本题考查曲线的切线的有关问题.解题的关键是设出切点 的坐标,求出切线的斜率.
解答此类题目时,所给的直线的倾斜角或斜率是解题的关键,由这些信息 得知函数在某点处的导数,进而可求此点的横坐标.解题时要注意解析几何知 识的应用,如直线的倾斜角与斜率的关系,平行,垂直等.
导数几何意义的应用
[小组合作型]
如图 3-1-3,点 A(2,1),B(3,0),E(x,0)(x≥0),过点 E 作 OB 的 垂线 l.记△AOB 在直线 l 左侧部分的面积为 S,则函数 S=f(x)的图象为下图中的 ()
(人教版)高中数学选修1-1课件:第3章 导数及其应用3.1.1、2

自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
求平均变化率
(1)计算函数f(x)=x2从x=1到x=1+Δx的平均变化 率,其中Δx的值为:
① 2;②1;③ 0.1;④ 0.01. (2)思考:当Δx越来越小时,函数f(x)在区间[1,1+Δx]上的 平均变化率有怎样的变化趋势? [思路点拨] 直接利用定义求平均变化率,先求出表达 式,再代入数据,就可以求出相应平均变化率的值.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
导数的概念
函数 y=f(x)在 x=x0 处的_瞬__时__变化率称为函数 y=f(x)在 __x_=__x_0__处的导数,记作 f′(x0)或 y′|x=x0,
即 f′(x0)= lim Δx→0
ΔΔyx=__Δlix_m→_0__f_x_0+__Δ_Δ_xx_-__f__x0___.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
求平均变化率的步骤: (1)先计算函数值的改变量 Δy=f(x1)-f(x0). (2)再计算自变量的改变量 Δx=x1-x0. (3)求平均变化率ΔΔyx=fxx11- -fx0x0.
数学 选修1-1
Δy Δx.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(2)导函数的函数值法,即先利用导数的定义求出导函数 f′(x),再把 x=x0 代入 f′(x)得 f′(x0).
求函数在某一点处的导数,一般是先求出函数的导数,再计 算这点的导数值.
人教A版数学选修1-1课件第三章导数及其应用3.1.3

『规律方法』 1.f ′(x0)即为过曲线y=f(x)上点P(x0, f(x0))切线的斜率.
2.若曲线y=f(x)在(a,b)上任一点处的导数值都大于零, 可以判断曲线y=f(x)在(a,b)上图象呈上升趋势,则函数y =f(x)在(a,b)上单调递增.而若y=f(x)在(a,b)上任一点处 的导数都小于零,则函数y=f(x)的图象在(a,b)上呈下降趋 势,y=f(x)在(a,b)单调递减.当函数y=f(x)在(a,b)上的 导数值都等于零时,函数y=f(x)的图象应为垂直于y轴的直 线的一部分.
=Δlixm→0[-(Δx)2-3x20-3x0·Δx]=-3x20.
∴2x0=-3x20,∴x0=0 或 x0=-23.
『规律方法』 求切点坐标可以按以下步骤进行: (1)设出切点坐标; (2)利用导数求出斜率; (3)利用斜率关系列方程,求出切点的横坐标; (4)把横坐标代入曲线或切线方程,求出切点纵坐标.
= lim Δx→0
12x+14Δx=12x,
∵点 P4,74不在抛物线 y=14x2 上, ∴点 P 不是切点.
设切点为(x0,y0),则 y0=14x20.
∴过切点(x0,y0)的切线的斜率为 k=12x0. 又∵切点过4,74和(x0,y0)两点, ∴12x0=xy00--744=14xx002--474. 解得 x0=1,或 x0=7. ∴过4,74的切线的斜率为12和72, 切线方程为 y-74=12(x-4)和 y-74=72(x-4) 即 2x-4y-1=0 和 14x-4y-49=0.
命题方向2 ⇨求切线方程
典例 2 已知曲线C:f(x)=x3. (1)求曲线C上横坐标为1的点处的切线的方程;
(2)求过点(1,1)与曲线C相切的直线方程.
高中数学人教版选修1-1 3.1.3导数的几何意义 课件1

(2)两者的联系:在 x=x0 处的导数 f′(x0)是导函数 f′(x) 在 x=x0 处的函数值,因此求函数在某一点处的导数.
课堂互动
1.导数几何意义的理解
例题 1 若函数 y=f(x)的导函数在区间[a,b]上是增函数,则函数 y =f(x)在区间[a,b]上的图象可能是( )
【思路探究】 (1)导数的几何意义是什么?(2)y=f(x)的导 函数在区间[a,b]上是增函数,说明 y=f(x)图象的切线有什么 特点?
重点难点
重点:导数的几何意义,求曲线上过一点处的切线方程. 难点:“以直代曲”的数学思想方法;以及切线定义的理 解——在每处“附近”变化率与瞬时变化率的近似关系的理 解.
教学设计
教学建议
为了更好的完成本节课的教学目标,帮助学生理解本节课 内容,突出重点,突破难点,宜设计了如下的教法和学法:
(1)教学设计:探讨教学法,即教师通过问题→诱导→演示 →讨论→探索结果→归纳总结.
【提示】 点 Pn 趋近于点 P 时,割线 PPn 趋近于过点 P 的 切线 PT.
3.第 2 题图中割线 PPn 的斜率 kn=fxxnn--xf0x0,当点 Pn 无 限趋近于点 P 时,此斜率与切线 PT 的斜率有何大小关系?
【提示】 kn 无限趋近于切线 PT 的斜率.
1.设点 P(x0,f(x0)),Pn(xn,f(xn))是曲线 y=f(x)上不同的点, 当点 Pn(xn,f(xn))(n=1,2,3,4…)沿着曲线 f(x)趋近于点 P(x0,f(x0)) 时,割线 PPn 趋近于确定的位置,这个确定位置的直线 PT 称为 过点 P 的 切线 ,且 PT 的斜率 k=lixn→m x0 fxxnn--fxx00= f′(x0) .
课堂互动
1.导数几何意义的理解
例题 1 若函数 y=f(x)的导函数在区间[a,b]上是增函数,则函数 y =f(x)在区间[a,b]上的图象可能是( )
【思路探究】 (1)导数的几何意义是什么?(2)y=f(x)的导 函数在区间[a,b]上是增函数,说明 y=f(x)图象的切线有什么 特点?
重点难点
重点:导数的几何意义,求曲线上过一点处的切线方程. 难点:“以直代曲”的数学思想方法;以及切线定义的理 解——在每处“附近”变化率与瞬时变化率的近似关系的理 解.
教学设计
教学建议
为了更好的完成本节课的教学目标,帮助学生理解本节课 内容,突出重点,突破难点,宜设计了如下的教法和学法:
(1)教学设计:探讨教学法,即教师通过问题→诱导→演示 →讨论→探索结果→归纳总结.
【提示】 点 Pn 趋近于点 P 时,割线 PPn 趋近于过点 P 的 切线 PT.
3.第 2 题图中割线 PPn 的斜率 kn=fxxnn--xf0x0,当点 Pn 无 限趋近于点 P 时,此斜率与切线 PT 的斜率有何大小关系?
【提示】 kn 无限趋近于切线 PT 的斜率.
1.设点 P(x0,f(x0)),Pn(xn,f(xn))是曲线 y=f(x)上不同的点, 当点 Pn(xn,f(xn))(n=1,2,3,4…)沿着曲线 f(x)趋近于点 P(x0,f(x0)) 时,割线 PPn 趋近于确定的位置,这个确定位置的直线 PT 称为 过点 P 的 切线 ,且 PT 的斜率 k=lixn→m x0 fxxnn--fxx00= f′(x0) .
人教A版高中数学选修1-1《三章 导数及其应用 3.1 变化率与导数 3.1.3 导数的几何意义》赛课课件_2

个确定的数.这样,当x变化时,f ' x0
便是x的一个函数,我们称它为f(x)的 导函数. 简称导数.
随堂练习
1.曲线y=x2在x=0处的( D ) A.切线斜率为1 B.切线方程为y=2x C.没有切线 D.切线方程为y=0
2.已知曲线y=2x2上的一点A(2,8),则点
A处的切线斜率为( C )
y
P
M
x
1j
x
-1 O 1
解 : k = lim f(x0 + Δx) - f(x0 )
Δx→0
Δx
= lim (1 + Δx)2 + 1- (1 + 1)
Δx→0
Δx
= lim 2Δx + (Δx)2 = 2.
Δx→0
Δx
因此,切线方程为y-2=2(x-1),即y=2x.
例3
如图1.1- 3,它表
旧知回顾
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
f (x0 ) 或 y|x=x0 , 即
f
(x
0
)
=
lim
Δx→0
f(x
0
+
Δx) Δx
f(x
0
)
= lim f(x) - f(x0 ) x→x0 x - x0
(1)求函数的增量 Δy = f(x0 + Δx) - f(x0 ).
开动脑筋,想象一下PPn的
动态变化效果吧?
y=f(x)
割
线
y
Q
T 切线
P o
结点论P处:当的割Q点线与无切限线逼存近在什P点么时关系,此?时 x 直线PQ就是P点处的切线PT.
便是x的一个函数,我们称它为f(x)的 导函数. 简称导数.
随堂练习
1.曲线y=x2在x=0处的( D ) A.切线斜率为1 B.切线方程为y=2x C.没有切线 D.切线方程为y=0
2.已知曲线y=2x2上的一点A(2,8),则点
A处的切线斜率为( C )
y
P
M
x
1j
x
-1 O 1
解 : k = lim f(x0 + Δx) - f(x0 )
Δx→0
Δx
= lim (1 + Δx)2 + 1- (1 + 1)
Δx→0
Δx
= lim 2Δx + (Δx)2 = 2.
Δx→0
Δx
因此,切线方程为y-2=2(x-1),即y=2x.
例3
如图1.1- 3,它表
旧知回顾
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
f (x0 ) 或 y|x=x0 , 即
f
(x
0
)
=
lim
Δx→0
f(x
0
+
Δx) Δx
f(x
0
)
= lim f(x) - f(x0 ) x→x0 x - x0
(1)求函数的增量 Δy = f(x0 + Δx) - f(x0 ).
开动脑筋,想象一下PPn的
动态变化效果吧?
y=f(x)
割
线
y
Q
T 切线
P o
结点论P处:当的割Q点线与无切限线逼存近在什P点么时关系,此?时 x 直线PQ就是P点处的切线PT.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合作探究 课堂互动
高效测评 知能提升
1.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( ) A.在点x0处的斜率 B.在点(x0,f(x0))处切线与x轴所夹锐角的正切值 C.曲线y=f(x)在点(x0,f(x0))处切线的斜率 D.点(x0,f(x0))与点(0,0)连线的斜率 解析: 由导数的几何意义知,选项C正确.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
3.1.3 导数的几何意义
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
自主学习 新知突破
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(2)“导函数”:如果函数 f(x)在开区间(a,b)内每一点都可
导,就说 f(x)在开区间(a,b)内可导,这时对于区间(a,b)内每一
个确定的值 x0,都对应着一个导数 f′(x0),这样就在开区间(a, b)内构成一个新的函数,我们把这一新函数叫做 f(x)在开区间(a,
b)内的导函数,记作 f′(x)或 y′,即 f′(x)=y′=li m
Δx→0
ΔΔyx=liΔmx→0
fx+Δx-fx
Δx
.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(3)导函数也简称导数.所以
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(4)函数 y=f(x)在点 x0 处的导数 f′(x0)就是导函数 f′(x)在 点 x=x0 处的函数值,f′(x0)=f′(x)|x=x0.
所以求函数在一点处的导数,一般是先求出函数的导函数, 再计算这点的导函数值.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
= lim
Δx→0
f-2+Δx-f-2 Δx
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
= lim
Δx→0
-2+2 Δx--22 Δx
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
[提示] 割线AB的斜率kAB无限接近于曲线在点A处的切线 的斜率k,k=f′(x0).
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
导数的几何意义
函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x) 在点P(x0,f(x0))处的切线的斜率.也就是说,曲线y=f(x)在点 P(x0,f(x0))处的切线的斜率是f′(x0).
高效测评 知能提升
1.了解平均变化率与割线之间、瞬时变化率与切线之间 的关系,通过函数的图象理解导数的几何意义.
2.了解导函数的概念,会求导函数. 3.根据导数的几何意义,会求曲线上某点处的切线方 程.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
设函数y=f(x)的图象如图所示,AB是过点A(x0,f(x0))与点 B(x0+Δx,f(x0+Δx))的一条割线,当点B沿曲线趋近于A时,割 线 AB 的 斜 率 kAB 与 曲 线 在 点 A 处 的 切 线 的 斜 率 k 之 间 有 什 么 关 系?与f′(x0)有什么关系?
切线方程为__y_-__f(_x_0)_=__f_′(_x_0_)(_x_-__x_0)___.
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
函数y=f(x)的导函数
从求函数 f(x)在 x=x0 处导数的过程可以看到,当 x=x0 时, f′(x0)是一个_确__定___的数.这样,当 x 变化时,f′(x)便是 x 的 一个函数,我们称它为 f(x)的导函数(简称__导__数__).y=f(x)的导 函数有时也记作 y′, fx+Δx-fx
解析: ∵ΔΔyx=3x+ΔΔxx2-3x2=6x+3Δx, ∴y′|x=1=lim (6+3Δx)=6.
Δx→0
通过验证得点 A(1,3)在曲线 y=3x2 上. ∴曲线在点 A(1,3)处的切线斜率为 6. ∴所求的切线方程为 y-3=6(x-1), 即 6x-y-3=0. 答案: 6x-y-3=0
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
4.求曲线 f(x)=2x在点(-2,-1)处的切线方程. 解析: ∵点(-2,-1)在曲线 y=2x上,
∴曲线 y=2x在点(-2,-1)处的切线斜率就等于 y=2x在点(-
2,-1)处的导数.
∴k=f′(-2)
即 f′(x)=y′=_Δlix_m→_0______Δ__x_____.
数ቤተ መጻሕፍቲ ባይዱ 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
“函数f(x)在点x0处的导数”“导函数”“导数”三者之间 的区别与联系
(1)“函数在一点处的导数”,就是在该点的函数的改变量 与自变量的改变量的比的极限,它是一个数值,不是变数.
=2 处的导数.
f′(2)= lim
Δx→0
ΔΔyx=Δlixm→0
22+Δx2-2×22 Δx
= lim
Δx→0
8Δx+Δ2xΔx2=8,故选 C.
答案: C
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
3.已知曲线y=3x2,则在点A(1,3)处的曲线的切线方程为 ____________.
答案: C
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.已知曲线y=2x2上一点A(2,8),则点A处的切线斜率为
()
A.4
B.16
C.8
D.2
数学 选修1-1
第三章 导数及其应用
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
解析: 曲线在点 A 处的切线的斜率就是函数 y=2x2 在 x
