数形结合思想在求参数范围中的应用
初中数学教学中数形结合思想的应用

初中数学教学中数形结合思想的应用摘要:数与形之间的结合转换,是目前数学课堂构成的核心。
了解数与形之间的对应关系,并对于目前数学课堂教学内容做出适当的转变,能够激发学生在课堂上学习的积极性。
强调数学课堂教学的应用发展,通过数形变换内容,丰富学生的想象能力以及认识能力,让学生在数学课堂上进行有效学习。
基于此,本文将就初中数学教学中数形结合思想应用进行分析,由数形转换知识储备、解题分析、答疑解惑为中心。
注重数形结合思想渗透化发展,注重数与形之间的对应关系,增强学生转换能力,化简为难,提高其学习效果。
关键词:初中数学;解决问题;数形结合引言数形结合思想在数学应用之中非常广泛,在初中阶段,正处于学生数学学习的启蒙和基础阶段。
在其中渗入数形结合的思想,化繁为简,能够为学生后续阶段的学习打好基础,同时也能够更好地锻炼学生的逻辑思维,帮助学生解决实际性的数学问题。
在数与形的相互转换过程中,通过分类讨论渗透相应的思想,让学生透过数形结合观念,正确解决问题。
培养学生新的认识思维,并在数与形的可操作化发展过程中,打好初中数学课程教学的基础,为学生的有效学习铺垫。
一、数形结合思想概述所谓数形结合思想,即是对应数与形之间的关系进行相互转换,将两者做出融合,共建一种更具思维化、可视化的教学方式。
数形结合思想对目前初中数学课堂的打造而言,是十分重要的。
它能够将数学知识做出简易化分析,最终提高数学课堂教学的有效性。
关于数与形两个关系的探讨,这始终是目前数学课堂教学的核心。
必须针对数与形两个基本观念进行分析,找准数与形结构关系,不论是数形的知识理解,还是习题的研究训练,都需要对于数形关系知识结构进行有效的划分。
结合数形结合思想教学应用,让学生的学习更显高效化。
对于学生而言,数形结合思想,能够开拓学生的视野。
避免复杂的计算以及推理过程,让数学解题内容更加简便。
数形结合思想正是空间思维以及抽象思维进行融合的一种教学模式,对应数与形之间的关系,让学生在学习过程中真正做好突破。
以形助数-以数解形——浅谈数形结合思想在初中数学中的应用

以形助数,以数解形—-浅谈数形结合思想在初中数学中的应用摘要:在初中数学中,数形结合思想无处不在,利用好它可以帮助解决较难问题,并提高解题速度。
笔者结合教学实际,对数形结合思想进行浅议,探讨其在数学教学中的应用.关键词:数形结合初中数学数学应用数形结合思想是初中数学中一种重要的数学思想.在近几年武汉中考数学试卷中,利用数形结合思想解决问题的题目屡见不鲜,而且有逐年加强的趋势,可见其重要性。
因此,笔者结合数学教学实际,探讨数形结合思想在初中数学中的应用.在《初中数学新课程标准》中提到:“数学中有一些重要内容、方法、思想是需要学生经历较长的认识过程,逐步理解和掌握的,如:数形结合思想等。
”[1]所谓数形结合,就是指把代数的精确刻划与几何的形象直观相统一,将抽象思维与形象直观相结合的一种思想方法。
利用它可以使复杂的问题简单化,抽象的问题具体化,很多难题便迎刃而解,而且解法简便易懂。
数与形是密切相关的两个数学表象,它们是一一对应的关系,且相互依存、相互促进.在解决数学问题时,我们要把它们有机的结合起来,并相互转化,即把几何图形转化为数量关系问题, 应用代数、三角函数等知识进行讨论,或者把数量关系问题转化为图形问题,借助几何知识加以解决,使学生看到“形”能想到“数”, 而看到“数”则能想到“形”,最终达到优化解题途径的目的.著名的数学家华罗庚说得好:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离" [2].初一我们就学习了数轴,它建立起了实数与数轴上的点的一一对应关系.进而,又引入了直角坐标系,它扩大成了有序实数对与坐标平面上的点的一一对应.到了初二、初三又陆续学习了一次函数、二次函数,我们知道它们跟直线、抛物线也是一一对应的关系,以至于后来的“用函数的观点看方程”,实质上就是曲线和方程的对应关系。
正是这些数与形的对应,才促使我们要利用它们之间的联系,相互结合,相互转化,最终达到解决数学问题的目的。
(完整版)数形结合思想例题分析(最新整理)

数形结合思想例题分析
一、构造几何图形解决代数与三角问题: 1、证明恒等式:
例 1 已知 x 、 y 、 z 、 r 均为正数,且 x2 y2 z2 , z
求证: rz xy.
C
x2 r2 x2
y A
r
x
B z
分析:由 x2 y2 z2 , 自然联想到勾股定理。由 z x2 r 2 x2. 可以联想到
则 G、E、D 三点共线时,GE+ED=DG 最短。作出图形,延长 DB 至 F,使 BF//AG 且
BF=AG,连接 GF.
2
则在 Rt△DGF 中,DF=1+2=3,GF=AB=2
D
1 a Eb B
2
DG DF 2 GF 2 32 22 13
G
2
F
CE+DE 的最小值是 13.
即 a2 4 b2 1 的最小值是 13.
AB CF > AC BE
当A 90时 , AB CF = AC BE .
3 /5
数形结合思想例题分析
综上: AB CF AC BE.
小结:以上两种证明方法,分别采用了三角法与代数法,较之纯几何证法来,易于想到。
例 7 如图,在正△ABC 的三边 AB、BC、CA 上分别有点 D、E、F.若 DE BC,EF AC,FD AB 同时成立,
射影定理。从而可以作出符合题设条件的图形(如图)。对照图形,由直角三角形面积的两种 算法,结论的正确性一目了然。
证明:(略) 小结:涉及到与平方有关的恒等式证明问题,可构造出与之对应的直角三角形或圆,然 后利用图形的几何性质去解决恒等式的证明问题。
2、证明不等式:
例 2 已知:0< a <1,0< b <1. 求证
专题:利用零点比大小秒杀参数取值范围
y
=
x
,当
a
³
1
ee
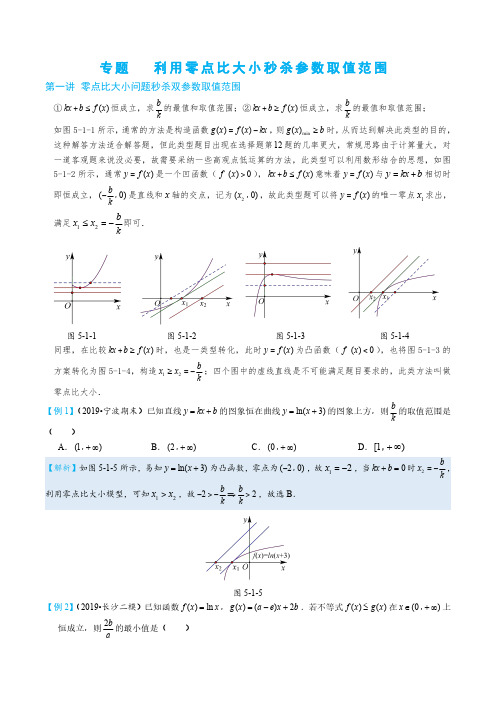
时,ax ³ loga x 恒成立,且切点为 (e ,e) ;当 ax ³ loga x 在区间 (m ,+ ¥) 恒成立,且 m > e ,则边界 x = m
就是 a 取得最小值的点,如图 5-2-2.找点法则通常是不考虑区间找出临界值,再考虑区间来分析端点值.
图 5-2-1
图 5-2-2
2
2
2
2
图 5-1-8
注意:关于双变量其中一个参数取得最值的时候,通常是两个函数在零点相切的时候取得.
【例 5】(2017•深圳一模)在平面直角坐标系 xOy 中,直线 y x b 是曲线 y a ln x 的切线,则当 a 0 时,
实数 b 的最小值是
.
【解析】法一 设出曲线上的一个切点为 (x ,y) ,由 y a ln x ,得 y a ,因为直线 y x b 是曲线 y a ln x x
线求出对应的 g(x) + m1 ,再根据过相同零点时的方程 g(x) + m2 ,从而得到一个取值范围,即为题目所求.
第二讲 构造零点比大小问题秒杀指对跨阶型单参数问题
在一些定义域为人为设计无零点,比如指数函数,需要通过构造并凑出零点,方法通常是指对互换(反
函数代换法),换元法,将 ex 转换成 ln x ,构造出定义域端点为零点后,再利用数形结合,解出参数的取值
可知 h2 (x) = ex - e ,此时显然 h2 (x) 与 t(x) 有两个交点,两凹凸性相反的函数在同一单调区间相交时无公切
线理论(参考公切线专题),故可知 -e < - b < -2 Þ b < e < 3 ,所以 m 3 .
巧用数形结合思想求函数最值

巧用数形结合思想求函数最值六招破解函数最值及巧用数形结合求参数问题一、六招破解函数最值问题函数最值问题一直是高考的一个重要的热点问题,在高考中占有极其重要的地位.为了让大家能够更加系统、全面地掌握函数最值问题的解决方法,下面就其问题的常用解法,分类浅析如下:1.配方法配方法是求二次函数最值的基本方法,如函数F(x)=6z/(x)2+/7/(x)+c(qHO)的最值问题,可以考虑用配方法.[例 1]已知函数 =(eA—a)2+(e A—tz)2(tzeR, aHO),求函数 y 的最小值.2.换元法换元法是指通过引入一个或几个新的变量,来替换原来的某些变量(或代数式),以便使问题得以解决的一种数学方法.在学习中,常常使用的换元法有两类,即代数换元和-:角换元,我们可以根据具体问题及题目形式灵活选择换元的方法,以便将复杂的函数最值问题转化为简单的函数最值问题.如可用三角换元解决形如/+/=1及部分根式函数形式的最值问题.3・不等式法利用不等式法求解函数最值,主要是指运用基本不等式及其变形公式來解决函数最值问题的一-种方法.常常使用的基本不等式有以下几种:aIb#a|b。
er2ab(a, b 为实数),° ^y[ab(a0, b20), abW。
J 些艺(a, b为实数).14[例3]函数fix) =-+t^(O<x< 1)的最小值为・兀1X4.函数单调性法先确定函数在给定区间上的单调性,然后依据单调性求函数的最值.这种利用函数单调性求最值的方法就是函数单调性法.这种方法在高考屮是必考的,多在解答题中的某一问出现.[例4]已知函数»=xln x,则函数心)在也r+2](r>0)上的最小值为.5.导数法设函数兀Q在区间[a, b]上连续,在区间(a, b)内可导,则的在[a, b]上的最大值和最小值应为兀0在(d, b)内的各极值与», fib) 中的最大值和最小值.利用这种方法求函数最值的方法就是导数法.[例5]函数»=x3-3x+l在闭区间[—3,0]上的最大值,最小值分别是,•6.数形结合法数形结合法是指利用函数所表示的几何意义,借助几何方法及函数的图象求函数最值的…种常用的方法.这种方法借助儿何意义,以形助数,不仅可以简捷地解决问题,还可以避免诸多失误,是我们开阔思路、正确解题、提高能力的-种重要途径.[a,[例 6]对 a, bWR,记 max|d, b\=\i1 函数=max||x+l|, |x—2||(x£R)的最小值是.二、巧用数形结合妙解3类求参数问题通过以下三个方面体会数形结合思想的运用.1.通过基本函数模型及变式的图象求参数的取值范围或值|lg x|, OvxWlO,若a,b,c互不相等,[例1]已知函数fix)=<1—2^+6,兀>10,_!»=»=»,则abc的取值范围是(2•通过函数的零点与方程的解的相互关系求函数零点和方程的解及参数的范围[例2]已知mGR,函数/(x)=x2+2(m2+l)x+7,g(x)=-(2m2—m+2)x+m.(1)设函数p(x)=/U)+g(x)・如果p(x)=0在区间(1,5)内有解但无重根,求实数加的取值范围;d,总存在唯一非零实数b(bHa),使得/2(d)=/z(b)成立?若存在,求加的值;若不存在,请说明理由.3.通过圆或圆锥曲线的部分图形与函数图象的关系来求参数的范围[例3]如果函数y=l+p4—F(|x|W2)的图象与函数2)。
浅谈确定解几问题中的参数取值范围的策略.

浅谈确定解几问题中的参数取值范围的策略重庆一中 李红林求参数的取值范围在中学数学中比比皆是,它使函数、方程与不等式、数与形、常量与变量有机地结合在一起。
这类问题不仅综合性强,而且情景新颖,能很好地考查考生的创新能力和潜在的数学素质,是历年高考命题的热点和重点.本文结合近几年的高考试题,对此问题的转化方法作简单探讨.转化策略一:构造关于目标参数的不等式建立关于目标参数的不等式,然后解出不等式,则得到所求参数的取值范围.建立目标参数的不等式有多种途径,常见的有:圆锥曲线的x,y 取值范围、函数的有界性、判别式、基本不等式及位置关系(点与曲线、曲线与曲线)等。
通过解不等式求参数的取值范围特别要注意必须进行等价变换,不然会扩大或缩小参数的取值范围。
例1(2004年高考题重庆卷10题)已知双曲线22221,(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,点P 在双曲线的右支上,且12||4||PF PF =,则此双曲线的离心率e 的最大值为( ) A 43 B 53 C 2 D 73分析:因题意涉及到双曲线的焦半径,故可考虑利用双曲线的两种定义。
若用第一定义则据焦半径存在一个取值范围能列出关于离心率的不等式;若用第二定义(焦半径公式)则据双曲线上的点的坐标存在取值范围也能列出关于离心率的不等式.略解1:由双曲线的定义可得:122232PF PF a PF a -=⇒= (点P 在双曲线的右支上) 2PF c a ≥- 523()533a c a a c e ∴≥-⇒≥⇒≤ 所以选B. 略解2:∵点P (x,y)在双曲线的右支上,由焦半径公式可得: 1PF a ex =+ 2PF a ex =-+ 5533ax x a e e ∴=≥∴≤ 例2(2002年高考题全国卷19题)设点P 到点)0,1(-M 、)0,1(N 距离之差为m 2,到x 轴、y 轴距离之比为2.求实数m 的取值范围.分析:显然点P 是直线与双曲线的交点,其交点P 的横坐标、纵坐标都与参数m 有,显化这种关系,则为实数的平方,根据其有界性即可列出关于参数m 的不等式。
浅谈集合中参数取值范围问题

185神州教育浅谈集合中参数取值范围问题董佳辽宁省实验中学东戴河分校随着新课改进程的加快,教材在内容及结构上也日益变化,以达到素质教育的要求。
高中数学应注重提高学生的数学思维能力,同时也是新课改中重要组成部分。
可是无论怎样变更,对于数学问题而言,解题方法永远是重要的一点,而众多问题中,含参问题的讨论则是高中数学的重中之重,它也是历年考试中的必考内容,并且对最近几年的试题分析情况来看,分值略有上升趋势。
纵观整个中学数学,参数问题是一条贯穿其中的脉络,参数与函数的定义域,值域(最值)相结合;与单调性结合;与方程问题相结合;与恒成立问题相结合。
可谓参数问题在高中数学中无处不在。
含参数问题的讨论,是训练和检查学生逻辑推理能力和分析问题能力的一种综合题型.求解这类问题的方法不复杂,但在一定程度上反映了学生数学素养的高低,因此,一直为人们所重视。
作为中学数学的重要内容,参数问题在课程教学中占有重要地位。
按照高中数学的教学脉络,这部分知识与集合、简易逻辑、函数思想、微积分应用、立体几何、数列等都有紧密的联系。
其中新课改之后,更是把导数中的参数问题的讨论和解决,变为重中之重。
学生们学习中的思维和视野角度都变宽泛了。
代数方法中关于参数问题解析和讨论,大多运用分离参数方法,多和分类讨论思想相结合。
在运用分类讨论思想的时候,少有著作详细分析常规的步骤。
在代数分析的时候,大多要注意导函数图象的大致形状,导函数对应方程的根,以及要注重根的大小的比较。
教者们在讲解时也因为知识点多,方法多,与其他知识交汇点众多,从而使得学生接受起来困难重重。
关于参数讨论,多和函数思想结合,这方的著作例如白建华[3]的《函数与方程思想在解题中的运用》提出了可以把函数中参数问题转换成方程有解问题来解决。
集合是高中数学的重要基础知识,它贯穿于整个中学数学教学之中,并且作为一种数学语言和工具在其他数学问题中有广泛的运用。
在高考中,它也是年年必考内容之一。
例谈“分段函数”中的参数范围问题

的 图 象 (如 图 1 所 示 ),因
为f(
0)是f(
x)的 最 小 值,
2
所 以 满 足 a ≤2+a,因 为
(
2
a-1)
x+4-3a,
x<1,
的
,
l
gx x≥1
{
图1
本题需 要 根 据 参 数 与 零 的 大 小 关 系 进 行 讨
论,分 a<0,
a=0,
a>0 三种情 况 .利 用 函 数
综上,
a 的取值范围是
[
0,
2].
.
的 图 象 易 知,为 满 足
题意应使 直 线 y= (
2
a-1)
x+
4-3
a 单调递增,且当 x=1 时,
y≥0,所以有
图2
2
a-1>0,
解得 1 <a≤3.故 a 的
2
(
)
,
2
a-1 ×1+4-3a≥0
{
取值范围是(1 ,
3].
2
本题侧重 考 查 了 “数 形 结 合 思 想 ”在 解 题 中
的灵活运用,有 利 于 进 一 步 提 升 学 生 对 分 段
函数图象与性质的理解与认识 .
x2 +x,-2≤x≤c,
例 3 已 知 函 数 f(
若
x)= 1
,
c<x≤3,
x
{
1 ],则实数 的取值范围是
函数 f(
x)的值域是[- ,
2
c
4
.
1
由c<x≤3 时,
x)= ,可知c≥0.画出二
f(
x
次函数 g(
构建不等式(组),求解参数的取值范围 .
(完整版)谈数形结合思想在中学数学解题中的应用毕业论文

目录摘要 (2)Abstrqct (3)1引言 (3)2 方程问题 (4)2.1 方程实根的正负情况 (4)2.2 求方程实根的个数 (4)2.3 含参数的方程 (5)3 不等式问题 (6)3.1 无理不等式 (6)3.2 二元二次不等式组 (6)3.3 高次不等式 (7)3.4 绝对值不等式 (7)3.5 含参数的不等式 (7)4 最值问题 (8)4.1 转化为直线的截距 (8)4.2 转化为直线的斜率 (8)4.3 转化为距离 (9)5 函数问题 (10)5.1 比较函数值的大小 (10)5.2 函数的定义域 (11)5.3 函数的值域 (11)5.4 函数求值 (12)5.5 函数的单调区间 (12)5.6 函数的奇偶性,单调性 (13)6解决线性规划问题 (13)参考文献 (14)致谢 (14)谈数形结合思想在中学数学解题中的应用XXX数学与信息学院数学与应用数学专业2011级指导老师:XXX摘要:数形结合思想在中学数学中应用广泛, 本文将例举说明数形结合思想方法在方程问题,不等式问题,最值问题,函数问题,线性规划问题等方面的实际应用。
充分说明在解题中运用数形结合的方法,借助几何图形的直观描述,如何使许多抽象的概念和复杂的关系形象化、简单化。
在中学数学解题中充分运用数形结合思想,有助于学生思维能力的培养, 有利于他们解题能力的提高。
关键词: 数形结合;数形结合思想;方程问题;不等式问题;最值问题;函数问题;线性规划问题On the combination of application of thought in middle schoolmathematicsXXXCollege of Mathematics and Information Mathematics and AppliedMathematicsGrade 2011 Instructor: XXXAbstrqct:Several form combining ideas is widely used in the middle school mathematics, this article will illustrate that number form combined with the thinking and methods in the equation, inequality problem, the most value problem, function problem, the practical application of linear programming problems.Full explanation in the problem solving, with the method of using the number form, with the help of a visual description of the geometry, how to make many abstract concepts and visual and simplify complex relationships. Full use of in the middle school mathematics problem-solving number form combining ideas, helps to develop students' thinking ability, is conducive to the improvement of their ability to problem solving.Key words:The number of combination form; Several form combining ideas; Equation problem; Inequality problem; The most value problems; Function problem; Linear programming problem1引言数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化。
数形结合思想

数形结合思想数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:或者是借助形的生动和直观性来阐明数之间的联系,即以形作为手段,数为目的,比如应用函数的图像来直观地说明函数的性质;或者是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.恩格斯曾说过:“数学是研究现实世界的量的关系与空间形式的科学.”数形结合就是根据数学问题的条件和结论之间的内在联系,既分析其代数意义,又揭示其几何直观,使数量关系的精确刻划与空间形式的直观形象巧妙、和谐地结合在一起,充分利用这种结合,寻找解题思路,使问题化难为易、化繁为简,从而得到解决.“数”与“形”是一对矛盾,华罗庚先生说过:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.数形结合的思想,其实质是将抽象的数学语言与直观的图形结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.在运用数形结合思想分析和解决问题时,要注意三点:第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二是恰当设参、合理用参,建立关系,由数思形,以形想数,做好数形转化;第三是正确确定参数的取值范围.数学中的知识,有的本身就可以看作是数形的结合.如:锐角三角函数的定义是借助于直角三角形来定义的;任意角的三角函数是借助于直角坐标系和单位圆来定义的.数形结合在解决集合运算、函数方程、不等式、解析几何、三角、向量等问题中均有广泛运用.应用数形结合的思想,应注意以下数与形的转化:数形结合思想解决的问题常有以下几种:(1)构建函数模型并结合其图象求参数的取值范围;(2)构建函数模型并结合其图象研究方程根的范围;(3)构建函数模型并结合其图象研究量与量之间的大小关系;(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式;(5)构建立体几何模型研究代数问题;(6)构建解析几何中的斜率、截距、距离等模型研究最值问题;(7)构建方程模型,求根的个数;(8)研究图形的形状、位置关系、性质等.数形结合的途径(1)通过坐标系形题数解借助于建立直角坐标系、复平面可以将图形问题代数化.这一方法在解析几何中体现的相当充分(在高考中主要也是以解析几何作为知识载体来考察的);值得强调的是,形题数解时,通过辅助角引入三角函数也是常常运用的技巧(这是因为三角公式的使用,可以大大简化代数推理)实现数形结合,常与以下内容有关:①实数与数轴上的点的对应关系;②函数与图象的对应关系;③曲线与方程的对应关系;④以几何元素和几何条件为背景,建立起来的概念,如复数、三角函数等;⑤所给的等式或代数式的结构含有明显的几何意义,如等式22(2)(1)4xy .常见方法有:(1)解析法:建立适当的坐标系(直角坐标系,极坐标系),引进坐标将几何图形变换为坐标间的代数关系.(2)三角法:将几何问题与三角形沟通,运用三角代数知识获得探求结合的途径. (3)向量法:将几何图形向量化,运用向量运算解决几何中的平行、垂直、夹角、距离等问题.把抽象的几何推理化为代数运算.特别是空间向量法使解决立体几何中平行、垂直、夹角、距离等问题变得有章可循.(2)通过转化构造数题形解许多代数结构都有着对应的几何意义,据此,可以将数与形进行巧妙地转化.例如,将|a |与距离互化,将a 2与面积互化,将a ≥b ≥c >0且b +c >a 中的a 、b 、c 与三角形的三边沟通,将有序实数对(或复数)和点沟通,将二元一次方程与直线、将二元二次方程与相应的圆锥曲线对应等等.这种代数结构向几何结构的转化常常表现为构造一个图形(平面的或立体的).另外,函数的图象也是实现数形转化的有效工具之一,正是基于此,函数思想和数形结合思想经常借助于相伴而充分地发挥作用.常见的转换途径为:1°方程或不等式问题常可以转化为两个图象的交点位置关系的问题,并借助函数的图象和性质解决相关的问题.2°利用平面向量的数量关系及模AB 的性质来寻求代数式性质.3°构造几何模型.通过代数式的结构分析,构造出符合代数式的几何图形,如将2a与正方形的面积互化,将abc 与勾股定理沟通等等.4°利用解析几何中的曲线与方程的关系,重要的公式(如两点间的距离,点到直线的距离002dA B,直线的斜率,直线的截距)、定义等来寻求代数式的图形背景及有关性质.2.数形结合的原则 (1)等价性原则在数形结合时,代数性质和几何性质的转换必须是等价的,否则解题将会出现漏洞.有时,由于图形的局限性,不能完整的表现数的一般性,这时图形的性质只能是一种直观而浅显的说明,但它同时也是抽象而严格证明的诱导.(2)双向性原则在数形结合时,既要进行几何直观的分析,又要进行代数抽象的探索,两方面相辅相成,仅对代数问题进行几何分析(或仅对几何问题进行代数分析)在许多时候是很难行得通的.例如,在解析几何中,我们主要是运用代数的方法来研究几何问题,但是在许多时候,若能充分地挖掘利用图形的几何特征,将会使得复杂的问题简单化.(3)简单性原则就是找到解题思路之后,至于用几何方法还是用代数方法、或者兼用两种方法来叙述解题过程,则取决于那种方法更为简单.而不是去刻意追求一种固定的模式——代数问题运用几何方法,几何问题寻找代数方法.一、引入1.函数()|log |(0a f x x a ,1)a 的单调递增区间是 A .(0]a , B .(0),C .(01],D .[1),2.方程2243xx x 的实数解的个数是A .1B .2C .3D .以上都不对3.已知不等式2log 0m xx在1(0)2x,时恒成立,则m 的取值范围是( )A .01mB .1116mC .1mD .1016m4.如果实数x y 、满足22(2)3x y ,则y x的最大值为A .12B .3C .2D .5.在平面直角坐标系中,点O (0,0),P (6,8),将向量OP 绕点O 按逆时针方向旋转34π后得向量OQ ,则点Q 的坐标是 A .(722), B .(722), C .(462), D .(462),6.若2()f x x bx c 对任意实数t ,都有(2)(2)f t f t ,则(1)f 、(3)f 、f ()4由小到大依次为___________.7.对a b R ,,记max{}.a ab a b b ab ,,,, 函数()max{|1||2|}f x x x ,的最小值是_________.8.若方程22320xax a 的一个根小于1,而另一根大于1,则实数a 的取值范围是______.9.已知奇函数()f x 在(0),上是增函数,且(3)0f ,不等式()0xf x 的解集为_________.10.已知定义在[11],上的函数()f x 为增函数,则不等式11()()21f x f x 的解集为 . 11.若关于x 的方程223320x xa 在[02],上只有一个根,则实数a 的取值范围是______. 12.讨论关于x 的方程|31|xk (k R )根的个数.二、例题:1.方程2221xx x 的实数解的个数是A .1B .2C .3D .以上都不对2.已知不等式2log 0xm x在1(0)2x,时恒成立,则m 的取值范围是 .3.点A (2,1)在圆225x y 上,将点A 绕原点O 顺时针旋转到点B ,求B 的坐标.4.当[1)x ,时,不等式222x ax a 恒成立,求a 的取值范围.5.设关于θsin 0θθa 在区间(02)π,内有相异的两个实根α,β,求实数a 的取值范围,并求α+β的值.三、练习:1.方程sin lg x x 的根的个数有 .2.设方程 22xx的实根为a ,2log 2xx的实根为b ,则ab.3.方程2||10xx a 有四个根,则a 的取值范围是 .4.设a b c ,,均为正数,且122log aa ,121()log 2b b ,21()log 2c c ,则A .ab c B .c b a C .c a b D .b a c5.设函数2log (1)2()1()1 2.2xx xf x x ,,,若0()1f x ,则0x 的取值范围是 A .(0)(2),, B .(02), C .(1)(3),, D .(13), 6.若log a 2<log b 2<0,则a ,b 的取值范围是A . 0<a <b <1B .0<b <a <1C .a >b >1D .b >a >1 7.已知0x 是函数1()21xf x x的一个零点,若10(1)x x ,,20()x x ,,则A .12()0()0f x f x ,B .12()0()0f x f x ,C .12()0()0f x f x , D .12()0()0f x f x ,8.已知01a ,则方程|||log |x a a x 的根的个数为A .1个B .2个C .3个D .1个或2个或3个 9.方程1sin()44πxx 的实数解的个数是( ) A . 2 B .3 C .4 D .以上均不对 10.函数||y a x 与y x a 的图象恰有两个公共点,则实数a 的取值范围是A .(1),B .(11),C .(1][1),,D .(1)(1),,11.若(12)x ,时,不等式2(1)log a x x 恒成立,则a 的取值范围为( )A .(0,1)B .(1,2)C .(1,2]D . [1,2]12.定义在R 上的函数()y f x 在(2),上为增函数,且(2)y f x 是偶函数,则( )A .(1)(3)f fB .(0)(3)f f C .(1)(3)f f D .(2)(3)f f13.已知51260xy 的最小值是A . 6013B .135C .1312D .1 14.已知()22ππx ,,则sin x ,tan x 与x 的关系是 A .tan sin xx x B .tan sin x x x C .|tan ||||sin |x x x D .不确定15.已知函数2()11([01])f x x x ,,对于满足121x x 的任意12x x ,,给出下列结论:①1212()[()()]0x x f x f x -;②2121()()()f x f x x x -;③2121()()()22f x f x x x f .其中正确的结论的序号是A .①B .②C .③D .①③ 16.若关于x 的方程24||5x x m 有四个互不相等的实根,则实数m 的取值范围是 . 17.函数2222613y x x x x 的最小值为___________.18.若直线yx m 与曲线21yx 有两个不同的交点,则实数m 的取值范围是 .19.若不等式|1||1|m x x 的解集是非空数集,那么实数m 的取值范围是_________. 20.对a bR ,,记min{}.b a b a b a ab ,,,, 函数1()min{|1|2}2f x x x ,的最大值是_________. 21.求函数sin 2cos 2x y x 的值域.22.关于x 的方程2230x kx k 的两根都在1和3之间,求k 的取值范围.23.已知向量(34)OA ,,(63)OB ,,(53)OC m m ,. (1)若点A B C ,,能够成三角形,求实数m 应满足的条件; (2)若△ABC 为直角三角形,且A 为直角,求实数m 的值.。
十种应用数形结合思想解题的方法

3
应用数形结合思想解题——十种典型题型
题型四、利用方程的根的关系解题
1 1 1、设 a,b,c 均为正数,且 2 = log 1 a , = log 1 b , = log 2 c .则( 2 2 2 2
a
b
c
)
A. a < b < c
B. c < b < a
C. c < a < b
A. 2a − 1 B. 1 − 2a C. 2− a − 1 D. 1 − 2− a
2、已知定义在 R 上的函数 f ( x) =
2 2x + 5 x + 2, x ∈ [0,1) f x ( ) ,且 f ( x + 2) = , g ( x) = , 2 x + 2 − ∈ − 2 x , x [ 1, 0) 0 在区间 [−5,1] 上的所有实根之和为( ) 则方程 f ( x) − g ( x) = B、 −6 C、 −7 D、 −8 A、 −5
应用数形结合思想解题——十种典型题型
题型一、求函数零点的个数或者图象交点的个数
= ) 2 − x ,则函数 y = 1、已知 f ( x
x 2
f ( x) 的零点个数是
.
2、函数 f ( x) = 2 ln x 的图象与函数 g ( x) = x 2 − 4 x + 5 的图象的交点个数为( A.3 B.2 C.1 D.0
x
取值范围是
.
2、已知函数 f ( x) = x − 2 + 1 , g ( x) = kx ,若方程 f(x)=g(x)有 两个不相等的实根,则实数 k 的取值范围是( ) 1 1 A. B. C. (1,2) 0,2 2,1
高中数学破题致胜微方法(集合应用剖析):“数形结合思想”在集合运算中的应用(含答案解析)

数形联合思想方法是高中数学中常用的一种解题思想方法,在解答相关会合运算7 及抽象会合问题时,一般要借助数轴或韦恩图求解,运用数形联合思想方法能够比较形象、直观地解决问题,常常有事半功倍的成效,平常我们要增强“数形联合”的思想训练 .下边我们看几个例题.例 1.设全集U R, A x| x 1 , B x | x a 0 ,且 BUe A, 务实数a的取值范围.解: e U A x | x 1 , B x| x a ,1a1.思路点拨:第一化简并求解会合,而后借助数轴由已知所给的会合间的关系求出 a 的取值范围 .例 2.设会合S x ||x 2| 3 ,T x | a x a 8 , S T R, 务实数a的取值范围.解:第一步:化简会合,S x | x1或x 5 ,T x | a x a 8 .第二步:借助数轴:第三步:依据所给会合间的关系列不等式求解参数,a1,得 3 a 1 .例 3.某班级共有30 人,此中15 人喜爱篮球, 8 人喜爱足球,两项都不喜爱的有8 人,则喜爱篮球但不喜爱足球的有_____人 .篮球足球x - 7x15- x8例 4.以下图, I 是全集, A,B, C 是它的子集,则暗影部分所表示的会合是()ACBA.(A B) CB.( A e I B) CC.( A B)e I CD.( e I B A) C解:选择 B.注:关于韦恩图所表述的会合应做以下理解:暗影部分波及谁就交谁,不波及谁就交其补集.就此,我们看下边暗影部分所表示的会合:A B C A B (e I C)(痧I A) ( I B) Ce I ( A B) C下边给出些练习来领会以上数形联合思想在会合中的应用.练习题:1.已知会合 A = { x ? R || x 2 |< 3} , 会合 B = { x ? R | ( x- m)( x- 2) 0} , 且 A B(- 1, n), 则m=________ ,n=________.分析:2.某网店统计了连续三天售出商品的种类状况:第一天售出19 种商品,次日售出13种商品,第三天售出 18 种商品;前两天都售出的商品有 3 种,后两天都售出的商品有4种,则该网店① 第一天售出但次日未售出的商品有________种;②这三天售出的商品最罕有________种 .分析:3.某班有 36 名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有同时参加物理和化学小组的有 4 人,则同时参加数学和化学小组的有______人 ..已知6 人,分析:4.已知全集U = R会合M = { x | - 2 ? x 1?2}, 和 N = { x | x = 2k - 1, k ? N * }, 的韦恩图如图所示,则暗影部分所表示的会合元素共有()A.2 个B.3 个C.1 个D. 无量多个UN M。
浅谈初中函数教学中的 “数形结合”思想方法

(追问)T: ⑸你能从解析式出发给出证明吗?
在上面的教学设计中,教师借助几何画板课件,帮助学生形象直观的理解了反比例函数图象的变化规律,发现变化过程中的特殊点的,自然的归纳出反比例函数增减性的性质及自变量的取值范围,并且通过结合符号语言和解析式全方位诠释增减性的意义。学生不但理解而且记忆,而且途径全面,更好的感受到函数的三种表示方法的整体一致性。
浅谈初中函数教学中的“数形结合”思想方法
函数是初中数学教学中的重要内容,学生初次接触函数,感觉难度大,不容易理解。那么怎样进行函数教学,学生会学的轻松一点呢?我在函数的教学过程中,针对学生的知识结构与年龄特点,结合自己的一点教学经验,谈谈函数教学中的“数形结合”思想方法。
一、数形结合的思想方法是初中数学中一种重要的思想方法。数学是研究现实世界数量关系和空间形式的科学。而数形结合就是通过数与形之间的对应和转化来解决数学问题。它包含以形助数和以数解形两个方面,利用它可使复杂问题简单化,抽象问题具体化,它兼有数的严谨与形的直观之长。
(2)切莫急于呈现画函数图象的简单画法。首先,在探索具体函数形状时,不能取得点太少,否则学生无法发现点分布的规律,从而猜想出图象的形状;其次,教师过早强调图象的简单画法,追求方法的“最优化”,缩短了学生知识探索的经历过程。所以,在教新知识时,教师要允许学生从最简单甚至最笨拙的方法做起,渐渐过渡到最佳方法的掌握,达到认识上的最佳状态。
(1)让学生经历绘制函数图象的具体过程。首先,对于函数图象的意义,只有学生在亲身经历了列表、描点、连线等绘制函数图象的具体过程,才能知道函数图象的由来,才能了解图象上点的横、纵坐标与自变量值、函数值的对应关系,为学生利用函数图象数形结合研究函数性质打好基础。其次,对于具体的一次函数、反比例函数、二次函数的图象的认识,学生通过亲身画图,自己发现函数图象的形状、变化趋势,感悟不同函数图象之间的关系,为发现函数图象间的规律,探索函数的性质做好准备。
中考数学专题复习:二次函数图象综合应用
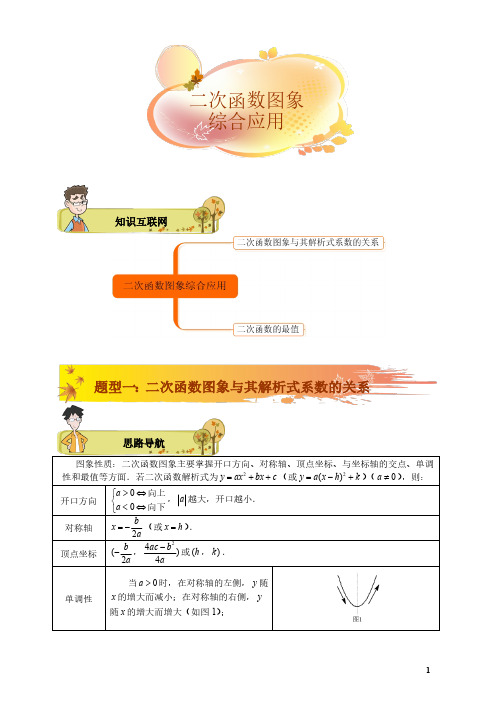
图象性质:二次函数图象主要掌握开口方向、对称轴、顶点坐标、与坐标轴的交点、单调性和最值等方面.若二次函数解析式为2y ax bx c =++(或2()y a x h k =-+)(0a ≠),则: 开口方向 00a a >⇔⎧⎨<⇔⎩向上向下,a 越大,开口越小. 对称轴 2bx a=-(或x h =). 顶点坐标(2ba-,24)4ac b a -或(h ,)k . 单调性当0a >时,在对称轴的左侧,y 随x 的增大而减小;在对称轴的右侧,y 随x 的增大而增大(如图1);知识互联网思路导航题型一:二次函数图象与其解析式系数的关系二次函数图象综合应用当0a <时,在对称轴的左侧,y 随x 的增大而增大;在对称轴的右侧,y 随x 的增大而减小(如图2)与坐标轴的交点① 与y 轴的交点:()0c ,; ② 与x 轴的交点:()()1200x x ,,,,其中12x x ,是方程()200ax bx c a ++=≠的两根.图象与x 轴的交点个数① 当240b ac ∆=->时,图象与x 轴有两个交点. ② 当0∆=时,图象与x 轴只有一个交点. ③ 当0∆<时,图象与x 轴没有交点.Ⅰ当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; Ⅱ当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.【引例】 二次函数2y ax bx c =++的图象如图所示,判断a ,b ,c ,24b ac -,2a b +,a b c ++,a b c -+的符号【解析】 由图知:图象开口向上,所以0a >;函数的对称轴02bx a=->,所以0b <;函数图象与y 轴的交点小于0,所以0c <;函数图象与x 轴有两个不同的交点,所以240b ac ->;同时12bx a=-<,所以20a b +>;1x =所对应的函数值小于0,所以0a b c ++<; 1x =-所对应的函数值大于0,所以0a b c -+>【例1】 ⑴ 二次函数2y ax bx c =++的图象如图所示,则点()a c ,在( )A .第一象限B .第二象限C .第三象限D .第四象限⑵ 二次函数c bx ax y ++=2的图象如图所示,则一次函数b ax y +=与反比例函数xcy =在同一平面直角坐标系中的大致图象为( ) 例题精讲典题精练A .B .C .D .⑶ 一次函数()0≠+=a b ax y 、二次函数bx ax y +=2和反比例函数()0≠=k xky 在同一直角坐标系中的图象如图所示,A 点的坐标为()02,-,则下列结论中,正确的是( )A .k a b +=2B .k b a +=C .0>>b aD .0>>k a【解析】 ⑴ B. ⑵ B .⑶D.【例2】 ⑴ 如图,抛物线2y ax bx c =++,OA OC =,下列关系中正确的是()A .1ac b +=B .1ab c +=C .1bc a +=D .1ac b+= )⑵ 如图,抛物线2y ax bx c =++与x 轴交于点A 、B ,与y 轴交于点C ,若12OB OC OA ==,则b 的值为 .【解析】 ⑴ A .提示:把()0c -,代入2y ax bx c =++即可.⑵ 12-.提示:先把B ()0c ,代入2y ax bx c =++,得1ac b =--,再把()0c ,代入()()2y a x c x c =+-即可.【例3】 ⑴ 函数2y ax bx c =++与x y =的图象如图所示,有以下结论:①ac b 42->0;②01=++c b ;③063=++c b ;④当1<x<3时,()012<c x b x +-+.其中正确的为.⑵ 已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列8 个结论:①0abc >;②b a c <+;③420a b c ++>;④23c b <;⑤()a b m am b +>+,(1m ≠的实数);⑥20a b += ;⑦240b ac -<,⑧22()a c b +>,其中正确的结论有( )A .2个B .3个C .4个D .5个【解析】 ⑴ ③④⑵ C .对称轴在y 轴的右边得0ab <(由开口向下得0a <,故0b >),抛物线与y 轴交于正半轴得0c >,∴0abc <,①不正确;当1x =-时,函数值为0a b c -+<,②不正确; 当2x =时,函数值420a b c ++>,③正确;其实0x =和2x =到对称轴1x =的距离相等,函数值相等得42a b c c ++=,∴2b a =-代入0a b c -+<,32bc <,即23c b <,④正确;当1x =,∵1m ≠,2max y a b c am bm c =++>++,可知⑤正确;由对称轴12ba-=得20a b +=,故⑥正确;抛物线与x 轴有两个交点,故240b ac ->,故⑦不正确;0a b c ++>,0a b c -+<,故()220a c b +-<,故⑧不正确.对于二次函数()20y ax bx c a =++>(max y 表示y 的最大值,min y 表示y 的最小值) ⑴ 若自变量x 的取值范围为全体实数,如图①,函数在顶点处2bx a=-时,取到最值. ⑵ 若2bm x n a<-≤≤,如图②,当x m =,max y y =;当x n =,min y y =. ⑶ 若2bm x n a-<≤≤,如图③,当x m =,min y y =;当x n =,max y y =. ⑷ 若m x n ≤≤,且2b m n a -≤≤,22b b n m a a +>--,如图④,当2bx a=-,min y y =; 当x n =,max y y =.【引例】 ⑴ 若x 为任意实数,求函数221y x x =-+的最小值;⑵ 若12x ≤≤,求221y x x =-+的最大值、最小值; ⑶ 若01x ≤≤,求221y x x =-+的最大值、最小值;b 思路导航例题精讲题型二:二次函数的最值⑷ 若20x -≤≤,求221y x x =-+的最大值、最小值; ⑸ 若x 为整数,求函数221y x x =-+的最小值.【解析】 ⑴ 套用求最值公式(建议教师讲配方法):当112224b x a -=-=-=⨯时,y 的最小值是24748ac b a -=. ⑵ 由图象可知:当12x ≤≤时,函数221y x x =-+单调递增,当1x =时,y 最小,且21112y =⨯-+=,当2x =时,y 最大,且222217y =⨯-+=.⑶ 由图象可知:当01x ≤≤时,函数221y x x =-+是先减后增,∴当14x =,y 最小,且78y =.∵当0x =时,20011y =⨯-+=;当1x =时, 211121y =⨯-+=>, ∴当1x =时,y 最大,且2y =.⑷ 由函数图象开口向上,且120<4x -≤≤,故当2x =-时,y 取最大值为11,当0x =时,y 取最小值为1.⑸ ∵112224b x a -=-=-=⨯,当0x =时,y 取最小值为1.【点评】 由此题我们可以得到:求二次函数2(0)y ax bx c a =++≠在给定区域内的最值,得看抛物线顶点横坐标2bx a=-是否在给定区域内.若在,则在顶点处取到一个最值,若不在,则在端点处取得最大值和最小值(其实求出端点值和顶点值,这三个值中最大的为最大值,最小的为最小值).【例4】 ⑴ 已知m 、n 、k 为非负实数,且121=+=+-n k k m ,则代数式6822+-k k 的最小值 为 .⑵ 已知实数x y ,满足2330x x y ++-=,则x y +的最大值为 .⑶当12x ≤时,二次函数223y x x =--的最小值为( ) A .4- B .154- C .12- D .12【解析】 ⑴∵m 、n 、k 为非负实数,且121=+=+-n k k m ,∴m 、n 、k 最小为0,当n =0时,k 最大为:21;∴210≤≤k ,故最小值为2.5.⑵ 4.提示:233y x x =--+,令()222314q x y x x x =+=--+=-++,当1x =-,q的最大值为4.本题属于x 为全体实数,求二次函数的最值,配方法要熟练掌握.⑶ B .提示:二次函数的对称轴为1122b x a =-=>,且抛物线的开口向上,故12x =时,y 的最小值为154-.【例5】 如图,抛物线211y ax ax =--+经过点1928P ⎛⎫- ⎪⎝⎭,,且与抛物线221y ax ax =--相交于典题精练A B ,两点.⑴ 求a 值; ⑵ 设211y ax ax =--+与x 轴分别交于M N ,两点(点M 在点N 的左边),221y ax ax =--与x 轴分别交于E F ,两点(点E 在点F 的左边),观察M N E F ,,,四点的坐标,写出一条正确的结论,并通过计算说明;⑶ 设A B ,两点的横坐标分别记为A B x x ,,若在x 轴上有一动点()0Q x ,,且A B x x x ≤≤,过Q 作一条垂直于x 轴的直线,与两条抛物线分别交于C D ,两点,试问当x 为何值时,线段CD 有最大值?其最大值为多少?【解析】 ⑴ ∵点1928P ⎛⎫- ⎪⎝⎭,在抛物线211y ax ax =--+上,∴1191428a a -++=,解得12a =.⑵ 由⑴知12a =,∴抛物线2111122y x x =--+,2211122y x x =--.当2111022x x --+=时,解得12x =-,21x =.∵点M 在点N 的左边,∴2M x =-,1N x =. 当2111022x x --=时,解得31x =-,42x =. ∵点E 在点F 的左边,∴1E x =-,2F x =.∵0M F x x +=,0N E x x +=,∴点M 与点F 关于y 轴对称,点N 与点E 关于y 轴对称. ⑶ ∵102a =>.∴抛物线1y 开口向下,抛物线2y 开口向上. 根据题意,得12CD y y =-22211111122222x x x x x ⎛⎫⎛⎫=--+---=-+ ⎪ ⎪⎝⎭⎝⎭.又21221112211122y x x y x x ⎧=--+⎪⎪⎨⎪=--⎪⎩,消y可解得12x x ==,则当0x =时,CD 的最大值为2.【例6】 ⑴ 二次函数2y ax bx c =++的图象的一部分如图所示,求a 的取值范围⑵ 二次函数2y ax bx c =++的图象的一部分如图所示,试求a b c ++的取值范围.【解析】 ⑴ 根据二次函数图象可知0a <,又此二次函数图象经过(10),,(01), 则有0a b c ++=,1c =,得(1)b a =-+,∵0a <,据图象得对称轴在y 轴左侧,∴0b <∴()10a -+<,∴1a >-于是有10a -<<. ⑵ 由图象可知0a >.又顶点在y 轴的右侧,在x 轴的下方,则:02ba->,2404ac b a -<,∴0b <. 又∵当0x =时,1y c =-=当0y =时,1x =-,∴0a b c -+= ∴10a b =+> ∴10b -<<.∴202a b c a b c b b ++=-++=+ ∴220b -<<,即20a b c -<++<.精讲:数形结合思想在二次函数中的应用探究【探究对象】数形结合思想在二次函数中的应用 【探究过程】【探究1】数形结合思想在含参二次函数中求参数的取值范围的应用;二次函数的图像信息:⑴ 根据抛物线的开口方向判断a 的正负性.⑵ 根据抛物线的对称轴的位置判断a 与b 之间的关系. ⑶ 根据抛物线与y 轴的交点,判断c 的大小.⑷ 根据抛物线与x 轴有无交点,判断24b ac -的正负性.⑸ 根据抛物线所经过的特殊点的坐标,可得到关于a b c ,,的等式. ⑹ 根据抛物线的顶点,判断244ac b a-的大小.例. 2y ax bx c =++的图象如图所示.设|||||2||2|M a b c a b c a b a b =++--+++--, 则( )A .0M >B .0M =C .0M <D .不能确定M 为正,为负或为0分析:依题意得0a >,012ba<-<,∴0b <,20a b +>,20a b ->, 又当1x =时,0y a b c =++<,当1x =-时,0y a b c =-+>,故()()(2)(2)2()0M a b c a b c a b a b a b c =-++--+++--=--+<,故选C .☆【探究2】数形结合思想在求解二次函数的区间最值中的应用;(区间最值问题为高中二次函数部分的重要内容,但在目前中考改革创新,部分高中思想下放初中的大 前提下,老师可以针对班里学生层次进行选讲) 区间最值分三种类型: “轴定区间定”、“轴动区间定”、“轴定区间动”;1、轴定区间定:2、轴动区间定:例.求2()22f x x ax =-+在[24],上的最大值和最小值. 分析: 先求最小值.因为()f x 的对称轴是x a =,可分以下三种情况:⑴ 当2a <时,()f x 在[24],上为增函数,所以min ()(2)64f x f a ==-; ⑵ 当24a ≤≤时,()f a 为最小值,2min ()2f x a =-;⑶ 当4a >时,()f x 在[24],上为减函数,所以min ()(4)188f x f a ==-.综上所述:2min 64, (2)()2, (24)188, (4)a a f x a a a a -<⎧⎪=-⎨⎪->⎩≤≤最大值为(2)f 与(4)f 中较大者:(2)(4)(64)(188)124f f a a a -=---=-+,(1)当3a ≥时,(2)(4)f f ≥,则max ()(2)64f x f a ==-; (2)当3a <时,(2)(4)f f <,则max ()(4)188f x f a ==-.故max 64, (3)()88, (3)a a f x a a -⎧=⎨-<⎩≥ 点评:本题属于二次函数在给定区间上的最值问题,由于二次函数的系数含有参数,对称轴是变动的,属于“轴动区间定”,由于图象开口向上,所以求最小值要根据对称轴x a = 与区间[24],的位置关系,分三种情况讨论;最大值在端点取得时,只须比较(2)f 与 (4)f 的大小,按两种情况讨论即可,实质上是讨论对称轴位于区间中点的左、右两 种情况. 3、轴定区间动:例.若函数2()22f x x x =-+当1t x t +≤≤时的最小值为()g t ,求函数()g t 当[32]t ∈-,时的最值. 分析:2()(1)1f x x =-+,按直线1x =与区间[1]t t +,的不同位置关系分类讨论:若1t >,则2min ()()(1)1f x f t t ==-+;若11t t +≤≤,即01t ≤≤,则min ()(1)1f x f ==; 若11t +<,即0t <,则2min ()(1)1f x f t t =+=+.∴22(1)1(1)()1(0)1(0)t t g t t t t ⎧-+>⎪=⎨⎪+<⎩≤≤1 函数()g t 在(0)-∞,内是减函数,在[01],内是常值函数,在(1)+∞,内是增函数,又(3)(2)g g ->,故在区间[32]-,内,min ()1g t =(当01t ≤≤时取得),max ()(3)10g t g =-=.小结:(i )解此类问题时,心中要有图象;(ii )含参数问题有两种:一种是“轴变区间定”,另一种是“轴定区间变”.讨论时,要紧紧抓住对称轴与所给区间的相对位置关系,这是进行正确划分的关键.☆【探究3】数形结合思想在求解二次函数的区间根中的应用;(区间根问题同样为高中二次函数部分的重要内容,但在目前中考改革创新,部分高中思想下放初中的大 前提下,老师可以针对班里学生层次进行选讲)二次方程的根其实质就是其相应二次函数的图像与x 轴交点的横坐标.因此, 可以借助于二次函数及其图像,利用数形结合的方法来研究二次方程的实根分布问题.设二次方程()002≠=++a c bx ax 的两个实根1x 、2x ()21x x <,ac b 42-=∆,方程对应的二次函数为()()02≠++=a c bx ax x f .1.当方程有一根大于m ,另一根小于m 时,对应二次函数()x f 的图像有下列两种情形:方程系数所满足的充要条件:()0<m af ;2.当方程两根均大于m 时,对应函数()x f 的图像有下列两种情形:方程系数所满足的充要条件:0>∆, m ab2-,()0>m af ; 3.当方程两根均在区间()n m ,内,对应二次函数()x f 的图像有下列两种情形:方程系数所满足的充要条件:0>∆, n abm <<2-,()0>m af ,()0>n af ; 4.当两根中仅有一根在区间()n m ,内,对应函数()x f 的图像有下列四种情形:方程系数所满足的充要条件: ()()0<n f m f ⋅;5.当两根在区间[]n m ,之外时:对应函数()x f 的图像有下列两种情形:方程系数所满足的充要条件:()0<m af ,()0<n af ;6.当两根分别在区间()n m ,、()t s ,内,且s n ≤,对应函数()x f 的图像有下列两种情形:方程系数所满足的充要条件:()0>m af ,()0<n af ,()0<s af , ()0>t af .小结: 由函数图像与x 轴交点的位置写出相应的充要条件,一般考虑三个方面:①判别式ac b 42-=∆的符号;②对称轴abx 2-=的位置分布;③二次函数在实根分布界点处 函数值的符号.例.若方程01222=+-+m mx x 的两个根均大于2,求实数m 的取值范围. 分析:令()1222+-+=m mx x x f ,如图得充要条件:()()⎪⎩⎪⎨⎧-+-+=≥+-⋅-=∆20124220124422>>m m m f m m ,解得4316-≤-m .训练1. 已知:a b c >>,且0a b c ++=,则二次函数2y ax bx c =++的图象可能是下列图象中的( )A B C D【解析】 B .由a b c >>,且0a b c ++=,可得0a >, 0c <,且过()10,点,由a b c >>,且a b c ++=0,利用不等式性质,可以进一步推出下列不等关系:a b a b >>--,∴112ba -<<, ∴11224b a -<-<.另一方法:∵a b >,∴330a b ->,330a b a b c -+++>,从而得到420a b c -+>.训练2.已知二次函数()2211y kx k x =+--与x 轴交点的横坐标为1x 、2x ()12x x <,则对于下列结论:⑴ 当2x =-时,1y =;⑵ 当2x x >时,0y >;⑶ 方程()22110kx k x +--=有两个不相等的实数根1x 、2x ;⑷11x <-,21x >-;⑸21x x -=确的结论是______.(只需填写序号)【解析】 ⑴⑶⑷.当2x =-时,代入得1y =,故⑴正确;因为k 的符号不确定,故开口不确定,因此无法确定当2x x >时,0y >,故⑵不正确;联立方程()22110y kx k x y ⎧=+--⎪⎨=⎪⎩可得()22110kx k x +--=,抛物线与x 轴有两个交点,即方程()22110kx k x +--=有两个不相等的实数根.当1x =-时,y k =-,若0k >,0y k =-<,若0k <,0y k =->,故⑷正确.21x x -=.训练3. 如图所示,二次函数2(2)5y x a x a =--+-的图象交x 轴于A 和B ,交y 轴于C ,当线段AB 最短时,求线段OC 的长.【解析】 设1(A x ,0),2(B x ,0),思维拓展训练(选讲)则1x ,2x 是方程2(2)50x a x a --+-=的两根,则12AB x x =-=== 当4a =时,AB 取最小值,即最短,此时,抛物线为221y x x =--, 可求得C 的纵坐标为1-,即线段OC 的长是1.训练4. 小明为了通过描点法作出函数21y x x =-+的图象,先取自变量x 的7个值满足:213276x x x x x x d -=-==-= ,再分别算出对应的y 值,列出表1:表1:x1x 2x3x4x 5x 6x7xy1 3 7 13 21 31 43记121m y y =-,232m y y =-,343m y y =-,454m y y =-,…; 121s m m =-,232s m m =-,343s m m =-,… ⑴ 判断1s 、2s 、3s 之间关系;⑵ 若将函数“21y x x =-+”改为“2(0)y ax bx c a =++≠”,列出表2:表2:x 1x 2x 3x 4x 5x 6x 7x y1y 2y 3y 4y 5y 6y 7y其他条件不变,判断1s 、2s 、3s 之间关系,并说明理由;⑶ 小明为了通过描点法作出函数2(0)y ax bx c a =++≠的图象,列出表3: 表3: x 1x 2x 3x4x 5x 6x7x y 10 50 110 190 290 420 550由于小明的粗心,表3中有一个y 值算错了,请指出算错的y 值(直接写答案).【解析】 ⑴ 123s s s ==;⑵ 123s s s ==.证明:()()222121111112m y y a x d b x d c ax bx c adx ad bd ⎡⎤⎡⎤=-=++++-++=++⎣⎦⎣⎦()222322122m y y adx ad bd ad x d ad bd =-=++=+++()2234331222m y y adx ad bd ad x d ad bd =-=++=+++()2245441223m y y adx ad bd ad x d ad bd =-=++=+++()22212111222s m m ad x d ad bd adx ad bd ad ⎡⎤⎡⎤=-=+++-++=⎣⎦⎣⎦ 同理22322s m m ad =-=,23432s m m ad =-=. ∴123s s s ==.⑶ 表中的420改为410.题型一 二次函数图象与其解析式系数的关系 巩固练习【练习1】 ⑴ 函数ky x=与22(0)y kx k k =+≠在同一坐标系中图象大致是图中的( )⑵ 二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b c y x++=在同一坐标系内的图象大致为( )【解析】 ⑴ A .⑵ D .【练习2】 如图所示,二次函数2y ax bx c =++的图象开口向上,图象经点()12-,和()10,且与y 轴交于负半轴.⑴ 下列四个结论:①0a >;②0b >;③0c >;④0a b c ++=, 其中正确的结论的序号是 . ⑵给出下列四个结论:①0abc <;②20a b +>;③1a c +=;④1a >.其中正确的结论的序号是 .【解析】 ⑴图象开口向上得0a >;对称轴02ba->可得0b <;当0x =时,0y <,即0c <;由1x =时,0y =,即0a b c ++=.故①④.⑵由⑴可知0abc >;对称轴12ba-<,∴20a b +>;∵点()12-,和()10,在抛物线上,代入解析式得20a b c a b c -+=⎧⎨++=⎩两式相加得1a c +=,得1a c =-,∵0c <,∴11c ->,即1a >.A BCD复习巩固故②③④.【练习3】 如图,表示抛物线2y ax bx c =++的一部分图象,它与x轴的一个交点为A ,与y 轴交于点B .则b 的取值范围是( )A .20b -<<B .10b -<<C .102b -<< D .01b <<【解析】 B .【练习4】 二次函数()20y ax bx c a =++≠的图象大致如图所示,⑴判别a ,b ,c 和24b ac -的符号,并说明理由; ⑵如果OA OC =,求证:10ac b ++=【解析】 ⑴ 解:因为抛物线开口向上,0a >.因为抛物线与y 轴交于负半轴,0c <.又因为抛物线对称轴在y 轴的右侧,02ba->,即a ,b 异号,由0a >,得0b <. 因为抛物线与x 轴有两个交点,所以方程20ax bx c ++=有两个不相等的实根,所以其判别式240b ac ->.⑵ 证明:由于C 点坐标为()0c ,,而OA OC =,所以A 点坐标为()0c ,,把()0A c ,代入2y ax bx c =++,得20ac bc c =++. 因为0c ≠,所以10ac b ++=.题型二 二次函数的最值 巩固练习【练习5】 已知:关于x 的一元二次方程22(2)0x n m x m mn +-+-=①.⑴ 求证:方程①有两个实数根;⑵ 若10m n --=,求证方程①有一个实数根为1;⑶ 在⑵的条件下,设方程①的另一个根为a . 当2x =时,关于m 的函数1y nx am =+与()2222y x a n m x m mn =+-+-的图象交于点A 、B (点A 在点B 的左侧),平行于y 轴的直线l 与1y 、2y 的图象分别交于点C 、D . 当l 沿AB 由点A 平移到点B 时,求CD 的最大值.【解析】 ⑴ 证明:()()22224n m m mn n ∆=---=.∵20n ≥, ∴0∆≥. ∴方程①有两个实数根.⑵ 解:由10m n --=,得1m n -=当x =1时,等号左边212n m m mn =+-+-()121210n m m m n n m m n m =+-+-=+-+=+-=. 等号右边=0. ∴左边=右边.∴ 1x =是方程①的一个实数根.⑶ 解:由求根公式,得22m n nx -±=.x =m 或x m n =-∵ 1m n -=, ∴ a m =.当2x =时,222122(1)22y n m m m m m =+=-+=+-,22222()()42(1)24y m n m m m m n m m m m m =+--+-=+--+=--+如图,当l 沿AB 由点A 平移到点B 时,22211273363(24CD y y m m m =-=--+=-++由12y y =,得222224m m m m +-=--+解得m =-2或m =1.∴ m A =-2,m B =1.∵-2<12-<1,∴当m =12-时,CD 取得最大值274.【测试1】 设二次函数()20y ax bx c a =++≠图像如图所示,试判断:24a b c a b c a b c b ac ++-+-、、、、、的符号.【解析】由图像可知0a >,102ba-<<,2404ac b a -<,2000a b c ⋅+⋅+<,0a b c -+=,0a b c ++>,于是20000040a b c a b c a b c b ac >><++>-+=->,,,,,.【测试2】 若01x ≤≤,求221y x x =-+的最大值、最小值;【解析】由图像可知:当01x ≤≤时,函数221y x x =-+是先减后增,∴当14x =,y 最小,且78y =. ∵当0x =时,20011y =⨯-+=当1x =时, 211121y =⨯-+=>, ∴当1x =时,y 最大,且2y =.课后测。
巧用“数形结合”求参数取值范围

巧用“数形结合”求参数取值范围数形结合是重要的数形思想方法之一,在数学解题中,有着广泛的应用。
尤其在求参数取值范围中,能简化计算、求解准确。
学生易于掌握。
请看下面例题:例1.当0<x≤时,4x ax,则a的取值范围是( )A. B.C.(1,) D.(,2)x,当a>1时解析:法一:构造函数f(x)=4x和g(x)=loga不满足条件,当0<a<1时,画出两个函数在上的图像,可知,f<g,即2a,则a>,所以a的取值范围为.x>4x>1,法二:∵0<x≤,∴1<4x≤2,∴loga∴0<a<1,排除选项C,D;取a=,x=,则有4=2,=1,显然4x ax不成立,排除选项A.答案:B例2.已知函数f(x)=若关于x的方程f(x)-a=0有两个实根,则a的取值范围是________.解析:当x≤0时,0<2x≤1,由图像可知方程f(x)-a=0有两个实根,即y=f(x)与y=a的图像有两个交点,所以由图像可知0<a≤1.即实数a的取值范围为(0,1].答案:(0,1]例3.已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的范围是________.解析:问题等价于函数y=f(x)与y=-x+a的图像有且只有一个交点,结合函数图像可知a>1.答案:(1,+∞)从上面例题可以看出,利用数形结合解题,一要合理转化模型;二要作图准确。
应用对数型函数的图像可求解的问题有:(1)对一些可通过平移、对称变换作出其图像的指数、对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想.(2)一些指数、对数型方程、不等式问题常转化为相应的函数图像问题,利用数形结合法求解。
一元一次不等式组中参数取值范围的确定方法

2022年8月下半月㊀学习交流㊀㊀㊀㊀一元一次不等式组中参数取值范围的确定方法◉白银区武川新村学校㊀刘振琴㊀㊀摘要:一元一次不等式组是学生在学完一元一次不等式㊁一元一次方程和二元一次方程组基础上接触到的新知识,该知识点本身难度不大.但是,如果一元一次不等式组中出现了另一个参数,那么这对学生求出解集和确定参数取值范围带来了很大困扰.如果借助数形结合与分类讨论的方法,采用 解㊁画㊁移㊁比 四个步骤,可顺利解决一元一次不等式组中关于参数取值范围的确定问题.关键词:一元一次不等式组;数形结合;分类讨论;参数;取值范围1引言含参数的一元一次不等式组中参数取值范围的确定是 一元一次不等组 这一节的重难点内容.从课堂教学情况来看,学生在该知识点上存在很大问题,出现了诸多错误.所以,笔者对一元一次不等式组中参数取值范围的确定方法进行了研究,希望对学生有更多帮助.2例题分析例1㊀若不等式组x<m,x>3{无解,则m的取值范围是.分析:本题中的不等式组无需进一步求解,只需在数轴上将x<m和x>3表示出来.然而,由于m是除未知数x之外的又一个字母,且m的值题中未给出,这就给在数轴上的表示解集增加了难度.所以,根据题意应该采用数形结合和分类讨论的方法,分析如下.第一步,画出数轴,在数轴上表示出x>3的解集,将x<m的解集表示图如图1所示画出;第二步,将x<m的解集表示图在数轴上移动,直至找出符合题意的情况;第三步,观察符合题意的x<m解集表示图所在的位置,比较m与3的大小.解:首先,将x<m和x>3在数轴上表示出来,如下图1所示.㊀图1然后,分析x<m的解集表示图有三个不同的位置可以放置,分别是数轴上3的左边㊁3的上面和3的右边,如图2所示.㊀图2再者,根据 无解 这一题意,可以确定(1)(2)两种情况符合.很明显,(1)中m<3,(2)中m=3.最后,综上分析可得出m的取值范围为mɤ3.例2㊀若不等式组x+1>a,xɤ2{有3个整数解,则a的取值范围是.分析:本题与例1的不同点在于本题中不等式组需要求解及不等式组有解集两个方面,同样用数形结合和分类讨论的方法分析如下.第一步,解出不等式的解集,分别是x>a-1和xɤ2;第二步,画出数轴,在数轴上表示出xɤ2的解集,将x>a-1的解集表示图如图3所示画出;第三步,将x>a-1的解集表示图在数轴上移动,直至找出符合题意的情况;第四步,观察符合题意情况下的x>a-1解集表示图所在的位置,比较a-1与2的大小.34Copyright博看网. All Rights Reserved.学习交流2022年8月下半月㊀㊀㊀解:解不等式组x +1>a ,x ɤ2,{得x >a -1,x ɤ2.{将不等式组的解集在数轴上表示,如图3所示:㊀图3因为原不等式组有3个整数解,所以a -1一定小于2.因为x ɤ2确定了原不等式组中的一个解,又由于x >a -1,a -1处是空心,所以在满足原不等式组有三个解的前提下,a -1一定要在0的左边㊁-1的右边,即-1ɤa -1<0,如图4所示.㊀图4所以,a 的取值范围是0ɤa <1.3解法总结通过以上两道例题的分析可以发现,一元一次不等式组中参数取值范围的确定,不仅要利用数形结合的方法将之直观地在数轴上表示出来,还需要借助分类讨论思想,对符合题意的几种情况逐个分析[1].对于这类问题,大致可采用以下思路解决:第一步,解.解出不等式的解集.第二步,画.画出数轴,在数轴上分别表示出不等式组的解集.对于含参数的解集,可像例1,2中一样先画出其形状待用.第三步,移.将含参数的解集表示图在数轴上移动,直至找出符合题意的情况.第四步,比.观察符合题意情况下含参数的解集表示图所在的位置,比较对应数字的大小[2].另外,在操作第三步和第四步时,需注意以下几个方面的问题:首先,为了让学生有更直观的移动体验,教师可以利用多媒体画图工具,先用一种颜色将不含参数的解集在数轴上画好,然后用另一种颜色将含参数的解集在数轴以外的地方画好,然后利用 平移 或 移动 工具移动该解集的表示图,让学生经历解集表示图移动的过程,更直观地感受符合题意的几种情况.这样操作,比教师包办效果更好.其次,在移动到相应位置取值时,一定要注意 空心 和 实心 的区别[3].空心 意味着取不到该点对应的数值,需继续移动. 实心 意味着可以取到该点对应的数值,移动时需结合题意谨慎进行.例如,在例2中a -1处是空心 ,那么在 不等式组x +1>a ,x ɤ2{有3个整数解 的条件下,a -1不能放在0上,因为这样不等式解集无法取到0,那么原不等式组只有1和2两个整数解,与题意矛盾,所以应将a -1处是 空心 移向-1的左边.但是,a -1处是 空心 可以放在-1处,因为即使a -1处是 空心 可以放在-1处时原不等式组也取不到-1这个整数解,原不等式组仍只有3个整数解,符合题意.最后,解㊁画㊁移㊁比是解这类问题的通用步骤,学生不仅要对这些步骤进行常规化练习,而且要进行变式训练,以不断激发思维和拓展解题思路[4].4结语综上所述,虽然含有参数的一元一次不等式组会给人以疑惑感,但如果能在 解 的基础上一步步尝试探究和深入,学生可能会获得不一样的学习心得.这种心得不仅体现在学习本身,更体现在与学生全面发展有关的诸多素养方面.所以,作为一线教师不仅要重视解㊁画㊁移㊁比这四个步骤的不断训练,更要借助变式练习激发学生的思维,培养学生更好的学习品质,为学生更全面的发展奠定基础.参考文献:[1]李进,王磊.解决含参数一元一次不等式问题 数形结合与分类讨论在解题中的运用[J ].初中生世界,2017(Z 3):28G29.[2]钮丹媛.数学思想方法在课堂教学中的应用 以 一元一次不等式 教学为例[J ].成长,2021(10):101G102.[3]曹元军.例谈一元一次不等式组中参数取值问题[J ].初中数学教与学,2017(5):13G14.[4]马永刚.用 三定法 解决一类一元一次不等式组中参数取值范围的问题[J ].中小学数学,2022(Z 1):69G70.Z44Copyright 博看网 . All Rights Reserved.。
高中数学恒成立问题中参数范围的求法

一、变换主元法
2
例1、已知函数f(x)=x+(a-6)x+9-3a,当-1≤a≤1时,f(x)>0恒成立,求x的取值范围。
二、判别式法
2 2
例2、已知函数f(x)=lg[x+(a-1) x+a 的定义域是实数集R,求实数a的取值范围
三、分离参数法例3、不等式x+ax+1≥0,对x (0, ]恒成立,求实数a 的取值范围221
四、利用根的分布例4(同例3)、不等式x+ax+1≥0,对x (0, ]恒成立,求实数a 的取值范围
212
五、数形结合法
x
例5、若函数f(x)=a-x-a(a>0,且a≠1)恒有两个零点,求实数a的取值范围
2
例6、当1<x<2时,不等式(x-1)<logx恒成立,求实数a的取值范围
六、根据函数的奇偶性、周期性等性质•若函数f(x)是奇(偶)函数,则对一切定义域中的x ,f(-x)=-f(x)•(f(-x)=f(x))恒成立;若函数y=f(x)的周期为T,则对一切定义域•中的x,f(x)=f(x+T)恒成立。
分析:告诉我们偶函数的条件,即相当于告诉我们一个恒成立问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数形结合思想在求参数范围中的应用
[典例] 已知函数y =|x 2
-1|x -1 的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是________.
[解析] 因为函数y =|x 2-1|x -1=⎩⎪⎨⎪⎧ x +1,x ≤-1或x >1,-x -1,-1<x <1,所以函数y =kx -2的图象恒
过点(0,-2),根据图象易知,两个函数图象有两个交点时,0<k <1或1<k <4.
[答案] (0,1)∪(1,4)
[题后悟道]
所谓数形结合思想,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的
几何性质.解答本题利用了数形结合思想,本题首先作出y =|x 2
-1|x -1
的图象,然后利用图象直观确定直线y =kx -2的位置.作图时应注意不包括B 、C 两点,而函数y =kx -2的图象恒过定点A (0,-2),直线绕A 点可以转动,直线过B 、C 两点是关键点.
针对训练
1. 设函数f (x )=|x +a |,g (x )=x -1,对于任意的x ∈R ,不等式f (x )≥g (x )恒成立,则实数a 的取值范围是________.
解析:如图作出函数f (x )=|x +a |与g (x )=x -1的图象,观
察图象可知:当且仅当-a ≤1,即a ≥-1时,不等式f (x )≥g (x )
恒成立,因此a 的取值范围是[-1,+∞).
答案:[-1,+∞)
2.已知函数f (x )=⎩⎪⎨⎪⎧ |2x -1|,x <2,3x -1
,x ≥2,若方程f (x )-a =0有三个不同的实数根,则
实数a 的取值范围为( ) A .(1,3)
B .(0,3)
C .(0,2)
D .(0,1) 解析:选D
因为方程f (x )-a =0的根,即是直线x =a 与函数f (x )=⎩⎪⎨⎪⎧
|2x
-1|,x <2,
3
x -1,x ≥2的图象交点的横坐标,画出函数图象进行观察可以得知,a 的取值范围是(0,1).。
