拱桥的计算例题
专题6:拱桥问题

专题6:拱桥问题一、拱桥问题1.右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加__________m。
2.如右图所示,有一座拱桥圆弧形,它的跨度为60米,拱高为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,•是否采取紧急措施?3.如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.则两盏景观灯之间的水平距离_________.4.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10 s时和26 s时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____________ s.5.一位运动员投掷铅球的成绩是14m,当铅球运行的水平距离是6m时达到最大高度4m,若铅球运行的路线是抛物线,则铅球出手时距地面的高度是m.二、能否通过问题1.一座拱桥的轮廓是抛物线型,拱高6m,跨度16m,为了安全起见,分别在桥的两侧安装如图1所示的不锈钢护栏(护栏包括支柱和衡量),相邻两支柱间的距离均为4m.(1)如图所示建立直角坐标系,求这条抛物线的函数表达式;(2)求安装护栏所需钢管的总长度;(3)拱桥下地平面是双向行车道,其中的一条行车道能否并排行驶宽2.4m,高3m的两辆汽车(汽车间的间隔忽略不计)?请说说你的理由.2.有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.(1)在如图1所示的坐标系中,求抛物线的解析式;(2)在正常水位基础上,当水位上升h(m)时,桥下水面的宽度为d(m),试写出用d表示h 的函数解析式;(3)设正常水位时桥下的水深2m,且桥下水面的宽度不得小于18m才能保证过往船只顺利通行,当水深超过多少米时,会影响过往船只在桥下通行?3.某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.(1)建立如图的平面直角坐标系,求此抛物线的解析式;(2)此球能否准确投中?(3)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?。
中考数学高频考点突破:实际问题与二次函数——拱桥问题

中考数学高频考点突破:实际问题与二次函数——拱桥问题一、选择题1.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )A.2.76米B.7米C.6米D.6.76米2.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=−0.01(x−20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )A.5米B.4米C.2.25米D.1.25米3.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面 1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )A.4√3米B.5√2米C.2√13米D.7米二、填空题4.如图所示是一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的髙度相同,则小强骑自行车通过拱梁部分的桥面OC共需秒.5.一个拱形桥架可以近似看做是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成的.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45∘,AC1=4米,点D2的坐标为(−13,−1.69),则桥架的拱高OH=米.6.闵行体育公园的圆形喷水池的水柱(如图1),如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度y(米)关于水平距离x(米)的函数解析式,那么圆形水池的半径至少为米时,才能使喷出的水流不落在为y=−x2+4x+94水池外.三、解答题7.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.(1) 求抛物线的解析式;(2) 一辆货运卡车高4.5m,宽2.4m,它能通过该隧道吗?8.如图是一个抛物线形拱桥示意图,已知河床宽度AB=40米,拱桥高度为10米.(1) 建立适当的坐标系,并求出抛物线的解析式;(2) 若测量得拱桥内水面宽度为28米,求拱桥内的水深.9.已知一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,且矩形的一条边长为2.5m.(1) 写出隧道截面的面积y(m2)与截面上部半圆的半径x(m)之间的函数表达式;(2) 当隧道截面上部半圆的半径为2m时,隧道截面的面积约是多少(精确到0.1m2)?10.桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A,C,B三点的抛物线,以桥面的水平线为x轴,经过抛物线的顶点C与x轴垂直的直线为y轴,建立平面直角坐标系,已知此桥垂直于桥面的相邻两柱之间的距离为2米(图中用线段AD,FG,CO,BE等表示桥柱),CO=1米,FG=2米.(1) 求经过A,B,C三点的抛物线的函数解析式;(2) 求桥柱AD的高度.11.有一个抛物线形蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为9米.4(1) 求该抛物线的解析式;(2) 若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,则横梁DE的长度是多少米?12.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m.水柱落地点D离池中心A处3m,建立适当的平面直角坐标系,解答下列问题.(1) 求水柱所在抛物线的函数解析式;(2) 求水管AB的长.13.如图为一座桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.(1) 建立平面直角坐标系,并求该抛物线的函数表达式.(2) 若水面上升1m,水面宽度将减少多少?14.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,以AB的中点O为原点,按如图②所示建立平面直角坐标系.(1) 求该抛物线对应的函数关系式;(2) 通过计算说明该货车能安全通过的最大高度.15.秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥非常令人喜爱,如图所示,玉带桥的桥拱是抛物线形,水面宽度AB=10m,桥拱最高点C到水面的距离为6m.(1) 建立适当的平面直角坐标系,求抛物线的表达式;(2) 现有一艘游船高度是 4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,通过计算说明这艘游船能否安全通过玉带桥.16.如图是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.(1) 经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填“方案一”“方案二”或“方案三”),则B点坐标是,求出你所选方案中的抛物线的表达式.(2) 因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.17.如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.(1) 画出直角坐标系xOy,并求出抛物线ADC的函数表达式;(2) 在抛物线型拱壁E,F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?18.如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1) 求足球开始飞出到第一次落地时,该抛物线的解析式.(2) 足球第一次落地点C距守门员多少米?(取4√3≈7)(3) 运动员乙要在第二个落地点D抢到足球,他应再向前跑多少米?(取2√6≈5)答案一、选择题1. 【答案】D【解析】设该抛物线的表达式为 y =ax 2,把 x =10,代入表达式得 −4=a ×102,解得 a =−125,故此抛物线的表达式为 y =−125x 2,∵ 桥下水面宽度不得小于 18m ,∴ 令 x =9 时,可得 y =−125×81=−3.24(m ), 此时水深 6+4−3.24=6.76(m ), 即桥下水深 6.76m 时正好通过, ∴ 超过 6.76m 时则不能通过.2. 【答案】C3. 【答案】B【解析】建立如图所示的平面直角坐标系,则 MN =4 米,EF =14 米,BC =10 米,DO =32 米,设大孔所在抛物线的解析式为 y =ax 2+32(a ≠0),∵BC =10 米, ∴ 点 B (−5,0),∴0=a ×(−5)2+32, ∴a =−350,∴ 大孔所在抛物线的解析式为 y =−350x 2+32,设点 A (b,0),则设顶点为 A 的小孔所在抛物线的解析式为 y =m (x −b )2, ∵EF =14 米,∴ 点 E 的横坐标为 −7, ∴ 点 E 的坐标为 (−7,−3625),当 m (x −b )2=−3625 时,解得 x 1=65√−1m +b ,x 2=−65√−1m +b , ∵MN =4 米, ∴∣∣∣∣65√−1m +b −(−65√−1m +b)∣∣∣∣=4, ∴m =−925,∴ 顶点为 A 的小孔所在抛物线的解析式为 y =−925(x −b )2,∵ 大孔水面宽度为 20 米,∴ 当 x =−10 时,y =−92, ∴−92=−925(x −b )2, ∴x 1=5√22+b ,x 2=−5√22+b ,∴ 当大孔水面宽度为 20 米时,单个小孔的水面宽度 =∣∣∣(5√22+b)−(−5√22+b)∣∣∣=5√2(米). 故选B .二、填空题4. 【答案】 36【解析】如图所示:设在 10 秒时到达 A 点,在 26 秒时到达 B , ∵10 秒时和 26 秒时拱梁的高度相同,∴A ,B 关于对称轴对称,则从 A 到 B 需要 16 秒,则从 A 到 D 需要 8 秒, ∴ 从 O 到 D 需要 10+8=18 秒, 从 O 到 C 需要 2×18=36 秒.5. 【答案】 7.24【解析】设抛物线 D 1OD 8 的解析式为 y =ax 2,将 x =−13,y =−1.69 代入,可得 a =−1100.因为横梁 D 1D 8=C 1C 8=AB −2AC 1=36 m ,所以点 D 1 的横坐标是 −18,代入 y =−1100x 2,得 y =−3.24. 因为 ∠A =45∘,所以 D 1C 1=AC 1=4 m ,所以 OH =3.24+4=7.24 m .6. 【答案】 92三、解答题7. 【答案】(1) 根据题意,A (−4,2),D (4,2),E (0,6),设抛物线的解析式为 y =ax 2+6(a ≠0),把 A (−4,2) 或 D (4,2) 代入得 16a +6=2,得 a =−14,抛物线的解析式为 y =−14x 2+6.(2) 根据题意,把 x =±1.2 代入解析式,得 y =5.64, ∵5.64>4.5,∴ 货运卡车能通过.【解析】(1) 方法二:设解析式为y=ax2+bx+c,代入A,D,E三点坐标得{16a−4b+c=216a+4b+c=2c=6,得{a=−14b=0c=6,抛物线的解析式为y=−14x2+6.8. 【答案】(1) 建立如图所示坐标系,设抛物线铁板式为y=ax2;由题意得,B(20,−10),∴−10=202a,解得a=−140,∴y=−140x2.(2) 由题意得,点D横坐标为28÷2=14,当x=14时,y=−140×142=−4.9,−4.9−(−10)=5.1.∴拱桥内的水深5.1米.9. 【答案】(1) y与x之间的函数表达式是y=12πx2+5x;(2) 当x=2时,y=12π×22+5×2=2π+10≈16.3(m2).所以隧道截面上部半圆的半径为2m时,隧道截面的面积约是16.3m2.10. 【答案】(1) 由题意可知:点C的坐标为(0,1),点F的坐标为(−4,2).设抛物线的函数解析式为y=ax2+c,所以{1=c,2=16a+c,解得{a=116,c=1.所以抛物线的函数解析式为y=116x2+1.(2) 点A的横坐标为−8,当x=−8时,y=5,所以桥柱AD的高度为5米.11. 【答案】(1) 由题意可得,抛物线经过(2,94),(8,0),故{64a+8b=0,4a+2b=94,解得{a=−316,b=32,故拋物线的解析式为y=−316x2+32x.(2) 由题意可得,当y=1.5时,1.5=−316x2+32x,解得x1=4+2√2,x2=4−2√2,故DE=x1−x2=4+2√2−(4−2√2)=4√2(米).12. 【答案】(1) 以池中心A为原点,竖直安装的水管为y轴,与水管垂直的方向为x轴建立平面直角坐标系.由于在距池中心的水平距离为1m时达到最高,高度为3m,则设抛物线的解析式为y =a (x −1)2+3,代入 (3,0),求得 a =−34, 故所求的函数解析式为 y =−34(x −1)2+3(0≤x ≤3).(2) 令 x =0,则 y =94=2.25.故水管 AB 的长为 2.25 m .13. 【答案】(1) 以 C 为坐标原点建立坐标系,则 A (−6,−4),B (6,−4),C (0,0),设 y =ax 2,把 B (6,−4) 代入上式,36a +4=0,解得:a =−19,∴y =−19x 2.(2) 令 y =−3 得:−19x 2=−3,解得:x =±3√3, ∴ 若水面上升 1 m ,水面宽度将减少 12−6√3.14. 【答案】(1) 如图,A (−4,0),C (0,4),设抛物线的解析式为 y =ax 2+k (a ≠0),由题意,得 {16a +k =0,k =4,解得 {a =−14,k =4,∴ 抛物线的解析式为 y =−14x 2+4.(2) 2+0.42=2.2,当 ∣x ∣=2.2 时,y =−14×2.22+4=2.79,2.79−0.5=2.29(m ).答:该货车能够安全通行的最大高度为 2.29 m .15. 【答案】(1) 以 AB 的中点为原点,建立如下的坐标系, 则点 C (0,6),点 B (5,0).设函数的表达式为 y =ax 2+c =ax 2+6(a ≠0),将点 B 的坐标代入上式,得 0=25a +6,解得 a =−625,故抛物线的表达式为 y =−625x 2+6.(2) 设船从桥的中心进入,则其最右侧点的横坐标为 2,当 x =2 时,y =−625x 2+6=−625×4+6=12625=5.04,船的顶部高为 4.5,4.5+0.5=5<5.04,故顶部通过符合要求,故这艘游船能安全通过玉带桥.16. 【答案】(1) 方案二;(10,0);由题意知,抛物线的顶点坐标为 A (5,5),且经过点 O (0,0),B (10,0), 设抛物线的解析式为 y =a (x −5)2+5(a ≠0),把点 (0,0) 代入,得 0=a (0−5)2+5,解得a=−15.∴抛物线的解析式为y=−15(x−5)2+5.(2) 在方案二的前提下,由题意知,当x=5−3=2时,−15(x−5)2+5=165,所以水面上涨的高度为165米.17. 【答案】(1) 画出直角坐标系xOy,如图:由题意可知,抛物线ADC的顶点坐标为(6,10),A点坐标为(0,4),可设抛物线ADC的函数表达式为y=a(x−6)2+10,将x=0,y=4代入得:a=−16,∴抛物线ADC的函数表达式为y=−16(x−6)2+10.(2) 由y=8得:−16(x−6)2+10=8,解得:x1=6+2√3,x2=6−2√3,则EF=x1−x2=4√3,即两盏灯的水平距离EF是4√3米.18. 【答案】(1) 根据题意,可设足球开始飞出到第一次落地时,抛物线的解析式为y=a(x−6)2+4,将点A(0,1)代入,得36a+4=1,解得a=−112,∴足球开始飞出到第一次落地时,该抛物线的解析式为y=−112(x−6)2+4.(2) 令y=0,得−112(x−6)2+4=0,解得x1=4√3+6≈13,x2=−4√3+6<0(舍去),∴足球第一次落地点C距守门员13米.(3) 如图,足球第二次弹起后的水平距离为CD,根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),∴−112(x−6)2+4=2,解得x1=6−2√6,x2=6+2√6,∴CD=x2−x1=4√6≈10(米),∴BD=13−6+10=17(米).答:运动员乙要在第二个落地点D抢到足球,他应再向前跑17米.。
桥梁工程-拱桥计算2
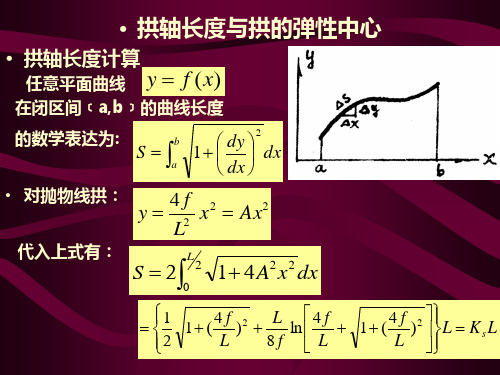
而
dx L dξ 1 1 ds = = , cos = = 2 cos 2 cos 1 + tg 1 + η 2 sh 2 kξ
1 α L2 2 2 2 2 故: 1 p = ∫ (1 ξ ) 1 + η sh kξ + (1 α ) ∫ 1 + η sh kξ dξ 4 EI α 0
S = 2∫
L
2
0
1 + 4 A x dx
2 2
1 4 f 2 L 4 f 4 f 2 = 1+ ( ) + ln + 1 + ( ) L = K s L L 8f L L 2
悬链线拱
dy L = ηshKξ , dx = dξ dx 2
1
1
S = 2∫
1
0
L 1 1 + η sh Kξ dξ = L 2 ν1
∫
∫
可分别查《拱桥》手册表Ⅲ , 可分别查《拱桥》手册表Ⅲ-9,Ⅲ-11 N = H g cos 主拱任意截面恒载弹性压缩影响内力为: 主拱任意截面恒载弹性压缩影响内力为: M = H g y
偏离内力
Q = H g sin
拱轴线偏离恒载压力线所产生的主拱内力称为偏离内力, 拱轴线偏离恒载压力线所产生的主拱内力称为偏离内力,对于大 中跨径空腹悬链拱应予考虑. 中跨径空腹悬链拱应予考虑.
分子可用分段总和法近似求取 11 MPy yi M Pi L yi M Pi L ∫ EI ds ≈ 2∑ EI cos i + i =∑ EI cos i i =1 0 ,12
拱顶控制弯矩为"+", 拱顶控制弯矩为" 拱脚为"-" 拱脚为"
人教版九年级上册数学22.3实际问题与二次函数--拱桥问题训练

人教版九年级上册数学22.3实际问题与二次函数--拱桥问题训练1.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;(2)求支柱EF的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.2.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC 为x轴,OE为y轴的直角坐标系.(1)求抛物线的解析式;(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?3.如图,隧道的截面由抛物线和长方形构成.长方形的长是8m ,宽是2m ,抛物线可以用2144y x =-+表示.()1一辆货运卡车高4m ,宽2m ,它能通过该隧道吗?()2如果该隧道内设双行道,那么这辆货运卡车是否可以通过?4.建立适当的坐标系,运用函数知识解决下面的问题:如图,是某条河上的一座抛物线形拱桥,拱桥顶部点E 到桥下水面的距离EF 为3米时,水面宽AB 为6米,一场大雨过后,河水上涨,水面宽度变为CD ,且CD=26米,此时水位上升了多少米?5.如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.(1)在如图所示的坐标系中求抛物线的解析式;(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?6.如图所示的是水面一桥拱的示意图,它的形状类似于抛物线,在正常水位时,该桥下水面宽度为20米,拱顶距离正常水面4米,建立平面直角坐标系如图所示,求抛物线的解析式.7.如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.(1)求该抛物线的表达式;(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?8.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m 时,桥洞与水面的最大距离是5m.(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填方案一,方案二,或方案三),则B点坐标是,求出你所选方案中的抛物线的表达式;(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.9.某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)如果设计成圆弧型,求该圆弧所在圆的半径;(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.10.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度)?(结果保留根号)11.如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,把拱桥的截面图放在平面直角坐标系中.(1)求抛物线对应的函数解析式,并写出自变量的取值范围;(2)求两盏景观灯之间的水平距离.12.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.(1)求抛物线的解析式;(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数关系h=-1128(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?13.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;(3)施工队计划在隧道门口搭建一个矩形脚手架CDAB,使A、D点在抛物线上.B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.14.有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图所示).(1)请你直接写出O、A、M三点的坐标;(2)一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)?15.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.(1)求该抛物线的解析式;(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?16.某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4 m,顶部C离地面高为4.4 m.(1)以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,求该抛物线对应的函数表达式;(2)现有一辆载满货物的汽车欲通过大门,货物顶点距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.17.某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,求涵洞所在抛物线的函数表达式.18.如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB =6m,建立如图所示的坐标系.(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?参考答案1.解:(1)根据题目条件,A 、B 、C 的坐标分别是(-10,0)、(10,0)、(0,6). 设抛物线的解析式为y =ax2+c ,将B 、C 的坐标代入y =ax2+c ,得60100c a c ⎧⎨⎩=,=+ 解得a =350-,c =6. 所以抛物线的表达式是y =350-x2+6. (2)可设()5F F y ,,于是2356 4.550F y -⨯=+=, 从而支柱EF 的长度是10-4.5=5.5米.(3)设DN 是隔离带的宽,NG 是三辆车的宽度和,则G 点坐标是()70,. 过G 点作GH 垂直AB 交抛物线于H ,则2376 3.06350H y -⨯==+>. 根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.2.(1)设抛物线的解析式为y =ax 2+c .∵点E (0,6),点A (﹣5,3)在此抛物线上,∴2653c a c =⎧⎨⨯-+=⎩(),得:3256a c ⎧=-⎪⎨⎪=⎩,∴此抛物线的解析式为y 2325x =-+6; (2)当x =±3时,y 23325=-⨯±+()6=4.92>4.5,即这辆货运卡车能顺利通过隧道. 3. 解:()1把422y =-=代入2144y x =-+得: 21244x =-+, 解得22x =±,∴此时可通过物体的宽度为()2222422--=>,∴能通过;()2∵一辆货运卡车高4m ,隧道的截面由抛物线和长方形构成.长方形的长是8m ,宽是2m ,∴货车上面有2m ,在矩形上面,当2y =时,21244x =-+, 解得22x =±,∵222>,∴能通过.4.以点E 为原点、EF 所在直线为y 轴,垂直EF 的直线为x 轴建立平面直角坐标系,根据题意知E (0,0)、A (﹣3,﹣3)、B (3,﹣3),设y=kx 2(k <0),将点(3,﹣3)代入,得:k=﹣13, ∴y=﹣13x 2, 将6代入,得:y=﹣2,∴上升了1米.5.解:(1)设所求抛物线的解析式为y =ax 2.∵CD =10 m ,CD 到拱桥顶E 的距离仅为1 m ,∴C (-5,-1).把点C 的坐标代入y =ax 2,得a =-,故抛物线的解析式为y =-x 2.(2)∵AB 宽20 m ,∴可设A (-10,b).把点A 的坐标代入抛物线的解析式y =-x 2中,解得b =-4,∴点A 的坐标为(-10,-4).设AB 与y 轴交于点F ,则F (0,-4),∴EF =3 m.∵水位以每小时0.3 m 的速度上升,∴3÷0.3=10(时).答:从正常水位开始,持续10小时到达警戒线.6.试题解析:设抛物线解析式为2y ax =,把点()104B -,代入解析式得:2410a -=⨯, 解得:125a =-, ∴抛物线的解析式为2125y x =-. 7.试题分析:(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;(2)令x=10,求出y 与6作比较;(3)求出y=8.5时x 的值即可得.试题解析:(1)根据题意,该抛物线的顶点坐标为(6,10),设抛物线解析式为:y=()26a x -+10,将点B (0,4)代入,得:36a+10=4,解得:a=16-, 故该抛物线解析式为y=()2166x --+10; (2)根据题意,当x=6+4=10时,y=16-×16+10=223>6, ∴这辆货车能安全通过.(3)当y=8.5时,有:()2166x --+10=8.5, 解得:1x =3,2x =9,∴2x ﹣1x =6,答:两排灯的水平距离最小是6米.考点:二次函数的应用.8.:解:方案1:(1)点B 的坐标为(5,0),设抛物线的解析式为:(5)(5)y a x x =+-.由题意可以得到抛物线的顶点为(0,5),代入解析式可得:15a =-,∴抛物线的解析式为:1(5)(5)5y x x =-+-; (2)由题意:把3x =代入1(5)(5)5y x x =-+-,解得:165y ==3.2,∴水面上涨的高度为3.2m .方案2:(1)点B 的坐标为(10,0).设抛物线的解析式为:(10)y ax x =-.由题意可以得到抛物线的顶点为(5,5),代入解析式可得:15a =-,∴抛物线的解析式为:1(10)5y x x =--; (2)由题意:把2x =代入1(10)5y x x =--解得:165y ==3.2,∴水面上涨的高度为3.2m . 方案3:(1)点B 的坐标为(5, 5-),由题意可以得到抛物线的顶点为(0,0).设抛物线的解析式为:2y ax =,把点B 的坐标(5, 5-),代入解析式可得:15a =-, ∴抛物线的解析式为:21y x 5=-; (2)由题意:把3x =代入21y x 5=-解得:95y =-= 1.8-,∴水面上涨的高度为5 1.8-=3.2m . 9.解析:(1)抛物线的解析式为y=ax 2+c ,又∵抛物线经过点C (0,8)和点B (16,0),∴0=256a+8,a=-132. ∴抛物线的解析式为y=-132x 2+8(-16≤x≤16); (2)设弧AB 所在的圆心为O ,C 为弧AB 的中点,CD ⊥AB 于D ,延长CD 经过O 点,设⊙O 的半径为R ,在Rt △OBD 中,OB 2=OD 2+DB 2∴R 2=(R-8)2+162,解得R=20;(3)①在抛物线型中设点F (x ,y )在抛物线上,x=OE=16-4=12,EF=y=3.5米;②在圆弧型中设点F′在弧AB 上,作F′E′⊥AB 于E′,OH ⊥F′E′于H ,则OH=D E′=16-4=12,O F′=R=20,在Rt △OH F′中,H F′= 222012-,∵HE′=OD=OC -CD=20-8=12,E′F′=HF′-HE′=16-12=4(米)∴在离桥的一端4米处,抛物线型桥墩高3.5米; 圆弧型桥墩高4米.10.解:(1)由图可设抛物线的解析式为:y=ax 2+2,由图知抛物线与x 轴正半轴的交点为(2,0),则:a×22+2=0, ∴a=﹣,∴抛物线的解析式为y=﹣x 2+2;(2)当y=1.60时,知1.6=﹣x 2+2,解得:x=,所以门的宽度最大为2×=米. 考点:二次函数的应用.11.(1)抛物线的顶点坐标为(5,5),与y 轴交点坐标是(0,1),设抛物线的解析式是y =a(x ﹣5)2+5,把(0,1)代入y =a (x ﹣5)2+5,得:a =﹣425,∴y =﹣425(x ﹣5)2+5(0≤x ≤10),即2481255y x x =-++(0≤x ≤10); (2)由已知得两景观灯的纵坐标都是4,∴4=﹣425(x ﹣5)2+5,∴425(x ﹣5)2=1,∴x 1=152,x 2=52,∴两景观灯间的距离为 152﹣52=5米. 12.二次函数的应用,待定系数法,曲线上点的坐标与方程的关系.(1)根据抛物线特点设出二次函数解析式,把B 坐标代入即可求解.(2)水面到顶点C 的距离不大于5米时,即水面与河底ED 的距离h 至多为6,把6代入所给二次函数关系式,求得t 的值,相减即可得到禁止船只通行的时间.13.(1)∵M (12,0),P (6,6).∴设这条抛物线的函数解析式为y=a(x -6)2+6,∵把(0,0)代入解得a=-16, ∴这条抛物线的函数解析式为y=-16(x -6)2+6, 即y=-16x 2+2x (0≤x≤12); (2)当x=6-0.5-2.5=3(或x=6+0.5+2.5=9)时,y=4.5<5∴不能行驶宽2.5米、高5米的特种车辆;(3)设点A的坐标为(m,-16m2+2m),∴OB=m,AB=DC=-16m2+2m根据抛物线的轴对称可得OB=CM=m,∴BC=12-2m,即AD=12-2m∴L=AB+AD+DC=-13m2+2m+12=-13(m-3)2+15∴当m=3,即OB=3米时,三根木杆长度之和L的最大值为15米.14.解:(1)0(0,0),A(6,0),M(3,3).(2)设抛物线的关系式为y=a(x-3)2+3,因为抛物线过点(0,0),所以0=a(0-3)2+3,解得a=,所以,要使木板堆放最高,依据题意,得B点应是木板宽CD的中点,把x=2代入,得,所以这些木板最高可堆放米.15.解:(1)由题意得M(0,4),F(4,0)可设抛物线的解析式为y=ax2+4,将F(4,0)代入y=ax2+4中,得a=-14,∴抛物线的解析式为y=-14x2+4;(2)当x=3,y=74, 74+2-12=3.25>3.2,∴能安全通过; (3)由GH=n ,可设H (24216n n -+,), ∴GH+GA+BH=n+(2416n -+)×2+2×2=21128n n -++, ∴L=21128n n -++, ∵a <0,抛物线开口向下,∴当n=-2b a=4时,L 有最大值,最大值为14. 16.解:(1)如图,过AB 的中点作AB 的垂直平分线,建立平面直角坐标系.点A ,B ,C 的坐标分别为 A(-2,0),B(2,0),C(0,4.4).设抛物线的表达式为y =a(x -2)(x +2).将点C(0,4.4)代入得a(0-2)(0+2)=4.4,解得a =-1.1,∴y =-1.1(x -2)(x +2)=-1.1x 2+4.4.故此抛物线的表达式为y =-1.1x 2+4.4.(2)∵货物顶点距地面2.8 m ,装货宽度为2.4,∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.将x =1.2代入抛物线,得 y =2.816>2.8,∴点(-1.2,2.8)和点(1.2,2.8)都在抛物线内.∴这辆汽车能够通过大门.17.解:设此抛物线所对应的函数表达式为:2y ax =,∵ 1.6AB m =,涵洞顶点O 到水面的距离为2.4m ,∴A 点坐标应该是()0.8, 2.4--,把A 点代入得:22.4(0.8)a -=-⨯, 解得:154a =-,故涵洞所在抛物线的函数表达式2154y x =-. 18. (1)设抛物线形桥洞的函数解析式为y=ax 2+c , 把A (3,0),E (0,3)代入得:解得: ∴由题意得:点C 与D 的纵坐标为0.5, ∴解得:∴(米), 则水面的宽度CD 为米;(2)当x =1时,∵ ∴这艘游船能从桥洞下通过.。
净矢高和计算矢高计算例题

净矢高和计算矢高是两个与桥梁或建筑相关的概念,通常用于描述拱桥的形状和特性。
净矢高是从拱顶截面的下缘到相邻拱梁中心线的垂直距离。
以字母f表示,单位为米。
计算矢高是考虑了桥面铺装层厚度后的矢高,以字母F表示,单位也是米。
下面是一个简单的计算例题:
假设一座拱桥的净矢高为10米,桥面铺装层的厚度为0.2米。
那么,计算矢高F可以通过以下公式计算:
F = f + 2t
其中,f是净矢高,t是桥面铺装层的厚度。
将给定的数值代入公式:
F = 10 + 2×0.2
F = 10.4米
所以,该拱桥的计算矢高为10.4米。
拱桥计算

gx d 2 y1 1 d 2M 2 2 dx H g dx Hg
(3)
由上式可知,为了计算拱轴线(压力线)的一般方程,需首先知道恒载 的分布规律,对于实腹式拱,其任意截面的恒载可以用下式表示:
g x g d y1 gd
拱顶处恒载强度;
(4)
拱上材料的容重。
由上式,取y1=f,可得拱脚处恒载强度 g j 为:
反双曲余弦函数对数表示
(10)
当m=1时 gx=gj,可以证明,在均布荷载作用下的压力线为二次抛 物线,其方程变为:
y1 f 2
由悬链线方程可以看出,当拱的跨度和失高确定后,拱轴线各点的坐 标取 确于拱轴系数m。其线形特征可用l/4点纵坐标y1/4的大小表示: 当
1 2
时, y1 y1/ 4 ;代
拱轴线与压力线不相符
不考虑弹性压缩
弹性压缩
1、不考虑弹性压缩的恒载内力 1)实腹拱 实腹式悬链线的拱轴线与压力线重和,恒载作用拱的任意截面存 在轴力,而无弯矩,此时拱中轴力可按以下公式计算。 在进行悬链线方程推导时有:
l12 g d k (m 1) Hg f
2
(11)
恒载水平推力Hg :利用上式有
y1
f (chk 1) m 1
(9)
上式为悬链线方程。
其中ch k为双曲余弦函数:
e k e k chk 2
对于拱脚截面有:=1,y1=f,代入式(9)可得:
chk m
通常m为已知,则可以用下式计算k值:
k ch1m ln(m m 2 1)
2、拱轴系数m值的确定 (1)实腹式拱m值的确定
m
gj gd
拱顶恒载分布集度 gd
midas拱桥算例

在此例题中为了提高熟练度在建模过程中尽量不去使用树形菜单或主菜单而是以使用图标菜单为主。
以下是为了有效地利用图标菜单将操作所需的图标在画面上给予显示的步骤。
1.在主菜单选择工具>用户定制>工具条
对新建立的横系梁激活之后,利用捕捉点功能和建立单元功能来完成纵向支撑(加强肋,Stringer)。
1.点击 选择最新建立的个体
2.点击 激活
3.点击 单元编号(Toggle on)
4.点击 建立单元
5.在单元类型选择栏确认‘一般梁/变截面梁’
6.在材料选择栏选择‘1 : Grade3’
7.在截面选择栏选择‘6 :水平斜支撑(包括纵向支撑)’
形成拱的主梁并复制构架
连接构架的两端来输入拱的主梁,并将所完成的一侧构架复制到另一侧。
1. 点击 点格、 捕捉点(Toggle off)
2.点击 标准视图
3.在单元工具条点击 建立单元
4.在单元类型选择栏确认‘一般梁/变截面梁’
5.在材料选择栏选择‘1 : Grade3’
6.在截面选择栏确认‘1 :主梁’
3.在一般的材料号输入栏确认‘1’(参考图6)
4.在类型选择栏确认‘钢材’
5.在钢材的规范选择栏选择‘GB(S)’
6.在数据库选择栏选择‘Grade3’
7.点击 键
8.用同样的方法参考上表输入虚设梁的材料
9.点击 键
图7. 截面数据的输入
1. 在材料和截面特性对话窗口(图5)选择截面表单
(或在特性工具条选择 截面)
跨 径 : 50m
设计车道数 : 2条车道
勾股定理之拱桥问题
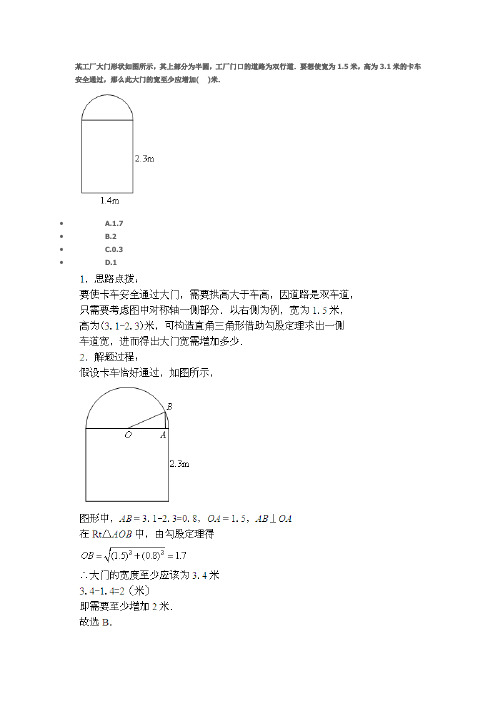
某工厂大门形状如图所示,其上部分为半圆,工厂门口的道路为双行道.要想使宽为1.5米,高为3.1米的卡车安全通过,那么此大门的宽至少应增加( )米.• A.1.7• B.2• C.0.3• D.1一辆卡车装满货物后宽3.2米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为4米的正方形),则装满货物后卡车的最大高度为( )米.• A.5.2• B.5.8• C.7.6• D.5.4如图所示,某住宅社区在相邻两楼之间修建一个上方是半圆,下方是长方形的仿古通道(AD=2.6米,AB=5米),现有一辆卡车装满家具后宽3米,卡车要通过通道,装满家具后的最大高度为____米.(上方是一个以AB为直径的半圆)如图所示,某住宅社区在相邻两楼之间修建一个上方是半圆,下方是长方形的仿古通道(AD=2.6米,AB=4米),现有一辆卡车装满家具后宽2.8米,高4米,这辆卡车能通过横截面如图所示这个通道吗?(上方是一个以AB为直径的半圆)能通过一辆装满货物的卡车,2.5米高,1.6米宽,想要开进某工厂,工厂厂门如图所示(上部分为半圆,下部分为长方形),则这辆卡车____通过.(填“能”或“不能”)答MN=1.6m,AB=2m∴OE=0.8m∵OC=OA=1m在Rt△OCE中,∴CM=2.3m+0.6m=2.9m>2.5m所以这辆卡车能通过一辆卡车装满货物后宽6.4米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为8米的正方形),则装满货物后卡车的最大高度为( )米.• A.10.4• B.11.6• C.15.2• D.10.8如图,由题意得,卡车从正中间通过的机会最大,且当卡车CDEB车顶刚好碰到隧道上方的半圆,接触点为B,E时,恰好通过,此时高度CB即为最大高度.由条件可知,,设AB为x,在Rt△OAB中,由勾股定理得,,得x=2.4,故最大高度为AB+AC=2.4+8=10.4,故选A一辆卡车装满货物后,高4米,宽2.8米.这辆卡车能通过横截面如图所示(上方是一个半圆)的隧道吗?案能通过解:∵卡车在隧道中间位置能通过的可能性最大∴如图,O为EF的中点,OE=1.4m,OG为圆的半径,OG=2m在直角△OEG中GE²=OG²-OE²=2²-1.4²=2.04∵(4-2.6)²=1.4²=1.96,2.04>1.96∴在相同宽度下隧道的高度高于卡车的高度,卡车能通过该隧道。
2024年中考数学高频考点专题复习-拱桥问题(实际问题与二次函数)

2024年中考数学高频考点专题复习-拱桥问题(实际问题与二次函数)1.某公园要修建一个截面抛物线形的拱门,其最大高度为4.5m,宽度OP为6米,现以地面(OP所在的直线)为x轴建立平面直角坐标系(如图1所示)(1)求这条抛物线的函数表达式;(2)如图所示,公园想在抛物线拱门距地面3米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?(3)为修建该拱门,施工队需搭建一个矩形“支架“ABCD(由四根木杆AB﹣BC﹣CD﹣DA组成),使B,C两点在抛物线上.A,D两点在地面OP上(如图2所示),请你帮施工队计算一下最多需要准备多少米该种木杆?2.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明.3.如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=16x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为172m.(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?4.陕北窑洞,具有十分浓厚的民俗风情和土气息. 如图所示,某窑洞口的下部近似为矩形 OABC ,上部近似为一条抛物线. 已知 3OA =米,2AB =米,窑洞的最高点 M (抛物线的顶点)高地面 OA 的距离为 258米.(1)建立如图所示的平面直角坐标系,求抛物线的表达式;(2)若在窑洞口的上部要安装一个正方形窗户DEFG ,使得点 D E 、在矩形 OABC 的边BC 上,点 F G 、在抛物线上,那么这个正方形窗户 DEFG 的边长为多少米?5.赛龙舟是中国端午节的习俗之一,也是一项广受欢迎的民俗体育运动.某地计划进行一场划龙舟比赛,图1是比赛途中经过的一座拱桥,图2是该桥露出水面的主桥拱的示意图,可看作抛物线的一部分,建立如图所示的平面直角坐标系xOy ,桥拱上的点到水面的竖直高度y (单位:m )与到点O 的水平距离x (单位:m )近似满足函数关系()20.01309y x =--+,据调查,龙舟最高处距离水面2m ,为保障安全,通过拱桥时龙舟最高处到桥拱的竖直距离至少3m .(1)水面的宽度OA =_______m ;(2)要设计通过拱桥的龙舟赛道方案,若每条龙舟赛道宽度为9m ,求最多可设计龙舟赛道的数量.6.如图,某长为800m 的隧道的横截面顶部为拋物线形,隧道的左侧是高为4m 的墙OA ,右侧是高为5m 的墙BC ,拱壁上某处离地面的高度()m y 与其离墙OA 的水平距离()m x 之间的关系满足216y x bx c =-++.现测得,OA BC 两墙体之间的水平距离为12m .(1)求该抛物线的函数关系式,并计算出拱顶D到地面OC的距离.(2)从隧道头到隧道尾,在拋物线形拱壁上安装若干排吊灯,每排吊灯与地面的距离都不低于203m32,每相邻两排吊灯之间的水平距离为2m,每排内相邻两盏吊灯之间的距离为10m.求共需要多少盏吊灯?(3)如果隧道内设双向行车道,每条车道的宽为5m,两条车道之间是宽为1m的绿化带,一辆货车载一个长方体集装箱后高为5m、宽为4m,那么这辆货车无论从哪条车道都能安全通过吗?请说明理由.7.(1)解方程:22125x x-+=(2)如图是抛物线形拱桥,当拱顶离水面2m时,水面AB宽4m.若水面上升1m,求水面的宽度.8.某公司生产A型活动板房的成本是每个3500元.图1表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长4mAD=,宽3mAB=,抛物线的最高点E到BC的距离为4m.(1)按图1中所示的平面直角坐标系,求该抛物线的函数表达式;(2)现将A型活动板房改造成为B型活动板房.如图2,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G、M在AD上,点F、N在抛物线上,窗户的成本为150元/2m.已知2mGM=,求每个B型活动板房的成本.(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)9.现要修建一条隧道,其截面为抛物线型,如图所示,线段OE 表示水平的路面,以O 为坐标原点,以OE 所在的直线为x 轴,以过点O 作垂直于x 轴的直线为y 轴,建立平面直角坐标系.根据设计要求12m OE =,该抛物线的顶点P 到OE 的距离为9m .(1)求满足设计要求的抛物线的函数解析式;(2)现需在这一隧道内壁的同样高度的A 、B 处安装上照明灯,如图所示,若要求A 、B 两个照明灯之间的水平距离为8m ,求出此时A 、B 两个照明灯距离地面的高度.10.湘雅公园人工湖上有一座拱桥,横截面呈抛物线形状,如图所示,现对此展开研究:跨度AB 为4米,桥墩露出水面的高度AE 为0.88米,在距点A 水平距离为2米的地点,拱桥距离水面的高度为2.88米,建立如图所示的平面直角坐标系,并设抛物线的表达式为()2y a x h k =-+,其中()m x 是横截水面,()m y 是拱桥距水面的高度.(1)求抛物线的表达式;(2)公园欲开设游船项目,为安全起见,公园要在水面上的C 、D 两处设置航行警戒线,并且CE DF =,要求游船能从C 、D 两点之间安全通过,则C 处距桥墩的距离CE 至少为多少米?11.如图所示的是一座古桥,桥拱为抛物线型,桥的跨径AB 为20m ,此时水位在OC 处,在水面以上的桥墩AO BC ,都为2m ,桥拱最高点P 离水面6m .以OC 所在的直线为x 轴、AO 所在的直线为y 轴建立平面直角坐标系.(1)求此桥拱所在抛物线的表达式.(2)当水位上涨2m 时,若有一艘船在水面以上部分高3m ,宽10.8m ,问此船能否通过桥洞?请说明理由. 12.一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为 2m ,隧道最高点P 位于AB 的中央且距地面6m ,建立如图所示的坐标系.(1)求抛物线的表达式;(2)一辆货车高4m ,宽4m ,能否从该隧道内通过,为什么?13.即墨古城某城门横断面分为两部分,上半部分为抛物线形状,下半部分为正方形(OMNE 为正方形),已知城门宽度为4米,最高处离地面6米,如图1所示,现以O 点为原点,OM 所在的直线为x 轴,OE 所在的直线为y 轴建立直角坐标系.(1)求出上半部分抛物线的函数表达式,并写出其自变量的取值范围;(2)有一辆宽3米,高4.5米的消防车需要通过该城门进入古城,请问该消防车能否正常进入?(3)为营造节日气氛,需要临时搭建一个矩形“装饰门”ABCD ,该“装饰门”关于抛物线对称轴对称,如图2所示,其中AB ,AD ,CD 为三根承重钢支架,A 、D 在抛物线上,B ,C 在地面上,已知钢支架每米50元,问搭建这样一个矩形“装饰门”,仅钢支架一项,最多需要花费多少元?14.如图,有一座抛物线型拱桥,在正常水位时水面宽20m AB =,当水位上升3m 时,水面宽10m CD =.(1)按如图所示的直角坐标系,求此抛物线的函数表达式;km h的速度向此桥径直驶来,当船距离此桥35km,桥下水位正好在AB处,之后水位每小时上涨(2)有一条船以5/0.25m,当水位达到CD处时,将禁止船只通行.如果该船的速度不变继续向此桥行驶35km时,水面宽是多少?它能否安全通过此桥?参考答案:1.(1)213(06)2y x x x =-+≤≤(2)33)最多需要准备11米该种木杆. 2.(1)y=-16x 2+2x .(0≤x≤12);(2)不能行驶宽2.5米、高5米的特种车辆. 3.(1)抛物线的函数关系式为y =16-x 2+2x +4,拱顶D 到地面OA 的距离为10m ;(2)可以通过(3)两排灯的水平距离最小是43m .4.(1)()2132503228y x x ⎛⎫=--+≤≤ ⎪⎝⎭ (2)1米5.(1)60(2)4条.6.(1)212510096496y x ⎛⎫=--+ ⎪⎝⎭,1009m 96 (2)486盏(3)货车无论从哪条车道都能安全通过7.(1)126,4x x ==-(2)22m8.(1)2114y x =-+ (2)每个B 型活动板房的成本为3725元9.(1)21(6)94y x =--+ (2)5m10.(1)()212 2.882y x =--+; (2)C 处距桥墩的距离CE 至少为0.8米.11.(1)抛物线解析式为()2110625y x =--+ (2)此船不能通过桥洞 12.(1) 21(4)64y x =--+;(2) 货车能通过隧道 13.(1)()2124042y x x x =-++≤≤;(2)能正常进入;(3)650元 14.(1)2125y x =- (2)水面宽是15m ,它能安全通过此桥。
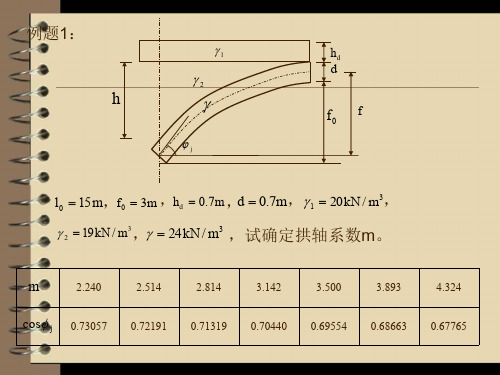
拱桥的计算例题
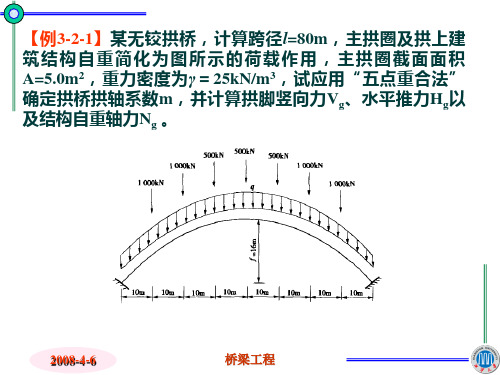
所有荷载:
所以 小于半级,因此取拱轴系数m=2.24 3)查表(III)-19得半拱悬臂自重对拱脚截面的竖向剪力为 半拱悬臂集中力对拱脚截面的竖向剪力为:
2008-4-6
桥梁工程
【例 3-2-2】某无铰拱桥,计算跨径 l=80m ,主拱圈及拱上建 筑结构自重简化为图所示的荷载作用,主拱圈截面面积 A=5.0m2 ,重力密度为 γ= 25kN/m3 ,由“五点重合法”确定 拱桥拱轴系数 m=2.24 ,截面抗弯惯矩 I=1.0m4 ,计算考虑弹 性压缩后,拱脚竖向力Vg、水平推力Hg以及结构自重轴力Ng, 以及弹性压缩引起的拱脚截面弯矩。
例322某无铰拱桥计算跨径l80m主拱圈及拱上建筑结构自重简化为图所示的荷载作用主拱圈截面面积a50m2重力密度为25knm3由五点重合法确定拱桥拱轴系数m224截面抗弯惯矩i10m4计算考虑弹性压缩后拱脚竖向力vg水平推力hg以及结构自重轴力ng以及弹性压缩引起的拱脚截面弯矩
【例 3-2-1】某无铰拱桥,计算跨径 l=80m ,主拱圈及拱上建 筑结构自重简化为图所示的荷载作用,主拱圈截面面积 A=5.0m2 ,重力密度为 γ= 25kN/m3 ,试应用“五点重合法” 确定拱桥拱轴系数m,并计算拱脚竖向力 Vg、水平推力Hg以 及结构自重轴力Ng 。
K M 19.478kN / m, K H 18.070, KV 16.879kN / m
3)根据
f / l 1 / 5, m 2.24
查《拱桥(上)》第774页的影响线面积:
M 0.01905l 2 , H 0.09067l 2 / f , V 0.16622l , N 0.44469l
2008-4-6 桥梁工程
4)拱脚最大弯矩:
midas拱桥算例

在此例题中为了提高熟练度在建模过程中尽量不去使用树形菜单或主菜单而是以使用图标菜单为主。
以下是为了有效地利用图标菜单将操作所需的图标在画面上给予显示的步骤。
1.在主菜单选择工具>用户定制>工具条
- 水平斜支撑(包括纵梁)
7 : Dummy Beam
- 虚设梁
截面1~5属于焊接制作的截面(Built-up Section)故可使用User功能,而截面6则可使用程序中内存的GB标准截面DB。
上面的虚设梁是为了指定车辆移动荷载而设的。其材料和截面可使用以下数据来输入。
Name
Type
Data
材料
3.在一般的材料号输入栏确认‘1’(参考图6)
4.在类型选择栏确认‘钢材’
5.在钢材的规范选择栏选择‘GB(S)’
6.在数据库选择栏选择‘Grade3’
7.点击 键
8.用同样的方法参考上表输入虚设梁的材料
9.点击 键
图7. 截面数据的输入
1. 在材料和截面特性对话窗口(图5)选择截面表单
(或在特性工具条选择 截面)
利用扩展单元功能将拱肋上生成的节点按竖直下方投影延长以输入吊杆。(参考图9)
1. 在单元工具条点击 扩展单元(图9的)
2.点击 节点编号(Toggle on)
3.点击 用窗口选择,选择为建立吊杆要进行投影延长的节点2~10
4.在扩展类型选择栏确认‘节点→线单元’
5.在单元属性选择栏的单元类型确认‘梁单元’
荷载条件2 : 人行道荷载 6.2 kN/m (只作用于主梁)
荷载条件3 : 车辆移动荷载 (C-AL, C-AD)
垂径定理---圆弧型拱桥问题
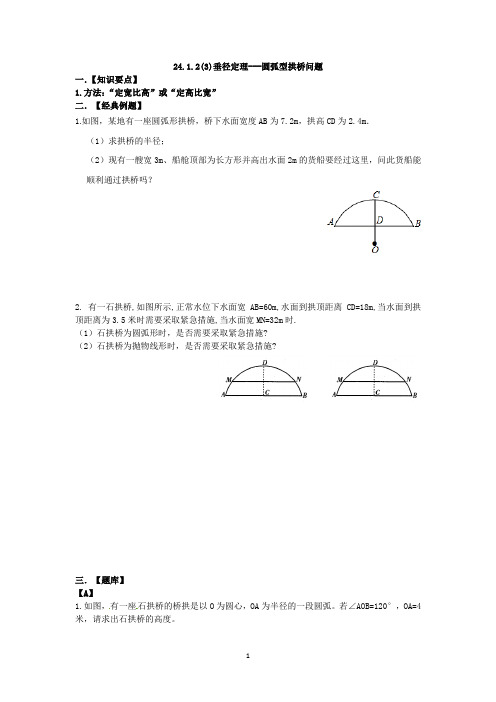
24.1.2(3)垂径定理---圆弧型拱桥问题
一.【知识要点】
1.方法:“定宽比高”或“定高比宽”
二.【经典例题】
1.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2m,拱高CD为
2.4m.
(1)求拱桥的半径;
(2)现有一艘宽3m、船舱顶部为长方形并高出水面2m的货船要经过这里,问此货船能顺利通过拱桥吗?
2.有一石拱桥,如图所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当水面到拱顶距离为
3.5米时需要采取紧急措施,当水面宽MN=32m时.
(1)石拱桥为圆弧形时,是否需要采取紧急措施?
(2)石拱桥为抛物线形时,是否需要采取紧急措施?
三.【题库】
【A】
1.如图,有一座石拱桥的桥拱是以O为圆心,OA为半径的一段圆弧。
若∠AOB=120°,OA=4米,请求出石拱桥的高度。
【B】【C】【D】
B
O
A。
1.有一抛物线形的拱形桥,其解析式为y=ax2,桥拱跨度为12m,桥高4m.按规定,通过该桥下的载货车最高处与桥拱

桥面
-5 0 5
x/m
这条抛物线的顶点坐标是 20,1. 由此可知桥面最低点到桥面的距离是1m.
•
⑵两条钢缆最低点之间的距离是多少?你是怎样计算的 ?与同伴交流. 想一想,你知道图中右面钢缆的表达式是什么吗? y 0.0225 x 2 0.9 x 10 2 y 0 . 0225 x 0.9 x 10 2
b 4ac b 由顶点坐标公式 2a , 4a b 0.9 20, 2a 2 0.0225
2
得:
2
y 0.0225 x 2 0.9 x 10
Y/m 10
桥面 -5 0 5
x/m
这条抛物线的顶点坐标是 20,1.
4ac b 2 4 0.0225 10 0.9 2 1. 4a 4 0.0225
根据对称性,如果不计其它因素,那么水池的半径至少要 2.5m,才能使喷出的水流不致落到池外 . •
喷泉与二次函数
解:(2)如图,根据题意得,A点坐标为(0,1.25),点C坐标为(3.5,0). y ●B(1.57,3.72)
●
A (0,1.25)
x
数学化
● ●
D(-3.5,0) O
C(3.5,0)
•
解: (1)
∵抛物线 y
25 2 2 ( x )2 6 5 3
2 2 ( 的顶点坐标为 , ), 5 3
∴ 运动员在空中运动的最大高度离水 面为10 2 米.
3 3 (2)当运动员距池边的水平距离为
3 8 时,即 x 3 5 2 5
时,y
此时,运动员距水面的高为: 10 16 14 5 3 3 因此,此次试跳会出现失误.
桥梁工程-拱桥计算1 - 其它内力计算分享

用GQJS程序计算某拱桥的模型图
裸拱模型图,不考虑拱上建筑联合作用 将腹拱圈与主拱一起建模,考虑拱上建筑联合作用
三、拱桥内力计算
(一)解析法计算主拱圈内力 (二)有限元法计算简介 (三)主拱附加内力计算 (四)主拱在横向力及偏心荷载作用下的计算 (五)拱上建筑的计算 (六)连拱计算简介 (七)拱桥动力及抗震计算要点 (八)主拱内力调整 (九)考虑几何非线性的主拱内力计算简介 (十)主拱圈结构验算
(二)有限元方法计算简介
等截面悬链线拱的附加内力计算
超静定拱中,温度变化、混凝土收缩变形和拱脚变位都会产 生附加内力。
我国许多地区温度变化大,温度引起的附加内力不容忽视。 混凝土收缩徐变引起拱桥开裂。 拱桥墩台变位的影响突出。据统计分析,两拱脚相对水平位
移超过L/1200时,拱桥的承载力就会大大降低,甚至破坏。
✓ 温度变化内力计算 ✓ 混凝土收缩变形影响 ✓ 拱脚变位引起的内力计算 ✓ 水浮力引起的内力计算
Ht
lt
' 22
lt '
22
(升温,t为正,反之,为负 )
升温时,轴力为正,在拱顶,
M t Ht y Ht ( y1 ys ) M为负,拱脚M为正,与该
Nt Ht cos
两截面的控制弯矩方向正好 相反,对拱圈受力有利。
Qt Ht sin
降温时,轴力为负,拱顶拱 脚的弯矩与控制弯矩方向相 同,对拱圈不利。
《公路圬工桥涵设计规范》(JTG D61-2005)
拱桥计算例题
4
N j'
Hg
cos j
1230.769 1704.879kN 0.72191
2、弹压内力计算
Nd'' 13.418kN
x
Qd '' 0kN
Md'' 13.4182.733 36.671kN m
ys S
y
N l '' 13.418 0.94042 12.619kN
4
Ql '' 13.418 0.34001 4.562kN
4
x
M l '' 13.418 0.986 13.230kN m
4
N
'' j
13.418 0.72191
9.687kN
Qj '' 13.418 0.69198 9.285kN
M
'' j
13.418 (8.125 2.733)
j
)
8.125m
Hg
M j 1230.769kN f
ys 1 f 0.336314 8.125 2.733m
d 0.260 12
1
11.0890
(
f
)2
0.011
9.16703
(
)2
0.009
f
S
1 1
Hg
13.418 kN
后保留三位有效数字。
查表已知各数据如下:1 0.336314
,1
11.0890
人教版九年级上册数学实际问题与二次函数——拱桥问题训练

5.如图所示,桥拱是抛物线形,其函数的表达式为y=﹣ ,当水位线在AB位置时,水面宽12m,这时水面离桥顶的高度为()
A.3mB. mC.4 mD.9m
6.吉林省某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距P地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)()
12.某涵洞的截面是抛物线型,如图所示,在图中建立的直角坐标系中,抛物线的解析式为 ,当涵洞水面宽 为 米时,水面到桥拱顶点 的距离为________米.
13.如图,花坛水池中央有一喷泉,水管 ,水从喷头 喷出后呈抛物线状先向上至最高点后落下,若最高点距水面 , 距抛物线对称轴 ,则为使水不落到池外,水池半径最小为________.
18.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m水面CFra bibliotek的宽是10m.
(1)求此抛物线的函数表达式.
(2)在正常水位时,有一艘宽8m、高2.5m的小船,它能通过这座桥吗?
(3)现有一艘船以每小时5km的速度向此桥径直驶来,当船距此桥35km时,桥下水位正好在AB处,之后水位每小时上涨0.25m,当水位在CD处时,将禁止船只通行.如果该船按原来的速度行驶,能否安全通过此桥?
参考答案:
1.C
2.D
3.C
4.A
5.D
6.B
7.B
8.B
9.
10.16
11.
12.
13. 米
14.6
15.
16. .
17.(1)抛物线的表达式 ,支柱EF的长度是5.5米
桥梁工程-拱桥计算2分享

Ht
lt
' 22
lt '
22
(升温,t为正,反之,为负 )
升温时,轴力为正,在拱顶,
M t Ht y Ht ( y1 ys ) M为负,拱脚M为正,与该
Nt Ht cos
两截面的控制弯矩方向正好 相反,对拱圈受力有利。
Qt Ht sin
降温时,轴力为负,拱顶拱 脚的弯矩与控制弯矩方向相 同,对拱圈不利。
(Finite Element Method)
1、有限元法在拱桥计算中的应用 (1)有限元方法是为能够求解弹性力学的偏微分
方程组(15个方程:3个平衡微分方程,6个几何方程 和6个物理方程)而发展的一种数值方法,随着计算 机的发展而得到迅速进步;
(2)用有限元方法计算三维空间的桥梁结构,可 以实现多种非线性影响的计算,例如,几何非线性、 材料非线性、动力问题及稳定问题等;
例题:
一缆索吊装施工钢筋砼拱桥,主拱合 拢温度为150C,最低气温00C,最高气温 400C,混凝土收缩内力按温度降低100C考虑, 计算考虑混凝土徐变的影响力。
《公路圬工桥涵设计规范》(JTG D61-2005)
(2)混凝土收缩影响力
《公路桥涵设计通用规范》(JTG D60-2004)
(2)混凝土收缩影响力
《公路钢筋混凝土与预应力混凝土桥涵设计规范》 (JTG D62-2004)
(2)混凝土收缩影响力
《公路钢筋混凝土与预应力混凝土桥涵设计规范》
(JTG D62-2004)
Page 57
(2)混凝土收缩影响力
《公路钢筋混凝土与预应力混凝土桥涵设计规范》
(JTG D62-2004)
Page 118-119
考虑混凝土徐变的影响
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-4-6
桥梁工程
解:
y1/4
2008-4-6
桥梁工程
【例3-2-2】某无铰拱桥,计算跨径l=80m,主拱圈及拱上建 筑结构自重简化为图所示的荷载作用,主拱圈截面面积 A=5.0m2,重力密度为γ=25kN/m3,由“五点重合法”确定 拱桥拱轴系数m=2.24,截面抗弯惯矩I=1.0m4,计算考虑弹性 压缩后,拱脚竖向力Vg、水平推力Hg以及结构自重轴力Ng, 以及弹性压缩引起的拱脚截面弯矩。
V KVV 216.8790.1662250 280.6kN N H1 cos j V sin j 819.2 0.7357 280.6 0.68284 790.1kN
2、拱脚最大负弯矩及相应轴力
1)根据
l 50m
拱脚最大负M及汽车-20查《基本资料》第79页的等代荷载:
KM 23.547kN / m, KH 10.932, KV 16.724kN / m
M1/4
1
f M j 2(m 1) 2
半拱悬臂集中力荷载作用时:
1)假定拱轴系数m=2.514, f/l=16/80 =1/5,查 表(III)-19得:
所有荷载: 所以
2008-4-6
桥梁工程
需重新计算
2)假定拱轴系数m=2.24
所有荷载:
所以 小于半级,因此取拱轴系数m=2.24
3)查表(III)-19得半拱悬臂自重对拱脚截面的竖向剪力为 半拱悬臂集中力对拱脚截面的竖向剪力为:
2)根据
f / l 1/ 5, m 2.24
查《拱桥(上)》第774页的影响线面积:
M 0.01465l2,H 0.03675l2 / f ,V 0.33378l,N 0.36216l
2008-4-6
桥梁工程
3)拱脚最大负弯矩及相应轴力:
Mmax KMM 2 23.547 0.01465502 1724.8kN m
2008-4-6
桥梁工程
解:(1)不考虑弹性压缩时Vg、Hg和Ng
(2)由弹性压缩引起的Vg、Hg和Ng
S
Hg
1 1
2008-g和Ng
2008-4-6
桥梁工程
【例3-2-3】等截面悬链线无铰拱,l=50m,f=10m,m= 2.24,桥 面宽度为净-7米,计算汽车20级荷载作用下拱脚最大正、负 弯矩及相应轴力。
H1 KHH 210.932 0.03675502 /10 200.9kN
V KVV 216.7240.3337850 558.2kN
N H1 cos j V sin j 200.9 0.73.57 558.2 0.68284 527.9kN
2008-4-6
桥梁工程
解:1、拱脚最大正弯矩及相应轴力
1)根据
f / l 1/ 5, m 2.24
查《拱桥(上)》第1010页的拱脚水平倾角的正弦和余弦:
sin j 0.68284 , cos j 0.73057
2)根据
l 50m
拱脚最大正M及汽车-20查《基本资料》第74页的等代荷载:
KM 19.478kN / m, KH 18.070, KV 16.879kN / m
3)根据
f / l 1/ 5, m 2.24
查《拱桥(上)》第774页的影响线面积:
M 0.01905l2 ,H 0.09067l2 / f ,V 0.16622l,N 0.44469l
2008-4-6
桥梁工程
4)拱脚最大弯矩:
Mmax KMM 219.478 0.01905 502 1855.3kN m H1 KHH 218.070 0.09067502 /10 819.2kN
