最短路线问题——标数法的应用
【思维拓展】数学六年级思维拓展之标数法(附答案)

六年级思维拓展之标数法求最短路线数1.阿雅和天天到图书馆参加活动。
如果他们从学校出发,共有多少种不同的最短路线?2.球球从A步行到Z,行走方向都是向右或者向下,路线如图所示。
那么球球一共有多少种不同的行走路线?3.下图是阿雅学校附近小区的平面图。
今天阿雅放学,要去同学家写作业。
请问:从学校到同学家有多少种不同的最短路线?4.B点有一群小羊在吃草,大灰狼在A点,它想到B点吃羊,最短路线有多少条?5.皮皮和天天准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,你们知道吗?6.下图是天天家附近小区的平面图。
今天下雨,路口G有积水,不能通过。
请问:今天天天从家去学校有多少种不同的最短路线可供选择?7.天天上学需要先经过K路口去买书。
请问:天天经过K路口到达学校有多少种不同的最短路线?8.如图,一只蜜蜂从A处出发,回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?9.城市街道如下图所示,有几处街区有积水不能通行。
那么从A到B的最短路线有几条?10.天天和皮皮结伴骑车去图书馆看书,他们先去公园看大熊猫再去图书馆。
聪明的小朋友们,请你帮天天和皮皮想想他们的最短路线有多少种不同的走法?参考答案1.【解答】标数法:三步走(1)确定方向;(2)从起点出发的两个方向上每个点标1;(3)其他点来源相加。
如下图所示。
一共有10种不同的最短路线。
2.【解答】分析:标数,如下图所示。
一共有13种不同的路线。
3.【解答】分析:标数,如下图所示。
一共有10种不同的路线。
4.【解答】分析:标数,如下图所示。
一共有12种不同的路线。
5.【解答】分析:标数,断点型标数法,不能通过的点打叉或者标0如下图所示。
一共有132种不同的路线。
6.【解答】分析:标数,如下图所示。
一共有11种不同的路线。
7.【解答】分析:标数,必经点型——可标“×”或者画大圈排除,简化标数图。
六年级上册数学讲义-小升初思维训练:最短路线 (解析版)全国通用

PC 第08讲最短路线教学目标:1、探索标数法在最短路径中的应用,掌握求最短路线的各种方法;2、探索最短路径的求法,总结最短路线的计算规律并加以应用;3、培养学生仔细认真的学习态度,激发学生的学习兴趣,并能提高解决实际问题的能力。
教学重点:理解并掌握“标数法”解最短路线问题。
教学难点:掌握“标数法”解较难的最短路线问题。
教学过程:【温故知新】1、两个数的和(差)与一个数相乘,可以把两个加数(被减数和减数)分别与这个数相乘,再把这两个积相加,所得的结果不变。
这叫做乘法分配律;2、如果用字母a、b分别表示两个加数,用字母c表示因数,乘法分配律可以写成:(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c;3、会运用乘法分配律进行巧算。
【巩固作业1】计算:99×29+29解析部分:在计算时,可以把算式99×29+29中的加数29看成1×29,99个29加1个29,结果正好是100个29.运用了乘法分配律。
给予新学员的建议:让学员了解乘法分配律的含义;哈佛案例教学法:鼓励学生独立完成,课堂上分享解题方法。
参考答案:99×29+29= 99×29+1×29=(99+1)×29=100×29=2900【巩固作业2】根据乘法分配律,用两种方法进行巧算:125×88。
解析部分:把88分成8×11,然后125乘8的积再乘11,运用了乘法结合律。
或者把88分成80+8,125分别去乘80和8,最后把所得积相加。
运用了乘法分配律。
给予新学员的建议:让学员熟练使用乘法分配律巧算;哈佛案例教学法:鼓励学生独立完成,课堂上分享解题方法。
参考答案:125×88 125×88=125×(8×11)=125×(80+8)=(125×8)×11 =125×80+125×8=1000×11 =10000+1000=11000 =11000【预习】一只蚂蚁在长方形格纸上的A点,它想沿着格子线走到B点玩,但是不知走哪条路最近。
标数法: 用来解决计算最短路线问题的方法,在给出的图形中

“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
7.
一只密蜂从 A 处出发, A 回到家里 B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而 不准逆行,共有多少种回家的方法?
1 A 2 3 4 5 6 7 8 9 B
8. 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出 “ APPLE ”的路线共有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
有问题跟我联系哦!wutong@ 【数学加油站答案】
1.
A E1 1 C 1 F2 3 1 D
3G 6 B
H
I
2. 首先明确三天所走的路线有什么不同?每天的路线有无限制条件?若有, 是什么?搞清 楚这些问题后,仍然用标数法求解.第一天(无限制条件)共有 16 条;第二天(必须 经过公园)共有 8 条;第三天(必须不经过公园)共有 8 条. 3. 因为 B 在 A 的右下方,由标号法可知,从 A 到 B 的最短路径上,到达任何一点的走法 数都等于到它左侧点的走法数与到它上侧点的走法数之和. 有积水的街道不可能有路线 经过,可以认为积水点的走法数是 0.接下来,可以从左上角开始,按照加法原理,依 次向下向右填上到各点的走法数.如右上图,从 A 到 B 的最短路线有 22 条.
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
标数法: 用来解决计算最短路线问题的方法,在给出的图形中 的每一个结点标出到达该点的方法 数,最后利用相加的原则求出到达目 的地的方法数。
从 A 到 B 的最短路线有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
5. 用“标数”求出:从学校到养老院共 126 条.必经过市中心的 60 条,所以可行的路有: 126 60 66 (条) .
标数法

一、加法原理概念引入生活中常有这样的情况,就是在做一件事时,有几类不同的方法,而每一类方法中,又有几种可能的做法.那么,考虑完成这件事所有可能的做法,就要用加法原理来解决.例如:王老师从北京到天津,他可以乘火车也可以乘长途汽车,现在知道每天有五次火车从北京到天津,有4趟长途汽车从北京到天津.那么他在一天中去天津能有多少种不同的走法?分析这个问题发现,王老师去天津要么乘火车,要么乘长途汽车,有这两大类走法,如果乘火车,有5种走法,如果乘长途汽车,有4种走法.上面的每一种走法都可以从北京到天津,故共有5+4=9种不同的走法.在上面的问题中,完成一件事有两大类不同的方法.在具体做的时候,只要采用一类中的一种方法就可以完成.并且两大类方法是互无影响的,那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数. 二、加法原理的定义一般地,如果完成一件事有k 类方法,第一类方法中有1m 种不同做法,第二类方法中有2m 种不同做法,…,第k 类方法中有k m 种不同做法,则完成这件事共有12 k N m m m =+++……种不同方法,这就是加法原理.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次,分类时要注意满足两条基本原则:① 完成这件事的任何一种方法必须属于某一类; ② 分别属于不同两类的两种方法是不同的方法.知识要点第8讲 标数法只有满足这两条基本原则,才可以保证分类计数原理计算正确.运用加法原理解题时,关键是确定分类的标准,然后再针对各类逐一计数.通俗地说,就是“整体等于局部之和”. 三、加法原理解题三部曲1、完成一件事分N 类;2、每类找种数(每类的一种情况必须是能完成该件事);3、类类相加树形图法、标数法及简单的递推 一、树形图法“树形图法”实际上是枚举的一种,但是它借助于图形,可以使枚举过程不仅形象直观,而且有条理又不重复遗漏,使人一目了然.【例 1】 (难度等级 ※※※)A 、B 、C 三个小朋友互相传球,先从A 开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A 手中,那么不同的传球方式共多少种?(2005年《小数报》数学邀请赛)【解析】 如图,A 第一次传给B ,到第五次传回A 有5种不同方式.同理,A 第一次传给C ,也有5种不同方式.所以,根据加法原理,不同的传球方式共有5510+=种.C B CC B AAB A B CCBA【巩固】 (难度等级 ※※※)一只青蛙在A ,B ,C 三点之间跳动,若青蛙从A 点跳起,跳4次仍回到A 点,则这只青蛙一共有多少种不同的跳法?【解析】 6种,如图,第1步跳到B ,4步回到A 有3种方法;同样第1步到C 的也有3种方法.根据加法原理,共有336+=种方法.AA A BCAB C BA【例 2】 (难度等级 ※※※)甲、乙二人打乒乓球,谁先连胜两局谁赢,若没有人连胜头两局,则谁先胜三局谁赢,打到决出输赢为止.问:一共有多少种可能的情况?【解析】 如下图,我们先考虑甲胜第一局的情况:图中打√的为胜者,一共有7种可能的情况.同理,乙胜第一局也有 7种可能的情况.一共有 7+7=14(种)可能的情况.二、标数法适用于最短路线问题,需要一步一步标出所有相关点的线路数量,最终得到到达终点的方法总数.标数法是加法原理与递推思想的结合.【例 3】 (难度等级 ※※)如图所示,沿线段从A 到B 有多少条最短路线?GFE D C BA111064332111AB【解析】 图中B 在A 的右上方,因此从A 出发,只能向上或者向右才能使路线最短,那么反过来想,如果到达了某一个点,也只有两种可能:要么是从这个点左边的点来的,要么是从这个点下边的点来的.那么,如果最后到达了B ,只有两种可能:或者经过C 来到B 点,或者经D 来到B 点,因此,到达B 的走法数目就应该是到达C 点的走法数和到达D 点的走法数之和,而对于到达C 的走法,又等于到达E 和到达F 的走法之和,到达D 的走法也等于到达F和到达G的走法之和,这样我们就归纳出:到达任何一点的走法都等于到它左侧点走法数与到它下侧点走法数之和,根据加法原理,我们可以从A点开始,向右向上逐步求出到达各点的走法数.如图所示,使用标号方法得到从A到B共有10种不同的走法.【巩固】(难度等级※※)如图,从A点到B点的最近路线有多少条?BA10204111111B6243310A【解析】使用标号法得出到B点的最近路线有20条.【例 4】(难度等级※※)如图,某城市的街道由5条东西向马路和7条南北向马路组成,现在要从西南角的A处沿最短的路线走到东北角B出,由于修路,十字路口C不能通过,那么共有____种不同走法.AA【解析】本题是最短路线问题.要找出共有多少种不同走法,关键是保证不重也不漏,一般采用标数法.如上图所示,共有120种.另解:本题也可采用排除法.由于不能经过C,可以先计算出从A到B的最短路线有多少条,再去掉其中那些经过C的路线数,即得到所求的结果.对于从A到B的每一条最短路线,需要向右6次,向上4次,共有10次向右或向上;而对于每一条最短路线,如果确定了其中的某6次是向右的,那么剩下的4次只能是向上的,从而该路线也就确定了.这就说明从A到B的最短路线的条数等于从10次向右或向上里面选择6次向右的种数,为610C.一般地,对于m n⨯的方格网,相对的两个顶点之间的最短路线有mm nC+种.本题中,从A到B的最短路线共有610C种;从A到C的最短路线共有26C种,从C到B的最短路线共有24C种,根据乘法原理,从A到B且必须经过C的最短路线有2264C C⨯种,所以,从A到B且不经过C的最短路线有622106421090120C C C-⨯=-=种.【例 5】(难度等级※※※)如图所示,从A点到B点,如果要求经过C点或D点的最近路线有多少条?【解析】1、方格图里两点的最短路径,从位置低的点向位置高的点出发的话,每到一点(如C、D点)只能向前或者向上.2、题问的是经过C点,或者D点;那么A到B点就可以分成两条路径了A--C---B;A---D---B,那么也就可以分成两类.但是需要考虑一个问题——A到B点的最短路径会同时经过C和D点吗?最短路径只能往上往前,经过观察发现C、D不会同时出现在最短路径上了.3、A---C---B,那么C就是必经之点了,就需要用到乘法原理了.A---C,最短路径用标数法标出,同样C---B点用标数法标注,然后相乘A---D---B,同样道理.最后结果是735+420=1155条.【例 6】如图1为一幅街道图,从A出发经过十字路口B,但不经过C走到D的不同的最短路线有条.【解析】到各点的走法数如图2所示.ACBD1118126666633211DB CA图1图2所以最短路径有18条.【例 7】小王在一年中去少年宫学习56次,如图所示,小王家在P点,他去少年宫都是走最近的路,且每次去时所走的路线正好互不相同,那么少年宫在________点处.EC【解析】本题属最短路线问题.运用标数法分别计算出从小王家P点到A、B、C、D、E点的不同路线有多少条,其中,路线条数与小王学习次数56相等的点即为少年宫.因为,从小王家P点到A点共有不同线路84条;到B点共有不同线路56条;到C点共有不同线路71条;到D点共有不同线路15条;到E点共有不同线路36条.所以,少年宫在B点处.【例 8】(难度等级※※※)在下图的街道示意图中,有几处街区有积水不能通行,那么从A 到B的最短路线有多少种?AB1111111111455511136162151422 1111 1311B A【解析】因为B在A的右下方,由标号法可知,从A到B的最短路径上,到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和.有积水的街道不可能有路线经过,可以认为积水点的走法数是0.接下来,可以从左上角开始,按照加法原理,依次向下向右填上到各点的走法数.如右上图,从A到B的最短路线有22条.【例 9】(难度等级※※※)在下图的街道示意图中,C处因施工不能通行,从A到B的最短路线有多少条?CBA6033311122221111CBA【解析】 因为B 在A 的右上方,由标号法可知,从A 到B 的最短路径上,到达任何一点的走法数都等于到它左侧点的走法数与到它下侧点的走法数之和.而C 是一个特殊的点,因为不能通行,所以不可能有路线经过C ,可以认为到达C 点的走法数是0.接下来,可以从左下角开始,按照加法原理,依次向上向右填上到各点的走法数.如图,从A 到B 的最短路线有6条.【巩固】 (难度等级 ※※※)在下图的街道示意图中,C 处因施工不能通行,从A 到B 的最短路线有多少种?CB A【解析】 因为B 在A 在右下方,由标号法可知,从A 到B 的最短路径上,到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和.而C 是一个特殊的点,因为不能通行,所以不可能有路线经过C ,可以认为到达C 点的走法数是0.接下来,可以从左上角开始,按照加法原理,依次向下向右填上到各点的走法数.如图,从A 到B 的最短路线有6条.【例 10】 (难度等级 ※※※)如下表,请读出“我们学习好玩的数学”这9个字,要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻),这里共有多少种完15111310146151132【解析】 方法一:标数法.第一个字只能选位于左上角的“我”,以后每一个字都只能选择前面那个字的下方或右方的字,所以本题也可以使用标号法来解:(如右上图,在格子里标数)共70种不同的读法.方法二:组合法.仔细观察我们可以发现,按“我们学习好玩的数学”走的路线就是向右走四步,向下走四步的路线,而向下和向右一个排列顺序则代表了一种路线.所以总共有4870C 种不同的读法.【例 11】 (难度等级 ※※※)如图,沿着“北京欢迎你”的顺序走(要求只能沿着水平或竖直方向走),一共有多少种不同的走法?北北京北北京欢京北欢迎欢你113112*********【解析】 沿着“北京欢迎你”的顺序沿水平或竖直方向走,北以后的每一个字都只能选择上面的或左右两边的字,按加法原理,用标号法可得右上图.所以一共有11种走法.【巩固】 (难度等级 ※※※)如下表,请读出“我们学习好玩的数学”这9个字,要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻),这里共有多少351511113451014610151512013570321【解析】第一个字只能选位于左上角的“我”,以后每一个字都只能选择前面那个字的下方或右方的字,所以本题也可以使用标号法来解:(在格子里标数)共70种不同的读法.【例 12】(难度等级※※※)在下图中,用水平或者垂直的线段连接相邻的字母,当沿着这些线段行走是,正好拼出“APPLE”的路线共有多少条?A|A—P—A| | |A—P—P—P—A| | | | |A—P—P—L—P—P—A| | | | | | |A—P—P—L—E—L—P—P—A1|1—3 —1| | |1—2—7 —2—1| | | | |1—2—4—15—4—2—1| | | | | | | 1—2—4—8—31—8—4—2—1【解析】要想拼出英语“APPLE”的单词,必须按照“A→P→P→L→E”的次序拼写.在图中的每一种拼写方式都对应着一条最短路径.如下图所示,运用标号法原理标号得出共有31种不同的路径.【巩固】如图1,用水平线或竖直线连结相邻汉字,沿着这些线读下去,正好可以读成“祖国明天更美好”,那么可读成“祖国明天更美好”的路线有条.【解析】如图2所示,利用加法原理,将读到各个字的路线数写在每个字下方,共有不同的路线721127-=(条).祖祖国祖祖国明国祖祖国明天明国祖祖国明天更天明国祖祖国明天更美更天明国祖祖国明天更美好美更天明国祖图1祖1祖1国3祖1祖1国2明7国2祖1祖1国2明4天15明4国2祖1祖1国2明4天8更31天8明4国2祖1祖1国2明4天8更16美63更16天8明4国2祖1祖1国2明4天8更16美32好127美32更16天8明4国2祖1图2【巩固】(第三届“希望杯”2试试题)右图中的“我爱希望杯”有______种不同的读法.杯杯杯杯杯望望望望希希希爱爱我161511353211111111杯杯杯杯杯望望望望希希希爱爱我【解析】“我爱希望杯”的读法也就是从“我”走到“杯”的方法.如上右图所示,共16种方法.【例 13】如图1所示,科学家“爱因斯坦”的英文名拼写为“Einstein”,按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”.i111111i图1图2【解析】由E n s t e i n→i→→→→→→的拼法如图2所示.根据加法原理可得共有303060+=(种)不同拼法.【例 14】(难度等级※※※)图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码走到小号码,从1号房间走到10号房间共有多少种不同的走法?【解析】 我们可以把这个图展开,用箭头标出来就更直观了,然后采用我们学的标数法.【例 15】 (难度等级 ※※※)国际象棋中“马”的走法如图1所示,位于○位置的“马”只能走到标有×的方格中, 类似于中国象棋中的“马走日”.如果“马”在88⨯的国际象棋棋盘中位于第一行第二列(图2中标有△的位置),要走到第八行第五列(图2中标有@的位置),最短路线有________条.【2008年北京“数学解题能力展示”读者评选活动】第@图图1题@图2【解析】 最后一步的可能如图1,倒数第二步的可能如图2,倒数第三步的可能如图3.最后36312++=(种).图3图2@11112122图1@111122163321111@【例 16】 (难度等级 ※※※)从北京出发有到达东京、莫斯科、巴黎和悉尼的航线,其他城市间的航线如图所示(虚线表示在地球背面的航线),则从北京出发沿航线到达其他所有城市各一次的所有不同路线有多少?【解析】 第一站到东京的路线有10条:⎧⎪⎪⎪⎧→→⎪→⎨⎪→→⎩⎪⎪⎧⎧→→⎪⎪⎨→⎪⎪⎩→→→⎨⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎪⎪⎧⎧→⎪→⎪⎨⎪→⎪⎩→⎪⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎩莫斯科巴黎悉尼纽约悉尼巴黎莫斯科巴黎悉尼纽约悉尼巴黎北京东京莫斯科纽约悉尼巴黎悉尼纽约巴黎莫斯科纽约莫斯科巴黎悉尼纽约莫斯科巴黎莫斯科纽约 同理,第一站到悉尼、巴黎、莫斯科的路线各有10条,不同的路线共有10440⨯=条.【例 17】 一个实心立方体的每个面分成了四部分.如图所示,从顶点P 出发,可找出沿图中相连的线段一步步到达顶点Q 的各种路径.若要求每步沿路径的运动都更加靠近Q ,则从P 到Q 的各种路径的数目为几?QP1818666333322111111QP【解析】因为正方体每个面的对面也有同样的路径,最靠近Q 的有三个点,从P 点到这三个点都是18种路径.故有18354⨯=三、简单递推:斐波那契数列的应用对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面的数,这种方法称为递推法.【例 18】(难度等级※※※)一楼梯共10级,规定每步只能跨上一级或两级,要登上第10级,共有多少种不同走法?【解析】登1级2级3级4级 ......10级1种方法2种3种5种 ......?我们观察每级的种数,发现这么一个规律:从第三个数开始,每个数是前面两个数的和;依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用:假如我们把这个人开始登楼梯的位置看做A0,那么登了1级的位置是在A1,2级在A2... A10级就在A10.到A3的前一步有两个位置;分别是A2和A1.在这里要强调一点,那么A2到A3既然是一步到了,那么A2、A3之间就是一种选择了;同理A1到A3也是一种选择了.同时我们假设到n级的选择数就是An .那么从A0到A3就可以分成两类了:第一类:A0 ---- A1 ------ A3,那么就可以分成两步.有A1×1种,也就是A1种;(A1 ------ A3是一种选择)第二类:A0 ---- A2 ------ A3,同样道理有A2.类类相加原理:A3 = A1+A2,依次类推An = An-1 + An-2.【例 19】(难度等级※※※)1×2的小长方形(横的竖的都行)覆盖2×10的方格网,共有多少种不同的盖法.【解析】 如果用12⨯的长方形盖2n ⨯的长方形,设种数为n a ,则11a =,22a =,对于3n ≥,左边可能竖放1个12⨯的,也可能横放2个12⨯的,前者有-1n a 种,后者有-2n a 种,所以-1-2n n n a a a =+,所以根据递推,覆盖210⨯的长方形一共有89种.【例 20】 (难度等级 ※※※)如下图,一只蜜蜂从A 处出发,回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?BAAB 1357946821235813213455891【解析】 蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房.明确了行走路径的方向,就可以运用标数法进行计算.如右图所示,小蜜蜂从A 出发到B 处共有89种不同的回家方法.【巩固】小蜜蜂通过蜂巢房间,规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B 房间有多少种方法?【解析】 斐波那契数列第八项.21种.【例 21】 每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有多少对兔子?【解析】 第一个月,有1对小兔子;第二个月,长成大兔子,所以还是1对;第三个月,大兔子生下一对小兔子,所以共有2对;第四个月,刚生下的小兔子长成大兔子,而原来的大兔子又生下一对小兔子,共有3对; 第五个月,两对大兔子生下2对小兔子,共有5对; ……这个特点的说明每月的大兔子数为上月的兔子数,每月的小兔子数为上月的大兔子数,即上上月的兔子数,所以每月的兔子数为上月的兔子数与上上月的兔子数相加. 依次类推可以列出下表:经过月数:---1---2---3---4---5---6---7---8---9---10---11---12 兔子对数:---1---1---2---3---5---8--13--21--34--55--89--144 所以十二月份的时候总共有144对兔子.【例 22】 树木生长的过程中,新生的枝条往往需要一段“休息”时间供自身生长,而后才能萌发新枝.一棵树苗在一年后长出一条新枝,第二年新枝“休息”,老枝依旧萌发新枝;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则依次“休息”.这在生物学上称为“鲁德维格定律”.那么十年后这棵树上有多少条树枝?【解析】 一株树木各个年份的枝桠数,构成斐波那契数列:1,2,3,5,8,13,21,34,55,89,……所以十年后树上有89条树枝.【例 23】 对一个自然数作如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行直到得数为1操作停止.问经过9次操作变为1的数有多少个?【解析】 可以先尝试一下,倒推得出下面的图:2410131112514302831643215167683421其中经1次操作变为1的1个,即2, 经2次操作变为1的1个,即4, 经3次操作变为1的2个,是一奇一偶,以后发现,每个偶数可以变成两个数,分别是一奇一偶,每个奇数变为一个偶数,于是,经1、2、…次操作变为1的数的个数依次为:1,1,2,3,5,8,…这一串数中有个特点:自第三个开始,每一个等于前两个的和,即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢?道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1,2a =1,3a =2,… 从上面的图看出,1n a +比n a 大.一方面,每个经过n 次操作变为1的数,乘以2,就得出一个偶数,经过1n +次操作变为1;反过来,每个经过1n +次操作变为1的偶数,除以2,就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面,每个经过n 次操作变为1的偶数,减去1,就得出一个奇数,它经过1n +次操作变为1,反过来.每个经过1n +次操作变为1的奇数,加上1,就得出一个偶数,它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多.而由上面所说,前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数,分为偶数、奇数两类,所以11n n n a a a +-=+,即上面所说的规律的确成立.。
三年级下册数学试题-竞赛思维能力训练:03最短路线(三年级竞赛)教师版
B C
B48 28 14 20 14 14 5 6 C9 52
65 4 32
1
A
1 1 1 11 A
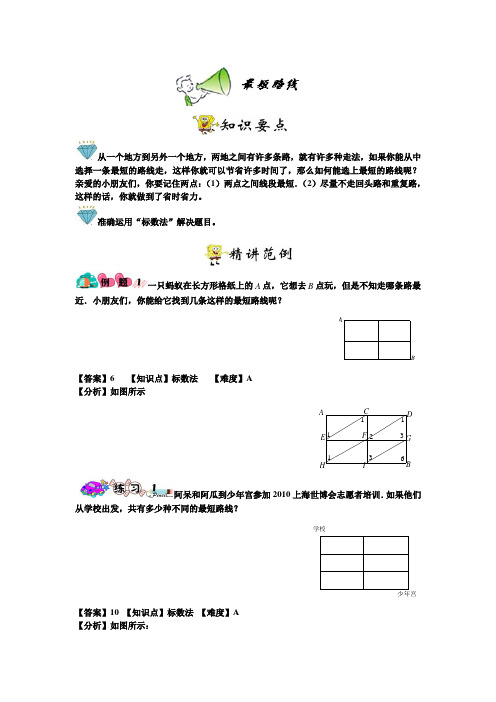
【答案】48,;1600 【知识点】标数法 【难度】C 【分析】用对角相加法,考虑到某些道路不能通行,在图形中用虚线标写出来,再在图中 依次标数,如上图所示:
所以,从 A 地到 B 地有 48 条最短路线。 从 A 地到 B 地最少要行使的距离:200×5+150×4=1600(米)
下面是一个街道的平面图,从街道的 A 地出发到 B 地,问有多少条最短路线?
【答案】18 【知识点】标数法 【难度】B 【分析】如图所示:
下图为某城市的街道示意图,C 处正在挖下水道,不能通车,从 A 到 B 处的最短路 线共有多少条?
B
【答案】431 【知识点】标数法 【难度】B 【分析】如图所示:
甲 C
A B D
乙
甲
1 11
1 2C 1
A 22 33 3
B 2 5 8 11
2D
8 19
2 2 10
2乙9
解:用虚线将不能通行的道路表示出来,再利用“对角线法”依次标数,如上图所示。 所以从甲地到乙地有 29 条最短路线。 从甲地到乙地至少要行驶的距离:5×180+320×5=2500(米)。
1
5
15
1
4
10
1
3
6
1
2
3
学校
1
1
市中心
养老院
25
40
66
10
15
26
5
11
4
5
6
1
1
1
是多少条?
如图,从 A 到 B 沿网格线不经过线段 CD 和 EF 的最短路径的条数
四年级组合计数

四年级名校第二讲组合计数——最短路线教学目标:1.让学生了解如何用标数法来解题。
2.让学生学会如何走最短路线。
3.让学生在学习中,学会数学的逻辑思维能力。
教学重点:如何用标数法解题。
教学难点:标数时我们应用什么样的方法去标数。
教学过程:导入:我们平时在出去玩的时候是不是有很多不同的路线可以选择,但是我们往往会选择一条最短的线路来走,但是事实上我们有的时候最短的路不止有一条。
这样就涉及到了我们数学当中一个非常有名的专题就是组合计数。
(出示课题)新授:例1下图是一个街道平面图,某人从A里走到B处(只能从南到北及从西到东)共有多少种不同的走法?分析:首先我们要看清楚题目,题目当中说的是只能从南到北及从西到东,那么我们只能怎么走呢?我们只能从下往上或者从左往右走。
我们可以这样想,从A点出发可以去2个地方,如果是这样我们是不是可以反过来想呢?到达那2个点只能从哪里来则我们可以这样标数。
那么从哪里来有几条路?(强调学生要注意标数的时候一定要一排一排的标,这样才能做到不重复不遗漏。
)那么我就可以这样标数,如图。
练习:演练一例2苏珊从A步行道Z,行走方向都是向东或向南,路线如图所示。
那么苏珊从A到Z有多少条不同的行走路线?分析:我们从A出发要到Z,可以随便走么?方向只能是向东或者向南,那么我们就可以用标数的方法将其标出来,这样就可以做出来了。
注意一定要一排一排的标,不能乱标。
要引导学生一个一个来。
练习:演练二例3 一直密封从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?分析:如果我们从蜂房的A出发回到B处,同学们可不可以将我们小蜜蜂的回家的路线试着画出来呢?将小蜜蜂的路线图画出来之后我们就可以用标数法将其做出来了。
例4如图所示科学家“爱因斯坦”的英文名拼写为“Einstein”,按见图所示方向有多少种不同的方法拼出英文单词“Einstein”?分析:我们在拼出英文单词的时候是不是可以随便拼写呢?我们一定要按照这个引文单词拼写的顺序来标数。
小学三年级奥数 第22讲最短路线
最短路线
【例1】(☆☆)
【课前铺垫】
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最
近。
小朋友们,你能给它找到几条这样的最短路线呢?
标数法:用来解决最短路线问题的方法,在给出的图形中的每一个结点标出
到达该点的
,。
【例2】(☆☆☆)【例3】(☆☆☆)
寒假到了,艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行。
聪明的小朋友们,请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?
1
【例4】(☆☆☆☆)【例5】(☆☆☆☆☆)
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行,共有多少种回家的方法?
【例6】(☆☆☆☆☆)
城市街道如下图所示,有几处街区有积水不能通行,那么从A到B的最
短路线有几条?
【本讲总结】
最短路线
宗旨:不走冤枉路,就要朝着目标走
方法:标数法
标数法四步:
1.找目标、定方向
2.从起点标数,起点标1
3.按顺序每个点都要标到
4.某点数字=指向该点箭头
尾巴上的数字相加
注意:
.坏点可以划去或看成
2.必须经过,分段标出
2。
标数法与牛顿台阶问题
标数法与牛顿台阶问题关于“标数法”,先来看两个最简单的例子。
例1:从A到B的最短路径有多少条?B1楚香凝解析:从A到C有一种路径,所以在C点标记个“1”;从A到D有一种路径,所以在D点也标记一个1;到B点有两类情况,可以从C过来,也可以从D过来,所以到达B点的情况数;(到达C点的情况数)+ (到达D点的情况数),所以在B点标记1+1="2”。
例2:从A到B的最短路径有多少条?楚香凝解析:从A到C有一种路径,所以在C点标记个“1”;从A到D有一种路径,所以在D点也标记一个1;到E点有两类情况,可以从C过来,也可以从D过来,所以在E 点标记1+1="2";从A到F有一种路径,所以在F点标记个“1”;到B点有两类情况,可以从F过来,也可以从E过来,所以在B点标记1+2="3”。
注意:标数法适用的前提条件为“最短路径”,更通俗来讲,即不能走“回头路”。
下面来看近几年出现过的三道真题。
例1:A、B、Cm地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路。
如要从A地到达B地,且途中只能向南、东和东南方向行进,有多少种不同的走法:【山东2014】A.9B.11C.13D.15楚香凝解析:标数法,共15种,选D例2:从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择?【黑龙江2015】A.14B.15C.18D.21楚香凝解析:标数法,共15种,选B例3:下图为某大厦走火通道逃离路线。
某大厦集中所有的人员开展火灾逃生演习,从入口A点出发,要沿某几条线段才到出口F点。
逃离中,同一个点或同一线段只能经过1 次。
假设所有逃离路线都是安全的,则不同的逃离路线最多有()种。
【广州2015】A.8B.9C.10D.11应闲B 匚『出口楚香凝解析:此题与标数法的区别在于,可以往上和斜上走,所以标数法不再适用,需分类计算;A―D,之后有四种;A—B―D,之后有三种;A—B―C,之后有三种;共10种,选C牛顿台阶问题(斐波那契递推数列)例1:十阶楼梯,小张每次只能走一阶或者两阶,请问走完此楼梯共有多少种方法?A.55B.67C.74D.89楚香凝解析:解法一:列举找规律;阶梯数:1 2 3 4 5 6 7 8 9 10方法数: 1 2 3 5 8 13 21 34 55 89走到1阶只有1种方法;走到2阶有2种(1+1或直接上2阶);走到3阶有3种(1+1+1 或1+2或2+1)…依次类推,选D解法二:到达第十阶的前一步只有两类情况:【从第九阶迈一步上来】或者【从第八阶迈两步上来工所以到达第十阶的情况数二(到达第九阶的情况数)+ (到达第八阶的情况数),以此类推,到达某阶的情况数等于前面两个数之和(前两项通过列举得到),由此可得斐波那契递推数列 1、2、3、5、8、13、21、34、55、89,选 D解法三:分类计算;走五次两阶、共五步,有1种;走四次两阶、共六步,选出四步来走两阶,有C (6 4) =15种;走三次两阶、共七步,选出三步来走两阶,有C (7 3) =35种;走两次两阶、共八步,选出两步来走两阶,有C (8 2) =28种;走一次两阶、共九步,选出一步来走两阶,有C (9 1)=9种;走0次两阶,有1种;共 1+15+35+28+9+1=89 种,选 D拓展:十阶楼梯,小张每次只能走一阶或者两阶或者三阶,请问走完此楼梯共有多少种 方法?A.89B.169C.230D.274楚香凝解析:到达第十阶的情况数=(到达第九阶的情况数)+(到达第八阶的情况数) + (到达第七阶的情况数),以此类推…到达某阶的情况数等于前面三个数之和(前三项通过 列举得到),由此可得斐波那契递推数列如下:阶梯数:1 2 3 4 5 6 7 8 9 10方法数: 1 2 4 7 13 24 44 81 149 274例2:小璐有8元钱,她准备从明天起,用这8元钱每天买一个冰激淋或者一包果冻吃。
matlab最短路径问题标号法

一、介绍MATLAB是一种非常流行的数学建模和仿真软件,被广泛应用于工程、科学和金融领域。
在MATLAB中,最短路径问题是一个常见的优化问题,通常会涉及到图论、线性代数和优化算法等知识。
在解决最短路径问题时,我们常常需要使用标号法来求解,本文将对MATLAB中最短路径问题的标号法进行介绍。
二、什么是最短路径问题最短路径问题是指在一个加权有向图或无向图中寻找两个顶点之间的最短路径。
在实际应用中,最短路径问题通常涉及到网络规划、路线规划、物流配送等方面。
我们需要求解城市之间的最短路径来设计公交线路,或者求解货物在仓库之间的最短路径来优化物流方案。
三、最短路径问题的标号法在MATLAB中,我们可以使用标号法(Label Correcting Algorithm)来求解最短路径问题。
标号法是一种基于节点标号的启发式算法,它通过不断更新节点的标号信息来逐步搜索最短路径。
下面是标号法的基本思路:1. 初始化:我们需要对图中的节点进行初始化,设置起点的标号为0,其他节点的标号为无穷大。
2. 标号更新:我们开始不断更新节点的标号。
对于每个节点,我们计算通过它能够到达的节点的距离,并将这些距离与当前节点的标号进行比较。
如果通过当前节点到达某个邻居节点的路径距离更短,则更新该邻居节点的标号为当前节点的标号加上当前节点到邻居节点的距离。
3. 节点选择:在标号更新的过程中,我们需要选择一个未加入最短路径的节点,并将其标记为已加入最短路径。
这个过程通常会涉及到优先级队列等数据结构的使用,以便快速找到最短路径的下一个节点。
4. 终止条件:当所有节点都已加入最短路径,或者找到目标节点时,算法终止,最短路径即为标号信息所指示的路径。
四、MATLAB实现最短路径问题的标号法在MATLAB中,我们可以利用图论工具箱和优化工具箱来实现最短路径问题的标号法。
下面是一个简单的MATLAB示例:```matlab创建图N = 5; 节点数E = [1, 2; 1, 3; 2, 3; 2, 4; 3, 4; 3, 5; 4, 5]; 边集L = [1, 2, 3, 4, 5]; 标号W = [1, 2, 3, 4, 5, 6, 7]; 权重G = digraph(E(:, 1), E(:, 2), W);最短路径求解[s, t] = deal(1, N); 起点和终点[P, D] = graphshortestpath(G, s, t, 'Method', 'positive');```在这个例子中,我们首先创建了一个有向图G,并指定了节点数N、边集E、节点标号L和边权重W。
第24讲 最短路线问题

小升初面试第二阶段数学课程---最短路线问题第一部分思维提升(45分钟)在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
方法:1、两点之间,线段最短;连接两点之间的线段,为两点之间的最短路线;A、B两点在直线CD的同侧,做A点关于直线CD的对称点A’,连接A’与B的线段与直线CD交于E点,则AE+BE最短;2、标数法:适用于求从点A到点B的最短路线的条数;从起点到达任何一点的最短路线数,都等于从起点出发到达与这一点相邻的点的最短路线数之和。
本质上是利用加法原理进行分类计数。
例1、直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线长度之和最短,问汽车站建在哪儿最好?例2、下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B 处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A到C只有一条路线。
最短路径问题-教案

最短路线问题一、教学对象:小学三四年级学生二、教学目标1.能够在理解的基础上准确运用“标数法”解决最短路线题目;2.能够运用“标数法”解决其他应用问题,提高学生综合运用知识解决问题的能力;3.在运用“标数法”解决最短路线问题的过程中,引导学生认识杨辉三角,通过找规律,体会数学的魅力;三、教学过程1.导入新知老师:同学们,在日常生活、工作中,我们其实经常会遇到有关行程路线的问题。
快递员送包裹,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求在走最少的路的同时能够游遍所有的景点。
而这些的问题,就是我们今天所要研究学习的“最短路线问题”2.讲解新知最短路线的选择老师:现在请大家看向讲义开头的那一张地图(图1)。
小明同学想从A点步行到达B点,怎么走才是最省时省力的呢?对,很好,在走的路线最短的情况下。
我们常常说两点之间直线最短,但同学们也应该注意到了,在现实生活中,我们的街道常常是纵横交错的,也就是说,小明是不可以直接从A飞到B的,而只能沿着地图上的街道行走。
为了解决这样的问题,我们不妨把问题简单化一下,假设我们要走的城市街道如图(图2)。
好的,现在请同学们拿出一支铅笔画一画从A到B的最短路径,并且尝试着数一数究竟有多少条可选择的最短路径,给大家一分钟的时间,现在开始。
老师:通过尝试,我们不难发现,像城市街道这样的道路布局,两点之间往往不止一条的最短路径,而这些最短路线也有着明显的相似之处。
B在A的右上(东北)方,我们其实只要在从A到B的过程中仅选择向右走或向上走,而不选择向左走或向下走,也就是我们常说的“不走回头路”,是不是就可以保证我们走的就是最短路线呀。
运用“标数法”计算最短路线数目老师:那么,从A到B到底有多少最短路径可供我们选择呢?现在请同学们看向例1,让我们一起来解决这一问题;老师:首先,我们在位于角上的起点标上1,因为只有一种方式选择起点;然后,我们将从这个点出发向东走或者向北走所有能够到达的点上标1。
最短路径与标号法

最短路径与标号法前面我们学习过动态规划的应用,图中没明显阶段求最短路径的问题属于无明显阶段的动态规划,通常用标号法求解,求最短路径问题是信息学奥赛中很重要的一类问题,许多问题都可转化为求图的最短路径来来解,图的最短路径在图论中有经典的算法,本章介绍求图的最短路径的dijkstra算法、Floyed算法,以及标号法。
一、最短路径的算法1、单源点最短路径(dijkstra算法)给定一个带权有向图G=(V,E),其中每条边的权是一个非负实数,另外,还给定V中的一个顶点,称为源点。
求从源点到所有其他各顶点的最短路径长度。
这个问题称为单源最短路径问题。
求单源最短路径可用dijkstra算法求解。
(dijkstra算法)算法思想:设源点为x0,dist[i]表示顶点i到源点x0的最短路径长度,map[i,j]表示图中顶点i到顶点j的长度,用数组mark对所有的顶点作标记,已求出源点到达该点J的最短路径的点J记为mark[j]=true,否则标记为false。
初始时,对源点作标记,然后从未作标记的点中找出到源点路径长度最短的顶点minj,对该顶点作标记,并对其它未作标记的点K作判断:if dist[minj]+map[minj,k]<dist[k] then dist[k]= dist[minj]+map[minj,k]。
重复处理,直到所有的顶点都已作标记,这时求出了源点到所有顶点的最短路径。
算法过程:const maxn=100;varmap: array[1..maxn,1..maxn] of integer;dist: array[1..maxn] of integer;mark: array[1..maxn] of Boolean;n,k: integer;procedure dijkstra;var I,j,min,minj,temp:integer;beginfillchar(mark,sizeof(mark),0);for I:=1 to n do dist[i]:=maxint;dist[k]:=0;for I:=1 to n-1 dobeginmin:=maxint;for j:=1 to n doif (not mark[j]) and (dist[j]<min) thenbeginmin:=dist[j]; minj:=j;end;mark[minj]:=true;for j:=1 to n doif (not mar[j]) and (map[minj,j]>0) thenbegintemp:=dist[minj]+map[minj,j];if temp<dist[j] then dist[j]:=temp;end;end;end;以上只是求出了从源点到其它所有点的最短路径长度,所经过的具体路径没有保存,如果要求出具体的路径来,那么在求最短路径的过程中要将经过的中间点记录下来。
标数法

下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B 处共有多少条最短路线错误!分析:为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A →E的一种走法。
3.看G点:从上向下走是D→G,从左向右走是F→G,那么从A→G我们在G点标上数字“3”.3=2+1,“2”是从A→F的两种走法,“1”是从A→D的一种走法。
4.看I点:从上向下走是F→I,从左向右走是H→I,那么从出发点在I点标上“3”.3=2+1.“2”是从A→F的两种走法;“1”是从A→H的一种走法。
5.看B点:从上向下走是G→B,从左向右走是I→B,那么从出发点A→B 可以这样走:共有六种走法.6=3+3,第一个“3”是从A→G共有三种走法,第二个“3”是从A→I共有三种走法.在B点标上“6”。
六年级下册奥数试题——最短路线.(含答案)人教版

1. 准确运用“标数法”解决题目.2. 培养学生的实际操作能力.知识点说明从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:⑴两点之间线段最短.⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力.【例 1】一只蚂蚁在长方形格纸上的A 点,它想去B 点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?BA11613321BA IHG F E DC【解析】 (方法一)从A 点走到B 点,不论怎样走,最短也要走长方形AHBD 的一个长与一个宽,因此,在水平方向上,所有线段的长度和应等于AD ;在竖直方向上,所有线段的长度和应等于DB .这样我们走的这条路线才是例题精讲知识精讲教学目标8-8最短路线最短路线.为了保证这一点,我们就不应该走“回头路”,只能向右和向下走.所有最短路线:→→→→→→→→、A E F G B→→→→、A C F G BA C D G B→→→→→→→→、A E H I BA C F I B→→→→、A E F I B这种方法不能保证“不漏”.如果图形再复杂些,做到“不重”也是很困难的.(方法二)遵循“最短路线只能向右和向下走”,观察发现这种题有规律可循.①看C点:只有从A到C的这一条路线.同样道理:从A到D、从A到E、从A到H也都只有一条路线.我们把数字“1”分别标在C D E H、、、这四个点上.②看F点:从A点出发到F,可以是A C F→→,也可以是→→,共有两种走法.那么我们在F点标上数字“2”(2=11+).③A E F看G点:从A G→→→、A C F G→→→、→有三种走法,即:A C D G→→→.在G点标上数字“3”(3=12+).④看I点:共有三种走A E F G法,即:A C F I→→→,在I点标上“3”→→→、A E H I→→→、A E F I(3=12+).⑤看B点:从上向下走是G B→,那么从→,从左向右走是I B 出发点A B→→→→、→→→→、A C F G B→有六种走法,即:A C D G B→→→→、A E H I B→→→→、A E F I B→→→→,→→→→、A C F I BA E F G B在B点标上“6”(633=+),观察发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到这点的所有最短路线的条数.此法能够保证“不重”也“不漏”,这种方法叫“对角线法”或“标号法”.【巩固】如图所示,从A点沿线段走最短路线到B点,每次走一步或两步,共有多少种不同走法?AB【解析】 这是一个较复杂的最短路线问题,我们退一步想想,先看看简单的情况.从A 到B 的各种不同走法中先选择一条路线来分析:如果按路线A →C →D →E →F →B 来走,这条路线共有5条线段,每次走一步或两步,要求从A 走到B ,会有几种走法?这不是“上楼梯”问题吗.根据“上楼梯”问题的解法可得在A →C →D →E →F →B 这条路线中有8种符合条件的走法.而对于从A 到B 的其他每条最短路线而言,每一条路线都有5条线段,所以每条路线都有8种走法. 进一步:从A 到B 共有多少条最短路线?这正是“最短路线”问题!用“标数法”来解决,有10条.综上所述,满足条件的走法有81080⨯=种.1032463111111B A BF ED CA BA【巩固】 从A 到B 的最短路线有几条呢?BA【解析】 图中从A 到B 的最短路线都为6条.【巩固】 有一只蜗牛从A 点出发,要沿长方形的边或对角线爬到C 点,中间不许爬回A 点,也不能走重复的路,那么,它有多少条不同的爬行路线?最短的是哪条呢?ODC BA【解析】 共有9种,即:A O C →→、 A O D C A O B C →→→→→→、 、 A B C →→A B O C →→→、 A B O D C →→→→、 A D C →→、 A D O C →→→ A D O B C →→→→,最短的路是:A O C →→.【例 2】阿呆和阿瓜到少年宫参加2008北京奥运会志愿者培训.如果他们从学校出发,共有多少种不 同的最短路线?少年宫学校J I HGF EDC B A 410633211111少年宫学校【解析】 从学校到少年宫的最短路线,只能向右或向下走.我们可以先看A 点:从学校到A 点最短路线只有1种走法,我们在A 点标上1.B 、E 、F 、G 点同理.再看J 点:最短路线可以是A J →、E J →共2条,我们在J 点标上2.我们发现211=+正好是对角线A 点和E 点上的数字和.所有的最短路线都符合这个规律,最终从学校到少年宫共有10种走法.【巩固】 方格纸上取一点A 作为起点,再在A 的右上方任取一点B 作为终点,画一条由A 到B 的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?BA【解析】 根据“标号法”可知共有10种,如图.【巩固】 如图,从F 点出发到G 点,走最短的路程,有多少种不同的走法?GF【分析】 共有115种.【巩固】 小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!南村北村【分析】 根据“对角线法”知共有126种,如图.12656703535216152015105541111南村北村410633211111【例 3】“五一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?黄山北京2黄山北京211410331111722【解析】 采用对角线法(如图)这道题的图形与前几题的图形又有所区别,因此,在解题时要格外注意是由哪两点的数之和来确定另一点的.从北京到黄山最近的道路共有10条.【巩固】 从甲到乙的最短路线有几条?乙甲【解析】 有11条.【例 4】古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.人一天一位将军向他请教一个问题:如下图,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为了使行走的路线最短,应该让马在什么地方饮水?乙地甲地河流【解析】 本题主要体现最值思想和对称的思想,教师应充分引导孩子观察行走路线的变化情况甲地逐步引导学生通过对称来找到相应的点,进一步了解图形最值问题中应该如何解决问题.【例 5】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图).爱动脑筋的嘟嘟就在想,从学校到李家村共有多少种不同的最短路线呢?李家村学校81461025李家村学校235216151051114106331111【解析】 我们采用对角线法(如图),从学校到李家村共有81种不同的最短路线.[拓展] 亲爱的小朋友们,你们觉得从A 到B 共有几条最短路线呢?BA【解析】 此题与上题不同,但方法相同.我们采用对角线法(如图)可知:可以选择的最短路线共有41条.【例 6】阿花和阿红到少年宫参加2008北京奥运会志愿者培训.他们从学校出发到少年宫最多有多少种不同的行走路线?少年宫学校904214482814少年宫学校2651143111114952052【解析】 采用对角线法(如图).可得从学校到少年宫共有90种走法.[铺垫] 小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?小猪家游乐场149小猪家游乐场2551114321【解析】 “对角线”法(如图),共14 条.【例 7】阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行.咱们学而思的小朋友都很聪明,请你们帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?【解析】仍然用对角线法求解.第一天(无限制条件)共有16条;第二天(必须经过公园)共有8条;第三天(必须不经过公园)共有8条.【巩固】大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,请你们快想想吧!【解析】(方法一)用“对角线法”求出:从学校到养老院共126条.必经过市中心的60 条,所以可行的路有:1266066-=(条).养老院(方法二)可以直接求,即把含有市中心的田字格挖去,共有66条.664026111010养老院学校2526155111463311115155411【例 8】如图,从X 到Y 最短路线总共有几种走法?【分析】 如图,共有716种.71637434217017220285511536212815218364115878536492836211515101077666554432YX1111111111111【例 9】如图,从A 到B 沿网格线不经过线段CD 和EF 的最短路径的条数是多少条?A C DE FB【解析】 由于不能经过线段CD 和EF ,所以我们必须先在网络图中拆除CD 和EF ,然后再在拆除了CD 和EF 以后的网络图中进行标数(如下图所示).运用标数法可求出满足条件的最短路径有78条.【巩固】 下图为某城市的街道示意图,C 处正在挖下水道,不能通车,从A 到B 处的最短路线共有多少条?【解析】 从A 到B 的最短路线有431条.CBA174551999558325743117411030552518121211C BA836410776543211111111【例 10】 按图中箭头所指的方向行走,从A 到I共有多少条不同的路线?CF H DIGE B A【解析】 本题中的运动方向已经由箭头标示出来,所以关键要分析每一点的入口情况.通过标数法我们可以得出从A 到I 共有29条不同的路径.【例 11】 按图中箭头方向所指行走,从A 到G 有多少种不同的路线?GF E DC B A【解析】 运用标数法原理进行标数,整个标数流程如下图2181AB CD EF G 2351313532GF ED CB A1881AB CDE F G2355332GF E D CB A11AB CDE F G22GF E DC B A11AB C DE F G从A 到G 共有21条不同的路线.【巩固】 ⑴按下图左箭头方向所指,从X到Y 有多少种不同的路线?⑵如下图右所示,这个问题有一个规则:只能沿着箭头指的方向走,你能否根据规则算出所有从入口到出口的路径共有多少条?[分析]⑴利用标数法求得X到Y有34种不同的路线,如下图左所示.⑵由题将路线图转化为下图右所示,根据标数法求得从入口到出口的路径共有10条.出口1【例 12】⑴如下图左,如果只允许向下移动,从A点到B点共有多少种不同的路线?⑵如下图右,要从A点到B点,要求每一步都是向右,向上或者斜上方,问共有多少种不同的走法?ABBA【解析】⑴按题目要求,只能向下移动,利用标数法求得A到B共有路线68种,如下图左所示.⑵按题目要求,只能走下图右的3个方向,利用标数法求得共有22种不同的走法,如下图右.2622166111201010644143468341444332111111A BB A 42622166111B A【巩固】 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间,从1号房间走到10号房间共有多少种不同走法?10987654321【分析】 图中并没有标出行走的方向,但题中“你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间”这句话实际上就规定了行走的方向.如下图所示,我们可以把原图转化成常见的城市网络图,然后再根据标数法的思想标数:从图中可以看出,从1号走到10号房间共有22种不同的走法.【例 13】 一只密蜂从A 处出发,A 回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?BA864297531【解析】 蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房.明确了行走路径的方向,就可运用标准法进行计算.如图所示,小蜜蜂从A 出发到B 处共有89种不同的回家方法.【例 14】 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE ”的路线共有多少条?AAPPLELPPA A P L P P P A A P P P A A P A[分析] 要想拼出英语“APPLE ”的单词,必须按照“A P P L E →→→→”的次序拼写.在图中的每一种拼写方式都对应着一条最短路径.如下图所示,运用标数法原理标数不难得出共有31种不同的路径.131127211224154112283184411AAPPLELPPA A P L P P P A A P P P A A P A[铺垫] 图中的“我爱希望杯”有多少种不同的读法.望杯望杯希杯爱望希杯杯望希爱我 杯杯杯杯杯望望望希希希爱爱我644332111111111[分析] 从我(1个)、爱(2个)、希(3个)、望(4个)、杯(5个)中组成“我爱希望杯”即相同的字只能选一个而且不能重复选,所以共有1464116++++=(种).[拓展] 如下图左所示,科学家“爱因斯坦”的英文名拼写为“Einstein ”,按图中箭头所示方向有多少种不同的方法拼出英文单词“Einstein ”.i111111i[分析] 因为“Einstein ”的拼读顺序为“E i n s t e i n →→→→→→→”,每一种拼法都对应着网络图中的一条最短路径,所以可以运用标数法来解决. 如上图右所示,从E 点到n 点的最短路径有30条,所以共有303060+=(种)不同拼法.注意图中的三个字母“i ”,左、右的两个字母“i ”只能由一个字母“e ”去到达.。
(word完整版)最短路线问题——标数法的应用
(word 完整版)最短路线问题——标数法的应用
计数的基本方法-—标数法
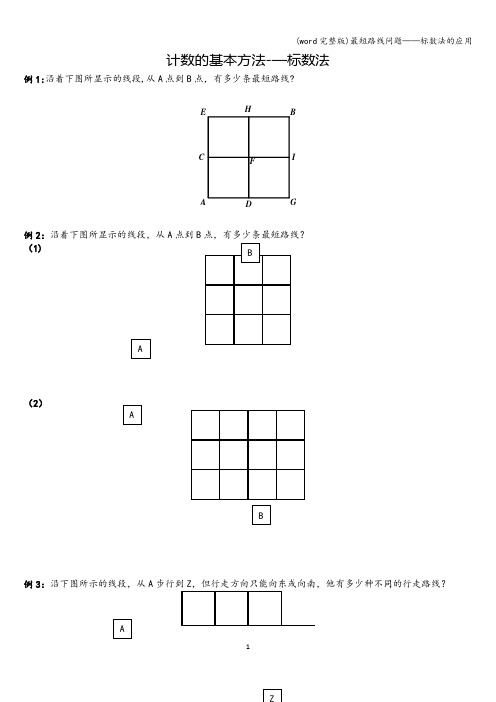
例1:沿着下图所显示的线段,从A 点到B 点,有多少条最短路线?
I
C
例2:沿着下图所显示的线段,从A 点到B 点,有多少条最短路线? (1)
(2)
例3:沿下图所示的线段,从A
完整版)最短路线问题——标数法的应用
例4:如图,求A 到B 沿网格线的最短路线数:
(1) 必须经过点C ; (2) 必须经过线段EF ; (3) 不经过点C ; (4) 不经过线段EF;
例5:按下图箭头所指的方向行走,从A 到达Z 有多少种不同行走路线?
本章小结:
1.什么是标数法?
答:在每个点上标记出从起点出发到此点的路线数的一种计数方法。
2.如何使用标数法解决长方形网络图中的最短路线问题? 答:
1. 确定标数的方向;
2. 将与起点共直线的点上标上数字1;
3. 画出每个小方格对角线;
(word完整版)最短路线问题——标数法的应用4.把每个小方格内对角线顶点上的两个数字相加,和标记在剩下的那个点上;
2。
如何使用标数法解决路线数问题?
答:
1.从某一点出发到另一点只有一条路线的时候,则后点上标记的数字应该和前一点相同;
2.如果到达某一点必须经过与这个点相邻的两个或几个点时,则该点上标记的数字是能够到达这一点的相
邻的两个或几个点上标记的数字之和。
标号法求最短路径问题

运筹学
教案
标题:标号法求最短路径问题
教学目标:
1.通过本节学习,使学生掌握标号法的步骤;
2.通过本节学习,学生能够应用标号法求解配送路径问题
教学重点及难点:
重点:标号法的求解步骤;难点:标号法在配送路径问题中的应用
教学内容(教学时数:2 )
一、标号法的概念
标号法也称Dijstra算法,是荷兰科学家Dijstra于1959年提出的求解指定两点间最短路径的有效算法。
二、标号法的适用范围和原理
条件:网络中所有的边(弧)的权重值 w
ij
≥0;
范围:指定两点间或指定一点到另一点的最短路径问题;
原理:最短路的子路还是最短路。
三、标号法的思想
从起点v
s 开始,逐步给每个结点v
j
标号[d
j
,v
i
],其中d
j
为起点
v s 到v
j
的最短距离, v
i
为该最短路线上的前一节点。
若给终点v
t
标上号[d
t
,v
i
], 表示已求出v
1
至v
t
的最短路其最
短路长为d
t ,最短路径可根据标号v
i
反向追踪而得。
四、标号法的求解步骤
备注:
五、例题讲解与练习
求解过程详见PPT。
练习:利用标号法求V
1
到V
8
的最短路径
备注:作业、讨论题、思考题:完成课本158页的第1、2题。
排列组合第阶表格最短路径问题

1. 如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有35种.【考点】计数原理的应用.【专题】排列组合.【分析】根据题意,从M到N的最短路程,只能向右、向下运动,将原问题转化为排列、组合问题,计算可得答案.【解答】解:根据题意,从M到N的最短路程,只能向右、向下运动,从M到N,最短的路程需要向下走3次,向右走4次,即从7次中任取3次向下,剩下4次向右,有C73=35种情况,故答案为:35【点评】本题考查排列、组合的应用,解题的关键将圆问题转化为排列、组合问题,由分步计数原理计算得到答案.2. 如图,某城市的街道由5条东西与7条南北向马路组成.现在要从西南角的A处沿最短路线走到东北角的B处,由于修路十字路口C不能通过,那么共有多少种不同走法?【考点】排列组合.【专题】传统应用题专题.【分析】利用逐步分析点的路线,列出表格,求得数据即可解决问题.【解答】解:用标数法可以求出一共有120种走法.答:共有120种不同走法.【点评】本题从每个交叉点得出有2条路可走是关键,然后利用标数法得出共有的走法就比较容易了,注意C不能通过.3.某城市有7条南北向的街,5条东西向的街.(1)如果从城的O点走向A点,最短的走法有几种?(2)从O点出发经过B点走向A点,最短的走法有几种?(3)从O点出发,不经过B、C两点,走向A点,最短的走法有几种?ACBO4.如图,沿着箭头从P 走到Q,有________种不同的最短路径【考点】标数法【答案】12问题16:查找表格的功能介绍与操作?一个族文件往往包含若干个类型,每一个类型都拥有自己的参数,手动复制修改每一个参数类型将会是一个很繁琐的事情,软件提供了查找表格的功能来自动控制这些不同类型的参数值,下面将带着大家一起看看查找表格的功能介绍。
1.如下图所示,打开一个常规T形三通族文件;2.点击“创建”选项卡下的“族类型”命令,打开“族类型”对话框;观察族类型对话框,T形三通用到了查找表格功能,使用的查找表格名称为“Tee - Generic”(软件安装完成,查找表格的文件被默认放置在了电脑系统盘,默认路径为:C:\ProgramData\Autodesk\RVT 2021\Lookup Tables),打开查找表格文件;打开默认路径发现有两个表格,“Conduit”表示线管表格,“Pipe”表示给排水管道表格;3.打开“Tee - Generic”文件(文件格式为:CSV格式);上图即为T形三通的查找表格文件,第一列是用来区分该管件类型名称的参数;观察表头“ND##length##millimeters”,“ND”是“Nominal Diameter”(公称直径)的缩写;“length”(长度)是ND的参数属性;“millimeters”是该列参数的单位;第三列“POD”表示管件外径;“CtE”表示中心到端点的距离。
三年级奥数标数法解题

数学原来是一件非常轻松快乐的事情!你发现了吗?- 1 -第12讲 标数法解题知识要点从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?我们可以用标数法解决。
亲爱的小朋友们,你要记住两点:⑴两点之间线段最短;⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力。
精典例题例1:一只蚂蚁在长方形格纸上的点,它想去点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢??模仿练习1.如图,从A 点沿最短线段到B 点,共有多少种不同的最短线路?ABBA要想最短要注意两点:一是不重复路线,二是不走回头路。
数学会让你变成一个善于发现的孩子!- 2 -2.下图是一个街道的示意图,实绩表示道路,从B 到A ,只能向右或向上方沿着道路前进,则一共有( )种不同的走法。
例2:如图,从甲地到乙地最近的道路有几条?模仿练习从甲到乙的最短路线有几条?采用标数法,这道题的图形与前几题的图形又有所区别。
因此,在解题时要格外注意是由哪两点的数之和来确定另一点的。
乙甲数学原来是一件非常轻松快乐的事情!你发现了吗?- 3 -精典例题例3: 如下图所示,淘气和笑笑从学校到电影院去看电影,但是由于文化宫在维修不能通过,请问从学校到电影院最短的路线有多少条?模仿练习如图为一幅街道图,小明要从A 出发走到D ,但由于B 、C 两个地方在修路不能通过,那么从A 到D 的不同的最短路线有多少条?例4:大熊和美子准备去看望养老院的李奶奶,可是他们要先去市中心购买鲜花,他们从学校经过市中心到养老院的最短路线共有几条呢?先到市中心,再到养老院,可以分两步来完成。
学校电影院文化宫数学会让你变成一个善于发现的孩子!- 4 -模仿练习阿强和牛牛结伴骑车去图书馆看书,他们想先去公园看大熊猫再去图书馆,请你们帮阿强和牛牛想一想:从学校到图书馆的最短路线分别有多少种不同的走法?家庭作业1.阿呆和阿瓜到少年宫参加北京奥运会志愿者培训.如果他们从学校出发,共有多少种不同的最短路线?2.小君家到学校的道路如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计数的基本方法——标数法
例1:沿着下图所显示的线段,从A 点到B 点,有多少条最短路线?
例2:沿着下图所显示的线段,从A 点到B 点,有多少条最短路线? (1)
(2)
F
I
C
A
G
E
B
B
A
A
B
例3:沿下图所示的线段,从A 步行到Z ,但行走方向只能向东或向南,他有多少种不同的行走路线?
例4:如图,求A 到B 沿网格线的最短路线数: (1) 必须经过点C ; (2) 必须经过线段EF ; (3) 不经过点C ; (4) 不经过线段EF ;
例5:按下图箭头所指的方向行走,从A 到达Z 有多少种不同行走路线?
A
Z
A
Z
B
A
C
F
E
本章小结:
1.什么是标数法?
答:在每个点上标记出从起点出发到此点的路线数的一种计数方法。
2.如何使用标数法解决长方形网络图中的最短路线问题?
答:
1.确定标数的方向;
2.将与起点共直线的点上标上数字1;
3.画出每个小方格对角线;
4.把每个小方格内对角线顶点上的两个数字相加,和标记在剩下的那个点上;
2.如何使用标数法解决路线数问题?
答:
1.从某一点出发到另一点只有一条路线的时候,则后点上标记的数字应该和前一点相
同;
2.如果到达某一点必须经过与这个点相邻的两个或几个点时,则该点上标记的数字是能
够到达这一点的相邻的两个或几个点上标记的数字之和。
