阶梯型标数法
[Excel]阶梯图——无规律阶跃类数据的可视化法
![[Excel]阶梯图——无规律阶跃类数据的可视化法](https://img.taocdn.com/s3/m/85ed619070fe910ef12d2af90242a8956becaac9.png)
[Excel]阶梯图——⽆规律阶跃类数据的可视化法阶梯图的介绍阶梯图顾名思义,是⼀种⽆规律、间歇型阶跃的⽅式表达数值的变化。
对⽐,以上的折线图和阶梯图,你可以发现:从数据上来看,从2002/6/30到2006/01/07,资费⼀直维持在0.37,⽽在2006/01/08那天起,资费上调⾄了0.39。
如果以折线图的形式表达,可能会让⼈误以为,这种变化是线性且连贯的;⽽如果以阶梯图表达,就可以避免这种可能的错误理解。
阶梯图的制作谈论完了阶梯图的作⽤,⽕箭君就带着⼤家聊⼀下如何制作阶梯图。
常⽤的⽅法有两种:折线图变形法以及散点图变形法。
折线图变形法0101折线图变形法利⽤折线图⼯具制作阶梯图,最主要的是对数据的改造:Step 1在按⽇期正序排列完原始数据后,需要新建⼀批数据,这批数据所对应的⽇期序列从原始数据的第⼆个⽇期开始,⽽这批数据所对应的资费数据则从原始数据的第⼀个资费数值开始。
举例说来,D3: =A4,⽽E3: =B3。
Step 2将原始数据复制到改造后数据的下⽅,组成⼀个新的数据集,包含数据总量为2倍原始数据少1。
Step 3使⽤这个新的数据集,⽣成⼀个折线图。
⽽这个折线图就是我们要做的阶梯图。
0202散点图变形法散点图变形法假设我们已有个税每档的税率以及对应的个⼈薪酬所得额度,想要利⽤散点图来制作阶梯图,可以如下操作:Step 1依旧是改造数据。
加两列辅助数列,分别对应x轴两点间、y轴两点间的差值。
增加⼀⾏,薪酬所得超过最⼤税率所对应的薪酬所得,税率与最⼤税率保持⼀致公式如上图所列。
Step 2给散点图增加误差线。
然后再按以下设置误差线的格式,并注意这两点:⽆线端将⽔平误差线和垂直误差线的末端形式均设置为 ⽆线端设置⽔平误差线误差量的正错误值为辅助数列dX(C2:C9),负错误值为{0};设置垂直误差线误差量的正错误值为{0},负错误值为辅助数列dY(D2:D9)这样设置完成后,你可以得到这样⼀个图表:Step 3将数据标记设置为⽆,并调整误差线格式。
标数法深入

这两道题来自小奥总复习,应该来说针对的可能是四、五六年级的孩子。
但是我们刚刚学过简单的标数法,标数法应用实际很广,尤其是阶梯型标数法。
如果孩子确实学有余力,可以让他见见这些题,解题过程图画方便用word画,有意向可以来问我。
大概需要十分钟时间解答。
方法提示:阶梯型标数法。
适用于两个量间存在先后,大小顺序的题目。
有一次小组长选举中,铮铮与昊昊两人作为候选人参加竞选,一共得了7张选票。
在将7张选票逐一唱票的过程中,昊昊的得票始终没有超过铮铮。
那么这样的唱票过程有几种不同的情况?
某体育馆,门票价格为50元,而且规定每人限购1张门票,现有10人排队购票。
其中5人均手持50元面值的钞票,另5人均手持100元面值的钞票,而售票员只带了门票,没有准备零钱,问共有多少种购票序列是不需要售票处另外找零的?。
数形结合详解

第三讲、数形结合答案1. 某区举行小学数学竞赛,结果不低于80分的人数比80分以下的人数的4倍还多2人;及格的人数比不低于80分的人数多22人,恰是不及格人数的6倍。
求参赛的总人数。
【解析】:由“不低于80分的比80分以下的4倍还多2人”可画出左下图,由“及格的比不低于80分的多22人”可画出右下图。
因为及格人数是不及格人数的6倍,由右上图知,22+22×4+2=112(人)是不及格人数的2倍,所以参赛总人数为(112÷2)×(1+6)=392(人)。
2. 农夫说:“如果卖掉75只鸡,那么鸡饲料可以维持20天;如果再买进100鸡,那么鸡饲料只能维持15天。
”问:农夫养了多少只鸡?【解析】由于“工作总量=工作效率×工作时间”,正好对应着矩形中“面积=长×宽”的关系,所以可以利用这种关系画出矩形图来理解。
注:只要满足A×B=C的关系式,都可以表示成矩形图。
设1只鸡1天吃的饲料为1份,那么x只鸡1天吃x份。
所以我们就可以用矩形的长来表示“鸡的只数”,而矩形的宽表示“吃的天数”,那么矩形的面积就表示“吃的饲料”,如图所示:由于饲料的总数不发生变化,所以矩形“A+C”的面积与矩形“B+C”的面积相等,由此可知:矩形A的面积=矩形B的面积。
而矩形B的面积为:(75+100)×15=2625所以矩形A的长为:2625÷(20-15)=525由此可知农夫公养鸡:525+75=600(只)3.某次数学竞赛原定一等奖10人,二等奖20人。
现在将一等奖中最后4人调整为一等奖,这样使二等奖的学生的平均分提高了1分,使一等奖的学生的平均分提高了3分。
那么原来一等奖平均分比二等奖平均分多多少分?【解析】长代表人数,宽代表平均数,那么对应矩形的面积则表示总分。
调整前一二等奖情况如下图根据人数的调整情况与平均分的变化,进一步画图调整后总面积不变,所以B=A+C 。
奥数:7-6计数方法与技巧综合

7 计数综合7-6 计数方法与技巧综合 7-6-1归纳法7-6-2整体法7-6-3对应法7-6-3-1图形中的对应关系 7-6-3-2数字问题中的对应关系 7-6-3-3对应与阶梯型标数法 7-6-3-4不完全对应关系7-6-4递推法前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.模块一、归纳法从条件值较小的数开始,找出其中规律,或找出其中的递推数量关系,归纳出一般情况下的数量关系. 【例 1】 (难度等级※※)一条直线分一个平面为两部分.两条直线最多分这个平面为四部分.问5条直线最多分这个平面为多少部分?【解析】 方法一:我们可以在纸上试着画出1条直线,2条直线,3条直线,……时的情形,于是得到下表:由上表已知5条直线最多可将这个平面分成16个部分,并且不难知晓,当有n 条直线时,最多可将平面分成2+2+3+4+…+n=()12n n ++1个部分. 方法二:如果已有k 条直线,再增加一条直线,这条直线与前k 条直线的交点至多k 个,因而至多被分成k+1段,每一段将原有的部分分成两个部分,所以至多增加k+1个部分.于是3条直线至多将平面分为4+3=7个部分,4条直线至多将平面分为7+4=11个部分,5条直线至多将平面分为11+5=16个部分.一般的有k 条直线最多将平面分成:1+1+2+…+k=()12k k ++1个部分,所以五条直线可以分平面为16个部分.例题精讲教学目标计数方法与技巧综合【巩固】(难度等级※※)平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?【解析】 假设用a k 表示k 条直线最多能把圆的内部分成的部分数,这里k =0,1,2,……a 0=1a 1=a 0+1=2 a 2=a 1+2=4 a 3=a 2+3=7 a 4=a 3+4=11 ……故5条直线可以把圆分成16部分,100条直线可以把圆分成5051部分【例 2】 (难度等级 ※※)平面上10个两两相交的圆最多能将平面分割成多少个区域? 【解析】 先考虑最简单的情形.为了叙述方便,设平面上k 个圆最多能将平面分割成k a 个部分.141312111098765432187652134431221从图中可以看出,12a =,24221a ==+⨯,38422a ==+⨯,414823a ==+⨯,…… 可以发现k a 满足下列关系式:()121k k a a k -=+-.实际上,当平面上的(1k -)个圆把平面分成1k a -个区域时,如果再在平面上出现第k 个圆,为了保证划分平面的区域尽可能多,新添的第k 个圆不能通过平面上前()1k -个圆之间的交点.这样,第k 个圆与前面()1k -个圆共产生2(1)k ⨯-个交点,如下图:这2(1)k ⨯-个交点把第k 个圆分成了2(1)k ⨯-段圆弧,而这2(1)k ⨯-段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了2(1)k ⨯-个部分.所以,()121k k a a k -=+-. 那么,10987292829272829a a a a =+⨯=+⨯+⨯=+⨯+⨯+⨯=12122...272829a =+⨯+⨯++⨯+⨯+⨯ ()2212...78992=+⨯+++++=.故10个圆最多能将平面分成92部分.【例 3】 10个三角形最多将平面分成几个部分?【解析】 设n 个三角形最多将平面分成n a 个部分.1n =时,12a =;2n =时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有236⨯=(个)交点.这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即2223a =+⨯.3n =时,第三个三角形与前面两个三角形最多有4312⨯=(个)交点,从而平面也增加了12个部分,即:322343a =+⨯+⨯.…… 一般地,第n 个三角形与前面()1n -个三角形最多有()213n -⨯个交点,从而平面也增加()213n -⨯个部分,故()()222343213224213332n a n n n n =+⨯+⨯++-⨯=++++-⨯=-+⎡⎤⎣⎦;特别地,当10n =时,2103103102272a =⨯+⨯+=,即10个三角形最多把平面分成272个部分.【例 4】 (难度等级※※)一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?【解析】 一个长方形把平面分成两部分.第二个长方形的每一条边至多把第一个长方形的内部分成2部分,这样第一个长方形的内部至多被第二个长方形分成五部分.同理,第二个长方形的内部至少被第一个长方形分成五部分.这两个长方形有公共部分(如下图,标有数字9的部分).还有一个区域位于两个长方形外面,所以两个长方形至多把平面分成10部分.第三个长方形的每一条边至多与前两个长方形中的每一个的两条边相交,故第一条边被隔成五条小线段,其中间的三条小线段中的每一条线段都把前两个长方形内部的某一部分一分为二,所以至多增加3×4=12个部分.而第三个长方形的4个顶点都在前两个长方形的外面,至多能增加4个部分. 所以三个长方形最多能将平面分成10+12+4=26.【小结】n 个图形最多可把平面分成部分数:直线:()112n n ⨯++;圆:()21n n +⨯-;三角形:()231n n +⨯⨯- ; 长方形:()241n n +⨯⨯-.【例 5】 (难度等级※※)在平面上画5个圆和1条直线,最多可把平面分成多少部分? 【解析】 先考虑圆.1个圆将平面分成2个部分.这时增加1个圆,这个圆与原有的1个圆最多有两个交点,成为2条弧,每条弧将平面的一部分一分为二,增加了2个部分,所以2个圆最多将平面分成4个部分.当有3个圆时,第3个圆与原有的2个产生4个交点而增加4个部分,所以3个圆最多将平面分成8个部分.同样的道理,5个圆最多将平面分成22个部分.再考虑直线.直线与每个圆最多有2个交点,这样与5个圆最多有10个交点.它们将直线分成11条线段或射线,而每条线段又将平面的一部分一分为二,2条射线增加了一部分,因此5个圆和1条直线最多可将平面分成32个部分.【例 6】在一个西瓜上切6刀,最多能将瓜皮切成多少片?【解析】将西瓜看做一个球体,球体上任意一个切割面都是圆形,所以球面上的切割线是封闭的圆周,考虑每一次切割能增加多少瓜皮片.当切1刀时,瓜皮被切成两份,当切第2刀时,由于切割线相交,所以瓜皮被切成4分,……,切第n次时,新增加的切割线与原来的切割线最多有()n-个交点.这21些交点将第n条切割线分成()n-,所以2121n-段,也就是说新增加的切割线使瓜皮数量增加了()在西瓜上切6刀,最多能将瓜皮切成11212223242532++⨯+⨯+⨯+⨯+⨯=片.【例 7】在一大块面包上切6刀最多能将面包切成多少块.(注:面包是一个立体几何图形,切面可以是任何方向)【解析】题目相当于6个平面能将空间划分为多少个部分.通过找规律来寻找递推关系,显然的1个平面能将空间划分成2块,2个平面能将空间划分成4块,3个平面能将空间划分成8个平面,当增加到第四个平面时,第四个平面这能将原来空间中的8个部分中的其中几个划分.如图:注意到第四个平面与其他三个平面相交形成3条直线,这三条直线将第四个平面分割成7个部分,而每一部分将原来三个平面划分的8个空间中的7个划分成两份,所以4个平面能将空间划分成+=个部分.8715同样的第五个平面与前四个平面分别相交成4条直线,这四条直线能将第5个平面分割成++++=个部分,每一部分都划分原空间中的某一区域,所以第五个平面能使空间中的区1123411域增加到151126+==个部分.当增加到6个平面时,第六个平面共被划分成11234516+++++=个部分,所以第6个平面能将空间中的区块数增加到261642+=个部分.所以6刀能将面包切成42块.模块二、整体法解决计数问题时,有时要“化整为零”,使问题变得简单;有时反而要从整体上来考虑,从全局、从整体来研究问题,反而有利于发现其中的数量关系.【例8】(难度等级※※※)一个正方形的内部有1996个点,以正方形的4个顶点和内部的1996个点为顶点,将它剪成一些三角形.问:一共可以剪成多少个三角形?如果沿上述这些点中某两点之间所连的线段剪开算作一刀,那么共需剪多少刀?【解析】 方法一:归纳法如下图,采用归纳法,列出1个点、2个点、3个点…时可剪出的三角形个数,需剪的刀数.不难看出,当正方形内部有n 个点时,可以剪成2n +2个三角形,需剪3n+l 刀,现在内部有1996个点,所以可以剪成2×1996+2=3994个三角形,需剪3×1996+1=5989刀.方法二:整体法.我们知道内部一个点贡献360度角,原正方形的四个顶点共贡献了360度角,所以当内部有n 个点时,共有360n+360度角,而每个三角形的内角和为180度角,所以可剪成(360n+360)÷180=2n+2个三角形.2n+2个三角形共有3×(2n+2)=6n+6条边,但是其中有4条是原有的正方形的边,所以正方形内部的三角形边有6n+6—4=6n+2条边,又知道每条边被2个三角形共用,即每2条边是重合的,所以只用剪(6n+2)÷2=3n+1刀.本题中n=1996,所以可剪成3994个三角形,需剪5989刀.【巩固】在三角形ABC 内有100个点,以三角形的顶点和这100点为顶点,可把三角形剖分成多少个小三角形?【解析】 整体法.100个点每个点周围有360度,三角形本身内角和为180度,所以可以分成()360100180180201⨯+÷=个小三角形.【例 9】 在一个六边形纸片内有60个点,以这60个点和六变形的6个顶点为顶点的三角形,最多能剪出_______个.【解析】 设正六边形内有n 个点,当1n =时有6个三角形,每增加一个点,就增加2个三角形,n 个点最多能剪出()()62122n n ++=+个三角形.60n =时,可剪出124个三角形.注:设最多能剪出x 个小三角形,则这些小三角形的内角和为180x ︒.换一个角度看,汇聚到正六边形六个顶点处各角之和为4180⨯︒,故这些小三角形的内角总和为603604180⨯︒+⨯︒.于是180603604180x ︒=⨯︒+⨯︒,解得124x =.模块三、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.一、图形中的对应关系【例 10】 (难度等级 ※※※)在8×8的方格棋盘中,取出一个由三个小方格组成的“L”形(如图),一共有多少种不同的方法?【解析】注意:数“不规则几何图形”的个数时,常用对应法.第1步:找对应图形每一种取法,有一个点与之对应,这就是图中的A点,它是棋盘上横线与竖线的交点,且不在棋盘边上.第2步:明确对应关系从下图可以看出,棋盘内的每一个点对应着4个不同的取法(“L”形的“角”在2×2正方形的不同“角”上).第3步:计算对应图形个数由于在8×8的棋盘上,内部有7×7=49(个)交叉点,第4步:按照对应关系,给出答案故不同的取法共有49×4=196(种).评注:通过上面两个范例我们知道,当直接去求一个集合元素的个数较为困难的时候,可考虑采用相等的原则,把问题转化成求另一个集合的元素个数.【例11】(难度等级※※※)在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?【解析】首先可以知道题中所讲的13⨯长方形中间的那个小主格为黑色,这是因为两个白格不相邻,所以不能在中间.显然,位于棋盘角上的黑色方格不可能被包含在这样的长方形中.下面分两种情况来分析:第一种情况,一个位于棋盘内部的黑色方格对应着两个这样的13⨯长方形(一横一竖);第二种情况,位于边上的黑色方格只能对应一个13⨯长方形.由于在棋盘上的32个黑色方格中,位于棋盘内部的18个,位于边上的有12个,位于角上的有2个,所以共有1821248⨯+=个这样的长方形.本题也可以这样来考虑:事实上,每一行都有6个13⨯长方形⨯长方形,所以棋盘上横、竖共有13⨯⨯=个.由于棋盘上的染色具有对称性,因此包含两个白色小方格与一个黑色小方格的长方68296形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系,这说明它们各占一半,因此所求的长方形个数为96248÷=个.【巩固】(难度等级※※)用一张如图所示的纸片盖住66⨯方格表中的四个小方格,共有多少种不同的放置方法?【解析】如图,将纸片中的一个特殊方格染为黑色,下面考虑此格在66⨯方格表中的位置.易见它不能位于四个角上;若黑格位于方格表中间如图浅色阴影所示的44⨯正方形内的某格时,纸片有4种不同的放法,共计44464⨯⨯=种;若黑格位于方格表边上如图深色阴影所示的方格中时,纸片的位置随之确定,即只有1种放法,此类放法有4416⨯=种.所以,纸片共有641680+=种不同的放置方法.【例12】(难度等级※※)图中可数出的三角形的个数为.【解析】这个图不像我们以前数三角形那样规则,粗看似乎看不出其中的规律,不妨我们取出其中的一个三角形,发现它的三条边必然落在这个图形中的三条大线段上,而每三条大线段也正好能构成一个三角形,因此三角形的个数和三条大线段的取法是一一对应的关系,图中一共有8条大线段,因此有3856C=个三角形.【例 13】如图所示,在直线AB上有7个点,直线CD上有9个点.以AB上的点为一个端点、CD上的点为另一个端点的所有线段中,任意3条线段都不相交于同一个点,求所有这些线段在AB与CD之间的交点数.C D【解析】常规的思路是这样的:直线AB上的7个点,每个点可以与直线CD上的9个点连9根线段,然后再分析这些线段相交的情况.如右图所示,如果注意到下面这个事实:对于直线AB上的任意两点M、N与直线CD上的任意两点P、Q都可以构成一个四边形MNQP,而这个四边形的两条对角线MQ、NP的交点恰好是我们要计数的点,同时,对于任意四点(AB与CD上任意两点)都可以产生一个这样的交点,所以图中两条线段的交点与四边形有一一对应的关系.这说明,为了计数出有多少个交点,我们只需要求出在直线AB与CD中有多少个满足条件的四边形MNQP就可以了!从而把问题转化为:在直线AB上有7个点,直线CD上有9个点.四边形MNQP有多少个?其中点M、N位于直线AB 上,点P、Q位于直线CD上.这是一个常规的组合计数问题,可以用乘法原理进行计算:由于线段MN有2721C=种选择方式,线段PQ有2936C=种选择方式,根据乘法原理,共可产生2136756⨯=个四边形.因此在直线AB与CD 之间共有756个交点.二、数字问题中的对应关系【例 14】 有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大? 【解析】 由于四位数的四个数位上的数的大小关系已经非常明确,而对于从0~9中任意选取的4个数字,它们的大小关系也是明确的,那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大,所以千位不能为0,本身已符合四位数的首位不能为0的要求,所以进行选择时可以把0包含在内),也就是说满足条件的四位数的个数与从0~9中选取4个数字的选法是一一对应的关系,那么满足条件的四位数有410109872104321C ⨯⨯⨯==⨯⨯⨯个.【巩固】 (难度等级 ※※※)三位数中,百位数比十位数大,十位数比个位数大的数有多少个? 【解析】 相当于在10个数字中选出3个数字,然后按从大到小排列.共有10×9×8÷(3×2×1)=120种.实际上,前铺中每一种划法都对应着一个数.【例 15】 数3可以用4种方法表示为一个或几个正整数的和,如3,12+,21+,111++.问:1999表示为一个或几个正整数的和的方法有多少种?【解析】 我们将1999个1写成一行,它们之间留有1998个空隙,在这些空隙处,或者什么都不填,或者填上“+”号.例如对于数3,上述4种和的表达方法对应:1 1 1,1+1 1,1 1+1,1+1+1. 可见,将1999表示成和的形式与填写1998个空隙处的方式之间是一一对应的关系,而每一个空隙处都有填“+”号和不填“+”号2种可能,因此1999可以表示为正整数之和的不同方法有1998199822222⨯⨯⨯=个相乘种.【例 16】 (2019年国际小学数学竞赛)请问至少出现一个数码3,并且是3的倍数的五位数共有多少个? 【解析】 五位数共有90000个,其中3的倍数有30000个.可以采用排除法,首先考虑有多少个五位数是3的倍数但不含有数码3.首位数码有8种选择,第二、三、四位数码都有9种选择.当前四位的数码确定后,如果它们的和除以余数为0,则第五位数码可以为0、6、9;如果余数为1,则第五位数码可以为2、5、8;如果余数为2,则第五位数码可以为1、4、7.可见只要前四位数码确定了,第五位数码都有3种选择,所以五位数中是3的倍数但不含有数码3的数共有8999317496⨯⨯⨯⨯=个. 所以满足条件的五位数共有300001749612504-=个.三、对应与阶梯型标数法【例 17】 游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?【解析】 与类似题目找对应关系.要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可以利用斜直角三角模型.在下图中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A 点沿格线走到B 点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求下图中从A 到B 有多少种不同走法.使用标数法,可求出从A 到B 有42种走法.AB424228145141494553221111111但是由于10个小朋友互不相同,必须将他们排队,可以分成两步,第一步排拿2元的小朋友,5个人共有5120=!种排法;第二步排拿到1元的小朋友,也有120种排法,所以共有5514400⨯=!!种排队方法.这样,使售票员能找得开零钱的排队方法共有4214400604800⨯=(种).【例 18】 (2008年第一届“学而思杯”五年级试题)学学和思思一起洗5个互不相同的碗,思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有 种不同的摞法.【解析】 我们把学学洗的5个碗过程看成从起点向右走5步(即洗几个碗就代表向右走几步),思思拿5个碗的过程看成是向上走5步(即拿几个碗就代表向上走几步),摞好碗的摞法,就代表向右、向上走5步到达终点最短路线的方法.由于洗的碗要多余拿的碗,所以向右走的路线要多余向上走的路线,所以我们用下面的斜三角形进行标数,共有42种走法,即代表42种摞法.421A【例 19】 (第七届走美试题)一个正在行进的8人队列,每人身高各不相同,按从低到高的次序排列,现在他们要变成并列的2列纵队,每列仍然是按从低到高的次序排列,同时要求并排的每两人中左边的人比右边的人要矮,那么,2列纵队有种不同排法.【解析】 首先,将8人的身高从低到高依次编号为12345678、、、、、、、,现在就相当于要将这8个数填到一个42 的方格中,要求每一行的数依次增大,每一列上面的要比下面的大.下面我们将12345678、、、、、、、依次往方格中填,按照题目规则,很容易就发现:第二行填的的数字的个数永远都小于或等于第一行数字填的个数.也就是说,不能出现下图这样的情况.而这个正好是“阶梯型标数”题型的基本原则.于是,我们可以把原题转化成:在这个阶梯型方格中,横格代表在第一行的四列,纵格代表第二行的四列,那么此题所有标数的方法就相当于从A 走到B 的最短路线有多少条.例如,我们选择一条路线:它对应的填法就是:.最后,用“标数法”得出从A 到B 的最短路径有14种,如下图:【巩固】将1~12这12个数填入到2行6列的方格表中,使得每行右边比左边的大,每一列上面比下面的大,共有多少种填法?【解析】 根据对应关系,再运用阶梯型标数法画图如下:13242141455211111111329048422820149654321共有132种填法.四、不完全对应关系【例 20】 圆周上有12个点,其中一个点涂红,还有一个点涂了蓝色,其余10个点没有涂色,以这些点为顶点的凸多边形中,其顶点包含了红点及蓝点的多边形称为双色多边形;只包含红点(蓝点)的多边形称为红色(蓝色)多边形.不包含红点及蓝点的称无色多边形.试问,以这12个点为顶点的所有凸多边形(边数可以从三角形到12边形)中,双色多边形的个数与无色多边形的个数,哪一种较多?多多少个?【解析】 从任意一个双色的N 边形出发(5N ≥时),在去掉这个双色多边形中的红色顶点与蓝色顶点后,将得到一个无色的2N -边形;另一方面,对于一个任意的无色的M 边形,如果加上红色顶点和蓝色顶点,就得到一个双色的2M +边形,所以无色多边形与双色多边形中的五边形以上的图形是一一对应的关系,所以双色多边形的个数比较多,多的是双色三角形和双色四边形的个数.而双色三角形有10个,双色四边形有21045C =个,所以双色多边形比无色多边形多104555+=个.【例 21】 有一类各位数字各不相同的五位数M ,它的千位数字比左右两个数字大,十位数字也比左右两位数字大.另有一类各位数字各不相同的五位数W ,它的千位数字比左右两个数字小,十位数字也比左右两位数字小.请问符合要求的数M 与W ,哪一类的个数多?多多少?【解析】 M 与W 都是五位数,都有千位和十位与其它数位的大小关系,所以两类数有一定的对应关系.比如有一个符合要求的五位数M ABCDE =(A 不为0),那么就有一个与之相反并对应的五位数(9)(9)(9)(9)(9)A B C D E -----必属于W 类,比如13254为M 类,则与之对应的86754为W 类. 所以对于M 类的每一个数,W 类都有一个数与之对应.但是两类数的个数不是一样多,因为M 类中0不能做首位,而W 类中9可以做首位.所以W 类的数比M 类的数要多,多的就是就是首位为9的符合要求的数.计算首位为9的W 类的数的个数,首先要确定另外四个数,因为要求各不相同,从除9外的其它9个数字中选出4个,有49126C =种选法.对于每一种选法选出来的4个数,假设其大小关系为4321A A A A >>>,由于其中最小的数只能在千位和十位上,最大的数只能在百位和个位上,所以符合要求的数有2类:①千位、十位排1A 、2A ,有两种方法,百位、十位排3A 、4A ,也有两种方法,故此时共有4种;②千位、十位排1A 、3A ,只能是千位3A ,百位4A ,十位1A ,个位2A ,只有1种方法.根据乘法原理,首位为9的W 类的数有()12641630⨯+=个.故W 类的数比M 类的数多630个.【例 22】 用1元,2元,5元,10元四种面值的纸币若干张(不一定要求每种都有),组成99元有P 种方法,组成101元有Q 种方法,则Q P -= .【解析】 由于101992-=,所以对于组成99元的每一种方法,只要再加上一张2元的,即可组成101元;而对于组成101元的方法,如果其中包含有一张2元的,那么去掉这张2元的,即可得到一种组成99元的方法.可见组成99元的方法与组成101元的某些方法之间存在一一对应的关系,组成101元的所有方法中,除去这些与组成99元的方法对应的方法,剩下的都是不包含有2元纸币的组成方法.所以Q 比P 多的就是用1元,5元,10元这三种面值的纸币组成101元的方法的总数. 假设用x 张1元的,y 张5元的,z 张10元的可以组成101元,则510101x y z ++=. 由于10101z ≤,所以10z ≤.即10元的可以有0~10张. 如果10元的张数确定了,那么有()()5101101010152021x y z z z +=-=-+=-+,那么y 的值可以为0到()202z -,也就是对每一个z 的值,y 都可以有2021212z z -+=-种可能,相应地5元纸币的张数也有212z -种取法.而当10元和5元的张数都确定了以后,1元纸币的张数也就确定了,这样也就确定了组成101元的方法.所以只需要看取10元和5元的共有多少种取法.如果10元的取0张,即0z =,则21221z -=,即5元的有21种取法; 如果10元的取1张,即1z =,则21219z -=,即5元的有19种取法; 如果10元的取2张,即2z =,则21217z -=,即5元的有17种取法; ……如果10元的取10张,即10z =,则2121z -=,即5元的有1种取法; 所以总数为2211917111121++++==. 那么121Q P -=.。
数学阶梯问题

数学阶梯问题阶梯问题是一种基础的数学难题,需要我们掌握基本的数学知识,比如等差数列,算术平均数,几何平均数等等。
在此非常荣幸能够为大家讲解阶梯问题的解决方法及其实际应用。
首先,什么是阶梯问题呢?在数学上,阶梯问题是指一组数排列成阶梯形式,其中每个数与它的相邻数的差都相同。
例如,一个简单的阶梯数列可能是1,5,9,13,17……,其中每一对相邻数的差都是4。
而解决这种问题的关键在于找到每个数之间的规律性。
接下来我们来探讨如何解决阶梯问题。
首先,我们需要确定差值,即相邻两项之间的差值。
这个差值被称为公差,通常用字母d表示。
对于任意的阶梯数列,公差的数值都是相等的。
例如,对于上述的例子,公差是4。
我们可以通过相邻两项的差值来计算公差,即:d = a(n) - a(n-1)其中a(n)表示数列中的第n项,a(n-1)表示数列中的第n-1项,d 表示公差。
有了公差,我们就可以利用以下公式推导出阶梯数列中任意一项的数值:a(n) = a(1) + (n-1)*d其中a(n)表示数列中的第n项,a(1)表示数列中的第一项,n表示数列中第n项的位置,d表示公差。
通过这个公式,我们可以计算出阶梯数列中任意一项的值。
这对于解决阶梯问题非常有用。
比如说,如果我们知道数列的首项和公差,那么我们就可以轻松地计算任意项的数值。
举例来说,假设我们有一个阶梯数列:3,7,11,15,19……,公差是4。
我们想计算第8项的数值。
根据上面的公式,我们可以得出:a(8) = a(1) + (8-1)*da(8) = 3 + 7*4a(8) = 31因此,第8项的数值是31。
这个解法非常简单,只需要将两个已知的量带入公式进行计算即可。
除了计算每个数值之外,阶梯问题还可以用于解决其他类型的问题。
比如,我们可以根据阶梯数列求出该数列的平均值。
这个平均值通常指的是算术平均数或者几何平均数。
算术平均数是数列中所有数值的总和再除以整个数列的项数。
3月试题答案-六年级奥数天天练

3.1【答案】根据对应关系,再运用阶梯型标数法画图如下:共有132种填法.3.2【答案】3.3【答案】3.4【答案】3.5【答案】由于四位数的四个数位上的数的大小关系已经非常明确,而对于从0~9中任意选取的4个数字,它们的大小关系也是明确的,那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大,所以千位不能为0,本身已符合四位数的首位不能为0的要求,所以进行选择时可以把0包含在内),也就是说满足条件的四位数的个数与从0~9中选取4个数字的选法是一一对应的关系,那么满足条件的四位数有3.6【答案】3.7【答案】取1个苹果有1种方法,取2个苹果有2种方法,取3个苹果有4种取法,以后取任意个苹果的种数等于取到前三个苹果所有情况之和,以此类推,参照上题列表如下:取完这堆苹果一共有81种方法.3.8【答案】按照蜜蜂只能从小号码的蜂房爬近相邻大号码的蜂房的原则,运用标号法进行计算.如图所示,小蜜蜂从A 出发到B处共有296种不同的回家方法.3.9【答案】3.10【答案】解:设公鸡买了x只,母鸡买了y只,小鸡买了z只,则3.11【答案】3.12【答案】3.13【答案】3.14【答案】3.15【答案】3.16【答案】3.17【答案】解答:如下图所示,在正六边形ABCDEF中,与面积相等,12个组成小正六角星形,那么由6个及12个组成的正六边形的面积为16÷12×(12+6)=24(平方厘米).而通过下图,我们知道,正六边形ABCDEF可以分成6个小正三角形,并且它们面积相等,且与六个角的面积相等,所以大正六角星形的积24÷6×12=48(平方厘米).3.18【答案】3.19【答案】3.20【答案】3.21【答案】因为3÷7=0.428571,6个数字一个循环,又2011÷6=335......1所以小数点后面第2011位上的数字是4.因为(4+2+8+5+7+1)×335+4=9049所以,从小数点后第一位到第2011位的所有数字之和是90493.22【答案】方法一:当十位为1时,共有111,210共2个;当十位为2时,共有:123;222;321;420共4个;当十位为3时,共有:135;234;333;432;531;630共6个;当十位为4时,共有:147;246;345;444;543;642;741;840共8个;当十位为5时,共有:159;258;357;456;555;654;753;852;951共9个;当十位为6时,共有:369;468;567;666;765;864;963;共7个;当十位为7时,共有:579;678;777;876;975;共5个;当十位为8时,共有:789;888;987共3个;当十位为9时,共有:999共1个;所以,中间数字恰好是首尾数字的平均值的好数共有:45个.方法二:(对应法)根据题意,如果百位和个位数字确定后,十位数字就确定,因此百位和个位数字的取法个数,就是好数的个数,又因为百位数字和个位数字的奇偶性相同,对于百位有9种选法,百位选定后个位数字有5种选择,因此有9×5=45个好数。
计数之对应法

7-6-3.计数之对应法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.例题精讲模块三、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.一、图形中的对应关系【例1】在8×8的方格棋盘中,取出一个由三个小方格组成的“L”形(如图),一共有多少种不同的方法?【例2】在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?【巩固】用一张如图所示的纸片盖住66方格表中的四个小方格,共有多少种不同的放置方法?【例3】图中可数出的三角形的个数为.【例4】如图所示,在直线AB上有7个点,直线CD上有9个点.以AB上的点为一个端点、CD上的点为另一个端点的所有线段中,任意3条线段都不相交于同一个点,求所有这些线段在AB与CD之间的交点数.C D二、数字问题中的对应关系【例5】有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大?【巩固】三位数中,百位数比十位数大,十位数比个位数大的数有多少个?【例6】数3可以用4种方法表示为一个或几个正整数的和,如3,12++.问:1999表示+,111+,21为一个或几个正整数的和的方法有多少种?【例7】请问至少出现一个数码3,并且是3的倍数的五位数共有多少个?三、对应与阶梯型标数法【例8】游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?【例9】学学和思思一起洗5个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有种不同的摞法.【巩固】学学和思思一起洗4个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,问学学摞好的碗一共有种不同的摞法。
标数法与XXX台阶问题

标数法与XXX台阶问题解法二:斐波那契数列递推公式,第十项为89,选D。
在标数法中,我们可以通过标记每个节点的情况数,来计算从起点到终点的最短路径的方案数。
这种方法适用于不能走“回头路”的情况。
举例来说,如果要从A到B,我们可以先走到C或者D,然后再从C或者D到达B,这样就可以通过标数法来计算从A到B的方案数。
最近几年的考题中,也出现了一些需要用到标数法的问题,例如从A到B的最短路径有多少种,或者在某些限制条件下,从一个点到另一个点有多少种走法等。
除了标数法,还有一种经典的问题叫做XXX台阶问题,也可以用斐波那契递推数列来解决。
例如在一个十阶楼梯上,XXX每次只能走一阶或者两阶,问走完此楼梯共有多少种方法。
我们可以通过斐波那契数列递推公式来计算,最终得到的结果为89.一年后可以繁殖的兔子总对数为斐波那契数列,选B。
假设刚出生的兔子,一个月后长成大兔子,两个月及以后的每个月可以生一对小兔子。
小兔子的来源只有一种:大兔子生出小兔子;大兔子的来源有两种:小兔子经过一个月变成大兔子、原来的大兔子依然是大兔子。
根据上述规律,可以得到每月的小兔子对数和大兔子对数,从而得到兔子总对数。
根据斐波那契数列的规律,从1号蜂房出发到达8号蜂房的不同走法数为21种,选C。
从1号出发,到达编号数分别为5、2、6、3、7、4、8的蜂房时,对应的方法数分别为1、2、3、5、8、13、21.到达7号的前一步有两类情况:从3号往右上过来或者从6号往右过来,所以到达7号的情况数等于到达3号的情况数加上到达6号的情况数。
从一个3×4的方格中的一个顶点A到顶点B的最短路线有15条。
可以使用组合数学或标数法来解决这个问题。
A。
1.2.3.5.8.13.21.34.55.89每次吃一颗或两颗,相当于每次可以走一步或两步,因此问题可以转化为在斐波那契数列中求第11项,即为89,选B。
例4:某人有7个球,其中3个红的、2个黄的、2个蓝的,他把这7个球随机地排成一行,那么红球在黄球两侧的排列方法有(。
六年级数学专题思维训练—计数综合(含答案及解析)

六年级数学专题思维训练—计数综合1、若4个两两不同的自然数的倒数之和为1,则这样的自然数组(次序不同认为是同共有组,2、如下图所示,在纸上画有A、B、C三点,经过其中任意两点画一条直线,可以画3条直线,如果在纸上画有5个点,其中任意三个点都不在一条直线上,经过每两点画一条直线,可以画____条直线.3、在右下图中,以最短的路径从点P到点Q,请问共有种不同的走法.4、科学家“爱因斯坦”的英文名拼写为“Einstein”,如下图所示,按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”.5、在下图中,用水平或者竖直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE”的路线共有多少条?6、甲队和乙队进行的一场足球赛的最终比分是4:2,已知甲队先进一球,而乙队在比赛过程中始终没有领先过,那么两队的入球次序共有种不同的可能.7、如下图所示,27个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有条.8、国际象棋中“马”的走法如图a所示,位于O位置的“马”只能走到标有×的格中,类似于中国象棋中的“马走日”.如果“马”在8×8的国际象棋棋盘中位于第一行第二列(图b)中标有△的位置),要走到第八行第五列(图b)中标有★的位置),最短路线有条.9、小思从X市开车到y市,她必须遵照下图箭头所指示的方向行驶:请问小思由X市到y市共有多少种不同的路径?10、 A,B两人进行象棋比赛,没有和棋,先比对方多胜三局的一方赢得比赛,如果经过11局比赛A才以7胜4负获胜,那么这11局比赛的胜负排列共有种.(例如:“胜负胜负胜负胜负胜胜胜”是一种胜负排列)11、一个正在行进的8人队列,每人身高各不相同,按从低到高的次序排列.现在他们要变成2列纵队,每列仍然是按从低到高的次序排列,同时要求并排的每两人中左边的人比右边的人要矮,那么,2列纵队有种不同排法.12、有7个相同的小球放人4个不同的盒子中,每个盒子中至少放一个球,则共有种不同的放法.A. 15 B.18 C.20 D.2413、以下图的黑点作为顶点,请问可作出多少个三角形?14、正整数2009的数码和为11,请问在2010到2999之间有多少个自然数其数码和为11 ?15、学学和思思一起洗已摞好的5个互不相同的碗,思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放人碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有种不同的摞法。
标数法口诀

标数法口诀以下是五个符合要求的口诀:《标数法口诀一》一二三四依次来,标数其实很简单。
一条路走到底,就像直线不拐弯。
二路分开左右看,选择清楚不犯难。
三路好比岔路口,仔细思考再向前。
四路如同多方向,冷静判断别慌乱。
从小数字开始算,一步一步记心间。
遇到复杂也别怕,耐心标数全搞定它。
《标数法口诀二》标数法呀真奇妙,小朋友们要记牢。
一是起点认真找,方向明确不能跑。
二是过程慢慢瞧,步骤清晰不混淆。
三看分支怎么绕,条理清楚才最好。
四要终点确认好,大功告成哈哈笑。
就像走路一步步,稳稳当当不会错。
大家快来一起学,轻松掌握没话说。
《标数法口诀三》标数如同走楼梯,一步一步向上移。
一是基础要打实,稳稳站立不偏移。
二把台阶看仔细,顺序不能出问题。
三走起来有规律,不慌不忙有秩序。
四到终点心欢喜,收获成果笑嘻嘻。
好像游戏玩通关,快乐感觉在心田。
学会标数用处大,解题不再困难啦。
《标数法口诀四》标数法,要学会,听我来讲小口诀。
一开头,别乱走,目标明确才不忧。
二中间,思路展,多种可能都看见。
三过程,耐心点,仔细分析不能倦。
四结尾,答案显,大功告成笑开颜。
如同搭积木一般,稳稳当当建家园。
快来一起用标数,知识海洋任你游。
《标数法口诀五》标数就像建房子,一砖一瓦有次序。
一是先把地基打,基础牢固才不怕。
二是开始砌墙壁,横竖整齐又美丽。
三将屋顶慢慢盖,遮风挡雨有依赖。
四等房子全建成,满心欢喜好高兴。
好比画画一步步,精彩作品就出炉。
小朋友们快练习,标数轻松就学会。
部编版数学六年级上册第1讲.数形结合

方形面积之和 .那么,可以构造一个图形,如下图:
4
3
2
1
12
3
4
一方面,图中大正方形的边长为“1+2+3+4”,面积为 (12 3 4)2 .
另一方面它又等于全部小正方形的面积之和.但是注意在放置两个 2×2 及 4×4 的正方形时, 两个正方形有重叠部分— — 图中浅色阴影正方形,再把重叠部分补到它的右上方的小正方 块— — 图中深色阴影正方形中去,这样一来这些小正方形的面积和正好等于边长为 “1+2+3+4”的大正方形面积.所以: 13 23 33 43 112 2 22 3 32 4 42 (1 2 3 4)2
c
d
c
d
c
d
a
S1
S2
a
S1
S2
S5
a
S1
S2
b
S3
S4
b
S3
S4
S6
(4)的答案是各个小长方体的体积之和
c a
f
e d
b
例6
试用图解法说明: 1 1 1 1 1 11
2 22 23 24
2n
2n
(学案对应:带号 2)
【分析】如图,将一个边长为的正方形,平均分成两块,然后再将剩下的平均分成两块,依次类推,
三、阶梯型标数法 (一)阶梯型标数指的是求图中从点 A 走到点 B 的最短路线的条数(图中虚线不能走) (二)阶梯型标数特征
1.走到图中任意一点的所有路线中,单位竖线段个数不多于单位横线段的个数。 2.走到虚线边上任意一点的路线条数,恰好是卡塔兰数(1,,2 ,5,14,4,,13,,429, )
标准阶梯形矩阵

标准阶梯形矩阵阶梯形矩阵是线性代数中的一个重要概念,它在矩阵运算和方程组求解中有着重要的应用。
本文将介绍标准阶梯形矩阵的定义、性质和应用,并对其相关概念进行详细解释。
1. 定义。
标准阶梯形矩阵是指在一个矩阵中,每一行的第一个非零元素为1,且每一行的1所在列的其他元素都为0,同时每一行的1所在列的行数递增。
简单来说,标准阶梯形矩阵就是一个上三角矩阵,但是它的每一行的第一个非零元素都为1。
2. 性质。
标准阶梯形矩阵有一些重要的性质:每个非零行的首个非零元素所在列的列号严格递增;任意两行之间的首个非零元素所在列的列号不同;每个非零行的首个非零元素为1;每个非零行的首个非零元素所在列的其他元素都为0。
3. 应用。
标准阶梯形矩阵在线性代数中有着广泛的应用,特别是在方程组的求解中。
通过将系数矩阵化为标准阶梯形矩阵,可以方便地求解方程组的解。
此外,标准阶梯形矩阵还可以用于矩阵的求逆、矩阵的秩计算等方面。
4. 实例分析。
下面我们通过一个实例来说明标准阶梯形矩阵的应用。
考虑方程组:```。
2x + y + z = 1。
4x + 3y + 4z = 2。
2x + 2y + 3z = 3。
```。
我们可以将其系数矩阵化为标准阶梯形矩阵:```。
2 1 1 | 1。
0 1 2 | 0。
0 0 1 | 1。
```。
通过对标准阶梯形矩阵进行化简,我们可以得到方程组的解为: ```。
x = 1。
y = -2。
z = 1。
```。
可以看到,通过将系数矩阵化为标准阶梯形矩阵,我们可以方便地求解出方程组的解。
5. 总结。
标准阶梯形矩阵是线性代数中的一个重要概念,它在方程组求解、矩阵运算等方面有着重要的应用。
通过本文的介绍,我们了解了标准阶梯形矩阵的定义、性质和应用,并通过实例分析说明了其在实际问题中的应用价值。
希望本文对读者对标准阶梯形矩阵有所帮助。
小学计数综合计数方法与技巧

计数方法与技巧知识结构(1)归纳法:从条件值较小的数开始,找出其中规律,或找出其中的递推数量关系,归纳出一般情况下的数量关系.(2)整体法:解决计数问题时,有时要“化整为零”,使问题变得简单;有时反而要从整体上来考虑,从全局、从整体来研究问题,反而有利于发现其中的数量关系.(3)对应法:将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.(4)递推法:对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.例题精讲【例 1】一条直线分一个平面为两部分.两条直线最多分这个平面为四部分.问5条直线最多分这个平面为多少部分?【考点】计数之归纳法【难度】3星【题型】解答【解析】方法一:我们可以在纸上试着画出1条直线,2条直线,3条直线,……时的情形,于是得到下表:由上表已知5条直线最多可将这个平面分成16个部分,并且不难知晓,当有n条直线时,最多可将平面分成2+2+3+4+…+n=()12n n++1个部分.方法二:如果已有k条直线,再增加一条直线,这条直线与前k条直线的交点至多k个,因而至多被分成k+1段,每一段将原有的部分分成两个部分,所以至多增加k+1个部分.于是3条直线至多将平面分为4+3=7个部分,4条直线至多将平面分为7+4=11个部分,5条直线至多将平面分为11+5=16个部分.一般的有k条直线最多将平面分成:1+1+2+…+k=()12k k++1个部分,所以五条直线可以分平面为16个部分.【答案】16【巩固】 平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】 假设用a k 表示k 条直线最多能把圆的内部分成的部分数,这里k =0,1,2,……a 0=1 a 1=a 0+1=2 a 2=a 1+2=4 a 3=a 2+3=7 a 4=a 3+4=11 ……故5条直线可以把圆分成16部分,100条直线可以把圆分成5051部分【答案】5051部分【例 2】 平面上10个两两相交的圆最多能将平面分割成多少个区域?【考点】计数之归纳法【难度】4星【题型】解答【解析】 先考虑最简单的情形.为了叙述方便,设平面上k 个圆最多能将平面分割成k a 个部分.从图中可以看出,12a =,24221a ==+⨯,38422a ==+⨯,414823a ==+⨯,…… 可以发现k a 满足下列关系式:()121k k a a k -=+-.实际上,当平面上的(1k -)个圆把平面分成1k a -个区域时,如果再在平面上出现第k 个圆,为了保证划分平面的区域尽可能多,新添的第k 个圆不能通过平面上前()1k -个圆之间的交点.这样,第k 个圆与前面()1k -个圆共产生2(1)k ⨯-个交点,如下图:141312111098765432187652134431221这2(1)k ⨯-个交点把第k 个圆分成了2(1)k ⨯-段圆弧,而这2(1)k ⨯-段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了2(1)k ⨯-个部分.所以,()121k k a a k -=+-.那么,10987292829272829a a a a =+⨯=+⨯+⨯=+⨯+⨯+⨯=12122...272829a =+⨯+⨯++⨯+⨯+⨯()2212...78992=+⨯+++++=.故10个圆最多能将平面分成92部分.【答案】92【巩固】 10个三角形最多将平面分成几个部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】 设n 个三角形最多将平面分成n a 个部分.1n =时,12a =;2n =时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有236⨯=(个)交点.这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即2223a =+⨯.3n =时,第三个三角形与前面两个三角形最多有4312⨯=(个)交点,从而平面也增加了12个部分,即:322343a =+⨯+⨯. ……一般地,第n 个三角形与前面()1n -个三角形最多有()213n -⨯个交点,从而平面也增加()213n -⨯个部分,故()()222343213224213332n a n n n n ⎡⎤=+⨯+⨯++-⨯=++++-⨯=-+⎣⎦;特别地,当10n =时,2103103102272a =⨯+⨯+=,即10个三角形最多把平面分成272个部分.【答案】272【例 3】 一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】 一个长方形把平面分成两部分.第二个长方形的每一条边至多把第一个长方形的内部分成2部分,这样第一个长方形的内部至多被第二个长方形分成五部分.同理,第二个长方形的内部至少被第一个长方形分成五部分.这两个长方形有公共部分(如下图,标有数字9的部分).还有一个区域位于两个长方形外面,所以两个长方形至多把平面分成10部分.第三个长方形的每一条边至多与前两个长方形中的每一个的两条边相交,故第一条边被隔成五条小线段,其中间的三条小线段中的每一条线段都把前两个长方形内部的某一部分一分为二,所以至多增加3×4=12个部分.而第三个长方形的4个顶点都在前两个长方形的外面,至多能增加4个部分.所以三个长方形最多能将平面分成10+12+4=26.【小结】n 个图形最多可把平面分成部分数:直线:()112n n ⨯++;圆:()21n n +⨯-; 三角形:()231n n +⨯⨯- ; 长方形:()241n n +⨯⨯-.【答案】26【巩固】 在平面上画5个圆和1条直线,最多可把平面分成多少部分?【考点】计数之归纳法【难度】5星【题型】解答【解析】先考虑圆.1个圆将平面分成2个部分.这时增加1个圆,这个圆与原有的1个圆最多有两个交点,成为2条弧,每条弧将平面的一部分一分为二,增加了2个部分,所以2个圆最多将平面分成4个部分.当有3个圆时,第3个圆与原有的2个产生4个交点而增加4个部分,所以3个圆最多将平面分成8个部分.同样的道理,5个圆最多将平面分成22个部分.再考虑直线.直线与每个圆最多有2个交点,这样与5个圆最多有10个交点.它们将直线分成11条线段或射线,而每条线段又将平面的一部分一分为二,2条射线增加了一部分,因此5个圆和1条直线最多可将平面分成32个部分.【答案】32【例 4】一个正方形的内部有1996个点,以正方形的4个顶点和内部的1996个点为顶点,将它剪成一些三角形.问:一共可以剪成多少个三角形?如果沿上述这些点中某两点之间所连的线段剪开算作一刀,那么共需剪多少刀?【考点】计数之整体法【难度】4星【题型】解答【解析】方法一:归纳法,如下图,采用归纳法,列出1个点、2个点、3个点…时可剪出的三角形个数,需剪的刀数.不难看出,当正方形内部有n个点时,可以剪成2n+2个三角形,需剪3n+l刀,现在内部有1996个点,所以可以剪成2×1996+2=3994个三角形,需剪3×1996+1=5989刀.方法二:整体法.我们知道内部一个点贡献360度角,原正方形的四个顶点共贡献了360度角,所以当内部有n个点时,共有360n+360度角,而每个三角形的内角和为180度角,所以可剪成(360n+360)÷180=2n+2个三角形.2n+2个三角形共有3×(2n+2)=6n+6条边,但是其中有4条是原有的正方形的边,所以正方形内部的三角形边有6n+6—4=6n+2条边,又知道每条边被2个三角形共用,即每2条边是重合的,所以只用剪(6n+2)÷2=3n+1刀.本题中n=1996,所以可剪成3994个三角形,需剪5989刀.【答案】可剪成3994个三角形,需剪5989刀【巩固】在三角形ABC内有100个点,以三角形的顶点和这100点为顶点,可把三角形剖分成多少个小三角形?【考点】计数之整体法【难度】4星【题型】解答【解析】整体法.100个点每个点周围有360度,三角形本身内角和为180度,所以可以分成()⨯+÷=个小三角形.360100180180201【答案】201个小三角形【例 5】在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】首先可以知道题中所讲的13⨯长方形中间的那个小主格为黑色,这是因为两个白格不相邻,所以不能在中间.显然,位于棋盘角上的黑色方格不可能被包含在这样的长方形中.下面分两种情况来分析:第一种情况,一个位于棋盘内部的黑色方格对应着两个这样的13⨯长方形(一横一竖);第二种情况,位于边上的黑色方格只能对应一个13⨯长方形.由于在棋盘上的32个黑色方格中,位于棋盘内部的18个,位于边上的有12个,位于角上的有2个,所以共有1821248⨯+=个这样的长方形.本题也可以这样来考虑:事实上,每一行都有6个13⨯长方形,所以棋盘上横、竖共有13⨯⨯=个.由于棋盘上的染色具有对称性,因此包含两个白色小方格与一⨯长方形68296个黑色小方格的长方形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系,这说明它们各占一半,因此所求的长方形个数为96248÷=个.【答案】48【巩固】用一张如图所示的纸片盖住66⨯方格表中的四个小方格,共有多少种不同的放置方法?【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】【解析】如图,将纸片中的一个特殊方格染为黑色,下面考虑此格在66⨯方格表中的位置.易见它不能位于四个角上;若黑格位于方格表中间如图浅色阴影所示的44⨯正方形内的某格时,纸片有4种不同的放法,共计44464⨯⨯=种;若黑格位于方格表边上如图深色阴影所示的方格中时,纸片的位置随之确定,即只有1种放法,此类放法有4416⨯=种.所以,纸片共有641680+=种不同的放置方法.【答案】80种【例 6】有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大?【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】由于四位数的四个数位上的数的大小关系已经非常明确,而对于从0~9中任意选取的4个数字,它们的大小关系也是明确的,那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大,所以千位不能为0,本身已符合四位数的首位不能为0的要求,所以进行选择时可以把0包含在内),也就是说满足条件的四位数的个数与从0~9中选取4个数字的选法是一一对应的关系,那么满足条件的四位数有41010987210 4321C⨯⨯⨯==⨯⨯⨯个.【答案】210个【巩固】三位数中,百位数比十位数大,十位数比个位数大的数有多少个?【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】相当于在10个数字中选出3个数字,然后按从大到小排列.共有10×9×8÷(3×2×1)=120种.实际上,前铺中每一种划法都对应着一个数.【答案】120种【例 7】 学学和思思一起洗5个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有 种不同的摞法.【考点】计数之对应与阶梯型标数法【难度】5星【题型】解答【关键词】2008年,第一届,学而思杯,5年级,第7题 【解析】 方法一:如下所示,共有42种不同的摞法:54321----,45321----,35421----,53421----,34521----,54231----,45231----,25431----,52431----,24531----,52341----,25341----,23541----,23451----,54312----,45312----,53412----,35412----,34512----,54132----,45132----,15432----,51432----,14532----,51342----,15342----,13542----,13452----,54123----,45123----,15423----,51423----,14523----,12543----,51243----,15243----,12453----,12354----,12534----,15234----,51234----, 12345----。
行测数量关系技巧:标数法进阶篇

行测数量关系技巧:标数法进阶篇通过标数法基础篇的学习相信大家已经基本掌握了标数法这一解题方法,并在涉及到最短路线的方法数这类题型中运用自如。
随着行测考试的日渐成熟,数学运算中的各种方法或多或少有一些延伸或变形,标数法也是如此,本文主要讲解标数法的进阶题型。
首先,回顾一道标准的标数法题目。
例1.小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方)。
假如他只能向东或者向北行走,则他上班不同走法共有:A.12种B.15种C.20种D.10种通过标数法基础篇的学习,我们已经了解了标数法是指将到达每个点的方法数标注在点的旁边的一种解题方法,通常运用在求最短路线方法数的题目中。
标数法的核心步骤是观察一个点能从哪些点走过来就把这些点的数加起来作为该点的方法数。
这道例题中规定了只能向东或者向北走,按照要求走就不会存在绕路的情况,那么这样从华兴园到软件公司的走法就是最短路线。
我们可以利用标数法的核心对原图进行标数:在路线方向和路线经过的点明确的情况下,我们能够利用标数法很快得出结果,上述例题从华兴园到到软件公司的方法数为10种,故答案为D。
其次,我们来学习标数法延伸后的第一类题目。
此类题目中不直接给出路线方向或路线经过的点,需要考生自行理解转化为标数模型求解。
例2.如图所示,有两排蜂房,一只蜜蜂从左下角的1号蜂房开始去8号蜂房,假设只朝右上或右下逐个爬行。
则不同的走法有:A.16种B.18种C.21种D.24种例题二中并没有给出明确的路线方向也没有路线中经过的点,需要我们根据题目的表述进行理解。
我们可以把每一个蜂房理解为路线中经过的点,路线方向是左下角的蜂房可以朝右侧相邻的两个蜂房移动(注意“只朝右上或右下逐个爬行”中的右上或右下应理解为整体观察的情况,即只向右侧的蜂房爬行)。
然后我们再采取标数法进行解题,如下图所示。
故从1号蜂房到8号蜂房共有21种方法,此题选C。
再次,我们来学习标数法延伸后的第二类题目。
小学奥数 计数之对应法 精选练习例题 含答案解析(附知识点拨及考点)

前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.模块一、图形中的对应关系【例 1】 在8×8的方格棋盘中,取出一个由三个小方格组成的“L ”形(如图),一共有多少种不同的方法? 【考点】计数之图形中的对应关系 【难度】3星 【题型】解答【解析】 注意:数“不规则几何图形”的个数时,常用对应法.第1步:找对应图形 每一种取法,有一个点与之对应,这就是图中的A 点,它是棋盘上横线与竖线的交点,且不在棋盘边上.第2步:明确对应关系 从下图可以看出,棋盘内的每一个点对应着4个不同的取法(“L ”形的“角”在2×2正方形的不同“角”上).第3步:计算对应图形个数 由于在 8×8的棋盘上,内部有7×7=49(个)交叉点, 第4步:按照对应关系,给出答案故不同的取法共有49×4=196(种).评注:通过上面两个范例我们知道,当直接去求一个集合元素的个数较为困难的时候,可考虑采用相等的原则,把问题转化成求另一个集合的元素个数.【答案】196【例 2】 在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个? 【考点】计数之图形中的对应关系 【难度】3星 【题型】解答例题精讲教学目标7-6-3计数之对应法【解析】首先可以知道题中所讲的13⨯长方形中间的那个小主格为黑色,这是因为两个白格不相邻,所以不能在中间.显然,位于棋盘角上的黑色方格不可能被包含在这样的长方形中.下面分两种情况来分析:第一种情况,一个位于棋盘内部的黑色方格对应着两个这样的13⨯长方形(一横一竖);第二种情况,位于边上的黑色方格只能对应一个13⨯长方形.由于在棋盘上的32个黑色方格中,位于棋盘内部的18个,位于边上的有12个,位于角上的有2个,所以共有1821248⨯+=个这样的长方形.本题也可以这样来考虑:事实上,每一行都有6个13⨯长方形,所以棋盘上横、竖共有13⨯长方形68296⨯⨯=个.由于棋盘上的染色具有对称性,因此包含两个白色小方格与一个黑色小方格的长方形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系,这说明它们各占一半,因此所求的长方形个数为96248÷=个.【答案】48【巩固】用一张如图所示的纸片盖住66⨯方格表中的四个小方格,共有多少种不同的放置方法?【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】如图,将纸片中的一个特殊方格染为黑色,下面考虑此格在66⨯方格表中的位置.易见它不能位于四个角上;若黑格位于方格表中间如图浅色阴影所示的44⨯正方形内的某格时,纸片有4种不同的放法,共计44464⨯⨯=种;若黑格位于方格表边上如图深色阴影所示的方格中时,纸片的位置随之确定,即只有1种放法,此类放法有4416⨯=种.所以,纸片共有641680+=种不同的放置方法.【答案】80种【例3】图中可数出的三角形的个数为.【考点】计数之图形中的对应关系【难度】4星【题型】填空【解析】这个图不像我们以前数三角形那样规则,粗看似乎看不出其中的规律,不妨我们取出其中的一个三角形,发现它的三条边必然落在这个图形中的三条大线段上,而每三条大线段也正好能构成一个三角形,因此三角形的个数和三条大线段的取法是一一对应的关系,图中一共有8条大线段,因此有3 856C=个三角形.【答案】56个三角形【例 4】 如图所示,在直线AB 上有7个点,直线CD 上有9个点.以AB 上的点为一个端点、CD 上的点为另一个端点的所有线段中,任意3条线段都不相交于同一个点,求所有这些线段在AB 与CD 之间的交点数. 【考点】计数之图形中的对应关系 【难度】4星 【题型】解答CD【解析】 常规的思路是这样的:直线AB 上的7个点,每个点可以与直线CD 上的9个点连9根线段,然后再分析这些线段相交的情况.如右图所示,如果注意到下面这个事实:对于直线AB 上的任意两点M 、N 与直线CD 上的任意两点P 、Q 都可以构成一个四边形MNQP ,而这个四边形的两条对角线MQ 、NP 的交点恰好是我们要计数的点,同时,对于任意四点(AB 与CD 上任意两点)都可以产生一个这样的交点,所以图中两条线段的交点与四边形有一一对应的关系.这说明,为了计数出有多少个交点,我们只需要求出在直线AB 与CD 中有多少个满足条件的四边形MNQP 就可以了!从而把问题转化为:在直线AB 上有7个点,直线CD 上有9个点.四边形MNQP 有多少个?其中点M 、N 位于直线AB 上,点P 、Q 位于直线CD 上.这是一个常规的组合计数问题,可以用乘法原理进行计算:由于线段MN 有2721C =种选择方式,线段PQ 有2936C =种选择方式,根据乘法原理,共可产生2136756⨯=个四边形.因此在直线AB 与CD 之间共有756个交点.【答案】756个交点模块二、数字问题中的对应关系【例 5】 有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大? 【考点】计数之数字问题中的对应关系 【难度】4星 【题型】解答【解析】 由于四位数的四个数位上的数的大小关系已经非常明确,而对于从0~9中任意选取的4个数字,它们的大小关系也是明确的,那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大,所以千位不能为0,本身已符合四位数的首位不能为0的要求,所以进行选择时可以把0包含在内),也就是说满足条件的四位数的个数与从0~9中选取4个数字的选法是一一对应的关系,那么满足条件的四位数有410109872104321C ⨯⨯⨯==⨯⨯⨯个.【答案】210个【巩固】 三位数中,百位数比十位数大,十位数比个位数大的数有多少个? 【考点】计数之数字问题中的对应关系 【难度】4星 【题型】解答【解析】 相当于在10个数字中选出3个数字,然后按从大到小排列.共有10×9×8÷(3×2×1)=120种.实际上,前铺中每一种划法都对应着一个数.【答案】120种【例 6】 数3可以用4种方法表示为一个或几个正整数的和,如3,12+,21+,111++.问:1999表示为一个或几个正整数的和的方法有多少种? 【考点】计数之数字问题中的对应关系 【难度】4星 【题型】解答【解析】 我们将1999个1写成一行,它们之间留有1998个空隙,在这些空隙处,或者什么都不填,或者填上“+”号.例如对于数3,上述4种和的表达方法对应:1 1 1,1+1 1,1 1+1,1+1+1. 可见,将1999表示成和的形式与填写1998个空隙处的方式之间是一一对应的关系,而每一个空隙处都有填“+”号和不填“+”号2种可能,因此1999可以表示为正整数之和的不同方法有1998199822222⨯⨯⨯=个相乘种.【答案】19982种【例 7】 请问至少出现一个数码3,并且是3的倍数的五位数共有多少个? 【考点】计数之数字问题中的对应关系 【难度】4星 【题型】解答 【关键词】小学数学竞赛【解析】 五位数共有90000个,其中3的倍数有30000个.可以采用排除法,首先考虑有多少个五位数是3的倍数但不含有数码3.首位数码有8种选择,第二、三、四位数码都有9种选择.当前四位的数码确定后,如果它们的和除以余数为0,则第五位数码可以为0、6、9;如果余数为1,则第五位数码可以为2、5、8;如果余数为2,则第五位数码可以为1、4、7.可见只要前四位数码确定了,第五位数码都有3种选择,所以五位数中是3的倍数但不含有数码3的数共有8999317496⨯⨯⨯⨯=个. 所以满足条件的五位数共有300001749612504-=个.【答案】12504个模块三、对应与阶梯型标数法【例 8】 游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱? 【考点】计数之对应与阶梯型标数法 【难度】5星 【题型】解答【解析】 与类似题目找对应关系.要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可以利用斜直角三角模型.在下图中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A 点沿格线走到B 点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求下图中从A 到B 有多少种不同走法.使用标数法,可求出从A 到B 有42种走法.AB424228145141494553221111111但是由于10个小朋友互不相同,必须将他们排队,可以分成两步,第一步排拿2元的小朋友,5个人共有5120=!种排法;第二步排拿到1元的小朋友,也有120种排法,所以共有5514400⨯=!!种排队方法.这样,使售票员能找得开零钱的排队方法共有4214400604800⨯=(种).【答案】604800种【例 9】 学学和思思一起洗5个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有 种不同的摞法. 【考点】计数之对应与阶梯型标数法 【难度】5星 【题型】解答 【关键词】学而思杯,5年级,第7题【解析】 方法一:如下所示,共有42种不同的摞法:54321----,45321----,35421----,53421----,34521----,54231----,45231----,25431----,52431----,24531----,52341----,25341----,23541----,23451----,54312----,45312----,53412----,35412----,34512----,54132----,45132----,15432----,51432----,14532----,51342----,15342----,13542----,13452----,54123----,45123----,15423----,51423----,14523----,12543----,51243----,15243----,12453----,12354----,12534----,15234----,51234----, 12345----。
阶梯型标数法原理

阶梯型标数法原理嘿,朋友们!今天咱来唠唠这个阶梯型标数法原理。
这玩意儿啊,就像是咱生活中的小梯子,一步一步带着咱往上走,可有意思啦!你想想看啊,咱平时走路是不是得一步一步来呀,这阶梯型标数法不也一样嘛!它能把一个大问题啊,拆分成一个个小步骤,就像把一条长长的路分成了好多级台阶。
每一级台阶就是一个小目标,等咱踏踏实实地踩上了这一级,再迈向下一步,可不就稳稳当当的嘛。
比如说咱要去爬山,那山看着好高好高啊,要是直接仰头就往上冲,那不得累得气喘吁吁呀。
但要是咱把这爬山的路看成是阶梯型的,一步一步地去走,是不是感觉就没那么难啦?这阶梯型标数法就是这样,让复杂的事情变得简单起来。
咱再打个比方,就像搭积木一样。
你要是一股脑儿地把所有积木都堆上去,那肯定得塌呀。
但要是一块一块有顺序地往上搭,按照一定的步骤来,那就能搭出漂亮的城堡啦!这和阶梯型标数法不是一个道理嘛。
它可真是个神奇的东西呢!能帮咱理清思路,找到解决问题的办法。
就好像在迷宫里找到了那根能指引方向的线一样。
你说要是没有它,咱在那迷宫里瞎转悠,得多晕乎呀!而且啊,这阶梯型标数法还能让咱看到自己的进步呢。
每踏上一级台阶,咱就知道自己又前进了一点,那种成就感啊,可别提多棒啦!这就像咱小时候学走路,一步一步,从摇摇晃晃到稳稳当当,每一步都是成长呀!你说咱生活中有多少事情是可以用这阶梯型标数法来解决的呀?学习上,工作中,甚至是咱平时做个小手工,都能派上用场呢!它就像是我们的小助手,默默地帮着我们把困难一点点攻克。
咱可别小瞧了这小小的阶梯型标数法哦,它虽然看起来简单,但是用处可大着呢!它能让咱做事更有条理,更有效率,还能让咱更有信心去面对各种挑战。
所以啊,朋友们,以后遇到什么难题,咱就试着用这阶梯型标数法来拆解看看,说不定就能找到解决问题的钥匙啦!让我们一起用好这个神奇的工具,在生活的道路上稳稳地向上攀登吧!。
阶梯型标数法
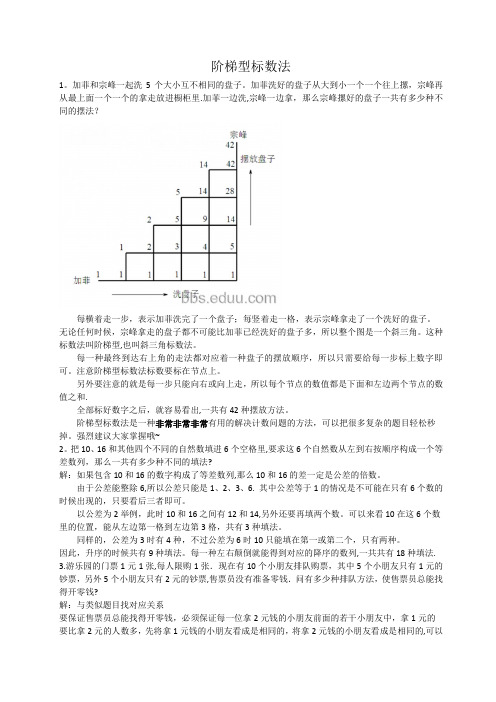
阶梯型标数法1。
加菲和宗峰一起洗5个大小互不相同的盘子。
加菲洗好的盘子从大到小一个一个往上摞,宗峰再从最上面一个一个的拿走放进橱柜里.加菲一边洗,宗峰一边拿,那么宗峰摞好的盘子一共有多少种不同的摆法?每横着走一步,表示加菲洗完了一个盘子;每竖着走一格,表示宗峰拿走了一个洗好的盘子。
无论任何时候,宗峰拿走的盘子都不可能比加菲已经洗好的盘子多,所以整个图是一个斜三角。
这种标数法叫阶梯型,也叫斜三角标数法。
每一种最终到达右上角的走法都对应着一种盘子的摆放顺序,所以只需要给每一步标上数字即可。
注意阶梯型标数法标数要标在节点上。
另外要注意的就是每一步只能向右或向上走,所以每个节点的数值都是下面和左边两个节点的数值之和.全部标好数字之后,就容易看出,一共有42种摆放方法。
阶梯型标数法是一种非常非常非常有用的解决计数问题的方法,可以把很多复杂的题目轻松秒掉。
强烈建议大家掌握哦~2。
把10、16和其他四个不同的自然数填进6个空格里,要求这6个自然数从左到右按顺序构成一个等差数列,那么一共有多少种不同的填法?解:如果包含10和16的数字构成了等差数列,那么10和16的差一定是公差的倍数。
由于公差能整除6,所以公差只能是1、2、3、6. 其中公差等于1的情况是不可能在只有6个数的时候出现的,只要看后三者即可。
以公差为2举例,此时10和16之间有12和14,另外还要再填两个数。
可以来看10在这6个数里的位置,能从左边第一格到左边第3格,共有3种填法。
同样的,公差为3时有4种,不过公差为6时10只能填在第一或第二个,只有两种。
因此,升序的时候共有9种填法。
每一种左右颠倒就能得到对应的降序的数列,一共共有18种填法.3.游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?解:与类似题目找对应关系要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可以利用斜直角三角模型.在下图中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A点沿格线走到B点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求下图中从A到B有多少种不同走法.使用标数法,可求出从A到B有42种走法。
小奥阶梯标数法

小奥阶梯标数法咱说这小奥阶梯标数法啊,这可不是个简单事儿。
我就见过好些个学数学的孩子,那脑子转得是快慢不一的。
就像我们那班级,有个小明,看着一副聪明样,脸上时常挂着微笑,淘气劲儿十足。
可一问他数学问题啊,他就皱起眉头,算个题半天算不出。
我就寻思着,得想个法子让大家都掌握这阶梯标数法。
首先呢,讲解是必不可少的。
我就把大家都召集起来,说:“咱呀都得学会这办法,就像那建筑,得一层一层盖,否则扣不上屋顶不是?”我站在黑板前,看着他们或迷茫或雀跃的眼神。
讲解内容可得生动,不能光是那些抽象的符号。
我就借来图示和动画,把那步骤一步步拆解开来,既然咱在讲数学,就得有点故事。
有一回,我就请来了老余,他那手里的粉笔都快磨成铜锣了。
老余站在讲台上,指着黑板就来了:“这阶梯标数法啊,就像走台阶,一步一步顺着来,别贪快,慢慢来。
”他讲起当年自己念书时的糗事,大家听得哈哈大笑,气氛一下子就轻松许多。
当然了,光会听也不成,得动手实际操作。
我就对校长说:“咱这孩子们得自己尝试,就像学骑自行车,摔几次也慢慢就掌握诀窍了。
”校长也有点犹豫,担心出错可怎么办。
我就说:“校长啊,这学数学跟下棋似的,得实践演练才行啊。
”校长被我这么一说,也点头同意了。
于是,我们就设计了一些可以实际应用的小项目。
有的孩子就对这项目犯难了。
像小丽,眼瞅着就愁眉苦脸,碰到问题就愈发急躁。
我就走到她跟前,鼓励她:“小丽啊,别着急,这啊就跟解谜游戏似的,一层层解,总能见着出口的。
”然后我就一步步给她分析,让她慢慢抠细节。
对于积极参与的学生啊,还得有激励措施。
光让人家练习,没个鼓励谁愿意啊?我就跟学校的教务处商量,设了个奖励机制。
每个月要是谁在掌握这方法上有明显提升,就给他们发个特别小奖励。
虽不是什么大奖,但个个心意。
大家一听有奖励,那学习积极性立马就高涨起来,像一群小鸡仔啄米似的,越想越来劲。
还有啊,得营造个好的学习氛围。
教室里不能总是死气沉沉的。
我就组织大家一起搞点儿活动,什么数学竞赛啦,解题比赛啦。
标数法与牛顿台阶问题
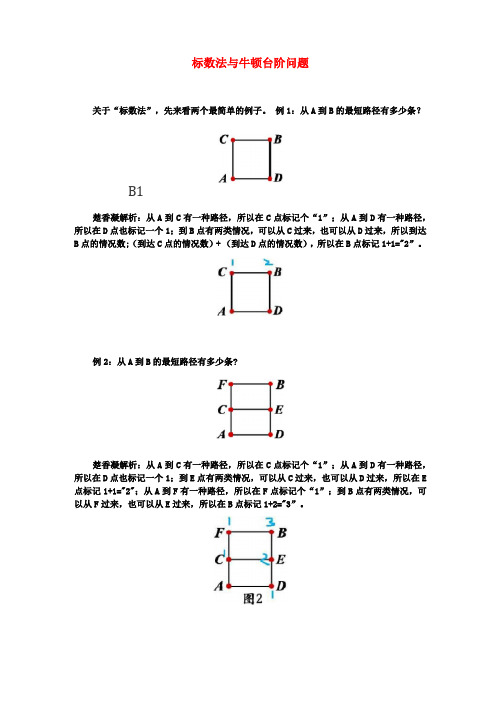
标数法与牛顿台阶问题关于“标数法”,先来看两个最简单的例子。
例1:从A到B的最短路径有多少条?B1楚香凝解析:从A到C有一种路径,所以在C点标记个“1”;从A到D有一种路径,所以在D点也标记一个1;到B点有两类情况,可以从C过来,也可以从D过来,所以到达B点的情况数;(到达C点的情况数)+ (到达D点的情况数),所以在B点标记1+1="2”。
例2:从A到B的最短路径有多少条?楚香凝解析:从A到C有一种路径,所以在C点标记个“1”;从A到D有一种路径,所以在D点也标记一个1;到E点有两类情况,可以从C过来,也可以从D过来,所以在E 点标记1+1="2";从A到F有一种路径,所以在F点标记个“1”;到B点有两类情况,可以从F过来,也可以从E过来,所以在B点标记1+2="3”。
注意:标数法适用的前提条件为“最短路径”,更通俗来讲,即不能走“回头路”。
下面来看近几年出现过的三道真题。
例1:A、B、Cm地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路。
如要从A地到达B地,且途中只能向南、东和东南方向行进,有多少种不同的走法:【山东2014】A.9B.11C.13D.15楚香凝解析:标数法,共15种,选D例2:从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择?【黑龙江2015】A.14B.15C.18D.21楚香凝解析:标数法,共15种,选B例3:下图为某大厦走火通道逃离路线。
某大厦集中所有的人员开展火灾逃生演习,从入口A点出发,要沿某几条线段才到出口F点。
逃离中,同一个点或同一线段只能经过1 次。
假设所有逃离路线都是安全的,则不同的逃离路线最多有()种。
【广州2015】A.8B.9C.10D.11应闲B 匚『出口楚香凝解析:此题与标数法的区别在于,可以往上和斜上走,所以标数法不再适用,需分类计算;A―D,之后有四种;A—B―D,之后有三种;A—B―C,之后有三种;共10种,选C牛顿台阶问题(斐波那契递推数列)例1:十阶楼梯,小张每次只能走一阶或者两阶,请问走完此楼梯共有多少种方法?A.55B.67C.74D.89楚香凝解析:解法一:列举找规律;阶梯数:1 2 3 4 5 6 7 8 9 10方法数: 1 2 3 5 8 13 21 34 55 89走到1阶只有1种方法;走到2阶有2种(1+1或直接上2阶);走到3阶有3种(1+1+1 或1+2或2+1)…依次类推,选D解法二:到达第十阶的前一步只有两类情况:【从第九阶迈一步上来】或者【从第八阶迈两步上来工所以到达第十阶的情况数二(到达第九阶的情况数)+ (到达第八阶的情况数),以此类推,到达某阶的情况数等于前面两个数之和(前两项通过列举得到),由此可得斐波那契递推数列 1、2、3、5、8、13、21、34、55、89,选 D解法三:分类计算;走五次两阶、共五步,有1种;走四次两阶、共六步,选出四步来走两阶,有C (6 4) =15种;走三次两阶、共七步,选出三步来走两阶,有C (7 3) =35种;走两次两阶、共八步,选出两步来走两阶,有C (8 2) =28种;走一次两阶、共九步,选出一步来走两阶,有C (9 1)=9种;走0次两阶,有1种;共 1+15+35+28+9+1=89 种,选 D拓展:十阶楼梯,小张每次只能走一阶或者两阶或者三阶,请问走完此楼梯共有多少种 方法?A.89B.169C.230D.274楚香凝解析:到达第十阶的情况数=(到达第九阶的情况数)+(到达第八阶的情况数) + (到达第七阶的情况数),以此类推…到达某阶的情况数等于前面三个数之和(前三项通过 列举得到),由此可得斐波那契递推数列如下:阶梯数:1 2 3 4 5 6 7 8 9 10方法数: 1 2 4 7 13 24 44 81 149 274例2:小璐有8元钱,她准备从明天起,用这8元钱每天买一个冰激淋或者一包果冻吃。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阶梯型标数法
1.加菲和宗峰一起洗5个大小互不相同的盘子。
加菲洗好的盘子从大到小一个一个往上摞,宗峰再从最上面一个一个的拿走放进橱柜里。
加菲一边洗,宗峰一边拿,那么宗峰摞好的盘子一共有多少种不同的摆法?
每横着走一步,表示加菲洗完了一个盘子;每竖着走一格,表示宗峰拿走了一个洗好的盘子。
无论任何时候,宗峰拿走的盘子都不可能比加菲已经洗好的盘子多,所以整个图是一个斜三角。
这种标数法叫阶梯型,也叫斜三角标数法。
每一种最终到达右上角的走法都对应着一种盘子的摆放顺序,所以只需要给每一步标上数字即可。
注意阶梯型标数法标数要标在节点上。
另外要注意的就是每一步只能向右或向上走,所以每个节点的数值都是下面和左边两个节点的数值之和。
全部标好数字之后,就容易看出,一共有42种摆放方法。
阶梯型标数法是一种非常非常非常有用的解决计数问题的方法,可以把很多复杂的题目轻松秒掉。
强烈建议大家掌握哦~
2.把10、16和其他四个不同的自然数填进6个空格里,要求这6个自然数从左到右按顺序构成一个等差数列,那么一共有多少种不同的填法?
解:如果包含10和16的数字构成了等差数列,那么10和16的差一定是公差的倍数。
由于公差能整除6,所以公差只能是1、2、3、6. 其中公差等于1的情况是不可能在只有6个数的时候出现的,只要看后三者即可。
以公差为2举例,此时10和16之间有12和14,另外还要再填两个数。
可以来看10在这6个数里的位置,能从左边第一格到左边第3格,共有3种填法。
同样的,公差为3时有4种,不过公差为6时10只能填在第一或第二个,只有两种。
因此,升序的时候共有9种填法。
每一种左右颠倒就能得到对应的降序的数列,一共共有18种填法。
3.游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?
解:与类似题目找对应关系
要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的
要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可
以利用斜直角三角模型.在下图中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A点沿格线走到B点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求下图中从A到B有多少种不同走法.使用标数法,可求出从A到B有42种走法。
但是由于10个小朋友互不相同,必须将他们排队,可以分成两步,第一步排拿2元的小朋友,5个人共有5!=120种排法;第二步排拿到1元的小朋友,也有120种排法,所以共有5!×5!=14400种排队方法。
这样,使售票员能找得开零钱的排队方法共有42×14400=604800种。
