2009年武平一中招收高一保送生加试卷数学试卷
2009年山西省中考数学试卷版含答案

2009年山西省初中毕业学业考试试卷数 学一、选择题(每小题2分,共20分)1.比较大小:2- 3-(填“>”、“=”或“<“). 2.山西有着丰富的旅游资源,如五台山、平遥古城、乔家大院等著名景点,吸引了众多的海内外游客,2008年全省旅游总收入739.3亿元,这个数据用科学记数法可表示为 .3.请你写出一个有一根为1的一元二次方程: .4= .5.如图所示,A 、B 、C 、D 是圆上的点,17040A ∠=∠=°,°,则C ∠= 度. 6.李师傅随机抽查了本单位今年四月份里6天的日用水量(单位:吨)结果如下:7,8,8,7,6,6,根据这些数据,估计四月份本单位用水总量为 吨.7.如图,ABC △与A B C '''△是位似图形,且顶点都在格点上,则位似中心的坐标是 .8.如图,ABCD Y的对角线AC 、BD 相交于点O ,点E 是CD 的中点,ABD △的周长为16cm ,则DOE △的周长是 cm .9.若反比例函数的表达式为3y x=,则当1x <-时,y 的取值范围是 .10.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .ABCD 1(第5题) A C D B E O (第8题)(1)(2)(3)…… ……二、选择题(在下列各小题中,均给出四个备选答案,其中只有一个正确答案,请将正确答案的字母号填入下表相应的空格内,每小题3分,共24分)11.下列计算正确的是( )A .623a a a ÷= B .()122--= C .()236326x x x -=-· D .()0π31-=12.反比例函数ky x=的图象经过点()23-,,那么k 的值是( )A .32-B .23- C .6- D .613.不等式组21318x x --⎧⎨->≥的解集在数轴上可表示为( )AB C D14.解分式方程11222x x x-+=--,可知方程( ) A .解为2x = B .解为4x = C .解为3x = D .无解15.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )A .5B .6C .7D .816.如图,AB 是O ⊙的直径,AD 是O ⊙的切线,点C 在O ⊙上,BC OD ∥,23AB OD ==,,则BC 的长为( )A .23B .32C D主视图左视图 俯视图(第15题)AB CDO(第16题)mnnn(2)(1) (第17题)17.如图(1),把一个长为m 、宽为n 的长方形(m n >)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )A .2m n -B .m n -C .2mD .2n18.如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32 B .76 C .256D .2三、解答题(本题共76分)19.(每小题4分,共12分)(1)计算:()()()2312x x x +---(2)化简:222242x x x x +---(3)解方程:2230x x --=20.(本题6分)已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.(1)填空:图1中阴影部分的面积是 (结果保留π);(2)请你在图2中以图1为基本图案,借助轴对称、平移或旋转设计一个完整的花边图案(要求至少含有两种图形变换).21.(本题8分)根据山西省统计信息网公布的数据,绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下:ADBEC(第18题)(第20题 图1)(第20题 图2)万户(1)填空:2004~2008移动电话年末用户的极差是 万户,固定电话年末用户的中位数是 万户; (2)你还能从图中获取哪些信息?请写出两条. 22.(本题8分)某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元. (1)该顾客至少可得到 元购物券,至多可得到 元购物券;(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.23.(本题8分)有一水库大坝的横截面是梯形ABCD ,AD BC EF ∥,为水库的水面,点E 在DC 上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB 的长为12米,迎水坡上DE 的长为2米,135120BAD ADC ∠=∠=°,°,求水深.(精确到0.11.73==)24.(本题8分)某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润y 甲(万元)与进货量x (吨)近似满足函数关系0.3y x =甲;乙种水果的销售利润y 乙(万元)与进货量x (吨)近似满足函数关系2y ax bx =+乙(其中0a a b ≠,,为常数),且进货量x 为1吨时,销售利润y 乙为1.4万元;进货量x 为2吨时,销售利润y 乙为2.6万元.(第23题)(1)求y 乙(万元)与x (吨)之间的函数关系式.(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为t 吨,请你写出这两种水果所获得的销售利润之和W (万元)与t (吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?25.(本题12分)在ABC △中,2120AB BC ABC ==∠=,°,将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A BC A B 111△,交AC 于点E ,11A C 分别交AC BC 、于D F 、两点.(1)如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系?并证明你的结论;(2)如图2,当α30=°时,试判断四边形1BC DA 的形状,并说明理由;(3)在(2)的情况下,求ED 的长.26.(本题14分)如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移,设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关于t 的函数关系式,并写出相应的t 的取值范围.ADBECF1A1CADBECF1A1C(第25题 图1)(第25题 图2)2009年山西省初中毕业学业考试试卷数 学一、选择题(每小题2分,共20分)1.> 2.107.39310⨯ 3.答案不唯一,如21x = 4 5.306.210 7.(9,0) 8.8 9.30y -<< 10.32n +二、选择题(在下列各小题中,均给出四个备选答案,其中只有一个正确答案,请将正确三、解答题(本题共76分)19.(1)解:原式=()226932x x x x ++--+ ·························································· (2分) =226932x x x x ++-+- ····························································· (3分) =97x +. ·················································································· (4分)(2)解:原式=()()()22222x x x x x +-+-- ································································· (2分) =222x x x --- ············································································· (3分) =1. ··························································································· (4分)(3)解:移项,得223x x -=,配方,得()214x -=, ············································· (2分)∴12x -=±,∴1213x x =-=,. ···························································· (4分) (注:此题还可用公式法,分解因式法求解,请参照给分)20.解:(1)π2-; ··························································································· (2分)(2)答案不唯一,以下提供三种图案.(注:如果花边图案中四个图案均与基本图案相同,则本小题只给2分;未画满四个“田”字格的,每缺1个扣1分.)21.(1)935.7,859.0; ························································································ (4分)(2)解:①2004~2008移动电话年末用户逐年递增.②2008年末固定电话用户达803.0万户. ··············································· (8分) (注:答案不唯一,只要符合数据特征即可得分) 22.解:(1)10,50; ························································································· (2分) (2)解:解法一(树状图):·················································································································· (6分)从上图可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,因此P (不低于30元)=82123=.······························································ (8分)解法二(列表法):··········································································································· (6分)(以下过程同“解法一”) ········································································· (8分)23.解:分别过A D 、作AM BC ⊥于M DG BC ⊥,于G .过E 作EH DG ⊥于H ,则四边形AMGD 为矩形.,135120AD BC BAD ADC ∠=∠=Q ∥°,°. 0 10 20 30 1020 30 10 2030 10 3040 0 10 30 20 2030 50 20 30 10 503040 第一次 第二次 和(第20题 图2) ···································(6分) (第23题)∴456030B DCG GDC ∠=∠=∠=°,°,°.在Rt ABM △中,sin 122AM ABB ==⨯=·∴DG = ······························································································ (3分)在Rt DHE △中,cos 22DH DEEDH =∠=⨯=· ······································ (6分)∴ 1.41 1.73HG DG DH =-=⨯-6≈6.7. ······································· (7分)答:水深约为6.7米. ···················································································· (8分)(其它解法可参照给分)24.解:(1)由题意,得: 1.442 2.6a b a b +=⎧⎨+=⎩,.解得0.11.5a b =-⎧⎨=⎩,.········································· (2分)∴20.1 1.5y x x =-+乙. ········································································· (3分)(2)()()20.3100.1 1.5W y y t t t =+=-+-+乙甲.∴20.1 1.23W t t =-++. ······································································· (5分) ()20.16 6.6W t =--+.∴6t =时,W 有最大值为6.6. ························· (7分)∴1064-=(吨).答:甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润之和最大,最大利润是6.6万元. ········································································· (8分)25.解:(1)1EA FC =. ······················································································· (1分)证明:(证法一)AB BC A C =∴∠=∠Q ,.由旋转可知,111AB BC A C ABE C BF =∠=∠∠=∠,,,∴ABE C BF 1△≌△. ··················································· (3分)∴BE BF =,又1BA BC =Q ,∴1BA BE BC BF -=-.即1EA FC =. ······························ (4分)(证法二)AB BC A C =∴∠=∠Q ,.由旋转可知,11A C A B CB ∠=∠,=,而1EBC FBA ∠=∠,∴1A BF CBE △≌△. ··················································· (3分)A DBE C F1A1CG∴BE BF =,∴1BA BE BC BF -=-,即1EA FC =. ······························································· (4分)(2)四边形1BC DA 是菱形. ····································································· (5分)证明:111130A ABA AC AB ∠=∠=∴Q °,∥,同理AC BC 1∥.∴四边形1BC DA 是平行四边形. ················································· (7分)又1AB BC =Q ,∴四边形1BC DA 是菱形. ····································· (8分)(3)(解法一)过点E 作EG AB ⊥于点G ,则1AG BG ==.在Rt AEG △中,1cos cos30AG AE A ===°……(10分)由(2)知四边形1BC DA 是菱形,∴2AD AB ==,∴2ED AD AE =-= ················································ (12分)(解法二)12030ABC ABE ∠=∠=Q °,°,∴90EBC ∠=°.在Rt EBC △中,tan 2tan 30BE BC C ==⨯=·°112EA BA BE ∴=-= ·············································· (10分)11111AC AB A DE A A DE A ∴∠=∠∴∠=∠Q ∥,..∴12ED EA ==-······················································· (12分)(其它解法可参照给分)26.(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=.········································································ (2分)由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ······························· (3分)∴111263622ABC C S AB y ==⨯⨯=△·.·················································· (4分) (2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,. ·········································································· (5分)又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,. ·········································································· (6分)∴8448OE EF =-==,. ································································ (7分)(3)解法一:①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =. Rt Rt AFH AMC Q △∽△,∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.·························································· (10分)(图3)(图1)(图2)。
2009年普通高等学校招生全国统一考试数学卷(江西.理)含详解

绝密★启用前2009年普通高等学校招生全国统一考试(江西卷)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分。
第Ⅰ卷考生注意:答题前,考生务必将自己的准考证号、姓名填写在答题卡上,考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
第Ⅱ卷用黑色墨水签字笔在答题卡上作答。
若在试题卷上作答,答案无效。
考试结束,监考员将试题卷、答题卡一并收回。
参考公式如果事件,A B 互斥,那么 球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件,A B ,相互独立,那么 其中R 表示球的半径 ()()()P A B P A P B ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是p ,那么 343V R π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)k k n k n n P k C p p -=- 一.选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数2(1)(1)z x x i =-+-为纯虚数,则实数x 的值为 A .1- B .0 C .1 D .1-或12.函数y =的定义域为A .(4,1)--B .(4,1)-C .(1,1)-D .(1,1]-3.已知全集U =A B 中有m 个元素,()()U U A B 痧中有n 个元素.若A B I 非空,则A B I 的元素个数为A .mnB .m n +C .n m -D .m n -4.若函数()(1)cos f x x x =,02x π≤<,则()f x 的最大值为A .1B .2 C1 D25.设函数2()()f x g x x =+,曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+,则曲线()y f x =在点(1,(1))f 处切线的斜率为A .4B .14-C .2D .12-6.过椭圆22221x y a b +=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=,则椭圆的离心率为A.2 B. C .12 D .137.(1)n ax by ++展开式中不含x 的项的系数绝对值的和为243,不含y 的项的系数绝对值的和为32,则,,a b n 的值可能为A .2,1,5a b n ==-=B .2,1,6a b n =-=-=C .1,2,6a b n =-==D .1,2,5a b n ===8.数列{}n a 的通项222(cos sin )33n n n a n ππ=-,其前n 项和为n S ,则30S 为A .470B .490C .495D .5109.如图,正四面体ABCD 的顶点A ,B ,C 分别在两两垂直的三条射线Ox ,Oy ,Oz 上,则在下列命题中,错误的为A .O ABC -是正三棱锥B .直线OB ∥平面ACDC .直线AD 与OB 所成的角是45D .二面角D OB A --为45 10.为了庆祝六一儿童节,某食品厂制作了3种不同的精美卡片,每袋食品随机装入一张卡片,集齐3种y xz OA B CD。
福建省武平县第一中学2014-2015学年高一(普通班)下学期期中考试数学试卷 Word版含答案

武平一中高一下半期考数学试卷 2015.5.14 一、选择题(12*5=60) 1、下列角中终边与330°相同的角是A.30° B.-30° C.630° D.-630° 若圆的半径是6cm,则圆心角为的扇形面积为A. B. C. D. 若点是角终边上一点,且,则的值为A. B. C. D. 已知函数,则是A.最小正周期为2π的偶函数 B.最小正周期为2π的奇函数 C.最小正周期为π的偶函数 D.最小正周期为π的奇函数 160人,其中有业务员104人,管理人员32人,后勤服务人员24人,要从中抽取一个容量为20的样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员人数为()A. 3B. 4C. 5D. 6 6、已知是方程的两根,则实数的值为 A. B. C. D. 点P在边长为1的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )A. B. C. D.π 为了得到函数的图像,只需把函数的图像A.向左平移个长度单位 B向右平移个长度单位 C向左平移个长度单位 D向右平移个长度单位 在函数①,,③,④中,最小正周期为的所有函数为( )A. B. C. D. 12、下图是某算法的程序框图,则程序运行后输的结果是() A. 2 B. 3 C. 5 D.6 月份x 1 2 3 4 用水量y 4.5 4 3 5 13、下表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是=-0.7x+a,则a=________.,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ . 15、化简为第二象限角_ ___ 16、函数f(x)=3sin 的图象为C________ (写出所有正确结论的编号) ①图象C关于直线x=π对称图象C关于对称函数f(x)在区间内是增函数;由y=3sin 2x 的图象向右平移个单位长度可以得到图象C. a,b,c,女生两名,分别记为x,y,现从中任选2名学生参加校数学竞赛, ⑴写出这种选法的基本事件。
2009年普通高等学校招生全国统一考试湖南卷含答案

2009年普通高等学校招生全国统一考试(湖南卷)含答案数学(文史类)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.2log 的值为 【 D 】A . B.C. 12-D. 122. 抛物线2y =-8x 的焦点坐标是 【 B 】A .(2,0) B. (- 2,0) C. (4,0) D. (- 4,0) 3.设n s 是等差数列{n a }的前n 项和,已知1a =3,5a =11,则7s 等于 【 C 】 A .13 B. 35 C. 49 D. 634.如图1 D ,E ,F 分别是∆ABC 的边AB ,BC ,CA 的中点,则 【 A 】A .AD + BE + CF =0B .BD CE DF -+=0C .AD CE CF +-=0D .BD BE FC --=0 图15.某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为【 B 】 A .14 B. 16 C. 20 D. 486.平面六面体ABCD - 1A 1B 1C 1D 中,既与AB 共面也与1CC 共面的棱的条数为【 C 】 A .3 B. 4 C.5 D. 67.若函数y=f(x)导函数在区间[a,b ]是增函数,则函数y=f(x)在区间[a,b ]上的图象可能是(A )8. 设函数()y f x =在(,)-∞+∞内有定义,对于给定的正数K ,定义函数{(),(),()()f x f x kk k f x kf x ≤>=取函数()2xf x -=。
当K =12时,函数()k f x 的单调递增区间为 【C 】 A (,0)-∞ B (0,)+∞ C (,1)-∞- D (1,)+∞二 填空题:本大题共七小题,没小题5分,共35分,把答案填在答题卡中对应题号后的横线上。
2009年普通高等学校招生全国统一考试文科数学(全国卷Ⅰ)(含答案解析)

集合 CU ( A B) 中共有 3 个元素,故选 A.
考点:集合的运算.
3.D
【分析】分类讨论解绝对值不等式与分式不等式即可.
【详解】
x x
1 1
1, 1
x x
1 1
1,
x
1 x
x 1
1
0
且
x
1 x
x 1
1
0
,
2x x 1
0
且
x
2 -1
<
0
,解得:
x
0
,
故不等式的解集是x x 0 ,
故选:D.
中各选出 2 名同学,则选出的 4 人中恰有 1 名女同学的不同选法共有
A.150 种
B.180 种
C.300 种
D.345 种
8.设非零向量 a , b
, c 满足
a
b
c
,ab
c ,则向量 a , b 的夹角为(
)
A.150
B.120
C. 60
D. 30
9.已知三棱柱 ABC - A1B1C1 的侧棱与底面边长都相等,若 A1在底面 ABC 上的射影为 BC
(2)乙组中选出一名女生有 C52C61C21 120 种选法.故共有 345 种选法 考点:排列组合
8.B
【分析】根据向量加法的几何意义确定正确选项.
【详解】设 AB a, AD b, AC c ,
a b c 表示 AB AD AC ,所以四边形 ABCD 是平行四边形,
故答案为: 240 .
【点睛】本题考查利用二项式定理求项的系数和,考查计算能力,属于基础题.
14.24 【分析】根据等差数列的性质与前 n 项和公式计算.
2009年全国高中数学联赛一试(经典试题参考答案及评分标准)

2009年全国高中数学联赛一试 试题参考答案及评分标准说明:1.评阅试卷时,请依据本评分标准,填空题只设7分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中至少4分为一个档次,不要增加其他中间档次. 一、填空(共8小题,每小题7分,共56分)1. 若函数()f x =且()()()n nf x f f f f x ⎡⎤=⎡⎤⎣⎦⎣⎦ ,则()()991f = . 【答案】 110【解析】 ()()()1f x f x =, ()()()2f x f f x =⎡⎤⎣⎦……()()99f x =.故()()991110f =.2. 已知直线:90L x y +-=和圆22:228810M x y x y +---=,点A 在直线L 上,B ,C 为圆M 上两点,在ABC ∆中,45BAC ∠=︒,AB 过圆心M ,则点A 横坐标范围为 .【答案】 []36, 【解析】 设()9A a a -,,则圆心M 到直线AC 的距离sin 45d AM =︒,由直线AC 与圆M相交,得d 解得36a ≤≤.3. 在坐标平面上有两个区域M 和N ,M 为02y y x y x ⎧⎪⎨⎪-⎩≥≤≤,N 是随t 变化的区域,它由不等式1t x t +≤≤所确定,t 的取值范围是01t ≤≤,则M 和N 的公共面积是函数()f t = .【答案】 212t t -++【解析】 由题意知()f t S =阴影部分面积 AOB OCD BEF S S S ∆∆∆=-- ()22111122t t =--- 212t t =-++4. 使不等式1111200712213a n n n +++<-+++ 对一切正整数n 都成立的最小正整数a的值为 . 【答案】2009 【解析】 设()1111221f n n n n =++++++ .显然()f n 单调递减,则由()f n 的最大值()1120073f a <-,可得2009a =.5. 椭圆22221x y a b +=()0a b >>上任意两点P ,Q ,若OP OQ ⊥,则乘积OP OQ ⋅的最小值为 . 【答案】 22222a b a b +【解析】 设()cos sin P OP OP θθ,,ππcos sin 22Q OQ OQ θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,.由P ,Q 在椭圆上,有222221cos sin a b OP θθ=+ ① 222221sin cos a b OQ θθ=+ ② ①+②得221111a b OP OQ+=+.于是当OP OQ =OP OQ 达到最小值22222a b a b +.6. 若方程()lg 2lg 1kx x =+仅有一个实根,那么k 的取值范围是 . 【答案】0k <或4k = 【解析】 ()20101kx x kx x ⎧>⎪⎪+>⎨⎪=+⎪⎩ 当且仅当 0kx > ① 10x +> ② ()2210x k x +-+=③对③由求根公式得1x,2122x k ⎡=-⎣ ④2400k k k ∆=-⇒≥≤或4k ≥.(ⅰ)当0k <时,由③得 12122010x x k x x +=-<⎧⎨=>⎩ 所以1x ,2x 同为负根.又由④知121010x x +>⎧⎨+<⎩所以原方程有一个解1x .(ⅱ)当4k =时,原方程有一个解112kx =-=. (ⅲ)当4k >时,由③得12122010x x k x x +=->⎧⎨=>⎩所以1x ,2x 同为正根,且12x x ≠,不合题意,舍去. 综上可得0k <或4k =为所求.7. 一个由若干行数字组成的数表,从第二行起每一行中的数字均等于其肩上的两个数之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是 (可以用指数表示) 【答案】981012⨯ 【解析】 易知:(ⅰ)该数表共有100行;(ⅱ)每一行构成一个等差数列,且公差依次为11d =,22d =,232d =,…,98992d =(ⅲ)100a 为所求.设第()2n n ≥行的第一个数为n a ,则 ()22111222n n n n n n a a a a -----=++=+3222222n n n a ---⎡⎤=++⎣⎦24223222222n n n n a ----⎡⎤=++⨯+⎣⎦323232n n a --=+⨯……()121212n n a n --=+-⨯()212n n -=+故981001012a =⨯.8. 某车站每天800~900∶∶,900~1000∶∶都恰有一辆客车到站,但到站的时刻是随机的,且两一旅客820∶到车站,则它候车时间的数学期望为 (精确到分).【答案】 27 【解析】 旅候车时间的数学期望为1111110305070902723361218⨯+⨯+⨯+⨯+⨯=二、解答题1. (本小题满分14分)设直线:l y kx m =+(其中k ,m 为整数)与椭圆2211612x y +=交于不同两点A ,B ,与双曲线221412x y -=交于不同两点C ,D,问是否存在直线l ,使得向量0AC BD += ,若存在,指出这样的直线有多少条?若不存在,请说明理由. 【解析】 由2211612y kx m x y =+⎧⎪⎨+=⎪⎩消去y 化简整理得()2223484480k xkmx m +++-=设()11A x y ,,()22B x y ,,则122834kmx x k +=-+()()()222184344480km k m ∆=-+-> ① (4)分由221412y kx m x y =+⎧⎪⎨-=⎪⎩消去y 化简整理得()22232120k xkmx m ----=设()34C x y ,,()44D x y ,,则34223kmx x k +=- ()()()2222243120km k m ∆=-+-+> ② ………………………………………………8分因为0AC BD +=,所以()()42310x x x x -+-=,此时()()42310y y y y -+-=.由1234x x x x +=+得 2282343km kmk k -=+-. 所以20km =或2241343k k -=+-.由上式解得0k =或0m =.当0k =时,由①和②得m -<m 是整数,所以m 的值为3-,2-,1-,0,1,2,3.当0m =,由①和②得k .因k 是整数,所以1k =-,0,1.于是满足条件的直线共有9条.………14分2. (本小题15分)已知p ,()0q q ≠是实数,方程20x px q -+=有两个实根α,β,数列{}n a 满足1a p =,22a p q =-,()1234n n n a pa qa n --=-= ,, (Ⅰ)求数列{}n a 的通项公式(用α,β表示);(Ⅱ)若1p =,14q =,求{}n a 的前n 项和.【解析】 方法一:(Ⅰ)由韦达定理知0q αβ⋅=≠,又p αβ+=,所以()1212n n n n n a px qx a a αβαβ------=+-,()345n = ,,,整理得()112n n n n a a a a βαβ----=-令1n n n b a a β+=-,则()112n n b b n α+== ,,.所以{}n b 是公比为α的等比数列. 数列{}n b 的首项为:()()222121b a a p q p ββαβαββαβα=-=--=+--+=. 所以21n n n b ααα-+=⋅=,即11n n n a a βα++-=()12n = ,,.所以11n n n a a βα++=+()12n = ,,. ①当240p q ∆=-=时,0αβ=≠,12a p ααα==+=,11n n n a a βα++=+()12n = ,,变为11n n n a a αα++=+()12n = ,,.整理得,111n n n n a a αα++-=,()12n = ,,.所以,数列n n a α⎧⎫⎨⎬⎩⎭成公差为1的等差数列,其首项为122a ααα==.所以()2111nna n n α=+-=+.于是数列{}n a 的通项公式为()1n n a n α=+;……………………………………………………………………………5分 ②当240p q ∆=->时,αβ≠,11n n n a a βα++=+1n n a βαβαβα+-=+-11n n n a βαβααβαβα++=+---()12n = ,,.整理得211n n n n a a ααββαβα+++⎛⎫+=+ ⎪--⎝⎭,()12n = ,,. 所以,数列1n n a αβα+⎧⎫+⎨⎬-⎩⎭成公比为β的等比数列,其首项为2221a ααβαββαβαβα+=++=---.所以121n n n a αβββαβα+-+=--. 于是数列{}n a 的通项公式为11n n n a βαβα++-=-. (10)分(Ⅱ)若1p =,14q =,则240p q ∆=-=,此时12αβ==.由第(Ⅰ)步的结果得,数列{}n a 的通项公式为()11122nn n n a n +⎛⎫=+= ⎪⎝⎭,所以,{}n a 的前n 项和为231234122222n n n n n s -+=+++++234112341222222n n n n s n ++=+++++以上两式相减,整理得1133222n n n s ++=-所以332n n n s +=-. (15)分 方法二:(Ⅰ)由韦达定理知0q αβ⋅=≠,又p αβ+=,所以1a αβ=+,222a αβαβ=++.特征方程20p q λλ-+=的两个根为α,β.①当0αβ=≠时,通项()()1212n n a A A n n α=+= ,,由12a α=,223a α=得()()122212223A A A A αααα+=⎧⎪⎨+=⎪⎩ 解得121A A ==.故 ()1n n a n α=+.……………………………………………………5分②当αβ≠时,通项()1212n n n a A A n αβ=+= ,,.由1a αβ=+,222a αβαβ=++得12222212A A A A αβαβαβαβαβ+=+⎧⎪⎨+=++⎪⎩ 解得1A αβα-=-,2A ββα=-.故1111n n n n n a αββαβαβαβα++++--=+=---.…………………………………………………………10分(Ⅱ)同方法一.3. (本小题满分15分)求函数y 【解析】 函数的定义域为[]013,.因为y=当0x =时等号成立.故y 的最小值为.……………………………………………5分又由柯西不等式得22y =()()()11122731312123x x x ⎛⎫+++++-= ⎪⎝⎭≤所以11y ≤. ………………………………………………………………………………10分 由柯西不等式等号成立的条件,得()491327x x x =-=+,解得9x =.故当9x =时等号成立.因此y 的最大值为1.…………………………………………………………………………………15分。
2009高考数学全国卷

2009年普通高等学校夏季招生考试(全国Ⅰ卷)数学(文史类)(必修+选修Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 参考公式:如果事件A 、B 互斥,那么 P(A+B)=P(A)+P(B)如果事件A 、B 相互独立,那么 P(A·B)=P(A)·P(B)如果事件A 在一次试验中发生的概率是p,那么n 次独立重复试验中事件A 恰好发生k 次的概念P n (k)=kn k k n p p C --)1((k=0,1,2,…,n)球的表面积公式 S=4πR 2其中R 表示球的半径 球的体积公式334R V π=其中R 表示球的半径第Ⅰ卷一、选择题1.(2009全国卷Ⅰ,文1)sin585°的值为( ) A.22-B.22C.23-D.23 答案:A2.(2009全国卷Ⅰ,文2)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A ∪B,则集合(A∩B)中的元素共有( )A.3个B.4个C.5个D.6个 答案:A3.(2009全国卷Ⅰ,文3)不等式|11-+x x |<1的解集为…( ) A.{x|0<x <1}∪{x|x >1} B.{x|0<x <1} C.{x|-1<x <0} D.{x|x <0} 答案:D4.(2009全国卷Ⅰ,文4)已知tanα=4,31cot =β,则tan(α+β)=( ) A.117 B.117- C.137 D.137- 答案:B5.(2009全国卷Ⅰ,文5)设双曲线12222=-by a x (a >0,b >0)的渐近线与抛物线y=x 2+1相切,则该双曲线的离心率等于( )A.3B.2C.5D.6 答案:C6.(2009全国卷Ⅰ,文6)已知函数)(x f 的反函数为g(x)=1+2lgx(x >0),则f(1)+g(1)=( ) A.0 B.1 C.2 D.4答案:C7.(2009全国卷Ⅰ,文7)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )A.150种B.180种C.300种D.345种 答案:D8.(2009全国卷Ⅰ,文8)设非零向量a 、b 、c 满足|a |=|b |=|c |,a+b =c ,则〈a,b 〉=( ) A.150° B.120° C.60° D.30° 答案:B9.(2009全国卷Ⅰ,文9)已知三棱柱ABC —A 1B 1C 1的侧棱与底面边长都相等,A 1在底面ABC 上的射影为BC 的中点,则异面直线AB 与CC 1所成的角的余弦值为( ) A.43 B.45 C.47 D.43 答案:D10.(2009全国卷Ⅰ,文10)如果函数y=3cos(2x+φ)的图像关于点(34π,0)中心对称,那么|φ|的最小值为( ) A.6π B.4π C.3π D.2π 答案:A11.(2009全国卷Ⅰ,文11)已知二面角α-l-β为60°,动点P 、Q 分别在面α,β内,P 到β的距离为3,Q 到α的距离为32,则P 、Q 两点之间距离的最小值为( )A.2B.2C.32D.4 答案:C12.(2009全国卷Ⅰ,文12)已知椭圆C:1222=+y x 的右焦点为F,右准线为l,点A ∈l,线段AF 交C 于点B.若FB FA 3=,则|AF |=( )A.2B.2C.3D.3 答案:A第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.(注意:在试题卷上作......答无效...) 13.(2009全国卷Ⅰ,文13)(x-y)10的展开式中,x 7y 3的系数与x 3y 7的系数之和等于__________. 答案:-24014.(2009全国卷Ⅰ,文14)设等差数列{a n }的前n 项和为S n .若S 9=72,则a 2+a 4+a 9=__________. 答案:2415.(2009全国卷Ⅰ,文15)已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M,若圆M 的面积为3π,则球O 的表面积等于____________. 答案:16π16.(2009全国卷Ⅰ,文16)若直线m 被两平行线l 1:x-y+1=0与l 2:x-y+3=0所截得的线段的长为22,则m 的倾斜角可以是____________.①15° ②30° ③45° ④60° ⑤75°其中正确答案的序号是___________.(写出所有正确答案的序号) 答案:①⑤三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)(注意:在试题卷上作答无........效)(2009全国卷Ⅰ,文17)设等差数列{a n }的前n 项和为S n ,公比是正数的等比数列{b n }的前n 项和为T n , 已知a 1=1,b 1=3,a 3+b 3=17,T 3-S 3=12,求{a n },{b n }的通项公式. 解:设{a n }的公差为d,{b n }的公比为q. 由a 3+b 3=17得1+2d+3q 2=17, ① 由T 3-S 3=12得q 2+q-d=4. ②由①②及q >0解得q=2,d=2.故所求的通项公式为a n =2n-1,b n =3×2n-1.18.(本小题满分12分)(注意:在试题卷上作答无效.........)(2009全国卷Ⅰ,文18)在△ABC 中,内角A 、B 、C 的对边长分别为a 、b 、c.已知a 2-c 2=2b,且sinB=4cosAsinC,求b. 解:由余弦定理得a 2-c 2=b 2-2bccosA. 又a 2-c 2=2b,b≠0, 所以b=2ccosA+2.①由正弦定理得C Bc b sin sin =, 又由已知得A CBcos 4sin sin =,所以b=4ccosA.② 故由①②解得b=4.19.(本小题满分12分)(注意:在试题卷上作答无效.........)(2009全国卷Ⅰ,文19) 如图,四棱锥S —ABCD 中,底面ABCD 为矩形,SD ⊥底面ABCD,2=AD ,DC=SD=2,点M 在侧棱SC 上,∠ABM=60°.(1)证明:M 是侧棱SC 的中点; (2)求二面角S-AM-B 的大小. 解法一:(1)作ME ∥CD 交SD 于点E,则ME ∥AB,ME ⊥平面SAD.连接AE,则四边形ABME 为直角梯形. 作MF ⊥AB,垂足为F,则AFME 为矩形. 设ME=x,则SE=x,2)2(222+-=+=x AD ED AE ,MF=AE=2)2(2+-x ,FB=2-x. 由MF=FB·tan60°,得)2(32)2(2x x -=+-,解得x=1,即ME=1,从而DC ME 21=. 所以M 为侧棱SC 的中点. (2)222=+=MC BC MB ,又∠ABM=60°,AB=2,所以△ABM 为等边三角形. 又由(1)知M 为SC 中点,2=SM ,6=SA ,AM=2,故SA 2=SM 2+AM 2,∠SMA=90°.取AM 中点G,连结BG ,取SA 中点H,连结GH,则BG ⊥AM,GH ⊥AM. 由此知∠BGH 为二面角S-AM-B 的平面角. 连接BH.在△BGH 中,323==AM BG ,2221==SM GH ,22222=+=AH AB BH , 所以362cos 222-=••-+=∠GH BG BH GH BG BGH .∴二面角S-AM-B 的大小为arccos(36-). 解法二:以D 为坐标原点,射线DA 为x 轴正半轴,建立如图所示的直角坐标系D —xyz. 设A(2,0,0),则B(2,2,0),C(0,2,0),S(0,0,2).(1)设MC SM λ=(λ>0),则 M(0,λλλ++12,12),MB =(λλ+-+12,12,2). 又AB =(0,2,0),〈MB ,AB 〉=60°, 故MB ·AB =|MB ||AB |cos60°,即222)12()12()2(14λλλ+-+++=+.解得λ=1,即MC SM =. 所以M 为侧棱SC 的中点.(2)由M(0,1,1),A(2,0,0),得AM 的中点G(21,21,22). 又GB =(21,23,22-),MS =(0,-1,1),AM =(2-,1,1). GB ·AM =0,MS ·AM =0,所以GB ⊥AM ,MS ⊥AM .因此〈GB ,MS 〉等于二面角S-AM-B 的平面角, cos 〈GB ,MS 〉36||||-=MS GB MS GB . 所以二面角S-AM-B 的大小为arccos(36-). 20.(本小题满分12分)(注意:在试题卷上作答无效.........)(2009......全国卷...Ⅰ.,.文.20..)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立.已知前2局中,甲、乙各胜1局. (1)求再赛2局结束这次比赛的概率; (2)求甲获得这次比赛胜利的概率.解:记A i 表示事件:第i 局甲获胜,i=3,4,5. B j 表示事件:第j 局乙获胜,j=3,4. (1)记A 表示事件:再赛2局结束比赛 A=A 3·A 4+B 3·B 4.由于各局比赛结果相互独立,故 P(A)=P(A 3·A 4+B 3·B 4)=P(A 3·A 4)+P(B 3·B 4) =P(A 3)P(A 4)+P(B 3)P(B 4) =0.6×0.6+0.4×0.4 =0.52.(2)记B 表示事件:甲获得这次比赛的胜利.因前两局中,甲、乙各胜一局,故甲获得这次比赛的胜利当且仅当在后面的比赛中,甲先胜2局,从而B=A 3·A 4+B 3·A 4·A 5+A 3·B 4·A 5. 由于各局比赛结果相互独立,故 P(B)=P(A 3·A 4)+P(B 3·A 4·A 5)+P(A 3·B 4·A 5)=P(A 3)P(A 4)+P(B 3)P(A 4)P(A 5)+P(A 3)P(B 4)P(A 5) =0.6×0.6+0.4×0.6×0.6+0.6×0.4×0.6 =0.648.21.(本小题满分12分)(注意:在试题卷上作答无效.........)(2009全国卷Ⅰ,文21)已知函数)(x f =x 4-3x 2+6.(1)讨论)(x f 的单调性;(2)设点P 在曲线y=)(x f 上,若该曲线在点P 处的切线l 通过坐标原点,求l 的方程.解:(1)f′(x)=4x 3-6x=4x·(26+x )(26-x ). 当x ∈(-∞,26-)和x ∈(0,26)时,f′(x)<0; 当x ∈(26-,0)和x ∈(26,+∞)时,f′(x)>0. 因此,)(x f 在区间(-∞,26-)和(0,26)上是减函数,)(x f 在区间(26-,0)和(26,+∞)上是增函数.(2)设点P 的坐标为(x 0,f(x 0)),由l 过原点知,l 的方程为y=f′(x 0)x. 因此f(x 0)=x 0f′(x 0),即x 04-3x 02+6-x 0(4x 03-6x 0)=0, 整理得(x 02+1)(x 02-2)=0. 解得20-=x 或20=x .因此切线l 的方程为x y 22-=或x y 22=.22.(本小题满分12分)(注意:在试题卷上作答无效.........)(2009全国卷Ⅰ,文22)如图,已知抛物线E:y 2=x 与圆M:(x-4)2+y 2=r 2(r >0)相交于A 、B 、C 、D 四个点.(1)求r 的取值范围;(2)当四边形ABCD 的面积最大时,求对角线AC 、BD 的交点P 的坐标. 解:(1)将y 2=x 代入(x-4)2+y 2=r 2, 并化简得x 2-7x+16-r 2=0.①E 与M 有四个交点的充要条件是方程①有两个不等的正根x 1、x 2.由此得⎪⎩⎪⎨⎧>-=>=+>---=∆.016,07,0)16(4)7(2212122r x x x x r解得515<r 2<16. 又r >0,所以r 的取值范围是(215,4). (2)不妨设E 与M 的四个交点的坐标为A(x 1,1x )、B(x 1,1x -)、C(x 2,2x -)、D(x 2,2x ).则直线AC 、BD 的方程分别为1112121)(x y x x x x x x x y +•-•---=-=)(11212x x x x x x -•-+,解得点P 的坐标为(21x x ,0). 设21x x t =,由216r t -=及(1)知0<t <27.由于四边形ABCD 为等腰梯形,因而其面积||)22(211221x x x x S -•+•=, 则S 2=(21212x x x x ++)·[(x 1+x 2)2-4x 1x 2], 将x 1+x 2=7,t x x =21代入上式,并令f(t)=S 2,得 f(t)=(7+2t)2·(7-2t)=-8t 3-28t 2+98t+343(0<t <27). 求导数,f′(t)=-24t 2-56t+98=-2(2t+7)(6t-7). 令f′(t)=0,解得67=t ,27=t (舍去). 当0<t <67时,f′(t)>0; 当67=t 时,f′(t)=0; 当2767<<t 时,f′(t)<0. 故当且仅当67=t 时,f(t)有最大值,即四边形ABCD 的面积最大, 故所求的点P 的坐标为(67,0).。
福建省武平县第一中学高一数学下学期期末练习试题(6.2

高一数学期末练习6.241.运用如右图所示的程序,输出的结果是( ) (第1题)A .1-B .1C .2D .3 2.气象台预报“龙岩市明天降雨的概率是80℅”,下列理解正确的是( ) A.龙岩市明天将有80℅的地区降雨 B. 龙岩市明天将有80℅的时间降雨 C.明天出行不带雨具肯定要淋雨 D. 明天出行不带雨具淋雨的可能性很大 3.下列各式中,值为21的是( ) A.oo15cos 15sin B.12sin12cos22ππ- C.o o5.22tan 15.22tan 2- D.26cos1π+4.如图,样本A 和B 分别取自两个不同的总体,它们的样本平均数分别为A x 和B x ,样本标准差分别为A S 和B S ,则下列结论正确的是( ) A. A x >B x ,A S >B S B. A x >B x ,A S <B S C. A x <B x ,A S >B S D. A x <B x ,A S <B S5.已知锐角βα、满足53cos =α,135)cos(-=+βα,则=βcos ( ) A.6556 B. 6533C. 6556-D. 6533-6.袋中装有黑、白两种颜色的球各三个,现从中取出两个球,设事件P :取出的都是黑球;事件Q :取出的都是白球;事件R :取出的球中至少有一个黑球.则下列结论正确的是( ) A .P 与R 互斥 B .任何两个均互斥 C .Q 和R 互斥 D .任何两个均不互斥 7.假设要抽查的某种品牌的850颗种子的发芽率,抽取60粒进行试验。
利用随机数表抽取种子时,先将850颗种子按001,002,。
,850进行编号,如果从随机数表第8行第7列的数从7开始向右读,则检测的第3颗种子的编号为( )(下面的数据摘自随机数表第7行至第9行)12a b a a b===-PRTNT a ENDA.785B. 555C. 567D.199 8.在△ABC 中,已知A A B sin sin cos 2=,则△ABC 一定为( )A.等腰三角形B.直角三角形C.钝角三角形D.正三角形9.设(1,2)a =r ,(1,1)b =r,c a kb =+r r r .若b c ⊥r r ,则实数k 的值等于( )A .32-B .53-C .53D .3210.某产品的广告费用x (万元)与销售额y (万元)的统计数据如下表(一个数据上有污渍):已知该公司根据原有数据统计(没有污渍前)得线性回归方程^1.94.9+=x y ,则污渍部分的数据是( )A.50B.52C.54D.5811.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( ) A .2 B .1 C .0 D .1-MBCAD(第11题) (第12题) ( 第14题)12.如图,四边形ABCD ,若M 是BC 的中点,则AB AM DM DC ⋅-⋅=u u u r u u uu r u u u u ru u u r( )A .1B .1-CD 13.样本数据4,2,1,0,-2,标准差是14.如图所示,墙上挂有边长为a 的正方形木板,它的四个角的阴影部分都是以正方形的顶点为圆心,半径为2a的圆弧.某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都相等,此人投镖4000次,镖击中空白部分的次数是854此.据此估算:圆周率π约为15.已知O 是正三角形ABC 内部的一点,230OA OB OC ++=u u u r u u u r u u u r r,则OAC ∆的面积与OAB ∆的面积之比为16.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.22sin 45cos 75+sin45cos75,+o o o o 22sin 36cos 66+sin36cos66,+o o o o22sin 15cos 45+sin15cos45,+o o o o 22sin (15)cos 15+sin(15)cos15,-+-o o o o22sin (45)cos (15)+sin(45)cos(15),-+---o o o o试将该同学的发现推广为三角恒等式17.统计某校1000名学生数学某单元水平测试成绩,得到频率分布直方图如图所示.已知频率分布直方图估计的平均分为71分,及格率是%80 (满分100分,规定不低于60分为及格).(1)分别求第三、第四组的频率;(2)若从优秀(]100,80[分)、合格()80,60[分)、 不合格()60,40[分)钟分层抽取20名学生参加座谈会, 问合格学生应抽取多少名?(3)在(2)的条件下,这20名参加座谈会的学生对本单元知识个人掌握程度作出估计(评价区间0分~100分,满分100分),得到下列一组数据:请选择适当的一个数字特征来描述这组数据,并据此评价学生该单元知识掌握情况.18.已知向量)cos 32sin ,(cos ),sin ,(cos x x x n x x m-=-=→→,R x ∈,设→→⋅=n m x f )(.(1)求函数)(x f 的最小正周期;(2)⎥⎦⎤⎢⎣⎡∈2,4ππx ,求函数)(x f 的值域. 19.如图,在平面直角坐标系xOy 中,点,,A B C 均在单位圆上,已知点A 在第一象限的横坐标是3,5点B 在第二象限,点()1,0.C (1)设,COA θ∠=求sin 2θ的值; (2)若AOB ∆为正三角形,求点B 的坐标20.某实验室一天的温度(单位:C ο)随时间t (单位:h )的变化近似满足函数关系;)24,0[,12sin12cos310)(∈--=t t t t f ππ.(1)求实验室这一天的最大温差;(2)若要求实验室温度不高于11C ο,则在哪段时间实验室需要降温?21.已知向量))4cos(3),4(sin(ππ+-+=x x ,))4cos(),4(sin(ππ-+=x x ,函数n m x f ⋅=)(,R x ∈.(1)求函数)(x f y =的图像的对称中心坐标; (2)将函数)(x f y =图像向下平移21个单位,再向左平移3π个单位得函数)(x g y =的图像,试写出)(x g y =的解析式并作出它在5[,]66ππ-上的图像.22.如图所示,某市政府决定在以政府大楼o 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径R OM =,∠OMOP 45=,OB 与OM之间的夹角为θ.(1)将图书馆底面矩形ABCD的面积S表示成θ的函数;(2)求当θ为何值时,矩形ABCD的面积S有最大值?最大值是多少?(用含θ的式子表示)高一数学期末练习6.24 1-12 ADCCB CDAAC CD13.N 2 14. 3.146 15. 2316.22sin cos()sin cos()66ππαααα++++=4317.18.19.(1)因为点A 在单位圆上,点A 在第一象限,点A 的横坐标是3,5所以点A 的坐标为34,.55⎛⎫⎪⎝⎭根据三角函数定义有34cos ,sin x y θθ====,从而24sin 22sin cos .θθθ==有因此点B 的坐标为.⎝⎭20.(1)因为)312sin(210)12sin 2112cos 23(210)(ππππ+-=+-=t t t t f , 又240<≤t ,所以373123ππππ<+≤t ,1)312sin(1≤+≤-ππt , 当2=t 时,1)312sin(=+ππt ;当14=t 时,1)312sin(-=+ππt ;于是)(t f 在)24,0[上取得最大值12,取得最小值8. (2)依题意,当11)(>t f 时实验室需要降温. 由(1)得)312sin(210)(ππ+-=t t f ,所以11)312sin(210>+-ππt ,即21)312sin(<+ππt , 又240<≤t ,因此61131267ππππ<+<t ,即1810<<t , 故在10时至18时实验室需要降温. 21.(1)x f ⋅=)()4cos()4cos(3)4(sin 2πππ-+-+=x x x21)32sin(2cos 23)2sin 1(21+-=-+=πx x x 4分由于0)32sin(=-πx 得:Z k k x ∈=-,32ππ,所以Z k k x ∈+=,621ππ. 所以)(x f 的图像的对称中心坐标为Z k k ∈+),21,621(ππ 6分 (2))(x g =)32sin(π+x ,列表:描点、连线得函数()y g x =在5[,]66ππ-上的图象如图所示:22.(1)由题意可知,点M 为»PQ 的中点,所以OM AD ⊥. 设OM 于BC 的交点为F ,则2sin BC R θ=,cos OF R θ=.1cos sin 2AB OF AD R R θθ=-=-.所以2sin (cos sin )S AB BC R R R θθθ=⋅=-22(2sin cos 2sin )R θθθ=- 2(sin 21cos 2)R θθ=-+222sin(2)4R R πθ=+-,(0,)4πθ∈ . (2)因为(0,)4πθ∈ ,则32(,)444πππθ+∈ .所以当242ππθ+=,即8πθ=时,S 有最大值.2max (21)S R =-.故当8πθ=时,矩形ABCD 的面积S 有最大值2(21)R -.。
福建省龙岩市武平一中2014_2015学年高一数学下学期期末试卷(含解析)

2014-2015学年福建省龙岩市武平一中高一(下)期末数学试卷一.选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.与角﹣80°终边相同的角是()A.80°B.100°C.260°D.280°2.有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的样本编号可能为()A. 5,10,15,20,25 B. 9,19,29,39,49C. 2,13,24,35,46 D. 5,15,20,30,403.为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度4.已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为()A. 4cm2B. 6cm2C. 8cm2D. 16cm25.某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛.在下列选项中,互斥而不对立的两个事件是()A.“至少有1名女生”与“都是女生”B.“至少有1名女生”与“至多1名女生”C.“恰有1名女生”与“恰有2名女生”D.“至少有1名男生”与“都是女生”6.下表是某厂1~4月份用水量(单位:百吨)的一组数据:月份x 1 2 3 4用水量y 4.5 4 3 2.5由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=﹣0.7x+a,则a等于()A. 10.5 B. 5.15 C. 5.2 D. 5.25 7.﹣sin10°(tan﹣15°﹣tan5°)=()A.B. 1 C. 2 D.8.阅读如图所示的程序框图,运行相应的程序,输出的结果是()A. 2 B. 4 C. 8 D. 169.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足,则等于()A.B.C.D.10.函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=()A. 10 B. 8 C.D.11.关于f(x)=3sin(2x+)有以下命题,其中正确命题的个数()①若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z);②f(x)图象与g(x)=3cos(2x﹣)图象相同;③f(x)在区间[﹣,﹣]上是减函数;④f(x)图象关于点(﹣,0)对称.A. 0 B. 1 C. 2 D. 312.在四边形ABCD中,==(1,1),+=,则四边形ABCD的面积为()A.B. 2C.D.二.填空题(本题共5个小题,每小题5分,共25分,请把正确答案填在题中横线上)13.用秦九韶算法计算多项式f(x)=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64当x=2时的值时,v4的值为.14.将二进制数1011010(2)化为十进制结果为;再将该数化为八进制数,结果为.15.在边长为2的正方形ABCD中,点O为边AB的中点,在正方形ABCD内随机取一点P,则点P到点O的距离大于1的概率为.16.在△ABC中,∠B=60°,O为△ABC的外心,P为劣弧AC上一动点,且=x+y(x,y∈R),则x+y的取值范围为.三.解答题(本大题共6小题,共75分,解答写出必要的文字说明、演算过程及步骤)17.如图,已知角α的终边在第二象限,且与单位圆交于点P(m,).(Ⅰ)求实数m的值;(Ⅱ)求的值.18.某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求高三(1)班全体女生的人数;(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)间的矩形的高;(3)若要从分数在[80,100)之间的试卷中任取两份分析女学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.19.设向量=(2,sinθ),,θ为锐角.(1)若∥,求tanθ的值;(2)若•=,求sinθ+cosθ的值.20.已知函数.(1)求f(x)的最小正周期;(2)求f(x)的单调递增区间;(3)求f(x)在上的最值及取最值时x的值.21.已知向量=(sin,﹣1),=(A,Acos)(A>0),函数f(x)=•的最大值为2.(1)求f(x)最小正周期和解析式;(2)设α,β∈[0,],f(3α+),f(3β+2π)=,求sin(α﹣β)的值.22.已知函数f(x)的图象是由函数g(x)=cosx的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍,横坐标不变,再将所得到的图象向右平移个单位长度.(1)求函数f(x)的解析式,并求其图象的对称轴方程;(2)已知关于x的方程f(x)+g(x)=m在[0,2π)内有两个不同的解α,β(i)求实数m的取值范围;(ii)证明:cos(α﹣β)=﹣1.2014-2015学年福建省龙岩市武平一中高一(下)期末数学试卷参考答案与试题解析一.选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.与角﹣80°终边相同的角是()A.80°B.100°C.260°D.280°考点:终边相同的角.专题:三角函数的求值.分析:根据与﹣80°终边相同的角是k×360°﹣80°,k∈z,从而求得结果.解答:解:与﹣80°终边相同的角是k×360°﹣80°,k∈z,当k=1时,1×360°﹣80°=280°.故选:D.点评:本题考查终边相同的角的定义和表示方法,属于容易题.2.有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的样本编号可能为()A. 5,10,15,20,25 B. 9,19,29,39,49C. 2,13,24,35,46 D. 5,15,20,30,40考点:系统抽样方法.专题:概率与统计.分析:由系统抽样的特点知,将总体分成均衡的若干部分是将总体分段,分段的间隔要求相等,间隔一般为总体的个数除以样本容量.从所给的四个选项中可以看出间隔相等且组距为10的一组数据是由系统抽样得到的.解答:解:从50件产品中随机抽取5件进行检验,采用系统抽样的间隔为50÷5=10,只有选项B中编号间隔为10,故选:B.点评:本题考查了系统抽样的方法应用问题,解题时要从容量为N的总体中抽取容量为n的样本,应将总体分成均衡的若干部分,按照预先制定的间隔,从每一部分抽取一个个体,得到所要的样本,是系统抽样.3.为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.解答:解:把函数y=sin2x的图象向右平移个单位长度,可得函数y=sin2(x﹣)=sin(2x﹣)的图象,故选:D.点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.4.已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为()A. 4cm2B. 6cm2C. 8cm2D. 16cm2考点:扇形面积公式.专题:计算题.分析:设出扇形的半径,求出扇形的弧长,利用周长公式,求出半径,然后求出扇形的面积.解答:解:设扇形的半径为:R,所以,2R+2R=8,所以R=2,扇形的弧长为:4,半径为2,扇形的面积为:=4(cm2).故选A.点评:本题是基础题,考查扇形的面积公式的应用,考查计算能力.5.某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛.在下列选项中,互斥而不对立的两个事件是()A.“至少有1名女生”与“都是女生”B.“至少有1名女生”与“至多1名女生”C.“恰有1名女生”与“恰有2名女生”D.“至少有1名男生”与“都是女生”考点:互斥事件与对立事件.专题:概率与统计.分析:互斥事件是两个事件不包括共同的事件,对立事件首先是互斥事件,再就是两个事件的和事件是全集,由此规律对四个选项逐一验证即可得到答案解答:解:A中的两个事件是包含关系,故不符合要求.B中的两个事件之间有都包含一名女的可能性,故不互斥;C中的两个事件符合要求,它们是互斥且不对立的两个事件;D中的两个事件是对立事件,故不符合要求故选:C.点评:本题考查互斥事件与对立事件,解题的关键是理解两个事件的定义及两事件之间的关系.属于基本概念型题.6.下表是某厂1~4月份用水量(单位:百吨)的一组数据:月份x 1 2 3 4用水量y 4.5 4 3 2.5由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=﹣0.7x+a,则a等于()A. 10.5 B. 5.15 C. 5.2 D. 5.25考点:线性回归方程.专题:概率与统计.分析:由条件利用回归直线经过样本的中心点(,),求得a的值.解答:解:由题意可得样本的中心点的坐标为(2.5,3.5),再把样本的中心点的坐标(2.5,3.5)代入其线性回归直线方程是=﹣0.7x+a,可得3.5=﹣0.7×2.5+a,求得a=5.25,故选:D.点评:本题主要考查回归直线经过样本的中心点(,),属于基础题.7.﹣sin10°(tan﹣15°﹣tan5°)=()A.B. 1 C. 2 D.考点:三角函数的化简求值.专题:三角函数的求值.分析:由条件利用同角三角函数的基本关系、倍角公式,把要求的式子化为=﹣2cos10°,通分后利用诱导公式、和差化积公式化为cos30°,从而得到结果.解答:解:原式==========cos30°=.故选D.点评:本题主要考查同角三角函数的基本关系、诱导公式、和差化积公式的应用,属于中档题8.阅读如图所示的程序框图,运行相应的程序,输出的结果是()A. 2 B. 4 C. 8 D. 16考点:循环结构.专题:阅读型;图表型.分析:根据程序框图可知,程序运行时,列出数值S与n对应变化情况,从而求出当S=2时,输出的n即可.解答:解:.由框图可知,程序运行时,数值S与n对应变化如下表:S ﹣1 2n 2 4 8故S=2时,输出n=8.故选C点评:本题主要考查了直到型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于基础题.9.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足,则等于()A.B.C.D.考点:平面向量数量积的运算.专题:计算题;平面向量及应用.分析:根据向量加法的几何意义,得出=2,从而所以=.解答:解:如图因为M是BC的中点,根据向量加法的几何意义,=2,又,所以==.故选:A.点评:本题考查向量加法的几何意义,向量数量积的计算,属于基础题.10.函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=()A. 10 B. 8 C.D.考点:余弦函数的图象.专题:三角函数的求值.分析:由题意求出函数的周期,与最值,过p作PD⊥x轴于D,解出∠APD与∠BPD的正切,利用两角和的正切函数求出tan∠APB.解答:解:由函数f(x)=cos(πx+φ)(φ>0)的图象可得,由题意可知T==2,最大值为:1;过P作PD⊥x轴于D,AD=,DB=,DP=1,所以tan ∠APD=,tan∠BPD=,所以tan∠APB=tan(∠APD+∠BPD)==8,故选:B.点评:本题主要考查三角函数的图象与两角和的正切函数公式的应用,题目新,考查理解能力计算能力,属于中档题.11.关于f(x)=3sin(2x+)有以下命题,其中正确命题的个数()①若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z);②f(x)图象与g(x)=3cos(2x﹣)图象相同;③f(x)在区间[﹣,﹣]上是减函数;④f(x)图象关于点(﹣,0)对称.A. 0 B. 1 C. 2 D. 3考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:考查f(x)=3sin(2x+)的零点、周期性、对称性、单调性,可得结论.解答:解:关于f(x)=3sin(2x+),由于它的周期为π,相邻的两个零点相差半个周期,故若f(x1)=f(x2)=0,则x1﹣x2=k•(k∈Z),故①不正确.由于g(x)=3cos(2x﹣)=3sin(2x﹣+)=f(x)=3sin(2x+),故②正确.由2kπ+≤2x+≤2kπ+,k∈z,求得 kπ+≤x≤kπ+,故函数f(x)的减区间为[kπ+≤x≤kπ+],k∈z,故f(x)在区间[﹣,﹣]上是减函数,故③正确.把x=﹣代入f(x)的解析式求得f(x)=0,可得f(x)图象关于点(﹣,0)对称,故④正确.故选:D.点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的零点、周期性、对称性、单调性,属于基础题.12.在四边形ABCD中,==(1,1),+=,则四边形ABCD的面积为()A.B. 2C.D.考点:平面向量的基本定理及其意义.专题:平面向量及应用.分析:根据已知条件可判定四边形ABCD是菱形,并且边长为,对等式两边平方可得cos∠ABC,从而求出sin∠ABC,根据三角形的面积公式:S=即可求出四边形ABCD的面积.解答:解:∵∴四边形ABCD是▱;∵都是单位向量;∴四边形ABCD是菱形,边长为;∴;整理得:;∴cos;∴sin;.故选:A.点评:求解本题的关键是判断出四边形ABCD是菱形,本题考查知识点是,根据向量的坐标求长度,菱形的概念,单位向量,向量加法的平行四边形法则,三角形的面积公式.二.填空题(本题共5个小题,每小题5分,共25分,请把正确答案填在题中横线上)13.用秦九韶算法计算多项式f(x)=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64当x=2时的值时,v4的值为80 .考点:秦九韶算法.专题:算法和程序框图.分析:由秦九韶算法计算多项式f(x)=(((((x﹣12)x+60)x﹣160)x+240)x﹣192)x+64.即可得出.解答:解:由秦九韶算法计算多项式f(x)=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64=(((((x﹣12)x+60)x﹣160)x+240)x﹣192)x+64.∴当x=2时的值时,v0=1,v1=1×2﹣12=﹣10,v2=﹣10×2+60=40,v3=40×2﹣160=﹣80,v4=﹣80×2+240=80.故答案为:80.点评:本题考查了秦九韶算法的应用,属于基础题.14.将二进制数1011010(2)化为十进制结果为90 ;再将该数化为八进制数,结果为132(8).考点:整除的定义.专题:算法和程序框图.分析:利用二进制数化为“十进制”的方法可得1011010(2)=1×26+0×25+1×24+1×23+0×22+1×21+0×20.再利用“除8取余法”即可得出.解答:解:二进制数1011010(2)=1×26+0×25+1×24+1×23+0×22+1×21+0×20=90.如图所示,∴90(10)=132(8)点评:本题考查了二进制数化为“十进制”的方法、“除8取余法”,属于基础题.15.在边长为2的正方形ABCD中,点O为边AB的中点,在正方形ABCD内随机取一点P,则点P到点O的距离大于1的概率为.考点:几何概型.专题:计算题;概率与统计.分析:本题考查的知识点是几何概型,关键是要找出点到O的距离大于1的点对应的图形的面积,并将其和正方形面积一齐代入几何概型计算公式进行求解.解答:解:在正方形ABCD内随机取一点P,点P到点O的距离等于1的轨迹是以O为圆心,1为半径的半圆,面积为,∵正方形的面积为4,∴点P到点O的距离大于1的概率为1﹣=.故答案为:.点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.16.在△ABC中,∠B=60°,O为△ABC的外心,P为劣弧AC上一动点,且=x+y(x,y∈R),则x+y的取值范围为[1,2] .考点:平面向量的基本定理及其意义.专题:不等式的解法及应用;平面向量及应用.分析:看能否建立关于x,y变量之间的式子,设外接圆的半径为r,则,对等式两边平方得:,整理便会得到x2﹣xy+y2=1,所以(x+y)2=3xy+1,因为P为劣弧上的点,所以x,y∈[0,1],根据,所以从而求出x+y的范围.解答:解:∠AOC=120°,设|OA|=|OC|=|OP|=r;∵;∴;∴r2=r2;∴(x+y)2=3xy+1;∵P为劣弧AC上一动点;∴0≤x≤1,0≤y≤1;∴x+y≥;∴xy≤∴1≤∴1≤(x+y)2≤4∴1≤x+y≤2.∴x+y的取值范围为[1,2].故答案为:[1,2].点评:求解本题的关键便是根据||=r,对等式||=r两边进行平方.考查圆周角与圆心角的关系,向量的数量积,基本不等式.三.解答题(本大题共6小题,共75分,解答写出必要的文字说明、演算过程及步骤)17.如图,已知角α的终边在第二象限,且与单位圆交于点P(m,).(Ⅰ)求实数m的值;(Ⅱ)求的值.考点:两角和与差的正弦函数;任意角的三角函数的定义;运用诱导公式化简求值.专题:三角函数的求值.分析:(I)利用单位圆的性质可得:=1,且m<0,解得m;(II)由(I)可得:sinα,cosα.再利用诱导公式即可得出.解答:解:(Ⅰ)根据题意得:=1,且m<0,解得:m=﹣;(Ⅱ)∵sinα=,cosα=﹣,∴原式====.点评:本题考查了三角函数化简求值、单位圆的性质、诱导公式、两角和差的正弦公式,考查了计算能力,属于基础题.18.某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求高三(1)班全体女生的人数;(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)间的矩形的高;(3)若要从分数在[80,100)之间的试卷中任取两份分析女学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.考点:列举法计算基本事件数及事件发生的概率;频率分布直方图.专题:概率与统计.分析:(1)根据条件所给的茎叶图看出分数在[50,60)之间的频数,由频率分布直方图看出分数在[50,60)之间的频率,根据频率、频数和样本容量之间的关系解出样本容量.(2)算出分数在[80,90)之间的人数,算出分数在[80,90)之间的频率,根据小矩形的面积是这一段数据的频率,做出矩形的高.(3)由题意知本题是一个古典概型,试验包含的所有事件可以通过列举得到结果数,看出满足条件的事件数,根据古典概型公式得到结果.解答:解:(1)由茎叶图知:分数在[50,60)之间的频数为2.由频率分布直方图知:分数在[50,60)之间的频率为0.008×10=0.08.∴全班人数为=25人.(2)∵分数在[80,90)之间的人数为25﹣2﹣7﹣10﹣2=4人∴分数在[80,90)之间的频率为=0.16,∴频率分布直方图中[80,90)间的矩形的高为=0.016.(3)将[80,90)之间的4个分数编号为1,2,3,4;[90,100]之间的2个分数编号为5,6.则在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.至少有一个在[90,100]之间的基本事件有(1,5)(1,6)(2,5)(2,6)(3,5)(3,6)(4,5)(4,6)(5,6)共9个,∴至少有一份分数在[90,100]之间的概率是.点评:这是一个统计综合题,频数、频率和样本容量三者之间的关系是知二求一,这种问题会出现在选择和填空中,有的省份也会以大题的形式出现,把它融于统计问题中.19.设向量=(2,sinθ),,θ为锐角.(1)若∥,求tanθ的值;(2)若•=,求sinθ+cosθ的值.考点:平面向量数量积的运算;平行向量与共线向量.专题:计算题;平面向量及应用.分析:(1)根据向量平行的坐标表示式,结合题中数据建立关于θ的关系式,用同角三角函数基本关系化简即可得到tanθ=2.(2)根据向量数量积的公式可得2+sinθcosθ=,解出sinθcosθ=.结合同角三角函数的平方关系,算出(sinθ+cosθ)2=,将两边开方并且注意到θ为锐角,即可得到sinθ+cosθ=(舍负).解答:解:(1)∵=(2,sinθ),,且∥,…(2分)∴2cosθ﹣sinθ=0,可得tanθ=2.…(5分)(2)∵•=,∴2+sinθcosθ=,化简得sinθcosθ=.…(8分)因此,(sinθ+cosθ)2=1+2 sinθcosθ=.…(10分)又∵θ为锐角,可得sinθ+cosθ是正数∴sinθ+cosθ=(舍负).…(12分)点评:本题给出向量含有三角函数的坐标形式,在满足、平行的情况和•=的情况下,求tanθ和sinθ+cosθ的值.着重考查了平面向量平行的坐标表示式、向量数量积的坐标公式和同角三角函数关系等知识,属于中档题.20.已知函数.(1)求f(x)的最小正周期;(2)求f(x)的单调递增区间;(3)求f(x)在上的最值及取最值时x的值.考点:二倍角的余弦;两角和与差的正弦函数;二倍角的正弦;三角函数的周期性及其求法;正弦函数的单调性.专题:三角函数的图像与性质.分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为,由此求得它的周期.(2)根据函数f(x)的解析式为,由,求得x的范围,可得函数的增区间.(3)根据x的范围,以及正弦函数的定义域和值域求得函数的最值.解答:解:(1)因为=…(1分)==,…(3分)所以f(x)的最小正周期.…..(4分)(2)因为,由,…(6分)得,…..(7分)所以f(x)的单调增区间是.…(8分)(3)因为,所以.…..…(9分)所以.…..…..….(10分)所以.…..…(12分)当,即x=0时,f(x)取得最小值1.…..…(13分)当,即时,f(x)取得最大值4.…..…(14分)点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的单调性、定义域和值域,属于中档题.21.已知向量=(sin,﹣1),=(A,Acos)(A>0),函数f(x)=•的最大值为2.(1)求f(x)最小正周期和解析式;(2)设α,β∈[0,],f(3α+),f(3β+2π)=,求sin(α﹣β)的值.考点:平面向量数量积的运算;三角函数中的恒等变换应用;正弦函数的图象.专题:三角函数的图像与性质;平面向量及应用.分析:(1)利用平面向量的数量积得到解析式,然后利用三角函数公式化简,由题意得到周期和A;(2)由(1)得到α,β的三角函数值,然后由两角和与差的三角函数公式求值.解答:解:(1)…(3分)f(x)的最小正周期…(4分)因为 A>0,由题意知A=2,…(5分)所以f(x)=2sin(x﹣)…(6分)(2)f(3α+)=2sin((3α+)﹣)=2sinα=,f(3β+2π)=2sin((3β+2π)﹣)=2sin()=2cosβ=,…(8分)∴sin,cos,α,β∈[0,],∴cosα==sinβ==…(10分)∴sin(α﹣β)=sinαcosβ﹣cosαsinβ==﹣…(12分)点评:本题考查了平面向量的数量积、三角函数式的化简以及三角函数公式;熟练掌握两角和与差的三角函数公式是关键.22.已知函数f(x)的图象是由函数g(x)=cosx的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍,横坐标不变,再将所得到的图象向右平移个单位长度.(1)求函数f(x)的解析式,并求其图象的对称轴方程;(2)已知关于x的方程f(x)+g(x)=m在[0,2π)内有两个不同的解α,β(i)求实数m的取值范围;(ii)证明:cos(α﹣β)=﹣1.考点:三角函数中的恒等变换应用;函数y=Asin(ωx+φ)的图象变换.专题:创新题型;函数的性质及应用;三角函数的图像与性质.分析:(1)由函数y=Asin(ωx+φ)的图象变换规律可得:f(x)=2sinx,从而可求对称轴方程.(2)(i)由三角函数中的恒等变换应用化简解析式可得f(x)+g(x)=sin(x+j)(其中sinj=,cosj=),从而可求||<1,即可得解.(ii)由题意可得sin(α+j)=,sin(β+j)=.当1<m<时,可求α﹣β=π﹣2(β+j),当﹣<m<1时,可求α﹣β=3π﹣2(b+j),由cos(α﹣β)=2sin2(β+j)﹣1,从而得证.解答:解:(1)将g(x)=cosx的图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y=2cosx的图象,再将y=2cosx的图象向右平移个单位长度后得到y=2cos(x﹣)的图象,故f(x)=2sinx,从而函数f(x)=2sinx图象的对称轴方程为x=k(k∈Z).(2)(i)f(x)+g(x)=2sinx+cosx=()=sin(x+j)(其中sinj=,cosj=)依题意,sin(x+j)=在区间[0,2π)内有两个不同的解α,β,当且仅当||<1,故m的取值范围是(﹣,).(ii)因为α,β是方程sin(x+j)=m在区间[0,2π)内有两个不同的解,所以sin(α+j)=,sin(β+j)=.当1<m<时,α+β=2(﹣j),即α﹣β=π﹣2(β+j);当﹣<m<1时,α+β=2(﹣j),即α﹣β=3π﹣2(β+j);所以cos(α﹣β)=﹣cos2(β+j)=2sin2(β+j)﹣1=2()2﹣1=.点评:本小题主要考查三角函数的图象与性质、三角恒等变换等基础知识,考查运算求解能力、抽象概括能力、推理论证能力,考查函数与方程思想、分类与整体思想、化归与转化思想、数形结合思想.。
武平县第一中学届高三数学试题及答案

数学练习题5-1一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.已知集合A={x|x2﹣3x﹣4≤0},B={x|x=,x∈Z,k∈Z},则A∩B=()A.{﹣1,1} B.{﹣1,1,3} C.{﹣3,﹣1,1} D.{﹣3,﹣1,1,3}2.已知命题p:∃x∈R,向量=(x2,1)与=(2,1﹣3x)垂直,则()A.p是假命题;¬p:∀x∈R,向量=(x2,1)与=(2,1﹣3x)不垂直B.p是假命题;¬p:∀x∈R,向量=(x2,1)与=(2,1﹣3x)垂直C.p是真命题;¬p:∀x∈R,向量=(x2,1)与=(2,1﹣3x)不垂直D.p是真命题;¬p:∃x∈R,使得向量=(x2,1)与=(2,1﹣3x)不垂直3.设a=cos,b=30.3,c=log53,则()A.c<b<q B.c<a<b C.a<c<b D.b<c<a4.某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林()A.14400亩B.172800亩C.17280亩D.20736亩5.已知,函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是()A.B.C.D.6.已知x0是的一个零点,x1∈(﹣∞,x0),x2∈(x0,0),则()A.f(x1)<0,f(x2)<0 B.f(x1)>0,f(x2)>0C.f(x1)>0,f(x2)<0 D.f(x1)<0,f(x2)>07.数列{a n}的前n项和为S n,若a1=1,a n+1=3S n(n≥1),则a6=()A.3×44B.3×44+1 C.44 D.44+18.若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx﹣2在x=1处有极值,则ab的最大值()A.2 B. 3 C. 6 D.99.已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,﹣π<φ≤π.若函数f(x)的最小正周期为6π,且当x=时,f(x)取得最大值,则()A . f (x )在区间上是增函数B . f (x )在区间上是增函数C . f (x )在区间上是减函数D . f (x )在区间上是减函数10.已知函数f (x )的定义域为R ,f (﹣1)=2,对任意x ∈R ,f′(x )>2,则f (x )>2x+4的解集为( )A . (﹣1,1)B . (﹣1,+∞)C . (﹣∞,﹣1)D . (﹣∞,+∞) 二、填空题11.若实数满足,则的最小值为.12.设,则m 与n的大小关系为 .13.一个几何体的三视图如图所示(单位:m ),则这个几何体的体积为 .14.设 与的等比中项,则的最小值为 . 15.具有性质:的函数,我们称为满足“倒负”交换的函数,下列函数:①y=x ﹣;②y=x+;③y=中满足“倒负”变换的函数是 .三、解答题16.如图,已知直角梯形ACDE 所在的平面垂直于平面ABC ,∠BAC=∠ACD=,∠EAC=,AB=AC=AE.,x y 22x y +0,0a b >>2a2b11a b+︒90︒60(1)在直线BC 上是否存在一点P ,使得DP//平面EAB ?请证明你的结论; (2)求平面EBD 与平面ACDE 所成的锐二面角的余弦值.17.设为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,; 当两条棱平行时,的值为两条棱之间的距离;当两条棱异面时,. (1)求概率P ();(2)求的分布列,并求其数学期望E ().18.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足csinA=acosC (1)求角C 大小; (2)求sinA ﹣cos (B+)的最大值,并求取得最大值时角A ,B 的大小.19.已知抛物线的焦点为椭圆的右焦点,且椭圆的长轴长为4,左右顶点分别为A ,B ,经过椭圆左焦点的直线与椭圆交于C 、D (异于A ,B )两点.(1)求椭圆标准方程;θξ0=ξξ1=ξ0=ξξξ2y =22221(0)x y a b a b+=>>l(2)求四边形的面积的最大值;(3)若是椭圆上的两动点,且满,动点满足(其中O 为坐标原点),是否存在两定点使得为定值,若存在求出该定值,若不存在说明理由.20.已知函数.(Ⅰ)求f (x )的单调区间;(Ⅱ)若对于任意的x ∈(0,+∞),都有f (x )≤,求k 的取值范围.21.在直角坐标系中,曲线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线的普通方程与曲线的直角坐标方程;(2)设为曲线上的动点,求点到上点的距离的最小值,并求此时点的坐标.22.设函数的最大值为M .(1)求实数M 的值;(2)求关于的不等式的解集.ADBC 1122(,)(,)M x y N x y 121220x x y y +=P 2OP OM ON =+12,F F 12PF PF+xoy 1C ⎩⎨⎧==a y ax sin cos 3a o x 2C 24)4sin(=+πθρ1C 2C P 1C P 2C P ()f x =x 12x x M -++≤数学练习题5-1答案1.解:由A中不等式变形得:(x﹣4)(x+1)≤0,解得:﹣1≤x≤4,即A=,由B中x=,x∈Z,k∈Z,得到2k﹣1可能为﹣3,﹣1,1,3,解得:k=﹣1,0,1,2,即x=﹣1,﹣3,3,1,∴B={﹣3,﹣1,1,3},则A∩B={﹣1,1,3},故选:B.2.解:命题p:∃x∈R,向量=(x2,1)与=(2,1﹣3x)垂直,它的否定是:¬p:∀x∈R,向量=(x2,1)与=(2,1﹣3x)不垂直,如果垂直则有:2x2+1﹣3x=0,解得x=1或x=,显然命题的否定是假命题.故选:C.3.C 解:∵<<,∴a=cos<,b=30.3>1,c=log53>log5=,c=log53<log55=1;故a<c<b,4.解:由题设知该林场第二年造林:10000×(1+20%)=12000亩,该林场第三年造林:12000×(1+20%)=14400亩,该林场第四年造林:14400×(1+20%)=17280.故选C.5.D解:=2sin(x+),函数y=f(x+φ)=2sin(x+φ+)的图象关于直线x=0对称,函数为偶函数,∴φ= 6.解:∵已知x0是的一个零点,x1∈(﹣∞,x0),x2∈(x0,0),可令h(x)=,g(x)=﹣,如下图:当0>x>x0,时g(x)>h(x),h(x)﹣g(x)=<0;当x<x0时,g(x)<h(x),h(x)﹣g(x)=>0;∵x1∈(﹣∞,x0),x2∈(x0,0),∴f(x1)>0,f(x2)<0,故选C;7.解:由a n+1=3S n,得到a n=3S n﹣1(n≥2),两式相减得:a n+1﹣a n=3(S n﹣S n﹣1)=3a n,则a n+1=4a n(n≥2),又a1=1,a2=3S1=3a1=3,得到此数列除去第一项后,为首项是3,公比为4的等比数列,所以a n=a2q n﹣2=3×4n﹣2(n≥2)则a6=3×44.故选A8.解:函数f(x)=4x3﹣ax2﹣2bx﹣2的导数f′(x)=12x2﹣2ax﹣2b,由于函数f(x)=4x3﹣ax2﹣2bx﹣2在x=1处有极值,则有f′(1)=0,即有a+b=6,(a,b>0),由于a+b≥2,即有ab≤()2=9,当且仅当a=b=3取最大值9.故选D.9.解:∵函数f(x)的最小正周期为6π,根据周期公式可得ω=,∴f(x)=2sin(φ),∵当x=时,f(x)取得最大值,∴2sin(φ)=2,φ=+2kπ,∵﹣π<φ≤π,∴φ=,∴,由可得函数的单调增区间:,由可得函数的单调减区间:,结合选项可知A正确,故选A.10.解:设g(x)=f(x)﹣2x﹣4,则g′(x)=f′(x)﹣2,∵对任意x∈R,f′(x)>2,∴对任意x∈R,g′(x)>0,即函数g(x)单调递增,∵f(﹣1)=2,∴g(﹣1)=f(﹣1)+2﹣4=4﹣4=0,则∵函数g(x)单调递增,∴由g (x )>g (﹣1)=0得x >﹣1,即f (x )>2x+4的解集为(﹣1,+∞),故选:B 11.. 12、解:∵e x ,lnx 的导数等于e x ,,∴m=e x |=e 1﹣e 0=e ﹣1;n=lnx|=lne ﹣ln1=1.而e ﹣1>1∴m >n .故答案为:m >n .13、解:由三视图可知,这是一个简单的组合体,上面是一个底面是边长为1的正方形,高是2的四棱柱,体积是1×1×2 下面是一个长为2,高为1,宽为1的长方体,体积是1×1×2 ∴几何体的体积是1×1×2+2×1×1=4m 3,故答案为:4 14.【解析】,又,,所以的最小值为. 15、①③16.(一)解:(1)线段BC 的中点就是满足条件的点P 。
2009年普通高等学校招生全国统一考试数学(理)试题汇编圆锥曲线方程部分(全解析)

2009年普通高等学校招生全国统一考试试题数学(理)汇编圆锥曲线方程部分1.(安徽3(A )22124x y -= (B )22142x y -= (C )22146x y -= (D )221410x y -=答案:B解析:由2e =得222222331,1,222c b b a a a =+==,选B2.(安徽20)(本小题满分13分)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>上,00cos ,sin ,0.2x a y b πβββ==<<直线2l 与直线00122:1x y l x y a b+=垂直,O 为坐标原点,直线OP 的倾斜角为α,直线2l 的倾斜角为γ.(I )证明: 点P 是椭圆22221x y a b+=与直线1l 的唯一交点;(II )证明:tan ,tan ,tan αβγ构成等比数列.解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。
考查综合运用知识分析问题、解决问题的能力。
本小题满分13分。
解:(I )(方法一)由00221x y x y a b +=得22020(),b y a x x a y =-代入椭圆22221x y a b +=,得22222002422200021()(1)0b x b x b x x a a y a y y +-+-=.将00cos sin x a y b ββ=⎧⎨=⎩代入上式,得2222cos cos 0,x a x a ββ-⋅+=从而cos .x a β= 因此,方程组2222002211x y a b x y x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩有唯一解00x x y y =⎧⎨=⎩,即直线1l 与椭圆有唯一交点P.(方法二)显然P 是椭圆与1l 的交点,若Q 111(cos ,sin ),02a b βββπ≤<是椭圆与1l 的交点,代入1l 的方程cos sin 1x y a bββ+=,得11cos cos sin sin 1,ββββ+= 即11cos()1,,ββββ-==故P 与Q 重合。
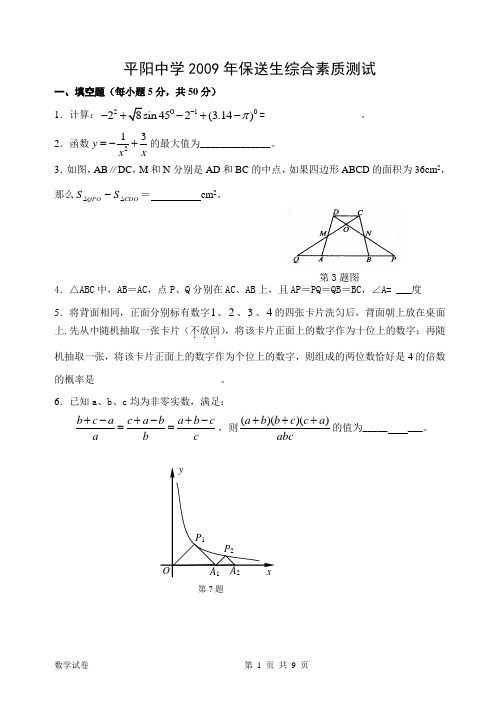
平阳中学2009年保送生综合素质测试及答案
平阳中学2009年保送生综合素质测试一、填空题(每小题5分,共50分)1.计算:21028sin 452(3.14)π--+-+- =___________________。
2.函数213y x x=-+的最大值为______________。
3.如图,AB ∥DC ,M 和N 分别是AD 和BC 的中点,如果四边形ABCD 的面积为36cm 2,那么CD O Q PO S S ∆∆-= cm 2。
4.△ABC 中,AB =AC ,点P 、Q 分别在AC 、AB 上,且AP =PQ =QB =BC ,∠A= 度 5.将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上.先从中随机抽取一张卡片(不放回...),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是_________________________。
6.已知a 、b 、c 均为非零实数,满足: b c a c a b a b ca b c+-+-+-==,则()()()a b b c c a abc +++的值为_____ ___。
第3题图P 1OxyA 1 A 2P 2 第7题7.如图,△P 1O A 1、△P 2 A 1 A 2是等腰直角三角形,点P 1、P 2在函数4y x=(x >0)的图象上,斜边OA 1、A 1A 2都在x 轴上,则点A 2的坐标是 。
8在△ABC 中,AB =BC =9,且∠BAC =45°,P 是线段BC 上任意一点,P 关于AB 、AC 的对称点为E 、F ,当△AEF 的面积最小时,AP = .9.已知关于x 的不等式0ax b ->的解是1x <,则关于x 的不等式()(2)0ax b x +->的解为_____________________________。
10.已知由小到大的10个正整数a 1,a 2,a 3,……,a 10的和是2009(a 1,a 2,a 3,……,a 10中任何两个数都不相等),那么a 5的最大值是 .二、解答题(每小题10分,共50分) 11.(每小题5分,满分10分) (1)先化简,再求值:232224xx x x x x ⎛⎫-÷ ⎪+--⎝⎭,其中45x =-;(2)解方程:2450x x --=。
2009年宁波市重点中学保送生招生考试数学试卷及答案

(A) 1(B)(D)39. 13个小朋友围成一圈做游戏, 规则是从某一个小朋友开始按顺时针方向数数,数到第13,该小朋友离开;这样继续下去•,直到最后剩下一个小朋友2009宁波重点中学保送生招生考试数学试卷、选择题(每小题 3分,共36 分)1如图是一个水平摆放的小正方体木块,图( 2)、( 3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去, 至第七个叠放的图形中, 小正方体木块总数应是 ()2、 有如下结论(1)有两边及一角对应相等的两个三角形全等; (2)菱形既是轴对称图形又是中心对称图形;(3)对角线相等的四边形是矩形; (4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。
其中正确结论的个数为( )(A ) 1 个 (B ) 2 个 (C ) 3 个(D ) 4 个3、 在1000个数据中,用适当的方法抽取 50个作为样本进行统计, 频数分布表中,54.5~57.5这一组的频率是0.12,那么,估计总体数据落在 54.5~57.5之间的约有 ( ) (A ) 6 个 (B ) 12 个 (C ) 60 个 (D ) 120 个 4、如图,O O 中,弦 AD // BC , DA = DC ,Z AOC = 160 ° 则/ BCO 等于().(A ) 20° (B ) 30° ( C ) 40° ( D ) 50°5、 若直角三角形的两条直角边长为 a 、b ,斜边长为c ,斜边上的高为h ,则有( )(D )120A 、ab=h ; B1+1 = 1 ; C1丄1 1 + = ; D 2 .2 .2a b h2 2a +b =2h6. 如图是一个切去了一个角的正方体纸盒,切面与棱的交点ABC7. 在平面直角坐标系中,横坐标、纵坐标都为整数的 点称为整点,观察图中每正方形(实线)四条边上的整 点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点的个数共有 ................... ( A 、35 个 B 、40 个 C 、45 个 D 、50 个&用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面•已知正11 1多边形的边数为x 、y 、z ,则-- -的值为()x y z将纸盒剪开展成平面,则展开图不可能是A 、B 、C 均是棱的中点,现小明是1号,要使最后剩下的是小明自己,他应该建议从()小朋友开始数起?A、7 号B 、8 号C 、13 号D 、2 号10、在1+11+111 +……+111……111(最后一项2009个1)的和之中,数字1共出现了()次. A 、224 B、225 C、1004 D、100511、一只船有一个漏洞,水以均匀速度进入船内。
2009年高考理科数学(全国卷Ⅰ)试题及答案

2009年普通高等学校招生全国统一考试全国卷I 理科数学(必修+选修Ⅱ)本试卷分第。
卷(选择题)和第。
卷(非选择题)两部分.第。
卷1至2页,第。
卷3至4页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意: 1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目. 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效..........3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.参考公式: 如果事件A B ,互斥,那么球的表面积公式()()()P A B P A P B +=+24πS R = 如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径一、选择题【2009/理/1】 设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A B ,则集合[()u AB I中的元素共有(A )(A )3个 (B )4个 (C )5个 (D )6个解:{3,4,5,7,8,9}AB =,{4,7,9}(){3,5,8}U A BC A B =∴=故选A 。
也可用摩根律:()()()U U U C A B C A C B =【2009/理/2】已知1iZ+=2+i,则复数z=(B ) (A )-1+3i (B)1-3i(C)3+i(D)3-i解:(1)(2)13,13z i i i z i =+⋅+=+∴=- 故选B 。
【2009/理/3】不等式11X X +-<1的解集为( D ) (A ){x }{}011x x x 〈〈〉 (B){}01x x 〈〈(C ){}10x x -〈〈 (D){}0x x 〈解:验x=-1即可。
2009年中考数学保送生招生试卷及答案(浙江省余姚)

(A)- 4S L 21 -------- T(B)- ,4S L(C)-L 2 1 — 4S (D)— . L 22223、方程(x 2 x 1) x 31的所有整数解的个数是()(A ) 5 个(B ) 4 个(C ) 3个(D ) 2 个4、已知梯形ABCD 中,AD // BC ,对角线 AC 、BD 交于0,△ AOD 的面积为4,△ BOC 的面积为 9,则梯形ABCD 的面积为( )4S(A ) 21 (B ) 22(C ) 25(D ) 265、方程 |xy |+|x+y|=1 的整数解的组数为() 。
(A ) 8(B) 6(C) 4(D) 26、已知一组正数x 1, X 2, X 3, &, 疋的方差为: S 2 土25 2 2 2X 2 X 3 X4X 52 20), 则关于数据洛 2, X 22, X 3 2, &2,x 2的说法: ①方差为S 2 ;②平均数为2③平均数为4;④方差为4S 2。
其中准确的说法是()(A ) ①②(B) ①③ (C) ②④(D ) ③④7、 一名模型赛车手遥控一辆赛车, 称为一次操作.若五次操作后, (A ) 7 2°( B ) 108° 或 14 4° (C ) 144° 8、 如图,已知圆心为 A 、B C 的三个圆彼此相切,且均与直线别为 a 、b 、c (0<c<a<b ),贝U a 、 2°或 A 、O 144°B 、OC 勺半径(A ) 2b=a+c(D)、填空题(每小题 5分,共30 分)9、已知a 、b 为正整数,a=b-2005,若关于x 方程x 2-ax+b=0有正整数解,则a 的最小值是 _____________ 10、如图,在△ ABC 中, AB=AC,AC L BC, CG/ AB, BG 分别交AD,AC 于EF 若f b ,那么籌等于余姚中学2009年4月保送生选拔卷(数学)2、菱形的两条对角线之和为 L,面积为S,则它的边长为().先前进 Oim a(0 a然后,原地逆时针方向旋转角 发现赛车回到出发点,则角 <a <180 ° )。
福建省龙岩市武平一中_学年高一数学下学期期末练习试卷(含解析)【含答案】

2014-2015学年福建省龙岩市武平一中高一(下)期末数学练习试卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.sin(﹣)的值等于()A.B.﹣C.D.﹣2.已知向量=(﹣2,1),=(4,k).若⊥,则实数k的值是()A. k=2 B. k=﹣2 C. k=8 D. k=﹣83.如果点P(tanθ,cosθ)位于第三象限,那么角θ所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.化简=()A.B.C.D.5.函数y=|sinx|的一个单调增区间是()A. [﹣,] B. [π,] C. [,] D. [,2π]6.已知||=4,||=8,与的夹角为120°,则|2|=()A. 8B. 6C. 5D. 87.已知等边三角形ABC的边长为1,则•=()A.B.﹣C.D.8.已知函数f(x)=sin(2x﹣)(x∈R)下列结论错误的是()A.函数f(x)的最小正周期为πB.函数f(x)是偶函数C.函数f(x)的图象关于直线x=对称D.函数f(x)在区间上是减函数9.若|+|=|﹣|=2||,则向量﹣与的夹角为()A.B.C.D.10.现有四个函数:①y=xsinx,②y=xcosx,③y=x|cosx|,④y=x•2x的部分图象如下,但顺序被打乱了,则按照从左到右将图象对应的函数序号排列正确的一组是()A.①②③④B.②①③④C.③①④②D.①④②③二、填空题(每小题5分)11.直线的倾斜角等于.12.已知一扇形的周长为20cm,当这个扇形的面积最大时,半径R的值为.13.已知=(3,﹣1),=(4,3),满足=(﹣9,18),则= .14.已知为一单位向量,与之间的夹角是120°,而在方向上的投影为﹣2,则||= .15.给出下列四个命题:①函数f(x)=sin|x|不是周期函数;②把函数f(x)=2sin2x图象上每个点的横坐标伸长到原来的4倍,然后再向右平移个单位得到的函数解析式可以表示为;③函数f(x)=2sin2x﹣cosx﹣1的值域是[﹣2,1];④已知函数f(x)=2cos2x,若存在实数x1、x2,使得对任意x都有f(x1)≤f(x)≤f(x2)成立,则|x1﹣x2|的最小值为;其中正确命题的序号为(把你认为正确的序号都填上).三、解答题(解答应写出必要的文字说明、证明或演算步骤.)16.函数已知向量,的夹角为,||=2,||=3,设=3﹣2,=2+k (1)若⊥,求实数k的值;(2)是否存在实数k,使得∥,说明理由.17.(Ⅰ)化简:;(Ⅱ)已知α为第二象限的角,化简:.18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.(1)求函数f(x)的解析式;(2)求函数f(x)的单调增区间;(3)若x∈[﹣,],求函数f(x)的值域.2014-2015学年福建省龙岩市武平一中高一(下)期末数学练习试卷参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.sin(﹣)的值等于()A.B.﹣C.D.﹣考点:三角函数的化简求值.专题:计算题.分析:要求的式子即 sin(﹣4π+),利用诱导公式可得,要求的式子即 sin=sin.解答:解:sin(﹣)=sin(﹣4π+)=sin =sin=,故选C.点评:本题考查利用诱导公式进行化简求值,把要求的式子化为sin(﹣4π+),是解题的关键.2.已知向量=(﹣2,1),=(4,k).若⊥,则实数k的值是()A. k=2 B. k=﹣2 C. k=8 D. k=﹣8考点:平面向量数量积的运算.专题:平面向量及应用.分析:利用⊥⇔=0,即可解出.解答:解:∵⊥,∴=﹣2×4+k=0,解得k=8.故选:C.点评:本题考查了向量垂直于数量积的关系,属于基础题.3.如果点P(tanθ,cosθ)位于第三象限,那么角θ所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限考点:三角函数值的符号;象限角、轴线角.专题:三角函数的求值.分析:利用角所在的象限与三角函数值的符号的关系即可得出.解答:解:∵点P(tanθ,cosθ)位于第三象限,∴,∴θ位于第二象限.故选B.点评:熟练掌握角所在的象限与三角函数值的符号的关系是解题的关键.4.化简=()A.B.C.D.考点:向量加减混合运算及其几何意义;零向量.专题:计算题.分析:根据向量加法的三角形法则,我们对几个向量进行运算后,即可得到答案.解答:解:∵.故选B点评:本题考查的知识点是向量加减混合运算及其几何意义,及零向量的定义,其中根据三角形法则对已知向量进行处理,是解答本题的关键.5.函数y=|sinx|的一个单调增区间是()A. [﹣,] B. [π,] C. [,] D. [,2π]考点:正弦函数的图象.专题:三角函数的图像与性质.分析:结合函数y=|sinx|的周期为π,结合它的图象,可得它的一个增区间.解答:解:结合函数y=|sinx|的周期为π,结合它的图象,可得它的一个增区间为[π,],故选:B.点评:本题主要考查正弦函数的图象特征,属于基础题.6.已知||=4,||=8,与的夹角为120°,则|2|=()A. 8B. 6C. 5D. 8考点:数量积表示两个向量的夹角.专题:平面向量及应用.分析:把已知数据代入向量的模长公式计算可得.解答:解:∵||=4,||=8,与的夹角θ=120°,∴|2|====8故选:A点评:本题考查数量积与向量的夹角,涉及模长公式,属基础题.7.已知等边三角形ABC的边长为1,则•=()A.B.﹣C.D.考点:平面向量数量积的运算.专题:平面向量及应用.分析:由向量数量积的定义,即,再将题目中条件代入计算即可.解答:解:由题意,COS120°=.故答案选:B.点评:本题是对数量积定义的考查,属于简单题,在选择时,学生往往可能因为对特殊角的三角函数值的不熟练而选错.8.已知函数f(x)=sin(2x﹣)(x∈R)下列结论错误的是()A.函数f(x)的最小正周期为πB.函数f(x)是偶函数C.函数f(x)的图象关于直线x=对称D.函数f(x)在区间上是减函数考点:正弦函数的图象.专题:三角函数的图像与性质.分析:由条件利用诱导公式,余弦函数的周期性、奇偶性、单调性以及图象的对称性,判断各个选项是否正确,从而得出结论.解答:解:函数f(x)=sin(2x﹣)=cos2x,故它的最小正周期为π,故A满足条件;显然,它是偶函数,故B正确;当x=时,求得函数值y=0,不是最值,故f(x)的图象不关于直线x=对称,故C错误;在区间上,f(x)=cos2x是减函数,故D正确,故选:C.点评:本题主要考查诱导公式,余弦函数的图象和性质,属于基础题.9.若|+|=|﹣|=2||,则向量﹣与的夹角为()A.B.C.D.考点:平面向量数量积的运算.专题:平面向量及应用.分析:由已知条件得,且||=||,由此能求出向量﹣与的夹角.解答:解:∵|+|=|﹣|=2||,∴,且||=||,∴cos<(),>==﹣=﹣=﹣,∴向量﹣与的夹角为.故选:A.点评:本题考查向量的夹角的求法,是中档题,解题时要认真审题,注意平面向量数量积的合理运用.10.现有四个函数:①y=xsinx,②y=xcosx,③y=x|cosx|,④y=x•2x的部分图象如下,但顺序被打乱了,则按照从左到右将图象对应的函数序号排列正确的一组是()A.①②③④B.②①③④C.③①④②D.①④②③考点:函数的图象.专题:函数的性质及应用.分析:依据函数的性质与图象的图象对应来确定函数与图象之间的对应关系,对函数的解析式研究发现,四个函数中有一个是偶函数,有两个是奇函数,还有一个是指数型递增较快的函数,由这些特征接合图象上的某些特殊点判断即可.解答:解:研究发现①是一个偶函数,其图象关于y轴对称,故它对应第一个图象②③都是奇函数,但②在y轴的右侧图象在x轴上方与下方都存在,而③在y轴右侧图象只存在于x轴上方,故②对应第三个图象,③对应第四个图象,④与第二个图象对应,易判断.故按照从左到右与图象对应的函数序号①④②③故选:D.点评:本题考点是正弦函数的图象,考查了函数图象及函数图象变化的特点,解决此类问题有借助两个方面的知识进行研究,一是函数的性质,二是函数值在某些点的符号即图象上某些特殊点在坐标系中的确切位置.二、填空题(每小题5分)11.直线的倾斜角等于120°.考点:直线的一般式方程.专题:直线与圆.分析:求出直线斜率即可得出tanα的值,由倾斜角的范围和正切函数的知识可得答案.解答:解:由题意可得:直线的斜率为﹣,即tanα=﹣,又α∈[0,π),故α=120°故答案为:120°点评:本题考查直线的斜率和倾斜角的关系,属基础题.12.已知一扇形的周长为20cm,当这个扇形的面积最大时,半径R的值为5cm .考点:扇形面积公式.专题:三角函数的求值.分析:根据条件求出扇形的面积公式,转化成关于R的二次函数,利用一元二次函数的性质进行求解.解答:解:∵扇形的周长为20cm,∴l=20﹣2R,∴S=lR=(20﹣2R)•R=﹣R2+10R=﹣(R﹣5)2+25,∴当半径R=5cm时,扇形的面积最大为25cm2.故答案为:5cm点评:本题考查扇形的面积的计算,利用一元二次函数的性质是解决本题的关键.13.已知=(3,﹣1),=(4,3),满足=(﹣9,18),则= (﹣1,2).考点:平面向量数量积的运算.专题:平面向量及应用.分析:由数量积的运算可得,代入已知由向量的坐标运算可得.解答:解:∵=(3,﹣1),=(4,3),∴=4×3﹣1×3=9,又=(﹣9,18),∴9=(﹣9,18),∴=(﹣1,2)故答案为:(﹣1,2)点评:本题考查平面向量的数量积运算,属基础题.14.已知为一单位向量,与之间的夹角是120°,而在方向上的投影为﹣2,则||= 4 .考点:向量的模.专题:计算题.分析:利用向量数量积的几何意义:向量的数量积等于一个向量的模乘以另一个向量在第一个向量上的投影.解答:解:在方向上的投影为=﹣2∴故答案为:4点评:本题考查向量数量积的几何意义;解答关键是利用数量积求出向量的投影.15.给出下列四个命题:①函数f(x)=sin|x|不是周期函数;②把函数f(x)=2sin2x图象上每个点的横坐标伸长到原来的4倍,然后再向右平移个单位得到的函数解析式可以表示为;③函数f(x)=2sin2x﹣cosx﹣1的值域是[﹣2,1];④已知函数f(x)=2cos2x,若存在实数x1、x2,使得对任意x都有f(x1)≤f(x)≤f(x2)成立,则|x1﹣x2|的最小值为;其中正确命题的序号为①④(把你认为正确的序号都填上).考点:命题的真假判断与应用;正弦函数的图象.专题:三角函数的图像与性质.分析:①根据三角函数的周期性进行判断.②根据三角函数的平移关系进行判断.③根据三角函数的性质结合一元二次函数的最值进行求解即可.④根据三角函数的对称性和最值性结合三角函数的周期性进行判断即可.解答:解:①函数f(x)=sin|x|=是偶函数,关于y轴对称,则函数f(x)不是周期函数,故①正确;②把函数f(x)=2sin2x图象上每个点的横坐标伸长到原来的4倍,得到y=2sin,然后再向右平移个单位得到的函数解析式可以表示为y=2sin,故②错误;③函数f(x)=2sin2x﹣cosx﹣1=2(1﹣cos2x)﹣cosx﹣1=﹣2cos2x﹣cosx+1=﹣2(cosx+)2+,∴当cosx=﹣时,函数取得最大值,当cosx=1时,函数取得最小值﹣2﹣1+1=﹣2,即函数的值域是[﹣2,];故③错误.④若存在实数x1、x2,使得对任意x都有f(x1)≤f(x)≤f(x2)成立,则f(x1)为函数f(x)的最小值,f(x2)为函数f(x)的最大值,则|x1﹣x2|的最小值为==,故④正确.故正确的命题是①④,故答案为:①④.点评:本题主要考查命题的真假判断,涉及的内容主要是三角函数的图象和性质以及三角函数的图象变换,综合考查三角形的性质的应用.三、解答题(解答应写出必要的文字说明、证明或演算步骤.)16.函数已知向量,的夹角为,||=2,||=3,设=3﹣2,=2+k(1)若⊥,求实数k的值;(2)是否存在实数k,使得∥,说明理由.考点:数量积判断两个平面向量的垂直关系;平行向量与共线向量.专题:平面向量及应用.分析:(1)由已知得=()(2)=0,由此能求出k=.(2)由∥,得,由此能求出k.解答:解:(1)∵向量,的夹角为,||=2,||=3,设=3﹣2,=2+k,⊥,∴=()(2)=6+(3k﹣4)﹣2k=24+6(3k﹣4)cos﹣18k=0,解得k=.(2)∵∥,∴,解得k=﹣.点评:本题考查实数值的求法,是基础题,解题时要注意向量垂直和向量平行的性质的合理运用.17.(Ⅰ)化简:;(Ⅱ)已知α为第二象限的角,化简:.考点:三角函数的化简求值;运用诱导公式化简求值.专题:三角函数的求值.分析:(Ⅰ)利用三角函数的诱导公式化简;(Ⅱ)利用三角函数的基本关系式对代数式变形、化简.解答:解:(Ⅰ)===﹣cosα.(Ⅱ)=•=.∵α是第二象限角,∴cosα<0,sinα>0上式=+=cosα﹣1+1﹣cosα=0.点评:本题考查了利用三角函数诱导公式以及基本关系式化简三角函数式;注意三角函数符号以及名称.18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.(1)求函数f(x)的解析式;(2)求函数f(x)的单调增区间;(3)若x∈[﹣,],求函数f(x)的值域.考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:(1)利用函数的图象求出A和函数的周期,求出ω,即可求函数f(x)的解析式;(2)利用正弦函数的单调增区间直接求解函数f(x)的单调增区间;(3)通过x∈[﹣,],求出相位的范围,利用正弦函数的值域,求函数f(x)的值域.解答:解:(1)由题意知:A=2,T=,∴ω=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)函数f(x)的解析式:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(2)由得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)减区间为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)(3)∵x∈[﹣,],∴,∴.∴函数的值域为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(16分)点评:本题考查三角函数的解析式的求法,函数的单调性以及正弦函数的值域的求法,考查计算能力.。
保送生考试数学试卷

2009年永定一中保送生考试数学试卷考试时间: 120分钟 满分: 120分注意:1、 本试卷共 8页,包含选择题(第1题~第10题,共10题,计40分)与非选择题(第11题~第21题,共11题,计80分)两部分.2、 请把选择题的答案写在选择题后的答题栏里....。
第Ⅰ卷(选择题 共40分)一、选择题:(本大题共101.已知一次函数y=kx+b 的图象(如图1),则当x >0时, y 的取值范围是( )A .y >0B .y <0C .-2<y <0D .y <-22.2009年,我国第一季度的国内生产总值大约为65800 ( ) A . 6.58×1014元 B . 6.58×1013元 C . 6.58×1012元 D . 6.58×1011元 3.下列运算正确的是( )A .633x x x =+B .12233)(x x x =C .633)(x x =D .20210x x x ÷=4.由一些大小相同的小正方体组成的简单几何体的 主视图和俯视图如图2所示,则组成该几何体的 小正方体个数的最小值是( ) A . 6 B . 7C . 8D . 9 5.定义一种数的运算:11a b 22a b ,1221b a b a -=的解为( )A . 2,1B . 1,2-C . 1,2-D . 无解 6.已知关于x 的方程0122=+++a ax ax 有实根,则实数a 的取值范围是( )A. 0≤aB. 0≥a C . 0<a D . 1>a7.把反比例函数xy 2=的图象关于x 轴对称后,再向左平移2个单位,则所得函数图象的表达式是( )A . 22+-=x y B . 22+=x y C . 22-=x y D .22--=x y 8.已知,73-=A 57-=B ,则A 、 B 的大小关系是( )A .A <B B .A >BC .A =BD . A 、 B 的大小关系不确定9.如图3,AD 、AE 分别是⊙O 的切线,D 、E 分别为切点,若AD=4a ,⊙O 的面积为29a π,则弦DE 的长为 ( ) A .512a B . 524aC . 12aD .不能确定10.连续掷一枚质地均匀的骰子2次,则所得点数之和不小于6的概率为( )A .32B . 97C .21D .1813 一、选择题答题栏:(每小题4分,满分40分) 第Ⅱ卷(非选择题 共80分)二、填空题(本大题共5小题,每小题4分,满分20分) 11.分解因式:=++m mx mx 652 。
09杭高保送生数学卷答案

数学部分(共50分)1.解:原方程可化为22240(2)x x ax x -++=-等价于22240x x a -++=且0,2x x ≠≠因此原方程只有一个实根有以下三种情形:① 方程22240x x a -++=有两个(除0,2)等根0= :72a =- 方程的根为12x =②方程22240x x a -++=有两根:一个为0,另一个除0,2的根将0x =代入得4a =-,此时另一根为1x =③方程22240x x a -++=有两根:一个为2,另一个除0,2的根将2x =代入得8a =-,此时另一根为1x=- 综上:72a =-,方程只有一个根为12x =4a =-,方程只有一个根为1x= 8a =-,方程只有一个根为1x =-2. 解:由题意可知:第x 年,每个甲鱼池平均产量为1y 万只,全县的甲鱼池数为2y ,满足10.20.8y x =+ 2434y x =-+(1)第二年甲鱼池的个数为26个,全县出产甲鱼31.2万只(2)212(0.20.8)(434)0.8 3.627.2y y x x x x =+-+=-++ =20.8( 2.25)31.25x --+第6年总产量为20万只,第1年为30万只,所以规模缩小(3)x 为正整数,故当2x=时规模最大全县出产甲鱼31.2万只3.解:由已知可知12009n n a a -= ① 或11n n a a -= ② (1)144a =,2442009a =,3200944a = 144a =,2442009a =,32442009a =,24200944a =(2)1n a -只能经过第①类变换或第②类变换变为n a (2,3,,2009)n = ,从1a 开始连续经过2008次这样的变换变为2009a连续两次②类变换相互抵消,保持原数不变。
连续三系变换依次为“第①类变换、第②类变换、第①类变换”时,其中两次第①类变换相互抵消,相当于只对原数进行了一次第②类的变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年武平县初中毕业生综合素质测试卷(数学部分)(答题时间:120分钟 满分:120分)一、选择题(本大题共8小题,每小题3分,共24分))A .15 B .-15C .5D .-5 2.若x 表示一个两位数,把数字3放在x 的左边,组成一个三位数是( ) A .3x B .3×100+x C .100x+3 D .10x+3 3.如图1,把一个长方形纸片沿EF 折叠,点D 、C 分别落在 D ′、C ′的位置,若∠EFB=65°,则∠AED ′等于 A .50° B .55° C .60° D .65°4.如图2,某一大坝的横断面是梯形ABCD ,坝顶宽CD=6米, 斜坡AD=16米,坝高8米,斜坡BC 的坡度i=1:3,则坝底宽 AB 是( )米。
A . B .30 C . D .5.如图3,矩形ABCD 中,AB=3cm ,BC=4cm ,对角线AC 、 BD 相交于点O ,点P 是线段AD 上的一动点,且PM ⊥BD 于M ,PN ⊥AC 于N ,则PM+PN 等于( ) A .65 B .125 C .3 D .2456.为迎接“五·四”青年节,九年级某班宿舍从包括李冰在内的8名内宿生中,随机地抽调2名内宿生整理宿舍,那么抽调到李冰的概率是( )A .14B .17 C .18 D .1287.已知点A (x 1,6),B (x 2,-2),C (x 3,-4)都是反比例函数y =-2a x(a ≠0)图象上的点,则x 1,x 2,x 3的大小关系是( )A .x 1<x 2<x 3B .x 1<x 3<x 2C .x 3<x 2<x 1D .x 2<x 3<x 18.一列数1,-23,12,-25,13,-27……中,观察该数列后,找出第15个数是( ) A .-215 B .215 C .-18 D .18二、填空题(本大题共10小题,每小题3分,共30分)9.已知∠A=23°45′6″,则∠A 的余角是 。
10.据统计,全球每小时约有523000000吨污水排入江河湖海,用科学记数法表示是吨。
11.化简:|2π-7|= 。
12.多项式3x 2-y -xy 3+x 3-1中最高次数项是 。
13.如图4在ΔABC 中,D 、E 、F 分别是AB 、BC 、AC的中点,若平移ΔCFE ,则图中能与它重合的三角形 是 (写一个即可)。
14.不等式组 4152x xxx>-+≤- 的解集为 。
15.数据0,3,1,-2,-1,4,1,2的方差是 。
16.一个长方体的主视图和左视图如图5所示(单位:cm )则其俯视图的面积是 cm 2。
17.如图6,AB 为⊙O 的弦,⊙O 的半径为4,OC ⊥AB 于点D ,交⊙O 于点C ,且CD=1, 则弦AB 的长是 。
18.分解因式:x 2+7x y -18y 2= 。
三、解答题(本大题共9小题,共66分)19.(本小题6分)计算题: 4sin45°+0-(13)—120.(本小题6分)先化简,再求值:24(1)3244a a a--÷-+++,其中21.(本小题6分)如图7在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)请在图中画出图形ABCD关于点M对称的图形。
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少?(注:只要写出对应边的比即可)(3)求图形A2B2C2D2的面积。
22.(本小题6分)“爱我中华,爱我家乡”的知识测验(试题满分为100分,得分取正整数),为了了解测试情况,从中抽取部分学生的成绩作样本进行统计,并绘制了下面尚未完成的频率分布表:(1)请你把尚未完成的频率分布表补充完整;(2)画出频率分布直方图。
(3)如果我县现有2300名中学生,请你估计80分以上的学生人数有多少?23.(本小题7分)地球半径R约为6400km,同步卫星运行到地球表面上P点的正上方F点时,PF=6R,从同步卫星上能拍摄到的地球上最远的点在什么位置?这样的最远点与P点的距离大约是多少?(结果保留小数点后一位)24.(本小题7分)2008年初我国南方发生雪灾,某地电线被压断,供电局的维修队要到30千米远的郊区进行抢修。
维修工骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果两车同时到达抢修点,已知抢修车每小时比摩托车快20千米,求这两种车的速度。
25.(本小题7分)如图9,以锐角ΔABC的一边BC为直径作半圆,交AB于D,交AC于E。
(1)求证ΔADE∽ΔABC;(2)若DE=12BC,求∠A的度数。
如图10,正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q。
(1)试证明:无论点P运动到AB上(不含A点)何处时,都有ΔADQ≌ΔABQ;(2)当点P在AB上运动到什么位置时,ΔADQ的面积是正方形ABCD面积的16;(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,指出当点P运动到什么位置时,ΔADQ恰为等腰三角形(不必说明理由)。
已知,如图11,抛物线y=a x2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于点A、B,点A的坐标为(3,0),点O为坐标原点。
(2)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。
问:是否存在这样的直线l,使得OF+DF最小?若存在,请求出点P的坐标;若不存在,请说明理由。
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ。
当ΔCQE 的面积最大时,求点Q的坐标。
2009年武平县初中毕业生综合素质测试卷数学部分参考答案及评分标准一、选择题(共24分)1—5:CBACB 6—8:ABD 二、填空题(共30分)9.66°14′54″ 10.5.23×10811.7-2π 12.-xy 313.ΔBED (或ΔADF ) 14.2<x ≤3 15.7216.6 17. 18.(x+9y )(x -2y) 三、解答题(共66分)19.原式=41-3+3- …………5分 =2 …………6分20.解原式=2222243244a a a a a a a -+---÷-+++ …………1分 =2(2)(2)32(2)(2)a a a a a a -+-++- ……………………4分=a -3 ……………………5分当 31 ……………………6分21.(1)画正确2分 (2)1:2或12……2分 (3)16 ……2分 22.(1)每空0.5分,8 0.16 0.28 50 (2)画完整2分。
(画错1个扣1分,扣完为止) (3)13800名 …………2分23.解:从同步卫星上拍摄到的地球上最远的点是切点, ……1分如图,FT 是⊙O 的切线,ΔFTO 是直角三形 ……2分∵cos ∠FDT=177OT R FE R == ……3分 ∴∠FDT ≈81.79° ……4分∴ (81.79)64009131.4180PTkm π⨯=⨯≈(π=3.14)(9136.0km ) ……6分答:最远点与P 点的距离大约是(9131.4)km 。
(直接代入9135.7km) ……7分 24.解:设摩托车的速度每小x 千米,则抢修车每小时(x+20)千米 ……1分由题意得:30301204x x -=+ …………4分 解得:x 1=40,x 2=-60。
…………5分经检验x 1=40,x 2=-60都是原方程的解,但x 2=-60不符合题意,应舍去。
∴x=40,x+20=60 ………6分 答:摩托车、抢修车的速度分别是40、60千米/时 ………7分25.(1)证明:∵四边形BCED 内接于半圆∴∠B=∠AED ,∠C=∠ADE …………1分 ∴ΔADE ∽ΔACB …………2分(2)解:连接BE 由ΔADE ∽ΔACB 得到,AE DEAB CB= …………3分 ∵DE=12BC∴12AE AB = …………4分 又∵BC 是直径∴∠BEC=90° …………5分 ∴cosA=12AE AB = …………6分 ∴∠A=60° …………7分26.(1)证明:在正方形ABCD 中,AD=AB ,∠DAQ=∠BAQ=45°又∵AQ 是公共边∴ΔADQ ≌ΔABQ ……2分(2)解:作QE ⊥AD 于E ,设正方形边长为a∵S ΔADQ =16×a 2∴EQ=13a ∴EQ=13a ,DE=23a而EQ ∥QP∴ΔDEQ ≈ΔDAP∴EQ DE AP DA = 即 1233a aAP a=, AP=12a ∴点P 在线段AB 中点时时条件。
…………6分(3)若ΔADQ 是等腰三角形,则有QD=QA 或DA=DQ 或AQ=AD①当点P 运动到与B 点重合时,由于四边形ABCD 是正方形知QD=QA ,此时ΔADQ 是等腰三角形。
……7分②当点P 运动到与点C 重合时,点Q 也与点C 重合,此时DA=DQ ,ΔADQ 是等腰三形。
…………8分③当CP=1)BC 时ΔADQ 是等腰三形。
…………9分27.解:(1)由题意得c=3 解得: a =-19a -6a+c=0 c=3 ……2分 ∴抛物线解析式:y =-x 2+2x+3(2)存在如图作D ′使D ′与D 关于直线AC 对称,连接D ′O ,D ′A 交AC 于F ,过点F 且平行于x 的直线l 与抛物线交于点P ,点P 为所求。
易求D ′(3,1),设直线OD ′解析式:y=k 1x ……4分3k 1=1,k 1=13,直线OD :y=13x 设直线AC 解析式:y=k 2x+33k 2+3=0, k 2=-1,直线CA :y =-x+3 ……5分由 133y x y x ==-+ 得 9434x y ==即F (94,34) ……6分 ∴直线l :y=34……7分 由 23423y y x x ==-++ 得 111234x y =+=221234x y =-= 即P (1+,34)或(134) …………8分(3)设Q(x,0),且-1≤m≤3 作EH⊥x轴于H,QE∥AC∴ΔBEQ∽ΔBCA∴EH BO OC BA=即134mEH m+=,EH=34(m+1)∴S=SΔBQ C-SΔBEQ=12(m+1)×3-12(m+1)×34(m+1)=38(m-1)2+32∵-1≤m≤3∴当m=1时,ΔCAE面积最大,此时Q(1,0)。
