小学数学立体图形表面积、体积公式
小学数学所有图形的周长,面积,体积,表面积公式大全

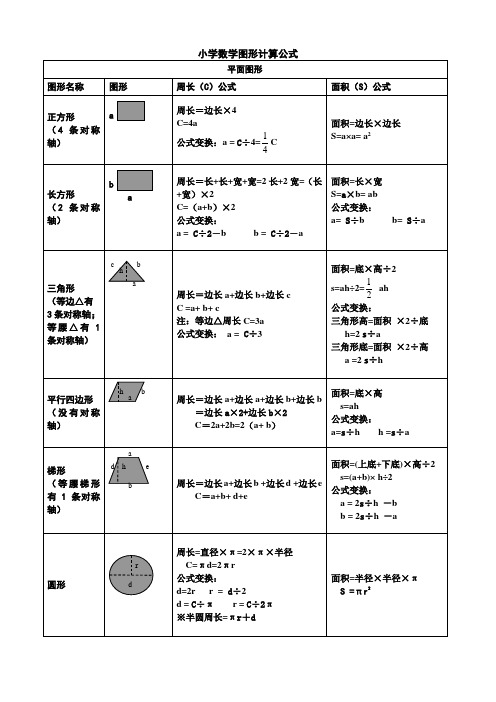
小学数学图形计算公式令狐采学平面图形图形名称图形周长(C)公式面积(S)公式正方形(4条对称轴)a周长=边长×4C=4a公式变换:a = C÷4=C面积=边长×边长S=a×a= a2长方形(2条对称轴)ba周长=长+长+宽+宽=2长+2宽=(长+宽)×2C=(a+b)×2公式变换:a = C÷2-bb = C÷2-a面积=长×宽S=a×b= ab公式变换:a= S÷bb= S÷a三角形(等边△有3条对称轴;等腰△有1条对称轴)周长=边长a+边长b+边长cC =a+ b+ c注:等边△周长C=3a公式变换: a = C÷3面积=底×高÷2s=ah÷2= ah公式变换:三角形高=面积 ×2÷底h=2s÷a三角形底=面积 ×2÷高a =2s÷h平行四边形(没有对称轴)周长=边长a+边长a+边长b+边长b=边长a×2+边长b×2C=2a+2b=2(a+ b)面积=底×高s=ah公式变换:a=s÷hh =s÷a梯形(等腰梯形有1条对称轴)周长=边长a+边长b +边长d +边长eC=a+b+ d+e面积=(上底+下底)×高÷2s=(a+b)× h÷2公式变换:a =2s÷h-bb = 2s÷h-aabhahbcabd eh圆形周长=直径×π=2×π×半径C=πd=2πr公式变换:d=2r r= d÷2d = C÷πr = C÷2π※半圆周长=πr+d面积=半径×半径×πS =πr2圆环周长=C大圆+C小圆=πD+πd=2πR+2πr=2π(R+r)面积= S大圆-S小圆=πR2-πr2=π(R2-r2)立体图形图形名称图形总棱长(L)公式表面积(S)公式体(容)积(V)公式正方体总棱长=棱长×12L=12aS=一个面的面积×6S=a×a×6 =6a2体积=棱长×棱长×棱长V= a×a×a=a3长方体总棱长=长×4+宽×4+高×4=4(长+宽+高)L=4(a+b+h)表面积=(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)体积=长×宽×高V=abh圆柱体侧面积=底面周长×高S侧=ch=dπh=2πrh表面积=底面积×2+侧面积S表= S底×2+ S侧圆柱的表面积公式:(1)有两个底面的圆柱的表面积公式:S表= S底×2+ S侧=πr2×2+πdh=πr2×2+2πrh=2πr(r+h)(2)只有1个底面的圆柱的表面积公式:S表= S底+ S侧=πr2+πdh=πr2+2πrh=πr(r+2h)(3)两个底面都没有的圆柱的表面积公式:S表=S侧=ch =πdh =2πrh体积=底面积×高=侧面积÷2×半径V= S底×h=πr2 h圆筒大圆柱直径为D,半径为R,周长为C;小圆柱直径为d,半径为r,周长为c;高都为hS表= S大圆柱侧+ S小圆柱侧+(S大圆柱底-S小圆柱底)×2= C大圆柱h+c小圆柱h+(πR2-πr2)×2=Dπh+dπh+(πR2-πr2)×2=πh(D+d)+2π(R2-r2)=2πh(R+r)+2π(R2-r2)V= V大圆柱-V小圆柱= S大圆柱底×h-S小圆柱底×h=πR2 h-πr2×h=πh(R2 -r2)圆锥体体积=底面积×高÷3V圆锥=V圆柱= S底×h=πr2 h draa bh。
小学数学苏教版六年级上册《立体图形表面积和体积总复习》课件(公开课)

高是50cm。 3)一个圆柱,底面周长是12.56cm,高是5cm。 4)一个圆锥,底面半径是3cm,高是4.5cm。
练习与实践
变式应用
已知长方体的底面积是3.14cm²,体积是9.42cm³,高是( )cm。
V=S h
已知圆锥的底面直径是 2dm,体积是12.56dm³,高是( )dm。
r=d÷2
S=πr²
h= V÷ ÷S V= S h
2÷2=1(dm)
12.56÷ ÷3.14=12(dm)
3.14×1²=3.14(dm²)
把一个圆柱切成若干等分,拼成一个近似的 长方体。圆柱的侧面积是72平方米,底面半 径是3米。求圆柱的体积是多少?
立体图形的表面积: 是指立体图形表面所有面的面积总和。
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积= 棱长×棱长×6
圆柱表面积= 侧面积+底面积×2 圆柱侧面积= 底面周长×高
体积:物体所占空间的大小。 容积:容器所能容纳的物体的体积。
体积单位: 立方厘米 1000 立方分米 1000 立方米
= =
容积单位: 毫升
1000
升
体积和容积有什么联系和区别?
联系:都是指所占空间的大小,计算方法是相同的,计量单位是有联系的。 区别:计算体积在物体的外面测量数据,计算容积要在容器的里面测量数据。
这几个立体图形的体积公式的推导过程是 怎样的?
知识回顾
h
a
b
长方体的体积 =长x宽 x高=底面积x高
h=V÷S 9.42÷3.14=3(cm)
已知圆柱的高是 2m,体积是10m³ቤተ መጻሕፍቲ ባይዱ底面积是( )m²。
几何体的表面积和体积

几何体的表面积和体积一、几何体的定义和分类几何体是指由平面图形绕某一轴线旋转或拉伸而成的立体图形。
常见的几何体包括圆柱体、圆锥体、球体、长方体等。
二、几何体的表面积1. 圆柱体表面积圆柱体表面积等于上下底面积之和加上侧面积。
公式为:S=2πr²+2πrh。
其中,r为底面半径,h为高。
2. 圆锥体表面积圆锥体表面积等于底面积加上侧面积。
公式为:S=πr²+πrl。
其中,r为底面半径,l为斜高线长。
3. 球体表面积球体表面积等于4倍的球半径平方乘以π。
公式为:S=4πr²。
其中,r为球半径。
4. 长方体表面积长方体表面积等于所有侧面积之和。
公式为:S=2(lw+lh+wh)。
其中,l、w、h分别代表长方体的长度、宽度和高度。
三、几何体的体积1. 圆柱体的容积圆柱的容积等于其底部面积与高度的乘积。
公式为:V=πr²h。
其中,r为底面半径,h为高。
2. 圆锥体的容积圆锥体的容积等于其底部面积乘以高度再除以3。
公式为:V=1/3πr²h。
其中,r为底面半径,h为高。
3. 球体的容积球体的容积等于4/3倍的球半径立方乘以π。
公式为:V=4/3πr³。
其中,r为球半径。
4. 长方体的容积长方体的容积等于其长度、宽度和高度之间的乘积。
公式为:V=lwh。
其中,l、w、h分别代表长方体的长度、宽度和高度。
四、几何体表面积和体积计算实例1. 计算一个底面直径为10cm、高20cm的圆柱体表面积和容积。
解:圆柱体表面积S=2πr²+2πrh=2×π×5²+2×π×5×20≈628.32cm²;圆柱体容积V=πr²h=π×5²×20≈1570.8cm³。
2. 计算一个半径为6cm、斜高线长10cm的圆锥体表面积和容积。
解:圆锥体表面积S=πr²+πrl=π×6²+π×6×10≈282.74cm²;圆锥体容积V=1/3πr²h=1/3×π×6²×10≈376.99cm³。
立体图形表面积体积

教育学科教师辅导讲义学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师: 授课 类型T (立体图形相关知识点) C (典型例题试题讲解) T (拓展提高)授课日期时段教学内容知识点一:表面积1、长方体表面积=长x 宽× 2+ 宽× 高× 2+ 长×高× 2 字母公式:S=ax b× 2+ a× c× 2+ b×c× 2 或者:长方体的表面积 =( 长×宽 + 长×高 + 宽×高 ) × 2 。
字母公式:S=(ax b+ a× c+ b×c)× 22、正方体的表面积 =棱长×棱长×6。
字母公式:S=a ×a× 63、圆柱体的表面积:圆柱表面积=上底+下底+侧面(侧面面积=底面圆的周长×圆柱的高) 用字母表示:22s r ch π=+注:侧面积的求法:已知底面半径和高,rh π侧2s = 已知底面直径和高,dh π侧=s知识点二:体积1、长方体体积:长方体体积= ① 长×宽×高 (V=abh)② 底面积×高=横截面积×长 (V =sh ) 2、正方体的体积:正方体体积=棱长×棱长×棱长检测题1:把一个圆柱的侧面展开,得到一个正方形.已知这个圆柱的高是10厘米,它的侧面积是( )平方厘米.A .50B .100C .50πD .100π答案:B检测题2.把一个棱长4厘米的正方体分割成两个长方体,表面积增加了______平方厘米.答案:64检测题3 一个正方体的棱长之和是48厘米,它的棱长是______厘米,表面积是______平方厘米,体积是______立方厘米. 答案:2 24 8检测题4 把两个棱长5厘米的正方体拼成一个长方体,这个长方体的表面积是______平方厘米.答案:250检测题5.一个练功房铺设了1600块长50厘米,宽10厘米,厚3厘米的木地板,这个练功房的面积有______平方米.答案:这个练功房的面积有80平方米.检测题6.圆柱的底面半径扩大2倍,高缩小到原来的21,它的体积就( )答案:扩大2倍检测题7.做一个圆柱体,侧面积是9.42平方厘米,高是3厘米,它的底面半径是______.答案:1.57cm一、专题精讲例1.如图是高为10厘米的圆柱,如果它的高增加4 厘米,那么它表面积就增加125.6平方厘米。
立体图形的表面积和体积

体图形的表面积和体积。 2、熟练掌握几种立体图形的表面积和体 积的计算公式。 3、形成初步的空间观念,运用所学知识 灵活解决生活中的实际问题。
学习提示 1、各种立体图形的表面积和体积 公式是什么?用字母怎样表示? 2、可以用文字、图表、图形、框 架图等自己喜欢的方式进行整理。
二、看图列式不计算求体积
12平方分米 24 32平方米 平 方 米
6 分 米
8米
24×8
1 12×6× 3
2 2
7分米
3 分 米
8 分 米
.
3.14 × 32 ×7
3.14 ×(6÷2)2 ×8
二、生活中的数学问题
1、 一个长方体的鱼池,长10米,宽6米, 深是2米。 ①这个这个鱼池的占地面积是多少平方米? 求底面面积 ②在池内的侧面和池底铺上瓷砖,瓷砖的面 积是多少平方米? 侧面(4个)+底面 ③鱼池内放满水后能盛放多少立方米的水? 求容积
算法(公式) 图形
项目
表面积
体积
一个立体图形所有面的面积总和叫做它的表面积。
一个立体图形所占空间的大小叫做它的体积。
a
h b
V= abh V=
a
3
a
a a
h
s
s
1
h
V= sh V=
3
sh
V = sh
正方体、长方体和圆柱有什 么相似的地方呢?
动画
va
V=abh
3
1 V= sh 3
下面的几种情况,你来判断一下分别求 得是什么?
1、油漆柱子的面积(圆柱的侧面积) 2、给教室粉刷白灰
(长方体6个面去掉上面,去掉门窗面积)
小学数学所有图形的周长-面积-体积-表面积公式大全

周长=边长 a+边长 b +边长 d +边长 e C=a+b+ d+e
面积=(上底+下底)×高÷2
s=(a+b)× h÷2 公式变换:
a = 2s÷h -b b = 2s÷h -a
圆形
周长=直径×π =2×π ×半径
r
C=π d=2π r
公式变换:
d
d=2r r = d÷2
面积=半径×半径×π S =πr2
面积=底×高÷2
1 s=ah÷2= ah
2 公式变换: 三角形高=面积 ×2÷底
h=2 s÷a 三角形底=面积 ×2÷高
a =2 s÷h
周长=边长 a+边长 a+边长 b+边长 b =边长 a×2+边长 b×2 C=2a+2b=2(a+ b)
面积=底×高 s=ah
公式变换: a=s÷h h =s÷a
体积=长×宽× 高
V=abh
侧面积=底面周长×高 S 侧=ch=dπh=2πrh
表面积=底面积×2+侧面积 S 表= S 底×2+ S 侧
圆柱的表面积公式: (1)有两个底面的圆柱的表面积公式: S 表= S 底×2+ S 侧=πr2×2+πdh
=πr2×2+2πrh =2πr(r+h) (2)只有 1 个底面的圆柱的表面积公式: S 表= S 底+ S 侧=πr2+πdh
=πr2+2πrh=πr(r+2h) (3)两个底面都没有的圆柱的表面积公 式: S 表=S 侧 =ch =πdh =2πrh
体积=底面积× 高=侧面积÷2 ×半径 V= S 底×h
小学六年级数学小升初珍藏版复习资料第19讲 组合图形的认识、表面积与体积(解析)

2022-2023学年小升初数学精讲精练专题汇编讲义第19讲 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体,这四种立体图形的表面积和体积的计算是小升初数学的热点内容,特别是涉及到立体图形的切拼时,立体图形的表面积和体积发生了变化,牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键,本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。
知识点一:立体图形的表面积和体积计算常用公式: 立体图形 表面积体积 长方体S=2)(bh ah ab ++a :长 b:宽 h :高 S :表面积 V abh = V Sh = 正方体S=26a a :棱长 S :表面积 3V a = V Sh = 圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱圆锥 22ππ360n S l r =+=+圆锥侧面积底面积 注:l 是母线,即从顶点到底面圆上的线段长 21π3V r h =圆锥体 知识点二:解决立体图形的表面积和体积问题时的注意事项(1)要充分利用正方体六个面的面积都相等,每个面都是正方形的特点.(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍;反之,把两个立体图形拼合到一起,减少的表面积等于重合部分面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来;若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
2.解答立体图形的体积问题时,要注意以下几点:(1)物体沉入水中,水面上升部分的体积等于物体的体积;把物体从水中取出,水面下降部分的体积等干物体的体积,这是物体全部浸没在水中的情况。
如果物h r hr 知识精讲体不全部浸在水中,那么排开水的体积就等于浸在水中的那部分物体的体积. (2)把一种形状的物体变为另一种形状的物体后,形状变了,但它的体积保持不变.(3)求一些不规则物体体积时,可以通过变形的方法求体积。
常用图形周长面积体积计算公式

常用图形周长面积体积计算公式:1、正方形C周长 S面积 a边长周长=边长×4面积=边长×边长C=4aS=a×a S=a22、正方体V体积 a棱长(1)表面积=棱长×棱长×6 (2)体积=棱长×棱长×棱长S表=a×a×6 表=6a2V=a×a×a V= a33、长方形C周长 S面积 a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4、长方体V体积 S面积 a长 b宽 h高(1)表面积=(长×宽+长×高+宽×高)×2(2)体积=长×宽×高S=2(ab+ah+bh)V=abh5、三角形S面积 a底 h高面积=底×高÷2S=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形S面积 a底 h高面积=底×高 S=ah7、梯形S面积 a上底 b下底 h高面积=(上底+下底)×高÷2S=(a+b)× h÷28、圆形S面积 C周长π圆周率d直径 r半径周长=直径×π周长=2×π×半径面积=半径×半径×πC=πd C=2πrS=πr2 d=C÷πd=2r r=d÷2r=C÷2÷π S环=π(R2-r2)9、圆柱体V体积 h高 S底面积 r底面半径 C底面周长侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高S侧=ChS侧=πdhV=Sh V=πr2h圆柱体积=侧面积÷2×半径10、圆锥体V体积 h高S底面积 r底面半径体积=底面积×高÷3V=Sh÷3长度单位换算1千米=1000米;1米=10分米;1分米=10厘米;1米=100厘米;1厘米=10毫米面积单位换算1平方千米=100公顷;1公顷=10000平方米;1平方米=100平方分米;1平方分米=100平方厘米;1平方厘米=100平方毫米;1平方米=0.0015亩;1万平方米=15亩;1公顷=15亩=100公亩=10000平方米;1公亩等于100平方米;1(市)亩等于666.66平方米体(容)积单位换算1立方米=1000立方分米;1立方分米=1000立方厘米;1立方分米=1升;1立方厘米=1毫升;1立方米=1000升重量单位换算1吨=1000千克;1千克=1000克;1千克=1公斤人民币单位换算1元=10角;1角=10分;1元=100分时间单位换算1世纪=100年;1年=12月;大月(31天)有:1\3\5\7\8\10\12月;小月(30天)的有:4\6\9\11月平年2月28天,闰年2月29天;平年全年365天,闰年全年366天1日=24小时1时=60分;1分=60秒1时=3600秒总数÷总份数=平均数和差问题的公式:(和+差)÷2=大数;(和-差)÷2=小数和倍问题:和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题:差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1、非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2、封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数 (大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)定义定理公式(一)三角形的面积=底×高÷2。
平面图形和立体图形公式汇总

文档. 平面图形和立体图形公式汇总1长方体的体积=长×宽×高2正方体的体积=棱长×棱长×棱长公式的逆用:v=sh h=v ÷s s=v ÷h3.长方体的表面积公式=(长×宽+长×高+宽×高)×24.正方体表面积公式=棱长×棱长×65.长方体的棱长之和=(长+宽+高)×46.正方体的棱长之和=棱长×127.圆柱侧面积=底面周长×高8.圆柱表面积=侧面积+底面积×29.圆柱的体积=底面积×高公式的逆用:s= h v h=s v10.半圆柱形表面积=整个圆柱的表面积÷2+高×直径11.半圆柱形体积=整个圆柱的体积÷212.圆锥的体积=31×底面积×高公式的逆用:s= h v 3 h=s v313.长方形的周长=(长+宽)×2 面积=长×宽14.正方形的周长=边长×4 面积=边长×边长15.三角形面积=底×高×2116.平行四边形面积=底×高17.梯形面积=(上底+下底)×高×2118.圆的周长=πd=2πr 面积=πr 219.半圆的周长=πr+2r 面积=πr 2÷220.圆周长的一半是πr21.圆的面积推导公式,变成近似的长方形,长方形的长是πr ,宽是r22.圆柱侧面展开图的长方形的长是底面周长,宽是圆柱的高23.圆柱体积推导公式,变成近似的长方体,长方体的长是πr ,宽是r ,高和圆柱的高相等。
小学数学常用图形周长面积体积计算公式

小学数学常用图形周长面积体积计算公式:1,正方形C周长S面积a边长周长=边长×4面积=边长×边长C=4aS=a×a S=a22,正方体V体积a棱长表面积=棱长×棱长×6体积=棱长×棱长×棱长S表=a×a×6 表=6a2V=a×a×a V= a33,长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4,长方体V体积S面积a长b宽h高(1)表面积=(长×宽+长×高+宽×高)×2(2)体积=长×宽×高S=2(ab+ah+bh)V=abh5,三角形S面积a底h高面积=底×高÷2S=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6,平行四边形S面积a底h高面积=底×高S=ah7,梯形S面积a上底b下底h高面积=(上底+下底)×高÷2S=(a+b)× h÷28,圆形S面积C周长π圆周率d直径r半径周长=直径×π周长=2×π×半径面积=半径×半径×πC=πd C=2πrS=πr2 d=C÷πd=2r r=d÷2r=C÷2÷πS环=π(R2-r2)9,圆柱体V体积h高S底面积r底面半径C底面周长侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高S侧=ChS侧=πdhV=Sh V=πr2h圆柱体积=侧面积÷2×半径10,圆锥体V体积h高S底面积r底面半径体积=底面积×高÷3V=Sh÷3长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米1平方米=0.0015亩,1万平方米=15亩1公顷=15亩=100公亩=10000平方米1公亩等于100平方米1(市)亩等于666.66平方米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒总数÷总份数=平均数和差问题的公式(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)小学定义定理公式(一)三角形的面积=底×高÷2。
面积体积公式大全

面积体积公式大全
面积和体积是几何学中重要的概念,用于描述平面图形和立体图形的大小。
在学习和应用数学时,了解面积和体积的计算公式是很必要的。
下面列出了一些常见图形的面积和体积公式。
1.平面图形的面积公式:
-正方形面积公式:$A=s^2$,其中$A$为面积,$s$为正方形的边长。
2.立体图形的体积公式:
-立方体体积公式:$V=s^3$,其中$V$为体积,$s$为立方体的边长。
3.其他图形和多边形的面积和体积公式:
这些是一些常见图形的面积和体积计算公式,掌握和理解这些公式可以帮助我们计算和解决与面积和体积相关的问题。
同时,在实际应用中,也会遇到更复杂的图形和立体体积的计算,此时可通过将复杂形状分解为简单形状来计算其面积和体积。
六年级数学下册课件立体图形的表面积和体积苏教版32

一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加多少平方厘米? 做一个长4米、宽3米、高2米的长方体的木箱,需要木板多少平方米?这个木箱的体积是多少?
做一个长4米、宽3米、高2米的长方体的木箱,需要木板多少平方米?这个木箱的体积是多少? A不变 B减少 C增加
常用的体积单位是立方米、立方分米、立方厘米
( B )。 常用的体积单位是立方米、立方分米、立方厘米
一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加多少平方厘米? ⑥至少用4块同样的小正方体就可以拼成一个较大的正方体 。
③长方体说:“把我熔铸成一个圆锥体,我的体 积不变。” ( )
④油桶说:“我最多能盛多少水,我的体积就是 多少。” ( ) ⑤正方体说:“我的棱长是6分米,我的表面积 和体积相等。” ( )
只列式不计算
①一个正方体棱长和是60厘米,这个正 方体的体积是多少? ②一个圆柱体的容积是42.39立方米,底 面积是7.065平方米,求这个圆柱的高。
的卡车几辆才能运完? A 2倍 B 2/3 C 3倍 D 1/3
常用的体积单位是立方米、立方分米、立方厘米 2、把一块圆柱形的木料平均截成两段表面积 ( ),体积( )。 ①圆柱说:“我的体积是圆锥的3倍。
④若在四周和底面贴上瓷砖,要贴多少面积? ②长方体说:“我和一个圆柱等底面积、等高,我俩的体积相等。
③若每立方米土重1400千克,需要载重1. 一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加多少平方厘米?
小升初专题复习-立体图形的表面积和体积(课件)人教版六年级下册数学

六、(江苏·盐城)如下图,用涂色部分做一个圆柱体(接头处不计),这 个圆柱体的体积是多少立方厘米?(9 分)
解:设圆柱的底面直径为 d 厘米。 3.14d+d=41.4 d=10
3.14×(10÷2)2×(10×2)=1570(cm3)
答:这个圆柱体的体积是 1570 立方厘米。
第18课时 立体图形的表面积和体 积
名称 长方体 正方体
圆柱
圆锥
图形
字母意义
表面积公
体积公式
a——长 b——宽
h——高 S 表——表面积 S 表=22((aabb++aahh++bbhh))V=aabbhh =S 底 h
S 底——底面积 V——体积
a——棱长 S 表——表面积 V——体积 S 底——底面积
6.小明新买了一管容积约为 45 cm3 的牙膏,牙膏圆形出口的直径为 6 mm。 他早晚各刷一次牙,每次挤出的牙膏长约 20 mm。这管牙膏估计能用
( 42 )天。(π 取 3) 7.一个长方体木料,横截面是边长 10 厘米的正方形,从这根木料上截 下 6 厘米长的一段,切削成一个最大的圆锥,圆锥的体积是( 157 )立 方厘米,削去部分的体积是( 443 )立方厘米。 8.(江苏·南京)一个圆锥和一个圆柱的底面积相等,体积的比是 1∶12。
4.(浙江·绍兴)学校体育馆底层用 10 根圆柱形柱子支撑着,每根柱子
高 3 m,底面直径为 5 dm,油漆这些柱子的面积是( 47.1 )m2。 5.如右图,如果这两个图形分别绕各自 3 cm 的边旋转一周,可以形成 一个圆锥和一个圆柱。圆柱的体积为( 150.72 )cm3,圆锥的体积为 ( 50.24 )cm3。
【答案】(1)60÷1.5=40(m) 60×40×2=4800(m3) 答:这个游泳池最多能蓄水 4800 立方米。 (2)60×40+(60×2+40×2)×2=2800(m2) 答:抹水泥的面积是 2800 平方米。
小学数学所有图形的周长-面积-体积-表面积公式大全
a
梯形 (等腰梯形 有 1 条对称 轴)
d
h
e b
a
r
圆形
d
周长=直径×π =2×π ×半径 C=π d=2π r 公式变换: d=2r r = d÷2 d = C÷π r = C÷2π ※半圆周长=π r+d
面积=半径×半径×π S =πr2
圆环
周长=C 大圆+C 小圆 =πD+πd =2πR+2πr =2π(R+r) 立体图形
d2r半圆周长rd面积半径半径圆环周长c大圆c小圆大圆s小圆v公式正方体12l12as一个面的面积6s2abahbh体积长宽vabh圆柱体侧面积底面周长高侧chdh2rh表面积底面积2侧面积圆柱的表面积公式
小学数学图形计算公式
平面图形
图形名称
图形
周长(C)公式 周长=边长×4 C=4a
面积(S)公式
圆锥体
1 3
1 1 S 底×h= πr2 h 3 3
V 圆柱=3 V 圆锥 等底等体积的圆柱与圆锥,圆锥的高=圆柱高的 3 倍
圆柱体
体积=底面积× 高=侧面积÷2 ×半径 V= S 底×h =πr2 h
圆筒
大圆柱直径为 D,半径为 R,周长为 C; V= V 大圆柱-V 小圆柱 小圆柱直径为 d,半径为 r,周长为 c;高都 = S 大圆柱底×h-S 为h 小圆柱底×h S 表= S 大圆柱侧+ S 小圆柱侧+(S 大圆柱底-S 小圆柱底)×2 2 2 =πR h-πr 2 2 = C 大圆柱 h+c 小圆柱 h+(πR -πr )×2 ×h =Dπh+dπh+(πR2-πr2)×2 2 2 =πh(R -r ) =πh(D+d)+2π(R2-r2) 2 2 =2πh(R+r)+2π(R -r ) 体积=底面积×高÷3 V 圆锥= V 圆柱=
4. 立体图形的体积、表面积、侧面积 几何重心与转动惯量计算公式

r,R分别为上,下底圆半径,h为高,l为母线
上下底平行, , 分别为上,下底面积, 为中截面面积,h为高
体积
表面积
侧面积
母线
重心
(Q为底圆中心,O为圆锥顶点)
转动惯量
取圆锥顶点为坐标原点,z轴与GQ重合
体积距离)
重心
(P,Q分别为上下底圆心)
两底为矩形,a’,b’,a,b分别为上下底边长,h为高, 为截头棱长
底为矩形,a,b为其边长,h为高,a’为上棱长
r为半径
体积
重心
(P,Q分别为上下底重心)
体积
重心
(P为上棱中点,Q为下底面重心)
体积
表面积
重心G与球心O重合
转动惯量
取球心O为坐标原点
图形
体积V、表面积S、侧面积M、几何重心G与转动惯量J
R为外半径,r为内半径,h为高
r为底圆半径,h,H分别为最小,最大高度, 为截角,D为截头椭圆轴
体积
表面积
侧面积
重心
(P,Q分别为上下底圆心)
转动惯量
取重心G为坐标原点,z轴垂直底面
体积
表面积
侧面积
式中t为管壁厚, 为平均半径
重心
转动惯量
取z轴与GQ重合
体积
表面积
侧面积
截头椭圆轴
重心
(GQ为重心到底面距离,GK
8
12
20
棱数k
6
12
30
30
顶点数e
4
6
20
12
体积V
表面积S
表中a为棱长.
[欧拉公式]一个多面体的面数为f,棱数为k,顶点数为e,它们之间满足
立体图形的知识点

立体图形的知识点在日常生活中,我们经常会接触到各种立体图形,比如球体、立方体、圆柱体等等。
这些立体图形在建筑、工程、艺术等领域有着广泛的应用。
为了更好地理解和应用这些图形,我们需要了解立体图形的基本概念、性质和公式。
一、基本概念1.立体图形立体图形是具有一定体积的图形,包括球体、立方体、圆柱体、圆锥体、棱锥体、棱柱体等。
2. 体积体积是立体图形所占的空间大小,用“立方米”等单位来表示。
立体图形的体积公式有很多,下面将分别介绍不同立体图形的体积公式。
3. 表面积表面积是立体图形外部的总面积,用“平方米”等单位表示。
同样,在下面将分别介绍不同立体图形的表面积公式。
二、性质和公式1. 球体球体的体积公式为V=4/3πr³,其表面积公式为S=4πr²。
这里,V表示体积,S表示表面积,r表示球的半径,π表示圆周率,约为3.1415。
2. 立方体立方体的体积公式为V=a³,其表面积公式为S=6a²。
这里,a 表示立方体的边长。
3. 圆柱体圆柱体的体积公式为V=πr²h,其表面积公式为S=2πrh+2πr²。
这里,r表示底面圆的半径,h表示圆柱的高。
4. 圆锥体圆锥体的体积公式为V=1/3πr²h,其表面积公式为S=πr(r+√(r²+h²))。
这里,r表示底面圆的半径,h表示圆锥的高。
5. 棱锥体棱锥体的体积公式为V=1/3Sh,其中S表示底面的面积,h表示棱锥的高。
其表面积公式为S=B+L,其中B表示底面的面积,L表示侧面的面积。
6. 棱柱体棱柱体的体积公式为V=Bh,其中B表示底面的面积,h表示棱柱的高。
其表面积公式为S=2B+Ph,其中P表示侧面的周长。
总结通过了解不同立体图形的基本概念、性质和公式,我们可以更好地理解和应用在不同领域中。
在实际应用过程中,应根据具体情况选择合适的公式,进行计算和应用。
因此,了解这部分知识点对我们的学习和工作都有一定的帮助。
所有面积体积公式

所有面积体积公式面积和体积是数学中常见的概念,用于描述物体的大小和形状。
面积表示平面上一个区域所覆盖的大小,而体积则表示一个立体物体所占据的空间大小。
在不同情况下,面积和体积的计算公式也会不同。
以下是常见的面积和体积的计算公式:一、平面图形的面积公式:1.矩形的面积公式:矩形的面积公式为:面积=长×宽,其中长和宽分别表示矩形的边长。
2.正方形的面积公式:正方形的面积公式与矩形相同,也是:面积=边长×边长。
3.三角形的面积公式:三角形的面积公式为:面积=底边长×高÷2,其中底边长表示三角形的底边长度,高表示从底边到顶点的垂直距离。
4.圆的面积公式:5.椭圆的面积公式:椭圆的面积公式为:面积=π×长半径×短半径,其中长半径和短半径分别表示椭圆的两个半径长度。
6.正多边形的面积公式:正多边形的面积公式为:面积= 1/4 × n × 边长的平方×cot(π/n),其中n表示正多边形的边数,边长表示正多边形的边长。
二、立体图形的体积公式:1.长方体的体积公式:长方体的体积公式为:体积=长×宽×高,其中长、宽和高分别表示长方体的三个边长。
2.立方体的体积公式:立方体的体积公式与长方体相同,也是:体积=边长×边长×边长。
3.圆柱体的体积公式:圆柱体的体积公式为:体积=圆的面积×高,其中圆的面积可使用上述的圆的面积公式计算。
4.圆锥体的体积公式:圆锥体的体积公式为:体积=1/3×圆的面积×高,其中圆的面积可使用上述的圆的面积公式计算。
5.球体的体积公式:6.椭球体的体积公式:椭球体的体积公式为:体积=4/3×π×长半径×短半径的平方,其中长半径和短半径分别表示椭球体的两个半径长度。
以上是一些常见的平面图形和立体图形的面积和体积公式,可以帮助我们计算不同形状的物体的大小。
小学数学平面图形、立体图形公式大全(三角形、梯形和长方体、正方体、圆柱)2

S表长=2 (ab+ah+bh)
体积单位进率: ×1000 1m³=1000dm³ 1dm³=1000cm³ 1m³=1000000cm³
【正方体 的表面积 】6个面 都相等;
S表正=棱长×棱长×6
S表正=6a²
【正方体 的体积】
正方体体积=棱长×棱长×棱长
V正=a³
4.圆锥:
实验证明,等底等高的圆锥容器倒水三次,正 好将倒满圆柱容器,这样的圆锥是圆柱体积的 三分之一。
小学平面、立体图形数学公式大全
(一)平面图形 1.长方形:
长度:指长短,是一 条线,即1维空间。
1cm 1cm
宽 b
1×1
长方形 周长= (长+ 宽)×2 C长 =(a+b)× 2
长方形 面积= 长 ×宽 S长=a×b
2.正方形:
边 长
1×1
边长 a
长a
1cm 边长为1cm 的小方片;
面积是两个长度单位 相乘,即2维空间。
面积:物体表面的大小,或
占地范围的大小。图形内
能摆多少个小方片,面积
1cm
是多少。
正方形周长=边长×4 C正=4a 正方形面积=边长×边长 S正=a²
3.平行四边形:
Author:laurence223
长度单位进率: ×10 1m=10dm 1dm=10cm
高 底
平行四边形面积=底×高
h a S平行四边形=ah
长方体棱长之和=(长+宽+高)×4
【正方体 棱长之和 】正方体 12条棱长 都相等;
4(a+b+h)
正方体棱长之和=棱长×12
12a
容积单位:
【长方体 的表面积 】3个对 面相等, 上下、前 后、左 右;
