基本图形在相似三角形中
相似三角形几种基本模型
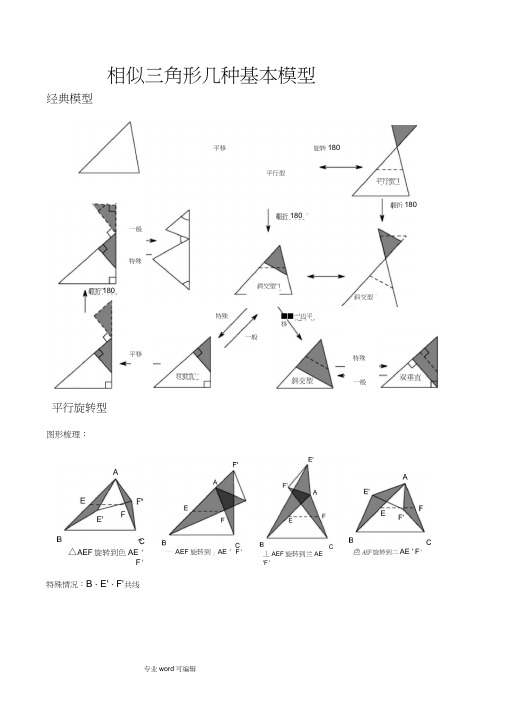
相似三角形几种基本模型经典模型平行旋转型图形梳理:特殊情况:B 、E'、F'共线平移一般平移特殊翻折180°旋转180°平行型平行型翻折180°翻折180°斜交型斜交型■■一边平移双垂直特殊一般特殊一般C△AEF 旋转到色AE 'F 'F'一 AEF 旋转到」AE ' F '丄AEF 旋转到兰AE 'F '色AEF 旋转到二AE ' F 'C , E', F'共线相似三角形有以下几种基本类型 :①平行线型常见的有如下两种 ,DE//BC ,则厶ADE S MBC②相交线型常见的有如下四种情形 ,如图,已知/仁/B ,则由公共角ZA 得,△ ADE s^ABCA B C△ AEF 旋转到厶AE‘ F 'A△ AEF 旋转至U 厶AE‘ F '八BC 一AEF 旋转至U 仝AE ‘ F 'AAEF 旋转到 A AE ‘ F 'E'A如下左图,已知Z1= ZB,则由公共角Z A 得,△ADC s^ACBZ1= Z得,△ ADE s^ABC 已知ZBAD= /CAE,Z B= ZD ,则厶ADE^A ABC,下图为常见的基本图形④母子型已知Z ACB=90 ° ,AB 丄CD ,则厶CBD ^A ABC^A ACD .如下右图,已知ZB= ZD,则由对顶角③旋转型相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形(1)如图:称为平行线型”的相似三角形(有A 型”与X 型”图)反A 共角共边型”、蝶型”)⑷如图:/仁Z2,/B= ZD ,则厶ADE ^A ABC ,称为 旋转型”的相似三角形2、几种基本图形的具体应用(1)若 DE//BC (A 型和 X 型)则厶 ADE S ^ABC(2)射影定理 若CD 为Rt △ ABC 斜边上的高(双直角图形)(3) 如图:称为 垂直型”有 双垂直共角型 型”)EC双垂直共角共边型 (也称 射影定理型 ”)”三垂直如图:其中/仁Z2 ,则厶ADE S ^ABC 称为 斜交型”的相似三角形(有反A 共角型ED则Rt△ ABC^Rt△ ACD^Rt △ CBD 且AC2=AD AB , CD2=AD BD , BC2=BD AB ;(3) 满足1、AC2=AD AB, 2、/ACD= ZB, 3、/ACB= Z ADC ,都可判定△ ADC ^A ACB ./ ⑴AD AE亠亠(4) 当或AD AB=AC AE 时,△ ADE ^△ACB .AC AB。
浅谈相似三角形中的基本图形

浅谈相似三角形中的基本图形浙江省苍南县钱库一中王昌汤一道几何问题,都会以一个图形以及这个图形所具有的各种性质为研究对象。
而出现在几何问题中的每一个几何图形,无论是怎样的简单还是怎样的复杂,经过观察和分析,都一定可以发现它是由一个或者若干个最简单、最基本也是最重要的图形组合而成的。
在对数以万计的几何问题进行图形剖析后,就会发现几何中的基本图形的数量并不很多,但就是这些数量不多的基本图形却演绎出一部能显现无穷变化的平面几何学。
对这数量不多的基本图形再进行分类,就可以分成:平行线、等腰三角形、与圆有关的角、全等三角形、相似三角形、特殊角三角形、与面积方法有关的三角形等七个部分。
现本人以相似三角形为例来说明如何将复杂图形转化为简单图形,培养学生分析问题和解决问题的能力。
通过寻找(或构造)相似三角形,用以计算或论证问题的方法,我称之为相似三角形法,在计算线段的长度,证明角相等,证明线段成比例等方面都有广泛的应用。
常见的基本图形有:例如:(2012•嘉兴)如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB 的直线相交于点G,连接DF.给出以下四个结论:①FBFGABAG;②点F是GE的中点;③AF= AB32④S△ABC=5S△BDF,其中正确的结论序号是.本题中的基本图形就有X字型和K字型等,只有从这个复杂图形中分离出基本图形,才能利用相似三角形的判定与性质和面积变换解答此类问题。
A字型反A型母子型双垂图X字型K字型风筝型又如上图:这样复杂的图形其实就包含四个基本图形,只要掌握这些基本图形的性质和应用,解决此类就不难了。
当若干个基本图形组合而成为一个几何问题的时候,许多图形的性质就难以发现了,变为隐蔽了,所以几何问题的分析和思考过程实质上就是要将这一综合过程逆过来进行,也就是要剖析并找到这些基本图形,并应用这些基本图形的性质,使问题得到解决。
三角形相似的判定方法

三角形相似的判定方法一1、定义法:三个对应角相等,三条对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似. 特殊、判定直角三角形相似的方法:(1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 注:射影定理:在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高, 则AD 2=BD ·DC ,AB 2=BD ·BC ,AC 2=CD ·BC 。
二 相似三角形常见的图形三、1,下面我们来看一看相似三角形的几种基本图形:(1) 如图:称为“平行线型”的相似三角形(有“A 型”与“X 型”图)(2) 如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜交型”的相似三角形。
(有“反A 共角型”、“反A 共角共边型”、 “蝶型”)ACD E 12AADDEE12412DBCEAD(3)BCAE (2)CB(3) 如图:称为“垂直型”(有“双垂直共角型”、“双垂直共角共边型(也称“射影定理型”)”“三垂直型”)(4)如图:∠1=∠2,∠B=∠D ,则△ADE ∽△ABC ,称为“旋转型”的相似三角形。
(完整版)相似三角形中的辅助线专题训练【2024版】

可编辑修改精选全文完整版相似三角形中的辅助线专题训练一、基本图形:二、基本方法:证相似,实不难,A字字仔细看;如没有,辅助线,各种情况常相见。
三、实例演习:(一)遇燕尾,作平行,构造字一般行。
1、BE=AD,求证:EF·BC=AC·DF(二)遇梯形,延长腰,构成A字瞧一瞧。
2、梯形ABCD中,AD∥BC,CH平分∠BCD,BH=3AH,四边形AHCD的面积为21,求△HBC的面积。
(三)遇平分,作等腰,三线合一要记牢。
3、AC⊥BC,AE⊥DE,2∠ADE=∠B,AC:BC=3:1,求AE:DG(四)直角多,垂线作,再难题目你能做。
4、平行四边形ABCD中,CE⊥AE,CF⊥AF,求证:AB·AE+AD·AF=AC2HDCBAEDCBAGEDCBAA BCDEF四、巩固练习:(做题目,看情况,灵活运用最恰当。
) 1、BD :DC =2:1,E 为AD 中点,求①BE :EF ②AF :FC2、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC3、D 为BC 中点,求证:AF :BF =AE :EC4、AC ⊥BC ,CD ⊥AB ,FG ⊥AB ,E 为CD 中点,求证:FG 2=CF ·BF 5、AB =AC ,AD 为中线,CF ∥AB ,求证:BP 2=PE ·PF6、AD 平分∠BAC ,EF 垂直平分AD ,求证:ED 2=EB ·EC7、矩形ABCD 中,E 为AD 中点,EF ⊥EC ,求证:△AEF ∽△ECF8、AB =AC ,AB ⊥BC ,AD 为中线,BE ⊥AD ,求证:①AE =2EC ②∠AEB =∠CED 9、∠BAC =90°,AE ⊥BC ,BD =DC =EC =1,求AC 的长10、AB =AC ,BD 为高,求证:BC 2=2AC ·CDFE DC BA G F E DC B A A BC DE FA B C D E F G PA BC D E F AB CD EF AB CD E F P AB C D E PAB CDEA BCDPA B CD E。
相似三角形M基本图形中点

如图,已知∠A=∠BCD=∠E=60°, 图中有没有相似三角形?并说明理由。
如图,已知∠A=∠BCD=∠E=120°, 图中有没有相似三角形?并说明理由。
如图,已知∠A=∠BCD=∠E=α, 图中有没有相似三角形,并写出证明过程
(2)设P为抛物线的对称轴上的一动点, 求当∠APC=900时的点P坐标。
P
(2)设P为抛物线的对称轴上的一动点, 求当∠APC=900时的点P坐标。
A
B
PCMP相似?如存在,求出点P坐标, 如不存在,请说明理由。
y
A
B P
C
M
x
若点N是第一象限内抛物线上的一动点, 当 ∠NAA’=900时,求N点坐标。
B α
D
α
α
A
C
E
A
△ABE∽ △ECF
F
B
E
C
A
A
A
60 ° α 60 ° α
F
F
F
BB
α 60 ° α 60 ° E EE
α 60 ° 60 ° α CC C
顺口溜:“一线三等角,相似容易找”
【学习目标】
1、会用“一线三等角”的基本图形(M型图)解决相似中 的相关问题 2、通过抽象模型,图形变换,方程思想,变式类比等方 法提高综合解题能力
要善于挖掘题 目中的隐含条 件
3,如图,三角形ABC中AB=AC=5,
BC=8,P为BC上一点(不与点B、C重合), ∠APE=∠B,点E在AC上.
求证:(1)△ABP∽△PCE; (2)设BP=x,CE=y,求y与x的解析式;
A E
三角形相似的基本类型

PA2 PB2
=x y
。
分析 ⑴如图 3-4 是图 3-3 的一部分,在△ACP 和△APB 中,∠A
是公共角,∠ACP=∠APB=120°,则△ACP∽△APB,其中 PA 为两个三
角形的公共边,即两三角形属于“共边型”相似。 同理,如图 3-5 也是图
3-3 的一部分,△PDB∽△APB 且同样属于“共边型”相似。 由于△ACP
3,点 F 在 AC 上,连接 EF,若△AEF 与△ABC 相似,则 AF=_________。
分析 △AEF 与△ABC 相似应分两种情况进行讨论。
⑴当 EF∥BC 时,△AEF 与△ABC 属于“正 A”型相似,即△AEF∽
△ABC。
37
⑵ 当 ∠AEF=∠C 时 ,△AEF 与 △ABC 属 于 “ 斜 A” 型 相 似 , 即
∴
PA2 PB2
= AC·AB BD·AB
= AC BD
=x y
。
39
△CBD,所以,我们称它们之间的相似为“母子型”相似。 且由“母子型”
相似得到三个很实用的结论:AC2=AD·AB,BC2=BD·BA,CD2=DA·DB。
例 3 如 图 3-3, 在△PAB 中 , 点 C、D 在 边 AB 上 ,PC=PD=CD,
∠APB=120°。
⑴找出图中相似的三角形;
⑵若 AC=x,BD=y,试证明
=
AF AC
,
即
4 3
= AF , 2
∴ AF= 8 。 3
当△AFE∽△ABC
时,
AE AC
=
AF AB
,即
4 2
=
AF 3
,
∴
AF=6
(完整版)相似三角形的几种基本图形
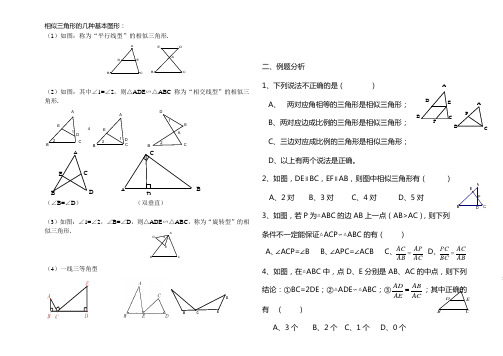
B EADC相似三角形的几种基本图形:(1)如图:称为“平行线型”的相似三角形.(2)如图:其中∠1=∠2,则△ADE ∽△ABC 称为“相交线型”的相似三角形.ABCD E12AABBCC DD EE12412(∠B=∠D ) (双垂直)(3)如图:∠1=∠2,∠B=∠D ,则△ADE ∽△ABC ,称为“旋转型”的相似三角形.(4)一线三等角型二、例题分析1、下列说法不正确的是( )A 、 两对应角相等的三角形是相似三角形;B 、两对应边成比例的三角形是相似三角形;C 、三边对应成比例的三角形是相似三角形;D 、以上有两个说法是正确。
2、如图,DE ∥BC ,EF ∥AB ,则图中相似三角形有( )A 、2对B 、3对C 、4对D 、5对 3、如图,若P 为△ABC 的边AB 上一点(AB>AC ),则下列条件不一定能保证△ACP ∽△ABC 的有( )A 、∠ACP=∠B B 、∠APC=∠ACBC 、ACAP ABAC = D 、ABAC BCPC =4、如图,在△ABC 中,点D 、E 分别是AB 、AC 的中点,则下列结论:①BC=2DE ;②△ADE ∽△ABC ;③AD AB AE AC =;其中正确的有 ( )A 、3个B 、2个C 、1个D 、0个ED CBAB EACD 12A BC D E A B CD A B C DE A AB BC CD DE EA BDE ABC PEFA B5、如图AD⊥AB于D,CE⊥AB于E交AB于F,则图中相似三角形的对数是。
;6、已知AD为Rt△ABC斜边BC上的高,且AB=15cm,BD=9cm,则AD= ,CD= 。
7、如图四,在平行四边形ABCD中,AB = 4cm ,AD =7cm , ∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF = ________cm8、已知:如图,ΔABC中,AD=DB,∠1=∠2.求证:ΔABC∽ΔEAD.9、已知,如图,D为△ABC内一点,连结ED、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD求证:△DBE∽△ABC10、已知△ABC中,AB=AC,∠A=36°,BD是角平分线,求证:△ABC∽△BCD11、矩形ABCD中,BC=3AB,E、F,是BC边的三等分点,连结AE、AF、AC,问图中是否存在非全等的相似三角形?请证明你的结论。
三角形相似的基本图例

三角形相似的基本图例[教材分析]本节内容是上科版《新时代数学》九上第24章《相似形》第二节《相似三角形判定》的第一节课.是在学习了第一节相似多边形的概念、比例线段的有关概念及性质,并具备了有关三角形中位线和平行四边形知识后,研究三角形一边的平行线的判定定理.一方面,该定理是前面知识的延伸和全等三角形性质的拓展;另一方面,不仅可以直接用来证明有关三角形相似的问题,而且还是证明其他三种判定定理的主要根据,所以有时也把它叫做相似三角形判定定理的“预备定理”.通过本节课的学习,还可培养学生实验、猜想、证明、探索等能力,对掌握分析、比较、类比、转化等思想有重要作用.因此,这节课在本章中有着举足轻重的地位.[教学目标]知识与技能目标:(1)、理解相似三角形的概念,能正确地找出相似三角形的对应边和对应边角.(2)、掌握相似三角形判定定理的“预备定理”.过程与方法目标:(1)、通过探索相似三角形判定定理的“预备定理”的过程,培养学生的动手操作能力,观察、分析、猜想和归纳能力,渗透类比、转化的数学思想方法.(2)、利用相似三角形的判定定理的“预备定理”进行有关判断及计算,训练学生的灵活运用能力,提高表达能力和逻辑推理能力.情感与态度目标:(1)、通过实物演示和电化教学手段,把抽象问题直观化,激发学生学习的求知欲,感悟数学知识的奇妙无穷.(2)、通过主动探究、合作交流,在学习活动中体验获得成功的喜悦.[教学重点]相似三角形判定定理的预备定理的探索[教学难点] 相似三角形判定定理的预备定理的有关证明[教学方法]探究法[教学媒体]多媒体课件直尺、三角板[教学过程]①相似三角形对应角相等②相似三角形的对边、对应高、对应中线、对应角平分线之比都相等,等于相似比③相似三角形对应周长比等于相似比④相似三角形对应面积比等于相似比的平方2、判定①两角相等②两边对应成比例,夹角相等③三边对应成比例二、观测图像归纳ABCDE三判断下列图像是否相似,为什么呢?ABCDEABCDEAB CA’B’C’AB CA’C’B’四、判断下列命题的真假,为什么呢?1、有一对角相等的三角形一定相似.( )2、有一对锐角相等的两个直角三角形一定相似.()3、有一个角等于1000的两个等腰三角形相似.( )4、有一个角等于300的两个等腰三角形相似.( )5、有一对角相等的两个等腰三角形一定相似.( )五、实际操作一、A型和反A型如图1、已知DE∥BC,证明△ADE∽△ABC如图2、已知∠ADE=∠C,证明△ADE∽△ACB二、8型和反8型如图3、已知AB∥CD,证明△AOB∽△DOC如图4、已知∠A=∠C,证明△AOB∽△COD三、射影型和仿射影型(经典)如图5、已知∠ACB=900,CD⊥AB;①证明△ACD∽△ABC进而证明:AC2=AD*AB②证明△ACD∽△ABC进而证明:AC2=AD*AB③证明△ACD∽△CBD进而证明:CD2=AD*DB④证明△CBD∽△ABC进而证明:BC2=BD*AB如图6、已知∠ACD=∠B,证明:△ACD∽△ABC进而证明:BC2=BD*AB相似中的基本图形一、A型和反A型二、8型和反8型三、射影型和仿射影型配套训练:1、△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)计算△A′B′C′的面积S.ABC图132、如图,△ABC∽△ADE,AE=3,EC=5,DE=1.2,则BC的长度6题EDCBA3、网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.图21[教学反思与剖析]1、以问题为出发点,唤起学生对知识的回忆虽然两节课都是设置一定的教学情景,但是两堂课唤起学生对知识的回忆的深度、挖掘度不同:前一节课是在教师设想上设置问题;而后一节课是从学生的生活实际中引出话题,进而进行问题设置,学生有切身的体验——从而让学生产生情绪高昂和智力振奋的内心状态。
初中数学_相似三角形中的基本图形教学设计学情分析教材分析课后反思

专题6:相似三角形中的基本图形教学目标:1.通过梳理使学生掌握相似三角形中的基本图形,熟悉这些基本图形的特征,能在复杂图形中加以识别。
2.在综合题目中较快识别出相似的基本图形,能根据条件找出隐藏的基本图形,或者通过添加辅助线构造出完整的基本图形来建立数学模型,从而解决相关问题。
3、通过问题的解决,体验探究问题成功的乐趣,提高学习几何的兴趣。
重点和难点重点:在综合题中识别出相似的基本图形,,灵活运用相似知识解决相关问题。
深化学生对基本图形模型的理解。
难点:从复杂图形中识别相似的基本图形,并利用相似知识解决问题。
相似有关的综合性问题的解决技巧和方法的渗透。
教学过程:一、教师赠言:每个人心中都有一座山世上最难攀登的山其实是自己往上走哪怕只有一小步也有新高度做最好的自己我能(设计意图:让学生斗志昂扬的宣读赠言,教师鼓励同学们每天都能更进一步,奋力拼搏,做最棒的自己。
)二、温故知新:1.判定三角形相似的方法:2.相似三角形的性质:(设计意图:新旧知识之间有相互一致的特征,学生通过复习旧知识,激活认知结构中的原有知识,为促其顺利迁移,获得本节知识奠定基础。
)三、相似三角形基本图形梳理:(8种类型)A BCD E D E A BC (D)E ABC ABCD EA BCD E AEBC(D)1221ABCD E(学生课前积累平时学习中的各类基本图形,体会这些基本图形之间的联系) 四、构建模型、探求方法:(设计意图:通过题组的形式帮助学生梳理各类型的基本图形。
掌握这些基本图形的性质与特点,熟悉的模型在已有知识经验的基础上抽象出数学概念是帮助学生理解数学知识的有效学习方法。
)(一)基本图形一:平行型相似三角形 如图①~③所示,在△ABC 中,点D,E 分别是AB ,AC 上(或延长线上或反向延长线上)的点,且DE ∥BC,则△ADE ∽ △ABC 。
(引导学生给每一个基本图形命名,“A ”型和“X ”型。
) 【培优训练】:1.(2014.随州)如图,在△ABC 中,两条中线BE,CD 相交于点O,则S △DOE ∶S △COB=( )A.1∶4B.2∶3C.1∶3D.1∶2 2.(2013•乌鲁木齐)如图,AB ∥GH ∥CD ,点H 在BC 上,AC 与BD 交于点G ,AB=2,CD=3,则GH的长为 .【方法归纳】:______________________________________________(学生抢答并总结方法) (二)基本图形二:相交型相似三角形 【知识点睛】如图①,∠AED=∠B,则△AED ∽△ABC; 如图②,∠ACD=∠B,则△ACD ∽△ABC; 如图③,∠A=∠D,则△AOB ∽△DOC.(引导学生给每一个基本图形命名,反“A ”型和反“X ”型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形中的基本图形
1.锐角△ABC 中,BC=6,S △ABC =12,两动点M,N 分别在边AB,AC 上滑动,且MN ∥BC ,以MN 为边向下作正方形MPQN ,设其边长为x ,正方形MPQN 与△ABC 公共部分的面积为y(y>0).
(1)△ABC 中BC 边上高AD= ;
(2)当x= 时,PQ 恰好落在BC 边上(如图1);
(3)当PQ 在△ABC 外部时(如图2),求y 关于x 的函数关系式(注明x 的取值范围),并求出x 为何值时y 最大,最大值是多少?
变式:现用一块直角三角形的边角料来加工一个正方形,已知两直角边AC=30cm,BC=40cm.甲,乙两种加工方法如图所示,请你通过计算说明哪种加工方法能使加工成的正方形面积更大。
2. 如图, 边长为4的正方形ABCD 中, P 是边BC 上的一点, QP ⊥AP 交 DC 于Q, 设BP= x, △ADQ 的面积为y.
(1) 求y 与x 之间的函数关系式,并求自变量x 的取值范围; (2) 问P 点在何位置时,△ADQ 的面积最小?最小面积是多少?
Q
B
C
P
D
A A A
B B C
M M N
N P P Q
Q D D
(图1
) (图2)
E E
X
变式1:如图,在直角梯形ABCD 中,AB ∥CD, ∠A=900,AB=2, AD=5,P 是AD 上一动点(不与A 、D 重合),PE⊥BP,PE交DC于点E. (1)△ABP 与△DPE 是否相似?请说明理由;
(2)设AP=x DE=y ,求y 与x 之间的函数关系式,并指出自变量x 的取值范围; (3)请你探索在点P 运动的过程中,四边形ABED 能否构成矩形?如果能,求出AP 的长;如果不能,请说明理由;
(4)请你探索在点P 运动的过程中,△BPE 能否成为等腰三角形?如果能,求出AP 的长,如果不能,请说明理由。
变式2:如图,梯形ABCD 中 AD ∥BC ,∠ABC=90°,AD=9,
BC=12,AB=10,在线段BC 上任取一P ,作射线PE ⊥PD ,与线段AB 交于点E. (1)试确定CP=5时点E 的位置;
(2)若设CP=x ,BE=y ,试写出y 关于自变量x 的函数关系式,
并求出自变量x 的取值范围.
变式3:如图,已知抛物线与x 轴交于A 、B 两点,与y 轴交于C 点. (1)求此抛物线的解析式;
(2)抛物线上有一点P ,满足∠PBC=90°,求点P 的坐标;
(3)在(2)的条件下,问在y 轴上是否存在点E ,使得以A 、O 、E 为顶点的三角形与⊿PBC 相似?若存在,求出点E 的坐标;若不存在,请说明理由.
A B D P E
C
B C A D E P
A
X=4
2
3 6
C
B
如图,二次函数22
++=bx ax y 的图像与x 轴相交于点A 、B ,与y 轴相交于点C ,经过点
A 的直线2-=kx y 与y 轴相交于点D ,与 直线BC 垂直于点E ,已知AB=3,求这个二次函数的解析式。
如图,已知AC=BC ,∠ACB=90°,点B 的坐标为(1,0),抛物线A 、B 、C 三点。
(1)求抛物线的解析式;
(2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积;
(3)在x 轴上方y 轴左侧的抛物线是否存在一点M ,过M 作MG ⊥x 轴于点G ,使以A ,
M ,G 三点为顶点的三角形与△PCA 相似。
若存在,请求出点M 的坐标;若不存在,请说明理由。
如图,直角坐标平面内,二次函数图象的顶点坐标为C ()
3,4-,且在x 轴上截得的线段AB 的长为6.
(1)求二次函数解析式;
(2)在x 轴上方的抛物线上,是否存在点D ,使得以A 、B 、D 三点为顶点的三角形与△ABC 相似?若存在,求出点D 的坐标,若不存在,请说明理由。
图1-5。
