第二章矩阵的运算及与矩阵的秩

合集下载

求矩阵的秩的三种方法实用2份

求矩阵的秩的三种方法实用2份求矩阵的秩的三种方法 1矩阵的`运算：矩阵的最基本运算包括矩阵加（减）法，数乘和转置运算。

被称为“矩阵加法”、“数乘”和“转置”的运算不止一种。

给出m×n矩阵 A 和B，可定义它们的和 A + B 为一m×n 矩阵，等i,j 项为(A + B)[i, j] = A[i, j] + B[i, j]。

举例：另类加法可见于矩阵加法。

若给出一矩阵A 及一数字c，可定义标量积cA，其中(cA)[i, j] = cA[i, j]。

例如这两种运算令M(m, n, R) 成为一实数线性空间，维数是mn.若一矩阵的列数与另一矩阵的行数相等，则可定义这两个矩阵的乘积。

如A 是m×n 矩阵和B 是n×p矩阵，它们是乘积AB 是一个m×p 矩阵，其中(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + . + A[i, n] *B[n, j] 对所有i 及j。

例如此乘法有如下性质：(AB)C = A(BC) 对所有k×m 矩阵A, m×n 矩阵 B 及n×p 矩阵 C (“结合律").(A + B)C = AC + BC 对所有m×n 矩阵 A 及 B 和n×k 矩阵 C ("分配律")。

C(A + B) = CA + CB 对所有m×n 矩阵 A 及 B 和k×m 矩阵 C ("分配律")。

要注意的是：可置换性不一定成立，即有矩阵A 及B 使得AB ≠ BA。

对其他特殊乘法，见矩阵乘法。

求矩阵的秩的三种方法 2矩阵的运算：矩阵的最基本运算包括矩阵加（减）法，数乘和转置运算。

被称为“矩阵加法”、“数乘”和“转置”的运算不止一种。

给出m×n 矩阵 A 和B，可定义它们的和 A + B 为一m×n 矩阵，等i,j 项为(A + B)[i, j] = A[i, j] + B[i, j]。

线性代数第二章

其中，
s
cij ai1b1 j ai2b2 j aisbsj aikbkj (i 1，2 ，，m ；j 1，2 ，，n) ．
k 1
注：（1）只有当左边矩阵的列数等于右边矩阵的行数时，两个矩阵才能相乘，否则 AB
没有意义．
（2）矩阵 C 中元素 cij 等于左矩阵 A 的第 i 行与右矩阵 B 的第 j 列对应元素乘积之和．
（3）矩阵加减法与矩阵数乘统称为矩阵的线性运算．
2.2.2 数与矩阵相乘
矩阵数乘的性质
（1）分配律： k( A B) kA kB，(k l)A kA lA ；（2）结合律： (kl) A k(lA) ；（3）1A A，0A O ．
2.2.2 数与矩阵相乘
例题
3 1 2
7 5 4
a11 a12
a21
a22
am1 am2
a1n a11 a12
a2n
或
a21
a22
amn
am1
am 2
a1n
a2n
，
amn
称为 m 行 n 列矩阵，简称 m n 矩阵．通常用大写字母 A，B ，C ，表示矩阵， aij 表示
矩阵中第 i 行、第 j 列的元素，一个 m n 矩阵可以简记为 A=Am×n=(aij) m×n
a11
只有一列的矩阵
A
a21
称为列矩阵或列向量。
am1
注：列矩阵也可记为 A a11 ，a12 ，，a1n 。
2.1.2 几种特殊形式的矩阵
3．零矩阵
所有元素全为零的矩阵称为零矩阵， m n 零矩阵记为 Omn 或简记为 O ． 4．方阵
对于矩阵 Amn ，当 m n 时，称为 n 阶方阵，记作 Ann 或 An ，即

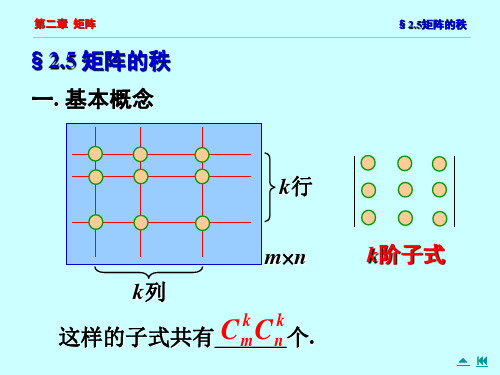
2.6-矩阵的秩

001
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵，则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵

线性代数第二章矩阵及其运算2-3PPT课件

例如，设实数k=2，矩阵A=[1 2; 3 4]，则kA=[2 4; 6 8]。
CHAPTER 02
矩阵的乘法
矩阵乘法的定义
01
矩阵乘法是将两个矩阵对应位置的元素相乘，得到一个新的矩阵。
02
矩阵乘法的结果是一个矩阵，其行数等于左矩阵的行数，列数
等于右矩阵的列数。
矩阵乘法的操作顺序是先进行行操作，再进行列操作。
CHAPTER 05
矩阵的秩
秩的定义
秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
秩的Байду номын сангаас质
矩阵的秩是唯一的，且其值满足特定的性质，如对于任何矩阵A， r(A)≤min(m,n)，其中m和n分别为矩阵A的行数和列数。
秩的计算方法
可以通过多种方法计算矩阵的秩，如高斯消元法、行变换法、初等行变换法等。
线性代数第二章矩阵及其运算2-3ppt课件
CONTENTS 目录
• 矩阵的加法与数乘 • 矩阵的乘法 • 逆矩阵与伴随矩阵 • 矩阵的行列式 • 矩阵的秩 • 矩阵的应用
CHAPTER 01
矩阵的加法与数乘
矩阵的加法
矩阵加法定义
两个矩阵A和B的和记作A+B，定义为满足以下条件的矩阵C，即C的元素Cij=Aij+Bij（i，j=1，2，…，n）。
03
矩阵乘法的性质
1 2
结合律
$(AB)C=A(BC)$，即矩阵乘法满足结合律。
分配律
$A(B+C)=AB+AC$，即矩阵乘法满足分配律。
3
单位元
存在一个单位矩阵，使得任意矩阵与单位矩阵相乘都等于原矩阵。

第二章矩阵的运算及与矩阵的秩ppt课件

钢笔 100 150
铅笔 300 260
.
§2.1 矩阵的基本运算
每种商品进货单价和销售单价（元）如下表：
圆珠笔钢笔铅笔
进货单价 6 9 3
销售单价 8 12 4
.
§2.1 矩阵的基本运算
求每个月的总进货额和总销售额。
金额月份
总进货额
总销售额
九月 200×6+100×9+300×3 200×8+100×12+300×4
0 0 2 5
0 1 8
0
0 0
A1
A2
0 0 0 3 2 0
A3
0 0 0 0 0 9
.
二、分块矩阵的运算
§2.2 分块矩阵
1．分块矩阵相加、减
设A、B是两个用相同方法分块的同型矩阵
A11
设Amn
A21 M
A12 L A22 L MO
Ap1 Ap2 L
A1q
B11 B12 L
001 a 31 a 32 a 33 a 3 4 a 31 a 32 a 33 a 34
.
§2.1 矩阵的基本运算
1 0 0 0
a11 A(E 2,3)a21
a12 a22
a13 a23
a a1 24 40 0
0 1
1 0
0 0a a1 21 1
a13 a23
a12 a22
a14 a24
P 1 P 2LP sA Q 1 Q 2LQ tB
.
三、矩阵的转置
§2.1 矩阵的基本运算
定义2.3：把m×n矩阵A的行和列依次互换得到的一个 n×m 矩阵，称为A的转置，记作AT或A’.

第二章矩阵

在n阶矩阵A (aij )中，若当i j时都有aij 0,
称A为上三角矩阵。
同样，若在n阶矩阵A中，当i j时都有aij 0，
称A为下三角矩阵。
5 1 2 4
0 2 4 3
0 0
0 0
3 0
5 7
1 0 0 0
2 3 0 0
0 6
5 8
4 9
10
2. 矩阵的运算
定义1.4 矩阵的和（矩阵的加法）
b22
b23
b21
b22
b23
0
1
0
0 1 1 b31 b32 b33 b31 b32 b33 0 1 1
b11
b12
b13 b11 b12 b13 b13
b21
b22
b23
b21
b22 b23
b23
b21 b31 b22 b32 b23 b33 b31 b22 b33 b33
AB
(aij
bij ) mn
am1 bm1
a1n b1n
amn bmn
A-B=A+(-B)
A+(-A)= 0
定义1.5 矩阵的数乘
数k与m n矩阵A (aij )的数量乘积仍是m n矩阵，
ka11 ka12 L ka1n
记为kA，定义为kA
(kaij )mn
ka21 M
b11 b12 0
得到 b13 b23 b21 0, b22 b33
B
0
b22
0
b31 b32 b22
例题1.3 下面的对角矩阵A满足aii a jj (i j;
a11 0 L 0
A
0
a22 L

矩阵的秩的性质以及矩阵运算和矩阵的秩的关系

高等代数第二次大作业1120133839 周碧莹30011303班矩阵的秩的性质1.阶梯型矩阵J的行秩和列秩相等，它们都等于J的非零行的数目；并且J的主元所在的列构成列向量的一个极大线性无关组。

2.矩阵的初等行变换不改变矩阵的行秩。

证明：设矩阵A的行向量组是a1，…,as.设A经过1型初等行变换变成矩阵B，则B的行向量组是a1，…,ai,kai+aj,…,as.显然a1，…,ai,kai+aj,…,as可以由a1，…,as线性表处。

由于aj=1*(kai+aj)-kai,因此a1，…,as可以由a 1，…,ai,kai+aj,…,as线性表处。

于是它们等价。

而等价的向量组由相同的秩，因此A的行秩等于B的行秩。

同理可证2和3型初等行变换使所得矩阵的行向量组与原矩阵的行向量组等价，从而不改变矩阵的行秩。

3.矩阵的初等行变换不改变矩阵的列向量组的线性相关性。

证明：一是为什么初等行变换不改变列向量的线性相关性?二是列向量进行初等行变换后，为什么可以根据行最简形矩阵写出不属于极大无关组的向量用极大无关组表示的表示式?第一个问题：设α1，α2，…，αn是n个m维列向量，则它们的线性相关性等价于线性方程组AX=0(其中A=(α1，α2，…，αn)，X=(x1，x2，…，xn)T)是否有非零解，即α1，α2，…，αn线性相关等价于AX=0有非零解，α1，α2，…，αn 线性无关等价于AX=0只有零解。

而对A进行三种行初等变换分别相当于对线性方程组中的方程进行：两个方程交换位置，对一个方程乘一个非零常数，将一个方程的常数倍对应加到另一个方程上。

显然进行三种变换后所得方程组与原方程组同解，若设所得方程组为BX=0，则B即为对A进行行初等变换后所得矩阵。

B 的列向量的线性相关性与BX=0是否有解等价，也就是与AX=0是否有解等价，即与A的列向量的线性相关性等价!第二个问题以一个具体例子来说明。

例：设矩阵，求A的列向量组的一个极大无关组，并把不属于极大无关组的列向量用极大无关组线性表示。

矩阵的秩

第二章矩阵的运算
22
几个常用的矩阵秩的性质.
(5) maxRA, RB RA, B RA RB,
特别地,当B=b为列向量时,有
RA RA,b RA1.
证 A的最高阶非零子式总是(A,B)的非零
子式,所以 RA RA, B. 同理有 RB RA, B.
r3 5 r4 r3
1 2 2 1 1 0 0 2 1 0 0 0 0 0 1 0 0 0 0 0
R( A) 2, R(B) 3.
第二章矩阵的运算
19
例2-24 设
1 1 1 2
A 3 1 2 5 3 6
综上,若 A 经有限次初等变换变为B( 即 A ~ B),则 R( A) R(B).
证毕
初等变换求矩阵秩的方法：把矩阵用初等行变换变成为行阶梯形矩阵，
行阶梯形矩阵中非零行的行数就是矩阵的秩.
第二章矩阵的运算
10
例2-22
3 2 0 5 0
设
A

3 2
2 0
3 1
6 5

又因为 RA E RE A, 所以
RA E RA E n.
第二章矩阵的运算
26
四、小结
1. 矩阵秩的概念 2. 求矩阵秩的方法 (1)利用定义 (即寻找矩阵中非零子式的最高阶数); (2)初等变换法 (把矩阵用初等行变换变成为行阶梯形矩阵，行阶梯形矩阵中非零行的行数就是矩阵的秩).
第二章矩阵的运算
16
例2-23
1 2 2 1 1
设A

2 2
4 4
8 2
0 3

矩阵的秩与运算

矩阵的秩与运算
一·矩阵秩的求法
求矩阵的秩主要有三种方法；(1)定义
法，利用定义寻找矩阵中非零子式的最高
阶数。

(2)初等变换法，对矩阵实施初等行变
换，将其变成为行阶梯形矩阵，行阶梯形矩
阵中非零行的行数就是矩阵的秩；(3)标准
形法，求矩阵的标准形，l的个数即为矩阵
的秩。

二·矩阵的秩与行列式
对于一个方阵A，如何判断它是
否可逆，除了根据它的行列式是否为零，还
可以根据方阵秩的大小来判断。

比如方阵A（nn）
其秩R, ，若R ＜ n，则显然矩阵行列式为零，不可逆；
若R = n ,则矩阵行列式不为零，矩阵可逆。

三·矩阵的秩与线性方程组
1齐次的
齐次线性方程组
●系数矩阵R = n ，则有且仅有一个0解
●系数矩阵R ＜ n，则有无数个解。

2非齐次的
费齐次线性方程组，设系数矩阵A ,增广矩阵B
●若R(A) = R(B) = n ，则有且仅有一个解；
●若R(A) = R(B)＜n，则有无数个解；
●若R(A)≠R(B) ，则方程组无解。

四·矩阵的秩与二次曲面
说二次曲面，其实就是与二次型的关系。

有定义知道，
二次型的秩定义为其矩阵的秩，这就为解决二次曲面问题找到了一个可转移的办法。

正所谓遇难则变，变则通。

道家之言，诚哉大哉！！
下面将具体举例阐述，二次型总可以经线性变换成CY化为标准形（比如合同变换），而且，同的非退化线性变换化为不同的标准形，但这些标准形中所含平方项的个数是相同的，所含平方项的个数就等于二次型的秩，也就是矩阵的秩。

工程数学第二章矩阵课件

68 34
上页
下页
返回
结束
例 6 若 A 为 n 阶方阵， k 为实数，则 kA kn A .
证由于 A 为 n 阶方阵， k 为实数，根据数与矩阵乘法的定义知， kA 是将 A 的每个元素都乘以 k ，在求 kA 时，根据行列式性质的单行可提性，每一行提出一个 k ，所以 kA kn A .
例1
已知
a
3
b
a
3
b
c
7
d
2c d 3
，求
a,b,c, d
．
解根据题意，得
a b 7,
2c d 3,
cd
3,
a b 3
故 a 5,b 2,c 2, d 1 .
上页
下页
返回
结束
例2 设
A
1 3
2 4
，
B
0 1
2 1
，
试求：（1） A 与 B 是否相等？（2） A , B .
；
0
0
A
0
0 0
0 0
0 2 1 0 4 2
0
3
2
5
1
3
10 2 5
4
1
.
0 A 称为 A 的负矩阵，记为 A，其中 A与 A 的每个对应元素都互为相反数．
上页
下页
返回
结束
矩阵加法具有如下性质：
假设 A, B,C, 0 均为 m n 矩阵，则（1） A B B A（交换律）；（2） (A B) C A (B C) （结合律）；（3） A 0 0 A A；（4） A (A) 0 .
5
3
7 5
4 2

矩阵的秩的运算

矩阵的秩的运算一、矩阵秩的定义1. 基本概念- 对于一个m× n矩阵A，它的秩r(A)是矩阵A中线性无关的行向量（或列向量）的最大个数。

- 例如，对于矩阵A=begin{pmatrix}1&2&32&4&6end{pmatrix}，通过观察可以发现第二行是第一行的2倍，所以矩阵A的行向量中最多只有一个线性无关的向量，r(A) = 1。

2. 等价定义- 矩阵A的秩等于矩阵A的行最简形矩阵中非零行的行数。

例如，将矩阵A=begin{pmatrix}1&1&11&2&31&3&5end{pmatrix}化为行最简形begin{pmatrix}1&0& - 10&1&20&0&0end{pmatrix}，非零行有2行，所以r(A)=2。

二、矩阵秩的基本运算性质1. r(A)=r(A^T)- 矩阵A与其转置矩阵A^T具有相同的秩。

这是因为矩阵A中行向量的线性相关性与A^T中列向量的线性相关性是对应的。

例如，若A=begin{pmatrix}1&2&34&5&6end{pmatrix}，A^T=begin{pmatrix}1&42&53&6end{pmatrix}，通过计算可知r(A)=2，r(A^T) = 2。

2. r(kA)- 若k≠0为常数，r(kA)=r(A)。

这是因为数乘矩阵只是对矩阵的每个元素进行数乘，不会改变向量之间的线性相关性。

例如，设A=begin{pmatrix}1&23&4end{pmatrix}，2A=begin{pmatrix}2&46&8end{pmatrix}，r(A)=2，r(2A)=2。

- 当k = 0时，r(0A)=0（零矩阵的秩为0）。

3. r(A + B)≤ r(A)+r(B)- 设A=begin{pmatrix}1&00&0end{pmatrix}，B=begin{pmatrix}0&00&1end{pmatrix}，r(A)=1，r(B)=1，A +B=begin{pmatrix}1&00&1end{pmatrix}，r(A + B)=2，此时r(A + B)=r(A)+r(B)；再设A=begin{pmatrix}1&00&0end{pmatrix}，B=begin{pmatrix}-1&00&0end{pmatrix}，r(A)=1，r(B)=1，A +B=begin{pmatrix}0&00&0end{pmatrix}，r(A + B)=0，r(A + B)<r(A)+r(B)。

矩阵秩的性质及矩阵秩与矩阵运算之间的联系

于是这个 r 阶子式的列向量组线性无关.从而它的延伸组，即 A 的第��1 , ⋯ , �� 列线性无关.由于 A 的列秩为 r，因此 A 的第��1 , ⋯ , �� 列构成 A 的列向量组的一个极大无关组. 类似地可证明 A 的行向量的极大无关组的结论. █ 【定理8】非零矩阵 A 不等于 0 的子式的最高阶数称为 A 的行列式秩，A 的行列式秩与 A 的秩相等证明设�� × ��的矩阵的秩为 r，则 A 的行向量组的秩为 r，有 r 个行向量线性无关，设为 αi1 ，αi2 ，…，αir . 取此 r 个向量组成的�� × ��子矩阵��1 ，则rank A1 = r.于是��1 列向量组秩也为 r.同理组成��1 的 r 级子矩阵��2 ，则��2 的列向量组线性无关.故 ��2 ≠ 0.而即是矩阵��1 的一个 r 阶子式 ��2 = �� 1 ��1 ��2 ��2 ⋯ �� ⋯ ��
所以 A 存在一个 r 阶不等于 0 的子式. 另一方面，当�� < �� , �� 时，任取 A 的一个 k 阶子式i（�� ≤ �� ≤ �� , �� ) �� ⋯ �� = �� 1 2 ��1 ��2 ⋯ �� 设 A 的列向量组为��1 ，��2 ， ⋯ ，�� ，其一个极大无关组为��1 , ��2 , ⋯ , �� .则 A 的列向量组�� 1 , �� 2 , ⋯ , �� 可由其线性表出.因�� > ��，故�� 1 , �� 2 , ⋯ , �� 相性相关. ∵子式 M 恰在此列向量组上 ∴M 的列向量组即其缩短组. 所以由�� 1 , �� 2 , ⋯ , �� 相性相关可得 M 列向量组也线性相关.因此�� = 0

第二章第一讲矩阵的秩

互换变换：A的i行与j行交换变为B，则B 的子式或为A的子式，或与A的子式差一个符号，秩不变。倍乘变换：A的i 行元素乘以 k (k≠0) 得到B，则B 的子式成为A的子式，或与A的子式差一个因子 k≠0。则秩不变。
首页上页返回下页结束铃
倍加变换：A由i行的k倍加到 j行，得到
矩阵B。：B的一个子式若不包含第j行元素，则也为A的一个子式；
1 2 1 1 0 3 4 4 , 0 5 1 0
5 0 , 由r(A)=2, 得 1 0
5. 即 1
首页
上页
返回
下页
结束
铃
四、小结
1. 矩阵秩的概念 2. 求矩阵秩的方法 (1) 利用定义寻找矩阵中非零子式的最高阶数; (2) 初等变换法
解：对Ａ作初等行变换，变成行阶梯形矩阵。
1 1 2 1 A 1 2 4 1
首页
2 2 0 4
1 4 3 2
上页
r2 2 r1 r3 r1 r4 4 r1
返回

1 1 2 1 0 3 2 2 0 3 2 2 0 3 4 2
对A作初等行变换，变成行阶梯形矩阵：
1 r r 1 3 2 5 1 1 8 1 1 3 4 7 3 5 0 1 2 4 11
解
A
7 11
首页
上页
返回
下页
结束
铃
5 1 2 1 7 1 11 8 r2 2r1
无解。
返回下页
因此，r(A) = 2 , r(B) = 3.
上页
结束

矩阵教学课件

例如:
13 2
6 2
5 2
是一个3 阶方阵.
2 2 2
(2) 只有一行的矩阵 A a1,a2 ,,an ,称为行矩阵(或行向量).
(3) 只有一列的矩阵
a1
B
a2
,
an
称为列矩阵(或列向量).
第二章矩阵
§1 矩阵的概念
(4) 元素全为零的矩阵称为零矩阵, 记作O.
注意：不同阶数的零矩阵是不相等的.
例8: 设列矩阵X = (x1 x2 ···xn)T, 满足XTX = 1, E为n 阶单位矩阵, H = E – 2XXT, 证明: H为对称矩阵, 且HHT = E.
证明: 自学（见P49）
第二章矩阵
§2 矩阵的运算
五、方阵的行列式定义:由n阶方阵A的元素所构成的行列式(各元素的位
置不变),称为方阵A的行列式,记作|A| 或det A. 例
第二章矩阵
§1 矩阵的概念 §2 矩阵的运算 §3 逆矩阵 §4 分块矩阵 §5 矩阵的初等变换 §6 矩阵的秩
第二章矩阵
§1 矩阵的概念
一、矩阵的定义定义: 由m×n个数aij (i = 1,2, ∙ ∙ ∙, m ; j = 1,2, ∙ ∙ ∙, n) 排
成的m行n列的数表
称为m行n列矩阵,简称m×n矩阵.
y1 a11x1 a12 x2 a1n xn ,
y2 a21x1 a22 x2 a2n xn ,
ym am1 x1 am2 x2 amn xn .
表示一个从变量x1、x2、…xn到变量y1、y2、…ym的线性变换，
其中aij为常数。
第二章矩阵
§1 矩阵的概念
,
x

第二章矩阵及其运算总结

§1 矩阵及其运算一、矩阵的基本概念（必考）矩阵，是由m*n个数组成的一个m行n列的矩形表格，通常用大写字母表示，组成矩阵的每一个数，均称为矩阵的元素，通常用小写字母其元素表示，其中下标都是正整数，他们表示该元素在矩阵中的位置.比如,或表示一个m*n 矩阵，下标ij 表示元素位于该矩阵的第行、第列.元素全为零的矩阵称为零矩阵. 特别地，一个m*1矩阵，也称为一个 m维列向量；而一个 1*n矩阵B=(b1,b2,…，bn)，也称为一个 n维行向量.当一个矩阵的行数m与烈数n 相等时，该矩阵称为一个 n阶方阵.若一个n阶方阵的主对角线上的元素都是，而其余元素都是零，则称为单位矩阵，记为，即： .单位矩阵与实数中的‘1’的运算相近.如一个阶方阵的主对角线上（下）方的元素都是零，则称为下（上）三角矩阵是一个阶下三角矩阵.例题：1.A既是上三角矩阵，又是下三角矩阵，则A必是对角矩阵2.两矩阵既可相加又可相乘的充要条件是两矩阵为同阶方阵.3.A=(l≠n)，则A的主对角线上个元素的和为 (设矩阵为2行3列的矩阵，找规律)二、矩阵的运算1、矩阵的加法：如果是两个同型矩阵（即它们具有相同的行数和列数，比如说），则定义它们的和仍为与它们同型的矩阵（即），的元素为和对应元素的和，即：.给定矩阵，我们定义其负矩阵为： .这样我们可以定义同型矩阵的减法为： .由于矩阵的加法运算归结为其元素的加法运算，容易验证，矩阵的加法满足下列运算律：(1)交换律：； (2)结合律：；(3)存在零元：;(4)存在负元：.2 、数与矩阵的乘法的运算律：（1)；（2)；（3)；（4) .3 、矩阵的乘法（必考）设为距阵，为距阵，则矩阵可以左乘矩阵（注意：距阵的列数等与矩阵的行数），所得的积为一个距阵，即,其中,并且(即左行乘右列)矩阵的乘法满足下列运算律（假定下面的运算均有意义）：(1）结合律：； (2）左分配律：；(3）右分配律：；(4）数与矩阵乘法的结合律：；(5）单位矩阵的存在性：.若为阶方阵，则对任意正整数，我们定义：，并规定：由于矩阵乘法满足结合律，我们有：， .注意：矩阵的乘法与通常数的乘法有很大区别，特别应该注意的是：（必考重要）（1)矩阵乘法不满足交换律：一般来讲即便有意义，也未必有意义；倘使都有意义，二者也未必相等.正是由于这个原因，一般来讲,在实数中的某些运算不再适应，如,，反过来，这些公式成立的条件又恰是A、B 可逆.例：A,B,C 是同阶矩阵，A ≠0,若AB=BC,必有B=C,则A满足可逆（2)两个非零矩阵的乘积可能是零矩阵，即未必能推出或者. 同理，A ≠0，B ≠0，而AB却肯能等于0.例题：（选择题5、6）（3)矩阵的乘法不满足消去律：如果并且，未必有 .4 、矩阵的转置：定义：设为矩阵，我们定义的转置为一个矩阵，并用表示的转置，即：.矩阵的转置运算满足下列运算律：（1)；（2)；（3)；（4) (重要).5、对称矩阵：n 阶方阵若满足条件：，则称为对称矩阵；若满足条件：，则称为反对称矩阵.若设，则为对称矩阵，当且仅当对任意的成立；为反对称矩阵，当且仅当对任意的成立.从而反对称矩阵对角线上的元素必为零.对称矩阵具有如下性质：（1)对于任意矩阵，为阶对称矩阵；而为阶对称矩阵；（2)两个同阶（反）对称矩阵的和，仍为（反）对称矩阵；（3)如果两个同阶（反）对称矩阵可交换，即，则它们的乘积必为对称矩阵，即.运算性质：1）（2）（3）（4）（5）三、逆矩阵1.定义对于n 阶矩阵A ，如果存在n 阶矩阵B ，使得E BA AB ==．则A 称为可逆矩阵或非奇异矩阵．B 称为A 的逆矩阵，．由定义可得，A 与B 一定是同阶的，而且A 如果可逆，则A 的逆矩阵是唯一的．这是因为（反证法），如果1B 、2B 都是A 的逆矩阵，则有E A B AB ==11，E A B AB ==22，那么22212111)()(B EB B A B AB B E B B =====所以逆矩阵是唯一的．我们把矩阵A 的逆矩阵记作1-A ．逆矩阵有下列性质：（1）如果A 可逆，则1-A 也可逆，且A A =--11)(．由可逆的定义，显然有A 与1-A 是互逆的．（2）如果A 、B 是两个同阶可逆矩阵，则)(AB 也可逆，且111)(---=A B AB ．（必考重点）这是因为 E A A AEA ABB A A B AB =⋅===------111111)())((E B B EB B B A A B AB A B ====------111111)())((，所以111)(---=A B AB ．（必考重点）这个结论也可以推广到有限个可逆矩阵想乘的情形. （3）可逆矩阵A 的转置矩阵T A 也是可逆矩阵，且T T A A )()(11--=．这是因为E E A A A A T T TT===--)()(11，E E AA A A T T T T ===--)()(11所以 T TA A )()(11--=．（4）如果A 是可逆矩阵，则有11--=A A ．这是因为E AA=-1，两边取行列式有 11=⋅-A A ，所以111--==A AA ．矩阵可逆的条件（1）n 阶方阵A 可逆的充分必要条件是| A | ≠ 0（也即r （A ）= n ）；（2）n 阶方阵A 可逆的充分必要条件是A 可以通过初等变换（特别是只通过初等行（列）变换）化为n 阶单位矩阵；（3）n 阶方阵A 可逆的充分必要条件是A 可以写成一些初等矩阵的乘积；（4）n 阶方阵A 可逆的充分必要条件是A 的n 个特征值不为零；（5）对于n 阶方阵A ，若存在n 阶方阵B 使得AB = E （或BA = E ），则A 可逆，且A -1= B. 逆矩阵的有关结论及运算必考 ——求法方法1 定义法：设A 是数域P 上的一个n 阶方阵，如果存在P 上的n 阶方阵B ，使得AB = BA= E ，则称A 是可逆的，又称B 为A 的逆矩阵.当矩阵A 可逆时，逆矩阵由A 惟一确定，记为A -1.例1：设A 为n 阶矩阵，且满足22A - 3A + 5E = 0，求A -1.【解】22 2 -12A - 3A + 5E = 02A - 3A = - 5E23-A - A =E 552323A (- A - E) = - A - E = E555523A A = - A - E55∴∴∴∴可逆且方法 2 伴随矩阵法：A -1= 1|A|A*.定理n 阶矩阵A = a ij 为可逆的充分必要条件是A 非奇异.且11211122221121n n nnnn A A A A A A A A A A A -⎛⎫ ⎪ ⎪=⎪ ⎪⎝⎭其中A ij 是|A|中元素a ij 的代数余子式.矩阵112111222212n n nnnn A A A A A A A A A ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭称为矩阵A 的伴随矩阵，记作A*，于是有A -1=1|A|A*. 注 ①对于阶数较低（一般不超过3阶）或元素的代数余子式易于计算的矩阵可用此法求其逆矩阵.注意A* = （A ji ）n ×n 元素的位置及符号.特别对于2阶方阵11122122a a A a a ⎛⎫= ⎪⎝⎭，其伴随矩阵22122111*a a A a a -⎛⎫=⎪-⎝⎭,即伴随矩阵具有“主对角元素互换，次对角元素变号”的规律.②对于分块矩阵A B C D ⎛⎫⎪⎝⎭不能按上述规律求伴随矩阵.例2：已知101A=210325⎛⎫ ⎪ ⎪ ⎪--⎝⎭，求A -1.【解】 ∵| A | = 2 ≠ 0 ∴A 可逆.由已知得111213212223313233A = - 5, A = 10, A = 7A = 2, A = - 2, A = - 2A = - 1, A = 2, A = 1 ， A -1= 1|A| A* = 5115212211022511272171122⎛⎫-- ⎪--⎛⎫ ⎪⎪-=- ⎪ ⎪ ⎪ ⎪-⎝⎭- ⎪⎝⎭方法3 初等变换法：注 ①对于阶数较高（n ≥3）的矩阵，采用初等行变换法求逆矩阵一般比用伴随矩阵法简便.在用上述方法求逆矩阵时，只允许施行初等行变换.②也可以利用1E A E A -⎛⎫⎛⎫−−−−→⎪ ⎪⎝⎭⎝⎭初等列变换求得A 的逆矩阵. ③当矩阵A 可逆时，可利用求解求得A -1B 和CA -1.这一方法的优点是不需求出A 的逆矩阵和进行矩阵乘法，仅通过初等变换即求出了A -1B 或CA -1.例3：:用初等行变换求矩阵231A 013125⎛⎫⎪= ⎪ ⎪⎝⎭的逆矩阵.【解】()231100125001125001A E 01301001301001301012500123110000611212500112500101301001301001910211100166311341006631310122111001663⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎛⎫ ⎪⎛⎫⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪---⎝⎭-- ⎪⎝⎭⎛--→---⎝⎫⎪⎪⎪⎪ ⎪⎪ ⎪⎭1113410066313A 010********1663-⎛⎫--⎪ ⎪ ⎪=- ⎪ ⎪ ⎪-- ⎪⎝⎭故方法4 用分块矩阵求逆矩阵：设A 、B 分别为P 、Q 阶可逆矩阵，则：1111111111111111A A 000B 0C O A A A CB A O A O BD B O B B DA B B O A O B B O AO ----------------⎛⎫⎛⎫⎛⎫-⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭例4：已知0052002112001100A ⎛⎫⎪ ⎪=⎪-⎪⎝⎭，求A -1.【解】将A 分块如下：12005200211200110O A A A O ⎛⎫ ⎪ ⎪⎛⎫⎪== ⎪⎪⎝⎭- ⎪ ⎪⎝⎭其中 125212,2111A A -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭可求得 1*1*1122121212111,2511||||3A A A A A A ---⎛⎫⎛⎫==== ⎪ ⎪--⎝⎭⎝⎭ 从而11211120033110331200250O A A A O ---⎛⎫ ⎪ ⎪ ⎪-⎛⎫ ⎪== ⎪⎪⎝⎭ ⎪ ⎪- ⎪-⎝⎭方法5 恒等变形法求逆矩阵：有些计算命题表面上与求逆矩阵无关,但实质上只有求出矩阵的逆矩阵才能算出来,而求逆矩阵须对所给的矩阵等式恒等变形,且常变形为两矩阵的乘积等于单位矩阵的等式.例8 已知，且，试求．解由题设条件得3.伴随矩阵如果n 阶矩阵A 的行列式0≠A ,则称A 是非奇异的(或非退化的).否则,称A 是奇异的(或退化的).（n 阶矩阵A 可逆的充要条件是:|A|≠0）设n n ij a A ⨯=)(,ij A 是A 中元素)21(n j i a ij ，，，， =的代数余子式.矩阵 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n A A A A A A A A A A 212221212111*（顺序变化，重点）称为A 的伴随矩阵. 矩阵n n ij a A ⨯=)(为可逆矩阵的充分必要条件是A 为非奇异矩阵,并且当A 可逆时,有*11A AA =-，伴随矩阵例1. 已知矩阵⎪⎪⎪⎭⎫ ⎝⎛---=313132121A 判断A 是否可逆,如果可逆,求1-A .解: 因为01313132121≠=---=A ,所以A 可逆.又.13221)1(11211)1(;11312)1(71321)1(;63311)1(53112)1(;11332)1(93312)1(;83113)1(333323321331322322221221311321121111=---==-==---=-=--=-=--=-=---==--==--==---=+++++++++A A A A A A A A A所以 ⎪⎪⎪⎭⎫⎝⎛---==-1711691581*1A A A 四、分块矩阵一、分块矩阵的概念对于行数和列数较高的矩阵, 为了简化运算，经常采用分块法，使大矩阵的运算化成若干小矩阵间的运算，同时也使原矩阵的结构显得简单而清晰. 具体做法是：将大矩阵用若干条纵线和横线分成多个小矩阵. 每个小矩阵称为A 的子块, 以子块为元素的形式上的矩阵称为分块矩阵.矩阵的分块有多种方式，可根据具体需要而定注：一个矩阵也可看作以n m ⨯个元素为1阶子块的分块矩阵. 二、分块矩阵的运算分块矩阵的运算与普通矩阵的运算规则相似. 分块时要注意，运算的两矩阵按块能运算，并且参与运算的子块也能运算，即，内外都能运算.1. 设矩阵A 与B 的行数相同、列数相同，采用相同的分块法, 若,,11111111⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=st s t st s t B B B B B A A A A A其中ij A 与ij B 的行数相同、列数相同, 则.11111111⎪⎪⎪⎭⎫ ⎝⎛++++=+st st s s t t B A B A B A B A B A2.设,1111⎪⎪⎪⎭⎫ ⎝⎛=st s t A A A A Ak 为数, 则.1111⎪⎪⎪⎭⎫ ⎝⎛=st s t kA kA kA kA kA 3．设A 为l m ⨯矩阵, B 为n l ⨯矩阵, 分块成,,11111111⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=tr t r st s t B B B B B A A A A A其中pt p p A A A ,,,21 的列数分别等于tq q q B B B ,,,21 的行数, 则,1111⎪⎪⎪⎭⎫ ⎝⎛=sr s r C C C C AB 其中).,,2,1;,,2,1(1r q s p B A C t k kqpk pq ===∑=4. 分块矩阵的转置设,1111⎪⎪⎪⎭⎫ ⎝⎛=st s t A A A A A则.1111⎪⎪⎪⎪⎭⎫ ⎝⎛=T st T tT s T TA A A A A 5. 设A 为n 阶矩阵, 若A 的分块矩阵只有在对角线上有非零子块, 其余子块都为零矩阵, 且在对角线上的子块都是方阵, 即⎪⎪⎪⎪⎪⎭⎫⎝⎛=s A O A O A A21, 其中),,2,1(s i A i =都是方阵, 则称A 为分块对角矩阵.分块对角矩阵具有以下性质：(1) 若 ),,2,1(0||s i A i =≠，则0||≠A ，且|;|||||||21s A A A A =(2) .112111⎪⎪⎪⎪⎪⎭⎫⎝⎛=----s A O A O A A(3) 同结构的对角分块矩阵的和、差、积、商仍是对角分块矩阵. 且运算表现为对应子块的运算。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Ps AQ1Q2
Qt B
§2.1 矩阵的基本运算
三、矩阵的转置
定义2.3：把m×n矩阵A的行和列依次互换得到的一个 n×m 矩阵，称为A的转置，记作AT或A’.
a11 a12 a21 a22 A a m1 am 2 a1n a2 n amn
k 1
s
由这个定义可知： 1）矩阵A、B相乘的条件：矩阵A的列数=矩阵B的行数.
§2.1 矩阵的基本运算
2）矩阵C的行数等于矩阵A的行数，矩阵 C的列数等于矩阵B的列数。 3）矩阵乘法法则：乘积C的第i行第j列的元素
Cij等于矩阵A的第i行的元素与矩阵B的第j列
的对应元素乘积之和。
例2.1 设
AE(i(k))：相当于用非零数k 乘矩阵A的第i列；
AE(i,j(k))：相当于A的第i列乘k加到第j列上．
§2.1 矩阵的基本运算
推论：若m×n矩阵A与B等价，则存在若干个
m×m初等矩阵Pi(i=1,2-----,s)和若干个n×n初等矩阵Qj(j=1,2-----,t)使得
PP 1 2
a11 a12 T A a 1n
a21 am1 a22 am 2 . a2 n amn
§2.1 矩阵的基本运算
相关性质： 1. (AT)T=A
2. (A+B)T=AT+BT
3. (kA)T=kAT （k为常数） 4. (AB)T=BTAT
l 0 0 l lI 0 0 0 0 l
称为数量矩阵
§2.1 矩阵的基本运算
称矩阵(-1)A=(-aij)为矩阵A的负矩阵，记为-A．矩阵的减法：A-B=A+(-B)=(aij-bij)
矩阵的加法矩阵的线性运算数与矩阵的乘法
§2.1 矩阵的基本运算
§2.1 矩阵的基本运算
例2.1
1 2 3 设 A 0 1 5
且A-2X=B,求X
1 1 3 B 2 4 2
§2.1 矩阵的基本运算
二、矩阵的乘法 1．矩阵乘法的定义
引例某文化用品商店售圆珠笔、钢笔和铅笔三种，每种商品的进货单价和数量如下表。
§2.1 矩阵的基本运算
1 0 0 a11 a E (2(k )) A 0 k 0 21 0 0 1 a31
a12 a22 a32
a13 a23 a33
a14 a11 ka a24 21 a34 a31
为n阶方阵A的m次多项式
a1 A a0 I
0 2 2-2x+3 例2.5 设 A 且 f(x)=x 1 1
求f(A)
§2.1 矩阵的基本运算
例2.6
用数学归纳法证
l 1 0 0 l 1 0 0 l
n
ln 0 0
nl
n 1 n
§2.1 矩阵的基本运算
1 1 例2.3 设 A 1 1
求AB
1 1 B 1 1
注：⑵由AB=0一般不能得到A=0或B=0.
1 2 例2.4 设 A 2 4
求AB，AC
7 1 1 3 B C 1 2 2 1
0 0 1 0
0 1 0 0
0 a11 0 a21 0 a31 1
a13 a23 a33
a12 a22 a32
a14 a24 a34
上述过程也可以等同于：
a11 a 21 a31 a12 a22 a32 a13 a23 a33 a14 a11 a C 2 C3 a24 21 a34 a31 a13 a23 a33 a12 a22 a32 a14 a24 a34
n ( n 1) 2
l n2
n 1
l
nl
0
ln

(n为任意自然数）．
§2.1 矩阵的基本运算
线性方程组的矩阵表示
a11 x1 a12 x2 a1n xn b1 a x a x a x b 21 1 22 2 2n n 2 am1 x1 am 2 x2 amn xn bm
矩阵C与A、B之间有什么关系？
矩阵C的第i行第j列的元素等于矩阵A的第i行的元素与矩阵B的第j列的对应元素乘积之和。
§2.1 矩阵的基本运算
定义2.2 设 A=(aij) m×s ，B=(bij)s×n ，那么称 C=AB=(cij) m×n 为矩阵A与B的乘积.其中
cij aik bkj (i 1,2 m; j 1,2 n)
ka12 ka22 ka32
a13 a23 a33
a14 a24 a34
a11 AE(2,3(k )) a21 a31
a12 a22 a32
a13 a23 a33
1 a14 0 a24 0 源自 a34 00 1 0 0
0 k 1 0
系数矩阵：
A
a11 a12 a a 21 22 am1 am 2
a1n a2 n amn
§2.1 矩阵的基本运算
a11 a12 a a 21 22 am1 am 2
a1n x1 b1 a2 n x2 b2 amn xn bm
上述过程也可以等同于：
a11 a 21 a31 a12 a22 a32 a13 a23 a33 a14 a11 a r2 r3 a24 31 a34 a21 a12 a32 a22 a13 a33 a23 a14 a34 a24
§2.1 矩阵的基本运算
例2.7
1 2 T T 设A 1 3 0 , B 0 3 ; 求B A . 1 2
十月
220×6+150×9+260× 3
220×8+150×12+260×4
§2.1 矩阵的基本运算
200 100 300 A 220 150 260
定义矩阵
6 8 B 9 12 3 4
200 6 100 9 300 3 200 8 100 12 300 4 C 220 6 150 9 260 3 220 8 150 12 260 4
a12 a22 ka32 a32
a13 a23 ka33 a33
a24 ka34 a34 a14
§2.1 矩阵的基本运算
a11 AE(2,3) a21 a31
a12 a22 a32
a13 a23 a33
1 a14 0 a24 0 a34 0
即：
E(i,j)A：相当于交换A的第i行与第j行；
E(i(k))A：相当于用非零数k乘矩阵A的第i行；
E(i,j(k))A：相当于A的第j行乘k加到第i行上；
§2.1 矩阵的基本运算
同理：（2）对A施行某种初等列变换，相当于对A右乘一个相应的n阶初等矩阵.
即：
AE(i,j)：相当于交换A的第i列与第j列；
§2.1 矩阵的基本运算
a11 AE(2(k )) a21 a31
a12 a22 a32
a13 a23 a33
1 a14 0 a24 0 a34 0
0 k 0 0
0 0 1 0
0 a11 0 a21 0 a31 1
方阵的幂设A是n阶方阵，k是正整数，k个A连乘称为
A的k次幂，记作 Ak ，即
约定A0=I
Ak AA
k个
A
相关结论：
A A A
k l
k l
,(A ) A
k l
kl
其中k,l为正整数．
一般地
( AB) k Ak B k
§2.1 矩阵的基本运算
矩阵的多项式：
f ( A) am Am am1 Am1
0 a11 0 a21 0 a31 1
a12 a22 a32
a13 ka12 a23 ka22 a33 ka32
a14 a24 a34
§2.1 矩阵的基本运算
定理2.1 设Am×n= (a )m×n,则：
ij
（1）对A施行某种行初等变换，相当于对A 左乘一个相应的m阶初等矩阵.
．
AX B
§2.1 矩阵的基本运算
2. 矩阵与初等矩阵的乘积
例如：计算下列矩阵与初等阵的乘积
1 0 0 a11 a12 a13 a14 a11 a12 a13 a14 a a a a E (2,3) A 0 0 1 a a a a 21 22 23 24 31 32 33 34 0 1 0 a31 a32 a33 a34 a21 a22 a23 a24
注：⑶若AB=AC，且A≠0,则一般不能得到B=C.
§2.1 矩阵的基本运算
矩阵乘法满足的运算律： 1) (AB)C=A(BC) （结律合）
k(AB)=(kA)B=A(kB)
2) A(B+C)=AB+AC （分配律）
(B+C)A=BA+CA 3) 设Am×n，则ImA=AIn=A
§2.1 矩阵的基本运算
a12 ka22 a32
a13 ka23 a33
a14 ka24 a34
1 0 0 a11 a E (2,3(k )) A 0 1 k 21 0 0 1 a31