算法流程图
算法流程图举例_课件
S←1,i←12
i←i-1
N
输出S
S←S×i
Y
结束
12.以下给出的是计算1/2+1/4+1/6+…+1/20的值的一个流程图, 判断框内应填入的条件为___.
开始 S←0,n←2,i←1
i←i+1 n←n+2 S←S+1/n
N Y 输出S 结束
13.下图流程图是计算1+1/3+1/5+…+1/99的流程图,请你补充完整. 开始
开始 x ← 1,S ← 0
x≤5 Nቤተ መጻሕፍቲ ባይዱ输出S
x←x+1 S←S+x2 Y
结束
5.如图所示的流程图输出的第2013个数为_1_0__0_7___.
开始 A←1,N←1
输出A N←N+1
N≤5000 N 结束
A←A+1/2 Y
6.下图所示流程图输入n=7,输出的结果为 13 .
开始 输入n A←1,B←1,K←3
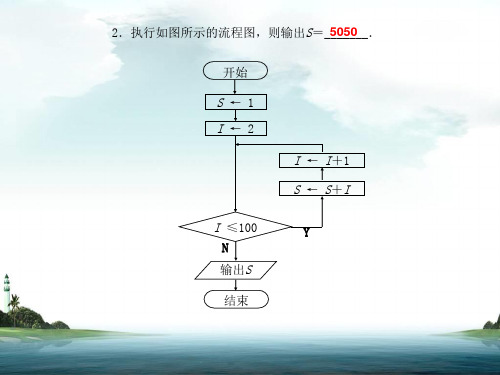
2.执行如图所示的流程图,则输出S=_5_0__5_0__.
开始 S←1 I←2
I ← I+1 S ← S+I
I ≤100
Y
N
输出S
结束
3.下图所示的流程图的输出结果为2_5__6_. 开始 p←0
i←1
p ← p+i
i ← i+2
i>31
N
Y
输出p
结束
4.下图所示的流程图的输出结果为_5_5__.
开始 i←1,m←0,T←0
输入x x>80 N
Y 输出x
T←T+x m←m+1
i←i+1
N
i>15
Y
P←T/m
输出P 结束
9.如下流程图,循环体执行的次数为 ( )
开始
算法流程图(循环结构)

i) 顺序结构
三种基本算法结构
ii) 选择结构
Y A B A
p
N B
循环结构
算法2流程图:
算法2:
开始 T←1
S1
S2
T←1;
S←2;
S←2
T←T×S S←S+1 S>5 Y 输出T 结束 N
S3
S4 S5
T←T×S;
S←S+1; 如果S不大于5,返 回 S3,否则输出T。
开始
开始
i ← 0,Sum ← 0
2010辽宁文数如果执行下图左的程序框图输入那么输出的等于a720b360c240d12010aa1b2b1输出b结束缚目录点击添加标题点击添加标题点击添加标题点击添加标题添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本01020304添加标添加文本点击添加文本点击添加文本点击添加文本点击添加文本会议基调年会视频
开始 Sum←0,i←1 Sum←Sum+1 i←i+1 否 i>100 是 输出Sum 结束
1.【2010· 浙江理数】 某程序框图如左图所 示,若输出的S=57, 则判断框内位( ) A. k>4? B.k>5? C. k>6? D.k>7?
2.【2010· 辽宁文数】 如果执行下图(左)的 程序框图,输入 n 6 , m 4那么输出的 等于( ) A.720 B.360 C.240 D.120
算法与程序框图(算法流程图)

程序框图的发展趋势
可视化编程
随着可视化技术的发展,程序框 图成为一种直观的编程方式。通 过图形化的方式描述程序逻辑, 降低了编程难度,提高了开发效 率。
交互式编程
交互式编程让用户在编程过程中 能够实时查看程序运行结果,及 时调整代码。这种编程方式提高 了开发效率和程序质量。
智能生成与自动优
化
基于机器学习和人工智能技术, 程序框图可以自动生成和优化程 序代码。这大大减少了编程工作 量,提高了开发效率。
算法的复杂度分析
随着计算机科学的发展,算法的复杂度分析越来越受到重 视。人们不断探索更高效的算法,以提高计算效率和准确 性。
机器学习与人工智能算法
随着人工智能的兴起,机器学习与人工智能算法成为研究 热点。这些算法能够从大量数据中自动提取有用的信息, 为决策提供支持。
并行计算与分布式算法
为了处理大规模数据和复杂问题,并行计算和分布式算法 成为研究重点。这些算法能够充分利用多核处理器和分布 式系统的优势,提高计算性能。
算法的表示方法
01
自然语言描述
用简洁明了的文字描述算法的步骤。
流程图
用图形符号表示算法的步骤和流程。
03
02
伪代码
用类似于编程语言的简化和结构化 形式描述算法。
程序代码
用编程语言实现算法的具体代码。
04
算法的复杂度分析
时间复杂度
评估算法执行时间随输入规 模增长的情况,表示为 O(f(n))。
空间复杂度
选择结构是根据条件判断选择不同的执行路径的程序框图 结构。它使用判断框来表示条件判断,根据条件的结果选 择不同的执行路径。选择结构可以有效地处理具有多个分 支的情况,提高程序的灵活性和适应性。
算法流程图的定义

算法流程图的定义An algorithm flowchart is a visual representation of the step-by-step process involved in solving a problem or completing a task. In computer science, these flowcharts help programmers and designers plan and organize their code in a clear and structured manner. By breaking down complex algorithms into simple, sequential steps, flowcharts make it easier to understand and optimize the logic behind the solution.算法流程图是解决问题或完成任务所涉及的逐步过程的视觉表示。
在计算机科学中,这些流程图帮助程序员和设计者以清晰和结构化的方式规划和组织他们的代码。
通过将复杂算法分解为简单的顺序步骤,流程图使得更容易理解和优化解决方案的逻辑。
When creating an algorithm flowchart, it is important to start with a clear understanding of the problem at hand. This involves breaking down the problem into smaller, more manageable components and identifying the specific inputs, processes, and outputs involved. By clearly defining these elements, you can create a roadmap for howthe algorithm will function and the steps needed to achieve the desired outcome.在创建算法流程图时,重要的是要先清楚地了解手头问题。
算法流程图

简介
计算机语言只是一种工具。光学习语言的规则还不够,最重要的是学会针对各种类型的问题,拟定出有效的 解决方法和步骤即算法。有了正确而有效的算法,可以利用任何一种计算机高级语言编写程序,使计算机进行工 作。因此,设计算法是程序设计的核心。为了表示一个算法,可以用不同的方法。常用的有自然语言,流程图, 伪代码,PAD图等。这其中以特定的图形符号加上说明,表示算法的图,称为算法流程图。
传统的流程图用流程线指出各框的执行顺序,对流程线的使用没有严格限制。因此,使用者可以毫不受限制 地使流程随意地转来转去,使流程图变得毫无规律,阅读者要花很大精力去追踪流程,使人难以理解算法的逻辑。 如果我们写出的算法能限制流程的无规律任意转向,而像一本书那样,由各章各节顺序组成,那样,阅读起来就 很方便,不会有任何困难,只需从头到尾顺序地看下去即可。
为了提高算法的质量,使算法的设计和阅读方便,必须限制箭头的滥用,即不允许无规律地使流程乱转向, 只能按顺序地进行下去。但是,算法上难免会包含一些分支和循环,而不可能全部由一个一个框顺序组成。如上 例不是由各框顺序进行的,包含一些流程的向前或向后的非顺序转移。为了解决这个问题,人们设想,如果规定 出几种基本结构,然后由这些基本结构按一定规律组成一个算法结构,整个算法的结构是由上而下地将各个基本 结构顺序排列起来的。1966年,Bohra和Jacoplni提出了以下三种基本结构,用这三种基本结构作为表示一个良 好算法的基本单元。
1、顺序结构:如图2所示的虚线框内,A和B两个框是顺序执行的。顺序结构是最简单的一种基本结构。
图2
2、选择结构:如图3所示的虚线框中包含一个判断框。
结构流程图
1973年美国学者提出了一种新的流程图形式。在这种流程图6中,完全去掉了带箭头的流程线。全部算法写 在一个矩形框内。在该框内还可以包含其它的从属于它的框,即可由一些基本的框组成一个大的框。这种适于结 构化程序设计的流程图称N-S结构化流程图,它用以下的流程图符号:
算法流程图
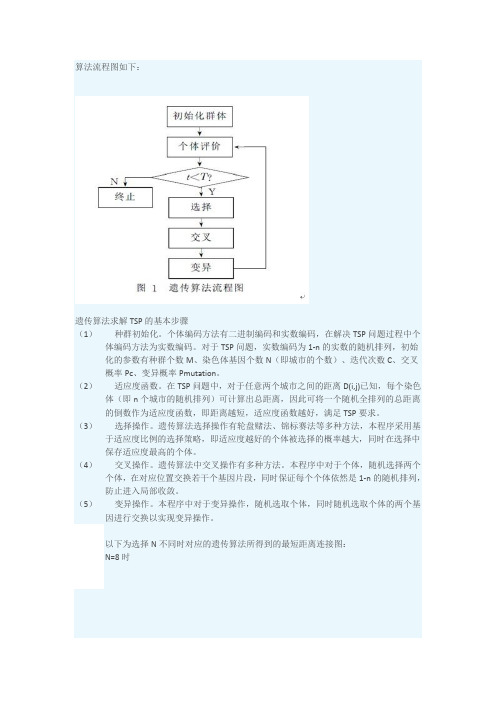
算法流程图如下:遗传算法求解TSP的基本步骤(1)种群初始化。
个体编码方法有二进制编码和实数编码,在解决TSP问题过程中个体编码方法为实数编码。
对于TSP问题,实数编码为1-n的实数的随机排列,初始化的参数有种群个数M、染色体基因个数N(即城市的个数)、迭代次数C、交叉概率Pc、变异概率Pmutation。
(2)适应度函数。
在TSP问题中,对于任意两个城市之间的距离D(i,j)已知,每个染色体(即n个城市的随机排列)可计算出总距离,因此可将一个随机全排列的总距离的倒数作为适应度函数,即距离越短,适应度函数越好,满足TSP要求。
(3)选择操作。
遗传算法选择操作有轮盘赌法、锦标赛法等多种方法,本程序采用基于适应度比例的选择策略,即适应度越好的个体被选择的概率越大,同时在选择中保存适应度最高的个体。
(4)交叉操作。
遗传算法中交叉操作有多种方法。
本程序中对于个体,随机选择两个个体,在对应位置交换若干个基因片段,同时保证每个个体依然是1-n的随机排列,防止进入局部收敛。
(5)变异操作。
本程序中对于变异操作,随机选取个体,同时随机选取个体的两个基因进行交换以实现变异操作。
以下为选择N不同时对应的遗传算法所得到的最短距离连接图:N=8时MATLAB实现程序如下:初始化的参数有种群个数M、染色体基因个数N(即城市的个数)、迭代次数C、交叉概率Pc、变异概率Pmutation。
(1)适应度函数fit.mfunction fitness=fit(len,m,maxlen,minlen)fitness=len;for i=1:length(len)fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;end(2)个体距离计算函数 mylength.mfunction len=myLength(D,p)[N,NN]=size(D);len=D(p(1,N),p(1,1));for i=1:(N-1)len=len+D(p(1,i),p(1,i+1));endend(3)交叉操作函数 cross.mfunction [A,B]=cross(A,B)L=length(A);if L<10W=L;else if ((L/10)-floor(L/10))>=rand&&L>10%%%Matlab取整函数有: fix, floor, ceil, round.具体应用方法如下:fix朝零方向取整,如fix(-1.3)=-1; fix(1.3)=1;floor,顾名思义,就是地板,所以是取比它小的整数,即朝负无穷方向取整,如floor(-1.3)=-2; floor(1.3)=1;floor(-1.8)=-2,floor(1.8)=1ceil,与floor相反,它的意思是天花板,也就是取比它大的最小整数,即朝正无穷方向取整,如ceil(-1.3)=-1; ceil(1.3)=2;ceil(-1.8)=-1,ceil(1.8)=2round四舍五入到最近的整数,如round(-1.3)=-1;round(-1.52)=-2;round(1.3)=1;round(1.52)=2。
算法流程图的三种基本结构

算法流程图的三种基本结构
算法流程图是软件开发中非常重要的一部分,它能够清晰地展现出程序的执行
流程,帮助开发人员更好地理解和调试代码。
在算法流程图中,有三种基本的结构,它们分别是顺序结构、选择结构和循环结构。
首先,顺序结构是最简单的一种结构,它表示程序按照从上到下的顺序依次执
行各个操作。
在算法流程图中,顺序结构通常用矩形框表示,框内包含了具体的操作步骤,每个步骤都按照一定的顺序执行。
这种结构清晰明了,直观易懂,能够很好地展现出程序的执行流程。
其次,选择结构是根据某个条件的成立与否,决定程序的执行路径。
在算法流
程图中,选择结构通常用菱形框表示,菱形框内包含了条件判断的具体内容,根据条件的成立与否,程序会选择不同的执行路径。
这种结构能够很好地展现出程序的分支逻辑,帮助开发人员理清程序的执行流程。
最后,循环结构是根据某个条件的成立与否,重复执行某段代码。
在算法流程
图中,循环结构通常用圆角矩形框表示,圆角矩形框内包含了需要重复执行的代码段,同时也包含了条件判断的具体内容。
这种结构能够很好地展现出程序的循环执行逻辑,帮助开发人员理清程序的重复执行流程。
综上所述,算法流程图的三种基本结构分别是顺序结构、选择结构和循环结构。
它们分别代表了程序按照顺序执行、根据条件选择执行路径以及重复执行某段代码的逻辑。
这三种结构在算法流程图中起着非常重要的作用,能够很好地帮助开发人员理清程序的执行流程,从而更好地理解和调试代码。
在实际的软件开发中,合理运用这三种结构,能够编写出结构清晰、逻辑严谨的程序,提高代码的可读性和可维护性。
算法流程图

【范例8-4】 求区间[100, 200]内10 个随机整数中的最大数、最小数。
输出max,min 结束
用传统流程图表示三种基本结构
1、顺序结构
A
2、选择结构
不成立 条件? A B 成立
B
用传统流程图表示三种基本结构
3、循环结构
A
不成立 条件? 成立
A条件?成立不成立当型循环
直到型循环
开始 输入n的值
流程图的基础
流程图的绘制
流程图中的元素及含义
流程图主要用两种:传统流程图和N-S流程图。 1.传统流程图
起止框
输入/输出框
处理框
判断框
流程线
连接符
2、N-S流程图
P成立? A A B A B 是 否 当P成立 A A 当P成立
处理
顺序结构元素
选择结构元素
当型循环结构元素
直到型循环结构元素
流程图的绘制
2. 将1到100之间 能用3或5整 除的数打印 出来。
开始
i赋初值为1 N
i<=100?
Y
i赋初值为1 i<=100?
N
i能被3或5整 除? Y
i能被3或5整 除? T 打印i i++
用N-S图表示
F
打印i
i++ 结束 用流程图表示
1.使用word自带的流程图绘图工具 2、使用Visio绘制工具
如何表示一个算法
用自然语言表示算法 用流程图表示算法 用传统流程图表示三种基本结构 用N-S图表示算法
用伪代码表示算法
用计算机语言表示算法
用流程图表示算法
流程图相对于自然语言来说更直观形象,易于理解简洁 直观。 一个流程图包括以下几部分:
算法流程图

. 算法的表示
可以用不同的方法表示算法,常用的有: 自然语言 传统流程图 结构化流程图 伪代码 PAD图
. 用流程图表示算法
美国国家标准化协会ANSI(American National Standard Institute)规定了一些常用的流程图 符号:
起止框
判断框
处理框
输入/输出框
总结:
两种流程图主要区别在于:N-S流程图完全
去掉了传统流程图的带箭头的流程线,比文 字描述直观、形象、 易于理解;比传统流程 图紧凑易画。而只能至上而下有序地运行, 避开了传统流程图运行的跳转。但是,两种 流程图都有确定性、有穷性、有效性。
Thank You !
Everyone !
N-S流程图用以下的流程图符号:
(1)顺序结构. (2)选择结构.
(3)循环结构.
用三种N-S流程图中的基本框,可以组成复杂 的N-S流程图。图中的A框或B框,可以是一个简 单的操作,也可以是三个基本结构之一。
A框可以是一个选择结构
B框可以是一个循环结构
例2.13 判定 闰年的算 法 将例2.3用 N-S图表 示
注释框
流向线
连接点
2.三种基本结构
Bohra和Jacopini提出了以下三种基本 结构:
顺序结构、选择结构、循环结构 用这三种基本结构作为表示一个良好算 法的基本单元。
三种基本结构的图示:
顺序结构
选择结构
循环结构的图示:
当型(While型)循环结构
直到型(Until型)循环
例2.8 将例 2.3判定闰年 的算法用流 程图表示
不正确的流程表示:
图中没有一条从入口到 出口的路径通过A框
算法初步 §13.1 流程图

算法初步§13.1 流程图一、知识导学1.流程图:是由一些图框和带箭头的流线组成的,其中图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流线表示操作的先后次序.2.算法的三种基本的逻辑结构:顺序结构、条件结构、循环结构.3.根据对条件的不同处理,循环结构又分为两种:直到型(until型)循环:在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体.满足则停止.如图13-1-3,先执行A框,再判断给定的条件是否为“假”,若为“假”,则再执行A,如此反复,直到为“真”为止.当型(while型)循环:在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止.如图13-1-4,当给定的条件成立(“真”)时,反复执行A 框操作,直到条件为“假”时才停止循环.图13-1-1 图13-1-2二、疑难知识导析1.“算法“没有一个精确化的定义,教科书只对它作了描述性说明,算法具有如下特点:(1)有限性:一个算法的步骤是有限的,必须在有限操作之后停止,不能是无限的.(2)确定性:算法的每一步骤和次序应当是确定的.(3)有效性:算法的每一步骤都必须是有效的.2. 画流程图时必须注意以下几方面:(1)使用标准的图形符号.(2)流程图一般按从上到下、从左到右的方向画.(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.(4)判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.(5)在图形符号内描述的语言要非常简练清楚.3. 算法三种逻辑结构的几点说明:(1)顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.在流程图中的体现就是用流程线自上而下地连接起来,按顺序执行算法步骤.(2)一个条件结构可以有多个判断框.(3)循环结构要在某个条件下终止循环,这就需要条件结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用语输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次.三、经典例题导讲[例1]已知三个单元存放了变量,,的值,试给出一个算法,顺次交换,,的值(即取的值,取的值,取的值),并画出流程图.正解:第一步{先将的值赋给变量,这时存放的单元可作它用}第二步{再将的值赋给,这时存放的单元可作它用}第三步{同样将的值赋给,这时存放的单元可作它用}第四步{最后将的值赋给,三个变量,,的值就完成了交换}流程图为图13-1-4点评:在计算机中,每个变量都分配了一个存储单元,为了达到交换的目的,需要一个单元存放中间变量.[例2]已知三个数,,.试给出寻找这三个数中最大的一个算法,画出该算法的流程图. 解:流程图为图13-1-5点评:条件结构可含有多个判断框,判断框内的内容要简明、准确、清晰.此题也可将第一个判断框中的两个条件分别用两个判断框表示,两两比较也很清晰.若改为求100个数中的最大数或最小数的问题则选择此法较繁琐,可采用假设第一数最大(最小)将第一个数与后面的数依依比较,若后面的数较大(较小),则进行交换,最终第一个数即为最大(最小)值.点评:求和时根据过程的类同性可用循环结构来实现,而不用顺序结构.[例3]画出求的值的算法流程图.解:这是一个求和问题,可采用循环结构实现设计算法,但要注意奇数项为正号,偶数项为负号.思路一:采用-1的奇偶次方(利用循环变量)来解决正负符号问题;图13-1-6 图13-1-7思路二:采用选择结构分奇偶项求和;图13-1-8思路三:可先将化简成,转化为一个等差数列求和问题,易利用循环结构求出结果.[例4]设计一算法,求使成立的最小正整数的值.解:流程图为图13-1-9点评:这道题仍然是考察求和的循环结构的运用问题,需要强调的是求和语句的表示方法.若将题改为求使成立的最大正整数的值时,则需注意的是输出的值.[例5]任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判断.解:算法为:S1 判断n是否等于2,若n=2,则n是质数;若n>2,则执行S2S2 依次从2~n-1检验是不是的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数.点评:要验证是否为质数首先必须对质数的本质含义作深入分析:(1)质数是只能被1和自身整除的大于1的整数.(2)要判断一个大于1的整数n是否为质数,只要根据定义,用比这个整数小的数去除n.如果它只能被1和本身整除,而不能被其它整数整除,则这个数便是质数.图13-1-10[例6]设计一个求无理数的近似值的算法.分析:无理数的近似值可看作是方程的正的近似根,因此该算法的实质是设计一个求方程的近似根的算法.其基本方法即运用二分法求解方程的近似解. 解:设所求近似根与精确解的差的绝对值不超过0.005,算法:S1 令.因为,所以设S2 令,判断是否为0,若是,则m为所求;若否,则继续判断大于0还是小于0.S3 若>0,则;否则,令.S4 判断是否成立,若是,则之间的任意值均为满足条件的近似根;若否,则返回第二步.点评:二分法求方程近似解的算法是一个重要的算法案例,将在第三节中详细阐述.四、典型习题导练1.已知两个单元分别存放了变量和的值,则可以实现变量交换的算法是(). A.S1 B.S1 C.S1 D.S1S2 S2 S2 S2 S3 S32.下面流程图中的错误是()图13-1-11A.没有赋值B.循环结构有错C.S的计算不对 D.判断条件不成立3.将“打电话”的过程描述成一个算法,这个算法可表示为,由此说明算法具有下列特性 .4. 在表示求直线(,为常数,且,不同时为0)的斜率的算法的流程图中,判断框中应填入的内容是5. 3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的流程图.6.一队士兵来到一条有鳄鱼的深河的左岸.只有一条小船和两个小孩,这条船只能承载两个小孩或一个士兵.试设计一个算法,将这队士兵渡到对岸,并将这个算法用流程图表示.。
算法流程图

1.输人一个数到变.., 输出它的绝对值。
(要求用单分支和双分支结构分别设计算法)单分支结构算法:
(1)输入任意数并赋值给变量a;
(2)判断a是否小于0, 如果a 小于0 , 取a 的相反数;
(3)输出a。
双分支结构算法:
(1)输人任意数并赋值给变量 a ;
(2)判断a 是否小于0 , 如果a 小于0 则输出a 的相反数, 否则输出a 。
(3)求输入的十个数中的最大值。
2.最值问题:
(1)求输人的两个数中的最大值。
(2)求输人的三个数中的最大值。
3.循环求和(不同的控制循环方法)
1.求输.
2.个数的和。
(知道循环次数, 可以采用循环变量i 来控制循环次数)
计数法2.求输入的若干个学生成绩
的和, 输.-1表示结束。
(不能确定次数, 可以用输
入的数据的值来进行控制)
标志法
3.对输入的数据求和, 当所求
的和超.10.则停止输入并输出
求和结果(设此题中输人的数
皆为正数)。
(没有指出输人数据的具体个
数, 且不能依据对输入数据的
值来控制循环, 控制循环的关
键就在于对循环体中变量s
的判断)
(没有指出输人数据的具体个
数,且不能依据对输入数据的
值来控制循环,控制循环的关
键就在于对循环体中变量s
的判断)
输出如下图形:
**********
**********
**********
**********
**********
如下算法能输出哪种图形?(A)。
算法流程图(循环结构)

目录
• 循环结构的概述 • 循环流程图的绘制 • 常见的循环结构算法 • 循环结构的应用场景 • 循环结构的注意事项 • 案例分析
01
循环结构的概述
循环结构的定义
循环结构是算法流程图中的一种基本结构,用于 01 重复执行一段代码,直到满足某个条件为止。
循环结构由三个基本部分组成:初始化、循环体 02 和终止条件。
详细描述
在for循环中,首先定义一个计数器变量和循环次数,然后在每次循 环中执行指定的操作,直到计数器达到设定的循环次数为止。
示例
以下是一个简单的for循环算法,用于计算1到10的累加和
for循环算法
```
sum = sum + i
for i = 1 to 10 do
for循环算法
end for ```
VS
详细描述
for循环通常用于已知循环次数的情况, 它包含三个基本部分:初始化、条件和后 续操作。在流程图中,for循环通常以矩 形表示,并在其中标明循环变量、初始值 、条件表达式和增量。例如,计算1到10 的累加和可以使用以下for循环实现
for循环的案例分析
```
for (int i = 1; i <= 10; i) {
控制条件的绘制
01 绘制一个菱形,标注为“条件”,表示循环的控
制条件。
02
在条件菱形内标注判断的具体内容,如“i<10” 。
循环次数的表示
使用一个数字标注在控制条件旁边,表示循环的 次数。
如果循环次数是动态变化的,可以使用变量代替 数字,如“n”。
03
常见的循环结构算法
for循环算法
总结词
for循环是一种预先设定循环次数的循环结构,通常用于已知循环次 数的情况。
算法流程图(附答案)
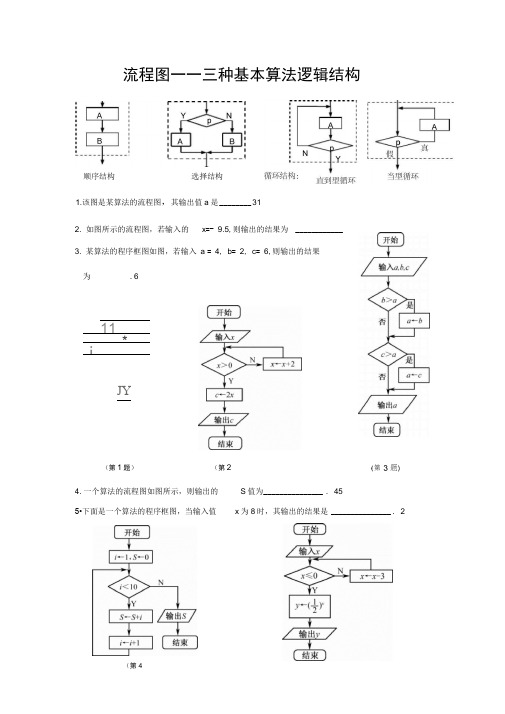
1.该图是某算法的流程图,其输出值a是________ 312. 如图所示的流程图,若输入的x=- 9.5,则输出的结果为 ____________3. 某算法的程序框图如图,若输入a = 4, b= 2, c= 6,则输出的结果为.611*iJY(第1题)4. 一个算法的流程图如图所示,则输出的5•下面是一个算法的程序框图,当输入值S值为_______________ . 45x为8时,其输出的结果是_______________ . 2流程图一一三种基本算法逻辑结构顺序结构选择结构(第2题)(第4题)6. 运行如图所示的程序框图,则输出的结果 S = ___________ . 617. 如图所示的算法流程框图中, 若输入a = 4,b = 48,则最后输出的a 的值是 ________________ .96 8. 如图,程序执行后输出的结果为 _________ 6410.阅读下面的流程图,若输入______________a = 10, b = 6,则输出的结果是 211. _____________________________________________ 右图是一个算法的流程图,则输出 S 的值是 _________________________________________________ 7500开始/输出P/ 卩/9•按如图所示的流程图运算 ,则输出的S 二 _________20 (第6题)(第7题)I —12. ___________________________________________ 右图是一个算法的流•程图,最后输出的k= _________________ . 1113•阅读右边的流程图,则输出S= ________ . 3015、图中是一个算法流程图,则输出的n= ______ 1116. 右图是一个算法的流程图,最后输出的x= ________ .-1017.执行右边的程序框图,若p =15,则输出的n二fT-li S^-0(第16题)5/输入/n=l,S=0沪針严/5丽7ZE~~TM=n+1 [结束](第15题)(第17题))如图所示,其输出结果是127开始(第14 题)结束14•程序框图(即算法流程图(第12题)(第13题)c-2cr+'l/输出口/18. 根据如图所示的算法流程图,可知输出的结果i为______________ .719. 右图是一个算法的流程图,最后输出的n = ____________ .10020. 右图是一个算法的流程图,则输出a的值是_____________. log2321. 已知某算法的流程图如图所示,若将输出的数组(x, y)依次记为(X1, y1), (X2, y2),…, (X n, y n),…,则程序运行结束时输出的最后一个数组为22. _________________________________ 如图,该程序运行后输出的结果为______________________________ 1623•执行右边的程序框图,若p= 9,则输出的s= _(第19题)(第18题)(开始〕1 rm2托(第20题)(第22 题)—• (27,—6)2.5苏州市第六中学2014数学必修三(算法)。
算法流程图的基本结构及优化原则

用于算法的学习和交流。
算法流程图的基本元素
处理步骤
表示算法中的各个处理步骤,通常用矩形表示。
判断/决策
表示算法中的判断或决策点,通常用菱形表示。
开始/结束
表示算法的起点和终点,通常用椭圆形表示。
算法流程图的基本元素
流程线:用来连接各个元素,表示算法的执行顺序。
以上这些基本元素,通过合理的组织和连接,可以构建出复杂算法的流程图,从而帮助我们更好地理 解和分析算法。在实际应用中,绘制算法流程图时,还需要遵循一些优化原则,如简化流程、减少冗 余步骤、提高流程线的清晰度和可读性等,以便更好地发挥流程图的作用。
以上三种基本结构是构成算法流程图 的核心元素,理解和掌握这些结构对 于绘制和理解算法流程图至关重要。 同时,在实际应用中,我们还需要遵 循一些优化原则,使得流程图更加清 晰、简洁和高效。
03
CATALOGUE
算法流程图的优化原则
简化流程
精简步骤
在流程图中尽量减少不必要的步骤和环节,突 出核心处理逻辑。
定义
选择结构用于描述算法中的决策点,根据条 件判断结果,选择执行不同的分支。
描述
在选择结构中,通常会有一个或多个判断条 件,每个条件对应一个或多个执行分支。根 据判断条件的真假,选择执行相应的分支, 直到某个分支执行完毕,然后将控制权转移 到后续步骤。这种结构常用于描述需要根据 不同情况执行不同操作的算法。
清晰明确
通过简洁明了的符号和连线,算法流程图能够明确地表达算法的逻辑和步骤。
算法流程图的作用
算法理解
01
流程图能够帮助人们更好地理解算法的逻辑和流程,
提高算法的可读性。
算法设计
02 在算法设计过程中,流程图可以帮助设计师更好地组
经典流程图
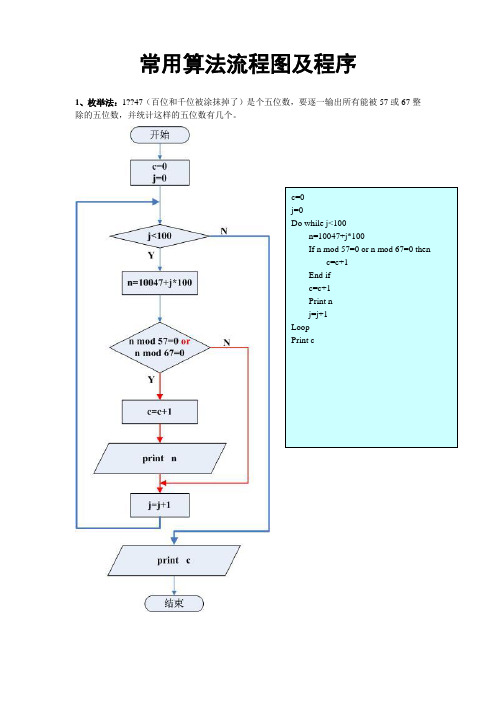
常用算法流程图及程序
1、枚举法:1??47(百位和千位被涂抹掉了)是个五位数,要逐一输出所有能被57或67整除的五位数,并统计这样的五位数有几个。
2、枚举法:1? 4?7(十位和千位被涂抹掉了)是个五位数,要逐一输出所有能被57或67整除的五位数。
3、枚举法:逐一输出所有3位数水仙花数(即个位数3+十位数3+百位数 3 =
这个数)
4、枚举法:百鸡百钱问题:100元买100只鸡(三种鸡,5元一只公鸡,3元一只母鸡,1元三只小鸡),输出每一种买法的各种鸡的数量。
5、枚举法:输出1000以内的所有的素数之和
6、冒泡排序:对十个数按非递减方式(即升序)冒泡排序,并输出排序后的这十个数。
其中i 是外循环变量,用来控制需要进行多少次处理,j 是内循环变量,用来控制每次处理需要进行多少次的俩俩比较。
7、顺序查找:100个数中顺序查找key,如找到则输出是第几个元素,否则输出0(如果输出0的话,表示没找到)。
8、对分查找:100个数(必须事先排好序)中对分查找key,如找到则输出是第几个元素,否则输出0(如果输出0的话,表示没找到)。
i 是用来表示对分查找的起点变量,j是用来表示对分查找的终点变量。
数值分析各算法流程图

01,,n1,,n1,,)n x及数值分析各算法流程图一、插值1、 拉格朗日插值流程图:( 相应程序:lagrintp(x,y,xx))2,,n ,,j n 1,2,,n 1,,)n 2、 牛顿插值流程图(1)产生差商表的算法流程图(相应程序:divdiff(x,y))注:1、另一程序divdiff1(x,y),输出的矩阵包含了节点向量。
而divdiff(x,y)不含节点向量。
2、另一程序tableofdd(x,y,m),输出的是表格形式,添加了表头。
1,,),,n m 及1,,m (2)非等距节点的牛顿插值流程图(相应程序:newtint11(x,y,xx,m)) 、注:1、虽然程序newtint11(x,y,xx,m)考虑了多种情形,看上去很复杂,但基本流程结构还是如上图所示。
2、程序中调用的子程序是divdiff 。
若调用的子程序是divdiff1的话,流程图中的第三,第四,第五步要相应的改一下数字。
2,3,,1m +1,,j1,2,,n=1,2,,)n m 及(3)求差分表的流程图(相应程序:difference(y,m))注:1、difference 输出的是矩阵D 。
而另一程序tableofd(y,m),输出的是带有表头的差分表。
n x m1,,),,1,,m注:1、程序newtforward1(x,y,xx,m))的结构与上述流程图一致,xx可以是数组。
2、另一程序newtforward(x,y,xx,m))先求出插值多项式,再求插值多项式在插值点的函数值。
基本结构还是和上面的流程图一样。
n x m1,,),,-x x1,,m注:1、程序newtbackward1(x,y,xx,m))的结构与上述流程图一致,xx可以是数组。
2、另一程序newtbackward(x,y,xx,m))先求出插值多项式,再求插值多项式在插值点的函数值。
基本结构还是和上面的流程图一样。
1,2,,n1,2,,n ,2,,)n x及3、Hermite 插值流程图(1) 已知条件中一阶导数的个数与插值节点的个数相等时的Hermite 插值流程图。
算法流程图学习方法

算法流程图学习方法Learning the algorithm flowchart can be a challenging but crucial aspect for students studying computer science. 算法流程图是计算机科学学生学习的一个具有挑战性但至关重要的方面。
Understanding and effectively implementing algorithm flowcharts is essential in developing problem-solving skills and mastering the art of programming. 理解和有效地实施算法流程图对于培养解决问题的能力和掌握编程艺术至关重要。
There are several methods for learning algorithm flowcharts, and each individual may find a different approach more helpful. 学习算法流程图有几种方法,每个人可能会发现不同的方法更有帮助。
In this article, we will explore some effective ways to learn algorithm flowcharts and provide insights into the importance of this skill in the field of computer science. 在本文中,我们将探讨学习算法流程图的一些有效方法,并提供关于这种技能在计算机科学领域中的重要性的见解。
One of the most basic yet effective ways to learn algorithm flowcharts is through visual representation. 通过视觉表现学习算法流程图是一种最基本但有效的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 输人一个数到变量 a ,输出它的绝对值。
(要求用单分支和双分支结构分别设计算法) 单分支结构算法:
(1) 输入任意数并赋值给变量 a ;
(2) 判断a 是否小于0,如果a 小于0 ,取a 的相反数; (3) 输出a 。
双分支结构算法:
(1) 输人任意数并赋值给变量 a ;
(2) 判断a 是否小于0,如果a 小于0则输出a 的相反数,否则输出 a 。
2. 最值问题:
max-x, i —1
i -i+1
/输出乜/
/ 输出
a /
单分支结构算法流程图
双分支结构算法流程医
(1 )求输人的两个数中的最大值。
(开始T
(3)求输入的十个数中的最大值。
「开始
J x 7 /输応
'」/输出b /
■ /输躬
]
(2 )求输人的三个数中的最大值。
3.循环求和(不同的控制循环方法)
1.求输人20个数的和。
(知道循环次数,可以采用循环变量i来控制循环次数)
计数法
3.对输入的数据求和,当所求的和超过100则停止输入并
输出求和结果(设此题中输人的
数皆为正数)。
(没有指出输人数据的具体个
数,且不能依据对输入数据的值
来控制循环,控制循环的关键就
在于对循环体中变量s
的判断)
2.求输入的若干个学生成绩
的和,输入-1表示结束。
(不能确定次数,可以用
输入的数据的值来进行控
标志法
输出a / / 输呼〃箱単b / / 輸匹
输出如下图形:
**********
**********
**********
**********
**********
A,o・o・o・o・
o・ o«o»o»oeo> o»o»o«o»o> o・o・o・o・o・ o ・o・o・o・o・B•o«o»o»c»o •©•o«oeo»o •o ・o・o・o・o •o ・o・o・o・o •o ・o・o・o・o c.・o・o・o・o・o o・o・o・o・o・•o・o・o・o ・o o*o»o«o»o«•oeoooeoeo a o ・o・o・o・o・•o・o・o・o・o
•o»o«o*o»o
o«o*oeo>o«。
