高等数学上机实验报告模板

合集下载

数值分析上机实验报告3

实验报告三题目：函数逼近——曲线拟合目的：掌握曲线拟合基本使用方法数学原理：[P,S]=polyfit(x,y,3)其中x，y为取样值，3为得出的结果的最高次数。

P为对应次数的系数，S为误差值向量，其中x,y是等长的向量，P是一个长度为m+1的向量。

结果分析和讨论：23.观察物体的运动，得出时间t与距离s的关系如表，求运动方程。

t=[0,0.9,1.9,3.0,3.9,5.0];s=[0,10,30,50,80,110];[P,S]=polyfit(t,s,5)P =-0.5432 6.4647 -26.5609 46.1436 -13.2601 -0.0000S =R: [6x6 double]df: 0normr: 1.2579e-012所以得到方程为：-13.2601x46.1436x-26.5609x6.4647x-0.5432x2345++24.在某化学反应堆里，根据实验所得分解物的质量分数y与时间t的关系，用最小拟合求y=F（t）；>> x=0:5:55;y=[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.62,4.64];>> [P,S]=polyfit(x,y,5)P =0.0000 -0.0000 0.0002 -0.0084 0.2851 0.0082S =R: [6x6 double]df: 6normr: 0.0487所以得到方程为：0082.02851.00084.00002.023++-xxx结论：在23题中计算的结果误差为4.5769，而在24中计算的结果误差为0.0487，说明对于曲线拟合来说，总会有误差，因为取样点并不是都过拟合的曲线的。

线代上机实验报告(3篇)

第1篇一、实验目的1. 掌握线性代数基本概念和基本运算方法。

2. 熟悉MATLAB软件在解决线性代数问题中的应用。

3. 提高实际操作能力和编程能力。

二、实验环境1. 操作系统：Windows 102. 软件环境：MATLAB R2019b3. 实验设备：计算机三、实验内容1. 矩阵的基本运算2. 矩阵的秩3. 矩阵的逆4. 线性方程组的求解5. 特征值和特征向量6. 二次型及其标准形四、实验步骤1. 矩阵的基本运算（1）创建矩阵A：A = [1, 2, 3; 4, 5, 6; 7, 8, 9]（2）计算矩阵A的转置：A_transpose = A'（3）计算矩阵A的行列式：det_A = det(A)（4）计算矩阵A的逆：A_inverse = inv(A)2. 矩阵的秩（1）创建矩阵B：B = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12]（2）计算矩阵B的秩：rank_B = rank(B)3. 矩阵的逆（1）创建矩阵C：C = [1, 2; 3, 4]（2）判断矩阵C是否可逆：is_inverse = rank(C) == size(C, 1)（3）如果可逆，计算矩阵C的逆：C_inverse = inv(C)4. 线性方程组的求解（1）创建矩阵A和B：A = [1, 2; 3, 4]B = [5; 6]（2）使用MATLAB内置函数求解线性方程组：x = A \ B5. 特征值和特征向量（1）创建矩阵D：D = [4, 1; 2, 3]（2）计算矩阵D的特征值和特征向量：[V, D] = eig(D)6. 二次型及其标准形（1）创建矩阵E：E = [2, 1; 1, 3]（2）计算矩阵E的特征值和特征向量：[V, D] = eig(E)（3）将二次型E化为标准形：Q = V D inv(V)五、实验结果与分析1. 矩阵的基本运算（1）矩阵A：1 2 34 5 67 8 9（2）矩阵A的转置：1 4 72 5 83 6 9（3）矩阵A的行列式：（4）矩阵A的逆：-1.5 0.50.5 -0.52. 矩阵的秩矩阵B的秩为2。

《数学建模与数学实验》上机实验报告

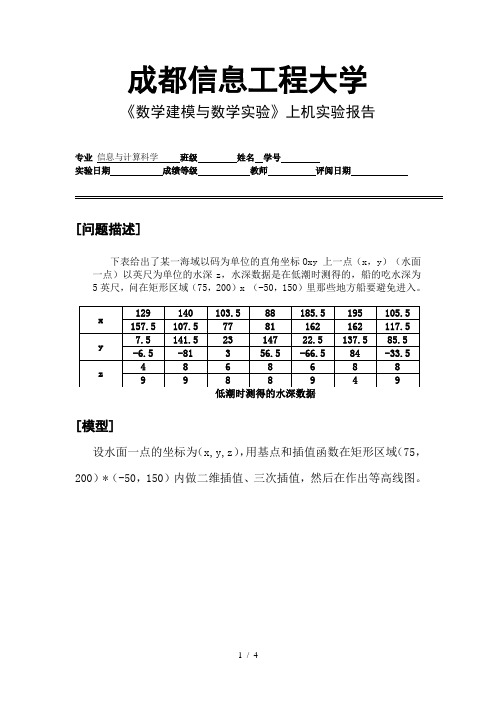
成都信息工程大学《数学建模与数学实验》上机实验报告专业信息与计算科学班级姓名学号实验日期成绩等级教师评阅日期[问题描述]下表给出了某一海域以码为单位的直角坐标Oxy 上一点（x，y）（水面一点）以英尺为单位的水深z，水深数据是在低潮时测得的，船的吃水深为5英尺，问在矩形区域（75，200）x （-50，150）里那些地方船要避免进入。

[模型]设水面一点的坐标为（x,y,z），用基点和插值函数在矩形区域（75，200）*（-50，150）内做二维插值、三次插值，然后在作出等高线图。

[求解方法]使用matlab求解：M文件：water.mx=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5];y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.584 -33.5];z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];cx = 75:0.5:200;cy = -50:0.5:150;[cx,cy]=meshgrid(cx,cy);作出曲面图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> meshz(cx,cy,cz)>> xlabel('X'),ylabel('Y'),zlabel('Z')>>作出等高线图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> figure(2)>> contour(cx,cy,cz,[-5,-5],'r')>> hold on>> plot(x,y,'*')>> xlabel('X'),ylabel('Y')[结果]插值结果等值图：[结果分析及结论]根据等值图可看出：红色区域为危险区域，所以船只要避免进入。

(完整word版)计算方法A上机实验报告

计算方法A上机实验报告姓名：苏福班级：硕4020 学号：3114161019一、上机练习目的1）复习和巩固数值计算方法的基本数学模型，全面掌握运用计算机进行数值计算的具体过程及相关问题。

2）利用计算机语言独立编写、调试数值计算方法程序，培养学生利用计算机和所学理论知识分析解决实际问题的能力。

二、上机练习任务1）利用计算机语言编写并调试一系列数值方法计算通用程序，并能正确计算给定题目，掌握调试技能。

2）掌握文件使用编程技能，如文件的各类操作，数据格式设计、通用程序运行过程中文件输入输出运行方式设计等。

3）写出上机练习报告。

三、上机题目1. 共轭梯度法求解线性方程组。

（第三章）2. 三次样条插值（第四章）3. 龙贝格积分（第六章）4. 四阶龙格－库塔法求解常微分方程的初值问题四、上机报告题目1：共轭梯度法求解线性方程组1．算法原理共轭梯度法是把求解线性方程组的问题转化为求解一个与之等价的二次函数极小值的问题。

从任意给定的初始点出发，沿一组关于矩阵A共轭的方向进行线性搜索，在无舍入误差的假定下，最多迭代n 次（其中n 为矩阵A 的阶数），就可求得二次函数的极小值，也就求得了线性方程组Ax b =的解。

定理：设A 是n 阶对称正定矩阵，则x *是方程组Ax b =的解得充分必要条件是x *是二次函数1()2TT f x x Ax b x =-的极小点，即 ()()min nx R Ax b f x f x **∈=⇔=共轭梯度法的计算公式：(0)(0)(0)()()()()(1)()()(1)(1)(1)()()()(1)(1)()k T k k k T k k k k k k k k T k k k T k k k k k d r b Ax r d d Ad xx d r b Ax r Ad d Ad d r d ααββ++++++⎧==-⎪⎪=⎪⎪=+⎪⎨=-⎪⎪⎪=-⎪⎪=+⎩2. 程序框图（1）编写共轭梯度法求解对称正定矩阵的线性方程组见附录（myge.m）：function x=myge(A,b)输入对称正定矩阵及对应的列向量，初始向量设为0，精度取为810 。

c++上机实验报告(精品)

XX大学C++上机实验报告（一）学院:XX学院班级：XXX姓名：XXX学号：*******指导老师：XXX日期：年月日实验三类的定义和使用一．实验目的1.掌握类的概念、类的定义格式、类与结构的关系、类的成员属性和类的封装性；2.掌握类对象的定义；3.理解类的成员的访问控制的含义，公有、私有和保护成员的区别；4.掌握构造函数和析构函数的含义与作用、定义方式和实现，能够根据要求正确定义和重载构造函数。

能够根据给定的要求定义类并实现类的成员函数；5.掌握友元函数的含义，友元函数和成员函数的区别。

二．实验内容及要求1、定义一个圆类，计算圆的面积和周长。

要求：分别用成员函数和友元函数来求圆的面积和周长。

2、定义一个学生类，其中有3个数据成员有学号、姓名、年龄，以及若干成员函数。

同时编写主函数使用这个类，实现对学生数据的赋值和输出。

要求：1）使用成员函数实现对输出的输入、输出；2）使用构造函数和析构函数实现对数据的输入、输出。

3、定义日期类型Date。

要求有以下面成员：1）可以设置日期；2）日期加一天操作；3）输入函数，输入格式为“XXXX年XX月XX日”。

三．实验要求1）写出程序，并调试程序，要给出测试数据和实验结果。

2）整理上机步骤，总结经验和体会。

3）完成实验日志和上交程序。

四．算法思想1.圆类程序中，用Circle构造函数和Length友元函数分别计算圆的的面积和周长。

再通过主函数调用：Date d;cout<<"请输入圆半径r:";cin>>m;Circle p(m);Length(p);实现输入半径r并输出相关计算值。

2.学生类根据要求分别用构造函数Student(double n,int o,char c[50])和析构函数~Student()，实现学生信息的录入与输出。

于是，当在主程序中，定义学生类Student s(n,o,c)是调用构造函数录入信息，所在作用范围结束时，系统会自动调用析构函数输出信息。

第一次上机实验报告

第一次上机实验报告1、求解线性规划问题：（1）max z=3x1+x2, (2) min z=3x1+x2-x3;x1-x2>=-2; x1+x2-2x3>=2;s.t. x1-2x2<=2; s.t. x1-2x2+x3>=2;3x1+2x2<=14; 3x1+2x2-x3=14;X1,x2,x3>=0.程序：（1）：f=[-3,-1];A=[-1,1;1,-2;3,2];b=[2,2,14];Aeq=[];beq=[];lb=[];ub=[];[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)z=-1*fval结果：x =4.00001.0000fval =-13.0000z =13.0000程序：（2）：f=[3,1,-1];A=[-1,-1,2;-1,2,-1];b=[-2,-2];Aeq=[3,2,-1];beq=[14];lb=[0,0,0];ub=[inf,inf,inf];[x,z]=linprog(f,A,b,Aeq,beq,lb,ub)结果：x =4.00002.00002.0000z =12.00002.由于已经到了高年级，小刚在这个学期必须要选修的课程（必修课）只有一门（2学分）；但可以供他选择的限定选修课程（限选课）有8门，任意选修课程（任选课）有10门，这18门课程的学分数和要求同时选修课程的相应信息如下表所示：限选课课号1 2 3 4 5 6 7 8学分5 5 4 4 3 3 3 2同时选修要求 1 2任选课课号 9 10 11 12 13 14 15 16 17 18学分 3 3 3 2 2 2 1 1 1 1同时选修要求 8 6 4 5 7 6按照学校规定，学生每学期选修的总学分不能少于21学分，上述至少选修19分，任意选修选修的课不能少于3分，也不能超过6分。

求出最优方案。

（1）条件假设：假设投资三种证券和银行存款的资金分别为1X ,2X ,03,X X ,总投资金M ，并设三种证券之间是相互独立的, 设总风险度为a ，且在投资的同一时期内各证券的收益率及风险均为定值，不受意外因素影响。

(完整版)哈工大-数值分析上机实验报告

实验报告一题目：非线性方程求解摘要：非线性方程的解析解通常很难给出，因此线性方程的数值解法就尤为重要。

本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。

前言：（目的和意义）掌握二分法与Newton法的基本原理和应用。

数学原理：对于一个非线性方程的数值解法很多。

在此介绍两种最常见的方法：二分法和Newton法。

对于二分法，其数学实质就是说对于给定的待求解的方程f(x)，其在[a,b]上连续，f(a)f(b)<0，且f(x)在[a,b]内仅有一个实根x*，取区间中点c，若，则c恰为其根，否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个，从而得出新区间，仍称为[a,b]。

重复运行计算，直至满足精度为止。

这就是二分法的计算思想。

Newton法通常预先要给出一个猜测初值x0，然后根据其迭代公式产生逼近解x*的迭代数列{x k}，这就是Newton法的思想。

当x0接近x*时收敛很快，但是当x0选择不好时，可能会发散，因此初值的选取很重要。

另外，若将该迭代公式改进为其中r为要求的方程的根的重数，这就是改进的Newton法，当求解已知重数的方程的根时，在同种条件下其收敛速度要比Newton法快的多。

程序设计：本实验采用Matlab的M文件编写。

其中待求解的方程写成function的方式，如下function y=f(x);y=-x*x-sin(x);写成如上形式即可，下面给出主程序。

二分法源程序：clear%%%给定求解区间b=1.5;a=0;%%%误差R=1;k=0;%迭代次数初值while (R>5e-6) ;c=(a+b)/2;if f12(a)*f12(c)>0;a=c;elseb=c;endR=b-a;%求出误差k=k+1;endx=c%给出解Newton法及改进的Newton法源程序：clear%%%% 输入函数f=input('请输入需要求解函数>>','s')%%%求解f(x)的导数df=diff(f);%%%改进常数或重根数miu=2;%%%初始值x0x0=input('input initial value x0>>');k=0;%迭代次数max=100;%最大迭代次数R=eval(subs(f,'x0','x'));%求解f(x0)，以确定初值x0时否就是解while (abs(R)>1e-8)x1=x0-miu*eval(subs(f,'x0','x'))/eval(subs(df,'x0','x'));R=x1-x0;x0=x1;k=k+1;if (eval(subs(f,'x0','x'))<1e-10);breakendif k>max;%如果迭代次数大于给定值，认为迭代不收敛，重新输入初值ss=input('maybe result is error,choose a new x0,y/n?>>','s');if strcmp(ss,'y')x0=input('input initial value x0>>');k=0;elsebreakendendendk;%给出迭代次数x=x0；%给出解结果分析和讨论：1.用二分法计算方程在[1，2]内的根。

数学的上机实验报告

实验题目：线性代数求解方程组一、实验目的1. 理解线性代数中方程组的求解方法。

2. 掌握利用计算机求解线性方程组的算法。

3. 熟悉数学软件（如MATLAB、Python等）在数学问题中的应用。

二、实验内容本次实验主要利用数学软件求解线性方程组。

线性方程组是线性代数中的一个基本问题，其求解方法有很多种，如高斯消元法、矩阵求逆法等。

本实验以高斯消元法为例，利用MATLAB软件求解线性方程组。

三、实验步骤1. 编写高斯消元法算法程序。

2. 输入方程组的系数矩阵和常数项。

3. 调用程序求解方程组。

4. 输出解向量。

四、实验代码及分析1. 高斯消元法算法程序```matlabfunction x = gaussElimination(A, b)[n, m] = size(A);assert(n == m, 'The matrix A must be square.');assert(n == length(b), 'The length of b must be equal to the number of rows in A.');% 初始化解向量x = zeros(n, 1);% 高斯消元for i = 1:n-1% 寻找最大元素[~, maxIdx] = max(abs(A(i:n, i)));maxIdx = maxIdx + i - 1;% 交换行A([i, maxIdx], :) = A([maxIdx, i], :);b([i, maxIdx]) = b([maxIdx, i]);% 消元for j = i+1:nfactor = A(j, i) / A(i, i);A(j, i:n) = A(j, i:n) - factor A(i, i:n); b(j) = b(j) - factor b(i);endend% 回代求解for i = n:-1:1x(i) = (b(i) - A(i, i+1:n) x(i+1:n)) / A(i, i); endend```2. 输入方程组的系数矩阵和常数项```matlabA = [2, 1, -1; 1, 2, 1; -1, 1, 2];b = [8; 5; 2];```3. 调用程序求解方程组```matlabx = gaussElimination(A, b);```4. 输出解向量```matlabdisp('解向量为：');disp(x);```五、实验结果与分析实验结果：```解向量为：2-13```实验分析：通过高斯消元法，我们成功求解了给定的线性方程组。

高等数学上机实验报告第5题2003

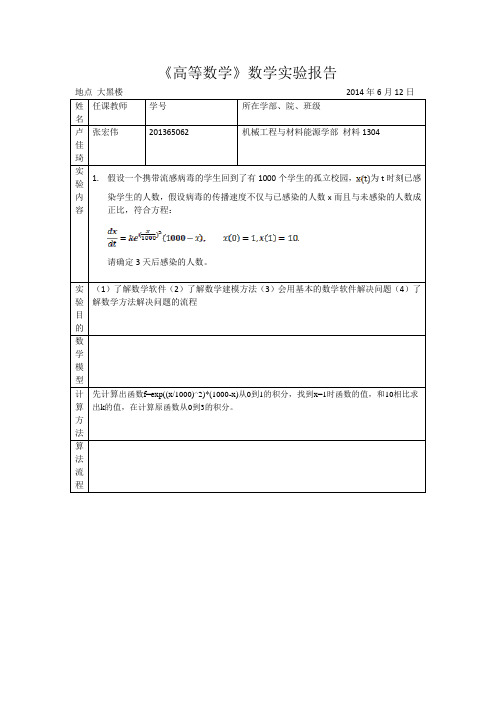
《高等数学》数学实验报告
姓
名
任课教师学号所在学部、院、班级
卢
佳
琦
张宏伟201365062 机械工程与材料能源学部材料1304
实
验
内
容
1.假设一个携带流感病毒的学生回到了有1000个学生的孤立校园，为t时刻已感
染学生的人数，假设病毒的传播速度不仅与已感染的人数x而且与未感染的人数成正比，符合方程：
请确定3天后感染的人数。

实
验
目
的
（1）了解数学软件（2）了解数学建模方法（3）会用基本的数学软件解决问题（4）了解数学方法解决问题的流程
数
学
模
型
计
算
方
法
先计算出函数f=exp((x/1000)^2)*(1000-x)从0到1的积分，找到x=1时函数的值，和10相比求出k的值，在计算原函数从0到3的积分。

算
法
流
程
实
验
结
果
与
分
析
当x=1时，y=1001,则k=10/1001
将函数从0到3积分，x=3的值为2997，乘以k，最后结果约为30 实
验
后
感
想。

西安交通大学数学建模上机实验报告

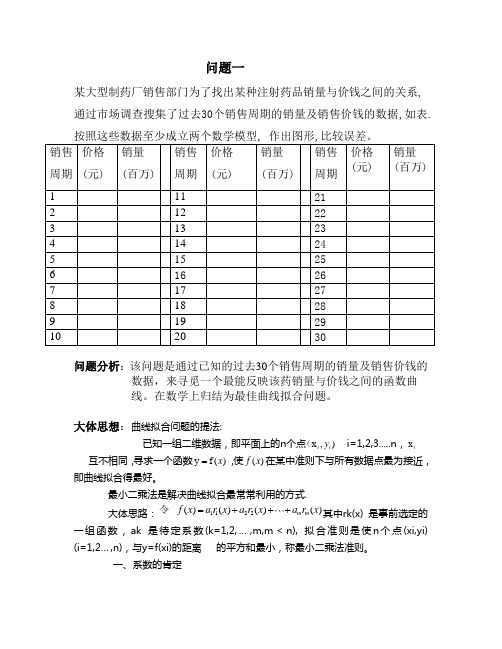
问题一某大型制药厂销售部门为了找出某种注射药品销量与价钱之间的关系,通过市场调查搜集了过去30个销售周期的销量及销售价钱的数据,如表.按照这些数据至少成立两个数学模型, 作出图形,比较误差。

问题分析：该问题是通过已知的过去30个销售周期的销量及销售价钱的数据，来寻觅一个最能反映该药销量与价钱之间的函数曲线。

在数学上归结为最佳曲线拟合问题。

大体思想：曲线拟合问题的提法:已知一组二维数据，即平面上的n 个点),x i i y （ i=1,2,3.....n ，i x 互不相同，寻求一个函数)(f y x =，使)(x f 在某中准则下与所有数据点最为接近，即曲线拟合得最好。

最小二乘法是解决曲线拟合最常常利用的方式.大体思路：1122 ()()()()m m f x a r x a r x a r x =+++令其中rk(x) 是事前选定的一组函数，ak 是待定系数(k=1,2,…,m,m ＜n), 拟合准则是使n 个点(xi,yi) (i=1,2…,n)，与y=f(xi)的距离的平方和最小，称最小二乘法准则。

一、系数的肯定22111 (,,)[()]n nm ii i i i J a a f x y δ====-∑∑记求m a a ,,1 使得使J 达到最小.0 (1,,)kJ k m a ∂==∂ 取得关于 m a a ,,1 的线性方程组：11111()[()]0 ()[()]0nmi k k i i i k n mm i k k i i i k r x a r x y r x a r x y ====⎧-=⎪⎪⎪⎨⎪⎪-=⎪⎩∑∑∑∑ 1 ,,().m a a f x 解出，即得散点图：程序： x=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; y=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; plot(x,y,'r.')通过观察，结合实际情形。

数值分析第三次上机练习实验报告

2 1 , k 0,1, 2...n. 这里唯一需要注意的就是 n 1 Pn ( xk ) Pn'1 ( xk )
还需要一个多项式微分运算（使用的是polyder函数），求解出这两项之后，剩下的就是 I n ( f ) 2.
A
k 0
n
k
f ( xk ) 。
Romberg积分公式计算函数主体是Romberg.m文件,以下只分析这个函数文件的结构: 第一部分是赋初值,对于积分表T还赋值T(1,1):
实现方法说明
程序语言采用Matlab语言，运行环境为Matlab R2009b。
注：主程序文件是First.m和Second.m，其他都是对应的自编函数文件。
1.
复化Guass-Legendre求积公式运算这个程序主体是First.m文件，在里面定义了变量x和函数f f=sym(100*sin(10*(2+x)^(-1))*(2+x).^(-2));由于Legendre多项式的使用条件是[-1,1]，因此对积分区间做了变换，函数体本身也就变成了f（x）=(100*sin(10/(x + 2)))/(x + 2)^2。其他都是调用自己编写的函数计算。 ① Legendre多项式生成函数：Legendre.m
2/5
水利系
2008010249
程国安
这个函数主要用于生成 Legendre 多项式，比较简短，最重要的就是一个迭代关系 P=((2*n-1)*x*Legendre(n-1)-(n-1)*Legendre(n-2))/(n);最后输出一个多项式，如果需要整合，另外加一句 expand（P）即可。 ② Guass-Legendre积分函数：Guass-Legendre.m 这个函数的相关输入输出说明见函数文件注释。积分实现主要需要求出 f ( xk ) 和 Ak ，对于 f ( xk ) ，重点就是建立内联函数 f ( x) 和变量序列 xk ，变量序列 xk 主要使用利用Legendre求出对应次数的Legendre多项式的零点（使用sym2poly求出系数，之后利用roots求零点）。对于 Ak ，利用 Ak

概率论上机实验报告

概率论上机实验报告《概率论上机实验报告》在概率论的学习中，实验是非常重要的一部分。

通过实验，我们可以验证概率论的理论，加深对概率的理解，同时也可以提高我们的实验能力和数据处理能力。

本次实验报告将详细介绍一次概率论的上机实验，包括实验目的、实验方法、实验结果和实验分析。

实验目的：本次实验的目的是通过随机抽样的方法，验证概率论中的一些基本概念和定理，包括概率的计算、事件的独立性、事件的互斥性等。

通过实际操作，加深对这些概念的理解，同时也提高我们的实验技能和数据处理能力。

实验方法：本次实验采用计算机模拟的方法进行。

首先，我们选择了几个经典的概率问题作为实验对象，包括掷骰子、抽球问题等。

然后，通过编写程序，模拟进行大量的随机实验，得到实验数据。

最后，通过对实验数据的统计分析，验证概率论中的一些基本概念和定理。

实验结果：通过实验，我们得到了大量的实验数据。

通过对这些数据的统计分析，我们验证了概率的计算方法，验证了事件的独立性和互斥性等基本概念和定理。

实验结果表明，概率论中的一些基本概念和定理在实际中是成立的，这也进一步加深了我们对概率论的理解。

实验分析：通过本次实验，我们不仅验证了概率论中的一些基本概念和定理，同时也提高了我们的实验能力和数据处理能力。

通过实验，我们深刻理解了概率论的一些基本概念和定理，并且也掌握了一些实验技能和数据处理技能。

这对我们今后的学习和工作都将有很大的帮助。

总结：通过本次实验，我们深刻理解了概率论的一些基本概念和定理，同时也提高了我们的实验能力和数据处理能力。

这对我们今后的学习和工作都将有很大的帮助。

希望通过这次实验，我们能更加深入地理解概率论，并且提高我们的实验技能和数据处理技能。

高数mathematica上机实验报告

15-16-2《高等数学》数学实验报告学号：姓名：得分： . ..实验：已知函数f(x)=（5≤x≤4）,作出并比较当c分别取1,0,1,2,3时的图形，并从图上观察极值点、驻点、单调区间、凹凸区间以及渐进线。

当c=时In[1]= f[x]:=1/(-1+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[3]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[5]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[7]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[7]=Out[8]=极大值点为x=，驻点为x=，单调递增区间为,单调递减区间为，下凸区间为，上凸区间为，渐进线为x=,x=当c=0时In[9]= f[x]:=1/(2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[11]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[13]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[15]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[15]=Out[16]=极大值点为x=，驻点为，单调递增区间为,单调递减区间为，下凸区间为，上凸区间为，渐进线为x=,x=0当c=1时In[17]= f[x]:=1/(1+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[19]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[21]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[23]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[23]=Out[24]=无极值点，无驻点，单调递增区间为,单调递减区间为，下凸区间为，无上凸区间，渐进线为x=当c=2时In[25]= f[x]:=1/(2+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[27]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[29]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[31]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[31]=Out[32]=极大值点为x=，驻点为，单调递增区间为单调递减区间，下凸区间为，上凸区间为，无渐进线当c=3时In[33]= f[x]:=1/(3+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[35]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[37]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[39]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[39]=Out[40]=极大值点为x=，驻点为，单调递增区间为单调递减区间，下凸区间为，上凸区间为，无渐进线。

上机实验报告怎么写

上机实验报告怎么写实验目的本次实验的目的是...实验环境本次实验使用的工具和软件环境如下：- 操作系统：Windows 10- 开发工具：Visual Studio Code- 编程语言：Python实验步骤步骤一：准备工作在开始实验之前，我们需要进行一些准备工作，包括安装相应的软件环境和准备实验材料等。

具体的准备工作如下：1. 安装操作系统：确保使用最新的操作系统，并安装所需的驱动程序。

2. 安装开发工具：下载并安装Visual Studio Code，并配置相应的插件和设置。

3. 安装Python：下载并安装Python解释器，并配置环境变量。

步骤二：实验设计在本次实验中，我们将实现一个简单的计算器功能，包括加法、减法、乘法和除法。

具体的实验设计如下：1. 设计界面：使用Tkinter库创建一个窗口，并在窗口中添加输入框和按钮等组件。

2. 实现功能：根据用户的输入，进行相应的数值计算，并将结果显示在窗口中。

步骤三：编写代码根据实验设计，我们开始编写代码。

代码的具体实现如下：pythonimport tkinter as tkdef calculate():获取用户输入的数值num1 = float(entry1.get())num2 = float(entry2.get())执行计算操作result = num1 + num2显示计算结果label.config(text="计算结果：" + str(result))创建窗口window = ()添加输入框entry1 = tk.Entry(window)entry1.pack()entry2 = tk.Entry(window)entry2.pack()添加按钮button = tk.Button(window, text="计算", command=calculate) button.pack()添加结果显示标签label = bel(window, text="计算结果：")label.pack()启动事件循环window.mainloop()步骤四：实验结果在编写完代码后，我们进行了实验测试，并记录下了实验结果。

上机报告总结模板下载(通用3篇)

上机报告总结模板下载第1篇一、实验原理（1）电子的自旋轨道磁矩与自旋磁矩 l原子中的电子由于轨道运动，具有轨道磁矩，其数值为：l号表示方向同Pl相反。

在量子力学中PePl2me，负，因而lB1)B2me称为玻尔磁子。

电子除了轨道运动外，其中e还具有自旋运动，因此还具有自旋磁矩，其数值表示为：se Psme。

由于原子核的磁矩可以忽略不计，原子中电子的轨道磁矩和自旋磁矩合成原子的总磁矩：jgej(j1)l(l1)s(s1)Pjg12me，其中g是朗德因子：2j(j1)。

在外磁场中原子磁矩要受到力的作用，其效果是磁矩绕磁场的方向作旋进，也就是Pj 绕着磁场方向作旋进，引入回磁比同时原子角动量Pj和原子总磁矩Pjm ,mj,j1,j2,e2me，总磁矩可表示成jPj。

j取向是量子化的。

Pj在外磁场方向上的投影为：其中m称为磁量子数，相应磁矩在外磁场方向上j。

的投影为： jmmgB ;mj,j1,j2,（2）电子顺磁共振 j。

如果在原子所在的稳定磁场区又叠加一个与之垂直的交变磁场，且角频率满足条件gB B，即EB，刚好满足原子在稳定外磁场中的邻近二能级差时，二邻近能级之间就有共振跃迁，我们称之为电子顺磁共振。

P当原子结合成分子或固体时，由于电子轨道运动的角动量常是猝灭的，即j近似为零，所以分子和固体中的磁矩主要是电子自旋磁矩的贡献。

根据泡利原理，一个电子轨道最多只能容纳两个自旋相反的电子，若电子轨道都被电子成对地填满了，它们的自旋磁矩相互抵消，便没有固有磁矩。

通常所见的化合物大多数属于这种情况，因而电子顺磁共振只能研究具有未成对电子的特殊化合物。

（3）弛豫时间实验样品是含有大量具有不成对电子自旋所组成的系统，虽然各个粒子都具有磁矩，但是在热运动的扰动下，取向是混乱的，对外的合磁矩为零。

当自旋系统处在恒定的外磁场H0中时，系统内各质点的磁矩便以不同的角度取向磁场H0的方向，并绕着外场方向进动，从而形成一个与外磁场方向一致的宏观磁矩M。

高等数学上机实验报告第1题2003

《高等数学》数学实验报告
姓
名
任课教师学号所在学部、院、班级
卢
佳
琦
张宏伟201365062 机械工程与材料能源学部材料1304
实验内容要在陆地城市A与海岛B之间敷设一条地下光缆（图2-28），经地质勘探后知，陆地区域与水下区域每公里敷设的成本不同，试问如何确定敷设路线，可使工程的总成本最低？
实验目的（1）了解数学软件（2）了解数学建模方法（3）会用基本的数学软件解决问题（4）了解数学方法解决问题的流程
数学模型设陆地和水下铺设的成本分别为c1,c2,AB相距水平距离为d，将问题转化为求方程y=(a^2+x^2)^0.5*c1+(b^2+(d-x)^2)^0.5*c2的最小值，即求
dy/dx=c1*x/(a^2+x^2)^0.5-c2*(d-x)/(b^2+(d-x)^2)^0.5
的零点。

计
算
方
法
令a=3,b=2,d=6,c1=100,c2=200,利用二分法球根
算
法
流
程
实
验
结
果
与
分
析
假设了上述初值后，计算结果为5.048 实
验
后
感
想。

数值积分上机实验报告

一、实验目的1. 理解数值积分的概念及其在实际应用中的重要性；2. 掌握数值积分的常用方法，如梯形法、辛普森法、高斯法等；3. 利用计算机编程实现数值积分算法，提高编程能力；4. 分析不同数值积分方法在精度和效率方面的差异。

二、实验内容1. 实现梯形法、辛普森法和高斯法；2. 对给定函数进行数值积分，比较不同方法的精度和效率；3. 分析误差来源，提出改进措施。

三、实验环境1. 操作系统：Windows 102. 编程语言：Python3. 数值计算库：NumPy四、实验步骤1. 实现梯形法：```pythonimport numpy as npdef trapezoidal_rule(f, a, b, n):h = (b - a) / nresult = 0.5 (f(a) + f(b))for i in range(1, n):result += f(a + i h)result = hreturn result```2. 实现辛普森法：```pythondef simpson_rule(f, a, b, n):h = (b - a) / nresult = f(a) + f(b)for i in range(1, n):if i % 2 == 1:result += 4 f(a + i h)else:result += 2 f(a + i h)result = h / 3return result```3. 实现高斯法：```pythondef gauss_quadrature(f, a, b, n):x = np.linspace(a, b, n)w = 2 (b - a) / (3 n) np.ones(n)return np.dot(w, f(x))```4. 对给定函数进行数值积分，比较不同方法的精度和效率：```pythondef f(x):return np.sin(x)a = 0b = np.pin = 10result_trapezoidal = trapezoidal_rule(f, a, b, n)result_simpson = simpson_rule(f, a, b, n)result_gauss = gauss_quadrature(f, a, b, n)print("梯形法结果：", result_trapezoidal)print("辛普森法结果：", result_simpson)print("高斯法结果：", result_gauss)```5. 分析误差来源，提出改进措施：通过比较梯形法、辛普森法和高斯法的结果，我们可以发现高斯法在精度和效率方面都优于梯形法和辛普森法。

二分法上机实验报告 2

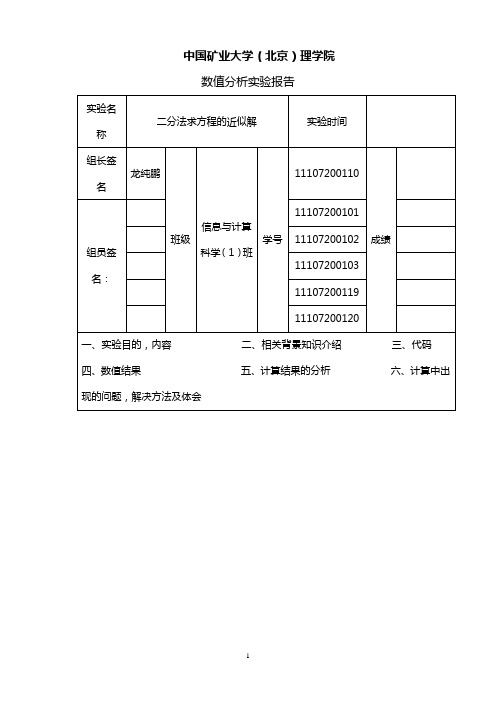
中国矿业大学（北京）理学院数值分析实验报告实验名称二分法求方程的近似解实验时间组长签名龙纯鹏班级信息与计算科学（1）班学号11107200110 成绩组员签名：1110720010111107200102 11107200103 1110720011911107200120一、实验目的，内容二、相关背景知识介绍三、代码四、数值结果五、计算结果的分析六、计算中出现的问题，解决方法及体会一、实验目的，内容通过用二分法求一个具体的方程02=--x x ，]1,0[∈x 精确到 510-的近似根，掌握二分法，会编写相关代码。

二、相关背景知识介绍（1）算法原理或计算公式二分法的基本思路是通过计算隔根区间的中点，逐步将隔根区间缩小，从而可得方程的近似根数列{}n x 。

ε<-≤-+1*2k k ab x x（2）程序设计思路二分法原理：不妨设方程0)(=x f 在隔根区间],[b a 上.0)(,0)(><b f a f . (1)将区间],[b a 二分得中点2b a +,计算)(x f 在中点的函数值)2(ba f +，若0)2(=+b a f ，则2ba x +=*就是方程的根；否则,若0)2(<+b a f ,由于)(x f 在]2,[b a a +内不变号，所以隔根区间变为],2[b ba +.同理，若0)2(>+b a f , 隔根区间变为]2,[ba a +.将新区间记为[]11,b a . (2)将[]11,b a 重复上述步骤(1).得到一系列隔根区间：[][][]⋯⋯⊃⊃⋯⋯⊃⊃k k b b a b ,a ,,a 11并有),(,0)(f )(f *k k k k b a x b a ∈<*，且后一区间的长度都是前一区间长度的一半，所以[]k k b ,a 的长度为)(,2∞→-=-k a b a b k k k ，区间[]k k b ,a 的长度趋向于零，即这些区间最终收缩于一点*x ，显然*x 就是方程0)(=x f 的根。