高等数学上册课后习题答案1-2
高等数学课后习题答案--第一章
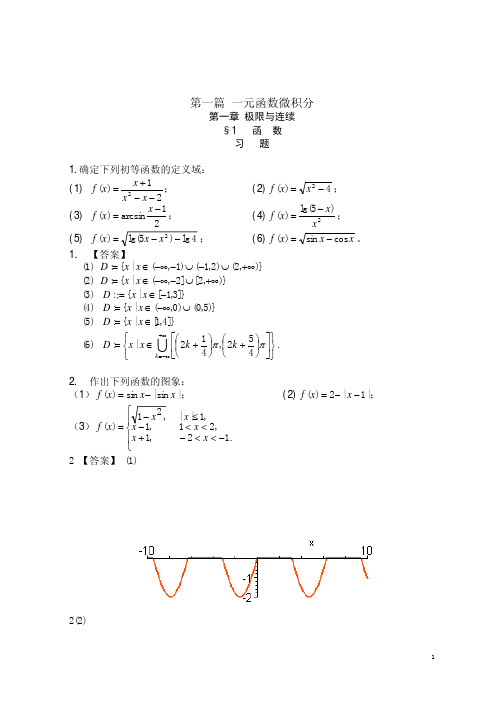
《高等数学》习题参考资料第一篇 一元函数微积分第一章 极限与连续§1 函 数习 题1.确定下列初等函数的定义域:(1) 21)(2−−+=x x x x f ;(2)4)(2−=x x f ;(3) 21arcsin )(−=x x f ;(4)2)5lg()(x x x f −=;(5) 4lg )5lg()(2−−=x x x f ;(6)x x x f cos sin )(−=。
1. 【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象:(1)|sin |sin )(x x x f −=;(2)|1|2)(−−=x x f ;(3)+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性:(1)x x x f ++−=11)(;(2)xxx f x x +−+−=11lg110110)(;(3)x x a a x f x x sin )(++=−;(4))1lg()(2x x x f ++=。
3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。
4. 【答案】 设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5.设函数f 满足:D (f )关于原点对称,且()xc x bf x af =+1)(,其中a ,b ,c 都是常数,||||b a ≠,试证明f 是奇函数。
高等数学上册课后习题答案1-2

习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)nn x 21=; n x n n 1)1(-= 解 当n →∞时, nn x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=; 解 当n →∞时, →0, 01)1(lim =-∞→nn n . (3)212nx n +=; 解 当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→n n . (4)11+-=n n x n ; 解 当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n . (5) x n =n (-1)n .解 当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 0lim =∞→n n x . n n n x n 1|2c o s ||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→n n ; 分析 要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim 2=∞→n n .(2)231213lim =++∞→n n n ; 分析 要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明 因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n . (3)1lim 22=+∞→na n n ; 分析 要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22n a n , 所以1lim 22=+∞→na n n . (4)19 999.0lim =⋅⋅⋅∞→ 个n n . 分析 要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n . 证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明 因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而 ||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→. 数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x . 证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M . 又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有My n ε<||. 从而当n >N 时, 有εε=⋅<≤=-M M y M y x y x n n n n n |||||0|, 所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞), 证明: x n →a (n →∞). 证明 因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0, ∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ; ∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε . 取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε . 因此x n →a (n →∞).。
(WORD)-高等数学课后习题(完整版)及答案

高等数学课后习题(完整版)及答案高等数学课后答案习题1 11设A ( 5) (5 ) B [10 3)写出A BA B A\B及A\(A\B)的表达式解 A B ( 3) (5 )A B [105)A\B ( 10) (5 )A\(A\B) [105)2设A、B是任意两个集合证明对偶律 (A B)C AC BC 证明因为x (A B)C x A B x A或x B x AC或x BC x ACBC所以 (A B)C AC BC3设映射f X Y A X B X 证明(1)f(A B) f(A) f(B)(2)f(A B) f(A) f(B)证明因为y f(A B) x A B使f(x) y(因为x A或x B) y f(A)或y f(B)y f(A) f(B)所以 f(A B) f(A) f(B)(2)因为y f(A B) x A B使f(x) y (因为x A且x B) y f(A)且y f(B) y f(A) f(B)所以 f(A B) f(A) f(B)4设映射f X Y若存在一个映射g Y X使g f IXf g IY其中IX、IY分别是X、Y上的恒等映射即对于每一个x X有IX x x 对于每一个y Y有IY y y证明 f是双射且g是f的逆映射 g f 1证明因为对于任意的y Y有x g(y) X且f(x) f[g(y)] Iy y y即Y中任意元素都是X中某元素的像所以f为X到Y的满射又因为对于任意的x1 x2必有f(x1) f(x2)否则若f(x1) f(x2) g[ f(x1)] g[f(x2)] x1 x2因此f既是单射又是满射即f是双射对于映射g Y X因为对每个y Y有g(y) x X且满足f(x) f[g(y)] Iy y y按逆映射的定义 g是f的逆映射5设映射f X Y A X 证明(1)f 1(f(A)) A(2)当f是单射时有f 1(f(A)) A证明 (1)因为x A f(x) y f(A) f 1(y) x f 1(f(A))所以 f 1(f(A)) A(2)由(1)知f 1(f(A)) A另一方面对于任意的x f 1(f(A)) 存在y f(A)使f1(y) x f(x) y 因为y f(A)且f是单射所以x A这就证明了f 1(f(A)) A因此f 1(f(A)) A6求下列函数的自然定义域(1)y x233 解由3x2 0得x 2函数的定义域为[2, )(2)y 1 1x2解由1x2 0得x 1函数的定义域为( 1) (11) (1 )(3)y 1x x2解由x 0且1x2 0得函数的定义域D [1 0) (0 1](4)y 14x2解由4x2 0得 |x| 2函数的定义域为(2 2)(5)y sinx解由x 0得函数的定义D [0 )(6) y tan(x1)2 解由x1 (k 0 1 2 )得函数的定义域为x k 1 (k 0 1 2 2)(7) y arcsin(x3)解由|x3| 1得函数的定义域D [2 4](8)y x1 x解由3x 0且x 0得函数的定义域D ( 0) (0 3)(9) y ln(x1)解由x1 0得函数的定义域D (1 )(10)y ex解由x 0得函数的定义域D ( 0) (0 )7下列各题中函数f(x)和g(x)是否相同?为什么?(1)f(x) lg x2 g(x) 2lg x(2) f(x) x g(x) x2(3)f(x) x4x3g(x) xx1(4)f(x) 1 g(x) sec2x tan2x解 (1)不同因为定义域不同(2)不同因为对应法则不同 x 0时 g(x) x(3)相同因为定义域、对应法则均相相同(4)不同因为定义域不同8 |sinx| |x|3设 (x) |x| 0 3 求 ( ) ( ) ( ) (2)并作出函数y (x)644的图形) |sin | 解 ( ) |sin | 1 (446622) |sin( )| (442 (2) 09试证下列函数在指定区间内的单调性(1)y x ( 1) 1x(2)y x ln x (0 )证明 (1)对于任意的x1 x2 ( 1)有1x1 0 1x2 0因为当x1 x2时y1y2 xxx x 0 1x11x2(1x1)(1x2) 所以函数y x在区间( 1)内是单调增加的 1x(2)对于任意的x1 x2 (0 )当x1 x2时有y1y2 (x1lnx1)(x2lnx2) (x1x2)lnx 0 x2所以函数y x ln x在区间(0 )内是单调增加的10设 f(x)为定义在(l l)内的奇函数若f(x)在(0 l)内单调增加证明f(x)在(l 0)内也单调增加证明对于x1 x2 (l 0)且x1 x2有x1x2 (0 l)且x1 x2因为f(x)在(0 l)内单调增加且为奇函数所以f(x2) f(x1)f(x2) f(x1) f(x2) f(x1)这就证明了对于x1 x2 (l 0)有f(x1) f(x2)所以f(x)在(l 0)内也单调增加11设下面所考虑的函数都是定义在对称区间(l l)上的证明(1)两个偶函数的和是偶函数两个奇函数的和是奇函数(2)两个偶函数的乘积是偶函数两个奇函数的乘积是偶函数偶函数与奇函数的乘积是奇函数证明 (1)设F(x) f(x)g(x)如果f(x)和g(x)都是偶函数则F(x) f(x)g(x) f(x)g(x) F(x)所以F(x)为偶函数即两个偶函数的和是偶函数如果f(x)和g(x)都是奇函数则F(x) f(x)g(x) f(x)g(x) F(x)所以F(x)为奇函数即两个奇函数的和是奇函数(2)设F(x) f(x) g(x)如果f(x)和g(x)都是偶函数则F(x) f(x) g(x) f(x) g(x) F(x)所以F(x)为偶函数即两个偶函数的积是偶函数如果f(x)和g(x)都是奇函数则F(x) f(x) g(x) [f(x)][g(x)] f(x) g(x) F(x)所以F(x)为偶函数即两个奇函数的积是偶函数如果f(x)是偶函数而g(x)是奇函数则F(x) f(x) g(x) f(x)[g(x)] f(x) g(x) F(x)所以F(x)为奇函数即偶函数与奇函数的积是奇函数12下列函数中哪些是偶函数哪些是奇函数哪些既非奇函数又非偶函数?(1)y x2(1x2)(2)y 3x2x3(3)y 1x2 1x2(4)y x(x1)(x1)(5)y sin x cos x1(6)y ax a x2解 (1)因为f(x) (x)2[1(x)2] x2(1x2) f(x)所以f(x)是偶函数(2)由f(x) 3(x)2(x)3 3x2x3可见f(x)既非奇函数又非偶函数(3)因为1(x)21x2f(x) f(x) 221x1x所以f(x)是偶函数(4)因为f(x) (x)(x1)(x1) x(x1)(x1) f(x)所以f(x)是奇函数(5)由f(x) sin(x)cos(x)1 sin x cos x1可见f(x)既非奇函数又非偶函数(6)因为(x)(x)xxa aa af(x) f(x) 22所以f(x)是偶函数13下列各函数中哪些是周期函数?对于周期函数指出其周期(1)y cos(x2)解是周期函数周期为l 2(2)y cos 4x解是周期函数周期为l 2(3)y 1sin x解是周期函数周期为l 2(4)y xcos x解不是周期函数(5)y sin2x解是周期函数周期为l14求下列函数的反函数(1)y x1解由y x1得x y31所以y x1的反函数为y x31(2)y 1x 1x解由y 1x得x 1y所以y 1x的反函数为y 1x1x1y1x1x(3)y ax b(ad bc 0) cx d解由y ax b得x dy b所以y ax b的反函数为y dx b cx dcy acx dcx a(4) y 2sin3xyarcsin所以y 2sin3x的反函数为y 1arcsinx解由y 2sin 3x 得x 13232(5) y 1ln(x2)x2(6)y 2 1 解由y 1ln(x2)得x ey12所以y 1ln(x2)的反函数为y ex122xx y 所以的反函数为y log2211x 解 y2xy x log由得21y2 115设函数f(x)在数集X上有定义试证 函数f(x)在X上有界的充分必要条件是它在X上既有上界又有下界证明先证必要性设函数f(x)在X上有界则存在正数M使|f(x)| M即M f(x) M这就证明了f(x)在X上有下界M和上界M再证充分性设函数f(x)在X上有下界K1和上界K2即K1 f(x) K2 取M max{|K1| |K2|}则M K1 f(x)K2 M即 |f(x)| M这就证明了f(x)在X上有界16在下列各题中求由所给函数复合而成的函数并求这函数分别对应于给定自变量值x1和x2的函数值(1) y u2 u sin x解 y sin2x x1 6x2 33y1 sin2 12 1y2 sin2 ()2 324624x1 x2 84 (2) y sin u u 2x解 y sin2x(3)y解 y1 sin(2 ) sin y2 sin(2 sin 1 842422u 1x x1 1 x2 2 y x2 y1 12 y2 22(4) y eu u x2 x1 0 x2 1解 y ex2 y1 e0 1 y2 e1 e 22(5) y u2 u ex x1 1 x2 1解 y e2x y1 e2 1 e2 y2 e2 (1) e217设f(x)的定义域D [0 1]求下列各函数的定义域(1) f(x2)解由0 x2 1得|x| 1所以函数f(x2)的定义域为[1 1](2) f(sinx)解由0 sin x 1得2n x (2n1) (n 0 1 2 )所以函数f(sin x)的定义域为[2n (2n1) ] (n 0 1 2 )(3) f(x a)(a>0)解由0 x a 1得a x 1a所以函数f(x a)的定义域为[a 1a](4) f(x a)f(x a)(a 0)22 解由0 x a 1且0 x a 1得 当0 a 1时 a x 1a 当a 1时无解因此当0 a 1时函数的定义域为[a 1a]当a 1时函数无意义2218设的图形解 |x| 1 1 x f(x) 0 |x| 1 g(x) e |x| 1 1 求f[g(x)]和g[f(x)]并作出这两个函数 1 |ex| 1 f[g(x)] 0|ex| 11 |ex| 1 即 1 x 0 f[g(x)] 0 x 0 1 x 0e1 |x| 1 g[f(x)] ef(x) e0 |x| 1e 1 |x| 1 e |x| 1 |x| 1即g[f(x)] 11 |x| 1 e19已知水渠的横断面为等腰梯形斜角 40 (图137)当过水断面ABCD的面积为定值S0周L(L AB BC CD)与水的函数关系式并指明其图137解 AB DC hsin40 0cot40 h所以又从1h[BC(BC2cot40 h)] S0得BC Sh时求湿深h之间定义域 2S2cos40L h hsin40自变量h的取值范围应由不等式组h 0确定定义域为0 h 0cot40S0 cot40 h 0 h20收敛音机每台售价为90元成本为60元厂方为鼓励销售商大量采购决定凡是订购量超过100台以上的每多订购1台售价就降低1分但最低价为每台75元(1)将每台的实际售价p表示为订购量x的函数(2)将厂方所获的利润P表示成订购量x的函数(3)某一商行订购了1000台厂方可获利润多少?解 (1)当0 x 100时 p 90令001(x0100) 9075得x0 1600因此当x 1600时p 75当100 x 1600时p 90(x100) 001 910 01x综合上述结果得到0 x 100 90 p 910.01x 100 x 1600 75 x 1600 30x 0 x 1002100 x 1600 (2)P (p60)x 31x0.01x 15x x 1600(3) P 31 1000001 10002 21000(元)习题1 21观察一般项xn如下的数列{xn}的变化趋势写出它们的极限 (1)xn 1 2n解当n 时(2)xn (1)n1 n1 0 0 xn 1limn 22 解当n 时(3)xn 2 12 nxn (1)n1 0 lim(1)n1 0 n nn解当n 时(4)xn n1 n1xn 21 2 lim(21) 2 n nn2解当n 时(5) xn n(1)n xn n1 12 0 limn1 1n n1n1n 1解当n 时 xn n(1)n没有极限2 cos设数列{xn}的一般项xn nx ? 求出N使当n N时 xn问nlim n与其极限之差的绝对值小于正数 当 0001时求出数N解limx 0n n要使|x n0| 只要1 也就是n 1取n|cos|1 0 |xn0| nnN [1]则n N有|xn0|当 0001时 N [1] 10003根据数列极限的定义证明1 0 (1)nlim 2n分析要使|120| 12 只须n2 1即nnn1nn证明因为 0N [3n1 3 (2)nlim1]1 0当n N时有|120| 所以nlim 2分析2n12n13| 1 1要使|3 2n122(2n1)4n4只须证明因为 0N [1]当n N (3)nlim 分析 n2a2 1 n1 即n 14 4n3n1 3时有|3n13| 所以nlim 2n122n12只须2an222222a a naa要使|1| 22nnn a n)n2aN []证明因为 022n alim 1 n n当n N时有|n2a21|n所以(4)nlim0. 999 9 1n个分析要使|099 91|110n 1只须1 10即n 1lg1证明因为 0N [1lg1]当n N时有|099 91| 所以n n个lim0.999 9 1|u| |a|并举例说明 如果数列{|xn|}有极限但数证明nlimn4limu an n列{xn}未必有极限u a所以 0N N当n N时有|un a| 从而证明因为nlim n||un||a|| |un a||un| |a|这就证明了nlim|(1)n| 1但lim(1)n 数列{|xn|}有极限但数列{xn}未必有极限例如nlimn不存在y 0证明 5设数列{xn}有界又nlim nn limxnyn 0证明因为数列{xn}有界所以存在M使n Z有|xn| Myn 0所以 0N N当n N时有|yn| 从而当n N时又nlim M有xy 0所以nlim nn|xnyn0| |xnyn| M|yn| M M6对于数列{xn}若x2k1 a(k ) x2k a(k )证明 xn a(n )证明因为x2k1 a(k ) x2k a(k )所以 0K1当2k1 2K11时有| x2k1a| K2当2k 2K2时有|x2k a| 取N max{2K11 2K2}只要n N就有|xn a| 因此xn a (n )习题1 31根据函数极限的定义证明(3x1) 8 (1)limx 3分析因为|(3x1)8| |3x9| 3|x3|所以要使|(3x1)8| 只须|x3| 1 3 证明因为 0 1 当0 |x3| 时有 3|(3x1)8|(3x1) 8所以limx 3(5x2) 12 (2)limx 2分析因为|(5x2)12| |5x10| 5|x2|所以要使|(5x2)12| 只须|x2| 1 5 证明因为 0 1 当0 |x2| 时有 5|(5x2)12|(5x2) 12所以limx 22x4 4(3)xlim 2x 2分析因为x24(4) x24x4 |x2| |x(2)| x2x 2所以要使x24(4) x2只须|x(2)| 证明因为 0 当0 |x(2)| 时有x24(4) x2x24 4lim所以x 2x2314x(4)lim 2 2x1x分析因为所以要使14x32 |12x2| 2|x(1)| 2x1214x32 2x1只须|x(1)| 1 2222 证明因为 0 1 当0 |x(1)| 时有 14x32 2x1 314x所以lim 2 2x1x 22根据函数极限的定义证明1x (1)xlim 1 22x3分析因为所以要使1x31 1x3x3 1 2x322x32|x|3 1x312x2只须1 2|x|即|x| 1证明因为 0X 1当|x| X时有 1x312x3231x 1所以xlim3 2x2sinx 0 (2)xlim x 分析因为所以要使证明sinx0 |sinx| 1 xxxsinx0 只须1 即x 12x x因为 0X 1当x X时有 2sinx0 xsinx 0所以xlim x 3当x 2时 y x2 4问 等于多少使当|x2|< 时 |y4|<0001?解由于当x 2时 |x2| 0故可设|x2| 1即1 x 3要使|x24| |x2||x2| 5|x2| 0001只要|x2| 0.001 0.0002 5取 00002则当0 |x2| 时就有|x24| 0 0014当x 时解要使y x21 1 x32问X等于多少使当|x| X时|y1| 001? 只要|x| 43 0.01x211 4 0.01x23x23故X5证明函数f(x) |x|当x 0时极限为零证明因为|f(x)0| ||x|0| |x| |x0|所以要使|f(x)0| 只须|x|因为对 0 使当0 |x0| 时有|f(x)0| ||x|0||x| 0所以limx 06求f(x) x, x (x) |x|当xx 0时的左﹑右极限并说明它们在x 0时的极限是否存在证明因为lim f(x) lim x lim1 1x 0x 0xx 0lim f(x) lim x lim1 1 x 0x 0xx 0x 0limf(x) lim f(x) x 0f(x)存在所以极限limx 0因为|x| lim x 1 x 0x 0xx 0x|x|x 1lim (x) lim limx 0x 0xx 0xlim (x) limx 0 lim (x) lim (x) x 0(x)不存在所以极限limx 07证明 若x 及x 时函数f(x)的极限都存在且都等于Af(x) A则xlimf(x) A证明因为xlim x limf(x) A所以 >0X1 0使当x X1时有|f(x)A|X2 0使当x X2时有|f(x)A|f(x) A取X max{X1 X2}则当|x| X时有|f(x)A| 即xlim8根据极限的定义证明 函数f(x)当x x0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等证明先证明必要性设f(x) A(x x0)则 >0 0使当0<|x x0|< 时有|f(x)A|<因此当x0 <x<x0和x0<x<x0 时都有|f(x)A|<这说明f(x)当x x0时左右极限都存在并且都等于A再证明充分性设f(x00) f(x00) A则 >01>0使当x0 1<x<x0时有| f(x)A<2>0使当x0<x<x0+ 2时有| f(x)A|<取 min{ 1 2}则当0<|x x0|< 时有x0 1<x<x0及x0<x<x0+ 2 从而有| f(x)A|<即f(x) A(x x0)9试给出x 时函数极限的局部有界性的定理并加以证明解 x 时函数极限的局部有界性的定理 如果f(x)当x 时的极限存在则存在X 0及M 0使当|x| X时 |f(x)| M证明设f(x) A(x )则对于 1X 0当|x| X时有|f(x)A| 1所以|f(x)| |f(x)A A| |f(x)A||A| 1|A|这就是说存在X 0及M 0使当|x| X时 |f(x)| M其中M 1|A|习题1 41两个无穷小的商是否一定是无穷小?举例说明之解不一定(x)2 例如当x 0时 (x) 2x (x) 3x都是无穷小但limx 0(x)3 (x)不 (x)是无穷小2根据定义证明2x9(1)y x当x 3时为无穷小; 3(2)y xsin1当x 0时为无穷小x2x9 |x3|时|y| x 3 证明 (1)当x 3有因为 0当0 |x3| 时2|y| x9 |x3| x 32x9所以当x 3时y x为无穷小 3(2)当x 0时|y| |x||sin1| |x0|因为 0 x|y| |x||sin1| |x0| x所以当x 0时y xsin1为无穷小 x当0 |x0| 时有3根据定义证明 函数y 12x为当x 0时的无穷大问x应满足什x么条件能使|y| 104?证明分析|y||x| 1 M212x 21 12 xx|x|2 M即要使|y| M只须|1x|证明因为M 0所以当取1使当0 |x0| 时有12x M xM2x 0时函数y 12x是无穷大 xM 104则 41当0 |x0| 41时|y| 104 10210 2 4求下列极限并说明理由2x1; (1)limx x21x(2)limx 01xxxxx1x2 1所以lim x 01x2x1 2解 (1)因为2x1 21而当x 时1是无穷小所以limx x (2)因为11x2 1x(x 1)而当x 0时x为无穷小5根据函数极限或无穷大定义填写下表解6函数y xcos x在( )内是否有界?这个函数是否为当x 时的无穷大?为什么?解函数y xcos x在( )内无界这是因为M 0在( )内总能找到这样的x使得|y(x)| M例如y(2k ) 2k cos2k 2k (k 0 1 2 )当k充分大时就有| y(2k )| M当x 时函数y xcos x不是无穷大这是因为M 0找不到这样一个时刻N使对一切大于N的x都有|y(x)| M例如y(2k (2k )cos(2k ) 0(k 0 1 2 ) 2222 对任何大的N当k充分大时总有x 2k N但|y(x)| 0 M7证明 函数y 1sin1在区间(0 1]上无界但这函数不是当x 0+时xx的无穷大证明函数y 1sin1在区间(0 1]上无界这是因为 xx M 0在(0 1]中总可以找到点xk使y(xk) M例如当xk2k 1(k 0 1 2 )2时有y(xk) 2k2当k充分大时 y(xk) M当x 0+ 时函数y 1sin1不是无穷大这是因为 xxM 0对所有的 0总可以找到这样的点xk使0 xk但y(xk) M例如可取xk 12k(k 0 1 2 )当k充分大时 xk 但y(xk) 2k sin2k 0 M习题1 51计算下列极限2xlim5 (1)x 2x3x25 225 9lim解 x 2x3232x(2)3 x x 1解 2()23x3 0 2x x1() 12 x (3)limx 12x1 2x 1解2(x1)2x2x1x1 0 0lim lim limx 1x 1(x1)(x1)x 1x12x2 14x32x2xlim(4)x 02 3x2x3224x2x x4x2x1 1 lim解lim x 03x2xx 03x22 (x h)2x2lim(5)h 0h222(x h)2x2x2hx h xlim lim lim(2x h) 2x解h 0h 0h 0hh(6)xlim(211) xx21lim1 2解xlim(211 2lim x xx xxx2x1(7)xlim 2x2x 1 解 1 121 limlimx 1 2x 2x x1x 22xx2(8)xlim解或 x2x 42x3x12xx 0lim42(分子次数低于分母次数x x3x1112x lim23 0lim4x2 x x3x1x 1xx2极限为零) x6x8 (9)limx 4x5x 4解 2(x2)(x4)limx26x8 lim limx2 42 2x 4x5x4x 4(x1)(x4)x 4x1413(10)xlim(11)(21) 2xx1) lim(21 1 2 2解xlim(11)(21 lim(1 xx2x xx x2(11)nlim(111 1) 242n1(1)n 1lim(111 1) lim 2 n n 2421 2n 解 123 (n1) (12)nlim(n1)n123 (n1) 1limn1 1解nlim lim n 2n n2nn(n1)(n2)(n3)(13)nlim5n(n1)(n2)(n3)1 (分子与分母的次数相同解nlim 55n3极限为最高次项系数之比)或(n1)(n2)(n3)11)(1213 1 lim(1 3n n 5nnn55n(14)lim(1 33 x 11x1xlim解2131x x3 lim(1x)(x2)lim() limx 11x1x3x 1(1x)(x 1(1x)(1x x2)1x x2) limx 21 x 11x x2计算下列极限32x2x(1)x lim 2(x2)2解 (x2)20lim 0因为x 2x2x162x所以limx 22x2 (x2)23 x (2)xlim 2x 1解 2xlim x 2x1(因为分子次数高于分母次数)(2x3x1) (3)xlim解 x lim(2x3x1) (因为分子次数高于分母次数)3计算下列极限(1)limx2sin1 x 0x2解 limx2sin1 0(当x 0时 x是无穷小而sin1是有界变量)x 0xxarctanx (2)xlim xarctanx lim1 arctanx 0(当x 时 1是无穷小解xlim x xxx而arctan x是有界变量)4证明本节定理3中的(2)习题1 51计算下列极限2xlim5 (1)x 2x322x52lim 5 9解 x 2x32 3 2x(2)23 x x 1解 2()23x3 0 x x21()2 12 x (3)limx 12x1 2x 1解2(x1)2x2x1x1 0 0lim lim limx 1x 1(x1)(x1)x 1x12x 1 324x2x x(4)limx 03x22x4x32x2x lim4x22x1 1解 limx 03x22xx 03x22 (x h)2x2lim(5)h 0h222(x h)2x2x2hx h xlim lim lim(2x h) 2x解h 0h 0h 0hh(6)xlim(211) xx21lim1 2解xlim(211 2lim x xx x2xx2(7)xlim解x21 22x x1112x1lim2 lim 1x 2x x1x 222xx x2x x x43x212x x 0解xlim(分子次数低于分母次数 x3x1(8)lim极限为零)或112x lim 0lim4x2 x x3x1x 21124xx2 x6x8 (9)limx 42x5x 4解 2(x2)(x4)xlim26x8 lim limx2 42 2x 4x5x4x 4(x1)(x4)x 4x1413(10)xlim(11)(21) 2xx1) lim(21 1 2 2解xlim(11)(21 lim(1 xx2x xx x2(11)nlim(111 1) 242n1(1)n 1lim(111 1) lim 2 nn n 2421 2n 解 123 (n1) (12)nlim 2(n1)n123 (n1) 1limn1 1解nlim lim n 2n n2n2n2(n1)(n2)(n3)(13)nlim3 5n(n1)(n2)(n3)1 (分子与分母的次数相同解nlim 55n3极限为最高次项系数之比)或(n1)(n2)(n3)11)(1213 1 lim(1 n 5n nnn55n3(14)lim(1 33 x 11x1xlim解2131x x3 lim(1x)(x2)lim() limx 11x1xx 1(1x)(x 1(1x)(1x x)1x x) limx 22 1 x 11x x2计算下列极限 32x2xlim(1)x 2(x2)2解 (x2)20lim3 0因为x 2x2x21632x2x 所以limx 2(x2)2 x2lim(2)x 2x1 x2 解 xlim 2x1(因为分子次数高于分母次数)(2x3x1) (3)xlim解 x lim(2x3x1) (因为分子次数高于分母次数)3计算下列极限(1)limx2sin1 x 0x2解 limx2sin1 0(当x 0时 x是无穷小而sin1是有界变量)x 0xxarctan x (2)xlim xarctanx lim1 arctanx 0(当x 时1是无穷小解 xlim x xxx而arctan x是有界变量)4证明本节定理3中的(2)习题 171当x 0时 2x x2 与x2x3相比哪一个是高阶无穷小?解232x xx x lim 0因为limx 02x xx 02x所以当x 0时 x2x3是高阶无穷小即x2x3 o(2x x2)2当x 1时无穷小1x和(1)1x3 (2)1(1x2)是否同阶?是否等2价?解 3(1x)(1x x2)1x lim lim(1x x2) 3 (1)因为limx 11xx 1x 11x所以当x 1时 1x和1x3是同阶的无穷小但不是等价无穷小1(1x2) 1lim(1x) 1 (2)因为limx 11x2x 1所以当x 1时 1x和1(1x2)是同阶的无穷小而且是等价无穷小 23证明 当x 0时有(1) arctan x~x2x(2)secx1~2arctanx lim 证明 (1)因为limx 0y 0xy 1(提示 tany令y arctan x则当x 0时y 0)所以当x 0时 arctanx~x2sin2x2sinxsecx1 2lim1cosx lim lim(2 1 (2)因为limx 02x 0x2cosxx 0x 0x2x2222xsecx1~ 2 所以当x 0时4利用等价无穷小的性质求下列极限tan3x (1)limx 02xsin(xn)(2)limx 0(sinx)m(n m为正整数)tanx sinx (3)limx 0sinx(4)limx 0sinx tanx 2(x1sinx1)tan3x lim3x 3解 (1)limx 0x 02x2x21 n mn sin(xn)x 0 n m lim(2)limx 0(sinx)mx 0xm n m1x2sinx(11)tanx sinx lim lim1cosx lim2 1(3)lim332x 0x 0x 0cosxsinxx 0xcosx2sinxsinx(4)因为sinx tanx tanx(cosx1) 2tanxsin2x~2x x)2 1x3(x 0) 222所以x21 x21x2(x 0) ~1x2)2x213sinx~sinx~x(x 0) sinx1sinx1 1x3sinx tanxlim lim 3x 0(x21sinx1)x 02x x35证明无穷小的等价关系具有下列性质(1) ~ (自反性)(2) 若 ~ 则 ~ (对称性)(3)若 ~ ~ 则 ~ (传递性)证明 (1)lim 1所以 ~1从而lim 1因此 ~ (2) 若 ~ 则lim(3) 若 ~ ~习题18 lim lim lim 1 因此 ~1研究下列函数的连续性并画出函数的图形(1) x2 0 x 1 f(x) 2x 1 x 2解已知多项式函数是连续函数所以函数f(x)在[0 1)和(1 2]内是连续的在x 1处因为f(1) 1并且x 12f(x) lim(2x) 1 limf(x) limx 1lim x 1x 1x 1f(x) 1从而函数f(x)在x 1处是连续的所以limx 1综上所述,函数f(x)在[0 2]上是连续函数x 1 x 1 (2)f(x) 1 |x| 1解只需考察函数在x 1和x 1处的连续性在x 1处因为f(1) 1并且x 1limf(x) lim1 1 f(1) x 1x 1 x 1limf(x) lim x 1 f(1)所以函数在x 1处间断但右连续在x 1处因为f(1) 1并且x 1limf(x) lim x 1 f(1) limf(x) lim1 1 f(1) x 1x 1x 1所以函数在x 1处连续综合上述讨论函数在( 1)和(1 )内连续在x 1处间断但右连续2下列函数在指出的点处间断说明这些间断点属于哪一类如果是可去间断点则补充或改变函数的定义使它连续2x(1)y 21 x 1 x 2 x3x 2解 2(x1)(x1)xy 21 x3x2(x2)(x1)因为函数在x 2和x 1处无定义所以x 2和x 1是函数的间断点2xlimy lim21 因为x 2x 2x3x2所以x 2是函数的第二类间断点(x1)y lim 2所以x 1是函数的第一类间断点并且是可去因为limx 1x 1(x2)间断点在x 1处令y 2则函数在x 1处成为连续的(2)y x x k x k tanx2(k 0 1 2 )2 解函数在点x k (k Z)和x k (k Z)处无定义因而这些点都是函数的间断点因xlim k x (k 0) tanxx 1 tanxlimx k 故x k (k 0)是第二类间断点2 因为limx 0x 0(k Z) tanx所以x 0和x k (k Z) 是第一2类间断点且是可去间断点令y|x 0 1则函数在x 0处成为连续的令x k 时 y 0则函数在x k 处成为连续的2(3)y cos21 x 0 x2xx 解因为函数y cos21在x 0处无定义所以x 0是函数y cos21的间断点又因为limcos21不存在所以x 0是函数的第二类间断点x 0xx 1 x 1 (4)y 3 x x 1 x 1解因为xlim1f(x) lim(x1) 0limf(x) lim(3x) 2x 1x 1x 1所以x 1是函数的第一类不可去间断点 3讨论函数解2n1xf(x) limx的连续性 n 1x2n若有间断点判别其类型x |x| 12n 1xf(x) limx 0 |x| 1 n 1x2nx |x| 1f(x) lim(x) 1 lim f(x) lim x 1x 1x 1x 1lim 在分段点x 1处因为x1所以x 1为函数的第一类不可去间断点在分段点x 1处因为xlim 1f(x) lim x 1 limf(x) lim(x) 1x 1x 1x 1所以x 1为函数的第一类不可去间断点4证明 若函数f(x)在点x0连续且f(x0) 0则存在x0的某一邻域U(x0)当x U(x0)时 f(x) 0证明不妨设f(x0)>0因为f(x)在x0连续所以xlimx的局部保号性定理存在x0的某一去心邻域U(x0)f(x) f(x0) 0由极限f(x)>0使当x U(x0)时从而当x U(x0)时 f(x)>0这就是说则存在x0的某一邻域U(x0)当x U(x0)时 f(x) 05试分别举出具有以下性质的函数f(x)的例子 (1)x 0 12无穷间断点1 n 1 是2nf(x)的所有间断点且它们都是解函数f(x) csc( x)csc 在点x 0 1 2 x 1 n 1 处是间断2n的且这些点是函数的无穷间断点(2)f(x)在R上处处不连续但|f(x)|在R上处处连续1 x Q 解函数f(x) 1 x Q在R上处处不连续但|f(x)| 1在R上处处连续(3)f(x)在R上处处有定义但仅在一点连续x x Q 解函数f(x) 在R上处处有定义它只在x 0处连续x x Q习题191求函数f(x) xlimf(x) x 233x2x3的连续区间 2x x6f(x)并求极限limx 0x 3limf(x)及33x2x3 (x3)(x1)(x1)f(x) x(x3)(x2)x x 6 解函数在( )内除点x 2和x 3外是连续的所以函数f(x)的连续区间为( 3)、(3 2)、(2 )在函数的连续点x 0处 limf(x) f(0) 1 x 02在函数的间断点x 2和x 3处limf(x) limx 2(x1)(x1)(x3)(x1)(x1) 8limf(x) limx 3x 3x 2x25(x3)(x2) 2设函数f(x)与g(x)在点x0连续证明函数(x) max{f(x) g(x)} (x) min{f(x) g(x)} 在点x0也连续证明已知xlim x可以验证(x) 1[f(x)g(x)|f(x)g(x)| ]因此2 (x) 1[f(x)g(x)|f(x)g(x)| ]2 (x0) 1[f(x0)g(x0)|f(x0)g(x0)| ]2 (x0) 1[f(x0)g(x0)|f(x0)g(x0)| ] 20f(x) f(x0)limg(x) g(x0) x x0因为lim (x) lim1[f(x)g(x)|f(x)g(x)| ]x x0x x02 1[limf(x)limg(x)|limf(x)limg(x)| ]x x0x x0x x02x x01[f(x0)g(x0)|f(x0)g(x0)| ] (x0) 2所以 (x)在点x0也连续同理可证明 (x)在点x0也连续3求下列极限(1)limx 0x 4x22x5 (sin2x)3 (2)limln(2cos2x) (3)limx 6(4)limx 0x11 xx4x (5)limx 1x 1(6)xlimsinx sina ax a(7)xlim(x2x x2x)解 (1)因为函数f(x) x 0x22x5是初等函数f(x)在点x 0有定义所以 limx22x5 f(0) 22 054 (2)因为函数f(x) (sin 2x)3是初等函数 f(x)在点x 有定义所以lim(sin2x)3 f( (sin2 3 1 44x 46 (3)因为函数f(x) ln(2cos2x)是初等函数 f(x)在点x 有定义所以limln(2cos2x) f( ) ln(2cos2 0 66x(4)limx 0x11 lim(x11)(x11) limxx 0x 0x(x11xx(x11) )11 111112 limx 0(5)limx 1x4x lim(x4xx4x)x 1x1(x1x4x) lim444x4 lim 2x 1x4xx 1(x1x4x) 142cosx asinx alimsinx sina lim(6)x ax ax ax asinx a cosa a 1 cosalimcosx a limx a2x a2222(x2x x2x)(x2x x2x)(x x x x) lim(7)xlim 22 x (x x x x)lim2x2 lim 1 x (x2x x2x)x (11)xx4求下列极限(1)xlim(2)limlnsinx x 0x1ex(11)2 (3)xlim x2x(13tan2x)cotx (4)limx 0x13x( (5)xlim 6x(6)limx 0tanx sinxx sin2x xlime e1lim1x 解 (1) (2) (3) x e0 1 limlnsinx ln(limsinx) ln1 0x 0x 0xxx1lim(1 2x x limx 11x2(1)x e 12(4)lim(13tan2x)cotx limx 02x 0 1(13tan2x)3tan2x3 e3x13x 3 (5)(6x) (16x)36x2因为3(1)3 e lim3 x1 3 xlim x 6x26x23x2 e2所以xlim 6x(tanx sinx)(sin2x1)tanx sinx lim(6)lim22x 0x 0x sinx xx(sinx1)(tanx sinx)2xtanx 2sin(ta nx sinx sinx1) lim limx 0xsin2x(tanx sinx)x 0xsinx22x (x21 limx 02x应当如何选择数a使得f(x)成为在( 5设函数 ex x 0f(x) a x x 0)内的连续函数?解要使函数f(x)在( )内连续只须f(x)在x 0处连续即只须 x 0limf(x) limf(x) f(0) a x 0x 0 x 0f(x) limex 1因为xlim 0x 0limf(x) lim(a x) a所以只须取a 1习题1101证明方程x53x 1至少有一个根介于1和2之间证明设f(x) x53x1则f(x)是闭区间[1 2]上的连续函数因为f(1) 3 f(2) 25 f(1)f(2) 0所以由零点定理在(1 2)内至少有一点(1 2)使f( ) 0即x 是方程x53x 1的介于1和2之间的根因此方程x53x 1至少有一个根介于1和2之间2证明方程x asinx b其中a 0 b 0至少有一个正根并且它不超过a b证明设f(x) asin x b x则f(x)是[0 a b]上的连续函数f(0) b f(a b) a sin (a b)b(a b) a[sin(a b)1] 0若f(a b) 0则说明x a b就是方程x asinx b的一个不超过a b的根若f(a b) 0则f(0)f(a b) 0由零点定理至少存在一点(0 a b)使f( ) 0这说明x 也是方程x=asinx b的一个不超过a b的根总之方程x asinx b至少有一个正根并且它不超过a b 3设函数f(x)对于闭区间[a b]上的任意两点x、y恒有|f(x)f(y)| L|x y|其中L为正常数且f(a) f(b) 0证明 至少有一点 (a b)使得f( ) 0证明设x0为(a b)内任意一点因为所以 0 lim|f(x)f(x0)| limL|x x0| 0 x x0x x0x x0 lim|f(x)f(x0)| 0即 x x0limf(x) f(x0)因此f(x)在(a b)内连续同理可证f(x)在点a处左连续在点b处右连续所以f(x)在[a b]上连续因为f(x)在[a b]上连续且f(a) f(b) 0由零点定理至少有一点 (a b)使得f( ) 04若f(x)在[a b]上连续 a x1 x2 xn b则在[x1 xn]上至少有一点 使f( ) f(x1)f(x2) f(xn) n证明显然f(x)在[x1 xn]上也连续设M和m分别是f(x)在[x1 xn]上的最大值和最小值因为xi [x1 xn](1 i n)所以有m f(xi) M从而有n m f(x1)f(x2) f(xn) n M m f(x1)f(x2)f(xn) Mn由介值定理推论在[x1 xn]上至少有一点 使f( ) f(x)f(x) f(x) nf(x)存在则f(x)必在( 5证明 若f(x)在( )内连续且xlim)内有界f(x) A则对于给定的 0存在X 0只要|x| X就有证明令xlim|f(x)A| 即A f(x) A又由于f(x)在闭区间[X X]上连续根据有界性定理存在M 0使|f(x)| M x [X X]取N max{M |A | |A |}则|f(x)| N x ()即f(x)在( )内有界6在什么条件下 (a b)内的连续函数f(x)为一致连续?总习题一1在“充分”、“必要”和“充分必要”三者中选择一个正确的填入下列空格内(1)数列{xn}有界是数列{xn}收敛的________条件数列{xn}收敛是数列{xn}有界的________的条件(2)f(x)在x0的某一去心邻域内有界是xlim xx x00f(x)存在的________条件 limf(x)存在是f(x)在x0的某一去心邻域内有界的________条件0 (3) f(x)在x0的某一去心邻域内无界是xlim xx x0f(x) 的________条件 limf(x) 是f(x)在x0的某一去心邻域内无界的________条件(4)f(x)当x x0时的右极限f(x0)及左极限f(x0)都存在且相等是x x0limf(x)存在的________条件解 (1) 必要充分(2) 必要充分(3) 必要充分(4) 充分必要2选择以下题中给出的四个结论中一个正确的结论设f(x) 2x3x2则当x 0时有( )(A)f(x)与x是等价无穷小 (B)f(x)与x同阶但非等价无穷小(C)f(x)是比x高阶的无穷小 (D)f(x)是比x低阶的无穷小解xxxxf(x)232213 lim lim lim 1 因为limx 0xx 0x 0xx 0xxxxt ln3limu ln2ln3 ln2lim(令21 t 31 u)t 0ln(1t)u 0ln(1u)所以f(x)与x同阶但非等价无穷小故应选B3设f(x)的定义域是[0 1]求下列函数的定义域(1) f(ex)(2) f(ln x)(3) f(arctan x)(4) f(cos x)解 (1)由0 ex 1得x 0即函数f(ex)的定义域为( 0](2) 由0 ln x 1得1 x e 即函数f(ln x)的定义域为[1 e](3) 由0 arctan x 1得0 x tan 1即函数f(arctan x)的定义域为[0 tan 1](4) 由0 cos x 1得2n x 2n (n 0 1 2) 22即函数f(cos x)的定义域为[2n , n ] (n 0 12 ) 224设x 0 0 0 x 0 f(x) g(x) 2x x 0x x 0求f[f(x)] g[g(x)] f[g(x)] g[f(x)]0 x 0 解因为f(x) 0所以f[f(x)] f(x) x x 0因为g(x) 0所以g[g(x)] 0因为g(x) 0所以f[g(x)] 00 x 0 因为f(x) 0所以g[f(x)] f 2(x) 2 x x 05利用y sin x的图形作出下列函数的图形(1)y |sin x|(2)y sin|x|(3)y 2sinx 26把半径为R的一圆形铁片自中心处剪去中心角为 的一扇形后围成一无底圆锥试将这圆锥的体积表为 的函数解设围成的圆锥的底半径为r高为h依题意有R(2 ) 2 r222r R(2 ) 22R2(2 )24 h R r R R2 4 2圆锥的体积为V 13 R2(2 )2 24 R2R324 2(2 )2 4 a2 (0 2 )7根据函数极限的定义证明limx2x 6x 3x3 5证明对于任意给定的 0要使|x2x 6x35| 只需|x3| 取当0 |x3| 时就有|x3| 即|x2x65| 所以limx2x 6x3x 3x3 58求下列极限(1)limx2x 1x 1(x1)2(2)xlim x(x21x)(3)3xlim (2x2x1x1(4)limtanx sinxx 0x3(5)limxxx 0(a b cx3)(a 0 b 0 c 0)(6)lim(sinx)tanx x 2解 (1)因为lim(x1)2所以limx2x 1x 1x2x1 0 x 1(x1)(2)xlim x(x21x) x(x21x)(x21x)xlim (x21 x) x1xlim x21x xlim 1112x2x322x1x1() lim(1 lim(1)22(3)xlim 2x1x x 2x12x 1222(1)(1 2 xlim 2x12x 122(1) lim(1) e xlim x 2x12x 1sinx(11)sinx(1cosx)tanx sinx lim lim(4)limx 0x 0x 0x3x3x3cosxsinx 2sin2x2x (x)2lim 1 limx 0x 02x3cosxx3(提示 用等价无穷小换)(a (5)limx 0x b3x cx)x lim(1a b c。
同济大学版高等数学课后习题答案第2章

习题2-11. 设物体绕定轴旋转, 在时间间隔[0, t ]内转过的角度为θ, 从而转角θ是t 的函数: θ=θ(t ). 如果旋转是匀速的, 那么称t θω=为该物体旋转的角速度, 如果旋转是非匀速的, 应怎样确定该物体在时刻t 0的角速度? 解 在时间间隔[t 0, t 0+∆t ]内的平均角速度ω为tt t t t ∆-∆+=∆∆=)()(00θθθω,故t 0时刻的角速度为)()()(lim lim lim 000000t tt t t t t t t θθθθωω'=∆-∆+=∆∆==→∆→∆→∆.2. 当物体的温度高于周围介质的温度时, 物体就不断冷却, 若物体的温度T与时间t 的函数关系为T =T (t ), 应怎样确定该物体在时刻t 的冷却速度? 解 物体在时间间隔[t 0, t 0+∆t ]内, 温度的改变量为 ∆T =T (t +∆t )-T (t ),平均冷却速度为tt T t t T t T ∆-∆+=∆∆)()(,故物体在时刻t 的冷却速度为)()()(lim lim 00t T tt T t t T t T t t '=∆-∆+=∆∆→∆→∆.3. 设某工厂生产x 单位产品所花费的成本是f (x )元, 此函数f (x )称为成本函数, 成本函数f (x )的导数f '(x )在经济学中称为边际成本. 试说明边际成本f '(x )的实际意义.解 f (x +∆x )-f (x )表示当产量由x 改变到x +∆x 时成本的改变量.xx f x x f ∆-∆+)()(表示当产量由x 改变到x +∆x 时单位产量的成本.xx f x x f x f x ∆-∆+='→∆)()(lim )(0表示当产量为x 时单位产量的成本.4. 设f (x )=10x 2, 试按定义, 求f '(-1).解 xx x f x f f x x ∆--∆+-=∆--∆+-=-'→∆→∆2200)1(10)1(10lim)1()1(lim )1( 20)2(lim 102lim 10020-=∆+-=∆∆+∆-=→∆→∆x xx x x x .5. 证明(cos x )'=-sin x .解 xxx x x x ∆-∆+='→∆cos )cos(lim )(cos 0xxx x x ∆∆∆+-=→∆2sin )2sin(2lim0 x x xx x x sin ]22sin )2sin([lim 0-=∆∆∆+-=→∆. 6. 下列各题中均假定f '(x 0)存在, 按照导数定义观察下列极限, 指出A 表示什么:(1)A xx f x x f x =∆-∆-→∆)()(lim000;解 xx f x x f A x ∆-∆-=→∆)()(lim 000)()()(lim 0000x f x x f x x f x '-=∆--∆--=→∆-.(2)A xx f x =→)(lim 0, 其中f (0)=0, 且f '(0)存在;解 )0()0()0(lim )(lim 00f x f x f x x f A x x '=-+==→→.(3)A hh x f h x f h =--+→)()(lim 000.解 hh x f h x f A h )()(lim 000--+=→hx f h x f x f h x f h )]()([)]()([lim 00000----+=→hx f h x f h x f h x f h h )()(lim)()(lim 000000----+=→→ =f '(x 0)-[-f '(x 0)]=2f '(x 0). 7. 求下列函数的导数: (1)y =x 4; (2)32x y =; (3)y =x 1. 6;(4)xy 1=;(5)21x y =;(6)53x x y =;(7)5322x x x y =; 解 (1)y '=(x 4)'=4x 4-1=4x 3 . (2)3113232323232)()(--=='='='x x x xy . (3)y '=(x 1. 6)'=1.6x 1. 6-1=1.6x 0. 6.(4)23121212121)()1(-----=-='='='x x x xy .(5)3222)()1(---='='='x x x y . (6)511151651653516516)()(x x x x xy =='='='-.(7)651616153226161)()(--=='='='x x x x x x y .8. 已知物体的运动规律为s =t 3(m). 求这物体在t =2秒(s )时的速度. 解v =(s )'=3t 2, v |t =2=12(米/秒).9. 如果f (x )为偶函数, 且f (0)存在, 证明f (0)=0. 证明 当f (x )为偶函数时, f (-x )=f (x ), 所以)0(0)0()(lim 0)0()(lim 0)0()(lim)0(000f x f x f x f x f x f x f f x x x '-=-----=---=--='→-→→,从而有2f '(0)=0, 即f '(0)=0. 10. 求曲线y =sin x 在具有下列横坐标的各点处切线的斜率: π32=x , x =π.解 因为y '=cos x , 所以斜率分别为 2132cos 1-==πk , 1cos 2-==πk .11. 求曲线y =cos x 上点)21 ,3(π处的切线方程和法线方程式.解y '=-sin x , 233sin 3-=-='=ππx y ,故在点)21 ,3(π处, 切线方程为)3(2321π--=-x y , 法线方程为)3(3221π--=-x y .12. 求曲线y =e x 在点(0,1)处的切线方程. 解y '=e x , y '|x =0=1, 故在(0, 1)处的切线方程为 y -1=1⋅(x -0), 即y =x +1.13. 在抛物线y =x 2上取横坐标为x 1=1及x 2=3的两点, 作过这两点的割线, 问该抛物线上哪一点的切线平行于这条割线? 解 y '=2x , 割线斜率为421913)1()3(=-=--=y y k . 令2x =4, 得x =2.因此抛物线y =x 2上点(2, 4)处的切线平行于这条割线. 14. 讨论下列函数在x =0处的连续性与可导性: (1)y =|sin x |;(2)⎪⎩⎪⎨⎧=≠=0001sin 2x x xx y . 解 (1)因为y (0)=0, 0)sin (lim |sin |lim lim 0=-==---→→→x x y x x x ,0sin lim |sin |lim lim 00===+++→→→x x y x x x ,所以函数在x =0处连续. 又因为1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000-=-=--=--='---→→→-xx x x x y x y y x x x ,1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000==--=--='+++→→→+xx x x x y x y y x x x , 而y '-(0)≠y '+(0), 所以函数在x =0处不可导.解 因为01sin lim )(lim 200==→→xx x y x x , 又y (0)=0, 所以函数在x =0处连续.又因为01sin lim 01sin lim 0)0()(lim0200==-=--→→→xx x x x x y x y x x x , 所以函数在点x =0处可导, 且y '(0)=0.15. 设函数⎩⎨⎧>+≤=1 1)(2x b ax x x x f 为了使函数f (x )在x =1处连续且可导, a , b 应取什么值? 解 因为1lim )(lim 211==--→→x x f x x , b a b ax x f x x +=+=++→→)(lim )(lim 11, f (1)=a +b ,所以要使函数在x =1处连续, 必须a +b =1 . 又因为当a +b =1时211lim )1(21=--='-→-x x f x , a x x a x b a x a x b ax f x x x =--=--++-=--+='+++→→→+1)1(lim 11)1(lim 11lim )1(111,所以要使函数在x =1处可导, 必须a =2, 此时b =-1.16. 已知⎩⎨⎧<-≥=0 0)(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在?解 因为f -'(0)=10lim )0()(lim 00-=--=---→→xx x f x f x x ,f +'(0)=00lim )0()(lim 200=-=-++→→xx x f x f x x ,而f -'(0)≠f +'(0), 所以f '(0)不存在. 17. 已知f (x )=⎩⎨⎧≥<0 0sin x x x x , 求f '(x ) .解 当x <0时, f (x )=sin x , f '(x )=cos x ; 当x >0时, f (x )=x , f '(x )=1;因为 f -'(0)=10sin lim )0()(lim 00=-=---→→xx x f x f x x ,f +'(0)=10lim )0()(lim 00=-=-++→→x x x f x f x x , 所以f '(0)=1, 从而f '(x )=⎩⎨⎧≥<0 10cos x x x .18. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 .解 由xy =a 2得x a y 2=, 22xa y k -='=. 设(x 0, y 0)为曲线上任一点, 则过该点的切线方程为)(02020x x x a y y --=-.令y =0, 并注意x 0y 0=a 2, 解得0022002x x ax y x =+=, 为切线在x 轴上的距.令x =0, 并注意x 0y 0=a 2, 解得00022y y x a y =+=, 为切线在y 轴上的距. 此切线与二坐标轴构成的三角形的面积为 200002||2|2||2|21a y x y x S ===.习题 2-21. 推导余切函数及余割函数的导数公式: (cot x )'=-csc 2x ; (csc x )'=-csc x cot x .解 x x x x x x x x 2sin cos cos sin sin )sin cos ()(cot ⋅-⋅-='=' x xx x x 22222csc sin 1sin cos sin -=-=+-=. x x xx x x cot csc sin cos)sin 1()(csc 2⋅-=-='='. 2. 求下列函数的导数: (1)1227445+-+=xx x y ;(2) y =5x 3-2x +3e x ; (3) y =2tan x +sec x -1; (4) y =sin x ⋅cos x ; (5) y =x 2ln x ; (6) y =3e x cos x ; (7)x x y ln =;(8)3ln 2+=xe y x ; (9) y =x 2ln x cos x ;(10)tt s cos 1sin 1++=;解 (1))12274()12274(14545'+-+='+-+='---x x x xx x y 2562562282022820x x x x x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3e x .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ⋅tan x =sec x (2sec x +tan x ). (4) y '=(sin x ⋅cos x )'=(sin x )'⋅cos x +sin x ⋅(cos x )' =cos x ⋅cos x +sin x ⋅(-sin x )=cos 2x . (5) y '=(x 2ln x )'=2x ⋅ln x +x 2⋅x1=x (2ln x +1) .(6) y '=(3e x cos x )'=3e x ⋅cos x +3e x ⋅(-sin x )=3e x (cos x -sin x ).(7)22ln 1ln 1)ln (x x x xx x x x y -=-⋅='='. (8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=⋅-⋅='+='. (9) y '=(x 2ln x cos x )'=2x ⋅ln x cos x +x 2⋅x1⋅cos x +x 2 ln x ⋅(-sin x )2x ln x cos x +x cos x -x 2 ln x sin x . (10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t tt t t t t t t t s +++=+-+-+='++='.3. 求下列函数在给定点处的导数: (1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=d d .(3)553)(2x x x f +-=, 求f '(0)和f '(2) . 解 (1)y '=cos x +sin x ,21321236sin 6cos 6+=+=+='=πππx y ,222224sin 4cos 4=+=+='=πππx y . (2)θθθθθθθθρcos sin 21sin 21cos sin +=-+=d d ,)21(4222422214cos 44sin 214πππππθρπθ+=⋅+⋅=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=.求:(1)该物体的速度v (t ); (2)该物体达到最高点的时刻. 解 (1)v (t )=s '(t )=v 0-gt . (2)令v (t )=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻. 5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程. 解 因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x , 所求的法线方程为x y 21-=, 即x +2y =0.6. 求下列函数的导数: (1) y =(2x +5)4 (2) y =cos(4-3x ); (3)23x e y -=; (4) y =ln(1+x 2); (5) y =sin 2x ; (6)22x a y -=; (7) y =tan(x 2); (8) y =arctan(e x ); (9) y =(arcsin x )2; (10) y =lncos x .解 (1) y '=4(2x +5)4-1⋅(2x +5)'=4(2x +5)3⋅2=8(2x +5)3. (2) y '=-sin(4-3x )⋅(4-3x )'=-sin(4-3x )⋅(-3)=3sin(4-3x ). (3)22233236)6()3(x x x xe x e x e y ----=-⋅='-⋅='. (4)222212211)1(11xx x x x x y +=⋅+='+⋅+='.(5) y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x . (6))()(21])[(22121222122'-⋅-='-='-x a x a x a y222122)2()(21xa x x x a --=-⋅-=-.(7) y '=sec 2(x 2)⋅(x 2)'=2x sec 2(x 2). (8)xx x x e e e e y 221)()(11+='⋅+='.(9) y '21arcsin 2)(arcsin arcsin 2x x x x -='⋅=.(10)x x xx x y tan )sin (cos 1)(cos cos 1-=-='⋅='.7. 求下列函数的导数: (1) y =arcsin(1-2x ); (2)211x y -=; (3)x e y x 3cos 2-=;(4)xy 1arccos =;(5)xx y ln 1ln 1+-=;(6)x x y 2sin =;(7)x y arcsin =; (8))ln(22x a x y ++=; (9) y =ln(sec x +tan x ); (10) y =ln(csc x -cot x ). 解 (1)2221)21(12)21()21(11xx x x x y --=---='-⋅--='.(2))1()1(21])1[(21212212'-⋅--='-='---x x x y222321)1()2()1(21xx x x x --=-⋅--=-.(3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y xxx x )3sin 63(cos 213sin 33cos 21222x x e x e x e xxx +-=--=---.(4)1||)1()1(11)1()1(1122222-=---='--='x x x x x x x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='. (6)222sin 2cos 212sin 22cos x x x x x x x x y -=⋅-⋅⋅='. (7)2222121)(11)()(11x x x x x x y -=⋅-='⋅-='. (8)])(211[1)(12222222222'+++⋅++='++⋅++='x a x a x a x x a x x a x y 2222221)]2(211[1xa x x a x a x +=++⋅++=. (9) x xx x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12=++='+⋅+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12=-+-='-⋅-='.8. 求下列函数的导数: (1)2)2(arcsin x y =;(2)2tan ln x y =;(3)x y 2ln 1+=; (4)xe y arctan=;(5)y =sin n x cos nx ;(6)11arctan -+=x x y ;(7)x x y arccos arcsin =;(8) y =ln[ln(ln x )] ; (9)x x x x y -++--+1111;(10)xx y +-=11arcsin .解 (1)'⋅=')2(arcsin )2(arcsin 2x x y)2()2(11)2(arcsin 22'⋅-⋅=x x x 21)2(11)2(arcsin 22⋅-⋅=x x . 242arcsin 2x x-=(2))2(2sec 2tan 1)2(tan 2tan 12'⋅⋅='⋅='x x x x x yx x x csc 212sec 2tan 12=⋅⋅=.(3))ln 1(ln 121ln 1222'+⋅+=+='x x x y )(ln ln 2ln 1212'⋅⋅+=x x x x x x1ln 2ln 1212⋅⋅+=x x x 2ln 1ln +=.(4))(arctan arctan '⋅='x e y x )()(112arctan '⋅+⋅=x x e x)1(221)(11arctan 2arctan x x e x x exx+=⋅+⋅=.(5) y '=n sin n -1x ⋅(sin x )'⋅cos nx +sin n x ⋅(-sin nx )⋅(nx )' =n sin n -1x ⋅cos x ⋅cos nx +sin n x ⋅(-sin nx )⋅n=n sin n -1x ⋅(cos x ⋅cos nx -sin x ⋅sin nx )= n sin n -1x cos(n +1)x . (6)222211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--⋅-++='-+⋅-++='. (7)222)(arccos arcsin 11arccos 11x x x x x y -+-=' 22)(arccos arcsin arccos 11x x x x +⋅-=22)(arccos 12x x -=π.(8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'⋅⋅='⋅='x xx x x y)ln(ln ln 11ln 1)ln(ln 1x x x x x x ⋅=⋅⋅=.(9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111xx -+-=. (10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-⋅+--='+-⋅+--=' )1(2)1(1x x x -+-=. 9. 设函数f (x )和g (x )可导, 且f 2(x )+g 2(x )≠0, 试求函数)()(22x g x f y +=的导数.解 ])()([)()(212222'+⋅+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'⋅+=)()()()()()(22x g x f x g x g x f x f +'+'=.10. 设f (x )可导, 求下列函数y 的导数dxdy : (1) y =f (x 2);(2) y =f (sin 2x )+f (cos 2x ).解 (1) y '=f '(x 2)⋅(x 2)'= f '(x 2)⋅2x =2x ⋅f '(x 2). (2) y '=f '(sin 2x )⋅(sin 2x )'+f '(cos 2x )⋅(cos 2x )'= f '(sin 2x )⋅2sin x ⋅cos x +f '(cos 2x )⋅2cos x ⋅(-sin x ) =sin 2x [f '(sin 2x )- f '(cos 2x )]. 11. 求下列函数的导数: (1) y =ch(sh x ); (2) y =sh x ⋅e ch x ; (3) y =th(ln x ); (4) y =sh 3x +ch 2x ; (5) y =th(1-x 2); (6) y =arch(x 2+1); (7) y =arch(e 2x ); (8) y =arctan(th x ); (9)xx y 2ch 21ch ln +=;(10))11(ch 2+-=x x y解 (1) y '=sh(sh x )⋅(sh x )'=sh(sh x )⋅ch x . (2) y '=ch x ⋅e ch x +sh x ⋅e ch x ⋅sh x =e ch x (ch x +sh 2x ) .(3))(ln ch 1)(ln )(ln ch 122x x x x y ⋅='⋅='.(4) y '=3sh 2x ⋅ch x +2ch x ⋅sh x =sh x ⋅ch x ⋅(3sh x +2) . (5))1(ch 2)1()1(ch 122222x x x x y --=-⋅-='.(6)222)1()1(112422++='+⋅++='x x x x x y .(7)12)(1)(142222-='⋅-='x xx x e e e e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11⋅+=⋅+='⋅+=' xx x 222sh 211sh ch 1+=+=.(9))ch (ch 21)ch (ch 124'⋅-'⋅='x xx x yx x xx x sh ch 2ch 21ch sh 4⋅⋅-=x x x x x x x x 323ch sh ch sh ch sh ch sh -⋅=-= x xxx x x 33332th ch sh ch )1ch (sh ==-⋅=. (10)'+-⋅+-⋅+-='+-⋅+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y)112(sh )1(2)1()1()1()112(sh 22+-⋅+=+--+⋅+-⋅=x x x x x x x x . 12. 求下列函数的导数: (1) y =e -x (x 2-2x +3); (2) y =sin 2x ⋅sin(x 2); (3)2)2(arctan x y =;(4)n x x y ln =;(5)t t t t ee e e y --+-=; (6)xy 1cos ln =;(7)x ey 1sin 2-=;(8)x x y +=;(9) 242arcsin x x x y -+=;(10)212arcsin tt y +=.解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2) =e -x (-x 2+4x -5).(2) y '=2sin x ⋅cos x ⋅sin(x 2)+sin 2x ⋅cos(x 2)⋅2x =sin2x ⋅sin(x 2)+2x ⋅sin 2x ⋅cos(x 2). (3)2arctan 44214112arctan 222x x x x y +=⋅+⋅='.(4)121ln 1ln 1+--=⋅-⋅='n n n n x x n x nx x x xy . (5)2222)1(4)())(())((+=+---++='-----t t t t t t t t t t t t e e e e e e e e e e e e y .(6)x x x x x x x y 1tan 1)1()1sin (1sec )1(cos 1sec 22=-⋅-⋅='⋅='. (7))1(1cos )1sin 2()1sin (21sin 21sin 22x x x e x ey x x -⋅⋅-⋅='-⋅='--x e x x1sin 222sin 1-⋅⋅=. (8))211(21)(21x xx x x x x y +⋅+='+⋅+='xx x x +⋅+=412.(9)2arcsin )2(421214112arcsin 22x x x x x x y =-⋅-+⋅-⋅+='.(10)22222222)1()2(2)1(2)12(11)12()12(11t t t t tt t t t t y +⋅-+⋅⋅+-='+⋅+-=' )1(|1|)1(2)1()1(2)1(1222222222t t t t t t t +--=+-⋅-+=.习题 2-31. 求函数的二阶导数: (1) y =2x 2+ln x ; (2) y =e 2x -1; (3) y =x cos x ; (4) y =e -t sin t ; (5)22x a y -=; (6) y =ln(1-x 2) (7) y =tan x ;(8)113+=x y ;(9) y =(1+x 2)arctan x ;(10)xe y x =; (11)2x xe y =;(12))1ln(2x x y ++=. 解 (1)x x y 14+=', 214xy -=''.(2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1. (3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x . (4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t .(5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a xa x a xx x a y ---=---⋅---=''.(6) 22212)1(11x x x x y --='-⋅-=',222222)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''.(7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y ,333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y . (9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y ,212arctan 2xx x y ++=''.(10)22)1(1x x e x e x e y x x x -=⋅-⋅=', 3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''. (12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=',xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222.2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3, f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxyd :(1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2). (2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=.4. 试从y dy dx '=1导出:(1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==. (2)(())(())dy dx y y dx d y y dy d dy xd ⋅'''-='''-=3333 52623)()(31)()(3)(y y y y y y y y y y y '''''-''='⋅''''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω.解 t A dt ds ωωcos =,t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0sin sin 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式: y ''-λ2y =0 . 解 y '=C 1λe λx -C 2λe -λx , y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx ) =(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 . 7. 验证函数y =e x sin x 满足关系式: y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x . y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x =2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数); (2) y =sin 2x ; (3) y =x ln x ; (4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1,y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! . (2) y '=2sin x cos x =sin2x , )22sin(22cos 2π+==''x x y ,)222sin(2)22cos(222ππ⋅+=+='''x x y ,)232sin(2)222cos(233)4(ππ⋅+=⋅+=x x y ,⋅ ⋅ ⋅,]2)1(2sin[21)(π⋅-+=-n x y n n .(3) 1ln +='x y , 11-==''x x y ,y '''=(-1)x -2, y (4)=(-1)(-2)x -3, ⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x , y '''=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) . 9. 求下列函数所指定的阶的导数: (1) y =e x cos x , 求y (4) ; (2) y =x sh x , 求y (100) ; (3) y =x 2sin 2x , 求y (50) . 解 (1)令u =e x , v =cos x , 有 u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x , 所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x . (2)令u =x , v =sh x , 则有 u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x ,所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x . (3)令u =x 2 , v =sin 2x , 则有 u '=2x , u ''=2, u '''=0;x x v 2sin 2)2482sin(24848)48(=⋅+=π,v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅= )50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''= )2sin 2(2cos 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2sin 212252cos 502sin (2250x x x x x ++-=.习题 2-31. 求函数的二阶导数: (1) y =2x 2+ln x ; (2) y =e 2x -1; (3) y =x cos x ; (4) y =e -t sin t ; (5)22x a y -=; (6) y =ln(1-x 2) (7) y =tan x ; (8)113+=x y ;(9) y =(1+x 2)arctan x ;(10)xe y x =;(11)2x xe y =;(12))1ln(2x x y ++=. 解 (1)x x y 14+=', 214xy -=''.(2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1. (3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x . (4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t . (5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a xa x a xx x a y ---=---⋅---=''.(6) 22212)1(11xx x x y --='-⋅-=',222222)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''. (7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y , 333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y .(9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y ,212arctan 2xx x y ++=''.(10)22)1(1x x e x e x e y x x x -=⋅-⋅=',3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''. (12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=',xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222. 2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3, f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxyd :(1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2). (2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=.4. 试从y dy dx '=1导出:(1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==.(2)(())(())dy dx y y dx d y y dy d dy xd ⋅'''-='''-=3333 52623)()(31)()(3)(y y y y y y y y y y y '''''-''='⋅''''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω. 解 t A dt ds ωωcos =,t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0sin sin 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式:y ''-λ2y =0 . 解 y '=C 1λe λx -C 2λe -λx , y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx ) =(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 . 7. 验证函数y =e x sin x 满足关系式: y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x . y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x =2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数); (2) y =sin 2x ;(3) y =x ln x ; (4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1,y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! . (2) y '=2sin x cos x =sin2x , )22sin(22cos 2π+==''x x y ,)222sin(2)22cos(222ππ⋅+=+='''x x y ,)232sin(2)222cos(233)4(ππ⋅+=⋅+=x x y ,⋅ ⋅ ⋅,]2)1(2sin[21)(π⋅-+=-n x y n n .(3) 1ln +='x y , 11-==''x x y ,y '''=(-1)x -2, y (4)=(-1)(-2)x -3, ⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x , y '''=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) . 9. 求下列函数所指定的阶的导数: (1) y =e x cos x , 求y (4) ; (2) y =x sh x , 求y (100) ; (3) y =x 2sin 2x , 求y (50) .解 (1)令u =e x , v =cos x , 有 u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x , 所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x . (2)令u =x , v =sh x , 则有 u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x , 所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x . (3)令u =x 2 , v =sin 2x , 则有 u '=2x , u ''=2, u '''=0;x x v 2sin 2)2482sin(24848)48(=⋅+=π,v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅= )50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''= )2sin 2(2cos 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2sin 212252cos 502sin (2250x x x x x ++-=.习题2-41. 求由下列方程所确定的隐函数y 的导数dxdy : (1) y 2-2x y +9=0; (2) x 3+y 3-3axy =0; (3) xy =e x +y ; (4) y =1-xe y .解 (1)方程两边求导数得2y y '-2y -2x y ' =0 , 于是 (y -x )y '=y , xy y y -='. (2)方程两边求导数得3x 2+3y 2y '-2ay -3axy '=0, 于是 (y 2-ax )y '=ay -x 2 ,axy x ay y --='22.(3)方程两边求导数得 y +xy '=e x +y (1+y '), 于是 (x -e x +y )y '=e x +y -y ,yx y x e x ye y ++--='.(4)方程两边求导数得 y '=-e y -xe y y ', 于是 (1+xe y )y '=-e y ,yy xe e y +-='1. 2.求曲线323232a y x =+在点)42 ,42(a a 处的切线方程和法线方程.解 方程两边求导数得 032323131='+--y y x ,于是 3131---='y x y ,在点)42 ,42(a a 处y '=-1.所求切线方程为)42(42a x a y --=-, 即a y x 22=+.所求法线方程为)42(42a x a y -=-, 即x -y =0.3. 求由下列方程所确定的隐函数y 的二阶导数22dxyd :(1) x 2-y 2=1;(2) b 2x 2+a 2y 2=a 2b 2; (3) y =tan(x +y ); (4) y =1+xe y .解 (1)方程两边求导数得 2x -2yy '=0, y '=y x ,3322221)(y y x y y y xx y y y x y y x y -=-=-='-='=''. (2)方程两边求导数得2b 2x +2a 2yy '=0,yx a b y ⋅-='22, 22222222)(y yx a b x y a b y y x y a b y ⋅--⋅-='-⋅-=''32432222222ya b y a x b y a a b -=+⋅-=. (3)方程两边求导数得y '=sec 2(x +y )⋅(1+y '),1)(cos 1)(sec 1)(sec 222-+=+-+='y x y x y x y 222211)(sin )(cos )(sin y y x y x y x --=+-+++=, 52233)1(2)11(22yy y y y y y +-=--='=''. (4)方程两边求导数得y '=e y +xe y y ',ye y e xe e y y y y y -=--=-='2)1(11, 3222)2()3()2()3()2()()2(y y e y y y e y y e y y e y y y y y --=-'-=-'---'=''.4. 用对数求导法求下列函数的导数:(1) x xx y )1(+=;(2)55225+-=x x y ;(3)54)1()3(2+-+=x x x y ;(4)x e x x y -=1sin . 解 (1)两边取对数得ln y =x ln|x |-x ln|1+x |, 两边求导得xx x x x x y y +⋅-+-⋅+='11)1ln(1ln 1,于是 ]111[ln )1(xx x x x y x ++++='.(2)两边取对数得)2ln(251|5|ln 51ln 2+--=x x y ,两边求导得22251515112+⋅--⋅='x x x y y , 于是 ]225151[25512552+⋅--=+-='x x x x x y .(3)两边取对数得)1ln(5)3ln(4)2ln(21ln +--++=x x x y ,两边求导得1534)2(211+---+='x x x y y ,于是 ]1534)2(21[)1()3(254+--+++-+='x x x x x x y。
高等数学上复旦第三版 课后习题答案

283高等数学上(修订版)(复旦出版社)习题六 无穷数级 答案详解1.写出下列级数的一般项: (1)1111357++++ ;(2)22242462468x x x x x ++++⋅⋅⋅⋅⋅⋅ ;(3)35793579a a a a -+-+ ;解:(1)121n U n =-; (2)()2!!2n n xU n =;(3)()211121n n n a U n ++=-+; 2.求下列级数的和: (1)()()()1111n x n x n x n ∞=+-+++∑;(2)()1221n n n n ∞=+-++∑;(3)23111555+++ ; 解:(1)()()()()()()()111111211n u x n x n x n x n x n x n x n =+-+++⎛⎫-=⎪+-++++⎝⎭284从而()()()()()()()()()()()()()()11111211212231111111211n S x x x x x x x x x n x n x n x n x x x n x n ⎛-+-= +++++++⎝⎫++-⎪+-++++⎭⎛⎫-=⎪++++⎝⎭因此()1lim 21n n S x x →∞=+,故级数的和为()121x x +(2)因为()()211n U n n n n =-+-++- 从而()()()()()()()()324332215443211211211221n S n n n n n n n n =-+-----+-++---+-++-=+-++-=+-+++所以lim 12n n S →∞=-,即级数的和为12-. (3)因为21115551115511511145n nn n S =+++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎣⎦=-⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎣⎦ 从而1lim 4n n S →∞=,即级数的和为14. 3.判定下列级数的敛散性: (1) ()11n n n ∞=+-∑;(2)()()11111661111165451n n +++++⋅⋅⋅-+ ; (3) ()23133222213333n n n --+-++- ;285(4)311115555n +++++ ; 解:(1) ()()()3212111n S n n n =+++-+--=+-从而lim n n S →∞=+∞,故级数发散. (2) 1111111115661111165451111551n S n n n ⎛⎫=-+-+-++-⎪-+⎝⎭⎛⎫=- ⎪+⎝⎭从而1lim 5n n S →∞=,故原级数收敛,其和为15. (3)此级数为23q =-的等比级数,且|q |<1,故级数收敛. (4)∵15n n U =,而lim 10n n U →∞=≠,故级数发散. 4.利用柯西审敛原理判别下列级数的敛散性:(1) ()111n n n +∞=-∑;(2)1cos 2nn nx∞=∑; (3)1111313233n n n n ∞=⎛⎫+- ⎪+++⎝⎭∑. 解:(1)当P 为偶数时,()()()()122341111112311111231111112112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n p n n n +++++++++++----=++++++++-+--=++++⎛⎫⎛⎫-=----- ⎪ ⎪+-+-++++⎝⎭⎝⎭<+当P 为奇数时,286()()()()1223411111123111112311111112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n n n +++++++++++----=++++++++-+-+=++++⎛⎫⎛⎫-=---- ⎪ ⎪+-++++⎝⎭⎝⎭<+因而,对于任何自然数P ,都有12111n n n p U U U n n++++++<<+ , ∀ε>0,取11N ε⎡⎤=+⎢⎥⎣⎦,则当n >N 时,对任何自然数P 恒有12n n n pU U U ε++++++< 成立,由柯西审敛原理知,级数()111n n n +∞=-∑收敛. (2)对于任意自然数P ,都有()()()1212121cos cos cos 12222111222111221121112212n n n p n n n p n n n p n p n p nU U U x n p x xn n ++++++++++++++++=+++≤+++⎛⎫- ⎪⎝⎭=-⎛⎫=- ⎪⎝⎭<于是, ∀ε>0(0<ε<1),∃N =21log ε⎡⎤⎢⎥⎣⎦,当n >N 时,对任意的自然数P都有12n n n p U U U ε++++++< 成立,由柯西审敛原理知,该级数收敛. (3)取P =n ,则287()()()()()121111113113123133213223231131132161112n n n pU U U n n n n n n n n n n ++++++⎛⎫=+-+++- ⎪++++++⋅+⋅+⋅+⎝⎭≥++++⋅+≥+> 从而取0112ε=,则对任意的n ∈N ,都存在P =n 所得120n n n p U U U ε++++++> ,由柯西审敛原理知,原级数发散.5.用比较审敛法判别下列级数的敛散性. (1)()()111465735n n ++++⋅⋅++ ;(2)22212131112131nn +++++++++++ (3)1πsin 3n n ∞=∑;(4) 3112n n∞=+∑;(5)()1101nn a a∞=>+∑;(6)()1121nn ∞=-∑.解:(1)∵ ()()21135n U nn n =<++而211n n ∞=∑收敛,由比较审敛法知1n n U ∞=∑收敛. (2)∵221111n n n U n n n n++=≥=++ 而11n n∞=∑发散,由比较审敛法知,原级数发散.(3)∵ππsinsin 33lim lim ππ1π33n nn n n n→∞→∞=⋅=288而1π3n n ∞=∑收敛,故1πsin 3n n ∞=∑也收敛.(4)∵33321112n U nnn=<=+ 而3121n n∞=∑收敛,故3112n n∞=+∑收敛.(5)当a >1时,111n n n U a a =<+,而11n n a ∞=∑收敛,故111nn a∞=+∑也收敛. 当a =1时,11lim lim 022n n n U →∞→∞==≠,级数发散. 当0<a <1时,1lim lim 101n n n n U a →∞→∞==≠+,级数发散. 综上所述,当a >1时,原级数收敛,当0<a ≤1时,原级数发散.(6)由021limln 2xx x →-=知121lim ln 211nx n→∞-=<而11n n∞=∑发散,由比较审敛法知()1121nn ∞=-∑发散.6.用比值判别法判别下列级数的敛散性:(1) 213n n n ∞=∑;(2)1!31nn n ∞=+∑; (3)232333*********nn n +++++⋅⋅⋅⋅ ; (1) 12!n n n n n ∞=⋅∑解:(1) 23n n n U =,()2112311lim lim 133n n n n n n U n U n ++→∞→∞+=⋅=<, 由比值审敛法知,级数收敛.289(2) ()()111!311lim lim 31!31lim 131n n n n n nn n n U n U n n ++→∞→∞+→∞++=⋅++=⋅++=+∞所以原级数发散.(3) ()()11132lim lim 2313lim 21312n nn n n n n nn U n U n n n +++→∞→∞→∞⋅=⋅⋅+=+=> 所以原级数发散.(4) ()()1112!1lim lim 2!1lim 21122lim 1e 11n nn n n n n nnn n n U n n U n n n n n +++→∞→∞→∞→∞⋅+=⋅⋅+⎛⎫= ⎪+⎝⎭==<⎛⎫+ ⎪⎝⎭故原级数收敛.7.用根值判别法判别下列级数的敛散性:(1) 1531nn n n ∞=⎛⎫⎪+⎝⎭∑;(2)()[]11ln 1nn n ∞=+∑;(3) 21131n n n n -∞=⎛⎫⎪-⎝⎭∑;(4) 1nn n b a ∞=⎛⎫⎪⎝⎭∑,其中a n →a (n →∞),a n ,b ,a 均为正数.解:(1)55lim lim 1313n n n n n U n →∞→∞==>+, 故原级数发散.(2) ()1lim lim 01ln 1n n n n U n →∞→∞==<+,290故原级数收敛.(3)121lim lim 1931nn nn n n U n -→∞→∞⎛⎫==< ⎪-⎝⎭, 故原级数收敛.(4) limlim nn n n n nb b b a a a →∞→∞⎛⎫== ⎪⎝⎭, 当b <a 时,ba <1,原级数收敛;当b >a 时,b a>1,原级数发散;当b =a 时,b a=1,无法判定其敛散性.8.判定下列级数是否收敛?若收敛,是绝对收敛还是条件收敛?(1)1111234-+-+ ;(2)()()1111ln 1n n n ∞-=-+∑;(3) 2341111111153535353⋅-⋅+⋅-⋅+ ;(4)()21121!n n n n ∞-=-∑; (5)()()1111n n R n αα∞-=∈-∑;(6) ()11111123nn n n ∞=⎛⎫-++++ ⎪⎝⎭∑ . 解:(1)()111n n U n -=-,级数1n n U ∞=∑是交错级数,且满足111n n >+,1lim 0n n →∞=,由莱布尼茨判别法级数收敛,又11121n n n U n∞∞===∑∑是P <1的P级数,所以1n n U ∞=∑发散,故原级数条件收敛.(2)()()111ln 1n n U n -=-+,()()1111ln 1n n n ∞---+∑为交错级数,且()()11ln ln 12n n >++,()1lim 0ln 1n n →∞=+,由莱布尼茨判别法知原级数收敛,但由于()11ln 11n U n n =≥++291所以,1n n U ∞=∑发散,所以原级数条件收敛.(3)()11153n n n U -=-⋅民,显然1111115353n n n n n n U ∞∞∞=====⋅∑∑∑,而113nn ∞=∑是收敛的等比级数,故1n n U ∞=∑收敛,所以原级数绝对收敛.(4)因为2112lim lim 1n n n n nU U n ++→∞→∞==+∞+. 故可得1n n U U +>,得lim0n n U →∞≠, ∴lim 0n n U →∞≠,原级数发散. (5)当α>1时,由级数11n nα∞=∑收敛得原级数绝对收敛. 当0<α≤1时,交错级数()1111n n n α∞-=-∑满足条件:()111n n αα>+;1lim 0n n α→∞=,由莱布尼茨判别法知级数收敛,但这时()111111n n n nn αα∞∞-===-∑∑发散,所以原级数条件收敛.当α≤0时,lim0n n U →∞≠,所以原级数发散. (6)由于11111123n nn ⎛⎫⋅>++++ ⎪⎝⎭而11n n∞=∑发散,由此较审敛法知级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 发散. 记1111123n U nn ⎛⎫=⋅++++ ⎪⎝⎭ ,则292()()()()()()1222111111123111111112311111111231110n n U U n n n n n n n n n n n n n n +⎛⎫⎛⎫-=-++++- ⎪⎪+⎝⎭⎝⎭+⎛⎫=-++++ ⎪⎝⎭++⎛⎫⎛⎫-=++++ ⎪ ⎪⎝⎭+++⎝⎭>即1n n U U +>又01111lim lim 12311d n n n n U n n x n x→∞→∞⎛⎫=++++ ⎪⎝⎭=⎰ 由0111lim d lim 01t t t t x t x→+∞→+∞==⎰ 知lim 0n n U →∞=,由莱布尼茨判别法,原级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 收敛,而且是条件收敛.9.判别下列函数项级数在所示区间上的一致收敛性.(1) ()1!1nn x n ∞=-∑,x ∈[-3,3]; (2) 21nn x n ∞=∑,x ∈[0,1];(3) 1sin 3n n nx∞=∑,x ∈(-∞,+∞); (4)1!nxn e n -∞=∑,|x |<5; (5)3521cos n nxn x∞=+∑,x ∈(-∞,+∞)解:(1)∵()()3!!11nnx n n ≤--,x ∈[-3,3],而由比值审敛法可知()13!1nn n ∞=-∑收敛,所以原级数在 [-3,3]上一致收敛.(2)∵221nx n n≤,x ∈[0,1],293而211n n∞=∑收敛,所以原级数在[0,1]上一致收敛. (3)∵1sin 33n n nx ≤,x ∈(-∞,+∞),而113nn ∞=∑是收敛的等比级数,所以原级数在(-∞,+∞)上一致收敛. (4)因为5!!nnx ee n n -≤,x ∈(-5,5), 由比值审敛法可知51!nn e n ∞=∑收敛,故原级数在(-5,5)上一致收敛.(5)∵53523cos 1nxn xn≤+,x ∈(-∞,+∞),而5131n n∞=∑是收敛的P -级数,所以原级数在(-∞,+∞)上一致收敛.10.若在区间Ⅰ上,对任何自然数n .都有|U n (x )|≤V n (x ),则当()1n n V x ∞=∑在Ⅰ上一致收敛时,级数()1n n U x ∞=∑在这区间Ⅰ上也一致收敛.证:由()1n n V x ∞=∑在Ⅰ上一致收敛知, ∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,于是,∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|U n +1(x )+U n +2(x )+…+U n +p (x )|≤V n +1(x )+V n +2(x )+…+V n +p (x ) ≤|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,因此,级数()1n n U x ∞=∑在区间Ⅰ上处处收敛,由x 的任意性和与x 的无关294性,可知()1n n U x ∞=∑在Ⅰ上一致收敛.11.求下列幂级数的收敛半径及收敛域:(1)x +2x 2+3x 3+…+nx n +…; (2)1!nn x n n ∞=⎛⎫⎪⎝⎭∑;(3)21121n n x n -∞=-∑; (4)()2112nn x n n∞=-⋅∑; 解:(1)因为11limlim 1n n n n a n a n ρ+→∞→∞+===,所以收敛半径11R ρ==收敛区间为(-1,1),而当x =±1时,级数变为()11n n n ∞=-∑,由lim(1)0n x nn →-≠知级数1(1)nn n ∞=-∑发散,所以级数的收敛域为(-1,1).(2)因为()()1111!11lim lim lim lim e 1!11nn n n n n n n n na n n n a n n n n ρ-+-+→∞→∞→∞→∞⎡⎤+⎛⎫⎛⎫==⋅===+ ⎪⎢⎥ ⎪+⎝⎭+⎝⎭⎣⎦ 所以收敛半径1e R ρ==,收敛区间为(-e,e).当x =e 时,级数变为1e nn n n n∞=∑;应用洛必达法则求得()10e e1lim 2xx x x →-+=-,故有111lim 12n n n a n a +→∞⎛⎫-=-<⎪⎝⎭由拉阿伯判别法知,级数发散;易知x =-e 时,级数也发散,故收敛域为(-e,e).(3)级数缺少偶次幂项.根据比值审敛法求收敛半径.211212221lim lim 2121lim21n n n n n nn U x n U n x n x n x ++-→∞→∞→∞-=⋅+-=⋅+= 所以当x 2<1即|x |<1时,级数收敛,x 2>1即|x |>1时,级数发散,故295收敛半径R =1.当x =1时,级数变为1121n n ∞=-∑,当x =-1时,级数变为1121n n ∞=--∑,由1121lim 012n n n→∞-=>知,1121n n ∞=-∑发散,从而1121n n ∞=--∑也发散,故原级数的收敛域为(-1,1). (4)令t =x -1,则级数变为212nn t n n∞=⋅∑,因为()()2122lim lim 1211n n n na n na n n ρ+→∞→∞⋅===⋅++ 所以收敛半径为R =1.收敛区间为 -1<x -1<1 即0<x <2.当t =1时,级数3112n n ∞=∑收敛,当t =-1时,级数()31112n n n ∞=-⋅∑为交错级数,由莱布尼茨判别法知其收敛.所以,原级数收敛域为 0≤x ≤2,即[0,2] 12.利用幂级数的性质,求下列级数的和函数: (1)21n n nx∞+=∑;(2) 22021n n x n +∞=+∑;解:(1)由()321lim n n n x n x nx++→∞+=知,当|x |=<1时,原级数收敛,而当|x |=1时,21n n nx ∞+=∑的通项不趋于0,从而发散,故级数的收敛域为(-1,1).记 ()23111n n n n S nxxnxx ∞∞+-====∑∑易知11n n nx∞-=∑的收敛域为(-1,1),记()111n n S n xx ∞-==∑296则()1011xn n x S x x x∞===-∑⎰ 于是()()12111x S x x x '⎛⎫== ⎪-⎝⎭-,所以()()()3211x S x x x =<-(2)由2422221lim 23n n n x n x n x++→∞+=⋅+知,原级数当|x |<1时收敛,而当|x |=1时,原级数发散,故原级数的收敛域为(-1,1),记()2221002121n n n n x x S x x n n ++∞∞====++∑∑,易知级数21021n n x n +∞=+∑收敛域为(-1,1),记()211021n n x S x n +∞==+∑,则()21211n n S x x x∞='==-∑, 故()1011d ln 21xx S x x x +'=-⎰ 即()()1111ln 021x S S x x +-=-,()100S =,所以()()()11ln 121x xS xS x x x x+==<-13.将下列函数展开成x 的幂级数,并求展开式成立的区间: (1)f (x )=ln(2+x ); (2)f (x )=cos 2x ; (3)f (x )=(1+x )ln(1+x ); (4)()221x f x x=+;(5)()23xf x x=+; (6)()()1e e 2x x f x -=-; (7)f (x )=e x cos x ;(8)()()212f x x =-.解:(1)()()ln ln 2ln 2ln 11222x x f x x ⎛⎫⎛⎫===++++ ⎪ ⎪⎝⎭⎝⎭由于()()0ln 111n nn x x n ∞==+-+∑,(-1<x ≤1)故()()110ln 11221n nn n x x n +∞+=⎛⎫=+- ⎪⎝⎭+∑,(-2≤x ≤2)297因此()()()11ln ln 22121n nn n x x n +∞+==++-+∑,(-2≤x ≤2) (2)()21cos 2cos 2x f x x +==由()()20cos 1!2nnn x x n ∞==-∑,(-∞<x <+∞)得()()()()()220042cos 211!!22n n n nn n n x x x n n ∞∞==⋅==--∑∑ 所以()()22011()cos cos 222114122!2n nn n f x x x x n ∞===+⋅=+-∑,(-∞<x <+∞) (3)f (x )=(1+x )ln(1+x ) 由()()()10ln 111n nn x x n +∞==+-+∑,(-1≤x ≤1)所以()()()()()()()()()()()()()1120111111111111111111111111111n nn n n nn n n n n nn n n n n n n n n n x f x x n x x n n x x x n n n n x xn n x xn n +∞=++∞∞==++∞∞+==+∞+=-∞+==+-+=+--++=++--+++--=+⋅+-=++∑∑∑∑∑∑∑ (-1≤x ≤1)(4)()2222111x f x x xx==⋅++由于()()()2211!!2111!!21n n n n x n x∞=-=+-+∑ (-1≤x ≤1)298故()()()()221!!2111!!2n n n n x f x x n ∞=⎛⎫-+=- ⎪⎝⎭∑()()()()2211!!211!!2n n n n x xn ∞+=-=+-∑ (-1≤x ≤1) (5)()()()()2202111313133133nn n n nn n xf x x x x x x ∞=+∞+==⋅+⎛⎫=⋅- ⎪⎝⎭=-<∑∑(6)由0e !nxn x n ∞==∑,x ∈(-∞,+∞)得()01e !n nxn x n ∞-=⋅-=∑,x ∈(-∞,+∞)所以()()()()()()0002101e e 2112!!1112!,!21x x n n n n n n n n n n f x x x n n x n x x n -∞∞==∞=+∞==-⎛⎫-=- ⎪⎝⎭=⋅⎡⎤--⎣⎦=∈-∞+∞+∑∑∑∑(7)因为e cos x x 为()()1e cos sin x x i e x i x +=+的实部, 而()()[]()10002011!1!ππ2cos sin !44ππ2cos sin !44nxi n nn n nn n n n n ex i n x i n x i n x n n i n ∞+=∞=∞=∞==+=+⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=⋅+ ⎪⎝⎭∑∑∑∑299取上式的实部.得2π2cos4cos !n xn n n e x x n ∞==⋅∑(-∞<x <+∞)(8)由于()1211n n nx x ∞-==-∑ |x |<1而()211412f x x =⋅⎛⎫- ⎪⎝⎭,所以()111001422n n n n n n x x f n x --∞∞+==⋅⎛⎫=⋅= ⎪⎝⎭∑∑ (|x |<2) 14.将()2132f x x x =++展开成(x +4)的幂级数.解:21113212x x x x =-++++而()()()0101113411431314413334713nn nn n x x x x x x x ∞=∞+==+-++=-⋅+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<∑∑又()()()0101122411421214412224622nn nn n x x x x x x x ∞=∞+==+-++=-+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<-∑∑300所以()()()()()2110011013244321146223n nn n n n nn n n f x x x x x x x ∞∞++==∞++==++++=-+⎛⎫=-+-<<- ⎪⎝⎭∑∑∑15.将函数()3f x x =展开成(x -1)的幂级数. 解:因为()()()()()2111111!2!m nmm mm m m x xx x n---+=++++++-<<所以()()[]()()()33221133333331121222222211111!2!!n f x x x n x x x n ==+-⎛⎫⎛⎫⎛⎫⎛⎫----+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=+++++---(-1<x -1<1) 即()()()()()()()()()()()()()2323133131313251111111222!23!2!3152111022!n nnnn n f x x x x x n n x x n ∞=⋅⋅⋅⋅⋅⋅--+--=+++++----⋅⋅⋅⋅⋅⋅--=+-<<⋅∑ 16.利用函数的幂级数展开式,求下列各数的近似值: (1)ln3(误差不超过0.0001); (2)cos20(误差不超过0.0001)解:(1)35211ln 213521n x x x x x x n -+⎛⎫=+++++ ⎪--⎝⎭,x ∈(-1,1)令131x x +=-,可得()11,12x =∈-,301故()35211111112ln3ln 212325222112n n -+⎡⎤+++++==⎢⎥⋅⋅⋅-⎣⎦-又()()()()()()()()()()2123212121232521242122112222123222212112222123252111222212112211413221n n n n n n n n n n n r n n n n n n n n n n +++++++++-⎡⎤++=⎢⎥⋅⋅++⎣⎦⎡⎤⋅⋅++=+++⎢⎥⋅⋅+++⎣⎦⎛⎫<+++ ⎪⎝⎭+=⋅+-=+ 故5810.000123112r <≈⨯⨯61010.000033132r <≈⨯⨯. 因而取n =6则35111111ln32 1.098623252112⎛⎫=≈++++ ⎪⋅⋅⋅⎝⎭(2)()()2420ππππ909090cos 2cos 11902!4!!2nn n ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭==-+-++-∵24π906102!-⎛⎫ ⎪⎝⎭≈⨯;48π90104!-⎛⎫⎪⎝⎭≈ 故2π90cos2110.00060.99942!⎛⎫⎪⎝⎭≈-≈-≈17.利用被积函数的幂级数展开式,求定积分0.5arctan d xx x⎰(误差不超过0.001)的近似值.302解:由于()3521arctan 13521n n x x x x x n +=-+-++-+ ,(-1≤x ≤1) 故()2420.50.5000.5357357arctan d d 113521925491111111292252492nx x x x x x x n x x x x ⎡⎤=-+-++-⎢⎥+⎣⎦⎛⎫=-+-+ ⎪⎝⎭=-⋅+⋅-⋅+⎰⎰ 而3110.013992⋅≈,5110.0013252⋅≈,7110.0002492⋅≈. 因此0.535arctan 11111d 0.487292252x x x ≈-⋅+⋅≈⎰ 18.判别下列级数的敛散性:(1)111n nnn nn n +∞=⎛⎫+ ⎪⎝⎭∑;(2)21cos 32n n nx n ∞=⎛⎫ ⎪⎝⎭∑; (3)()1ln 213nn n n ∞=+⎛⎫+ ⎪⎝⎭∑.解:(1)∵122111n nnnnn nn n n n n n n +⎛⎫>= ⎪+⎝⎭⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭ 而()22211221lim lim 10111nnn n n n nn n --++→∞→∞⎡⎤⎛⎫-⎛⎫==≠+⎢⎥⎪ ⎪+⎝⎭+⎝⎭⎣⎦故级数2211nn n n ∞=⎛⎫⎪+⎝⎭∑发散,由比较审敛法知原级数发散. (2)∵2cos 3022n nnx n n ⎛⎫⎪⎝⎭<≤ 由比值审敛法知级数12n n n ∞=∑收敛,由比较审敛法知,原级数21cos 32nn nx n ∞=⎛⎫ ⎪⎝⎭∑303收敛. (3)∵()()ln ln 220313nnn n n ++<<⎛⎫+ ⎪⎝⎭ 由()()()()11ln 33lim lim 3ln 21ln 3lim3ln 2113nn n n n nn U n U n n n ++→∞→∞→∞+=⋅++=+=< 知级数()1ln 23nn n ∞=+∑收敛,由比较审敛法知,原级数()1ln 213n n n n ∞=+⎛⎫+ ⎪⎝⎭∑收敛. 19.若2lim n nn U →∞存在,证明:级数1n n U ∞=∑收敛. 证:∵2lim n n n U →∞存在,∴∃M >0,使|n 2U n |≤M , 即n 2|U n |≤M ,|U n |≤2M n而21n Mn ∞=∑收敛,故1n n U ∞=∑绝对收敛. 20.证明,若21n n U ∞=∑收敛,则1nn U n∞=∑绝对收敛. 证:∵222211111222n n n nU U n U U n n n+=⋅≤=+⋅而由21n n U ∞=∑收敛,211n n∞=∑收敛,知 22111122n n U n ∞=⎛⎫+⋅ ⎪⎝⎭∑收敛,故1n n U n∞=∑收敛, 因而1nn U n∞=∑绝对收敛.30421.若级数1n n a ∞=∑与1n n b ∞=∑都绝对收敛,则函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.证:U n (x )=a n cos nx +b n sin nx ,∀x ∈R 有()cos sin cos sin n n n n n n n U a nx b nx a nx b nx a b x =+≤+≤+由于1n n a ∞=∑与1n n b ∞=∑都绝对收敛,故级数()1n n n a b ∞=+∑收敛.由魏尔斯特拉斯判别法知,函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.22.计算下列级数的收敛半径及收敛域:(1) 1311nn n n x n ∞=⎛⎫+ ⎪+⎝⎭∑;(2)()1πsin12nnn x ∞=+∑; (3) ()2112nn n x n ∞=-⋅∑解:(1)()111lim 1331lim 3123311311lim lim lim 22313e e 3n n nn nn nnn n n a a n n n n n n n n n n ρ+→∞+→∞→∞→∞→∞-=+⎛⎫⎛⎫++=⋅ ⎪ ⎪+⎝⎭+⎝⎭⎛⎫++++⎛⎫+=⋅⋅ ⎪ ⎪++⎝⎭+⎝⎭=⋅⋅=∴133R ρ==, 又当33x =±时,级数变为()113133311333nnnn n n n n n n ∞∞==⎛⎫⎛⎫⎛⎫++=±± ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭∑∑, 因为33333lim 033nn n en -→∞⎛⎫+=≠ ⎪+⎝⎭305所以当33x =±,级数发散,故原级数的收敛半径33R =,收敛域(-33,33). (2) 111ππsin122lim lim lim ππ2sin 22n n n n n n nnna a ρ+++→∞→∞→∞==== 故12R ρ==,又∵πsinπ2limsin 2lim ππ0π22n n n n n n→∞→∞⋅==≠.所以当(x +1)=±2时,级数()1πsin12n n n x ∞=+∑发散, 从而原级数的收敛域为-2<x +1<2,即-3<x <1,即(-3,1)(3) ()212121lim lim 221n n n n n na n a n ρ++→∞→∞⋅===⋅+ ∴2R =,收敛区间-2<x -1<2,即-1<x <3. 当x =-1时,级数变为()2111nn n∞=-∑,其绝对收敛,当x =3时,级数变为211n n ∞=∑,收敛. 因此原级数的收敛域为[-1,3]. 23.将函数()0arctan d xtF t x t=⎰展开成x 的幂级数. 解:由于()21arctan 121n nn t t n +∞==-+∑306所以()()()()()20002212000arctan d d 121d 112121nxx n n n n xnnn n t t F t t x t n t x t n n ∞=+∞∞====-+==--++∑⎰⎰∑∑⎰(|x |≤1)24.判别下列级数在指定区间上的一致收敛性:(1)()113n nn x ∞=-+∑,x ∈[-3,+∞); (2)1n n n x ∞=∑,x ∈(2,+∞); (3)()()222211n nx x n n ∞=⎡⎤+++⎣⎦∑,x ∈(-∞,+∞);解:(1)考虑n ≥2时,当x ≥-3时,有()1111133333nn n n nx x --=<<+-+ 而1113n n ∞-=∑收敛,由魏尔斯特拉斯判别法知,级数()113nnn x ∞=-+∑在[-3,+∞)上一致收敛. (2)当x >2时,有2n nn nx=< 由1112lim 122n n nn n +→∞+=<知级数12n n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数1n n nx ∞=∑在(2,+∞)上一致收敛. (3)∀x ∈R 有()()()22224322111nn n x n n nx n n n ≤<=⎡⎤+⋅+++⎣⎦而311n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数()()222211n n x x n n ∞=⎡⎤+++⎣⎦∑在(-∞,+∞)上一致收敛. 25.求下列级数的和函数:307(1)()211121n n n x n ∞-=--∑; (2)2121n n x n +∞=+∑; (3)()11!1n n nxn ∞-=-∑; (4)()11n n x n n ∞=+∑.解:(1)可求得原级数的收敛半径R =1,且当|x |=1时,级数()111121n n n ∞-=--∑是收敛的交错级数,故收敛域为[-1,1] 记()()()()22111111112121n n n n n n x x S x xS x x n n -∞∞--=====----∑∑ 则S 1(0)=0,()()122121111n n n S x x x∞--='==-+∑ 所以()()1121d arctan 01xS S x x x x-==+⎰ 即S 1(x )=arctan x ,所以S (x )=x arctan x ,x ∈[-1,1].(2)可求得原级数的收敛半径R =1,且当|x |=1时,原级数发散.记()21021n n x S x n +∞==+∑则()22011n n S x x x ∞='==-∑ ()200111d d ln 121xxx S x x x x x +'==--⎰⎰,即()()11ln 021xS S x x+-=-,S (0)=0 所以()11ln 21xS x x+=-,(|x |<1)(3)由()11!lim lim 0!1n n n n n a n n a n +→∞→∞+==-知收敛域为(-∞,+∞).记()()11!1n n n S x x n ∞-==-∑则()()()1011d e !!11nn xx n n x x S x x x x n n -∞∞=====--∑∑⎰,所以()()()e 1e x x S x x x '==+,(-∞<x <+∞)(4)由()()()112lim111n n n n n →∞++=+知收敛半径R =1,当x =1时,级数变为308()111n n n ∞=+∑,由()2111n n n <+知级数收敛,当x =-1时,级数变为()()111n n n n ∞=-+∑是收敛的交错级数,故收敛域为[-1,1].记()()11nn x S x n n ∞==+∑则S (0)=0,()()111n n x xS x n n +∞==+∑,()[]1111n n x xS x x∞-=''==-∑ (x ≠1) 所以()[]()0d ln 1xxS x x x ''=--⎰ 即()[]()ln 1xS x x '=--()[]()()()00d ln 1d 1ln 1xxxS x x x x x x x '=--=--+⎰⎰ 即()()()1ln 1xS x x x x =--+当x ≠0时,()()111ln 1S x x x⎛⎫=+-- ⎪⎝⎭,又当x =1时,可求得S (1)=1(∵()1lim lim 111n n S x n →∞→∞⎛⎫=-= ⎪+⎝⎭) 综上所述()()[)()0,01,1111ln 1,1,00,1x S x x x x x =⎧⎪==⎪⎨⎛⎫⎪+--∈- ⎪⎪⎝⎭⎩ 26.设f (x )是周期为2π的周期函数,它在(-π,π]上的表达式为()32π0,0π.x f x x x -<≤⎧=⎨<≤⎩ 试问f (x )的傅里叶级数在x =-π处收敛于何值?解:所给函数满足狄利克雷定理的条件,x =-π是它的间断点,在x =-π处,f (x )的傅里叶级数收敛于()()[]()33ππ11π22π222f f -+-+-=+=+30927.写出函数()21π00πx f x x x --≤≤⎧=⎨<≤⎩的傅里叶级数的和函数. 解:f (x )满足狄利克雷定理的条件,根据狄利克雷定理,在连续点处级数收敛于f (x ),在间断点x =0,x =±π处,分别收敛于()()00122f f -++=-,()()2πππ122f f -++-=,()()2πππ122f f -+-+--=,综上所述和函数.()221π00π102π1π2x x x S x x x --<<⎧⎪<<⎪⎪=-=⎨⎪⎪-=±⎪⎩28.写出下列以2π为周期的周期函数的傅里叶级数,其中f (x )在[-π,π)上的表达式为:(1)()π0π,4ππ0;4x f x x ⎧≤<⎪⎪=⎨⎪--≤<⎪⎩(2)()()2πx π=-≤≤f x x ;(3)()ππ,π,22ππ,,22ππ,π;22⎧--≤<-⎪⎪⎪=-≤<⎨⎪⎪≤<⎪⎩x f x x x x (4)()()cosππ2=-≤≤x f x x .310解:(1)函数f (x )满足狄利克雷定理的条件,x =n π,n ∈z 是其间断点,在间断占处f (x )的傅里叶级数收敛于()()ππ0044022f f +-⎛⎫+- ⎪+⎝⎭==,在x ≠n π,有()π0π-ππ011π1πcos d cos d cos d 0ππ4π4n a f x nx x nx x nx x -⎛⎫==-+= ⎪⎝⎭⎰⎰⎰ ()π0π-ππ011π1πsin d sin d sin d ππ4π40,2,4,6,,1,1,3,5,.n b f x nx x nx x nx xn n n-⎛⎫==-+ ⎪⎝⎭=⎧⎪=⎨=⎪⎩⎰⎰⎰于是f (x )的傅里叶级数展开式为()()11sin 2121n f x n x n ∞==--∑(x ≠n π) (2)函数f (x )在(-∞,+∞)上连续,故其傅里叶级数在(-∞,+∞)上收敛于f (x ),注意到f (x )为偶函数,从而f (x )cos nx 为偶函数,f (x )sin nx 为奇函数,于是()π-π1sin d 0πn b f x nx x ==⎰,2π20-π12πd π3a x x ==⎰,()()ππ22-π0124cos d cos d 1ππnn a f x nx x x nx x n ===-⋅⎰⎰ (n =1,2,…) 所以,f (x )的傅里叶级数展开式为:()()221π41cos 3nn f x nx n∞==+-⋅∑ (-∞<x <∞)(3)函数在x =(2n +1)π (n ∈z )处间断,在间断点处,级数收敛于0,当x ≠(2n +1)π时,由f (x )为奇函数,有a n =0,(n =0,1,2,…)311()()()πππ2π002222πsin d sin d sin d ππ212π1sin 1,2,π2n nb f x nx x x nx x nx x n n n n ⎡⎤==+⎢⎥⎣⎦=--+=⎰⎰⎰ 所以()()12112π1sin sin π2n n n f x nx n n ∞+=⎡⎤=-⋅+⎢⎥⎣⎦∑ (x ≠(2n +1)π,n ∈z )(4)因为()cos 2xf x =作为以2π为周期的函数时,处处连续,故其傅里叶级数收敛于f (x ),注意到f (x )为偶函数,有b n =0(n =1,2,…),()()ππ-π0π0π1212cos cos d cos cos d π2π2111cos cos d π2211sin sin 12211π224110,1,2,π41n n x xa nx x nx xn x n x x n x n x n n n n +==⎡⎤⎛⎫⎛⎫=++- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫⎛⎫+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥=+⎢⎥+-⎢⎥⎣⎦⎛⎫=-= ⎪-⎝⎭⎰⎰⎰所以f (x )的傅里叶级数展开式为:()()12124cos 1ππ41n n nxf x n ∞+==+--∑ x ∈[-π,π]29.将下列函数f (x )展开为傅里叶级数: (1)()()πππ42x f x x =--<<(2)()()sin 02πf x x x =≤≤解:(1) ()ππ0-ππ11ππcos d d ππ422x a f x nx x x -⎛⎫==-= ⎪⎝⎭⎰⎰[]()ππππ-π-πππ1π11cos d cos d x cos d π4242π1sin 001,2,4n x a nx x nx x nx x nx n n--⎛⎫=-=- ⎪⎝⎭=-==⎰⎰⎰312()ππππ-π-π1π11sin d sin d xsin d π4242π11n n x b nx x nx x nx x n-⎛⎫=-=- ⎪⎝⎭=-⋅⎰⎰⎰故()()1πsin 14n n nxf x n∞==+-∑ (-π<x <π)(2)所给函数拓广为周期函数时处处连续, 因此其傅里叶级数在[0,2π]上收敛于f (x ),注意到f (x )为偶函数,有b n =0,()ππ0πππ011cos0d sin d ππ24sin d ππa f x x x x x x x --====⎰⎰⎰ ()()()()()()ππ0ππ02222cos d sin cos d ππ1sin 1sin 1d π211π10,1,3,5,4,2,4,6,π1n na f x nx x x nx x n x n x x n n n n -===+--⎡⎤⎣⎦-⎡⎤=+-⎣⎦-=⎧⎪-=⎨=⎪-⎩⎰⎰⎰所以()()2124cos2ππ41n nxf x n ∞=-=+-∑ (0≤x ≤2π) 30.设f (x )=x +1(0≤x ≤π),试分别将f (x )展开为正弦级数和余弦级数. 解:将f (x )作奇延拓,则有a n =0 (n =0,1,2,…)()()()()ππ0022sin d 1sin d ππ111π2πn nb f x nx x x nx x n==+--+=⋅⎰⎰从而()()()1111π2sin πnn f x nx n∞=--+=∑ (0<x <π)313若将f (x )作偶延拓,则有b n =0 (n =1,2,…)()()ππ00222cos d 1cos d ππ0,2,4,64,1,3,5,πn a f x nx x x nx x n n n ==+=⎧⎪=-⎨=⎪⎩⎰⎰ ()()ππ0π012d 1d π2ππa f x x x x -==+=+⎰⎰ 从而()()()21cos 21π242π21n n xf x n ∞=-+=--∑ (0≤x ≤π) 31.将f (x )=2+|x | (-1≤x ≤1)展开成以2为周期的傅里叶级数,并由此求级数211n n∞=∑的和. 解:f (x )在(-∞,+∞)内连续,其傅里叶级数处处收敛,由f (x )是偶函数,故b n =0,(n =1,2,…)()()11010d 22d 5a f x x x x -==+=⎰⎰()()()1112cos d 22cos d 0,2,4,64,1,3,5,πn a f x nx x x nx xn n n -==+=⎧⎪-=⎨=⎪⎩⎰⎰所以()()()221cos 21π542π21n n xf x n ∞=-=--∑,x ∈[-1,1]取x =0得,()2211π821n n ∞==-∑,故 ()()22222111111111π48212n n n n n n n n ∞∞∞∞=====+=+-∑∑∑∑ 所以211π6n n∞==∑31432.将函数f (x )=x -1(0≤x ≤2)展开成周期为4的余弦级数.解:将f (x )作偶延拓,作周期延拓后函数在(-∞,+∞)上连续,则有b n =0 (n =1,2,3,…)()()220201d 1d 02a f x x x x -==-=⎰⎰ ()()()222022221ππcos d 1cos d 2224[11]π0,2,4,6,8,1,3,5,πn nn x n xa f x x x x n n n n -==-=--=⎧⎪=⎨-=⎪⎩⎰⎰ 故()()()22121π81cos π221n n xf x n ∞=-=-⋅-∑(0≤x ≤2)33.设()()011,0,2cos π1222,1,2n n x x a f x s x a n x x x ∞=⎧≤≤⎪⎪==+⎨⎪-<<⎪⎩∑,-∞<x <+∞,其中()12cos πd n a f x n x x =⎰,求52s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作偶延拓到[-1,1],再以2为周期延拓到(-∞,+∞)将f (x )展开成余弦级数而得到 s (x ),延拓后f (x )在52x =-处间断,所以515511122222221131224s f f f f +-+-⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+-=-+-⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎛⎫=+= ⎪⎝⎭34.设函数f (x )=x 2(0≤x <1),而()1s i n πn n s x b nx ∞==∑,-∞<x <+∞,其中()12sin πd n b f x n x x =⎰ (n =1,2,3,…),求12s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作奇延拓到,[-1,1],再以2为周期延拓到(-∞,+∞),并将315f (x )展开成正弦级数得到s (x ),延拓后f (x )在12x =-处连续,故.211112224s f ⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 35.将下列各周期函数展开成为傅里叶级数,它们在一个周期内的表达式分别为:(1)f (x )=1-x 2 1122x ⎛⎫-≤< ⎪⎝⎭;(2)()21,30,1,0 3.x x f x x +-≤<⎧=⎨≤<⎩解:(1) f (x )在(-∞,+∞)上连续,故其傅里叶级数在每一点都收敛于f (x ),由于f (x )为偶函数,有b n =0 (n =1,2,3,…)()()112221002112d 41d 6a f x x x x -==-=⎰⎰, ()()()()112221021222cos2n πd 41cos2n πd 11,2,πn n a f x x x x x x n n -+==--==⎰⎰所以()()12211111cos 2π12πn n f x n x n +∞=-=+∑ (-∞<x <+∞)(2) ()()303033011d 21d d 133a f x x x x x --⎡⎤==++=-⎢⎥⎣⎦⎰⎰⎰, ()()()()330330221πcos d 331π1π21cos d cos d 3333611,1,2,3,πn nn xa f x x n x n x x x x n n --==++⎡⎤=--=⎣⎦⎰⎰⎰316()()()()33033011πsin d 331π1π21sin d sin d 333361,1,2,πn n n xb f x x n x n x x x x n n --+==++=-=⎰⎰⎰ 而函数f (x )在x =3(2k +1),k =0,±1,±2,…处间断,故()()()122116π6π11cos 1sin 2π3π3n n n n x n x f x n n ∞+=⎧⎫⎡⎤=-+--+-⎨⎬⎣⎦⎩⎭∑ (x ≠3(2k +1),k =0,±1,±2,…)36.把宽为τ,高为h ,周期为T 的矩形波(如图所示)展开成傅里叶级数的复数形式.解:根据图形写出函数关系式()0,22,220,22T t u t h t T t ττττ⎧-≤<-⎪⎪⎪=-≤<⎨⎪⎪≤≤⎪⎩()()22022111d d d 2T l T l h c u t t u t t h t l T T Tτττ---====⎰⎰⎰ ()()π2π222π2π22222π2211e d e d 212πe d e d 2ππsin e 2ππn T n i t l i t l T T n l n n i t i t T T n i t T c u t t u t tl T h T n h t i t T T n i T h h n n i n T τττττττ----------==-⎛⎫⎛⎫==⋅- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎡⎤=-= ⎪⎣⎦⎝⎭⎰⎰⎰⎰。
高等数学同济第七版上册课后习题答案

习题1-11.求下列函数的自然定义域:(1)1(3)(5)sin (7)arcsin(3);(9)ln(1);y y x y y x y x ====-=+211(2);1(4);(6)tan(1);1(8)arctan ;(10).xe y xy y x y xy e =-==+=+=解:2(1)3203x x +≥⇒≥-,即定义域为2,3⎡⎫-+∞⎪⎢⎣⎭2(2)101,x x -≠⇒≠±即定义域为(,1)(1,1)(1,)-∞-⋃-⋃+∞(3)0x ≠且2100x x -≥⇒≠且1x ≤即定义域为[)(]1,00,1-⋃2(4)402x x ->⇒<即定义域为(2,2)-(5)0,x ≥即定义域为[)0,+∞(6)1(),2x k k Z ππ+≠+∈即定义域为1(1,2x x R x k k Z π⎧⎫∈≠+-∈⎨⎬⎩⎭且(7)3124,x x -≤⇒≤≤即定义域为[]2,4(8)30x -≥且0x ≠,即定义域为(](,0)0,3-∞⋃(9)101x x +>⇒>-即定义域为(1,)-+∞(10)0,x ≠即定义域为(,0)(0,)-∞⋃+∞2.下列各题中,函数()f x 和()g x是否相同?为什么?222(1)()lg ,()2lg (2)(),()(3)()()(4)()1,()sec tan f x x g x x f x x g x f x g x f x g x x x========-解:(1)不同,因为定义域不同(2)不同,因为对应法则不同,,0(),0x x g x x x ≥⎧==⎨-<⎩(3)相同,因为定义域,对应法则均相同(4)不同,因为定义域不同3.设sin ,3()0,3x x x x πϕπ⎧<⎪⎪=⎨⎪≥⎪⎩求(),((),(2),644πππϕϕϕϕ--并指出函数()y x ϕ=的图形解:1()sin ,()sin 66244()sin(),(2)0,44ππππϕϕππϕϕ====-=-=-=()y x ϕ=的图形如图11-所示4.试证下列函数在指定区间内的单调性:(1);1(2)ln ,(0,)xy xy x x =-=++∞证明:1(1)()1,(,1)11x y f x x x===-+-∞--设121x x <<,因为212112()()0(1)(1)x x f x f x x x --=>--所以21()(),f x f x >即()f x 在(,1)-∞内单调增加(2)()ln ,(0,)y f x x x ==++∞设120x x <<,因为221211()()ln 0x f x f x x x x -=-+>所以21()()f x f x >即()f x 在(0,)+∞内单调增加5.设()f x 为定义在(,)l l -内的奇函数,若()f x 在(0,)l 内单调增加,证明()f x 在(,0)l -内也单调增加证明:设120l x x -<<<,则210x x l<-<-<由()f x 是奇函数,得2121()()()()f x f x f x f x -=-+-因为()f x 在(0,)l 内单调增加,所以12()()0f x f x --->即()f x 在(,0)l -内也单调增加6.设下面所考虑的函数都是定义在区间(,)l l -上的。
中国人民大学出版社(第四版)高等数学一第1章课后习题详解

中国人民大学出版社(第四版)高等数学一第1章课后习题详解第一章函数、极限与连续内容概要名称主要内容(1.1、1.2)函数邻域(){}δδ<-=axxaU,(即(){},U a x a x aδδδ=-<<+)(){}0,0U a x x aδδ=<-<((){}0,,0U a x a x a xδδδ=-<<+≠)函数两个要素:对应法则f以及函数的定义域D由此,两函数相等⇔两要素相同;(与自变量用何字母表示无关)解析表示法的函数类型:显函数,隐函数,分段函数;特性局部有界性对集合DX⊂,若存在正数M,使对所有Xx∈,恒有()Mxf<,称函数()xf在X上有界,或()xf是X上的有界函数;反之无界,即任意正数M(无论M多大),总存在(能找到)Xx∈,使得()Mxf>局部单调性区间DI⊂,对区间上任意两点21xx,当21xx<时,恒有:()()21xfxf<,称函数在区间I上是单调增加函数;反之,若()()21xfxf>,则称函数在区间I上是单调减小函数;奇偶性设函数()xf的定义域D关于原点对称;若Dx∈∀,恒有()()xfxf=-,则称()xf是偶函数;若Dx∈∀,恒有()()xfxf-=-,则称()x f是奇函数;周期性若存在非零常数T,使得对Dx∈∀,有()DTx∈±,且()()x fTxf=+,则称()x f是周期函数;初等函数几类基本初等函数:幂函数;指数函数;对数函数;三角函数;反三角函数;反函数求法和性质;复合函数性质;初等函数课后习题全解习题1-1★1.求下列函数的定义域:知识点:自然定义域指实数范围内使函数表达式有意义的自变量x 的取值的集合; 思路:常见的表达式有 ① alog□,( □0>) ② /N □, ( □0≠) ③ (0)≥④ arcsin([]1,1-∈)等解:(1)[)(]1,00,11100101122⋃-∈⇒⎩⎨⎧≤≤-≠⇒⎩⎨⎧≥-≠⇒--=x x x x x x x y ; (2)31121121arcsin ≤≤-⇒≤-≤-⇒-=x x x y ;(3)()()3,00,030031arctan 3⋃∞-∈⇒⎩⎨⎧≠≤⇒⎩⎨⎧≠≥-⇒+-=x x x x x x x y ;(4)()()3,11,1,,1310301lg 3⋃-∞-∈⇒⎩⎨⎧-<<<⇒⎩⎨⎧-<-<⇒-=-x x or x x x x x y x;(5)()()4,22,11601110)16(log 221⋃∈⇒⎪⎩⎪⎨⎧-<-≠-<⇒-=-x x x x x y x ; ★2.下列各题中,函数是否相同?为什么?(1)2lg )(x x f =与x x g lg 2)(=;(2)12+=x y 与12+=y x知识点:函数相等的条件;思路:函数的两个要素是f (作用法则)及定义域D (作用范围),当两个函数作用法则f 相同(化简后代数表达式相同)且定义域相同时,两函数相同;解:(1)2lg )(x x f =的定义域D={}R x x x ∈≠,0,xx g lg )(=的定义域{},0R x x x D ∈>=,虽然作用法则相同x x lg 2lg 2=,但显然两者定义域不同,故不是同一函数;(2)12+=x y ,以x 为自变量,显然定义域为实数R ;12+=y x ,以x 为自变量,显然定义域也为实数R ;两者作用法则相同“2□1+”与自变量用何记号表示无关,故两者为同一函数;★3.设⎪⎪⎩⎪⎪⎨⎧≥<=3,03,sin )(ππϕx x x x ,求)2()4()4()6(--ϕπϕπϕπϕ,,,,并做出函数)(x y ϕ=的图形知识点:分段函数; 思路:注意自变量的不同范围;解:216sin )6(==ππϕ,224sin 4==⎪⎭⎫⎝⎛ππϕ,224sin 4=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππϕ()02=-ϕ;如图:★4.试证下列各函数在指定区间内的单调性 :(1)()1,1∞--=xxy (2)x x y ln 2+=,()+∞,0 知识点:单调性定义。
高等数学一上册教材答案

高等数学一上册教材答案第一章:函数与极限1.1 函数的概念与性质函数的概念函数是一种特殊的关系,它将一个集合中的每个元素对应到另一个集合中的唯一元素。
用数学符号表示为:y = f(x),其中 x 是自变量,y 是因变量,f(x) 是函数关系。
函数的性质(1)定义域和值域定义域是自变量可能的取值范围,值域是因变量对应的所有可能取值的范围。
(2)奇偶性如果对任意 x,有 f(-x) = f(x),则函数为偶函数;如果对任意 x,有f(-x) = -f(x),则函数为奇函数。
(3)单调性如果对任意 x1、x2,当 x1 < x2 时有f(x1) ≤ f(x2),则函数为增函数;如果对任意 x1、x2,当 x1 < x2 时有f(x1) ≥ f(x2),则函数为减函数。
1.2 一次函数与二次函数一次函数一次函数的标准式表示为 y = kx + b,其中 k 是斜率,b 是 y 轴截距。
一次函数的图像是一条直线,它的性质包括:与 y 轴平行的直线的斜率为零,与 x 轴平行的直线的斜率为无穷大。
例题:已知函数 f(x) = 3x + 2,求 f(2) 的值。
解:将 x 替换为 2,得到 f(2) = 3(2) + 2 = 8。
二次函数二次函数的标准式表示为 y = ax^2 + bx + c,其中a ≠ 0。
二次函数的图像是一个抛物线,它的性质包括:抛物线开口向上(a > 0)或向下(a < 0),顶点的横坐标为 -b/2a。
例题:已知函数 f(x) = x^2 + 2x - 1,求 f(-1) 的值。
解:将 x 替换为 -1,得到 f(-1) = (-1)^2 + 2(-1) - 1 = -2。
1.3 幂函数与指数函数幂函数幂函数的定义形式为 y = x^p,其中 p 是常数。
幂函数的图像随着 p 的取值不同,可能是增函数、减函数或常数函数。
例题:已知函数 f(x) = x^3,求 f(2) 的值。
高等数学教材详细答案

高等数学教材详细答案1. 极限与连续1.1 数列极限的定义与性质(1) 数列极限的定义(2) 数列极限的性质1.2 函数极限的定义与性质(1) 函数极限的定义(2) 函数极限的性质1.3 极限运算法则(1) 四则运算法则(2) 复合函数的极限(3) 三角函数的极限1.4 连续与间断(1) 连续的定义与性质(2) 间断点与间断类型2. 导数与微分2.1 导数的概念(2) 导数的几何意义2.2 导数的基本运算法则(1) 乘积法则(2) 商法则(3) 复合函数的导数2.3 高阶导数与高阶微分(1) 高阶导数的定义(2) 高阶导数的性质2.4 微分的概念与运算(1) 微分的定义(2) 微分运算法则3. 微分中值定理与应用3.1 罗尔定理与拉格朗日中值定理(1) 罗尔定理(2) 拉格朗日中值定理3.2 柯西中值定理与洛必达法则(2) 洛必达法则3.3 泰勒公式与极值问题(1) 泰勒公式的推导(2) 极值问题的求解4. 不定积分与定积分4.1 不定积分的概念与性质(1) 不定积分的定义(2) 不定积分的基本性质 4.2 基本积分表与常用公式(1) 基本积分表(2) 常用公式与性质4.3 定积分的概念与性质(1) 定积分的定义(2) 定积分的性质4.4 定积分的计算方法(1) 几何与物理应用(2) 牛顿-莱布尼茨公式5. 定积分的应用5.1 平面图形的面积(1) 平面图形的面积计算5.2 几何体的体积(1) 旋转体的体积计算(2) 截面法计算体积5.3 物理应用(1) 质量和质心的计算(2) 转动惯量和转动中心的计算6. 多元函数微分学6.1 二元函数与二元函数的极限(1) 二元函数的定义与极限(2) 二元函数的性质6.2 偏导数与全微分(1) 偏导数的定义与计算(2) 全微分的概念与性质6.3 多元函数的微分学定理(1) 多元函数的极值定理(2) 多元函数的条件极值问题7. 重积分7.1 二重积分的概念与性质(1) 二重积分的定义(2) 二重积分的性质7.2 二重积分的计算方法(1) 矩形区域的二重积分(2) 极坐标下的二重积分7.3 三重积分的概念与性质(1) 三重积分的定义(2) 三重积分的性质7.4 三重积分的计算方法(1) 柱面坐标和球面坐标下的三重积分(2) 三元函数的体积计算8. 曲线与曲面积分8.1 曲线积分的概念与性质(1) 第一类曲线积分(2) 第二类曲线积分8.2 曲线积分的计算方法(1) 参数方程下的曲线积分(2) 平面曲线的曲线积分8.3 曲面积分的概念与性质(1) 第一类曲面积分(2) 第二类曲面积分8.4 曲面积分的计算方法(1) 参数方程下的曲面积分(2) 线面积分的转化9. 常微分方程9.1 高阶常微分方程(1) 二阶常微分方程(2) 高阶常微分方程的线性方程 9.2 变量可分离方程与齐次方程(1) 变量可分离方程(2) 齐次方程9.3 一阶线性微分方程(1) 一阶线性微分方程的求解 9.4 常系数线性微分方程(1) 齐次线性微分方程的解法(2) 非齐次线性微分方程的解法10. 线性代数基础10.1 向量的基本概念与运算(1) 向量的定义与性质(2) 向量的线性运算10.2 矩阵与矩阵运算(1) 矩阵的定义与性质(2) 矩阵的运算法则10.3 行列式的定义与性质(1) 行列式的定义(2) 行列式的性质10.4 线性方程组与解的判定(1) 线性方程组的解的性质(2) 线性方程组的解的判定。
(完整版)高等数学第六版(同济大学)上册课后习题答案解析

y1
y2
x1 1 x1
x2 1 x2
(1
x1 x2 x1)(1
x2)
0
所以函数 y x 在区间( 1)内是单调增加的 1 x
(2)对于任意的 x1 x2(0 ) 当 x1x2 时 有
这就证明了对于x1 x2(l 0) 有 f(x1) f(x2) 所以 f(x)在(l 0)内也单调 增加
11 设下面所考虑的函数都是定义在对称区间(l l)上的 证明 (1)两个偶函数的和是偶函数 两个奇函数的和是奇函数 (2)两个偶函数的乘积是偶函数 两个奇函数的乘积是偶函数 偶函数与奇 函数的乘积是奇函数 证明 (1)设 F(x)f(x)g(x) 如果 f(x)和 g(x)都是偶函数 则
1
(10) y e x
解 由 x0 得函数的定义域 D( 0)(0 ) 7 下列各题中 函数 f(x)和 g(x)是否相同?为什么? (1)f(x)lg x2 g(x)2lg x
(2) f(x)x g(x) x2
(3) f (x)3 x4 x3 g(x) x3 x 1
(4)f(x)1 g(x)sec2xtan2x 解 (1)不同 因为定义域不同 (2)不同 因为对应法则不同 x0 时 g(x)x (3)相同 因为定义域、对应法则均相相同 (4)不同 因为定义域不同
f(x1)f(x2)g[ f(x1)]g[f(x2)] x1x2 因此 f 既是单射 又是满射 即 f 是双射 对于映射 g YX 因为对每个 yY 有 g(y)xX 且满足 f(x)f[g(y)]Iy
yy 按逆映射的定义 g 是 f 的逆映射 5 设映射 f XY AX 证明 (1)f 1(f(A))A (2)当 f 是单射时 有 f 1(f(A))A 证明 (1)因为 xA f(x)yf(A) f 1(y)xf 1(f(A))
高等数学第1章课后习题答案(科学出版社)

第一章 函数、极限、连续习题1-11.求下列函数的自然定义域:(1)321x y x=+-(2) 1arctany x=+(3) 1arccosx y -=;(4) 313 , 1x y x ⎧≠⎪=⎨⎪=⎩. 解:(1)解不等式组23010x x +≥⎧⎨-≠⎩得函数定义域为[3,1)(1,1)(1,)---+∞U U ; (2)解不等式组230x x ⎧-≥⎨≠⎩得函数定义域为[U ;(3)解不等式组2111560x x x -⎧-≤≤⎪⎨⎪-->⎩得函数定义域为[4,2)(3,6]--U ; (4)函数定义域为(,1]-∞.2.已知函数()f x 定义域为[0,1],求(cos ),()() (0)f f x f x c f x c c ++->的定义域.解:函数f要有意义,必须01≤≤,因此f 的定义域为[0,1];同理得函数(cos )f x 定义域为[2π-,2π]22k k ππ+;函数()()f x c f x c ++-要有意义,必须0101x c x c ≤+≤⎧⎨≤-≤⎩,因此,(1)若12c <,定义域为:[],1c c -;(2)若12c =,定义域为:1{}2;(3)若12c >,定义域为:∅. 3.设21()1,||x a f x x x a ⎛⎫-=- ⎪-⎝⎭0,a >求函数值(2),(1)f a f .解:因为21()1||x a f x x x a ⎛⎫-=- ⎪-⎝⎭,所以 21(2)104a f a a a ⎛⎫=-= ⎪⎝⎭,22 ,>1,11(1)10 ,0<<111a a f a a ⎛⎫⎧-=-= ⎪⎨ ⎪-⎩⎝⎭. 4. 证明下列不等式:(1) 对任何x R ∈有 |1||2|1x x -+-≥; (2) 对任何n Z +∈有 111(1)(1)1n n n n++>++;(3) 对任何n Z +∈及实数1a >有 111na a n--≤.证明:(1)由三角不等式得|1||2||1(2)|1x x x x -+-≥---= (2)要证111(1)(1)1n n n n++>++,即要证111n +>+= 111(1)(1)(1)11111n n n n n +++++++<=+++L 得证。
高等数学上册第六版课后习题详细图文答案第二章

高等数学上册第六版课后习题详细答案第二章习题2-11. 设物体绕定轴旋转, 在时间间隔[0, t ]内转过的角度为θ, 从而转角θ是t 的函数: θ=θ(t ). 如果旋转是匀速的, 那么称tθω=为该物体旋转的角速度, 如果旋转是非匀速的, 应怎样确定该物体在时刻t 0的角速度?解 在时间间隔[t 0, t 0+∆t ]内的平均角速度ω为tt t t t ∆-∆+=∆∆=)()(00θθθω, 故t 0时刻的角速度为)()()(l i m l i m l i m 000000t tt t t t t t t θθθθωω'=∆-∆+=∆∆==→∆→∆→∆. 2. 当物体的温度高于周围介质的温度时, 物体就不断冷却, 若物体的温度T 与时间t 的函数关系为T =T (t ), 应怎样确定该物体在时刻t 的冷却速度? 解 物体在时间间隔[t 0, t 0+∆t ]内, 温度的改变量为∆T =T (t +∆t )-T (t ),平均冷却速度为tt T t t T t T ∆-∆+=∆∆)()(, 故物体在时刻t 的冷却速度为)()()(lim lim 00t T tt T t t T t T t t '=∆-∆+=∆∆→∆→∆. 3. 设某工厂生产x 单位产品所花费的成本是f (x )元, 此函数f (x )称为成本函数, 成本函数f (x )的导数f '(x )在经济学中称为边际成本. 试说明边际成本f '(x )的实际意义.解 f (x +∆x )-f (x )表示当产量由x 改变到x +∆x 时成本的改变量.xx f x x f ∆-∆+)()(表示当产量由x 改变到x +∆x 时单位产量的成本. xx f x x f x f x ∆-∆+='→∆)()(lim )(0表示当产量为x 时单位产量的成本. 4. 设f (x )=10x 2, 试按定义, 求f '(-1).解 xx x f x f f x x ∆--∆+-=∆--∆+-=-'→∆→∆2200)1(10)1(10lim )1()1(lim)1( 20)2(lim 102lim 10020-=∆+-=∆∆+∆-=→∆→∆x x x x x x . 5. 证明(cos x )'=-sin x .解 xx x x x x ∆-∆+='→∆cos )cos(lim )(cos 0xx x x x ∆∆∆+-=→∆2s i n )2s i n (2lim 0 x x x x x x s i n ]22s i n )2s i n ([lim 0-=∆∆∆+-=→∆. 6. 下列各题中均假定f '(x 0)存在, 按照导数定义观察下列极限, 指出A 表示什么:(1)A xx f x x f x =∆-∆-→∆)()(lim000; 解 xx f x x f A x ∆-∆-=→∆)()(lim 000 )()()(lim 0000x f xx f x x f x '-=∆--∆--=→∆-. (2)A xx f x =→)(lim 0, 其中f (0)=0, 且f '(0)存在; 解 )0()0()0(lim )(lim 00f xf x f x x f A x x '=-+==→→. (3)A hh x f h x f h =--+→)()(lim 000. 解 hh x f h x f A h )()(lim 000--+=→ hx f h x f x f h x f h )]()([)]()([lim 00000----+=→ h x f h x f h x f h x f h h )()(lim )()(lim 000000----+=→→ =f '(x 0)-[-f '(x 0)]=2f '(x 0).7. 求下列函数的导数:(1)y =x 4;(2)32x y =;(3)y =x 1. 6;(4)xy 1=; (5)21xy =; (6)53x x y =;(7)5322x x x y =; 解 (1)y '=(x 4)'=4x 4-1=4x 3 .(2)3113232323232)()(--=='='='x x x x y . (3)y '=(x 1. 6)'=1.6x 1. 6-1=1.6x 0. 6.(4)23121212121)()1(-----=-='='='x x x x y . (5)3222)()1(---='='='x x x y . (6)511151651653516516)()(x x x x x y =='='='-. (7)651616153226161)()(--=='='='x x x x x x y . 8. 已知物体的运动规律为s =t 3(m). 求这物体在t =2秒(s )时的速度. 解v =(s )'=3t 2, v |t =2=12(米/秒).9. 如果f (x )为偶函数, 且f (0)存在, 证明f (0)=0.证明 当f (x )为偶函数时, f (-x )=f (x ), 所以)0(0)0()(l i m 0)0()(l i m 0)0()(l i m )0(000f x f x f x f x f x f x f f x x x '-=-----=---=--='→-→→, 从而有2f '(0)=0, 即f '(0)=0.10. 求曲线y =sin x 在具有下列横坐标的各点处切线的斜率: π32=x , x =π. 解 因为y '=cos x , 所以斜率分别为2132c o s 1-==πk , 1cos 2-==πk . 11. 求曲线y =cos x 上点)21 ,3(π处的切线方程和法线方程式. 解y '=-sin x , 233sin 3-=-='=ππx y , 故在点)21 ,3(π处, 切线方程为)3(2321π--=-x y , 法线方程为)3(3221π--=-x y . 12. 求曲线y =e x 在点(0,1)处的切线方程.解y '=e x , y '|x =0=1, 故在(0, 1)处的切线方程为y -1=1⋅(x -0), 即y =x +1.13. 在抛物线y =x 2上取横坐标为x 1=1及x 2=3的两点, 作过这两点的割线, 问该抛物线上哪一点的切线平行于这条割线?解 y '=2x , 割线斜率为421913)1()3(=-=--=y y k . 令2x =4, 得x =2. 因此抛物线y =x 2上点(2, 4)处的切线平行于这条割线.14. 讨论下列函数在x =0处的连续性与可导性:(1)y =|sin x |;(2)⎪⎩⎪⎨⎧=≠=000 1sin 2x x x x y . 解 (1)因为y (0)=0, 0)sin (lim |sin |lim lim 000=-==---→→→x x y x x x , 0sin lim |sin |lim lim 000===+++→→→x x y x x x , 所以函数在x =0处连续.又因为1s i n l i m 0|0s i n ||s i n |l i m 0)0()(l i m )0(000-=-=--=--='---→→→-xx x x x y x y y x x x , 1s i n lim 0|0sin ||sin |lim 0)0()(lim )0(000==--=--='+++→→→+xx x x x y x y y x x x , 而y '-(0)≠y '+(0), 所以函数在x =0处不可导.解 因为01sin lim )(lim 200==→→xx x y x x , 又y (0)=0, 所以函数在x =0处连续. 又因为01s i n l i m 01s i n l i m 0)0()(l i m 0200==-=--→→→xx x x x x y x y x x x , 所以函数在点x =0处可导, 且y '(0)=0.15. 设函数⎩⎨⎧>+≤=1 1 )(2x b ax x x x f 为了使函数f (x )在x =1处连续且可导, a , b 应取什么值?解 因为1lim )(lim 211==--→→x x f x x , b a b ax x f x x +=+=++→→)(lim )(lim 11, f (1)=a +b , 所以要使函数在x =1处连续, 必须a +b =1 .又因为当a +b =1时211l i m )1(21=--='-→-x x f x ,a x x a xb a x a x b ax f x x x =--=--++-=--+='+++→→→+1)1(lim 11)1(lim 11lim )1(111, 所以要使函数在x =1处可导, 必须a =2, 此时b =-1.16. 已知⎩⎨⎧<-≥=00 )(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在? 解 因为f -'(0)=10lim )0()(lim 00-=--=---→→xx x f x f x x , f +'(0)=00lim )0()(lim 200=-=-++→→xx x f x f x x , 而f -'(0)≠f +'(0), 所以f '(0)不存在. 17. 已知f (x )=⎩⎨⎧≥<0 0 sin x x x x , 求f '(x ) . 解 当x <0时, f (x )=sin x , f '(x )=cos x ;当x >0时, f (x )=x , f '(x )=1;因为 f -'(0)=10sin lim )0()(lim 00=-=---→→xx x f x f x x , f +'(0)=10lim )0()(lim 00=-=-++→→xx x f x f x x , 所以f '(0)=1, 从而 f '(x )=⎩⎨⎧≥<0 10 cos x x x . 18. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 .解 由xy =a 2得x a y 2=, 22x a y k -='=. 设(x 0, y 0)为曲线上任一点, 则过该点的切线方程为)(02020x x x a y y --=-. 令y =0, 并注意x 0y 0=a 2, 解得0022002x x a x y x =+=, 为切线在x 轴上的距. 令x =0, 并注意x 0y 0=a 2, 解得00022y y x a y =+=, 为切线在y 轴上的距. 此切线与二坐标轴构成的三角形的面积为200002||2|2||2|21a y x y x S ===.习题 2-21. 推导余切函数及余割函数的导数公式:(cot x )'=-csc 2x ; (csc x )'=-csc x cot x .解 xx x x x x x x 2sin cos cos sin sin )sin cos ()(cot ⋅-⋅-='=' x xx x x 22222c s c s i n 1s i n c o s s i n -=-=+-=. x x xx x x c o t c s c s i n c os )s i n 1()(c s c 2⋅-=-='='. 2. 求下列函数的导数:(1)1227445+-+=xx x y ; (2) y =5x 3-2x +3e x ;(3) y =2tan x +sec x -1;(4) y =sin x ⋅cos x ;(5) y =x 2ln x ;(6) y =3e x cos x ;(7)xx y ln =; (8)3ln 2+=xe y x ; (9) y =x 2ln x cos x ;(10)tt s cos 1sin 1++=; 解 (1))12274()12274(14545'+-+='+-+='---x x x xx x y 2562562282022820x x x x x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3e x .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ⋅tan x =sec x (2sec x +tan x ).(4) y '=(sin x ⋅cos x )'=(sin x )'⋅cos x +sin x ⋅(cos x )'=cos x ⋅cos x +sin x ⋅(-sin x )=cos 2x .(5) y '=(x 2ln x )'=2x ⋅ln x +x 2⋅x1=x (2ln x +1) . (6) y '=(3e x cos x )'=3e x ⋅cos x +3e x ⋅(-sin x )=3e x (cos x -sin x ).(7)22ln 1ln 1)ln (x x x x x x x x y -=-⋅='='. (8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=⋅-⋅='+='. (9) y '=(x 2ln x cos x )'=2x ⋅ln x cos x +x 2⋅x1⋅cos x +x 2 ln x ⋅(-sin x )2x ln x cos x +x cos x -x 2 ln x sin x .(10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t t t t t t t t tt s +++=+-+-+='++='.3. 求下列函数在给定点处的导数:(1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=d d .(3)553)(2x x x f +-=, 求f '(0)和f '(2) . 解 (1)y '=cos x +sin x ,21321236s i n 6c o s 6+=+=+='=πππx y , 222224s i n 4c o s 4=+=+='=πππx y . (2)θθθθθθθρcos sin 21sin 21cos sin +=-+=d d , )21(4222422214c o s 44s i n 214πππππθρπθ+=⋅+⋅=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=. 求:(1)该物体的速度v (t );(2)该物体达到最高点的时刻.解 (1)v (t )=s '(t )=v 0-gt .(2)令v (t )=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻. 5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程. 解 因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x ,所求的法线方程为x y 21-=, 即x +2y =0. 6. 求下列函数的导数:(1) y =(2x +5)4(2) y =cos(4-3x );(3)23x e y -=;(4) y =ln(1+x 2);(5) y =sin 2x ;(6)22x a y -=;(7) y =tan(x 2);(8) y =arctan(e x );(9) y =(arcsin x )2;(10) y =lncos x .解 (1) y '=4(2x +5)4-1⋅(2x +5)'=4(2x +5)3⋅2=8(2x +5)3.(2) y '=-sin(4-3x )⋅(4-3x )'=-sin(4-3x )⋅(-3)=3sin(4-3x ).(3)22233236)6()3(x x x xe x e x e y ----=-⋅='-⋅='.(4)222212211)1(11xxx x x x y +=⋅+='+⋅+='. (5) y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x .(6))()(21])[(221122122'-⋅-='-='-x a x a x a y 222122)2()(21x a x x x a --=-⋅-=-. (7) y '=sec 2(x 2)⋅(x 2)'=2x sec 2(x 2).(8)xx x x e e e e y 221)()(11+='⋅+='. (9) y '21arcsin 2)(arcsin arcsin 2xx x x -='⋅=. (10)x x xx x y tan )sin (cos 1)(cos cos 1-=-='⋅='. 7. 求下列函数的导数:(1) y =arcsin(1-2x );(2)211x y -=; (3)x e y x3cos 2-=;(4)xy 1arccos =; (5)xx y ln 1ln 1+-=; (6)xx y 2sin =; (7)x y arcsin =;(8))ln(22x a x y ++=;(9) y =ln(sec x +tan x );(10) y =ln(csc x -cot x ).解 (1)2221)21(12)21()21(11x x x x x y --=---='-⋅--='. (2))1()1(21])1[(21212212'-⋅--='-='---x x x y 222321)1()2()1(21xx x x x --=-⋅--=-. (3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y x xx x )3s i n 63(c o s 213s i n 33c o s 21222x x e x e x e x xx +-=--=---. (4)1||)1()1(11)1()1(1122222-=---='--='x x x x xx x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='. (6)222sin 2cos 212sin 22cos x x xx x x xx y -=⋅-⋅⋅='. (7)2222121)(11)()(11x x x x x x y -=⋅-='⋅-='.(8)])(211[1)(12222222222'+++⋅++='++⋅++='x a x a x a x x a x x a x y 2222221)]2(211[1x a x x a x a x +=++⋅++=. (9) x xx x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12=++='+⋅+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12=-+-='-⋅-='.8. 求下列函数的导数:(1)2)2(arcsin x y =; (2)2tan ln x y =; (3)x y 2ln 1+=;(4)x e y arctan =;(5)y =sin n x cos nx ;(6)11arctan -+=x x y ; (7)xx y arccos arcsin =; (8) y =ln[ln(ln x )] ;(9)xx x x y -++--+1111; (10)xx y +-=11arcsin . 解 (1)'⋅=')2(arcsin )2(arcsin 2x x y )2()2(11)2(a r c s i n 22'⋅-⋅=x x x21)2(11)2(a r c s i n 22⋅-⋅=x x . 242a r c s i n 2x x -= (2))2(2sec 2tan 1)2(tan 2tan 12'⋅⋅='⋅='x x x x xy x x x c s c 212s e c 2t a n 12=⋅⋅=. (3))ln 1(ln 121ln 1222'+⋅+=+='x xx y )(l n ln 2ln 1212'⋅⋅+=x x x x x x1ln 2ln 1212⋅⋅+= xx x 2ln 1ln +=. (4))(arctan arctan '⋅='x e y x )()(112arctan '⋅+⋅=x x e x)1(221)(11a r c t a n 2a r c t a n x x e x x e x x +=⋅+⋅=. (5) y '=n sin n -1x ⋅(sin x )'⋅cos nx +sin n x ⋅(-sin nx )⋅(nx )'=n sin n -1x ⋅cos x ⋅cos nx +sin n x ⋅(-sin nx )⋅n=n sin n -1x ⋅(cos x ⋅cos nx -sin x ⋅sin nx )= n sin n -1x cos(n +1)x .(6)222211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--⋅-++='-+⋅-++='. (7)222)(arccos arcsin 11arccos 11x x x x x y -+-=' 22)(a r c c o s a r c s i n a r c c o s 11x x x x +⋅-=22)(a r c c o s 12x x -=π. (8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'⋅⋅='⋅='x xx x x y )l n (l n ln 11ln 1)ln(ln 1x x x x x x ⋅=⋅⋅=.(9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111x x -+-=. (10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-⋅+--='+-⋅+--=' )1(2)1(1x x x -+-=. 9. 设函数f (x )和g (x )可导, 且f 2(x )+g 2(x )≠0, 试求函数)()(22x g x f y +=的导数.解 ])()([)()(212222'+⋅+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'⋅+= )()()()()()(22x g x f x g x g x f x f +'+'=. 10. 设f (x )可导, 求下列函数y 的导数dx dy : (1) y =f (x 2);(2) y =f (sin 2x )+f (cos 2x ).解 (1) y '=f '(x 2)⋅(x 2)'= f '(x 2)⋅2x =2x ⋅f '(x 2).(2) y '=f '(sin 2x )⋅(sin 2x )'+f '(cos 2x )⋅(cos 2x )'= f '(sin 2x )⋅2sin x ⋅cos x +f '(cos 2x )⋅2cos x ⋅(-sin x )=sin 2x [f '(sin 2x )- f '(cos 2x )].11. 求下列函数的导数:(1) y =ch(sh x );(2) y =sh x ⋅e ch x ;(3) y =th(ln x );(4) y =sh 3x +ch 2x ;(5) y =th(1-x 2);(6) y =arch(x 2+1);(7) y =arch(e 2x );(8) y =arctan(th x );(9)xx y 2ch 21ch ln +=; (10))11(ch 2+-=x x y 解 (1) y '=sh(sh x )⋅(sh x )'=sh(sh x )⋅ch x .(2) y '=ch x ⋅e ch x +sh x ⋅e ch x ⋅sh x =e ch x (ch x +sh 2x ) .(3))(ln ch 1)(ln )(ln ch 122x x x x y ⋅='⋅='. (4) y '=3sh 2x ⋅ch x +2ch x ⋅sh x =sh x ⋅ch x ⋅(3sh x +2) .(5))1(ch 2)1()1(ch 122222x x x x y --=-⋅-='. (6)222)1()1(112422++='+⋅++='x x x x x y . (7)12)(1)(142222-='⋅-='x x x x e ee e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11⋅+=⋅+='⋅+=' xx x 222sh 211sh ch 1+=+=. (9))ch (ch 21)ch (ch 124'⋅-'⋅='x xx x y x x xx x sh ch 2ch 21ch sh 4⋅⋅-= xx x x x x x x 323ch sh ch sh ch sh ch sh -⋅=-= x xx x x x 33332th ch sh ch )1ch (sh ==-⋅=. (10)'+-⋅+-⋅+-='+-⋅+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y )112(sh )1(2)1()1()1()112(sh 22+-⋅+=+--+⋅+-⋅=x x x x x x x x . 12. 求下列函数的导数:(1) y =e -x (x 2-2x +3);(2) y =sin 2x ⋅sin(x 2);(3)2)2(arctan x y =; (4)n xx y ln=;(5)t t t t ee e e y --+-=; (6)xy 1cos ln =; (7)x e y 1sin 2-=;(8)x x y +=;(9) 242arcsin x x x y -+=; (10)212arcsin tty +=. 解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2)=e -x (-x 2+4x -5).(2) y '=2sin x ⋅cos x ⋅sin(x 2)+sin 2x ⋅cos(x 2)⋅2x=sin2x ⋅sin(x 2)+2x ⋅sin 2x ⋅cos(x 2).(3)2arctan 44214112arctan 222x x xx y +=⋅+⋅='. (4)121ln 1ln 1+--=⋅-⋅='n n n n x x n x nx x x xy . (5)2222)1(4)())(())((+=+---++='-----t t t t t t t t t t t t e e e e e e e e e e e e y . (6)x x x x x x x y 1tan 1)1()1sin (1sec )1(cos 1sec 22=-⋅-⋅='⋅='. (7))1(1cos )1sin 2()1sin (21sin 21sin 22x x x e xe y x x -⋅⋅-⋅='-⋅='-- x e x x1s i n 222s i n 1-⋅⋅=. (8))211(21)(21x xx x x x x y +⋅+='+⋅+=' xx x x +⋅+=412. (9)2arcsin )2(421214112arcsin 22x x x x x x y =-⋅-+⋅-⋅+='.(10)22222222)1()2(2)1(2)12(11)12()12(11t t t t tt t t t t y +⋅-+⋅⋅+-='+⋅+-=' )1(|1|)1(2)1()1(2)1(1222222222t t t t t t t +--=+-⋅-+=.习题 2-31. 求函数的二阶导数:(1) y =2x 2+ln x ;(2) y =e 2x -1;(3) y =x cos x ;(4) y =e -t sin t ;(5)22x a y -=;(6) y =ln(1-x 2)(7) y =tan x ;(8)113+=x y ; (9) y =(1+x 2)arctan x ;(10)xe y x =; (11)2x xe y =;(12))1ln(2x x y ++=.解 (1)x x y 14+=', 14x y -=''. (2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1.(3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x .(4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t .(5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a x a x a x x x a y ---=---⋅---=''.(6) 22212)1(11xxx x y --='-⋅-=', 22)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''. (7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y , 333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y . (9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y , 212a r c t a n 2xxx y ++=''. (10)22)1(1xx e x e x e y x x x -=⋅-⋅=', 3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''.(12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=', xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222. 2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3,f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxy d : (1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2).(2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=. 4. 试从y dy dx '=1导出: (1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==. (2)(())(())dy dx y y dx d y y dy d dy x d ⋅'''-='''-=3333 223)()(31)()(3)(y y y y y y y y y y y ''''-''=⋅'''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω. 解 t A dtds ωωcos =, t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0s i n s i n 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式:y ''-λ2y =0 .解 y '=C 1λe λx -C 2λe -λx ,y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx )=(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 .7. 验证函数y =e x sin x 满足关系式:y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x .y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x=2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数);(2) y =sin 2x ;(3) y =x ln x ;(4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1, y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! .(2) y '=2sin x cos x =sin2x ,)22s i n (22c o s 2π+==''x x y , )222s i n (2)22c o s (222ππ⋅+=+='''x x y , )232s i n (2)222c o s (233)4(ππ⋅+=⋅+=x x y , ⋅ ⋅ ⋅,]2)1(2s i n [21)(π⋅-+=-n x y n n . (3) 1ln +='x y ,11-==''x xy , y '''=(-1)x -2,y (4)=(-1)(-2)x -3,⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x ,y '''=2e x +e x +xe x =3e x +xe x ,⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) .9. 求下列函数所指定的阶的导数:(1) y =e x cos x , 求y (4) ;(2) y =x sh x , 求y (100) ;(3) y =x 2sin 2x , 求y (50) .解 (1)令u =e x , v =cos x , 有u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x ,所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x .(2)令u =x , v =sh x , 则有u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x ,所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x .(3)令u =x 2 , v =sin 2x , 则有u '=2x , u ''=2, u '''=0;x x v 2s i n 2)2482sin(24848)48(=⋅+=π, v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅=)50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''=)2s i n 2(2c o s 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2s i n 212252c o s 502sin (2250x x x x x ++-=.习题2-41. 求由下列方程所确定的隐函数y 的导数dxdy : (1) y 2-2x y +9=0;(2) x 3+y 3-3axy =0;(3) xy =e x +y ;(4) y =1-xe y .解 (1)方程两边求导数得2y y '-2y -2x y ' =0 ,于是 (y -x )y '=y ,xy y y -='. (2)方程两边求导数得3x 2+3y 2y '-2ay -3axy '=0,于是 (y 2-ax )y '=ay -x 2 ,axy x ay y --='22. (3)方程两边求导数得y +xy '=e x +y (1+y '),于是 (x -e x +y )y '=e x +y -y ,yx y x e x y e y ++--='. (4)方程两边求导数得y '=-e y -xe y y ',于是 (1+xe y )y '=-e y ,y y xeey +-='1. 2. 求曲线323232a y x =+在点)42 ,42(a a 处的切线方程和法线方程. 解 方程两边求导数得 032323131='+--y y x , 于是 3131---='y x y , 在点)42 ,42(a a 处y '=-1. 所求切线方程为)42(42a x a y --=-, 即a y x 22=+. 所求法线方程为)42(42a x a y -=-, 即x -y =0. 3. 求由下列方程所确定的隐函数y 的二阶导数22dx y d : (1) x 2-y 2=1;(2) b 2x 2+a 2y 2=a 2b 2;(3) y =tan(x +y );(4) y =1+xe y .解 (1)方程两边求导数得2x -2yy '=0,y '=yx , 3322221)(y y x y y y xx y y y x y y x y -=-=-='-='=''. (2)方程两边求导数得2b 2x +2a 2yy '=0,yx a b y ⋅-='22, 22222222)(y y x a b x y a by y x y a by ⋅--⋅-='-⋅-='' 32432222222ya b y a x b y a a b -=+⋅-=. (3)方程两边求导数得y '=sec 2(x +y )⋅(1+y '),1)(c o s 1)(s e c 1)(s e c 222-+=+-+='y x y x y x y 222211)(s i n )(c o s )(s i n y y x y x y x --=+-+++=, 52233)1(2)11(22yy y y y y y +-=--='=''. (4)方程两边求导数得y '=e y +xe y y ',ye y e xe e y y y y y -=--=-='2)1(11, 3222)2()3()2()3()2()()2(y y e y y y e y y e y y e y y y y y --=-'-=-'---'=''. 4. 用对数求导法求下列函数的导数:(1) x xx y )1(+=;(2)55225+-=x x y ;(3)54)1()3(2+-+=x x x y ; (4)x e x x y -=1sin .解 (1)两边取对数得ln y =x ln|x |-x ln|1+x |,两边求导得xx x x x x y y +⋅-+-⋅+='11)1l n (1ln 1, 于是 ]111[l n )1(xx x x x y x ++++='. (2)两边取对数得)2l n (251|5|ln 51ln 2+--=x x y , 两边求导得22251515112+⋅--⋅='x x x y y , 于是 ]225151[25512552+⋅--=+-='x x x x x y . (3)两边取对数得)1l n (5)3l n (4)2l n (21ln +--++=x x x y , 两边求导得1534)2(211+---+='x x x y y , 于是 ]1534)2(21[)1()3(254+--+++-+='x x x x x x y (4)两边取对数得)1l n (41s i n ln 21ln 21ln x e x x y -++=, 两边求导得)1(4c o t 21211x e e x x y y --+=', 于是 ])1(4c o t 2121[1s i n x x xe e x x e x x y --+-=' ]1c o t 22[1s i n 41-++-=x x x e e x x e x x . 5. 求下列参数方程所确定的函数的导数dxdy : (1) ⎩⎨⎧==22bt y at x ; (2) ⎩⎨⎧=-=θθθθcos )sin 1(y x .解 (1)t ab at bt x y dx dy t t 23232==''=. (2)θθθθθθθθcos sin 1sin cos ---=''=x y dx dy . 6. 已知⎩⎨⎧==.cos ,sin t e y t e x t t 求当3π=t 时dx dy 的值. 解 tt t t t e t e t e t e x y dx dy t t t t t t cos sin sin cos cos sin sin cos +-=+-=''=, 当3π=t 时, 23313123212321-=+-=+-=dx dy . 7. 写出下列曲线在所给参数值相应的点处的切线方程和法线方程:(1) ⎩⎨⎧==t y t x 2cos sin , 在4π=t 处; (2) ⎪⎩⎪⎨⎧+=+=2221313taty t atx , 在t =2处.解 (1)tt x y dx dy t t cos 2sin 2-=''=. 当4π=t 时, 222224cos )42sin(2-=-=⋅-=ππdx dy , 220=x , 00=y , 所求切线方程为)22(22--=x y , 即0222=-+y x ; 所求法线方程为)22(221---=x y , 即0142=--y x . (2)222222)1(6)1(23)1(6t at t t at t at y t +=+⋅-+=', 222222)1(33)1(23)1(3t at a t t at t a x t +-=+⋅-+=', 2212336ttat a atx y dx dy t t -=-=''=. 当t =2时, 3421222-=-⋅=dx dy , a x 560=, a y 5120=, 所求切线方程为)56(34512a x a y --=-, 即4x +3y -12a =0; 所求法线方程为)56(43512a x a y -=-, 即3x -4y +6a =0. 8. 求下列参数方程所确定的函数的二阶导数22dxy d : (1) ⎪⎩⎪⎨⎧-==.122t y t x ;(2) ⎩⎨⎧==t b y t a x sin cos ; (3) ⎩⎨⎧==-t t ey e x 23; (4) ⎩⎨⎧-==)()()(t f t tf y t f x t t , 设f ''(t )存在且不为零. 解 (1) t x y dx dy t t 1-=''=, 322211)(t t t x y dx y d t t x =='''=. (2) t ab t a t b x y dx dy t t cot sin cos -=-=''=, ta b t a t a b x y dx y d t t x 32222sin sin csc )(-=-='''=. (3) t t t t t e e e x y dx dy 23232-=-=''=-, t t t t x e e e x y dx y d 322943232)(=-⋅-=''=. (4) t t f t f t f t t f x y dx dy t t ='''-''+'=''=)()()()(, )(1)(22t f x y dx y d t t x ''='''=. 9. 求下列参数方程所确定的函数的三阶导数33dxy d : (1)⎩⎨⎧-=-=321t t y t x ; (2)⎩⎨⎧-=+=t t y t x arctan )1ln(2. 解(1)tt t t t dx dy 231)1()(223--='-'-=, )31(412)231(3222t t t t t dx y d +-=-'--=,)1(832)31(4125333t t t t t dx y d +-=-'+-=. (2)t tt t t t t dx dy 2112111])1[ln()arctan (22=++-='+'-=, t t t t t dxy d 4112)21(2222+=+'=, 3422338112)41(t t tt t t dx y d -=+'+=. 10. 落在平静水面上的石头, 产生同心波纹, 若最外一圈波半径的增大率总是6m/s , 问在2秒末扰动水面面积的增大率为多少?解 设波的半径为r , 对应圆面积为S , 则S =πr 2, 两边同时对t 求导得 S t '=2πrr '.当t =2时, r =6⋅2=12, r 't =6,故S t '|t =2=2⋅12⋅6π=144π (米2/秒).11. 注水入深8m 上顶直径8m 的正圆锥形容器中, 其速率为4m 2/min . 当水深为5m 时, 其表面上升的速度为多少?解 水深为h 时, 水面半径为h r 21=, 水面面积为π241h S =, 水的体积为3212413131h h h hS V ππ=⋅==, dt dh h dt dV ⋅⋅=2312π, dtdV h dt dh ⋅=24π. 已知h =5(m),4=dtdV (m 3/min), 因此 πππ2516425442=⋅=⋅=dt dV h dt dh (m/min).12. 溶液自深18cm 直径12cm 的正圆锥形漏斗中漏入一直径为10cm 的圆柱形筒中, 开始时漏斗中盛满了溶液, 已知当溶液在漏斗中深为12cm 时, 其表面下降的速率为1cm/min . 问此时圆柱形筒中溶液表面上升的速率为多少? 解 设在t 时刻漏斗在的水深为y , 圆柱形筒中水深为h . 于是有h y r 22253118631=-⋅⋅ππ. 由186y r =, 得3y r =, 代入上式得 h y y 2225)3(3118631=-⋅⋅ππ, 即 h y 233253118631=-⋅⋅π. 两边对t 求导得h y y t '='-222531. 当y =12时, y 't =-1代入上式得64.025165)1(1231222≈=-⋅⋅-='t h (cm/min)..2-71. 已知y =x 3-x , 计算在x =2处当∆x 分别等于1, 0.1, 0.01时的∆y 及dy . 解 ∆y |x =2, ∆x =1=[(2+1)3-(2+1)]-(23-2)=18,dy |x =2, ∆x =1=(3x 2-1)∆x |x =2, ∆x =1=11;∆y |x =2, ∆x =0.1=[(2+0.1)3-(2+0.1)]-(23-2)=1.161,dy |x =2, ∆x =0.1=(3x 2-1)∆x |x =2, ∆x =0.1=1.1;∆y |x =2, ∆x =0.01=[(2+0.01)3-(2+0.01)]-(23-2)=0.110601,dy |x =2, ∆x =0.01=(3x 2-1)∆x |x =2, ∆x =0.01=0.11.2. 设函数y =f (x )的图形如图所示, 试在图(a )、(b )、(c )、(d )中分别标出在点x 0的dy 、∆y 及∆y -d y 并说明其正负.解 (a )∆y >0, dy >0, ∆y -dy >0.(b )∆y >0, dy >0, ∆y -dy <0.(c )∆y <0, dy <0, ∆y -dy <0.(d )∆y <0, dy <0, ∆y -dy >0.3. 求下列函数的微分:(1)x xy 21+=; (2) y =x sin 2x ;(3)12+=x xy ;(4) y =ln 2(1-x );(5) y =x 2e 2x ;(6) y =e -x cos(3-x );(7)21arcsin x y -=;(8) y =tan 2(1+2x 2);(9)2211arctan x x y +-=; (10) s =A sin(ωt +ϕ) (A , ω, ϕ是常数) .解 (1)因为xx y 112+-=', 所以dx x x dy )11(2+-=. (2)因为y '=sin2x +2x cos2x , 所以dy =(sin2x +2x cos2x )dx .(3)因为1)1(111122222++=++⋅-+='x x x x x x y , 所以dx x x dy 1)1(122++=. (4)dx x x dx x x dx x dx y dy )1ln(12])1(1)1ln(2[])1([ln 2--=--⋅-='-='=. (5)dy =y 'dx =(x 2e 2x )'dx =(2xe 2x +2x 2e 2x )dx =2x (1+x )e 2x .(6) dy =y 'dx =[e -x cos(3-x )]dx =[-e -x cos(3-x )+e -x sin(3-x )]dx=e -x [sin(3-x )-cos(3-x )]dx .(7)dx xx x dx x x dx x dx y dy 22221||)12()1(11)1(arcsin --=--⋅--='-='=. (8) dy =d tan 2(1+2x 2)=2tan(1+2x 2)d tan(1+2x 2)=2tan(1+2x 2)⋅sec 2(1+2x 2)d (1+2x 2)=2tan(1+2x 2)⋅sec 2(1+2x 2)⋅4xdx=8x ⋅tan(1+2x 2)⋅sec 2(1+2x 2)dx .(9))11()11(1111arctan 2222222x x d x x x x d dy +-+-+=+-= dx x x dx x x x x x x x 4222222214)1()1(2)1(2)11(11+-=+--+-⋅+-+=.(10) dy =d [A sin(ω t +ϕ)]=A cos(ω t +ϕ)d (ωt +ϕ)=A ω cos(ωt +ϕ)dx .4. 将适当的函数填入下列括号内, 使等式成立:(1) d ( )=2dx ;(2) d ( )=3xdx ;(3) d ( )=cos tdt ;(4) d ( )=sin ωxdx ;(5) d ( )dx x 11+=; (6) d ( )=e -2x dx ;(7) d ( )dx x1=; (8) d ( )=sec 23xdx .解 (1) d ( 2x +C )=2dx .(2) d (C x +223)=3xdx . (3) d ( sin t +C )=cos tdt .(4) d (C x +-ωωcos 1)=sin ωxdx . (5) d ( ln(1+x )+C )dx x 11+=. (6) d (C e x +--221)=e -2x dx . (7) d (C x +2)dx x1=. (8) d (C x +3tan 31)=sec 23xdx .5. 如图所示的电缆B O A的长为s , 跨度为2l , 电缆的最低点O 与杆顶连线AB 的距离为f , 则电缆长可按下面公式计算:)321(222lf l s +=, 当f 变化了∆f 时, 电缆长的变化约为多少?解 f f l df lf l dS S ∆='+=≈∆38)321(222. 6. 设扇形的圆心角α=60︒, 半径R =100cm(如图), 如果R 不变, α 减少30', 问扇形面积大约改变了多少?又如果α 不变, R 增加1cm , 问扇形面积大约改变了多少?解 (1)扇形面积221R S α=, αααα∆='=≈∆2221)21(R d R dS S . 将α=60︒3π=, R =100, 36003πα-='-=∆ 代入上式得 63.43)360(100212-≈-⋅⋅≈∆πS (cm 2). (2) R R dR R dS S R ∆='=≈∆αα)21(2. 将α=60︒3π=, R =100, ∆R =1代入上式得 72.10411003≈⋅⋅≈∆πS (cm 2). 7. 计算下列三角函数值的近似值:(1) cos29︒;(2) tan136︒.解 (1)已知f (x +∆x )≈f (x )+f '(x )∆x , 当f (x )=cos x 时, 有cos(x +∆x )≈cos x -sin x ⋅∆x , 所以cos29︒=87467.01802123)180(6sin 6cos )1806cos(≈⋅+=-⋅-≈-ππππππ. (2)已知f (x +∆x )≈f (x )+f '(x )∆x , 当f (x )=tan x 时, 有tan(x +∆x )≈tan x +sec 2x ⋅∆x , 所以。
川大版高等数学(第一册)部分课后题详细答案

高数第一册 第一章 习题1.13.(1)(,1)(1,)(2){|1,}1(1,1)(1,)(3)(1,1)x x x R -∞-⋃-+∞≠±∈∞-⋃-⋃+∞-或(-,)(4)22903[3,1)(1,3]10x x x x x ⎧⎫-≥⇒-⎪⎪⇒--⋃⎨⎬-⇒⎪⎪⎩⎭≤ ≤3>>1或<-12222(5)(,3)(6)sin 0,,()241(7)114(1),11(1)3x x k x k k z x x x x x x πππ-∞≠≠≠∈⎡⎤≤⇒≤⇒≤+⇒-⎢⎥++⎣⎦(8)0ln 0x x x x x ⎧⎫⇒⇒⎨⎬⇒⎩⎭> >0>1>>1(9)[1,2]-(10)21()x x x f x x x x x x x x ⎧⎫⇒⎪⎪⎪⎪=⇒⇒≠⇒∴⎨⎬⎪⎪⎪⎪⇒⎩⎭-1 <00≤≤10即0<<1 < 0和0<≤2e 1≤≤27.(1)(2)(3)(4)(5)奇函数偶函数偶函数偶函数非奇非偶(6)2()()f x f x -=+=偶函数(7)11()lnln ()11x xf x f x x x+--==-=--+奇函数)(8)2112()()2112x xx xf x f x -----===-++奇函数(9)()sin cos f x x x -=--非奇非偶 13.(1)22(())(2)24,(())2,xxxx f x f f x x Rϕϕ====∈(2)11(())(0,1)111x f f x x xx-==≠--(3)32221,()(1)3(1)256()56(1)(1)5(1)6x t f t t t t t f x x x f x x x +==---+=-+∴=-++=+-++则x=t-1,或:14.[]22(1)(0)0.(2)0,111111(3)01(4)1lg ,lg 1,lg 1,.1(5)11()(6)1log (16)y x x y x y y x y x x y y y xx y x y y x xy xx x y x x x =≤≤+∞=≥=++===≠-+==-=--=≠-+∞⎧=≤≤∞反函数反函数x=,x-1=,x=1+反函数y ,定义域反函数定义域x >0反函数,定义域(x )-<<1反函数16)<<+⎫⎪⎬⎪⎩⎭习题1.2 2。
高等数学第六版(同济大学)上册课后习题答案解析

高等数学第六版上册课后习题答案及解析第一章习题1-11. 设A=(-, -5)(5, +), B=[-10, 3), 写出A B, A B, A\B及A\(A\B)的表达式.解A B=(-, 3)(5, +),A B=[-10, -5),A\B=(-, -10)(5, +),A\(A\B)=[-10, -5).2. 设A、B是任意两个集合, 证明对偶律: (A B)C=A C B C.证明因为x(A B)C x A B x A或x B x A C或x B C x A C B C,所以(A B)C=A C B C.3. 设映射f : X Y, A X, B X . 证明(1)f(A B)=f(A)f(B);(2)f(A B)f(A)f(B).证明因为y f (A B )x A B , 使f (x )=y(因为x A 或x B ) y f (A )或y f (B )y f (A )f (B ), 所以 f (AB )=f (A )f (B ). (2)因为y f (A B )x A B , 使f (x )=y (因为x A 且x B ) y f (A )且y f (B ) y f (A )f (B ), 所以 f (A B )f (A )f (B ).4. 设映射f : X Y , 若存在一个映射g : Y X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个xX , 有I X x =x ; 对于每一个y Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的yY , 有x =g (y )X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1x 2, 必有f (x 1)f (x 2), 否则若f (x 1)=f (x 2)g [ f (x 1)]=g [f (x 2)]x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y X , 因为对每个y Y , 有g (y )=x X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X Y , A X . 证明:(1)f -1(f (A ))A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x A f (x )=y f (A ) f -1(y )=x f -1(f (A )),所以 f -1(f (A ))A . (2)由(1)知f -1(f (A ))A .另一方面, 对于任意的xf -1(f (A ))存在y f (A ), 使f -1(y )=x f (x )=y . 因为y f (A )且f 是单射, 所以x A . 这就证明了f -1(f (A ))A . 因此f -1(f (A ))=A .6. 求下列函数的自然定义域:(1)23+=x y ; 解 由3x +20得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 20得x 1. 函数的定义域为(-, -1)(-1, 1)(1, +). (3)211x xy --=; 解 由x0且1-x 20得函数的定义域D =[-1, 0)(0, 1].(4)241x y -=; 解 由4-x 20得 |x | 2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x 0得函数的定义D =[0, +¥).(6) y =tan(x +1);解 由21π≠+x (k =0, 1, 2, )得函数的定义域为 12-+≠ππk x (k =0, 1, 2, ). (7) y =arcsin(x -3);解 由|x -3|1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解 由3-x 0且x 0得函数的定义域D =(-¥, 0)È(0, 3).(9) y =ln(x +1);解 由x +10得函数的定义域D =(-1, +¥). (10)x e y 1=.解 由x0得函数的定义域D =(-¥, 0)È(0, +¥). 7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x 0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, j (-2), 并作出函数y =j (x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-, 1); (2)y =x +ln x , (0, +).证明 (1)对于任意的x 1, x 2(-, 1), 有1-x 10, 1-x 20. 因为当x 1x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数xx y -=1在区间(-, 1)内是单调增加的. (2)对于任意的x 1, x 2(0, +), 当x 1x 2时, 有0ln)()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于"x 1, x 2Î(-l , 0)且x 1<x 2, 有-x 1, -x 2Î(0, l )且-x 1-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以 f (-x 2)f (-x 1), -f (x 2)-f (x 1), f (x 2)f (x 1),这就证明了对于"x1, x2Î(-l, 0), 有f(x1)f(x2), 所以f(x)在(-l, 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(-l, l)上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明(1)设F(x)=f(x)+g(x). 如果f(x)和g(x)都是偶函数, 则F(-x)=f(-x)+g(-x)=f(x)+g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的和是偶函数.如果f(x)和g(x)都是奇函数, 则F(-x)=f(-x)+g(-x)=-f(x)-g(x)=-F(x),所以F(x)为奇函数, 即两个奇函数的和是奇函数.(2)设F(x)=f(x)×g(x). 如果f(x)和g(x)都是偶函数, 则F(-x)=f(-x)×g(-x)=f(x)×g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的积是偶函数.如果f(x)和g(x)都是奇函数, 则F(-x)=f(-x)×g(-x)=[-f(x)][-g(x)]=f(x)×g(x)=F(x),所以F(x)为偶函数, 即两个奇函数的积是偶函数.如果f(x)是偶函数, 而g(x)是奇函数, 则F(-x)=f(-x)×g(-x)=f(x)[-g(x)]=-f(x)×g(x)=-F(x),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211xxy +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2p .(2)y =cos 4x ;解 是周期函数, 周期为2π=l .(3)y =1+sin px ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =p .14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。
(整理)高等数学(1)-2习题册答案(第十一章1-4节)

第十一章 曲线积分与曲面积分第17次课 对弧长的曲线积分1.计算下列各题中的曲线积分: (1)cos d Ly s ⎰,其中L 为原点至点(2,1)的直线段;解:2200cos 2L x yds ⎤===⎥⎦⎰⎰ (2)d Lx s ⎰,其中L 为抛物线221y x =-介于1x =及0x =之间的一段弧;解:131222001121(116)(116)3232348Lxds x x ⎡⎤==+=+=⎢⎥⎣⎦⎰⎰⎰(3)()d Lx y s +⎰,其中L 是以(0,0),(1,0),(0,1)O A B 为顶点的三角形的边界;解:()()()()LOAABOBx y ds x y ds x y ds x y ds +=+++++⎰⎰⎰⎰111((0x y =++++⎰⎰⎰11221000122x y =++=+(4)222()d Lx y s +⎰,其中L 为圆周222x y a +=;解:2222245()()22LLx y ds a ds a a a ππ+==⋅=⎰⎰(5)||d Lxy s ⎰,其中L 为圆周222x y a +=;解:根据xy 在四个象限的对称性,有14LL xy ds xy ds =⎰⎰(其中1L 是在第一象限的四分之一圆周),则12044(cos )(sin LL xyds xyds a t a t π==⎰⎰⎰333220sin 2(2)(cos 2)2atd t a t a ππ==-=⎰(6)222d z s x y Γ+⎰,其中Γ为圆周cos ,sin ,,02x a t y a t z at t π===≤≤. 解:22220z dsx yπτ=+⎰⎰222330013t dt t a ππ===⎰2.计算曲线积分22d x y Les +⎰,其中L 为圆周222x y a +=,直线y x =及x 轴在第一象限内所围成的扇形的整个边界.解:2240ax y Leds π+=++⎰⎰⎰ 4002(1)4aax a a ae t e ae e ππ=++=+-3.有一铁丝成半圆形cos ,sin (0)x a t y a t t π==≤≤,其上每一点的密度等于该点的纵坐标,求铁丝的质量.解:220sin (cos )2LM yds a a t a ππ===-=⎰⎰提高题:1.已知椭圆23:143x y L +=周长为a ,求22(234)d L xy x y s ++⎰. 解:原式(122)121212012LLLxy ds ds xyds a a =+=+=+=⎰⎰⎰2.计算曲线积分4433()d Lx y s +⎰,其中L 为星形线33cos ,sin (0)2x a y a πθθθ==≤≤在第一象限内的弧.解:4444433320()d (sin cos Lx y s a πθθθ+=+⎰⎰7772556633322000113(sin sin cos cos )3sin cos 66a d d a a πππθθθθθθ⎛⎫=-=-= ⎪⎝⎭⎰⎰第18次课 对坐标的曲线积分1.计算下列各题中的曲线积分: (1)(2)d Lx y x +⎰,其中L 为从点(2,0)-到点(0,2)的直线段.解:02(2)(22)2Lx y dx x x dx -+=++=-⎰⎰(2)22d d Lxy y x y x -⎰,其中L 为圆周221x y +=,逆时针方向.解:2222220cos sin cos cos sin sin Lxy dy x ydx t t tdt t t tdt ππ-=+⎰⎰⎰2222000sin 21cos 411sin 4244162t t dt dt t t ππππ-⎛⎫===-= ⎪⎝⎭⎰⎰(3)d Lxy x ⎰,其中L 为圆周222()(0)x a y a a -+=>及x 轴所围成的在第一象限内的区域的整个边界曲线弧(按逆时针方向). 解:LAOOAxydx xydx xydx =+⎰⎰⎰半圆周232320(cos )sin (sin )0sin sin cos aa a t a t a t dt dx a tdt a t tdt πππ=+⋅-+=--⎰⎰⎰⎰33233330001cos 2111sin sin sin 2sin 22432t a dt a td t a t t a ta πππππ-⎛⎫=--=---=-⎪⎝⎭⎰⎰(4)d d d Lx x y y z z ++⎰,其中Γ为从(1,1,1)到(2,3,4)的直线段.解:()1112[(1)(12)2(13)3](614)6713Lxdx ydy zdz t t t dt t dt t t++=+++⋅++⋅=+=+=⎰⎰⎰(5)d d L x yx y ++⎰,其中L 为从点(0,1)A -到点(1,0)B 再到点(0,1)C 的折线段.解:1001(11)(11)2L AB BC dx dy dx dy dx dydx dx x y x y x y +++=+=++-=+-+⎰⎰⎰⎰⎰2.计算()d ()d Lx y x y x y ++-⎰,其中L :(1)抛物线2y x =上从点(1,1)到点(4,2)的一段弧; (2)从点(1,1)到点(4,2)的直线段;(3)曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧. 解:(1)2222321134=[()2()](2)3y y y y y dy y y y dy ++-=++=⎰⎰原式 (2)441112121108=[()()]()113333399x x x x dx x dx ++++-⋅=+=⎰⎰原式 (3)122220{(211)(41)[1(21)]2}t t t t t t t t dt =+++++++-++⎰原式132032(10592)3t t t dt =+++=⎰3.计算曲线积分2(12)d d Lxy x x y ++⎰,其中L 为从点(1,0)到点(1,0)-的上半椭圆周2221(0)y x y +=≥.解::cos ,,:02L x t y t t π==→20=[(1cos )(sin )cos cos ]2t t t tt dt π+-+⎰原式220sin sin sin (1sin )sin 2tdt td t t d t πππ=-+-⎰⎰ 2=-提高题: 1.计算曲线积分2sin 2d 2(1)d Lx x x y y +-⎰,其中L 是曲线sin y x =上从点(0,0)到点(,0)π的一段.解:220=[sin 22(1)sin cos ]sin 2x x x x dx x xdx ππ+-=⎰⎰原式2200011cos 2cos 2cos 222x d x x x x xdx πππ⎡⎤=-=-+⎣⎦⎰⎰ []2200011111sin 2sin 2sin 222222xd x x x xdx πππππ=-+=-+-⎰⎰212π=-2.设在力场F y x z (,,)=-作用下,质点由(,0,0)A R 沿Γ移动到(,0,2)B R k π,其中Γ为 (1)cos ,sin ,x R t y R t z kt ===; (2)AB . 试求力场对质点所作的功. 解:(1)222220d d d ()d 2()W y x x y z z R k t t k R πππΓ==-+=-+=-⎰⎰(2)直线的参数方程为,0,2,:01x R y z kt t π===→12220d d d (2)d 2ABW y x x y z z k t t k ππ=-+==⎰⎰第19次课 格林公式及其应用1.应用格林公式计算下列各题中的积分: (1)22d d Lx y x xy y -⎰,其中L 为正向圆周222(0)x y a a +=>.解:22,Q Py x x y∂∂=-=∂∂,由格林公式 原式2222440011()()2()42a Dy x dxdy d r rdr a a πθππ=--=-=⋅-=-⎰⎰⎰⎰(2)()d (3)d Lx y y x y x -++⎰,其中L 为以(1,0),(2,0),(2,1),(1,1)A B C D 为顶点的正方形沿顺时针方向. 解:1,3Q Px y∂∂==∂∂,由格林公式 原式(13)222DDDdxdy dxdy S=--===⎰⎰⎰⎰(3)22222(32)d (223)d x x Ly e x xy y x ye x xy y y ++++++-⎰,其中L 是半圆周y =自点(1,0)A 至(0,1)B .解:222,222x x Q Pye x y ye x y x y∂∂=++=++∂∂,由格林公式 原式L BO OABO OA++=--⎰⎰⎰012210(23)3Ddxdy y y x dx =---⎰⎰⎰⎰1=-(4)22()d (sin )d Lx y x x y y --+⎰,其中L 是在圆周y =上由点(0,0)到(1,1)的一段弧. 解:1,1Q Px y∂∂=-=-∂∂ 设(1,1),(1,0)B A ,由格林公式 原式L BA AOBAAO++=--⎰⎰⎰0022110[(1sin )]Ddxdy y dy x dx =---+-⎰⎰⎰⎰311710(sin 2)sin 224364=--+=-+2.利用曲线积分计算星形线33cos ,sin (0,02)x a t y a t a t π==>≤≤所围成图形的面积.解:23232011[cos 3sin cos sin (3cos sin )]22L A xdy ydx a t a t t a t a t t dt π=-=⋅-⋅-⎰⎰ 2222222220003331c o s 4s i n c o s s i n 22882t a t t d t a t d t a d t πππ-===⎰⎰⎰ 238a π=3.证明曲线积分21d d L y x y x x -⎰在右半平面内与路径无关,并求(1,2)2(2,1)1d d y x y x x -⎰.解:21Q Px x y∂∂==∂∂(0)x > ∴曲线积分在区域{}(,)0x y x >与路径无关 设(2,1),(1,2),:3,:21A B AB y x x =-+→则(1,2)1222(2,1)21131d d d d [(1)]AB y y x x y x y dx x xx x x x -+-=-=-⋅-⎰⎰⎰ 12332x =-=-4.验证表达式:2222(2)d (2)d x xy y x x xy y y +-+--在整个平面内是某一函数(,)u x y 的全微分,并求这样的一个(,)u x y .解:22Q Px y x y∂∂=-=∂∂ ∴2222(2)d (2)d x x y y x x x y y y +-+--是某一函数(,)u x y 的全微分(,)2222(0,0)(,)(2)d (2)d x y u x y x xy y x x xy y y =+-+--⎰(,0)(,)222(0,0)(,0)(2)x x y xyx x d x x x y y d y=+=+--⎰⎰⎰⎰ 32231133x x y xy y =+--提高题:1.设曲线积分2d ()d L xy x y x y ϕ+⎰与路径无关,其中()x ϕ具有连续导数,且(0)0ϕ=,求()x ϕ,并求积分(1,1)2(0,0)d ()d xy x y x y ϕ+⎰的值. 解:曲线积分与路径无关可得2()Q P xy y x x yϕ∂∂'==∂∂即 从而2()2()x x x x C ϕϕ'=⇒=+,又(0)0ϕ=有2()x x ϕ= 故(1,1)123(0,0)01d ()d 22xy x y x y x dx ϕ+==⎰⎰2.[()]d [()]d x x L f y e my x f y e m y '-+-⎰,其中()f y 有连续的一阶导数,L 是连续点1(0,)A y ,2(0,)B y 的任何路径,且L 与直线AB 所围成区域的面积为定值S ,L 总是位于直线AB 的左方. 解:(),()x x Q P f y e f y e m x y∂∂''==-∂∂ 不妨设12y y <,由格林公式 原式12[()]y L BA BA y D mdxdy f y m dy +'=-=---⎰⎰⎰⎰⎰ 212121[()]()()()y D y mS f y my mS f y f y m y y =-+-=-+---第20 次课 对面积的曲面积分1.计算下列各题中的曲面积分:(1)d z S ∑⎰⎰,其中∑为上半球面z =解:222:xy D x y R +≤xy D zdS ∑=⎰⎰⎰⎰ 23xy D Rdxdy R R R ππ==⋅=⎰⎰(2)()d x y z S ∑++⎰⎰,其中∑为锥面z =被平面1z =所截下的有限部分. 解:22:1xy D x y +≤()d (xy D x y z S x y ∑++=+⎰⎰⎰⎰2100(cos 1)d r sin rdr πθθθ=++⋅⎰20(cos sin 1)3d πθθθ=++⎰=(3)d S ∑⎰⎰,其中∑是平面1=++z y x 在第一卦限被0,0,0===z y x 截下的部分.解:∑的等边三角形,其面积为2S ∑=d S S ∑∑==⎰⎰(4)S ∑,其中∑为抛物面22z x y =+被平面1z =所截下的有限部分.解:22:1xy D x y +≤xyD S ∑=⎰⎰ 2122200(144)(14)xy D x y dxdy d r rdr πθ=++=+⎰⎰⎰⎰ 3232ππ=⋅=(5)()xy yz zx dS ∑++⎰⎰,其中∑为锥面z =被柱面222(0)x y ax a +=> 所截得的部分.解:222:()xy D x a y a -+≤()d [(xy D xy yz zx S xy x y ∑++=++⎰⎰⎰⎰2cos 22202[sin cos (sin cos )]a d r r rdr πθπθθθθθ-=++⎰454522(sin cos sin cos cos )d ππθθθθθθ-=++⎰422420(1sin )sin d πθθ=-=⎰(6)d ,:xy S ∑∑⎰⎰曲面22(01)z x y z =+≤≤在第一卦限的部分. 解:22:1(0,0)xy D x y x y +≤≥≥d xy D xy S ∑=⎰⎰⎰⎰12200sin cos d r πθθ=⎰⎰12001sin cos 2d πθθθ=⋅⎰⎰2201111sin 22242t d t dt πθθ-=⋅⋅⎰25311111cos 232253240o t t πθ⎛⎫⎛=-⋅-= ⎪ ⎝⎭⎝2.计算曲面积分(,,)d f x y z S ∑⎰⎰,:∑抛物面222z x y =--在xOy 平面上方的部分,(,,)f x y z 分别如下:(1)(,,)1f x y z =; (2)22(,,)f x y z x y =+; (3)(,,)3f x y z z =.解:22:2xy D x y +≤(1)(,,)d xyD f x y z S S ∑∑==⎰⎰⎰⎰20d πθ=⎰1313263ππ=⋅=(2) 22(,,)d (xy D f x y z S x y ∑=+⎰⎰⎰⎰200d πθ=⎰ 14914926030ππ=⋅=(3) 22(,,)d 3(2xyD f x y z S xy ∑=--⎰⎰⎰⎰2200d r πθ=-⎰11111122010ππ=⋅=提高题: 1.设曲面:1x y z ∑++=,求()d x y S ∑+⎰⎰. 解:由曲面的对称性和函数x 的奇偶性可知0xdS ∑=⎰⎰又曲面∑对坐标,,x y z 具有轮换对称性()d d d x y S x S y S∑∑∑∴+=+⎰⎰⎰⎰⎰⎰ 10()3x y z dS ∑=+++⎰⎰11183332dS S ∑∑===⋅=⎰⎰第21次课 对坐标的曲面积分1.计算下列各题中的曲面积分:(1)d d z x y ∑⎰⎰,其中∑为平面1x y z ++=位于第一卦限部分的上侧.(2)22d d x y z x y ∑⎰⎰,:∑球面2222x y z R ++=的下半部分的下侧.(3)222d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑为球面2221x y z ++=上半部分外侧.(4)d d d d d d z x y x y z y z x ∑++⎰⎰,:∑柱面221(03)x y z +=≤≤在第一卦限内的部分的前侧.(5)d d d d xy z x z x y ∑+⎰⎰,其中∑为抛物面22z x y =+在0,0,01x y z ≥≥≤≤内部分的上侧.2.求()d d ()d d ()d d y z y z z x z x x y x y ∑-+-+-⎰⎰,其中∑为曲面z =及平面(0)z h h =>所围成的空间区域的整个边界曲面的外侧.3.计算()d d ()d d ()d d f x y z g y z x h z x y ∑++⎰⎰,其中(),(),()f x g y h z 为连续函数,∑为直角平行六面体0,0,0x a y b z c ≤≤≤≤≤≤的表面外侧.提高题:1.把对坐标的曲面积分:(,,)d d (,,)d d (,,)d d P x y z y z Q x y z z x R x y z x y ∑++⎰⎰化成对面积的曲面积分,其中:∑是平面236x y z -+=在第二卦限部分的上侧.2.设曲面∑是z =的上侧,求2d d d d d d xy y z x z x x x y ∑++⎰⎰.第22次课 第十一章 总复习题1.计算下列曲线积分:(1)d L x S ⎰, 其中L 为星形线332cos 2sin x t,y t ==经过点(2,0)A ,(0,2)C ,(2,0)B -的ACB 弧段.(2)22d d L y x y x y x -⎰,其中L 是圆周222x y a +=,沿顺时针方向.(3)求zds Γ⎰,其中Γ为曲线0cos sin ,(0)x t t y t t t t z t =⎧⎪=≤≤⎨⎪=⎩.(4)求(sin 2)d (cos 2)d x x L e y y x e y y -+-⎰,其中L 为上半圆周222()(0)x a y a y -+=≥,沿逆时针方向.2.验证22(e cos 2)d (2e sin )d x xy xy x x y y y ++-是否是某一函数()u x,y 的全微分.若是,试求出()u x,y .3.设L 为平面曲线:222x y R +=,计算下列各积分:(1)22()d L x y s +⎰; (2)22()d L x y x +⎰,其中L 取正向; (3)22()d D x y σ+⎰⎰,其中D 为曲线L 所围成的平面区域.4.计算33d d L y x x y -⎰,其中L 是从(,0)A R -到(,0)B R 的上半圆周y =5.设曲面:∑2222x y z R ++=,计算下列各曲面积分:(1)222()d x y z S ∑++⎰⎰; (2)222()d d x y z z x ∑++⎰⎰,其中∑取其外侧; (3)222()d x y z V Ω++⎰⎰⎰,其中Ω为曲面∑所围成的空间区域.6.计算∑∑为介于0z =及(0)z H H =>之间的柱面222R x y =+.。
高等数学上册(第六版)课后习题答案

高等数学上册(第六版)课后习题答案习题1-11.设A=(-∞,-5)⋃(5,+∞),B=[-10, 3),写出A⋃B,A⋂B,A\B及A\(A\B)的表达式.解A⋃B=(-∞, 3)⋃(5,+∞),A⋂B=[-10,-5),A\B=(-∞,-10)⋃(5,+∞),A\(A\B)=[-10,-5).2.设A、B是任意两个集合,证明对偶律: (A⋂B)C=A C ⋃B C.证明因为x∈(A⋂B)C⇔x∉A⋂B⇔ x∉A或x∉B⇔ x∈A C或x∈B C⇔ x∈A C ⋃B C,所以(A⋂B)C=A C ⋃B C.3.设映射f:X→Y,A⊂X,B⊂X.证明(1)f(A⋃B)=f(A)⋃f(B);(2)f(A⋂B)⊂f(A)⋂f(B).证明因为y∈f(A⋃B)⇔∃x∈A⋃B,使f(x)=y⇔(因为x∈A或x∈B) y∈f(A)或y∈f(B)⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1. 证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射. 又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )), 所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f-1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A .6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0,±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时,0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数x x y -=1在区间(-∞, 1)内是单调增加的.(2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0ln )()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2. 因为f (x )在(0, l )内单调增加且为奇函数, 所以f(-x2)<f(-x1),-f(x2)<-f(x1), f(x2)>f(x1),这就证明了对于∀x1,x2∈(-l, 0),有f(x1)< f(x2),所以f(x)在(-l, 0)内也单调增加.11.设下面所考虑的函数都是定义在对称区间(-l,l)上的,证明:(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数.证明(1)设F(x)=f(x)+g(x).如果f(x)和g(x)都是偶函数,则F(-x)=f(-x)+g(-x)=f(x)+g(x)=F(x),所以F(x)为偶函数,即两个偶函数的和是偶函数.如果f(x)和g(x)都是奇函数,则F(-x)=f(-x)+g(-x)=-f(x)-g(x)=-F(x),所以F(x)为奇函数,即两个奇函数的和是奇函数.(2)设F(x)=f(x)⋅g(x).如果f(x)和g(x)都是偶函数,则F(-x)=f(-x)⋅g(-x)=f(x)⋅g(x)=F(x),所以F(x)为偶函数,即两个偶函数的积是偶函数.如果f(x)和g(x)都是奇函数,则F(-x)=f(-x)⋅g(-x)=[-f(x)][-g(x)]=f(x)⋅g(x)=F(x),所以F(x)为偶函数,即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211x xy +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数.13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2π.(2)y =cos 4x ;解 是周期函数, 周期为2π=l . (3)y =1+sin πx ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y ;解 由31+=x y 得x =y 3-1, 所以31+=x y 的反函数为y =x 3-1.(2)xx y +-=11; 解 由xx y +-=11得y y x +-=11, 所以x x y +-=11的反函数为x x y +-=11. (3)d cx b ax y ++=(ad -bc ≠0);解 由d cx b ax y ++=得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为acx b dx y -+-=.(4) y =2sin3x ;解 由y =2sin 3x 得2arcsin 31y x =, 所以y =2sin3x 的反函数为2arcsin 31x y =. (5) y =1+ln(x +2);解 由y =1+ln(x +2)得x =e y -1-2, 所以y =1+ln(x +2)的反函数为y =e x -1-2.(6)122+=x x y . 解 由122+=x x y 得y y x -=1log 2, 所以122+=x x y 的反函数为x x y -=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明 先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即-M ≤f (x )≤M . 这就证明了f (x )在X 上有下界-M 和上界M . 再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 -M ≤ K 1≤f (x )≤ K 2≤M , 即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ;解 y =sin 2x , 41)21(6sin 221===πy ,43)23(3sin 222===πy . (2) y =sin u , u =2x , 81π=x ,42π=x ; 解 y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy . (3)u y =, u =1+x 2, x 1=1, x 2= 2;解 21x y +=, 21121=+=y , 52122=+=y .(4) y =e u , u =x 2, x 1 =0, x 2=1;解 2x e y =, 1201==e y , e e y ==212. (5) y =u 2 , u =e x , x 1=1, x 2=-1.解 y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(-1)=e -2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域:(1) f (x 2);解 由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[-1, 1].(2) f (sin x );解 由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为[2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) .(3) f (x +a )(a >0);解 由0≤x +a ≤1得-a ≤x ≤1-a , 所以函数f (x +a )的定义域为[-a , 1-a ].(4) f (x +a )+f (x -a )(a >0).解 由0≤x +a ≤1且0≤x -a ≤1得: 当210≤<a 时, a ≤x ≤1-a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1-a ], 当21>a 时函数无意义. 18. 设⎪⎩⎪⎨⎧>-=<=1||11||01|| 1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形.解 ⎪⎩⎪⎨⎧>-=<=1|| 11|| 01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>-=<=0 1000 1)]([x x x x g f . ⎪⎩⎪⎨⎧>=<==-1|| 1|| e 1|| )]([101)(x e x x e e x f g x f , 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g .19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40︒(图1-37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式,并指明其定义域.图1-37解40sin h DC AB ==, 又从0)]40cot 2([21S h BC BC h =⋅++ 得h hS BC ⋅-= 40cot 0, 所以 h h S L40sin 40cos 20-+=.自变量h 的取值范围应由不等式组h >0, 040cot 0>⋅-h hS 确定, 定义域为 40cot 00S h <<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数;(2)将厂方所获的利润P 表示成订购量x 的函数;(3)某一商行订购了1000台, 厂方可获利润多少?解 (1)当0≤x ≤100时, p =90.令0.01(x 0-100)=90-75, 得x 0=1600. 因此当x ≥1600时, p =75. 当100<x <1600时,p =90-(x -100)⨯0.01=91-0. 01x .综合上述结果得到⎪⎩⎪⎨⎧≥<<-≤≤=1600 75160010001.0911000 90x x x x p . (2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 151600100 01.0311000 30)60(2x x x x x x x x p P . (3) P =31⨯1000-0.01⨯10002=21000(元).习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)n n x 21=; 解 当n →∞时, n n x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=; 解 当n →∞时, n x n n 1)1(-=→0, 01)1(lim =-∞→nn n . (3)212nx n +=; 解 当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→nn . (4)11+-=n n x n ; 解 当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n . (5) x n =n (-1)n .解 当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N . 解 0lim =∞→n n x . n n n x n 1|2c o s ||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n .取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→nn ; 分析 要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim 2=∞→n n . (2)231213lim =++∞→n n n ; 分析 要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明 因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n . (3)1lim 22=+∞→na n n ; 分析 要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22na n , 所以1lim 22=+∞→na n n . (4)19 999.0lim =⋅⋅⋅∞→个n n . 分析 要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n .证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明 因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→. 数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x .证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M . 又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有My n ε<||. 从而当n >N 时, 有εε=⋅<≤=-MM y M y x y x n n n n n |||||0|, 所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞),证明: x n →a (n →∞).证明 因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0,∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ;∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε .取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε .因此x n →a (n →∞).习题1-31. 根据函数极限的定义证明:(1)8)13(lim 3=-→x x ; 分析 因为|(3x -1)-8|=|3x -9|=3|x -3|,所以要使|(3x -1)-8|<ε , 只须ε31|3|<-x . 证明 因为∀ε>0, ∃εδ31=, 当0<|x -3|<δ时, 有 |(3x -1)-8|<ε ,所以8)13(lim 3=-→x x . (2)12)25(lim 2=+→x x ; 分析 因为|(5x +2)-12|=|5x -10|=5|x -2|,所以要使|(5x +2)-12|<ε , 只须ε51|2|<-x .证明 因为∀ε >0, ∃εδ51=, 当0<|x -2|<δ时, 有 |(5x +2)-12|<ε ,所以12)25(lim 2=+→x x . (3)424lim 22-=+--→x x x ; 分析 因为|)2(||2|244)4(2422--=+=+++=--+-x x x x x x x , 所以要使ε<--+-)4(242x x , 只须ε<--|)2(|x . 证明 因为∀ε >0, ∃εδ=, 当0<|x -(-2)|<δ时, 有ε<--+-)4(242x x , 所以424lim 22-=+--→x x x .(4)21241lim 321=+--→x x x . 分析 因为|)21(|2|221|212413--=--=-+-x x x x , 所以要使ε<-+-212413x x , 只须ε21|)21(|<--x . 证明 因为∀ε >0, ∃εδ21=, 当δ<--<|)21(|0x 时, 有 ε<-+-212413x x , 所以21241lim 321=+--→x x x .2. 根据函数极限的定义证明:(1)2121lim 33=+∞→x x x ; 分析 因为333333||21212121x x x x x x =-+=-+, 所以要使ε<-+212133x x , 只须ε<3||21x , 即321||ε>x . 证明 因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有 ε<-+212133x x , 所以2121lim 33=+∞→x x x . (2)0sin lim =+∞→xx x . 分析 因为xx x x x 1|sin |0sin ≤=-. 所以要使ε<-0sin x x , 只须ε<x1, 即21ε>x . 证明 因为∀ε>0, ∃21ε=X , 当x >X 时, 有 ε<-0sin xx , 所以0sin lim =+∞→xx x . 3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x -2|<δ时, |y -4|<0.001?解 由于当x →2时, |x -2|→0, 故可设|x -2|<1, 即1<x <3.要使|x 2-4|=|x +2||x -2|<5|x -2|<0.001, 只要0002.05001.0|2|=<-x . 取δ=0.0002, 则当0<|x -2|<δ时, 就有|x 2-4|<0. 001.4. 当x →∞时, 13122→+-=x xy , 问X 等于多少, 使当|x |>X 时, |y -1|<0.01?解 要使01.034131222<+=-+-x x x, 只要397301.04||=->x , 故397=X . 5. 证明函数f (x )=|x |当x →0时极限为零.证明 因为|f (x )-0|=||x |-0|=|x |=|x -0|,所以要使|f (x )-0|<ε, 只须|x |<ε.因为对∀ε>0, ∃δ=ε, 使当0<|x -0|<δ, 时有|f (x )-0|=||x |-0|<ε,所以0||lim 0=→x x . 6. 求,)(x x x f = xx x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在.证明 因为11lim lim )(lim 000===---→→→x x x x x x f , 11lim lim )(lim 000===+++→→→x x x x x x f ,)(lim )(lim 00x f x f x x +→→=-, 所以极限)(lim 0x f x →存在. 因为1lim ||lim )(lim 000-=-==---→→→xx x x x x x x ϕ, 1lim ||lim )(lim 000===+++→→→x x x x x x x x ϕ, )(lim )(lim 00x x x x ϕϕ+→→≠-, 所以极限)(lim 0x x ϕ→不存在. 7. 证明: 若x →+∞及x →-∞时, 函数f (x )的极限都存在且都等于A , 则A x f x =∞→)(lim . 证明 因为A x f x =-∞→)(lim , A x f x =+∞→)(lim , 所以∀ε>0, ∃X 1>0, 使当x <-X 1时, 有|f (x )-A |<ε ;∃X 2>0, 使当x >X 2时, 有|f (x )-A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )-A |<ε , 即A x f x =∞→)(lim . 8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明 先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ 时, 有|f (x )-A |<ε .因此当x 0-δ<x <x 0和x 0<x <x 0+δ 时都有|f(x)-A|<ε.这说明f(x)当x→x0时左右极限都存在并且都等于A.再证明充分性.设f(x0-0)=f(x0+0)=A,则∀ε>0,∃δ1>0,使当x0-δ1<x<x0时,有| f(x)-A<ε;∃δ2>0,使当x0<x<x0+δ2时,有| f(x)-A|<ε.取δ=min{δ1,δ2},则当0<|x-x0|<δ时,有x0-δ1<x<x0及x0<x<x0+δ2,从而有| f(x)-A|<ε,即f(x)→A(x→x0).9.试给出x→∞时函数极限的局部有界性的定理,并加以证明.解x→∞时函数极限的局部有界性的定理:如果f(x)当x→∞时的极限存在,则存在X>0及M>0,使当|x|>X时, |f(x)|<M.证明设f(x)→A(x→∞),则对于ε=1,∃X>0,当|x|>X时,有|f(x)-A|<ε=1.所以|f(x)|=|f(x)-A+A|≤|f(x)-A|+|A|<1+|A|.这就是说存在X>0及M>0,使当|x|>X时, |f(x)|<M,其中M=1+|A|.习题1-41.两个无穷小的商是否一定是无穷小?举例说明之.解不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim=→x x x βα, )()(x x βα不是无穷小. 2. 根据定义证明:(1)392+-=x x y 当x →3时为无穷小;(2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2-=+-=x x x y . 因为∀ε>0, ∃δ=ε , 当0<|x -3|<δ时, 有εδ=<-=+-=|3|39||2x x x y , 所以当x →3时392+-=x x y 为无穷小. (2)当x ≠0时|0||1sin |||||-≤=x xx y . 因为∀ε>0, ∃δ=ε , 当0<|x -0|<δ时, 有εδ=<-≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数xx y 21+=为当x →0时的无穷大. 问x 应满足什么条件, 能使|y |>104?证明 分析2||11221||-≥+=+=x xxx y , 要使|y |>M , 只须M x >-2||1, 即21||+<M x . 证明 因为∀M >0, ∃21+=M δ, 使当0<|x -0|<δ时, 有M xx >+21,所以当x →0时, 函数xx y 21+=是无穷大.取M =104, 则21014+=δ. 当2101|0|04+<-<x 时, |y |>104.4. 求下列极限并说明理由:(1)xx x 12lim +∞→; (2)xx x --→11lim 20. 解 (1)因为x x x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→x x x . (2)因为x xx +=--1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=--→x x x .5. 根据函数极限或无穷大定义, 填写下表:解6.函数y=x cos x在(-∞,+∞)内是否有界?这个函数是否为当x→+∞时的无穷大?为什么?解函数y=x cos x在(-∞,+∞)内无界.这是因为∀M>0,在(-∞,+∞)内总能找到这样的x,使得|y(x)|>M.例如y(2kπ)=2kπ cos2kπ=2kπ (k=0, 1, 2,⋅⋅⋅),当k充分大时,就有| y(2kπ)|>M.当x→+∞时,函数y=x cos x不是无穷大.这是因为∀M>0,找不到这样一个时刻N,使对一切大于N的x,都有|y(x)|>M.例如0)22cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数xxy 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明 函数xxy 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xxy 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅), 当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M . 习题1-51. 计算下列极限:(1)35lim 22-+→x x x ;解 9325235lim 222-=-+=-+→x x x .(2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)x x x x x x 2324lim 223++-→; 解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x . (5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2xx x +-∞→;解 21lim 1lim 2)112(lim 22=+-=+-∞→∞→∞→x x xx x x x .(7)121lim 22---∞→x x x x ; 解 2111211lim 121lim 2222=---=---∞→∞→xx x x x x x x . (8)13lim 242--+∞→x x x x x ; 解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零).或 012111lim 13lim 4232242=--+=--+∞→∞→xx x x x x x x x x . (9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x . (10))12)(11(lim 2xx x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→xx x x x x x .(11))21 41211(lim n n +⋅⋅⋅+++∞→;解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n .(12)2)1( 321lim nn n -+⋅⋅⋅+++∞→;解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n nn n n n n n . (13)35)3)(2)(1(lim nn n n n +++∞→;解 515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同, 极限为最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim 3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31xx x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112lim 21-=+++-=→xx x x .2. 计算下列极限:(1)2232)2(2lim -+→x x x x ;解 因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2limx x x x . (2)12lim 2+∞→x x x ;解 ∞=+∞→12lim 2x x x (因为分子次数高于分母次数). (3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限: (1)xx x 1sin lim 20→;解 01sin lim 20=→x x x (当x →0时, x 2是无穷小, 而x1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量). 4. 证明本节定理3中的(2). 习题1-61. 计算下列极限: (1)xx x ωsin lim 0→;解 ωωωωω==→→x x xx x x sin lim sin lim 00.(2)xx x 3tan lim 0→;解 33cos 133sin lim 33tan lim 00=⋅=→→xx x x x x x .(3)xx x 5sin 2sin lim 0→;解 52525sin 522sin lim 5sin 2sin lim 00=⋅⋅=→→x x x x x x x x .(4)x x x cot lim 0→;解 1cos lim sin lim cos sin lim cot lim 0000=⋅=⋅=→→→→x x x x xx x x x x x x .(5)xx x x sin 2cos 1lim 0-→;解 2)sin (lim 2sin 2lim 2cos 1lim sin 2cos 1lim 20220200===-=-→→→→x x x x x x x x x x x x x . 或 2s i n lim 2sin sin 2lim sin 2cos 1lim 0200===-→→→xx x x x x x x x x x . (6)n n n x 2sin 2lim ∞→(x 为不等于零的常数).解 x x xxx nn n n n n =⋅=∞→∞→22sin lim2sin 2lim . 2. 计算下列极限: (1)x x x 1)1(lim -→;解 11)(10)1()(1010})](1[lim {)](1[lim )1(lim ---→--→→=-+=-+=-e x x x x x x x x x .(2)x x x 1)21(lim +→;解222122101])21(lim [)21(lim )21(lim e x x x x x x x x x =+=+=+→⋅→→.(3)x x xx 2)1(lim +∞→;解 222])11(lim [)1(lim e xx x x x x x =+=+∞→∞→.(4)kx x x)11(lim -∞→(k 为正整数).解 k k x x kx x e xx ---∞→∞→=-+=-))(()11(lim )11(lim .3. 根据函数极限的定义, 证明极限存在的准则I '. 证明 仅对x →x 0的情形加以证明.设ε为任一给定的正数, 由于A x g x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ1>0, 使得当0<|x -x 0|<δ1时, 恒有|g (x )-A |<ε, 即 A -ε<g (x )<A +ε.由于A x h xx =→)(lim 0, 故由定义知, 对ε>0, 存在δ2>0, 使得当0<|x -x 0|<δ2时, 恒有|h (x )-A |<ε, 即 A -ε<h (x )<A +ε.取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ时, A -ε<g (x )<A +ε与A -ε<h (x )<A +ε 同时成立, 又因为 g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε,因此A x f xx =→)(lim 0.证明 仅对x →x 0的情形加以证明. 因为A x g x x =→)(lim 0, A x h x x =→)(lim 0,所以对任一给定的ε>0, 存在δ>0, 使得当0<|x -x 0|<δ时, 恒有 |g (x )-A |<ε及|h (x )-A |<ε, 即 A -ε<g (x )<A +ε及A -ε<h (x )<A +ε. 又因为 g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε,因此A x f xx =→)(lim 0.4. 利用极限存在准则证明: (1)111lim =+∞→nn ;证明 因为nn11111+<+<,而 11lim =∞→n 且1)11(lim =+∞→nn ,由极限存在准则I , 111lim =+∞→nn .(2)1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n ;证明 因为πππππ+<++⋅⋅⋅++++<+2222222)1 211(n n n n n n n n n n , 而 1l i m 22=+∞→πn n n n , 1lim 22=+∞→πn n n , 所以 1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n .(3)数列2, 22+, 222++, ⋅ ⋅ ⋅ 的极限存在; 证明 21=x , n n x x +=+21(n =1, 2, 3, ⋅ ⋅ ⋅). 先证明数列{x n }有界.当n =1时221<=x , 假定n =k 时x k <2, 则当n =k +1时, 22221=+<+=+k k x x ,所以x n <2(n =1, 2, 3, ⋅ ⋅ ⋅), 即数列{x n }有界. 再证明数列单调增. 因为nn n n n n n n n n n n x x x x x x x x x x x x +++--=++-+=-+=-+2)1)(2(22221, 而x n -2<0, x n +1>0, 所以x n +1-x n >0, 即数列{x n }单调增. 因为数列{x n }单调增加有上界, 所以此数列是有极限的. (4)11lim 0=+→n x x ;证明 当|x |≤1时, 则有 1+x ≤1+|x |≤(1+|x |)n , 1+x ≥1-|x |≥(1-|x |)n , 从而有 ||11||1x x x n +≤+≤-. 因为 1|)|1(lim |)|1(lim 0=+=-→→x x x x ,根据夹逼准则, 有 11lim 0=+→n x x .(5)1]1[lim 0=+→xx x .证明 因为xxx1]1[11≤<-, 所以1]1[1≤<-xx x .又因为11lim )1(lim 0==-++→→x x x , 根据夹逼准则, 有1]1[lim 0=+→xx x .习题 1-71. 当x →0时, 2x -x 2 与x 2-x 3相比, 哪一个是高阶无穷小?解 因为02lim 2lim 202320=--=--→→xx x x x x x x x , 所以当x →0时, x 2-x 3是高阶无穷小, 即x 2-x 3=o (2x -x 2).2. 当x →1时, 无穷小1-x 和(1)1-x 3, (2))1(212x -是否同阶?是否等价?解 (1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=-++-=--→→→x x xx x x x x x x x , 所以当x →1时, 1-x 和1-x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim121=+=--→→x x x x x , 所以当x →1时, 1-x 和)1(212x -是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ;(2)2~1sec 2x x -.证明 (1)因为1tan limarctan lim 00==→→yyxx y x (提示: 令y =arctan x , 则当x →0时, y →0),所以当x →0时, arctan x ~x .(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x , 所以当x →0时, 2~1s e c 2x x -. 4. 利用等价无穷小的性质, 求下列极限: (1)xx x 23tan lim 0→;(2)mn x x x )(sin )sin(lim 0→(n , m 为正整数); (3)xx x x 3sin sin tan lim -→; (4))1sin 1)(11(tan sin lim32-+-+-→x x x x x . 解 (1)2323lim 23tan lim 00==→→xx xx x x .(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim 00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x -=⋅--=-=-(x →0),23232223231~11)1(11x x x x x ++++=-+(x →0), x x x x x ~sin ~1sin 1sin 1sin 1++=-+(x →0), 所以 33121lim )1sin 1)(11(tan sin lim 230320-=⋅-=-+-+-→→x x x x x x x x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim =αα, 所以α ~α ;(2) 若α ~β, 则1lim =βα, 从而1lim =αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim lim lim =⋅=βαγβγα. 因此α~γ.习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ;解 已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的.在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x .所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的.综上所述,函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f . 解 只需考察函数在x =-1和x =1处的连续性. 在x =-1处, 因为f (-1)=-1, 并且 )1(11lim )(lim 11-≠==---→-→f x f x x ,)1(1lim )(lim 11-=-==++-→-→f x x f x x ,所以函数在x =-1处间断, 但右连续. 在x =1处, 因为f (1)=1, 并且1lim )(lim 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1),所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续.2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x x y , x =1, x =2;解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的. (2)xx y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅);解 函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点. 因∞=→xx k x tan limπ(k ≠0), 故x =k π(k ≠0)是第二类间断点; 因为1tan lim 0=→xx x ,0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的;令2ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的.(3)xy 1cos 2=, x =0;解 因为函数xy 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点. 又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点.(4)⎩⎨⎧>-≤-=1311x x x x y , x =1.解 因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nn n 2211lim )(+-=∞→的连续性, 若有间断点, 判别其类型. 解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1||1|| 01|| 11lim)(22x x x x x x x x x f nn n . 在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x ,所以x =-1为函数的第一类不可去间断点.在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U , 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;解 函数xx x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解 函数⎩⎨⎧∉∈-=QQx x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解 函数⎩⎨⎧∉-∈=QQ x x x x x f )(在R 上处处有定义, 它只在x =0处连续. 习题1-91. 求函数633)(223-+--+=x x x x x x f 的连续区间, 并求极限)(lim 0x f x →, )(lim 3x f x -→及)(lim 2x f x →.解 )2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f , 函数在(-∞, +∞)内除点x =2和x =-3外是连续的, 所以函数f (x )的连续区间为(-∞, -3)、(-3, 2)、(2, +∞).在函数的连续点x =0处, 21)0()(lim 0==→f x f x .在函数的间断点x =2和x =-3处,∞=-++-+=→→)2)(3()1)(1)(3(lim )(lim 22x x x x x x f x x , 582)1)(1(lim )(lim 33-=-+-=-→-→x x x x f x x .2. 设函数f (x )与g (x )在点x 0连续, 证明函数ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )}在点x 0也连续.证明 已知)()(lim 00x f x f x x =→, )()(lim 00x g x g x x =→. 可以验证] |)()(|)()([21)(x g x f x g x f x -++=ϕ, ] |)()(|)()([21)(x g x f x g x f x --+=ψ. 因此 ] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ, ] |)()(|)()([21)(00000x g x f x g x f x --+=ψ. 因为] |)()(|)()([21lim )(lim 00x g x f x g x f x x x x x -++=→→ϕ ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→-++= ] |)()(|)()([210000x g x f x g x f -++==ϕ(x 0), 所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限:(1)52lim 20+-→x x x ; (2)34)2(sin lim x x π→;(3))2cos 2ln(lim 6x x π→;(4)xx x 11lim 0-+→; (5)145lim 1---→x x x x ; (6)ax a x a x --→sin sin lim ; (7))(lim 22x x x x x --++∞→. 解 (1)因为函数52)(2+-=x x x f 是初等函数, f (x )在点x =0有定义, 所以55020)0(52lim 220=+⋅-==+-→f x x x . (2)因为函数f (x )=(sin 2x )3是初等函数, f (x )在点4π=x 有定义, 所以 1)42(sin )4()2(sin lim 334=⋅==→πππf x x . (3)因为函数f (x )=ln(2cos2x )是初等函数, f (x )在点6π=x 有定义, 所以0)62cos 2ln()6()2cos 2ln(lim 6=⋅==→πππf x x .(4))11(lim )11()11)(11(lim 11lim 000++=++++-+=-+→→→x x x x x x x x x x x x 211101111lim 0=++=++=→x x . (5))45)(1()45)(45(lim 145lim 11x x x x x x x x x x x x +--+---=---→→)45)(1(44lim1x x x x x +---=→214154454lim 1=+-⋅=+-=→x x x . (6)ax ax a x a x a x a x a x --+=--→→2sin 2cos 2lim sin sin lim a a a a x ax a x a x a x cos 12cos 22sin lim 2cos lim =⋅+=--⋅+=→→. (7))())((lim )(lim 22222222x x x x x x x x x x x x x x x x x x -++-++--+=--++∞→+∞→ 1)1111(2lim )(2lim22=-++=-++=+∞→+∞→xx x x x x x x x . 4. 求下列极限:(1)x x e 1lim ∞→;(2)x x x sin ln lim 0→; (3)2)11(lim xx x+∞→; (4)x x x 2cot 20)tan 31(lim +→; (5)21)63(lim -∞→++x x xx ; (6)xx x x x x -++-+→20sin 1sin 1tan 1lim . 解 (1) 1lim 01lim 1===∞→∞→e e e x x x x .。
高等数学第六版上册课后习题答案与及解析

高等数学第六版上册课后习题答案与及解析第一章习题111设A (5)(5)B [103)写出ABABA \B 及A \(A \B )的表达式 解AB (3)(5) AB [105) A \B (10)(5)A \(A \B )[105)2设A 、B 是任意两个集合证明对偶律(AB )C A C B C 证明因为x (AB )C xABxA 或xBxA C 或xB C xA C B C 所以(AB )C A C B C3设映射fXYAXBX 证明 (1)f (AB )f (A )f (B ) (2)f (AB )f (A )f (B ) 证明因为yf (AB )xAB 使f (x )y(因为xA 或xB )yf (A )或yf (B ) yf (A )f (B )所以f (AB )f (A )f (B ) (2)因为yf (AB )xAB 使f (x )y (因为xA 且xB )yf (A )且yf (B )yf (A )f (B ) 所以f (AB )f (A )f (B )4设映射fXY 若存在一个映射gYX 使X I f g =οY I g f =ο其中I X 、I Y 分别是X 、Y 上的恒等映射即对于每一个xX 有I X xx 对于每一个yY 有I Y yy 证明f 是双射且g 是f 的逆映射gf 1 证明因为对于任意的yY 有xg (y )X 且f (x )f [g (y )]I y yy 即Y 中任意元素都是X 中某元素的像所以f 为X 到Y 的满射又因为对于任意的x 1x 2必有f (x 1)f (x 2)否则若f (x 1)f (x 2)g [f (x 1)]g [f (x 2)]x 1x 2 因此f 既是单射又是满射即f 是双射对于映射gYX 因为对每个yY 有g (y )xX 且满足f (x )f [g (y )]I y yy 按逆映射的定义g 是f 的逆映射5设映射fXYAX 证明 (1)f 1(f (A ))A(2)当f 是单射时有f 1(f (A ))A证明(1)因为xAf (x )yf (A )f 1(y )xf 1(f (A )) 所以f 1(f (A ))A(2)由(1)知f 1(f (A ))A另一方面对于任意的xf 1(f (A ))存在yf (A )使f 1(y )xf (x )y 因为yf (A )且f 是单射所以xA 这就证明了f 1(f (A ))A 因此f 1(f (A ))A 6求下列函数的自然定义域 (1)23+=x y解由3x 20得32->x 函数的定义域为) ,32[∞+-(2)211x y -=解由1x 20得x 1函数的定义域为(1)(11)(1) (3)211x x y --=解由x 0且1x 20得函数的定义域D [10)(01] (4)241x y -=解由4x 20得|x |2函数的定义域为(22) (5)x y sin =解由x 0得函数的定义D [0) (6)y tan(x 1)解由21π≠+x (k 012)得函数的定义域为 12-+≠ππk x (k 012)(7)y arcsin(x 3)解由|x 3|1得函数的定义域D [24] (8)x x y 1arctan 3+-=解由3x 0且x 0得函数的定义域D (0)(03) (9)y ln(x 1)解由x 10得函数的定义域D (1) (10)xe y 1=解由x 0得函数的定义域D (0)(0)7下列各题中函数f (x )和g (x )是否相同?为什么? (1)f (x )lg x 2g (x )2lg x (2)f (x )xg (x )2x(3)334)(x x x f -=31)(-=x x x g (4)f (x )1g (x )sec 2x tan 2x 解(1)不同因为定义域不同(2)不同因为对应法则不同x 0时g (x )x (3)相同因为定义域、对应法则均相相同 (4)不同因为定义域不同8设⎪⎩⎪⎨⎧≥<=3||03|| |sin |)(ππϕx x x x 求)6(πϕ)4(πϕ)4(πϕ-(2)并作出函数y (x )的图形 解21|6sin |)6(==ππϕ22|4sin |)4(==ππϕ22|)4sin(|)4(=-=-ππϕ0)2(=-ϕ9试证下列函数在指定区间内的单调性 (1)x x y -=1(1)(2)yx ln x (0)证明(1)对于任意的x 1x 2(1)有1x 101x 20因为当x 1x 2时 所以函数x x y -=1在区间(1)内是单调增加的(2)对于任意的x 1x 2(0)当x 1x 2时有所以函数yx ln x 在区间(0)内是单调增加的10设f (x )为定义在(ll )内的奇函数若f (x )在(0l )内单调增加证明f (x )在(l 0)内也单调增加证明对于x 1x 2(l 0)且x 1x 2有x 1x 2(0l )且x 1x 2 因为f (x )在(0l )内单调增加且为奇函数所以f (x 2)f (x 1)f (x 2)f (x 1)f (x 2)f (x 1)这就证明了对于x 1x 2(l 0)有f (x 1)f (x 2)所以f (x )在(l 0)内也单调增加 11设下面所考虑的函数都是定义在对称区间(ll )上的证明 (1)两个偶函数的和是偶函数两个奇函数的和是奇函数(2)两个偶函数的乘积是偶函数两个奇函数的乘积是偶函数偶函数与奇函数的乘积是奇函数证明(1)设F (x )f (x )g (x )如果f (x )和g (x )都是偶函数则 F (x )f (x )g (x )f (x )g (x )F (x )所以F (x )为偶函数即两个偶函数的和是偶函数 如果f (x )和g (x )都是奇函数则 F (x )f (x )g (x )f (x )g (x )F (x )所以F (x )为奇函数即两个奇函数的和是奇函数 (2)设F (x )f (x )g (x )如果f (x )和g (x )都是偶函数则F (x )f (x )g (x )f (x )g (x )F (x )所以F (x )为偶函数即两个偶函数的积是偶函数 如果f (x )和g (x )都是奇函数则F (x )f (x )g (x )[f (x )][g (x )]f (x )g (x )F (x )所以F (x )为偶函数即两个奇函数的积是偶函数 如果f (x )是偶函数而g (x )是奇函数则 F (x )f (x )g (x )f (x )[g (x )]f (x )g (x )F (x )所以F (x )为奇函数即偶函数与奇函数的积是奇函数12下列函数中哪些是偶函数哪些是奇函数哪些既非奇函数又非偶函数? (1)yx 2(1x 2)(2)y 3x 2x 3(3)2211x x y +-= (4)yx (x 1)(x 1) (5)y sin x cos x 1(6)2x x a a y -+= 解(1)因为f (x )(x )2[1(x )2]x 2(1x 2)f (x )所以f (x )是偶函数 (2)由f (x )3(x )2(x )33x 2x 3可见f (x )既非奇函数又非偶函数(3)因为())(111)(1)(2222x f xx x x x f =+-=-+--=-所以f (x )是偶函数 (4)因为f (x )(x )(x 1)(x 1)x (x 1)(x 1)f (x )所以f (x )是奇函数(5)由f (x )sin(x )cos(x )1sin x cos x 1可见f (x )既非奇函数又非偶函数(6)因为)(22)()()(x f a a a a x f xx x x =+=+=-----所以f (x )是偶函数13下列各函数中哪些是周期函数?对于周期函数指出其周期 (1)y cos(x 2)解是周期函数周期为l 2 (2)y cos4x解是周期函数周期为2π=l(3)y 1sin x解是周期函数周期为l 2 (4)yx cos x解不是周期函数 (5)y sin 2x解是周期函数周期为l 14求下列函数的反函数(1)31+=x y解由31+=x y 得xy 31所以31+=x y 的反函数为yx 31 (2)xx y +-=11解由x x y +-=11得y yx +-=11所以x x y +-=11的反函数为xx y +-=11(3)dcx b ax y ++=(adbc 0)解由d cx b ax y ++=得a cy bdy x -+-=所以d cx b ax y ++=的反函数为acx b dx y -+-=(4)y 2sin3x解由y 2sin3x 得2arcsin 31yx =所以y 2sin3x 的反函数为2arcsin 31x y =(5)y 1ln(x 2)解由y 1ln(x 2)得xe y 12所以y 1ln(x 2)的反函数为ye x 12(6)122+=xxy 解由122+=x x y 得y y x -=1log 2所以122+=x x y 的反函数为x x y -=1log 215设函数f (x )在数集X 上有定义试证函数f (x )在X 上有界的充分必要条件是它在X上既有上界又有下界证明先证必要性设函数f (x )在X 上有界则存在正数M 使|f (x )|M 即Mf (x )M 这就证明了f (x )在X 上有下界M 和上界M再证充分性设函数f (x )在X 上有下界K 1和上界K 2即K 1f (x )K 2取M max{|K 1||K 2|}则MK 1f (x )K 2M 即|f (x )|M这就证明了f (x )在X 上有界16在下列各题中求由所给函数复合而成的函数并求这函数分别对应于给定自变量值x 1和x 2的函数值(1)yu 2u sin x 61π=x 32π=x解y sin 2x 41)21(6sin 221===πy 43)23(3sin 222===πy(2)y sin uu 2x 81π=x 42π=x解y sin2x 224sin )82sin(1==⋅=ππy 12sin )42sin(2==⋅=ππy(3)u y =u 1x 2x 11x 2 2解21x y +=21121=+=y 52122=+=y (4)ye u ux 2x 10x 21解2x e y =1201==e y e e y ==212(5)yu 2ue x x 11x 21 解ye 2x y 1e 21e 2y 2e 2(1)e 217设f (x )的定义域D [01]求下列各函数的定义域 (1)f (x 2)解由0x 21得|x |1所以函数f (x 2)的定义域为[11] (2)f (sin x )解由0sin x 1得2nx (2n 1)(n 012)所以函数f (sin x )的定义域为 [2n (2n 1)](n 012) (3)f (xa )(a >0)解由0xa 1得ax 1a 所以函数f (xa )的定义域为[a 1a ] (4)f (xa )f (xa )(a 0)解由0xa 1且0xa 1得当210≤<a 时ax 1a 当21>a 时无解因此当210≤<a 时函数的定义域为[a 1a ]当21>a 时函数无意义18设⎪⎩⎪⎨⎧>-=<=1||11||01||1)(x x x x f g (x )e x 求f [g (x )]和g [f (x )]并作出这两个函数的图形 解⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)]([x x x e e e x g f 即⎪⎩⎪⎨⎧>-=<=0 10 001)]([x x x x g f ⎪⎩⎪⎨⎧>=<==-1|| 1|| e 1|| )]([101)(x e x x e e x f g x f 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g19已知水渠的横断面为等腰梯形斜角40(图137)当过水断面ABCD 的面积为定值S 0时求湿周L (LABBCCD )与水深h 之间的函数关系式并指明其定义域 图137解ο40sin h DC AB ==又从)]40cot 2([21S h BC BC h =⋅++ο得h hS BC ⋅-=ο40cot 0所以自变量h 的取值范围应由不等式组h 0040cot 0>⋅-h hS ο确定定义域为ο40cot 00S h <<20收敛音机每台售价为90元成本为60元厂方为鼓励销售商大量采购决定凡是订购量超过100台以上的每多订购1台售价就降低1分但最低价为每台75元 (1)将每台的实际售价p 表示为订购量x 的函数 (2)将厂方所获的利润P 表示成订购量x 的函数 (3)某一商行订购了1000台厂方可获利润多少? 解(1)当0x 100时p 90令001(x 0100)9075得x 01600因此当x 1600时p 75 当100x 1600时p 90(x 100)00191001x 综合上述结果得到(2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 151600100 01.0311000 30)60(2x x x x x x x x p P(3)P 3110000011000221000(元)习题121观察一般项x n 如下的数列{x n }的变化趋势写出它们的极限 (1)nn x 21=解当n 时n n x 21=0021lim =∞→nn (2)nx n n 1)1(-=解当n 时n x n n 1)1(-=001)1(lim =-∞→nn n(3)212nx n +=解当n 时212n x n +=22)12(lim 2=+∞→n n (4)11+-=n n x n解当n 时12111+-=+-=n n n x n 0111lim =+-∞→n n n(5)x n n (1)n解当n 时x n n (1)n 没有极限2设数列{x n }的一般项n n x n 2cos π=问n n x ∞→lim 求出N 使当nN 时x n 与其极限之差的绝对值小于正数当0001时求出数N 解0lim =∞→n n xn n n x n 1|2cos ||0|≤=-π0要使|x n 0|只要ε<n 1也就是ε1>n 取]1[ε=N 则nN 有|x n 0| 当0001时]1[ε=N 10003根据数列极限的定义证明(1)01lim 2=∞→n n分析要使ε<=-221|01|n n 只须ε12>n 即ε1>n 证明因为0]1[ε=N 当nN 时有ε<-|01|2n 所以01lim 2=∞→n n (2)231213lim =++∞→n n n分析要使ε<<+=-++n n n n 41)12(21|231213|只须ε<n41即ε41>n 证明因为0]41[ε=N 当nN 时有ε<-++|231213|n n 所以231213lim =++∞→n n n(3)1lim22=+∞→na n n分析要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|只须ε2a n >证明因为0][2εa N =当nN 时有ε<-+|1|22n a n 所以1lim 22=+∞→n a n n(4)19 999.0lim =⋅⋅⋅∞→43421个n n 分析要使|09991|ε<=-1101n 只须1101-n 即ε1lg 1+>n 证明因为0]1lg 1[ε+=N 当nN 时有|09991|所以19 999.0lim =⋅⋅⋅∞→43421个n n 4a u n n =∞→lim 证明||||lim a u n n =∞→并举例说明如果数列{|x n |}有极限但数列{x n }未必有极限证明因为a u n n =∞→lim 所以0N N 当nN 时有ε<-||a u n 从而||u n ||a |||u n a |这就证明了||||lim a u n n =∞→数列{|x n |}有极限但数列{x n }未必有极限例如1|)1(|lim =-∞→n n 但n n )1(lim -∞→不存在5设数列{x n }有界又0lim =∞→n n y 证明0lim =∞→n n n y x证明因为数列{x n }有界所以存在M 使n Z 有|x n |M 又0lim =∞→n n y 所以0N N 当nN 时有M y n ε<||从而当nN 时有 所以0lim =∞→n n n y x6对于数列{x n }若x 2k 1a (k )x 2k a (k ) 证明x n a (n )证明因为x 2k 1a (k )x 2k a (k )所以0 K 1当2k 12K 11时有|x 2k 1a | K 2当2k 2K 2时有|x 2k a |取N max{2K 112K 2}只要nN 就有|x n a | 因此x n a (n ) 习题131根据函数极限的定义证明 (1)8)13(lim 3=-→x x分析因为|(3x 1)8||3x 9|3|x 3|所以要使|(3x 1)8|只须ε31|3|<-x证明因为0εδ31=当0|x 3|时有|(3x 1)8| 所以8)13(lim 3=-→x x(2)12)25(lim 2=+→x x分析因为|(5x 2)12||5x 10|5|x 2|所以要使|(5x 2)12|只须ε51|2|<-x证明因为0εδ51=当0|x 2|时有 |(5x 2)12|所以12)25(lim 2=+→x x(3)424lim 22-=+--→x x x分析因为所以要使ε<--+-)4(242x x 只须ε<--|)2(|x 证明因为0εδ=当0|x (2)|时有所以424lim 22-=+--→x x x(4)21241lim 321=+--→x x x 分析因为所以要使ε<-+-212413x x 只须ε21|)21(|<--x 证明因为0εδ21=当δ<--<|)21(|0x 时有所以21241lim 321=+--→x x x 2根据函数极限的定义证明(1)2121lim 33=+∞→x x x 分析因为所以要使ε<-+212133x x 只须ε<3||21x 即321||ε>x 证明因为0321ε=X 当|x |X 时有所以2121lim 33=+∞→x x x (2)0sin lim =+∞→x x x分析因为所以要使ε<-0sin x x 只须ε<x1即21ε>x证明因为021ε=X 当xX 时有所以0sin lim =+∞→xx x3当x 2时yx 24问等于多少使当|x 2|<时|y 4|<0001? 解由于当x 2时|x 2|0故可设|x 2|1即1x 3要使|x 24||x 2||x 2|5|x 2|0001 只要0002.05001.0|2|=<-x取00002则当0|x 2|时就有|x 24|00014当x 时13122→+-=x x y 问X 等于多少使当|x |X 时|y 1|001 解要使01.034131222<+=-+-x x x 只要397301.04||=->x 故397=X5证明函数f (x )|x |当x 0时极限为零证明因为|f (x )0|||x |0||x ||x 0| 所以要使|f (x )0|只须|x | 因为对0使当0|x 0|时有 |f (x )0|||x |0| 所以0||lim 0=→x x6求,)(xx x f =x x x ||)(=ϕ当x 0时的左﹑右极限并说明它们在x 0时的极限是否存在证明因为所以极限)(lim 0x f x →存在因为所以极限)(lim 0x x ϕ→不存在7证明若x 及x 时函数f (x )的极限都存在且都等于A 则A x f x =∞→)(lim证明因为A x f x =-∞→)(lim A x f x =+∞→)(lim 所以>0X 10使当xX 1时有|f (x )A | X 20使当xX 2时有|f (x )A |取X max{X 1X 2}则当|x |X 时有|f (x )A |即A x f x =∞→)(lim8根据极限的定义证明函数f (x )当xx 0时极限存在的充分必要条件是左极限、右极限各自存在并且相等证明先证明必要性设f (x )A (xx 0)则>00使当0<|xx 0|<时有 |f (x )A |<因此当x 0<x <x 0和x 0<x <x 0时都有 |f (x )A |<这说明f (x )当xx 0时左右极限都存在并且都等于A 再证明充分性设f (x 00)f (x 00)A 则>0 1>0使当x 01<x <x 0时有|f (x )A <2>0使当x 0<x <x 0+2时有|f (x )A |<取min{12}则当0<|xx 0|<时有x 01<x <x 0及x 0<x <x 0+2从而有 |f (x )A |< 即f (x )A (xx 0)9试给出x 时函数极限的局部有界性的定理并加以证明解x 时函数极限的局部有界性的定理如果f (x )当x 时的极限存在则存在X 0及M 0使当|x |X 时|f (x )|M证明设f (x )A (x )则对于1X 0当|x |X 时有|f (x )A |1所以 |f (x )||f (x )AA ||f (x )A ||A |1|A |这就是说存在X 0及M 0使当|x |X 时|f (x )|M 其中M 1|A | 习题141两个无穷小的商是否一定是无穷小?举例说明之 解不一定例如当x 0时(x )2x (x )3x 都是无穷小但32)()(lim0=→x x x βα)()(x x βα不是无穷小2根据定义证明(1)392+-=x x y 当x 3时为无穷小; (2)xx y 1sin =当x 0时为无穷小证明(1)当x 3时|3|39||2-=+-=x x x y 因为0当0|x 3|时有所以当x 3时392+-=x x y 为无穷小 (2)当x 0时|0||1sin |||||-≤=x xx y 因为0当0|x 0|时有所以当x 0时xx y 1sin =为无穷小3根据定义证明函数xx y 21+=为当x 0时的无穷大问x 应满足什么条件能使|y |104?证明分析2||11221||-≥+=+=x x x x y 要使|y |M 只须M x >-2||1即21||+<M x证明因为M 021+=M δ使当0|x 0|时有M xx >+21所以当x 0时函数xx y 21+=是无穷大取M 104则21014+=δ当2101|0|04+<-<x 时|y |104 4求下列极限并说明理由 (1)xx x 12lim +∞→;(2)xx x --→11lim 20 解(1)因为xx x 1212+=+而当x 时x 1是无穷小所以212lim =+∞→x x x(2)因为x xx +=--1112(x 1)而当x 0时x 为无穷小所以111lim 20=--→x x x5根据函数极限或无穷大定义填写下表f (x )Af (x )f (x )f (x )xx 0 00使当0|xx 0|时 有恒|f (x )A |xx 0 xx 0x 0X 0使当|x |X 时 有恒|f (x )|Mx x解f (x )A f (x ) f (x ) f (x ) xx 000使当0|xx 0|时有恒|f (x )A | M 00使当0|xx 0|时有恒|f (x )|M M 00使当0|xx 0|时有恒f (x )M M 00使当0|xx 0|时有恒f (x )M xx 000使当0xx 0时有恒|f (x )A | M 00使当0xx 0时有恒|f (x )|M M 00使当0xx 0时有恒f (x )M M 00使当0xx 0时有恒f (x )M xx 000使当0x 0x 时有恒|f (x )A | M 00使当0x 0x 时有恒|f (x )|M M 00使当0x 0x 时有恒f (x )M M 00使当0x 0x 时有恒f (x )M x0X 0使当|x |X 时有恒|f (x )A | 0X 0使当|x |X 时有恒|f (x )|M 0X 0使当|x |X 时有恒f (x )M 0X 0使当|x |X 时有恒f (x )M x0X 0使当xX 时有恒|f (x )A | 0X 0使当xX 时有恒|f (x )|M 0X 0使当xX 时有恒f (x )M 0X 0使当xX 时有恒f (x )Mx0X 0使当xX 时有恒|f (x )A | 0X 0使当xX 时有恒|f (x )|M 0X 0使当xX 时有恒f (x )M 0X 0使当xX 时有恒f (x )M6函数yx cos x 在()内是否有界?这个函数是否为当x 时的无穷大?为什么? 解函数yx cos x 在()内无界这是因为M 0在()内总能找到这样的x 使得|y (x )|M 例如y (2k )2k cos2k 2k (k 012)当k 充分大时就有|y (2k )|M 当x 时函数yx cos x 不是无穷大这是因为M 0找不到这样一个时刻N 使对一切大于N 的x 都有|y (x )|M 例如0)22cos()22()22(=++=+ππππππk k k y (k 012)对任何大的N 当k 充分大时总有N k x >+=22ππ但|y (x )|0M7证明函数xx y 1sin 1=在区间(01]上无界但这函数不是当x 0+时的无穷大证明函数xx y 1sin 1=在区间(01]上无界这是因为M 0在(01]中总可以找到点x k 使y (x k )M 例如当221ππ+=k x k (k 012)时有当k 充分大时y (x k )M当x 0+时函数xx y 1sin 1=不是无穷大这是因为M 0对所有的0总可以找到这样的点x k 使0x k 但y (x k )M 例如可取πk x k 21=(k 012)当k 充分大时x k 但y (x k )2k sin2k 0M 习题151计算下列极限(1)35lim 22-+→x x x 解9325235lim222-=-+=-+→x x x (2)13lim 223+-→x x x 解01)3(3)3(13lim 22223=+-=+-→x x x (3)112lim 221-+-→x x x x 解02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x (4)x x x x x x 2324lim 2230++-→ 解2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x (5)hx h x h 220)(lim -+→解x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→(6))112(lim 2x x x +-∞→解21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x (7)121lim 22---∞→x x x x 解2111211lim 121lim 2222=---=---∞→∞→xx x x x xx x (8)13lim 242--+∞→x x x x x 解013lim 242=--+∞→x x x x x (分子次数低于分母次数极限为零) 或012111lim 13lim 4232242=--+=--+∞→∞→x x x x x x x x x x (9)4586lim 224+-+-→x x x x x 解32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x (10))12)(11(lim 2x x x -+∞→解221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x (11))21 41211(lim n n +⋅⋅⋅+++∞→ 解2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n (12)2)1( 321limn n n -+⋅⋅⋅+++∞→解211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n n n n n n n n (13)35)3)(2)(1(limn n n n n +++∞→解515)3)(2)(1(lim3=+++∞→n n n n n (分子与分母的次数相同极限为 最高次项系数之比)或51)31)(21)(11(lim 515)3)(2)(1(lim3=+++=+++∞→∞→n n n n n n n n n (14))1311(lim 31x x x ---→解)1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 2计算下列极限(1)2232)2(2lim -+→x x x x 解因为01602)2(lim 2322==+-→x x x x 所以∞=-+→2232)2(2lim x x x x (2)12lim 2+∞→x x x解∞=+∞→12lim 2x x x (因为分子次数高于分母次数) (3))12(lim 3+-∞→x x x解∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数)3计算下列极限 (1)xx x 1sin lim 20→解01sin lim 20=→x x x (当x 0时x 2是无穷小而x 1sin 是有界变量) (2)xx x arctan lim ∞→解0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x 时x 1是无穷小 而arctan x 是有界变量) 4证明本节定理3中的(2) 习题151计算下列极限(1)35lim 22-+→x x x解9325235lim222-=-+=-+→x x x (2)13lim 223+-→x x x解01)3(3)3(13lim 22223=+-=+-→x x x (3)112lim 221-+-→x x x x 解02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x (4)xx x x x x 2324lim 2230++-→ 解2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x (5)hx h x h 220)(lim -+→解x h x h x h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→ (6))112(lim 2x x x +-∞→解21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x (7)121lim 22---∞→x x x x 解2111211lim 121lim 2222=---=---∞→∞→xx x x x x x x (8)13lim 242--+∞→x x x x x 解013lim 242=--+∞→x x x x x (分子次数低于分母次数极限为零) 或012111lim 13lim 4232242=--+=--+∞→∞→x x x x x x x x x x (9)4586lim 224+-+-→x x x x x解32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x (10))12)(11(lim 2xx x -+∞→解221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x (11))21 41211(lim n n +⋅⋅⋅+++∞→解2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n (12)2)1( 321limnn n -+⋅⋅⋅+++∞→ 解211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n nn n n n n n (13)35)3)(2)(1(limn n n n n +++∞→解515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同极限为 最高次项系数之比)或51)31)(21)(11(lim 515)3)(2)(1(lim 3=+++=+++∞→∞→n n n n n n n n n (14))1311(lim 31x x x ---→解)1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 2计算下列极限(1)2232)2(2lim -+→x x x x 解因为01602)2(lim 2322==+-→x x x x 所以∞=-+→2232)2(2limx x x x (2)12lim 2+∞→x x x 解∞=+∞→12lim 2x x x (因为分子次数高于分母次数) (3))12(lim 3+-∞→x x x解∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数)3计算下列极限 (1)xx x 1sin lim 20→解01sin lim 20=→x x x (当x 0时x 2是无穷小而x 1sin 是有界变量) (2)xx x arctan lim ∞→解0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x 时x 1是无穷小 而arctan x 是有界变量) 4证明本节定理3中的(2) 习题171当x 0时2xx 2与x 2x 3相比哪一个是高阶无穷小?解因为02lim 2lim 202320=--=--→→xx x x x x x x x 所以当x 0时x 2x 3是高阶无穷小即x 2x 3o (2xx 2)2当x 1时无穷小1x 和(1)1x 3(2))1(212x -是否同阶?是否等价?解(1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=-++-=--→→→x x xx x x x x x x x 所以当x 1时1x 和1x 3是同阶的无穷小但不是等价无穷小(2)因为1)1(lim 211)1(21lim 121=+=--→→x x x x x 所以当x 1时1x 和)1(212x -是同阶的无穷小而且是等价无穷小3证明当x 0时有 (1)arctan x ~x(2)2~1sec 2x x - 证明(1)因为1tan limarctan lim 00==→→y yxx y x (提示令y arctan x 则当x 0时y 0) 所以当x 0时arctan x ~x(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x 所以当x 0时2~1sec 2x x -4利用等价无穷小的性质求下列极限 (1)xx x 23tan lim 0→(2)mn x x x )(sin )sin(lim 0→(nm 为正整数)(3)x x x x 30sin sin tan lim -→ (4))1sin 1)(11(tan sin lim320-+-+-→x x x x x 解(1)2323lim 23tan lim 00==→→x x x x x x(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00 (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x x x x x x x x x x x (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x -=⋅--=-=-(x 0)23232223231~11)1(11x x x x x ++++=-+(x 0) x x x x x ~sin ~1sin 1sin 1sin 1++=-+(x 0) 所以33121lim )1sin 1)(11(tan sin lim 230320-=⋅-=-+-+-→→x x x x x x x x x 5证明无穷小的等价关系具有下列性质 (1)~(自反性)(2)若~则~(对称性) (3)若~~则~(传递性) 证明(1)1lim =αα所以~(2)若~则1lim =βα从而1lim=αβ因此~ (3)若~~1lim limlim =⋅=βαγβγα因此~ 习题181研究下列函数的连续性并画出函数的图形(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f解已知多项式函数是连续函数所以函数f (x )在[01)和(12]内是连续的 在x 1处因为f (1)1并且所以1)(lim 1=→x f x 从而函数f (x )在x 1处是连续的综上所述,函数f (x )在[02]上是连续函数(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f解只需考察函数在x 1和x 1处的连续性在x 1处因为f (1)1并且所以函数在x 1处间断但右连续 在x 1处因为f (1)1并且1lim )(lim 11==--→→x x f x x f (1)11lim )(lim 11==++→→x x x f f (1)所以函数在x 1处连续综合上述讨论函数在(1)和(1)内连续在x 1处间断但右连续2下列函数在指出的点处间断说明这些间断点属于哪一类如果是可去间断点则补充或改变函数的定义使它连续(1)23122+--=x x x y x 1x 2 解)1)(2()1)(1(23122---+=+--=x x x x x x x y 因为函数在x 2和x 1处无定义所以x 2和x 1是函数的间断点因为∞=+--=→→231lim lim 2222x x x y x x 所以x 2是函数的第二类间断点因为2)2()1(limlim 11-=-+=→→x x y x x 所以x 1是函数的第一类间断点并且是可去间断点在x 1处令y 2则函数在x 1处成为连续的 (2)xx y tan =xk 2ππ+=k x (k 012)解函数在点xk (k Z)和2ππ+=k x (k Z)处无定义因而这些点都是函数的间断点因∞=→x x k x tan lim π(k 0)故xk (k 0)是第二类间断点 因为1tan lim0=→x x x 0tan lim2=+→xx k x ππ(k Z)所以x 0和2 ππ+=k x (k Z)是第一类间断点且是可去间断点令y |x 01则函数在x 0处成为连续的令2 ππ+=k x 时y 0则函数在2ππ+=k x 处成为连续的(3)xy 1cos 2=x 0解因为函数x y 1cos 2=在x 0处无定义所以x 0是函数x y 1cos 2=的间断点又因为xx 1cos lim 20→不存在所以x 0是函数的第二类间断点(4)⎩⎨⎧>-≤-=1 31 1x x x x y x 1解因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x 所以x 1是函数的第一类不可去间断点3讨论函数x x x x f nnn 2211lim )(+-=∞→的连续性若有间断点判别其类型 解⎪⎩⎪⎨⎧<=>-=+-=∞→1||1|| 01|| 11lim )(22x x x x x x xx x f nnn 在分段点x 1处因为1)(lim )(lim 11=-=---→-→x x f x x 1lim )(lim 11-==++-→-→x x f x x 所以x 1为函数的第一类不可去间断点在分段点x 1处因为1lim )(lim 11==--→→x x f x x 1)(lim )(lim 11-=-=++→→x x f x x 所以x 1为函数的第一类不可去间断点4证明若函数f (x )在点x 0连续且f (x 0)0则存在x 0的某一邻域U (x 0)当xU (x 0)时f (x )0 证明不妨设f (x 0)>0因为f (x )在x 0连续所以0)()(lim 00>=→x f x f x x 由极限的局部保号性定理存在x 0的某一去心邻域)(0x U ο使当x )(0x U ο时f (x )>0从而当xU (x 0)时f (x )>0这就是说则存在x 0的某一邻域U (x 0)当xU (x 0)时f (x )0 5试分别举出具有以下性质的函数f (x )的例子(1)x 01221±n n1±是f (x )的所有间断点且它们都是无穷间断点解函数x x x f ππcsc )csc()(+=在点x 01221±n n1±处是间断的且这些点是函数的无穷间断点(2)f (x )在R 上处处不连续但|f (x )|在R 上处处连续解函数⎩⎨⎧∉∈-=Q Qx x x f 1 1)(在R 上处处不连续但|f (x )|1在R 上处处连续(3)f (x )在R 上处处有定义但仅在一点连续解函数⎩⎨⎧∉-∈=Q Qx x x x x f )(在R 上处处有定义它只在x 0处连续习题191求函数633)(223-+--+=x x x x x x f 的连续区间并求极限)(lim 0x f x →)(lim 3x f x -→及)(lim 2x f x → 解)2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f 函数在()内除点x 2和x 3外是连续的所以函数f (x )的连续区间为(3)、(32)、(2) 在函数的连续点x 0处21)0()(lim 0==→f x f x 在函数的间断点x 2和x 3处2设函数f (x )与g (x )在点x 0连续证明函数 (x )max{f (x )g (x )}(x )min{f (x )g (x )} 在点x 0也连续证明已知)()(lim 00x f x f x x =→)()(lim 00x g x g x x =→可以验证因此] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ因为] |)()(|)()([210000x g x f x g x f -++=(x 0) 所以(x )在点x 0也连续同理可证明(x )在点x 0也连续 3求下列极限 (1)52lim 20+-→x x x(2)34)2(sin lim x x π→(3))2cos 2ln(lim 6x x π→(4)xx x 11lim 0-+→(5)145lim 1---→x x x x(6)a x a x a x --→sin sin lim(7))(lim 22x x x x x --++∞→解(1)因为函数52)(2+-=x x x f 是初等函数f (x )在点x 0有定义所以(2)因为函数f (x )(sin2x )3是初等函数f (x )在点4π=x 有定义所以(3)因为函数f (x )ln(2cos2x )是初等函数f (x )在点6π=x 有定义所以(4))11(lim)11()11)(11(lim 11lim 000++=++++-+=-+→→→x x x x x x x x x x x x (5))45)(1()45)(45(lim 145lim 11x x x x x x x x x x x x +--+---=---→→(6)ax ax a x a x a x a x a x --+=--→→2sin 2cos 2limsin sin lim (7))())((lim )(lim 22222222x x x x x x x x x x x x x x x x x x -++-++--+=--++∞→+∞→4求下列极限 (1)xx e 1lim∞→(2)x x x sin ln lim 0→(3)2)11(lim xx x +∞→ (4)x x x 2cot 20)tan 31(lim +→(5)21)63(lim -∞→++x x xx (6)x x x x x x -++-+→20sin 1sin 1tan 1lim解(1)1lim 01lim 1===∞→∞→e ee xxx x(2)01ln )sin lim ln(sin ln lim 00===→→x x x x x x(3)[]e e x x x x xx ==+=+∞→∞→21212)11(lim )11(lim(4)[]33tan 312cot 222)tan31(lim )tan 31(lim e x x x x x x =+=+→→(5)21633621)631()63(-+-⋅-+-+-+=++x x x x xx x 因为 所以2321)63(lim --∞→=++e xx x x(6))sin 1tan 1)(1sin 1()1sin 1)(sin 1tan 1(limsin 1sin 1tan 1lim 22020x x x x x x x x x x x x x x +++-++++-+=-++-+→→ 5设函数⎩⎨⎧≥+<=0 0)(x x a x e x f x 应当如何选择数a 使得f (x )成为在()内的连续函数?解要使函数f (x )在()内连续只须f (x )在x 0处连续即只须 因为1lim )(lim 0==-→-→x x x e x f a x a x f x x =+=+→+→)(lim )(lim 00所以只须取a 1习题1101证明方程x 53x 1至少有一个根介于1和2之间 证明设f (x )x 53x 1则f (x )是闭区间[12]上的连续函数因为f (1)3f (2)25f (1)f (2)0所以由零点定理在(12)内至少有一点 (12)使f ()0即x 是方程x 53x 1的介于1和2之间的根 因此方程x 53x 1至少有一个根介于1和2之间2证明方程xa sin xb 其中a 0b 0至少有一个正根并且它不超过ab 证明设f (x )a sin xbx 则f (x )是[0ab ]上的连续函数f (0)bf (ab )a sin(ab )b (ab )a [sin(ab )1]0若f (ab )0则说明xab 就是方程xa sin xb 的一个不超过ab 的根若f (ab )0则f (0)f (ab )0由零点定理至少存在一点(0ab )使f ()0这说明x 也是方程x =a sin xb 的一个不超过ab 的根总之方程xa sin xb 至少有一个正根并且它不超过ab3设函数f (x )对于闭区间[ab ]上的任意两点x 、y 恒有|f (x )f (y )|L |xy |其中L 为正常数且f (a )f (b )0证明至少有一点(ab )使得f ()0 证明设x 0为(ab )内任意一点因为 所以0|)()(|lim 00=-→x f x f x x即)()(lim 00x f x f x x =→因此f (x )在(ab )内连续同理可证f (x )在点a 处左连续在点b 处右连续所以f (x )在[ab ]上连续因为f (x )在[ab ]上连续且f (a )f (b )0由零点定理至少有一点(ab )使得f ()0 4若f (x )在[ab ]上连续ax 1x 2x n b 则在[x 1x n ]上至少有一点使证明显然f (x )在[x 1x n ]上也连续设M 和m 分别是f (x )在[x 1x n ]上的最大值和最小值因为x i [x 1x n ](1in )所以有mf (x i )M 从而有 由介值定理推论在[x 1x n ]上至少有一点使5证明若f (x )在()内连续且)(lim x f x ∞→存在则f (x )必在()内有界证明令A x f x =∞→)(lim 则对于给定的0存在X 0只要|x |X 就有|f (x )A |即Af (x )A又由于f (x )在闭区间[XX ]上连续根据有界性定理存在M 0使|f (x )|Mx [XX ] 取N max{M |A ||A |}则|f (x )|Nx ()即f (x )在()内有界 6在什么条件下(ab )内的连续函数f (x )为一致连续? 总习题一1在“充分”、“必要”和“充分必要”三者中选择一个正确的填入下列空格内 (1)数列{x n }有界是数列{x n }收敛的________条件数列{x n }收敛是数列{x n }有界的________的条件(2)f (x )在x 0的某一去心邻域内有界是)(lim 0x f x x →存在的________条件)(lim 0x f x x →存在是f (x )在x 0的某一去心邻域内有界的________条件(3)f (x )在x 0的某一去心邻域内无界是∞=→)(lim 0x f x x 的________条件∞=→)(lim 0x f x x 是f (x )在x 0的某一去心邻域内无界的________条件(4)f (x )当xx 0时的右极限f (x 0)及左极限f (x 0)都存在且相等是)(lim 0x f x x →存在的________条件 解(1)必要充分 (2)必要充分 (3)必要充分 (4)充分必要2选择以下题中给出的四个结论中一个正确的结论 设f (x )2x 3x 2则当x 0时有()(A )f (x )与x 是等价无穷小(B )f (x )与x 同阶但非等价无穷小 (C )f (x )是比x 高阶的无穷小(D )f (x )是比x 低阶的无穷小解因为x x xx x f x x x x x x x x 13lim 12lim 232lim )(lim 0000-+-=-+=→→→→3ln 2ln )1ln(lim 3ln )1ln(lim 2ln 00+=+++=→→u u t t u t (令2x 1t 3x 1u )所以f (x )与x 同阶但非等价无穷小故应选B 3设f (x )的定义域是[01]求下列函数的定义域 (1)f (e x ) (2)f (ln x ) (3)f (arctan x ) (4)f (cos x )解(1)由0e x 1得x 0即函数f (e x )的定义域为(0] (2)由0ln x 1得1xe 即函数f (ln x )的定义域为[1e ](3)由0arctan x 1得0x tan1即函数f (arctan x )的定义域为[0tan1] (4)由0cos x 1得2222ππππ+≤≤-n x n (n 012)即函数f (cos x )的定义域为[2,22ππππ+-n n ](n 012)4设求f [f (x )]g [g (x )]f [g (x )]g [f (x )]解因为f (x )0所以f [f (x )]f (x )⎩⎨⎧>≤=0 00x x x因为g (x )0所以g [g (x )]0因为g (x )0所以f [g (x )]0因为f (x )0所以g [f (x )]f 2(x )⎩⎨⎧>-≤=0 002x x x5利用y sin x 的图形作出下列函数的图形(1)y |sin x | (2)y sin|x | (3)2sin 2x y =6把半径为R 的一圆形铁片自中心处剪去中心角为的一扇形后围成一无底圆锥试将这圆锥的体积表为的函数解设围成的圆锥的底半径为r 高为h 依题意有R (2)2r παπ2)2(-=R r圆锥的体积为22234)2(24a R -⋅-=πααππ(02) 7根据函数极限的定义证明536lim 23=---→x x x x证明对于任意给定的0要使ε<----|536|2x x x 只需|x 3|取当0|x 3|时就有|x 3|即ε<----|536|2x x x 所以536lim 23=---→x x x x8求下列极限(1)221)1(1lim -+-→x x x x (2))1(lim 2x x x x -++∞→(3)1)1232(lim +∞→++x x x x(4)30sin tan lim x x x x -→ (5)x x x x x c b a 10)3(lim ++→(a 0b 0c 0) (6)x x x tan 2)(sin lim π→解(1)因为01)1(lim 221=+--→x x x x 所以∞=-+-→221)1(1lim x x x x (2))1()1)(1(lim )1(lim 2222x x x x x x x x x x x x ++++-+=-++∞→+∞→(3)2121211)1221(lim )1221(lim )1232(lim ++∞→+∞→+∞→++=++=++x x x x x x x x x x (4)xx x x x x x x x x x x x cos )cos 1(sin lim )1cos 1(sin lim sin tan lim 303030-=-=-→→→ (提示用等价无穷小换)(5)x c b a c b a x x x x x x x x x x x x x x x c b a c b a 3333010)331(lim )3(lim -++⋅-++→→-+++=++因为所以3ln 103)3(lim abc e c b a abc x x x x x ==++→提示求极限过程中作了变换a x 1tb x 1uc x1v(6)xx x x xx x x tan )1(sin 1sin 12tan 2)]1(sin 1[lim )(sin lim -⋅-→→-+=ππ因为 所以1)(sin lim 0tan 2==→e x x x π9设⎪⎩⎪⎨⎧≤+>=01sin )(2x x a x xx x f 要使f (x )在()内连续应怎样选择数a 解要使函数连续必须使函数在x 0处连续 因为f (0)a a x a x f x x =+=--→→)(lim )(lim 20001sin lim )(lim 00==++→→xx x f x x所以当a 0时f (x )在x 0处连续因此选取a 0时f (x )在()内连续10设⎪⎩⎪⎨⎧≤<-+>=-01 )1ln(0 )(11x x x e x f x 求f (x )的间断点并说明间断点所属类形 解因为函数f (x )在x 1处无定义所以x 1是函数的一个间断点因为0lim )(lim 1111==-→→--x x x e x f (提示-∞=--→11lim 1x x )∞==-→→++1111lim )(lim x x x e x f (提示+∞=-+→11lim 1x x )所以x 1是函数的第二类间断点又因为0)1ln(lim )(lim 0=+=--→→x x f x x ee xf x x x 1lim )(lim 11==-→→++所以x 0也是函数的间断点且为第一类间断点11证明()11 2111lim 222=++⋅⋅⋅++++∞→nn n n n 证明因为()11 211122222+≤++⋅⋅⋅++++≤+n n n n n n n n n 且所以()11 2111lim 222=++⋅⋅⋅++++∞→nn n n n 12证明方程sin xx 10在开区间)2,2(ππ-内至少有一个根证明设f (x )sin xx 1则函数f (x )在]2,2 [ππ-上连续因为2121)2 (πππ-=+--=-f 22121)2 (πππ+=++=f 0)2 ()2 (<⋅-ππf f所以由零点定理在区间)2,2 (ππ-内至少存在一点使f ()0这说明方程sin xx 10在开区间)2,2 (ππ-内至少有一个根13如果存在直线Lykxb 使得当x (或xx )时曲线yf (x )上的动点M (xy )到直线L 的距离d (ML )0则称L 为曲线yf (x )的渐近线当直线L 的斜率k 0时称L 为斜渐近线 (1)证明直线Lykxb 为曲线yf (x )的渐近线的充分必要条件是 (2)求曲线xe x y 1)12(-=的斜渐近线证明(1)仅就x 的情况进行证明按渐近线的定义ykxb 是曲线yf (x )的渐近线的充要条件是 必要性设ykxb 是曲线yf (x )的渐近线则0)]()([lim =+-∞→b kx x f x于是有0])([lim =--∞→x b k x x f x x 0)(lim =-∞→k x x f x xx f k x )(lim∞→= 同时有0])([lim =--∞→b kx x f x ])([lim kx x f b x -=∞→充分性如果xx f k x )(lim∞→=])([lim kx x f b x -=∞→则 因此ykxb 是曲线yf (x )的渐近线(2)因为212lim lim 1=⋅-==∞→∞→x x x e x x x y k。
