矩形波导模式和场结构分析毕业设计论文
波导论文

1 导行电磁波的分类图:任意界面的均匀波导把坐标的z 轴选作波导的轴线方向,这样波导的横截面就是x0y 平面,如图所示,同时做以下假设:(1)波导的横截面形状和媒质特性沿轴线z 不变化,即具有轴向均匀性。
(2)金属波导为理想导体,即γ= 。
波导内填充均匀、线性、各向同性的理想介质。
(3)波导内没有激励源存在,即0,0ρ==J 。
(4)电磁波沿z 轴传播,且场随时间作正弦变化。
在以上假设下,电磁场基本方程组的复数形式如下0j j ωεμω∇⨯=∇⨯=-∇⨯=∇⨯=H EE HH E (1)由此可以得到,电磁场的电场分量E 和磁场分量H 均满足齐次的波动方程222200k k ∇+=∇+=E E H H (2) 式中k ωμε=是波数。
既然波导轴线沿z 方向,那么不论波的传播情况在波导内怎样复杂,其最终的效果只能是一个沿z 方向前进的导行电磁波。
因而可以把波导内电场分量E 和磁场分量H 写成(,)(,)zz E x y H x y e e γγ--==E H (3)其中E (x ,y )和H (x ,y )是待定函数。
γ为波沿z 方向的传播常数。
将(3)代入(2)式,得22(,)(,)0t c x y k x y ∇+=E E22(,)(,)0t c x y k x y ∇+=H H (4)这里22222tx y ∂∂∇=+∂∂是横向拉普拉斯算子。
式中 222c k k γ=+可以由方程(4)得到E (x ,y )和H (x ,y )各分量的标量波动方程。
也可先求解纵向场分z y x,εμ量的波动方程,得到两个纵向分量z E 和z H ,然后再根据电磁场基本方程组所求得所有横向分量。
纵向分量z E 和z H 满足的标量波动方程为222222222200z z c z z z c z E E k E x yH H k H x y∂∂++=∂∂∂∂++=∂∂ 由上述两个方程求得z E 和z H 后,即可从电磁场基本方程组的两个旋度方程得到四个横向场分量22221()1()1()1()z z x c z z y c z z x c z z y c E H E j k x y E H E j k y xE H H j k x yE H H j k x y γωμγωμγωμωεγ∂∂=-+∂∂∂∂=-+∂∂∂∂=--∂∂∂∂=-+∂∂上式中所有场量只与坐标x 和y 有关。
矩形波发生器论文

矩形波发生器小论文一、开题报告矩形波发生器电路有多种方案,该设计以运算放大器为核心,由矩形波振荡电路、幅值调节电路两部分组成。
使用元件包括:LF353p运算放大器、12V电压源、电阻、可调电位器(滑动变阻器)、电容、二极管、单刀双掷开关、示波器。
电路设计方案和元器件选择的原则是:工作稳定可靠、结构简单合理、安装调试方便、性能参数达标。
二、设计内容图1 矩形波发生器1、矩形波振荡电路矩形波振荡电路(又称多谐振荡器)有反向输入的滞回比较器和RC电路组成。
滞回比较器起开关作用,RC电路的作用是产生暂态过程。
RC回路即使延迟环节,又是反馈网络,通过RC充放电过程是先输出状态的自动转换。
在运放的输出端引入限流电阻就组成了如图2所示的双向限幅矩形波。
图2中的滞回比较器的阈值电压±UT=±R1/(R1+R2)UZ (1)假设接通电源时,电容C两端电压uc=0,输入电压uo=+UZ,则运放通向输入端电压up=+UT,二极管VD2导通,VD1截止,u0通过电阻R3和R6给电容C充电,忽略二极管的动态电阻,充电时间常数近似为(R3+R6)C,使运放反向输入端电压uN由0逐渐上升,在uN<up时,u0=+UZ保持不变。
当uN≥up时,uo立即从+UZ跃变成-UZ,同时up从+UT跃变为-UT,二极管VD1导通,VD2截止,电容C开始通过R3和R5放电,放电时间常数近似为(R3+R5)C,使运放反向输入端电压uN逐渐下降,在uN〉up时,u0=-UZ保持不变。
当uN≤up时,uo立即从-UZ跃变成+UZ,电容C又开始充电,运放输出状态再次翻转。
如此周而复始,电路产生自激振荡,输出端输出矩形波信号。
图2 矩形波振荡电路通常将矩形波输出高电平的持续时间与振荡周期的比定义为占空比。
上图所示电路利用二极管的单向导电性使电容充、放电的通路不同,从而使它们的时间常数不同,实现了输出电压占空比的调节。
上图矩形波发生器的输出电压幅值等于稳压管的稳压值,电路输出电压正、负幅度对称。
标准矩形波导

标准矩形波导标准矩形波导是一种常见的波导结构,广泛应用于微波通信、雷达系统、天线设计等领域。
它具有良好的传输特性和较低的传输损耗,因此备受工程师和研究人员的青睐。
本文将对标准矩形波导的结构特点、工作原理和应用领域进行介绍,希望能为相关领域的研究和应用提供参考。
结构特点。
标准矩形波导通常由金属材料制成,其截面呈矩形形状,具有固定的宽度和高度。
波导内部充满介质,通常为空气或真空。
波导的长度通常为波长的整数倍,以保证波的传输稳定。
在波导的两端通常设置有适当的耦合装置,用于与其他器件或系统连接。
工作原理。
当电磁波通过波导传输时,波导内部会产生电场和磁场的分布。
这些电场和磁场的分布会受到波导结构和工作频率的影响,从而影响波导的传输特性。
标准矩形波导的工作原理可以通过电磁场理论和传输线理论进行描述,通过分析波导内部的电磁场分布和传输线的特性,可以得到波导的传输特性参数,如传输损耗、衰减系数等。
应用领域。
标准矩形波导广泛应用于微波通信、雷达系统、天线设计等领域。
在微波通信系统中,标准矩形波导可以用作信号的传输线路,用于连接各种微波器件和系统。
在雷达系统中,标准矩形波导可以用于天线的馈源系统,用于将雷达信号传输到天线中。
在天线设计中,标准矩形波导可以用于天线的馈源系统和辐射系统,用于实现天线的高效工作。
总结。
标准矩形波导是一种重要的波导结构,具有良好的传输特性和较低的传输损耗。
它在微波通信、雷达系统、天线设计等领域有着广泛的应用。
通过对标准矩形波导的结构特点、工作原理和应用领域进行了解,可以更好地应用和设计波导系统,推动相关领域的研究和发展。
以上就是对标准矩形波导的介绍,希望能为相关领域的研究和应用提供一些帮助。
如果您对标准矩形波导还有更多的了解和应用,欢迎继续探讨和交流。
矩形波导的模式

矩形波导的模式
矩形波导是使⽤最⼴泛的⼀种传输线。
给定尺⼨的波导可以传播⽆限多频率的电磁波,本⽂主要写矩形波导的场求解问题及矩形波导的相关特性。
在波导内部,认为为⽆源空间,所以不存在传导电流和电荷,即J = 0
⼀
对式2继续取旋度,得
同理对式1取旋度,可得到两个Helmheltz⽅程如下
求解的过程可总结为
每个Helmholtz⽅向是⼀个⽮量⽅程,在矩形波导中可以分解为三个⽅向x\y\z的三个标题⽅程,从⽽得到波传播⽅向z⽅向的标量⽅程
假设E z\H z可分离变量,分离变量法可得到
且
其中为截⽌波数,
解的第⼀部分是⼊射波,第⼆部分是反射波。
只考虑⼊射波得
横向分量⽤纵向分量表⽰
整理Ex、Hy得
整理Hx、Ey得
写成矩阵形式
⼆以TE波为例
H(x,y)可分离变量,H(x,y)=X(x)Y(y)
得
⼀般解为:
总的解为
矩形波导的基模是TE10模
TE10模功率容量。
矩形波导的特点

矩形波导的特点矩形波导是一种常用的传输线结构,广泛应用于微波和毫米波领域。
它具有以下几个特点:1. 结构简单:矩形波导由一条矩形截面的金属管道组成,截面形状为长方形。
这种简单的结构使得制造和安装都相对容易,适用于各种不同的应用场景。
同时,矩形波导还可以通过连接多个截面不同的金属截面,实现不同通道的复用,进一步提高了其应用的灵活性。
2. 宽频工作范围:矩形波导的工作频段通常在几十GHz到几百GHz之间。
并且由于其结构简单,波导内部没有电流分布,所以可以在宽频带范围内工作。
这使得矩形波导具有很高的频带传输能力,适用于高频率和宽带宽的应用,如雷达、通信和卫星通信等。
3. 低损耗:矩形波导由于截面为长方形,电磁波在其中传播时,相对于同等宽度的其他类型的传输线,波导的截面较大,从而使电磁波的功率分布较为均匀。
这可以减少能量损失,降低传输损耗。
因此,矩形波导在高频率、高功率和长距离传输中,具有较低的传输损耗。
4. 承载高功率:矩形波导由于其结构简单而坚固,能够承受较大的功率。
由于矩形波导的能量传播主要限制在波导内部,不会在周围空间中传播,因此能够承受相对较高的功率密度,稳定可靠。
5. 良好的屏蔽性能:矩形波导由金属材料构成,具有良好的屏蔽性能,能够阻挡外界的电磁干扰,防止波导内部电磁波的干扰和泄漏。
这对于保证信号的稳定传输和提高系统的抗干扰能力非常重要。
除了以上特点,矩形波导还具有易于制造和安装、适用于高温和高真空环境、可实现复杂的分支网络等优点。
这使得矩形波导在军事、航空航天、通信、医疗和科学研究等领域得到广泛应用。
综上所述,矩形波导具有结构简单、宽频工作范围、低损耗、承载高功率和良好的屏蔽性能等特点。
这些特点使得矩形波导在微波和毫米波传输中具有广泛的应用前景。
参考文献:1. Pozar, D. M. (2009). Microwave engineering. New York, NY: John Wiley & Sons.2. Collin, R. (1991). Foundations for Microwave Engineering. New York, NY: IEEE Press.3. Gupta, K. C., Garg, R., & Bahl, I. J. (2002). Microstrip lines and slotlines. Norwood, MA: Artech House.4. Sarkar, T. K., Salazar-Palma, M., & Oliner, A. A. (2001). History of wireless. Hoboken, NJ: John Wiley & Sons.。
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
电磁场与微波技术实验2矩形波导仿真与分析

实验二 矩形波导仿真与分析一、实验目的:1、 熟悉HFSS 软件的使用;2、 掌握导波场分析和求解方法,矩形波导高次模的基本设计方法;3、 利用HFSS 软件进行电磁场分析,掌握导模场结构和管壁电流结构规律和特点。
二、预习要求1、 导波原理。
2、 矩形波导模式基本结构,及其基本电磁场分析和理论。
3、 HFSS 软件基本使用方法。
三、实验原理由于矩形波导的四壁都是导体,根据边界条件波导中不可能传输TEM 模,只能传输TE 或TM 模。
这里只分析TE 模(Ez=0)对于TE 模只要解Hz 的波动方程。
即采用分离变量,并带入边界条件解上式,得出TE 模的横向分量的复振幅分别为(1)矩形波导中传输模式的纵向传输特性①截止特性波导中波在传输方向的波数β由式9 给出222000220z z c z H H k H x y ∂∂++=∂∂式7000220002200020002()cos()sin()()sin()cos()()sin()cos()()cos()sin()z x c c z y c c y x H c x y H c H n m n E j j H x y k y k b a b H m m n E j j H x y k x k a a b E m m n H j H x y Z k a a b E n m n H j H x y Z k b a b ωμωμπππωμωμπππβπππβπππ∂⎧==⎪∂⎪⎪∂==-⎪∂⎪⎨⎪=-=⎪⎪⎪==⎪⎩式822222c c k k ππβλλ=-=-式9式中k 为自由空间中同频率的电磁波的波数。
要使波导中存在导波,则β必须为实数,即k 2>k 2c 或λ<λc(f >f c ) 式10如果上式不满足,则电磁波不能在波导内传输,称为截止。
故k c 称为截止波数。
矩形波导中TE 10模的截止波长最长,故称它为最低模式,其余模式均称为高次模。
由于TE 10模的截止波长最长且等于2a,用它来传输可以保证单模传输。
矩形波导

微波技术基础考察小论文请讨论矩形波导TE 10模的截止波长、相速、波导波长、波阻抗;其外形结构尺寸的确定遵循什么原则? 一、理论依据1) 通常将由金属材料制成的、矩形截面的、内充空气介质的规则金属波导称为矩形波导, 它是微波技术中最常用的传输系统之一 矩形波导TE 波的截止波数:22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=b n a m K c ππ它与波导尺寸、传输波型有关。
m 和n 分别代表TE 波沿x 方向和y 方向分布的半波个数, 一组m 、n, 对应一种TE 波, 称作TE mn 模; 但m 和n 不能同时为零, 否则场分量全部为零。
因此,矩形波导能够存在TE m0模和TE 0n 模及TE mn (m,n ≠0)模; 其中TE 10模是最低次模(主模), 其余称为高次模。
2)单模传输在传输过程中,如若我们需要传输TE 10模,我们需要抑制高次模的传输。
因此工作波长应该满足:1020TE TE λλλ<<1001TE TE λλλ<<二、问题解答对于TE 10模即m = 1, n = 01)TE 10模的截止波数c K 为:a K c π=2) 截止波长c λ:a aK cc 222===πππλ 3)相速p v 表示波的等相位面沿波导的轴向(z )传播的速度, 其值:22211⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==a v v wv c p λλλβ4)波导波长g λ表示波导内沿其轴向传播的电磁波,它的相邻的两个同相位点之间的距离, 其值:21⎪⎪⎭⎫ ⎝⎛-==c p g fv λλλλ将截止波长代入,则: 波导波长:22211⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==a fv c p g λλλλλλ 5)在不计损耗的情况下,在行波状态下,电场的横向分量Et 和磁场的横向分量Ht 不仅构成了沿波导轴正Z 方向传播的波,而且对于同一波形而言,t E 和t H 的比值在波导横截面内处处相等,它与坐标Z 无关,并具有阻抗的量纲。
矩形波导中传播模式的研究

矩形波导中传播模式的研究矩形波导是一种常见的光波导结构,其具有独特的特性和广泛的应用。
研究矩形波导中的传播模式是了解其工作原理、优化设计以及应用于光电子器件中的重要一步。
本文将以1200字以上介绍矩形波导中传播模式的研究。
首先,我们来介绍矩形波导的基本结构。
矩形波导通常由一个矩形的导波区域和四个边界组成。
导波区域被限制在一个矩形的空间内,而边界则由两条长边和两条短边组成。
导波区域的尺寸会直接影响传播模式的特性。
当导波区域的尺寸远小于光波的波长时,可以将矩形波导看作一个简单的光纤结构,其中只有一个模式可以沿波导传播。
然而,当导波区域的尺寸达到或超过光波的波长时,将会出现多个模式同时传播的情况。
研究矩形波导中传播模式的独特性质是很重要的。
通常,我们可以利用数值模拟方法来计算和分析矩形波导的传播模式。
其中一种常用的方法是有限差分法(FDM),它将波导的导模问题转化为一个二维矢量波动方程。
利用FDM,可以计算出波导中的场分布、传播常数等参数。
另一种常用的方法是有限元法(FEM),它通过将域离散化为有限数量的元素,将波导的导模问题转化为一个矢量强度方程。
利用FEM,可以计算出波导中的电场、磁场分量等参数。
这些数值模拟方法不仅可以计算出传播模式的分布特性,还可以分析波导的传输损耗、耦合特性等。
在矩形波导中,常见的传播模式有基模、高次模等。
基模是指在导波区域内仅有一条主要能量传输路径的模式。
基模是最常用的一种模式,通常具有低传输损耗和较大的传输带宽。
高次模则是指在导波区域内还存在其他能量传输路径的模式。
由于高次模的能量传输路径更多,会导致较大的传输损耗和较窄的传输带宽。
因此,在矩形波导的设计和应用中,我们通常希望尽可能地利用基模,并且减小高次模的影响。
传播模式的研究不仅仅局限于矩形波导的基模和高次模,还可以进一步探究更复杂的模式现象。
例如,当矩形波导的宽度和高度相等时,可以得到一种特殊的模式,称为TE/TM模式。
开缝矩形波导

开缝矩形波导开缝矩形波导是一种常用的微波器件,广泛应用于通信、雷达、微波炉等领域。
它是由一块金属板制成,通过在金属板上开缝来实现微波的传输和耦合。
本文将介绍开缝矩形波导的基本原理、结构特点、优缺点以及应用领域等方面的内容。
一、基本原理开缝矩形波导的基本原理是利用金属板上的开缝来实现微波的传输和耦合。
在金属板上开一条长短适中的缝隙,微波信号可以从缝隙中通过,并在波导内沿着金属板的表面传输。
当微波信号到达开口处时,一部分能量会透过缝隙穿过金属板,形成辐射场,另一部分则会沿着金属板传输。
在波导的另一端,开口处的微波信号再次透过缝隙穿过金属板,形成辐射场,从而实现了微波的传输和耦合。
二、结构特点开缝矩形波导的结构特点是由一块金属板制成,上面开有一条长短适中的缝隙。
波导的宽度和高度通常比较大,可以容纳较大的微波信号。
开缝矩形波导的结构简单,制作成本低廉,易于加工和制造。
同时,它的传输带宽比较大,能够传输较宽的频率范围内的微波信号,具有较好的通用性和适应性。
三、优缺点开缝矩形波导的优点是由于其结构简单,制作成本低廉,易于加工和制造。
同时,它的传输带宽比较大,能够传输较宽的频率范围内的微波信号,具有较好的通用性和适应性。
缺点是由于其开口处会产生辐射场,因此会存在一定的能量损耗。
此外,开缝矩形波导的尺寸较大,不适合在一些场合中使用。
四、应用领域开缝矩形波导广泛应用于通信、雷达、微波炉等领域。
在通信领域中,它主要用于微波通信系统中的信号传输和耦合。
在雷达领域中,它主要用于雷达信号的传输和接收。
在微波炉领域中,它主要用于微波炉内部的微波信号传输和辐射。
开缝矩形波导是一种常用的微波器件,具有结构简单、制作成本低廉、易于加工和制造等优点,广泛应用于通信、雷达、微波炉等领域。
实验二矩形波导TE10的仿真设计与电磁场分析解读

实验⼆矩形波导TE10的仿真设计与电磁场分析解读]实验⼆、矩形波导TE10的仿真设计与电磁场分析⼀、实验⽬的:1、熟悉HFSS软件的使⽤;2、掌握导波场分析和求解⽅法,矩形波导TE10基本设计⽅法;3、利⽤HFSS 软件进⾏电磁场分析,掌握导模场结构和管壁电流结构规律和特点。
⼆、预习要求1、《2、导波原理。
3、矩形波导TE10模式基本结构,及其基本电磁场分析和理论。
4、HFSS软件基本使⽤⽅法。
三、实验原理与参考电路导波原理3.1.1. 规则⾦属管内电磁波对由均匀填充介质的⾦属波导管建⽴如图1 所⽰坐标系, 设z轴与波导的轴线相重合。
由于波导的边界和尺⼨沿轴向不变, 故称为规则⾦属波导。
为了简化起见, 我们作如下假设:\①波导管内填充的介质是均匀、线性、各向同性的;②波导管内⽆⾃由电荷和传导电流的存在;③波导管内的场是时谐场。
图1 矩形波导结构本节采⽤直⾓坐标系来分析,并假设波导是⽆限长的,且波是沿着z⽅向⽆衰减地传输,由电磁场理论, 对⽆源⾃由空间电场E和磁场H满⾜以下⽮量亥姆霍茨⽅程:`式中β为波导轴向的波数,E0(x,y)和H0(x,y)分别为电场和磁场的复振幅,它仅是坐标x和y的函数。
以电场为例⼦,将上式代⼊亥姆霍兹⽅程 ,并在直⾓坐标内展开,即有(,)(,)j zj zE E x y eH H x y eββ--==式1220E k E+=222222222222222220T c E E EE k E k Ex y zE EE k E x yE k E β+=+++?=+-+??=?+=式2k c 表⽰电磁波在与传播⽅向相垂直的平⾯上的波数,如果导波沿z ⽅向传播,则 k 为⾃由空间中同频率的电磁波的波数。
由麦克斯韦⽅程组的两个旋度式,很易找到场的横向分量和纵向分量的关系式。
具体过程从略,这⾥仅给出结果:《从以上分析可得以下结论: ^(1)场的横向分量即可由纵向分量;(2)既满⾜上述⽅程⼜满⾜边界条件的解有许多, 每⼀个解对应⼀个波型也称之为模式,不同的模式具有不同的传输特性;(3)k c 是在特定边界条件下的特征值, 它是⼀个与导波系统横截⾯形状、尺⼨及传输模式有关的参量。
矩形波导仿真实验报告

矩形波导仿真实验报告标题:矩形波导仿真实验报告摘要:本实验报告旨在通过矩形波导的仿真实验,深入探讨矩形波导的基本原理、工作特性以及其在通信领域中的应用。
通过仿真实验,我们可以更好地理解矩形波导的电磁波传输机制,验证其传输效果,并对其性能进行评估。
本报告还包括对矩形波导在微波、光通信等领域的应用前景的讨论。
1. 引言1.1 研究背景1.2 实验目的2. 矩形波导的基本原理2.1 电磁波传输原理2.2 矩形波导的结构与特点3. 矩形波导的仿真实验设计3.1 实验所用软件和工具3.2 实验所用材料和设备3.3 实验步骤4. 实验结果与分析4.1 矩形波导的传输效果评估4.2 电磁场分布和损耗分析4.3 参数对传输性能的影响分析5. 矩形波导在通信领域中的应用5.1 微波通信领域中的应用案例5.2 光通信领域中的应用案例5.3 应用前景与展望6. 总结与展望在本实验中,我们首先对矩形波导的基本原理进行了介绍,包括其电磁波传输原理以及结构特点。
我们详细描述了矩形波导的仿真实验设计,包括所用软件和工具、材料和设备以及实验步骤。
我们给出了实验结果与分析,评估了矩形波导的传输效果,并对电磁场分布和损耗进行了分析。
我们还研究了参数对传输性能的影响。
随后,我们讨论了矩形波导在通信领域中的应用案例,包括微波和光通信领域,并对其应用前景和发展进行了展望。
通过本次矩形波导仿真实验,我们对矩形波导的基本原理有了更深入的理解,并对其在通信领域中的应用进行了探讨。
期望该实验报告能为研究者和工程师提供有价值的参考和启示,进一步推动矩形波导技术的发展与应用。
观点与理解:矩形波导作为一种重要的波导结构,具有许多独特的优势和应用前景。
从基本原理到仿真实验,我深入探索了矩形波导的特性和性能,并对其在通信领域中的应用进行了评估。
通过本次实验,我认识到矩形波导有着广泛的应用前景,特别是在微波和光通信领域。
希望通过我对这个主题的深入研究和理解,能够为更多人提供有价值的知识和见解,促进该领域的发展与创新。
矩形波导中场结构模拟实验

实验 矩形波导中场结构模拟实验一、实验目的要求:1.通过实验编程及图像动态演示,形象具体的了解电磁波在波导中传播特性。
2.通过编写Matlab 程序,加深矩形波导中电磁波公式推导以及单模电磁波在矩形波导中的传播理解。
二、实验内容:电磁场本身比较复杂和抽象,是涉及空间和时间的多维矢量场,需要具有较强的空间想象能力来理解它。
1.实验原理:矩形波导是截面形状为矩形的金属波导管,如图一所示。
波导内壁面位置坐标设为:x=0和x=a ;y=0和y=b 。
波导中填充介电常数为ε、磁导率为μ、电导率为σ的媒质,通常波导内填充理想介质(σ=0)。
由于波导内没有自由电荷和传导电流,所以传播的电磁波是正弦电磁波。
理想导电壁矩形波导中不可能传输TEM 模,只能传输TE 模或TM 模。
对于矩形波导中TE MN 模的电场强度E 、磁场强度H 场分量表达式为:(02cos sin j t z x c j n m n E H x y e k ba b )ωβωμπππ−⎛⎞⎛⎞⎛⎞=⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ (1) (02sin cos j t z y c j m m n E H x y e k aa b )ωβωμπππ−⎛⎞⎛⎞⎛⎞=⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ (2) (3)0z E =(02sin cos j t z x c j m m n H H x y e k a a b )ωββπππ−⎛⎞⎛⎞⎛⎞=⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠(4) (02cos sin j t z y c j n m n H H x y e k b a b )ωββπππ−⎛⎞⎛⎞⎛⎞=⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠(5) (0cos cos j t z z m n H H x y e a b )ωβππ−⎛⎞⎛⎞=⎜⎟⎜⎟⎝⎠⎝⎠ (6)其中:ω为微波角频率;m 和n 值可以取0或正整数,代表不同的TE 波场结构模式,称为TE 模,波导中可有无穷多个TE 模式;k c 为临界波束,k c 2=(m π/2)2+(n π/b )2;β为相位常数,β=。
本科毕设论文-—矩形波导模式和场结构分析

毕业设计(论文)题目:矩形波导模式和场结构分析目录第一章绪论 (1)1.1 选题背景及意义 (3)1.2 国内外研究概况及发展趋势 (3)1.3 本课题研究目标及主要内容 (4)1.4 本章小结 (6)第二章矩形波导的基本原理 (7)2.1 导波的一般分析 (7)2.1.1规则矩形波导内的电磁波 (7)2.1.2波导传输的一般特性 (8)2.2 矩形波导的分析 (8)2.2.1矩形波导电磁场解 (8)2.2.2矩形波导中的波型及截止波长 (11)2.3 本章小结 (12)第三章矩形波导的设计 (13)3.1 创建矩形波导模型 (13)3.2 求解设置 (20)3.3 设计检查和运行仿真 (22)3.3.1设计检查 (22)3.3.2运行仿真分析 (23)3.4 本章小结 (24)第四章HFSS仿真结果及其分析 (25)4.1 HFSS软件仿真原理 .............................. 错误!未定义书签。
4.2 HFSS仿真实现 (26)4.3 仿真结果分析 (32)4.4 本章小结....................................... 错误!未定义书签。
第五章小结与展望 .. (33)5.1 工作总结 (33)5.2 工作展望 (33)参考文献 (33)致谢 (35)附录 A 常用贝塞尔函数公式错误!未定义书签。
矩形波导模式和场结构分析第一章 绪论1.1选题背景及意义矩形波导(circular waveguide)简称为矩波导,是截面形状为矩形的长方形的金属管。
若将同轴线的内导线抽走,则在一定条件下,由外导体所包围的矩形空间也能传输电磁能量,这就是矩形波导。
矩波导加工方便,具有损耗小和双极化特性,常用于要求双极化模的天线的馈线中,也广泛用作各种谐振腔、波长计,是一种较常用的规则金属波导。
矩波导有两类传输模式,即TM 模和TE 模。
其中主要有三种常用模式,分别是主模TE 11模、矩对称TM 01模、低损耗的TE 01模。
矩形波导中传播模式的研究

矩形波导中传播模式的研究矩形介质光波导作为波导光学系统最基本的单元之一,是研究光电器件以及波导传播技术等课题的核心内容。
为研究矩形介质波导中的传播模式,本文将从平板介质波导入手,运用电磁场基本理论,结合边界条件求解麦克斯韦方程组,得到光场传播模式的表达式,模的传播常数以及截止条件等相关参数。
再以此为基础,分别以马卡蒂里理论、库玛尔理论以及有效折射率法在不同电磁波模式下分析比较矩形介质波导,并结合MMI耦合器分析单模和多模中的模场分布。
最后使用Matlab绘制传播曲线并且基于BPM算法对不同条件的矩形波导进行模拟,分析并比较其传播模式。
1.1 引言随着为微纳加工工艺技术的不断提高,晶体管的特征尺寸越来越小,单片集成的晶体管数目越来越多,由此带来的金属互联问题、漏电流问题以及散热问题难以解决。
紧靠减小晶体管尺寸、提高工作频率的手段提高处理器性能的方式已遇到瓶颈[1]。
光具有高传播速度、高宽带、并行性等本征的特质,使得光非常适用于海量数据传输处理等领域,研究并开发以此为核心的新型信息处理技术已成为普遍共识。
而随着光通讯正在朝着高速率大容量的方向发展,在SOI材料上制备光波导是技术发展的必然趋势。
在此背景下,研究矩形光波导中的传播模式是尤为重要的[2]。
本课题中的矩形波导是指由半导体材料制成的,具有矩形的波导芯层以及包围着芯层但折射率更低的包层结构,可以使光限制在芯层内传播的器件。
本课题主要分析矩形光波导中存在的传播模式以及各种模式的传播特性。
在第二章中,首先对平板波导理论进行推导,分析了平板波导中单模和多模条件。
第三章中运用第二章中的关于平板波导的相关知识,分别在马卡蒂里理论、库玛尔理论以及有效折射率法下对矩形波导进行计算。
前两者给出了不同区域内的两种光场分布重点讨论在有效折射率法矩形波导中可以存在的模式同波导横向长度和材料的折射率之间的关系以及不同模式下的场分布,并结合MMI(多模干涉)耦合器对单模和多模的模场分布进行具体分析。
微波元件矩形波导的理论和仿真分析
• 90•随着信息化的不断深入,为满足大容量、高速率的社会需求,各通信系统的通信频段都呈上升趋势,波导以其高频段传输的低损耗特性开始受到越来越多的关注。
本文利用电磁波传输的交链特性以及电磁场在矩形波导中的各分量表达式,针对实际应用对矩形波导主要传输的TE 10型波进行了场域和矢量线的高频仿真,仿真结果对理论分析进行了很好的验证。
随着电子化、信息化的不断深入,电子电气设备已经普及到我们生活的各个领域,传输线作为各类电子电气以及通信系统的连接和通信纽带,无论在军用还是民用等各个方面都有着不可或缺的地位。
通常在直流和波长小于3m 的低频电力系统中采用双线传输线(如双绞线)、频率较高时采用同轴线避免电磁波向外辐射损耗和干扰、频率更高时采用波导管(以下简称波导)来避免高频传输时同轴线的导体及介质中的损耗。
波导是由金属(如黄铜、铝、镀银等)拉制而成的空心管,填充的介质一般为空气。
在性能上可将其分为硬波导和软波导;在结构上可将其分为矩形波导、椭圆波导、扭波导、充气波导等。
1 理论分析以矩形波导为例创建模型,根据导波系统的横截面创建直角坐标系,令其沿Z 轴放置,且传播方向为正Z 方向。
为了简化数学分析,假设矩形波导由理想导体壁构成,其间的媒质是均匀、线性、无耗和各向同性的。
此外,还假设所讨论的波导部分远离波源,波导中无自由电荷和传导电流。
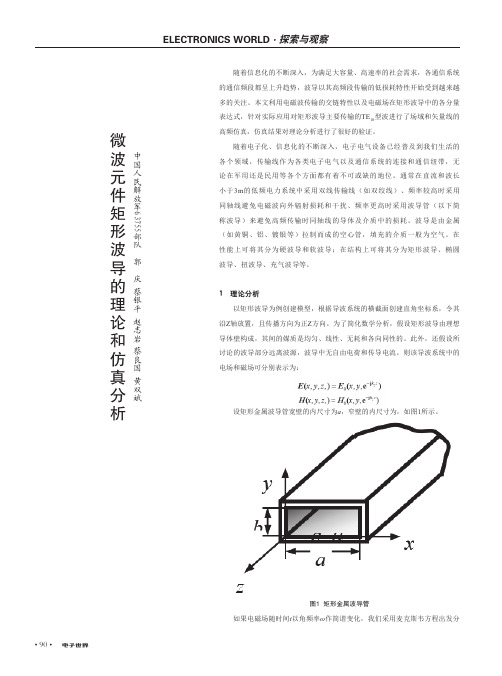
则该导波系统中的电场和磁场可分别表示为:设矩形金属波导管宽壁的内尺寸为a ,窄壁的内尺寸为,如图1所示。
图1 矩形金属波导管如果电磁场随时间t 以角频率ω作简谐变化,我们采用麦克斯韦方程出发分中国人民解放军63755部队 郭 庆 蔡银平 赵志岩 蔡良国 黄双斌微波元件矩形波导的理论和仿真分析• 91•析这个问题,从其复数形式可写为:(1)(2)(3)(4)消去方程中的和可得到:(5)(6)式中,(5)(6)方程组称为亥姆霍兹方程,拆开其分量可写为:(7)(12)式中。
已知金属波导中只能传输 TE 波及TM 波,现在分别讨论他们在矩形波导中的传播特性。
一种平面形式的矩形波导和微带线集成结构研究

摘要:通常从微带线到矩形波导的过渡是通过三维(3D)复杂的安装结构实现的。
现提出一种新的平面结构,将微带线和矩形波导完全集成在同一衬底上,并通过一个简单的锥度相互连接。
实验结果表明,在回波损耗为20 dB时,该结构的有效带宽为12%,带内插入损耗优于0.4 dB。
新的过渡结构可以在同一衬底上实现波导组件与MIC和MMIC的完全集成。
关键词:矩形波导;微带线到波导的过渡;集成0 引言矩形波导可用于设计高Q值的元件,但需要复杂的转换结构实现与平面电路的集成。
目前已经有一些针对微带线和矩形波导转换结构的研究,然而,传统的矩形波导平面结构集成方案体积庞大,通常也需要精密的加工工艺。
在毫米波频段,这类结构很难实现大规模生产。
微带与矩形波导的过渡一般是由两个或多个模块组成,需要通过精密的组装实现,而且需要配备一些调谐结构设计;此外,平面基板必须被切割成特定的形状。
上述要求都较难实现,也使得集成的成本十分高昂。
一个比较直接的解决方案就是将矩形波导集成到微带衬底中。
这样设计会因为填充电介质、减小体积而减小波导Q值的影响,但是整个电路包括平面电路、转换器和波导都可以使用标准PCB或其他平面加工技术来实现。
本文提出了一种新的微带线和矩形波导集成形式,其中两种不同的结构放置在同一轴上,从而减小了过渡所需的总尺寸。
这种过渡结构利用一个锥形微带线来激发波导模式。
在实验中,波导是在衬底上用线性阵列的金属化通孔合成的,也可以使用金属化凹槽实现。
由于所有组件都设计在同一衬底上,平面制造技术就可以保证优良的机械公差,不需要额外的调谐设计,这对多层结构特别是低温共烧陶瓷(LTCC)平台等多层工艺来说解决了很多难题。
1 介质集成波导技术理论基片集成波导(SIW)就是由两排阵列的金属通孔或槽连接介质基板顶部和底部的金属接地平面而制成的平面结构,使用SIW技术,非平面的金属波导可以建模成一个平面的集成波导,从而集成在平面电路上。
介质集成波导[1]设计步骤如下:步骤1,选择s/f(<2.0);步骤2,选择f/e(<0.2);步骤3,根据工作频率计算Weff;步骤4,根据求解Weff计算e;步骤5,根据f/e和s/f计算f和s。
矩形金属波导传输模式研究

枣庄学院学报
J OUR NA L O F Z AO Z HUA NG UN I VE RS I T Y
S e p . 2 01 7
第3 4卷
第 5期
Vo 1 . 3 4 NO. 5
矩 形 金 属 波 导 传 输 模 式 研 究
薛冬 , 刘珊 珊 , 高珊 , 张裕 仕 , 宗 明 吉 , 陈淑 瑜
导 模 式 特性 进 行 研 究 , 得 出单 负 材 料 包 层 的矩 形 波 导 传 输 条 件 , 并 实 现 宽 孔 径 多 模 传 输 和 小 孔 径 单 模 传 输 的 功 能 .中 北 大 学 的 陈 慧 斌 等 设 计 了 一 种 基 于 金 属 一介 质 一金 属 波
导 的半 圆形 谐 振 腔 与 矩 形 谐 振 腔 的耦 合 结 构 , 为 设 计 芯 片 上 基 于 表 面 等 离 极 化 激 元 波 导
用 在 超 材 料 的设 计 中 . 中 国 窀 问 技 术 研 究 院 的刘 高 见 等 人 设 计 _ r一 种 中 心 频 率 2 2 0 GHz
[ 收稿 日期 ] 2 0 1 7— 0 6—1 0 [ 基金项 目]国家 F 1 然科 学 基 金 项 目 ( 项 目编 号: 1 1 4 4 7 2 0 0; 6 1 7 0 1 4 3 4) ; 山 东 省 自然 科 学 基 金 面 上项 目( 项 目编 号: Z R 2 0 1 7 0 2 2 0 0 4 0 0 ) ; 山东省高等学校科技计划项 目( 项 臼编 号: J 1 7 K A 0 8 7 ) ; 枣庄市科 技成果转 化及重点研 发项 ( 项 目编 号 : 2 0 1 6 GH1 9 ) ; 枣 『 { 彳 科 技 计划 项 目( 项 目编 号 : 2 0 1 6 G X 3 1 ) ; 枣J L 学 院教 改 重点 项 日( 项 目编 号 :
开缝矩形波导

开缝矩形波导开缝矩形波导是一种支持电磁波传输的结构,其特点是在矩形波导的上表面开缝形成共振腔,使电磁波在波导中形成谐振现象,从而实现高效的电磁波传输。
本文将介绍开缝矩形波导的基本原理、应用、优缺点以及未来发展趋势。
一、基本原理开缝矩形波导的基本结构由两个矩形波导组成,其中一个波导在顶部开缝,形成一个共振腔。
电磁波在共振腔内形成谐振现象,从而提高了电磁波的传输效率。
开缝矩形波导支持的电磁模式具有高质量因子、低损耗和高效率等优点。
这种波导结构适用于高频通讯、微波加热和雷达系统等领域。
二、应用目前,开缝矩形波导已广泛应用于微波器件、射频电路、天线、毫米波通讯等领域。
它在无线通讯中的应用可以提高电磁波传输的效异性,实现高速数据传输和抗干扰能力。
另外,开缝矩形波导在微波加热技术中的应用可以提高加热效率,节约能源和降低成本。
此外,它还可以用于寻找目标及成像方面的雷达系统,其优点体现在节省空间和消除互连问题上。
三、优缺点优点:与其他传输介质相比,开缝矩形波导具有高效、稳定、可靠、低损失等优点。
同时,它还具有良好的频带选择性,可以实现较高的带宽。
开缝矩形波导利用谐振模式来传输电磁波,可以提高能量的转移效率,从而减少了能量损失和波浪的反射现象。
缺点:开缝矩形波导的缺点主要体现在制作成本较高,需要采用精密的工艺和高质量的材料。
此外,它的尺寸比其他传输介质较大,需要较高的空间用于安装和维护。
四、未来发展趋势随着通讯技术和电子设备的不断发展,开缝矩形波导将会得到广泛的应用。
其主要发展趋势包括:1、进一步提高频带选择性,实现更高的带宽。
2、加强对材料和工艺技术的研究,进一步优化制作成本和性能指标。
3、将开缝矩形波导应用于新领域和新技术的探索和开发,如可穿戴设备、无线充电、微波通讯和量子通信等。
总之,开缝矩形波导是一种高效、稳定和可靠的电磁波传输结构,具有广泛的应用前景和市场空间。
未来,有望进一步发展和完善,成为通讯技术和电子工业领域中不可或缺的重要组成部分。
矩形波导te模式

矩形波导te模式
矩形波导是一种常见的电磁波传输结构,由一对平行金属平面构成,并围合成矩形的截面。
它主要用于微波和毫米波领域的高频电磁波传输。
矩形波导的TE模式是指横电场模式,即电场只有垂直于波导截面方向的分量。
在TE模式下,波导中的电场沿着横截面的一条方向分布,在垂直方向上,则没有电场分量。
TE模式的电场分布可以通过解决矩形波导中的麦克斯韦方程得到。
TE模式的电场分布呈现出横直矩形的形状,其分布在纵向上可以有多个节点,与波导的截面尺寸有关。
每个TE模式都有自己的截止频率,只有当工作频率高于截止频率时,才能激发出该TE模式。
TE模式的矩形波导具有很好的模式选择性和低损耗特性,因此被广泛应用于微波电路、通信系统、雷达系统等领域中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
毕业设计(论文)题目:矩形波导模式和场结构分析目录第一章绪论 (1)1.1 选题背景及意义 (3)1.2 国内外研究概况及发展趋势 (3)1.3 本课题研究目标及主要内容 (4)1.4 本章小结 (6)第二章矩形波导的基本原理 (7)2.1 导波的一般分析 (7)2.1.1规则矩形波导内的电磁波 (7)2.1.2波导传输的一般特性 (8)2.2 矩形波导的分析 (8)2.2.1矩形波导电磁场解 (8)2.2.2矩形波导中的波型及截止波长 (11)2.3 本章小结 (12)第三章矩形波导的设计 (13)3.1 创建矩形波导模型 (13)3.2 求解设置 (20)3.3 设计检查和运行仿真 (22)3.3.1设计检查 (22)3.3.2运行仿真分析 (23)3.4 本章小结 (24)第四章HFSS仿真结果及其分析 (25)4.1 HFSS软件仿真原理 .............................. 错误!未定义书签。
4.2 HFSS仿真实现 (26)4.3 仿真结果分析 (32)4.4 本章小结....................................... 错误!未定义书签。
第五章小结与展望 .. (33)5.1 工作总结 (33)5.2 工作展望 (33)参考文献 (33)致谢 (35)附录 A 常用贝塞尔函数公式错误!未定义书签。
矩形波导模式和场结构分析第一章 绪论1.1选题背景及意义矩形波导(circular waveguide)简称为矩波导,是截面形状为矩形的长方形的金属管。
若将同轴线的内导线抽走,则在一定条件下,由外导体所包围的矩形空间也能传输电磁能量,这就是矩形波导。
矩波导加工方便,具有损耗小和双极化特性,常用于要求双极化模的天线的馈线中,也广泛用作各种谐振腔、波长计,是一种较常用的规则金属波导。
矩波导有两类传输模式,即TM 模和TE 模。
其中主要有三种常用模式,分别是主模TE 11模、矩对称TM 01模、低损耗的TE 01模。
在不同工作模式下,截止波长、传输特性以及场分布不尽相同,同时,各种工作模式的用途也不相同。
导模的场描述了电磁波在波导中的传输状态,可以通过电力线的疏密来表示场得强与弱。
本毕业课题是分析矩形波导中存在的模式、各种模式的场结构和传播特性,着重讨论11TE 、01TE 和01TM 三个常用模式,并利用MATLAB 和三维高频电磁仿真软件HFSS 可视化波导中11TE 、01TE 和01TM 三种模式电场和磁场波结构。
1.2国内外研究概况及发展趋势由于电磁场是以场的形态存在的物质,具有独特的研究方法,采取重叠的研究方法是其重要的特点,即只有理论分析、测量、计算机模拟的结果相互佐证,才可以认为是获得了正确可信的结论。
时域有限差分法就是实现直接对电磁工程问题进行计算机模拟的基本方法。
在近年的研究电磁问题中,许多学者对时域脉冲源的传播和响应进行了大量的研究,主要是描述物体在瞬态电磁源作用下的理论。
另外,对于物体的电特性,理论上具有几乎所有的频率成分,但实际上,只有有限的频带内的频率成分在区主要作用。
英国物理学家汤姆逊(电子的发现者) 在1893 年发表了一本论述麦克斯韦电磁理论的书,肯定了矩金属壁管子(即矩波导) 传输电磁波的可实现性, 预言波长可与矩柱直径相比拟, 这就是微波。
他预言的矩波导传输, 直到1936 年才实现。
汤姆逊成为历史上第一位预言波导的科学家。
这证明科学预言可以大大早于技术的发展, 同时也表明了应用数学的威力。
英国物理学家瑞利在1897 年发表了论文, 讨论矩形截面和矩形截面“空柱”中的电磁振动, 它们对应后来的矩形波导和矩波导, 并引进了截止波长的概念。
瑞利得到了矩形波导中主模的场方程组,这是雷达中最常用的模式,并讨论了矩波导中的主模。
到1931 年, 人们看出了波导技术会有实用价值。
1933 年, 已经有波长为15 cm 的信号源了。
美国贝尔实验室在20 世纪30 年代已经是一个庞大的研究机构, 它吸收了一大批科学家从事超高频技术的研究。
1936 年, 贝尔的科学家做实验, 实验波导线是长度为260 m 的青铜管, 直径12.5cm, 信号源输出波长为9 cm 。
实验表明, 在截止频率以上, 信号传输衰减很小。
后来, 人们把1936 年当作微波技术开始的年份。
为了对波导做出深刻的阐述, 贝尔实验室的专家继续作数学分析, 推出了完整的本征值方程, 并证明汤姆逊早年的方程是本征值方程的一个特例。
传输线技术发展到今天, 只用简短的文字已不能描述其品种的繁杂、发展的迅速和理论的艰深了。
例如, 就同轴电缆来说, 新技术之一是稳相同轴电缆, 其相位常数随环境温度和机械影响很小, 适用于对相位敏感的电子系统( 如卫星跟踪站和天文台) ; 就波导来说, 矩波导的主模11TE 模的极化平面不稳定, 使它甚至不能用于长度较大的天线馈线, 因此出现了椭矩波导。
目前椭矩波导已经广泛用于微波中继站和地球卫星站; 就传输线的集成化来说, 出现了微带传输线, 使传输线的小型化和平面化成为可能。
当然, 传输线新品种的开发, 又激发了理论工作的深入研究。
为了适应新的需求,需要是各种传输线模式之间进行变化,各种模式变化方面的研究应运而生,如同轴TEM 到矩波导11TE 模式变换。
经变换这种模式变换器可以承受高功率,中心频率上的转换效率大,反射损耗低等优点,是最近的热点研究。
1.3 本课题研究目标及主要内容1、研究目标该课题是在HFSS 的平台上实现矩形波导的设计与仿真,通过在HFSS 平台上对矩形波导的半径、主模工作频率等的设置来设计出要求所需的矩形波导。
其中要求矩形波导的半径为19.05mm ;主模的工作频率为5GHz ;完成对矩形波导的设计后要求画出矩形波导端口前10个模式的电场分布。
2、主要内容:本文针对矩形波导在HFSS 平台上的设计和仿真,需进行矩形波导的相关理论的理解,要求了解其工作原理。
要分析好矩形波导,首先求解电磁场纵向分量的波动方程, 求出纵向分量的通解, 并根据边界条件求出它的特解; 然后利用横向场与纵向场的关系式, 求出横向场的表达式; 最后讨论截止特性、传输特性、场结构和主要波型。
矩波导中11TE 、01TE 和01TM 是三种常用的模式, 根据它们不同的特点有着不同的应用。
下面就这三种模式的场分布特点和应用情况作介绍。
1.11TE 模11TE 模是矩波导的主模, 其截止波长为c λ= 3 .41 R 。
图3 .1 是矩波导11TE 模的场结构图。
由图可见, 矩波导的11TE 模与矩形波导的10TE 模很相似, 因此它们之间的波型转换是很方便的。
矩形波导10TE 模与矩波导11TE 模的波型转换器如图3 .2 所示:图1 .1 矩波导11TE 模的场结构图))2.01TM 模01TM 模是矩波导中的最低型横磁模,01TM 模有如下特点:(1 ) 磁场只有H ϕ分量, 磁力线是横截面上的同心矩。
(2 ) 电力线是平面曲线, 与ϕ无关, 电力线在矩波导中心最强。
(3 ) 01TM 模不存在极化简并模式。
(4 ) 01TM 模在波导管壁上电流只有纵向分量。
利用这一特点, 01TM 模可以用于天线馈线系统的旋转连接工作模式。
3.01TE 模01TE 模是矩波导中的高次模,01TE 模有如下特点:(1 ) 电场只有E ϕ分量, 电力线是横截面上的同心矩。
(2 ) 磁力线是平面曲线, 与ϕ无关。
(3 ) 01TE 模不存在极化简并模式。
(4 ) 01TE 模的一个突出特点是在波导管壁上电流没有纵向分量, 管壁电流只沿矩周方向流动, 并且当传输功率一定时, 随着频率的升高, 波导管壁的热损耗下降。
01TE 模的这个特点, 使它既适合作高Q 谐振腔, 又适合用于毫米波远距离波导通信。
(5 ) 01TE 模不是矩波导中的主模, 因此使用时需要抑制高次模。
1.4 本章小结本章首先介绍了课题选题的意义,波导导波技术的国内外现阶段发展现状及趋势,以及本课题主要研究内容基于HFSS 的仿真平台设计和仿真矩形波导,并画出仿真结果中的电场图。
第二章 矩形波导的基本原理2.1导波的一般分析2.1.1 规则金属管内的电磁波任意截面形状的金属波导如图2.1 所示, 电磁波沿纵向(z 轴方向)传输, 为求解简单, 作如下假设:(1)波导内壁的电导率为无穷大。
(2)波导内的介质是均匀无耗、线性、各向同性的。
(3)波导远离源。
(4)波导无限长。
图2.1 任意截面形状的金属波导由电磁场理论,对无源自由空间电场E 和磁场H 满足以下矢量赫姆霍茨方程:220E k E ∇+= (2-1-1) 220H k H ∇+= (2-1-2)式中,22k ωμε=。
现将电场和磁场分解为横向分量和纵向分量,即t z z E E a E =+ (2-1-3)t z z H H a H =+ (2-1-4)式中,z a 为z 向单位矢量,t 表示横坐标,由于分析的是矩形波导,以矩柱坐标为例讨论从以上分析可以得出以下结论:在规则波导中场得纵向分量满足标量其次波动方程,结合相应边界条件即可求得纵向分量z E 和z H ,而场得横向分量即可由纵向分量求得。
既满足上述方程又满足边界条件的解很多,每一个解对应一个波型也称之为模式,不同的模式具有不同的传输特性。
c k 是为传输系统的特征值,它是一个与波导系统横截面形状、尺寸及传输模式有关的参量。
由于当相移常数β=0时,意味着波导系统不再传播,亦称为及位置,此时c k =k ,故称c k 为截止波数。
2.1.2 波导传输的一般特性1.波导中传输模的种类所谓模式(或称模、波型)是指能够单独在波导中存在的电磁场结构, 按其有无场的纵向分量z E 和z H , 可以分为三类:(1)z E =0且z H =0的传输模称为横电磁模, 也称横电磁波, 记作TEM 波。
这种对于TEM 波, 20c k =,k β==。
相速度1/p v =与频率无关, 是无色散波型。
(2) z E =0而z H ≠0 的传输模称为横电模或磁模, 记为TE 模或H 模; z E ≠0 而z H =0的传输模称为横磁模或电模, 记为TM 模或E 模。
空心金属管波导只能传输这类模。
(3) z E ≠0且z H ≠0的传输模称为混合模, 分为EH 模和HE 模。
这类模存在于开放式波导中, 波在波导表面附近的空间传输, 故又称表面波。
2.2 矩形波导的分析2.2.1 矩形波导电磁场解截面为矩形的金属波导称为矩波导, 如图2.2所示。
矩波导具有损耗较小和双极化的特性, 常用于双极化天线馈线中, 也用作远距离波导通信, 并广泛用作微波谐振腔。
00(i 0E图2.2 矩形波导矩形波导在矩柱坐标中进行讨论,其中可以独立存在TM 模和TE 模。
