《直积》课件
矩阵直积

,t )nt,B=(1,
,
s
)则 ps
A B=(1 1,
,1 s ,
,t 1,
,t
s
) npts
.
注:由1)2)即可得3),下面只证1)和2).
证明:1)由定义得
(aij )
(cij
)
(bij ) (dij )
F
(aij )
(cij
)
F F
(bij (dij
) )
F F
)
(A
B
2
2
)
(AkBk );
范数有以下性质:
命题:1)x 时,x 是范数为一的向量(单位化);
x 2) -x = x ; 3)x,y V,有 x y x y .
证明:只证3) 我们有 x x-y+y x-y y 和 y y-x+x x-y x , 所以 - x-y x - y x-y ,也就是
定义2:设V是有限维线性空间,x , x 是V中任意两种
范数,若存在正数k1及k2,使得x V,都有:
k1
x
x
k2
x
,
称 x 与 x 是等价的.
定理1:有限维线性空间中的任何两种范数等价.
证明:设V是n维线性空间,e1, , en是V的一组基,则x V,
有唯一表达式: x=1e1 nen (e1, , en ) , 其中 =(1, ,n )T为x的坐标向量.
A C
F F
BF
D
F
2)设 =(a1, ,an )T ,则
a1
a1 B a1 (1, ,s )
B
an
an B an (1, ,s )
a1 1,a1 2
人教版《圆的面积》ppt课件4
第十二页,编辑于星期一:点 十八分。
五 课堂小结
圆的半径扩大2倍,直径就扩大( )倍,周长就扩大( )倍,面积就扩大( )倍。
(教科书第68页例1)
答:这个羊圈的周长是25.
一个运动场如下图,两端是半圆形,中间是长方形。
圆的半径扩大2倍,直径就扩大( )倍,周长就扩大( )倍,面积就扩大( )倍。
半径为2cm的圆,它的周长和面积相等。
()
()
把半径为2cm的圆的等分成16等份,拼成一个近似的
长方形,长方形的周长比圆的周长大。
()
一个圆的周长是25.12cm,它的半径是4cm,面积
是12.56cm2。
()
第六页,编辑于星期一:点 十八分。
小明骑自行车经过一座长2260.8m的桥,自行车车轮 的直径是0.6m,如果车轮每分钟转100圈,那么多 少分钟可以通过这座桥?
322= 3.14× 圆的周长越大,半径和面积也越大。
14×322=3215.
3215.36(平方米)
这个运动场的面积是多少平方米?
100× (32× 2)=6400(平方米) 把半径为2cm的圆的等分成16等份,拼成一个近似的长方形,长方形的周长比圆的周长大。
(教科书第68页例1)
圆形草坪的直径是20m,每平方米草皮8元。
圆的周长C=πd 或 C=2πr
答:这个大轮的半径是6分米。
圆的周长越大,半径和面积也越大。
半径为2cm的圆,它的周长和面积相等。
圆的周长C=πd 一个水桶的底面是圆形,周长是94.
圆形草坪的直径是20m,每平方米草皮8元。
在一张长9厘米,宽6厘米的长方形纸上剪一个最大的圆,圆的面积是多少?
或
圆的半径扩大2倍,直径就扩大( )倍,周长就扩大( )倍,面积就扩大( )倍。
高等量子力学 课件

进而 对于任意的 fr(q) , 总可以进行如下的幺正变换:
(q) 是任意实函数. 于是上式成为:
21
因而, 只要选择 (q) 使得
就有 即 譬如:
(通过适当选择基矢的相因子)
22
于是, 对于任一依赖于坐标和动量的算符
有
小结 在坐标表象中,坐标算符和动量算符对态矢量的作 用, 对应于以下算符对波函数的作用:
15
形式上, 可以把(k), A(k, k)理解为下标连续改变的矩阵:
16
§1.3.4 坐标表象
1 基矢 以体系的Descartes直角坐标本征态为基矢的
表象称为坐标表象, 或Schrodinger表象.
选取全体Descartes直角坐标
为厄米
算符完备组, 可以证明, 其本征值有连续谱, 于是正交归
反之 i = Ui 上述即为矢量的表象变换.
11
二、算符的表象变换
设算符A在K表象、L表象中分别表示为{Aij}和{A}:
Aij = iAj , A = A.
于是, A = ij iiAjj
即
一化关系和完备性公式分别为:
17
2 态矢量|和坐标算符函数的表示
其中,
是
在 |q 上的本征值.
进而,
18
3 动量算符的表示
利用原理3, 即 Heisenberg 对易关系 有
我们知道 (x) 具有性质:
19
将 与 则知, 若
取如下形式
对比
可使上述等式恒成立. 其中 fr(q)是q的任意实函数.
第一章 Hilbert空间
§1.1 矢量空间
1 定义; 2 正交性和模; 3 基矢; 4 子空间
§1.2 线性算符
《高等数学》电子课件(同济第六版)01第一章 第1节 函数

一、集合
二、函数概念 三、映射 四、函数的特性 五、反函数
六、基本初等函数 七、复合函数 初等函数
1
第一节 映射与函数
一.集合:
1、集合
M {x x具有特定性质}
有限集 如 M {0,1,2, ,9}
无限集 如 M2 {( x, y) x2 y2 1}
2、集合间的关系:
(1) 子 集 ;(2) 集 合 相 等 ;(3) 空 集 ;
2
故定义域为
D
[
0
,
1 2
)
12
3、几个特殊的函数举例
(1) 符号函数
1 当x 0
y
sgn
x
0
当x 0
1 当x 0
定义域 D (, ), 值域 W {1,0,1}
图形:
y
1
o
x
-1
x sgn x x 13
(2) 取整函数: y=[x] [x]表示不超过 x 的最大整数
如 [3] 0, [ 3] 1, [8] 8, [3.8] 4.
x, x 1
f
(x)
min{ x , x2}
x
2
,
1 x 1
三、映射(自学)x, x 1
19
四、函数的特性
1.函数的有界性:
若X D,M 0,x X,有 f (x) M 成立,
则称函数f ( x)在X上有界.否则称无界.
如 y cos x 在( , )上有界, 2 x2
y
1 x2
作业
习题11 P21
4(1)(3)(5)(7)(9),5(2)(3),6,7(1),10,11, 12(1)(3)(5),14(1)(3)(5),16,17,18
群的基本概念ppt课件

S3 置换群表:
S3
E (132) (123) (23) (13) (12)
E E (132) (123) (23) (13) (12)
(132) (132) (123) E (12) (23) (13)
(123) (123) E (132) (13) (12) (23)
Eˆ ECˆ31
Cˆ32
Aˆˆvv((12)) ˆv(3)
同构与同态在构造群表和群的特征标表中作用很大。
2.4 群的直积:直积群
2.4.1 子群 若一个群 H 的群元素皆包含于另一个群 G 之中,就称群 H 是群 G 的子群。 或者说,群 H 的阶为 h,群 G 的阶为 g,且 h ≤ g,H ∈ G。就称群 H 是群 G 的子群。 因为有相同的乘法关系,子群 H 与群 G 有相同的单位元素。
例 1 C6 群包含 C2 子群和 C3 子群。
C 6:
E ˆ C ˆ6 2(C ˆ3 1) C ˆ6 3(C ˆ2 1) C ˆ6 5
C ˆ6 4(C ˆ3 2) C ˆ6 1
C 6 C 3 C 2
例 1 C6 群包含 C2 子群和 C3 子群。
Eˆ
C2v Eˆ Cˆ 2 (Z)
ˆ XZ
ˆYZ
Eˆ Eˆ Cˆ 2 (Z)
ˆ XZ ˆYZ
Cˆ 2 (Z) Cˆ 2 (Z)
Eˆ
ˆYZ
ˆ XZ
ˆ XZ
ˆ XZ
ˆYZ
Eˆ Cˆ 2 (Z)
ˆYZ
ˆYZ
ˆ XZ
Cˆ 2 (Z) Eˆ
例 2-5 S3 置换群
S3 置换群是三个数码 1,2,3 的所有可能的置换,共有 6 个群 元素:
人教版A版高中数学选修3-4直积

定理2.4.3 设G1 和G2分别是m阶及n阶的循环 群。 则G1 G2 是循环群的充要条件是 (m,n) 1。
证 设 G1 a ,G2 b. 假设 G1 G2是循环群。若 (m,n) t 1 。 则由于 orda m, ordb n, 而am/t 和 bn/t的阶都是 t, 因此
(1) G中每个元可惟一地表为hk的形式, 其中 hH, k K;
(2) H 中任意元与 K中任意元可交换, 即: 对任 意h H,k K , 有 hk kh。
证 如果 G 是 H 和K 的内直积, 则G HK 。 所以, G 中每个元 g 都可表为hk的形式, 其中
h H ,k K 。 如果 g hk hk, h H ,k K,
所以G 是交换群。 反之, 如果G 是交换群, 那么对任意的 a1,b1 G, a2,b2 G 有
a1,a2 b1,b2 b1,b2 a1,a2 ,
即 a1b1,a2b2 b1a1,b2a2 .
故 a1b1 b1a1, a2b2 b2a2 , 所以 G1,G2 都是交换群。 (3) 构造映射
9,12),b 也有4种选择,从而共有16个5阶元。 (2) orda 5,ordb 1. 此时 a 仍有4种选择,
而 b 只有一种选择, 故共有4个5阶元。 (3) orda 1,ordb 5 此时 a 只有一种选择,
而 b 有4种选择, 故也有4个5阶元。 于是,Ζ15 Ζ5 共有24个5阶元。
定理2.4.2 设 G1,G2 是群,a 和 b 分别是 G1和 G2中 的有限阶元素。则对于(a,b) G1 G2, 有
ord(a,b) [orda,ordb].
证 设 orda m,ordb n, s [m,n]. 则
矩阵的直积课件

v2
v2
所以 AB 2 A 2 B 2 .此范数称为Frobenious范数,简称F-范数,
v2
v2
v2
常记为 A ,它有很好的性质. F
定理4:1)A Cnn,x Cn,则 Ax A x ;
2
F2
2)U ,V为酉矩阵,有
UA = AV = UAV = A =(tr(AH A))1/2.
F
A C
F F
BF
D
F
2)设 =(a1, ,an )T ,则
a1
a1 B a1 (1, ,s )
B
an
an B an (1, ,s )
a1 1,a1 2
an 1,an 2,
,a1 s
,an s
a1
1,
an
,
a1
s
an
m,n
例3:设 A Cmn ,则
A
v1
=
i,j 1
aij
,
A
v
= max i, j
aij
,以及
A
vp
m,n =
i,j1
aij
1/ p
p
( p 1)均是A的范数.
类似的前面的讨论,我们有如下定理:
定理3:
1)A Cmn的任一种范数均是A的元素的连续函数;
2)Cmn的任两种范数均是等价的,即对 A ,A ,存在
)
(A
B
2
2
)
(AkBk );
范数有以下性质:
命题:1)x 时,x 是范数为一的向量(单位化);
x 2) -x = x ; 3)x,y V,有 x y x y .
证明:只证3) 我们有 x x-y+y x-y y 和 y y-x+x x-y x , 所以 - x-y x - y x-y ,也就是
矢量空间的直和与直积ppt课件

算符的加法和乘法可根据上述定义得出:
(A L) (B M ) (A B) (L M ) (5.7)
(A L)( ) A L
(A L)(B M ) AB LM
(5.8)
证明:将其左边作用于直和空间中的任一矢量 上,有
(A L()A(BL)M(B)(M)( )(A)L()ABL)BM M
中的全部矢量,都是形如 的矢量。
在 R1 中取一组基矢{i },i 1,2,, n1, ,设这组基矢是算
符 K 的本征矢量( K 表象);在 R2 中取 P 表象,其基矢为
{ m },m 1,2,, n2 , 那么直和空间中的任意矢量 都可
以写成下列的形式:
i i m m
最后讨论一下子空间中的直和。若 R1 和 R2 是大空间的两个子空间, 则只有当 R1 和 R2 除零矢量 O 外不含公共矢量时,才可以谈论二者的直 和。这是因为大空间中的加法适用于所有矢量,从 R1 和 R2 中各取一个矢
量构成的双矢量 与二者之和 是等价的,前面公式中矢量
的直和号 可以径直改写为加号。直和空间不只包含 R1 和 R2 中的所有矢 量,还包含更多的矢量。例如在三维物理空间中,若 R1 是 xy 平面上的所 有矢量,R2 是沿 z 轴的矢量,则 R1 R2 包含这个三维空间中的全部矢量。 由于算符在整个大空间中都有定义,所以一切算符在 R1 和 R2 中是通用的, 这时没有算符的直和这一概念,(5.6)式和(5.14)式都不存在。
功了一个新的矢量空间 R ,我们说空间 R 是 R1 和 R2 的直和空间,
表为
R R1 R2
(5.5)
现在,用 R1 中的算符 A,B, 和 R2 中的算符 L,M,
去构造直和空间中的算符 A L ,称为 A,L 两算符的直和,其
近世代数群的概念课件

反身性
任何元素与自己相乘的结果仍为该元素本身。
可交换性
对于任意$a, b$在群中,有$a cdot b = b cdot a$。
可结合性
对于任意$a, b, c$在群中,有$(a cdot b) cdot c = a cdot (b cdot c)$。
子群与商群
子群
一个子群是一个集合在某个二元运算 下构成一个群,且该子集是原群的非 空子集。
05
有限群的结构
有限群的分 类
阿贝尔群和非阿贝尔群
01
根据群中元素的乘法是否满足交换律,可以将有限群分为阿贝
尔群和非阿贝尔群。
循环群和非循环群
02
根据群中是否存在循环子群,可以将有限群分为循环群和非循
环群。
素数阶群和非素数阶群
03
根据群的阶是否为素数,可以将有限群分为素数阶群和非素数
阶群。
有限群的Sylow定理
近世代数群的概念
目 录
• 群的定义与性质 • 群的表示与同态 • 循环群与交换群 • 群的扩张与直积 • 有限群的结构 • 群的应用
contents
01
群的定义与性质
群的定 义
群的定义
一个群是由一个集合和一个 在其上的二元运算所组成, 满足结合律、存在单位元、 存在逆元的代数系统。
结合律
群中的二元运算满足结合律, 即对于任意$a, b, c$在群中, 有$(a cdot b) cdot c = a cdot (b cdot c)$。
单位元
群中存在一个元素$e$,使 得对于任意$a$在群中,有 $e cdot a = a cdot e = a$。
逆元
对于任意$a$在群中,存在 一个元素$b$,使得$a cdot b = b cdot a = e$,其中 $e$是单位元。
吉林大学微积分(高等数学) PPT课件

AC A {x x 0 或 x 1 }.
9
二、集合的基本运算
1. 集合的并、交、差
设 A、B 是两个集合,由所有属于A 或者属 于B 的元素组成的集合, 称为A 与 B 的并集(简称 并), 记作 A B,
即 A B {x x A 或 x B};
[a,b] {x a x b}.
oa
b
x
a 和 b 称为闭区间[a, b]的端点, a [a, b], b [a, b].
16
类似地可定义半开区间:
[a,b) { x a x b},(a,b] { x a x b}. 有限区间 [a, b]、(a, b)、(a, b]、[a, b).
a
a
a
点 a 叫做这个邻域的中心,
叫做这个邻域的半径.
x
19
去心邻域的定义:
点 a 的 邻域去掉中心a 后, 称为a 的去心
o
邻域, 记作U (a, ),即
o
U(a, ) { x 0 x a }.
开区间(a ,a) 称为a 的左 邻域, 开区间 (a, a ) 称为a 的右 邻域.
(,) {x x R} R
ob x
18
4.邻域的定义
设 是任一正数, 则开区间(a ,a ) 是 a 的一个邻域, 称为点a 的 邻域, 记作U(a, ). U(a, ) {x x a } {x a x a }.
22
按 照 定 义 , 如 果 数 集E有 界 , 则 存 在 常 数l与L(l L), 使 得 对 一 切x E, 都 有
第8讲矩阵的直积及其应用

第8讲矩阵的直积及其应用内容:1.矩阵直积的定义与性质2.矩阵直积在解矩阵方程中的应用矩阵直积(Kronecker 积)在矩阵论及系统控制等工程 研究领域有十分重要的应用.运用矩阵直积运算,能够将线 性矩阵方程转化为线性代数方程组.§ 1矩阵直积的定义与性质 1.1矩阵直积定义1.1 设A=(a j )・c mn , Bwc pq ,称如下的分块积,张量积),记为A ® B . A ®B 是一个m"个块的分块矩阵, 简写为 A 二 B =(a ij B) C mp nq .显然A _ B 与Bi A 为同阶矩阵,但一般 A : B = B : A ,即矩例1.1 设 A t ;], —Jxy T 二X : y T ,称xy T 为向量x 与y 的外积.#1 -1 0 0、*1 0-1 0B =,A =2 0 1T 」 7<0 1 0T 」右 x = (X 1,X 2,…,X n )T , y = (%”2,…,y n )T • C n , 则a n Ba 12B … a 1n B矩阵B =a 21B I-a 22B … a 2n B al a m1Ba m2B …amnB为A 与B 的直积(Krionecker阵的直积不满足交换律对单位矩阵, 有 E m : E n 二 E n : E mmn ・定义1.21.2 矩阵直积的性质定理1.1 矩阵的直积具有如下基本性质:(1)k(A :B) =(kA) :B = A :(kB);(2)(A:B):C=A:(B:C);(3) A :工(B C) = A:." B A:.“ C , (B C ):." A = B :.“ A C :.“ A ;(4)(A :B)^A T:B T;(5)(A :B)H= A H:B H;(6)若A C m n B C p q,C • C n s,D C q t,则(A :B)(C :D) =(AC) :(BD),若 B 二E g , C 二E n,贝y (A :E g)(E n :D) = A _ D ;(7)若A , B均可逆,则A _ B可逆,且(A: B)"1"':B J;(8)若A和B都是对角矩阵、上(下)三角矩阵、实对称矩阵、Hermite矩阵、正交矩阵、酉矩阵,则A二B也分别是这种类型的矩阵.l定义 1.3二元复系数多项式为 f (x, y)二為cx y j,若矩阵,j=0A C m m,BC n n,则mn阶矩阵f(A,B) l八 C j A i : B j,其中A^ E m , i,j £B— E n .定理1.2l设 f (x, y) = V C ij X i y j,i,j=0lf(A,B)八• C j A,:B j, A m m 的i, j=0特征值为‘1,‘2,…,'m , B nn的特征值为」1匕,…,J,则f (代B)的全体特征值为fU j),(i =1,2/ ,m, j =1,2/ ,n).证明由Schur定理知存在酉矩阵P,Q使得% *、佔*、P H AP = '-2+=A , QH AQ =+=B1 ,I '-m丿其中A , B i为上三角矩阵,由定理 1.1知,P:Q为酉矩阵,A : B i j为上三角矩阵,贝Ul(P . Q)」f(A, B)(P _ Q)=為q(p H _ Q H)(A i - B j)(P : Q)i,j=0l l二 ' C j(P H A i P^ (Q H B j Q)二 ' C j A;:B?二f(A,BJi,j =0 i,j=0也是上三角矩阵.且f (代B)与f(A;,B i)有相同的特征值.则f(A,,B;)的对角元即为f (A,B)的全部特征值.因为勺 1 B1j* ' 个k出* \A1@ =爲B j+,,-k B1 =< 几j 2 i A j< 人kh因此,f(A;,B i)的对角元为f('「j),(i =12…,m, j =1,2,…,n).推论1.1 设A m渐的特征值为几入2,…,g , B n濒的特征值为•1匕,…C,则(1 ) A:B 的特征值为v l j , (i =1,2,…,m, j =1,2,…,n);(2 ) A:E n E m:B的mn个特征值为「和,i=1,2,…,m , j =12 ,n ;(3)det(A : B) =(det A))n (det(B))m;(4)tr(A : B) =(trA)(trB).定理1.3 设 A C m n,B C p q,贝》rank(A : B) =rank(A) rank(B).证明记rank(A)=「A , rank(B)=「B,有相应阶数的可逆矩阵PQS,T 使得PAQ=£A :L A I'SB T J] :1=B I , 1 0 0 1 0 0贝U A: B =(P J A I Q J^(S^B I T」)=(P「S」)(A I:B I)(Q‘:T‘),由S」,Q「T 1可逆,则rank(A : B)=rank(A : BJ = r A r B二rank (A) rank(B).§ 2矩阵直积在解矩阵方程中的应用2.1 矩阵的拉直定义2/ 设 A =®)乏C m妙,码=(%®,…&)丁, (i =1,2,…,n),令vec(A)=以;,称vec(A)为矩阵A的列拉直.矩阵A也可以按行拉芒n丿直为行向量,记作rvec(A),有rvec( A) = (vec(A T ))T, vec(A T) = (rvec(A))T.定理 2.1 设A c m n,B• c n P,C • C p q,贝yvec(ABC) =(C T _ A)vec(B).证明记B^bb, ,b p),C=(cpC2, ,C q),则广AB GAB C2vec(ABC) = (ABc「AB C2,…,ABc q)=lABC q而AB G = 5人6 c2i Ab2飞pi Ab p = (5 A,c2i A, ,c pi A)vec(B),c11A c21A …c p1A'_pz. c|2 A C22A c p2 A T故vec(ABC) = :::: vec(B) = (C T竖A)vec(B).fjqAGqA C pq A 』 推论 2.1 设 A E C m >m ,B E C n >n ,X E C 吶,贝U(1) vec(AX) =(En : A)vec(X); (2) vec(XB) =(B] E m )vec(X);(3)vec(AX XB)=(E n : A 〜丁 : E m )vec(X).2.2线性矩阵方程在系统控制等工程领域,经常遇到矩阵方程( Lyapunov 型方程)AX XB 二F 的求解问题,其中A C m m ,C nn ,F • C m n 为已知常数矩阵,x c mn 为未知矩阵.利用矩阵的直积和拉 直,可以给出线性矩阵方程的可解性及解法一般的线性矩阵方程可表示为A .XB 1 • A 2XB 2• A p XB p 二C ,其中A ・C mm ,B 「C nn (i =12 ,P ),C C mn 为已知常数矩阵,X C mn 未知矩阵.定理2.2 线性矩阵方程 MBr A 2XB 2A p XB p 二c 有解的充分必要条件是 rank(A) = rank(A :b),其中 A -、B 「: A ,b = vec(C),imA C mm ,B 「C nn (i =1,2' ,p),^ C m n 为已知常数矩阵,X- C mn 未知 矩阵.pp证明 7 AXB j =C 有解,=vecL A XB j )=vec(C)有解i =1i =1pp='、vec (AXBj =vec(C)有解,=' (Bj : AJvec(X) =vec(C)有解i =1i dau rank (A) = rank (A b)定理2.3 设A mm 的特征值为■1/2/ ,'m ,B n n 的特征值为 人廿…,叫,则矩阵方程 AX • XB 二F 有唯一解的充要条件是i」j =0 , (i =1,2,…,m, j =1,2,…,n),其中 A C m m, B C n n, F • C m n 为已知常数矩阵,X c mn为未矩阵.证明AX X^F 有唯一解,二vec(AX • XB)二vec(F)有唯一解二(E「A • Bj E m)vec(X)二vec(F)有唯一解= E^ A B^ Em的特征值不为零二i W =0 (i =1,2, ,m, j =1,2/ ,n)推论2.1 设A^xm的特征值为九」2,…丄m,B n述的特征值为•1,廿…,叫,则矩阵方程AX XB =0有非零解的充分必要条件是存在i 与j,使入+u j =0,(1 兰i 兰m,1 兰j 兰n).推论2.2 设A^C叹,则矩阵方程AX+XA—F有唯一解的充分必要条件是'S时必有• X /■ (A),其中-(A)为A的谱,—为的共轭复数•定理2.4 设A mm的特征值为■1,'2/' ,-m , B n n的特征值为l,…,^n ,则矩阵方程V A'XB^ F有唯一解的充分必要条件是i m1 • Jj •…(C。
群论及应用ppt课件

xAB cii
aij b ji
i
i
j
xBA d jj
b ji aij
b ji aij
aij b ji xAB
j
ji
i
j
i
j
3、共轭矩阵特征标相同
B X 1 AX
xB bii
X
a 1
ij
jk
X
ki
i
i jk
X
ki
X
a 1
ij
jk
jk i
kj a jk a jj xA
(5)所有群都有一个全对称表示
(6) xi2 (R) 4 xi2 (R) 1 R
(7)正交性: xi (R)x j (R) 0
R
x(R) 1
(8)特征标表
C 2V
E
A1
1
A2
1
B1
1
B2
1
C2
1 V
2 V
1
1
1
1
-1
-1
-1
1
-1
-1
-1
1
熊夫利符号 对称操作 A,B 一维 E 二维 T 三维 g, u 中心对称与反对称
还是(x,y,z),设P’点在OXYZ坐标系的坐标为(x’,y’,z’),则: OP' e' r er '
因为
e ' eD(R)
OP' eD(R)r er'
r ' D(R)r
(3)
比较(3)和(2)式, 将物体固定变换基矢与将基矢固定使物体 作相反方向变动时,物体上各点的坐标变换情况是一样的。
R
h lil j
群的直积PPT课件

由于 (e,a)(e,a)=(e,e),
(a,e)(a,e)=(e,e),
(a,a)(a,a)=(e,e),
故G×G与Klein四元群同构, G×G K4 。 第2页/共13页
2.4.2 群的直积的性质 (Property of Direct Product of Group)
G G1×G2×…×Gn。 注:推论中的两个条件
(1) G1,G2,…,Gn是G的不变子群; (2) G的每一元均可唯一地表示
G1, G2,…,Gn 的元的积,等价于以下三个条件:
(1)
(2)
G
Gi
=
Gn1GG2j…
G{en}
j 1
ji
(3) ai∈Gi,aj∈Gj,i≠j,有aiaj=ajai
则G A×B.
第4页/共13页
证明:由(2)可将G表示为 G = { ab | a∈A,b∈B},
而 A×B= {(a, b) | a∈A,b∈B} 作映射 f: G→A×B, ab→(a,b)
∵a1b1=a2b2 a1-1a2=b1b2-1∈A∩B a1-1a2=b1b2-1={e} a1=a2,b1=b2, ∴ f 是映射且为单射,f 也是满射。
注. 两个投影 fi,fj 称为正交的,若 fi fj =0,
f1,…,fn 称为正交投影组,若i≠j 有 fi fj =0
定义:群G叫做可分解的,若存在真正规子群G1, G2,使G=G1×G2,否则称G是不可分解的。
定理1 群G可分解 存在投影 f ≠0,ε (ε为恒等映射)
定理2. 若群G≠{e}满足正规子群的降链条件,则G 存在不等于{e}的正规第子10页群/共H13页1,…Hr,使
1.5群的直积同构同态
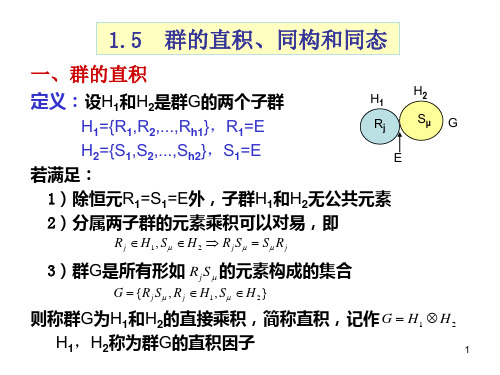
一、群的直积
定义: 是群G的两个子群 定义:设H1和H2是群 的两个子群
H1 H2 Sµ G Rj H1={R1,R2,...,Rh1},R1=E H2={S1,S2,...,Sh2},S1=E E 若满足: 若满足: 除恒元R 1)除恒元 1=S1=E外,子群 1和H2无公共元素 外 子群H 2)分属两子群的元素乘积可以对易,即 分属两子群的元素乘积可以对易,
而集合G'中任一元素 至少对应G中的一个元素R 集合 中任一元素R'至少对应 中的一个元素 中任一元素 至少对应
且这种一一对应或一多对应的关系对元素乘积保持不变 且这种一一对应或一多对应的关系对元素乘积保持不变 一一对应 ●则集合 构成群,且与已知群 同构或同态 则集合G'构成群 且与已知群G同构 构成群, 同构或 证明定理( 证明定理(二) 思路: 思路: 该定理的证明只需证G'构成群 构成群, 该定理的证明只需证 构成群,然后由定理给出的条件就可知 道它与群G同构或同态。证明方法仍利用群G元素对应集合 道它与群 同构或同态。证明方法仍利用群 元素对应集合G' 同构或同态 元素对应集合 10 中元素的唯一性。 中元素的唯一性。
9
定理( 3. 定理(二)
●设群G是一已知群, 是一已知群, 是一已知群
集合G'是一个定义了乘积规则 集合 是一个定义了乘积规则 又对乘积规则封闭的集合 ●若
中任一元素R都按某种规则唯一地对应集合G'中的一个确定元素R', 群G中任一元素 都按某种规则唯一地对应集合 中的一个确定元素 , 中任一元素 都按某种规则唯一地对应集合 中的一个确定元素
2
注 意
1)两个群的恒元与恒元对应 2)同构无方向性 G′ ≈ G ⇔ G ≈ G′
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a1
1,
an
,
a1
s
an
a1
1,
an
a1
,
s
an
( 1 ,, s) .
直积的基本性质: 1)k(AB)=(kA)B=A(kB),k为常数; 2)分配律(A+B)CACBC,C(A+B)CACB; 3)结合律(AB)CA(BC); 4)吸收律(AB)(CD)(AC)(BD),AC与BD有意义.
证明:只证3) 我们有 x x-y+y x-y y 和 y y-x+x x-y x , 所以 - x-y x - y x-y ,也就是
x y xy
n
例 1: x=(1,2, ,n)TCn,定 义x1 i, xm axi,
i1
1in
A k) ( B 1 B 2
B) ; k
2 ) ( A 1 A 2A k)(B 1 B 2 B k) ( A 1 B 1) (A 2 B 2) (A kB k) ;
范数有以下性质:
命题: 1)x时,x 是范数为一的向量(单位化) ;
x 2) -x = x ; 3)x,yV,有x y xy .
a1
a n
a 1 B a1 (1,
B
a n B an (1,
,s )
, s )
a11,a12
an 1,an 2,
,a1s
,an s
直积
直积的定义与性质
定义:设A=(aij )mn,B=(bij )pq,称分块矩阵
a11B a12B a21B a22B am1B am2B
a12B a2nB
amnBmpnq
为A与B的直积(张量积或Kronecker积).记为AB=(aijB)mpnq.
例 如 : A=a c d b,B=2 3, 则
推 论 : 1)(A B) k=Ak Bk,k=1,2,; 2)(A In)(Im B)(Im B)(A In)A B.(乘 法 可 交 换 )
性 质 4 可 推 广 到 一 般 情 形 :
1 ) ( A 1 B 1 ) ( A 2 B 2) ( A k B k) ( A 1 A 2
2
2
2
2
x22x y y2 x y 2
2
22
2
2
2
所 以x+y x y .
2
2
2
n
1
例 2: 设 1p , x=(1,2, ,n)T C n,定 义 xp( i p)p,
i 1
则 x 是 C n中 的 范 数 .称 为 p-范 数 . p
p = 1 时 , 为 1 - 范 数 ; p = 2 时 , 为 2 - 范 数 ; 令 p , 得 -范 数 . 这 三 种 范 数 为 常 见 范 数 .
定义2:设V是有限维线性空间, x,x是V中任意两种 范数,若存在正数k1及k2,使得xV, 都有:
k1 x x k2 x, 称x与x是等价的.
定 理 1 : 有 限 维 线 性 空 间 中 的 任 何 两 种 范 数 等 价 .
证 明 : 设 V 是 n 维 线 性 空 间 , e 1 , ,e n 是 V 的 一 组 基 , 则 x V ,
定 理 1: 1)两 个 上 三 角 矩 阵 的 直 积 是 上 三 角 阵 ; 2)两 个 对 角 矩 阵 的 直 积 是 对 角 阵 ; 3)InImImInImn.
直 积 具 有 以 下 运 算 规 律 :
命题1:1)AC DBF=AC FF DB FF;
n
1
x ( 2
i 2)2=
xHx
(x,x),即x 是 由 酉 空 间 Cn 2
i1
中 内 积 诱 导 的 范 数 ,故 由 Cauchy不 定 式 得
x+y2 (xy,xy)(x,x)(x,y)(y,x)(y,y) 2
x22Re(x,y) y2 x22(x,y) y2
n
1
x ( 2
i 2)2,则x1, x及x2均 是 Cn中 的 范 数 .
i1
证 明 : 不 难 验 证 x, x均 是 范 数 , 对 于 x, 正 定 性 和
1
2
齐 次 性 显 然 满 足 . 下 证 满 足 三 角 不 定 式 :
设 x=(1,2, ,n)T,y=(1,2, ,n)TCn.注 意 到
2)设为列向量,且B=(1, ,s),则
B=(1, ,s);
3)设A=(1,
,t )nt,B=(1,
,s
)则 ps
AB=(1 1, ,1 s, ,t 1, ,t s)npts.
注 : 由 1 ) 2 ) 即 可 得 3 ) , 下 面 只 证 1 ) 和 2 ) .
证 明 : 1)由 定 义 得
(aij) (cij)
((d biijj)) F ((a ciijj)) F F((d biijj)) F F A C F FD B F F
2 ) 设 = (a 1 ,, a n )T ,则
2a 2b
2a 2b
AB=a cB B b dB B=3 2 3a cc
2 3 3d b d,BA=3 2A A=3 2 3a cc
2d. 3b 3d
A B ,B A 的 阶 数 相 同 , 但 一 般 A B B A . 直 积 不 满 足 交 换 律 . 由 直 积 的 定 义 容 易 推 出 以 下 定 理 :
