四年级奥数第一讲一笔画问题
小学奥数知识讲解-一笔画问题

第一讲一笔画问题小朋友们,你们能把下面的图形一笔画出来吗?如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画。
那么是不是所有的图形都能一笔画成呢?这一讲我们就一起来学习一笔画的规律。
典型例题例【 1】下面这些图形,哪个能一笔画?哪个不能一笔画?( 1)(2)(3)(4)分析图(1)一笔画出,可以从图中任意一点开始画该图,画到同一点结束。
经过尝试后,可以发现图(2)不能一笔画出。
图(3)不是连通的,显然也不能一笔画出。
图(4)也可以一笔画出,且从任何一点出发都可以。
通过观察,我们可以发现一个几何图形中和一点相连通的线的条数不同。
由一点发出有偶数条线,那么这个点叫做偶点。
相应的,由一点出发有奇数条数,则这个点叫做奇点。
再看图( 1)、(4),其中每一点都是偶点,都可以一笔画,且可以从任意一点画起。
而图(2)有 4 个奇点, 2 个偶点,不能一笔画成。
这样我们发现,一个图形能否一笔画和这个图形奇点,偶点的个数有某种联系,到底存在什么样的关系呢,我们再看一个例题。
例【 2】下面各图能否一笔画成?(1)(2)(3)分析图(1)从任意一点出都可以一笔画成,因为它的每一个点都是与两条线相连的偶点。
关于图(2),经过反复试验,也可找到画法:由 A B C AD C。
图中 B、D 为偶点, A、C 为奇点,即图中有两个奇点,两个偶点。
要想一笔画,需从奇点出发,回到奇点。
经过尝试,图( 3)无法一笔画成,而图中有 4 个奇点, 5 个偶点。
解图( 1)、(2)可以一笔画。
这样我们可以发现能否一笔画和奇点、偶点的数目有着紧密的关系。
如果图形只有偶点,可以以任意一点为起点,一笔画出。
如果只有两个奇点,也可以一笔画出,但必须从奇点出发,由另一点结束。
如果图形的奇点个数超过两个,则图形不能一笔画出。
例【 3】下面的图形,哪些能一笔画出?哪些不能一笔画出?分析图( 1)有两个奇点,两个偶点,可以一笔画,须由 A 开始或由 B 开始到 B 结束或到 A 结束。
四年级奥数第一讲-一笔画问题

第十二讲一笔画问题那么,什么叫一笔画1什么样的图可以一笔画出■?欧竝又是如何彻底证明尢桥冋题的不可能性呢?下面,我们就来介貂这一方面的简单知谋数学书我们把由有限个点和连接这些点的线(线段或弧)所组成的图形叫做圈(如圈3 )S圈中的点叫做曙的结点!连按两結点的线叫做圏的边. 如图(b)中,有三个结点:氐F. G,四条边:线段臥FG以及连接臥F的两段呱•从图Q、0>)中可以看岀,任意两点之间都有一条通路〔即可臥从其中一点出发,沿着图的边走到另一点左WJI的通路为或A-Df I…”这样的图,我扪称为连通图;而下图中〔亡)的一些^点之间却不存在通略(如M与N),像这样的图就不是连逋图将所谓图的一笔ML指的就是;从图的一点出发,笔不离纟氐遍历每条边恰好一次,即每条边都只画一次,不推重复■从上图中容曷看出;能一笔画出的图首先必须是连逋图-但是否所有的连逋图都可以一笔画出呢?下面,我们就来探求醉抉这个问题的方法。
为了叙述的方使’我们把与奇数条边相连的结点叫做奇吊把与偶数条边相连的点称为播点■如I上鹵申的八个给点全是寄■点,上扇(b)申卫、F衣奇為G为偶点。
容易知道,上图00可以一笔画出,即从奇点E出发,沿箭头所指方向. 经过匚G> E.最后到达奇点心同理,从奇点F出发也可以一笔画也最后到达奇点氐而从偶点G岀发,却不能一笔画出•这是为什么呢?G事实上,这并不杲偶然现象•假定某个图可以一笔画成,且它的结点X既不是起点,也不是终点,而是中何点,那么X—定是一个偶点.这杲因为无论何时通过一条边到达X,由于不能重复,必须从另一董边离开X.这样与X连纟吉的边 -定成对出现,所以X必为偶点,也就是说:奇点在」笔画中只能作为起或终点•由此可臥看出,在一个可以一笔画出的图中,奇点的个数最多只有两个。
在七桥问题的图中有四个奇点,因此,欧拉断言’这个图无法一笔画岀,也即游人不可能不重复地1次走遍七座桥.更逬1步地,欧拉在解决七桥问题的同时彻底地解决了一笔画的问题,给出了下面的欧拉定理;①凡是由偶点组成的连通图,一定可以一笔画成;画时可以任一偶点为起点,最后一定能以这个点为终点画完此图。
小学奥数一笔画课件

单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。您的内容已经简明扼要,字字珠玑,但信息却千丝万缕、错综复杂,需要用更多的文字来表述;但请您尽可能提炼思想的精髓,否则容易造成观者的阅读压力,适得其反。正如我们都希望改变世界,希望给别人带去光明,但更多时候我们只需要播下一颗种子,自然有微风吹拂,雨露滋养。恰如其分地表达观点,往往事半功倍。当您的内容到达这个限度时,或许已经不纯粹作用于演示,极大可能运用于阅读领域;无论是传播观点、知识分享还是汇报工作,内容的详尽固然重要,但请一定注意信息框架的清晰,这样才能使内容层次分明,页面简洁易读。如果您的内容确实非常重要又难以精简,也请使用分段处理,对内容进行简单的梳理和提炼,这样会使逻辑框架相对清晰。为了能让您有更直观的字数感受,并进一步方便使用,我们设置了文本的最大限度,当您输入的文字到这里时,已濒临页面容纳内容的上限,若还有更多内容,请酌情缩小字号,但我们不建议您的文本字号小于14磅,请您务必注意。单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。您的内容已经简明扼要,字字珠玑,但信息却千丝万缕、错综复杂,需要用更多的文字来表述;但请您尽可能提炼思想的精髓,否则容易造成观者的阅读压力,适得其反。正如我们都希望改变世界,希望给别人带去光明,但更多时候我们只需要播下一颗种子,自然有微风吹拂,雨露滋养。恰如其分地表达观点,往往事半功倍。当您的内容到达这个限度时,或许已经不纯粹作用于演示,极大可能运用于阅读领域;无论是传播观点、知识分享还是汇报工作,内容的详尽固然重要,但请一定注意信息框架的清晰,这样才能使内容层次分明,页面简洁易读。如果您的内容确实非常重要又难以精简,也请使用分段处理,对内容进行简单的梳理和提炼,这样会使逻辑框架相对清晰。为了能让您有更直观的字数感受,并进一步方便使用,我们设置了文本的最大限度,当您输入的文字到这里时,已濒临页面容纳内容的上限,若还有更多内容,请酌情缩小字号,但我们不建议您的文本字号小于14磅,请您务必注意。单击此处添加正文,
一笔画(奥数)

一笔画【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
2 下列图形中各有几个单数点?能一笔画成吗?3 判断下面图形能不能一笔画成?如果能,应该怎样画?A4下面图形能不能一笔画成?这什么?5 如图是一个大型花池中小路的平面图,你能否不重复地一次走完所有的小路?进出口应设在什么地方?6 将下图加上最少的线改成一笔画的图形。
7.将下图去掉最少的线改成一笔画图形。
8.下图中的线段代表小路,请小朋友想一想,能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁?该怎么爬?9.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?10.下图是一个公园的平面图,应怎样走才能使游客走通每条路而不重复,设计一条最佳路线。
11 一个公园的平面图如下,请你设计好入口、出口,并给出一条浏览路线,要求走遍每一条路且不重复。
12.如图,是一个公园的平面图,请你设计好入口、出口,并给出一种游玩路线,要求走遍每一条路且不重复。
13.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?14.黑色的鱼与白色的鱼所能游动的河道如下图所示。
黑色的鱼在A点位置,白色的鱼在B点位置。
哪条鱼能不重复地游遍所有的河道?15.能用一根铁丝弯成下面的图形吗?16.一个邮递员投递信件要走的街道如图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?17.一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?18.你能用一笔画成4条线段把下图的9个点都连起来吗?19.下图能否一笔画成?如果能,应怎样画?20.如图,在一个六面体的顶点A和B处各有一只蜗牛,它们比赛看谁能不重复地爬遍每一棱线到达C点。
小学奥数模块教程一笔画问题
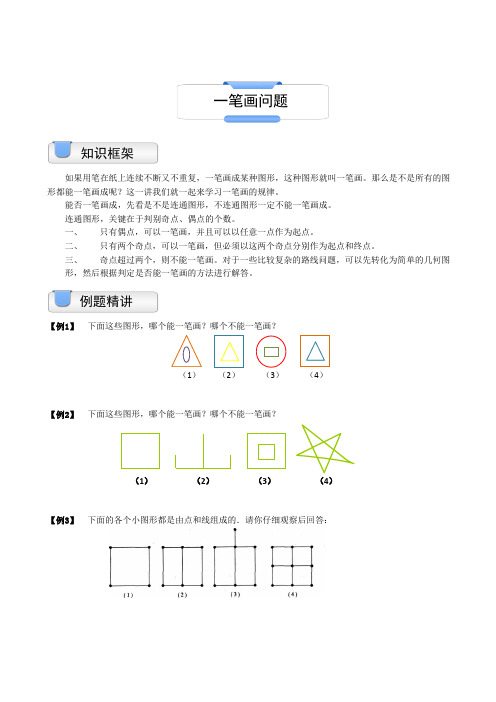
如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画。
那么是不是所有的图形都能一笔画成呢?这一讲我们就一起来学习一笔画的规律。
能否一笔画成,先看是不是连通图形,不连通图形一定不能一笔画成。
连通图形,关键在于判别奇点、偶点的个数。
一、只有偶点,可以一笔画,并且可以以任意一点作为起点。
二、只有两个奇点,可以一笔画,但必须以这两个奇点分别作为起点和终点。
三、奇点超过两个,则不能一笔画。
对于一些比较复杂的路线问题,可以先转化为简单的几何图形,然后根据判定是否能一笔画的方法进行解答。
【例1】下面这些图形,哪个能一笔画?哪个不能一笔画?(1)(2)(3)(4)【例2】下面这些图形,哪个能一笔画?哪个不能一笔画?(1)(2)(3)(4)【例3】下面的各个小图形都是由点和线组成的.请你仔细观察后回答:例题精讲知识框架一笔画问题发现不同①与一条线相连的有哪些点?②与二条线相连的有哪些点?③与三条线相连的有哪些点?④与四条线或四条以上的线相连的有哪些点?【例4】下面各图能否一笔画成?(1)(2)(3)【例5】下面这几个字都能一笔写出来吗?【例6】下面这几个字母都能一笔写出来吗?【例7】下面的图形,哪些能一笔画出?哪些不能一笔画出?【例8】下图中,至少要画几笔才能画成?【随练1】德国有个城市叫哥尼斯堡.城中有条河,河中有个岛,河上架有七座桥,这些桥把陆地和小岛连接起来,这样就给人们提供了一个游玩的好去处(见下图).俗话说,“人是万物之灵”,他们就是在游玩时候想出了这样一个问题:如果在陆地上可以随便走,而对每座桥只许通过一次,那么一个人要连续地走完这七座桥怎么个走法?好动脑筋的小朋友请先不要接着往下读,你也试一试,走一走.【随练2】在我国著名数学家陈景润写的《数学趣谈》一书中,有下面的这样一道题,大意是说:在法国的首都巴黎有一条河,河中有两个小岛,那里的人们建了15座桥把两个小岛和河岸连接起来,如下图所示,请你说一说,从任一岸出发,一次连续地通过所有的桥到达另一岸,可能吗?(每座桥只能走一次)课堂检测AB CD【作业1】 下面的图形都是由点和线组成的.请你仔细观察后回答:①与一条线相连的有哪些点?②与三条线相连的有哪些点?③与四条线或四条以上的线相连的有哪些点?【作业2】 下面各图能否一笔画成?(1)(2) (3) (4)【作业3】 下面这几个字母都能一笔写出来吗?【作业4】 下面这几个字都能一笔写出来吗?【作业5】 下图中,至少要画几笔才能画成?PONMLKJIHGFEDCBA家庭作业。
一笔画(奥数)

一
笔画
【知识要点】 1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】
1 判断下面图形中哪些点是单数点哪些点是双数点。
2
3
45
6
78
910 11 12重复。
13.如图, 14不重复地游遍所有的河道? 1516条街道,你能帮帮他吗? 17 18.你能用一笔画成41920C 21 A
22.下图是某新村小区主干道平面图,甲、乙两人分别从A、B出发,以相同的速度走遍所有的主干道,最后到达C,问谁能先到达C?
23.下面是某游艺宫的平面图,它由五个厅组成,每两厅之间有门相通,整个游艺宫还有一个进口和一个
23
24
25
26
S
27
28。
奥数只是讲解第一讲一笔画问题

word 文档仅供参照第一讲一笔划问题小朋友们 , 你们能把下边的图形一笔划出来吗?假如用笔在纸上连续不停又不重复, 一笔划成某种图形, 这类图形就叫一笔划。
那么能否是全部的图形都能一笔划成呢?这一讲我们就一同来学习一笔划的规律。
典型例题例【 1】下边这些图形,哪个能一笔划?哪个不可以一笔划?〔1〕〔2〕〔3〕〔4〕剖析图〔1〕一笔划出,能够从图中随意一点开始画该图, 画到同一点结束。
经过试试后 , 能够发现图〔 2〕不可以一笔划出。
图〔 3〕不是连通的 , 明显也不可以一笔划出。
图〔4〕也能够一笔画出 , 且从任何一点出发都能够。
经过察看 , 我们能够发现一个几何图形中和一点相连通的线的条数不一样。
由一点发出有偶数条线 , 那么这个点叫做偶点。
相应的 , 由一点出发有奇数条数 , 那么这个点叫做奇点。
再看图〔 1〕、〔4〕, 此中每一点都是偶点, 都能够一笔划 , 且能够从随意一点画起。
而图〔2〕有 4 个奇点 ,2 个偶点 , 不可以一笔划成。
这样我们发现 , 一个图形可否一笔划和这个图形奇点 , 偶点的个数有某种联系 , 究竟存在什么样的关系呢 , 我们再看一个例题。
例【 2】下边各图可否一笔划成?〔1〕〔2〕〔3〕剖析图〔 1〕从随意一点出都能够一笔划成, 由于它的每一个点都是与两条线相连的偶点。
对于图〔2〕, 经过频频试验 , 也可找到画法:由 A B C AD C 。
图中 B、D为偶点 ,A 、C为奇点 , 即图中有两个奇点 , 两个偶点。
要想一笔划 , 需从奇点出发 , 回到奇点。
经过试试 , 图〔 3〕没法一笔划成 , 而图中有 4 个奇点 ,5 个偶点。
解图〔 1〕、〔2〕能够一笔划。
这样我们能够发现可否一笔划和奇点、偶点的数量有着密切的关系。
假如图形只有偶点 , 能够以随意一点为起点, 一笔划出。
假如只有两个奇点 , 也能够一笔划出 , 但一定从奇点出发 , 由另一点结束。
假如图形的奇点个数超出两个, 那么图形不可以一笔划出。
一笔画问题及解决策略

一笔画问题及解决策略一、问题提出一笔画是一个大问题,为了更好的解决这个问题,我们从生活提出一笔画问题。
我们先看一个公路检查员的问题:他为了检查几个城市之间的若干公路,希望在这些城市和公路组成的公路系统中找出一条路线,使他能不重复地恰好通过每条公路一次,而经过每个城市的次数不限.这就是拓扑学中的数学问题。
二、问题解决(一) 数学化我们把这问题数学化,以点表示城市,以弧表示公路,这样构成的网络图就表示某个简单公路系统。
(二)点线图用点线图表示四个不同的公路系统。
如图所示:(三)一笔画的含义一个图形由一笔构成叫一笔画.对于平面图形的一笔画与多笔画问题,通常的几何方法是无能为力的,因为一个图形能否一笔画,与图形的大小、形状等几何概念都没有关系,而是与图形中线段的数目及连接关系有关,我们可以随意地将图形拉伸、压缩或弯曲,甚至在保持端点不动的前提下,还可以将某些线段“搬家”,只要图形的整体结构不变,能否一笔画的性质也就不会改变.(四)一笔画图形的判别著名的哥尼斯堡七桥问题实质上就是一个一笔画问题。
欧拉最终证明了这个图形是不能一笔画成的,并在关于七桥问题的报告中得到了任一网络图能否一笔画的判别法则。
1。
必要条件一个网络图是由有限个点和有限条曲线组成的平面图形,这些点和线分别称为网络的顶点和弧。
如果从网络的一个顶点出发,一条弧连着一条弧地把所有的弧都画出,且每条弧都只画一次,而经过每个顶点的次数不限,就称该网络能一笔画.当一个网络能一笔画时,只有两种情形:一是开放图形,只有起点和终点的指数为奇数,其余顶点的指数均为偶数;二是封闭图形,所有顶点的指数均为偶数。
我们称指数为奇数的顶点为奇顶点,指数为偶数的顶点为偶顶点,那么当一个网络能一笔画时,奇顶点个数必为0或2,所以,连通且奇顶点的个数是0或2,是一个网络图能一笔画的必要条件。
(1)。
凡是由偶点组成的连通图,一定可以一笔画成.画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
小学奥数—奇妙的一笔画

知识点拨
所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次, 不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢? 下面,我们就来探求解决这个问题的方法.
什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题: (1)能一笔画出的图形必须是连通的图形; (2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题: 我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于 任意的连通图来说,如果有 2n 个奇点(n 为自然数),那么这个图一定可以用 n 笔画成.
【例 17】 下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.
A
E
D
G
H
B
C
F
【例 18】 如图所示,某小区花园的道路为一个长 480 米,宽 200 米的长方形;一个边长为 260 米的菱形和十 字交叉的两条道路组成.一天,王大爷 A 处进入花园,走遍花园的所有道路并从 A 处离开.如果
【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一 次不重复地走遍这七座桥?
【例 21】 一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发, 要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米?
四年级数学竞赛辅导讲义04一笔画.doc

四年级数学竞赛辅导讲义(四)年月日一笔画一笔画是指一笔画成一个图形,是一种有名的数学游戏。
一个图形能不能一笔画成,怎样一笔画成,就是一笔画问题。
一笔画问题在实际生活中是有用的,如设计最短路线(最短邮路、最短运输路线)等,都要用一笔画的解决方法。
“一笔画”问题中最著名的当属“哥尼斯堡七桥问题”:在十八世纪的东普鲁士的哥尼斯堡有一条普莱格尔河流过,河中有两座小岛,河上有7座桥,爱动脑筋的人们提出了一个问题:一个散步者能否一次走遍7座桥,而且每座桥只通过一次,最后仍回到起始地点。
许多人作过尝试始终没有能找到答案,最后瑞士大数学家欧拉解决了这个问题。
这个问题为什么怎么有趣呢?在本课的最后我们一起来看看。
怎样才算一笔画呢?我们规定:1、从图形上的某个点出发,笔不能离开纸;2、每条线都只画一次,不能重复。
按照一笔画的要求,下面三个图形,哪个能一笔画出,哪个不能。
(一)(二)(三)我们会发现,图一、二能够一笔画出,图三无论怎样也不能。
怎样的图形能够一笔画呢?我们要观察图中的点和线,看从每个点出发有几条线。
1、如果从一个点出发的线的总数是偶数(双数),称该点为偶点。
2、如果从一个点出发的线的总数是奇数(单数),称该点为奇点。
从大量实验中,我们得出结论:1、全由偶点组成的图形,一定可以一笔画出,画时从任意一点为起点,最后仍回该点。
(如图一)2、只有两个奇点的图形,一定可以一笔画出,画时必须从其中一个奇点为起点,另一个奇点为终点。
(如图二)A B CD EFGH IA BCD3、超过两个奇点的图形,一定不能一笔画出。
(如图三) 例1、先判断下面的图形能不能一笔画出,然后画一画。
A B C D E [分析]: 图A 、C 所有点都是偶点,能一笔画出。
图B 有4个奇点,不能一笔画出。
图D 、E 各有2个奇点,能一笔画出。
例2、下面是一个公园的平面路线图,要使游客进入公园后,走遍每条路而且不重复,请问出入口分别应设在哪里? [分析]:要使游客走遍每条路而且不重复, 也就要求一笔画出路线图。
四年级奥数第一讲 一笔画问题
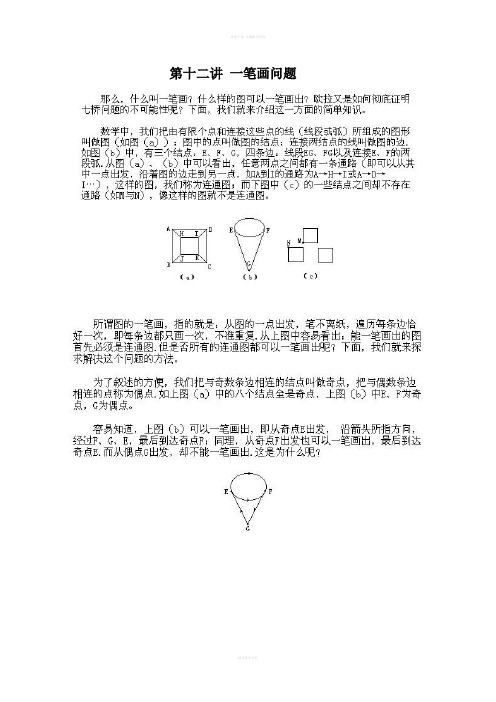
第十二讲一笔画问题例2下图是国际奥委会的会标,你能一笔把它画出来吗?分析与解答一个图能否一笔画出,关键取决于这个图中奇点的个数.通过观察可以发现,上图中所有的结点都是偶点,因此,这个图可以一笔画出.画时可以任一结点作为起点。
例3下图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析与解答本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C。
容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和。
仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C。
例4(1)能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?(2)能否用剪刀一次连续剪下右下图中六个三角形?【解析】:上面两个图形都只有两个奇点(红色交点),都是一笔画图形,但用笔画和用剪刀剪,这两种操作是有区别的。
第一、用笔画,笔要经过图中的每一条线段,用剪刀剪只能剪图形内部线段,四周的边框是不能剪的;第二,用笔画一条经过某个点的直线后,图形还是完整的,用剪刀沿直线经过某个点剪一刀后,这个图形会被剪成两段。
因此在剪的过程中要注意技巧,可以分别准备好这样的两张纸片,在纸片上画出对应的线段,让孩子在剪纸的操作中慢慢体验这一点。
这两个图形都可以按题目要求一次连续剪下。
上面左边图形在剪的时候注意:可以从图形左边奇点开始先向右剪,遇到第一个交点后拐弯向上,再向右下,再向左剪,最后向下到第二个奇点结束。
例5 下图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析与解答这种应用题,表面看起来不易解决,事实上,只要认真分析,就可以发现:我们并不关心展室的大小以及路程的远近,关心的只是能否一次不重复地走遍所有的门,与七桥问题较为类似.因此,仿照七桥问题的解法,我们可以把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A。
小学奥数一笔画课件ppt

为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
怎样走才能不重复不遗漏地逛完整个超市? 为了规范事业单位聘用关系,建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度,保障用人单位和职工的合法权益
能
2个
2个
能
2个
4个
能
0个6个能源自0个 10个能0个
8个
能
0个
9个
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
欧拉:“一笔画图”的规 规律律1:凡能一笔画的图形必须是一个连通图;
规律2:凡能一笔画的图形,与偶点个数无关, 与奇点个数有关,其个数是0或2.
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
“一笔画”是指笔不 离开纸,而且每条线 都只画一次不准重复 而画成的图形。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
交点分为两种
(1)从这点出发的线的数目 是双数的,叫双数点(偶点)。 (2)从这点出发的线的数目 是单数的,叫单数点(奇点)。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
一笔画问题例题加解析

一笔画问题例题加解析一、什么是一笔画问题。
一笔画问题呀,就像是一个超有趣的小谜题呢。
简单来说,就是在一个图形里,能不能一笔就把这个图形画出来,而且笔不能离开纸,也不能重复画已经画过的线。
这就像是在走迷宫,但是这个迷宫是用线条画出来的。
比如说,一个圆形,那肯定能一笔画出来,就顺着圆的边画一圈就好啦,简单得很。
二、一笔画问题的小规则。
这里面可是有小秘密的哦。
有个叫欧拉的超级聪明的人发现了一些规律。
对于一个连通图(就是这个图里的各个部分都是连着的,没有分开的小块),如果这个图里的奇点(就是从这个点出发的线的数量是奇数条的点)个数是0或者2的时候,这个图就能一笔画出来。
要是奇点个数是0呢,就可以从任何一个点开始画,最后还能回到这个点;要是奇点个数是2呢,就得从其中一个奇点开始画,然后到另一个奇点结束。
三、例题来啦。
1. 比如说这个三角形,我们来看看它能不能一笔画出来呢。
三角形的每个顶点,都有两条线连着,那就是说,它的奇点个数是0。
按照我们刚刚说的规则,它肯定能一笔画出来啦。
怎么画呢?就从三角形的一个顶点开始,顺着边画,绕一圈就画好啦,是不是很容易呢?2. 再看这个正方形加上一条对角线的图形。
这个图形的四个顶点本来都是有两条线连着的,但是加上对角线之后呢,对角线的两个端点就变成了奇点,这时候奇点个数是2。
那按照规则,我们从其中一个奇点开始,沿着边画,就能一笔画出来啦。
四、解析例题。
1. 对于三角形那个例子,因为每个顶点都是偶点(从这个点出发的线的数量是偶数条的点),所以我们在画的时候,就可以很顺畅地绕着图形走一圈,不会出现画不下去或者必须重复的情况。
这就像是在一个没有障碍的小路上散步,一路畅通无阻。
2. 在正方形加对角线的例子里,由于有两个奇点,这就像是两个特殊的出入口。
我们从一个奇点这个特殊的入口进去,然后沿着图形的边和线走,最后到达另一个奇点这个出口,就刚好把整个图形一笔画完了。
如果我们不按照这个规则,从别的点开始画,就会发现画到一半就会走不下去,或者必须要重复画某些线了。
一笔画(奥数)教学内容

一笔画(奥数)一笔画【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
2 下列图形中各有几个单数点?能一笔画成吗?3 判断下面图形能不能一笔画成?如果能,应该怎样画?4下面图形能不能一笔画成?这什么?ADEA B CC A B A B C DE F ADCBB C A5 如图是一个大型花池中小路的平面图,你能否不重复地一次走完所有的小路?进出口应设在什么地方?6 将下图加上最少的线改成一笔画的图形。
7.将下图去掉最少的线改成一笔画图形。
8.下图中的线段代表小路,请小朋友想一想,能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁?该怎么爬?9.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?10.下图是一个公园的平面图,应怎样走才能使游客走通每条路而不重复,设计一条最佳路线。
11 一个公园的平面图如下,请你设计好入口、出口,并给出一条浏览路线,要求走遍每一条路且不重复。
12不重复。
A BHCG FE D13.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?14.黑色的鱼与白色的鱼所能游动的河道如下图所示。
黑色的鱼在A 点位置,白色的鱼在B 点位置。
哪条鱼能不重复地游遍所有的河道?15.能用一根铁丝弯成下面的图形吗?16.一个邮递员投递信件要走的街道如图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?17.一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?18.你能用一笔画成4条线段把下图的9个点都连起来吗?19.下图能否一笔画成?如果能,应怎样画?20.如图,在一个六面体的顶点A 和B 处各有一只蜗牛,它们比赛看谁能不重复地爬遍每一棱线到达C点。
四年级数学思维拓展:一笔画问题

【四年级数学思维拓展】趣味入门—神奇的森林王国(一)
------白猫侦探一笔画问题
知道能否一笔画的判断法则,明白0个奇点和2个奇点图形的一笔画区别。
1.简单图形的一笔画。
2.一笔画的规则。
3.0奇点和2奇点一笔画出发点的区别。
例题1:小白猫有天问他爸爸白猫侦探,这个图形能不重复一笔画出来么?白猫侦探一看,这有何难!然后直接一笔画出来了。
大家知道怎么画么?
例题2小白猫又拿出一些形状,这些图形能不重复一笔画出来么?
例题3:白猫侦探要巡视一遍街道,街道平面图如图所示,问白猫侦探能否不重复的巡视完所有街道?
例题4:河马邮递员要给一个村子的每户送信,村庄街道形状如下图,请为河马设计一条路线能够不重复的走完每条路。
例题5:一条河中有两个小岛,一共有7座桥负责交通。
问能否一口气不重复走完所有的桥?
(即是该课程的课后测试)
1、尝试把下图不重复的一笔画出。
2、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
3、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
4、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
5、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
1、略。
2、没有奇点,所以可以一笔画出。
3、有4个奇点,所以不能一笔画出。
4、没有奇点,所以可以一笔画出。
5、有4个奇点,所以不能一笔画出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二讲一笔画问题
例2下图是国际奥委会的会标,你能一笔把它画出来吗?
分析与解答
一个图能否一笔画出,关键取决于这个图中奇点的个数.通过观察可以发现,上图中所有的结点都是偶点,因此,这个图可以一笔画出.画时可以任一结点作为起点。
例3下图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问
两人谁能最先到达C?
分析与解答
本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C。
容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和。
仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C。
例4(1)能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?
(2)能否用剪刀一次连续剪下右下图中六个三角形?
【解析】:
上面两个图形都只有两个奇点(红色交点),都是一笔画图形,但用笔画和用剪刀剪,这两种
操作是有区别的。
第一、用笔画,笔要经过图中的每一条线段,用剪刀剪只能剪图形内部线段,四周的边框是不
能剪的;
第二,用笔画一条经过某个点的直线后,图形还是完整的,用剪刀沿直线经过某个点剪一刀后,这个图形会被剪成两段。
因此在剪的过程中要注意技巧,可以分别准备好这样的两张纸片,在纸片
上画出对应的线段,让孩子在剪纸的操作中慢慢体验这一点。
这两个图形都可以按题目要求一次连续剪下。
上面左边图形在剪的时候注意:可以从图形左边奇点开始先向右剪,遇到第一个交点后拐弯向上,再向右下,再向左剪,最后向下到第二个奇点结束。
例5 下图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?
分析与解答
这种应用题,表面看起来不易解决,事实上,只要认真分析,就可以发现:我们并不关心展室的大小以及路程的远近,关心的只是能否一次不重复地走遍所有的门,与七桥问题较为类似.因此,仿照七桥问题的解法,我们可以把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即
能否从A出发,一笔画完此图,最后再回到A。
上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.
也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.
下面仅给出一种参观路线:
A→E→B→C→E→F→C→D→F→A。
注意:本题中,必须以A分别作为起点和终点.这就要求图中必须没有奇点,否则,若有两个奇点,虽能一笔画出,但与从入口入、出口出(即游人的出发和终止点都在展厅外)有矛盾,其他有多个奇点的情况则根本不可能一笔画出。
另外,通过前面的学习,大家已经知道:一个图如果能够一笔画出,则画的方法不止一种,但各种方法大同小异.因此,本书中,一
笔画的问题,一般我们只给出一种画法。
练习题
1.下面的图形可以一笔画成吗?如果可以,请你用一笔画成。
2.判断下列各图能否一笔画出,并说明理由。
3一只蚂蚁由A点出发,到达B点,必须不重复地经过每一条线,你能想出好办法吗?
4.游人在林间小路上(见图)散步,问能否一次不重复地走遍所有的路线后回到出发点?
5.下图是某个花房的平面图,它由六间展室组成,每相邻两室有一门相同,请你设计一个出口,使参观者能够从入口处进去,一次不重复地经过所有的门,最后由出口走出花房。
答案:
3:蚂蚁可以这样走:
4:图中有6个单数点,因此游人不能一次不重复的走遍所有路线后返回出发点
5:把原图转化为右图,如果添一条与A相连的边,此图就能成为以A点为起点一笔画出,所以,应连接A、F,把出口处开在花房F处.。
