哈工大机械原理大作业
(完整word版)哈工大机械原理大作业3齿轮传动设计

4、滑移齿轮变速传动中每对齿轮几何尺寸及重合度的计算
4.1滑移齿轮5和齿轮6
序号
项目
代号
计算公式及计算结果
1
齿数
齿轮5
17
齿轮6
39
2
模数
2
3
压力角
20°
4
齿顶高系数
1
5
令 =4
则可得定轴齿轮传动部分的传动比为 = =6.4667
滑移齿轮传动的传动比 = =2.308
= =2.857
定轴齿轮传动由3对齿轮传动组成,则每对齿轮的传动比为
3、齿轮齿数的确定
根据滑移齿轮变速传动系统中对齿轮齿数的要求,选择齿轮5、6为标准齿轮,7、8、9和10为角度变位齿轮。设 17, = 39满足传动比,由于是标准齿轮,可得中心距a=76mm ,h*a=1, =17,因此不会发生根切,开始设计下面的角度变位。
顶隙系数
0.25
6
标准中心距
= ( )/2=56
7
实际中心距
56
8
啮合角
9
变位系数
齿轮5
0
齿轮6
0
10
齿顶高
齿轮5
2mm
齿轮6
2mm
11
齿根高
齿轮5
2.5mm
齿轮6
2.5mm
12
分度圆直径
齿轮5
34mm
齿轮6
78mm
13
齿顶圆直径
齿轮5
38mm
齿轮6
82mm
14
齿根圆直径
哈尔滨工业大学机械原理大作业_连杆26题

1.运动分析题目如图所示机构,已知机构各构件的尺寸为AB=108mm,EF=320mm,BC=CE=CD=200mm,FG=162mm,AD=258mm,AG=514mm,DG=384mm,β=80º,构件1的角速度为ω1=10rad/s,试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
2.机构的结构分析,组成机构的基本杆组划分3.各基本杆组的运动分析数学模型(1)RR基本杆组:delt=0xB = xA + AB * Cos(f + delt)yB = yA + AB* Sin(f + delt)vxB = vxA - w * AB * Sin(f + delt)vyB = vyA + w * AB* Cos(f + delt)axB = axA - w ^ 2 * AB * Cos(f + delt):ayB = ayA - w ^ 2 * AB* Sin(f + delt)(2)RRR基本杆组Ci = lbc * Cos(fbc)Si = lbc * Sin(fbc)Cj = lcd * Cos(fcd)Sj = lcd * Sin(fcd)G1 = Ci * Sj - Cj * Siwbc = (Cj * (vxD - vxB) + Sj * (vyD - vyB)) / G1wcd = (Ci * (vxD - vxB) + Si * (vyD - vyB)) / G1vxC = vxB - wbc * lbc * Sin(fbc)vyC = vyB + wbc * lbc * Cos(fbc)G2 = axD - axB + wbc ^ 2 * Ci - wcd ^ 2 * CjG3 = ayD - ayB + wbc ^ 2 * Si - wcd ^ 2 * Sjebc = (G2 * Cj + G3 * Sj) / G1ecd = (G2 * Ci + G3 * Si) / G1axC = axB - ebc * lbc * Sin(fbc) - wbc ^ 2 * lbc * Cos(fbc)ayC = ayB + ebc * lbc * Cos(fbc) - wbc ^ 2 * lbc * Sin(fbc)EB = 2 * BC * Cos(febc)xE = xB + EB* Cos(fbc + febc)yE = yB + EB * Sin(fbc + febc)vxE = vxB – wbc * EB* Sin(fbc + febc)vyE = vyB + wbc * EB* Cos(fbc + febc)axE = axB - wbc ^ 2 * EB * Cos(fbc + delt) - ebc * EB * Sin(fbc + febc)ayE = ayB - wbc ^ 2 * leb * Sin(fbc + delt) + ebc * leb * Sin(fbc + febc) Ci = lef * Cos(fef)Si = lef * Sin(fef)Cj = lfg * Cos(ffg)Sj = lfg * Sin(ffg)G1 = Ci * Sj - Cj * Siwef = (Cj * (vxG - vxE) + Sj * (vyG - vyE)) / G1wfg = (Ci * (vxG - vxE) + Si * (vyG - vyE)) / G1vxF = vxE - wef * lef * Sin(fef)vyF = vyE + wef * lef * Cos(fef)G2 = axG - axE + wef ^ 2 * Ci - wfg ^ 2 * CjG3 = ayG - ayE + wef ^ 2 * Si - wfg ^ 2 * Sjeef = (G2 * Cj + G3 * Sj) / G1efg = (G2 * Ci + G3 * Si) / G1axF = axE - eef * lef * Sin(fef) - wef ^ 2 * lef * Cos(fef)ayF = ayE + eef * lef * Cos(fef) - wef ^ 2 * lef * Sin(fef)4.计算编程Dim xA As DoubleDim yA As DoubleDim vxA As DoubleDim vyA As DoubleDim axA As Double 'A '点加速度x轴分量Dim ayA As Double 'A '点加速度y轴分量Dim xB As Double 'B'点'x轴坐标Dim yB As Double 'B点y轴坐标Dim vxB As Double 'B点速度x轴分量Dim vyB As Double 'B点速度y轴分量Dim axB As Double 'B点加速度x轴分量Dim ayB As Double 'B点加速度y轴分量Dim xC As Double 'C点x轴坐标Dim yC As Double C'点y轴坐标Dim vxC As Double 'C点速度x轴分量Dim vyC As Double 'C点速度y轴分量Dim axC As Double 'C点加速度x轴分量Dim ayC As Double 'C点加速度y轴分量Dim xD As Double 'D点x轴坐标Dim yD As Double 'D点y轴坐标Dim vxD As Double 'D点速度x轴分量Dim vyD As Double 'D点速度y轴分量Dim axD As Double 'D点加速度x轴分量Dim ayD As Double 'D点加速度y轴分量Dim xE As Double 'E点x轴坐标Dim yE As Double 'E点y轴坐标Dim vxE As Double 'E点速度x轴分量Dim vyE As Double 'E点速度y轴分量Dim axE As Double 'E点加速度x轴分量Dim ayE As Double 'E点加速度y轴分量Dim xF As Double 'F点x轴坐标Dim yF As Double 'F点y轴坐标Dim vxF As Double 'F点速度x轴分量Dim vyF As Double 'F点速度y轴分量Dim axF As Double 'F点加速度x轴分量Dim ayF As Double 'F点加速度y轴分量Dim xG As Double 'G点x轴坐标Dim yG As Double 'G点y轴坐标Dim vxG As Double 'G点速度x轴分量Dim vyG As Double 'G点速度y轴分量Dim axG As Double 'G点加速度x轴分量Dim ayG As Double 'G点加速度y轴分量Dim delt As Double ' AB杆初始转角Dim lab As Double 'AB杆长Dim lbc As Double 'BC杆长Dim lcd As Double ' CD杆长Dim lce As Double 'CE杆长Dim lef As Double 'EF杆长Dim lfg As Double 'FG杆长Dim leb As Double 'ED杆长Dim f As Double 'AB杆转角Dim fbc As Double 'BC杆转角Dim fcd As Double 'CD杆转角Dim fce As Double 'CE杆转角Dim fef As Double 'EF杆转角Dim ffg As Double 'FG杆转角Dim fge As Double 'ge杆转角Dim w As Double 'AB杆角速度Dim wbc As Double ' BC角速度Dim wcd As Double 'CD角速度Dim wce As Double 'CE角速度Dim wef As Double 'EF角速度Dim wfg As Double 'FG角速度Dim e As Double 'AB杆角加速度Dim ebc As Double ' BC杆角加速度Dim ecd As Double 'CD杆角加速度Dim ece As Double 'CE杆角加速度Dim eef As Double 'EF杆角加速度Dim efg As Double 'FG杆角加速度Dim LBD As Double 'BD距离Dim leg As Double 'EG距离Dim JCBD As Double '角CBDDim jfeg As Double '角FEGDim fBD As Double 'BD转角Dim feg As Double 'EG转角Dim Ci As DoubleDim Cj As DoubleDim Si As DoubleDim Sj As DoubleDim G1 As DoubleDim G2 As DoubleDim G3 As DoubleDim val As DoubleDim pi As DoubleDim pa As DoubleDim febc As Double '角EBCDim i As DoubleDim fj1 As DoublePrivate Sub Command1_Click() '求点E的轨迹Picture1.Scale (-300, 400)-(10, -15)Picture1.Line (-300, 0)-(10, 0) 'XPicture1.Line (0, 400)-(0, -15) 'YFor i = -300 To 0 Step 50 'X轴坐标Picture1.DrawStyle = 2Picture1.Line (i, 400)-(i, 0)Picture1.CurrentX = i - 10: Picture1.CurrentY = 0 Picture1.Print iNext iFor i = 0 To 350 Step 50 'Y轴坐标Picture1.DrawStyle = 2Picture1.Line (0, i)-(-400, i)Picture1.CurrentX = -20: Picture1.CurrentY = i + 7 Picture1.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Picture1.PSet (xE, yE)Next fj1End SubPrivate Sub Command2_Click() '求构件5的角位移Picture2.Scale (-20, 5)-(380, -0.5)Picture2.Line (-20, 0)-(380, 0) 'XPicture2.Line (0, 3)-(0, -0.5) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture2.DrawStyle = 2Picture2.Line (i, 3)-(i, 0)Picture2.CurrentX = i - 10: Picture2.CurrentY = 0 Picture2.Print iNext iFor i = -0.5 To 3 Step 0.5 'Y轴坐标Picture2.Line (0, i)-(380, i)Picture2.CurrentX = -25: Picture2.CurrentY = i Picture2.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture2.PSet (fj1, ffg)Next fj1End SubPrivate Sub Command3_Click() '求构件5的角速度Picture3.Scale (-20, 10)-(380, -10)Picture3.Line (-20, 0)-(380, 0) 'XPicture3.Line (0, 10)-(0, -10) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture3.DrawStyle = 2Picture3.Line (i, 10)-(i, -10)Picture3.CurrentX = i - 10: Picture3.CurrentY = 0 Picture3.Print iNext iFor i = -8 To 8 Step 2 'Y轴坐标Picture3.Line (0, i)-(380, i)Picture3.CurrentX = -20: Picture3.CurrentY = i Picture3.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture3.PSet (fj1, wfg)Next fj1End SubPrivate Sub Command4_Click() '求构件5的角加速度Picture4.Scale (-20, 300)-(380, -200)Picture4.Line (-20, 0)-(380, 0) 'XPicture4.Line (0, 300)-(0, -200) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture4.DrawStyle = 2Picture4.Line (i, 300)-(i, -200)Picture4.CurrentX = i - 10: Picture4.CurrentY = 0 Picture4.Print iNext iFor i = -200 To 300 Step 50 'Y轴坐标Picture4.Line (0, i)-(380, i)Picture4.CurrentX = -25: Picture4.CurrentY = i + 5 Picture4.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture4.PSet (fj1, efgNext fj1End SubPrivate Sub Form_Load() '赋初值lab = 108lce = 200lbc = 200lcd = 200lef = 320lfg = 162w = 10e = 0delt = 0xA = 0yA = 0vyA = 0axA = 0ayA = 0xD = -178.311284yD = 186.464704vxD = 0vyD = 0axD = 0ayD = 0xG = -514yG = 0vxG = 0vyG = 0axG = 0ayG = 0pi = 3.1415926pa = pi / 180febc = pa * 50End SubPrivate Sub RR1() 'RR基本杆组xB = xA + lab * Cos(f + delt)yB = yA + lab * Sin(f + delt)vxB = vxA - w * lab * Sin(f + delt)vyB = vyA + w * lab * Cos(f + delt)axB = axA - w ^ 2 * lab * Cos(f + delt) - e * lab * Sin(f + delt)ayB = ayA - w ^ 2 * lab * Sin(f + delt) + e * lab * Sin(f + delt)End SubPrivate Sub RR2() 'RR基本杆组leb = 2 * lbc * Cos(febc)xE = xB + leb * Cos(fbc + febc)yE = yB + leb * Sin(fbc + febc)vxE = vxB - wbc * leb * Sin(fbc + febc)vyE = vyB + wbc * leb * Cos(fbc + febc)axE = axB - wbc ^ 2 * leb * Cos(fbc + delt) - ebc * leb * Sin(fbc + febc) ayE = ayB - wbc ^ 2 * leb * Sin(fbc + delt) + ebc * leb * Sin(fbc + febc) End SubPrivate Sub RRR1() 'RRR基本杆组LBD = Sqr((xD - xB) ^ 2 + (yD - yB) ^ 2)If LBD > lbc + lcd And LBD < Abs(lbc - lcd) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndEnd IfElseEnd IfIf LBD < lbc + lcd And LBD > Abs(lbc - lcd) Then val = (lbc ^ 2 + LBD ^ 2 - lcd ^ 2) / (2 * lbc * LBD) JCBD = Atn(-val / Sqr(-val * val + 1)) + 2 * Atn(1) ElseEnd IfIf LBD = lbc + lcd ThenJCBD = 0ElseEnd IfIf LBD = Abs(lbc - lcd) ThenIf lbc > lcd ThenJCBD = 0ElseEnd IfIf lbc < lcd ThenJCBD = piElseEnd IfElseEnd IfIf xD > xB And yD >= yB Then '第一象限fBD = Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD = xB And yD > yB ThenfBD = pi / 2ElseEnd IfIf xD < xB And yD >= yB Then '第二象限fBD = pi + Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD < xB And yD < yB Then '第三象限fBD = pi + Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD = xB And yD < yB ThenfBD = 3 * pi / 2ElseEnd IfIf xD > xB And yD <= yB Then '第四象限fBD = 2 * pi + Atn((yD - yB) / (xD - xB))ElseEnd Iffbc = fBD - JCBDxC = xB + lbc * Cos(fbc)yC = yB + lbc * Sin(fbc)If xC > xD And yC >= yD Then '第一象限fcd = Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And yC >= yD Thenfcd = pi / 2ElseEnd IfIf xC < xD And yC >= yD Then '第二象限fcd = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC < xD And yC < yD Then '第三象限fcd = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And yC < yD Thenfcd = 3 * pi / 2ElseEnd IfIf xC > xD And yC <= yD Then '第四象限fcd = 2 * pi + Atn((yC - yD) / (xC - xD))ElseEnd IfCi = lbc * Cos(fbc)Si = lbc * Sin(fbc)Cj = lcd * Cos(fcd)Sj = lcd * Sin(fcd)G1 = Ci * Sj - Cj * Siwbc = (Cj * (vxD - vxB) + Sj * (vyD - vyB)) / G1 wcd = (Ci * (vxD - vxB) + Si * (vyD - vyB)) / G1 vxC = vxB - wbc * lbc * Sin(fbc)vyC = vyB + wbc * lbc * Cos(fbc)G2 = axD - axB + wbc ^ 2 * Ci - wcd ^ 2 * CjG3 = ayD - ayB + wbc ^ 2 * Si - wcd ^ 2 * Sj ebc = (G2 * Cj + G3 * Sj) / G1ecd = (G2 * Ci + G3 * Si) / G1axC = axB - ebc * lbc * Sin(fbc) - wbc ^ 2 * lbc * Cos(fbc)ayC = ayB + ebc * lbc * Cos(fbc) - wbc ^ 2 * lbc * Sin(fbc)End SubPrivate Sub RRR2() 'RRR基本杆组leg = Sqr((xG - xE) ^ 2 + (yG - yE) ^ 2)If leg > lef + lfg And leg < Abs(lef - lfg) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndElseEnd IfElseEnd IfIf leg < lef + lfg And leg > Abs(lef - lfg) Thenval = (lef ^ 2 + leg ^ 2 - lfg ^ 2) / (2 * lef * leg)jfeg = Atn(-val / Sqr(-val * val + 1)) + 2 * Atn(1)ElseEnd IfIf leg = lef + lfg Thenjfeg = 0ElseEnd IfIf leg = Abs(lef - lfg) ThenIf lef > lfg Thenjfeg = 0ElseEnd IfIf lef < lfg Thenjfeg = piElseEnd IfElseEnd IfIf xG > xE And yG >= yE Then '第一象限feg = Atn((yG - yE) / (xG - xE))ElseEnd IfIf xG = xE And yG > yE Thenfeg = pi / 2ElseEnd IfIf xG < xE And yG >= yE Then '第二象限feg = pi + Atn((yG - yE) / (xG - xE))ElseEnd IfIf xG < xE And yG < yE Then '第三象限feg = pi + Atn((yG - yE) / (xG - xE)) ElseEnd IfIf xG = xE And yG < yE Thenfeg = 3 * pi / 2ElseEnd IfIf xG > xE And yG <= yE Then '第四象限feg = 2 * pi + Atn((yG - yE) / (xG - xE)) ElseEnd Iffef = feg - jfegxF = xE + lef * Cos(fef)yF = yE + lef * Sin(fef)If xF > xG And yF >= yG Then '第一象限ffg = Atn((yF - yG) / (xF - xG))ElseEnd IfIf xF = xG And yF >= yG Thenffg = pi / 2ElseEnd IfIf xF < xG And yF >= yG Then '第二象限ffg = pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfIf xF < xG And yF < yG Then '第三象限ffg = pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfIf xF = xG And yF < yG Thenffg = 3 * pi / 2ElseEnd IfIf xF > xG And yF <= yG Then '第四象限ffg = 2 * pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfCi = lef * Cos(fef)Si = lef * Sin(fef)Cj = lfg * Cos(ffg)Sj = lfg * Sin(ffg)G1 = Ci * Sj - Cj * Siwef = (Cj * (vxG - vxE) + Sj * (vyG - vyE)) / G1wfg = (Ci * (vxG - vxE) + Si * (vyG - vyE)) / G1vxF = vxE - wef * lef * Sin(fef)vyF = vyE + wef * lef * Cos(fef)G2 = axG - axE + wef ^ 2 * Ci - wfg ^ 2 * CjG3 = ayG - ayE + wef ^ 2 * Si - wfg ^ 2 * Sjeef = (G2 * Cj + G3 * Sj) / G1efg = (G2 * Ci + G3 * Si) / G1axF = axE - eef * lef * Sin(fef) - wef ^ 2 * lef * Cos(fef)ayF = ayE + eef * lef * Cos(fef) - wef ^ 2 * lef * Sin(fef)End Sub5.结果及分析图1 E点的运动轨迹(1)由图1所示,E点的运动轨迹呈稍倾斜“8字形”。
哈工大—机械原理凸轮大作业
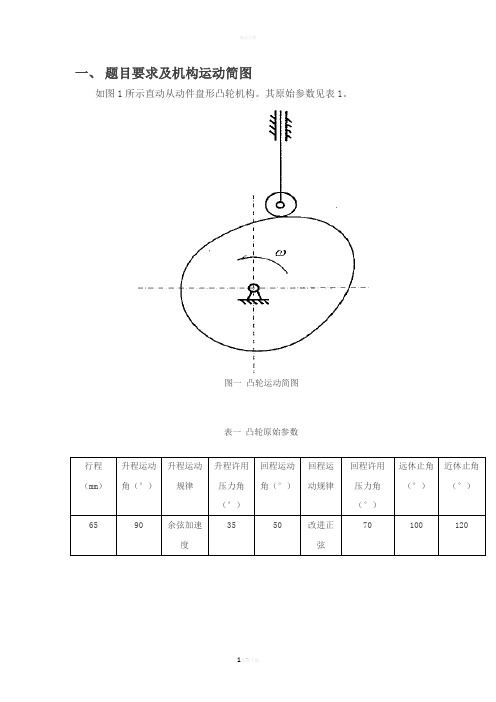
一、题目要求及机构运动简图如图1所示直动从动件盘形凸轮机构。
其原始参数见表1。
图一凸轮运动简图表一凸轮原始参数二、计算流程框图凸轮机构分析建立数学模型位移方程速度方程加速度方程速度线图位移线图加速线图ds/dΨ-s曲线升程压力角回程压力角确定轴向及基圆半径压力角图确定滚子半径实际轮廓理论轮廓轮廓图结束三、建立数学模型1.从动件运动规律方程首先,由于设计凸轮轮廓与凸轮角速度无关,所以不妨设凸轮运动角速度为w = 1rad/s。
(1)推程运动规律 (0 < φ < 90°)s=h2×[1−cos(πφ0×φ)]v=πhw2φ0×sin(πφ0×φ)a=π2ℎw22φ02×cos(πφ0×φ)式中:h=65mm,Φ0=π/2(2)远休程运动规律 (90°< φ < 190°)s = 65mmv = 0a = 0(3)回程运动规律 (190°< φ < 240°)s1=h−h4+π∗(π∗(φ−φ0−φs)φ0′−sin(4∗π∗φ−φ0−φsφ0)4)(190°< φ < 196.25°)s2=h−h4+π∗(2+π∗(φ−φ0−φs)φ0′−9∗sin(π3+4∗π∗φ−φ0−φs3∗φ0′)4)(196.25°< φ < 233.75°)s3=h−h4+π∗(4+π∗(φ−φ0−φs)φ0′−sin(4∗π∗φ−φ0−φsφ0′)4)(233.75°< φ < 240°)回程运动中的速度和加速度为位移对时间t的倒数:v=ds dta=dv dt(4)近休程运动规律 (240°< φ < 360°)s = 0v = 0a = 02.从动件位移、速度、加速度线图(1)位移线图(2)速度线图(3)加速度线图(4)位移、速度、加速度线图MATLAB源程序%% 已知条件h = 65; %mmphi_0 = 90./180*pi; %radalpha_up_al = 35./180*pi; %升程许用压力角phi_00 = 50./180*pi;alpha_down_al = 70./180*pi; %回程许用压力角phi_s = 100./180*pi;phi_ss = 120./180*pi;w = 1;%% 绘制从动件位移、速度、加速度线图% 推程阶段t_up = 0 : 0.5 : 90;t_up1 = t_up./180*pi;syms t_up1 phi_up s_up v_up a_upphi_up = w.*t_up1;s_up = h./2.*(1 - cos(pi.*phi_up./phi_0));v_up = diff(s_up,t_up1);a_up = diff(v_up,t_up1);s_up1 = double(subs(s_up,t_up./180*pi));v_up1 = double(subs(v_up,t_up./180*pi));a_up1 = double(subs(a_up,t_up./180*pi));% 远休程t_s = 90 : 0.5 : (90+100);t_s1 = t_up./180*pi;s_s(1:201) = h;v_s(1:201) = 0;a_s(1:201) = 0;% 回程阶段1t_down1 = (90+100) : 0.5 : (90+100+50/8);t_down11 = t_down1./180*pi;syms t_down11 phi_down1 s_down1 v_down1 a_down1phi_down1 = w.*t_down11;s_down1 = h - h./(4+pi).*(pi.*(phi_down1 - phi_0 - phi_s)./phi_00 - ...sin(4.*pi.*(phi_down1 - phi_0 - phi_s)./phi_00)./4);v_down1 = diff(s_down1,t_down11);a_down1 = diff(v_down1,t_down11);s_down11 = double(subs(s_down1,t_down1./180*pi));v_down11 = double(subs(v_down1,t_down1./180*pi));a_down11 = double(subs(a_down1,t_down1./180*pi));% 回程阶段2t_down2 = (90+100+50/8) : 0.5 : (90+100+7*50/8);t_down22 = t_down2./180*pi;syms t_down22 phi_down2 s_down2 v_down2 a_down2phi_down2 = w.*t_down22;s_down2 = h - h./(4+pi).*(2+pi.*(phi_down2 - phi_0 - phi_s)./phi_00 - 9.*sin(pi./3 + 4.*pi.*(phi_down2 - phi_0 - phi_s)./(3.*phi_00))./4); v_down2 = diff(s_down2,t_down22);a_down2 = diff(v_down2,t_down22);s_down22 = double(subs(s_down2,t_down2./180*pi));v_down22 = double(subs(v_down2,t_down2./180*pi));a_down22 = double(subs(a_down2,t_down2./180*pi));% 回程阶段3t_down3 = (90+100+7*50/8) : 0.5 : (90+100+50);t_down33 = t_down3./180*pi;syms t_down33 phi_down3 s_down3 v_down3 a_down3phi_down3 = w.*t_down33;s_down3 = h - h./(4+pi).*(4+pi.*(phi_down3 - phi_0 - phi_s)./phi_00 - …sin(4.*pi.*(phi_down3 - phi_0 - phi_s)./phi_00)./4);v_down3 = diff(s_down3,t_down33);a_down3 = diff(v_down3,t_down33);s_down33 = double(subs(s_down3,t_down3./180*pi));v_down33 = double(subs(v_down3,t_down3./180*pi));a_down33 = double(subs(a_down3,t_down3./180*pi));% 近休程t_ss = (90+100+50) : 0.5 : 360;s_ss(1:241) = 0;v_ss(1:241) = 0;a_ss(1:241) = 0;% 绘图位移t = [t_up t_s t_down1 t_down2 t_down3 t_ss];phi = w .* t ./ 180 .*pi;s = [s_up1 s_s s_down11 s_down22 s_down33 s_ss];v = [v_up1 v_s v_down11 v_down22 v_down33 v_ss];a = [a_up1 a_s a_down11 a_down22 a_down33 a_ss];figure('Name','从动件位移-时间线图');plot(t,s,'k','linewidth',1.0);grid on;title('从动件位移-时间线图');xlabel('转角\phi / 度');ylabel('位移h/mm');% 绘图速度figure('Name','从动件速度-时间线图');plot(t,v,'k','linewidth',1.0);grid on;title('从动件速度-时间线图');xlabel('转角\phi / 度');ylabel('速度v/mm*s^{-1}');% 绘图加速度figure('Name','从动件加速度-时间线图'); plot(t,a,'k','linewidth',1.0);grid on;title('从动件加速度-时间线图');xlabel('转角\phi / 度');ylabel('加速度a/mm*s^{-2}');3.绘制ds/dΦ线图并确定基圆半径和偏距(1)绘制ds/dΦ线图及源程序① MATLAB源程序:%% 绘制ds/dphi-s线图,确定基圆半径和偏距ds_dphi = v ./ w;figure('Name','凸轮ds/dphi - s线图');plot(ds_dphi,s,'k','linewidth',1.5);hold on;axis([-150 150 -70 70]);grid on;title('凸轮ds/dphi - s线图');xlabel('ds/dphi / (mm*s^{-2})');ylabel('s/mm');% 三条临界线x = linspace(-150,150,301);k_up = tan(pi/2 - alpha_up_al);y_up = k_up.*x - 66;plot(x,y_up,'linewidth',1.5);k_down = - tan(pi/2 - alpha_down_al);y_down = k_down.*x - 24.7;plot(x,y_down,'linewidth',1.5);x0 = linspace(0,150,151);k0 = - tan(alpha_up_al);y0 = k0.*x0;plot(x0,y0,'--');% 由图像选取凸轮基圆半径为r0 = sqrt(23^2 + 34^2) = 41 mm,偏距e = 23mm plot(23,-34,'or');r0 = 41;e = 23;plot(linspace(0,23,10),linspace(0,-34,10),'r',linspace(0,23,10),linsp ace(-34,-34,10),'r',linspace(23,23,10),linspace(0,-34,10),'r','linewi dth',1.0);(2)确定基圆半径和偏距在凸轮机构的ds/dφ-s线图里再作斜直线Dt-dt与升程的[ds/dφ-s]曲线相切并使与纵坐标夹角为升程许用压力角[α],则Dt-dt 线的右下方为选择凸轮轴心的许用区。
哈工大机械原理大作业3

Harbin Institute of Technology机械原理大作业三课程名称:设计题目:院系:班级:设计者:学号:指导教师:设计时间:哈尔滨工业大学大作业3 齿轮传动设计 1、设计题目1.1机构运动简图1.2机械传动系统原始参数2、传动比的分配计算由已知条件,电动机转速n=1450r/min ,输出转速n 1=27 r/min ,n 2=31 r/min ,n 3=37 r/min ,带传动最大传动比max p i =2.5,滑移齿轮传动最大传动比=4,定轴齿轮传动最大 传动比=4。
可求得:传动系统的总传动比为:11n ni == 1450/27=53.70322n ni == 1450/31=46.774 33n ni == 1450/37=39.189 传动系统的总传动比分别由带传动、滑移齿轮传动和定轴齿轮传动三部分实现。
设带传的传送比为其最大传送比5.2max =p i ,滑移齿轮的传动比为321,,v v v i i i ,定轴齿轮传动的传动比为f i ,则总传动比由于1i > 2i > 3i ,故取1max 4v v i i ==则定轴齿轮传动部分的传动比为1max max5.37f p v i i i i ==滑移齿轮传动的传动比22max3.49v f p i i i i ==33m a x2.92v f p i i i i ==定轴齿轮传动由3对齿轮传动组成, 每对齿轮的传动比为:1.754d i ==≤3、齿轮齿数的确定滑移齿轮齿数3=v i 65622.9521z z == 2=v i 8766 3.4719z z ==1=v i 10967 3.9417z z ==齿轮7,齿轮8:719z = 866z =781()852a m z z =+=齿轮9,齿轮10:917z =1067z =此时已知条件为'a =85mm ,910211()842()ni i a m z z X X ==+=-∑mm ''arccos(cos )21.78a aαα==总变位系数:'910()0.552tan z z x inv inv ααα∑+=-=根据x ∑值和1093.94 3.0z uz ==>,按选择变位系数线图左部斜线⑤分配变位系数,得90.45x =齿轮5,齿轮6:5=21z662z =此时已知'a =85mm ,561()832a m z z =+= ''arccos(cos )23.42a a αα==100.10x =总变位系数:'65() 1.082tan z z x inv inv ααα∑+=-=根据x ∑值和652.953z u z ==>,按选择变位系数线图左部斜线④分配变位系数,得 50.5x =60.58x =定轴圆柱齿轮齿数=d i 1214111326 1.5317z z z z ===齿轮11,齿轮12:角度变位正传动。
哈工大机械原理连杆和凸轮大作业24题

班级学号机械原理大作业说明书题目 1、连杆机构运动分析2、凸轮机构设计学生姓名1连杆机构运动分析1.设计题目:一、先建立如下坐标系:二、划分杆组如下,进行结构分析:该机构由I级杆组RR(如图1)、II级杆组RPR(如图2、3)和II级杆组RRP(如图4)组成。
(1)(2)(3)(4)三、运动分析数学模型:(1)同一构件上点的运动分析:如右图所示的原动件1,已知杆1的角速度=10/rad s ω,杆长1l =170mm,A y =0,A x =110mm 。
可求得下图中B 点的位置B x 、B y ,速度xB v 、yB v ,加速度xB a 、yB a 。
θcos 1l xB =,θsin 1l yB =θωυsin 1l xB -=,θωυcos 1l yB =,222B2==-cos =-BxB i d x a l x dt ωϕω2222==-sin =-B yB i B d y a l y dtωϕω。
(2)RPRII 级杆组的运动分析:a. 如右图所示是由2个回转副和1个移动副组成的II 级组。
已知两个外运动副C 、B 的位置(B x 、B y 、c x =110mm 、C y =0)、速度(xB υ,yB υ,xC υ=0,yC υ=0)和加速度(0,0,,==yC xC yB xB a a a a )。
可确定下图中D 点的位置、速度和加速度。
确定构件3的角位移1ϕ、角速度1ω、角加速度1α。
1sin 31..ϕϕl x dt dx C B -= 1s i n 131c o s 13.....2ϕϕϕϕl l x dt x d C B --= 1cos 31..ϕϕl y dt dy C B += 1c o s 131s i n 13.....2ϕϕϕϕl l y dty d C B +-= 根据关系:1111d 122..11.αϕϕωϕϕ====dtd dt , 故可得出: D x =)1cos(4βϕ++l x CD y =)1sin(4βϕ++l y Cb. 如右图所示是由2个回转副和1个移动副组成的II级组。
哈工大-机械原理大作业-连杆机构运动分析

机械原理大作业(一)作业名称:连杆机构运动分析设计题目: 20院系:英才学院班级: XXXXXXX设计者:邵广斌学号: XXXXXXXXXX指导教师:林琳设计时间: 2013年05月19日哈尔滨工业大学机械设计1.运动分析题目如图所示机构,已知机构各构件的尺寸为150AB mm =,97β=︒,400BC mm =,300CD mm =,320AD mm =,100BE mm =,230EF mm =,400FG mm =,构件1的角速度为110/rad s ω=,试求构件2上点F 的轨迹及构件5上点G 的位移、速度和加速度,并对计算结果进行分析。
2. 机构分析该机构由原动件AB (Ⅰ级杆组)、BCD (RRR Ⅱ级杆组)和FG (RRP Ⅱ级杆组)组成。
3. 建立坐标系如图3,建立以定点A 为原点的平面直角坐标系A-xy 。
图1 运动机构结构图4. 运动分析数学模型4.1 原动件AB原动件AB 的转角: 10~2ψπ= 原动件AB 的角速度:110/rad s ω=原动件AB 的角加速度: 10α= 运动副A 的位置坐标: 0A x = 0A y =运动副A 的速度: 0xA v = 0yA v = 运动副A 的加速度: 0xA a = 0yA a =原动件AB 长度:150AB l mm =运动副B 的位置坐标: 1B A AB x x l cos ψ=+1B A AB y x l sin ψ=+运动副B 的速度: 11 xB xA AB v v l sin ωψ=-11 yB yA AB v v l cos ωψ=+运动副B 的加速度: 2 1111 xBxA AB AB a a l cos l sin ωψαψ=--21111yB yA AB AB a a l sin l cos ωψαψ=-+4.2 RRR Ⅱ级杆组BCD运动副D 的位置坐标: 320D x mm = 0D y = 运动副D 的速度: 0xD v = 0yD v = 运动副D 的加速度: 0xD a = 0yD a = 杆BC 长度: 400BC l mm = 杆CD 长度:300CD l mm =BC 相对于x 轴转角:200ψ=其中02BC D B A l x x =-() 0 2 BC D B B l y y =-()2220B B C C l C l D l D =+- 222())(BDD B D B l x x y y =-+- CD 相对于x 轴转角: 3C DC Dy y arctanx x ψ-=-求导可得BC 角速度2ω、角加速度2α以及CD 角速度3ω、角加速度3α。
哈工大机械原理大作业——齿轮——1号

Harbin Institute of Technology机械原理大作业3课程名称:机械原理设计题目:齿轮传动设计哈尔滨工业大学一、设计题目:如下图一个机械传动系统,运动运动由电动机1输入,经过机械传动系变速后由圆锥齿轮16输出三种不同转速。
选择一组传动系统的原始参数,据此设计该传动系统。
序号电机转速〔r/min〕输出轴转速〔r/min〕带传动最大传动比滑移齿轮传动定轴齿轮传动最大传动比模数圆柱齿轮圆锥齿轮一对齿轮最大传动比模数一对齿轮最大传动比模数7 1450 17 23 30 ≤2.8 ≤4.5 2 ≤4.5 3 ≤4 3二、传动比的分配计算:电动机转速n=1450r/min,输出转速n1=17r/min,n2=23 r/min,n3=30 r/min,带传动的最大传动比=2.8,滑移齿轮传动的最大传动比=4.5,圆柱齿轮传动的最大传动比=4.5,圆锥齿轮最大传动比=4。
根据传动系统的原始参数可知,传动系统的总传动比为:i1=1450/30=48.333i2=1450/23=63.043i3=1450/17=85.294传动系统的总传动比由带传动、滑移齿轮传动和定轴齿轮传动三局部实现。
设带传动的传动比为ipmax =2.8,滑移齿轮的传动比为iv1,iv2和iv3,令iv3=ivmax=4.5,那么定轴的传动比为if =85.294/(4.5*2.8)=6.769,从而iv1=48.333/〔6.769*2.8〕=2.550,iv2=3.326。
定轴齿轮每对的传动比为id==1.89。
三、滑移齿轮变速传动中每对齿轮的几何尺寸及重合度:经过计算、比拟,确定出三对滑移齿轮的齿数,其分别为:z5=17,z6=44,z 7=14,z8=47,z9=11,z10=50。
变位系数确实定:x5=x6=0; x7≥ha*(17-14)/17=0.176,取x7=0.18,x8=-0.18;x9≥ha*(17-11)/17=0.353,取x9=0.36;x10=-0.36。
哈尔滨工业大学机械原理大作业凸轮设计
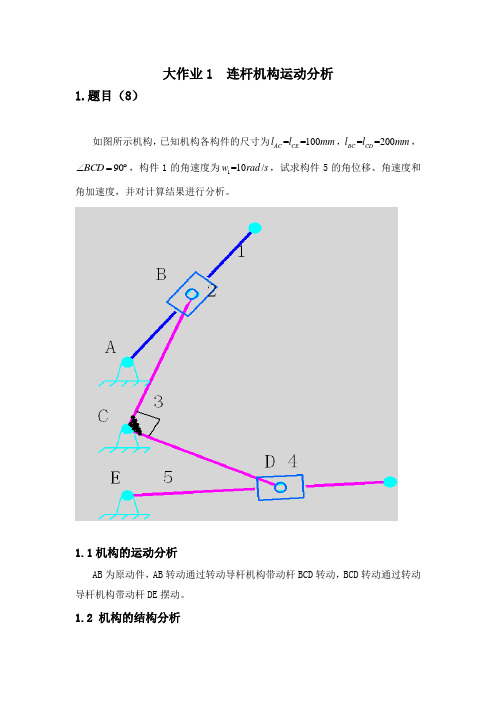
大作业1连杆机构运动分析1.题目(8)如图所示机构,已知机构各构件的尺寸为==100AC CE l l mm ,==200BC CD l l mm ,90BCD ∠=︒,构件1的角速度为1=10/w rad s ,试求构件5的角位移、角速度和角加速度,并对计算结果进行分析。
1.1机构的运动分析AB 为原动件,AB 转动通过转动导杆机构带动杆BCD 转动,BCD 转动通过转动导杆机构带动杆DE 摆动。
1.2 机构的结构分析杆组可以划分为一个RR I级杆组(杆1)、RRPII级杆组(滑块2,杆3)、RPRII 级杆组(滑块4,杆5)(1)RRI级杆组1:(2)RRPII级杆组2,3:(3)RPRII级杆组4,5:2.分析过程 2.1 建立坐标系建立以点E 为原点的固定平面直角坐标系x-E-y ,如图所示。
2.2 建立数学模型(1)构件1、2、3的分析原动件杆1的转角:1θ=0--360。
原动件杆1的角速度:1ω=.1θ=10/rad s 原动件杆1的角加速度:..1αθ==0运动副A 的坐标:0200A A x y mm =⎫⎬=⎭运动副A 的速度及加速度都为零。
构件1为BC (RRP Ⅱ级杆组)上滑块B 的导路 滑块B 的位置为:132cos cos B A C x x s x l θθ=+=+132sin sin B A C y y s x l θθ=+=+消去s,得:0212arcsinA l θθ=+式中:011()sin ()cos C A C A A x x y y θθ=---构件3的角速度i ω和滑块B 沿导路的移动速度D υ:.211213(Q sin Q cos )/Q ωϕθθ==-+ 1322323(Q cos Q sin )/Q D s l l υθθ⋅==-+式中:..11111211321212Q sin ;Q cos ;Q sin sin cos sin l l l θθθθθθθθ=-==+构件3的角加速度和滑块B 沿导路移动的加速度:..241513(Q sin Q cos )/Q αθθθ==-+..4325323(Q cos Q sin )/Q B s l l υθθ==-+式中:122......21142211111Q cos sin cos 2sin l l l s θθθθθθθθ=---- 122......21152211111Q sin cos sin 2cos l l l s θθθθθθθθ=+-+(2)构件3,4,5的分析构件3,4,5,由1个Ⅰ级基本杆组和一个RRP Ⅱ级杆组组成,与构件1,2,3结构相同,只运动分析过程与其相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y大作业设计说明书课程名称:机械原理设计题目:凸轮机构院系:机电学院班级:姓名:学号:指导教师:丁刚设计时间:哈尔滨工业大学1.设计题目2.运动方程式及运动线图由题目要求凸轮逆时针旋转(1)确定凸轮机构推杆升程、回程运动方程,并绘制推杆位移、速度、加速度线图。
升程第一段:(0 <φ< pi /4)φ0=pi/2;s1 = 73*φ^2;v1=146*w*φ;a1 = 146*w^2;升程第二段:(pi/4 <φ< pi /2)s2 =90-73*(pi/2-φ)^2;v2=146*w*( pi/2-φ);a2 =-146*w.^2;远休止程:(pi/2 <φ< 10*pi/9)s3 = 90;v3 = 0;a3 = 0;回程:(10*pi/9)< φ< ( 14*pi/9)s4 =45*(1+cos(9/4*(φ-10*pi/9)));v4 =*w*sin(9/4*(φ-10*pi/9)) ;a4 =*w^2* cos(9/4*(φ-10*pi/9));近休止程:(14*pi/9)< φ < ( 2*pi);s5 =0;v5 =0;a5 =0;1.由上述公式通过编程得到位移、速度、加速度曲线如下:(编程见附录).2. 凸轮机构的线图及基圆半径和偏距的确定凸轮机构的线图如下图所示(代码详见附录):因为凸轮逆时针旋转,,所以滚子从动件右偏,但由于绘图原因,采用向左为正方向,由此确定凸轮基圆半径与偏距:基圆半径为r0 = (50^2+100^2)=112mm,偏距e = 50mm。
3.凸轮实际轮廓,理论轮廓,基圆,偏距圆绘制4.整体图像附录1.求位移、速度、加速度的程序(matlab)w = input('请输入W=');x = 0:(pi/1000):(pi/4);s1 = 73*x.^2;v1=146*w*x;a1 = 146*w.^2;y = (pi/4):(pi/1000):(pi/2);s2 =90-73*(pi/2-y).^2;v2=146*w*( pi/2-y);a2 =-146*w.^2;z = (pi/2 ):(pi/1000):(10*pi/9);s3 = 90;v3 = 0;a3 = 0;c = (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));v4 =*w*sin(9/4*( c-10*pi/9)) ;a4 =*w.^2* cos(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0; v5 =0; a5 =0;subplot (2,2,1)plot(x,s1,'b',y,s2,'b',z,s3,'b',c,s4,'b', d,s5,'b');xlabel('转角/rad')ylabel('位移/(mm/s)')title('位移与转角曲线')grid onsubplot (2,2,2)plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g', d,v5,'g')xlabel('转角/rad')ylabel('速度/(mm/s)')title('转角与速度曲线')grid onsubplot (2,2,3)plot(x,a1,'r',y,a2,'r',z,a3,'r ',c,a4,'r',d,a5,'r')xlabel('转角/rad')ylabel('加速度/(mm/s)')title('转角与加速度曲线')grid on2.绘制凸轮机构dφ/ds – s线图w = input('请输入W=');x = 0:(pi/1000):(pi/4);s1 = 73*x.^2;ds1 =-73*2*x;y = (pi/4):(pi/1000):(pi/2);s2 =90-73*(pi/2-y).^2;ds2 =-73*2*(pi/2-y);z = (pi/2 ):(pi/1000):(10*pi/9);s3 = 90;ds3 =0;c = (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));ds4 =45*9/4*sin(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0;ds5 =0;plot(ds1,s1,'b',ds2,s2,'b',ds3,s3,'b',ds4,s4,'b',ds5,s5,'b'); xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s曲线')grid onhold onx3=-150::0;y3 = *x3;plot (x3,y3,'r');hold onx1=-150::150;for i=1:1:250;k1=(s1(i+1)-s1(i))/ (ds1(i+1)-ds1(i));if(k1>= && k1<=y1=k1*(x1-ds1(i))+s1(i);plot (x1,y1,'r');endendhold onx1=-150::150;for i=1:1:250;k2=(s2(i+1)-s2(i))/ (ds2(i+1)-ds2(i));if(k2>= && k2<=y1=k2*(x1-ds1(i))+s2(i);plot (x1,y1,'r');endendhold onx2=-150::150;for i=1:1:444;k3=(s4(i+1)-s4(i))/ (ds4(i+1)-ds4(i));if(k3>= && k3<=y2=k3*(x2-ds4(i))+s4(i);plot (x2,y2,'r');endendhold ony3=*(x2-ds1(251))+s1(251);plot(x2,y3,'r')text(-50,-100,'O点(-50,-100)')3.确定滚子半径(1)先求凸轮理论轮廓曲线,程序如下:Clc;clear;w = input('请输入w=');s0 = 100;s = 90;e = 50; x = 0:(pi/100):(pi/4);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (pi/4):(pi/100):(pi/2);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi/2 ):(pi/100):(10*pi/9);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (10*pi/9):(pi/1000):( 14*pi/9);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);d=(14*pi/9):(pi/1000):( 2*pi);x5 = (s + s0)*cos(d)-e*sin(d);y5 = (s0 + s)*sin(d) - e*cos(d);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b',x5,y5,'b');xlabel('x/mm')ylabel('y/mm')title('理论轮廓曲线')grid on(2)理论轮廓线最小曲率半径编程代码:由下程序结果可知pmin =这里滚子半径为 r r < pmin-ΔΔ=3~5mm;取r r=10mm; clear;clc;v=[];syms x1 x2 x3 x4 x5s0 = 100;e = 50;s1 = 73*x1.^2;t1 = (s1 + s0)*cos(x1)-e*sin(x1);y1 = (s0 + s1)*sin(x1) - e*cos(x1);tx1=diff(t1,x1);txx1=diff(t1,x1,2);yx1=diff(y1,x1);yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(pi/4);k1=subs(abs((tx1*yxx1-txx1*yx1)/(tx1^2+yx1^2)^,{x1},{xx1}); v=[v,1/k1];ends2 =90-73*(pi/2-x2).^2;t2 = (s2 + s0)*cos(x2)-e*sin(x2);y2 = (s0 + s2)*sin(x2) - e*cos(x2);tx2=diff(t2,x2);txx2=diff(t2,x2,2);yx2=diff(y2,x2);yxx2=diff(y2,x2,2);for xx2=(pi/4):(pi/100):(pi/2);k2=subs(abs((tx2*yxx2-txx2*yx2)/(tx2^2+yx2^2)^,{x2},{xx2}); v=[v,1/k2];ends3 = 90;t3 = (s3 + s0)*cos(x3)-e*sin(x3);y3 = (s0 + s3)*sin(x3) - e*cos(x3);tx3=diff(t3,x3);txx3=diff(t3,x3,2);yx3=diff(y3,x3);yxx3=diff(y3,x3,2);for xx3=(pi/2 ):(pi/100):(10*pi/9);k3=subs(abs((tx3*yxx3-txx3*yx3)/(tx3^2+yx3^2)^,{x3},{xx3}); v=[v,1/k3];ends4 =45*(1+cos(9/4*(x4-10*pi/9)));t4 = (s4 + s0)*cos(x4)-e*sin(x4);y4 = (s0 + s4)*sin(x4) - e*cos(x4);tx4=diff(t4,x4);txx4=diff(t4,x4,2);yx4=diff(y4,x4);yxx4=diff(y4,x4,2);for xx4=(10*pi/9):(pi/100):( 4*pi/3);k4=subs(abs((tx4*yxx4-txx4*yx4)/(tx4^2+yx4^2)^,{x4},{xx4}); v=[v,1/k4];ends5 =0;t5 = (s5 + s0)*cos(x5)-e*sin(x5);y5 = (s0 + s5)*sin(x5) - e*cos(x5);tx5=diff(t5,x5);txx5=diff(t5,x5,2);yx5=diff(y5,x5);yxx5=diff(y5,x5,2);for xx5=(10*pi/9):(pi/100):( 4*pi/3);k5=subs(abs((tx5*yxx5-txx5*yx5)/(tx5^2+yx5^2)^,{x5},{xx5}); v=[v,1/k5];endpmin=min(v)4.绘制凸轮轮廓曲线clear ;clc;syms x y z c dw= input('请输入w=');s0= 100;e = 50;r = 10;xx =0:(pi/100):(pi/4);s1 = 73*x.^2;x1 = (s1 + s0).*cos(x) - e*sin(x);y1 = (s0 + s1).*sin(x) - e*cos(x);n1 = diff (x1);m1 = diff(y1);xt1 = subs(x1+(r*m1)./(sqrt(n1.^2+m1.^2)),x,xx);yt1 = subs(y1 - (r*n1)./sqrt(m1.^2 +n1.^2),x,xx);yy = (pi/4):(pi/100):(pi/2);s2 = 90-73*(pi/2-y).^2;x2 = (s2 + s0).*cos(y)-e*sin(y);y2 = (s0 + s2).*sin(y) - e*cos(y);n2 = diff(x2);m2 = diff(y2);xt2 = subs(x2 + (r*m2)./sqrt(m2.^2+n2.^2),y,yy);yt2 = subs(y2 - (r*n2)./sqrt(m2.^2+n2.^2),y,yy);zz = (pi/2 ):(pi/100):(10*pi/9);s3 = 90;x3 = (s3 + s0).*cos(z)-e*sin(z);y3 = (s0 + s3).*sin(z) - e*cos(z);n3 = diff(x3);m3 = diff(y3);xt3= subs(x3 + (r*m3)./sqrt(m3.^2+n3.^2),z,zz);yt3 = subs(y3 - (r*n3)./sqrt(m3.^2+n3.^2),z,zz);cc= (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = (s0 +s4).*sin(c) - e*cos(c);n4 = diff(x4);m4 = diff(y4);xt4= subs(x4 + (r*m4)./sqrt(m4.^2+n4.^2),c,cc);yt4 =subs( y4 - (r*n4)./sqrt(m4.^2+n4.^2),c,cc);dd=(14*pi/9):(pi/1000):( 2*pi);s5 =0;x5 = (s5 + s0).*cos(d)-e*sin(d);y5 = (s0 +s5).*sin(d) - e*cos(d);n5 = diff(x5);m5 = diff(y5);xt5= subs(x5 + (r*m5)./sqrt(m5.^2+n5.^2),d,dd);yt5 =subs( y5 - (r*n5)./sqrt(m5.^2+n5.^2),d,dd);plot(xt1,yt1,'b',xt2,yt2,'b',xt3,yt3,'b',xt4,yt4,'b',xt5,yt5,'b');hold onxlabel('x/mm')ylabel('y/mm')title('凸轮工作曲线')grid on由于分步程序有很多重复,所以采用条件判断语句,求出分段的位移,速度,加速度表达式。
