应力圆法
材料力学应力圆法课件

(1)主应力数值
B1 B
A1 和 B1 两点为与主平面
y
D′
E D
2 20
C F A A1
对应的点,其横坐标 为主应力
1,2
x 1
OA1
OC
CA1
x
2
y
(
x
2
y )2
2 xy
max
1
OB1
OC
CB1
x
2
y
(
x
2
y )2
2 xy
角坐标系内的轨迹是一个圆.
1.圆心的坐标
C(
x
y
,0)
(Coordinate of circle center)
2
2.圆的半径(Radius of circle)
R
(
x
2
y
)2
2 xy
此圆习惯上称为 应力圆( plane stress circle),或称为莫 尔圆(Mohr’s circle)
y
20
tan1( 2 xy x y
)
0 确定后,1 对应的主平面方位即确定
3.求最大切应力(Determine
maximum shearing stress by
2
using stress circle)
G1和G两点的纵坐标分别代 o B1
表最大和最小切应力
CG1
2
材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

x
y
2
R cos[180o
(2
20 )]
xy
x
2
y
R cos(2
20 )
O
xy
x
y
2
R(cos 2
cos 20
sin 2
sin 20 )
x
y
2
x
2
y
cos 2
xy
sin
2
D
A ( x , xy )
y R 2 20
E
C
x
B ( y , xy )
13
单元体与应力圆的对应关系
y y
y
10
a
64103 110103 3.206107 1012
219.6MPa
200
b
64103 100103 3.206107 1012
199.6MPa
10
c
64103 0 3.206107 1012
0.0MPa
120
10
c z
b a y
30
(Fs 160kN; M 64kN m)
xy
(3)以C 为圆心,AC为半径画圆
—应力圆或莫尔圆
O
xy
y
y
xy x
Ox
A ( x , xy )
y C
B ( y , xy )
x
10
3、单元体公式与应力圆的关系
以上由单元体公式
应力圆(原变换)
下面寻求由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价 换句话,单元体与应力圆是否有一一对应关系?
x
x
x
0
y 1
应力莫尔圆(课堂PPT)

下面寻求: 由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价
换句话,单元体与应力圆是否有一一对应关系?
为什么说有这种对应关系?
DE R sin[180o ( 2a 2a0 )] R sin( 2a 2a0 )
( R cos 2a0 ) sin 2a ( R cos 2a0 )cos 2a
解: (1)主应力坐标系如图 (2)在坐标系内画出点
A(95,25 3)
25 3
s2
45 95
150° 25 3
a0
B(45,25 3)
(3)AB的垂直平分线与sa
轴的交点 C 即是圆心,
a (MPa)
B
以 C 为圆心,以 AC为
半径画圆 ——
s3
O
s2
应力圆
A
2a 0
C
s1
20MPa
s1
sa
(MPa)
§9.3 应力圆 ( Stresses Circle )
为什么叫莫尔圆 ( Mohr’s Circle ) ?
首先由Otto Mohr(1835-1918)提出 ( 又是一位工程师)
《来由》 一点无穷多个微元上的应力
能否在一张图上表示?
或者说,
把a看成参数,能否找到 s a与 a的函数关系?
sy
一、斜截面应力
s3 s y
D
2a o s x s1
a0
180 36.86 2
71.57
C
O
s 5、画出主单元体
B
(1)A点对应于右垂面
(2)右垂面逆时针转a o
30
得主单元体的最大
80
s 2 80
s1
三轴试验莫尔应力圆画法

三轴试验莫尔应力圆画法三轴试验莫尔应力圆画法是由奥地利地质学家莫尔爵士于1862年首先提出的一种经典的力学分析方法。
它是研究岩石和土壤力学性质的基础。
三轴试验是通过向试样施加不同的压力来研究材料的力学性质。
这种试验通常是在实验室环境下进行的。
试验装置包括一个气压或水压马达,用于施加垂直于试样顶部的压力。
通过对试验数据的分析,可以将应力状态转换为一个圆形轴载状态,称为莫尔应力圆。
在三轴试验中,试样被置于一个保持恒定应力状态的装置中。
然后通过改变施加在试样上的应力大小和方向来对试样施加压力。
试样最多可以承受三个压力:垂直于样品顶部的主压力,垂直于样品底部的副压力以及在两个侧面施加的轴向压力。
根据三轴试验的结果,可以得出应力状态的三个参数:主应力(或最大应力)、次应力(或中等应力)和剪应力(或最小应力)。
这三个参数确定了材料所处的应力状态。
莫尔应力圆是通过将主应力和剪切应力绘制在平面上,并使其形成一个圆的方式来表示这种状态。
莫尔应力圆的画法起始于选择一个坐标系,通常是水平的x和y坐标轴。
然后主应力和剪应力被绘制在这些坐标轴上:在这个图中,应力的最高点表示主应力σ1,最低点表示剪应力τ。
试样周围的其他三个顶点代表主剪应力状态。
通过连接这些顶点,画出一个正方形,其边界代表试样所处的力学状态。
为了得到与试样状态更接近的圆形图案,需要作出如下改进:尤奇然圆心沿尤圆心各个方向绘制刻度线连接刻度线上相同切效态下τ的点,可以得到莫尔圆的形状。
莫尔应力圆具有很高的实用价值。
它不仅可以提供岩土工程方面的理论基础,还可以用于解释和分析地质灾害和矿产资源开发等方面的问题。
此外,它还可以应用于深海海底油气勘探过程中的各种应力条件下试样的力学特性分析。
产值的调查和保守利用的要求。
应力圆法

x y 1 1 OC OB (OA OB ) (OA OB ) 2 2 2
CD CA AD (
2 2
x y
2
2 )2 xy
三、应力圆的应用(Application of stress-circle)
1.求单元体上任一 截面上的应力(Determine the stresቤተ መጻሕፍቲ ባይዱes on any inclined plane by using stress-circle) 从应力圆的半径 CD 按方位角的转向转动2得到半径CE. 圆周上 E 点的坐标就依次为斜截面上的正应力 和切应力.
σx σ y σx σ y cos 2 xy sin 2 σ α 2 2 σ x σ y sin 2 cos 2 xy 2
2 2 2
二、主应变数值及其方位 (The principal strains and it’s
(
x y
(2)主平面方位
由 CD顺时针转 20 到CA1 所以单元体上从 x 轴顺时 针转 0 (负值)即到 1对应 o 的主平面的外法线
2
B1 B 20 D
C
A
y
D′
A1
2 xy DA tan( 2 0 ) CA x y 2 xy tan 2 0 x y
§ 7-5 平面应变状态分析 (Analysis of plane strain-state)
平面应力状态下,已知一点的应变分量x ,y , xy ,欲求方 向上的线应变和切应变 ,可根据弹性小变形的几何条件,分别 找出微单元体(长方形)由于已知应变分量x ,y , xy在此方向上 引起的线应变及切应变,再利用叠加原理. 一、任意方向的应变(The strain of any direction)
应力状态分析2图解法

D
20 MPa 60 MPa
20 MPa
C B1 O
D
20 20
A1
60
解: 1)画应力圆
按选定比例尺,由 y = 20 MPa、yx = -60 MPa 确定 D′点,由 = -20 MPa、 = 0 确定 B1 点。由于B1、 D′均在应力圆的圆周上,故 作B1D′的垂直平分线,交 轴于点 C ;以点 C 为圆心、CD′为半径
8
[例2] 图示单元体,试用图解法确定主应力以及主平面位置。 解: 画应力圆
y yx
xy x
按选定比例尺,由 x = 80 MPa、xy = - 60 MPa 确定 D 点,由 y = - 40 MPa、yx = 60 MPa 确定 D′点;连接 DD′,交 轴
于点 C ;以点 C 为圆心、CD 为半径作出应力圆。
作出应力圆。
11
D
20 MPa 60 MPa
20 MPa
C B1 O
2)确定主应力和主平面
D
20 20 70 110
根据应力圆,按选定比例尺,量得主应力
60
A1
20 MPa
1 OA1 110 MPa 2 0 3 OB1 20 MPa
延长 D′C 连线交圆周于 D ,即得 x 截面上的正应力
OF
EF
要点: 点面对应、基准一致、转向相同、倍角关系
2
D x , xy
2 0
0
D y , yx
三、由图解法(应力圆)确定主平面与主应力
Байду номын сангаас主应力
1 OA1
2 OB1
根据点面对应、基准一致、转向相同、倍角关系的原则即可确定 主平面的方位
确定主应力大小和方向问题分析解读

确定主应力大小和方向问题分析基础部秦定龙一问题的提出在工程结构设计中,为了全面评价梁的强度安全,确保工程结构万无一失,经常要遇到计算结构中的主应力的大小和确定主应力的方向问题,以便于分析结构破坏的原因,或者合理布置结构形式,或者正确布置结构内的受力钢筋等。
图一(a)所示的钢筋混凝土简支梁,为什么会在轴线以下部分出现斜裂缝而破坏?图一(b)所示的铸铁试件在受到压缩或扭转时,为什么会沿与轴线成的斜面上发生破坏?这些都与结构内的主应力大小和方向有关。
在图二(a)中,钢筋混凝土简支梁的两组主应力轨迹线是根据主应力的方向绘制出来的,而图二(b)中梁内的弯起钢筋和纵向受力钢筋则是根据图二(a)中梁的主应力轨迹线布置的。
图一(a)q(a)图二(b)上述情况说明,在对结构进行强度分析或计算时,都要涉及到结构内主应力大小的计算和确定主应力方向的问题。
一般情况下,主应力的大小可按特定的公式算出来,而在确定应力的方向时,人们往往不容易正确确定出来。
本文就怎样快速准确确定主应力大小和方向作阐述和介绍。
二主应力大小及方向的确定方法图三表示从某一构件中取出的单元体,设它处于平面应力状态下。
假定在一对竖向平面上的正应力为,切应力为;在一对水平面上的正应力为y,切应力为y,它们的大小和方向已经求出。
现要求出这个单元体的最大正应力、最小正应力即主应力的大小和方向。
对应力、和角度的正负号规定如下:正应力(或主应力)以拉应力为正,压应力为负;切应力对单元体内的任一点以顺时针转为正,以反时针转时为负;角度以从x轴的正向出发量到截面的外法成n是反时针转为正,是顺时针转为负。
按照上述的规定,可以判断出,、、及是正值;是正值,是正值,角是负值。
(a)主应力的确定方法有两种:一种是解析法,一种是应力圆法。
下面分别讨论之。
1.确定主应力大小和主平面位置的解析法(b)图三根据对主应力的定义,进行严格的数学推导,得出计算平面应力状态下单元的主应力公式如下: (1)由式(1)可以看出, α有两个根。
应力圆的画法课件

实例三:多向应力圆
多向应力圆,考虑多种受力方向和大小
输入 标题
详细描述
当物体受到多个方向的力和力矩作用时,应力圆呈现 多向性,圆心位于所有力和力矩的合力矩中心,半径 表示各方向应力的合力大小。
总结词
公式
F表示合力,F_i表示各方向力,M表示合力矩,M_i表 示各方向力矩。
解释
F=ΣF_i, M=ΣM_i
应力圆的应用
应力圆被广泛应用于工程和科学领域,特别是在材料力学、结构分析和机械设计中。通过 应力圆,工程师可以直观地了解应力的分布和变化,从而优化设计、提高结构的稳定性和 安全性。
对未来研究的展望
01
应力圆理论的发展
随着科学技术的发展,对应力圆理论的深入研究有望进一步揭示其内在
规律和性质,为解决更复杂的应力问题提供更有效的工具。
02
应力圆与其他领域的交叉研究
可以探索应力圆与其他领域(如物理学、生物学等)的交叉研究,以发
现新的应用和研究方向。
03
应力圆的计算机辅助分析
随着计算机技术的发展,利用计算机辅助分析工具进行应力圆的分析和
模拟将成为一个重要的研究方向,有助于提高分析的效率和准确性。
THANK YOU
应力圆的画法课件
目 录
• 应力圆的基本概念 • 应力圆的画法 • 应力圆的应用 • 应力圆的实例分析 • 总结与展望
01
应力圆的基本概念
定义与特性
定义
应力圆是一种表示平面应力状态 的工具,通过将平面内的应力分 量表示为圆周上的角度,以直观 地展示应力分布。
特性
应力圆具有直观性、易理解性、 易绘制性等特点,是工程中常用 的应力分析工具。
公式ቤተ መጻሕፍቲ ባይዱ
平面应力状态的解析法和应力圆法详解
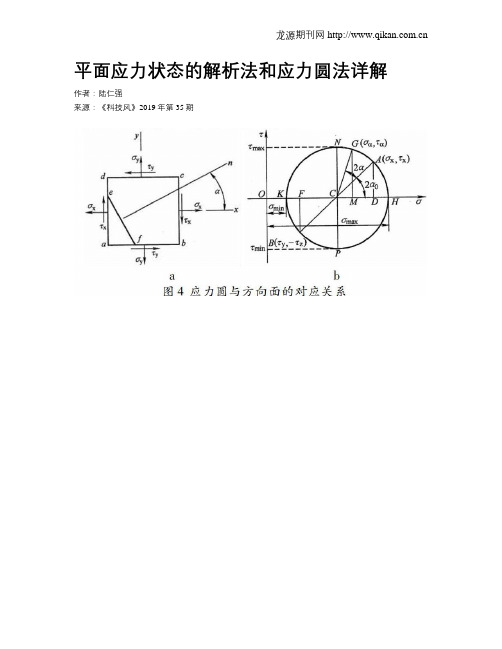
平面应力状态的解析法和应力圆法详解作者:陆仁强来源:《科技风》2019年第35期摘要:材料力学是土木类专业学生必修的一门专业基础课,对于后续专业课程的学习具有重要的基础作用。
但是材料力学由于其力学研究过程的复杂性和抽象性,使得学生在学习过程中存在较大的困难,而且感觉枯燥无味。
笔者通过对材料力学课程的多年讲授,总结了一套简单易懂的教学方法,本文以“平面应力状态任意方向面上应力”的求法为例,通过例题讲述及结论分析,教学效果反思发现能够让学生很容易的理解该部分内容。
本文的教学成果和方法,对于地方高校应用型专业课程的讲授具有一定的示范作用,可值得同类课程的借鉴采用。
关键词:平面应力状态;解析法;应力圆法1 平面应力状态的概念及表示研究一个点的应力状态,通常围绕该点作一微小单元体,称为单元体,一般情形下,微元的不同方位面上的应力各不相同,用任意截面把该微元体截开,则截开面上也存在正应力和切应力,过一点处的所有方位面的应力集合,称为该点的应力状态。
平面应力状态:微元各个面上所受应力的作用线都处于同一平面内,这种应力状态称为平面应力状态。
根据立体几何知识可知,图1所示的空间应力状态要转变为平面应力状态,则σx、σy、σz三者中至少有一个为0,即(τzy、τzx)、(τxy、τxz)、(τyx、τyz)三对中至少有一对为0,由于通常习惯于用x、y平面,故假设σz和(τzy、τzx)等于0,这样,图1的空间应力状态就可以表示为图2所示的平面应力状态了。
2 平面应力状态的解析法如图3所示,假设用任意一个截面把图中的平面应力状态截开以后,得到右边部分,截开面称为方向面,设方向面的法线方向为n。
根据微元的局部平衡,列静力学平衡方程:∑Fx=0∑Fy=0画应力圆的技巧:1)若知道圆心坐标和半径,可画圆;2)若知道任何一条直径的两个端点也可以画圆。
假设某应力状态为下图4a图,画出的应力圆为图4b图,也就是说图4a和图4b是等价的。
确定主应力大小和方向问题分析

确定主应力大小和方向问题分析基础部秦定龙一问题的提出在工程结构设计中,为了全面评价梁的强度安全,确保工程结构万无一失,经常要遇到计算结构中的主应力的大小和确定主应力的方向问题,以便于分析结构破坏的原因,或者合理布置结构形式,或者正确布置结构内的受力钢筋等。
图一(a)所示的钢筋混凝土简支梁,为什么会在轴线以下部分出现斜裂缝而破坏?图一(b)所示的铸铁试件在受到压缩或扭转时,为什么会沿与轴线成的斜面上发生破坏?这些都与结构内的主应力大小和方向有关。
在图二(a)中,钢筋混凝土简支梁的两组主应力轨迹线是根据主应力的方向绘制出来的,而图二(b)中梁内的弯起钢筋和纵向受力钢筋则是根据图二(a)中梁的主应力轨迹线布置的。
图一(a)q(a)图二(b)上述情况说明,在对结构进行强度分析或计算时,都要涉及到结构内主应力大小的计算和确定主应力方向的问题。
一般情况下,主应力的大小可按特定的公式算出来,而在确定应力的方向时,人们往往不容易正确确定出来。
本文就怎样快速准确确定主应力大小和方向作阐述和介绍。
二主应力大小及方向的确定方法图三表示从某一构件中取出的单元体,设它处于平面应力状态下。
假定在一对竖向平面上的正应力为σ,切应力为τ;在一对水平面上的正应力为σy,切应力为τy,它们的大小和方向已经求出。
现要求出这个单元体的最大正应力、最小正应力即主应力的大小和方向。
对应力σ、τ和角度α的正负号规定如下:正应力(或主应力)以拉应力为正,压应力为负;切应力对单元体内的任一点以顺时针转为正,以反时针转时为负;角度α以从x轴的正向出发量到截面的外法成n是反时针转为正,是顺时针转为负。
按照上述的规定,可以判断出,、、及是正值;是正值,是正值,角是负值。
(a)主应力的确定方法有两种:一种是解析法,一种是应力圆法。
下面分别讨论之。
1.确定主应力大小和主平面位置的解析法(b)图三根据对主应力的定义,进行严格的数学推导,得出计算平面应力状态下单元的主应力公式如下: (1)由式(1)可以看出,有两个根。
复杂应力状态分析2应力圆法

O
px A
OBC的面积为mdA
pz C
(A) OCA的面积为ndA
3
OAB的面积为ldA
z
2 1
x
y B
py
1 O
pz C
(B)平衡方程
X 0 px dA 1 mdA 0
2
Y 0 p y dA 3 ndA 0
px
Ax
Z 0 pz dA 2 ndA 0
(C)
p2
则E 点坐标: E(52.3,-18.7)
50
σ2
20 σ1
D′(50,20)
30 x A
C
σ1
σ2 0
20
B
3、主应力及主单元体
D(30,-20)
C(40,0) r 22.4 o 31.7o B点: 1 40 22.4 62.4(MPa)
A点: 2 40 22.4 17.6(MPa) 3 0
( n
2
3 )2
2
2 n
(
2
3
)2
2
(
n
3
2
1
)2
2 n
(
3
2
1
)2
(
n
1
2
2
)2
2 n
(
1
2
2
)2
结论:
σ3 σ2
σ1
任意斜截面上的应力,都落在图示阴影部分内,既阴影部 分内每一个点与一个截面上的应力相对应。
三、一点处应力状态中的 最大剪应力
max
1
3
2
★与二向应力状态中最大剪应力的区别:
与x轴的夹角为a,则
推论:
1
2
确定主应力大小和方向问题分析

确定主应力大小与方向问题分析基础部秦定龙一问题得提出在工程结构设计中,为了全面评价梁得强度安全,确保工程结构万无一失,经常要遇到计算结构中得主应力得大小与确定主应力得方向问题, 以便于分析结构破坏得原因,或者合理布置结构形式,或者正确布置结构内得受力钢筋等。
图一(a)所示得钢筋混凝土简支梁,为什么会在轴线以下部分出现斜裂缝而破坏?图一(b)所示得铸铁试件在受到压缩或扭转时,为什么会沿与轴线成得斜面上发生破坏?这些都与结构内得主应力大小与方向有关。
在图二(a)中,钢筋混凝土简支梁得两组主应力轨迹线就是根据主应力得方向绘制出来得,而图二(b)中梁内得弯起钢筋与纵向受力钢筋则就是根据图二(a)中梁得主应力轨迹线布置得。
图一(a)q(a)图二(b)上述情况说明,在对结构进行强度分析或计算时,都要涉及到结构内主应力大小得计算与确定主应力方向得问题.一般情况下,主应力得大小可按特定得公式算出来,而在确定应力得方向时,人们往往不容易正确确定出来。
本文就怎样快速准确确定主应力大小与方向作阐述与介绍。
二主应力大小及方向得确定方法图三表示从某一构件中取出得单元体,设它处于平面应力状态下。
假定在一对竖向平面上得正应力为,切应力为;在一对水平面上得正应力为y,切应力为y,它们得大小与方向已经求出。
现要求出这个单元体得最大正应力、最小正应力即主应力得大小与方向。
对应力、与角度得正负号规定如下:正应力(或主应力)以拉应力为正,压应力为负;切应力对单元体内得任一点以顺时针转为正,以反时针转时为负;角度以从x轴得正向出发量到截面得外法成n就是反时针转为正,就是顺时针转为负.按照上述得规定,可以判断出,、、及就是正值;就是正值,就是正值,角就是负值。
(a)主应力得确定方法有两种:一种就是解析法,一种就是应力圆法.下面分别讨论之。
1。
确定主应力大小与主平面位置得解析法(b)图三根据对主应力得定义,进行严格得数学推导,得出计算平面应力状态下单元得主应力公式如下:……(1)由式(1)可以瞧出, 有两个根。
莫尔应力圆

2 这表明:在σ 3=30kPa的条件下,该点如处
于极限平衡,则最大主应力为90kPa。 故可判断该点已破坏。
3.3 壁面最大主应力方向
库仑粉体:
C C
t
IYE
粉体在壁面处的滑移
WYF
B
条件在(σ,τ)坐标中
也是直线:WYF;壁
A
Φ D C WYE IYF
s
面粗糙时, WYF与
Christian Otto Mohr (1835-1918)
2、研究内容 研究粉体体内任一微小单元体的应力状态。
1)主应力与主应力面
2)主应力相互正交 3)任意一面上:正应力和剪应力 一点应力状态的表示方法:???
◇任意斜面上的应力
在微元体上取任一截面,与大主应力面即水平面成角,斜 面上作用法向应力和剪应力。现在求、与1、3之间的关 系。 取厚度为1,按平面问题计算。根据静力平衡条件与竖向合 力为零。
3.2 莫尔-库仑定律
莫尔最初提出的强度理论,认为材料破坏是剪
切破坏,在破坏面上τ f=f(σ ),由此函数关系所
定的曲线,称为莫尔破坏包络线。1776年,库仑 总结出粉体(土)的抗剪强度规律。 库仑定律是莫尔强度理论的特
例。此时莫尔破坏包线为一直
线。以库仑定律表示莫尔破坏包络 线的理论称莫尔—库仑破坏定律。
1 sin i 1 sin i P yy B gy K P B gy 1 sin i 1 sin i
c=0
3.4 朗肯(Rankine,1957)应力状态
1 sin i KP 1 sin i
Kp-朗肯被动应力系数,简称被动态系数
Molerus I 类粉体:KP是临界流动状态时, 最大主应力与最小主应力之比。被动态应 力σP与主动态应力σA之比等于
三向应力状态应力圆的画法

三向应力状态应力圆的画法应力圆是一种用于描述材料内部应力分布的图形方法,它可以直观地展示材料在不同方向上的应力大小和方向关系。
在三向应力状态下,应力圆的画法可以帮助我们更好地理解材料的应力分布情况。
在三向应力状态下,材料同时受到三个方向上的应力作用,这三个方向可以是任意的,通常分别称为x、y、z方向。
为了绘制应力圆,我们需要确定这三个方向上的应力大小和方向,并将其表示在一个平面上。
我们选择一个平面作为绘制应力圆的基准平面,通常选择x-y平面。
在这个平面上,我们可以用一个坐标系来表示应力的大小和方向。
在x-y平面上,我们以x轴为横轴,y轴为纵轴建立坐标系。
接下来,我们需要确定应力圆的中心位置。
在三向应力状态下,应力圆的中心位置通常表示为(x0, y0),即应力圆的圆心坐标。
根据材料的应力状态,我们可以计算出x、y方向上的应力值,然后将其代入应力圆方程中,求解出圆心坐标。
在得到圆心坐标后,我们可以绘制出应力圆的圆心。
圆心表示的是材料在该点上的平均应力状态。
接下来,我们需要确定应力圆的半径。
在三向应力状态下,应力圆的半径表示的是切应力的大小。
根据材料的应力状态,我们可以计算出x、y方向上的切应力值,然后将其代入应力圆方程中,求解出半径值。
在得到半径值后,我们可以绘制出应力圆的圆周。
圆周表示的是材料在该点上的切应力大小和方向。
还可以在应力圆上标注出一些特殊点和线。
例如,我们可以标注出主应力方向,即切应力达到最大或最小值的方向;我们还可以标注出主应力值,即切应力的最大或最小值。
通过绘制应力圆,我们可以直观地了解材料在不同方向上的应力分布情况。
这对于工程设计和材料分析都是非常重要的。
通过对应力圆的分析,我们可以判断材料的强度和稳定性,进而优化设计方案,提高材料的使用寿命。
应力圆的画法是一种用于描述材料内部应力分布的图形方法。
在三向应力状态下,应力圆可以帮助我们更好地理解材料的应力分布情况。
通过绘制圆心、圆周和标注特殊点和线,我们可以清晰地了解材料在不同方向上的应力大小和方向关系。
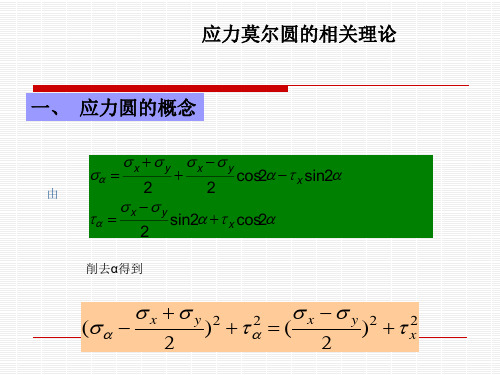
应力莫尔圆的相关理论
B1D1 2t x tg (-2a 0 ) = = CB1 (s x - s y )
再根据应力圆判断α0的合理范围
t
σ2
o
D1
由此可定出主应力s1 所在平面的
A2
sy
B2 C
位置。由于A1A2 为应力圆的直径, 则s2
所在的另一主平面与s1 所在的主平面垂 直。
B1
A1
s
D2
2
αo
σx
σ1
例题7-1 从水坝体内某点处取出的单元体如图所示, sx= - 1MPa , sy= - 0.4MPa , tx= - 0.2MPa , ty= 0.2MPa ,
(b)
B2 C
B1 s
τy
σy
σx τx
τy
σx τx
σy
t
该圆的圆心 C 点到 坐标
原点的 距离为
(b)
D1
sx +s y
2
o
2 +tx
B2 C sy D2 sx
B1 s
半径为
(
s x -s y
2
)
2
该圆就是相应于该单元体
应力状态的应力圆
D1 点的坐标为 ( sx , tx ) 因而 D1 点代表单元体 x 平面上的应力 。
a 0 = -19.3
a 0 = -19.30
s1
主平面及主应力如图所示。
(122.5 , 64.6)
D1
A2
τy
s A1
σ3 σx
B2
O C
2α 0
B1
σx τx
τy
D1 (0 , - 64.6)
τx σ1
α0
应力圆的画法

T (x)i P
dxi
li
N (x) N (x) i
i
dxi
EA P i
第十六页,课件共有23页
莫 弯曲: 尔
l
M
x
M
EI
x
dx
积 拉、压: 分 公 扭转:
n N i N i li
i 1
EAi
l
T
x
T x
GI p
dx
式
l
组合变形的圆截面杆
N
(
x) N ( EI
x)dx
l
T
x
T x
1 3
1([
2
1
)2
2
2
2
3
3
1 2 ]
r
r
莫尔强度理论:
1
[ t ] [ c ]
3
[ t
]
r3 2 4 2 r4 2 3 2
第十一页,课件共有23页
危险点处于单相应力状态
双向弯曲(原形横截面)
M
M
2 Z
M
2 Y
M
W
M
2 Z
M
2 Y
W
max
( M Z WZ
MY WY
)
x
FN A
Mz I
y
Myz I
第十二页,课件共有23页
r3 2 4 2 r4 2 3 2
圆形截面:Wt 2W
r3
( M )2 4( T )2
W
Wt
r3
1 W
M2 T2
r4
( M )2 3( T )2
W
Wt
r4
1 W
M 2 0.75T 2
11.3 平面应力状态分析的图解法 应力圆
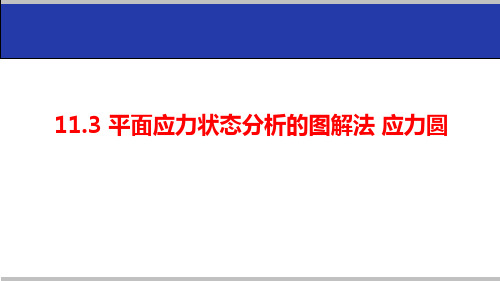
11.3 平面应力状态分析的图解法应力圆由 ⎪⎪⎩⎪⎪⎨⎧+-=--++=ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy y x xy y x y x 2222)2()2(xyyx yx τσστσσσαα+-=++-ατασσσσσα2sin 2cos 22xy yx y x --=+-sin 2cos 22x yxy ασστατα-=+应力圆CασατO2x yσσ+圆心( ,0)半径一点应力状态的另一种表示方法2()2x yασσσ+-222()2x yxyασσττ-+=+2x yσσ+222x y xyR σστ-⎛⎫=+ ⎪⎝⎭应力圆的画法DE σττx τyσx(σx +σy )/2σyOxyC222x y xyR σστ-⎛⎫=+ ⎪⎝⎭Rcos 2sin 222x yx yx σσσσατα+-=+-0cos(22)H C R σσαα=++00cos2cos2sin 2sin 2C R R σαααα=+-cos 2sin 22x yC x σσσατα-=+-应力圆与单元体之间的对应关系DEH (σH , τH )σττxτy2ασx(σx +σy )/2σyOαxynτασα (σx -σy )/2Csin 2cos 22x yx σσατα-=+0sin(22)H R ταα=+00sin 2cos 2cos 2sin 2R R αααα=+1222()22x yx y xy σσσσστσ+-=±+主应力DEσττxτy σx(σx +σy )/2σyOxy(σx -σy )/2CA B 主平面的方位02tan(2)xx yτασσ-=-σ1σ2σ2σ1maxτσ145°2x yσσ+2x yσσ+12max 2R σστ-==面内最大切应力KE σττxτyσx(σx +σy )/2σyOx y(σx -σy )/2Cmaxτ D单元体应力圆 A. 点面对应 一面上的应力 一点的坐标值B. 转向对应 斜面法线转向 半径转向C. 二倍角对应斜面转角α半径转角 2α 对应相同D. 互相垂直的两个方向 90° 直径的两个端点E. 互相平行的一个方向 180°应力圆上一点应力圆与单元体之间的对应关系σyτxσxτyαxy n τασα α20σHE στxτy2α σx(σx +σy )/2σyO(σx -σy )/2CH (σH , τH )Dτ有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)σστ1σσ2,3σ30º30º30σ30τ60º30cos6022σσσ=+30sin 602στ=30σ30τ( )1. 单向拉伸应力状态2. 纯剪切应力状态τσ1σ3σ1στ=20σ=3στ=-1σ3σ45ºτ平面应力状态分析的图解法——应力圆AB小结平面应力状态分析方法 1. 平衡方程 2. 解析法 3. 几何法平面应力状态分析方法——图解法 通过画应力圆分析一点的应力状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
80°
60°
30
30
0
0.2 0.4 0.6
-40
例7-4-2 :讨论圆轴扭转时的应力状态,并分析铸铁 件受扭转时的破坏现象。
解:1.取单元体ABCD,其中
xy
T , ,这是纯剪切应力状态。 WP
x y 0,
2.作应力圆 主应力为 1 , 3 ,并可 确定主平面的法线。
σx σ y σx σ y cos 2 xy sin 2 σ α 2 2 σ x σ y sin 2 cos 2 xy 2
2 2 2
二、主应变数值及其方位 (The principal strains and it’s
1.圆心的坐标 C( (Coordinate of circle center) 2.圆的半径(Radius of circle)
x y
2
,0)
2 )2 xy
R (
x y
2
此圆习惯上称为 应力圆( plane stress circle),或称为莫 尔圆(Mohr’s circle)
x y
cos 2 xy sin 2
把上面两式等号两边平方,然后相加便可消去,得
(
x y
2
) (
2 2
x y
2
2 )2 xy
因为x ,y ,xy 皆为已知量,所以上式是一个以,为变量的 圆周方程.当斜截面随方位角 变化时,其上的应力 , 在 - 直 角坐标系内的轨迹是一个圆.
C B A
3
2
1
2
c
abc 截面表示与三个主平 面斜交的任意斜截面
1
a b
1
该截面上应力 和 对应 的D点必位于上述三个应力圆 所围成的阴影内
3
2
结论 三个应力圆圆周上的 点及由它们围成的阴影部 分上的点的坐标代表了空 间应力状态下所有截面上 的应力
B A
该点处的最大正应力 O C (指代数值)应等于最大 3 应力圆上A点的横坐标1
A
B 2
A
B
O C
2.求主应力数值和主平面位置 (Determine principle stress and the direction of principle plane by using stress circle) (1)主应力数值 A1 和 B1 两点为与主平面
2
B1 B CF
1
x
1
2 xy 2 0 tan ( ) x y
0 确定后,1 对应的主平面方位即确定
3.求最大切应力(Determine maximum shearing stress by using stress circle) G1和G两点的纵坐标分别代 表最大和最小切应力
G1
y n
E 2 20 D
e
yx x xy
f
x
o
x
B
CF
A
y
D′
a
x
证明:
OF OC CF OC CE cos(20 2 ) OC CD cos 20 cos 2 CD sin 20 sin 2 x y x y cos 2 xy sin 2 2 2
x
(4)连接 DD′两点的直线与 轴相交于C 点 (5)以C为圆心, CD 为半径作圆,该圆就是相应于该单元体的 应力圆
2.证明(Prove)
D
(1)该圆的圆心C点到 坐 标原点的 距离为
x y
2
(2)该圆半径为
o
y
B C D′ A
R (
x y
2
)
2
2 xy
x
x y 1 1 OC OB (OA OB) (OA OB) 2 2 2
)
2
2 xy
max 1
(2)主平面方位
由 CD顺时针转 20 到CA1 所以单元体上从 x 轴顺时 针转 0 (负值)即到 1对应 o 的主平面的外法线
2
B1 B 20 D
C
A
y
D′
A1
2 xy DA tan( 2 0 ) CA x y 2 xy tan 2 0 x y
3.分析 纯剪切应力状态的两个主应力绝对值相等 ,但一为拉应力,另一为压应力。由于铸铁抗拉强度 较低,圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
§7-4 三向应力状态分析 (analysis of three-dimensional stress-state)
一、 空间应力状态下的最大正应力和最大切应力 (the maximum normal stress and shear stress in threedimensional stress-state)
2
1
max 1
最大切应力则等于最
大的应力圆的半径
max
1 ( 1 3 ) 2
O
C B A
最大切应力所在的 截面与 2 所在的主平面 垂直,并与1和3所在的 主平面成45°角.
3
2
1
例题9 单元体的应力如图所示,作应力圆, 并求出主应力和最 大切应力值及其作用面方位. 解: 该单元体有一个已知主应力
二、应力圆作法(The method for drawing a stress circle)
y
y x
yx
x xy y
x o
1.步骤(Steps)
(1)建 - 坐标系,选定比例尺
y
yx
D
x
x xy
x
o
y
B
C
D′
A
(2)量取 OA= x AD = xy 得D点 (3)量取 OB= y BD′= yx 得D′点
已知受力物体内某一点处三个主 应力1, 2, 3 利用应力圆确定该点的最大正应 力和最大切应力.
2
3
1
1 3 2
首先研究与其中一个主平 面 (例如主应力3 所在的平 面)垂直的斜截面上的应力 用截面法,沿求应力的
2
截面将单元体截为两部分,
取左下部分为研究对象
1 1
1
§ 7-5 平面应变状态分析 (Analysis of plane strain-state)
平面应力状态下,已知一点的应变分量x ,y , xy ,欲求方 向上的线应变和切应变 ,可根据弹性小变形的几何条件,分别 找出微单元体(长方形)由于已知应变分量x ,y , xy在此方向上 引起的线应变及切应变,再利用叠加原理. 一、任意方向的应变(The strain of any direction)
§7-3 平面应力状态分析-图解法 (Analysis of plane stress-state with graphical means)
一、莫尔圆(Mohr’s circle)
将斜截面应力计算公式改写为
2 2 x y sin 2 xy cos 2 2
x y
y 20MPa
z 20MPa
因此与该主平面正交的各截 面上的应力与主应力z 无关, 依据 x截面和y 截面上的应力画出应力 圆. 求另外两个主应力
z
20MPa 40MPa
x 20MPa
x 40MPa
xy 20MPa 由 x , xy 定出 D 点
y 20MPa yx 20MPa 由 y , yx 定出 D′ 点
3 2 2
主应力 3 所在的两平面上是一 对自相平衡的力,因而该斜面上的应 力 , 与3 无关, 只由主应力1 , 2 决定 与3 垂直的斜截面上的应力可 由 1 , 2 作出的应力圆上的点来表 示
1
3
1
3
2
2
该应力圆上的点对应 于与3 垂直的所有斜截面 上的应力 与主应力 2 所在主平 面垂直的斜截面上的应力, 可用由1 ,3作出的应力 圆上的点来表示 O 与主应力1所在主平 面垂直的斜截面上的应力 , 可用由2 ,3作出的应 力圆上的点来表示
FE CE sin(2 o 2 ) CD sin 2 0 cos 2 CD cos 2 0 sin 2 x y sin 2 xy cos 2 2
说明
(1)点面之间的对应关系:单元体某一面上的应力,必对应于 应力圆上某一点的坐标. (2)夹角关系:圆周上任意两点所引半径的夹角等于单元体 上对应两截面夹角的两倍.两者的转向一致.
以 DD′为直径作应力圆 A1,A2 两点的横坐标分别代 表另外两个主应力 1 和 3
D′ A2 O D A1
1 =46MPa
3 =-26MPa
该单元体的三个主应力
1 =46MPa 2 =20MPa 3 =-26MPa
根据上述主应力,作出三个应 力圆
3 1
max 36MPa
CD CA AD (
2 2
x y
2
2 )2 xy
三、应力圆的应用(Application of stress-circle)
1.求单元体上任一 截面上的应力(Determine the stresses on any inclined plane by using stress-circle) 从应力圆的半径 CD 按方位角的转向转动2得到半径CE. 圆周上 E 点的坐标就依次为斜截面上的正应力 和切应力.
